Đề khảo sát HSG Toán 8 năm 2015 – 2016 phòng GD&ĐT Ý Yên – Nam Định
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 đề khảo sát HSG Toán 8 năm 2015 – 2016 phòng GD&ĐT Ý Yên – Nam Định; đề thi có đáp án, lời giải và hướng dẫn chấm điểm.
Preview text:
PHÒNG GIÁO DỤC - ĐÀO TẠO ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI THCS HUYỆN Ý YÊN NĂM HỌC 2015 - 2016 MÔN : TOÁN – LỚP 8 ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút Đề gồm 01 trang Bài 1. (3 điểm) 1) Chứng minh : 3 2 2 3 4 4
(x y)(x x y xy y ) x y .
2) Phân tích đa thức thành nhân tử : 2
x(x 2)(x 2x 2) 1. 3) Tìm a, b, c biết : 2 2 2
a b c ab bc ca và 8 8 8 a b c 3.
Bài 2. (4 điểm) Cho biểu thức : 2 2 2 2 2 x y x y x y P . với x 0, y , 0 x y . 2 2 2 2 x x xy xy xy y x xy y
1) Rút gọn biểu thức P.
2) Tính giá trị của biểu thức P biết x, y thỏa mãn đẳng thức: 2 2
x y 10 2(x 3y) . Bài 3. (4 điểm) 1) Giải phương trình: 2
(6x 8)(6x 6)(6x 7) 72 .
2) Tìm các cặp số nguyên (x; y) thỏa mãn: 2 2 x x 3 y .
Bài 4. (2 điểm) Cho các số a, b, c thỏa mãn1 a, ,
b c 0 . Chứng minh rằng :
a + b2 + c3 – ab – bc – ca 1. Bài 5. (5,5 điểm)
Cho hình vuông ABCD có cạnh bằng a, biết hai đường chéo cắt nhau tại O. Lấy điểm I
thuộc cạnh AB, điểm M thuộc cạnh BC sao cho 0
IOM 90 (I và M không trùng với các
đỉnh của hình vuông). Gọi N là giao điểm của AM và CD, K là giao điểm của OM và BN.
1) Chứng minh ΔBIO = ΔCMO và tính diện tích tứ giác BIOM theo a. 2) Chứng minh BKM BCO . 3) Chứng minh 1 1 1 = + . 2 2 2 CD AM AN Bài 6. (1,5 điểm)
Cho tam giác ABC (AB < AC), trọng tâm G. Qua G vẽ đường thẳng d cắt các cạnh
AB, AC thứ tự ở D và E. Tính giá trị biểu thức AB AC + . AD AE .
Họ và tên thí sinh: …………………
Họ, tên chữ ký GT 1: ………………………….
Số báo danh:………………………… Họ, tên chữ ký GT 2: ………………………….
HƯỚNG DẪN CHẤM MÔN TOÁN LỚP 8 I. Hướng dẫn chung:
1) Hướng dẫn chấm chỉ trình bày một cách giải với các ý cơ bản học sinh phải trình bày, nếu
học sinh giải theo cách khác mà đúng và đủ các bước thì vẫn cho điểm tối đa.
2) Điểm toàn bài là tổng điểm của các ý, các câu và không làm tròn.
II. Đáp án và thang điểm: Bài Ý Nội dung trình bày Điểm Chứng minh : 3 2 2 3 4 4
(x y)(x x y xy y ) x y . Ta có: (x y)( 3 2 2 3 x x y xy y ) 1) 0,25 4 3 2 2 3 3 2 2 3 (0,5đ) = 4
x x y x y xy x y x y xy y = 4 4 x y 0,25
Vậy đẳng thức được chứng minh.
Phân tích đa thức thành nhân tử : 2
x(x 2)(x 2x 2) 1. Ta có: 2
x(x 2)(x 2x 2) 1 2 2
(x 2x)(x 2x 2) 1 0,25 2) 2 2 2 1. (1đ)
(x 2x) 2(x 2x) 1 0,25 (3đ) 2 2 (x 2x 1) 0,25 4 (x 1) 0,25 Tìm a, b, c biết : 2 2 2
a b c ab bc ca và 8 8 8 a b c 3. Biến đổi 2 2 2
a b c ab bc ca về 2 2 2
(a b) (b c) (c a) 0 0,5 3) Lập luận suy ra a = b = c 0,25
(1,5đ) Thay vào a = b = c vào 8 8 8 a b c 3 ta có 0,5 8 8
3a 3 a 1 a 1.
Vậy a = b = c = 1 và a = b = c = -1. 0,25 Với x , 0 y , 0 x y ta có: 2 2 2 2
2 x y (x y )(x y) xy x y 0,5 P = . 2 2 x xy(x y) x xy y 2
xy(x y) (x y).(x y)2 x y = - . 0,5 x xy(x y) 2 2 x xy y 1) 2 2 (2đ) 2 (x y)(x xy y ) x y = + . 0,5 x xy(x y) 2 2 x xy y 2 x y 2. = + 0,25 (4đ) x xy x y = 0,25 xy Ta có: 2 2 x y 10 2(x 3y) 2 2
x 2x 1 y 6y 9 0 0,5 2) 2 2 (2đ) x 1 y 3 0
Lập luận suy ra x 1; y 3 0,5
Ta thấy x = 1; y = -3 thỏa mãn điều kiện: x , 0 y , 0 x y 1,0 x y 1 ( ) 3 2
nên thay x = 1; y =- 3 vào biểu thức P = ta có: P= xy . 1 ( ) 3 3 Giải phương trình: 2
(6x 8)(6x 6)(6x 7) 72 Đặt 6x 7 t. Ta có 2 2 2 4 2
(t 1)(t 1)t 72 (t 1)t 72 t t 72 0 0,5 4 2 2 2 2 2 2 2
t 9t 8t 72 0 t (t 9) 8(t 9) 0 (t 9)(t 8) 0 0,5 1) Mà 2 t 8 0 nên 2 2
t 9 0 t 9 t 3 (2đ) 0,5 2 5
Từ đó tìm được x hoặc x . 3 3 0,5 2 5
Vậy phương trình có tập nghiệm là S = ; . 3 3
x x y x x y x 2 2 2 2 2 2 3 4 4 12 4 2 1 4y 1 1 0, 25 3. 2x 2y 1 2x 2y (4đ) 1 1 1 0,25
Do x, y nguyên nên 2x 2 y 1 và 2x 2 y 1 là các số nguyên 0,25
Do đo xảy ra các trường hợp sau
2x 2 y 1=1 và 2x 2 y 1 = -11. Tìm được x =-3 và y = 3 0,25 2) (2đ)
2x 2 y 1=-1 và 2x 2 y 1 = 11. Tìm được x = 2 và y = -3 0,25
2x 2 y 1=11 và 2x 2 y 1 = -1. Tìm được x = 2 và y = 3 0,25
2x 2 y 1= -11 và 2x 2 y 1 = 1. Tìm được x = -3 và y = - 3 0,25
KL:……………………….. 0,25
Cho các số a, b, c 0 ;
1 . Chứng minh rằng : a + b2 + c3 – ab – bc – ca 1. Vì b, c 0; 1 nên suy ra 2 3 b b; c c . 0,25 4.
Do đó: a + b2 + c3 – ab – bc – ca a + b + c – ab – bc – ca (1). 0,5 (2đ)
Lại có: a + b + c – ab – bc – ca = (a – 1)(b – 1)(c – 1) – abc + 1 (2) 0,5 Vì a, b, c 0 ;
1 nên (a – 1)(b – 1)(c – 1) 0 ; – abc 0 0,25
Do đó từ (2) suy ra a + b + c – ab – bc – ca 1 (3). 0,25
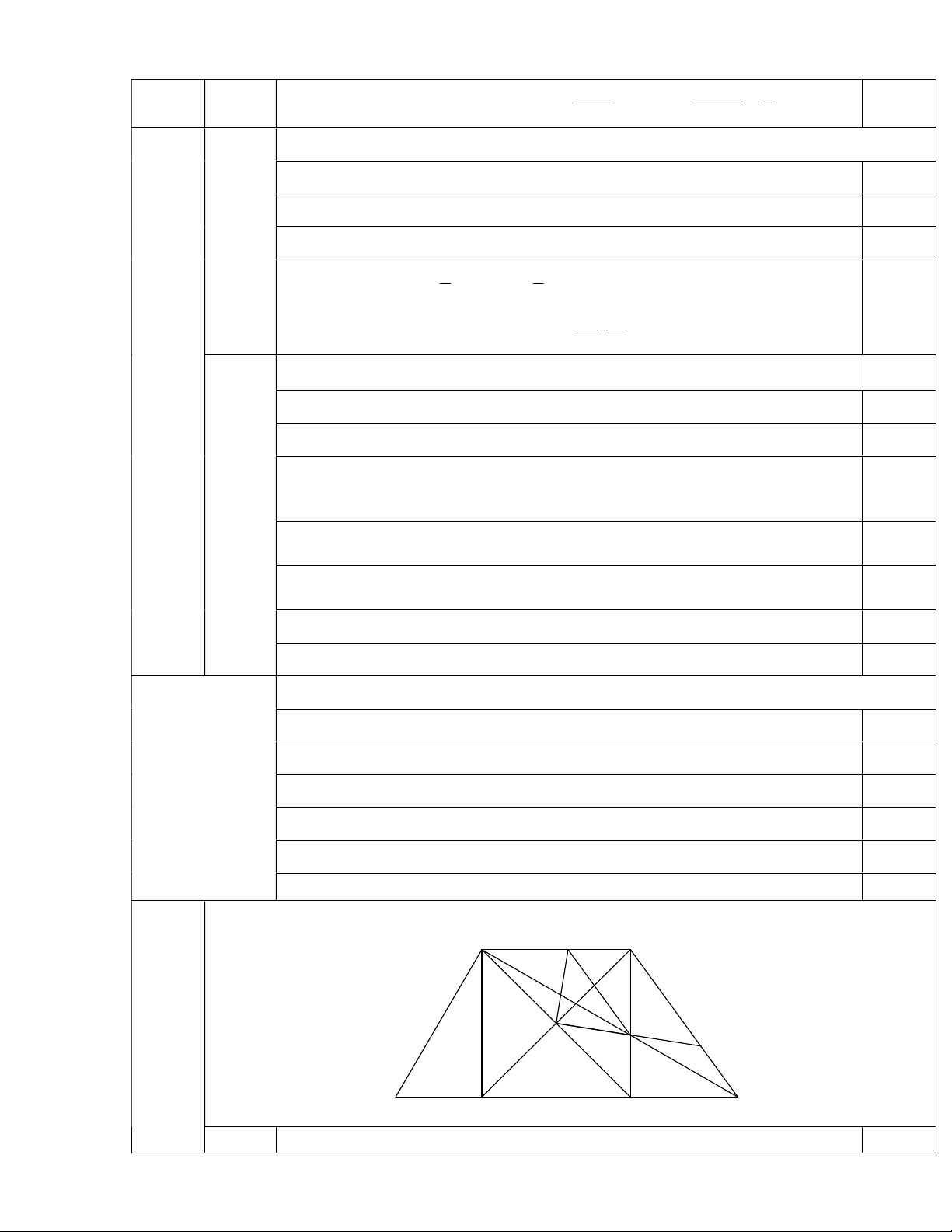
Từ (1) và (3) suy ra a + b2 + c3 – ab – bc – ca 1. 0,25 Hình vẽ: A I B O M K E D C N 1) Xét B IO và C MO có: 1,0 5. (2đ) IBO 0
MCO ( 45 ) ( tính chất đường chéo hình vuông) ( 5,5đ)
BO = CO ( tính chất đường chéo hình vuông) BOI COM ( cùng phụ với BOM ) B IO = C MO (g.c.g) S S mà S S S BIO CMO BMOI BOI BMO 1 1 1,0 Do đó 2 S S S S S a BMOI CMO BMO BOC 4 ABCD 4 Ta có B IO = C MO (cmt)
CM = BI ( cặp cạnh tương ứng) BM = AI 1,0 2) BM AM IA AM Vì CN // AB nên . Từ đó suy ra IM // BN (1,5đ) CM MN IB MN Ta có OI = OM ( vì B IO = C MO ) I OM cân tại O IMO 0 MIO 45 0,5 Vì IM // BN BKM 0 IMO 45 BKM BCO
Qua A kẻ tia Ax vuông góc AN cắt CD tại E.
Chứng minh ADE ABM (g. . c g) AE AM 0,5 Ta có A
NE vuông tại A có AD NE nên A . D NE AN.AE S 2 2 A . D NE AN.AE (A . D NE) (AN.AE) 0,5 3) AEN 2 2 (2đ)
Áp dụng định lí Pitago vào A NE ta có AN2 + AE2 = NE2 2 2 AN AE 1 1 1 1 0,5 2 2 2 2 2
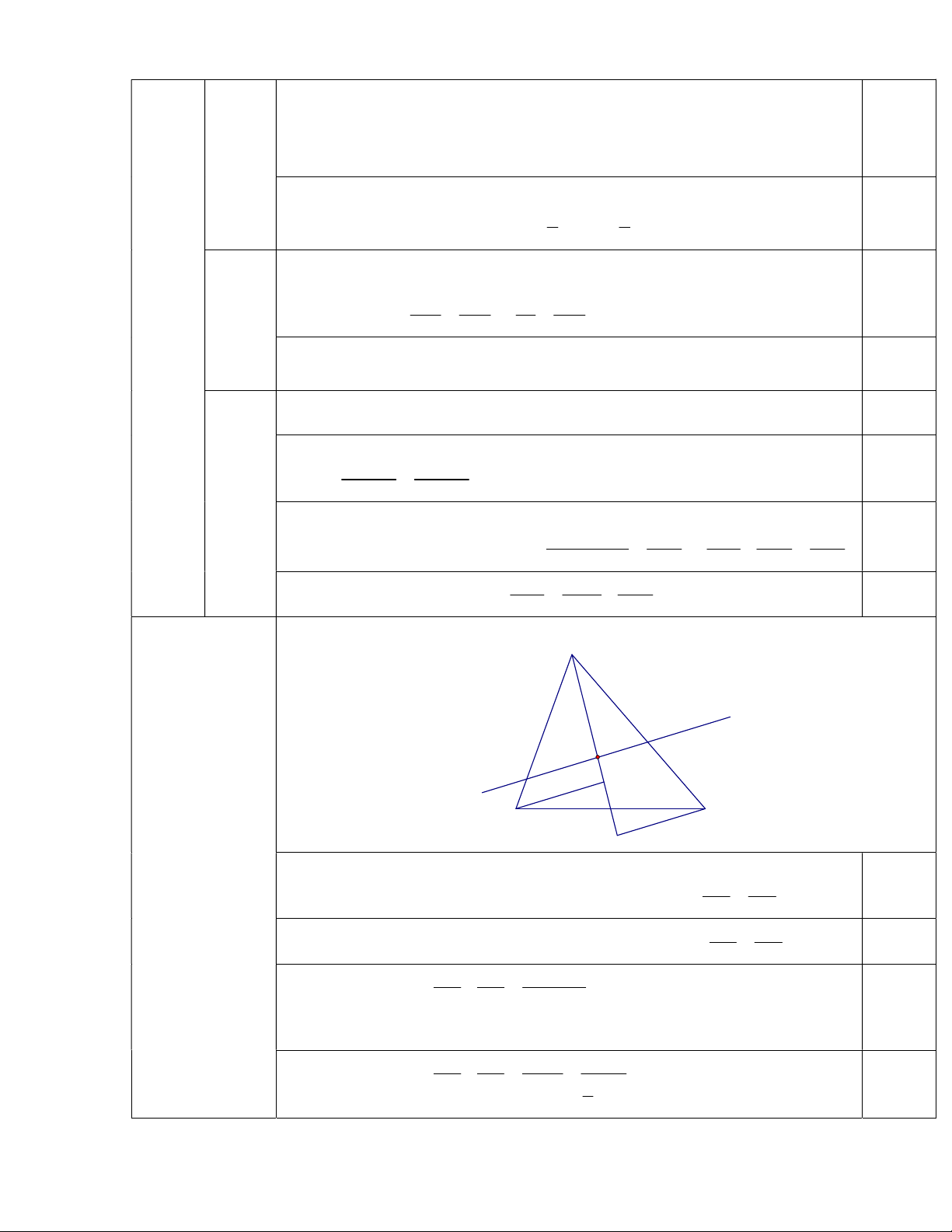
AD .(AN AE ) AN .AE 2 2 2 2 2 2 AN .AE AD AE AN AD 1 1 1 Mà AE AM và CD = AD 0,5 2 2 2 CD AM AN Hình vẽ: A d E G D I M B C K 5.
Gọi M là trung điểm của BC. (1,5 đ) AB AI
Qua B vẽ đường thẳng song song với d cắt AM tại I, ta có: (1) 0,25 AD AG AC AK
Qua C vẽ đường thẳng song song với d cắt AM tại K, ta có: (2) 0,25 AE AG AB AC AI AK Từ (1) và (2) suy ra: (3) AD AE AG 0,5
Mặt khác: AI + AK = (AM - MI) + (AM + MK) = 2AM (4)
(vì MI = MK do BMI = CMK) AB AC 2AM 2AM Từ (3) và (4) suy ra: 3 AD AE AG 2 0,5 AM 3