Đề khảo sát HSG Toán 8 năm 2024 – 2025 phòng GD&ĐT Kim Thành – Hải Dương

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI HUYỆN KIM THÀNH MÔN: TOÁN 8 NĂM HỌC 2024-2025
Thời gian làm bài: 120 phút
(Không tính thời gian phát đề)
(Đề khảo sát gồm có 05 câu, 01 trang) Câu 1 (2,0 điểm)  2 2  x +1  x −1
1) Cho biểu thức: A = −  . − x −  1 :
(với x ≠ 0; x ≠ 1; − x ≠ 1)
3x x +1  3x  x
Rút gọn A và tìm giá trị nguyên của x để A nhận giá trị nguyên.
2) Tìm đa thức f (x) biết: f (x) chia cho x - 3 dư 2, f (x) chia cho x + 4 dư 9, và f (x) 2
: x + x −12 được thương là 2 x + 3 và còn dư Câu 2 (2,0 điểm). 1) Giải phương trình : 1 1 1 1 + + = 2 2 2
x + 9x + 20 x +11x + 30 x +13x + 42 18
x  y  xy 1  0
2) Giải hệ phương trình 3x 2y   22 Câu 3 (2,0 điểm)
1) Tìm các cặp số (x; y) thỏa mãn x, y∈ và 2 2
6x + y + 5xy −8x − 3y + 7 = 0 P
 = (x + 2023)5 + (2y − 2024)5 + (3z + 2025)5
2) Cho x;y;z là các số nguyên và  S
 = x + 2y + 3z + 2024 
Chứng minh rằng P chia hết cho 30 khi và chỉ khi S chia hết cho30 . Câu 4 ( 3,0 điểm). 
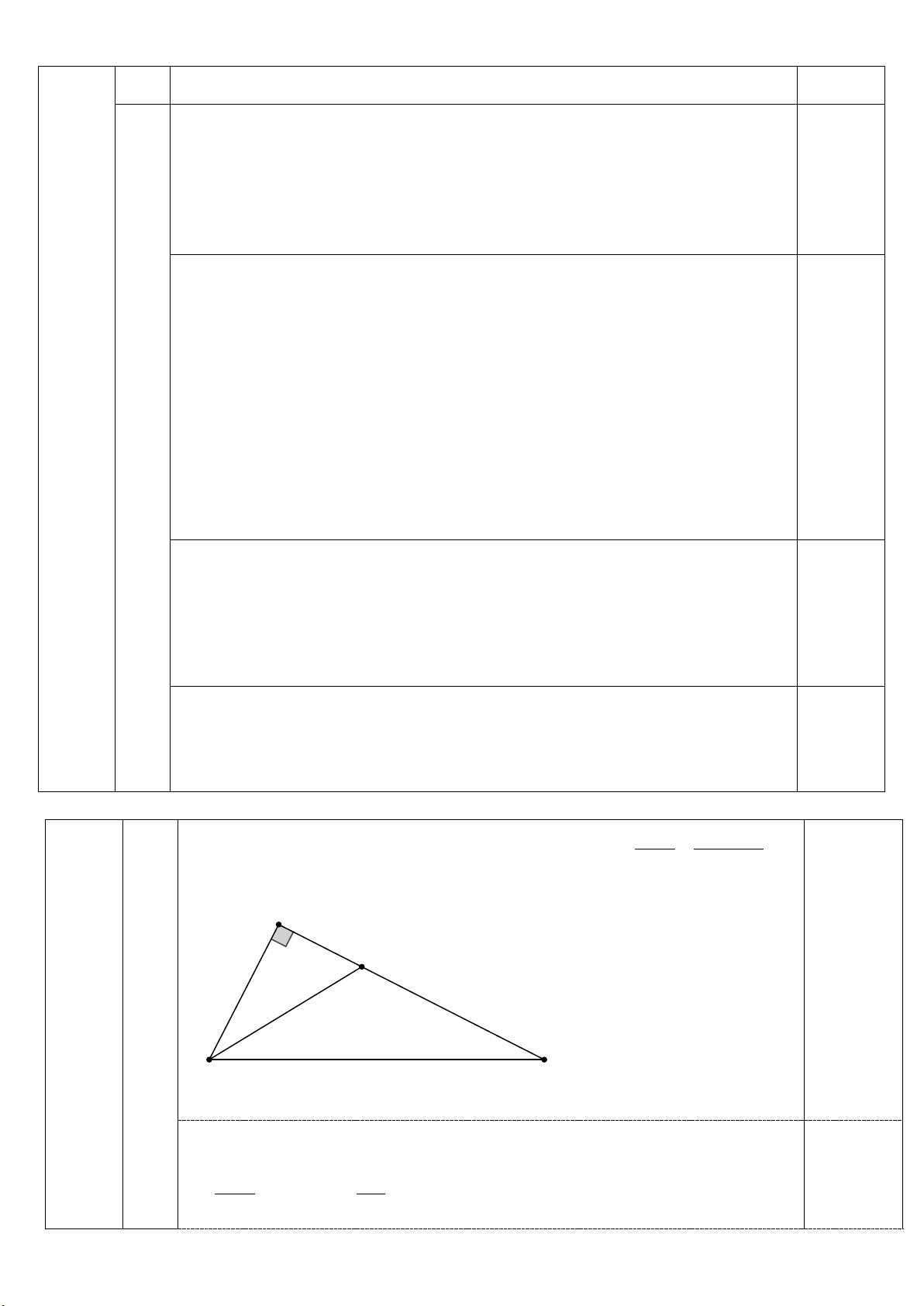
1) Cho tam giác ABC vuông tại A. Chứng minh rằng: tan ABC AC = 2 AB + BC
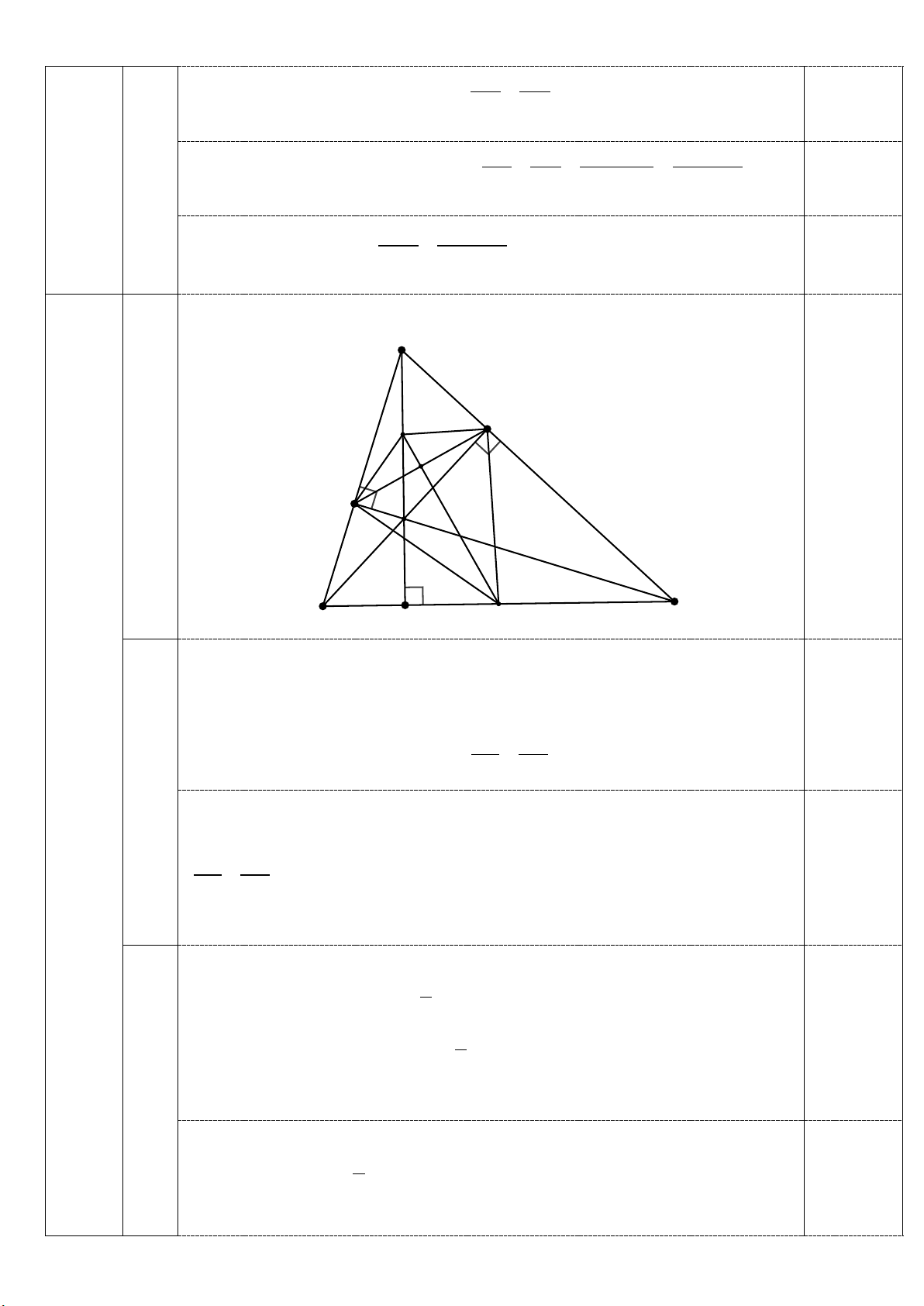
2) Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE,CF cắt nhau tại H .
a) Chứng minh tam giác AEF đồng dạng với tam giác ABC .
b) Gọi O là trung điểm của BC, I là trung điểm của AH . Giao điểm EF và
OI cắt nhau tại K . Chứng minh rằng : 2
AH = 4IK.IO Câu 5 (1,0 điểm)
Xét hai số thực a, b sao cho 1≤ a ≤ 2; 1≤ b ≤ 2 . Tìm giá trị lớn nhất của biểu thức  2 4 2  2 4 2 A a b b a  = + + + + + +  . 2 2 a b b a    
-------------HẾT------------
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM HUYỆN KIM THÀNH
ĐỀ KHẢO SÁT HỌC SINH GIỎI MÔN: TOÁN 8 NĂM HỌC 2024-2025
(Hướng dẫn chấm gồm có 05 trang) Câu Ý Nội dung Điểm  2 2  x +1  x −1 A = −  . − x −  1 :
3x x +1  3x  x  2
2 (x +1) − 3x(x +1) x −1 A = − . :  0,25 3x x 1 3x  +  x  2 2(1− 3x) = − . x A  3x 3x  x −1 1 x 2 = 2. x A = 0,25 x −1 x −1 2x 2
+ Với x ≠ 0; x ≠ 1 ± . Ta có A = = 2 + x −1 x −1 0,25
+ Để A∈ Z thì (x - 1) phải là ước của 2 suy ra x −1∈{ 1; ± ± } 2
+ Xét từng trường hợp tìm x 0,25 1
+ Đối chiếu điều kiện tìm được x = 2 hoặc x = 3 thỏa mãn và kết luận
Do f (x) chia cho 2
x + x −12 = (x − 3)(x + 4) được thương là 2 x + 3 còn 0,25
dư nên ta có : f (x) = (x + )(x − )( 2 4
3 x + 3)+ .ax +b Cho x = 4
− ⇒ f (x) = 4 − a + b = 9 0,25
Cho x = 3 ⇒ f (x) = 3a + b = 2 Khi đó ta có hệ:  4 − a + b = 9  7 − a = 7 a = 1 − a = 1 − 2  ⇔  ⇔  ⇔ 0,25 3  a b 2 3  a b 2 3.(  1) b 2  + = + = − + = b = 5
f (x) = (x + 4)(x −3)( 2 x + 3) − x + 5 = ( 2 x + x −12)( 2
x + 3) − x + 5 0,25 4 3 2
= x + x − 9x + 2x − 31 1) 1 1 1 1 + + = 2 2 2
x + 9x + 20 x +11x + 30 x +13x + 42 18 1 1 1 1 0,25 + + =
(x + 4)(x + 5) (x + 5)(x + 6) (x + 6)(x + 7) 18 Câu 2 1
ĐK : x ≠ -4 ;x ≠ -5 ;x ≠ -6 ;x ≠ -7 ( 2 1 1 1 1 1 1 1 − + − + − = điểm)
(x + 4) (x + 5) (x + 5) (x + 6) (x + 6) (x + 7) 18 0,25 1 1 1 − = x + 4 x + 7 18 2
x +11x − 26 = 0 ( 0,25
x +13)(x − 2) = 0 x = -13 (t/m) ; x = 2 (t/m) 0.25
Vậy phương trình có các nghiệm x = 1 − 3; x = 2 . 1 2
x  y  xy 1   0.25  0
3x 2y   22 
Viết được thành x  1y  1   0
3x 2y   22 2 x  1     0 y     hoặc 1 0  0.25   3x  2y     22 3x  2y  22    1/ x 1   0 x  1 0.25  giải được    3x  2y     22 y    12, 5  y  1 0.25 2/ y 1   0   giải được   3x  2y  20    22 x   3 Ta có: 2 2
6x + y + 5xy −8x − 3y + 7 = 0 2 2 2
4x + 4xy + y + 2x + xy −8x − 3y + 7 = 0 0,25
(2x + y)2 + x(2x + y)−3(2x + y) − 2(x −3) +1= 0
(2x + y)2 +(2x + y)(x −3)− 2(x −3)+1= 0 ( x + y)2 2
+ (x − 3)(2x + y − 2) +1 = 0
(2x + y − 2)(2x + y + 2+ x −3)+5 = 0 0,25 Câu 3
(2x + y − 2)(3x + y − ) 1 = 5 − ( 2 1
2x + y − 2 = 5 − x = 5 điểm) TH1:  ⇔  (TM ) 3
 x + y −1 = 1 y = 13 − 0,25
TH2: 2x + y − 2 =1 x = 7 −  ⇔  (TM ) 3
 x + y −1 = 5 − y = 17
TH3: 2x + y − 2 = 5 x = 7 −  ⇔  (TM ) 3
 x + y −1 = 1 − y = 21 0,25
TH4: 2x + y − 2 = 1 − x = 5  ⇔  (TM ) 3
 x + y −1 = 5 y = 9 − Vậy (x;y) là(5; 13 − );(5; 9 − );( 7 − ;17);( 7 − ; ) 21
Đặt a = x + 2023;b = 2y − 2024;c = 3z + 2025 với a; ;
b c là các số nguyên. 5 5 5  = + + Khi đó ta có: P a b c 
S = a + b + c 0,25 
Xét − = ( 5 − ) + ( 5 − ) + ( 5 P S a a b b c − c)
Ta có chứng minh với mọi số nguyên m thì 5
m − m chia hết cho 30 Thật vậy: 5 4 2 2
m − m = m(m − 1) = m(m − 1)(m + 1) 2 2 2
= m(m − 1)(m − 4) + 5m(m − 1)
= m(m − 1)(m + 1)(m − 2)(m + 2) + 5m(m − 1)(m + 1) 0,25
Với mọi số nguyên m thì m;(m − 1);(m + 1);(m − 2);(m + 2) là 5 số
2 nguyên liên tiếp nên trong đó có một thừa số chia hết cho 2; một thừa số
chia hết cho3 ; một thừa số chia hết cho 5 mà 2;3;5 nguyên tố cùng nhau
từng đôi một nên tích của chúng chia hết cho 2.3.5 .
Do đó m(m − 1)(m + 1)(m − 2)(m + 2) chia hết cho 30 .
Tương tự m(m − 1)(m + 1) chia hết cho 6 , mà (5,6) = 1 nên 0,25
5m(m − 1)(m + 1) chia hết cho 30 .
Vậy với mọi số nguyên m thì 5
m − m chia hết cho 30 .
Do đó − = ( 5 − ) + ( 5 − ) + ( 5 P S a a b b
c − c) chia hết cho 30 với a; ; b c là các
số nguyên. Suy ra P − S 30 0,25
do đó P chia hết cho 30 khi và chỉ khi S chia hết cho 30 . 
Cho tam giác ABC vuông tại A. Chứng minh rằng: tan ABC AC = 2 AB + BC A D Câu 4.1 ( 1 điểm) B C
Vẽ phân giác AD của tam giác ABC,  ABC =  tan tan AD ABD = (1) 2 AB AD DC =
Mà BD là phân giác góc ABC nên AB BC AD DC AD + DC AC = = = (2)
Theo tính chất dãy tỉ số bằng nhau , AB BC AB + BC AB + BC  tan ABC AC = Từ (1) và (2) suy ra 2 AB + BC A I E K F H B C D O 2a Xét ∆ E A B và A ∆ FC có:  BAC chung Câu 4.2  =  0 E A B AFC = 90 0,5 ( 2 Do đó: A ∆ EB AB ∽ A
∆ FC (g.g) suy ra: AE = điểm) AF AC Xét A ∆ EF và A ∆ BC có:  BAC chung AE AB = (cmt) 0,5 AF AC Nên ∆ E A F ∽ A
∆ BC ( .cg.c) Các ∆ E A H và A
∆ FH vuông tại E và F có EI và FI là trung tuyến thuộc cạnh huyền AH nên 1
IE = IF= AH ⇒ I ∈ đường trung trực của EF (1) 2 0,25 Chứng minh tương tự: 1
OE = OF= BC ⇒ O ∈ đường trung trực EF (2) 2
Từ (1) và (2) suy ra: OI là đường trung trực của EF nên tại K OI ⊥ EF 0,25 2b Mặt khác:  1 IA IF AH  = = ⇒ A ∆   IF cân tại I nên   FAI = AFI  2  Tương tự:  =  OFB OBF  +  0 OBF A
F I = 90 ( do ∆ D A B vuông tại D) Do đó:  +  0 = ⇒  0 AFI B O F 90 IFO = 90 Tương tự:  0 IEO = 90 Ta có: ∆ ∽ ∆   =  IKF IFO( 0
FIO chung, IKF IFO = 90 ) 0,25 Nên IF IK 2 =
⇒ IF = IK.IO IO IF Mà 1 2 1 2
IF = AH ⇒ IF = AH 0,25 2 4 Vậy 2
AH = 4IK.IO (x + y)2 Áp dụng BĐT xy ≤ ta có 4 2  2 2 4 4  0,25 Câu 5 2 2
a + + b + + a + + b +  2 2   2 4 2  2 4 2   a b a b A a b b a  = + + + + + + ≤ ( 1 2 2 a b b a     4 điểm) 0,25 Đặt 2 2 a + = ; x b + = y a b 2 4 2 2 4 2 ⇒ a +
= x − 4; b + = y − 4 2 a b
Lại có 1≤ a ≤ 2 ;1≤ b ≤ 2 suy ra (a − )(a − ) 2 1
2 ≤ 0 ⇒ a ≤ 3a − 2 2
2 a + 2 3a − 2 + 2 < ≤ a + = ≤ = 3 nên 0 x 3 a a a (b − )(b − ) 2 1
2 ≤ 0 ⇒ b ≤ 3b − 2 2
2 b + 2 3b − 2 + 2 b + = ≤
= 3 nên 0 < y ≤ 3 0,25 b b b ( 2 2
x + y + x + y − 8)2 (3+ 3+ 9 + 9 −8)2 Nên A ≤ ≤ = 64 4 4  2 4 2 2 4 2 a + b + + = b + a + +  2 2 a b b a  a = b = 1 Đẳng thức xảy ra khi (  a − ) 1 (a − 2) = 0 ⇔   a = b = 2
(b − )1(b − 2) = 0  0,25  a = b = 1
Vậy Max A = 64 ⇔  . a = b = 2
Xem thêm: ĐỀ THI HSG TOÁN 8
https://thcs.toanmath.com/de-thi-hsg-toan-8
Document Outline

• Toán 8_CHÍNH THÚC
• HSG 8