Đề khảo sát HSG vòng 5 Toán 8 năm 2024 – 2025 phòng GD&ĐT Đông Hưng – Thái Bình

UBND HUYỆN ĐÔNG HƯNG
ĐỀ KHẢO SÁT CHỌN NGUỒN HỌC SINH GIỎI VÒNG 5
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2024 - 2025 MÔN TOÁN 8
(Thời gian làm bài 120 phút) Bài 1 (5,5 điểm) 1. Rút gọn biểu thức: 2  x  3x 3   1 6x  x  3 A     :   3 2 2  3 2  2
 x  3x  9x  27 x  9   x  3 x  3x  9x  27  x  7
2. Cho x,y là các số thực thỏa mãn 3x  y  1. Tìm giá trị nhỏ nhất của 2 2 M  3x  y 3. Cho   3 2
f x  x  ax  bx  c với a, b, c là các số thực.
Biết f (x) chia cho x 1dư – 4, f(x) chia cho x  2 dư 5. Tính: A   2025 2025 a  b  2025 2025 b  c  2025 2025 c  a x3 Bài 2 (4,0 điểm). 1. Tìm x biết:
 x  3    x3  x  3  x   2 2 5 2 3 3 7 x  2052 x  2054
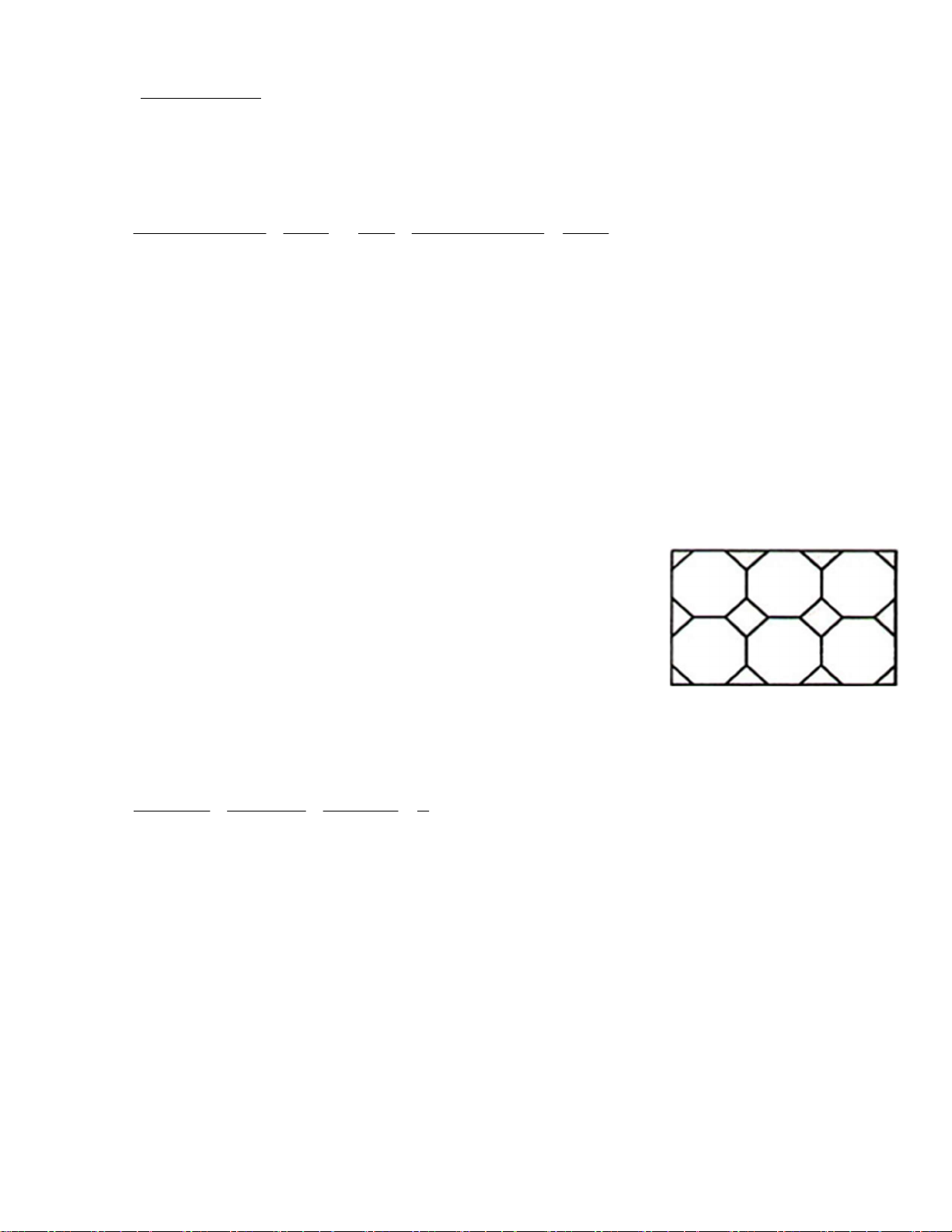
2. Một sân vườn hình chữ nhật được lát bởi các viên gạch hình bát giác
đều và các viên gạch hình vuông hoặc hình tam giác vuông cân (hình vẽ
minh họa). Biết cạnh bát giác đều bằng 2dm và số gạch hình bát giác
đều là 2025 viên. Tính diện tích phần sân vườn được lát bởi những viên
gạch không phải là hình bát giác đều. Bài 3 (4,0 điểm).
1. Tìm x, y nguyên tố biết: x  2 2 4 2 2 2 2  2y 11y  x y  9
2. Với các số thực x, y, z thỏa mãn xyz  1; x  y  z  4 và x y z 4  
 . Tính giá trị của biểu thức 2 2 2 P  x  y  z . 2 2 2
x  3x 1 y  3y 1 z  3z 1 9 Bài 4 (6,5 điểm)
1. Cho tam giác ABC có ba góc nhọn, gọi F là trung điểm của cạnh AB. Tia phân giác trong của góc
BFC cắt BC tại N, tia phân giác trong của góc AFC cắt AC tại Q.
a. Chứng minh rằng QN / / AB
b. Lấy điểm P thuộc FQ sao cho AP  A .
Q Gọi G là giao điểm của AP và FC, M là giao điểm của FN
và BG. Chứng minh APF ∽ C  QF và BM  BN 2. Cho tam giác ABC có ˆ ˆ
B  2C . Tính độ dài các cạnh của tam giác ABC biết rằng số đo các cạnh là
ba số tự nhiên liên tiếp. ------ Hết ------ HƯỚNG DẪN CHẤM Câu Nội dung Điểm 1. Rút gọn biểu thức: 2  x  3x 3   1 6x  x  3 Bài 1 A     :   3 2 2  3 2  2
 x  3x  9x  27 x  9   x  3 x  3x  9x  27  x  7 (5,5đ)
2. Cho x,y là các số thực thỏa mãn 3x  y  1. Tìm giá trị nhỏ nhất của 2 2 M  3x  y 3. Cho   3 2
f x  x  ax  bx  c với a, b, c là các số thực.
Biết f (x) chia cho x 1dư – 4, f(x) chia cho x  2 dư 5. Tính: A   2025 2025 a  b  2025 2025 b  c  2025 2025 c  a x3 1. Rút gọn biểu thức: 2  x  3x 3   1 6x  x  3 A     :   3 2 2  3 2  2
 x  3x  9x  27 x  9   x  3 x  3x  9x  27  x  7     x  x  3 3 1 6x x  3     :    2 2 2 2 0,5 
  x  9 x  3 x  9   x  3  x  3   x 9 x 7  2 x  3 x  9  6x x  3  :  2 x  9  x  3 2 x  9 2 x  7 0,5 x  3  x  3 2 x  9  x 3    0,5 2 2 2 x  9 x  3 x  7 Ý 1   (2đ) x  3  0,5 2 x  7 Kl… 2. Có 3x  y  1 y  1 3x Ý 2 0,25 (1,5đ) Xét
M  3x  y  3x  1 3x2 2 2 2 2 2  3x 1 6x  9x 0,25  1 1   1 1 1 2 2 2 
 12x  6x 1  12 x  x   12 x  2x         2 12   4 16 48  0,5 2  1  1 12 x     0,5  4  4 Lập luận chỉ ra M 1
 . Dấu bằng xảy ra khi 1 x  y  4 4 Ý 3 3. (2 đ)   3 2 f x  x  ax  bx  c
f(x) chia cho x 1dư – 4 nên f   1  4  0,5
suy ra a  b  c  3 . (1)
f(x) chia cho x  2 dư 5 nên f 2  5 0,5
Suy ra 4a  2b  c  3. (2)
Lấy (2) –(1) vế với vế ta được 3a  3b  0 0,5 a  b  0 a  b  0,5 Suy ra 2025 2025 a  b  0 . Vậy A   2025 2025 a  b  2025 2025 b  c  2025 2025 c  a x3  0 1. Tìm x biết:
 x  3    x3  x  3  x   2 2 5 2 3 3 7 x  2052 x  2054
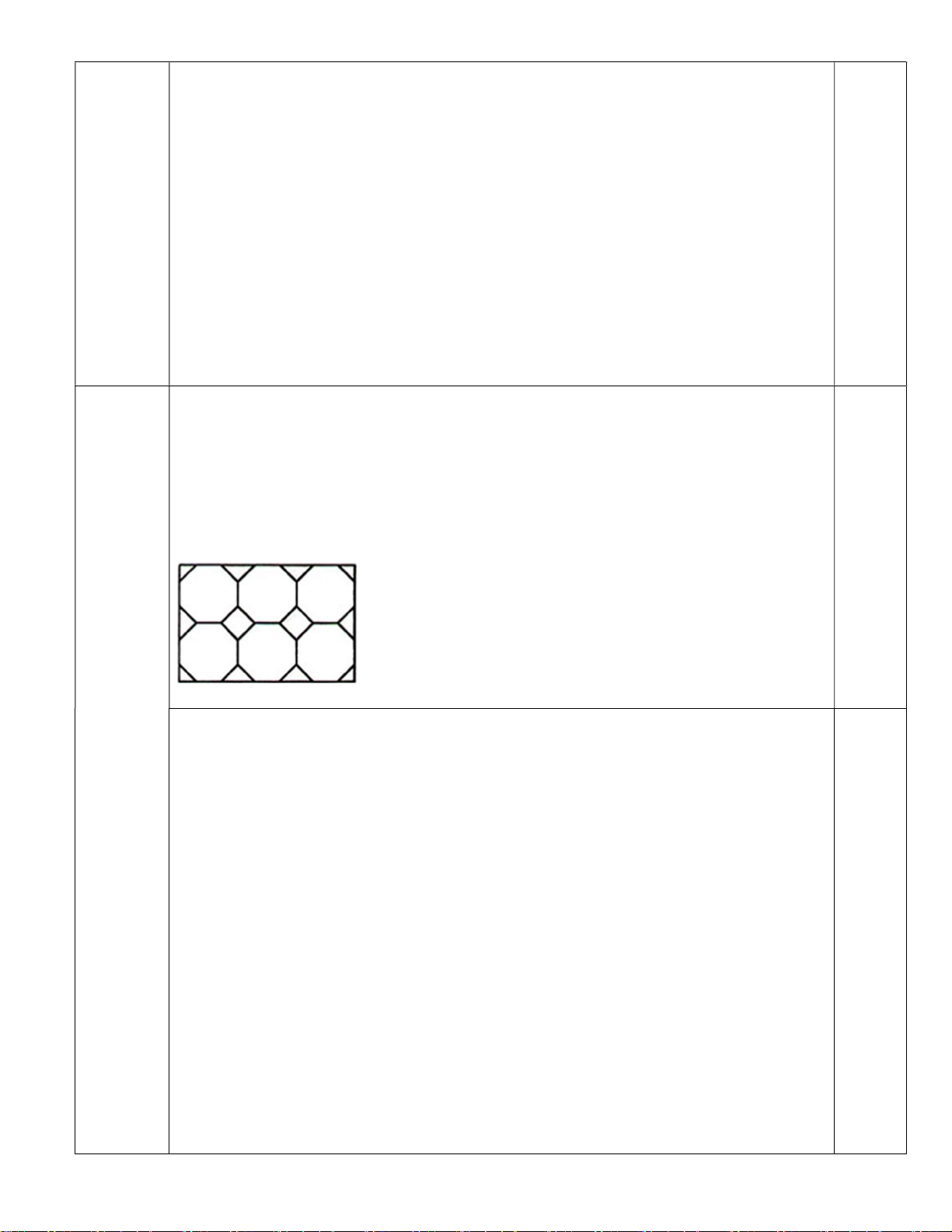
2. Một sân vườn hình chữ nhật được lát bởi các viên gạch hình bát giác đều và
các viên gạch hình vuông hoặc hình tam giác vuông cân (hình vẽ minh họa). Biết
cạnh bát giác đều bằng 2dm và số gạch hình bát giác đều là 2025 viên. Tính diện
tích phần sân vườn được lát bởi những viên gạch không phải là hình bát giác đều. 1. 3 3 3 Bài 2
 x     x  x   x   2 2 5 2 3
3 7x  2052x  2054. (1) (4,0đ)
Đặt a  2x  5; b  2  x Suy ra a  b  x  3 Có a  b  a  b3 3 3  3aba  b
Hay  x  3    x3   x  3 2 5 2
3  32x  52  x x  3 . 0,5 Khi đó (1) có dạng 
x  3   x    x x     x  3   x   2 3 3 2 5 2 3 3 3 7x  2052x  2054 x 3 2
7x  2052x  2054  32x  52  xx  3  0 0,5  x  3 2 7x  2052x  2054  3   2
4x  2x 10  5x  0  x 3 2 2
7x  2052x  2054  27x  6x  30  0    0,5 x  3 2
x  2025x  2024  0  
x 3x  1x  2024  0 0,5
Suy ra x  1; x  3; x  2024 Vậy …. 2.
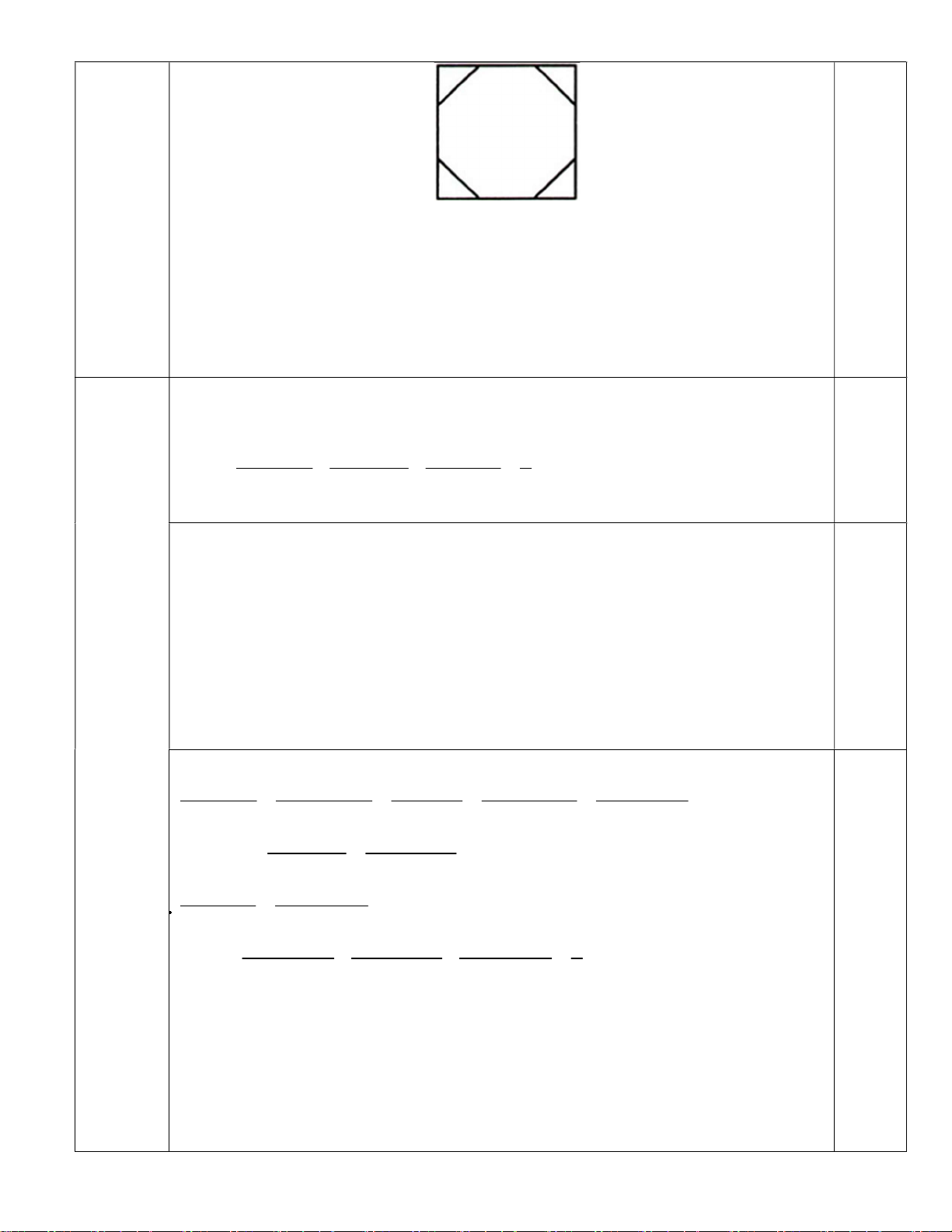
Xét một hình vuông chứa viên gạch hình bát giác đều cạnh 2 dm. 0,75
Bốn tam giác vuông cân nằm ngoài viên gạch hình bát giác đều ghép lại
được một hình vuông cạnh 2 dm có diện tích bằng 4 dm2.
Như vậy ứng với mỗi viên gạch hình bát giác đều, có diện tích 4 dm2 được 0,5
lát bởi các viên gạch không phải là hình bát giác đều. 0,75
Vậy diện tích phải tìm là 2025 x 4 = 8100 (dm2) = 81 (m2).
1. Tìm x, y nguyên tố biết: x  2 2 4 2 2 2 2  2y 11y  x y  9 2. Với các số thực ,
x y, z thỏa mãn xyz  1; x  y  z  4 và x y z 4  
 . Tính giá trị của biểu thức 2 2 2
x  3x 1 y  3y 1 z  3z 1 9 2 2 2 P  x  y  z . 1. Có  x  22 2 4 2 2 2  2y 11y  x y  9 4 2 4 2 2 2
x  4x  4  2 y 11y  x y  9  0 0,5 Biến đổi được  2 2 x  y   2 2 5 x  2 y   1  0 0,75 0,5 Bài 3 Suy ra 2 2
x  2y 1  0 . Lập luận chỉ ra y=2; x=3 0,25 Kl… (4,0 2. Ta có: 0,5 điểm). x x 1 1 1     2 2 x  3x 1 x  3x  xyz
x  3  yz 1 y  z  yz ( y 1)(z 1) Tương tự y 1  ; 2 y  3y 1 (x 1)(z 1) 0,5  z 1  . 2
z  3z 1 (x 1)( y 1) Suy ra 1 1 1 4   
( y 1)(z 1) (x 1)(z 1) (x 1)( y 1) 9 0,5 0,5 x 1 y 1 z 1 4 9
  (x 1)(y 1)(z 1)  (x 1)( y 1)(z 1) 9 4 9
 1 (x  y  z)  (xy  yz  zx)  4 1   xy  yz  zx  4 33 2 2 2 2
 x  y  z  (x  y  z)  2(xy  yz  zx)  2 Vậy 33 2 2 2 x  y  z  . 2
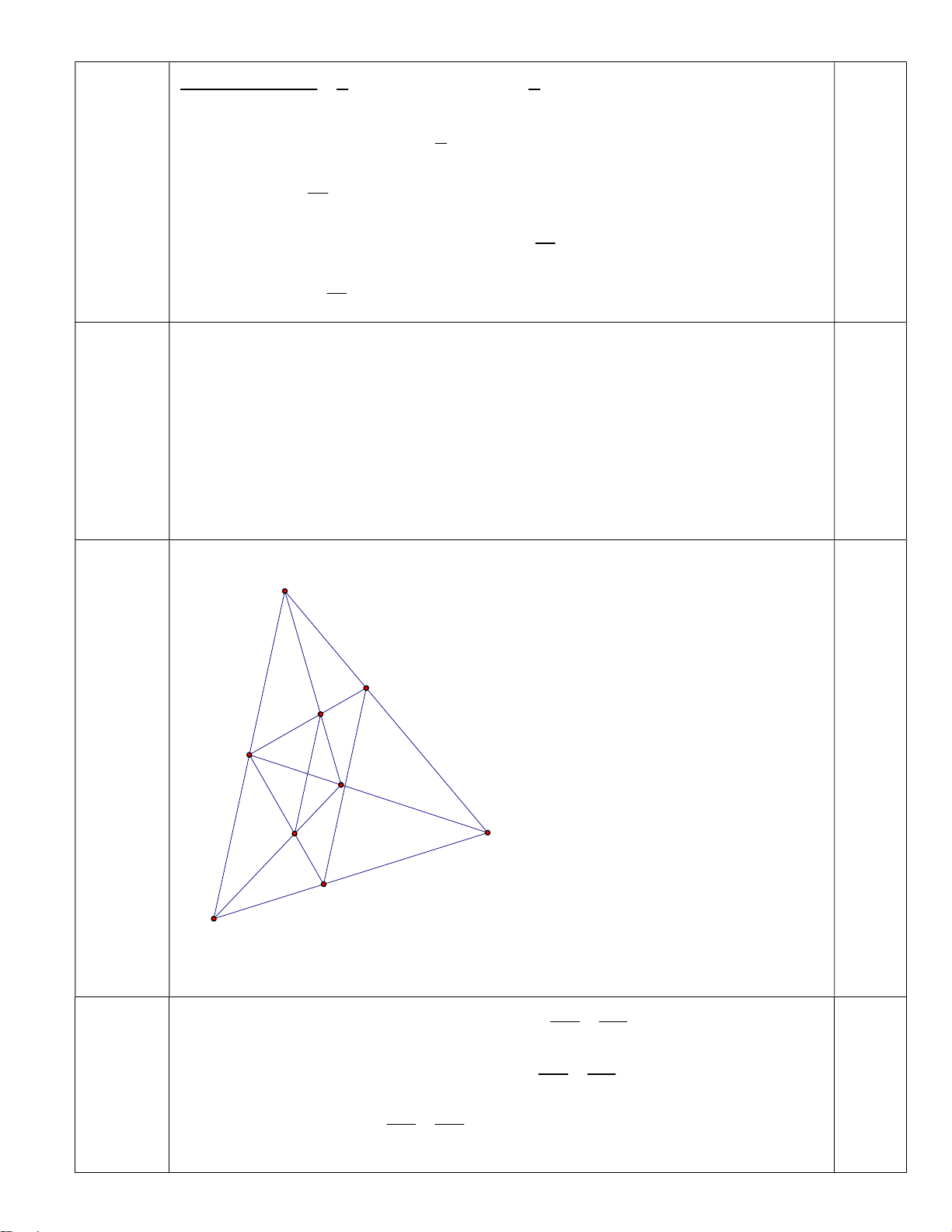
1. Cho tam giác ABC có ba góc nhọn, gọi F là trung điểm của cạnh A . B Tia
phân giác trong của góc BFC cắt BC tại N, tia phân giác trong của góc AFC cắt AC tại Q. Bài 4
a) Chứng minh rằng QN / / AB (6,5 đ)
b) Lấy điểm P thuộc FQ sao cho AP  A .
Q Gọi G là giao điểm của AP
và FC, M là giao điểm của FN và BG. Chứng minh APF ∽ C  QF và BM  BN A Q P F G M C N B A
 FC có FQ là tia phân giác của AQ FA 0,5 C  FA   QC FC 1a)  0,5
BFC có FN tia phân giác của  BN BF BFC   (2,0 đ) NC FC
Mà FA  FB nên suy ra AQ BN  QC NC 0,5 0,5
Theo Định lí Talet đảo ta suy ra QN / / AB (1)
Vì AP  AQ  APQ cân tại A  APQ  AQP 0,25 0 ˆ ˆ 0 ˆ ˆ
Mà APQ  APF  180 và AQP  CQF  180 ˆ ˆ 0,25 Nên APF  CQF Xét APF và CQF có : PFA  QFC  gt 0,5    ∽  APF  CQF  cmt APQ CQF (g.g) Từ PF FA APF ∽ CQF(g.g)   2 QF FC
Theo tính chất phân giác trong GAF và GBF ta có 0,25 1b) AP FA FB BM AP BM ( 2,5đ)       MP / / AB 3 PG FG FG GM PG AB (thales đảo) Từ (1) và (3) suy ra FP FM 0,25 QN / /PM   4 FQ FN Từ (2) và (4) suy ra FM FA FB   0,25 FN FC FC Xét BFM và CFN có :  B  FM  C  FN gt 0,5     ∽          BFM CFN ( . c g.c) BMF CNF FM FB cmt  FN FC
Từ đó c/m được góc BMN = góc BNM, nên tam giác BMN cân tại B 0,25 => BM = BN 2. Cho tam giác ABC có ˆ ˆ
B  2C . Tính độ dài các cạnh của tam giác
ABC biết rằng số đo các cạnh là ba số tự nhiên liên tiếp. A 2. B (2,0 đ) C D
Trên tia đối tia BA lấy điểm D sao cho BD = BC Chứng minh: A  CD  A  BC(g  g) 0,5 AC AD 2    AC  A . B AD AB AC Mà AD = AB + BC nên 2 2 AC  AB  A . B BC 0,5
Đặt AC = b, AB = c, BC = a ( a,b,c > 0)
Ta có b2 = c2 + ac suy ra b > c > 0 mà a,b,c là 3 số tự nhiên liên tiếp
+) Nếu b = c +1 ta có ( c +1) 2 = c2 +ac => 2c +1 = ac => c(a-2) = 1 0,5
Suy ra c = 1; a= 3; b= 2 ( loại) vì số đo trên không thể là các cạnh của một tam giác.
+) Nếu b = c +2 suy ra ( c +2) 2 = c2 + ac => 4c + 4 = ac => c(a -4) = 4 Suy ra c 1;2;  4 0,5
Xét từng TH thì chỉ có c = 4; a = 5; b= 6 thỏa mãn yêu cầu bài toán. Vậy: ......