Đề khảo sát tháng 1 Toán 9 năm 2024 – 2025 phòng GD&ĐT Gia Lâm – Hà Nội

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG THÁNG 1 HUYỆN GIA LÂM NĂM HỌC 2024-2025 MÔN: TOÁN 9
Đề thi gồm 2 trang
Thời gian làm bài: 120 phút
Bài I. (1,5 điểm)
Cô giáo chủ nhiệm lớp 9A đã thống kê tháng sinh nhật của các bạn học sinh trong lớp và thu
được kết quả dưới đây. Tháng 1 2 3 4 5 6 7 8 9 10 11 12 Nam 2 1 2 1 0 1 0 1 2 2 2 2 Nữ 1 2 1 0 1 2 2 2 1 1 1 0
Hãy sử dụng bảng dữ liệu trên để trả lời:
a) Lớp 9A có bao nhiêu bạn học sinh nam và bao nhiêu bạn học sinh nữ?
b) Chọn ngẫu nhiên một bạn học sinh lớp 9A, xác suất chọn được bạn nam sinh tháng 10 là bao nhiêu?
c) Chọn ngẫu nhiên một bạn học sinh lớp 9A, xác suất chọn được bạn nữ sinh từ tháng 8
đến tháng 12 là bao nhiêu?
Bài II. (1,5 điểm) Cho hai biểu thức: x + 5 A = và 1 2 x 3 x 10 B − + = − + với x − 2 x + 2 x − 2 x − 4
x ≥ 0; x ≠ 4.
1) Tính giá trị của biểu thức A khi x = 64. 2) Rút gọn biểu thức B
3) Tìm giá trị nhỏ nhất của biểu thức P = . A B
Bài III. (2,5 điểm)
1) Một xe khách và một xe du lịch khởi hành đồng thời từ A đi đến B. Biết vận tốc của xe
du lịch lớn hơn vận tốc của xe khách là 20 km/h. Do đó xe du lịch đến B trước xe khách 50
phút. Tính vận tốc của mỗi xe, biết quãng đường AB dài 100 km.
2) Bạn Phong đi siêu thị nếu mua 1 chiếc áo polo Lacoste và 1 đôi giày hãng Li-Ning theo
giá niêm yết hết 800 000 đồng. Nhưng gặp đợt khuyến mãi nên 1 chiếc áo polo Lacoste giảm
5% và 1 đôi giày hãng Li-Ning giảm 10%, vì vậy bạn Phong chỉ phải trả 735 000 đồng.
a) Hãy tính giá niêm yết ban đầu của 1 chiếc áo polo Lacoste và 1 đôi giày hãng Li-Ning ?
b) Ngoài ra, Siêu thị có thêm ưu đãi nếu khách hàng có hóa đơn từ 2 000 000 đồng trở lên sẽ
được giảm tiếp 10% trên tổng số tiền đã mua. Trong dịp này, bạn Phong đã mua 4 chiếc áo
polo Lacoste và 2 đôi giày hãng Li-Ning. Hỏi bạn Phong trả hết tất cả bao nhiêu tiền ? mx + 2y = 7
3) Cho hệ phương trình:  với ,
m n là tham số. Tính tổng m + n biết hệ
2x − 3ny = 10 −
phương trình trên có nghiệm ( ; x y) = (1;2).
Bài IV. (4,0 điểm)
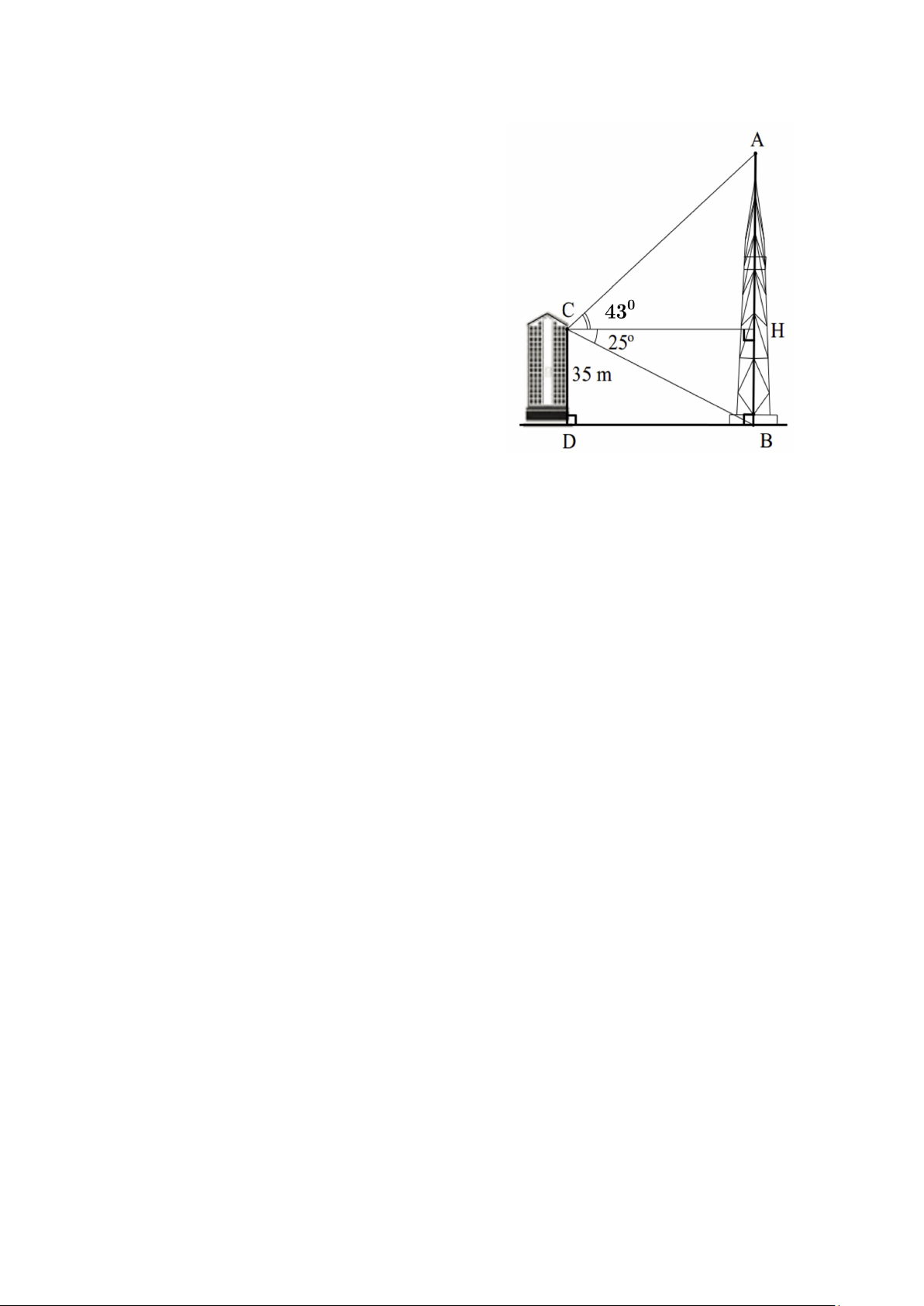
1) Cho hình vẽ bên, từ trên vị trí C của một tòa
nhà có chiều cao CD = 35m , người ta nhìn thấy
đỉnh A của một tháp truyền hình với góc nâng  0
ACH = 43 (góc nâng là góc tạo bởi phương
nằm ngang và tia đi qua đỉnh tháp) và từ vị trí C
nhìn thấy chân của tháp với góc hạ  0 HCB = 25
(góc hạ là góc tạo bởi phương nằm ngang và tia đi qua chân tháp)
a) Tính khoảng cách BD từ tòa nhà đến chân tháp.
b) Tính chiều cao AB của tháp truyền hình.
(Các kết quả làm tròn đến hàng đơn vị).
2) Từ điểm A nằm ngoài (O) vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp
điểm). Kẻ đường kính CD của (O).
a) Chứng minh 4 điểm O, B, A, C cùng thuộc một đường tròn
b) Kẻ AD cắt (O) tại E sao cho E nằm giữa A và D. Chứng minh rằng: CE ⊥ AD và 2
AC = AE.AD .
c) Vẽ BH ⊥ DC tại H. Gọi I là trung điểm của BH. Chứng minh ba điểm A, I, D thẳng hàng.
Bài V. (0,5 điểm)
Cửa hàng nhà bác Nghĩa chuyên kinh doanh máy tính loại ASUS tại Hà Nội. Giá nhập vào
một chiếc là 18 triệu đồng và bán ra với giá 22 triệu đồng. Với giá bán như trên thì một năm số
lượng máy tính bán được dự kiến là 500 chiếc. Để tăng thêm lượng tiêu thụ dòng máy tính
này, bác Nghĩa dự định giảm giá bán và ước lượng cứ giảm 200 nghìn đồng một chiếc thì số
lượng máy tính bán ra trong một năm sẽ tăng 50 chiếc. Vậy bác Nghĩa phải bán với giá bao
nhiêu để sau khi giảm giá lợi nhuận thu được sẽ cao nhất ? __________Hết__________
Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh:…………………………………………..Số báo danh:…………………… …………
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM HUYỆN GIA LÂM
ĐỀ KIỂM TRA KHẢO SÁT THÁNG 1 NĂM HỌC 2024-2025 Môn: TOÁN Bài Ý Nội dung Điểm I
Cô giáo chủ nhiệm lớp 9A đã thống kê tháng sinh nhật của các bạn học sinh 1,5
trong lớp và thu được kết quả dưới đây. Tháng 1 2 3 4 5 6 7 8 9 10 11 12 Nam 2 1 2 1 0 1 0 1 2 2 2 2 1 Nữ 1 2 1 0 1 2 2 2 1 1 1 0
Hãy sử dụng bảng dữ liệu trên để trả lời:
a) Lớp 9A có bao nhiêu bạn học sinh nam và bao nhiêu bạn học sinh nữ?
b) Chọn ngẫu nhiên một bạn học sinh lớp 9A, xác suất chọn được bạn nam sinh
tháng 10 là bao nhiêu?
c) Chọn ngẫu nhiên một bạn học sinh lớp 9A, xác suất chọn được bạn nữ sinh
từ tháng 8 đến tháng 12 là bao nhiêu?
a Lớp 9A có 16 bạn học sinh nam và 14 bạn học sinh nữ 0,5
b Xác suất chọn được bạn nam sinh tháng 10 là: 2 1 = 0,5 30 15
Xác suất chọn được bạn nữ sinh từ tháng 8 đến tháng 12 là: 2 +1+1+1 5 1 = = c 30 30 6 0,5
(HS không rút gọn đến tối giản trừ 0,25 điểm) II 0,5
Cho hai biểu thức: x + 5 A = và 1 2 x 3 x 10 B − + = − +
với x ≥ 0; x ≠ 4. x − 2 x + 2 x − 2 x − 4
Tính giá trị của biểu thức A khi x = 64.
1 Thay x = 64 vào biểu thức A Tính được 69 23 A = = 0,5 6 2
(HS không rút gọn đến tối giản trừ 0,25 điểm)
Rút gọn biểu thức B 0,75 1 2 x 3 x 10 0,25 B − + = − + 2 x + 2 x − 2 x − 4
x − 2 − 2( x + 2)+ x −3 x +10 0,25 = ( x + 2)( x − 2) ( x 0,25 x x − − + )2 2 4 4 x − 2 = ( = =
x + 2)( x − 2) ( x + 2)( x − 2) x + 2
3 Tìm giá trị nhỏ nhất của biểu thức P = .AB 0,25 Ta có: x + 5 9 P = . A B = = x + 2 + − 4 x + 2 x + 2
Áp dụng BĐT Cô-si ta có: 9 P = x + + − ≥ ( x + ) 9 2 4 2 2 . − 4 = 2 x + 2 x + 2
Vậy giá trị nhỏ nhất của P bằng 2 khi ( x + )2 2 = 9 hay x =1 0,25 III
Một xe khách và một xe du lịch khởi hành đồng thời từ A đi đến B. Biết vận tốc 1,0
1 của xe du lịch lớn hơn vận tốc của xe khách là 20 km/h. Do đó xe du lịch đến B
trước xe khách 50 phút. Tính vận tốc của mỗi xe, biết quãng đường AB dài 100 km. Đổi 5 50' = giờ 6
Gọi vận tốc của xe khách là x(km / ; h x > 0)
Vận tốc của xe du lịch là x + 20(km / h) 0,25
Thời gian xe khách đi từ A đến B là: 100 (giờ) x
Thời gian xe du lịch đi từ A đến B là: 100 (giờ) x + 20
Theo bài ta có phương trình: 100 100 5 = + x x + 20 6 x = 40(TM ) Giải được  x = 60( − L) 0,5
Vậy vận tốc xe khách là 40 km/h và vận tốc xe du lịch là 40 + 20 = 60 km/h 0,25
Bạn Phong đi siêu thị nếu mua 1 chiếc áo polo Lacoste và 1 đôi giày hãng Li-Ning 1,0
theo giá niêm yết hết 800 000 đồng. Nhưng gặp đợt khuyến mãi nên 1 chiếc áo polo
Lacoste giảm 5% và 1 đôi giày hãng Li-Ning giảm 10%, vì vậy bạn Phong chỉ phải
2 trả 735 000 đồng.
a) Hãy tính giá niêm yết ban đầu của 1 chiếc áo polo Lacoste và 1 đôi giày hãng Li- Ning ?
b) Ngoài ra, Siêu thị có thêm ưu đãi nếu khách hàng có hóa đơn từ 2 000 000 đồng
trở lên sẽ được giảm tiếp 10% trên tổng số tiền đã mua. Trong dịp này, bạn Phong
đã mua 4 chiếc áo polo Lacoste và 2 đôi giày hãng Li-Ning. Hỏi bạn Phong trả hết
tất cả bao nhiêu tiền ?
a) Gọi giá niêm yết của 1 chiếc áo polo Lacoste và 1 đôi giày hãng Li-Ning lần lượt là
x, y (nghìn đồng, x, y > 0)
Theo bài ta có hệ phương trình: x + y = 800 
0,95x + 0,9y = 735 0,25 x = 300
Giải được y =500 0,25
Vậy giá niêm yết của chiếc áo polo Lacoste và 1 đôi giày hãng Li-Ning lần lượt là
300.000 đồng và 500.000 đồng. 0,25
b) Số tiền bạn Phong trả khi mua 4 chiếc áo polo Lacoste và 2 đôi giày hãng Li-Ning là:
4.300.0,95 + 2.500.0,9 = 2040 (nghìn đồng)
Do hóa đơn từ 2 000 000 đồng trở lên sẽ được giảm tiếp 10% nên số tiền bạn Phong phải trả là: 2040.0,9 =1836 0,25 (nghìn đồng)
Vậy số tiền bạn Phong đã trả là 1.836.000 đồng mx + 2y = 7 0,5
Cho hệ phương trình:  với ,
m n là tham số
2x − 3ny = 10 −
Tính tổng m + n biết hệ phương trình trên có nghiệm ( ; x y) = (1;2). 3 m + 4 = 7
Thay x =1, y = 2 vào hệ phương trình, ta có:  2 − 6n = 10 − 0,25
Từ các phương trình trong hệ ta tìm được m = 3,n = 2
Suy ra m + n = 3 + 2 = 5 0,25 IV
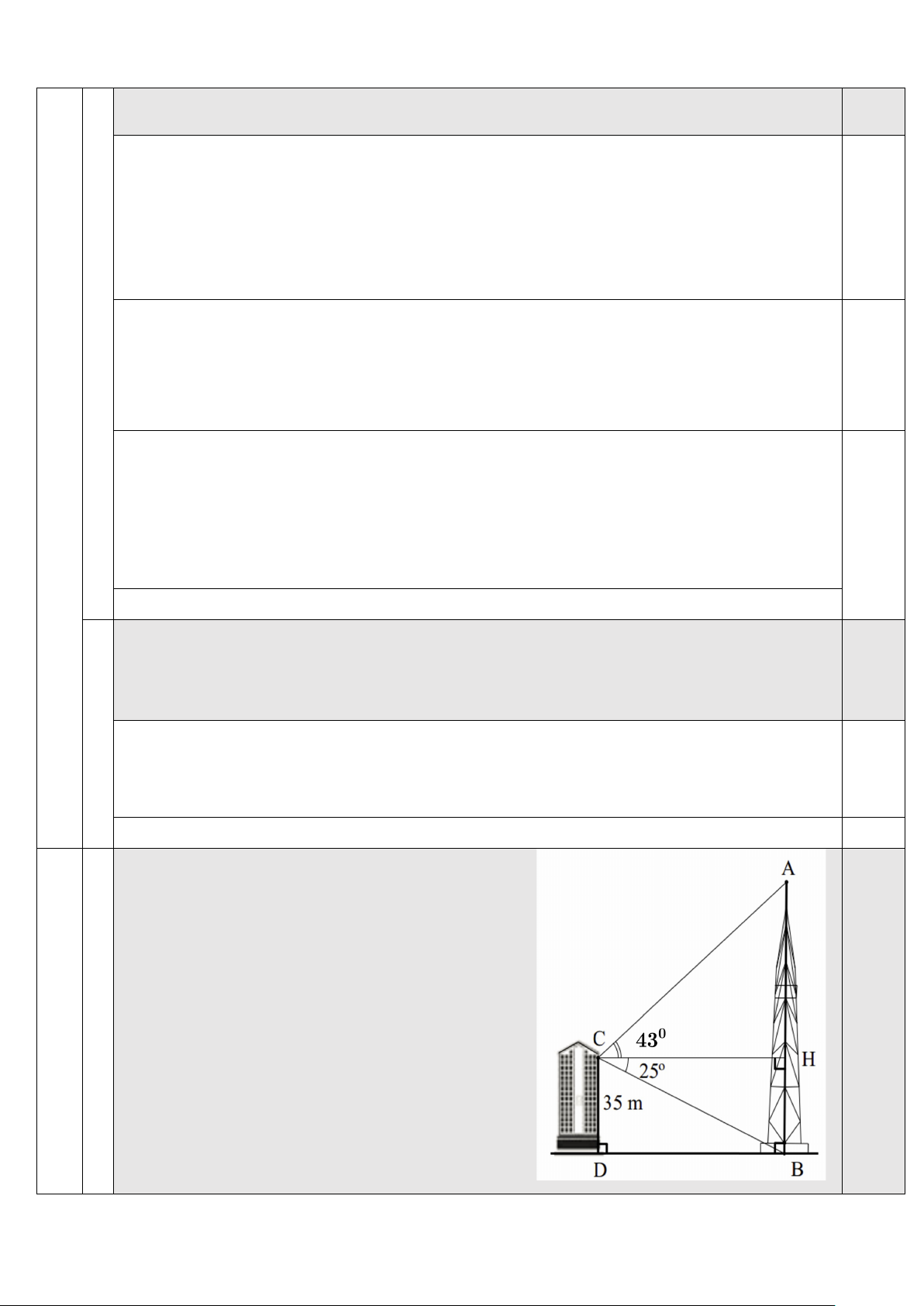
Cho hình vẽ bên, từ trên vị trí C của 1,0
một tòa nhà có chiều cao CD = 35m ,
người ta nhìn thấy đỉnh A của một
tháp truyền hình với góc nâng  0
ACH = 43 (góc nâng là góc tạo bởi
phương nằm ngang và tia đi qua đỉnh
1 tháp) và từ vị trí C nhìn thấy chân của
tháp với góc hạ  0
HCB = 25 (góc hạ là
góc tạo bởi phương nằm ngang và tia đi qua chân tháp)
a) Tính khoảng cách BD từ tòa
nhà đến chân tháp.
b) Tính chiều cao AB của tháp truyền hình. ((C
ác kết quả làm tròn đến hàng đơn vị ) a) Ta có  =  0
CBD BCH = 25 (so le trong vì BD / /CH ) Xét BC ∆
D vuông tại D ta có: tan CD CBD = suy ra CD 35 BD = = ≈ 75 (m) BD 0 tanCBD tan 25
Vậy khoảng cách từ tòa nhà đến chân Tháp là khoảng 75 m. b) 0,5
Tứ giác BDCH là hình chữ nhật suy ra: BH = CD = 35m CH = BD = 75 m Xét AC
∆ H vuông tại H ta có: tan AH ACH = suy ra 0
AH = CH.tan ACH = 75.tan 43 ≈ 70 (m) CH
Suy ra: AB = AH + BH ≈ 70 + 35 =105 (m) 0,5
Vậy chiều cao của tháp truyền hình là khoảng 105 m.
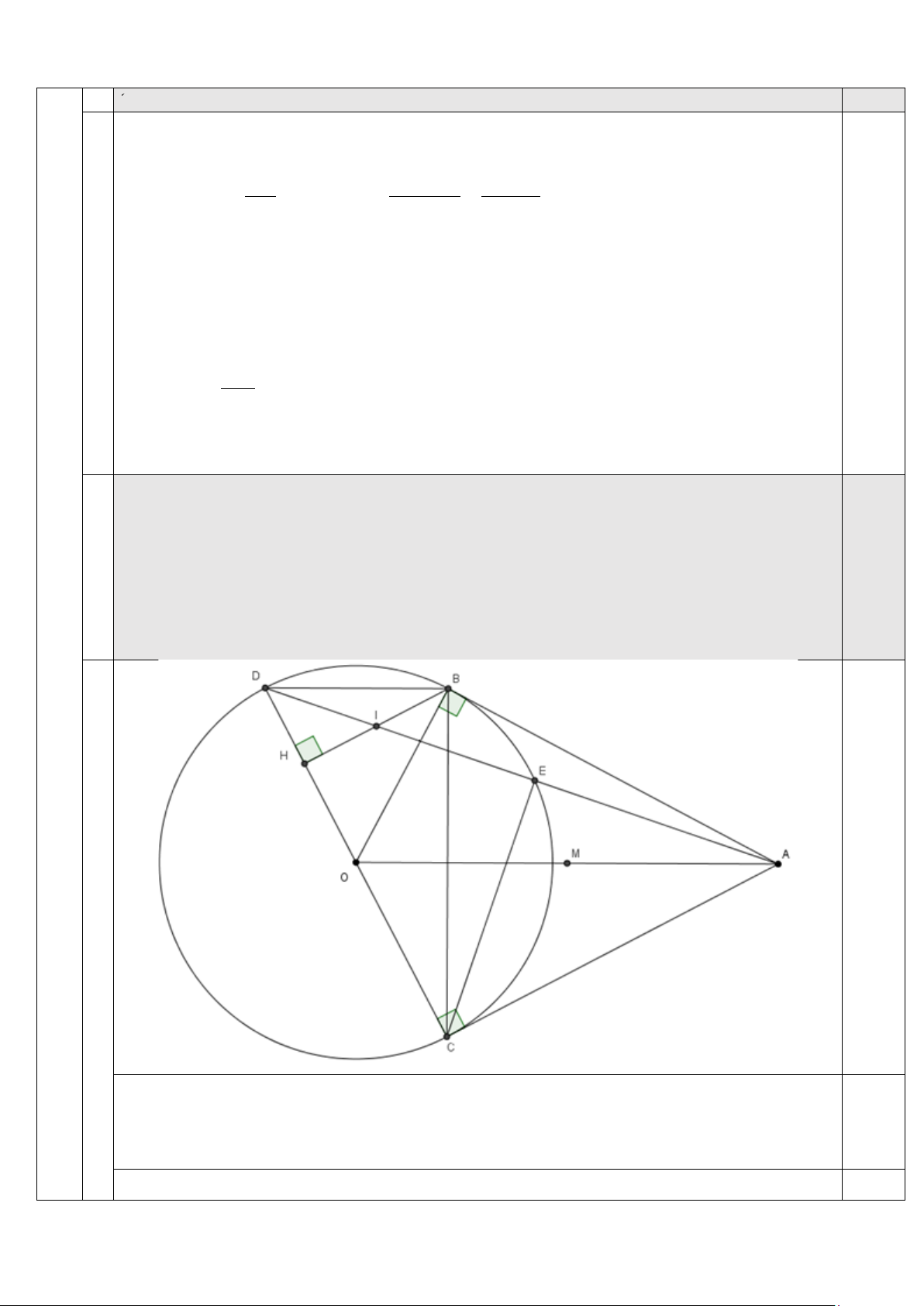
Từ điểm A nằm ngoài (O) vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là các 3.0
tiếp điểm). Kẻ đường kính CD của (O). 2
a) Chứng minh 4 điểm O, B, A, C cùng thuộc đường tròn
b) Kẻ AD cắt (O) tại E sao cho E nằm giữa A và D. Chứng minh rằng:
CE ⊥ AD và 2
AC = AE.AD
c) Vẽ BH ⊥ DC tại H. Gọi I là trung điểm của BH. Chứng minh ba điểm A,I,D thẳng hàng. 0,25 a
Gọi M là trung điểm OA, ta có:
+ M là tâm đường tròn đường kính OA
+ BM là đường trung tuyến OA ∆ B 0,5
+ CM là đường trung tuyến OA ∆ C - OA ∆
B vuông tại B, BM là đường trung tuyến Suy ra OA
OM = MA = BM =
nên ta có , , ∈( ; OA O B A M ) (1) 0,25 2 2 - OA ∆
C vuông tại C, CM là đường trung tuyến Suy ra OA
MO = MA = CM =
nên ta có , , ∈( ; OA O A C M ) (2) 0,25 2 2
(1)(2) suy ra , , , ∈( ; OA O B A C M ) 2 0,25 Chứng minh: 2
AC = AE.AD 1,0 Chứng minh được C ∆ ED vuông tại E ⊥ b Suy ra CE AD 0.5
Chứng minh được AEC ∆ đồng dạng AC ∆
D (g.g) suy ra AE AC = AC AD 0.5 Suy ra 2
AC = AE.AD
Chứng minh ba điểm A,I,D thẳng hàng 0,5
Chứng minh được BD//OA suy ra  = 
HDB COA hai góc đồng vị
Chứng minh được HDB ∆ đồng dạng C ∆ OA(g.g) HD BH HD BH Suy ra = = OC
AC suy ra 2OC 2AC
Mà CD = 2OC, BH = 2HI c HD HI Suy ra = CD AC 0,25
Chứng minh được HDI ∆ đồng dạng C ∆ DA (c.g.c) Suy ra  =  HDI CDA 0,25
Suy ra hai tia DI, DA trùng nhau
Vậy ba điểm A,I,D thẳng hàng
Cửa hàng nhà bác Nghĩa chuyên kinh doanh máy tính loại ASUS tại Hà Nội. Giá 0,5
nhập vào một chiếc là 18 triệu đồng và bán ra với giá 22 triệu đồng. Với giá bán
như trên thì một năm số lượng máy tính bán được dự kiến là 500 chiếc. Để tăng
thêm lượng tiêu thụ dòng máy tính này, bác Nghĩa dự định giảm giá bán và ước
lượng cứ giảm 200 nghìn đồng một chiếc thì số lượng máy tính bán ra trong một
năm sẽ tăng 50 chiếc. Vậy bác Nghĩa phải bán với giá bao nhiêu để sau khi giảm V
giá lợi nhuận thu được sẽ cao nhất ?
Đổi 200 nghìn đồng = 0,2 triệu đồng
Gọi x là giá bán mới mà cửa hàng bán một chiếc máy tính loại ASUS (triệu đồng, x>18)
Số tiền bị giảm khi bán một chiếc máy tính là 22 − x (triệu đồng) 0,25
Khi đó số lượng máy tính bán ra trong một năm là:
500 + 50(22 − x) : 0,2 = 6000 − 250x (chiếc)
Lợi nhuận mà cửa hàng nhà bác Nghĩa thu được khi bán giá mới là:
(6000 − 250x).(x −18) 2 = 250 −
x +10500x −108000 = 250 −
( 2x −42x + 432) = 250 − (x − )2 21 + 2250 ≥ 2250
Dấu “=” xảy ra khi x − 21 = 0 hay x = 21
Vậy giá bán mới của một chiếc máy tính loại ASUS là 21 triệu đồng và giá lợi nhuận 0,25
thu được cao nhất là 2250 triệu đồng
 HS làm cách khác có kết quả đúng vẫn được điểm tối đa.
Xem thêm: KHẢO SÁT CHẤT LƯỢNG TOÁN 9
https://thcs.toanmath.com/khao-sat-chat-luong-toan-9
Document Outline

• Đề KS Toán 9 Tháng 1 năm 24-25
• HD chấm đề KS toán 9 tháng 1 năm 2024-2025_done
• KS 9