Đề khảo sát tháng 2 Toán 9 năm 2024 – 2025 phòng GD&ĐT Thanh Trì – Hà Nội

UBND HUYỆN THANH TRÌ
ĐỀ KIỂM TRA KHẢO SÁT
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2024 - 2025 Môn: TOÁN 9 (Đề gồm 01 trang)
Thời gian làm bài: 120 phút
Ngày 21 tháng 02 năm 2025
Bài I (2 điểm).
1) Biết rằng parabol y = ax2 ( a ≠ 0 ) đi qua điểm A(1; 2). a) Tìm hệ số a.
b) Tìm các điểm thuộc parabol có tung độ bằng y = 8.
2) Một hộp đựng 20 tấm thẻ giống nhau được đánh số 1; 2; 3;…; 20. Bạn Nam rút ngẫu nhiên một
tấm thẻ trong hộp. Tính xác suất của các biến cố sau:
a) E: “Rút được tấm thẻ ghi số chia hết cho 3”.
b) F: “Rút được tấm thẻ ghi số không lớn hơn 5”. +
Bài II (1,5 điểm). Cho hai biểu thức: A = 1 x +
và B = 2 x 1 với x ≥ 0; x ≠ 1 x −1 x −1 x + x − 2
1) Tính giá trị của biểu thức B khi x = 9. +
2) Biết M = A : B. Chứng minh rằng M = x 2 . x +1
3) Tìm giá trị lớn nhất của M.
Bài III (2,0 điểm).
1) Một người đi xe đạp từ A đến B cách nhau 24 km. Khi từ B trở về A, người đó tăng vận tốc thêm
4 km/h so với lúc đi, vì vậy thời gian về ít hơn thời gian đi là 30 phút. Tính thời gian của người đi
xe đạp lúc đi từ A đến B.
2) Cô Mai chia số tiền 1 tỉ đồng của mình cho hai khoản đầu tư. Sau một năm, tổng số tiền lãi thu
được là 63 triệu đồng. Lãi suất cho khoản đầu tư thứ nhất là 5% một năm. Lãi suất cho khoản đầu
tư thứ hai là 7% một năm. Tính số tiền cô Mai đầu tư cho mỗi khoản.
Bài IV (4,0 điểm).
1) Một chiếc quạt giấy khi xòe ra có dạng nửa hình tròn bán kính 20cm.
Tính diện tích phần giấy của chiếc quạt, biết rằng khi gấp lại, phần
giấy có chiều dài 15cm (cho π ≈ 3,14 ; làm tròn kết quả đến hàng đơn vị của cm2).
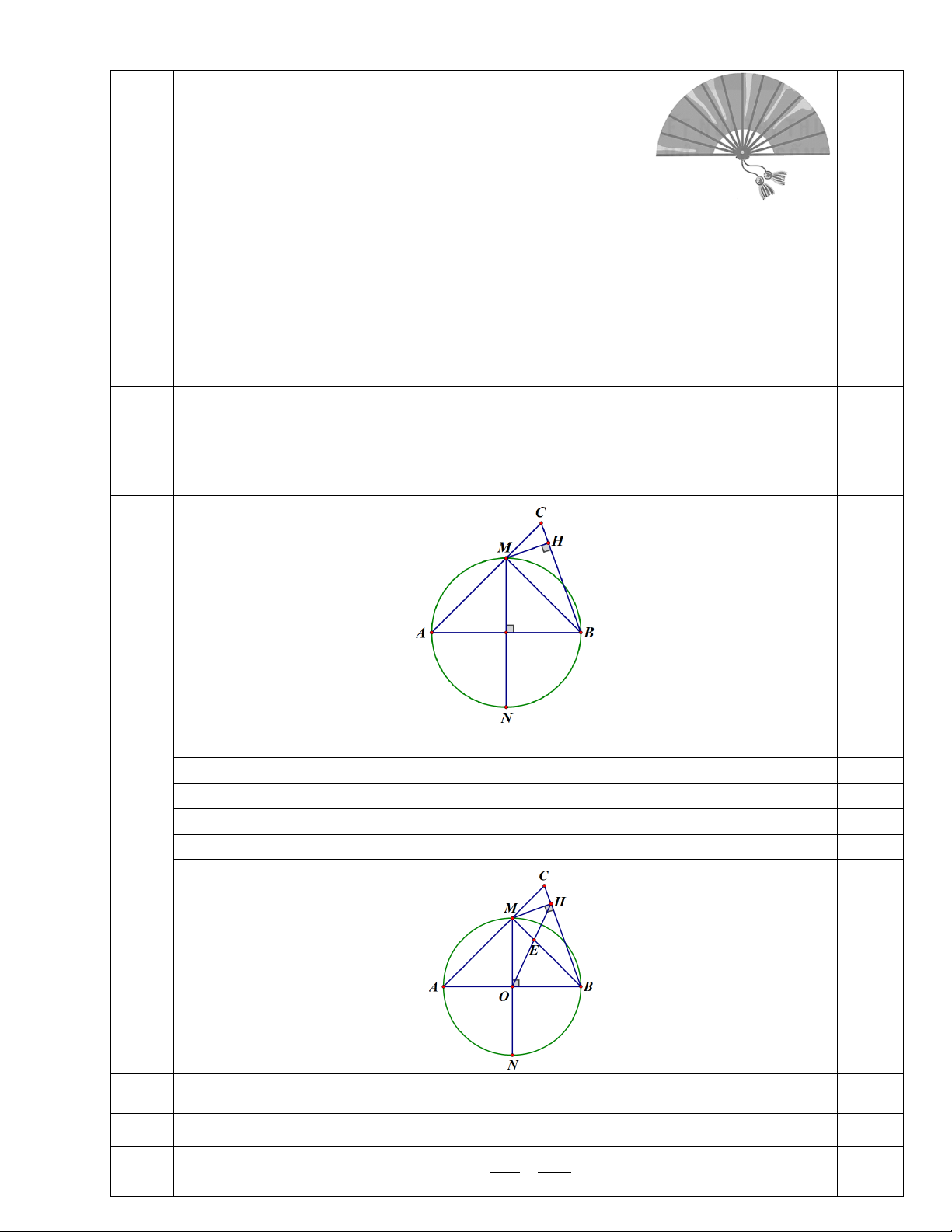
2) Cho đường tròn (O) có hai đường kính AB và MN vuông góc với
nhau. Trên tia đối của tia MA lấy điểm C khác điểm M. Kẻ MH vuông góc với BC (H thuộc BC).
a) Chứng minh B, O, M, H cùng thuộc một đường tròn.
b) MB cắt OH tại E. Chứng minh HO là tia phân giác của 
MHB và ME.MB = EB.MC.
c) Gọi giao điểm của đường tròn (O) với đường tròn ngoại tiếp MH ∆ C là K.
Chứng minh 3 điểm C, K, E thẳng hàng.
Bài V (0,5 điểm) Một cửa hàng phân phối bán ra 1000 sản phẩm mỗi năm. Mỗi lần đặt hàng có chi
phí là 50 USD và chi phí lưu kho là 2 USD cho một sản phẩm mỗi năm. Hãy tìm số lượng hàng hóa
cần đặt mỗi lần để tối thiểu hóa tổng chi phí đặt hàng và lưu kho.
-----------Hết----------
UBND HUYỆN THANH TRÌ
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM BÀI KIỂM TRA KHẢO SÁT MÔN: TOÁN 9
Năm học: 2024 – 2025 Bài Nội dung Điểm I
1) Biết rằng parabol y = ax2 ( a ≠ 0 ) đi qua điểm A(1; 2).
2,0đ a) Tìm hệ số a.
b) Tìm các điểm thuộc parabol có tung độ bằng y = 8
2) Một hộp đựng 20 tấm thẻ giống nhau được đánh số 1; 2; 3;…; 20. Bạn Nam
rút ngẫu nhiên một tấm thẻ trong hộp. Tính xác suất của các biến cố sau:
a) E : “Rút được tấm thẻ ghi số chia hết cho 3”.
b) F : “Rút được tấm thẻ ghi số không lớn hơn 5”. 1)
a) Thay x = 1; y = 2 vào y = ax2 ( a ≠ 0 ), tìm được a = 2 (thỏa mãn) 0,50 b) Ta có 2 2x = 8 2 x = 4 0,25 x = 2 ± 0,25
Với x = - 2 thì y = 8; với x = 2 thì y = 8. Vậy hai điểm là (-2; 8) và (2; 8) 2)
Có 20 kết quả có thể, đó là 1; 2; 3; …; 20. Do rút ngẫu nhiên nên các kết quả có thể này 0,50 là đồng khả năng.
a) Có 6 kết quả thuận lợi cho biến cố E là: 3; 6; 9; 12; 15; 18. Vậy 6 3 P(E) = = 20 10 0,25
b) Có 5 kết quả thuận lợi cho biến cố F là: 1; 2; 3; 4; 5.. Vậy 5 1 P(F) = = 20 4 0,25 II x x +
1,5đ Cho hai biểu thức: A = 1 + và B = 2
1 với x ≥ 0;x ≠1 x −1 x −1 x + x − 2
1) Tính giá trị của biểu thức B khi x = 9. +
2) Biết M = A : B. Chứng minh rằng M = x 2 . x +1
3) Tìm giá trị lớn nhất của M. + +
1) Thay x = 9 (TMĐKXĐ) vào biểu thức B ta có: B = 2 9 1 2.3 1 7 = = 9 + 9 − 2 9 + 3− 2 10 0,25
Vậy với x = 9 thì biểu thức B có giá trị là 7 10 0,25   + 2) Ta có: M = A : B = 1 x x  +   : 2
1 với x ≥ 0;x ≠1 x −  1 x 1
−  x + x − 2  x 1 x  + + 2 x +1 0,25 M  (  =  x − ) 1 ( x +  ) :
1  x − x + 2 x − 2  2 x +1 2 x +1 =
( x − )( x + ) : 1 1 ( x − ) 1 ( x + 2) ( 2 x + ) 1 ( x − ) 1 ( x + 2) x + 2 = ( = x − ) 1 ( x + ) 1 (2 x + ) 1 x +1 0,25 x + 3) M = 2 1 =1+ x +1 x +1
Vì x ≥ 0 nên x ≥ 0 do đó x +1≥1. Suy ra: 1 ≤1suy ra M ≤1+1 = 2 0,25 x +1
Dấu “=” xảy ra khi x = 0 (thỏa mãn ĐKXĐ). Vậy GTLN của M bằng 2 khi x = 0 0,25
III 1) Một người đi xe đạp từ A đến B cách nhau 24 km. Khi từ B trở về A, người đó 2,0đ
tăng vận tốc thêm 4 km/h so với lúc đi, vì vậy thời gian về ít hơn thời gian đi là
30 phút. Tính thời gian của người đi xe đạp lúc đi từ A đến B.
2) Cô Mai chia số tiền 1 tỉ đồng của mình cho hai khoản đầu tư. Sau một năm,
tổng số tiền lãi thu được là 63 triệu đồng. Lãi suất cho khoản đầu tư thứ nhất
là 5% một năm. Lãi suất cho khoản đầu tư thứ hai là 7% một năm. Tính số
tiền cô Mai đầu tư cho mỗi khoản.
1) Gọi vận tốc lúc đi của người đi xe đạp là x (km/h) (ĐK: x > 0) 0,25
Vận tốc lúc về của người đi xe đạp là: x + 4 (km/h)
Thời gian lúc đi của người đi xe đạp là: 24 (h). x 0,25
Thời gian lúc về của người đi xe đạp là: 24 (h) x + 4 0,25
Thời gian lúc về ít hơn lúc đi 30 phút = 1 (h) nên có phương trình: 24 24 1 − = 2 x x + 4 2
Biến đổi về phương trình: 2
x + 4x −192 = 0 . Tìm: x =12 (tmđk) ; x = 16 − (loại) 1 2
Vậy thời gian lúc đi của người đi xe đạp là 2 giờ. 0,25
Đổi 1 tỉ = 1000 triệu đồng
2) Gọi số tiền cô Mai đầu tư cho khoản đầu tư thứ nhất và khoản đầu tư thứ hai lần lượt là 0,25
x, y (triệu đồng) (0 < x, y < 1000)
Số tiền cô Mai đầu tư cho khoản đầu tư thứ nhất và khoản đầu tư thứ hai là 1000 triệu
đồng nên ta có phương trình: x + y = 1000 (1)
Sau một năm, số tiền lãi cho khoản đầu tư thứ nhất là: 5%.x = 0,05x (triệu đồng)
Sau một năm, số tiền lãi cho khoản đầu tư thứ hai là: 7%.y = 0,07y (triệu đồng) 0,25
Sau một năm, tổng số tiền lãi thu được là 63 triệu đồng, nên ta có phương trình: 0,05x + 0,07y = 63 (2) x + y = 1000 
0,05x + 0,07 y = 63
Từ (1), (2) ta có hệ phương trình: 0,25 x = 350  (TMÐK)  y = 650
Vậy số tiền cô Mai đầu tư cho khoản đầu tư thứ nhất là 350 triệu đồng và khoản đầu tư
thứ hai là 650 triệu đồng. 0,25
IV 1) Một chiếc quạt giấy khi xòe ra có dạng nửa hình tròn
4,0đ bán kính 20cm. Tính diện tích phần giấy của chiếc quạt,
biết rằng khi gấp lại, phần giấy có chiều dài 15cm (cho
π ≈ 3,14 ; làm tròn kết quả đến hàng đơn vị của cm2).
2) Cho đường tròn (O) có hai đường kính AB và MN
vuông góc với nhau. Trên tia đối của tia MA lấy điểm C
khác điểm M. Kẻ MH vuông góc với BC (H thuộc BC).
a) Chứng minh B, O, M, H cùng thuộc một đường tròn.
b) MB cắt OH tại E. Chứng minh HO là tia phân giác của 
MHB và ME.MB = EB.MC.
c) Gọi giao điểm của đường tròn (O) với đường tròn ngoại tiếp ∆MHC là K.
Chứng minh 3 điểm C, K, E thẳng hàng. 1)
Bán kính của đường tròn nhỏ là: 20 – 15 = 5cm 0,25
Diện tích hình vành khuyên tạo bởi hai đường tròn bán kính 20cm và 5cm là: 2 2 π (20 − 5 ) = 375π (cm2) 0,50
Diện tích phần giấy của chiếc quạt là: 375π : 2 =187,5π ≈ 589 (cm2) 0,25 2) o 0,25 Vẽ hình đến câu a
Chứng minh B, O, M, H cùng thuộc một đường tròn. 0,75
- Gọi I là trung điểm của MB. 0,25
- Chứng minh: IM = IB = IH = IO 0,25
- Chứng minh 4 điểm B, M, H, O thuộc đường tròn (I) 0,25 b)
- Chứng minh:  =   =   =  MHO MB ; O OHB MB ; O OMB OBM 0,25
Từ đó suy ra HO là tia phân giác của  MHB 0,25
- Có HO là tia phân giác của  MHB nên ME MH = 0,25 EB HB - Chứng minh: MH ∆
B đồng dạng C
∆ MB (g.g) MH MC ⇒ = HB MB 0,25
- Lập luận chứng minh được: ME.MB = EB.MC c)
Chứng minh C, E, K thẳng hàng 1,0 - Chứng minh:  90O CKM = ;  90O MKN = 0,25 ⇒  +  CKM N =180O MK
⇒ C, K, N thẳng hàng (1) 0,25 - Chứng minh MC ∆ E ∽ B
∆ NE (c.g.c) 0,25
⇒ 3 điểm C, E, N thẳng hàng (2). Từ (1) và (2) ⇒ 3 điểm C, E, K thẳng hàng 0,25 V
Một cửa hàng phân phối bán ra 1000 sản phẩm mỗi năm. Mỗi lần đặt hàng có chi
0,5đ phí là 50 USD và chi phí lưu kho là 2 USD cho một sản phẩm mỗi năm. Hãy tìm số
lượng hàng hóa cần đặt mỗi lần để tối thiểu hóa tổng chi phí đặt hàng và lưu kho.
Gọi x là số lượng hàng hóa đặt mỗi lần (x > 0)
Vì hàng tồn kho luôn giảm dần từ x sản phẩm đến 0 sản phẩm nên chi phí lưu kho là x + 0 ⋅ 2 = x (USD) 2
Chi phí đặt hàng của cửa hàng là 1000 50000 ⋅50 = (USD) x x
Tổng chi phí của cửa hàng là: 50000 T = x + (USD) x
Chứng minh và áp dụng bất đẳng thức Cosi ta có T ≥ 200 5 0,25
Dấu = xảy ra khi x =100 5 ≈ 224
Vậy số lượng hàng hóa cần đặt mỗi lần là khoảng 224 sản phẩm để tối thiểu hóa tổng 0,25 chi phí.
* Lưu ý: HS làm cách khác đúng vẫn cho điểm tối đa!