Đề khảo sát tháng 5 Toán 9 năm 2024 – 2025 phòng GD&ĐT Gia Lâm – Hà Nội

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT THÁNG 5 HUYỆN GIA LÂM MÔN: TOÁN, LỚP 9 NĂM HỌC 2024 - 2025 (Đề có 02 trang)
Thời gian làm bài: 120 phút
Bài I. (1,5 điểm)
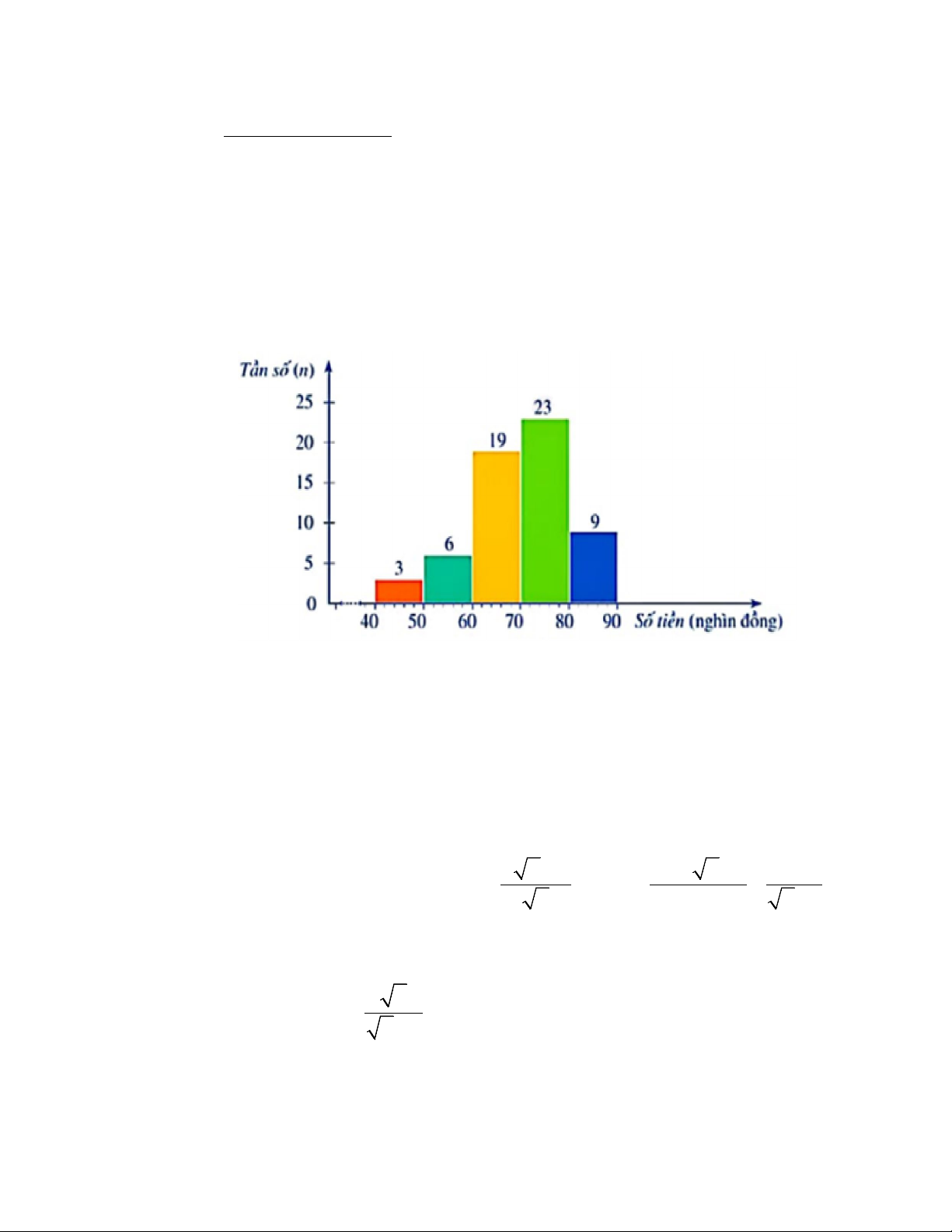
1) Một cửa hàng sách thống kê số tiền (đơn vị: nghìn đồng) mà 60 khách hàng
mua sách ở cửa hàng đó trong một ngày. Số liệu được ghi lại trong biểu đồ tần số ghép nhóm dưới đây:
Tìm tần số ghép nhóm và tần số tương đối ghép nhóm của nhóm [40; 50).
2) Một chiếc hộp chứa 3 viên bi: 1 viên bi xanh, 1 viên bi đỏ, 1 viên bi vàng.
Các viên bi có cùng kích thước và cùng khối lượng. Bạn An lần lượt lấy ra một cách
ngẫu nhiên từng viên bi từ trong hộp cho đến khi hết bi.
a) Xác định không gian mẫu của phép thử.
b) Tính xác suất của biến cố A: “Viên bi màu xanh được lấy ra cuối cùng”.
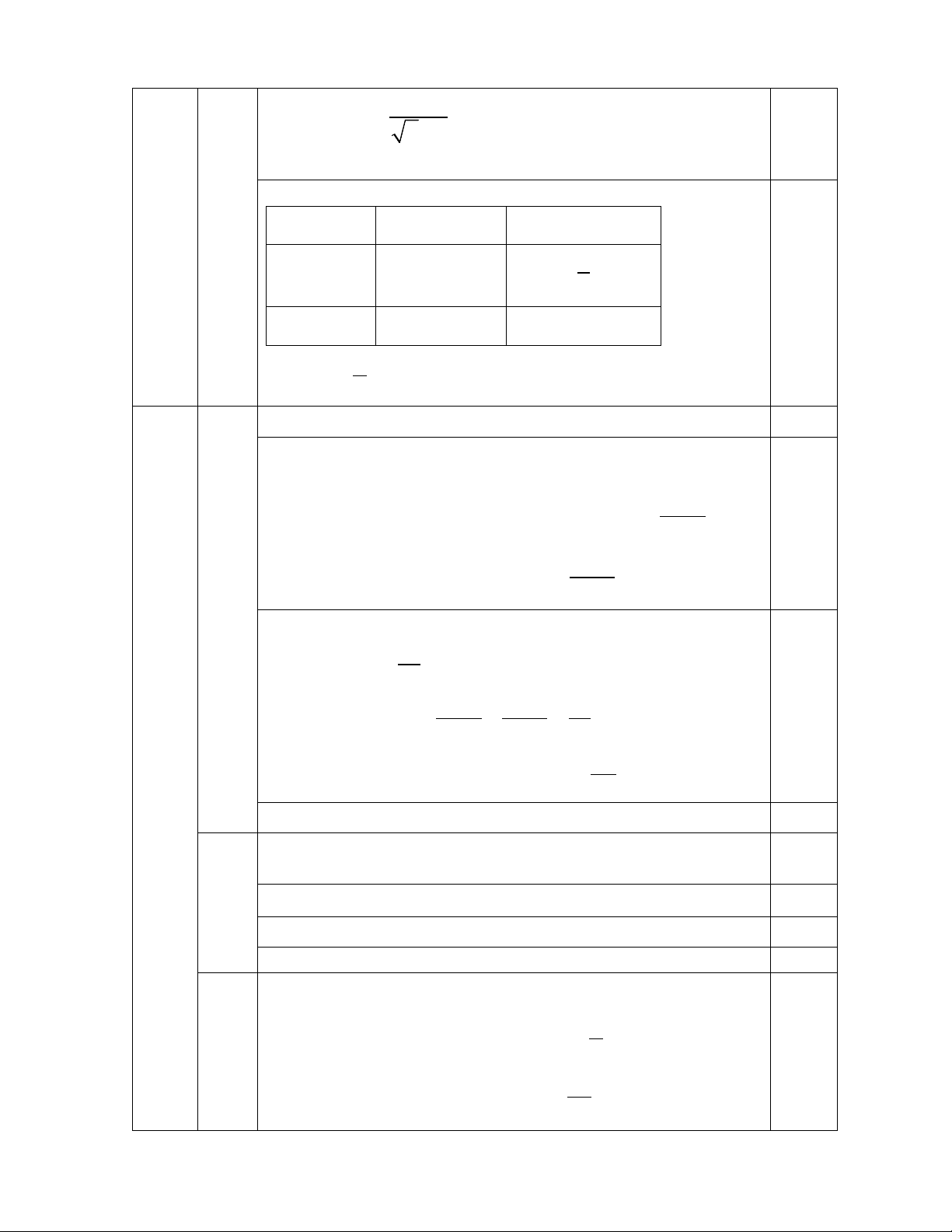
Bài II. (1,5 điểm). Cho hai biểu thức 2 x + 5 A = và x − 2 x −1 1 B = + với x x −1 x −1
x > 0 và x ≠1.
1) Tính giá trị của biểu thức A khi x =16. 2) Chứng minh x B = . x +1 3) Đặt M = .
A B . Tìm tất cả các giá trị của x để M nhận giá trị nguyên.
Bài III. (2,5 điểm).
1) Một ca nô xuôi dòng từ A đến B cách nhau 63 km, rồi ngược dòng trở lại
56 km. Tổng thời gian cả đi lẫn về của ca nô hết 3 giờ 45 phút. Tính vận tốc thực
của ca nô biết vận tốc dòng nước là 4 km/h.
2) Một tam giác vuông có độ dài cạnh huyền bằng 10 cm, độ dài hai cạnh góc
vuông hơn kém nhau 2 cm. Tính độ dài cạnh góc vuông nhỏ.
3) Cho phương trình 2
2x − 7x −1= 0 có hai nghiệm phân biệt x , x . Tính giá 1 2 trị của biểu thức 2 2
S = x + x − 3x x . 1 2 1 2 Bài IV (4,0 điểm)
1) Có một cốc hình trụ có đường kính đáy bằng 10 cm đựng
nước với mực nước trong cốc cao 15 cm và một viên bi sắt hình cầu có bán kính là 2 cm.
a) Tính thể tích lượng nước trong cốc (bỏ qua bề dày của thành
cốc, lấy π ≈ 3,14).
b) Nếu thả viên bi vào cốc thì lượng nước trong cốc dâng lên
bao nhiêu milimet, biết rằng viên bi chìm hẳn trong nước và nước không bị tràn ra ngoài ?
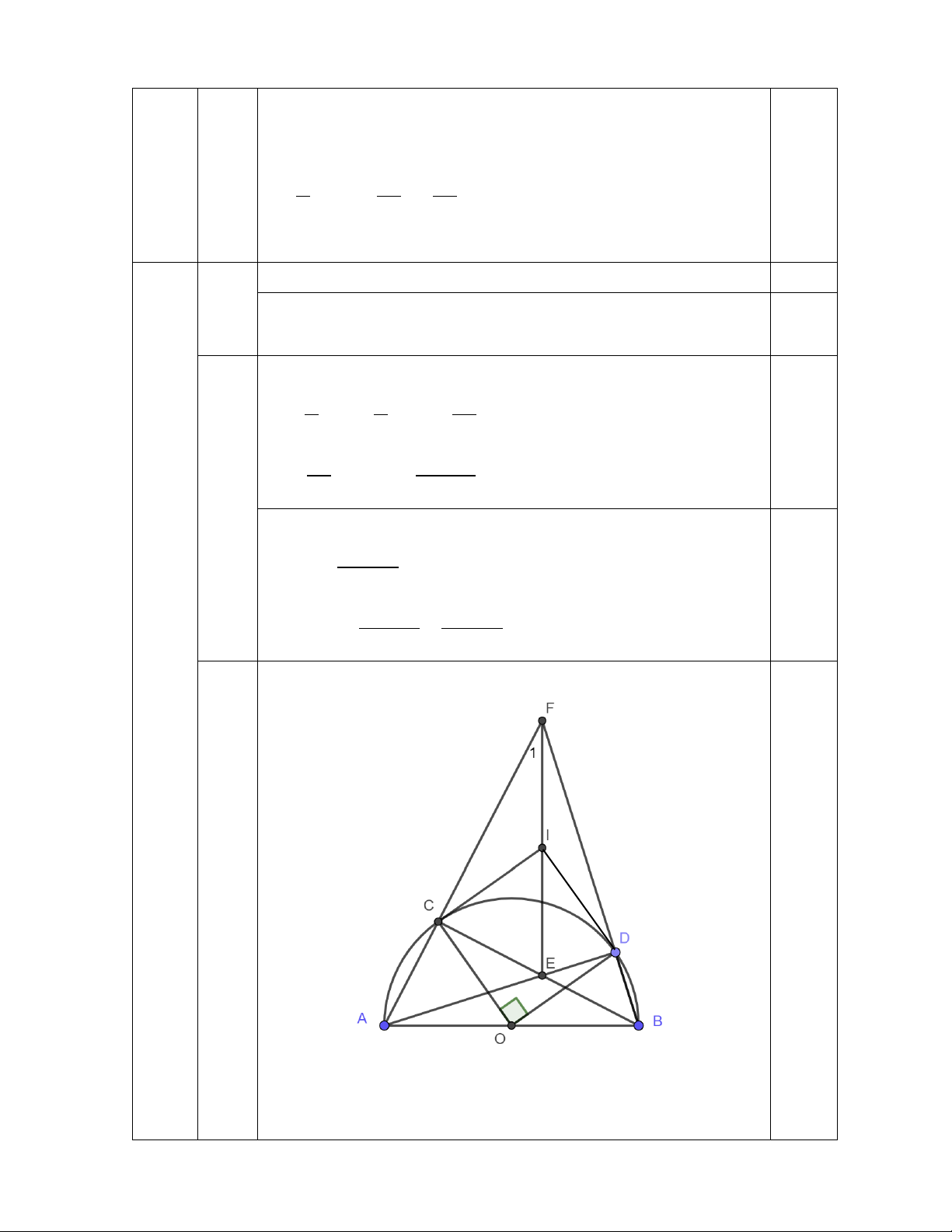
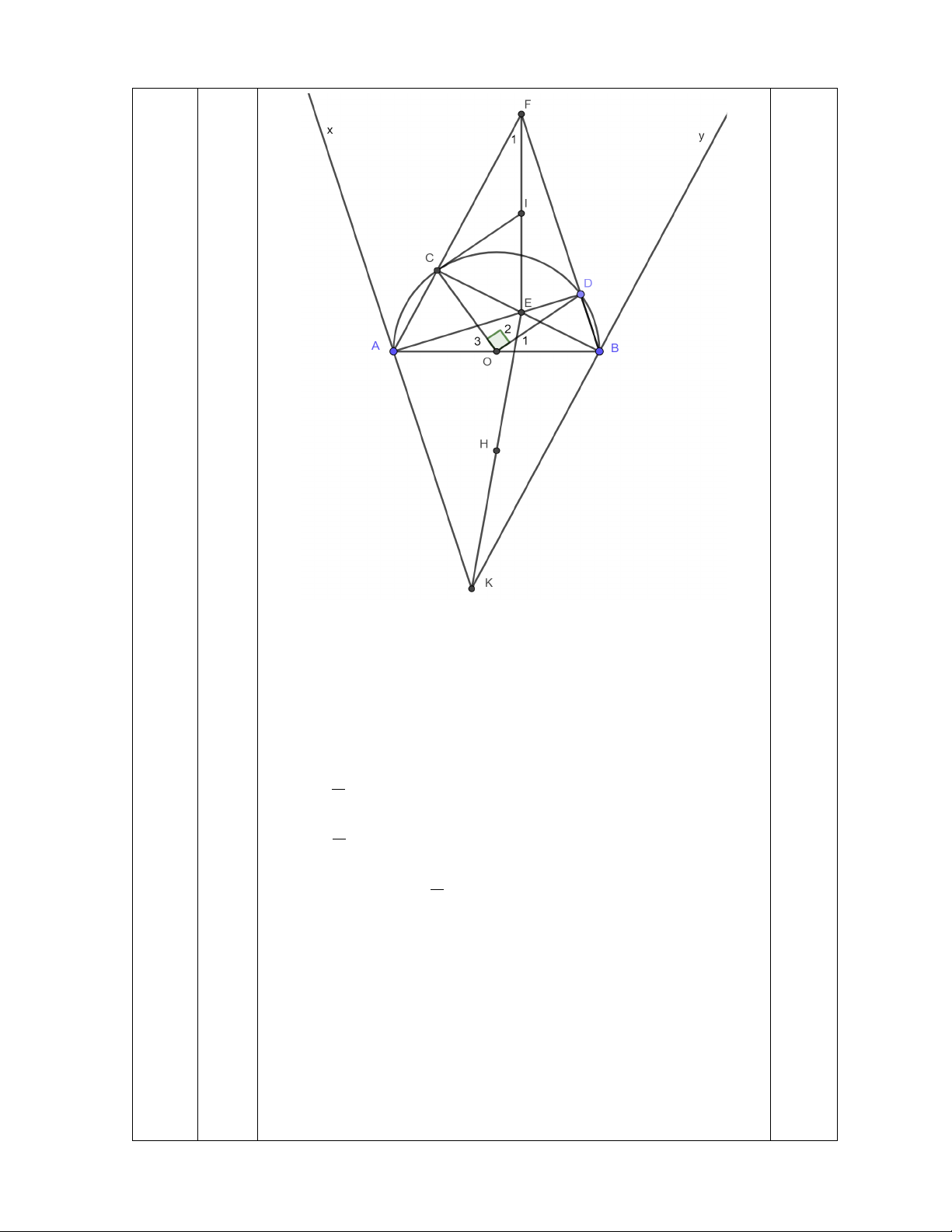
2) Cho nửa đường tròn (O) đường kính AB = 2R và C là điểm bất kì nằm
trên nửa đường tròn sao cho C khác A và AC < CB . Điểm D thuộc cung nhỏ BC sao cho  0
COD = 90 . Gọi E là giao điểm của AD và BC , F là giao điểm của AC và
BD , I là trung điểm của EF .
a) Chứng minh: CEDF là tứ giác nội tiếp.
b) Chứng minh: FC.FA = F .
D FB và IC là tiếp tuyến của (O).
c) Khi vị trí điểm C thay đổi thỏa mãn điều kiện bài toán, điểm E thuộc đường tròn cố định nào?
Bài V. (0,5 điểm) Ở một rạp xiếc, người ta có bán hai loại vé: Vé người lớn 100
nghìn đồng và vé trẻ em có giá 50 nghìn đồng. Một ngày nọ, vị quản lý nói rằng đã
có ít hơn 400 vé được bán ra và tổng số tiền thu được là 23 triệu 250 nghìn đồng.
Hỏi có ít nhất bao nhiêu vé người lớn đã được bán ra trong ngày hôm đó?
(Cán bộ coi thi không giải thích gì thêm)
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM HUYỆN GIA LÂM
ĐỀ KHẢO SÁT THÁNG 5 MÔN: TOÁN, LỚP 9 NĂM HỌC 2024 - 2025 Bài câu Đáp án Điểm 1
- Tần số ghép nhóm của nhóm [40; 50) là 3 0,25
- Tần số tương đối ghép nhóm của nhóm [40; 50) là 3 .100% 0,25 = 5% 60
Bài I 2.a Không gian mẫu của phép thử là:
Ω = {(xanh, đỏ, vàng); (xanh, vàng, đỏ); (vàng, xanh, đỏ); 0,5
(vàng, đỏ, xanh); (đỏ, vàng, xanh); (đỏ, xanh, vàng)}.
2.b Có hai kết quả thuận lợi cho biến cố A là: (vàng, đỏ, 0,25 xanh), (đỏ, vàng, xanh)
Vì các kết quả là đồng khả năng nên xác suất biến cố A 0,25 là: P(A) = 2 1 = 6 3 Bài 1
Thay x =16 (TM) vào A, ta có: 0,25 II 2 16 5 2.4 5 13 A + + = = = 16 4 4 Vậy 13 A = với x =16. 4 2 x − 2 x −1 1 0,25 B = + x −1 x −1 x 0,25 B − x = x −1 x ( x − )1 x 0,25 B = ( = x − )1( x + )1 x +1 3 Ta có 0,25 2 x + 5 x 2 x + 5 3 M = . A B = . = = 2 + x x +1 x +1 x +1 suy ra 3 2 < 2 + < 5 x +1
Để M nhận giá trị nguyên thì M ∈{3, } 4
Từ đó ta có bảng giá trị: 0,25 M 3 4 x 4 1 4 Kiểm tra thỏa mãn thỏa mãn Vậy 1 x  ;4 ∈
thì M đạt giá trị nguyên. 4    0,25 1
Gọi vận tốc thực của ca nô là x (km/h; x > 4) 0,25
Vận tốc ca nô khi xuôi dòng là x + 4 (km/h) 0,25
Vận tốc ca nô khi ngược dòng là x − 4 (km/h)
Thời gian ca nô đi xuôi dòng từ A đến B là : 63 (h) x + 4
Thời gian ca nô đi ngược dòng là : 56 (h) x − 4
Theo đề bài, tổng thời gian cả đi lẫn về của ca nô hết 3 0,25 giờ 45 phút ( 15 =
giờ). Ta có phương trình: 4 63 56 15 + = x + 4 x − 4 4
Giải ra, ta được: x = 32 (TM) và 4 x − = (Không TM) 15
Vậy vận tốc thực của ca nô là 32 km/h 0,25 2
Gọi độ dài cạnh góc vuông nhỏ là x ( x > 0) 0,25
thì cạnh góc vuông lớn là x + 2 (cm)
Theo định lý Pythagore, ta có : 2 2 x + (x + 2) =100 0,25
Giải phương trình, ta được x = 6(tm); x = 8 − 1 2 (loại) 0,25
Độ dài cạnh góc vuông nhỏ là: 6 cm . 0,25 3
Do phương trình có hai nghiệm phân biệt x , x 1 2  7 x + x =  0,25 1 2
Theo hệ thức Viète, ta có:  2  1 x x −  = 1 2  2 Ta có: 2 2 2
S = x + x − 3x x = x + x − 5x x 1 2 1 2 ( 1 2) 1 2 0,25 2  7   1 −  59 = −  5. =  2  2      4 Kết luận
Bài 1-a Bán kính đáy cốc là: R = 10:2 = 5 (cm) 0,25 IV
Thể tích nước trong cốc là: 0,25
V = πR2h ≈ 3,14.52.15 = 1177,5 (cm3)
1-b Thể tích của viên bi là: 0,25 4 3 4 3 32
V = πr = .π.2 = π (cm3) 3 3 3
Đổi 32π cm3 = 32 000π mm3 3 3
Gọi chiều cao mực nước dâng lên là x (mm), ta có: 0,25 2 32 000 π R x = π 3 suy ra 32 000 32 000 x = = ≈ 4 (mm) 2 2 3.R 3.50 Hình 0,25
(vẽ đúng đến ý a và b) 2-a Xét (O) có: +  0
ACB = 90 (góc nội tiếp chắn nửa đường tròn) nên BC ⊥ F Α , suy ra  0 ECF = 90 E
∆ CF vuông tại C có CI là đường trung tuyến nên EF
CI = IE = IF = 2 0,25 +  0
ADB = 90 (góc nội tiếp chắn nửa đường tròn) nên
AD ⊥ BF , suy ra  0 EDF = 90 E
∆ DF vuông tại D có DI là đường trung tuyến nên EF 0,25
DI = IE = IF = 2
Khi đó CI = DI = IE = IF , suy ra 4 điểm C, D, E, F cùng
thuộc đường tròn tâm I đường kính EF. 0,25
Vậy tứ giác CEDF là tứ giác nội tiếp. 0,25
2-b - Chứng minh được F
∆ DA đồng dạng với F ∆ CB (g.g) nên FA FD 0,25 =
(cặp cạnh tương ứng tỉ lệ) FB FC
suy ra FC.FA = F . D FB (đpcm) 0,25 - Ta có
CI = IF (cmt) nên IC
∆ F cân tại I, suy ra  =  F FCI (1) 1 Xét OA ∆
C cân tại O nên  =  CAO OCA (2) 0,25 Xét A
∆ BF ta có BC, AD là hai đường cao cắt nhau tại E
Nên E là trực tâm của A ∆ BF
Do đó EF ⊥ AB , suy ra  +  0 F CAO = 90 (3) 1 0,25
Từ (1); (2); (3) suy ra  +  0 ICF OCA = 90 Do đó  0
OCI = 90 hay OC ⊥ CI Vậy
CI là tiếp tuyến của đường tròn (O) 0,25 2-c Ta có  +  +  O O O =180° 1 2 3  O = 90° 2  +  nên O O = 90° 1 3 Xét (O) ta có:  1 =  DAB O 1 2  1 =  ABC O 3 2  +  1
nên DAB ABC = ⋅90° = 45° 2 Xét A
∆ EB ta có  +  0 DAB ABC = 45 nên  0 AEB =135
Qua A kẻ đường thẳng vuông góc với AE tại A, qua B kẻ
đường thẳng vuông góc với BE tại B, hai đường thẳng này cắt nhau tại K.
Ta chứng minh được tứ giác EAKB nội tiếp. Suy ra  +  0 AKB AEB =180 Mà  0 AEB =135 nên  0 AKB = 45
Gọi H là trung điểm của EK.
Xét đường tròn tâm H đường kính EK có  1 =  AKB 2 AHB , suy ra  0 AHB = 90 0,25 Xét A
∆ HB vuông tại H có HA = HB (bán kính đường
tròn tâm H ) nên A
∆ HB vuông cân tại H .
Mà đoạn thẳng AB cố định nên H cố định.
Áp dụng định lí Pytago vào A ∆ HB ta có: 2 2 2
HA + HB = AB 2 2 2HA = 4R 2 2 HA = 2R HA = 2R
Vậy khi C thay đổi thì E chạy trên đường tròn (H; 2R ) cố định. 0,25 Bài
Gọi a và b theo thứ tự là số vé người lớn và số vé trẻ em V
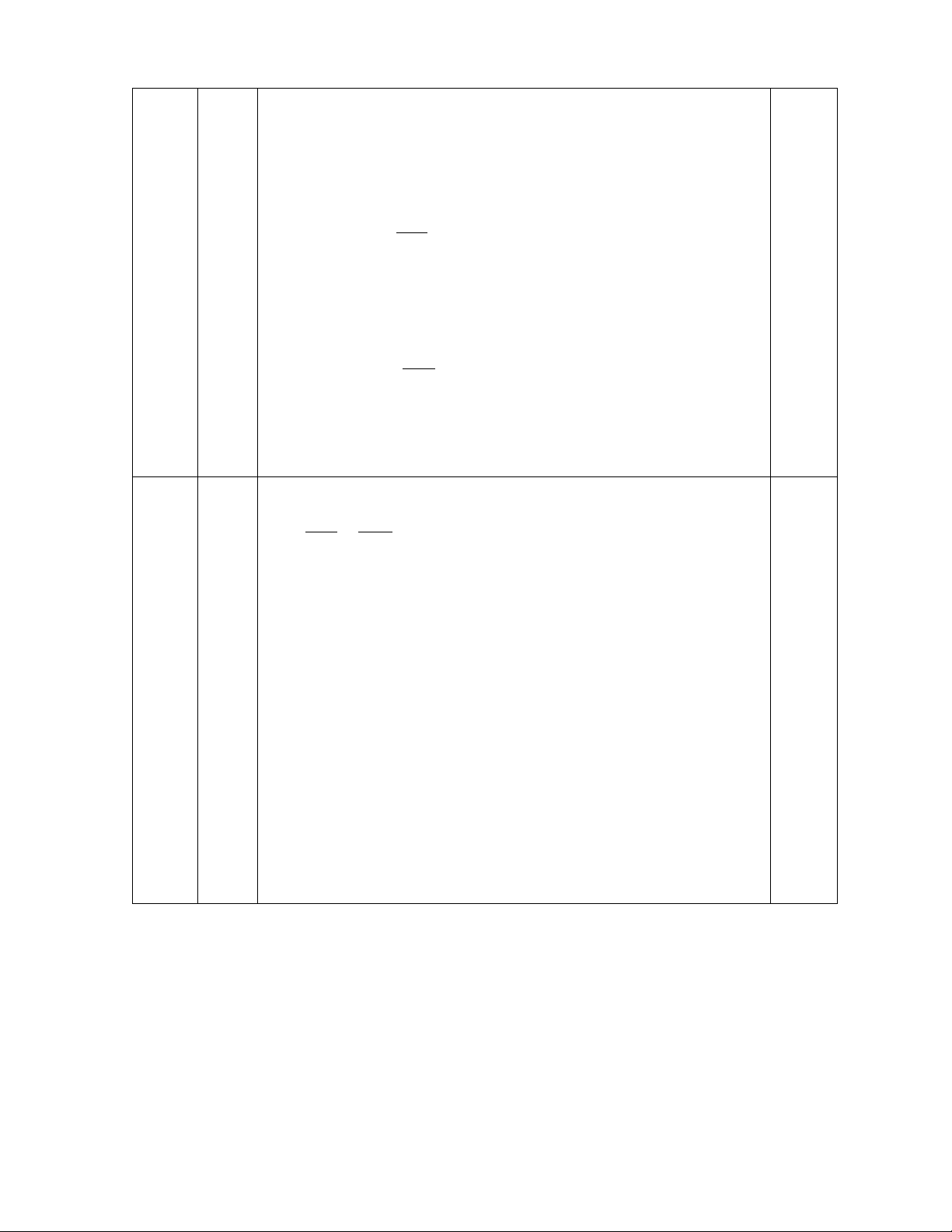
được bán ra trong ngày hôm đó (a,b∈ N ) Theo đề bài, ta có:
a + b < 400
a + b < 399 suy ra 100    a + 50b = 23250 2a + b = 465
Từ đó suy ra a ≥ 66 0,25
Dấu bằng xảy ra nếu có 66 vé người lớn và 333 vé trẻ em đã được bán ra.
Vậy có ít nhất 66 vé người lớn đã được bán ra trong ngày hôm đó. 0,25
(Học sinh có cách giải khác đúng vẫn cho điểm tương đương)
Xem thêm: KHẢO SÁT CHẤT LƯỢNG TOÁN 9
https://thcs.toanmath.com/khao-sat-chat-luong-toan-9
Document Outline

• Đề KS tháng 5
• Hướng dẫn chấm môn Toán_KS tháng 5
• KS 9