Đề khảo sát Toán 11 đầu năm học 2019 – 2020 trường Thuận Thành 1 – Bắc Ninh

Với mục đích kiểm tra đánh giá toàn diện lại các kiến thức Toán 10 đối với học sinh lớp 11, để chuẩn bị cho chương trình Toán 11 năm học 2019 – 2020, trường THPT Thuận Thành số 1, tỉnh Bắc Ninh đã tổ chức kỳ thi khảo sát chất lượng đầu năm học 2019 – 2020 môn Toán 11.

33 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

20 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
1/6 - Mã đề 832
SỞ GD&ĐT BẮC NINH
TRƯỜNG THPT THUẬN THÀNH SỐ 1
(Đề thi có 06 trang)
ĐỀ KHẢO SÁT ĐẦU NĂM HỌC 2019-2020
MÔN TOÁN – LỚP 11
Thời gian làm bài : 90 phút (không kể thời gian phát đề)
Họ và tên học sinh :..................................................... Số báo danh : ...................
Câu 1. Cho hai điểm
4;1
A
,
2;3
B
. Phương trình đường tròn đường kính
AB
là
A.
2 2
3 1 5
x y
. B.
2
2
1 20
x y
.
C.
2 2
1 2 10
x y
. D.
2 2
1 2 10
x y
.
Câu 2. Số nghiệm của phương trình
2 4 1 0
x x
là
A.
2
. B. Vô số. C.
1
. D.
0
.
Câu 3. Cho
, , ,
a b c d
hữu hạn,
4 3
3 1 2
f x
x x
. Tập nghiệm của bất phương trình
0
f x
có dạng
A.
; ;a b c

. B.
; ;
a b c
 . C.
; \ ;
a b
  . D.
; ;
a b c d
.
Câu 4. Cho góc
thỏa mãn
tan 2
. Giá trị của biểu thức
2 2
2 2
2sin 3sin .cos 4cos
5sin 6cos
P
là
A.
9
13
P
. B.
9
65
P
. C.
24
29
P
. D.
9
65
P
.
Câu 5. Cho hai điểm
1;2
A ,
3;1
B và đường thẳng
1
:
2
x t
y t
. Tọa độ điểm
C
thuộc
để tam giác
ABC
cân tại
C
là
A.
7 13
;
6 6
. B.
7 13
;
6 6
. C.
13 7
;
6 6
. D.
5 11
;
6 6
.
Câu 6. Tập các giá trị của tham số
m
để phương trình
2 2
1 2 0
m x x m
có hai nghiệm trái dấu là
A.
1;1
. B.
; 1 0;1

. C.
; 1 0;1

. D.
1;0 1;
.
Câu 7. Trong các công thức sau, công thức đúng là
A.
cos cos .cos sin .sin
a b a b a b
. B.
sin sin .cos cos .sin
a b a b a b
.
C.
sin sin .sin cos .cos
a b a b a b
. D.
cos cos .cos sin .sin
a b a b a b
.
Câu 8. Tọa độ các tiêu điểm của Elip
2 2
1
9 1
x y
là
A.
1 2
3 0 3 0
; , ;
F F
. B.
1 2
8 0 8 0
; , ;
F F .
C.
1 2
8 0 0 8
; , ;F F . D.
1 2
0 2 2 0 2 2
; , ;F F .
Mã đề 832
2/6 - Mã đề 832
x
y
O
1

2

Câu 9. Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số được liệt
kê ở bốn phương án A, B, C, D dưới đây. Hàm số đó là
A.
2
2 4 1
y x x
. B.
2
2 2
y x x
.
C.
2
2 1
y x x
. D.
2
2 4 1
y x x
.
Câu 10. Cho tam giác
ABC
có
6cm, 10
AB BC cm
. Độ dài đường trung tuyến xuất phát từ đỉnh
A
của
tam giác bằng
5
cm
. Diện tích tam giác
ABC
là
A. 30cm. B. 48cm. C. 24cm. D. 60cm.
Câu 11. Số đo góc
o
22 30
được đổi sang rađian là
A.
6
. B.
7
12
. C.
8
. D.
5
.
Câu 12. Rút gọn biểu thức
tan sin
sin cot
P
ta được kết quả là
A.
2sin
. B.
sin
. C.
cos
. D.
tan
.
Câu 13. Cho hai góc nhọn
,
a b
thỏa mãn
1 1
cos ;cos
3 4
a b
. Giá trị của biểu thức
cos( ).cos( )
P a b a b
là
A.
115
144
. B.
113
144
. C.
117
144
. D.
119
144
.
Câu 14. Phương trình
2
0 0
ax bx c a
có hai nghiệm âm phân biệt khi và chỉ khi
A.
0
0
0
P
S
. B.
0
0
P
. C.
0
0
0
P
S
. D.
0
0
0
a
S
.
Câu 15.
2
và
3
là hai nghiệm của phương trình
A.
2
2 3 6 0
x x
. B.
2
2 3 6 0
x x
.
C.
2
2 3 6 0
x x
. D.
2
2 3 6 0
x x
.
Câu 16. Cho
2 3
cos , 2
3 2
. Giá trị của
tan
là
A.
5
2
. B.
5
2
. C.
5
4
. D.
1
2
.
Câu 17. Góc giữa hai đường thẳng
1
:2 10 0
x y
và
2
: 3 9 0
x y
là
A.
0
0
. B.
0
90
. C.
0
60
. D.
0
45
.
Câu 18. Cho tam giác
ABC
biết
1; 2
A
,
5; 4
B
,
1;4
C
. Đường cao
'
AA
của tam giác
ABC
có
phương trình là
3/6 - Mã đề 832
A.
3 4 11 0
x y
. B.
8 6 20 0
x y
. C.
3 4 11 0
x y
. D.
8 6 4 0
x y
.
Câu 19. Tập nghiệm của bất phương trình
3 2 1
x
là
A.
1;2
. B.
1;2
. C.
;1 2;
 
. D.
;1 2;
 
.
Câu 20. Cho điểm
1; 1
M
và đường thẳng
:3 4 0
x y m
. Số giá trị
0
m
sao cho khoảng cách từ
M
đến
bằng
1
là
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 21. Cho đường tròn
2 2
: 3 1 5
C x y
. Tiếp tuyến của
C
song song với đường thẳng
: 2 10 0
d x y
có phương trình là
A.
2 0
x y
hoặc
2 10 0
x y
. B.
2 1 0
x y
hoặc
2 1 0
x y
.
C.
2 1 0
x y
. D.
2 0
x y
.
Câu 22. Phương trình tiếp tuyến tại
3 4
( ; )
M
của đường tròn
2 2
2 4 3 0
( ):C x y x y
là
A.
1 0
x y
. B.
1 0
x y
. C.
7 0
x y
. D.
7 0
x y
.
Câu 23. Tập nghiệm của hệ bất phương trình
2
2 1 5
3 2
3 5 0
2 1 0
x x
x x
x x
là
A.
13;5
. B.
1;5
. C.
3;5 \ 1
. D.
3;5 \ 1
.
Câu 24. Số nghiệm nguyên và lớn hơn
4
của bất phương trình
2
4 2 0
x x
là
A. 3. B. 4. C. 5. D. Vô số.
Câu 25. Phương trình tham số của đường thẳng đi qua 2 điểm
2;1 , 1;0
A B
là
A.
1 3
x t
y t
. B.
2 3
1 2
x t
y t
. C.
1 3
x t
y t
. D.
2 3
1
x t
y t
.
Câu 26. Hai cạnh của hình chữ nhật nằm trên hai đường thẳng có phương trình
4 – 3 5 0, 3 4 – 5 0
x y x y
. Một đỉnh của hình chữ nhật là
2;1
A . Diện tích của hình chữ nhật là
A. 3. B. 4. C. 1. D. 2.
Câu 27. Đường thẳng
d
có một vectơ chỉ phương là
2;1
u
. Một vectơ pháp tuyến của
d
là
A.
1; 2
n
. B.
1;2
n
. C.
3;6
n
. D.
3;6
n
.
Câu 28. Cho bất phương trình
2
3
1 *
4
x
x
và các mệnh đề
(I):
2
3x
* 1 1
4
x
.(II): Điều kiện xác định của
*
là
2
x
.
(III):
2
3x
* 1
4
x
.(IV):
2
* 3 4
x x
.
4/6 - Mã đề 832
Số mệnh đề đúng trong các mệnh đề trên là
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 29. Biết
, ,
A B C
là các góc trong tam giác
ABC
. Mệnh đề đúng là
A.
cot cot
A C B
. B.
sin sin
A C B
. C.
tan tan
A C B
. D.
cos cos
A C B
.
Câu 30. Mệnh đề sai trong các mệnh đề sau là
A.
2 2
sin cos 1
x x
. B.
4 4 2 2
sin cos 1 2sin cos
x x x x
.
C.
6 6 2 2
sin cos 1 3sin cos
x x x x
. D.
8 8 2 2
sin cos 1 4sin cos
x x x x
.
Câu 31. Rút gọn biểu thức
cos 2020 2019
x
ta được kết quả là
A.
sin 2020
x
. B.
cos2020
x
. C.
sin2020
x
. D.
cos2020
x
.
Câu 32. Nếu tam giác
ABC
có
2 2 2
a b c
thì
A.
A
là góc vuông. B.
A
là góc tù.
C.
A
là góc nhỏ nhất. D.
A
là góc nhọn.
Câu 33. Khi giải phương trình
2
3 1 2 1 1
x x
, một học sinh làm theo các bước sau:
Bước 1: Bình phương hai vế của phương trình
1
ta được:
2
2
2
3 1 2 1x x .
Bước 2: Khai triển và rút gọn
2
ta được:
2
0
4 0
4
x
x x
x
.
Bước 3: Khi
0
x
, ta có
2
3 1 0
x
. Khi
4
x
, ta có
2
3 1 0
x
.
Vậy tập nghiệm của phương trình là
0;–4
.
Nhận xét đúng nhất về lời giải trên là
A. Sai ở bước 2. B. Sai ở bước 3. C. Sai ở bước 1. D. Đúng.
Câu 34. Trong các khẳng định sau, khẳng định đúng là
A.
2
1 3 1 9
x x x x
. B.
2 2
x x
.
C.
( 2)
2 2
2
x x
x
x
. D.
2 2
3 2 2 3
x x x x x x
.
Câu 35. Biết bất phương trình
2
1 9 3
m x x m
nghiệm đúng với mọi
x
khi
0
m m
. Khẳng định đúng
nhất về
0
m
là
A.
0
2
m
. B.
0
5; 1
m
.
C. Có đúng hai giá trị
0
m
. D.
0
0;5
m .
Câu 36. Cho hình thoi
ABCD
có diện tích
20
S
, một đường chéo có phương trình
: 2 4 0
d x y
và
1; 3
D
. Biết đỉnh
A
có tung độ âm. Tọa độ đỉnh
A
là
A.
1; 2
A
. B.
5; 6
A
. C.
11; 18
A
. D.
1;2
A
.
5/6 - Mã đề 832
Câu 37. Cho đường tròn
2 2
: 4 2 1 0
C x y x y
và đường thẳng
d
có phương trình
1 0
x y
. Gọi
;
M a b
là điểm thuộc đường thẳng
d
sao cho từ
M
kẻ được hai tiếp tuyến vuông góc đến
C
. Khi đó
A.
a b
. B.
2 2
4
a b
. C.
2
2
a
. D.
2
4
a
.
Câu 38. Số giá trị
1
m
để phương trình
2
1
x x m
có đúng hai nghiệm là
A. 0. B. Vô số. C. 1. D. 2.
Câu 39. Điều kiện cần và đủ của tham số
m
để phương trình
2
2 2
2 4 – 2 2 4 4 –1 0
x x m x x m
có
đúng hai nghiệm là
A.
2 3
2 3
m
m
. B.
3 4
m
. C.
2 3 4
m
. D.
2 3
4
m
m
.
Câu 40. Cho hai đường thẳng
1 2
: 1 0, : 2 1 0
x y x y
và điểm
2;1
P
. Gọi
là đường thẳng đi
qua
P
và cắt hai đường thẳng
1 2
,
tại hai điểm
,
A B
sao cho
P
là trung điểm của
AB
. Phương trình của
là
A.
4 6 0
x y
. B.
4x 9 0
y
. C.
4x 7 0
y
. D.
9 14 0
x y
.
Câu 41. Từ hai vị trí
,
A B
của một tòa nhà, người
ta quan sát đỉnh
C
của một ngọn núi. Biết rằng độ
cao
70
AB m
, phương nhìn
AC
tạo với phương
nằm ngang một góc
0
30
, phương nhìn
BC
tạo với
phương nằm ngang một góc
0
15 30'
. Ngọn núi có
độ cao so với mặt đất gần nhất với giá trị sau
A.
135
m
. B.
195
m
.
C.
234
m
. D.
165
m
.
Câu 42. Cho Elip
E
có tiêu cự bằng
6
và đi qua điểm
0;5
A . Gọi
S
là diện tích lớn nhất của hình chữ
nhật nội tiếp
E
. Khi đó
A.
40
S
. B.
5
34
2
S . C.
10 34
S . D.
5 34
S .
Câu 43. Số giá trị nguyên thuộc đoạn
20;20
của tham số
a
để bất phương trình
2
( 5)(3 ) 2
x x x x a
nghiệm đúng với mọi
5;3
x
là
A.
36
. B.
10
. C.
16
. D.
15
.
Câu 44. Ta biết rằng Mặt Trăng chuyển động quanh Trái Đất theo một quỹ đạo là một elip mà Trái Đất là
một tiêu điểm. Elip có chiều dài trục lớn và trục nhỏ lần lượt là
769 266
km
và
768 106
km
. Tính
khoảng cách ngắn nhất từ Trái Đất đến Mặt Trăng, biết rằng các khoảng cách đó đạt được khi Trái Đất và
Mặt Trăng nằm trên trục lớn của elip, ta được kết quả là
6/6 - Mã đề 832
A.
384 053
km
. B.
363 517
km
. C.
384 633
km
. D.
363 518
km
.
Câu 45. Cho tam giác
ABC
với các cạnh , ,
AB c AC b BC a
. Trong các mệnh đề sau, mệnh đề sai là
A. Với mọi điểm
M
trong mặt phẳng ta luôn có
2 2 2
aMA bMB cMC abc
.
B. Nếu
I
là tâm đường tròn nội tiếp tam giác
ABC
thì
0
aIA bIB cIC
.
C. Nếu
H
là trực tâm của tam giác
ABC
thì
sinA sinB sinC 0
HA HB HC
.
D. Một vectơ chỉ phương của đường phân giác trong của góc
A
của tam giác
ABC
là
1 1
u AB AC
AB AC
.
Câu 46. Số giá trị nguyên thuộc đoạn
100;100
của tham số
m
để phương trình
2
2
1 1
2 1 2 0
x m x m
x x
có nghiệm là
A. 2. B. 200. C. 199. D. 1.
Câu 47. Cho
, ,
a b c
là các số thực dương thỏa mãn
2
0
f x ax bx c
với mọi
x
. Giá trị nhỏ nhất
min
F
của biểu thức
4
a c
F
b
là
A.
min
2
F
. B.
min
5
F
. C.
min
1
F
. D.
min
3
F
.
Câu 48. Số giá trị nguyên của tham số
m
để phương trình
2 2
2 1 2 0
x m x m m
có hai nghiệm trái
dấu, trong đó nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương là
A. 1. B. 2. C. 0. D. Vô số.
Câu 49. Tam giác
ABC
thỏa mãn hệ thức
3 3 3
2
cos 3cos 1
b c a
a
b c a
A C B
. Khẳng định đúng nhất về tam giác
ABC
là
A. Tam giác
ABC
vuông cân. B. Tam giác
ABC
vuông.
C. Tam giác
ABC
cân. D. Tam giác
ABC
đều.
Câu 50. Cho tam giác
ABC
nhọn có trực tâm H thuộc đường thẳng
3 4 4 0.
x y
Đường tròn ngoại tiếp
tam giác
HBC
có phương trình là
2 2
1 5 25
: .
2 2 4
C x y
Giả sử
2;3
M
là trung điểm của cạnh
BC
. Tọa độ đỉnh A là
A.
1
;0
2
A
. B.
3;1
A
. C.
1
1;
2
A
. D.
3
5;
2
A
.
------ HẾT ------
x
y
O
1

2

SỞ GD&ĐT BẮC NINH
TRƯỜNG THPT THUẬN THÀNH SỐ 1
Đ/A CHI TIẾT ĐỀ KS ĐẦU NĂM HỌC 2019-2020
MÔN TOÁN – LỚP 11
Câu 1: Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D
dưới đây. Hàm số đó là
A.
2
2 2
y x x
. B.
2
2 4 1
y x x
.
C.
2
2 4 1
y x x
. D.
2
2 1
y x x
.
Hướng dẫn giải
Chọn B.
Câu 2: Tập nghiệm của bất phương trình
3 2 1
x
là
A.
1;2
. B.
1;2
. C.
;1 2;
 
. D.
;1 2;
 
.
Hướng dẫn giải
Chọn C.
Ta có:
3 2 1
x
3 2 1
3 2 1
x
x
1
2
x
x
.
Vậy tập nghiệm của bất phương trình là
;1 2;S

.
Câu 3: Cho
2 3
cos , 2
3 2
. Giá trị của
tan
là
A.
5
2
. B.
5
2
. C.
5
4
. D.
1
2
.
Hướng dẫn giải
Chọn A.
Do
3
2 tan 0
2
.
Lại có
2
2
1 9 5
tan 1 1 tan
cos 4 2
.
Câu 4: Số nghiệm nguyên và lớn hơn
4
của bất phương trình
2
4 2 0
x x
là
A. 3. B. Vô số. C. 4. D. 5.
Hướng dẫn giải
Chọn C.
2
2
2
4 2 0 2 2 0
2
x
x x x x
x
.
Vậy có 4 nghiệm thỏa mãn yêu cầu.
Câu 5: Phương trình tiếp tuyến tại
3 4
( ; )
M
của đường tròn
2 2
2 4 3 0
( ):C x y x y
là
A.
7 0
x y
. B.
1 0
x y
.
C.
7 0
x y
. D.
1 0
x y
.
Hướng dẫn giải
Chọn A.
Ta có:
2 2
2 2
2 4 3 0 1 2 8
x y x y x y
.
Phương trình tiếp tuyến với đường tròn
( )
C
tại điểm
3 4
( ; )
M
là
3 1 3 4 2 4 0 2 3 2 4 0 7 0
( )( ) ( )( ) ( ) ( )
x y x y x y
.
Câu 6: Cho hai điểm
1;2
A ,
3;1
B và đường thẳng
1
:
2
x t
y t
. Tọa độ điểm
C
thuộc
để tam giác
ABC
cân tại
C
là
A.
7 13
;
6 6
. B.
13 7
;
6 6
. C.
7 13
;
6 6
. D.
5 11
;
6 6
.
Hướng dẫn giải
Chọn C.
1 ;2
C C t t
.
Ta có
2 2 2 2
2 2
1 1 2 2 3 1 1 2
CA CB CA CB t t t t
2 2 2
2
1
2 2 1
6
t t t t t
.
Suy ra
7 13
;
6 6
C
.
Câu 7: Cho tam giác
ABC
biết
1; 2
A
,
5; 4
B
,
1;4
C
. Đường cao
'
AA
của tam giác
ABC
có
phương trình là
A.
3 4 11 0
x y
. B.
3 4 11 0
x y
.
C.
8 6 4 0
x y
. D.
8 6 20 0
x y
.
Hướng dẫn giải
Chọn A.
Đường cao
AA
có vectơ pháp tuyến
6; 8
CB
, qua
1; 2
A
Nên phương trình tổng quát
AA
là:
6 1 8 2 0
x y
3 4 11 0
x y
.
Câu 8: Cho điểm
1; 1
M
và đường thẳng
:3 4 0
x y m
. Số giá trị
0
m
sao cho khoảng cách từ
M
đến
bằng
1
là
A.
0
. B.
1
. C.
2
. D.
3
.
Hướng dẫn giải
Chọn B.
2 2
3 4 1
,
5
3 4
m m
d M
.
1 5 6
1
, 1 1 1 5
1 5 4
5
m m
m
d M m
m m
.
Vậy có 1 giá trị của
m
thỏa mãn yêu cầu bài toán.
Câu 9: Cho bất phương trình
2
3
1 *
4
x
x
và các mệnh đề
(I):
2
3x
* 1 1
4
x
. (II): Điều kiện xác định của
*
là
2
x
.
(III):
2
3x
* 1
4
x
. (IV):
2
* 3 4
x x
.
Số mệnh đề đúng trong các mệnh đề trên là
A.
4
. B.
1
. C.
2
. D.
3
.
Hướng dẫn giải
Chọn A.
Câu 10: Đường thẳng
d
có một vectơ chỉ phương là
2;1
u
. Một vectơ pháp tuyến của
d
là
A.
1;2
n
. B.
3;6
n
. C.
3;6
n
. D.
1; 2
n
.
Hướng dẫn giải
Chọn B.
Câu 11: Biết bất phương trình
2
1 9 3
m x x m
nghiệm đúng với mọi
x
khi
0
m m
. Khẳng định đúng
nhất về
0
m
là
A. Có đúng hai giá trị
0
m
. B.
0
5; 1
m
.
C.
0
0;5
m
. D.
0
2
m
.
Hướng dẫn giải
Chọn B.
Bất phương trình đã cho tương đương với
2
9 3 1 0
m x m
.
Bất phương trình trên đúng với mọi
x
2
9 0
3 1 0
m
m
3
1
3
m
m
3
m
.
Vậy
0
5; 1
m
.
Câu 12: Cho
, , ,
a b c d
hữu hạn,
4 3
3 1 2
f x
x x
. Tập nghiệm của bất phương trình
0
f x
có dạng
A.
; ;
a b c d
. B.
; ;a b c

.
C.
; ;
a b c

. D.
; \ ;
a b
 
.
Hướng dẫn giải
Chọn B.
Ta có:
4 3 5 11
3 1 2 3 1 2
x
f x
x x x x
5 11 11 1
0 0 ; 2;
3 1 2 5 3
x
f x x
x x
.
Câu 13: Góc giữa hai đường thẳng
1
:2 10 0
x y
và
2
: 3 9 0
x y
là
A.
0
90
. B.
0
60
. C.
0
0
. D.
0
45
.
Hướng dẫn giải
Chọn D.
Ta có:
1
2; 1 ,
n
2
1; 3 .
n
0
1 2 1 2
2.1 1 . 3
1
cos , , 45 .
5. 10 2
Câu 14: Phương trình tham số của đường thẳng đi qua 2 điểm
2;1 , 1;0
A B là
A.
2 3
1
x t
y t
. B.
1 3
x t
y t
. C.
2 3
1 2
x t
y t
. D.
1 3
x t
y t
.
Hướng dẫn giải
Chọn B.
Câu 15: Cho hai điểm
4;1
A ,
2;3
B . Phương trình đường tròn đường kính
AB
là
A.
2 2
3 1 5
x y
. B.
2 2
1 2 10
x y
.
C.
2 2
1 2 10
x y
. D.
2
2
1 20
x y
.
Hướng dẫn giải
Chọn B.
Câu 16: Rút gọn biểu thức
tan sin
sin cot
P
ta được kết quả là
A.
cos
. B.
sin
. C.
tan
. D.
2sin
.
Hướng dẫn giải
Chọn A.
Câu 17: Cho hai góc nhọn
,
a b
thỏa mãn
1 1
cos ;cos
3 4
a b
. Giá trị của biểu thức
cos( ).cos( )
P a b a b
là
A.
119
144
. B.
113
144
. C.
117
144
. D.
115
144
.
Hướng dẫn giải
Chọn A.
Ta có:
2 2
1 1
cos( ).cos( ) (cos 2 cos 2 ) ( 2 cos 1 2 cos 1)
2 2
P a b a b b a b a
1 1 1 119
( 2. 2. 2 )
2 16 9 144
Câu 18: Nếu tam giác
ABC
có
2 2 2
a b c
thì
A.
A
là góc tù. B.
A
là góc vuông.
C.
A
là góc nhọn. D.
A
là góc nhỏ nhất.
Hướng dẫn giải
Chọn C.
Theo hệ quả định lí hàm số cosin ta có
2 2 2
b c a
cosA 0
2bc
.
Vậy
A
là góc nhọn.
Câu 19: Tọa độ các tiêu điểm của Elip
2 2
1
9 1
x y
là
A.
1 2
3 0 3 0
; , ;
F F . B.
1 2
8 0 0 8
; , ;F F
.
C.
1 2
0 2 2 0 2 2
; , ;F F
. D.
1 2
8 0 8 0
; , ;
F F
.
Hướng dẫn giải
Chọn D.
E
:
2 2
1
9 1
x y
có
3
a
;
1
b
2 2
8
c a b
.
Vậy
E
có các tiêu điểm là:
1
8 0
; ;
F
2
8 0
;
F
.
Câu 20: Mệnh đề sai trong các mệnh đề sau là
A.
8 8 2 2
sin cos 1 4sin cos
x x x x
. B.
6 6 2 2
sin cos 1 3sin cos
x x x x
.
C.
2 2
sin cos 1
x x
. D.
4 4 2 2
sin cos 1 2sin cos
x x x x
.
Hướng dẫn giải
Chọn A
Ta có:
2 2 2
8 8 4 4 4 4 4 4
sin cos sin cos sin cos 2sin cos
x x x x x x x x
2
2 2
2 2 2 2 4 4 2 2 4 4
sin cos 2sin cos 2sin cos 1 2sin cos 2sin cos
x x x x x x x x x x
2 2 4 4
1 4 sin cos 2sin cos
x x x x
.
Câu 21: Tập nghiệm của hệ bất phương trình
2
2 1 5
3 2
3 5 0
2 1 0
x x
x x
x x
là
A.
13;5
. B.
1;5
. C.
3;5 \ 1
. D.
3;5 \ 1
.
Hướng dẫn giải
Chọn C
2
2 1 5
3 2
3 5 0
2 1 0
x x
x x
x x
13
3 5
1
x
x
x
3 5
1
x
x
.
Câu 22: Rút gọn biểu thức
cos 2020 2019
x
ta được kết quả là
A.
cos2020
x
. B.
cos2020
x
. C.
sin2020
x
. D.
sin 2020
x
.
Hướng dẫn giải
Chọn A.
Câu 23: Tập các giá trị của tham số
m
để phương trình
2 2
1 2 0
m x x m
có hai nghiệm trái dấu là
A.
; 1 0;1

. B.
1;1
.
C.
1;0 1;

. D.
; 1 0;1

.
Hướng dẫn giải
Chọn A.
Ycbt
2
1
1 0
0 1
m
m m
m
.
Câu 24: Trong các công thức sau, công thức đúng là
A.
sin sin .cos cos .sin
a b a b a b
. B.
cos cos .cos sin .sin
a b a b a b
.
C.
sin sin .sin cos .cos
a b a b a b
. D.
cos cos .cos sin .sin
a b a b a b
.
Hướng dẫn giải
Chọn B.
Ta có:
sin sin .cos cos .sin
a b a b a b
;
cos cos .cos sin .sin
a b a b a b
.
Câu 25: Số đo góc
o
22 30
được đổi sang rađian là
A.
8
. B.
7
12
. C.
6
. D.
5
.
Hướng dẫn giải
Chọn A.
Câu 26: Trong các khẳng định sau, khẳng định đúng là
A.
( 2)
2 2
2
x x
x
x
. B.
2
1 3 1 9
x x x x
.
C.
2 2
3 2 2 3
x x x x x x
. D.
2 2
x x
.
Hướng dẫn giải
Chọn A.
Câu 27: Số nghiệm của phương trình
2 4 1 0
x x
là
A.
0
. B.
1
. C.
2
. D. Vô số.
Hướng dẫn giải
Chọn A.
Ta có
2 4 1 0
x x
2 4 0
1 0
x
x
2
1
x
x
x
.
Câu 28: Khi giải phương trình
2
3 1 2 1 1
x x , một học sinh làm theo các bước sau:
Bước 1: Bình phương hai vế của phương trình
1
ta được:
2
2
2
3 1 2 1x x .
Bước 2: Khai triển và rút gọn
2
ta được:
2
0
4 0
4
x
x x
x
.
Bước 3: Khi
0
x
, ta có
2
3 1 0
x
. Khi
4
x
, ta có
2
3 1 0
x
.
Vậy tập nghiệm của phương trình là
0;–4
.
Nhận xét đúng nhất về lời giải trên là
A. Đúng. B. Sai ở bước 1.
C. Sai ở bước 2. D. Sai ở bước 3.
Hướng dẫn giải
Chọn D.
Vì phương trình
2
là phương trình hệ quả nên ta cần thay nghiệm
0
x
;
4
x
vào phương
trình
1
để thử lại.
Câu 29: Phương trình
2
0 0
ax bx c a
có hai nghiệm âm phân biệt khi và chỉ khi
A.
0
0
P
. B.
0
0
0
P
S
. C.
0
0
0
P
S
. D.
0
0
0
a
S
.
Hướng dẫn giải
Chọn C.
Câu 30:
2
và
3
là hai nghiệm của phương trình
A.
2
2 3 6 0
x x
. B.
2
2 3 6 0
x x
.
C.
2
2 3 6 0
x x
. D.
2
2 3 6 0
x x
.
Hướng dẫn giải
Chọn B
Ta có:
2 3
6
S
P
2
: 0
pt x Sx P
2
2 3 + 6 0
x x
.
Câu 31: Cho đường tròn
2 2
: 3 1 5
C x y
. Tiếp tuyến của
C
song song với đường thẳng
:2 10 0
d x y
có phương trình là
A.
2 1 0
x y
hoặc
2 1 0
x y
. B.
2 1 0
x y
.
C.
2 0
x y
hoặc
2 10 0
x y
. D.
2 0
x y
.
Hướng dẫn giải
Chọn D.
Đường tròn
C
có tâm
3; 1
I
, bán kính
5
R
.
Tiếp tuyến
//
d
:2 0 10
x y c c
.
,
d I R
5
5
5
c
5 5
c
0
10
c
c
:2 0
:2 10 0
x y tm
x y L
.
Câu 32: Hai cạnh của hình chữ nhật nằm trên hai đường thẳng có phương trình
4 – 3 5 0, 3 4 – 5 0
x y x y
. Một đỉnh của hình chữ nhật là
2;1
A . Diện tích của hình chữ nhật là
A. 1. B. 2. C. 3. D. 4.
Hướng dẫn giải
Chọn B.
Khoảng cách từ đỉnh
2;1
A
đến đường thẳng
4 3 5 0
x y
là 2
Khoảng cách từ đỉnh
2;1
A đến đường thẳng
3 4 5 0
x y
là 1
Diện tích hình chữ nhật bằng
2.1 2
.
Câu 33: Biết
, ,
A B C
là các góc trong tam giác
ABC
. Mệnh đề đúng là
A.
sin sin
A C B
. B.
cos cos
A C B
.
C.
tan tan
A C B
. D.
cot cot
A C B
.
Hướng dẫn giải
Chọn B.
Vì
, ,
A B C
là ba góc của một tam giác suy ra
.
A C B
Khi đó
sin sin sin ; cos cos cos .
A C B B A C B B
tan tan tan ; cot cot cot .
A C B B A C B B
Câu 34: Cho góc
thỏa mãn
tan 2
. Giá trị của biểu thức
2 2
2 2
2sin 3sin .cos 4cos
5sin 6cos
P
là
A.
9
13
P
. B.
9
65
P
. C.
9
65
P
. D.
24
29
P
.
Hướng dẫn giải
Chọn A.
Chia cả tử và mẫu của
P
cho
2
cos
ta được
2 2
2 2
2tan 3tan 4 2.2 3.2 4 9
.
13
5tan 6 5.2 6
P
Câu 35: Cho tam giác
ABC
có
6cm, 10
AB BC cm
. Độ dài đường trung tuyến xuất phát từ đỉnh
A
của tam
giác bằng
5
cm
. Diện tích tam giác
ABC
là
A. 24cm. B. 48cm. C. 30cm. D. 60cm.
Hướng dẫn giải
Chọn A.
Áp dụng công thức đường trung tuyến
2 2 2
2
2 4
a
b c a
m ta suy ra
8
AC cm
.
Nhận xét: tam giác
ABC
vuông tại A nên
1
. 24 .
2
S AB AC cm
Câu 36: Tam giác
ABC
thỏa mãn hệ thức
3 3 3
2
cos 3cos 1
b c a
a
b c a
A C B
. Khẳng định đúng nhất về tam giác
ABC
là
A. Tam giác
ABC
vuông cân. B. Tam giác
ABC
đều.
C. Tam giác
ABC
vuông. D. Tam giác
ABC
cân.
Hướng dẫn giải
Chọn B.
Ta có
*
3 3 3
2
b c a
a
b c a
3 3 2
b c a b c
2 2 2
b c bc a
2cos 1 60
A A
.
*
cos 3cos 1
A C B
cos 3cos 1
B B
1
cos 60
2
B B
.
* Vậy
ABC
là tam giác đều.
Câu 37: Cho
, ,
a b c
là các số thực dương thỏa mãn
2
0
f x ax bx c
với mọi x
. Giá trị nhỏ nhất
min
F
của biểu thức
4
a c
F
b
là
A.
min
5
F
. B.
min
1
F
. C.
min
3
F
. D.
min
2
F
.
Hướng dẫn giải
Chọn D
Vì
2
0
f x ax bx c
với mọi x
nên ta có
2
4 0
b ac
2
4
ac b
2
ac b
Xét
4 4
2
a c ac
F
b b
.
Vậy
min
2
F
.
Câu 38: Cho hai đường thẳng
1 2
: 1 0, : 2 1 0
x y x y
và điểm
2;1
P . Gọi
là đường thẳng đi
qua
P
và cắt hai đường thẳng
1 2
,
tại hai điểm
,
A B
sao cho
P
là trung điểm của
AB
. Phương trình của
là
A.
4 6 0
x y
. B.
4x 9 0
y
.
C.
4x 7 0
y
. D.
9 14 0
x y
.
Hướng dẫn giải
Chọn C.
Gọi
là đường thẳng cần tìm.
Ta có
1
; 1
A A a a
.
2
;1 2
B B b b
.
P
là trung điểm của
8
4 4
3
2 2 2 2 0 4
3
a
a b a b
AB
a b a b
b
8 11 4 5
; ; ;
3 3 3 3
A B
4 16
; .
3 3
AB
Đường thẳng
qua
P
và có một véc tơ pháp tuyến
4; 1
n
có phương trình
4 2 1 1 0 4 7 0.
x y x y
Câu 39: Số giá trị nguyên của tham số
m
để phương trình
2 2
2 1 2 0
x m x m m
có hai nghiệm trái
dấu, trong đó nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương là
A. 0. B. 1. C. 2. D. Vô số.
Hướng dẫn giải
Chọn A.
Phương trình có hai nghiệm trái dấu khi:
2
2 0 0 2
m m m
(*).
Giả sử phương trình có hai nghiệm
1 2
0
x x
.
Theo yêu cầu bài toán ta có:
1 2
0
x x
1 2
0
x x
1 2
0
x x
1 0
m
1
m
(**).
Kết hợp (*), (**) ta có
0 1
m
.
Vậy không có giá trị nguyên nào của m thỏa mãn ycbt.
Câu 40: Cho đường tròn
2 2
: 4 2 1 0
C x y x y
và đường thẳng
d
có phương trình
1 0
x y
.
Gọi
;
M a b
là điểm thuộc đường thẳng
d
sao cho từ
M
kẻ được hai tiếp tuyến vuông góc đến
C
. Khi
đó
A.
2
2
a
. B.
2
4
a
. C.
2 2
4
a b
. D.
a b
.
Hướng dẫn giải
Chọn A.
Đường tròn
C
có tâm
2;1
I
, bán kính
6
R
.
Điểm
M
thuộc đường thẳng
d
nên
; 1
M a a
.
Theo bài ra
M
kẻ được đến
C
hai tiếp tuyến hợp với nhau góc
0
90
nên dựa vào hình vẽ dưới ta
có:
0
90
BMA
0
45
BMI
,
6
BI R
2 3
MI
.
I
B
A
M
Do đó:
2 2
2
2 2 12 2
a a a
.
Câu 41: Số giá trị nguyên thuộc đoạn
20;20
của tham số
a
để bất phương trình
2
( 5)(3 ) 2
x x x x a
nghiệm đúng với mọi
5;3
x là
A.
10
. B.
36
. C.
16
. D.
15
.
Hướng dẫn giải
Chọn C.
Đặt
2 2 2 2
( 5)(3 ) 2 15 2 15
t x x t x x x x t
. (đk:
0 4
t
).
Bất phương trình trở thành:
2 2
15 15 0(1)
t t a t t a
. Ta có hệ số đi với
2
t
dương.
Yêu cầu đề bài xảy ra bpt
(1)
nghiệm đúng với mọi
0 4
t
Phương trình
2
15 0
t t a
có 2 nghiệm phân biệt
1 2
0 4
t t
*
Cách 1:
1. (0) 0 15 0 15
* 5
1. (4) 0 5 0 5
f a a
a
f a a
.
Mà
20;20
a
nên có 16 giá trị nguyên của
a
.
Cách 2:
1 2
1 2 1 2
1 2
1 2 1 2
0
0 0
*
4 4 0
4 4 0 4
t t
t t t t
t tt t t t
1 2
1 2 1 2
0
4 16 0
t t
t t t t
15 0 15
5
5 0 5
a a
a
a a
Mà
20;20
a
nên có 16 giá trị nguyên của
a
.
Câu 42: Số giá trị nguyên thuộc đoạn
100;100
của tham số
m
để phương trình
2
2
1 1
2 1 2 0
x m x m
x x
có nghiệm là
A. 1. B. 2. C. 200. D. 199.
Hướng dẫn giải
Chọn D.
Điều kiện
0
x
Đặt
1
t x
x
suy ra
2
t
hoặc
2
t
.
Phương trình đã cho trở thành
2
2 1 2 0
t mt m
, phương trình này luôn có hai nghiệm là
1
1
t
;
2
2 1
t m
.
Theo yêu cầu bài toán ta suy ra
2 1 2
2 1 2
m
m
3
2
1
2
m
m
.
Mà
100;100
m nên có 199 giá trị nguyên của
a
.
Câu 43: Điều kiện cần và đủ của tham số
m
để phương trình
2
2 2
2 4 – 2 2 4 4 –1 0
x x m x x m
có đúng hai nghiệm là
A.
3 4
m
. B.
2 3 4
m
.
C.
2 3
2 3
m
m
. D.
2 3
4
m
m
.
Hướng dẫn giải
Chọn D.
Đặt
2
2 4
t x x
,
2
1 3 3
t x
.
Phương trình trở thành
2
2 4 1 0 2
t mt m
.
Nhận xét: Ứng với mỗi nghiệm
3
t
của phương trình
2
cho ta hai nghiệm của phương trình
1
. Do đó phương trình
1
có đúng hai nghiệm khi phương trình
2
có đúng một nghiệm
3
t
.
2
2
4 1 0
2 3
1. 3 2 .3 4 1 0
m m
m
m m
2 3
4
m
m
.
Câu 44: Số giá trị
1
m
để phương trình
2
1
x x m
có đúng hai nghiệm là
A. 0. B. 1. C. 2. D. Vô số.
Hướng dẫn giải
Chọn B.
2
1
x x m
m
2
2
1 0
1 0
x x khi x
f x
x x khi x
.
Biểu diễn đồ thị hàm số
f x
lên hệ trục tọa độ như hình vẽ bên trên. Dựa vào đồ thị ta suy ra với
5
4
1
m
m
thì phương trình
2
1
x x m
có đúng 2 nghiệm.
Vì
1
m
nên
5
4
m
.
Câu 45: Ta biết rằng Mặt Trăng chuyển động quanh Trái Đất theo một quỹ đạo là một elip mà Trái Đất là
một tiêu điểm. Elip có chiều dài trục lớn và trục nhỏ lần lượt là
769 266
km
và
768 106
km
. Tính
khoảng cách ngắn nhất từ Trái Đất đến Mặt Trăng, biết rằng các khoảng cách đó đạt được khi Trái Đất và
Mặt Trăng nằm trên trục lớn của elip.
A.
384 633
km
. B.
384 053
km
.
C.
363 518
km
. D.
363 517
km
.
Hướng dẫn giải
Chọn C.
Phương trình chính tắc của elip có dạng
2 2
2 2
1 , 0
x y
a b
a b
.
Theo giả thiết:
2 769266 384633
a a
;
2 768106 384053
b b
.
2 2
21115
c a b .
Khoảng cách ngắn nhất từ Trái Đất đến Mặt Trăng là:
363518
a c km
.
Câu 46: Từ hai vị trí
,
A B
của một tòa nhà, người ta quan sát đỉnh
C
của một ngọn núi. Biết rằng độ cao
70
AB m
, phương nhìn
AC
tạo với phương nằm ngang một góc
0
30
, phương nhìn
BC
tạo với phương
nằm ngang một góc
0
15 30'
. Ngọn núi có độ cao so với mặt đất gần nhất với giá trị sau
A.
135
m
. B.
234
m
. C.
165
m
. D.
195
m
.
Hướng dẫn giải
Chọn A.
Tam giác
ABC
có:
0 0 0
60 , 105 30' 14 30'
BAC ABC ACB
.
Áp dụng định lí hàm số sin trong tam giác
ABC
ta có:
269,4
AC AB
AC m
B C
Chiều cao của ngọn núi là:
0
.sin30 135
CH AC m
.
Câu 47: Cho tam giác
ABC
nhọn có trực tâm H thuộc đường thẳng
3 4 4 0.
x y
Đường tròn ngoại tiếp
tam giác
HBC
có phương trình là
2 2
1 5 25
: .
2 2 4
C x y
Giả sử
2;3
M là trung điểm của cạnh
BC. Tọa độ đỉnh A là
A.
1
1;
2
A
. B.
1
;0
2
A
. C.
3;1
A
. D.
3
5;
2
A
.
Hướng dẫn giải
Chọn D.
Tọa độ điểm H là nghiệm của hệ phương trình:
2 2
3 4 4 0
2
1
2; .
1
1 5 25
2
2
2 2 4
x y
x
H
y
x y
Gọi
'
H
là điểm đối xứng với
H
qua đường thẳng
.
BC
Khi đó
'
H
thuộc đường tròn ngoại tiếp tam giác
ABC
.
Đường tròn
C
có tâm
1 5
;
2 2
I
, bán kính
5
2
R
.
Giả sử đường tròn ngoại tiếp tam giác
ABC
có tâm
'
I
, bán kính
'
R
.
Phép đối xứng qua đường thẳng
BC
biến tam giác
HBC
thành tam giác
'
H BC
do đó biến đường tròn
ngoại tiếp tam giác
HBC
thành đường tròn ngoại tiếp tam giác
'
H BC
hay chính là đường tròn ngoại tiếp
tam giác
ABC
.
Ta có
M
là trung điểm của
'
II
và
5
' .
2
R R
Suy ra
7 7
' ; .
2 2
I
Ta có
3
2 ' 5; .
2
AH I M A
Câu 48: Cho hình thoi
ABCD
có diện tích
20
S
, một đường chéo có phương trình
: 2 4 0
d x y
và
1; 3
D
. Biết đỉnh
A
có tung độ âm. Tọa độ đỉnh
A
là
A.
5; 6
A
. B.
1;2
A
. C.
1; 2
A
. D.
11; 18
A
.
Hướng dẫn giải
Chọn A.
Vì
D d
nên đường thẳng
d
là phương trình của đường chéo
AC
.
Phương trình của
BD
là
2 7 0
x y
.
Gọi
3; 2
I AC BD I
.
Mặt khác
I
là trung điểm của
BD
nên
5; 1 5
B IB .
Diện tích hình thoi là
1
. 2 .
2
S AC BD IA IB
. Mà
20 2 5
S IA .
Lại có
;4 2
A d A a a
.
1 1;2
2 5
5 5; 6
a A
IA
a A
Vì đỉnh
A
có tung độ âm nên
5; 6
A
.
Câu 49: Cho Elip
E
có tiêu cự bằng
6
và đi qua điểm
0;5
A
. Gọi
S
là diện tích lớn nhất của hình chữ
nhật nội tiếp
E
. Khi đó
A.
5
34
2
S . B.
10 34
S .
C.
40
S
. D.
5 34
S
.
Hướng dẫn giải
Chọn B.
* Phương trình chính tắc của elip có dạng
2 2
2 2
1 , 0
x y
a b
a b
.
Theo giả thiết:
2 6 3
c c
. Vì
0;5 A
E
nên ta có phương trình:
2 2
2
2 2
0 5
1 25
b
a b
.
Khi đó:
2 2 2 2 2 2
5 3
a b c a
2
34 34
a a .
* Gọi
;
M x y
là một đỉnh của hình chữ nhật nội tiếp
E
. Khi đó
2 2
1
34 25
x y
.
Diện tích hình chữ nhật này là
4
xy
.
Áp dụng bđt Cauchy:
2 2
2 4
1 = = 4 10 34
34 25
5 34 10 34
xy xy
x y
xy .
Dấu “=” xảy ra khi
2 2
1
34 25 2
x y
.
Vậy
10 34
S .
Câu 50: Cho tam giác
ABC
với các cạnh , ,
AB c AC b BC a
. Trong các mệnh đề sau, mệnh đề sai là
A. Nếu
I
là tâm đường tròn nội tiếp tam giác
ABC
thì
0
aIA bIB cIC
.
B. Với mọi điểm
M
trong mặt phẳng ta luôn có
2 2 2
aMA bMB cMC abc
.
C. Một vectơ chỉ phương của đường phân giác trong của góc
A
của tam giác
ABC
là
1 1
u AB AC
AB AC
.
D. Nếu
H
là trực tâm của tam giác
ABC
thì
sinA sinB sinC 0
HA HB HC
.
Hướng dẫn giải
Chọn D.
Nếu
H
là trực tâm của tam giác
ABC
thì
tanA tanB tanC 0
HA HB HC
.
| 1/20
| | Tải xuống

Có thể bạn quan tâm:

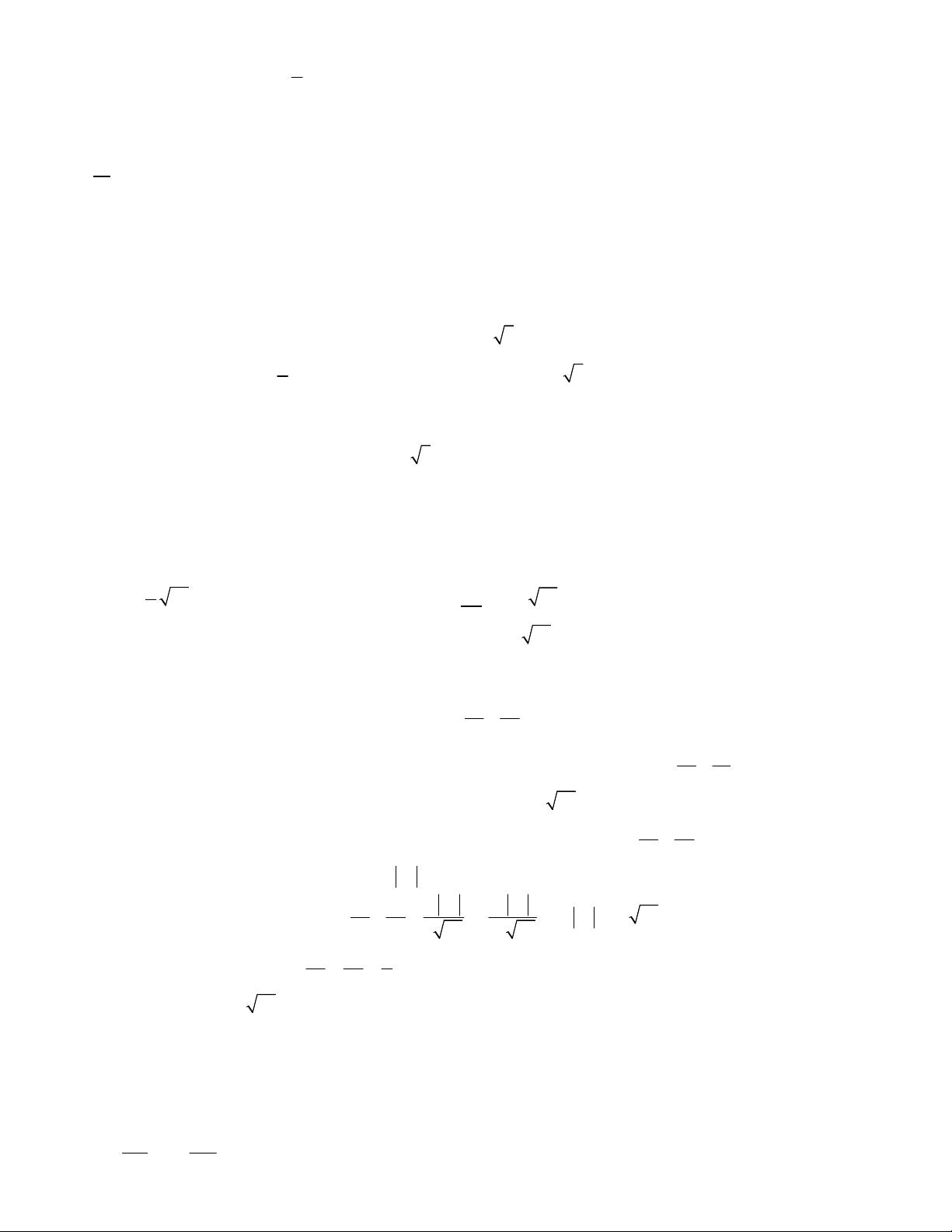
Preview text:

SỞ GD&ĐT BẮC NINH
ĐỀ KHẢO SÁT ĐẦU NĂM HỌC 2019-2020
TRƯỜNG THPT THUẬN THÀNH SỐ 1
MÔN TOÁN – LỚP 11
(Đề thi có 06 trang)
Thời gian làm bài : 90 phút (không kể thời gian phát đề)
Họ và tên học sinh :..................................................... Số báo danh : ................... Mã đề 832
Câu 1. Cho hai điểm A4 
;1 , B 2;3 . Phương trình đường tròn đường kính AB là 2 2
A.x  3   y   1  5 .
B. x   y  2 2 1  20 . 2 2 2 2
C. x   1
  y  2  10 . D. x  
1   y  2  10 .
Câu 2. Số nghiệm của phương trình 2x 4  x 1  0 là A. 2 . B. Vô số. C. 1. D. 0 . 4 3 Câu 3. Cho a, , b ,
c d hữu hạn, f x  
. Tập nghiệm của bất phương trình f x  0 có dạng 3x 1 2  x
A. a;b  c;  . B.  ;  a    ; b c . C.  ;   \  ; a b .
D. a;b   ; c d  . 2 2 2 sin  3sin .
cos  4 cos
Câu 4. Cho góc thỏa mãn tan  2 . Giá trị của biểu thức P  là 2 2
5 sin  6 cos 9 9 24 9 A. P  . B. P   . C. P  . D. P  . 13 65 29 65 x  1 t
Câu 5. Cho hai điểm A1; 2 , B 3 
;1 và đường thẳng  : 
. Tọa độ điểm C thuộc  để tam giác y  2  t
ABC cân tại C là  7 13   7 13   13 7   5 11  A. ;    . B. ;   . C. ;   . D. ;   .  6 6   6 6   6 6   6 6 
Câu 6. Tập các giá trị của tham số m để phương trình  2 m   2
1 x  2x m  0 có hai nghiệm trái dấu là A. 1  ;1 . B.  ;    1 0  ;1 . C.  ;    1  0  ;1 .
D. 1; 0  1;  .
Câu 7. Trong các công thức sau, công thức đúng là
A. cos a b  cos .
a cos b  sin . a sin b .
B. sin a b  sin .
a cos b  cos . a sin b .
C. sin a b  sin .
a sin b  cos . a cos b .
D. cos a b  cos .
a cos b  sin . a sin b . 2 2 x y
Câu 8. Tọa độ các tiêu điểm của Elip   1 là 9 1 A. F 3  ; 0 , F 3; 0 .
B. F  8; 0 , F 8;0 . 1   2   1   2   C. F
8; 0 , F 0;  8 .
D. F 0; 2 2 , F 0; 2 2 . 1   2   1   2   1/6 - Mã đề 832
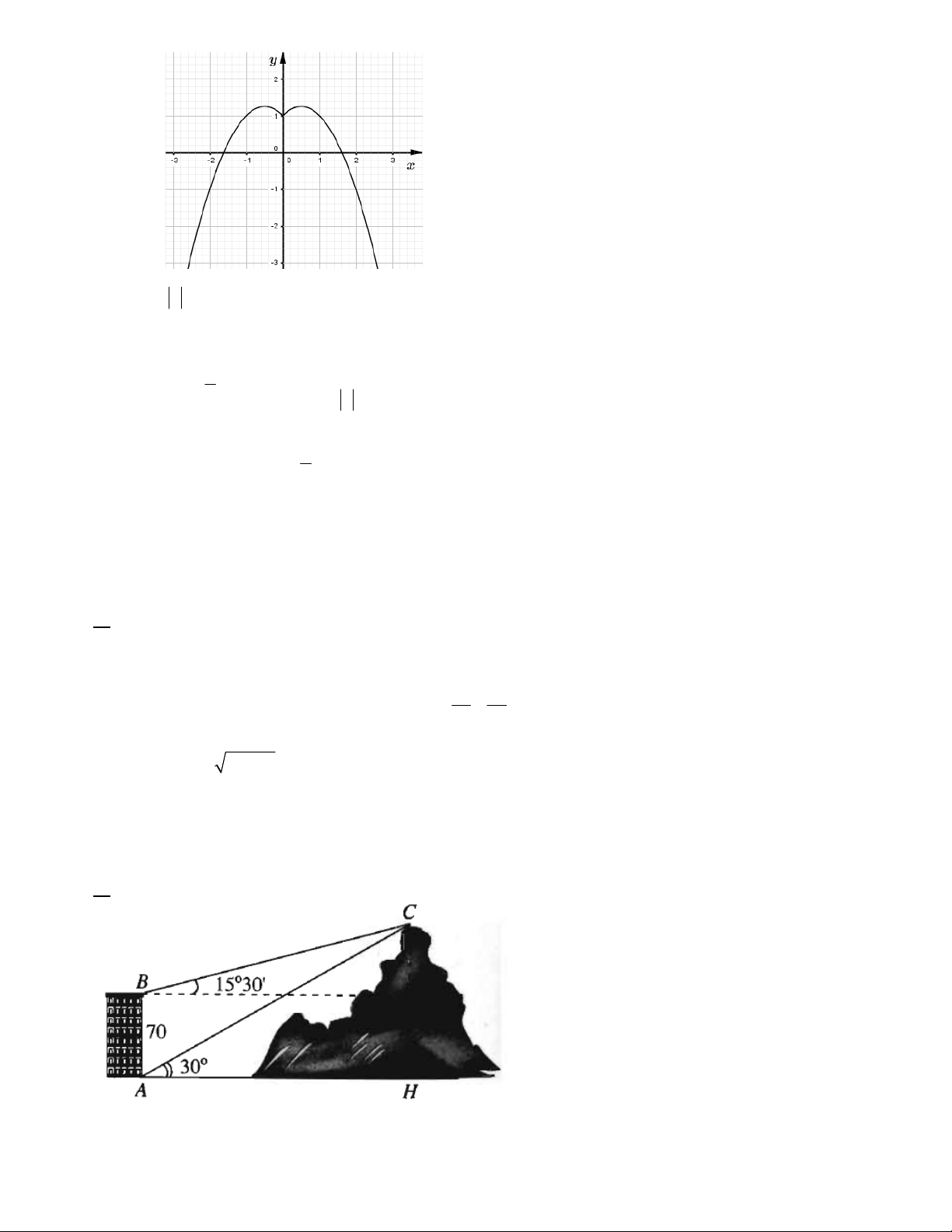
Câu 9. Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số được liệt y x
kê ở bốn phương án A, B, C, D dưới đây. Hàm số đó là O 1 2 A. 2
y  2x  4x 1. B. 2
y x  2x  2 .  C. 2
y x  2x 1. D. 2
y  2x  4x 1 . 
Câu 10. Cho tam giác ABC có AB  6cm, BC  10cm . Độ dài đường trung tuyến xuất phát từ đỉnh A của
tam giác bằng 5cm . Diện tích tam giác ABC là A. 30cm. B. 48cm. C. 24cm. D. 60cm. Câu 11. Số đo góc o
22 30 được đổi sang rađian là 7 A. . B. . C. . D. . 6 12 8 5 tan sin
Câu 12. Rút gọn biểu thức P   ta được kết quả là sin cot
A. 2 sin .
B. sin .
C. cos. D. tan . 1 1
Câu 13. Cho hai góc nhọn a, b thỏa mãn cos a  ; cos b
. Giá trị của biểu thức 3 4
P  cos(a b).cos(a b) là 115 113 117 119 A.  . B.  . C.  . D.  . 144 144 144 144
Câu 14. Phương trình 2
ax bx c  0
a  0 có hai nghiệm âm phân biệt khi và chỉ khi   0   0 a  0    0  
A.P  0 . B.  .
C.P  0 . D.   0.  P  0  S  0    S  0  S  0 
Câu 15. 2 và 3 là hai nghiệm của phương trình A. 2
x   2  3 x  6  0 . B. 2
x   2  3 x  6  0 . C. 2
x   2  3 x  6  0. D. 2
x   2  3 x  6  0 . 2 3
Câu 16. Cho cos ,
 2. Giá trị của tan là 3 2 5 5 5 1 A. . B.  . C. . D. . 2 2 4 2
Câu 17. Góc giữa hai đường thẳng  : 2x y 10  0 và  : x  3 y  9  0 là 1 2 A. 0 0 . B. 0 90 . C. 0 60 . D. 0 45 .
Câu 18. Cho tam giác ABC biết A1; 2
  , B5;4 , C 1
 ;4 . Đường cao AA' của tam giác ABC có phương trình là 2/6 - Mã đề 832
A. 3x  4 y 11  0 .
B. 8x  6 y  20  0 .
C. 3x  4 y 11  0 .
D. 8x  6 y  4  0 .
Câu 19. Tập nghiệm của bất phương trình 3  2x  1 là
A. 1; 2 . B. 1;2. C.   ;1 2; . D.   ;1  2;  .
Câu 20. Cho điểm M 1;  
1 và đường thẳng  : 3x  4 y m  0 . Số giá trị m  0 sao cho khoảng cách từ
M đến  bằng 1 là A. 0 . B. 3 . C. 1. D. 2 . 2 2
Câu 21. Cho đường tròn C  :  x  3   y   1
 5 . Tiếp tuyến của C song song với đường thẳng
d : 2x y 10  0 có phương trình là
A. 2x y  0 hoặc 2x y 10  0 .
B. 2x y 1  0 hoặc 2x y 1  0 .
C. 2x y 1  0 .
D. 2x y  0 .
Câu 22. Phương trình tiếp tuyến tại M 3 ( ;4) của đường tròn 2 2
(C) : x y  2x  4y  3  0 là
A. x y 1  0 .
B. x y 1  0 .
C. x y  7  0 .
D. x y  7  0 .  2x 1 x  5   3 2 
Câu 23. Tập nghiệm của hệ bất phương trình 
x  3 5  x  0 là  2
x  2x 1  0  
A. 13;5 . B. 1;5 .
C. 3;5 \   1 .
D. 3;5 \   1 .
Câu 24. Số nghiệm nguyên và lớn hơn 4 của bất phương trình  2
4  x  x  2  0 là A. 3. B. 4. C. 5. D. Vô số.
Câu 25. Phương trình tham số của đường thẳng đi qua 2 điểm A 2  ;  1 , B 1;0 là x  1 3t
x  2  3tx  1 3t
x  2  3t A.  . B.  . C.  . D.  . y ty  1 2ty ty  1 t
Câu 26. Hai cạnh của hình chữ nhật nằm trên hai đường thẳng có phương trình
4x – 3y  5  0, 3x  4 y – 5  0 . Một đỉnh của hình chữ nhật là A2 
;1 . Diện tích của hình chữ nhật là A. 3. B. 4. C. 1. D. 2. 
Câu 27. Đường thẳng d có một vectơ chỉ phương là u   2  ; 
1 . Một vectơ pháp tuyến của d là    
A. n  1;2 .
B. n  1;2 .
C. n  3;6. D. n   3  ; 6 . 3x
Câu 28. Cho bất phương trình  1 * và các mệnh đề 2 x  4 3x (I): *  1  
 1.(II): Điều kiện xác định của * là x  2 . 2 x  4 3x (III): *   1 .(IV):   2
*  3x x  4 . 2 x  4 3/6 - Mã đề 832
Số mệnh đề đúng trong các mệnh đề trên là A. 1. B. 4 . C. 2 . D. 3 . Câu 29. Biết ,
A B, C là các góc trong tam giác ABC . Mệnh đề đúng là
A. cotA C  cot B .
B. sin AC  sin B .
C. tan AC  tan B .
D. cosA C   cos B .
Câu 30. Mệnh đề sai trong các mệnh đề sau là A. 2 2
sin x  cos x  1 . B. 4 4 2 2
sin x  cos x  1 2 sin x cos x . C. 6 6 2 2
sin x  cos x  1 3sin x cos x . D. 8 8 2 2
sin x  cos x  1 4 sin x cos x .
Câu 31. Rút gọn biểu thức cos 2020x  2019 ta được kết quả là
A. sin 2020x .
B. cos 2020x .
C.  sin 2020x .
D.  cos 2020x .
Câu 32. Nếu tam giác ABC có 2 2 2
a b c thì  
A. A là góc vuông. B. A là góc tù.  
C. A là góc nhỏ nhất.
D. A là góc nhọn.
Câu 33. Khi giải phương trình 2
3x 1  2x 1  
1 , một học sinh làm theo các bước sau:
Bước 1: Bình phương hai vế của phương trình   1 ta được: 2
3x 1  2x  2 1 2 .  x  0
Bước 2: Khai triển và rút gọn 2 ta được: 2
x  4x  0   . x  4 
Bước 3: Khi x  0 , ta có 2
3x  1  0 . Khi x  4 , ta có 2 3x 1  0 .
Vậy tập nghiệm của phương trình là 0; –  4 .
Nhận xét đúng nhất về lời giải trên là
A. Sai ở bước 2.
B. Sai ở bước 3.
C. Sai ở bước 1. D. Đúng.
Câu 34. Trong các khẳng định sau, khẳng định đúng là A. 2
x 1  3x x 1  9x .
B. x  2  x  2 . x(x  2) C.
 2  x  2 . D. 2 2 3x
x  2  x
x  2  3x x . x  2
Câu 35. Biết bất phương trình 2
m x 1  9x  3m nghiệm đúng với mọi x khi m m . Khẳng định đúng 0 nhất về m là 0
A. m  2 .
B. m  5; 1 . 0   0
C. Có đúng hai giá trị m . D. m  0;5 . 0   0
Câu 36. Cho hình thoi ABCD có diện tích S  20 , một đường chéo có phương trình d : 2x y  4  0 và
D 1;3 . Biết đỉnh A có tung độ âm. Tọa độ đỉnh A là
A. A1; 2 . B. A5; 6   .
C. A11; 18 .
D. A1; 2 . 4/6 - Mã đề 832
Câu 37. Cho đường tròn C  2 2
: x y  4x  2 y 1  0 và đường thẳng d có phương trình x y 1  0 . Gọi M  ;
a b là điểm thuộc đường thẳng d sao cho từ M kẻ được hai tiếp tuyến vuông góc đến C  . Khi đó
A. a  b . B. 2 2
a b  4 . C. 2 a  2 . D. 2 a  4 .
Câu 38. Số giá trị m  1 để phương trình 2
x 1  x m có đúng hai nghiệm là A. 0. B. Vô số. C. 1. D. 2. 2
Câu 39. Điều kiện cần và đủ của tham số m để phương trình  2 x x    2
2 4 – 2m x 2x  4 4m–10 có đúng hai nghiệm là m  2 3  m  2  3 A.  .
B. 3  m  4 .
C. 2  3  m  4 . D.  . m  2  3  m  4 
Câu 40. Cho hai đường thẳng  : x y 1  0,  : 2x y 1  0 và điểm P 2 
;1 . Gọi  là đường thẳng đi 1 2
qua P và cắt hai đường thẳng  ,  tại hai điểm ,
A B sao cho P là trung điểm của AB . Phương trình của 1 2  là
A. x  4 y  6  0 .
B. 4x  y  9  0 .
C. 4x  y  7  0 .
D. x  9 y 14  0 .
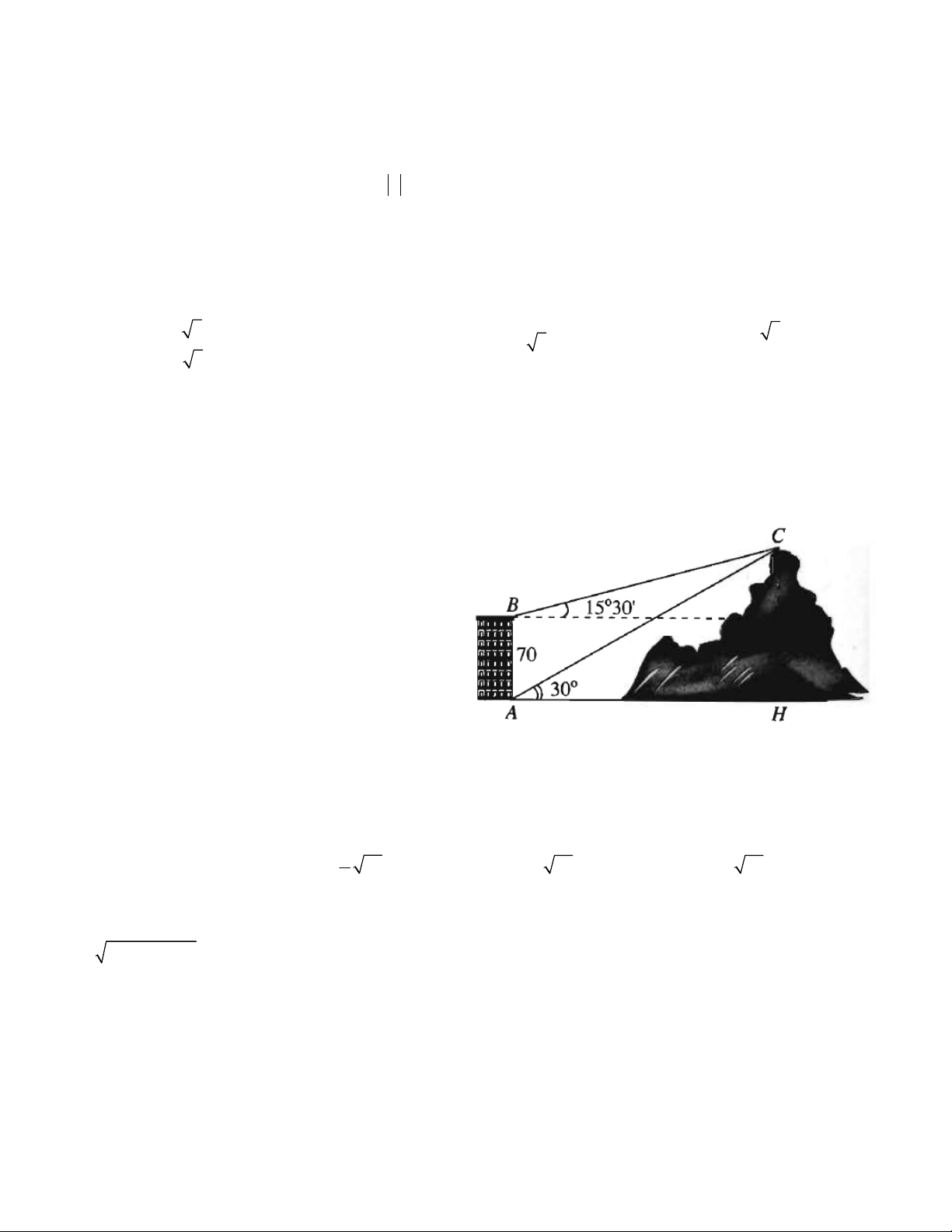
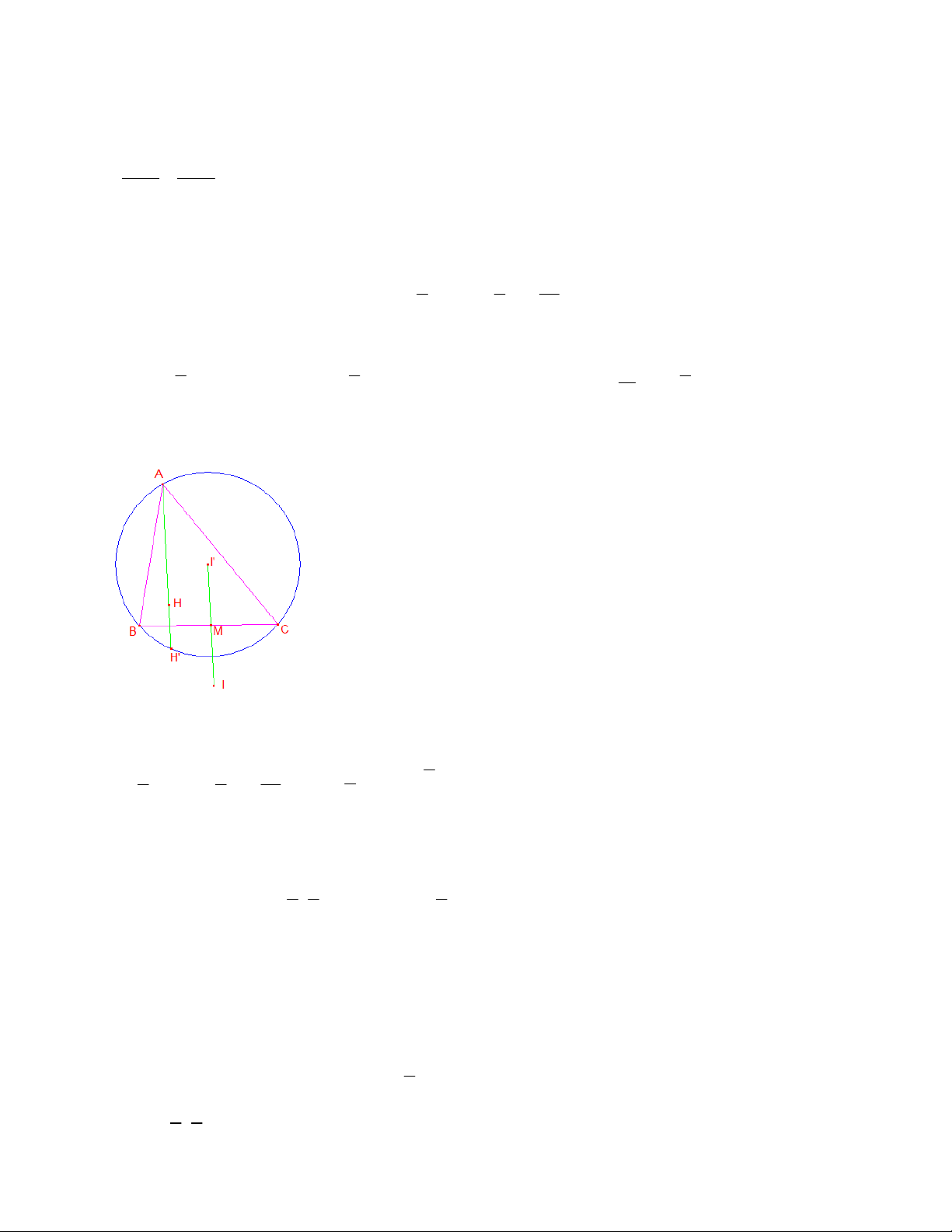
Câu 41. Từ hai vị trí ,
A B của một tòa nhà, người
ta quan sát đỉnh C của một ngọn núi. Biết rằng độ
cao AB  70m , phương nhìn AC tạo với phương nằm ngang một góc 0
30 , phương nhìn BC tạo với
phương nằm ngang một góc 0 15 30 ' . Ngọn núi có
độ cao so với mặt đất gần nhất với giá trị sau
A. 135m .
B. 195m . C. 234m . D. 165m .
Câu 42. Cho Elip  E  có tiêu cự bằng 6 và đi qua điểm A0;5 . Gọi S là diện tích lớn nhất của hình chữ
nhật nội tiếp  E  . Khi đó 5
A. S  40 . B. S  34 .
C. S  10 34 . D. S  5 34 . 2
Câu 43. Số giá trị nguyên thuộc đoạn 20; 20 của tham số a để bất phương trình 2
(x  5)(3  x)  x  2x a nghiệm đúng với mọi x 5;  3 là A. 36 . B. 10 . C. 16 . D. 15 .
Câu 44. Ta biết rằng Mặt Trăng chuyển động quanh Trái Đất theo một quỹ đạo là một elip mà Trái Đất là
một tiêu điểm. Elip có chiều dài trục lớn và trục nhỏ lần lượt là 769 266 km và 768 106 km . Tính
khoảng cách ngắn nhất từ Trái Đất đến Mặt Trăng, biết rằng các khoảng cách đó đạt được khi Trái Đất và
Mặt Trăng nằm trên trục lớn của elip, ta được kết quả là 5/6 - Mã đề 832 A. 384 053 km . B. 363 517 km . C. 384 633 km . D. 363 518 km .
Câu 45. Cho tam giác ABC với các cạnh AB c, AC b, BC a . Trong các mệnh đề sau, mệnh đề sai là
A. Với mọi điểm M trong mặt phẳng ta luôn có 2 2 2
aMA bMB cMC abc .    
B. Nếu I là tâm đường tròn nội tiếp tam giác ABC thì aIA bIB cIC  0 .    
C. Nếu H là trực tâm của tam giác ABC thì sinA HA  sinB HB  sinC HC  0 .
D. Một vectơ chỉ phương của đường phân giác trong của góc A của tam giác ABC là  1  1  u AB AC . AB AC
Câu 46. Số giá trị nguyên thuộc đoạn 100;100 của tham số m để phương trình  1   1  2 x    2mx   1 2m  0 2       xx có nghiệm là A. 2. B. 200. C. 199. D. 1.
Câu 47. Cho a,b, c là các số thực dương thỏa mãn f x 2
ax bx c  0 với mọi x   . Giá trị nhỏ nhất 4a c F
của biểu thức F  là min b A. F  2 . B. F  5 . C. F  1 . D. F  3 . min min min min
Câu 48. Số giá trị nguyên của tham số m để phương trình 2
x  m   2 2
1 x m  2m  0 có hai nghiệm trái
dấu, trong đó nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương là A. 1. B. 2. C. 0. D. Vô số. 3 3 3
b c a 2   a
Câu 49. Tam giác ABC thỏa mãn hệ thức  b c a
. Khẳng định đúng nhất về tam giác
cos A C  3cos B 1  ABC là
A. Tam giác ABC vuông cân.
B. Tam giác ABC vuông.
C. Tam giác ABC cân.
D. Tam giác ABC đều.
Câu 50. Cho tam giác ABC nhọn có trực tâm H thuộc đường thẳng 3x  4 y  4  0. Đường tròn ngoại tiếp 2 2  1   5  25
tam giác HBC có phương trình là C  : x   y   .    
Giả sử M 2; 3 là trung điểm của cạnh  2   2  4
BC . Tọa độ đỉnh A là  1   1   3  A. A ;0   . B. A3  ;1 . C. A 1;    . D. A 5;   .  2   2   2 
------ HẾT ------ 6/6 - Mã đề 832 SỞ GD&ĐT BẮC NINH
Đ/A CHI TIẾT ĐỀ KS ĐẦU NĂM HỌC 2019-2020
TRƯỜNG THPT THUẬN THÀNH SỐ 1
MÔN TOÁN – LỚP 11
Câu 1: Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D
dưới đây. Hàm số đó là y A. 2
y x  2x  2 . B. 2
y  2x  4x 1. 2 x O 1 C. 2
y  2x  4x 1. D. 2
y x  2x 1.  Hướng dẫn giải Chọn B. 
Câu 2: Tập nghiệm của bất phương trình 3  2x  1 là A. 1; 2 . B. 1; 2. C.   ;1  2;  . D.   ;1  2;  . Hướng dẫn giải Chọn C. 3  2x  1  x  1
Ta có: 3 2x 1     . 3  2x  1  x  2 
Vậy tập nghiệm của bất phương trình là S   ;   1 2; . 2 3
Câu 3: Cho cos ,
 2. Giá trị của tan là 3 2 5 5 5 1 A.  . B. . C. . D. . 2 2 4 2 Hướng dẫn giải Chọn A. 3 Do
 2 tan  0 . 2 1 9 5 2 Lại có tan
1  1 tan  . 2 cos 4 2
Câu 4: Số nghiệm nguyên và lớn hơn 4 của bất phương trình  2
4  x  x  2  0 là A. 3. B. Vô số. C. 4. D. 5. Hướng dẫn giải Chọn C.     x x 2 4
x  2  0  2  xx  22 2  0   . x  2  
Vậy có 4 nghiệm thỏa mãn yêu cầu.
Câu 5: Phương trình tiếp tuyến tại M 3 ( ;4) của đường tròn 2 2
(C) : x y  2x  4y  3  0 là
A. x y  7  0 .
B. x y 1  0 .
C. x y  7  0 .
D. x y 1  0 . Hướng dẫn giải Chọn A.
Ta có: x y x y  
  x  2   y  2 2 2 2 4 3 0 1 2  8 .
Phương trình tiếp tuyến với đường tròn (C ) tại điểm M 3 ( ; 4) là
(3  1)( x  3)  (4  2)(y  4)  0  2( x  3)  2(y  4)  0  x y  7  0 . x  1 t
Câu 6: Cho hai điểm A1; 2, B 3 
;1 và đường thẳng  : 
. Tọa độ điểm C thuộc  để tam giác y  2  t
ABC cân tại C là  7 13   13 7   7 13   5 11  A. ;    . B. ;   . C. ;   . D. ;   .  6 6   6 6   6 6   6 6  Hướng dẫn giải Chọn C.
C   C 1 t;2 t. 2 2 2 2 Ta có 2 2
CA CB CA CB  11 t   2  2  t   3 1 t   1 2  t  1
 2  t 2  t  2  t 2  1 t 2 2  t  . 6  7 13  Suy ra C ;  .  6 6 
Câu 7: Cho tam giác ABC biết A1; 2
  , B5;4 , C 1; 4 . Đường cao AA' của tam giác ABC có phương trình là
A. 3x  4 y 1  1 0 .
B. 3x  4 y 11  0 .
C. 8x  6 y  4  0 .
D. 8x  6 y  20  0 . Hướng dẫn giải Chọn A. 
Đường cao AA có vectơ pháp tuyến CB  6;  8 , qua  A 1;  2
Nên phương trình tổng quát AA là: 6x   1 8 y  
2  0  3x  4 y 11  0 .
Câu 8: Cho điểm M 1;  
1 và đường thẳng  : 3x  4 y m  0 . Số giá trị m  0 sao cho khoảng cách từ M đến  bằng 1 là A. 0 . B. 1. C. 2 . D. 3 . Hướng dẫn giải Chọn B. 3  4  m m  1
d M ,     2 2 5 3  4 . m 1 m 1  5 m  6
d M ,   1 
 1  m 1  5     . 5 m 1  5  m  4  
Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán. 3x
Câu 9: Cho bất phương trình  1   * và các mệnh đề 2 x  4 3x (I): *  1    1.
(II): Điều kiện xác định của * là x  2 . 2 x  4 3x (III): *   1 . (IV):   2
*  3x x  4 . 2 x  4
Số mệnh đề đúng trong các mệnh đề trên là A. 4 . B. 1. C. 2 . D. 3 . Hướng dẫn giải Chọn A.
Câu 10: Đường thẳng d có một vectơ chỉ phương là u   2  ; 
1 . Một vectơ pháp tuyến của d là     A. n   1  ; 2 .
B. n  3;6 .
C. n  3;6 .
D. n  1;2 . Hướng dẫn giải Chọn B.
Câu 11: Biết bất phương trình 2
m x 1  9x  3m nghiệm đúng với mọi x khi m m . Khẳng định đúng 0 nhất về m là 0
A. Có đúng hai giá trị m .
B. m  5; 1 . 0   0 C. m  0;5 .
D. m  2 . 0   0 Hướng dẫn giải Chọn B.
Bất phương trình đã cho tương đương với  2
m  9x  3m  1  0 .  2  m  9  0     m 3  
Bất phương trình trên đúng với mọi x    m     3. 3  m 1  0  1    m     3 Vậy m  5  ; 1 . 0   4 3
Câu 12: Cho a, , b ,
c d hữu hạn, f x  
. Tập nghiệm của bất phương trình f x  0 có dạng 3x 1 2  x
A. a;b   ; c d .
B. a;b  c;  . C.  ;  a    ; b c . D.  ;
  \ a;  b . Hướng dẫn giải Chọn B.  Ta có: 4 3 5 x 11 f x     3 x  1 2  x
3x  12  x  5x 11  11 1 
f x  0   0  x   ; 2;    . 3x   1 2  x  5 3 
Câu 13: Góc giữa hai đường thẳng  : 2x y 10  0 và  : x  3y  9  0 là 1 2 A. 0 90 . B. 0 60 . C. 0 0 . D. 0 45 . Hướng dẫn giải Chọn D.   Ta có: n  2; 1  , n  1; 3  . 2   1   2.1   1 . 3   1 cos  ,       ,   0  45 . 1 2 1 2 5. 10 2
Câu 14: Phương trình tham số của đường thẳng đi qua 2 điểm A 2  ;  1 , B 1;0 là
x  2  3tx  1 3t
x  2  3tx  1 3t A.  . B.  . C.  . D.  . y  1 ty ty  1 2ty tHướng dẫn giải Chọn B.
Câu 15: Cho hai điểm A4 
;1 , B 2;3 . Phương trình đường tròn đường kính AB là 2 2 2 2
A. x  3   y   1  5 . B. x  
1   y  2  10 . 2 2 C. x  
1   y  2  10 .
D. x   y  2 2 1  20 . Hướng dẫn giải Chọn B. tan sin
Câu 16: Rút gọn biểu thức P   ta được kết quả là sin cot A. cos. B. sin . C. tan .
D. 2 sin. Hướng dẫn giải Chọn A. 1 1
Câu 17: Cho hai góc nhọn a, b thỏa mãn cos a  ; cos b
. Giá trị của biểu thức 3 4
P  cos(a b).cos(a b) là 119 113 117 115 A.  . B.  . C.  . D.  . 144 144 144 144 Hướng dẫn giải Chọn A. 1 1 Ta có: 2 2
P  cos( a b ).cos( a b ) 
(cos 2b  cos 2a ) 
( 2 cos b  1  2 cos a  1 ) 2 2 1 1 1 119  ( 2.  2.  2 )   2 16 9 144
Câu 18: Nếu tam giác ABC có 2 2 2
a b c thì   A. A là góc tù. B. A là góc vuông.   C. A là góc nhọn.
D. A là góc nhỏ nhất. Hướng dẫn giải Chọn C.
Theo hệ quả định lí hàm số cosin ta có  2 2 2 b  c  a cosA   0 . 2bc  Vậy A là góc nhọn. 2 2 x y
Câu 19: Tọa độ các tiêu điểm của Elip   1 là 9 1
A. F 3;0 , F 3; 0 . B. F 8; 0 , F 0;  8 . 1   2   1   2  
C. F 0; 2 2 , F 0; 2 2 .
D. F  8;0 , F 8;0 . 1   2   1   2   Hướng dẫn giải Chọn D. 2 2 x yE : 
1 có a  3 ; b  1 2 2  c a b  8 . 9 1
Vậy E  có các tiêu điểm là: F  8;0 ; F 8; 0 . 2   1  
Câu 20: Mệnh đề sai trong các mệnh đề sau là A. 8 8 2 2
sin x  cos x  1 4 sin x cos x . B. 6 6 2 2
sin x  cos x  1 3sin x cos x . C. 2 2
sin x  cos x  1 . D. 4 4 2 2
sin x  cos x  1 2 sin x cos x . Hướng dẫn giải Chọn A Ta có: x x   x 2   x 2   x x 2 8 8 4 4 4 4 4 4 sin cos sin cos sin cos
 2 sin x cos x   2  x x 2  x x   x x    x x 2 2 2 2 2 4 4 2 2 4 4 sin cos 2 sin cos 2 sin cos 1 2 sin cos
 2 sin x cos x 2 2 4 4
 1  4 sin x cos x  2 sin x cos x .  2x 1 x  5   3 2 
Câu 21: Tập nghiệm của hệ bất phương trình 
x  3 5  x  0 là  2
x  2x 1  0  
A. 13;5 . B. 1;5 .
C. 3;5 \   1 .
D. 3;5 \  1 . Hướng dẫn giải Chọn C  2x 1 x  5   3 2 x  1  3    3   x  5 
x  3 5  x  0   3   x  5   .   x  1  2
x  2x 1  0 x  1   
Câu 22: Rút gọn biểu thức cos 2020x  2019 ta được kết quả là A.  cos 2020x .
B. cos 2020x .
C.  sin 2020x . D. sin 2020x . Hướng dẫn giải Chọn A.
Câu 23: Tập các giá trị của tham số m để phương trình  2 m   2
1 x  2x m  0 có hai nghiệm trái dấu là A.  ;    1  0  ;1 . B. 1  ;1 .
C. 1; 0  1;  . D.  ;    1 0  ;1 . Hướng dẫn giải Chọn A. m  1 Ycbt   2
m  1 m  0   . 0  m  1 
Câu 24: Trong các công thức sau, công thức đúng là
A. sin a b  sin .
a cos b  cos . a sin b .
B. cos a b  cos .
a cos b  sin . a sin b .
C. sin a b  sin .
a sin b  cos . a cos b .
D. cos a b  cos .
a cos b  sin . a sin b . Hướng dẫn giải Chọn B.
Ta có: sin a b  sin .
a cos b  cos .
a sin b ; cosa b  cos . a cosb  sin . a sin b . Câu 25: Số đo góc o
22 30 được đổi sang rađian là 7 A. . B. . C. . D. . 8 12 6 5 Hướng dẫn giải Chọn A.
Câu 26: Trong các khẳng định sau, khẳng định đúng là x(x  2) A.  2  x  2 . B. 2
x 1  3x x 1  9x . x  2 C. 2 2 3x
x  2  x
x  2  3x x .
D. x  2  x  2 . Hướng dẫn giải Chọn A.
Câu 27: Số nghiệm của phương trình 2x  4  x 1  0 là A. 0 . B. 1. C. 2 . D. Vô số. Hướng dẫn giải Chọn A. Ta có  x  x  2 2x4  x 1   2 4 0 0           x . x 1   0  x 1 
Câu 28: Khi giải phương trình 2
3x 1  2x 1  
1 , một học sinh làm theo các bước sau:
Bước 1: Bình phương hai vế của phương trình   1 ta được: 2
3x 1  2x  2 1 2 .  x  0
Bước 2: Khai triển và rút gọn 2 ta được: 2
x  4x  0   . x  4 
Bước 3: Khi x  0 , ta có 2
3x 1  0 . Khi x  4 , ta có 2 3x  1  0 .
Vậy tập nghiệm của phương trình là 0; –  4 .
Nhận xét đúng nhất về lời giải trên là A. Đúng. B. Sai ở bước 1. C. Sai ở bước 2.
D. Sai ở bước 3. Hướng dẫn giải Chọn D.
Vì phương trình 2 là phương trình hệ quả nên ta cần thay nghiệm x  0 ; x  4 vào phương trình   1 để thử lại.
Câu 29: Phương trình 2
ax bx c  0
a  0 có hai nghiệm âm phân biệt khi và chỉ khi   0   0 a  0   0    A.  . B. P  0 . C. P  0 .
D.   0 . P  0  S  0    S  0  S  0  Hướng dẫn giải Chọn C.
Câu 30: 2 và 3 là hai nghiệm của phương trình A. 2
x   2  3 x  6  0. B. 2
x   2  3 x  6  0 . C. 2
x   2  3 x  6  0 . D. 2
x   2  3 x  6  0. Hướng dẫn giải Chọn B  S  2  3 Ta có: 2 2 
pt : x Sx P  0  x   2  3 x+ 6  0 . P  6  2 2
Câu 31: Cho đường tròn C  :  x  3   y   1
 5 . Tiếp tuyến của C  song song với đường thẳng
d : 2x y 10  0 có phương trình là
A. 2x y 1  0 hoặc 2x y 1  0 .
B. 2x y 1  0 .
C. 2x y  0 hoặc 2x y 10  0 .
D. 2x y  0 . Hướng dẫn giải Chọn D.
Đường tròn C có tâm I 3;   1 , bán kính R 5.
Tiếp tuyến  / /d   : 2x y c  0 c  1  0 . 5  c c   0
 : 2x y  0 tm
d I,  R
 5  5  c  5     . 5 c  1  0 
 : 2x y 10  0 L 
Câu 32: Hai cạnh của hình chữ nhật nằm trên hai đường thẳng có phương trình
4x – 3y  5  0, 3x  4 y – 5  0 . Một đỉnh của hình chữ nhật là A2 
;1 . Diện tích của hình chữ nhật là A. 1. B. 2. C. 3. D. 4. Hướng dẫn giải Chọn B.
Khoảng cách từ đỉnh A2; 
1 đến đường thẳng 4x  3y  5  0 là 2
Khoảng cách từ đỉnh A2; 
1 đến đường thẳng 3x  4 y  5  0 là 1
Diện tích hình chữ nhật bằng 2.1  2 . Câu 33: Biết ,
A B, C là các góc trong tam giác ABC . Mệnh đề đúng là
A. sin AC  sin B .
B. cosA C   cos B .
C. tanA C  tan B .
D. cotA C  cot B . Hướng dẫn giải Chọn B. Vì ,
A B, C là ba góc của một tam giác suy ra A C B.
Khi đó sinA C   sinB  sin B; cosA C   cosB  cos B.
tan A C   tanB  tan B; cot A C   cot B  cot B. 2 2 2sin  3sin .
cos  4cos
Câu 34: Cho góc thỏa mãn tan  2 . Giá trị của biểu thức P  là 2 2
5sin  6 cos 9 9 9 24 A. P  . B. P  . C. P   . D. P  . 13 65 65 29 Hướng dẫn giải Chọn A.
Chia cả tử và mẫu của P cho 2 cos ta được 2 2
2 tan  3 tan  4 2.2  3.2  4 9 P    . 2 2 5 tan  6 5.2  6 13
Câu 35: Cho tam giác ABC có AB  6cm, BC  10cm . Độ dài đường trung tuyến xuất phát từ đỉnh A của tam
giác bằng 5cm . Diện tích tam giác ABC là A. 24cm. B. 48cm. C. 30cm. D. 60cm. Hướng dẫn giải Chọn A. 2 b  2 2 c a
Áp dụng công thức đường trung tuyến 2 m  
ta suy ra AC  8cm . a 2 4 1
Nhận xét: tam giác ABC vuông tại A nên S
AB.AC  24cm. 2 3 3 3
b c a 2   a
Câu 36: Tam giác ABC thỏa mãn hệ thức  b c a
. Khẳng định đúng nhất về tam giác
cos A C  3cos B  1  ABC là
A. Tam giác ABC vuông cân.
B. Tam giác ABC đều.
C. Tam giác ABC vuông.
D. Tam giác ABC cân. Hướng dẫn giải Chọn B. Ta có 3 3 3
b c a 2 *  a 3 3 2
b c a b c 2 2 2
b c bc a  2 cos A  1  A  60 .
b c a 1
* cos  AC  3cos B 1   cos B  3cos B  1  cos B   B  60 . 2
* Vậy ABC là tam giác đều.
Câu 37: Cho a, ,
b c là các số thực dương thỏa mãn f x 2
ax bx c  0 với mọi x   . Giá trị nhỏ nhất 4a c F
của biểu thức F  là min b A. F  5 . B. F  1 . C. F  3 . D. F  2 . min min min min Hướng dẫn giải Chọn D Vì f x 2
ax bx c  0 với mọi x nên ta có 2
  b  4ac  0 2
 4ac b  2 ac b 4a c 4 ac Xét F    2 . b b Vậy F  2 min .
Câu 38: Cho hai đường thẳng  : x y 1  0,  : 2x y 1  0 và điểm P 2 
;1 . Gọi  là đường thẳng đi 1 2
qua P và cắt hai đường thẳng  ,  tại hai điểm ,
A B sao cho P là trung điểm của AB . Phương trình của 1 2  là
A. x  4 y  6  0 .
B. 4x  y  9  0 .
C. 4x  y  7  0 .
D. x  9 y 14  0 . Hướng dẫn giải Chọn C.
Gọi là đường thẳng cần tìm.
Ta có A      A ; a a 1 1   .
B      B ; b 1 2b 2   .  8 a  a b  4 a b  4   P 3
là trung điểm của AB      
a  2  2b  2 a  2b  0 4   b    3  8 11  4 5   4 16  A ; ; B ;      AB  ; .    3 3   3 3   3 3  
Đường thẳng  qua P và có một véc tơ pháp tuyến n 4;  1 có phương trình 4 x  2   1 y  
1  0  4x y  7  0.
Câu 39: Số giá trị nguyên của tham số m để phương trình 2
x  m   2 2
1 x m  2m  0 có hai nghiệm trái
dấu, trong đó nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương là A. 0. B. 1. C. 2. D. Vô số. Hướng dẫn giải Chọn A. 2
Phương trình có hai nghiệm trái dấu khi: m 2m 0 0  m 2(*).
Giả sử phương trình có hai nghiệm 1 x 0 2 x .
Theo yêu cầu bài toán ta có:  x
x   x x  1 x  2 x  0 1 2 0 1 2
0  m 1  0  m 1 (**).
Kết hợp (*), (**) ta có 0  m  1 .
Vậy không có giá trị nguyên nào của m thỏa mãn ycbt.
Câu 40: Cho đường tròn C  2 2
: x y  4x  2 y 1  0 và đường thẳng d có phương trình x y 1  0 . Gọi M  ;
a b là điểm thuộc đường thẳng d sao cho từ M kẻ được hai tiếp tuyến vuông góc đến C  . Khi đó A. 2 a  2 . B. 2 a  4 . C. 2 2 a b  4 .
D. a  b . Hướng dẫn giải Chọn A.
Đường tròn C có tâm I 2 
;1 , bán kính R 6 .
Điểm M thuộc đường thẳng d nên M  ; a 1   a . 0
Theo bài ra M kẻ được đến C  hai tiếp tuyến hợp với nhau góc 90 nên dựa vào hình vẽ dưới ta  0 0 có: BMA  
90  BMI  45 , BI R  6 MI  2 3. B M I A
Do đó: a  2  a  2 2 2 2  12  a  2 .
Câu 41: Số giá trị nguyên thuộc đoạn 20;20 của tham số a để bất phương trình 2
(x  5)(3  x)  x  2x a nghiệm đúng với mọi x 5;  3 là A. 10 . B. 36 . C. 16 . D. 15 . Hướng dẫn giải Chọn C. Đặt 2 2 2 2
t  (x  5)(3 )
x t  x  2x 15  x  2x 15  t . (đk: 0  t  4 ). 2 2
Bất phương trình trở thành: t 15t a t t a 1
 5 0(1) . Ta có hệ số đi với 2 t dương.
Yêu cầu đề bài xảy ra bpt (1) nghiệm đúng với mọi 0  t  4
 Phương trình 2t t a  15  0 có 2 nghiệm phân biệt t 0 4t 1 2 * Cách 1: 1  . f (0)  0 a 15  0 a  15 *        a  5 . 1. f (4)  0 5  a  0 a  5   
Mà a 20; 20 nên có 16 giá trị nguyên của a . Cách 2: t   0  t t   0  t tt  0   * 1 2 1 2 1 2       t  4  t
t  4  0  t  4
t  4 t  4  0  1 2  1 2    1  2  tt  0  1 2 a 15  0 a  15        a  5
t t  4 t t 16  0   5  a  0 a  5 1 2  1 2   
Mà a 20; 20 nên có 16 giá trị nguyên của a .
Câu 42: Số giá trị nguyên thuộc đoạn 100;100 của tham số m để phương trình  1   1  2 x    2mx   1 2m  0 2       xx có nghiệm là A. 1. B. 2. C. 200. D. 199. Hướng dẫn giải Chọn D.
Điều kiện x  0 1
Đặt t x
suy ra t  2 hoặc t  2 . x
Phương trình đã cho trở thành 2
t  2 mt  1  2 m  0 , phương trình này luôn có hai nghiệm là t 1  t 2m 1  1 ; 2 .  3  m  2m1 2 
Theo yêu cầu bài toán ta suy ra  2    . 2m1 2    1 m   2
Mà m 100;100 nên có 199 giá trị nguyên của a . Câu 43: Điều kiện cần và đủ của tham số m để phương trình
x x  2 2 m 2 2 4 – 2
x  2x  4  4m –1  0 có đúng hai nghiệm là
A. 3  m  4 .
B. 2  3  m  4 . m  2 3  m  2  3 C.  . D.  . m  2  3  m  4  Hướng dẫn giải Chọn D. Đặt 2
t x  2x  4 , t   x  2 1  3  3. Phương trình trở thành 2
t  2mt  4m 1  0 2 .
Nhận xét: Ứng với mỗi nghiệm t 3 của phương trình 2  cho ta hai nghiệm của phương trình  
1 . Do đó phương trình  
1 có đúng hai nghiệm khi phương trình 2 có đúng một nghiệm t 3. 2
  m  4m 1  0  m  2  3  2m  3    .  m  4  1.   2 3  2 .
m 3  4m   1  0 
Câu 44: Số giá trị m  1 để phương trình 2
x 1  x m có đúng hai nghiệm là A. 0. B. 1. C. 2. D. Vô số. Hướng dẫn giải Chọn B. 2
x x 1 khi x  0 2 
x 1  x m m f x   . 2 
x x 1 khi x  0 
Biểu diễn đồ thị hàm số f x lên hệ trục tọa độ như hình vẽ bên trên. Dựa vào đồ thị ta suy ra với  5 m  4  thì phương trình 2
x 1  x m có đúng 2 nghiệm. m1  5
Vì m  1 nên m  . 4
Câu 45: Ta biết rằng Mặt Trăng chuyển động quanh Trái Đất theo một quỹ đạo là một elip mà Trái Đất là
một tiêu điểm. Elip có chiều dài trục lớn và trục nhỏ lần lượt là 769 266 km và 768 106 km . Tính
khoảng cách ngắn nhất từ Trái Đất đến Mặt Trăng, biết rằng các khoảng cách đó đạt được khi Trái Đất và
Mặt Trăng nằm trên trục lớn của elip. A. 384 633 km . B. 384 053 km . C. 363 518 km . D. 363 517 km . Hướng dẫn giải Chọn C. 2 2 x y
Phương trình chính tắc của elip có dạng 
 1 a, b  0 . 2 2   a b
Theo giả thiết: 2a  769266  a  384633 ; 2b  768106  b  384053 . 2 2
c a b  21115 .
Khoảng cách ngắn nhất từ Trái Đất đến Mặt Trăng là: a c  363518 km .
Câu 46: Từ hai vị trí ,
A B của một tòa nhà, người ta quan sát đỉnh C của một ngọn núi. Biết rằng độ cao
AB  70m , phương nhìn AC tạo với phương nằm ngang một góc 0
30 , phương nhìn BC tạo với phương nằm ngang một góc 0
15 30 ' . Ngọn núi có độ cao so với mặt đất gần nhất với giá trị sau A. 135m . B. 234m . C. 165m . D. 195m . Hướng dẫn giải Chọn A.   Tam giác ABC có: 0 0 0
BAC  60 , ABC  105 30'  ACB  14 30' .
Áp dụng định lí hàm số sin trong tam giác ABC ta có: AC AB   AC  269,4 m sin B sin C
Chiều cao của ngọn núi là: 0
CH AC.sin 30  135 m.
Câu 47: Cho tam giác ABC nhọn có trực tâm H thuộc đường thẳng 3x  4 y  4  0. Đường tròn ngoại tiếp 2 2  1   5  25
tam giác HBC có phương trình là C : x   y   .    
Giả sử M 2; 3 là trung điểm của cạnh  2   2  4 BC. Tọa độ đỉnh A là  1   1   3  A. A 1;    . B. A ;0   . C. A3  ;1 . D. A 5;   .  2   2   2  Hướng dẫn giải Chọn D.
Tọa độ điểm H là nghiệm của hệ phương trình:
3x  4 y  4  0 x  2    1  2 2  1   5  25   1  H 2; .   x   y   y   2         2    2  4  2
Gọi H ' là điểm đối xứng với H qua đường thẳng BC.Khi đó H ' thuộc đường tròn ngoại tiếp tam giác ABC .  1 5  5
Đường tròn C  có tâm I ;   , bán kính R  .  2 2  2
Giả sử đường tròn ngoại tiếp tam giác ABC có tâm I ' , bán kính R' .
Phép đối xứng qua đường thẳng BC biến tam giác HBC thành tam giác H ' BC do đó biến đường tròn
ngoại tiếp tam giác HBC thành đường tròn ngoại tiếp tam giác H ' BC hay chính là đường tròn ngoại tiếp tam giác ABC . 5
Ta có M là trung điểm của II ' và R'  R  . 2  7 7  Suy ra I ' ; .    2 2     3 
Ta có AH  2I ' M A 5; .    2 
Câu 48: Cho hình thoi ABCD có diện tích S  20 , một đường chéo có phương trình d : 2x y  4  0 và
D 1; 3 . Biết đỉnh A có tung độ âm. Tọa độ đỉnh A là
A. A5; 6 .
B. A1; 2 .
C. A1; 2 .
D. A11; 18 . Hướng dẫn giải Chọn A.
Vì D d nên đường thẳng d là phương trình của đường chéo AC .
Phương trình của BD là x  2 y  7  0 .
Gọi I AC BD I 3; 2 .
Mặt khác I là trung điểm của BD nên B 5;   1  IB  5 . 1
Diện tích hình thoi là S
AC.BD  2I .
A IB . Mà S  20  IA  2 5 . 2
Lại có A d A a; 4  2a .
a  1  A1;2 IA  2 5  
a  5  A5; 6   
Vì đỉnh A có tung độ âm nên A5; 6 .
Câu 49: Cho Elip  E có tiêu cự bằng 6 và đi qua điểm A0;5 . Gọi S là diện tích lớn nhất của hình chữ
nhật nội tiếp  E . Khi đó 5 A. S  34 .
B. S  10 34 . 2 C. S  40 .
D. S  5 34 . Hướng dẫn giải Chọn B. 2 2 x y
* Phương trình chính tắc của elip có dạng 
 1 a, b  0 . 2 2   a b 2 2 0 5
Theo giả thiết: 2c  6  c  3 . Vì A0;5  E  nên ta có phương trình: 2   1 b  25 . 2 2 a b Khi đó: 2 2 2 2 2 2
a b c a  5  3 2
a  34  a  34 . 2 2 x y * Gọi M  ;
x y  là một đỉnh của hình chữ nhật nội tiếp  E  . Khi đó   1 . 34 25
Diện tích hình chữ nhật này là 4 xy . 2 2 x y 2 xy 4 xy Áp dụng bđt Cauchy: 1 =   =  4 xy  10 34 . 34 25 5 34 10 34 2 2 x y 1 Dấu “=” xảy ra khi   . 34 25 2 Vậy S  10 34 .
Câu 50: Cho tam giác ABC với các cạnh AB c, AC b, BC a . Trong các mệnh đề sau, mệnh đề sai là    
A. Nếu I là tâm đường tròn nội tiếp tam giác ABC thì aIA bIB cIC  0 .
B. Với mọi điểm M trong mặt phẳng ta luôn có 2 2 2
aMA bMB cMC abc .
C. Một vectơ chỉ phương của đường phân giác trong của góc A của tam giác ABC là  1  1  u AB AC . AB AC    
D. Nếu H là trực tâm của tam giác ABC thì sinA HA  sinB HB  sinC HC  0 . Hướng dẫn giải Chọn D.    
Nếu H là trực tâm của tam giác ABC thì tanA HA  tanB HB  tanC HC  0 .
Document Outline

  • 11_Toan_DE_KHAO_SAT_TOAN_10_MA_832
  • 11_Toan_DAP_AN_CHI_TIET_KS_TOAN_10