Đề khảo sát Toán 9 đợt 1 năm 2024 – 2025 phòng GD&ĐT Ba Đồn – Quảng Bình

PHÒNG GD&ĐT TX BA ĐỒN KỲ THI KHẢO SÁT CHẤT LƯỢNG LỚP 9 ĐỢT 1 NĂM HỌC 2024-2025 ĐỀ CHÍNH THỨC
Khóa ngày 11 tháng 02 năm 2025 Môn thi: TOÁN
Thời gian: 120 phút (không kể thời gian giao đề)
SỐ BÁO DANH:……………
Đề gồm có 02 trang và 20 câu MÃ ĐỀ: 01
I. PHẦN TRẮC NGHIỆM (4,0 điểm) Trong các câu từ câu 1 đến câu 16 đều có 4
phương án trả lời A,B,C,D .Trong đó chỉ có một phương án đúng .Hãy chọn và ghi vào bài
làm chữ cái đứng trước phương án trả lời đúng Mỗi câu chọn đúng được 0,25 điểm.
Câu 1 Căn bậc ba của -27 là A. 3. B. 9. C. -9. D. -3.
Câu 2 Kết quả của phép tính 2 2 ( 3) − 7 bằng A. -21 B. 21 C. -42 D. 42
Câu 3 Phương trình bậc hai x2 + 3x - 2 = 0 có hệ số a,b,c lần lượt là A. 1 ; 3; 2 B. 1; -3; -2 C. 1; 3; -2 D. 1; -3; 2
Câu 4 Cặp số (x;y) nào là nghiệm của hệ phương trình 2x + y =1 
x − y = 2 A. (-1;-1);
B.(1; 1); C. (-1;1).; D. (1;-1).
Câu 5 Hàm số y = x2 có đồ thị là một parabol đi qua điểm
A. (-1;1) B. (1;-1) C. (1; 0) D. (0; -1)
Câu 6 Điều kiện xác định của phương trình 3 2x + 3 3− x − = là x −1 x + 2 2 A. x ≠ 1, − x ≠ 2
− . B. x ≠1, x ≠ 2 − .
C. x ≠1, x ≠ 2. D. x ≠ 1, − x ≠ 2.
Câu 7 . Giá trị của a để điểm M(− 2;2) thuộc đồ thị hàm số y = ax2 là A. 1 − B. 1 C. 1 − D. 2 2 2
Câu 8 Mức lương tối thiểu cho một giờ làm việc của người lao động là 50000 đồng. Nếu
gọi mức lương một giờ làm việc của người lao động đó là x (đồng) thì
A. x < 50000.
B. x > 50000.
C. x ≤ 50000. D. x ≥ 50000.
Câu 9 Cho tam giác ABC vuông tại A có AB = 18; AC = 24. Bán kính đường tròn ngoại tiếp tam giác đó bằng A. 30. B. 20. C. 15. D. 15 2 .
Câu 10 Tâm đường tròn ngoại tiếp tam giác vuông nằm ở
A.đỉnh góc vuông. B.trong tam giác. C.trung điểm cạnh huyền. D.ngoài tam giác.
Câu 11 Cho (O;2cm) và dây AB = 2cm. Khoảng cách từ tâm O đến AB bằng A. 1 cm. B. 3 cm. C. 1 cm. 2 3 D. 3 cm. 2
Câu 12 Trong tam giác ABC vuông tại A có AC = 3; AB = 4. Khi đó tanB bằng A. 3 . B. 3 . C. 4 . D. 4 . 4 5 5 3
Câu 13 Trong tam giác ABC vuông tại A có AC = 3; AB = 4. Khi đó sinB bằng A. 3 . B. 3 . C. 4 . D. 4 . 4 5 5 3 A
Câu 14 Tam giác ABC nội tiếp đường tròn (O; 5cm) (như hình vẽ ).
Biết AB = 5 cm. Khi đó số đo của cung nhỏ AC là B A. 300 B. 600 C. 1200 D. 1500 O C
Câu 15 Trên hình bên, số đo cung nhỏ PQ bằng 800. Số đo góc QMP M bằng P A. 400. B. 500. C. 600. D. 700. O
Câu 16 Nếu hai đường tròn (O;5cm), (O’;3cm) và khoảng cách hai tâm
là 7cm thì hai đường tròn Q A.tiếp xúc ngoài. B.tiếp xúc trong. C.không có điểm chung.
D.cắt nhau tại hai điểm.
II. PHẦN TỰ LUẬN (6,0 điểm)
Câu 17. (1,5 điểm)
1) Thực hiện phép tính: 1 1 48 − 32 − 75 − 50 . 2 5 2) Cho biểu thức 3 1 1 P = ( + ) :
với x ≥ 0, x ≠1. x −1 x +1 x −1 a) Rút gọn P b) So sánh P với 1
Câu 18. (2,0 điểm) Giải các phương trình, hệ phương trình sau: a) 2
3x − 4x − 4 = 0. 5x −3y =13 b)   2x − + y = 6
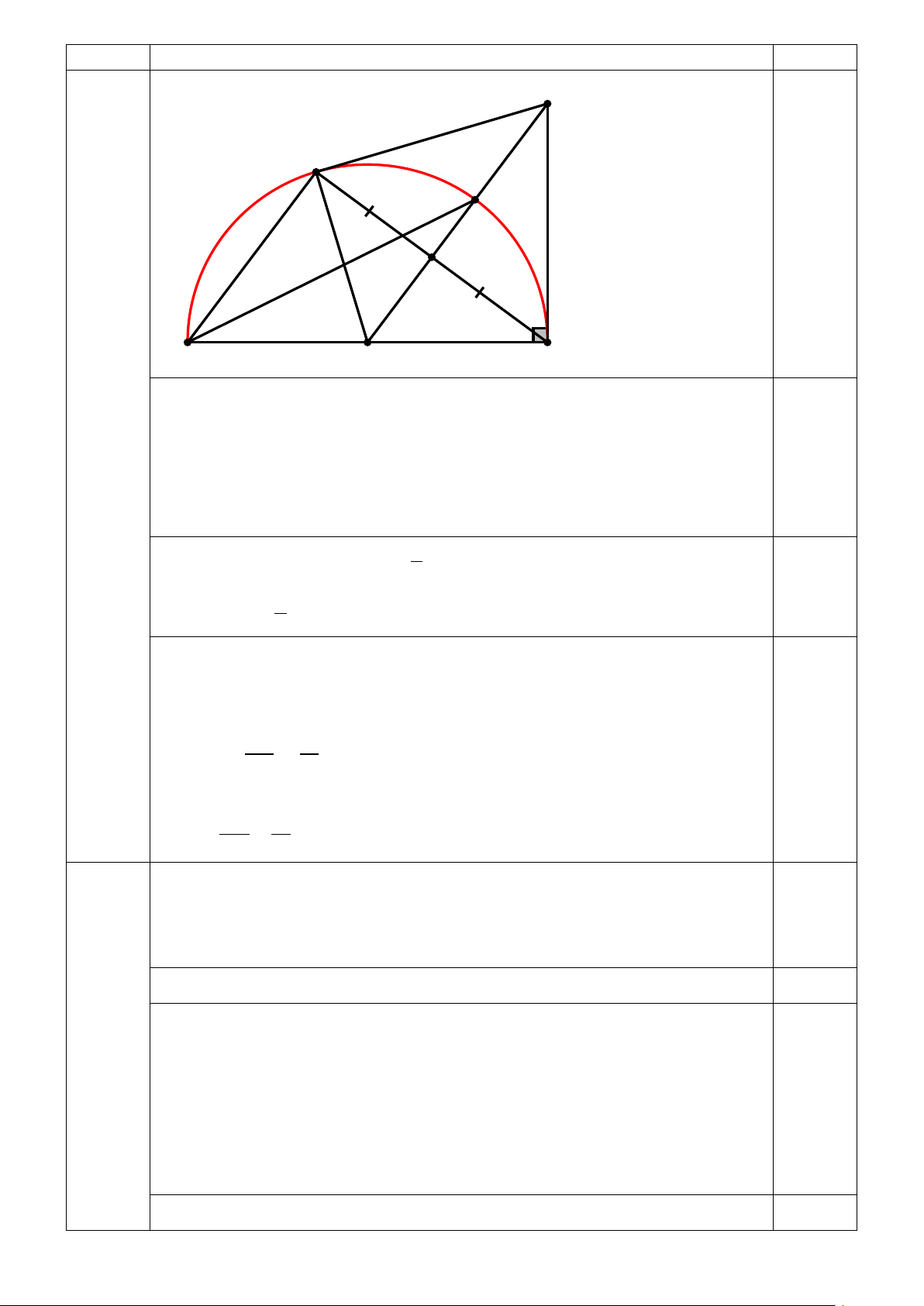
Câu 19 (1,5 điểm) Cho nửa đường tròn (O) đường kính AB . Lấy điểm C nằm trên nửa
đường tròn (O) . Gọi K là trung điểm của dây cung BC . Qua B dựng tiếp tuyến với (O)
cắt OK tại D .
a) Chứng minh DC là tiếp tuyến của đường tròn (O)
b) Gọi E là giao điểm của OD với (O) . Chứng minh  1 =  CAE DOB 2 c) Cho  CAE 30° =
. Hãy tính độ dài cung BC và diện tích hình quạt tròn COB với
AB =12cm . (lấy π = 3,14 )
Câu 20 (1,0 điểm) Thực hiện tung hai con xúc xắc cân đối và quan sát số chấm xuất hiện ở mỗi con xúc xắc.
a) Có bao nhiêu kết quả có thể?
b) Tính xác suất để “Tổng số chấm xuất hiện ở hai xúc xắc bằng 6”.
------------------ Hết ------------------
Giám thị không giải thích gì thêm
PHÒNG GD&ĐT TX BA ĐỒN KỲ THI KHẢO SÁT CHẤT LƯỢNG LỚP 9 ĐỢT 1 NĂM HỌC 2024-2025 ĐỀ CHÍNH THỨC
Khóa ngày 11 tháng 02 năm 2025 Môn thi: TOÁN
Thời gian: 120 phút (không kể thời gian giao đề)
SỐ BÁO DANH:……………
Đề gồm có 02 trang và 20 câu MÃ ĐỀ: 02
I. PHẦN TRẮC NGHIỆM (4,0 điểm) Trong các câu từ câu 1 đến câu 16 đều có 4
phương án trả lời A,B,C,D .Trong đó chỉ có một phương án đúng .Hãy chọn và ghi vào bài
làm chữ cái đứng trước phương án trả lời đúng Mỗi câu chọn đúng được 0,25 điểm.
Câu 1 Căn bậc hai của 36 là A. 6. B. 18. C. -6. D. ±6.
Câu 2 Kết quả của phép tính 2 2 3 ( 7) − bằng
A. 21 B. -21 C. -4 D. 10
Câu 3 Phương trình bậc hai : 5x2 - 3x - 2 = 0 có hệ số a,b,c lần lượt là A. 5; 3; 2 B. 5; -3; -2 C. 5; 3; -2 D. 5; -3; 2
Câu 4 Nghiệm (x;y) của hệ phương trình x +3y = 23  là 2x − y = 4 A. (5; 6 − ) . B. (5;6). C. ( 5; − 6). D. ( 5; − 6 − ) .
Câu 5 Điểm nào sau đây thuộc đồ thị của hàm số 2 y = 4 − x ?
A. 1;4. B. 1;4 C. 4;  1 . D. 4;  1 .
Câu 6 Điều kiện xác định của phương trình là A. B. C. D.
Câu 7 Điểm P(-1;-2) thuộc đồ thị hàm số y = ax2 khi a bằng A. 2 B. -2 C. 4 D. -4
Câu 8 Nghiệm của bất phương trình là: A. . B. . C. . D. .
Câu 9 Cho tam giác ABC vuông tại A có AB = 18; AC = 24. Bán kính đường tròn ngoại tiếp tam giác đó bằng A. 30. B. 20. C. 15. D. 15 2 .
Câu 10 Tâm đường tròn nội tiếp tam giác là giao điểm ba … của tam giác
A. đường cao B. đường trung tuyến C. đường trung trực D. đường phân giác
Câu 11 Cho (O;1cm) và dây AB = 1cm. Khoảng cách từ tâm O đến AB bằng A. 1 cm. 2 B. 3 cm. C. 3 cm. D. 3 cm. 3 2
Câu 12 Trong tam giác ABC vuông tại A có AC = 3; AB = 4. Khi đó tanC bằng A. 3 . B. 3 . C. 4 . D. 4 . 4 5 5 3
Câu 13 Trong tam giác ABC vuông tại A có AC = 3; AB = 4. Khi đó sinC bằng A. 3 . B. 3 . C. 4 . D. 4 . 4 5 5 3 A
Câu 14 Tam giác ABC nội tiếp đường tròn (O;4cm) (Như hình vẽ ).
Biết AB = 4cm. Khi đó số đo của cung nhỏ AB là B A. 300 B. 600 C. 1200 D. 1500 O C
Câu 15 Trên hình bên, số đo cung nhỏ PQ bằng 700. Số đo góc QMP M bằng P A. 350. B. 400. C. 700. D. 1400. O
Câu 16 Nếu hai đường tròn (O;5cm), (O’;3cm) và khoảng cách hai tâm
là 8cm thì hai đường tròn Q A.tiếp xúc ngoài. B.tiếp xúc trong. C.không có điểm chung.
D.cắt nhau tại hai điểm.
II. PHẦN TỰ LUẬN (6,0 điểm)
Câu 17. (1,5 điểm)
1) Thực hiện phép tính: A = − − ( − )2 3 8 50 2 1 . 2) Cho biểu thức 1 1 4 B = − +
x + 2 2 − x x − 4 với x ≥ 0 và x ≠4 a) Rút gọn B
b) Tính giá trị của B khi x = 9
Câu 18. (2,0 điểm) Giải các phương trình, hệ phương trình sau: a) 2
3x + 4x − 4 = 0.  4x −3y =17 b)   3x − + y = 9 −
Câu 19 (1,5 điểm) Cho nửa đường tròn (O) đường kính MN. Lấy điểm P nằm trên nửa
đường tròn (O). Gọi A là trung điểm của dây cung NP. Qua N dựng tiếp tuyến với (O) cắt OA tại B.
a) Chứng minh BP là tiếp tuyến của đường tròn (O)
b) Gọi C là giao điểm của OB với (O). Chứng minh  1 =  PMC NOB 2 c) Cho  0
PMC = 30 . Hãy tính độ dài cung PN và diện tích hình quạt tròn PON với
MN = 6cm. (lấy π = 3,14 )
Câu 20 (1,0 điểm) Thực hiện tung hai con xúc xắc cân đối và quan sát số chấm xuất hiện ở mỗi con xúc xắc.
a) Có bao nhiêu kết quả có thể?
b) Tính xác suất để “Tổng số chấm xuất hiện ở hai xúc xắc bằng 7”.
------------------ Hết ------------------
Giám thị không giải thích gì thêm.
PHÒNG GD&ĐT TX BA ĐỒN
KỲ THI KHẢO SÁT CHẤT LƯỢNG LỚP 9 ĐỢT 1
Khóa ngày 11 tháng 02 năm 2025 HƯỚNG DẪN CHẤM Môn thi: TOÁN
Đáp án này gồm có 06 trang YÊU CẦU CHUNG
* Đáp án chỉ trình bày một lời giải cho mỗi bài. Trong bài làm của thí sinh yêu cầu
phải lập luận lôgic chặt chẽ, đầy đủ, chi tiết và rõ ràng.
* Trong mỗi bài, nếu thí sinh giải sai ở bước giải trước thì cho điểm 0 đối với những
bước giải sau có liên quan.
* Ở câu 19 nếu thí sinh không vẽ hình thì cho 0 điểm.
* Điểm thành phần của mỗi bài nói chung phân chia đến 0,25 điểm. Đối với điểm
thành phần là 0,5 điểm hoặc 0,75 điểm thì tuỳ tổ giám khảo thống nhất để chiết thành từng 0,25 điểm.
* Thí sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tuỳ theo mức điểm của từng bài.
* Điểm của toàn bài là tổng (không làm tròn số) của điểm tất cả các bài. MÃ ĐỀ: 01
I. TRẮC NGHIỆM (4,0 điểm)
Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Đáp án D B C D A B B D C C B A B C A D
II. TỰ LUẬN (6,0 điểm) Câu Nội dung Điểm
1) Thực hiện phép tính: 1 1 48 − 32 − 75 − 50 . 0,5 2 5 1 1 48 − 32 − 75 − 50 2 5 1 1
= .4 3 − 4 2 − 5 3 − .5 2 0,25 2 5
= 2 3 − 4 2 − 5 3 − 2 = (2 − 5) 3 − (4 +1) 2 = 3 − 3 − 5 2 0,25 17 2) Cho biểu thức 3 1 1 P = ( + ) :
với x ≥ 0, x ≠1. x −1 x +1 x −1 (1,5 1.0 a) Rút gọn P điểm) b) So sánh P với 1 a) 3 1 1 P = ( + ) :
với x ≥ 0, x ≠ 1. 0,5 x −1 x +1 x −1 3 1 1 P = ( + ) : 0,25 ( x −1)( x +1) x +1 x −1 3 + x −1 x −1 x + 2 = . = ( x −1)( x +1) 1 x +1 0,25 1 Câu Nội dung Điểm b) So sánh P với 1 0,5 với x + x + +
x ≥ 0, x ≠ 1 ta có 2 1 1 1 P = = = 1+ 0,25 x +1 x +1 x +1
Do 1 > 0 nên P >1 x +1 0,25 Vậy P >1
Giải các phương trình, hệ phương trình 2,0 a) 2
3x − 4x − 4 = 0. 1,0 Pt có: a = 3, b = -4, c = -4 2 2
∆ = b − 4ac = ( 4) − − 4.3.( 4) − = 16 + 48 = 64 0,25 ∆ = 64 = 8
Do ∆ = 64 > 0nên phương trình có hai nghiệm phân biệt 0,25 b − + ∆ −( 4) − + 8 12 x = = = = 2 1 2a 2.3 6 0,25 b − − ∆ −( 4) − − 8 4 − 2 x − = = = = 2 2a 2.3 6 3
Vậy phương trình có hai nghiệm 2 18 x 2, x − = = 1 2 3 0,25 (2,0 điểm) 5x −3y =13 b)   1,0  2x − + y = 6  5x −3y =13   0,25  6 − x +3y =18  −x = 31   0,25  6 − x +3y =18 x = 31 −  0,25 y = 56 −
Vậy hệ phương trình đã cho có nghiệm duy nhất: (–31; –56) 0,25
Cho nửa đường tròn (O) đường kính AB . Lấy điểm C nằm trên
đường tròn (O) . Gọi K là trung điểm của dây cung BC . Qua B
dựng tiếp tuyến với (O) cắt OK tại D .
a) Chứng minh DC là tiếp tuyến của đường tròn (O) 19 1,5
(1,5 b) Gọi E là giao điểm của OD với (O) . Chứng minh  1 =  CAE DOB điểm) 2 c) Cho  CAE 30° =
. Hãy tính độ dài cung BC và diện tích hình quạt
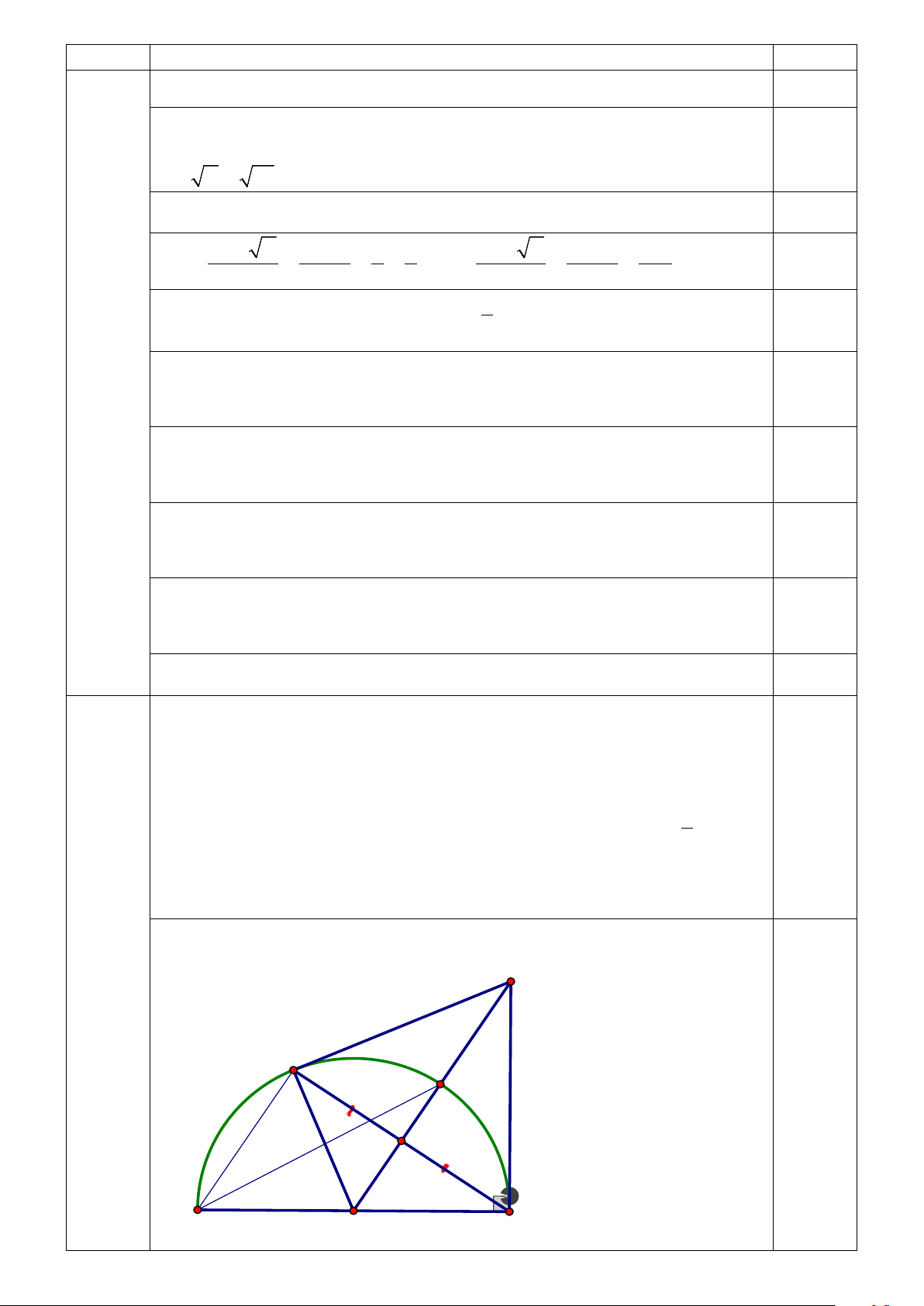
tròn COB với AB =12cm. (lấy π = 3,14 ) Vẽ hình đúng 0,25 2 Câu Nội dung Điểm D C E K A O B a) Ta có K ∆ OC = K
∆ OB (c − c − c) nên  =  KOC KOB Từ đó DOC ∆ = DOB ∆
(c − g − c) suy ra 0,25  =  DCO DBO
Suy ra DC ⊥ OC tại C Vậy 0,25
DC là tiếp tuyến với (O) b) Có  =  COD DOB 1 mà  =  CAE
COD (góc nội tiếp đường tròn) 2 0,25 Do đó  1 =  CAE DOB 2 c) Vì  CAE 30° = nên  COD 60° = Mà  
COB 2 COD 2 60° 120° = ⋅ = ⋅ = Độ dài cung tròn BC 120 12 l 0,25  = ⋅π. = 3,14⋅4 =12,56cm BC 180 2
Diện tích hình quạt tròn COB 120 12 2 2 S = π = = 0,25 qCOB ( ) 3,14.12 37,68cm 360 2
Thực hiện tung hai con xúc xắc cân đối và quan sát số chấm xuất
hiện ở mỗi con xúc xắc.
a) Có bao nhiêu kết quả có thể? 1,0
b) Tính xác suất để “Tổng số chấm xuất hiện ở hai xúc xắc bằng 6”.
a) Có bao nhiêu kết quả có thể? 0,5
Các kết quả có thể là:
1−1;1− 2;1− 3;1− 4;1− 5;1− 6;
2 −1;2 − 2;2 − 3;2 − 4;2 − 5;2 − 6 20 0,25 (1,0
3−1;3− 2;3− 3;3− 4;3− 5;3− 6
điểm) 4 −1;4 − 2;4−3;4− 4;4−5;4− 6
5 −1;5 − 2;5 − 3;5 − 4;5 − 5;5 − 6
6 −1;6 − 2;6 − 3;6 − 4;6 − 5;6 − 6.
Số kết quả có thể là: 36. 0,25 3 Câu Nội dung Điểm
b) Tính xác suất để “Tổng số chấm xuất hiện ở hai xúc xắc bằng 6”. 0,5
Theo bảng trên, số kết quả thuận lợi cho biến cố: “Tổng số chấm xuất hiện 0,25
ở hai xúc xắc bằng 6” là 5.
Do đó xác suất để “Tổng số chấm xuất hiện ở hai xúc xắc bằng 6” xuất 0,25
hiện ở hai xúc xắc là 5 . 36 MÃ ĐỀ: 02
I. TRẮC NGHIỆM (4,0 điểm)
Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Đáp án D A B B A D B C C D C D C B A A
II. TỰ LUẬN (6,0 điểm) Câu Nội dung Điểm
1) Thực hiện phép tính: A = − − ( − )2 3 8 50 2 1 . 0,5
A = 6 2 − 5 2 − 2 −1 0,25
= 2 − 2 +1 =1(vì 2 −1 > 0 ) 0,25 2) Cho biểu thức 1 1 4 B = − +
x + 2 2 − x x − 4 với x ≥ 0 và x ≠4 1.0 a) Rút gọn B
b) Tính giá trị của B khi x = 9 a) 1 1 4 B = + +
với x ≥ 0, x ≠ 4 . 0,5 x + 2 x − 2 ( x + 2)( x − 2) x − 2 x + 2 4 17 B = + +
( x + 2)( x − 2) ( x − 2)( x + 2) ( x − 2)( x + 2) (1,5 điểm) x − 2 x + 2 4 = + + 0,25
( x + 2)( x − 2) ( x − 2)( x + 2) ( x − 2)( x + 2) x − 2 + x + 2 + 4 + + = 2 x 4 2( x 2) = = ( x + 2)( x − 2)
( x + 2)( x − 2) ( x + 2)( x − 2) 2 B = 0,25 x − 2
b) Tính giá trị của B khi x = 9 0,5 với 2
x ≥ 0, x ≠ 4 ta có B = 0,25 x − 2
Thay x = 9 (TM) vào biểu thức B ta được A = 2 = 2 = 2 0,25 9 − 2 1
Giải các phương trình, hệ phương trình 2,0 4 Câu Nội dung Điểm 18 a) 2
3x + 4x − 4 = 0. 1,0 (2,0
điểm) Pt có: a = 3, b = 4, c = -4 2 2
∆ = b − 4ac = 4 − 4.3.( 4) − = 16 + 48 = 64 0,25 ∆ = 64 = 8
Do ∆ = 64 > 0 nên phương trình có hai nghiệm phân biệt 0,25 b − + ∆ 4 − + 8 4 2 x − − ∆ − − − = = = = b 4 8 12 x = = = = 2 − 0,25 1 2a 2.3 6 3 2 2a 2.3 6
Vậy phương trình có hai nghiệm 2 x = , x = 2 − 1 2 3 0,25  4x −3y =17 b)   1,0  3x − + y = 9 −  4x −3y =17   0,25  9 − x +3y = 27 −  5 − x = 10 −   0,25  3x − + y = 9 −  x = 2  0,25 y = 3 −
Vậy hệ phương trình đã cho có nghiệm duy nhất: (x;y) = (2;–3) 0,25
Cho nửa đường tròn (O) đường kính MN. Lấy điểm P nằm trên
đường tròn (O). Gọi A là trung điểm của dây cung NP. Qua N dựng
tiếp tuyến với (O) cắt OA tại B.
a) Chứng minh BP là tiếp tuyến của đường tròn (O) 1,5
b) Gọi C là giao điểm của OB với (O). Chứng minh  1 =  PMC NOB 2 c) Cho  0
PMC = 30 . Hãy tính độ dài cung PN và diện tích hình quạt
tròn PON với MN = 6cm. (lấy π = 3,14 ) Vẽ hình đúng 0,25 19 (1,5 B điểm) P C A M O N 5 Câu Nội dung Điểm
a) Ta có A là trung điểm của NP và ON = OP
Từ đó OB là đường trung trực của NP Nên BP = BN 0,25 Suy ra OP ∆ B = ON ∆ B (c-c-c)
Suy ra PB ⊥ OP tại P 0,25
Vậy BP là một tiếp tuyến của (O) b) Có OP ∆ B = ON ∆ B nên  =  POB BON Mà  1 =  PMC
POB (góc nội tiếp đường tròn) 0,25 2 Do đó  1 =  PMC NOB 2 c) Vì  0 PMC = 30 nên  0 POB = 60 Mà  =  0 0
PON 2.POB = 2.60 =120
Độ dài cung tròn PN 120 6 l = π = = 0,25 PN 3,14.2 6,28cm 180 2
Diện tích hình quạt tròn PON 120 6 2 2 S = π = = 0,25 qPON ( ) 3,14.3 9,42cm 360 2
Thực hiện tung hai con xúc xắc cân đối và quan sát số chấm xuất
hiện ở mỗi con xúc xắc.
a) Có bao nhiêu kết quả có thể? 1,0
b) Tính xác suất để “Tổng số chấm xuất hiện ở hai xúc xắc bằng 7”.
a) Có bao nhiêu kết quả có thể? 0,5
Các kết quả có thể là:
1−1;1− 2;1− 3;1− 4;1− 5;1− 6;
2 −1;2 − 2;2 − 3;2 − 4;2 − 5;2 − 6
3−1;3− 2;3− 3;3− 4;3− 5;3− 6 0,25
4 −1;4 − 2;4 − 3;4 − 4;4 − 5;4 − 6 20
5 −1;5 − 2;5 − 3;5 − 4;5 − 5;5 − 6 (1,0
6 −1;6 − 2;6 − 3;6 − 4;6 − 5;6 − 6.
điểm) Số kết quả có thể là: 36. 0,25
b) Tính xác suất để “Tổng số chấm xuất hiện ở hai xúc xắc bằng 7”. 0,5
Theo bảng trên, số kết quả thuận lợi cho biến cố: “Tổng số chấm xuất hiện 0,25
ở hai xúc xắc bằng 7” là 6.
Do đó xác suất để “Tổng số chấm xuất hiện ở hai xúc xắc bằng 7” xuất 0,25
hiện ở hai xúc xắc là 6 1 = . 36 6
------------------ Hết ------------------ 6
Xem thêm: KHẢO SÁT CHẤT LƯỢNG TOÁN 9
https://thcs.toanmath.com/khao-sat-chat-luong-toan-9
Document Outline

• De thi-IN
• HD cham-IN
• KS 9