Đề khảo sát Toán 9 lần 1 năm 2024 – 2025 phòng GD&ĐT TP Hải Dương

UBND THÀNH PHỐ HẢI DƯƠNG
ĐỀ KHẢO SÁT LỚP 9-LẦN 1
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC 2024 – 2025 MÔN: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút (Đề gồm 02 trang) Câu 1 (1,5 điểm)
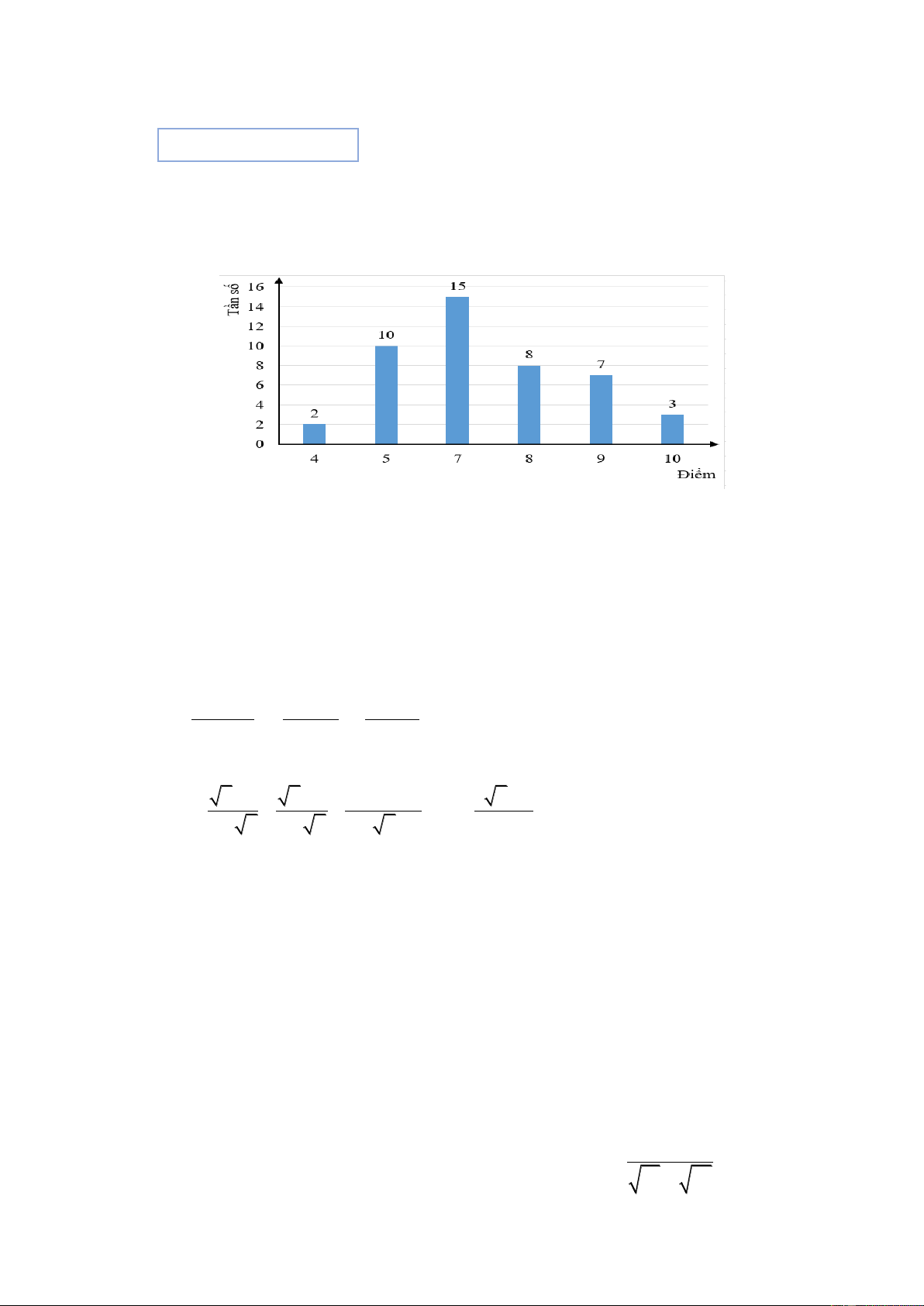
1. Biểu đồ dưới đây biểu diễn kết quả một bài kiểm tra của lớp 9A.
a) Có bao nhiêu giá trị khác nhau của mẫu dữ liệu trên, đó là những giá trị nào?
b) Lập bảng tần số cho dữ liệu được biểu diễn bởi biểu đồ.
2. Một hộp chứa 4 tấm thẻ cùng loại được đánh số 1; 4; 7; 9. Bạn Hùng và bạn Dũng
lần lượt mỗi người lấy ngẫu nhiên ra 1 tấm thẻ từ hộp. Tính xác suất của biến cố A:
“Tổng các số ghi trên 2 tấm thẻ mà hai bạn lấy được là số lẻ”. Câu 2 (2,0 điểm)
1. Giải phương trình và hệ phương trình sau:  + = x + 1 1 1 2x y 5 a) = + b)  2 1 - 9x 1 + 3x 1 - 3x
x − 3y = −8 2. Rút gọn biểu thức:  x −3 x + 2 9 − x   3 x − 9  P =  + −  :1−    
 (với x  0; x  4; x  9 ) 2 − x 3 + x x + x − 6 x − 9     Câu 3 (2,0 điểm)
1. Bác Tuấn chia số tiền 700 triệu đồng của mình cho hai khoản đầu tư. Lãi
suất cho khoản đầu tư thứ nhất và thứ hai lần lượt là 5,5% ; 6% một năm. Sau một
năm tổng số tiền lãi thu được là 40,5 triệu đồng. Tính số tiền bác Tuấn đầu tư cho mỗi khoản.
2. a) Một người đi bộ trên quãng đường AB dài 18 km. Lúc đầu người đó đi
với tốc độ 5 km/h, về sau đi với tốc độ 4 km/h. Tính độ dài ngắn nhất có thể của
đoạn đường người đó đi với vận tốc 5 km/h để hoàn thành cả quãng đường AB trong
khoảng thời gian không nhiều hơn 4 giờ. b) Cho phương trình 2
x − 12x + 4 = 0 có hai nghiệm là x , x . 1 2 2 x + 2 Không giải x
phương trình, hãy tính giá trị của biểu thức T = 1 2 . x + x 1 2 Câu 4 (1,0 điểm)
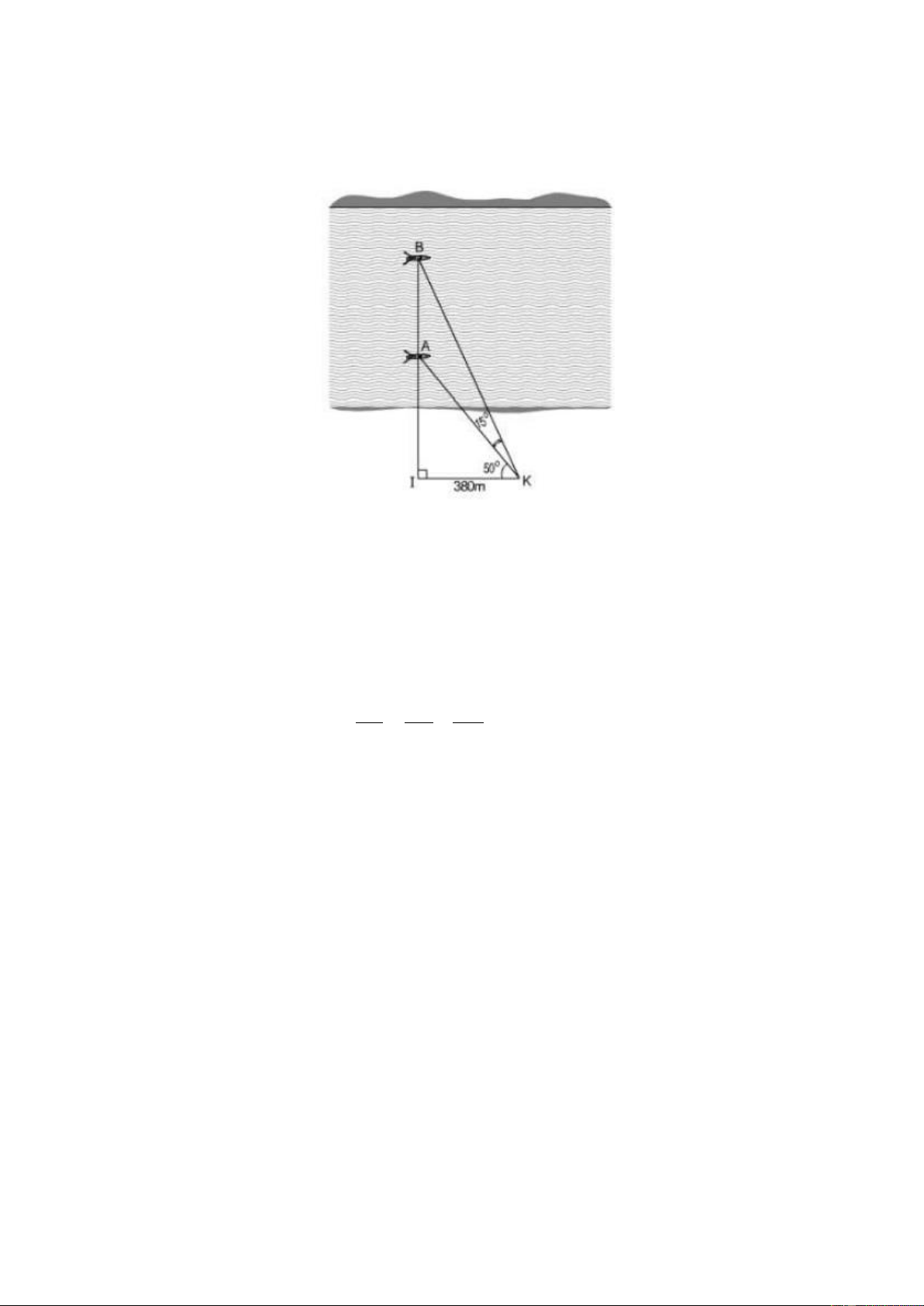
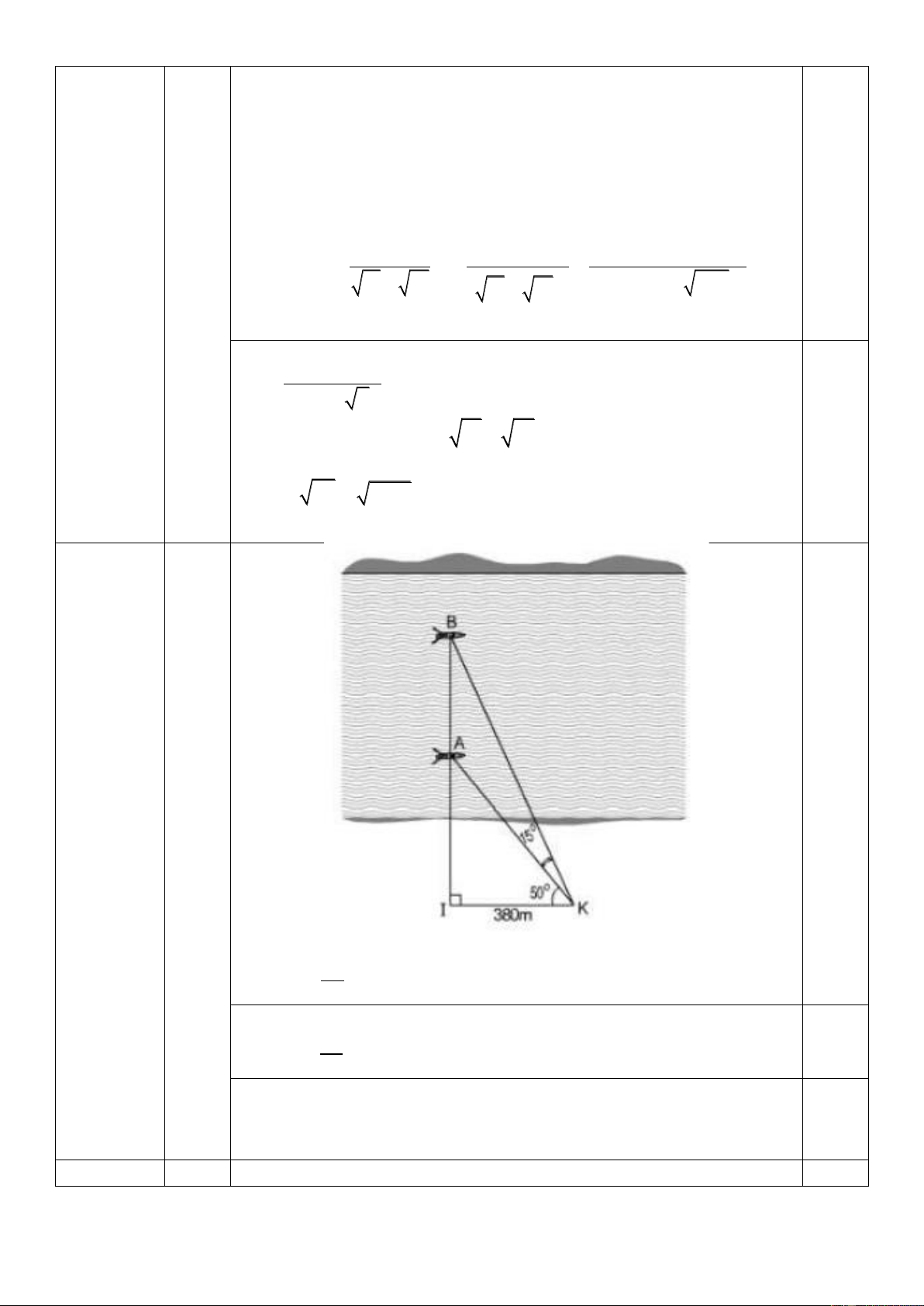
Tính khoảng cách giữa hai chiếc thuyền ở vị trí A và B được minh họa như
hình dưới đây. Biết BKA = 0 15 , AKI = 0
50 , KI ⊥ AB , IK = 380m. (Kết quả làm tròn đến mét) Câu 5 (3,0 điểm)
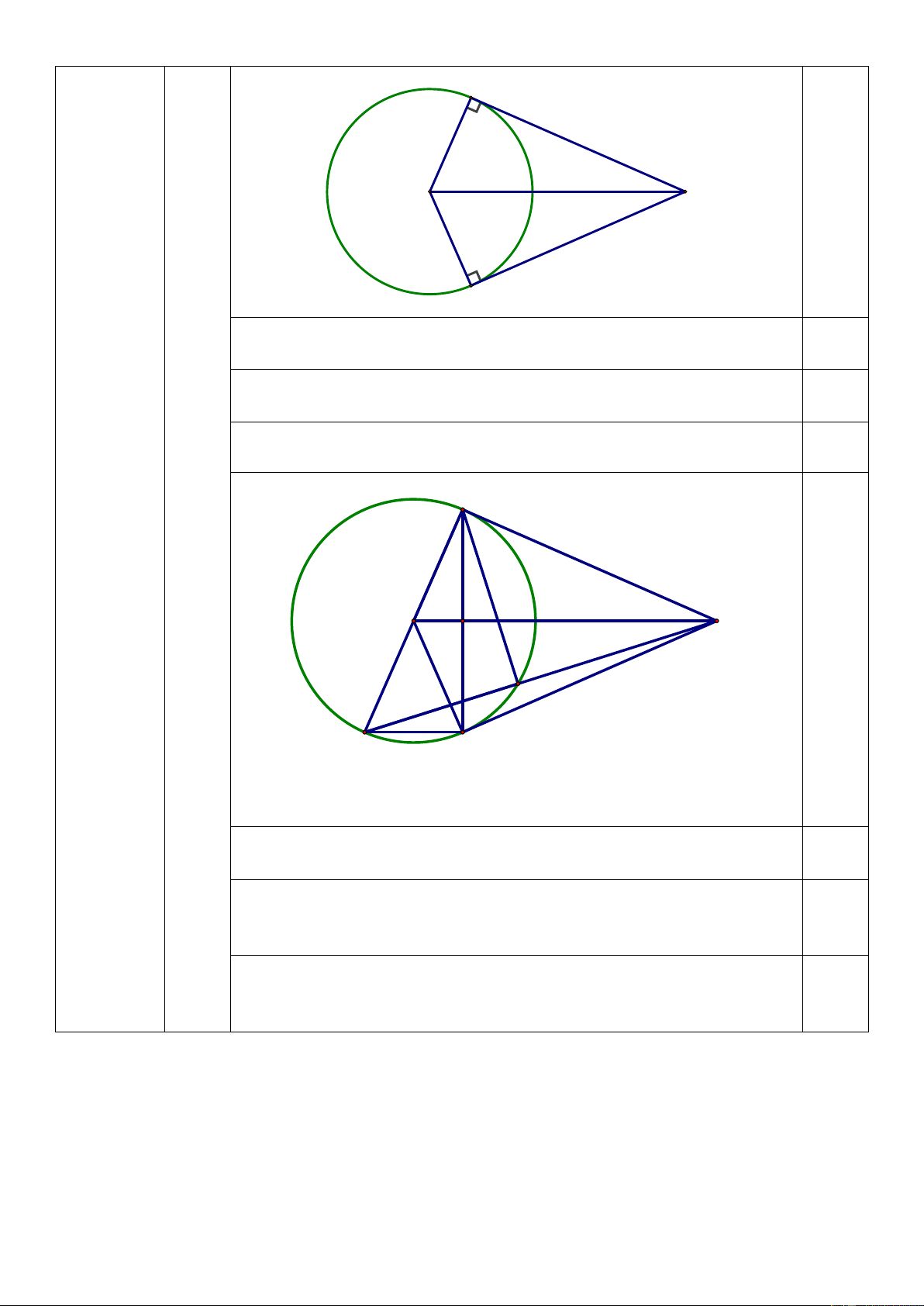
Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Từ A kẻ hai tiếp tuyến
AB và AC với đường tròn (O) (B và C là các tiếp điểm).
a) Chứng minh: Bốn điểm A, B, O, C cùng thuộc đường tròn.
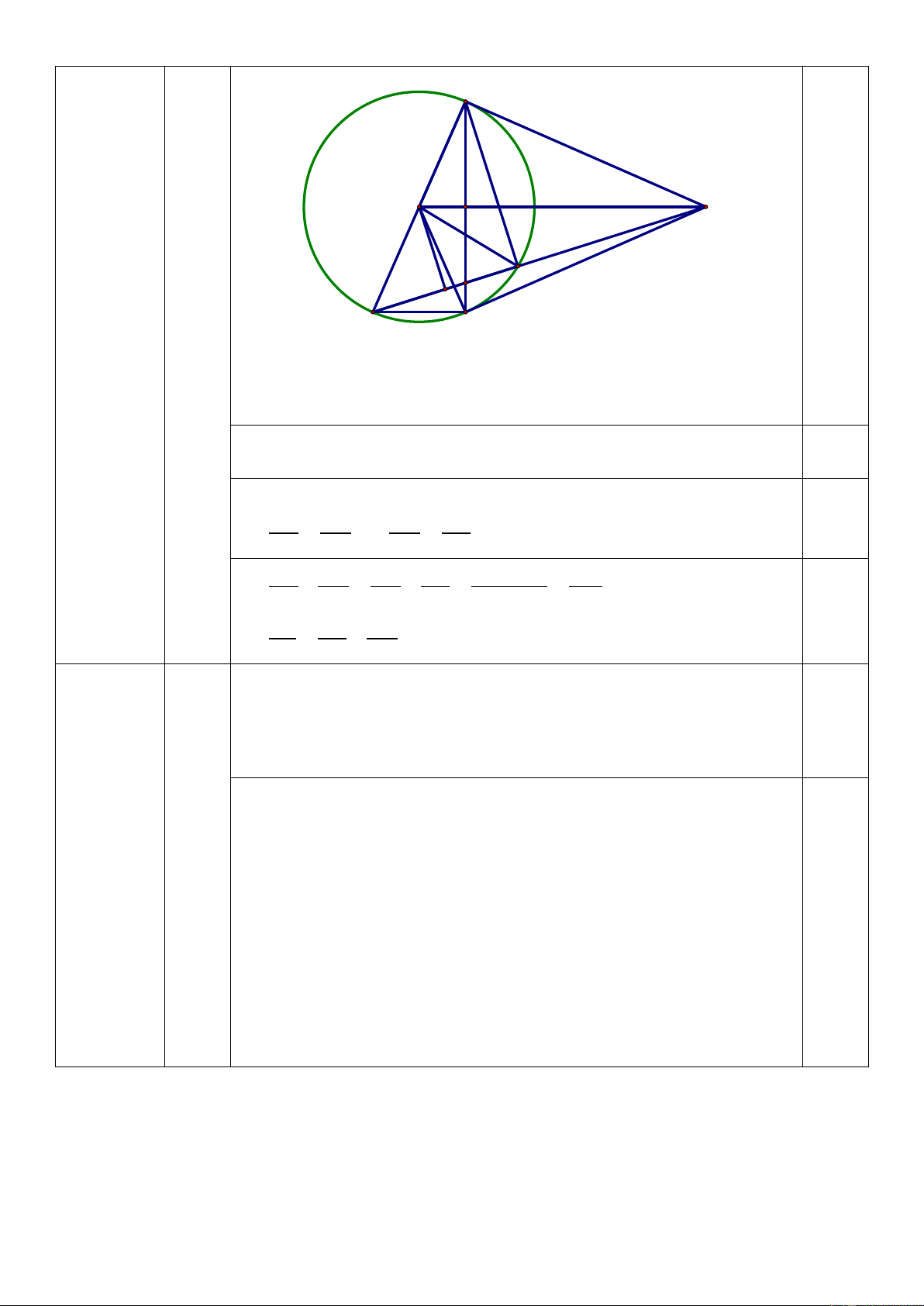
b) Kẻ đường kính BD của đường tròn (O), gọi H là giao điểm của AO và BC.
Tia AD cắt đường tròn (O) tại điểm E (E khác D) và cắt BC tại F. Chứng minh: AH.AO = AE.AD c) Chứng minh rằng: 2 1 1 = + AF AE AD Câu 6 (0,5 điểm)
Một rạp chiếu phim có 120 ghế, giá vé hiện tại là 100 nghìn đồng mỗi vé. Với
giá vé này, tất cả các ghế đều được bán hết cho mỗi suất chiếu. Ban quản lý rạp phim
đang xem xét việc tăng giá vé để tối ưu hóa doanh thu. Sau khi thử nghiệm, rạp phim
nhận thấy cứ mỗi lần tăng giá thêm 5 nghìn đồng thì số ghế bị bỏ trống sẽ tăng thêm
là 4. Hỏi mức giá vé mới là bao nhiêu để rạp phim đạt doanh thu lớn nhất? ----- Hết -----
SBD: .................. Họ và tên thí sinh: ....................................................................................
Giám thị 1: ............................................... Giám thị 2: .........................................................
UBND THÀNH PHỐ HẢI DƯƠNG HƯỚNG DẪN CHẤM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT LỚP 9 - LẦN 1 MÔN TOÁN NĂM HỌC 2024 – 2025
(Hướng dẫn chấm gồm 05 trang) Câu Phần Nội dung Điểm
Có 6 giá trị khác nhau của mẫu dữ liệu trên 0,25 1.a
Những giá trị đó là: 4; 5; 7; 8; 9; 10. 0,25 Bảng tần số: 1.b Điểm 4 5 7 8 9 10 0,5 Tần số 2 10 15 8 7 3 1
Vì 4 tấm thẻ là cùng loại nên các thẻ có cùng khả năng được
chọn. Số cách lấy có thể có là: (1; 4), (1; 7), (1; 9), (4; (1,5 điểm) 1), (4; 7), 0,25
(4; 9), (7; 1), (7; 4), (7; 9), (9; 1), (9; 4); (9; 7). Do đó có 12 cách chọn. 2
Có 6 kết quả thuận lợi cho biến cố A là:
(1; 4), (4; 1), (7; 4), (4; 7), (4; 9), (9; 4) 0,25 Xác suất biến cố A: 6 1 P( ) A = = 12 2 x + 1 1 1 1 1 = + ĐKXĐ: x ¹ - ;x ¹ 2 1 - 9x 1 + 3x 1 - 3x 3 3 x + 1 1 - 3x 1 + 3x 0,25 = +
(1 + 3x)(1- 3x) (1 + 3x)(1- 3x) (1 + 3x )(1- 3x ) 1.a
x + 1 = 1 + 3x + 1 - 3x x + 1 = 2
x = 1 (t / m ) 0,25
Vậy phương trình đã cho có nghiệm là: x = 1
Nhân cả hai vế của phương trình thứ nhất với 3, giữ nguyên 2
phương trình thứ hai, ta được: (2,0 điểm) 6x + 3y = 15   0,25 x − 3y = −8 1.b
Cộng từng vế hai phương trình của hệ mới, ta được 7x = 7 hay x = 1
Thế x = 1 vào phương trình thứ nhất của hệ đã cho ta được 2.1 + y = 5, suy ra y = 3 0,25
Vậy hệ phương trình có nghiệm duy nhất là (x; y) = (1;3)  x −3 x + 2 9 − x   3 x − 9  2 P =  + −  :1−      0,25 2 − x 3 + x x + x − 6 x − 9       x − 3 x + 2 9 − x  3 x − 9  P =  + +   −     2 − x 3 + x
(2− x)(3+ x) : 1  x − 9    
(x−9)+(4− x)+(9− x) x−9−3 x +9 P = ( 0,25 2 − x )(3+ x ) : x − 9 − + − x ( x 3)( x 3 4 ) P = ( 0,25 − x )( + x) : 2 3 x ( x −3) 2 + x + P = . Vậy 2 x P =
(với x  0; x  4; x  9 ) 0,25 x x
2. Gọi x (triệu đồng) là số tiền đầu tư vào khoản thứ nhất.
Gọi y (triệu đồng) là số tiền đầu tư vào khoản thứ hai. Điều kiện: 0 < , x y  700 0,25
Bác Tuấn chia 700 triệu đồng thành hai khoản đầu tư nên x + y = 700 ( ) 1
Tiền lãi của khoản đầu tư thứ nhất: 1
5,5%x = 0,055x (triệu đồng)
Tiền lãi của khoản đầu tư thứ hai: 0,25
6%y = 0,06y (triệu đồng)
Ta có 0,055x + 0,06y = 40,5 (2)
Giải hệ phương trình: được x = 300; y = 400 (thỏa mãn bài toán) 0,25
Số tiền đầu tư vào khoản thứ nhất là 300 triệu đồng
Số tiền đầu tư vào khoản thứ hai là 400 triệu đồng 0,25
Gọi quãng đường người đó đi với vận tốc 5 km/h là x (km) 3   (2,0 điểm ( 0 x 18 ) )
Quãng đường người đó đi với vận tốc 4 km/h là: 18 − x(km) x
Thời gian người đó đi với vận tốc 5 km/h 0,25 là: (h) 5 −
Thời gian người đó đi với vận tốc 4 km/h là: 18 x (h) 4 2a
Vì người đó hoàn thành cả quãng đường AB trong khoảng thời
gian không nhiều hơn 4 giờ nên ta có: x 18 − x +  4 5 4 90 − x  80 0,25 x  10
Vậy độ dài ngắn nhất có thể của đoạn đường người đó đi với vận tốc 5 km/h là 10 km. Xét phương trình: 2
x − 12x + 4 = 0 Ta có  = − 2
' ( 6) − 1.4 = 32  0 nên phương trình có hai nghiệm
phân biệt x ,x 1 2
x + x = 12  0
Theo định lí Viète ta có:  1 2
 x  0,x  x x = 0  4  1 2 0 1 2 0,25 2  2 2 2 x + x ( 2 + 2 2 2 ) (x x 2x x x x 1 2 )  + −  1 2  1 2 1 2 2  Ta có:  T =   = x + 2  x x x 2 x x 1 2  ( x x 1 2 ) =   + + + 1 2 1 2 2b
(Nếu học sinh không chỉ ra x  0, x  0 không trừ điểm) 1 2 (12 −2.4)2 2 2 T = = 1156 12 + 2 4 Nhận xét 2 x + 2
x  0 và x + x  0 với mọi x , x  0 1 2 1 2 1 2 0,25 suy ra T  0 T = 2 T = 1156 = 34 Vây T = 34 . 4 (1,0 điểm ) 0,25
Xét tam giác AIK vuông tại I ta có: AI 0 tan AKI =
 AI = IK.tan AKI = 380.tan 50 IK
Xét tam giác BIK vuông tại I ta có: BI 0,25 tan BKI =
 BI = IK.tan BKI = 380.tan (15 + 50) IK Ta có
AB + AI = BI  AB = BI − AI = ( + ) 0 380.tan 15
50 − 380.tan 50  362(m) 0,5
Vậy khoảng cách giữa chúng là 362m 5 a
Vẽ hình đúng đến câu a 0,25 (3,0 điểm) B O A C
Vì AB là tiếp tuyến của đường tròn (O) nên ABO vuông tại B
=> điểm B thuộc đường tròn đường kính OA 0,25 (1)
Vì AC là tiếp tuyến của đường tròn (O) nên ACO vuông tại C => điểm 0,25
C thuộc đường tròn đường kính OA (2)
Từ (1) và (2) suy ra bốn điểm A, B, O, C cùng thuộc một đường tròn (đpcm) 0,25 B O A H E D C 0,25 Ta có 0
BED = 90 (góc nội tiếp chắn nửa đường tròn)  BE ⊥ AD
Xét ABD vuông tại B, đường cao BE. 0,25
Theo HTL ta có: AB2 = AE. AD (3)
Vì AB, AC là 2 tiếp tuyến cắt nhau tại A nên AB = AC,
mà OB = OC nên OA là đường trung trực của BC, suy ra OA 0,25 vuông góc BC tại H
Xét OAB vuông tại B, đường cao BH. Theo HTL ta có: AB2 = AH. AO (4) 0,25
Từ (3) và (4) ta có AH. AO = AE. AD (đpcm) (5) B O A H E F I D C 0,25 c
Gọi I là trung điểm DE nên AD + AE = 2AI
Vì DOE cân tại O, có OI là đường trung tuyến nên OI đồng
thời là đường cao, suy ra OI vuông góc AD.
C/m được AHF đồng dạng AIO (g.g)  AF. AI = AH. AO (6) 0,25
Từ (5) và (6)  AE. AD = AF. AI  AF AD AF AE 0,25 = và = AE AI AD AI  AF AF AD AE AD + AE 2AI + = + = = = 2 AE AD AI AI AI AI 0,25  2 1 1 = + (đpcm) AF AE AD
Gọi số lần tăng giá là x (lần) ( x  N )
Giá tiền 1 vé sau x lần tăng là (100+5x) (nghìn đồng)
Số ghế đã bán sau x lần tăng giá là 120 – 4 0,25
x (ghế) ( x  30 )
Tổng số tiền thu được: A = (100 + 5x)(120−4x) (nghìn đồng)
Để có doanh thu lớn nhất thì A đạt giá trị lớn nhất 2 A = 2
− 0x + 200x +12000 2 2 2 6 = 2
− 0(x −10x + 5 ) +12500 = 2 − 0(x −5) +12500 (0,5 điểm ) Ta có: - 20(x - 5)2 £ 0 0,25 2 - 20(x - 5) + 12500 £ 12500 A £ 12500
A đạt giá trị lớn nhất khi x = 5 .
Vậy mức giá mới cho một vé là 100 + 25 = 125 (nghìn đồng)
thì rạp phim sẽ đạt doanh thu lớn nhất.
* Chú ý: Nếu học sinh làm cách khác mà đúng thì vẫn cho điểm tối đa