Đề khảo sát Toán 9 năm 2024 – 2025 cụm trường THCS quận Ba Đình – Hà Nội

UBND QUẬN BA ĐÌNH
ĐỀ KHẢO SÁT CHẤT LƯỢNG LỚP 9
CỤM TRƯỜNG: THCS NGUYỄN TRÃI NĂM HỌC 2024 - 2025
THCS NGUYỄN TRI PHƯƠNG Môn: TOÁN THCS THỐNG NHẤT
Ngày khảo sát: 29/05/2025
Thời gian làm bài: 120 phút ĐỀ CHÍNH THỨC Bài I. (1,5 điểm)
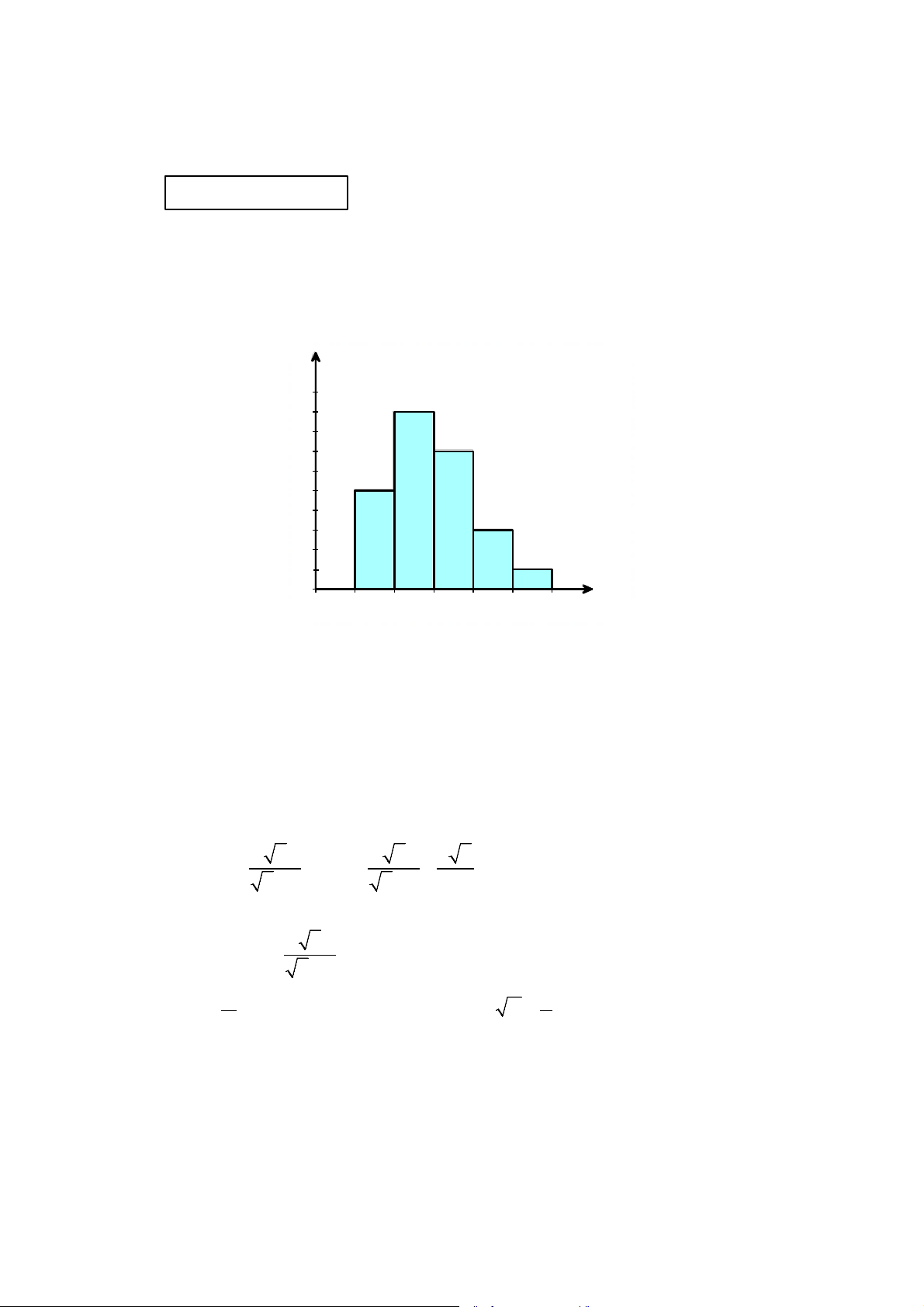
1) Thời gian tự học trong tuần (đơn vị: giờ) của 50 học sinh lớp 9A được biểu diễn trong biểu đồ
tần số ghép nhóm bên dưới. Tần số (n) 20 18 18 16 14 14 12 10 108 6 64 2 2 0 2 9 16 23 30 37 Số giờ
a) Lập bảng tần số ghép nhóm cho dữ liệu được biểu diễn trên biểu đồ.
b) Có ý kiến cho rằng 56% số học sinh của lớp 9A có thời gian tự học trong tuần ít hơn 16
giờ. Thông tin đó có chính xác không? Vì sao?
2) Viết ngẫu nhiên một số tự nhiên nhỏ hơn 20. Tính xác suất của biến cố A: “Số tự nhiên được
viết ra là bội của 5”. Bài II. (1,5 điểm) Cho hai biểu thức x A = và x 4 x B = −
với x ≥ 0, x ≠ 4. x + 7 x + 2 4 − x
1) Tính giá trị của biểu thức A biết x =16 . 2) Chứng minh x B = . x − 2 3) Cho A
P = . Tìm tất cả các giá trị của x để 1 P < . B 2
Bài III. (2,5 điểm)
Giải các bài toán sau bằng cách lập phương trình hoặc hệ phương trình
1) Một nhà hàng buffet áp dụng hai mức giá: một mức giá dành cho người lớn và một mức
giá dành cho trẻ em. Một gia đình gồm ba người lớn và hai trẻ em, khi vào nhà hàng đã thanh toán
1 375 000 đồng. Một gia đình khác gồm hai người lớn và một trẻ em, khi vào nhà hàng đã thanh
toán 875 000 đồng. Hãy xác định giá buffet cho mỗi người lớn và mỗi trẻ em.
2) Một khu vườn hình chữ nhật có chiều dài lớn hơn chiều
rộng là 5 m. Người ta để một lối đi xung quanh vườn rộng 1 m. Phần
đất còn lại dùng để trồng cây có diện tích 644 m2. Tính chiều dài và
chiều rộng của khu vườn đó.
3) Cho phương trình bậc hai (ẩn x): 2
x − ax − 4 = 0 (1). Biết rằng phương trình (1) có hai
nghiệm x , x thỏa mãn hệ thức x − 3x x + x = 5 . Tính giá trị của biểu thức 2
T = x x − 4x . 1 2 1 1 2 2 1 2 1 Bài IV. (4,0 điểm)
1) Một chiếc ly thủy tinh (như hình vẽ), phần phía trên có dạng hình nón có chiều
cao 8 cm, đường kính miệng ly 12 cm.
a) Hỏi chiếc ly trên đựng đầy được bao nhiêu centimet khối nước?
(lấy π ≈ 3,14, coi độ dày của ly không đáng kể).
b) Trong một sự kiện, người ta sử dụng rượu vang và sử dụng loại ly trên.
Mỗi chai rượu vang có dung tích 750ml. Hỏi một chai rượu vang rót được bao nhiêu ly trên biết
rằng lượng rượu rót vào ly mỗi lần chiếm 80% dung tích ly.
2) Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp đường tròn (O; R). Các đường cao AD,
CE, BF của tam giác ABC cắt nhau tại H.
a) Chứng minh tứ giác AEHF là tứ giác nội tiếp.
b) Tia AD cắt đường tròn (O) tại điểm thứ hai là K. Tia KE cắt (O) tại điểm thứ hai là I. Gọi
N là giao điểm của CI và EF. Chứng minh  = 
CIE NEC và CE2 = CN.CI.
c) Gọi M là trung điểm BC. Gọi P là tâm đường tròn ngoại tiếp tam giác AEF. Chứng minh
ba điểm M, N, P thẳng hàng. Bài V. (0,5 điểm)
Bạn Nam gấp một hình lăng trụ đứng tam giác đều có diện tích toàn phần bằng 18 3 dm2. Muốn
hình lăng trụ đứng tam giác đều đó có thể tích lớn nhất thì bạn Nam phải chọn cạnh đáy bằng bao nhiêu dm?
------------------ HẾT ----------------
Cán bộ coi thi không giải thích gì thêm!