Đề kiểm tra 1 tiết chương 1 Giải tích 12 NC trường THPT Thị xã Quảng Trị

Đề kiểm tra 1 tiết chương 1 Giải tích 12 NC trường THPT Thị xã Quảng Trị gồm 4 mã đề 135, 246, 357, 485, mỗi đề gồm 25 câu hỏi trắc nghiệm khách quan, yêu cầu học sinh làm bài trong thời gian 45 phút, đề nhằm kiểm tra kiến thức chủ đề hàm số và đồ thị, đề kiểm tra có đáp án.

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

30 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
---------------------------------------------------------
Họ và tên học sinh: …………………..……………………………………..Lớp: …………..
PHẦN ĐÁP ÁN
Câu Đáp án Câu Đáp án Câu Đáp án
01
09
17
02
10
18
03
11
19
04
12
20
05
13
21
06
14
22
07
15
23
08
16
24
25
Lưu ý: Đối với mỗi câu hỏi, thí sinh chọn và tô kín một ô tròn tương ứng với phương án trả lời đúng.
Câu 1: Cho hàm số

yfx
có đồ thị như hình vẽ bên. Hỏi đồ thị của hàm số

yfx
có bao nhiêu điểm cực trị ?
A. 1 B. 2
C. 3 D. 4
Câu 2: Cho hàm số f (x) có bảng biến thiên như hình vẽ sau
Hàm số f (x) đồng biến trên khoảng nào dưới đây ?
A.

;3 .
B.
(2;0).
C.

2; 2 .
D.

0; 2 .
Câu 3. Cho hàm số

yfx
có đồ thị (C) như hình vẽ. Đường thẳng
1y
cắt (C) tại bao nhiêu điểm ?
A.
0.
B.
1.
C.
2.
D.
3.
Câu 4: Cực tiểu của hàm số
32
31yx x là.
A. 1 B. 0 C. 2 D. - 3
Mã đề 135
-2
-4
O
-3
-1
1
Câu 5: Tâm đối xứng của đồ thị hàm số
21
1
x
y
x
có toạ độ là.
A. (1;2). B. (2;1). C. (-1;2). D. (2; -1).
Câu 6: Giá trị lớn nhất của hàm số
3
231
y
xx trên đoạn [-1; 2] là.
A.

1;2
max 2.y
B.

1;2
max 1.y
C.

1;2
max 15.y
D.

1;2
max 11.y
Câu 7. Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số sau ?
A.
42
31yx x . B.
3
31yx x
C.
21
1
x
y
x
D.
21
1
x
y
x
Câu 8: Cho hàm số
()
f
x
xác định, liên tục trên
và có bảng xét dấu
'( )
f
x
như
sau:
x
– –1 1 2 +
'( )
f
x
+ 0 – 0 – || +
Hàm số
()
f
x
có bao nhiêu điểm cực trị ?
A. 0 B. 1. C. 2. D. 3.
Câu 9. Cho hàm số
21
2
x
y
x
(C). Tiếp tuyến của (C) tại điểm có hoành độ
3x 
có phương trình là.
A.
58.yx
B.
522yx
C.
522yx
D.
58yx
Câu 10. Cho hàm số

yfx
xác định trên
\1
, liên tục trên mỗi khoảng xác định của nó và có bảng biến
thiên như hình vẽ dưới đây.
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số

f
x
là.
A. 1. B. 2. C. 3 D. 4
Câu 11: Cho hàm số

f
x
xác định, liên tục trên R và có đạo hàm cấp một xác định bởi công thức
2
'1fx x
. Mệnh đề nào sau đây đúng ?
A.
12ff
. B.

32ff
. C.

10ff
. D.
01ff
.
+
1
3
++
0
+
+
0
1
x
y
y'
+
1
2
6
4
2
-2
5
O
1
I
Câu 12. Bảng biến thiên sau đây là của hàm số nào trong bốn hàm số được cho ở bốn phương án A, B, C, D ?
x
0
y’ - 0 +
y
2
A.
42
32yx x B.
42
22yx x C.
42
22yx x D.
42
2yx x
Câu 13: Gọi M, N là giao điểm của đường thẳng
1yx
và đường cong
3
1
x
y
x
. Tìm toạ độ trung điểm I của
đoạn thẳng MN là.
A.
1; 1I
B.
11
;
22
I



C.
11
;
22
I



D.

1; 2I
Câu 14: Trong tất cả các giá trị thực của tham số
m
làm cho hàm số

32
32
f
xx mx m xm
đồng
biến trên R, giá trị lớn nhất của
m
là.
A. 0 B. 1 C. 2 D.
2
3
Câu 15: Đồ thị hàm số
2
12
3
x
y
x
x

có bao nhiêu đường tiệm cận ?
A.1 B. 2 C. 3 D. 4
Câu 16. Cho hàm số
2
212
2
xx
y
x

. Xét các mệnh đề sau :
1) Hàm số có hai điểm cực trị.
2) Hàm số đồng biến trên tập

;5 1; . 
3) Hàm số nghịch biến trên khoảng

5;1 .
4) Điểm cực tiểu của đồ thị hàm số là
1; 5
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng ?
A. 1 B. 2 C. 3 D. 4
Câu 17: Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số sau
đây ?
A.
32
32yx x B.
3
31
y
xx
C.
32
31yx x D.
32
31yx x
Câu 18: Tìm m để giá trị nhỏ nhất của hàm số
32
39
y
xxxm 
trên đoạn

0; 4
bằng – 25, khi đó hãy tính
giá trị của biểu thức
21.Pm
A.1 B. 3 C. 5 D. 7.
Câu 19: Tính tổng tất cả các giá trị của tham số m để đồ thị hàm số
2
1
2
x
y
x
xm

luôn có hai đường tiệm cận.
A.
2.
B.
5.
C.
4.
D.
4.
Câu 20: Có bao nhiêu đường thẳng đi qua điểm

1; 2A
và tiếp xúc với đồ thị của hàm số
3
34yx x
?
A. 0 B. 1 C. 2 D. 3
Câu 21: Cho hàm số

yfx
có bảng biến thiên như sau:
x 0 4

y’ + 0 0 +
y 5

3
Có bao nhiêu giá trị nguyên của tham số m để phương trình

0fx m
có 4 nghiệm phân biệt .
A.
6.
B.
7.
C.
8.
D. 9.
Câu 22: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số
422
22yx xm m
có 5 điểm
cực trị. Tìm số phần tử của S.
A. 0. B. 1 C. 2. D. 3
Câu 23: Cho hàm số

yfx
xác định trên
và có đạo hàm

f' x
thỏa
 
f' x 2 x x 3 g x 2018
với
gx 0, x .
Hàm số
y f 1 x 2018x 2019
đồng biến trên khoảng nào ?
A.
4;1
B.

3; 2
C.

0;3
D.

4;5
Câu 24: Cho hàm số

yf
x
. Hàm số

'
yf
x
xác định, liên tục trên R và có đồ thị như hình vẽ. Hàm số
 
42
46
g
x
f
xx x
có bao nhiêu điểm cực trị ?
A.
0.
B.
1.
C.
3.
D.
5.
Câu 25: Có bao nhiêu giá trị nguyên của tham số thực m để phương trình

2
2
cos cos 2 2cos cos cos 2 0m x x x xm xm
có nghiệm thực ?
A. 6. B. 5. C. 4. D. 3.
------------- Hết ---------------


TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
-----------------------------

----------------------------
Họ và tên học sinh: …………………..……………………………………..Lớp: …………..
PHẦN ĐÁP ÁN
Câu Đáp án Câu Đáp án Câu Đáp án
01
09
17
02
10
18
03
11
19
04
12
20
05
13
21
06
14
22
07
15
23
08
16
24
25
Lưu ý:
Đối với mỗi câu hỏi, thí sinh chọn và tô kín một ô tròn tương ứng với phương án trả lời đúng.
Câu 1:
Cho hàm số

yfx
có đồ thị như hình vẽ bên. Hỏi đồ thị của hàm số

yfx
có bao nhiêu điểm cực
trị ?
A.
1
B.
2
C.
3
D.
4
Câu 2:
Cho hàm số f (x) có bảng biến thiên như sau.
Hàm số f (x) nghịch biến trên khoảng nào dưới đây ?
A
.

;0 .
B.
(0;2).
C.

2; 2 .
D.

2; .
Câu 3.
Cho hàm số

yfx
có đồ thị (C) như hình vẽ. Đường thẳng
2y 
cắt (C)
tại bao nhiêu điểm ?
A.
0.
B
.
1.
C.
2.
D
.
3.
Câu 4:
Tâm đối xứng của đồ thị hàm số
1
2
x
y
x
có toạ độ là.
A.
(1;2).
B.
(2;1).
C.
(-2;1).
D.
(2; -1).
Mã đề 246
-2
-4
O
-3
-1
1
Câu 5: Cực đại của hàm số
3
32
y
xx là.
A. 0 B. -1 C. 1 D. 4
Câu 6: Giá trị lớn nhất của hàm số
32
3917yx x x trên đoạn [-2; 4] là.
A.

2;4
max 22.y
B.

2;4
max 20.y
C.

2;4
max 44.y
D.

2;4
max 15.y
Câu 7. Đường cong ở hình vẽ bên là đồ thị của hàm số nào trong bốn hàm số dưới
đây ?
A.
42
31.yx x B.
3
.
2
x
y
x
C.
32
331. yx x x D.
32
31. yx x
Câu 8: Hàm số
42
43yx x có bao nhiêu điểm cực trị ?
A. 0. B. 1. C. 2. D. 3
Câu 9. Cho hàm số
1
2
x
y
x
(C). Tiếp tuyến của (C) tại điểm có hoành độ
3x 
có phương trình là.
A.
35.yx
B.
35.yx
C.
313.yx
D.
35.yx
Câu 10. Cho hàm số

yfx
xác định trên
\1
, liên tục trên mỗi khoảng xác định của nó và có bảng biến
thiên như hình vẽ dưới đây.
Đồ thị của hàm số

f
x
có bao nhiêu tiệm cận ngang ?
A. 1. B. 2. C. 3 D. 4
Câu 11: Cho hàm số

f
x
xác định, liên tục trên R và có đạo hàm xác định bởi công thức

2
'2fx x
.
Mệnh đề nào sau đây sai ?
A.

12ff
. B.

23ff
. C.

11
f
f
. D.
01ff
+∞
-∞
-∞
+∞
0
_
x
y
/
y
+∞
- ∞
_
-1 0
-2
+
-2
+
1
1
Câu 12. Bảng biến thiên sau đây là của hàm số nào trong bốn hàm số được cho ở bốn phương án A, B, C, D ?
x 0
y’ + 0 -
y 2


A.
42
32yx x B.
42
22yx x C.
42
22yx x D.
42
2yx x
Câu 13: Gọi P, Q là giao điểm của đường thẳng
5yx
và đường cong
23
1
x
y
x
. Tìm toạ độ trung điểm I
của đoạn thẳng PQ.
A.

1; 4 .I 
B.

1; 4 .I
C.

1; 4 .I
D.

1; 4 .I
Câu 14: Có bao nhiêu giá trị nguyên của tham số m để hàm số
32
34
f
xxmxmxm
nghịch biến
trên R.
A. 0 B. 1 C. 2 D.
3.
Câu 15: Đồ thị hàm số
2
1
3
x
y
x
x
có bao nhiêu đường tiệm cận ?
A.1 B. 2 C. 3 D. 4
Câu 16. Cho hàm số
2
57
2
xx
y
x

. Xét các mệnh đề sau :
1) Hàm số đồng biến trên mỗi khoảng

;1
và

3; 
2) Hàm số có ba điểm cực trị.
3) Hàm số nghịch biến trên khoảng

1; 3 .
4) Điểm cực đại của đồ thị hàm số là
3;1
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng ?
A. 1 B. 2 C. 3 D. 4
Câu 17: Đường cong trong hình bên là đồ thị của hàm số nào trong bốn
hàm số sâu đây ?
A.
21
1
x
y
x
B.
12
1
x
y
x
C.
21
1
x
y
x
D.
12
1
x
y
x
Câu 18: Tìm m để giá trị nhỏ nhất của hàm số
3
3
y
xxm
trên đoạn

0; 2
bằng 1 ? Khi đó
35m
có giá
trị bằng.
A.2 B. 3 C. - 4 D. 4
4
2
-2
-
5 5
y
x
O
1
-1
Câu 19: Tổng tất cả các giá trị của tham số m để đồ thị hàm số
2
1
4
x
y
x
xm

có đúng một tiệm cận đứng là.
A.
1.
B.
7.
C.
4.
D.
4.
Câu 20: Có bao nhiêu đường thẳng đi qua điểm A ( 0 ; - 1) và tiếp xúc với đồ thị của hàm số
3
31yx x
?
A. 1 B. 2 C. 3 D. 0
Câu 21: Cho hàm số

yfx
có bảng biến thiên như sau:
x 0 2

y’ + 0 0 +
y 2

1
Có bao nhiêu giá trị nguyên của m để phương trình

30fx m
có 4 nghiệm phân biệt.
A.
0.
B.
1.
C.
2.
D. 3.
Câu 22: Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số
422
23
y
xxmm
có 5
điểm cực trị. Tìm số phần tử của S.
A. 0. B. 1 C. 2. D. 3
Câu 23: Cho hàm số

yfx
xác định trên và có đạo hàm

f' x
thỏa
 
f ' x 2 x x 3 g x 2018
với

gx 0, x .
Hàm số

y f 1 x 2018x 2019
có bao nhiêu điểm cực trị ?
A. 0. B. 1 C. 2. D. 3
Câu 24: Cho hàm số
()yfx
có đạo hàm
22
( ) ( 1) ( 9).fx xx x mx
Có bao nhiêu số nguyên dương m để
hàm số
(3 )yf x
đồng biến trên khoảng
(3; ).
A. 5. B. 6. C. 7. D. 8.
Câu 25: Có bao nhiêu giá trị nguyên của tham số m để phương trình
3
3
33sinsin mm x x có nghiệm thực
A.
2.
B.
3.
C.
5.
D.
7.
------------- Hết ---------------


TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
-----------------------------

----------------------------
Họ và tên học sinh: …………………..……………………………………..Lớp: …………..
PHẦN ĐÁP ÁN
Câu Đáp án Câu Đáp án Câu Đáp án
01
09
17
02
10
18
03
11
19
04
12
20
05
13
21
06
14
22
07
15
23
08
16
24
25
Lưu ý:
Đối với mỗi câu hỏi, thí sinh chọn và tô kín một ô tròn tương ứng với phương án trả lời đúng.
Câu 1:
Cho hàm số

yfx
có đồ thị như hình vẽ bên. Hỏi đồ thị của hàm số

yfx
có bao nhiêu điểm cực trị ?
A.
0
B.
1
C.
2
D.
3
Câu 2:
Cho hàm số f (x) có bảng biến thiên như hình vẽ sau
Hàm số f (x) đồng biến trên khoảng nào dưới đây ?
A
.

2;0 .
B.

;2.
C.

2; 2 .
D.

1; 3 .
Câu 3.
Cho hàm số

yfx
có đồ thị (C) như hình vẽ. Đường thẳng
2y 
cắt (C) tại bao nhiêu điểm ?
A.
0.
C
.
1.
B.
2.
D
.
3.
Câu 4:
Cực đại của hàm số
32
31yx x
là.
Mã đề 357
-2
-4
O
-3
-1
1
A. 1 B. 0 C. 2 D. - 3
Câu 5: Tâm đối xứng của đồ thị hàm số
1
2
x
y
x
có toạ độ là.
A. (1;2). B. (2;1). C. (-1;2). D. (-2; 1).
Câu 6: Giá trị lớn nhất của hàm số
3
32yx x
trên đoạn [0; 2] là.
A.

0;2
max 2.y B.

0;2
max 1.y C.

0;2
max 4.y D.

0;2
max 6.y
Câu 7. Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số sau ?
A.
42
31yx x
. B.
3
31yx x
C.
21
1
x
y
x
D.
21
1
x
y
x
Câu 8: Cho hàm số
()
f
x
xác định, liên tục trên
và có bảng xét dấu
'( )
f
x
như sau:
x
– –1 1 2 +
'( )
f
x
- 0 + 0 – || +
Hàm số
()
f
x
có bao nhiêu điểm cực trị ?
A. 0 B. 1. C. 2. D. 3.
Câu 9. Cho hàm số
21
2
x
y
x
(C). Tiếp tuyến của (C) tại điểm có hoành độ
1x 
có phương trình là.
A.
52.yx
B.
58.yx
C.
58.yx
D.
52yx
Câu 10. Cho hàm số

yfx
xác định trên tập
;2 \ 2
, liên tục trên mỗi khoảng xác định của nó và có
bảng biến thiên như hình vẽ dưới đây.
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số

f
x
là.
A. 4. B. 3. C. 2. D. 1.
Câu 11: Cho hàm số

f
x
xác định, liên tục trên R và có đạo hàm cấp một xác định bởi công thức

2
'2fx x
. Mệnh đề nào sau đây đúng ?
-2
2
2
+
y'
y
x
2
0
+
+
0
+
3+
6
4
2
-
2
5
O
1
I
A.
12ff
. B.

32ff
. C.
20ff
. D.
01
f
f
.
Câu 12. Bảng biến thiên sau đây là của hàm số nào trong bốn hàm số được cho ở bốn phương án A, B, C, D ?
x
0
y’ - 0 +
y
1
A.
42
31yx x
B.
42
21yx x
C.
42
21yx x
D.
42
1yx x
Câu 13: Gọi M, N là giao điểm của đường thẳng
3yx
và đường cong
3
1
x
y
x
. Tìm toạ độ trung điểm I của
đoạn thẳng MN là.
A.

5; 2I
B.
15
;
22
I



C.
51
;
22
I



D.
53
;
22
I



Câu 14: Trong tất cả các giá trị thực của tham số
m
làm cho hàm số

32
32
f
xx mx m xm
đồng
biến trên R, giá trị nhỏ nhất của
m
là.
A. 0 B. 1 C. 2 D.
2
3
Câu 15: Đồ thị hàm số
2
11
2
x
y
x
x

có bao nhiêu đường tiệm cận ?
A.4 B. 3 C. 2 D. 1
Câu 16. Cho hàm số
2
212
2
xx
y
x

. Xét các mệnh đề sau :
1) Hàm số có hai điểm cực trị.
2) Hàm số đồng biến trên tập
;5 1; . 
3) Hàm số nghịch biến trên khoảng

5;1 .
4) Điểm cực tiểu của đồ thị hàm số là
1; 5
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng ?
A. 1 B. 2 C. 3 D. 4
Câu 17: Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số sau
đây ?
A.
32
32yx x
B.
32
31yx x
C.
3
31yx x
D.
32
31yx x
Câu 18: Tìm m để giá trị lớn nhất của hàm số
32
39
y
xxxm
trên đoạn

0; 4
bằng 3, khi đó hãy tính giá
trị của biểu thức
21.Pm
A.1 B. 3 C. 5 D. 7.
Câu 19: Tính tổng tất cả các giá trị của tham số m để đồ thị hàm số
2
1
4
x
y
x
xm

luôn có hai đường tiệm cận.
A.
3.
B.
5.
C.
7.
D.
4.
Câu 20: Có bao nhiêu đường thẳng đi qua điểm

1; 2A
và tiếp xúc với đồ thị của hàm số
3
34yx x
?
A. 0 B. 1 C. 2 D. 3
Câu 21: Cho hàm số

yfx
có bảng biến thiên như sau:
x 0 2

y’ + 0 0 +
y 3

1
Có bao nhiêu giá trị nguyên của tham số m để phương trình

20fx m
có đúng 3 nghiệm.
A.
0.
B.
1.
C.
2.
D. 3.
Câu 22: Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số
422
22yx xm m
có 5
điểm cực trị. Tìm số phần tử của S.
A. 0. B. 1 C. 2. D. 3
Câu 23: Cho hàm số

yfx
xác định trên
và có đạo hàm

f' x
thỏa
 
f' x 2 x x 3 g x 2018
với
gx 0, x .
Hàm số
y f 1 x 2018x 2019
nghịch biến trên khoảng nào ?
A.

4;1
B.

3; 2
C.

0;3
D.

4;5
Câu 24: Cho hàm số

yf
x
. Hàm số

'
yf
x
xác định, liên tục trên R và có đồ thị như hình vẽ. Hàm số
 
42
46
g
x
f
xx x
có bao nhiêu điểm cực trị ?
A.
0.
B.
1.
C.
3.
D.
5.
Câu 25: Có bao nhiêu giá trị nguyên dương của tham số thực m để phương trình

2
2
cos cos 2 2cos cos cos 2 0m x x x xm xm
có nghiệm thực ?
A. 4. B. 5 . C. 2. D. 3.
------------- Hết ---------------


TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
-----------------------------

----------------------------
Họ và tên học sinh: …………………..……………………………………..Lớp: …………..
PHẦN ĐÁP ÁN
Câu Đáp án Câu Đáp án Câu Đáp án
01
09
17
02
10
18
03
11
19
04
12
20
05
13
21
06
14
22
07
15
23
08
16
24
25
Lưu ý:
Đối với mỗi câu hỏi, thí sinh chọn và tô kín một ô tròn tương ứng với phương án trả lời đúng.
Câu 1:
Cho hàm số

yfx
có đồ thị như hình vẽ bên. Hỏi đồ thị của hàm số

yfx
có bao nhiêu điểm cực
trị ?
A.
1
C.
2
B.
3
D.
4
Câu 2:
Cho hàm số f (x) có bảng biến thiên như sau.
Hàm số f (x) nghịch biến trên khoảng nào dưới đây ?
A
.

;0 .
B.
(0;2).
C.

2; 2 .
D.

2;0 .
Câu 3.
Cho hàm số

yfx
có đồ thị (C) như hình vẽ. Đường thẳng
2y
cắt (C) tại
bao nhiêu điểm ?
A.
0.
B
.
1.
C.
2.
D
.
3.
Câu 4:
Tâm đối xứng của đồ thị hàm số
1
2
x
y
x
có toạ độ là.
A.
(1;2).
B.
(2;1).
C.
(-2;1).
D.
(2; -1).
Mã đề 485
-2
-4
O
-3
-1
1
Câu 5: Cực tiểu của hàm số
3
32
y
xx là.
A. 0 B. -1 C. 1 D. 4
Câu 6: Giá trị lớn nhất của hàm số
32
3917yx x x trên đoạn [-2; 4] là.
A.

2;4
max 44.y
B.

2;4
max 20.y
C.

2;4
max 22.y
D.

2;4
max 15.y
Câu 7. Đường cong ở hình vẽ bên là đồ thị của hàm số nào trong bốn hàm số dưới
đây ?
A.
42
31.yx x C.
3
.
2
x
y
x
B.
32
331. yx x x D.
32
31. yx x
Câu 8: Hàm số
42
43yx x có bao nhiêu điểm cực trị ?
A. 0. B. 1. C. 2. D. 3
Câu 9. Cho hàm số
1
2
x
y
x
(C). Tiếp tuyến của (C) tại điểm có hoành độ
1x 
có phương trình là.
A.
35.yx
B.
35.yx
C.
313.yx
D.
31.yx
Câu 10. Cho hàm số

yfx
xác định trên
\1
, liên tục trên mỗi khoảng xác định của nó và có bảng biến
thiên như hình vẽ dưới đây.
Đồ thị của hàm số

f
x
có bao nhiêu tiệm cận đứng ?
A. 1. B. 2. C. 3 D. 4
Câu 11: Cho hàm số

f
x
xác định, liên tục trên R và có đạo hàm xác định bởi công thức

2
'2fx x
.
Mệnh đề nào sau đây sai ?
A.

12ff
. B.

23ff
. C.

30ff
. D.
01
f
f
+∞
-∞
-∞
+∞
0
_
x
y
/
y
+∞
- ∞
_
-1 0
-2
+
-2
+
1
1
Câu 12. Bảng biến thiên sau đây là của hàm số nào trong bốn hàm số được cho ở bốn phương án A, B, C, D ?
x 0
y’ + 0 -
y 1


A.
42
31yx x B.
42
21yx x C.
42
21yx x D.
42
1yx x
Câu 13: Gọi P, Q là giao điểm của đường thẳng
3yx
và đường cong
23
1
x
y
x
. Tìm toạ độ trung điểm I
của đoạn thẳng PQ.
A.

1; 2 .I
B.

2; 1 .I
C.

1; 2 .I
D.
2;1 .I
Câu 14: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số
32
34
f
xxmxmxm
nghịch
biến trên R.
A. 0 B. 1 C. 2 D.
3.
Câu 15: Đồ thị hàm số
2
12
3
x
y
x
x

có bao nhiêu đường tiệm cận ?
A.1 B. 2 C. 3 D. 4
Câu 16. Cho hàm số
2
57
2
xx
y
x

. Xét các mệnh đề sau :
1) Hàm số đồng biến trên mỗi khoảng

;1
và

3; 
2) Hàm số có ba điểm cực trị.
3) Hàm số nghịch biến trên khoảng

1; 3 .
4) Điểm cực đại của đồ thị hàm số là
3;1
Trong các mệnh đề trên, có bao nhiêu mệnh đề sai ?
A. 1 B. 2 C. 3 D. 4
Câu 17: Đường cong trong hình bên là đồ thị của hàm số nào trong bốn
hàm số sâu đây ?
A.
21
1
x
y
x
B.
12
1
x
y
x
C.
21
1
x
y
x
D.
12
1
x
y
x
Câu 18: Tìm m để giá trị nhỏ nhất của hàm số
3
3
y
xxm
trên đoạn

0; 2
bằng 1 ? Khi đó
36m
có giá
trị bằng.
A.2 B. 3 C. - 4 D. 4
4
2
-2
-
5 5
y
x
O
1
-1
Câu 19: Tổng tất cả các giá trị của tham số m để đồ thị hàm số
2
1
2
x
y
x
xm

có đúng một tiệm cận đứng là.
A.
1.
B.
2.
C.
4.
D.
4.
Câu 20: Có bao nhiêu đường thẳng đi qua điểm A ( 0 ; 1) và tiếp xúc với đồ thị của hàm số
3
31yx x
?
A. 1 B. 2 C. 3 D. 0
Câu 21: Cho hàm số

yfx
có bảng biến thiên như sau:
x 0 2

y’ + 0 0 +
y 2

1
Có bao nhiêu giá trị nguyên dương của m để phương trình

30fx m
có 4 nghiệm phân biệt.
A.
0.
B.
1.
C.
2.
D. 3.
Câu 22: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số
422
23
y
xxmm
có 5 điểm
cực trị. Tìm số phần tử của S.
A. 4. B. 3 C. 2. D. 1
Câu 23: Cho hàm số

yfx
xác định trên và có đạo hàm

f' x
thỏa
 
f ' x 3 x x 3 g x 2018
với

gx 0, x .
Hàm số

y f 1 x 2018x 2019
có bao nhiêu điểm cực trị ?
A. 0. B. 1 C. 2. D. 3
Câu 24: Cho hàm số
()yfx
có đạo hàm
22
( ) ( 1) ( 9).fx xx x mx
Có bao nhiêu số nguyên dương m để
hàm số
(3 )yf x
đồng biến trên khoảng
(3; ).
A. 6. B. 5. C. 7. D. 8.
Câu 25: Có bao nhiêu giá trị nguyên âm của tham số m để phương trình
3
3
33sinsin mm x x có nghiệm
thực
A.
2.
B.
3.
C.
5.
D.
7.
------------- Hết ---------------


TRƯỜNG THPT TX QUẢNG TRỊ ĐÁP ÁN ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
---------------------------------------------------------
Mã đề thi: 135
Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án
1 B 6 D 11 D 16 B 21 B
2 D 7 D 12 D 17 D 22 A
3 C 8 C 13 B 18 C 23 C
4 D 9 C 14 B 19 A 24 C
5 A 10 C 15 B 20 B 25 B
Mã đề thi: 246
Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án
1 C 6 A 11 C 16 A 21 B
2 D 7 C 12 B 17 A 22 D
3 D 8 D 13 C 18 D 23 C
4 C 9 C 14 D 19 A 24 B
5 D 10 A 15 B 20 A 25 C
Mã đề thi: 357
Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án
1 C 6 C 11 C 16 B 21 A
2 B 7 C 12 C 17 B 22 A
3 B 8 D 13 C 18 D 23 D
4 A 9 A 14 D 19 C 24 B
5 B 10 B 15 C 20 C 25 C
Mã đề thi: 485
Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án
1 B 6 C 11 D 16 C 21 A
2 D 7 B 12 A 17 C 22 A
3 B 8 B 13 A 18 B 23 C
4 B 9 D 14 B 19 B 24 A
5 A 10 B 15 B 20 A 25 A
Tran
g 5/17 - WordToan
1.B 2.D 3.C 4.D 5.A 6.D 7.D 8.C 9.C 10.C
11.D 12.D 13.B 14.B 15.B 16.B 17.D 18.C 19.A 20.B
21.B 23.C 24.C 25.B
LỜI GIẢ
I CHI TIẾT
Câu 1. Cho hàm số
y f x
có đ
ồ thị như hình vẽ bên. Hỏi đồ thị của hàm số
y f x
có bao
nhiêu
điểm cực trị?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giả
i
Chọn B
Dựa vào đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt và
. 0
CÐ C
T
y y
đồ thị
hàm số có 2 điểm
cực trị.
Câu 2. Cho hàm số
f x
có bảng biến thiên như hình vẽ sau
Hàm số đồng biến trên khoảng nào dưới đây?
A.
;3
. B.
2;0
. C.
2;2
. D.
0;2
.
Lời giả
i
Chọn D
D
ựa vào bảng biến thiên ta thấy
0
y
,
0;2
x
chọ
n D.
Câu 3: Cho hàm số
y f x
co đô th
i (C) như hinh ve. Đương thăng
1y
căt (C) tai bao nhiêu điêm?
BẢNG ĐÁP ÁN
Trang 6/17 – Diễn đàn giáo viên Toán
A.
0
.
B.
1
.
C.
2
.
D.
3
.
Lờ
i giải
Chọn C
Theo đồ
thị ta tháy có 2 giao điểm
Câu 4: Cực tiểu của hàm số
3
2
3
1
y
x x
là.
A.
1
. B.
0
. C.
2
. D.
3
.
Lờ
i giải
Chọn D
2
0
'
3 6 0
2
x
y
x x
x
'
' 6 6y x
;
'
'(0) 6 0
y
h
àm số đạt CĐ tại
0
x
.
'
'(2) 6 0
y
h
àm số đạt CT tại
2
; 3
CT
x
y
C
âu 5. Tâm đôi xưng cua đô thị hàm số
2
1
1
x
y
x
có toa đô la
A.
1;2
. B.
2;1
. C.
1;2
. D
2; 1
.
Lời giải
Chọn A
Tập
xác định
\
1
D
.
Ta c
ó:
+
2
1
lim 2
1
x
x
x

nê
n
2
y
l
à tiệm cận ngang.
+
1
2
1
lim
1
x
x
x

nê
n
1x
l
à tiệm cận đứng.
Vậy tâm đối xứng của đồ thị hàm số trên có tọa độ là
1
;2
.
Câu 6. Giá trị lớn nhất của hàm số
3
2
3 1y x x
tr
ên đoạn
1;
2
l
à
A.
1
;2
m
ax 2
y
. B.
1
;2
ma
x 1y
. C.
1
;2
m
ax 15
y
. D.
1
;2
m
ax 11
y
.
Lời gi
ải
Chọn D
Xét
hàm số
3
2
3 1y f x x x
trên đoạn
1;
2
:
Ta có
2
6
3
y
x
.
Cho
0
y
2
6
3 0
x
2
1;2
2
2
1;2
2
x
x
.
Tran
g 7/17 - WordToan
Khi đó:
1 2f
,
2 11f
,
2
1 2
2
f
,
2
1 2
2
f
.
Vậy
1;2
max
11y
.
Câu 7.
Đường cong trong hình bên là đồ thị của hàm số nào trong 4 hàm số sau?
A.
4 2
3 1y x
x
. B.
3
3 1y x
x
.
C.
2 1
1
x
y
x
.
D.
2 1
1
x
y
x
.
Lời giải
:
Chọn D
Dựa vào đồ thị ta nhận biết đây là đồ thị bậc nhất trên bậc nhất →
Loại A và B
Dựa vào đồ thị ta tìm được TCĐ và TCN
TCĐ:
1x
TCN:
2y
Chọn đáp
án đúng là D.
Câu 8. Cho hàm số
( )f x
xác
định, liên tục trên
có bảng xét d
ấu
( )f x
như sau:
Hàm số
( )f x
có bao nhiêu điểm cực trị?
A. 0. B. 1. C. 2 D. 3.
Lời giả
i
Chọn C
Dựa vào
BBT và áp dụng định lí 1 của SGK, hàm số đạt cực đại tại
1x
, đạt
cực tiêu tại
2x
.
Su
y ra hàm số có 2 điểm cực trị.
Câu 9. Cho hàm số
2 1
2
x
y
x
(C). Ti
ếp tuyến của (C) tại điểm có hoành độ
3x
có phương trinh
la
A.
5 8
y x
. B.
5 22y
x
. C.
5 22y
x
. D.
5 8y x
.
Tr
ang 8/17 – Diễn đàn giáo viên Toán
Lời
giải
Chọn
C
Ta có
2
5
2
y
x
.
Gọi
3;
M
M y
C
.
Khi đó tung độ của điểm
M
là
2. 3 1
7
3 2
M
y
tọa đ
ộ
3;
7M
.
Hệ số góc
của tiếp tuyến của (C) tại
M
là
2
5
3 5
3
2
k y
.
Vậy
phương trình tiếp tuyến của (C) tại
M
là:
5 3
7 5 22 y x y x
.
Câu 10. Cho h
àm số
y f x
xac đinh trên
\ 1
, liên tuc trên môi khoang xac đinh cua no va co bảng
biến thiên như hình vẽ dưới đây.
Tông sô tiêm cân đưng va tiêm cân ngang cua đô thi ham sô
f x
la.
A.
1
. B.
2
. C.
3
. D.
4
.
Lời
giải
Chọn
C
Theo bảng biến thiên của hàm số
y f x
ta
có:
*Tiệm cận đứng:
Ta có
1
lim


x
f x
hàm
số
y f
x
có
tiệm cận đứng
1 x
.
1
li
m
x
f x
hàm số
y f x
có tiệm cận đứng
1x
.
Vậy đồ thị hàm số có
2
tiệm cận đứng.
*Tiệm cận ngang:
Ta có
lim
3

x
f x
hàm
số
y f
x
có
tiệm cận ngang
3y
.
Vậy đồ thị
hàm số có
1
tiệm cậ
n ngang.
Kết luận: Tổng số tiệm cận đứng và ngang của đồ thị hàm số
y f
x
là
3
.
Câu 11. Cho ham sô
f x
xac đ
inh, liên tuc trên
va
 co đao ham câp môt xac đinh bơi công thưc
2
1f x
x
. Mênh đê
 nao sau đây đung?
A.
1 2f f
. B.
3 2f f
. C.
1 0f f
. D.
0 1f f
.
Tr
ang 9/17 - WordToan
Lời
giải
Chọn
D
Vì
2
1 0f x x
,
x
nê
n hàm số nghịch biến trên
.
Vì th
ế:
Do
1 2
nên
1 2f
f
.
Suy ra A sai.
Do
3 2
nên
3 2f
f
.
Suy ra B sai.
Do
1 0
nên
1 0f
f
. Suy ra C sai.
Do
0 1
nên
0 1f
f
.
Suy ra D đúng.
Câu 12. Bảng biến thiên sau đây là của hàm số nào trong bôn ham sô đươc cho ơ bôn phương an A, B, C,
D?
A.
4 2
3 2y x x . B.
4 2
2 2y x x . C.
4 2
2 2y x x . D.
4 2
2y x x .
Lời
giải
Chọn
D
Các hàm số ở bốn phương án A, B, C, D đều có dạng
4 2
y ax
bx c .
Dựa vào bảng biến thiên ta thấy hàm số cần tìm có hệ số
0a
,
nên loại A, B.
Cũng dựa vào bảng biến thiên ta thấy hàm số cần tìm chỉ có 1 điểm cực trị.
Xét hàm số ở phương án C:
4 2
2 2y
x x , ta có:
3
4 4y
x x
;
0
0 1
1
x
y
x
x
. Suy
ra hàm số này có 3 điểm cực trị.
Do đó loại phương án C.
Vậy chọn đáp án là D.
Câu 13. Gọi M, N là giao điểm của đường thẳng
1y x
và
đường cong
3
1
x
y
x
. Ti
m toa đô trung điêm I
cua đoan thăng MN la
A.
1;
1I
. B.
1 1
;
2
2
I
. C.
1 1
;
2
2
I
. D.
1;
2I
.
Lời
giải
Trang 10/17 – Diễn đàn giáo viên Toán
Chọn B
Hoành
độ
,
M
N
x
x
của M, N là nghiệm của phương trình
3
1
1
x
x
x
(1).
Ta có
2
2
(
1) ( 1) 3 2 0
x
x x x
.
Hoà
nh đô trung điêm I cua đoan thăng MN la
1
2
2
M N
I
x
x
x
(theo định lí Viet).
Điểm I nằm trên đường thẳng
1y x
nên
có tung độ là
1
1
2
I I
y
x
.
Vậy
, tọa độ điểm I là
1 1
;
2 2
I
.
Cách khác: Tìm tọa độ điểm M, N rồi tìm tọa độ điểm I.
Câu 14. Trong tất cả các giá trị thưc của tham sô
m
làm cho hàm số
3
2
3 2
f x x mx m x m
đồng
biến trên R, giá trị lớn nhất của
m
l
à
A. 0. B. 1. C. 2. D.
2
3
.
Lời giải
Chọn B
Ta c
ó
2
3
6 2
f
x x mx m
.
Hàm
số đồng biến trên R
(
) 0,
f
x x R
v
à dấu bằng chỉ xảy ra tại hữu hạn điểm
2
2
3 0
2
( ) 0, (3 ) 3( 2) 0 9 3 6 0 1
0
3
a
f x x R m m m m m
Do vậy, giá trị lớn nhất cần tìm của m là 1.
Câu 15. Đồ thị hàm số
2
1
2
3
x
y
x
x
có
bao nhiêu đường tiệm cận?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời gi
ải
Chọn B
Hàm
số
2
1
2
3
x
y
x
x
c
ó tập xác định
1
; \ 0;3
D

.
Ta c
ó
2
0
0
1
2
lim lim
3
x x
x
y
x x

n
ên đồ thị hàm số nhận đường thẳng
0
x
làm
tiệm cận đứng.
2
2
3
3 3 3
1
2 3 1 1
l
im lim lim lim
3
12
3
1 2 1 2
x x x x
x
x
y
x x
x x x x x
.
Do
đó đồ thị hàm số chỉ có duy nhất 1 đường tiệm cận đứng.
Tr
ang 11/17 - WordToan
Lại
có
2
1 2
lim lim 0
3
x
x
x
y
x x
 
n
ên đồ thị hàm số nhận đường thẳng
0y
làm
tiệm cận ngang.
Câu 16. Cho hàm số
2
2
12
2
x x
y
x
.
Xét các mệnh đề sau :
1) Hàm số có hai điểm cực trị.
2) Hàm số đồng biến trên tập
; 5 1;
.
3) Hàm số ng
hịch biến trên tập
5
;1
.
4) Điểm
cực tiểu của đồ thị hàm số là
1
;5
.
Trong
các mệnh đề trên, có bao nhiêu mệnh đề đúng?
A.
1
. B.
2
. C
.
3
. D.
4
.
Lời giải
Chọn B
Xét
2
'
2
2
1
8 2 8 10
2
2 2
x x
y
x x
'
2
1
18
0
2 0
5
2
x
y
x
x
.
Ta có bảng biến thiên của hàm số đã cho
Do đó mệnh đề 1) đúng, mệnh đề 2) sai, mệnh đề 3) sai và mệnh đề 4) đúng.
Câu 17. Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số sau đây?
A.
3
2
3
2y x x . B.
3
3
1y x x . C.
3
2
3
1y x x . D.
3
2
3
1y x x .
Lời giải
Chọn
D
Dựa vào đồ thị ta có:
Điểm cực đại
0
;1
v
à điểm cực tiểu
2
; 3
nên
đó là đồ thị của hàm số
3
2
3
1y x x .
Câu 18. Tìm
m
để giá trị nhỏ nhất của hàm số
3
2
3 9y x x x m trên đoạn
0;4
bằng
2
5
, khi đó hãy
tính giá trị của biểu thức
2
1P m
A.
1
. B.
3
. C.
5
. D.
7
.
Lời giải
x
5
2
1
y
0
0
y
19

5
Trang 12/17 – Diễn đàn giáo viên Toán
Chọn C
+
2
3 6
9y x x
.
+
2
1 0
;4
0 3
6 9 0
3 0
;4
x
y x
x
x
.
+
0
, 3 27 , 4 20
y m
y m y m
.
Hàm số đã cho liên tục trên đoạn
0;
4
do đó
hàm số đạt giá trị nhỏ nhất bằng
27
m
Suy ra
27
25 2
m m
.
Vậy
2 1
5
P m
.
Câu 19. Tính
tổng tất cả các giá trị của tham số m để đồ thị của hàm số
2
1
2
x
y
x x
m
luôn
có hai đường
tiệm cận.
A. –2. B. 5. C. –4. D. 4.
Lời giải
Ch
ọn A
Ta có
lim
lim 0
x x
y y

Đồ
thị hàm số có tiệm cận ngang y = 0.
Để đồ thị hàm số có hai đường tiệm cận
đồ t
hị hàm số chỉ có 1 tiệm cận đứng.
Xét phương trình
2
2 0
x x m
(1). Ta có
4 4m
.
TH1: Phương trình (1) có 1 nghiệm duy nhất.
1
m
. V
ới m = 1, phương trình có nghiệm x = 1
nhận
.
TH2: Phương trình (2) có hai nghiệm phân biệt trong đó có một nghiệm x = –1
2
0
1
3.
3
1 2
1 0
m
m
m
m
Vậy tổng các giá trị của m thỏa mãn bằng
1 3
2.
Câu 20.
Có bao nhiêu đường thẳng đi qua điểm
1;
2
A
và
tiếp xúc với đồ thị của hàm số
3
3 4
y x
x
?
A. 0. B. 1. C. 2. D. 3.
Lời
giải
Ch
ọn B
Gọi d là đường thẳng đi qua
1;
2
A
và
tiếp xúc với đồ thị của hàm số
3
3 4
y f
x x x
.
d là t
iếp tuyến đi qua điểm
1;
2
A
của đồ
thị hàm số
y f
x
.
Ta
có
2
3 3
f x
x
. Gi
ả sử tọa độ tiếp điểm là
3
0 0 0
; 3 4
x x x
2 3
0 0
0 0
: 3
3 3 4
d y
x x x x x
.
Vì d đi qua
1;
2
A
, th
ay tọa độ điểm A vào d ta được :
2 3
0 0
0 0
2 3
3 1 3 4
x x
x x
2
3
0 0 0
0
2
2
0 0 0 0 0
2
0 0 0
0
0
0
0
0
0 0
3 1
1 3 2 0
3 1
1 1 2 0
1 2
5 5 0
1 0
1
1.
2 5 5 0
x x x x
x x x x x
x x x
x
x
x
x
x x
Như
vậy qua A chỉ kẻ được một tiếp tuyến. Chọn B
Câu 21. Cho hàm số
y f x
có bảng biến thiên như sau:
Trang
13/17 - WordToan
Co bao
nhiêu gia tri nguyên cua tham sô m đê phương trình
0f x m
co 4
nghiêm phân
biêt .
A. 6. B. 7. C. 8. D. 9.
Lời giải
Chọn B
Phương trình (1):
0f x m
f x m
.
Số nghiệm củ
a phương trình (1) là số điểm chung của hai đồ thị:
( ):C
y f x
và
( ) :d
y m
.
Hàm số
y f x
là hàm
số chẵn
( )C
nhận trụ
c Oy làm trục đối xứng.
Mà
( ) 0
(
) 0
f x khi x
y f x
f x khi x
.
Bảng biến thiên của hàm số
y f x
:
Dựa v
ào bảng biến thiên ta có: phương trình (1) có 4 nghiệm phân biệt
3;5m
.
Mà
m
2; 1
;0;1;2;3;4m
Có 7 giá trị m thỏa mãn.
Câu 22. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số
4 2 2
2 2y x
x m m
có 5
điểm cực trị. Tìm số phần tử của S.
A. 0. B. 1 C. 2. D. 3
Lời giả
i
Chọn A
Xét hàm
số
4 2 2
( ) 2
2y f x x x m m
.
Tập xá
c định:
D
.
3
( ) 4
4f x x x
.
( ) 0
0f x x
.
Bảng bi
ến thiên của hàm số
( )y f
x
:
Xét hàm
số
4 2 2
( ) 2 2y f x x x m m
.
Tr
ang 14/17 – Diễn đàn giáo viên Toán
Ta
có
( ) ( ) 0
( )
( ) ( ) 0
f x khi f x
f x
f x khi f x
.
Bảng
biến thiên của hàm số
( )y
f x
có
những trường hợp sau:
TH1:
0
CT
y
(là
bảng biến thiên của hàm số
( )y
f x
)
TH2:
0
CT
y
(
0
x
,
0
x
là các nghiệm của phương trình
( )
0f x
)
Hàm số
4 2
2
2 2y
x x m m
có
tối đa 3 điểm cực trị Không có m.
Cho hàm số
f x
xá
c định trên
và
có đạo hàm
f x
thỏa
2 3
2018f x x x g x
với
0,g x x
. H
àm số
1 2018 2019y f x x
đồng biến
trên khoảng nào?
A.
4;1
. B.
3;
2
. C.
0;
3
. D.
4;
5
.
Lời
giải
Chọn C
Ta có:
1 2
018 2019 ' 1 2018y f x x y f x
.
Theo gi
ả thuyết của đề, ta có:
2 3
2018 2 3 2018f x x x g x f x x x g x
.
2018 2 3f x x x g x
.
2
2018 0
3
x
f x
x
.
Ta có bảng xét dấu là
Dựa vào bảng xét dấu, ta suy ra
20
18 0, 3;2f x x
.
Tr
ang 15/17 - WordToan
'
1 2018 0 3 1 2 1 4y f x x x
.
Vậy
, Hàm số
1
2018 2019y f x x
đồng
biến trên khoảng
1
;4
m
à
0
;3 1;4
.
Câu
23. Cho hàm số
f
x
xác định trên
và có đạo hàm
f
x
thỏa
2
3 2018f x x x g x
với
0
,g x x
.
Hàm số
1
2018 2019y f x x
đồng
biến trên khoảng nào?
A.
4
;1
. B.
3
;2
. C.
0
;3
. D.
4
;5
.
Lờ
i giải
Chọn C
Ta c
ó:
1
2018 2019 ' 1 2018y f x x y f x
.
Theo
giả thuyết của đề, ta có:
2 3 2018 2 3 2018f x x x g x f x x x g x
.
2
018 2 3f x x x g x
.
2
2018 0
3
x
f x
x
.
Ta có bảng xét dấu là
Dựa vào bảng xét dấu, ta suy ra
2
018 0, 3;2f x x
.
'
1 2018 0 3 1 2 1 4y f x x x
.
Vậy
, Hàm số
1 2018 2019y f x x
đồng
biến trên khoảng
1;4
m
à
0;3 1;4
.
Câu
24. Cho hàm số
f
x
. Hàm số
y
f x
xác định, liên tục trên
và có đồ thị như hình vẽ.
Tran
g 16/17 – Diễn đàn giáo viên Toán
Hàm
số
4 2
4 6g x
f x x x
có b
ao nhiêu điểm cực trị ?
A.
0
. B.
1
. C.
3
. D.
5
.
Lời giả
i
Chọn C
Ta có:
4 2 3
4 6 4 4
12g x f x x x g x f x x x
.
3 3
0 4 4
12 0 ' 3g x f x x x f x x x h x
.
3 2
3 3 3h
x x x h x x
.
2
1
0 3 3 0
1
x
h x x
x
.
Ta có bảng biến thiên của hàm số
3
3h x x
x
là
Ta có đ
ồ thị của hai hàm số
y f x
và
3
3h x x x
là
Dựa vào đồ thị ta thấy 2 đồ thị cắt nhau tại 3 điểm phân biệt có hoành độ lần lượt là
1 2
A A A
x x x
.
Ta có bảng xét dấu của hàm số
3
4 4 1
2g x f x x x
là
Trang 17/17 - WordToan
Dự
a vào BBT , ta suy ra hàm số
4
2
4 6g x f x x x
có
3 điểm cực trị.
Câu 25 Có bao nhiêu giá trị nguyên của tham số thực m để phương trình
2
2
c
os cos 2 2cos cos cos 2 0
m
x x x x m x m
có nghiệm thực ?
A.
6
. B.
5
. C.
4
. D.
3
.
Lời gi
ải
Chọn B
Ta có:
2
2
cos cos 2 2cos cos cos 2 0
m x x x x m x m
2
2
c
os cos cos 2 cos cos cos 2 0
x
x x x m x m x m
(1)
Đặt
c
ost x m
Ta được phương trình :
2
2
c
os cos cos 2 2 0
x
x x t t t
2
2
cos
cos cos 2 ( ) ( ) 2 *
x
x x t t t
Xét
hàm số
2
2
f
u u u u
với
u
ta
có
2
2
2
1 2 0 , u
2
u
f u u
u
n
ên
f u
l
à hàm số đồng biến trên
*
c
ó dạng:
c
os cos cosf x f t x t t x
Với
cost x
t
a được
c
os cos 2cos **
x
m x m x
Phư
ơng trình đã cho có nghiệm thực khi và chỉ khi phương trình
*
*
có
nghiệm thực . Khi đó điều
kiện của
m
l
à
2
2
m
.
Vì
m
là
số nguyên nên
2
; 1;0
m
.
Có 5 giá trị nguyên của
m
.
| 1/30
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
--------------------------------------------------------- Mã đề 135
Họ và tên học sinh: …………………..……………………………………..Lớp: ………….. PHẦN ĐÁP ÁN Câu Đáp án Câu Đáp án Câu Đáp án 01 09 17 02 10 18 03 11 19 04 12 20 05 13 21 06 14 22 07 15 23 08 16 24 25
Lưu ý: Đối với mỗi câu hỏi, thí sinh chọn và tô kín một ô tròn tương ứng với phương án trả lời đúng.
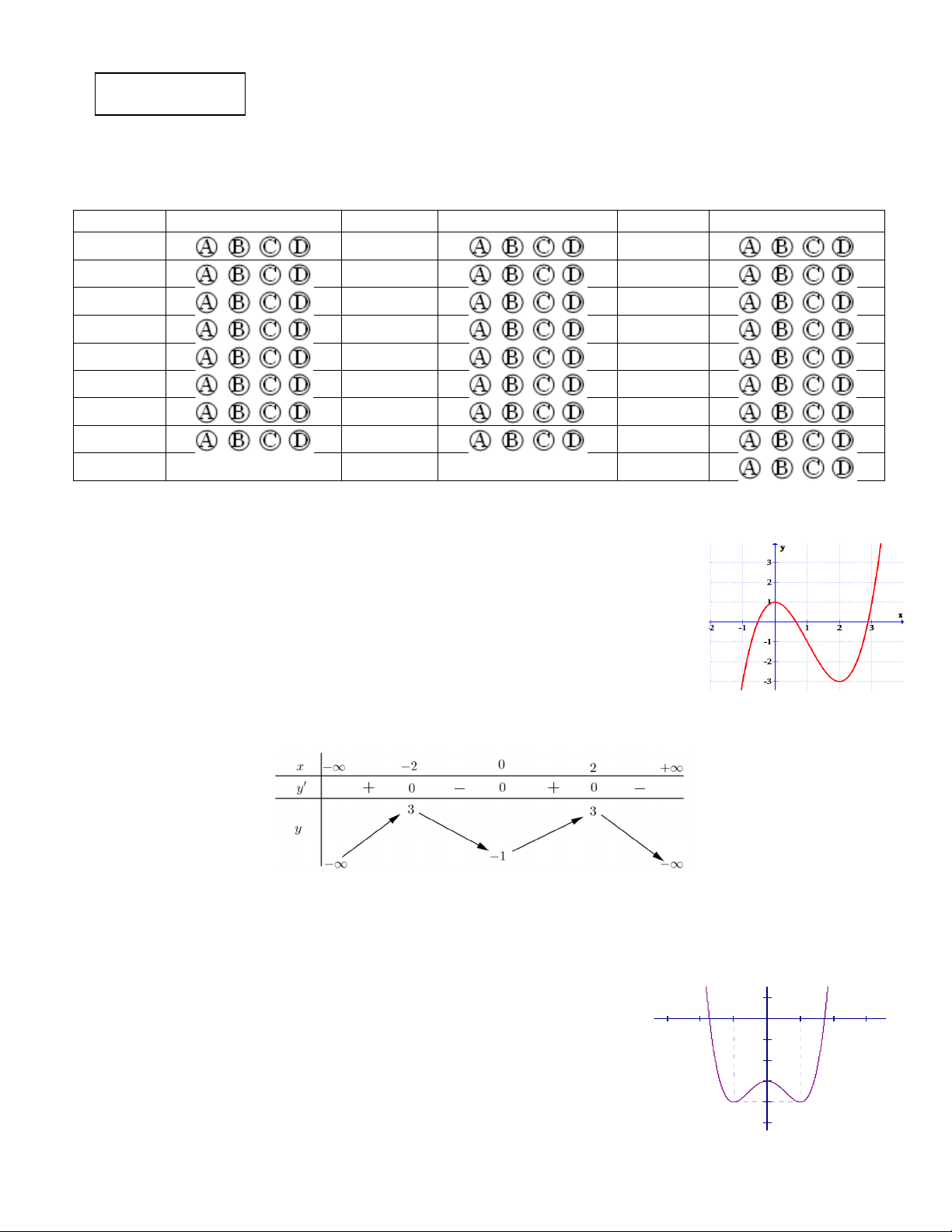
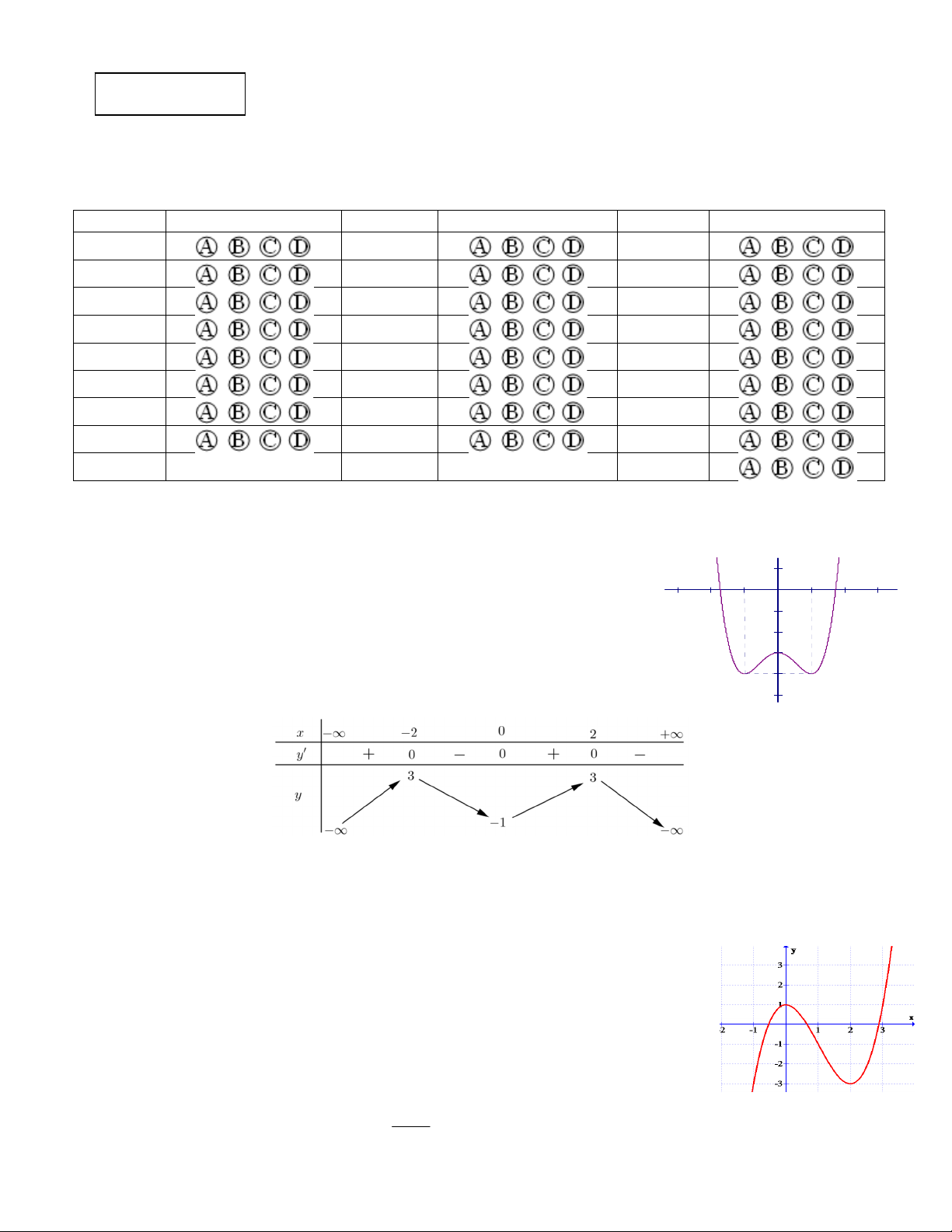
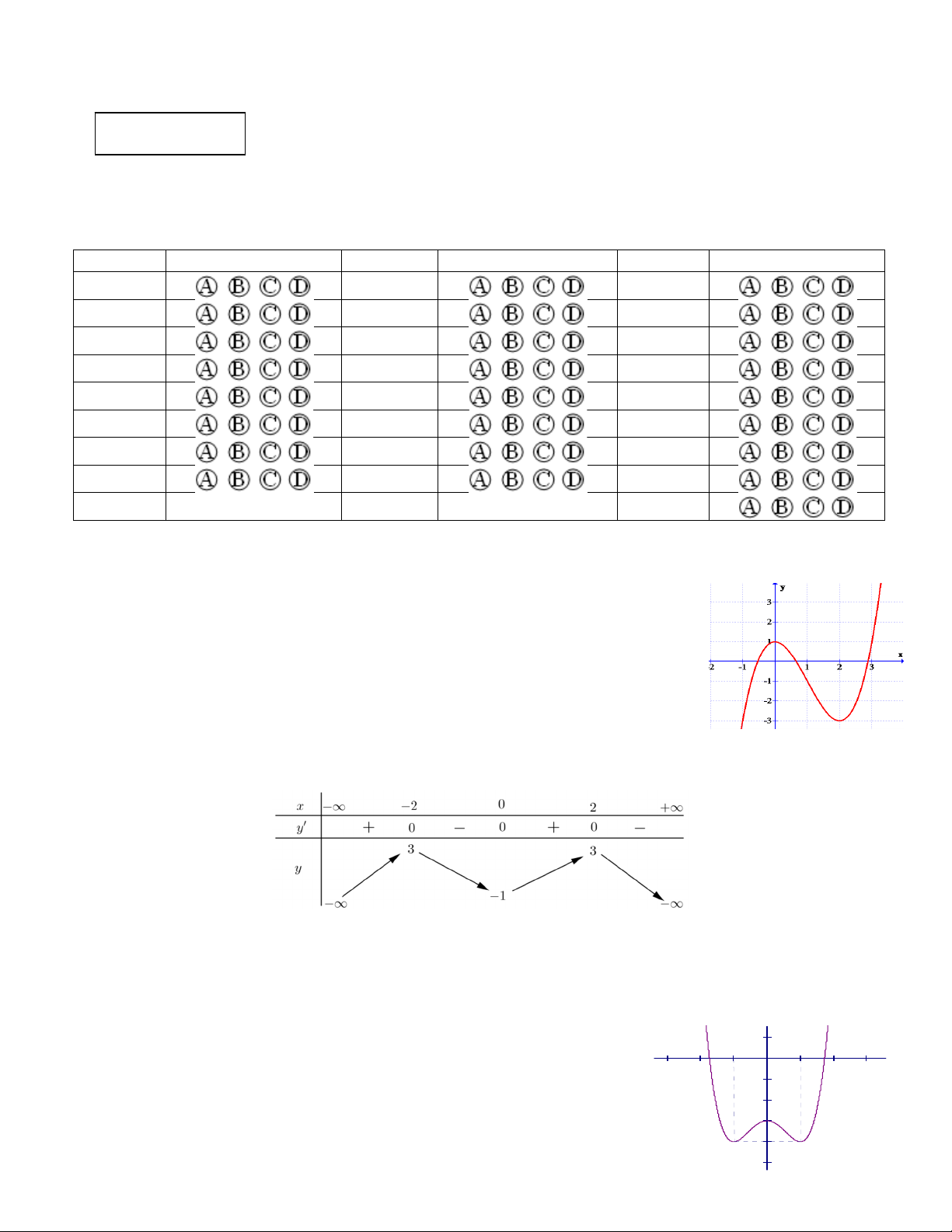
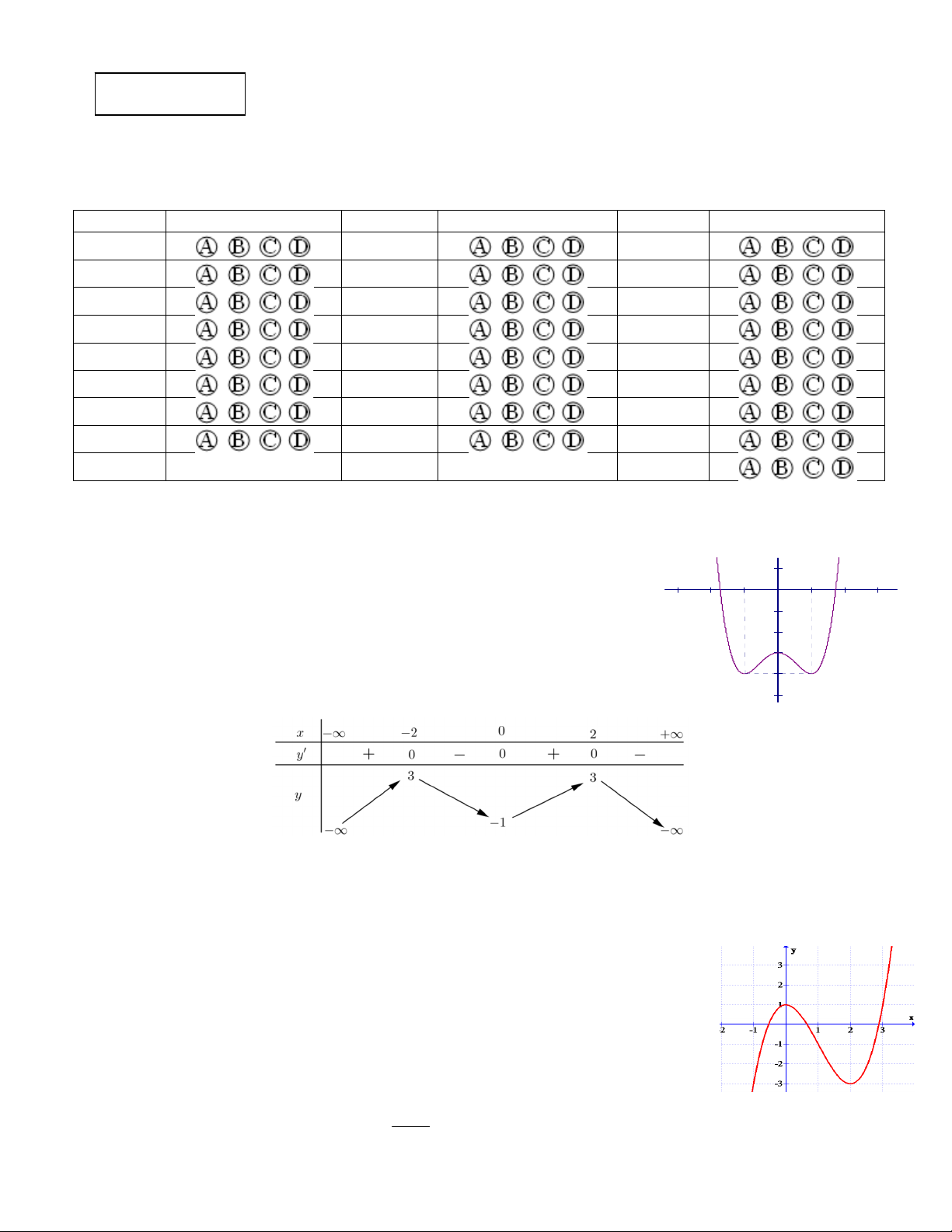
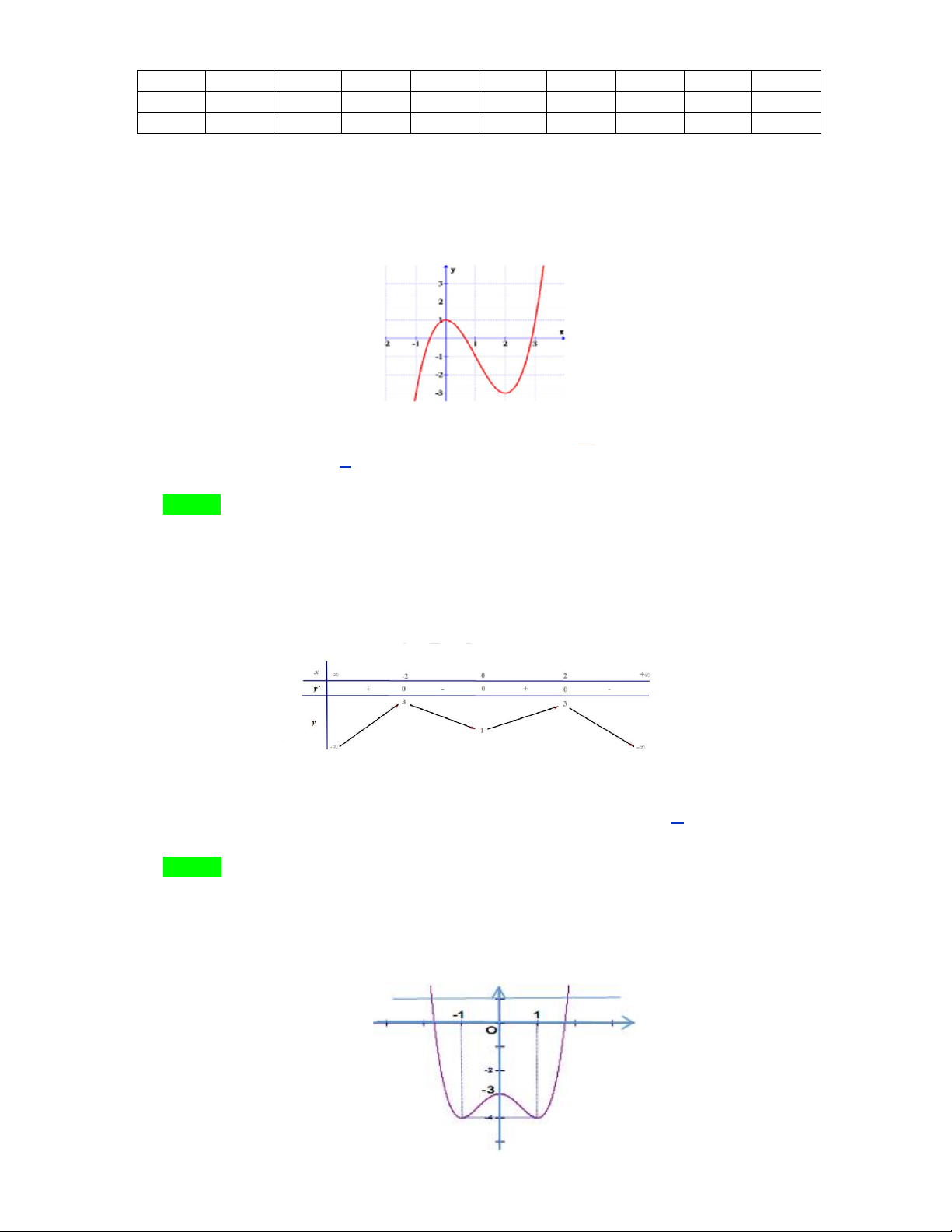
Câu 1: Cho hàm số y  f x có đồ thị như hình vẽ bên. Hỏi đồ thị của hàm số
y  f x có bao nhiêu điểm cực trị ? A. 1 B. 2 C. 3 D. 4
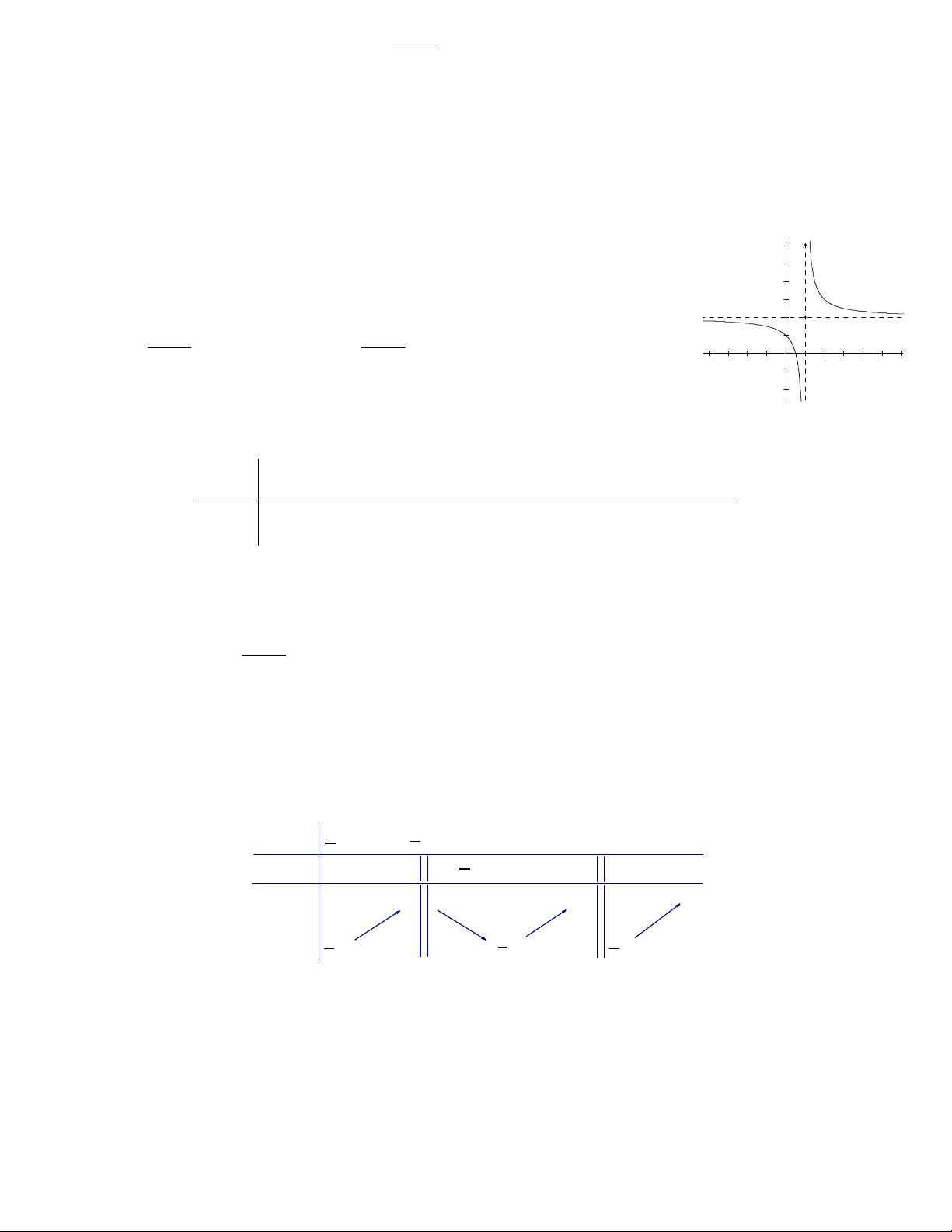
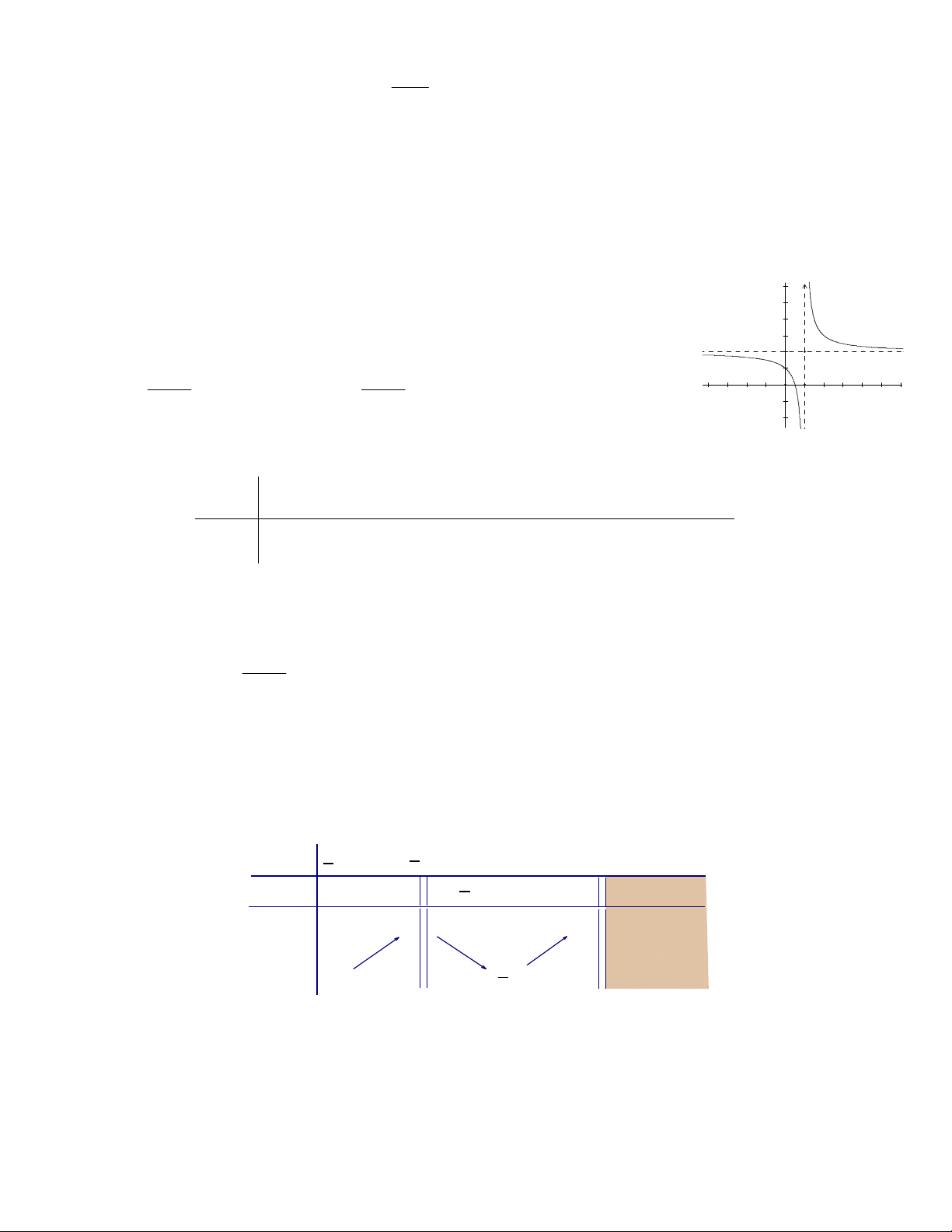
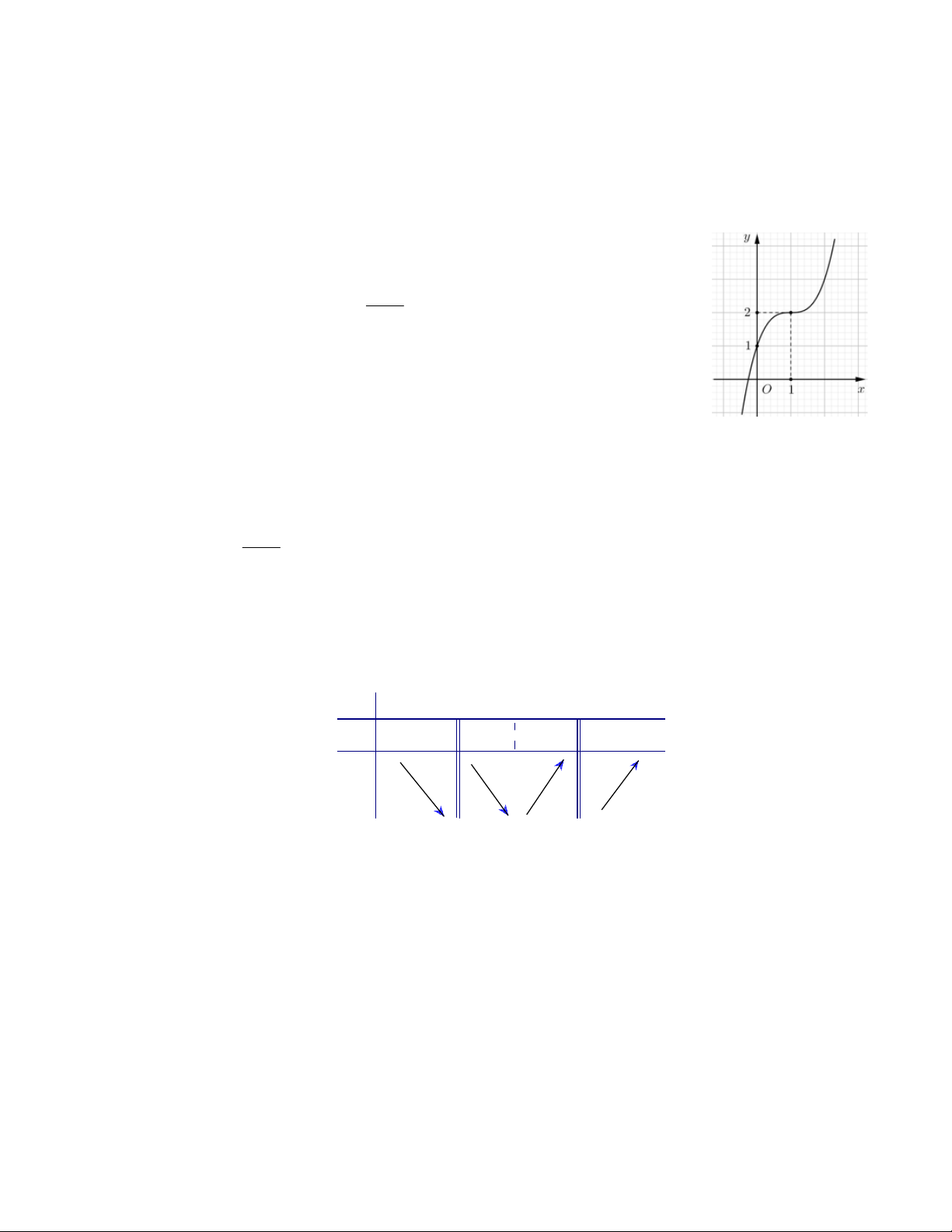
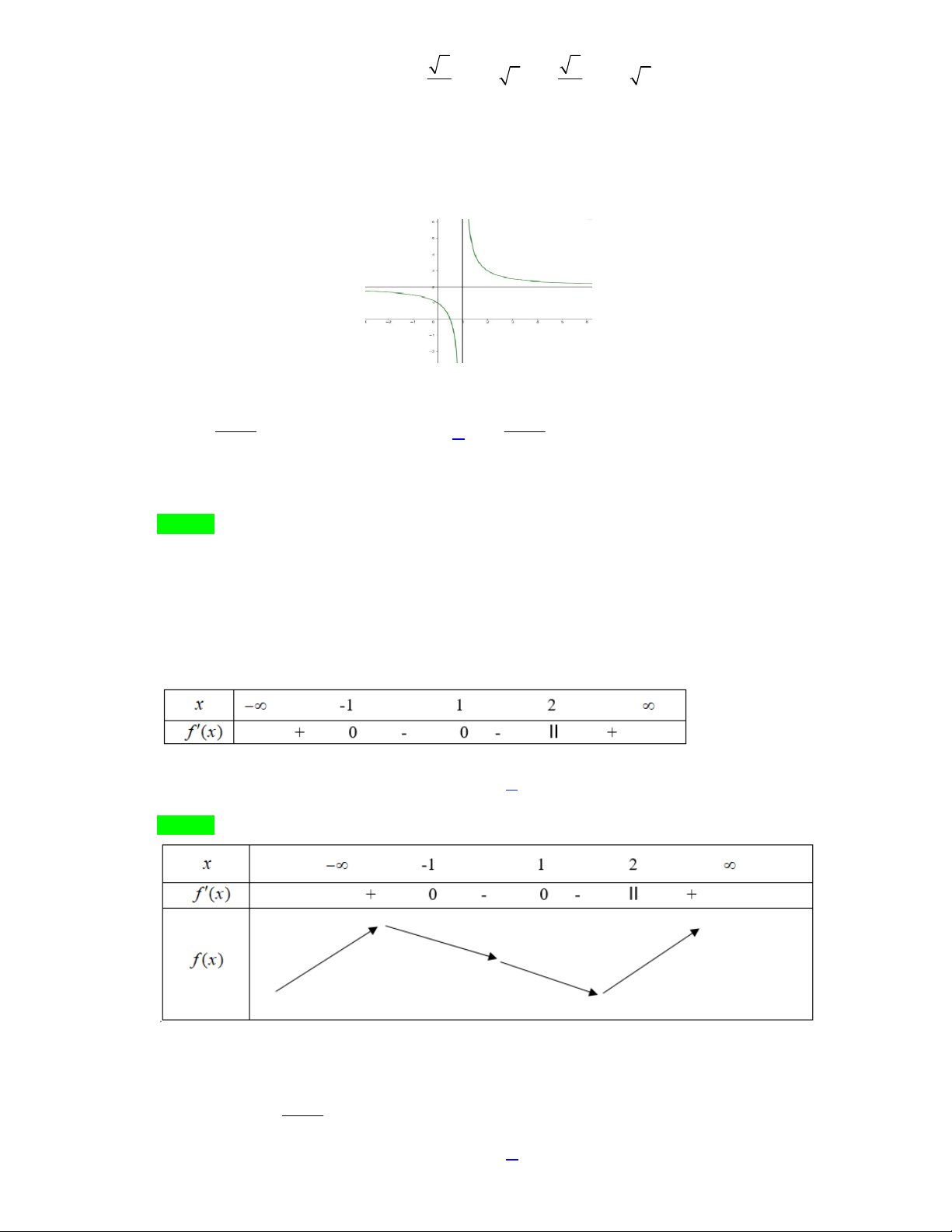
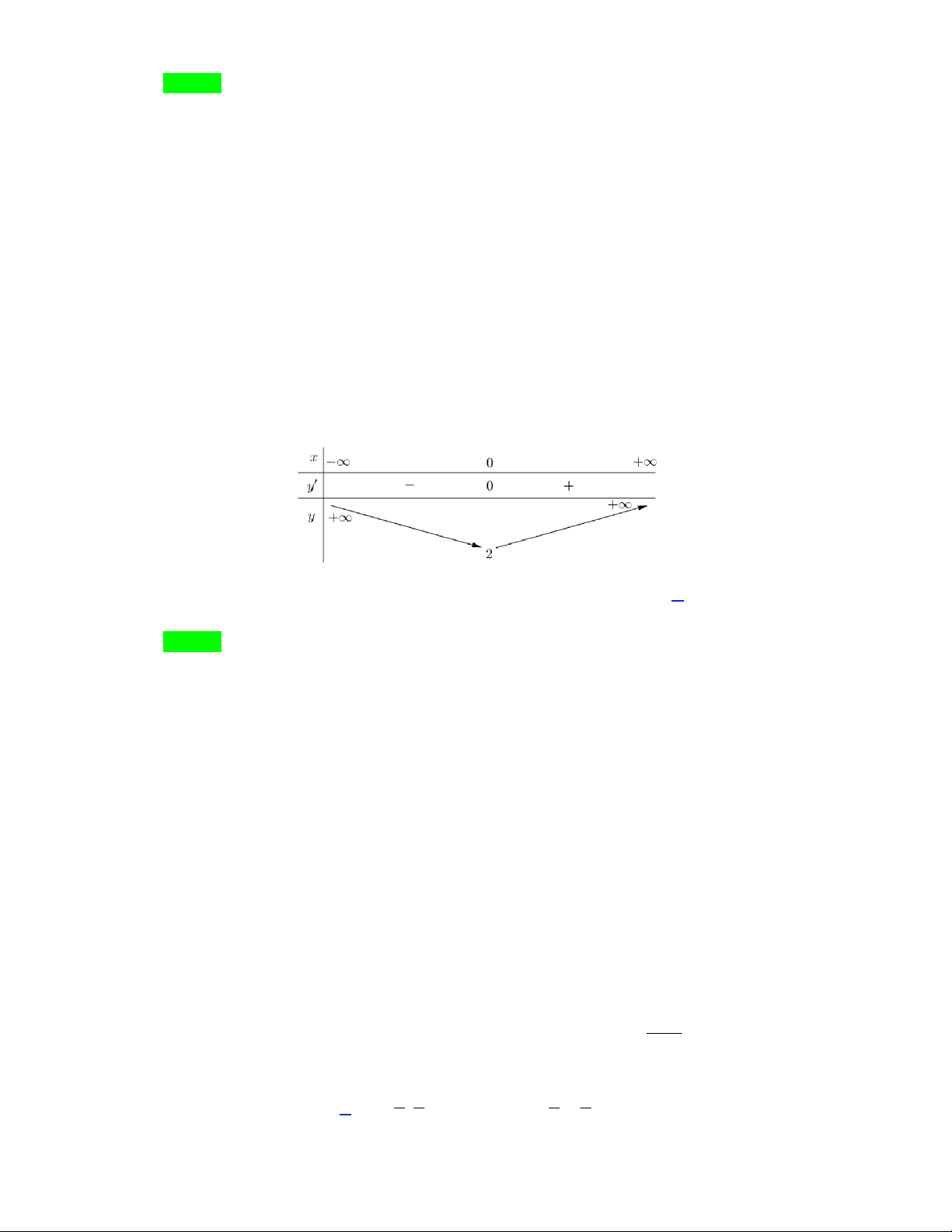
Câu 2: Cho hàm số f (x) có bảng biến thiên như hình vẽ sau
Hàm số f (x) đồng biến trên khoảng nào dưới đây ? A.   ;3 . B. ( 2  ;0). C.  2;
 2. D. 0;2.
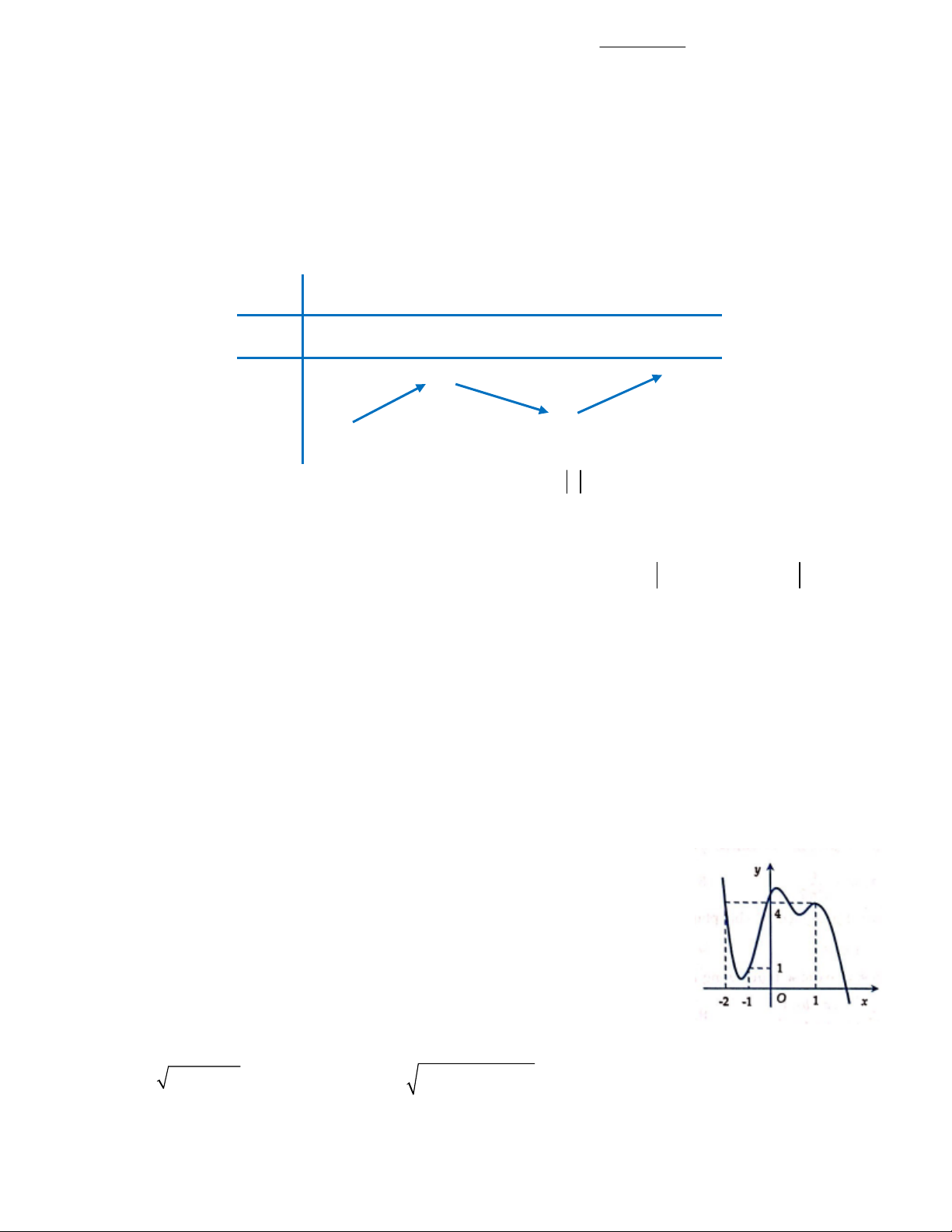
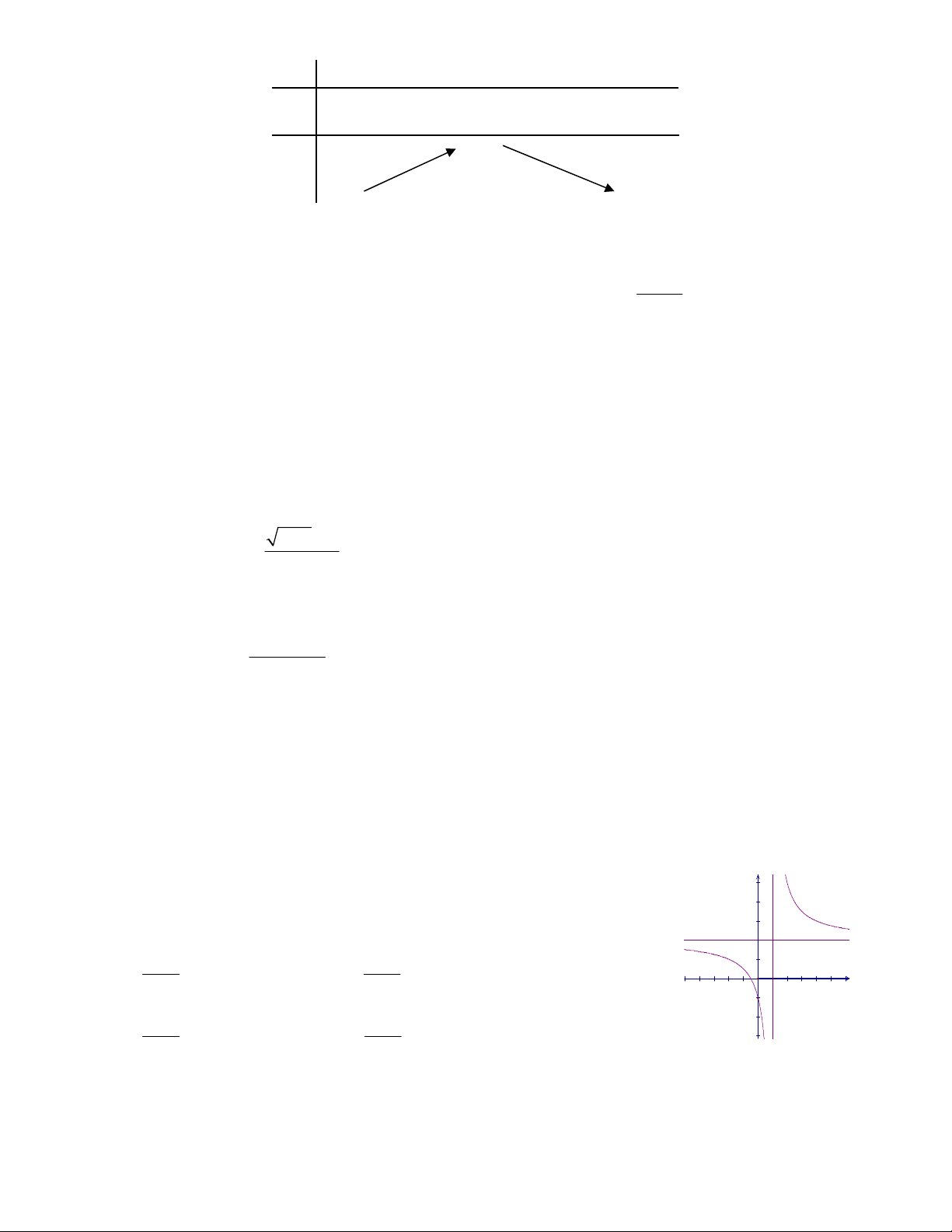
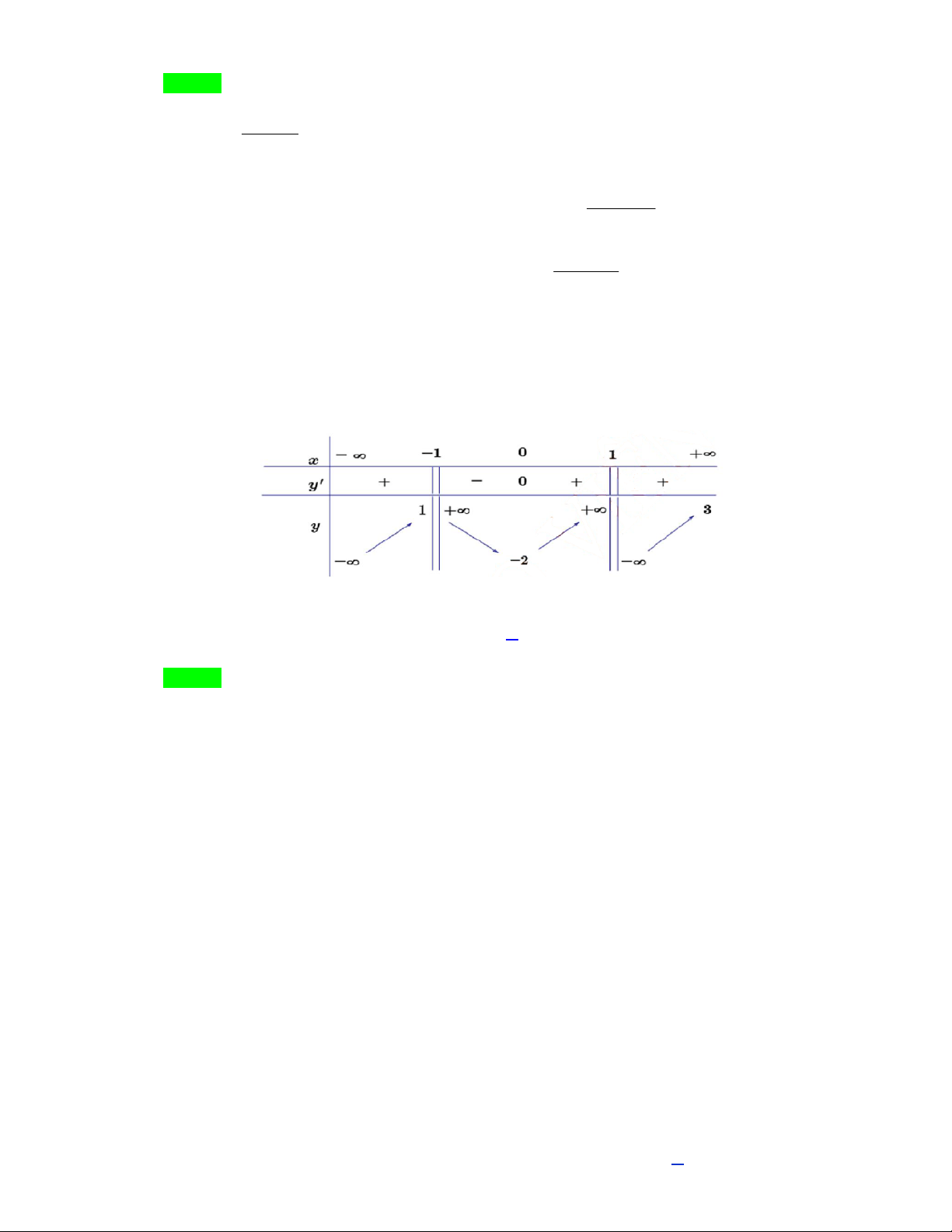
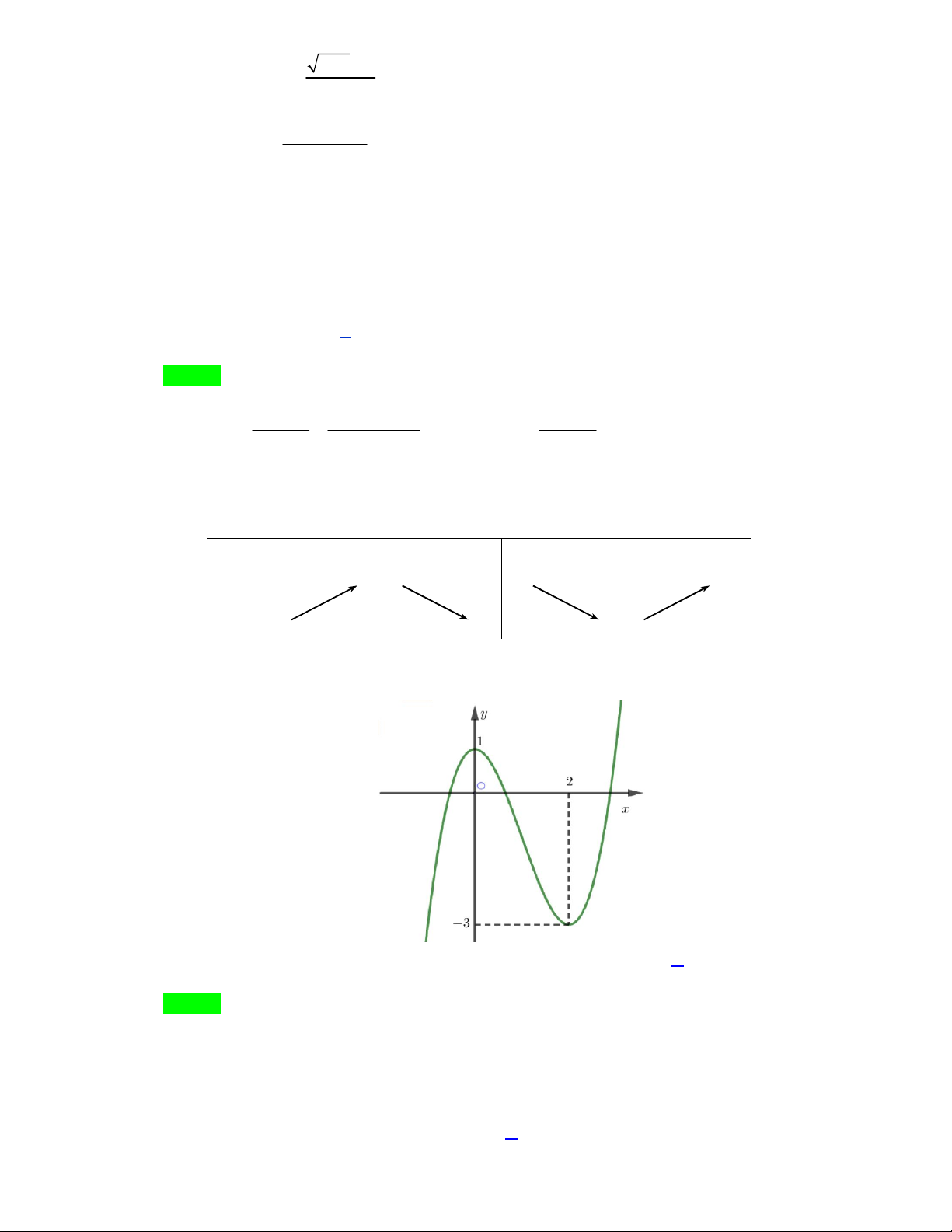
Câu 3. Cho hàm số y f x có đồ thị (C) như hình vẽ. Đường thẳng y 1 -1 1
cắt (C) tại bao nhiêu điểm ? O A. 0. B.1. -2 -3 C. 2. D. 3. -4
Câu 4: Cực tiểu của hàm số 3 2
y x  3x 1 là. A. 1 B. 0 C. 2 D. - 3
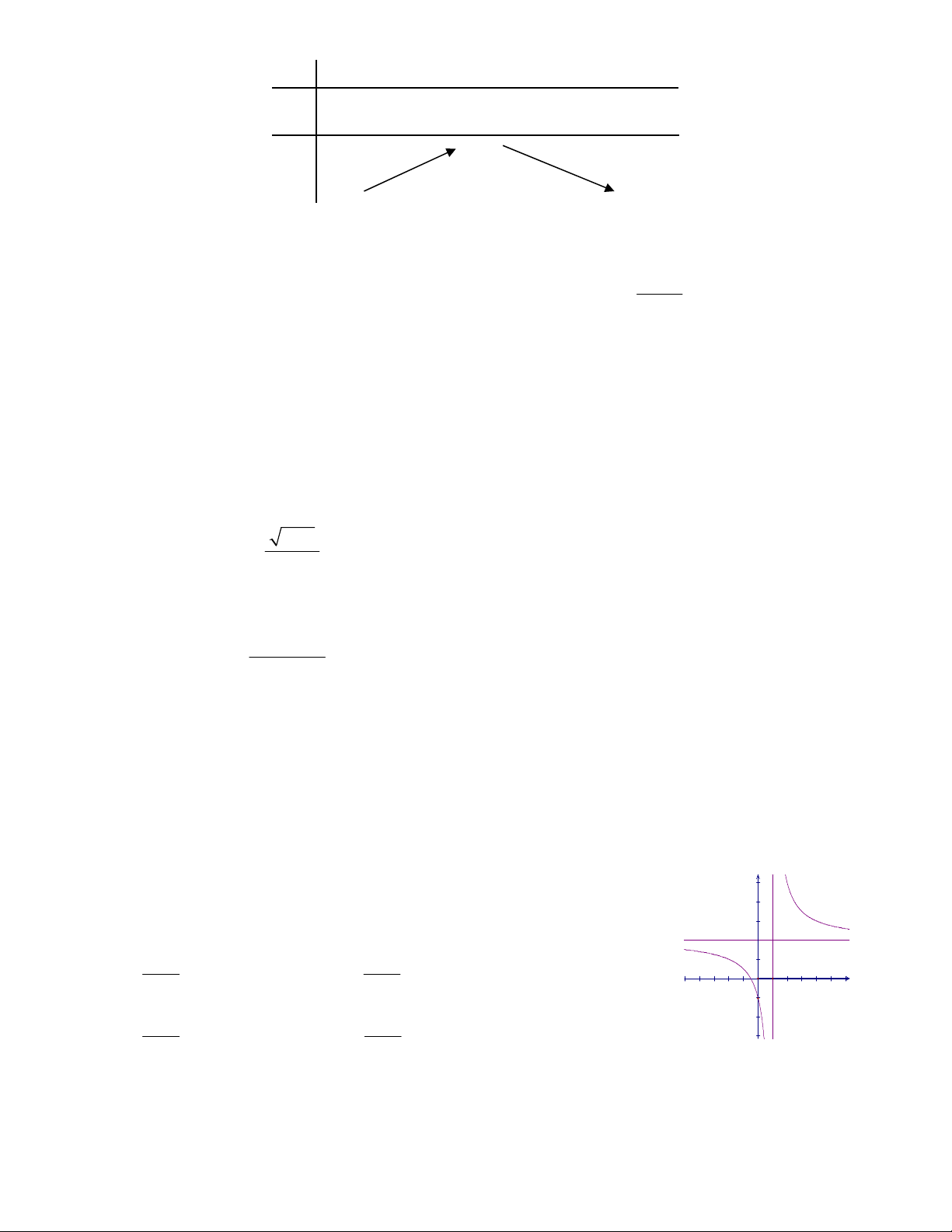
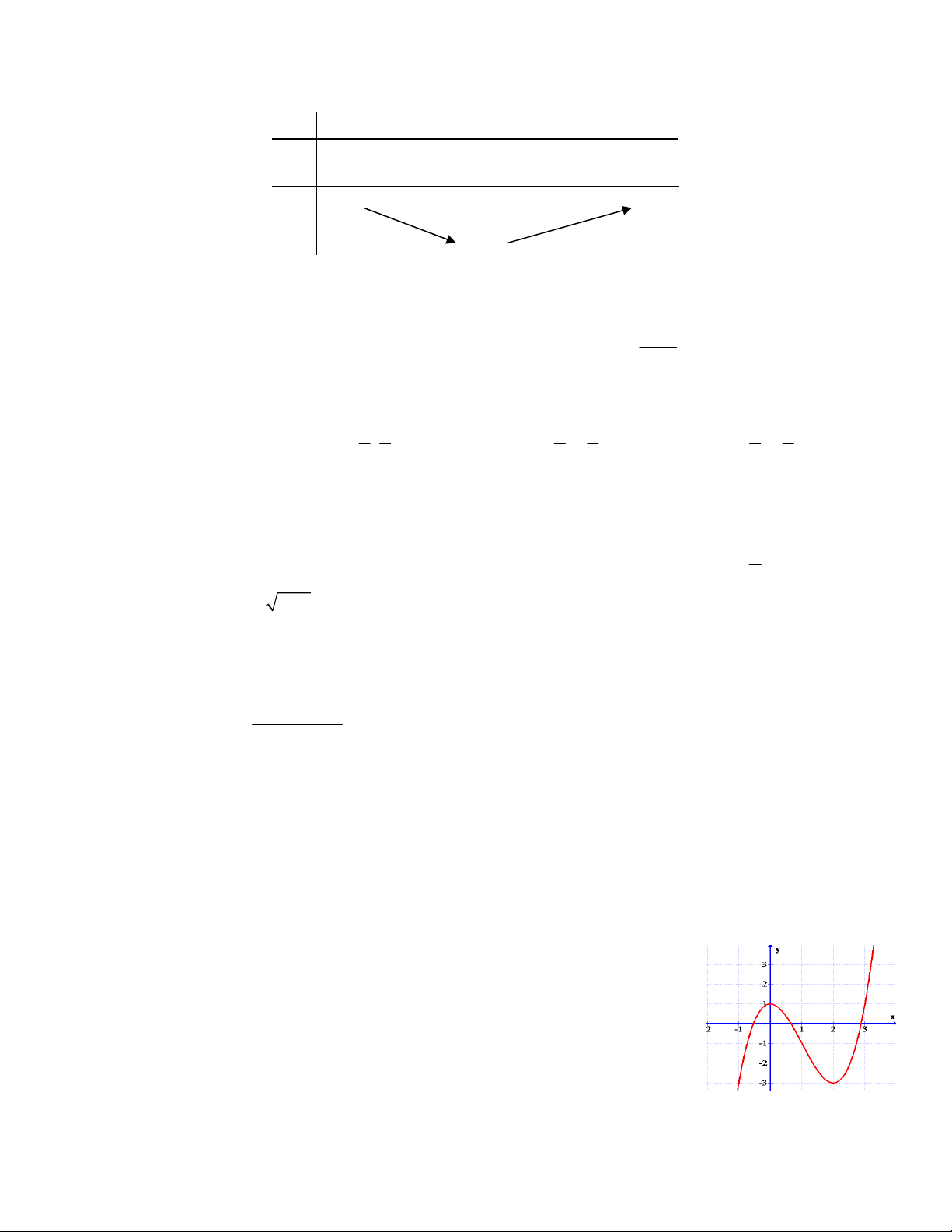
Câu 5: Tâm đối xứng của đồ thị hàm số 2x 1 y  có toạ độ là. x 1
A. (1;2). B. (2;1). C. (-1;2). D. (2; -1).
Câu 6: Giá trị lớn nhất của hàm số 3
y  2x  3x 1 trên đoạn [-1; 2] là.
A. max y  2. B. max y  1. C. max y  15. D. max y  11.  1;  2  1;  2  1;  2  1;  2
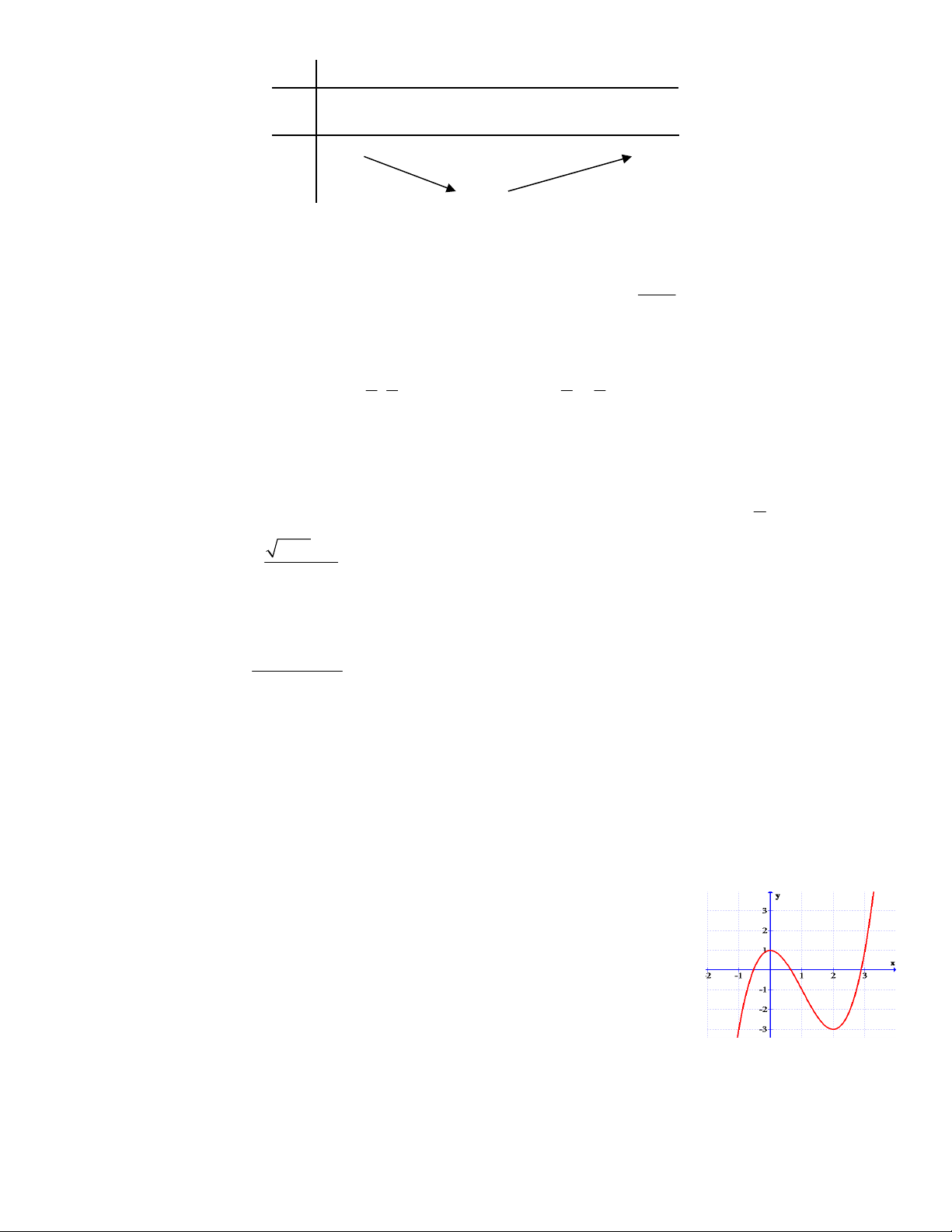
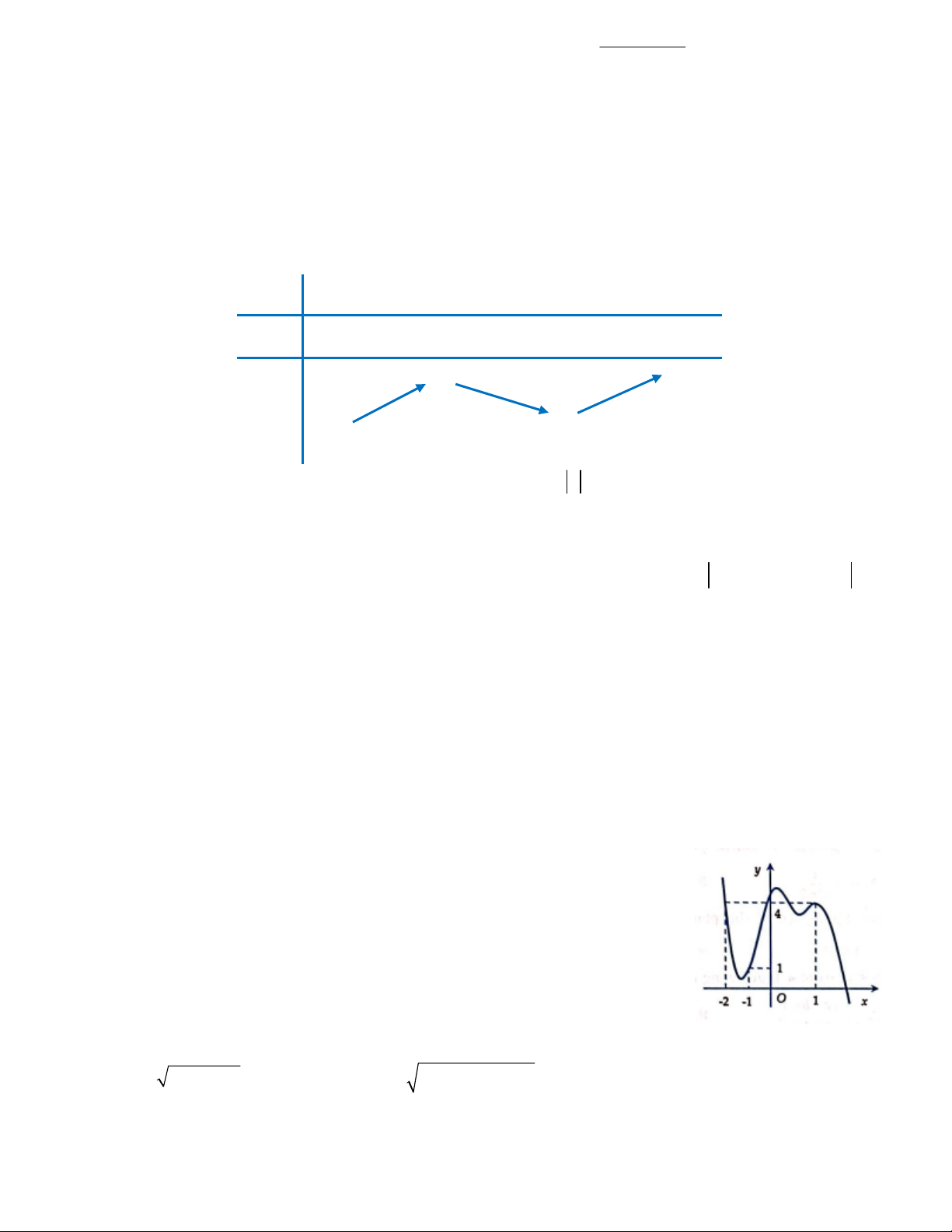
Câu 7. Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số sau ? 6 A. 4 2
y x  3x 1 . B. 3
y x  3x  1 4 I 2 2x 1 2x 1 C. y D. y x 1 x 1 O 1 5 -2
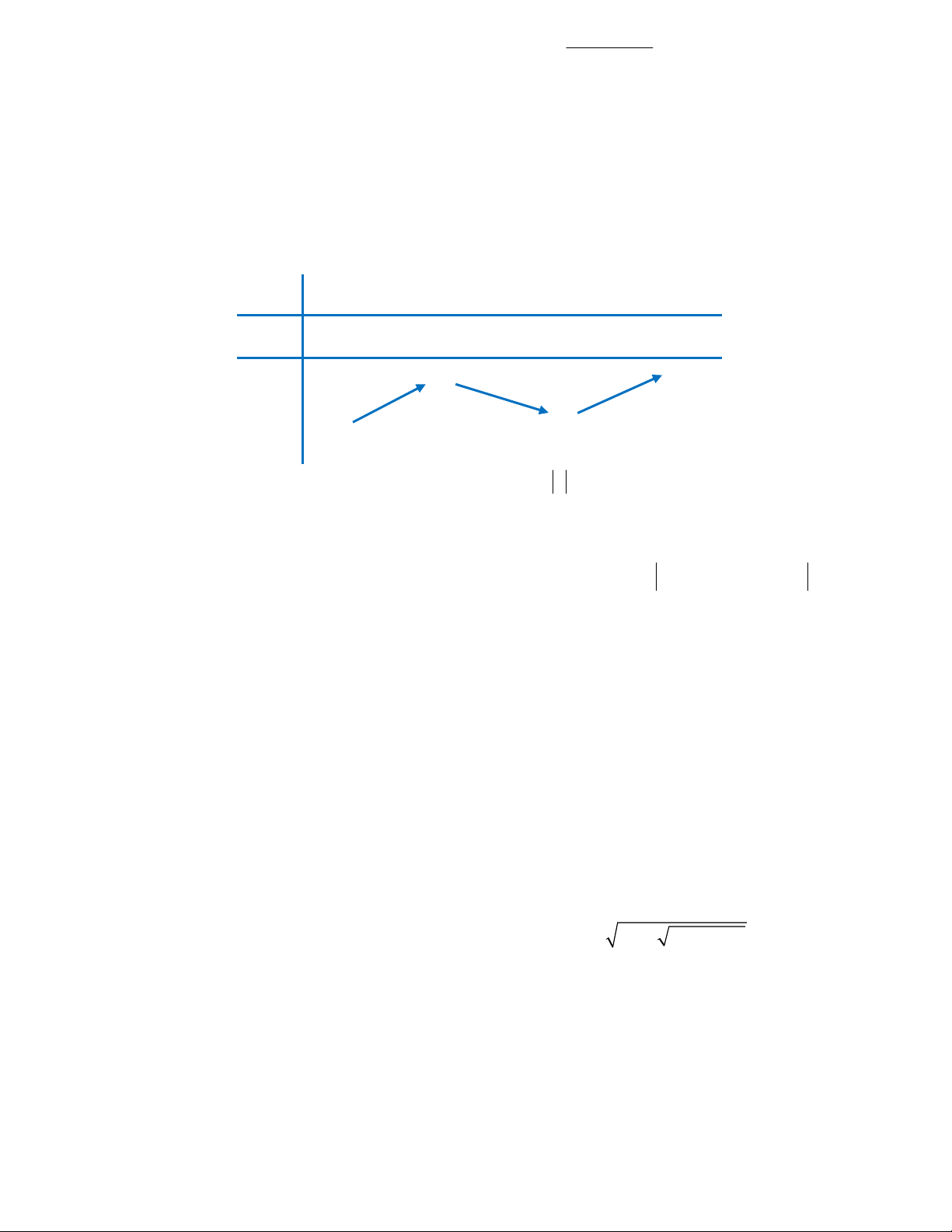
Câu 8: Cho hàm số f (x) xác định, liên tục trên  và có bảng xét dấu f '(x) như sau: x – –1 1 2 + f '(x) + 0 – 0 – || +
Hàm số f (x) có bao nhiêu điểm cực trị ? A. 0
B. 1. C. 2. D. 3. 2x 1
Câu 9. Cho hàm số y
(C). Tiếp tuyến của (C) tại điểm có hoành độ x  3 có phương trình là. x  2
A. y  5
x 8. B. y  5
x  22 C. y  5x  22 D. y  5x 8
Câu 10. Cho hàm số y f x xác định trên  \ 
1 , liên tục trên mỗi khoảng xác định của nó và có bảng biến
thiên như hình vẽ dưới đây. 1 0 x 1 ++ y' 0 + + 1 ++3 y2
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số f x là. A. 1. B. 2. C. 3 D. 4
Câu 11: Cho hàm số f x xác định, liên tục trên R và có đạo hàm cấp một xác định bởi công thức f x 2 '
 x 1. Mệnh đề nào sau đây đúng ? A. f  
1  f 2 .
B. f 3  f 2 . C. f  
1  f 0 . D. f 0  f   1 .
Câu 12. Bảng biến thiên sau đây là của hàm số nào trong bốn hàm số được cho ở bốn phương án A, B, C, D ? x   0   y’ - 0 + y     2 A. 4 2
y  x  3x  2 B. 4 2
y  x  2x  2 C. 4 2
y x  2x  2 D. 4 2
y x x  2 x  3
Câu 13: Gọi M, N là giao điểm của đường thẳng y x 1và đường cong y
. Tìm toạ độ trung điểm I của x 1 đoạn thẳng MN là.  1 1   1 1  A. I  1  ;  1 B. I  ;   C. I ;   D. I 1;2  2 2   2 2 
Câu 14: Trong tất cả các giá trị thực của tham số m làm cho hàm số f x 3 2
x  3mx  m  2 x m đồng
biến trên R, giá trị lớn nhất của m là. 2 A. 0 B. 1 C. 2 D.  3
Câu 15: Đồ thị hàm số x  1  2 y
có bao nhiêu đường tiệm cận ? 2 x  3x
A.1 B. 2 C. 3 D. 4 2 2x x 12
Câu 16. Cho hàm số y
. Xét các mệnh đề sau : x  2
1) Hàm số có hai điểm cực trị.
2) Hàm số đồng biến trên tập ;5  1;.
3) Hàm số nghịch biến trên khoảng 5;  1 .
4) Điểm cực tiểu của đồ thị hàm số là 1;5
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng ? A. 1 B. 2 C. 3 D. 4
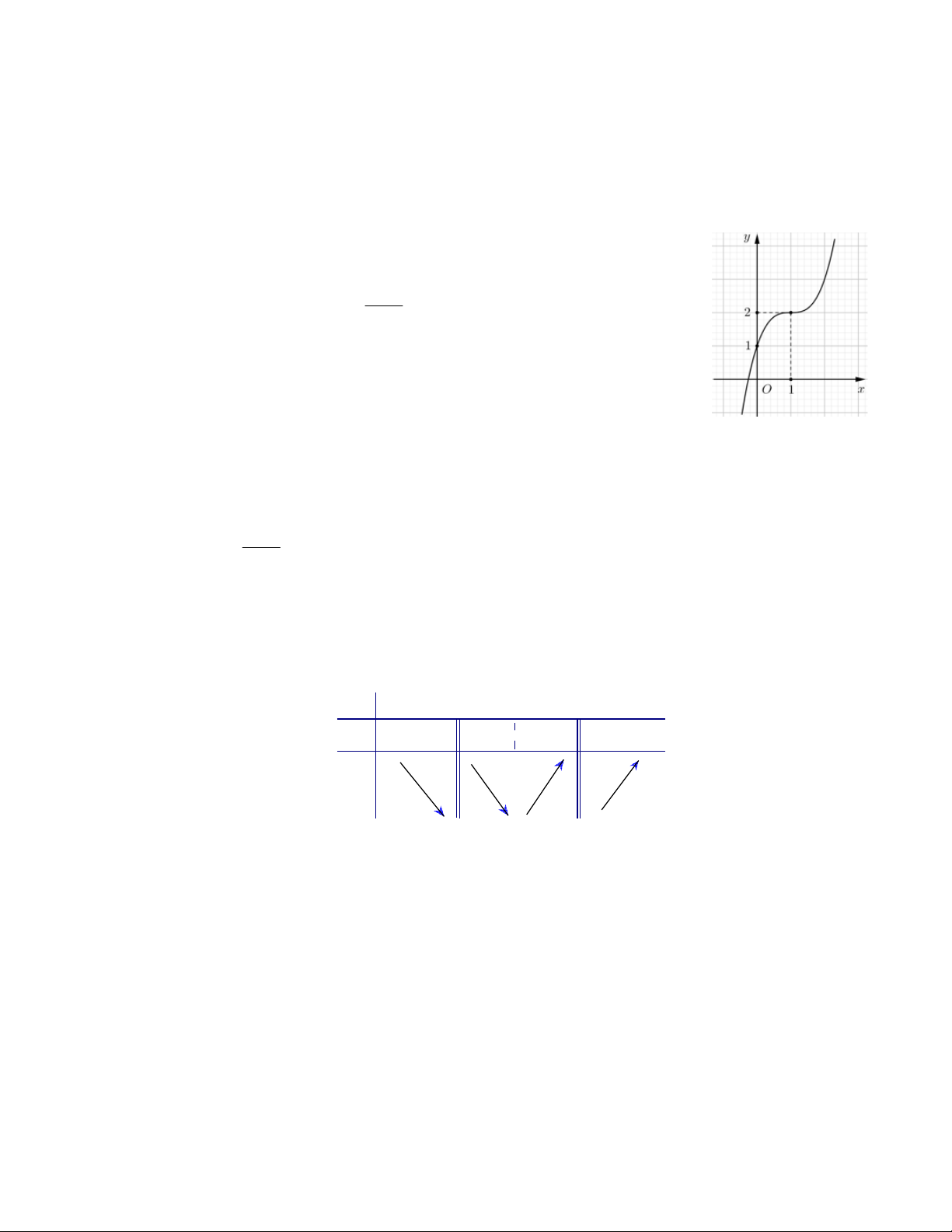
Câu 17: Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số sau đây ? A. 3 2
y x  3x  2 B. 3
y x  3x 1 C. 3 2
y x  3x 1 D. 3 2
y x  3x 1
Câu 18: Tìm m để giá trị nhỏ nhất của hàm số 3 2
y x  3x  9x m trên đoạn 0; 4 bằng – 25, khi đó hãy tính
giá trị của biểu thức P  2m 1.
A.1 B. 3 C. 5 D. 7. x 1
Câu 19: Tính tổng tất cả các giá trị của tham số m để đồ thị hàm số y
luôn có hai đường tiệm cận. 2
x  2x m
A. 2. B. 5. C. 4. D. 4.
Câu 20: Có bao nhiêu đường thẳng đi qua điểm A 1
 ;2 và tiếp xúc với đồ thị của hàm số 3
y x 3x  4 ? A. 0 B. 1 C. 2 D. 3
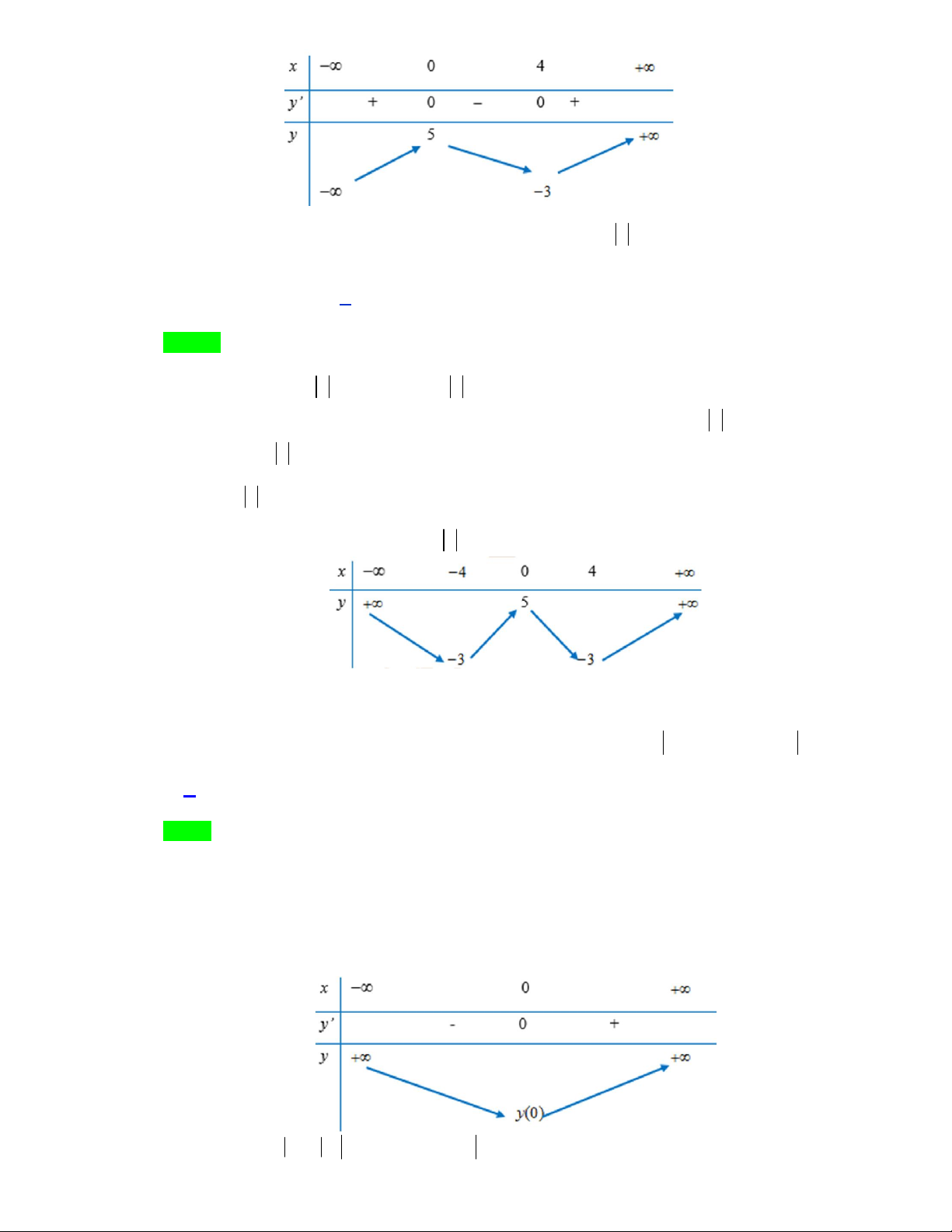
Câu 21: Cho hàm số y f x có bảng biến thiên như sau: x  0 4  y’ + 0  0 + y 5   3
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x   m  0 có 4 nghiệm phân biệt . A. 6.
B. 7. C. 8. D. 9.
Câu 22: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số 4 2 2
y x  2x m  2m có 5 điểm
cực trị. Tìm số phần tử của S. A. 0. B. 1 C. 2. D. 3
Câu 23: Cho hàm số y  f x xác định trên  và có đạo hàm f 'x thỏa f 'x  2  xx  3gx  2018với gx  0, x   .
 Hàm số y  f 1 x  2018x  2019 đồng biến trên khoảng nào ? A.  4;   1 B.  3;
 2 C. 0;3 D. 4;  5
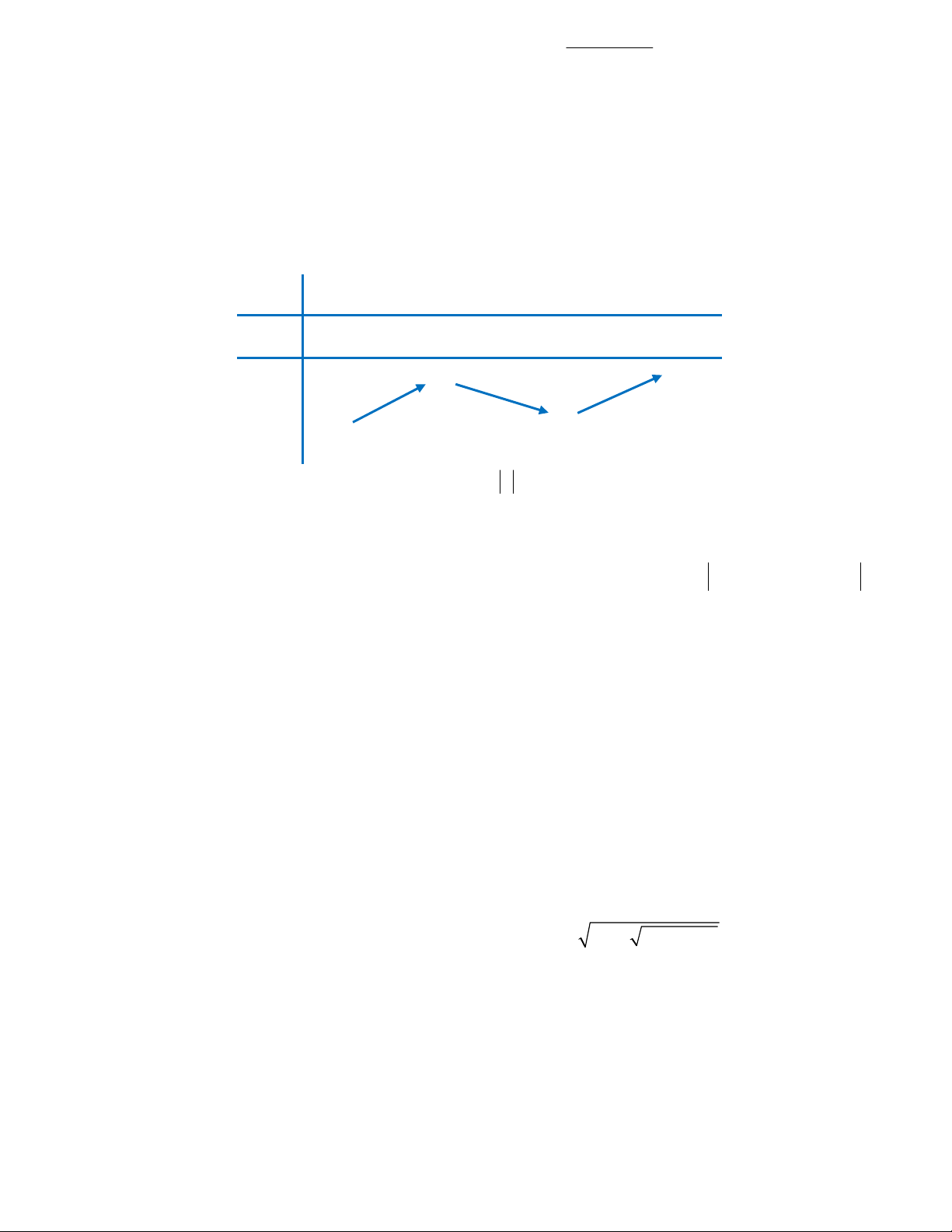
Câu 24: Cho hàm số y f x . Hàm số y f ' x xác định, liên tục trên R và có đồ thị như hình vẽ. Hàm số
g x  f x 4 2 4
x  6x có bao nhiêu điểm cực trị ? A. 0. B. 1. C. 3. D. 5.
Câu 25: Có bao nhiêu giá trị nguyên của tham số thực m để phương trình m x x   x   x m  x m2 2 cos cos 2 2cos cos cos
 2  0 có nghiệm thực ? A. 6. B. 5. C. 4. D. 3.
------------- Hết ---------------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
--------------------------------------------------------- Mã đề 246
Họ và tên học sinh: …………………..……………………………………..Lớp: ………….. PHẦN ĐÁP ÁN Câu Đáp án Câu Đáp án Câu Đáp án 01 09 17 02 10 18 03 11 19 04 12 20 05 13 21 06 14 22 07 15 23 08 16 24 25
Lưu ý: Đối với mỗi câu hỏi, thí sinh chọn và tô kín một ô tròn tương ứng với phương án trả lời đúng.
Câu 1: Cho hàm số y  f x có đồ thị như hình vẽ bên. Hỏi đồ thị của hàm số y  f x có bao nhiêu điểm cực trị ? -1 1 O A. 1 B. 2 -2 C. 3 D. 4 -3 -4
Câu 2: Cho hàm số f (x) có bảng biến thiên như sau.
Hàm số f (x) nghịch biến trên khoảng nào dưới đây ? A.  ;0  .
B. (0;2). C.  2;  2. D. 2;.
Câu 3. Cho hàm số y f x có đồ thị (C) như hình vẽ. Đường thẳng y  2  cắt (C) tại bao nhiêu điểm ? A. 0. B.1. C. 2. D.3. 
Câu 4: Tâm đối xứng của đồ thị hàm số x 1 y  có toạ độ là. x  2
A. (1;2). B. (2;1). C. (-2;1). D. (2; -1).
Câu 5: Cực đại của hàm số 3
y x  3x  2 là. A. 0 B. -1 C. 1 D. 4
Câu 6: Giá trị lớn nhất của hàm số 3 2
y x  3x  9x 17 trên đoạn [-2; 4] là.
A. max y  22. B. max y  20. C. max y  44. D. max y 15.  2;  4  2;  4  2;  4  2;  4
Câu 7. Đường cong ở hình vẽ bên là đồ thị của hàm số nào trong bốn hàm số dưới đây ? x  3 A. 4 2
y x  3x 1. B. y  . x  2 C. 3 2
y x  3x  3x 1. D. 3 2
y  x  3x 1. Câu 8: Hàm số 4 2
y x  4x  3 có bao nhiêu điểm cực trị ?
A. 0. B. 1. C. 2. D. 3 x 1
Câu 9. Cho hàm số y
(C). Tiếp tuyến của (C) tại điểm có hoành độ x  3 có phương trình là. x  2
A. y  3x  5. B. y  3x  5. C. y  3x 13. D. y  3x  5.
Câu 10. Cho hàm số y f x xác định trên  \  1
 , liên tục trên mỗi khoảng xác định của nó và có bảng biến
thiên như hình vẽ dưới đây. x - ∞ -1 0 1 +∞ _ _ y / 0 + + +∞ -2 +∞ -2 y -∞ 1 -∞
Đồ thị của hàm số f x có bao nhiêu tiệm cận ngang ? A. 1. B. 2. C. 3 D. 4
Câu 11: Cho hàm số f x xác định, liên tục trên R và có đạo hàm xác định bởi công thức f x 2 '  x  2 .
Mệnh đề nào sau đây sai ? A. f  
1  f 2 . B. f 2  f 3 . C. f   1  f  
1 . D. f 0  f   1
Câu 12. Bảng biến thiên sau đây là của hàm số nào trong bốn hàm số được cho ở bốn phương án A, B, C, D ? x   0   y’ + 0 - y 2   A. 4 2
y  x  3x  2 B. 4 2
y  x  2x  2 C. 4 2
y x  2x  2 D. 4 2
y x x  2 2x  3
Câu 13: Gọi P, Q là giao điểm của đường thẳng y x  5 và đường cong y
. Tìm toạ độ trung điểm I x 1 của đoạn thẳng PQ.
A. I 1;4. B. I 1;4. C. I 1;4.
D. I 1;4.
Câu 14: Có bao nhiêu giá trị nguyên của tham số m để hàm số f x 3 2
 x  3mx  m  4 x m nghịch biến trên R. A. 0 B. 1 C. 2 D. 3.
Câu 15: Đồ thị hàm số x 1 y
có bao nhiêu đường tiệm cận ? 2 x  3x
A.1 B. 2 C. 3 D. 4 2   Câu 16. Cho hàm số x 5x 7 y
. Xét các mệnh đề sau : x  2
1) Hàm số đồng biến trên mỗi khoảng   ;1 và 3; 
2) Hàm số có ba điểm cực trị.
3) Hàm số nghịch biến trên khoảng 1;3.
4) Điểm cực đại của đồ thị hàm số là 3;  1
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng ? A. 1 B. 2 C. 3 D. 4 y
Câu 17: Đường cong trong hình bên là đồ thị của hàm số nào trong bốn 4 hàm số sâu đây ? 2 A. 2x 1  x y B. 1 2 y x 1 x 1 -5 O 1 5 x -1 -2 C. 2x 1  x y D. 1 2 y x 1 x 1
Câu 18: Tìm m để giá trị nhỏ nhất của hàm số 3
y x  3x m trên đoạn 0;2 bằng 1 ? Khi đó 3m  5 có giá trị bằng.
A.2 B. 3 C. - 4 D. 4 x 1
Câu 19: Tổng tất cả các giá trị của tham số m để đồ thị hàm số y
có đúng một tiệm cận đứng là. 2
x  4x m A. 1.
B. 7. C. 4. D. 4. 
Câu 20: Có bao nhiêu đường thẳng đi qua điểm A ( 0 ; - 1) và tiếp xúc với đồ thị của hàm số 3
y x 3x 1 ? A. 1 B. 2 C. 3 D. 0
Câu 21: Cho hàm số y f x có bảng biến thiên như sau: x  0 2  y’ + 0  0 + y 2   1 
Có bao nhiêu giá trị nguyên của m để phương trình f x  3m  0 có 4 nghiệm phân biệt. A. 0.
B. 1. C. 2. D. 3.
Câu 22: Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số 4 2 2
y  x  2x m  3m có 5
điểm cực trị. Tìm số phần tử của S. A. 0. B. 1 C. 2. D. 3
Câu 23: Cho hàm số y  f x xác định trên  và có đạo hàm f 'x thỏa f 'x  2  xx  3gx  2018với gx  0, x   .
 Hàm số y  f 1 x  2018x  2019 có bao nhiêu điểm cực trị ? A. 0. B. 1 C. 2. D. 3
Câu 24: Cho hàm số y f (x) có đạo hàm 2 2 f (
x)  x(x 1) (x mx  9). Có bao nhiêu số nguyên dương m để
hàm số y f (3  x) đồng biến trên khoảng (3;   ). A. 5. B. 6. C. 7. D. 8.
Câu 25: Có bao nhiêu giá trị nguyên của tham số m để phương trình 3 3
m  3 m  3sin x  sin x có nghiệm thực
A. 2. B. 3. C. 5. D. 7.
------------- Hết ---------------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
--------------------------------------------------------- Mã đề 357
Họ và tên học sinh: …………………..……………………………………..Lớp: ………….. PHẦN ĐÁP ÁN Câu Đáp án Câu Đáp án Câu Đáp án 01 09 17 02 10 18 03 11 19 04 12 20 05 13 21 06 14 22 07 15 23 08 16 24 25
Lưu ý: Đối với mỗi câu hỏi, thí sinh chọn và tô kín một ô tròn tương ứng với phương án trả lời đúng.
Câu 1: Cho hàm số y  f x có đồ thị như hình vẽ bên. Hỏi đồ thị của hàm số
y  f x có bao nhiêu điểm cực trị ? A. 0 B. 1 C. 2 D. 3
Câu 2: Cho hàm số f (x) có bảng biến thiên như hình vẽ sau
Hàm số f (x) đồng biến trên khoảng nào dưới đây ? A.  2;  0. B.  ;  2  . C.  2;  2. D.  1  ;3.
Câu 3. Cho hàm số y f x có đồ thị (C) như hình vẽ. Đường thẳng y  2  -1 1
cắt (C) tại bao nhiêu điểm ? O A. 0. C.1. -2 -3 B. 2. D. 3. -4
Câu 4: Cực đại của hàm số 3 2
y x  3x 1 là. A. 1 B. 0 C. 2 D. - 3
Câu 5: Tâm đối xứng của đồ thị hàm số x 1 y  có toạ độ là. x  2
A. (1;2). B. (2;1). C. (-1;2). D. (-2; 1).
Câu 6: Giá trị lớn nhất của hàm số 3
y x  3x  2 trên đoạn [0; 2] là.
A. max y  2. B. max y  1. C. max y  4. D. max y  6. 0;2 0;2 0;2 0;2
Câu 7. Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số sau ? 6 4 A. 4 2
y x  3x 1 . B. 3
y x  3x  1 I 2 2x 1 2x 1 C. y D. y O 1 5 x 1 x 1 -2
Câu 8: Cho hàm số f (x) xác định, liên tục trên  và có bảng xét dấu f '(x) như sau: x – –1 1 2 + f '(x) - 0 + 0 – || +
Hàm số f (x) có bao nhiêu điểm cực trị ? A. 0
B. 1. C. 2. D. 3. 2x 1
Câu 9. Cho hàm số y
(C). Tiếp tuyến của (C) tại điểm có hoành độ x  1 có phương trình là. x  2
A. y  5x  2. B. y  5x 8. C. y  5
x 8. D. y  5  x  2
Câu 10. Cho hàm số y f x xác định trên tập ;2 \ 
2 , liên tục trên mỗi khoảng xác định của nó và có
bảng biến thiên như hình vẽ dưới đây. 0 2 +x 2 y' + 0 + 3 ++y -2 2
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số f x là. A. 4. B. 3. C. 2. D. 1.
Câu 11: Cho hàm số f x xác định, liên tục trên R và có đạo hàm cấp một xác định bởi công thức f x 2 '
 x  2 . Mệnh đề nào sau đây đúng ? A. f  
1  f 2 .
B. f 3  f 2 . C. f  2
   f 0. D. f 0  f   1 .
Câu 12. Bảng biến thiên sau đây là của hàm số nào trong bốn hàm số được cho ở bốn phương án A, B, C, D ? x   0   y’ - 0 + y     1 A. 4 2
y  x 3x 1 B. 4 2
y  x  2x 1 C. 4 2
y x  2x 1 D. 4 2
y x x 1 x  3
Câu 13: Gọi M, N là giao điểm của đường thẳng y x  3và đường cong y
. Tìm toạ độ trung điểm I của x 1 đoạn thẳng MN là.  1 5   5 1   5 3 
A. I 5;2 B. I  ;   C. I ;   D. I ;    2 2   2 2   2 2 
Câu 14: Trong tất cả các giá trị thực của tham số m làm cho hàm số f x 3 2
x  3mx  m  2 x m đồng
biến trên R, giá trị nhỏ nhất của m là. 2 A. 0 B. 1 C. 2 D.  3
Câu 15: Đồ thị hàm số x  1 1 y
có bao nhiêu đường tiệm cận ? 2 x  2x
A.4 B. 3 C. 2 D. 1 2 2x x 12
Câu 16. Cho hàm số y
. Xét các mệnh đề sau : x  2
1) Hàm số có hai điểm cực trị.
2) Hàm số đồng biến trên tập  ;
 5 1;.
3) Hàm số nghịch biến trên khoảng 5;  1 .
4) Điểm cực tiểu của đồ thị hàm số là 1;5
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng ? A. 1 B. 2 C. 3 D. 4
Câu 17: Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số sau đây ? A. 3 2
y x  3x  2 B. 3 2
y x 3x 1 C. 3
y x  3x 1 D. 3 2
y x  3x 1
Câu 18: Tìm m để giá trị lớn nhất của hàm số 3 2
y x  3x  9x m trên đoạn 0; 4 bằng 3, khi đó hãy tính giá
trị của biểu thức P  2m 1.
A.1 B. 3 C. 5 D. 7. x 1
Câu 19: Tính tổng tất cả các giá trị của tham số m để đồ thị hàm số y
luôn có hai đường tiệm cận. 2
x  4x m
A. 3. B. 5. C. 7. D. 4.
Câu 20: Có bao nhiêu đường thẳng đi qua điểm A1;2 và tiếp xúc với đồ thị của hàm số 3
y x 3x  4? A. 0 B. 1 C. 2 D. 3
Câu 21: Cho hàm số y f x có bảng biến thiên như sau: x  0 2  y’ + 0  0 + y 3   1
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x   2m  0 có đúng 3 nghiệm. A. 0.
B. 1. C. 2. D. 3.
Câu 22: Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số 4 2 2
y x  2x m  2m có 5
điểm cực trị. Tìm số phần tử của S. A. 0. B. 1 C. 2. D. 3
Câu 23: Cho hàm số y  f x xác định trên  và có đạo hàm f 'x thỏa f 'x  2  xx  3gx  2018với gx  0, x   .
 Hàm số y  f 1 x  2018x  2019 nghịch biến trên khoảng nào ? A.  4;   1 B.  3;
 2 C. 0;3 D. 4;  5
Câu 24: Cho hàm số y f x . Hàm số y f ' x xác định, liên tục trên R và có đồ thị như hình vẽ. Hàm số
g x  f x 4 2 4
x  6x có bao nhiêu điểm cực trị ? A. 0. B. 1. C. 3. D. 5.
Câu 25: Có bao nhiêu giá trị nguyên dương của tham số thực m để phương trình m x x   x   x m  x m2 2 cos cos 2 2 cos cos cos
 2  0 có nghiệm thực ? A. 4. B. 5 . C. 2. D. 3.
------------- Hết ---------------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
--------------------------------------------------------- Mã đề 485
Họ và tên học sinh: …………………..……………………………………..Lớp: ………….. PHẦN ĐÁP ÁN Câu Đáp án Câu Đáp án Câu Đáp án 01 09 17 02 10 18 03 11 19 04 12 20 05 13 21 06 14 22 07 15 23 08 16 24 25
Lưu ý: Đối với mỗi câu hỏi, thí sinh chọn và tô kín một ô tròn tương ứng với phương án trả lời đúng.
Câu 1: Cho hàm số y  f x có đồ thị như hình vẽ bên. Hỏi đồ thị của hàm số y  f x có bao nhiêu điểm cực trị ? -1 1 O A. 1 C. 2 -2 B. 3 D. 4 -3 -4
Câu 2: Cho hàm số f (x) có bảng biến thiên như sau.
Hàm số f (x) nghịch biến trên khoảng nào dưới đây ? A.  ;0  .
B. (0;2). C.  2;  2. D.  2;  0.
Câu 3. Cho hàm số y f x có đồ thị (C) như hình vẽ. Đường thẳng y  2 cắt (C) tại bao nhiêu điểm ? A. 0. B.1. C. 2. D.3. 
Câu 4: Tâm đối xứng của đồ thị hàm số x 1 y  có toạ độ là. x  2
A. (1;2). B. (2;1). C. (-2;1). D. (2; -1).
Câu 5: Cực tiểu của hàm số 3
y x  3x  2 là. A. 0 B. -1 C. 1 D. 4
Câu 6: Giá trị lớn nhất của hàm số 3 2
y x  3x  9x 17 trên đoạn [-2; 4] là.
A. max y  44. B. max y  20. C. max y  22. D. max y 15.  2;  4  2;  4  2;  4  2;  4
Câu 7. Đường cong ở hình vẽ bên là đồ thị của hàm số nào trong bốn hàm số dưới đây ? x  3 A. 4 2
y x  3x 1. C. y  . x  2 B. 3 2
y x  3x  3x 1. D. 3 2
y  x  3x 1. Câu 8: Hàm số 4 2
y x  4x  3 có bao nhiêu điểm cực trị ?
A. 0. B. 1. C. 2. D. 3 x 1
Câu 9. Cho hàm số y
(C). Tiếp tuyến của (C) tại điểm có hoành độ x  1 có phương trình là. x  2
A. y  3x  5. B. y  3x  5. C. y  3x 13. D. y  3x 1.
Câu 10. Cho hàm số y f x xác định trên  \  1
 , liên tục trên mỗi khoảng xác định của nó và có bảng biến
thiên như hình vẽ dưới đây. x - ∞ -1 0 1 +∞ _ _ y / 0 + + +∞ -2 +∞ -2 y -∞ 1 -∞
Đồ thị của hàm số f x có bao nhiêu tiệm cận đứng ? A. 1. B. 2. C. 3 D. 4
Câu 11: Cho hàm số f x xác định, liên tục trên R và có đạo hàm xác định bởi công thức f x 2 '  x  2 .
Mệnh đề nào sau đây sai ? A. f  
1  f 2 . B. f 2  f 3 .
C. f 3  f 0 . D. f 0  f   1
Câu 12. Bảng biến thiên sau đây là của hàm số nào trong bốn hàm số được cho ở bốn phương án A, B, C, D ? x   0   y’ + 0 - y 1   A. 4 2
y  x  3x 1 B. 4 2
y  x  2x 1 C. 4 2
y x  2x 1 D. 4 2
y x x 1 2x  3
Câu 13: Gọi P, Q là giao điểm của đường thẳng y x  3 và đường cong y
. Tìm toạ độ trung điểm I x 1 của đoạn thẳng PQ.
A. I 1; 2. B. I 2; 
1 . C. I 1;2. D. I 2;  1 .
Câu 14: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số f x 3 2
 x  3mx  m  4 x m nghịch biến trên R. A. 0 B. 1 C. 2 D. 3.  
Câu 15: Đồ thị hàm số x 1 2 y
có bao nhiêu đường tiệm cận ? 2 x  3x
A.1 B. 2 C. 3 D. 4 2   Câu 16. Cho hàm số x 5x 7 y
. Xét các mệnh đề sau : x  2
1) Hàm số đồng biến trên mỗi khoảng   ;1 và 3; 
2) Hàm số có ba điểm cực trị.
3) Hàm số nghịch biến trên khoảng 1;3.
4) Điểm cực đại của đồ thị hàm số là 3;  1
Trong các mệnh đề trên, có bao nhiêu mệnh đề sai ? A. 1 B. 2 C. 3 D. 4 y
Câu 17: Đường cong trong hình bên là đồ thị của hàm số nào trong bốn 4 hàm số sâu đây ? 2 A. 2x 1  x y B. 1 2 y x 1 x 1 -5 O 1 5 x -1 -2 C. 2x 1  x y D. 1 2 y x 1 x 1
Câu 18: Tìm m để giá trị nhỏ nhất của hàm số 3
y x  3x m trên đoạn 0;2 bằng 1 ? Khi đó 3m  6 có giá trị bằng.
A.2 B. 3 C. - 4 D. 4 x 1
Câu 19: Tổng tất cả các giá trị của tham số m để đồ thị hàm số y
có đúng một tiệm cận đứng là. 2
x  2x m A. 1.
B. 2. C. 4. D. 4. 
Câu 20: Có bao nhiêu đường thẳng đi qua điểm A ( 0 ; 1) và tiếp xúc với đồ thị của hàm số 3
y x 3x 1 ? A. 1 B. 2 C. 3 D. 0
Câu 21: Cho hàm số y f x có bảng biến thiên như sau: x  0 2  y’ + 0  0 + y 2   1 
Có bao nhiêu giá trị nguyên dương của m để phương trình f x  3m  0 có 4 nghiệm phân biệt. A. 0.
B. 1. C. 2. D. 3.
Câu 22: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số 4 2 2
y  x  2x m  3m có 5 điểm
cực trị. Tìm số phần tử của S. A. 4. B. 3 C. 2. D. 1
Câu 23: Cho hàm số y  f x xác định trên  và có đạo hàm f 'x thỏa f 'x  3 xx  3gx  2018 với gx  0, x   .
 Hàm số y  f 1 x  2018x  2019 có bao nhiêu điểm cực trị ? A. 0. B. 1 C. 2. D. 3
Câu 24: Cho hàm số y f (x) có đạo hàm 2 2 f (
x)  x(x 1) (x mx  9). Có bao nhiêu số nguyên dương m để
hàm số y f (3  x) đồng biến trên khoảng (3;   ). A. 6. B. 5. C. 7. D. 8.
Câu 25: Có bao nhiêu giá trị nguyên âm của tham số m để phương trình 3 3
m  3 m  3sin x  sin x có nghiệm thực
A. 2. B. 3. C. 5. D. 7.
------------- Hết ---------------
TRƯỜNG THPT TX QUẢNG TRỊ ĐÁP ÁN ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
--------------------------------------------------------- Mã đề thi: 135 Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án 1 B 6 D 11 D 16 B 21 B 2 D 7 D 12 D 17 D 22 A 3 C 8 C 13 B 18 C 23 C 4 D 9 C 14 B 19 A 24 C 5 A 10 C 15 B 20 B 25 B
Mã đề thi: 246 Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án 1 C 6 A 11 C 16 A 21 B 2 D 7 C 12 B 17 A 22 D 3 D 8 D 13 C 18 D 23 C 4 C 9 C 14 D 19 A 24 B 5 D 10 A 15 B 20 A 25 C Mã đề thi: 357 Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án 1 C 6 C 11 C 16 B 21 A 2 B 7 C 12 C 17 B 22 A 3 B 8 D 13 C 18 D 23 D 4 A 9 A 14 D 19 C 24 B 5 B 10 B 15 C 20 C 25 C
Mã đề thi: 485 Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án 1 B 6 C 11 D 16 C 21 A 2 D 7 B 12 A 17 C 22 A 3 B 8 B 13 A 18 B 23 C 4 B 9 D 14 B 19 B 24 A 5 A 10 B 15 B 20 A 25 A BẢNG ĐÁP ÁN 1.B 2.D 3.C 4.D 5.A 6.D 7.D 8.C 9.C 10.C 11.D 12.D 13.B 14.B 15.B 16.B 17.D 18.C 19.A 20.B 21.B 23.C 24.C 25.B
LỜI GIẢI CHI TIẾT Câu 1.
Cho hàm số y f x có đồ thị như hình vẽ bên. Hỏi đồ thị của hàm số y f x có bao nhiêu điểm cực trị? A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn B
Dựa vào đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt và y .y
 0 đồ thị hàm số có 2 điểm CÐ CT cực trị. Câu 2.
Cho hàm số f x có bảng biến thiên như hình vẽ sau
Hàm số đồng biến trên khoảng nào dưới đây? A. ;3 . B.  2  ; 0 . C.  2  ; 2 . D. 0; 2 . Lời giải Chọn D
Dựa vào bảng biến thiên ta thấy y  0 , x  0; 2  chọn D. Câu 3:
Cho hàm số y f x có đồ thị (C) như hình vẽ. Đường thẳng y  1 cắt (C) tại bao nhiêu điểm? Trang 5/17 - WordToan A. 0. B. 1. C. 2. D. 3. Lời giải Chọn C
Theo đồ thị ta tháy có 2 giao điểm Câu 4: Cực tiểu của hàm số 3 2
y x  3x 1 là. A. 1 . B. 0 . C. 2 . D. 3  . Lời giải Chọn D x  0 2
y '  3x  6x  0  x  2 
y '  6x  6 ; y ' (0)  6  0 hàm số đạt CĐ tại x  0 .
y ' (2)  6  0 hàm số đạt CT tại x  2; y  3 CT 2x 1 Câu 5.
Tâm đối xứng của đồ thị hàm số y  có toạ độ là x 1 A. 1; 2 . B. 2;  1 . C. 1; 2 . D 2;   1 . Lời giải Chọn A
Tập xác định D   \   1 . Ta có: 2x 1 + lim
 2 nên y  2 là tiệm cận ngang. x x 1 2x 1 + lim
  nên x  1 là tiệm cận đứng.  x  1 x 1
Vậy tâm đối xứng của đồ thị hàm số trên có tọa độ là 1; 2 . Câu 6.
Giá trị lớn nhất của hàm số 3
y  2x  3x 1 trên đoạn  1;  2 là
A. max y  2 . B. max y  1.
C. max y  15 . D. max y  11.  1  ;2 1;2 1;2 1;2 Lời giải Chọn D
Xét hàm số y f x 3
 2x  3x 1 trên đoạn  1;  2 : Ta có 2
y  6x  3 .  2 x      1;  2 2 Cho y  0 2
 6x  3  0   .  2  x   1  ; 2  2
Trang 6/17 – Diễn đàn giáo viên Toán  2   2  Khi đó: f  
1  2 , f 2  11 , f     1 2 , f    1 2 .  2      2   Vậy max y  11.  1  ;2
Câu 7. Đường cong trong hình bên là đồ thị của hàm số nào trong 4 hàm số sau? A. 4 2
y x  3x 1 . B. 3
y x  3x 1. 2x 1 2x 1 C. y  . D. y  . x 1 x 1 Lời giải: Chọn D
Dựa vào đồ thị ta nhận biết đây là đồ thị bậc nhất trên bậc nhất → Loại A và B
Dựa vào đồ thị ta tìm được TCĐ và TCN TCĐ: x  1 TCN: y  2
Chọn đáp án đúng là D.
Câu 8. Cho hàm số f (x) xác định, liên tục trên có bảng xét dấu f (  x) như sau:
Hàm số f (x) có bao nhiêu điểm cực trị? A. 0. B. 1. C. 2 D. 3. Lời giải Chọn C
Dựa vào BBT và áp dụng định lí 1 của SGK, hàm số đạt cực đại tại x  1
 , đạt cực tiêu tại x  2 .
Suy ra hàm số có 2 điểm cực trị. 2x 1 Câu 9. Cho hàm số y
(C). Tiếp tuyến của (C) tại điểm có hoành độ x  3 có phương trình là x  2 A. y  5  x  8 . B. y  5  x  22 .
C. y  5x  22 .
D. y  5x  8 . Trang 7/17 - WordToan Lời giải Chọn C 5 Ta có y  .  x  22 2. 3   1
Gọi M 3; y  C . Khi đó tung độ của điểm M là y
 7  tọa độ M 3; 7 . M   M 3   2 5
Hệ số góc của tiếp tuyến của (C) tại M là k y3   5 .  3   22
Vậy phương trình tiếp tuyến của (C) tại M là: y  5 x  3  7  y  5x  22 .
Câu 10. Cho hàm số y f x xác định trên  \   1 
, liên tục trên mỗi khoảng xác định của nó và có bảng
biến thiên như hình vẽ dưới đây.
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số f x là. A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C
Theo bảng biến thiên của hàm số y f x ta có: *Tiệm cận đứng:
Ta có lim f x    hàm số y f x có tiệm cận đứng x  1  . x 1 
lim f x    hàm số y f x có tiệm cận đứng x 1. x 1 
Vậy đồ thị hàm số có 2 tiệm cận đứng. *Tiệm cận ngang:
Ta có lim f x  3  hàm số y f x có tiệm cận ngang y  3 . x
Vậy đồ thị hàm số có 1 tiệm cận ngang.
Kết luận: Tổng số tiệm cận đứng và ngang của đồ thị hàm số y f x là 3 .
Câu 11. Cho hàm số f x xác định, liên tục trên  và có đạo hàm cấp một xác định bởi công thức f  x 2
 x 1. Mệnh đề nào sau đây đúng? A. f   1  f 2 .
B. f 3  f 2 . C. f   1  f 0 .
D. f 0  f   1 .
Trang 8/17 – Diễn đàn giáo viên Toán Lời giải Chọn D
Vì f  x 2
 x 1  0 , x
   nên hàm số nghịch biến trên  . Vì thế:
Do 1  2 nên f  
1  f 2 . Suy ra A sai.
Do 3  2 nên f 3  f 2 . Suy ra B sai.
Do 1  0 nên f  
1  f 0 . Suy ra C sai. Do 0  1
 nên f 0  f   1 . Suy ra D đúng.
Câu 12. Bảng biến thiên sau đây là của hàm số nào trong bốn hàm số được cho ở bốn phương án A, B, C, D? A. 4 2
y  x  3x  2 . B. 4 2
y  x  2x  2 . C. 4 2
y x  2x  2 . D. 4 2
y x x  2 . Lời giải Chọn D
Các hàm số ở bốn phương án A, B, C, D đều có dạng 4 2
y ax bx c .
Dựa vào bảng biến thiên ta thấy hàm số cần tìm có hệ số a  0 , nên loại A, B.
Cũng dựa vào bảng biến thiên ta thấy hàm số cần tìm chỉ có 1 điểm cực trị.
Xét hàm số ở phương án C: 4 2
y x  2x  2 , ta có: x  0 3 
y  4x  4x ; y  0  x  1
 . Suy ra hàm số này có 3 điểm cực trị.  x  1 
Do đó loại phương án C. Vậy chọn đáp án là D. x  3
Câu 13. Gọi M, N là giao điểm của đường thẳng y x 1và đường cong y
. Tìm toạ độ trung điểm I x 1
của đoạn thẳng MN là  1 1   1 1  A. I  1  ;  1 . B. I  ;   . C. I ;    . D. I 1;2 .  2 2   2 2  Lời giải Trang 9/17 - WordToan Chọn B x  3
Hoành độ x , x của M, N là nghiệm của phương trình x 1  (1). M N x 1 Ta có 2 2
(1)  ( x  1)  x  3  x x  2  0 . x x 1
Hoành độ trung điểm I của đoạn thẳng MN là M N x
  (theo định lí Viet). I 2 2 1
Điểm I nằm trên đường thẳng y x 1 nên có tung độ là y x  1  . I I 2  1 1 
Vậy, tọa độ điểm I là I  ;   .  2 2 
Cách khác: Tìm tọa độ điểm M, N rồi tìm tọa độ điểm I.
Câu 14. Trong tất cả các giá trị thực của tham số m làm cho hàm số f x 3 2
x  3mx  m  2 x m đồng
biến trên R, giá trị lớn nhất của m là 2 A. 0. B. 1. C. 2. D.  . 3 Lời giải Chọn B
Ta có f  x 2
 3x  6mx m  2 .
Hàm số đồng biến trên R  f (  x)  0, x
  R và dấu bằng chỉ xảy ra tại hữu hạn điểm a  3  0 2 2 2  f (
x)  0,x R  
 (3m)  3(m  2)  0  9m  3m  6  0    m  1   0 3 
Do vậy, giá trị lớn nhất cần tìm của m là 1. x 1  2
Câu 15. Đồ thị hàm số y
có bao nhiêu đường tiệm cận? 2 x  3x A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn B x 1  2 Hàm số y
có tập xác định D   1  ;  \ 0;  3 . 2 x  3x x 1  2 Ta có lim y  lim
  nên đồ thị hàm số nhận đường thẳng x  0 làm tiệm cận đứng.   2 x0 x0 x  3x x 1  2 x  3 1 1 lim y  lim  lim  lim  . 2 x3 x3 x3 x  3x  2
x  3x x 1  2 x3 xx 1  2 12
Do đó đồ thị hàm số chỉ có duy nhất 1 đường tiệm cận đứng.
Trang 10/17 – Diễn đàn giáo viên Toán x 1  2 Lại có lim y  lim
 0 nên đồ thị hàm số nhận đường thẳng y  0 làm tiệm cận ngang. 2 x x x  3x 2 2x x 12
Câu 16. Cho hàm số y
. Xét các mệnh đề sau : x  2
1) Hàm số có hai điểm cực trị.
2) Hàm số đồng biến trên tập  ;  5   1; .
3) Hàm số nghịch biến trên tập  5  ;  1 .
4) Điểm cực tiểu của đồ thị hàm số là 1;5 .
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng? A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn B 2 18 2x  8x 10 18 x  1 Xét ' y  2   '  y  0  2   0  .  2  x  22  x  22  x  2 x  5  
Ta có bảng biến thiên của hàm số đã cho x  5 2  1  y  0   0  19   y   5
Do đó mệnh đề 1) đúng, mệnh đề 2) sai, mệnh đề 3) sai và mệnh đề 4) đúng.
Câu 17. Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số sau đây? A. 3 2
y x  3x  2 . B. 3
y x  3x 1. C. 3 2
y x  3x 1 . D. 3 2
y x  3x 1. Lời giải Chọn D
Dựa vào đồ thị ta có: Điểm cực đại 0; 
1 và điểm cực tiểu 2; 3
  nên đó là đồ thị của hàm số 3 2
y x  3x 1.
Câu 18. Tìm m để giá trị nhỏ nhất của hàm số 3 2
y x  3x  9x m trên đoạn 0; 4 bằng 25 , khi đó hãy
tính giá trị của biểu thức P  2m 1 A. 1. B. 3 . C. 5 . D. 7 . Lời giải Trang 11/17 - WordToan Chọn C + 2
y  3x  6x  9 . x  1   0; 4 + 2
y  0  3x  6x  9  0   .
x  3 0; 4 
+ y 0  m , y 3  m  27 , y 4  m  20 .
Hàm số đã cho liên tục trên đoạn 0; 4 do đó hàm số đạt giá trị nhỏ nhất bằng m  27
Suy ra m  27  25  m  2 .
Vậy P  2m 1  5 . x  1
Câu 19. Tính tổng tất cả các giá trị của tham số m để đồ thị của hàm số y  luôn có hai đường 2
x  2x m tiệm cận. A. –2. B. 5. C. –4. D. 4. Lời giải Chọn A
Ta có lim y  lim y  0  Đồ thị hàm số có tiệm cận ngang y = 0. x   x  
Để đồ thị hàm số có hai đường tiệm cận  đồ thị hàm số chỉ có 1 tiệm cận đứng. Xét phương trình 2
x  2x m  0 (1). Ta có   4  4m .
TH1: Phương trình (1) có 1 nghiệm duy nhất.
m  1. Với m = 1, phương trình có nghiệm x = 1  nhận.
TH2: Phương trình (2) có hai nghiệm phân biệt trong đó có một nghiệm x = –1   0  m  1      m  3.    2 1  2  1  m  0 m  3  
Vậy tổng các giá trị của m thỏa mãn bằng 1   3    2  .
Câu 20. Có bao nhiêu đường thẳng đi qua điểm A 1
 ;2 và tiếp xúc với đồ thị của hàm số 3
y x  3x  4 ? A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B
Gọi d là đường thẳng đi qua A 1
 ;2 và tiếp xúc với đồ thị của hàm số y f x 3
x  3x  4 .
d là tiếp tuyến đi qua điểm A 1
 ;2 của đồ thị hàm số y f x .
Ta có f  x 2
 3x  3 . Giả sử tọa độ tiếp điểm là  3
x ; x  3x  4 0 0 0 
d : y   2
3x  3 x x  3
x  3x  4 . 0 0 0 0
Vì d đi qua A 1
 ;2 , thay tọa độ điểm A vào d ta được : 2   2
3x  31  x  3
x  3x  4 0 0 0 0  3   x  2 1  x   3
1  x  3x  2  0 0 0 0 0  3   x   1  x  2 1   x   1  2
x x  2  0 0 0 0 0 0    x   1  2
2x  5x  5  0 0 0 0   x  1  0  x  1 0 0    x  1.   0 0
2x  5x  5  0 x    0 0  0
Như vậy qua A chỉ kẻ được một tiếp tuyến. Chọn B
Câu 21. Cho hàm số y f x có bảng biến thiên như sau:
Trang 12/17 – Diễn đàn giáo viên Toán
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x   m  0 có 4 nghiệm phân biệt . A. 6. B. 7. C. 8. D. 9. Lời giải Chọn B
Phương trình (1): f x   m  0  f x   m .
Số nghiệm của phương trình (1) là số điểm chung của hai đồ thị: (C) : y f x  và (d) : y m .
Hàm số y f x  là hàm số chẵn  (C) nhận trục Oy làm trục đối xứng.  f (x) khi x  0
Mà y f x    .
f (x) khi x  0 
 Bảng biến thiên của hàm số y f x  :
Dựa vào bảng biến thiên ta có: phương trình (1) có 4 nghiệm phân biệt  m  3  ;5 .
Mà m    m  2  ; 1  ;0;1; 2;3; 
4  Có 7 giá trị m thỏa mãn.
Câu 22. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số 4 2 2
y x  2 x m  2m có 5
điểm cực trị. Tìm số phần tử của S. A. 0. B. 1 C. 2. D. 3 Lời giải Chọn A Xét hàm số 4 2 2
y f (x)  x  2x m  2m .
Tập xác định: D   . 3 f (
x)  4x  4x . f (
x)  0  x  0 .
Bảng biến thiên của hàm số y f (x) : Xét hàm số 4 2 2
y f ( x)  x  2 x m  2m . Trang 13/17 - WordToan f (x) khi f (x)  0
Ta có f (x)   .
f (x) khi f (x)  0 
Bảng biến thiên của hàm số y f (x) có những trường hợp sau: TH1: y  0 CT
(là bảng biến thiên của hàm số y f (x) ) TH2: y  0 CT
(  x , x là các nghiệm của phương trình f (x)  0 ) 0 0  Hàm số 4 2 2
y x  2 x m  2m có tối đa 3 điểm cực trị  Không có m.
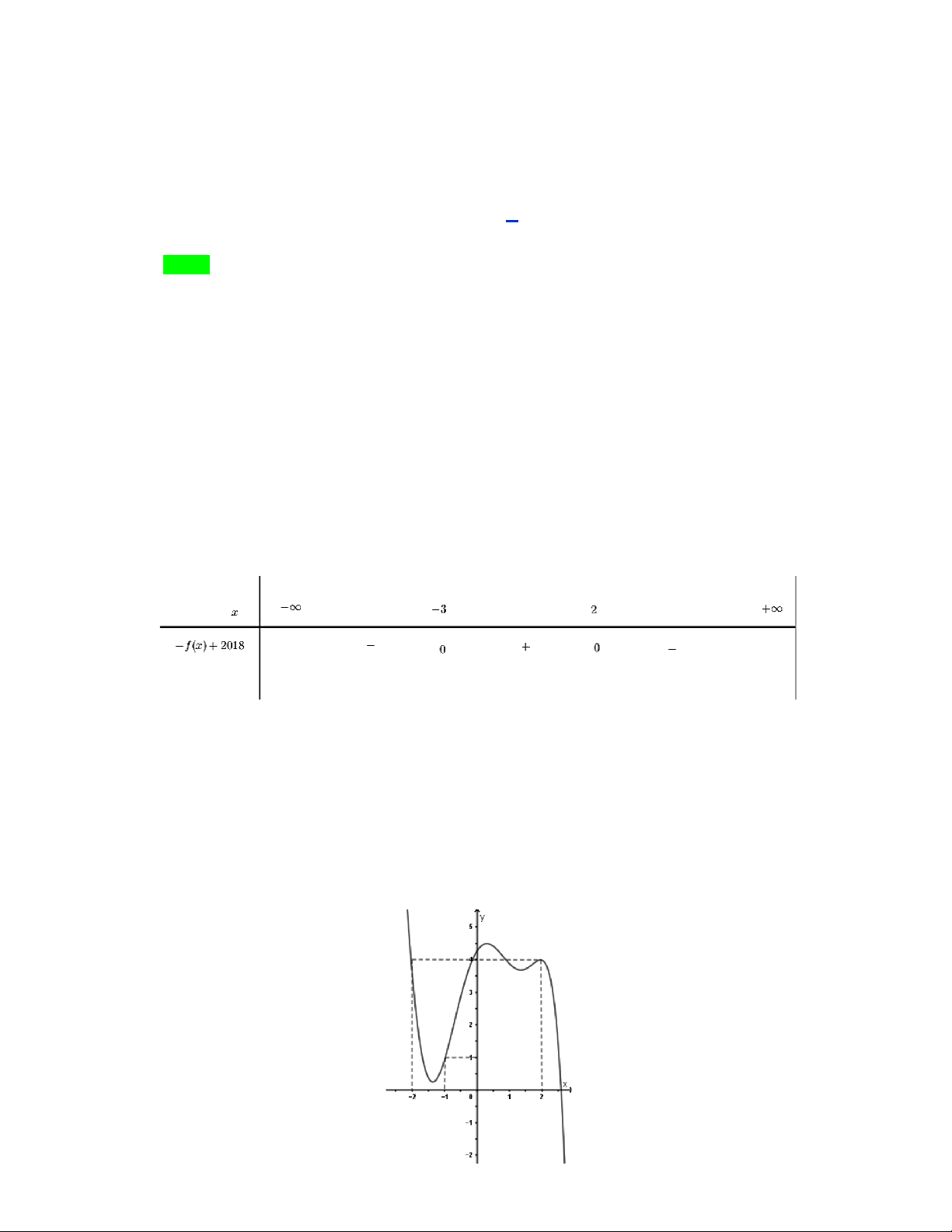
Cho hàm số f x xác định trên  và có đạo hàm f  x thỏa f  x  2  x x  
3 g x  2018
với g x  0, x
   . Hàm số y f 1 x  2018x  2019 đồng biến trên khoảng nào? A.  4   ;1 . B.  3  ; 2 . C. 0;  3 . D. 4;5 . Lời giải Chọn C
Ta có: y f 1 x  2018x  2019  y   f '1 x  2018 .
Theo giả thuyết của đề, ta có:
f  x  2  x x  3 g x  2018   f  x  2  x x  3 g x  2018 .
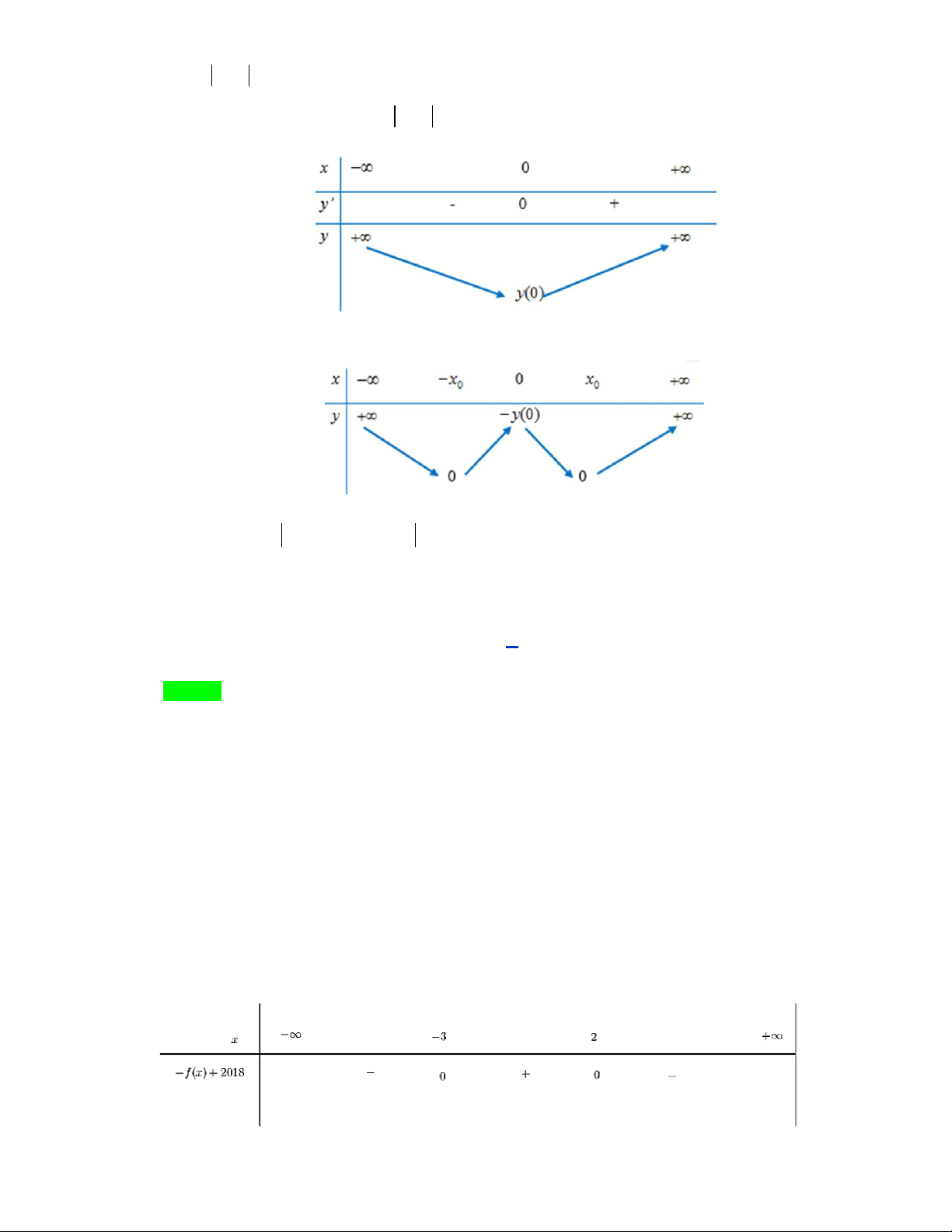
  f  x  2018  2  x x  3 g x .  x  2
  f  x  2018  0   . x  3  Ta có bảng xét dấu là
Dựa vào bảng xét dấu, ta suy ra  f  x  2018  0, x   3  ; 2 .
Trang 14/17 – Diễn đàn giáo viên Toán
y   f '1 x  2018  0  3
  1 x  2  1   x  4 .
Vậy, Hàm số y f 1 x  2018x  2019 đồng biến trên khoảng  1  ; 4 mà 0;  3   1  ; 4 .
Câu 23. Cho hàm số f x xác định trên  và có đạo hàm f  x thỏa f  x  2  x x  3 g x  2018
với g x  0, x
   . Hàm số y f 1 x  2018x  2019 đồng biến trên khoảng nào? A.  4   ;1 . B.  3  ; 2 . C. 0;  3 . D. 4;5 . Lời giải Chọn C
Ta có: y f 1 x  2018x  2019  y   f '1 x  2018 .
Theo giả thuyết của đề, ta có:
f  x  2  x x  3 g x  2018   f  x  2  x x  3 g x  2018 .
  f  x  2018  2  x x  3 g x .  x  2
  f  x  2018  0   . x  3  Ta có bảng xét dấu là
Dựa vào bảng xét dấu, ta suy ra  f  x  2018  0, x   3  ; 2 .
y   f '1 x  2018  0  3
  1 x  2  1   x  4 .
Vậy, Hàm số y f 1 x  2018x  2019 đồng biến trên khoảng  1  ; 4 mà 0;  3   1  ; 4 .
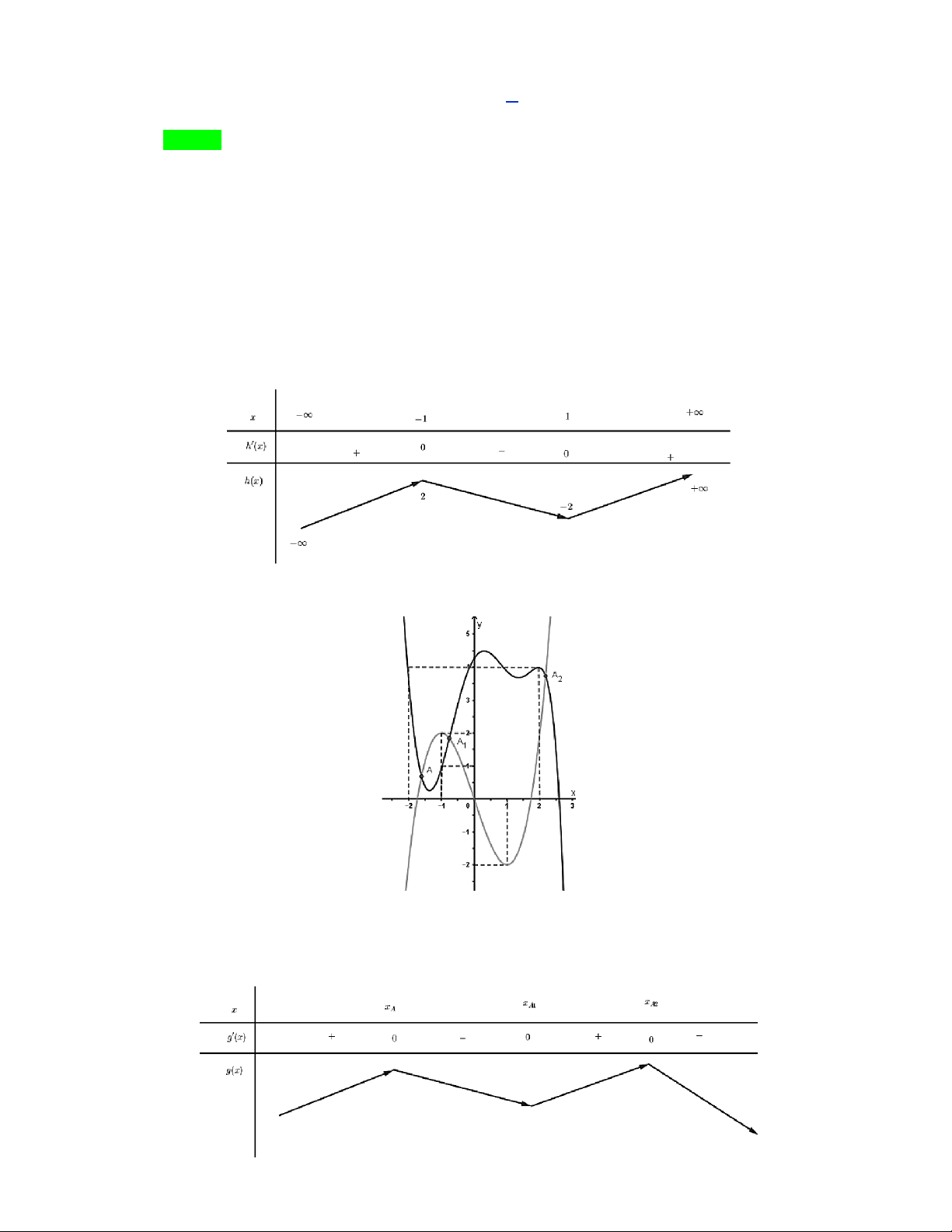
Câu 24. Cho hàm số f x . Hàm số y f  x xác định, liên tục trên  và có đồ thị như hình vẽ. Trang 15/17 - WordToan
Hàm số g x  f x 4 2 4
x  6x có bao nhiêu điểm cực trị ? A. 0 . B. 1. C. 3 . D. 5 . Lời giải Chọn C
Ta có: g x  f x 4 2
x x g x  f  x 3 4 6 4  4x 12x .
g x   f  x 3  x
x   f x 3 0 4 4 12 0 '
x  3x h x . h x 3
x x h x 2 3  3x  3 .  x  1   h x 2
 0  3x  3  0   . x  1 
Ta có bảng biến thiên của hàm số h x 3
x  3x là
Ta có đồ thị của hai hàm số y f  x và hx 3
x  3x là
Dựa vào đồ thị ta thấy 2 đồ thị cắt nhau tại 3 điểm phân biệt có hoành độ lần lượt là x x x . A 1 A A2
Ta có bảng xét dấu của hàm số g x  f  x 3 4
 4x 12x là
Trang 16/17 – Diễn đàn giáo viên Toán
Dựa vào BBT , ta suy ra hàm số g x  f x 4 2 4
x  6x có 3 điểm cực trị.
Câu 25 Có bao nhiêu giá trị nguyên của tham số thực m để phương trình m x x   x   x m  x m2 2 cos cos 2 2 cos cos cos
 2  0 có nghiệm thực ? A. 6 . B. 5 . C. 4 . D. 3 . Lời giải Chọn B Ta có: m x x   x   x m  x m2 2 cos cos 2 2 cos cos cos  2  0  x x x   
x m   x m  x m2 2 cos cos cos 2 cos cos cos  2  0 (1)
Đặt t  cos x m Ta được phương trình : 2 2
cos x  cos x cos x  2  t t t  2  0  x x x   t t  t 2 2 cos cos cos 2 ( ) ( )  2 *
Xét hàm số f u 2
u u u  2 với u   2 u
ta có f u 2  1 u  2   0 , u
   nên f u là hàm số đồng biến trên  2 u  2
* có dạng: f cos x  f t
   cos x t
  t   cos x
Với t   cos x ta được cos x m   cos x m  2  cos x *  *
Phương trình đã cho có nghiệm thực khi và chỉ khi phương trình * 
* có nghiệm thực . Khi đó điều
kiện của m là 2  m  2 . Vì m là số nguyên nên m  2  ; 1  ; 
0 . Có 5 giá trị nguyên của m . Trang 17/17 - WordToan
Document Outline

  • 321312
  • 1566877459_WT03-GT12-C1-KIỂM-TRA-1-TIẾT-CHƯƠNG-HÀM-SỐ-THPT-QUẢNG-TRỊ-NĂM-201