Đề kiểm tra 1 tiết chương 1 Hình học 12 NC năm 2018 – 2019 trường Thị Xã Quảng Trị

Giới thiệu đến quý thầy, cô cùng các em học sinh lớp 12 đề kiểm tra 1 tiết chương 1 Hình học 12 NC năm học 2018 – 2019 trường THPT Thị Xã Quảng Trị, đây là đề kiểm tra được sử dụng cho các lớp học chương trình nâng cao

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

32 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Hình học 12 NC . Thời gian làm bài : 45 phút
---------------------------------------------------------
Họ và tên học sinh: …………………..……………………………………..Lớp: …………..
Trả lời trắc nghiệm:
Câu 1
2 3 4 5 6 7 8 9 10
Đáp án
Câu 11
12 13 14 15 16 17 18 19 20
Đáp án
Chú ý: -Từ câu 1 đến câu 16 thí sinh điền đáp án trắc nghiệm A, B, C hay D vào bảng trên
- Từ câu 17 đến câu 20 thí sinh điền đáp số vào các ô tương ứng ở bảng trên ( điền khuyết).
Câu hỏi trắc nghiệm:
Phần I: Câu hỏi trắc nghiệm A,B,C, hay D
Câu 1: Khối chóp có diện tích đáy là
,B
chiều cao bằng
h
. Thể tích
V
khối chóp là:
A.
1
.
3
Bh
B.
.Bh
C.
1
.
2
Bh
D.
1
.
6
Bh
Câu 2: Hình nào dưới đây không phải là hình đa diện?
A. . B. C. D.
Câu 3: Cho hình chóp tứ giác
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
,
SA ABCD
và
6SA a
.
Thể tích của khối chóp
.
S ABCD
bằng
A.
3
6
6
a
. B.
3
6
a
. C.
3
6
3
a
. D.
3
6
2
a
.
Câu 4: Cho khối lăng trụ đứng có cạnh bên bằng
5
, đáy là hình vuông có cạnh bằng
. Hỏi thể tích khối lăng
trụ là:
A.
100
. B.
20
. C.
64
. D.
80
.
Câu 5: Cho khối chóp
.
S ABC
, trên ba cạnh
, , SA SB SC
lần lượt lấy ba điểm
, ,
A B C
sao cho
1
2
SA SA
,
1
3
SB SB
,
1
4
SC SC
. Gọi
V
và
V
lần lượt là thể tích của các khối chóp
.
S ABC
và
.
S A B C
. Khi đó tỉ số
V
V
là: A.
24.
B.
1
24
. C.
1
12
. D.
1
8
.
Câu 6: Cho khối chóp
OABC
có
OA
,
OB
,
OC
đôi một vuông góc tại
O
và
2
OA
,
3
OB
,
6
OC
. Thể
tích khối chóp bằng
Mã đề 135
A.
12
. B.
. C.
24
. D.
36
.
Câu 7: Cho hình chóp .
S ABC
có
SA
vuông góc mặt đáy, tam giác
ABC
vuông tại
A
,
4
SA
,
3
AB
,
5
BC
. Tính thể tích khối chóp
.
S ABC
.
A.
8.
B.
16.
C.
48.
D.
24.
Câu 8: Cho hình chóp đều
.
S ABCD
có chiều cao bằng
2a
và độ dài cạnh bên bằng
6a
. Tính thể tích
khối chóp
.
S ABCD
.
A.
3
10 2
3
a
. B.
3
8 3
3
a
. C.
3
10 3
3
a
. D.
3
8 2
3
a
.
Câu 9: Cho hình hộp chữ nhật .
ABCD A B C D
có
2AB
cm
,
3
AD
cm
,
7
AA
cm
. Tính thể tích khối
hộp
.
ABCD A B C D
.
A.
12
3
cm
. B.
42
3
cm
. C.
24
3
cm
. D.
36
3
cm
.
Câu 10: Cho khối lăng trụ đứng
.
ABC A B C
có
2CC a
, đáy
ABC
là tam giác vuông cân tại
B
và
2AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
V a
. B.
3
2
a
V . C.
3
2V a
. D.
3
3
a
V .
Câu 11: Cho khối lăng trụ tam giác
.
ABC A B C
có thể tích bằng
1
. Tính thể tích
V
của khối chóp
. ' ' 'A A B C
.
A.
3
V
. B.
1
4
V
. C.
1
3
V
. D.
1
2
V
.
Câu 12: Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh
2a
và thể tích bằng
3
a
. Tính chiều cao
h
của
hình chóp đã cho.
A.
3
6
a
h
. B.
3
2
a
h
. C.
3
3
a
h
. D.
3
h a
.
Câu 13: Cho hình chóp
.
S ABCD
có đáy hình vuông cạnh
a
;
SA
vuông góc mặt đáy; Góc giữa
SC
và mặt đáy
của hình chóp bằng
0
60
. Thể tích khối chóp
.
S ABCD
là
A.
3
6
.
3
a
B.
3
3
.
3
a
C.
3
2
.
3
a
D.
3
.
3
a
Câu 14: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
SAB
đều cạnh a nằm trong mặt phẳng
vuông góc với
ABCD
. Biết
SC
tạo với
ABCD
một góc bằng
0
30
. Tính thể tích
V
của khối chóp
. .S ABCD
A.
3
6
.
3
a
V
B.
3
6
.
6
a
V
C.
3
3
.
3
a
V
D.
3
3
.
6
a
V
Câu 15: Cho hình hộp đứng
.
ABCD A B C D
có đáy
ABCD
là hình thoi cạnh
và
60
BAD
,
'AC
hợp với
đáy
ABCD
một góc
60
. Thể tích của khối hộp là
A.
3
3
.
2
a
B.
3
3 3
4
a
. C.
3
3
4
a
. D.
3
3 3
.
2
a
Câu 16: Cho lăng trụ đứng tam giác
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
B
với
2BA BC a
. Gọi M là trung điểm
' ',A C
biết
BM
hợp với mặt phẳng
ABC
một góc
0
30
. Thể tích khối
lăng trụ
.
ABC A B C
là:
A.
3
3
3
a
. B.
3
2 3
3
a
. C.
3
3
9
a
. D.
3
2 3
9
a
.
Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 17: Cho khối lăng trụ tam giác
.
ABC A B C
. Tính tỉ số thể tích giữa khối đa diện
A B C BC
và khối lăng
trụ
.
ABC A B C
.
Câu 18: Cho tứ diện đều
ABCD
có cạnh bằng 3. Gọi
,M N
lần lượt là các điểm thuộc các cạnh
,AD BD
sao
cho
1
.
3
DM DN
DA DB
Lấy điểm bất kỳ
P
trên cạnh
AB
(khác
,A B
). Tính thể tích khối tứ diện
.PMNC
Câu 19: Cho lăng trụ
.
ABCD A B C D
có đáy
ABCD
là hình chữ nhật với
6
AB
,
3
AD
,
3
A C
và
mặt phẳng
AA C C
vuông góc với mặt đáy. Biết hai mặt phẳng
AA C C
,
AA B B
tạo với nhau góc
thỏa mãn
3
tan
4
. Tính thể tích khối lăng trụ
.
ABCD A B C D
.
Câu 20: Cho tam giác
OAB
đều cạnh
a
. Trên đường thẳng
d
qua
O
và vuông góc với mặt phẳng
OAB
lấy
điểm
M
sao cho
OM x
. Gọi
, E F
lần lượt là hình chiếu vuông góc của
A
trên
MB
và
OB
. Gọi
N
là giao
điểm của
EF
và
d
(hình vẽ minh họa bên dưới). Tìm giá trị của
x
theo
a
để thể tích khối tứ diện
ABMN
có
giá trị nhỏ nhất.
---------------------HẾT----------------------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Hình học 12 NC . Thời gian làm bài : 45 phút
---------------------------------------------------------
Họ và tên học sinh: …………………..……………………………………..Lớp: …………..
Trả lời trắc nghiệm:
Câu 1
2 3 4 5 6 7 8 9 10
Đáp
án
Câu 11
12 13 14 15 16 17 18 19 20
Đáp
án
Chú ý: -Từ câu 1 đến câu 16 thí sinh điền đáp án trắc nghiệm A, B, C hay D vào bảng trên
- Từ câu 17 đến câu 20 thí sinh điền đáp số vào các ô tương ứng ở bảng trên ( điền khuyết).
Câu hỏi trắc nghiệm:
Phần I: Câu hỏi trắc nghiệm A,B,C hay D
Câu 1: Số cạnh của một hình hộp chữ nhật là:
A. 8. B. 16. C.12. D. 9.
Câu 2: Khối lăng trụ có diện tích đáy là
,B
chiều cao bằng
h
. Thể tích
V
khối lăng trụ là:
A.
1
.
3
Bh
B.
.Bh
C.
1
.
2
Bh
D.
1
.
6
Bh
Câu 3: Hình chóp tam giác đều có độ dài cạnh bên khác độ dài cạnh đáy có mấy mặt phẳng đối xứng?
A.
4
. B.
3
. C.
6
. D.
5
.
Câu 4: Cho hình chóp
.
S ABC
có
,SA ABC
ABC
vuông cân tại A,
.SA AC a
Tính theo a thể tích V
của khối chóp
.
S ABC
A.
3
.
6
a
V
B.
3
.
4
a
V
C.
3
2 .V a
D.
3
.
2
a
V
Câu 5: Cho hình hộp chữ nhật
. .ABCD A B C D
Biết
,AB a
2 ,AD a
3 .AA a
Tính thể tích khối hộp
. .ABCD A B C D
A.
3
2 .a
B.
2
6 .a
C.
3
6 .a
D.
2
2 .a
Câu 6: Cho tứ diện
MNPQ
. Gọi
I
;
J
;
K
lần lượt là trung điểm của các cạnh
MN
;
MP
;
MQ
. Tỉ số thể tích
MIJK
MNPQ
V
V
bằng:
A.
1
3
. B.
1
4
. C.
1
6
. D.
1
8
.
Mã đề 248
Câu 7: Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
3a
, đường cao bằng
a
. Tính thể tích
V
của
khối chóp
.
S ABC
.
A.
3
3
4
a
V
. B.
3
3 3
2
a
V
. C.
3
3 3
4
a
V
. D.
3
3
4
a
V
.
Câu 8: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
2 3a
, mặt bên
SAB
là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp
.
S ABCD
là:
A.
3
12a
. B. 14a
3
. C.
3
15a
. D.
3
17a
.
Câu 9: Cho khối chóp
.
S ABC
có
SA
vuông góc với
ABC
, đáy
ABC
là tam giác vuông cân tại
A
,
2AB a
,
2 2SB a
. Tính thể tích khối chóp
.
S ABC
.
A.
3
4 2
3
a
. B.
3
4a
. C.
3
8
3
a
. D.
3
4
3
a
.
Câu 10: Cho lăng trụ đứng tam giác
.
MNP M N P
có đáy
MNP
là tam giác đều cạnh
a
, đường chéo
MP
tạo
với mặt phẳng đáy một góc bằng
60
. Tính theo
a
thể tích của khối lăng trụ
.
MNP M N P
.
A.
3
3
2
a
. B.
3
2
3
a
. C.
3
3
4
a
. D.
3
2
4
a
.
Câu 11: Cho khối lăng trụ đứng
.
ABC A B C
có
2CC a
, đáy
ABC
là tam giác vuông cân tại
B
và
2AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
V a
. B.
3
2
a
V
. C.
3
2V a
. D.
3
3
a
V
.
Câu 12: Cho khối chóp
.
S ABC
có thể tích bằng 60. Gọi
M
là trung điểm cạnh
SB
và
N
là điểm thuộc cạnh
SC
sao cho
2 .CN NS
Tính thể tích khối chóp
.
S AMN
A.
20.
B.
15.
C.
7,5.
D.
10.
Câu 13: Cho khối tứ diện
ABCD
có thể tích bằng
80.
Tam giác
BCD
vuông cân tại
B
và
4.
BC
Khoảng
cách từ điểm
A
đến mặt phẳng
BCD
bằng:
A.
10.
B.
15.
C.
5.
D.
30.
Câu 7: Cho hình chóp
.
S ABC
có
SAB
đều cạnh
a
, tam giác
ABC
vuông cân tại
C
. Hình chiếu vuông
của
S
lên
ABC
là trung điểm của cạnh
AB
. Thể tích khối chóp
.
S ABC
tính theo
a
là:
A.
3
3
8
a
V
B.
3
3
12
a
V
C.
3
3
4
a
V
D.
3
3
24
a
V
.
Câu 8: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
SAB
đều cạnh a nằm trong mặt phẳng
vuông góc với
ABCD
. Biết
SCD
tạo với
ABCD
một góc bằng
0
30
. Tính thể tích
V
của khối chóp
. .S ABCD
A.
3
3
.
8
a
V
B.
3
3
.
4
a
V
C.
3
3
.
2
a
V
D.
3
3
.
3
a
V
Câu 16: Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với đáy,
SC
tạo với mặt phẳng
SAB
một góc
0
30
. Tính thể tích khối chóp
.
S ABCD
A.
3
2a
B.
3
2
3
a
C.
3
2
3
a
D.
3
6
3
a
Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 17: Cho khối lăng trụ tam giác
.
ABC A B C
. Tính tỉ số thể tích giữa khối chóp
. ' 'A AB C
và khối lăng trụ
.
ABC A B C
.
Câu 18: Cho tứ diện đều
ABCD
có cạnh bằng 4. Gọi
,M N
lần lượt là các điểm thuộc các cạnh
,AD BD
sao
cho
1
.
4
DM DN
DA DB
Lấy điểm bất kỳ
P
trên cạnh
AB
(khác
,A B
). Tính thể tích khối tứ diện
.PMNC
Câu 19: Cho lăng trụ
.
ABCD A B C D
có đáy
ABCD
là hình chữ nhật với
6
AB
,
3
AD
,
3
A C
và
mặt phẳng
AA C C
vuông góc với mặt đáy. Biết hai mặt phẳng
AA C C
,
AA B B
tạo với nhau góc
thỏa mãn
tan 2
. Tính thể tích khối lăng trụ
.
ABCD A B C D
.
Câu 20: Cho tam giác
OAB
đều cạnh
2a
. Trên đường thẳng
d
qua
O
và vuông góc với mặt phẳng
OAB
lấy
điểm
M
sao cho
OM x
. Gọi
, E F
lần lượt là hình chiếu vuông góc của
A
trên
MB
và
OB
. Gọi
N
là giao
điểm của
EF
và
d
(hình vẽ minh họa bên dưới). Tìm giá trị của
x
theo
a
để thể tích khối tứ diện
ABMN
có
giá trị nhỏ nhất.
------------------------HẾT------------------------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Hình học 12 NC . Thời gian làm bài : 45 phút
---------------------------------------------------------
Họ và tên học sinh: …………………..……………………………………..Lớp: …………..
Trả lời trắc nghiệm:
Câu 1
2 3 4 5 6 7 8 9 10
Đáp án
Câu 11
12 13 14 15 16 17 18 19 20
Đáp án
Chú ý: -Từ câu 1 đến câu 16 thí sinh điền đáp án trắc nghiệm A, B, C hay D vào bảng trên
- Từ câu 17 đến câu 20 thí sinh điền đáp số vào các ô tương ứng ở bảng trên ( điền khuyết).
Câu hỏi trắc nghiệm:
Phần I: Câu hỏi trắc nghiệm A,B,C hay D
Câu 1: Cho hình chóp
.
S ABC
có
SA
vuông góc mặt đáy, tam giác
ABC
vuông tại
A
,
4
SA
,
3
AB
,
5
BC
. Tính thể tích khối chóp
.
S ABC
.
A.
8.
B.
16.
C.
48.
D.
24.
Câu 2: Khối chóp có diện tích đáy là
,B
chiều cao bằng
. Thể tích
V
khối chóp là:
A.
.Bh
B.
1
.
2
Bh
C.
1
.
3
Bh
D.
1
.
6
Bh
Câu 3: Hình nào dưới đây không phải là hình đa diện?
A. . B. C. D.
Câu 4: Cho khối lăng trụ đứng có cạnh bên bằng
5
, đáy là hình vuông có cạnh bằng
. Hỏi thể tích khối lăng
trụ là:
A.
100
. B.
20
. C.
64
. D.
80
.
Câu 5: Cho hình chóp tứ giác
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
,
SA ABCD
và
6SA a
.
Thể tích của khối chóp
.
S ABCD
bằng
A.
3
6
a
. B.
3
6
2
a
. C.
3
6
3
a
. D.
3
6
6
a
.
Mã đề 357
Câu 6: Cho khối chóp
.
S ABC
, trên ba cạnh
, , SA SB SC
lần lượt lấy ba điểm
, ,
A B C
sao cho
1
2
SA SA
,
1
3
SB SB
,
1
4
SC SC
. Gọi
V
và
V
lần lượt là thể tích của các khối chóp
.
S ABC
và
.
S A B C
. Khi đó tỉ số
V
V
là:
A.
1
24
. B.
1
12
. C.
24.
D.
1
8
.
Câu 7: Cho khối chóp
OABC
có
OA
,
OB
,
OC
đôi một vuông góc tại
O
và
2
OA
,
3
OB
,
6
OC
. Thể
tích khối chóp bằng
A.
12
. B.
24
. C.
36
. D.
.
Câu 8: Cho khối lăng trụ đứng
.
ABC A B C
có
2CC a
, đáy
ABC
là tam giác vuông cân tại
B
và
2AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
V a
. B.
3
2
a
V . C.
3
2V a
. D.
3
3
a
V .
Câu 9: Cho hình hộp chữ nhật
.
ABCD A B C D
có
2AB
cm
,
3
AD
cm
,
7
AA
cm
. Tính thể tích khối
hộp
.
ABCD A B C D
.
A.
12
3
cm
. B.
42
3
cm
. C.
24
3
cm
. D.
36
3
cm
.
Câu 10: Cho hình chóp đều
.
S ABCD
có chiều cao bằng
2a
và độ dài cạnh bên bằng
6a
. Tính thể tích
khối chóp
.
S ABCD
.
A.
3
10 2
3
a
. B.
3
8 3
3
a
. C.
3
10 3
3
a
. D.
3
8 2
3
a
.
Câu 11: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
SAB
đều cạnh a nằm trong mặt phẳng
vuông góc với
ABCD
. Biết
SC
tạo với
ABCD
một góc bằng
0
30
. Tính thể tích
V
của khối chóp
. .S ABCD
A.
3
6
.
3
a
V
B.
3
6
.
6
a
V
C.
3
3
.
3
a
V
D.
3
3
.
6
a
V
Câu 12: Cho khối lăng trụ tam giác
.
ABC A B C
có thể tích bằng
1
. Tính thể tích
V
của khối chóp
. ' ' 'A A B C
.
A.
1
4
V
. B.
1
3
V
. C.
3
V
. D.
1
2
V
.
Câu 13: Cho hình hộp đứng
.
ABCD A B C D
có đáy
ABCD
là hình thoi cạnh
và
60
BAD
,
'AC
hợp với
đáy
ABCD
một góc
60
. Thể tích của khối hộp là
A.
3
3
.
2
a
B.
3
3 3
4
a
. C.
3
3
4
a
. D.
3
3 3
.
2
a
Câu 14: Cho hình chóp
.
S ABCD
có đáy hình vuông cạnh
a
;
SA
vuông góc mặt đáy; Góc giữa
SC
và mặt đáy
của hình chóp bằng
0
60
. Thể tích khối chóp
.
S ABCD
là
A.
3
3
.
3
a
B.
3
2
.
3
a
C.
3
6
.
3
a
D.
3
.
3
a
Câu 15: Cho lăng trụ đứng tam giác
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
B
với
2BA BC a
. Gọi M là trung điểm
' ',A C
biết
BM
hợp với mặt phẳng
ABC
một góc
0
30
. Thể tích khối
lăng trụ
.
ABC A B C
là:
A.
3
3
9
a
. B.
3
3
3
a
. C.
3
2 3
3
a
. D.
3
2 3
9
a
.
Câu 16: Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh
2a
và thể tích bằng
3
a
. Tính chiều cao
h
của hình
chóp đã cho.
A.
3
h a
. B.
3
2
a
h
. C.
3
3
a
h
. D.
3
6
a
h
.
Phần II: Câu hỏi trắc nghiệm điền khuyết
Câu 17: Cho khối lăng trụ tam giác
.
ABC A B C
. Tính tỉ số thể tích giữa khối chóp
. ' 'C AA B B
và khối lăng
trụ
.
ABC A B C
.
Câu 18: Cho tứ diện đều
ABCD
có cạnh bằng 6. Gọi
,M N
lần lượt là các điểm thuộc các cạnh
,AD BD
sao
cho
1
.
6
DM DN
DA DB
Lấy điểm bất kỳ
P
trên cạnh
AB
(khác
,A B
). Tính thể tích khối tứ diện
PMNC
.
Câu 19: Cho lăng trụ
.
ABCD A B C D
có đáy
ABCD
là hình chữ nhật với
6
AB
,
3
AD
,
3
A C
và
mặt phẳng
AA C C
vuông góc với mặt đáy. Biết hai mặt phẳng
AA C C
,
AA B B
tạo với nhau một góc
0
45
. Tính thể tích khối lăng trụ
.
ABCD A B C D
.
Câu 20: Cho tam giác
OAB
đều cạnh
3a
. Trên đường thẳng
d
qua
O
và vuông góc với mặt phẳng
OAB
lấy
điểm
M
sao cho
OM x
. Gọi
, E F
lần lượt là hình chiếu vuông góc của
A
trên
MB
và
OB
. Gọi
N
là giao
điểm của
EF
và
d
(hình vẽ minh họa bên dưới). Tìm giá trị của
x
theo
a
để thể tích khối tứ diện
ABMN
có
giá trị nhỏ nhất.
----------------------------HẾT----------------------------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Hình học 12 NC . Thời gian làm bài : 45 phút
---------------------------------------------------------
Họ và tên học sinh: …………………..……………………………………..Lớp: …………..
Trả lời trắc nghiệm:
Câu 1
2 3 4 5 6 7 8 9 10
Đáp án
Câu 11
12 13 14 15 16 17 18 19 20
Đáp án
Chú ý: -Từ câu 1 đến câu 16 thí sinh điền đáp án trắc nghiệm A, B, C hay D vào bảng trên
- Từ câu 17 đến câu 20 thí sinh điền đáp số vào các ô tương ứng ở bảng trên ( điền khuyết).
Câu hỏi trắc nghiệm:
Phần I: Câu hỏi trắc nghiệm A,B,C hay D
Câu 1: Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
3a
, đường cao bằng
. Tính thể tích
V
của
khối chóp
.
S ABC
.
A.
3
3
4
a
V
. B.
3
3 3
2
a
V
. C.
3
3 3
4
a
V
. D.
3
3
4
a
V .
Câu 2: Số cạnh của một hình hộp chữ nhật là:
A. 16. B. 12. C. 8. D. 9.
Câu 3: Khối lăng trụ có diện tích đáy là
,B
chiều cao bằng
. Thể tích
V
khối lăng trụ là:
A.
1
.
2
Bh
B.
1
.
3
Bh
C.
1
.
6
Bh
D.
.Bh
Câu 4: Cho hình chóp
.
S ABC
có
,SA ABC
ABC
vuông cân tại A,
.SA AC a
Tính theo a thể tích V
của khối chóp
.
S ABC
A.
3
.
6
a
V B.
3
.
4
a
V C.
3
2 .V a
D.
3
.
2
a
V
Câu 5: Hình chóp tam giác đều có độ dài cạnh bên khác độ dài cạnh đáy có mấy mặt phẳng đối xứng?
A.
3
. B.
5
. C.
6
. D.
.
Câu 6: Cho hình hộp chữ nhật
. .ABCD A B C D
Biết
,AB a
2 ,AD a
3 .AA a
Tính thể tích khối hộp
. .ABCD A B C D
A.
2
6 .a
B.
3
6 .a
C.
3
2 .a
D.
2
2 .a
Câu 7: Cho tứ diện
MNPQ
. Gọi
I
;
J
;
K
lần lượt là trung điểm của các cạnh
MN
;
MP
;
MQ
. Tỉ số thể tích
MIJK
MNPQ
V
V
bằng:
Mã đề 468
A.
1
3
. B.
1
6
. C.
1
8
. D.
1
4
.
Câu 8: Cho lăng trụ đứng tam giác
.
MNP M N P
có đáy
MNP
là tam giác đều cạnh
a
, đường chéo
MP
tạo
với mặt phẳng đáy một góc bằng
60
. Tính theo
a
thể tích của khối lăng trụ
.
MNP M N P
.
A.
3
3
2
a
. B.
3
2
3
a
. C.
3
3
4
a
. D.
3
2
4
a
.
Câu 9: Cho khối chóp
.
S ABC
có
SA
vuông góc với
ABC
, đáy
ABC
là tam giác vuông cân tại
A
,
2AB a
,
2 2SB a
. Tính thể tích khối chóp
.
S ABC
.
A.
3
4 2
3
a
. B.
3
4a
. C.
3
8
3
a
. D.
3
4
3
a
.
Câu 10: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
2 3a
, mặt bên
SAB
là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp
.
S ABCD
là:
A.
3
12a
. B. 14a
3
. C.
3
15a
. D.
3
17a
.
Câu 11: Cho hình chóp
.
S ABC
có
SAB
đều cạnh
a
, tam giác
ABC
vuông cân tại
C
. Hình chiếu vuông
của
S
lên
ABC
là trung điểm của cạnh
AB
. Thể tích khối chóp
.
S ABC
tính theo
a
là:
A.
3
3
.
8
a
V
B.
3
3
.
12
a
V
C.
3
3
.
4
a
V
D.
3
3
24
a
V
.
Câu 12: Cho khối lăng trụ đứng
.
ABC A B C
có
2CC a
, đáy
ABC
là tam giác vuông cân tại
B
và
2AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
2
a
V . B.
3
2V a
. C.
3
V a
. D.
3
3
a
V .
Câu 13: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
SAB
đều cạnh a nằm trong mặt phẳng
vuông góc với
ABCD
. Biết
SCD
tạo với
ABCD
một góc bằng
0
30
. Tính thể tích
V
của khối chóp
. .S ABCD
A.
3
3
.
8
a
V
B.
3
3
.
4
a
V
C.
3
3
.
2
a
V
D.
3
3
.
3
a
V
Câu 14: Cho khối tứ diện
ABCD
có thể tích bằng
80.
Tam giác
BCD
vuông cân tại
B
và
4.
BC
Khoảng
cách từ điểm
A
đến mặt phẳng
BCD
bằng:
A.
15.
B.
5.
C.
10.
D.
30.
Câu 15: Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với đáy,
SC
tạo với mặt phẳng
SAB
một góc
0
30
. Tính thể tích khối chóp
.
S ABCD
A.
3
2
.
3
a
B.
3
2a
.
C.
3
2
3
a
D.
3
6
3
a
Câu 16: Cho khối chóp
.
S ABC
có thể tích bằng 60. Gọi
M
là trung điểm cạnh
SB
và
N
là điểm thuộc cạnh
SC
sao cho
2 .CN NS
Tính thể tích khối chóp
.
S AMN
A.
10.
B.
15.
C.
7,5.
D.
20.
Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 17: Cho khối lăng trụ tam giác
.
ABC A B C
. Tính tỉ số thể tích giữa khối chóp
'. ' 'C AA B
và khối lăng trụ
.
ABC A B C
.
Câu 18: Cho tứ diện đều
ABCD
có cạnh bằng 5. Gọi
,M N
lần lượt là các điểm thuộc các cạnh
,AD BD
sao
cho
1
.
5
DM DN
DA DB
Lấy điểm bất kỳ
P
trên cạnh
AB
(khác
,A B
). Tính thể tích khối tứ diện
.PMNC
Câu 19: Cho lăng trụ
.
ABCD A B C D
có đáy
ABCD
là hình chữ nhật với
6
AB
,
3
AD
,
3
A C
và
mặt phẳng
AA C C
vuông góc với mặt đáy. Biết hai mặt phẳng
AA C C
,
AA B B
tạo với nhau một góc
0
60
. Tính thể tích khối lăng trụ
.
ABCD A B C D
.
Câu 20: Cho tam giác
OAB
đều cạnh
4a
. Trên đường thẳng
d
qua
O
và vuông góc với mặt phẳng
OAB
lấy
điểm
M
sao cho
OM x
. Gọi
, E F
lần lượt là hình chiếu vuông góc của
A
trên
MB
và
OB
. Gọi
N
là giao
điểm của
EF
và
d
(hình vẽ minh họa bên dưới). Tìm giá trị của
x
theo
a
để thể tích khối tứ diện
ABMN
có
giá trị nhỏ nhất.
------------------------------HẾT-------------------------------
ĐÁP ÁN ĐỀ KIỂM TRA 1 TIẾT HH12 CHƯƠNG I.
Mã đề 135:
Câu 1
2 3 4 5 6 7 8 9 10
Đáp án
A
C
C
D
B
B
A
D
B
A
Câu 11
12 13 14 15 16 17 18 19 20
Đáp án
C
D
A
B
D
A
2
3
2
2
8
2
2
a
Mã đề 248:
Câu 1
2 3 4 5 6 7 8 9 10
Đáp án
C
B
B
A
C
D
A
A
D
C
Câu 11
12 13 14 15 16 17 18 19 20
Đáp án
A
D
D
D
B
C
1
3
2
9 14
4
2a
Mã đề 357:
Câu 1
2 3 4 5 6 7 8 9 10
Đáp án
A
C
B
D
C
A
D
A
B
D
Câu 11
12 13 14 15 16 17 18 19 20
Đáp án
B
B
D
C
B
A
2
3
5 2
2
9 2
3
2
a
Mã đề 468:
Câu 1
2 3 4 5 6 7 8 9 10
Đáp án
A
B
D
A
A
B
C
C
D
A
Câu 11
12 13 14 15 16 17 18 19 20
Đáp án
D
C
B
D
A
A
1
3
5 2
3
3 10
2 2a
ĐÁP ÁN CHI TIẾT CÂU 19-20 MÃ ĐỀ 135
(Các câu 19,20 các mã đề còn lại giải tương tự)
Câu 19:
Lời giải
M
C'
B'
D'
C
D
A
B
A'
I
H
K
Từ
B
kẻ
BI AC
BI AA C C
. Từ
I
kẻ
IH AA
,
B
AA C C A B B
I
A
H
.
Theo giải thiết ta có
3
AC
.AB BC
BI
AC
2
.
Xét tam giác vuông
BIH
có
tan
BI
BHI
IH
tan
BI
IH
BHI
4 2
3
IH
.
Xét tam giác vuông
ABC
có
2
.
AI AC AB
2
2
AB
AI
AC
.
Gọi
M
là trung điểm cả
AA
, do tam giác
AA C
cân tại
C
nên
CM AA
//CM IH
.
Do
2
3
AI AH
AC AM
2
3
AH
AM
1
3
AH
AA
.Trong tam giác vuông
AHI
kẻ đường cao
HK
ta có
4 2
9
HK
chiều cao của lăng trụ
.
ABCD A B C D
là
3
h HK
4 2
3
.
Vậy thể tích khối lăng trụ
.
ABCD A B C D
là
.
. .
ABCD A B C D
V AB AD h
4 2
6 3
3
8
.
Câu 20: Lời giải.
Do tam giác
OAB
đều cạnh
,a
suy ra
F
là trung điểm
.
2
a
OB OF
Ta có
.
AF OB
AF MOB AF MB
AF MO
Lại có
MB AE
nên suy ra
.MB AEF MB EF
Suy ra
OBM ONF
∽
nên
2
.
.
2
OB ON OB OF a
ON
OM OF OM x

Ta có
ABMN ABOM ABON
V V V
2 2 3
1 3 6
.
3 12 2 12
OAB
a a a
S OM ON x
x
Đẳng thức xảy ra khi và chỉ khi
2
2
2 2
a a
x x
x
.
Câu 17: Cho lăng trụ đứng
. ' ' 'ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
và
8 2
BC
. Mặt phẳng
'
A BC
hợp với mặt đáy
ABC
một góc
thỏa mãn
tan 2.
Thể tích khối lăng trụ
. ' ' 'ABC A B C
bằng:
A.
256.
B.
512.
C.
256
.
3
D.
128.
Câu 18: Cho lăng trụ tam giác
.
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
, cạnh
2 2
AC
. Biết
AC
tạo với mặt phẳng
ABC
một góc
60
và
4
AC
. Tính thể tích
V
của khối đa diện
ABCB C
.
A.
8
3
V
B.
16
3
V
C.
8 3
3
V
D.
16 3
3
V
Câu 19: Cho khối chóp
.
S ABCD
có thể tích là
V
. Gọi
G
là trọng tâm tam giác
SAB
,
'V
là thể tích khối đa
diện
GABCD
. Khẳng định nào sau đây đúng?
A.
4 '.V V
B.
3 '.V V
C.
2 '.V V
D.
2 3 '.V V
Câu 20: Cho khối chóp
.
S ABCD
có thể tích bằng
3
a
. Mặt bên
SAB
là tam giác đều cạnh
a
và đáy
ABCD
là
hình bình hành. Tính theo
a
khoảng cách giữa
SA
và
CD
.
A.
2 3a
. B.
3a
. C.
2
3
a
. D.
2
a
.
Câu 21: Cho hình chóp tứ giác
.
S ABCD
có đáy là hình vuông cạnh bằng
2a
. Tam giác
SAD
cân tại
S
và
mặt bên
SAD
vuông góc với mặt phẳng đáy. Biết thể tích khối chóp
.
S ABCD
bằng
3
4
3
a
. Tính khoảng cách
h
từ
B
đến mặt phẳng
SCD
A.
2
3
h a
B.
4
3
h a
C.
8
3
h a
D.
3
4
h a
Câu 22: Cho tứ diện đều
ABCD
có cạnh bằng 3. Gọi
,M N
lần lượt là trung điểm các cạnh
,AD BD
sao cho
1
.
4
DM DN
DA DB
Lấy điểm bất kỳ
P
trên cạnh
AB
(khác
,A B
). Thể tích khối tứ diện
PMNC
bằng:
A.
81 2
.
64
B.
27 2
.
32
C.
27 2
.
64
D.
81 2
.
32
Câu 8: Cho hàm số
( )y f x
có bảng biến như hình vẽ bên
Số điểm cực trị của hàm số
y f x
bằng: A. 5. B. 2. C. 3. D. 4
Câu 15: Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với đáy,
SC
tạo với mặt phẳng
SAB
một góc
0
30
. Tính thể tích khối chóp
.
S ABCD
A.
3
2a
B.
3
2
3
a
C.
3
2
3
a
D.
3
6
3
a
Câu 20: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
2a
, cạnh bên bằng
SA
vuông góc với đáy
,
SA a
. Tính khoảng cách từ
A
đến mặt phẳng
SBC
?
A.
3
.
2
a
d
B.
2
.
2
a
d
C.
6
.
2
a
d
D.
6
.
3
a
d
Câu 21: Cho hình chóp
.
S ABCD
có
SA ABCD
,
ABCD
là hình chữ nhật.
2SA AD a
. Góc giữa
SBC
và mặt đáy
ABCD
là
60
. Gọi
G
là trọng tâm tam giác
SBC
. Tính thể tích khối chóp
.
S AGD
là
A.
3
32 3
27
a
. B.
3
8 3
27
a
. C.
3
4 3
9
a
. D.
3
16
9 3
a
.
Câu 22: Cho tứ diện đều
ABCD
có cạnh bằng 3. Gọi
,M N
lần lượt là trung điểm các cạnh
,AD BD
sao cho
1
.
3
DM DN
DA DB
Lấy điểm bất kỳ
P
trên cạnh
AB
(khác
,A B
). Thể tích khối tứ diện
PMNC
bằng:
A.
2
.
2
B.
3 2
.
2
C.
3 2.
D.
2
.
4
Câu 23: Cho lăng trụ tam giác
.
ABC A B C
có đáy là tam giác đều cạnh
a
. Độ dài cạnh bên bằng
4a
. Mặt
phẳng
BCC B
vuông góc với đáy và
30
B BC
. Thể tích khối chóp
.
ACC B
là:
A.
3
3
2
a
. B.
3
3
12
a
. C.
3
3
18
a
. D.
3
3
6
a
.
Câu 24: Cho lăng trụ
.
ABCD A B C D
có đáy
ABCD
là hình chữ nhật với
6
AB
,
3
AD
,
3
A C
và
mặt phẳng
AA C C
vuông góc với mặt đáy. Biết hai mặt phẳng
AA C C
,
AA B B
tạo với nhau góc
thỏa mãn
3
tan
4
. Thể tích khối lăng trụ
.
ABCD A B C D
bằng?
A.
10
V
. B.
12
V
. C.
8
V
. D.
6
V
.
Câu 25: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông,
SA
vuông góc với đáy, mặt bên
SCD
hợp
với đáy một góc bằng
60
,
M
là trung điểm của
BC
. Biết thể tích khối chóp
.
S ABCD
bằng
3
3
3
a
. Khoảng
cách từ
M
đến mặt phẳng
SCD
bằng:
A.
3
6
a
. B.
3
4
a
. C.
3
2
a
. D.
3a
.
Câu 24: Cho lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
A
và góc
0
30 .
ABC
Gọi
M
là trung
điểm của
,AB
tam giác
MA C
đều cạnh
a
và nằm trong mặt phẳng vuông góc với đáy
.ABC
Thể tích khối
lăng trụ đã cho bằng
A.
3
.
7
a
B.
3
2
.
7
a
C.
3
3
.
7
a
D.
3
5
.
7
a
Câu 6: Tổng diện tích tất cả các mặt của hình bát diện đều cạnh bằng
là
A.
2
4a
. B.
2
2 3
a
. C.
2
4 3
a
. D.
2
3
a
.
Tr
ang 3/15 - WordToan
LỜI GIẢI CHI TIẾT
Câu 1. Khối chóp có diện tích đáy là
,B
chi
ều cao bằng
h
. T
hể tích
V
khối c
hóp là:
A.
1
.
3
Bh
B.
.Bh
C.
1
.
2
Bh
D.
1
.
6
Bh
Lời giải
Chọn A
Thể tích
V
của khối chóp có diện tích đáy là
B
, chiều cao bằng
h
là:
1
.
3
V Bh
Câu 2.
Hình nào dưới đây không phải là hình đa diện?
A. . B. C. D.
Lời giả
i
Chọn
C
Giả sử ta đặt tên cho các cạnh như sau:
Khi đó BC là cạnh chung của 3 tam giác ABC, BCD, BCE.
Như vậy không thỏa mãn định nghĩa của khối đa diện.
Câu 3. Cho hình chóp tứ giác
.S A
BCD
có đ
áy
AB
CD
là
hình vuông cạnh
a
,
SA
ABCD
và
6SA a
. Th
ể tích của khối chóp
.S A
BCD
bằng
A.
3
6
6
a
. B.
3
6a
. C.
3
6
3
a
. D.
3
6
2
a
.
Lời giả
i
Chọn C
A
D
C
B
E
Tr
ang 4/15 – Diễn đàn giáo viên Toán
+ Diện tích hình vuông
A
BCD
có cạnh bằng
a
là
2
.
A
BCD
S a
+
S
A ABCD
S
A
l
à chiều cao hình chóp,
6SA a
+ Thể
tích khối chóp
.S
ABCD
3
2
1
1 6
. . . 6 .
3 3 3
AB
CD
a
V
S SA a a
Câu 4. Cho khối lăng trụ đứng có cạnh bên bằng
5
, đáy là hình vuông có cạnh bằng
4
. Tính thể tích
khối lăng trụ.
A.
100
. B.
20
. C
.
64
. D.
80
.
Lời
giải
Chọn D
Thể tí
ch khối lăng trụ là
2
.
4 .5 80V B h
.
Câu
5. Cho khối chóp
.S
ABC
,
trên ba cạnh
,
, SA SB SC
lầ
n lượt lấy ba điểm
,
,
A B C
s
ao cho
1
2
SA
SA
,
1
3
S
B SB
,
1
4
SC
SC
.
Gọi
V
v
à
V
lầ
n lượt là thể tích của các khối chóp
.S
ABC
v
à
.
S A B C
.
Khi đó tỉ số
V
V
là:
A.
2
4
B.
1
24
. C
.
1
12
. D.
1
8
.
Lời giải
Chọn B
T
rang 5/15 - WordToan
.
.
V SA SB SC
V SA SB SC
1
1 1 1
. .
2 3 4 24
.
Câu
6. Cho khối chóp
O
ABC
có
O
A
,
O
B
,
O
C
đôi một vuông góc tại
O
và
2O
A
,
3O
B
,
6OC
.
Thể tích khối chóp bằng
A.
1
2
. B.
6
. C
.
24
. D.
3
6
.
Lời
giải
Chọn B
1
1
. . .2.3.6 6
6 6
OABC
V
OA OB OC
.
Câu
7. Cho hình chóp
.S
ABC
có
SA
vuông góc với đáy, tam giác
A
BC
vuông tại
,
4A SA 3, 5AB BC
.
Tính thể tích khối chóp
.S ABC
A.
8
. B.
16
. C
.
4
8
. D.
24
.
Lời
giải
Chọn
A
A
BC
vuông tại
A
2
2
25 9 4AC BC AB
.
Thể tích khối chóp là
1 1 1 1
. . . . . . .3.4.4 8
3 3 2 6
A
BC
V
S SA AB AC SA
.
Câu 8. Cho hình chóp đều
.S
ABCD
có
chiều cao bẳng
2a
v
à độ dài cạnh bên bẳng
6a .
Thể tích
khối chóp
.S
ABCD
.
A.
3
10 2
3
a
. B.
3
8 3
3
a
. C
.
3
10 3
3
a
. D.
3
8 2
3
a
.
Lời giả
i
A
'
S
A
B
C
B
'
C'
A
O
B
C
Tr
ang 6/15 – Diễn đàn giáo viên Toán
Chọn D
Gọi
O
AC BD SO ABCD
.
S
AO
v
uông tại
2
2 2 2
6
2 2O AO SA SO a a a
4AC
a
.
Thể
tích khối chóp là
3
2
2
1
1 1 1 8 2
. . . . . .16 . 2
3 3 2 6 3
AB
CD
a
V
S SO AC SO a a
.
Câu
9. Cho hình hộp chữ nhật
.A
BCD A B C D
c
ó
2A
B
cm,
3A
D
cm
,
7A
A
c
m. Tính thể
tích khối hộp
.AB
CD A B C D
.
A.
12
3
c
m
. B.
4
2
3
c
m
. C
.
2
4
3
c
m
. D.
3
6
3
cm
.
Lời giải
Chọn B
Ta có
.
.
.
A
BCD A B C D
V
AB AD AA
4
2
3
cm
.
Câu
10. Cho khối lăng trụ đứng
.ABC
A B C
có
2CC
a
,
đáy
A
BC
là
tam giác vuông cân tại
B
v
à
2AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
V a
. B.
3
2
a
V . C
.
3
2V a
. D.
3
3
a
V .
Lời
giải
Chọn A
O
D
A
C
B
S
T
rang 7/15 - WordToan
Ta
m giác
A
BC
v
uông cân tại
B
2
A
C
AB a .
Khi đó
2
.
1
.
.
2
A
BC A B C
V
AB AA
3
a
.
Vậy
3
.ABC A B C
V
a
.
Câu
11. Cho khối lăng trụ tam giác
.ABC A B C
c
ó thể tích bằng 1. Tính thể tích
V
của
khối chóp
.A
A B C
?
A.
3V
. B.
1
4
V
. C.
1
3
V
. D.
1
2
V
.
Lời giải
Chọn
C
Chiều cao
h
của
khối lăng trụ
.ABC
A B C
chính
bằng chiều cao của khối chóp
.A
A B C
.
Ta
có:
.
1
.
1
A
BC A B C ABC ABC
V
h S S
h
.
Thể tí
ch
V
của
khối chóp
.A
A B C
l
à:
.
1
1
.
3 3
ABC A B C ABC
V
h S
.
A'
A
B
'
B
C
'
C
Tr
ang 8/15 – Diễn đàn giáo viên Toán
Câu
12. Cho hình chóp
.S
ABC
có
đáy là tam giác đều cạnh
2a
v
à thể tích bằng
3
a
.
Tính chiều cao
h
của
khối chóp
.S
ABC
?
A.
3
6
a
h
. B.
3
2
a
h
. C
.
3
3
a
h
. D.
3h
a
.
Lời
giải
Chọn D
Diện tích tam giác
A
BC
l
à:
2
2
3
2
a . 3
4
S a
.
Ta
có:
.
.
3
.
1
. 3
3
S
ABC
S ABC ABC
ABC
V
V
h S h a
S
.
Câu
13. Cho hình chóp
.S
ABCD
có
đáy là hình vuông cạnh a;
SA
vuôn
g góc với mặt đáy; góc giữa
SC
và mặt đáy của hình chóp bằng
0
6
0
. Thể tích khối chóp
.S ABCD
là
A.
3
6
3
a
. B.
3
3
3
a
. C
.
3
2
3
a
. D.
3
3
a
.
Lời
giải
Chọn A
Ta
có
SA
ABCD gt
AC
là hình chiếu của
SC
lên mặt phẳng
A
BCD
.
Khi đó
0
;
; 60SC ABCD SC AC SCA
.
Ta
có
2
2 2 2 2 2
2
2AC AB BC a a a AC a
.
Xét
S
AC
v
uông tại A.
0
tan .tan 60 2. 3 6
SA
SCA SA AC a a
AC
.
3
2
.
1
1 6
. . 6
3 3 3
S
ABCD ABCD
a
V
S SA a a
.
Câu
14. Cho hình chóp
.S
ABCD
có
đáy
AB
CD
là
hình chữ nhật;
S
AB
đều
cạnh a nằm trong mặt
phẳng vuông góc với
ABCD
. Biết
S
C
tạo với
ABCD
một góc bằng
0
3
0
. Tính thể tích
V
của khối
chóp
.S
ABCD
.
A.
3
6
3
a
V
. B.
3
6
6
a
V
. C.
3
3
3
a
V
. D.
3
3
6
a
V
.
Lời
giải
Chọn B
Tr
ang 9/15 - WordToan
Gọi
H
là trung điểm của
AB
.
Vì
SAB
đều nên
SH
AB
. Mà
SAB
nằm trong mặt phẳng vuông góc với
AB
CD
và
SAB ABC
D AB
. Khi đó
SH A
BCD
.
Vì
SH ABCD SH HC HC
là hình chiếu của
SC
lên mặt phẳng
ABCD
.
0
; ; 30SC ABCD SC HC SCH
.
Xét
SH
C
vuông tại
H
ta có:
tan 1
SH
S
CH
HC
.
Mà
SH
là
đường cao trong tam giác đều cạnh
3
2
a
a SH
.
Từ
3
3
2
1
1
2
ta
n
3
a
SH a
HC
SCH
.
Xét
CB
H
vuông
tại
B
.
2 2
2 2 2 2 2 2
9
2 2
4
4
a a
CH CB BH CB CB a CB a
.
2
. .
2 2
ABCD
S A
B BC a a a
.
Vậy
3
2
1 1 3 6
. 2.
3 3 2 6
ABCD
a a
V S SH a
.
Câu 15.
Cho hình hộp đứng
.ABC
D A B C D
có đáy
ABC
D
là hình thoi cạnh
a
và
60B
AD
,
'AC
hợp với đáy
ABC
D
một góc
60
. Thể tích khối hộp là
A.
3
3
.
2
a
V
B.
3
3 3
.
4
a
V
C.
3
3
.
4
a
V
D.
3
3 3
.
2
a
V
Lời gi
ải
Chọn D
Tran
g 10/15 – Diễn đàn giáo viên Toán
Gọi
O
là
giao điểm của
AC
và
BD
, khi
đó
O
là
trung điểm của hai cạnh này.
Vì
AC
là
hình chiếu của
AC
xuống mặ
t phẳng
ABC
D
nên
ta có:
0
, '
, 60AC ABCD AC AC CAC
Ta có:
.
1
. .
.
2
ABCD A B C D ABCD
V S CC AC BD CC
Tam giác
AB
D
cân
tại
A
(vì
AB A
D a
) có
60B
AD
nên
là tam giác đều
Suy ra:
BD a
và
3
2
a
OA
. Mà
2 3AC OA AC a
Vì hình
hộp này là hình hộp đứng nên các cạnh bên vuông góc với đáy, nghĩa là
CC ABCD CC AC ACC
vuông tại
C
Khi
đó:
0
.t
an 3.tan60 3CC AC CAC a a
Vậy
.
1 1 3
3
. . . 3. .3
2 2 2
AB
CD A B C D
a
V AC
BD CC a a a
(đv
tt)
Câu 16. Cho lăng trụ đứng tam giác
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
B
với
2BA BC
a
. G
ọi M là trung điểm
' '
,A C
biết
BM
hợp v
ới mặt phẳng
AB
C
một g
óc
0
30
.
Thể tích khối lăng trụ
.AB
C A B C
là:
A.
3
3
3
a
. B.
3
2 3
3
a
. C.
3
3
9
a
. D.
3
2 3
9
a
.
Lời giải
Chọn A
Tr
ang 11/15 - WordToan
Gọi
saochoH AC HA HC MH ABC
0
, ,
30 .BM ABC MB BH
do
BA
C
vuông
cân tại B
2 0
; s
in45 .
ABC
S a
BH BA a
3
ta
n
3
a
h MH BH
(do
HB
M
vuông
cân tại H).
3
. '
' '
3
.
3
ABC A
B C ABC
a
V hS
Câu 17.
(Tự luận) Cho khối lăng trụ tam giác
.ABC A B C
.
Tính tỉ số thể tích giữa khối đa diện
A B
C BC
và
khối lăng trụ
.AB
C A B C
.
Lời giả
i
Ta gọi
.ABC
A B C
V V
khi
đó ta có
. . .
1
3
A ABC
C A B B C A BC
V V
V V
.
Ta có
. .A
B C BC C A B B C A BC
V V
V
nên
2
3
A B
C BC
V V
. T
ừ đó suy ra
.
2 2
:
3
3
A B
C BC
ABC A B C
V
V V
V
.
Câu 18.
(Tự luận) Tự luận)Cho tứ diện đều
ABC
D
có c
ạnh bằng 3. Gọi
, M
N
lần l
ượt là các điểm
thuộc các cạnh
, A
D BD
sao c
ho
1
.
3
DM DN
DA DB
Lấy
điểm bất kỳ
P
trê
n cạnh
AB
( khác
A
,
B
). Tính thể tích khối tứ diện
.PMNC
Lời giải
Tr
ang 12/15 – Diễn đàn giáo viên Toán
Gọi
I
là tâm đường tròn ngoại tiếp tam giác
AB
D
,
E
là trung điểm của
A
B
.
Ta có:
0
2
2
.sin 60 3.
3 3
DI DE BD
Vì
ABC
D
là tứ diện đều nên
2
2
(
) 6.CI ABD CI ID CI CD ID
0
1
1 9 2
. . . .sin 60 .
3 6 4
AB
CD ABD
V
CI S CI AB AD
Ta
m giác
AB
D
c
ó
1
1
. / /
3 3
DM DN
MN AB MN AB
DA DB
v
à
2
(
, ) ( , ).
3
d P MN d D AB
Do
đó,
1
1 1 2 2
. ( , ) . . . ( , ) .
2 2 3 3 9
PMN ABD
S
MN d P MN AB d D AB S
Vậy
1
1 2 2 2
. . .
3 3 9 9 2
PM
NC PMN ABD ABCD
V
CI S CI S V
Câu 19. (Tự luận) Cho lăng trụ
.ABC
D A B C D
có đáy
ABC
D
là hình chữ nhật với
6A
B
,
3AD
,
3A C
v
à mặt phẳng
(
)AA C C
v
uông góc với mặt phẳng đáy
(
)ABCD
.
Biết rằng
hai mặt phẳng
(
)AA C C
và
(
)AA B B
tạo với nhau góc
thỏa mãn
3
tan
4
. Tính thể tích
khối
lăng trụ.
Lời giải
T
rang 13/15 - WordToan
+ Ta có đáy là hình chữ nhật với
6A
B
,
3A
D
suy ra, diện tích đáy lăng trụ là:
.
6. 3 3 2
A
BCD
S
AB AD
.
+ Do mặt ph
ẳng
( )AA C C
vuôn
g góc với mặt phẳng đáy
( )ABCD
và
(
) ( )ACC A ABCD AC
( ; )d A AC h
l
à đường cao của hình bình hành và cũng là
đường cao của lăng trụ.Tính
?h
Gọi
H
l
à hình chiếu của
B
lê
n
( )AA C C
thì
điểm
H
nằ
m trên cạnh
A
C
v
à
(
' ')BH ACC A
'
(1)BH AA
.
Ta
có:
ABCD
l
à hình chữ nhật
2
2
3AC AB BC
;
Trong
tam giác
A
BC
v
uông tại
B
có
.
6. 3
2
3
BA BC
BH
AC
;
Trong t
am giác
HBC
v
uông tại
H
có
2
2
1H
C BC BH
;
2AH
AC CH
.
Trong
(
)AA C C
, kẻ
'
,( ')HK AA K AA (2)
.
Từ
(
1)
v
à
(
2) ' ( ) 'AA BHK AA BK
.
Ta
có,
( ) ( )
( ), (( );( ))
( ),
ABB A ACC A AA
BK ABB A BK AA ABB A ACC A BKH
HK ACC A HK AA
.
BKH
vuông tại
H
có
3 2 4 2
tan
4 3
BH
BKH KH
KH KH
;
2
2
2
3
A
K AH AK
.
Xét tam giác
'A
CA
câ
n tại
C
(d
o
'
3AC A C
). Kẻ
C
M AA
th
ì
M
là
trung điểm
'AA
v
à
/
/CM HK
A
CM AHK
3
3
2 2
2 2
CM AC
CM HK
HK AH
.
Xét tam giác vuông
'C
MA
(có
C
M AA
)
2
2 2 2
3 (2 2) 1A M A C CM
2
2AA A M
.
Ta
có, diện tích hình bình hành
A
CC A
l
à:
. 4 2
. ( ; ). .
3
ACC A
CM AA
S CM AA d A AC AC h AC h
AC
.
Vậy
,
.
4
2
.S .3 2 8
3
ABCD
A B C D ACC A
V
h
.
Câu
20. (Tự luận) Cho tam giác
O
AB
đều
cạnh
a
.
Trên đường thẳng
d
qua
O
v
à vuông góc với mặt
AB
CD
Trang
14/15 – Diễn đàn giáo viên Toán
phẳng
OAB
lấy đ
iểm
M
sao cho
OM x
. G
ọi
, E F
lần l
ượt là hình chiếu vuông góc của
A
trên
MB
và
OB
. Gọi
N
là g
iao điểm của
EF
và
d
(hình v
ẽ minh họa bên dưới). Tìm giá
trị của
x
theo
a
để th
ể tích khối tứ diện
ABM
N
có g
iá trị nhỏ nhất.
Lời giải
Ta có:
AF O
B
mà
tam giác
ABC
đều n
ên
F
là tr
ung điểm cạnh
OB
.
Mà
AF O
M
.
Do đó,
AF MNB
Vậy,
1
. .
3
MNAB MNB
V S A
F
.
Mặt khác
, ta có:
3
2
a
AF
;
1 1
. .
2
2
MNB
S BO MN a MN
.
Nên
2
1 3
. .
.
3 12
MNAB MNB
a
V S AF
MN
.
Vậy,
thể tích khối tứ diện
ABMN
có g
iá trị nhỏ nhất khi và chỉ khi độ dài
MN
nhỏ nh
ất.
* Tính
MN
T
rang 15/15 - WordToan
Cá
ch 1:
Ta c
ó:
A
F MNB AF MB
Mà
AE MB
nê
n
MB FE
.
Xét
M
EB
,
ta có:
.
.
.
M
O FB
M
O FB FE MB FE
MB
.
Mặt khác:
2
2
2
2 2 2 2 2
2
.
M
O FB
M
E MF FE ME MO OF
MB
.
Ta lại có:
.
M
N ME ME
M
EN MBO g g MN MB
MB MO MO
.
2
2 2 2
2
2 2 2
2 2 2
.
.
.
M
E MB MO FB
M
N MB MO OF
MO MO MB
.
2
2 2
2
2 2 2 2 2 2 2
2 2
1
.
.
4
4
OF a a
MN
MB MB FB x a x a
M
O x
.
2
4
2 2
2
2 2
2
1
.
4
2 2
a a a
M
N x a x MN x
x
x x
.
* Các
h 2:
Ta c
ó:
A
F MNB AF MB
Mà
A
E MB
nê
n
M
B FE MB NE
.
Mặt
khác, ta có:
O
B MN
.
Do
đó,
F
là
trực tâm
M
NB
.
Ta c
ó:
N
O OF MN MO OF
N
FO MBO g g
O
B MO OB MO
.
2
2
2
MN x a a
MN
x
a
x x
.
Áp
dụng bất đẳng thức Cauchy cho 2 số
x
v
à
2
2
a
x
, ta c
ó:
2
2
2
a
x a
x
.
Do
đó,
2
2
a
MN
x
x
đạt giá trị nhỏ nhất là
2a
khi và chỉ khi
2
2
2
2
a
a
x x
x
.
Vậy, giá trị của
x
t
heo
a
là
2
2
a
x
.
| 1/32
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Hình học 12 NC . Thời gian làm bài : 45 phút
--------------------------------------------------------- Mã đề 135
Họ và tên học sinh: …………………..……………………………………..Lớp: ………….. Trả lời trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 Đáp án Câu 11 12 13 14 15 16 17 18 19 20 Đáp án
Chú ý: -Từ câu 1 đến câu 16 thí sinh điền đáp án trắc nghiệm A, B, C hay D vào bảng trên
- Từ câu 17 đến câu 20 thí sinh điền đáp số vào các ô tương ứng ở bảng trên ( điền khuyết). Câu hỏi trắc nghiệm:
Phần I: Câu hỏi trắc nghiệm A,B,C, hay D
Câu 1: Khối chóp có diện tích đáy là B, chiều cao bằng h . Thể tích V khối chóp là: 1 1 1 A. . Bh B. . Bh C. . Bh D. . Bh 3 2 6
Câu 2: Hình nào dưới đây không phải là hình đa diện? A. . B. C. D.
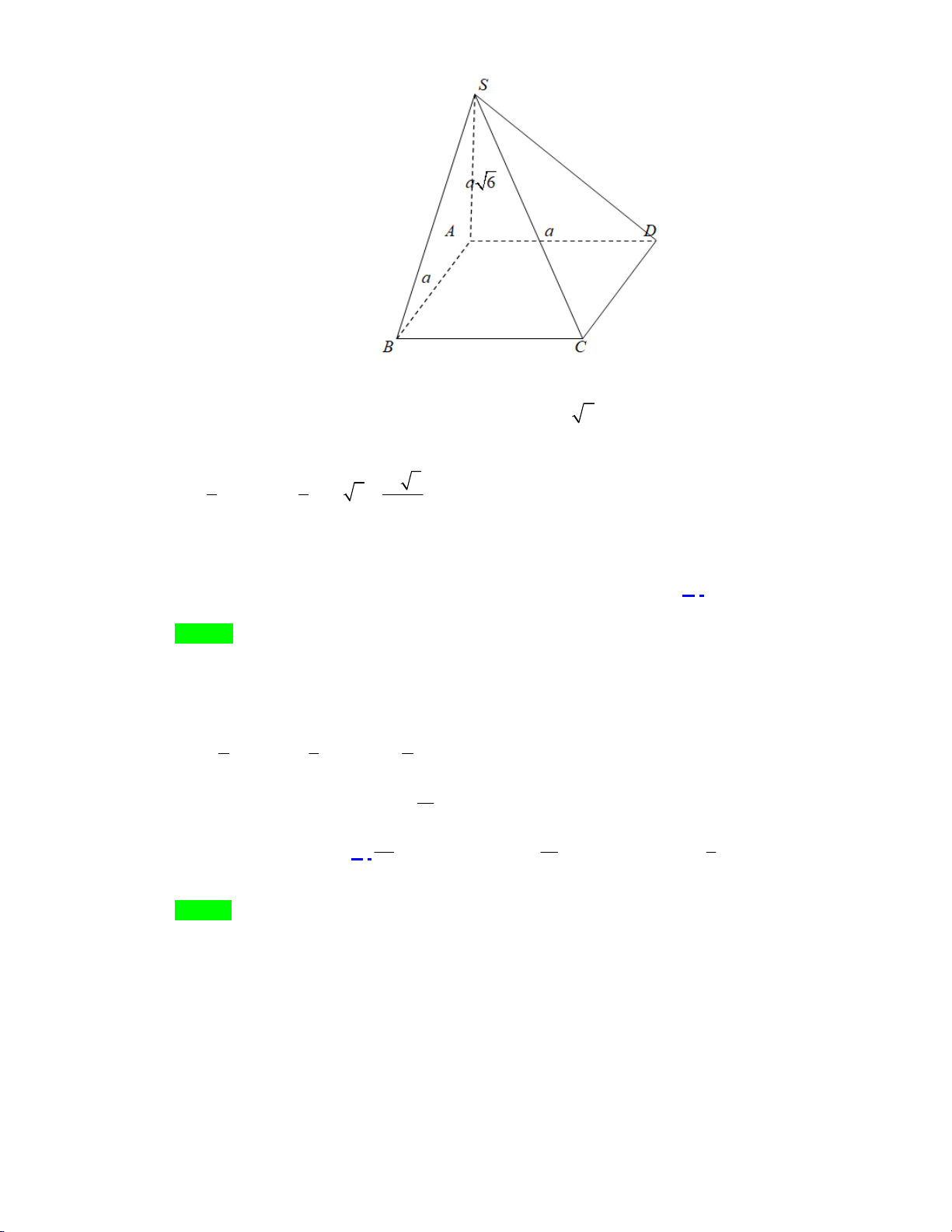
Câu 3: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a , SA   ABCD và SA a 6 .
Thể tích của khối chóp S.ABCD bằng 3 a 6 3 a 6 3 a 6 A. . B. 3 a 6 . C. . D. . 6 3 2
Câu 4: Cho khối lăng trụ đứng có cạnh bên bằng 5 , đáy là hình vuông có cạnh bằng 4 . Hỏi thể tích khối lăng trụ là: A. 100 . B. 20 . C. 64 . D. 80 . 1 Câu 5: Cho khối chóp .
S ABC , trên ba cạnh SA, SB, SC lần lượt lấy ba điểm A , B , C sao cho SA  SA , 2 1 1 S
B SB , SC 
SC . Gọi V và V  lần lượt là thể tích của các khối chóp .
S ABC và S.  A B C . Khi đó tỉ số 3 4 V 1 1 1 là: A. 24. B. . C. . D. . V 24 12 8
Câu 6: Cho khối chóp OABC có OA , OB , OC đôi một vuông góc tại O và OA  2 , OB  3 , OC  6 . Thể tích khối chóp bằng A. 12 . B. 6 . C. 24 . D. 36 .
Câu 7: Cho hình chóp S.ABC có SA vuông góc mặt đáy, tam giác ABC vuông tại A , SA  4 , AB  3 ,
BC  5 . Tính thể tích khối chóp S.ABC . A. 8. B. 16. C. 48. D. 24.
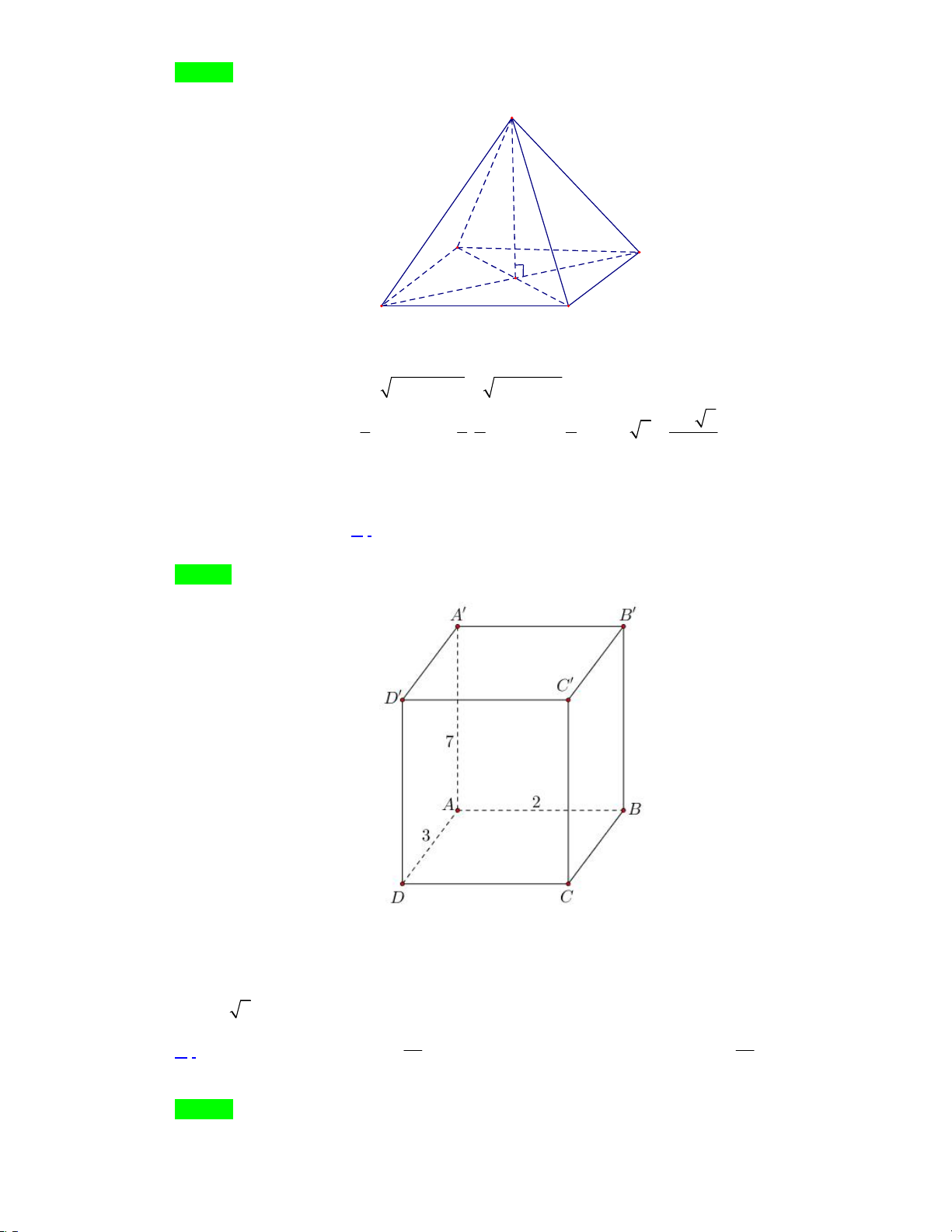
Câu 8: Cho hình chóp đều S.ABCD có chiều cao bằng a 2 và độ dài cạnh bên bằng a 6 . Tính thể tích
khối chóp S.ABCD . 3 10a 2 3 8a 3 3 10a 3 3 8a 2 A. . B. . C. . D. . 3 3 3 3
Câu 9: Cho hình hộp chữ nhật ABC . D A BCD
  có AB  2 cm , AD  3 cm , AA  7 cm . Tính thể tích khối hộp ABC . D A BCD   . A. 12 3 cm . B. 42 3 cm . C. 24 3 cm . D. 36 3 cm .
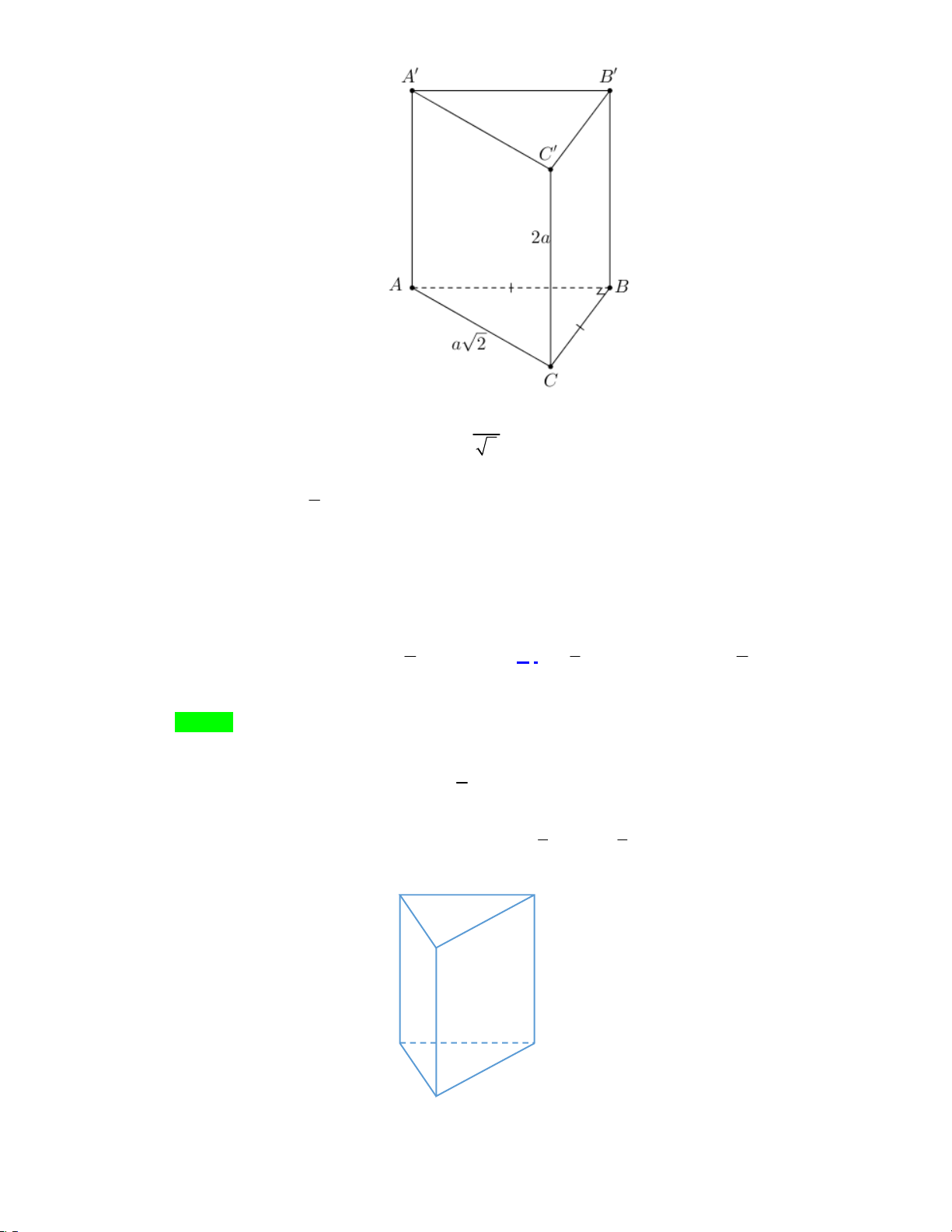
Câu 10: Cho khối lăng trụ đứng ABC.AB C
  có CC  2a , đáy ABC là tam giác vuông cân tại B và
AC a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a A. 3 V a . B. V  . C. 3 V  2a . D. V  . 2 3
Câu 11: Cho khối lăng trụ tam giác AB . C A BC
  có thể tích bằng 1. Tính thể tích V của khối chóp .
A A' B 'C ' . 1 1 1 A. V  3 . B. V  . C. V  . D. V  . 4 3 2 Câu 12: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh 2a và thể tích bằng 3
a . Tính chiều cao h của hình chóp đã cho. 3a 3a 3a A. h  . B. h  . C. h  . D. h  3a . 6 2 3
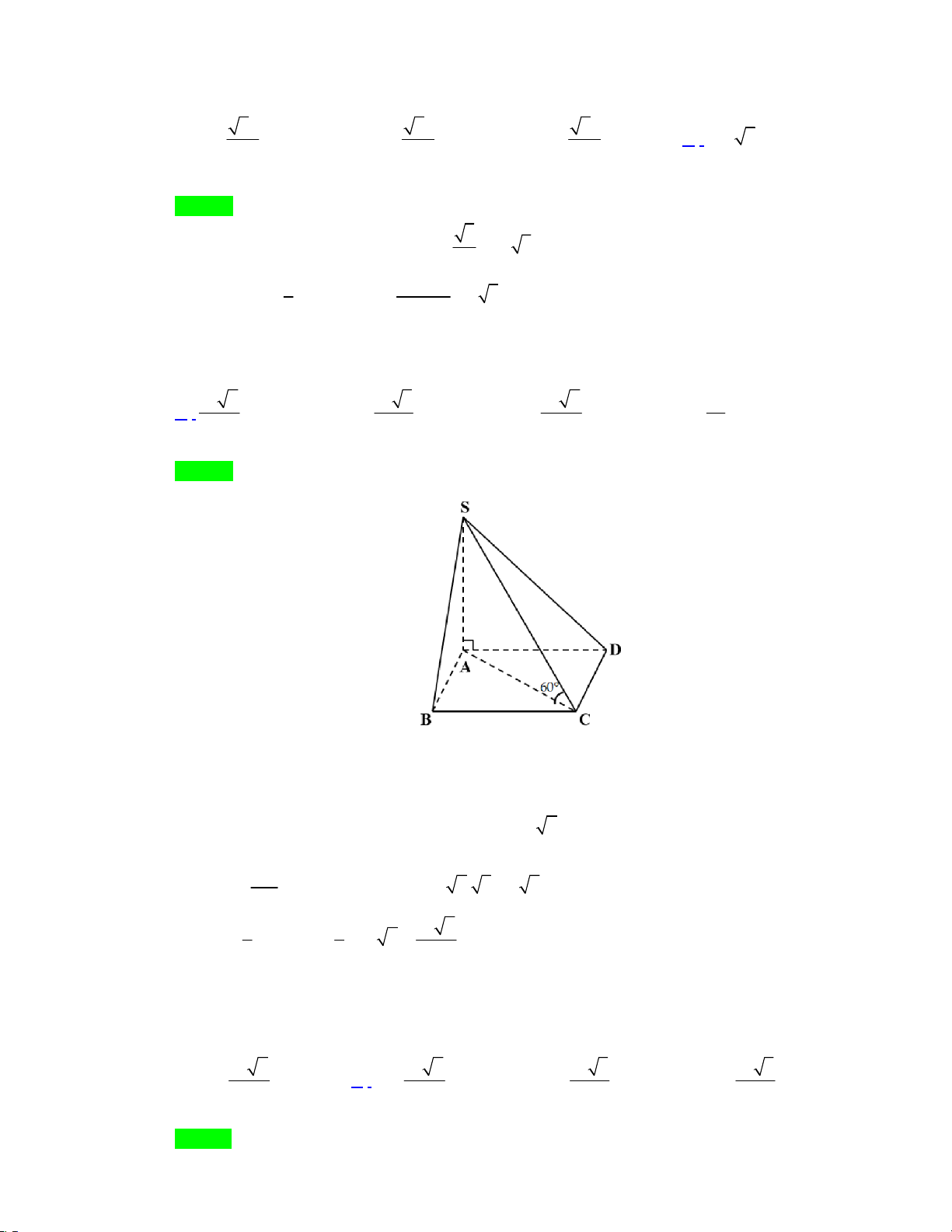
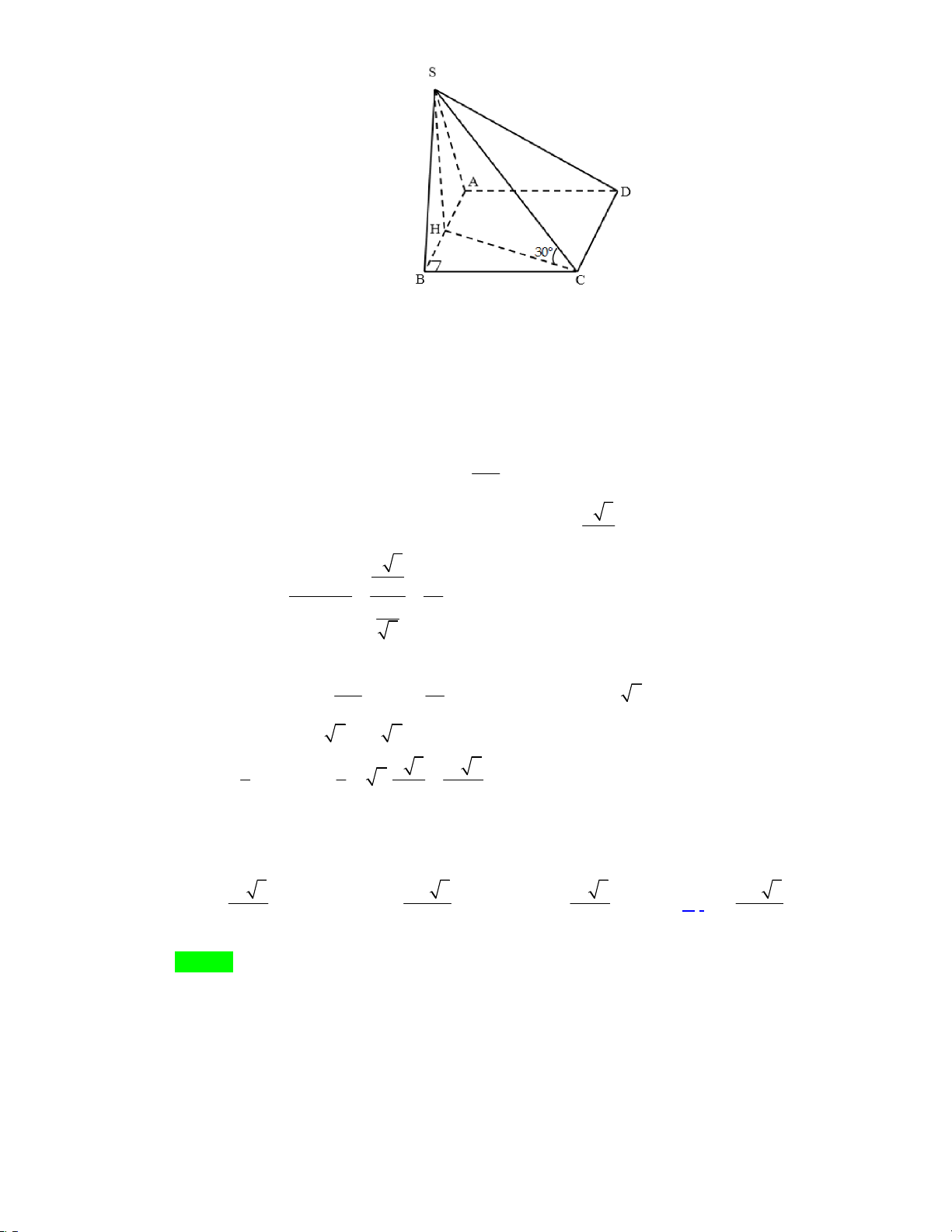
Câu 13: Cho hình chóp S.ABCD có đáy hình vuông cạnh a ; SA vuông góc mặt đáy; Góc giữa SC và mặt đáy của hình chóp bằng 0
60 . Thể tích khối chóp S.ABCD là 3 a 6 3 a 3 3 a 2 3 a A. . B. . C. . D. . 3 3 3 3
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SAB đều cạnh a nằm trong mặt phẳng
vuông góc với  ABCD . Biết SC tạo với  ABCD một góc bằng 0
30 . Tính thể tích V của khối chóp S.ABC . D 3 a 6 3 a 6 3 a 3 3 a 3 A. V  . B. V  . C. V  . D. V  . 3 6 3 6 
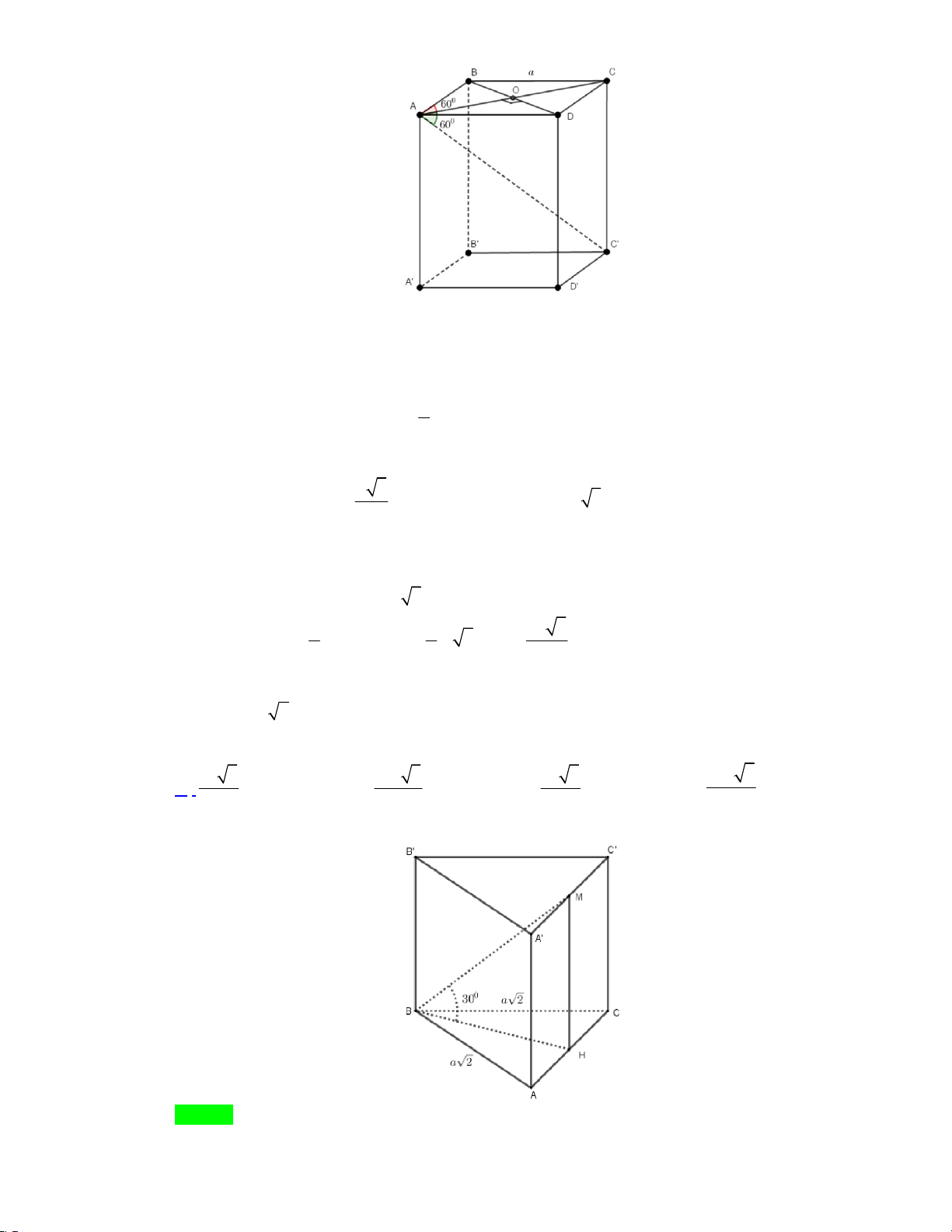
Câu 15: Cho hình hộp đứng ABC . D A BCD
  có đáy ABCD là hình thoi cạnh a và BAD  60 , AC ' hợp với
đáy  ABCD một góc 60 . Thể tích của khối hộp là 3 a 3 3 3a 3 3 a 3 3 3a 3 A. . B. . C. . D. . 2 4 4 2
Câu 16: Cho lăng trụ đứng tam giác AB . C A BC
  có đáy ABC là tam giác vuông cân tại B với
BA BC a 2 . Gọi M là trung điểm A'C ', biết BM hợp với mặt phẳng  ABC  một góc 0 30 . Thể tích khối lăng trụ AB . C A BC   là: 3 a 3 3 2a 3 3 a 3 3 2a 3 A. . B. . C. . D. . 3 3 9 9
Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 17: Cho khối lăng trụ tam giác ABC.AB C
  . Tính tỉ số thể tích giữa khối đa diện A BCB
C và khối lăng
trụ ABC.AB C   .
Câu 18: Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M , N lần lượt là các điểm thuộc các cạnh AD, BD sao DM DN 1 cho 
 . Lấy điểm bất kỳ P trên cạnh AB (khác ,
A B ). Tính thể tích khối tứ diện PMNC. DA DB 3
Câu 19: Cho lăng trụ ABC . D AB CD
  có đáy ABCD là hình chữ nhật với AB  6 , AD  3 , AC  3 và
mặt phẳng  AAC C
  vuông góc với mặt đáy. Biết hai mặt phẳng  AAC C
  ,  AAB B
  tạo với nhau góc  3 thỏa mãn tan 
. Tính thể tích khối lăng trụ ABC . D AB CD   . 4
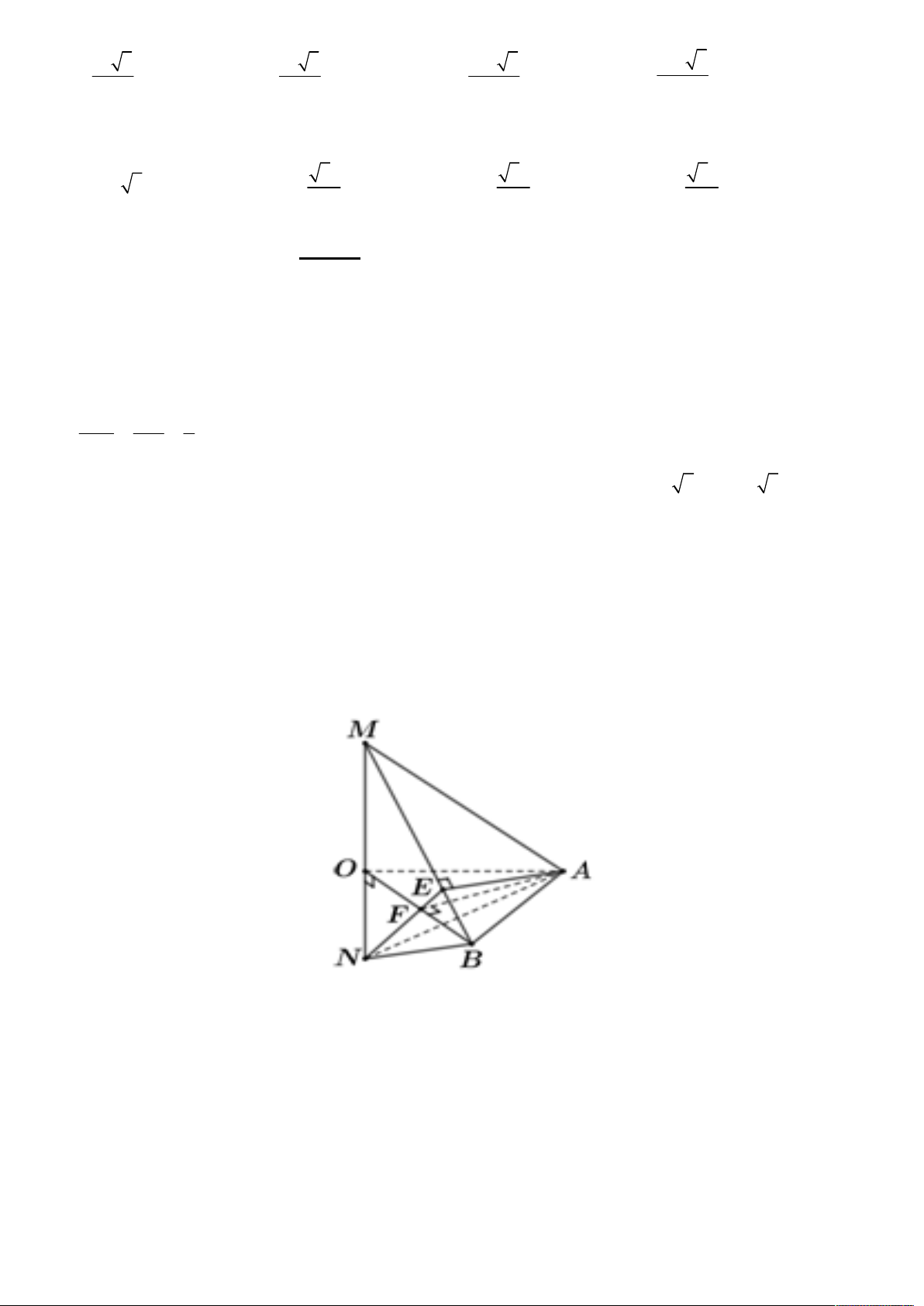
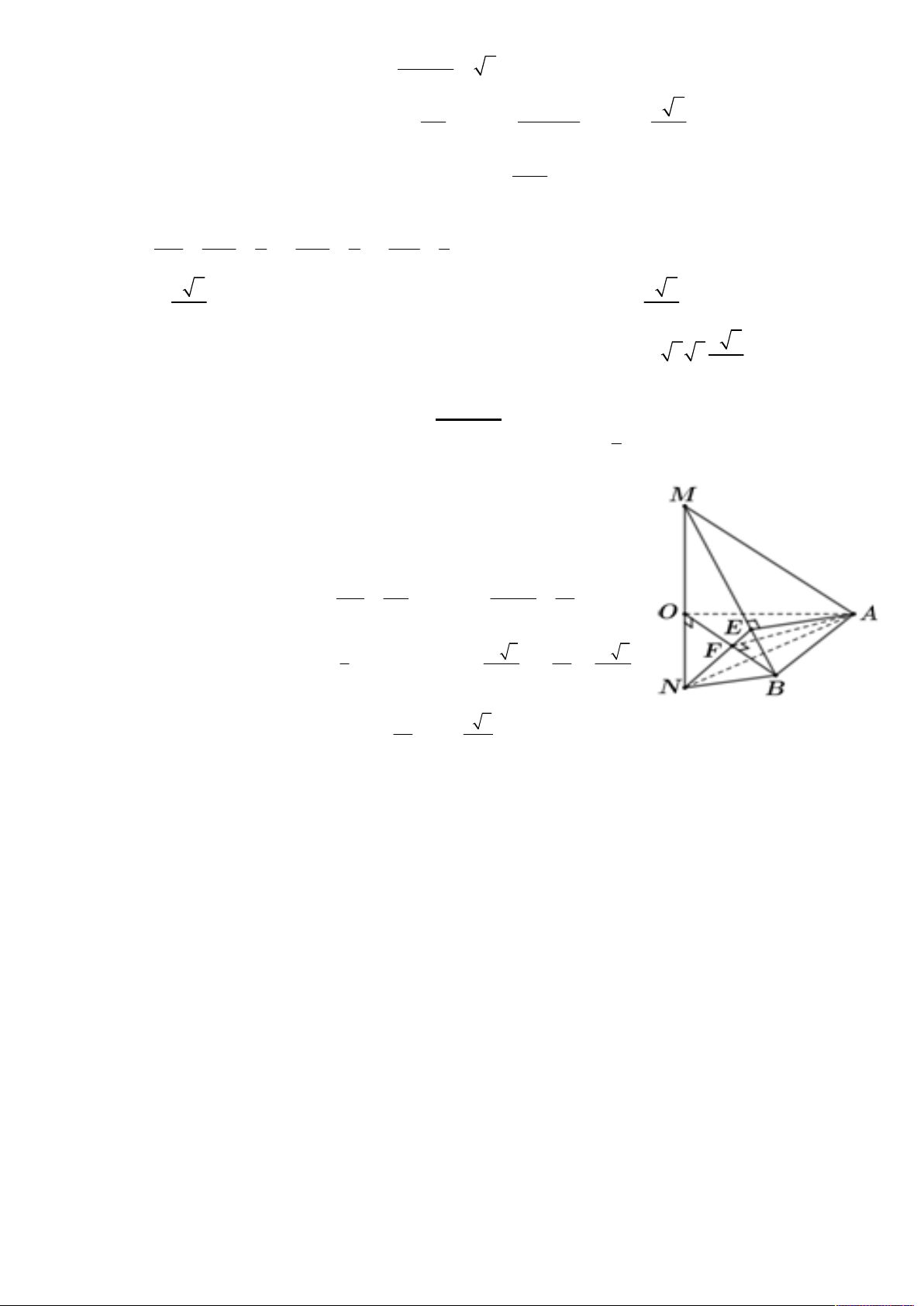
Câu 20: Cho tam giác OAB đều cạnh a . Trên đường thẳng d qua O và vuông góc với mặt phẳng OAB lấy
điểm M sao cho OM x . Gọi E, F lần lượt là hình chiếu vuông góc của A trên MB và OB . Gọi N là giao
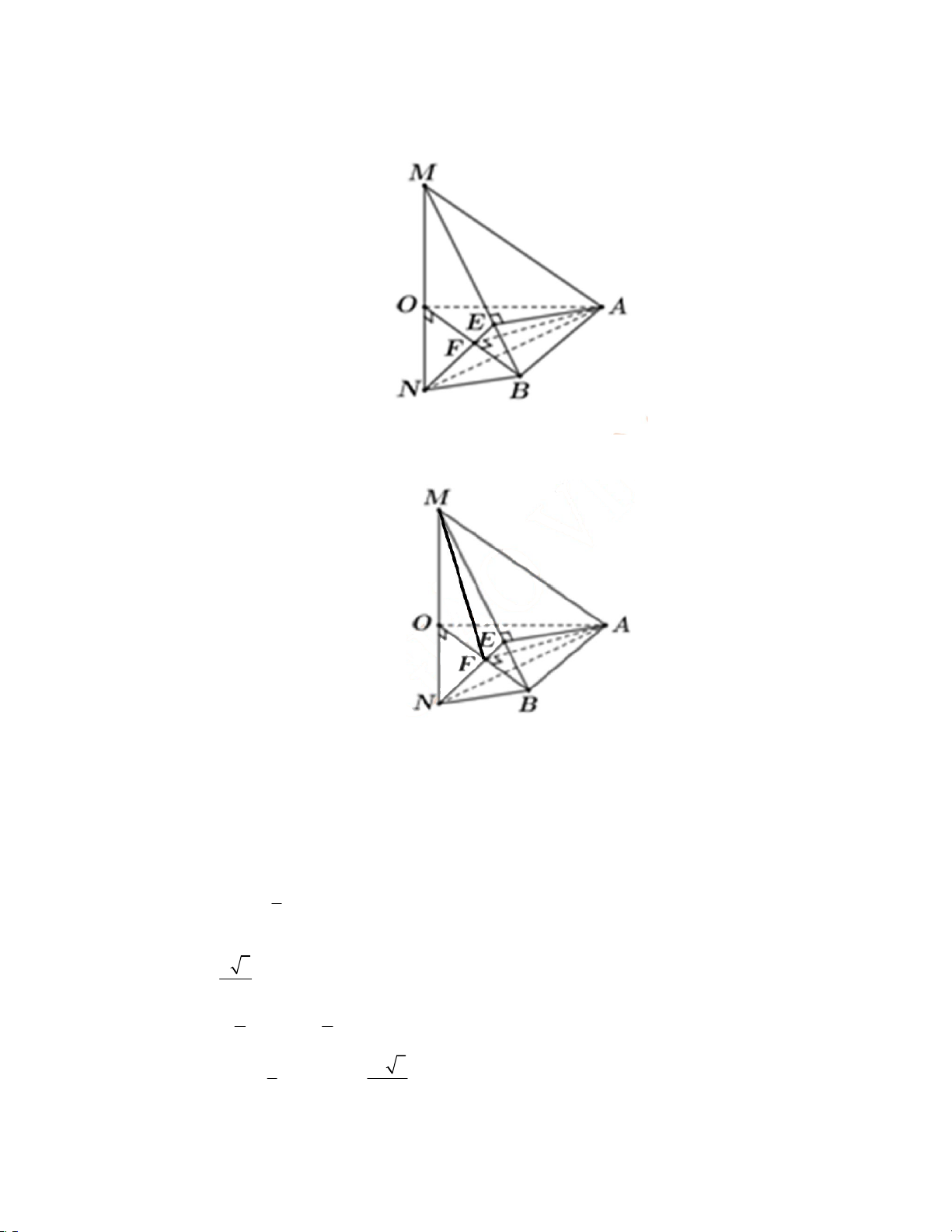
điểm của EF và d (hình vẽ minh họa bên dưới). Tìm giá trị của x theo a để thể tích khối tứ diện ABMN có giá trị nhỏ nhất.
---------------------HẾT----------------------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Hình học 12 NC . Thời gian làm bài : 45 phút
--------------------------------------------------------- Mã đề 248
Họ và tên học sinh: …………………..……………………………………..Lớp: ………….. Trả lời trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 Đáp án Câu 11 12 13 14 15 16 17 18 19 20 Đáp án
Chú ý: -Từ câu 1 đến câu 16 thí sinh điền đáp án trắc nghiệm A, B, C hay D vào bảng trên
- Từ câu 17 đến câu 20 thí sinh điền đáp số vào các ô tương ứng ở bảng trên ( điền khuyết). Câu hỏi trắc nghiệm:
Phần I: Câu hỏi trắc nghiệm A,B,C hay D
Câu 1: Số cạnh của một hình hộp chữ nhật là: A. 8. B. 16. C.12. D. 9.
Câu 2: Khối lăng trụ có diện tích đáy là B, chiều cao bằng h . Thể tích V khối lăng trụ là: 1 1 1 A. . Bh B. . Bh C. . Bh D. . Bh 3 2 6
Câu 3: Hình chóp tam giác đều có độ dài cạnh bên khác độ dài cạnh đáy có mấy mặt phẳng đối xứng? A. 4 . B. 3 . C. 6 . D. 5 . Câu 4: Cho hình chóp .
S ABC có SA   ABC , A
BC vuông cân tại A, SA AC  .
a Tính theo a thể tích V
của khối chóp S.ABC 3 a 3 a 3 a A. V  . B. V  . C. 3 V  2a . D. V  . 6 4 2
Câu 5: Cho hình hộp chữ nhật ABC . D A BCD
 . Biết AB a, AD  2a, AA  3 .
a Tính thể tích khối hộp ABC . D A BCD  . A. 3 2a . B. 2 6a . C. 3 6a . D. 2 2a .
Câu 6: Cho tứ diện MNPQ . Gọi I ; J ; K lần lượt là trung điểm của các cạnh MN ; MP ; MQ . Tỉ số thể tích VMIJK bằng: VMNPQ 1 1 1 1 A. . B. . C. . D. . 3 4 6 8
Câu 7: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a 3 , đường cao bằng a . Tính thể tíchV của
khối chóp S.ABC . 3 a 3 3 3a 3 3 3a 3 3 3a A.V  . B.V  . C.V  . D.V  . 4 2 4 4
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a 3 , mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABCD là: A. 3 12a . B. 14a 3 . C. 3 15a . D. 3 17a .
Câu 9: Cho khối chóp S.ABC có SA vuông góc với  ABC  , đáy ABC là tam giác vuông cân tại A , AB  2a
, SB  2a 2 . Tính thể tích khối chóp S.ABC . 3 4a 2 3 8a 3 4a A. . B. 3 4a . C. . D. . 3 3 3
Câu 10: Cho lăng trụ đứng tam giác MN . P M NP
  có đáy MNP là tam giác đều cạnh a , đường chéo MP tạo
với mặt phẳng đáy một góc bằng 60 . Tính theo a thể tích của khối lăng trụ MN . P M NP   . 3 3a 3 2a 3 3a 3 2a A. . B. . C. . D. . 2 3 4 4
Câu 11: Cho khối lăng trụ đứng AB . C A BC
  có CC  2a , đáy ABC là tam giác vuông cân tại B và
AC a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a A. 3 V a . B. V  . C. 3 V  2a . D. V  . 2 3
Câu 12: Cho khối chóp S.ABC có thể tích bằng 60. Gọi M là trung điểm cạnh SB và N là điểm thuộc cạnh
SC sao cho CN  2NS. Tính thể tích khối chóp S.AMN A. 20. B.15. C. 7,5. D.10.
Câu 13: Cho khối tứ diện ABCD có thể tích bằng 80. Tam giác BCD vuông cân tại B và BC  4. Khoảng
cách từ điểm A đến mặt phẳng  BCD bằng: A.10. B.15. C. 5. D. 30.
Câu 7: Cho hình chóp S.ABC có SAB đều cạnh a , tam giác ABC vuông cân tại C . Hình chiếu vuông
của S lên  ABC  là trung điểm của cạnh AB . Thể tích khối chóp S.ABC tính theo a là: 3 a 3 3 a 3 3 a 3 3 a 3 A. V  B. V  C. V  D.V  . 8 12 4 24
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, S
AB đều cạnh a nằm trong mặt phẳng
vuông góc với  ABCD . Biết SCD tạo với  ABCD một góc bằng 0
30 . Tính thể tích V của khối chóp S.ABC . D 3 a 3 3 a 3 3 a 3 3 a 3 A. V  . B. V  . C. V  . D. V  . 8 4 2 3
Câu 16: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SC tạo với mặt phẳng SAB một góc 0
30 . Tính thể tích khối chóp S.ABCD 3 2a 3 2a 3 6a A. 3 2a B. C. D. 3 3 3
Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 17: Cho khối lăng trụ tam giác ABC.AB C
  . Tính tỉ số thể tích giữa khối chóp A .AB 'C ' và khối lăng trụ
ABC.AB C   .
Câu 18: Cho tứ diện đều ABCD có cạnh bằng 4. Gọi M , N lần lượt là các điểm thuộc các cạnh AD, BD sao DM DN 1 cho  
. Lấy điểm bất kỳ P trên cạnh AB (khác ,
A B ). Tính thể tích khối tứ diện PMNC. DA DB 4
Câu 19: Cho lăng trụ ABC . D AB CD
  có đáy ABCD là hình chữ nhật với AB  6 , AD  3 , AC  3 và
mặt phẳng  AAC C
  vuông góc với mặt đáy. Biết hai mặt phẳng  AAC C
  ,  AAB B
  tạo với nhau góc 
thỏa mãn tan   2 . Tính thể tích khối lăng trụ ABC . D AB CD   .
Câu 20: Cho tam giác OAB đều cạnh 2a . Trên đường thẳng d qua O và vuông góc với mặt phẳng OAB lấy
điểm M sao cho OM x . Gọi E, F lần lượt là hình chiếu vuông góc của A trên MB và OB . Gọi N là giao
điểm của EF và d (hình vẽ minh họa bên dưới). Tìm giá trị của x theo a để thể tích khối tứ diện ABMN có giá trị nhỏ nhất.
------------------------HẾT------------------------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Hình học 12 NC . Thời gian làm bài : 45 phút
--------------------------------------------------------- Mã đề 357
Họ và tên học sinh: …………………..……………………………………..Lớp: ………….. Trả lời trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 Đáp án Câu 11 12 13 14 15 16 17 18 19 20 Đáp án
Chú ý: -Từ câu 1 đến câu 16 thí sinh điền đáp án trắc nghiệm A, B, C hay D vào bảng trên
- Từ câu 17 đến câu 20 thí sinh điền đáp số vào các ô tương ứng ở bảng trên ( điền khuyết). Câu hỏi trắc nghiệm:
Phần I: Câu hỏi trắc nghiệm A,B,C hay D
Câu 1: Cho hình chóp S.ABC có SA vuông góc mặt đáy, tam giác ABC vuông tại A , SA  4 , AB  3 ,
BC  5 . Tính thể tích khối chóp S.ABC . A. 8. B. 16. C. 48. D. 24.
Câu 2: Khối chóp có diện tích đáy là B, chiều cao bằng h . Thể tích V khối chóp là: 1 1 1 A. B . h B. . Bh C. B . h D. . Bh 2 3 6
Câu 3: Hình nào dưới đây không phải là hình đa diện? A. . B. C. D.
Câu 4: Cho khối lăng trụ đứng có cạnh bên bằng 5 , đáy là hình vuông có cạnh bằng 4 . Hỏi thể tích khối lăng trụ là: A. 100 . B. 20 . C. 64 . D. 80 .
Câu 5: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a , SA   ABCD và SA a 6 .
Thể tích của khối chóp S.ABCD bằng 3 a 6 3 a 6 3 a 6 A. 3 a 6 . B. . C. . D. . 2 3 6 1 Câu 6: Cho khối chóp .
S ABC , trên ba cạnh SA, SB, SC lần lượt lấy ba điểm A , B , C sao cho SA  SA , 2 1 1 S
B SB , SC 
SC . Gọi V và V  lần lượt là thể tích của các khối chóp .
S ABC và S.  A B C . Khi đó tỉ số 3 4 V là: V 1 1 1 A. . B. . C. 24. D. . 24 12 8
Câu 7: Cho khối chóp OABC có OA , OB , OC đôi một vuông góc tại O và OA  2 , OB  3 , OC  6 . Thể tích khối chóp bằng A. 12 . B. 24 . C. 36 . D. 6 .
Câu 8: Cho khối lăng trụ đứng ABC.A BC
  có CC  2a , đáy ABC là tam giác vuông cân tại B và
AC a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a A. 3 V a . B. V  . C. 3 V  2a . D. V  . 2 3
Câu 9: Cho hình hộp chữ nhật AB . CD A BCD
  có AB  2 cm , AD  3 cm , AA  7 cm . Tính thể tích khối hộp AB . CD AB CD   . A. 12 3 cm . B. 42 3 cm . C. 24 3 cm . D. 36 3 cm .
Câu 10: Cho hình chóp đều S.ABCD có chiều cao bằng a 2 và độ dài cạnh bên bằng a 6 . Tính thể tích
khối chóp S.ABCD . 3 10a 2 3 8a 3 3 10a 3 3 8a 2 A. . B. . C. . D. . 3 3 3 3
Câu 11: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SAB đều cạnh a nằm trong mặt phẳng
vuông góc với  ABCD . Biết SC tạo với  ABCD một góc bằng 0
30 . Tính thể tích V của khối chóp S.ABC . D 3 a 6 3 a 6 3 a 3 3 a 3 A. V  . B. V  . C. V  . D. V  . 3 6 3 6
Câu 12: Cho khối lăng trụ tam giác AB . C A BC
  có thể tích bằng 1. Tính thể tích V của khối chóp .
A A ' B 'C ' . 1 1 1 A. V  . B. V  . C. V  3 . D. V  . 4 3 2 
Câu 13: Cho hình hộp đứng ABC . D A BCD
  có đáy ABCD là hình thoi cạnh a và BAD  60 , AC ' hợp với
đáy  ABCD một góc 60 . Thể tích của khối hộp là 3 a 3 3 3a 3 3 a 3 3 3a 3 A. . B. . C. . D. . 2 4 4 2
Câu 14: Cho hình chóp S.ABCD có đáy hình vuông cạnh a ; SA vuông góc mặt đáy; Góc giữa SC và mặt đáy của hình chóp bằng 0
60 . Thể tích khối chóp S.ABCD là 3 a 3 3 a 2 3 a 6 3 a A. . B. . C. . D. . 3 3 3 3
Câu 15: Cho lăng trụ đứng tam giác AB . C A BC
  có đáy ABC là tam giác vuông cân tại B với
BA BC a 2 . Gọi M là trung điểm A'C ', biết BM hợp với mặt phẳng  ABC  một góc 0 30 . Thể tích khối lăng trụ AB . C A BC   là: 3 a 3 3 a 3 3 2a 3 3 2a 3 A. . B. . C. . D. . 9 3 3 9 Câu 16: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh 2a và thể tích bằng 3
a . Tính chiều cao h của hình chóp đã cho. 3a 3a 3a A. h  3a . B. h  . C. h  . D. h  . 2 3 6
Phần II: Câu hỏi trắc nghiệm điền khuyết
Câu 17: Cho khối lăng trụ tam giác ABC.AB C
  . Tính tỉ số thể tích giữa khối chóp C.AA' B ' B và khối lăng
trụ ABC.AB C   .
Câu 18: Cho tứ diện đều ABCD có cạnh bằng 6. Gọi M , N lần lượt là các điểm thuộc các cạnh AD, BD sao DM DN 1 cho  
. Lấy điểm bất kỳ P trên cạnh AB (khác ,
A B ). Tính thể tích khối tứ diện PMNC . DA DB 6
Câu 19: Cho lăng trụ ABC . D AB CD
  có đáy ABCD là hình chữ nhật với AB  6 , AD  3 , AC  3 và
mặt phẳng  AAC C
  vuông góc với mặt đáy. Biết hai mặt phẳng  AAC C
  ,  AAB B
  tạo với nhau một góc 0
45 . Tính thể tích khối lăng trụ ABC . D AB CD   .
Câu 20: Cho tam giác OAB đều cạnh 3a . Trên đường thẳng d qua O và vuông góc với mặt phẳng OAB lấy
điểm M sao cho OM x . Gọi E, F lần lượt là hình chiếu vuông góc của A trên MB và OB . Gọi N là giao
điểm của EF và d (hình vẽ minh họa bên dưới). Tìm giá trị của x theo a để thể tích khối tứ diện ABMN có giá trị nhỏ nhất.
----------------------------HẾT----------------------------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1
TỔ TOÁN Môn : Hình học 12 NC . Thời gian làm bài : 45 phút
--------------------------------------------------------- Mã đề 468
Họ và tên học sinh: …………………..……………………………………..Lớp: ………….. Trả lời trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 Đáp án Câu 11 12 13 14 15 16 17 18 19 20 Đáp án
Chú ý: -Từ câu 1 đến câu 16 thí sinh điền đáp án trắc nghiệm A, B, C hay D vào bảng trên
- Từ câu 17 đến câu 20 thí sinh điền đáp số vào các ô tương ứng ở bảng trên ( điền khuyết). Câu hỏi trắc nghiệm:
Phần I: Câu hỏi trắc nghiệm A,B,C hay D
Câu 1: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a 3 , đường cao bằng a . Tính thể tíchV của
khối chóp S.ABC . 3 a 3 3 3a 3 3 3a 3 3 3a A. V  . B. V  . C. V  . D. V  . 4 2 4 4
Câu 2: Số cạnh của một hình hộp chữ nhật là: A. 16. B. 12. C. 8. D. 9.
Câu 3: Khối lăng trụ có diện tích đáy là B, chiều cao bằng h . Thể tích V khối lăng trụ là: 1 1 1 A. . Bh B. B . h C. . Bh D. B . h 2 3 6
Câu 4: Cho hình chóp S.ABC có SA   ABC , A
BC vuông cân tại A, SA AC  .
a Tính theo a thể tích V
của khối chóp S.ABC 3 a 3 a 3 a A. V  . B. V  . C. 3 V  2a . D. V  . 6 4 2
Câu 5: Hình chóp tam giác đều có độ dài cạnh bên khác độ dài cạnh đáy có mấy mặt phẳng đối xứng? A. 3 . B. 5 . C. 6 . D. 4 .
Câu 6: Cho hình hộp chữ nhật ABC . D A BCD
 . Biết AB a, AD  2a, AA  3 .
a Tính thể tích khối hộp ABC . D A BCD  . A. 2 6a . B. 3 6a . C. 3 2a . D. 2 2a .
Câu 7: Cho tứ diện MNPQ . Gọi I ; J ; K lần lượt là trung điểm của các cạnh MN ; MP ; MQ . Tỉ số thể tích VMIJK bằng: VMNPQ 1 1 1 1 A. . B. . C. . D. . 3 6 8 4
Câu 8: Cho lăng trụ đứng tam giác M . NP M NP
  có đáy MNP là tam giác đều cạnh a , đường chéo MP tạo
với mặt phẳng đáy một góc bằng 60 . Tính theo a thể tích của khối lăng trụ M . NP M NP   . 3 3a 3 2a 3 3a 3 2a A. . B. . C. . D. . 2 3 4 4
Câu 9: Cho khối chóp S.ABC có SA vuông góc với  ABC  , đáy ABC là tam giác vuông cân tại A , AB  2a
, SB  2a 2 . Tính thể tích khối chóp S.ABC . 3 4a 2 3 8a 3 4a A. . B. 3 4a . C. . D. . 3 3 3
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a 3 , mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABCD là: A. 3 12a . B. 14a 3 . C. 3 15a . D. 3 17a .
Câu 11: Cho hình chóp S.ABC có SAB đều cạnh a , tam giác ABC vuông cân tại C . Hình chiếu vuông
của S lên  ABC  là trung điểm của cạnh AB . Thể tích khối chóp S.ABC tính theo a là: 3 a 3 3 a 3 3 a 3 3 a 3 A. V  . B. V  . C. V  . D. V  . 8 12 4 24
Câu 12: Cho khối lăng trụ đứng ABC.AB C
  có CC  2a , đáy ABC là tam giác vuông cân tại B và
AC a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a A. V  . B. 3 V  2a . C. 3 V a . D. V  . 2 3
Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, S
AB đều cạnh a nằm trong mặt phẳng
vuông góc với  ABCD  . Biết SCD tạo với  ABCD  một góc bằng 0
30 . Tính thể tích V của khối chóp S.AB . CD 3 a 3 3 a 3 3 a 3 3 a 3 A. V  . B. V  . C. V  . D. V  . 8 4 2 3
Câu 14: Cho khối tứ diện ABCD có thể tích bằng 80. Tam giác BCD vuông cân tại B và BC  4. Khoảng
cách từ điểm A đến mặt phẳng  BCD bằng: A. 15. B. 5. C. 10. D. 30.
Câu 15: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SC tạo với mặt phẳng SAB một góc 0
30 . Tính thể tích khối chóp S.ABCD 3 2a 3 2a 3 6a A. . B. 3 2a . C. D. 3 3 3
Câu 16: Cho khối chóp S.ABC có thể tích bằng 60. Gọi M là trung điểm cạnh SB và N là điểm thuộc cạnh
SC sao cho CN  2NS. Tính thể tích khối chóp S.AMN A. 10. B. 15. C. 7,5. D. 20.
Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 17: Cho khối lăng trụ tam giác ABC.A BC
  . Tính tỉ số thể tích giữa khối chóp C '.AA' B ' và khối lăng trụ ABC.A BC   .
Câu 18: Cho tứ diện đều ABCD có cạnh bằng 5. Gọi M , N lần lượt là các điểm thuộc các cạnh AD, BD sao DM DN 1 cho  
. Lấy điểm bất kỳ P trên cạnh AB (khác ,
A B ). Tính thể tích khối tứ diện PMNC. DA DB 5
Câu 19: Cho lăng trụ ABCD.AB CD
  có đáy ABCD là hình chữ nhật với AB  6 , AD  3 , AC  3 và
mặt phẳng  AAC C
  vuông góc với mặt đáy. Biết hai mặt phẳng  AAC C
  ,  AAB B
  tạo với nhau một góc 0
60 . Tính thể tích khối lăng trụ ABCD.AB CD   .
Câu 20: Cho tam giác OAB đều cạnh 4a . Trên đường thẳng d qua O và vuông góc với mặt phẳng OAB lấy
điểm M sao cho OM x . Gọi E, F lần lượt là hình chiếu vuông góc của A trên MB và OB . Gọi N là giao
điểm của EF và d (hình vẽ minh họa bên dưới). Tìm giá trị của x theo a để thể tích khối tứ diện ABMN có giá trị nhỏ nhất.
------------------------------HẾT-------------------------------
ĐÁP ÁN ĐỀ KIỂM TRA 1 TIẾT HH12 CHƯƠNG I. Mã đề 135: Câu 1 2 3 4 5 6 7 8 9 10 Đáp án A C C D B B A D B A Câu 11 12 13 14 15 16 17 18 19 20 Đáp án C D A B D A 2 8 2 a 2 3 2 2 Mã đề 248: Câu 1 2 3 4 5 6 7 8 9 10 Đáp án C B B A C D A A D C Câu 11 12 13 14 15 16 17 18 19 20 Đáp án A D D D B C 1 2 9 14 a 2 3 4 Mã đề 357: Câu 1 2 3 4 5 6 7 8 9 10 Đáp án A C B D C A D A B D Câu 11 12 13 14 15 16 17 18 19 20 Đáp án B B D C B A 2 3a 5 2 9 2 3 2 2 Mã đề 468: Câu 1 2 3 4 5 6 7 8 9 10 Đáp án A B D A A B C C D A Câu 11 12 13 14 15 16 17 18 19 20 Đáp án D C B D A A 1 5 2 3 10 2a 2 3 3
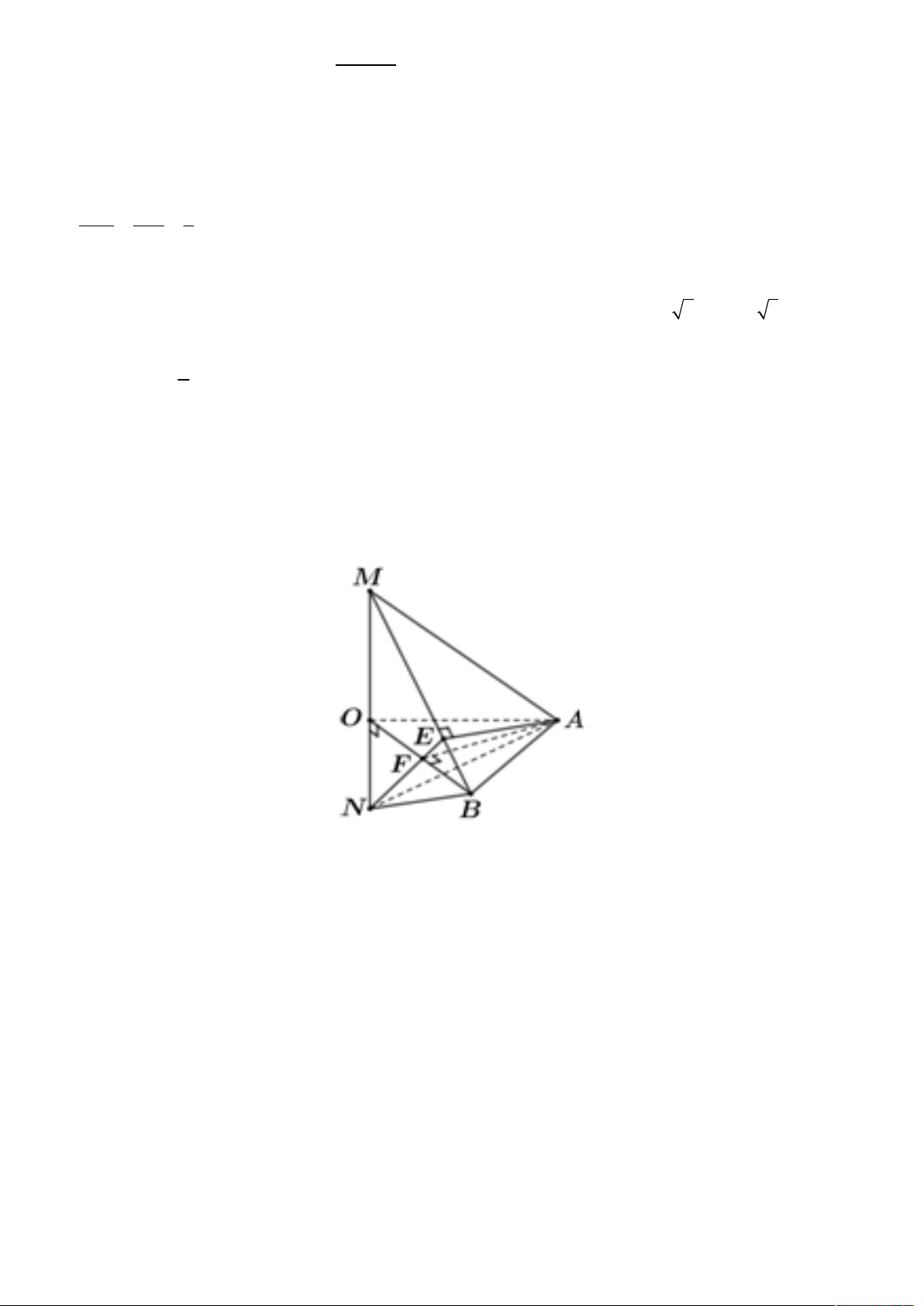
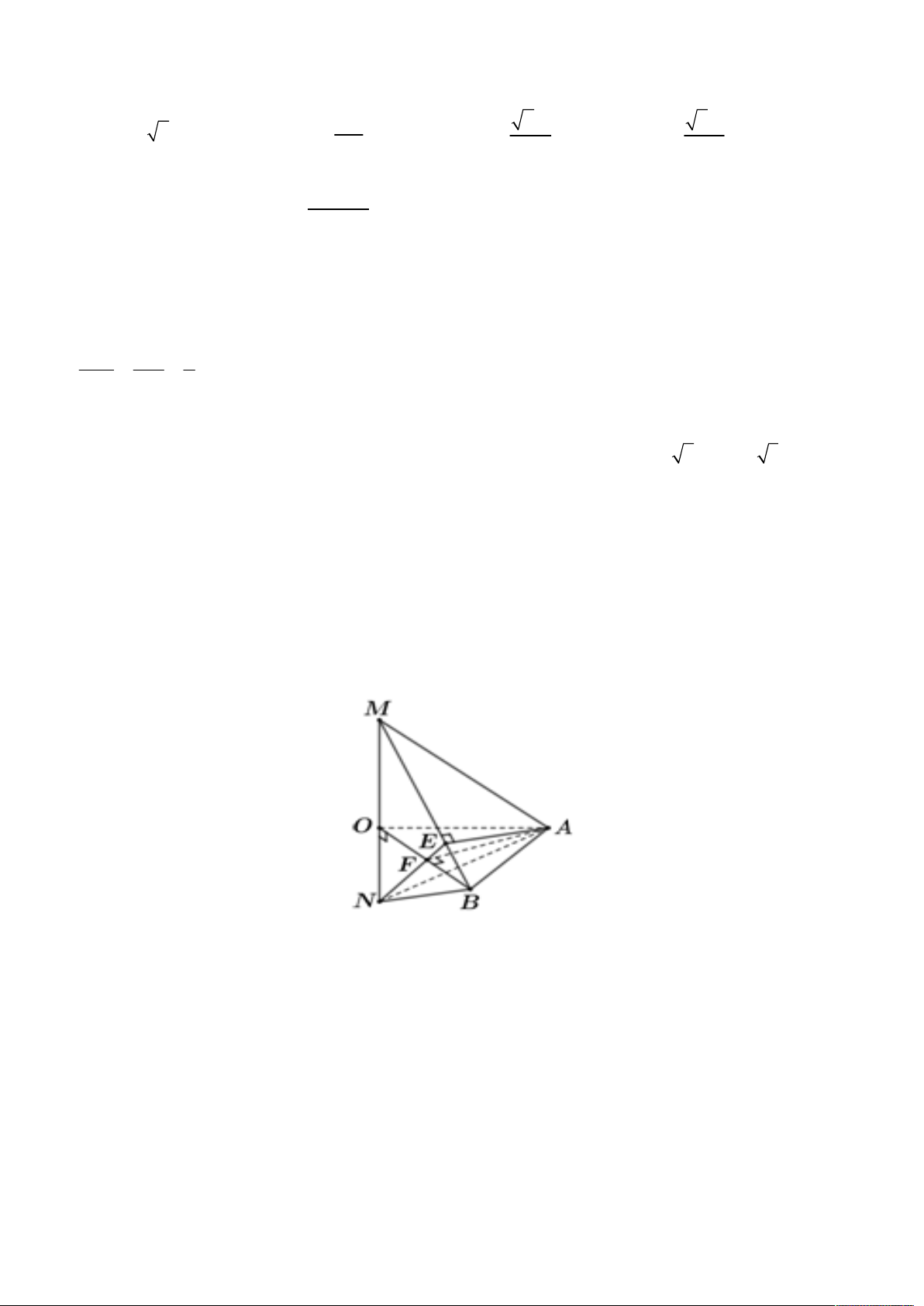
ĐÁP ÁN CHI TIẾT CÂU 19-20 MÃ ĐỀ 135
(Các câu 19,20 các mã đề còn lại giải tương tự) Câu 19: Lời giải A' B' D' M C' H A B K I D C
Từ B kẻ BI AC BI   AAC C
  . Từ I kẻ IH AA   AAC C
   AAB B     ,  B I H . . AB BC
Theo giải thiết ta có AC  3  BI   2 . AC BI BI 4 2
Xét tam giác vuông BIH có  tan BHI   IH   IH  . IH  tan BHI 3 2 AB
Xét tam giác vuông ABC có 2
AI.AC AB AI   2 . AC
Gọi M là trung điểm cả AA , do tam giác AA C
cân tại C nên CM AA  CM // IH . AI AH 2 AH 2 AH 1 Do      
.Trong tam giác vuông AHI kẻ đường cao HK ta có AC AM 3 AM 3 AA 3 4 2 4 2 HK
 chiều cao của lăng trụ ABC . D AB CD
  là h  3HK  . 9 3 4 2
Vậy thể tích khối lăng trụ ABC . D AB CD   là V  . AB . AD h  6 3  8 .
ABCD. AB CD   3 Câu 20: Lời giải. a
Do tam giác OAB đều cạnh ,
a suy ra F là trung điểm OB OF  . 2 AF OB Ta có 
AF  MOB  AF MB.  AF MO 
Lại có MB AE nên suy ra MB  AEF   MB EF. 2 OB ON OB.OF a Suy ra OBM ∽ ONF nên   ON   . OM OF OM 2x 2 2 3 1 a 3  a    a 6 Ta có VVVS        OM ON x . ABMN ABOM ABON   3 OAB 12  2x  12 2 a a 2
Đẳng thức xảy ra khi và chỉ khi x   x  . 2x 2
Câu 17: Cho lăng trụ đứng ABC.A ' B 'C ' có đáy ABC là tam giác vuông cân tại A và BC  8 2 . Mặt phẳng
A' BC hợp với mặt đáy  ABC  một góc  thỏa mãn tan  2. Thể tích khối lăng trụ ABC.A' B 'C ' bằng: 256 A. 256. B. 512. C. . D.128. 3
Câu 18: Cho lăng trụ tam giác ABC. 
A BC có đáy ABC là tam giác vuông cân tại A , cạnh AC  2 2 . Biết
AC tạo với mặt phẳng  ABC  một góc 60 và AC  4 . Tính thể tích V của khối đa diện ABCBC . 8 16 8 3 16 3 A. V  B. V  C. V  D. V  3 3 3 3
Câu 19: Cho khối chóp S.ABCD có thể tích là V . Gọi G là trọng tâm tam giác SAB , V ' là thể tích khối đa
diện GABCD . Khẳng định nào sau đây đúng? A. V  4V '. B. V  3V '.
C. V  2V '. D. 2V  3V '.
Câu 20: Cho khối chóp S.ABCD có thể tích bằng 3
a . Mặt bên SAB là tam giác đều cạnh a và đáy ABCD là
hình bình hành. Tính theo a khoảng cách giữa SA và CD . 2a a A. 2 3a . B. a 3 . C. . D. . 3 2
Câu 21: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh bằng 2a . Tam giác SAD cân tại S và 4
mặt bên SAD vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng 3
a . Tính khoảng cách 3
h từ B đến mặt phẳng  SCD  2 4 8 3 A. h a B. h a C. h a D. h a 3 3 3 4
Câu 22: Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M , N lần lượt là trung điểm các cạnh AD, BD sao cho DM DN 1  
. Lấy điểm bất kỳ P trên cạnh AB (khác ,
A B ). Thể tích khối tứ diện PMNC bằng: DA DB 4 81 2 27 2 27 2 81 2 A. . B. . C. . D. . 64 32 64 32
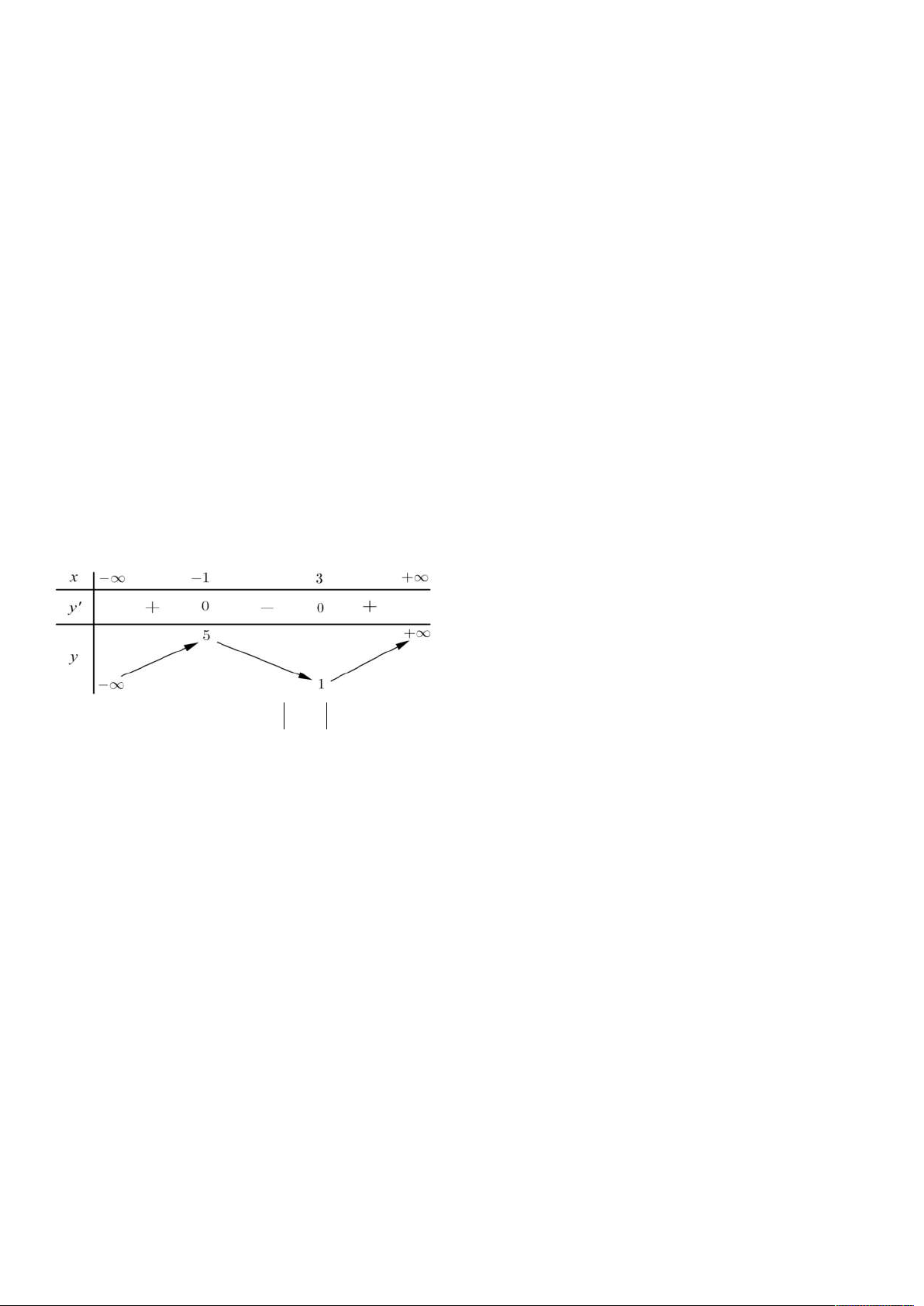
Câu 8: Cho hàm số y f (x) có bảng biến như hình vẽ bên
Số điểm cực trị của hàm số y f x bằng: A. 5. B. 2. C. 3. D. 4
Câu 15: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SC tạo với mặt phẳng SAB một góc 0
30 . Tính thể tích khối chóp S.ABCD 3 2a 3 2a 3 6a A. 3 2a B. C. D. 3 3 3
Câu 20: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a , cạnh bên bằng SA vuông góc với đáy
, SA a . Tính khoảng cách từ A đến mặt phẳng  SBC  ? a 3 a 2 a 6 a 6 A. d  . B. d  . C. d  . D. d  . 2 2 2 3
Câu 21: Cho hình chóp S.ABCD có SA   ABCD , ABCD là hình chữ nhật. SA AD  2a . Góc giữa
SBC  và mặt đáy  ABCD là 60 . Gọi G là trọng tâm tam giác SBC . Tính thể tích khối chóp S.AGD là 3 32a 3 3 8a 3 3 4a 3 3 16a A. . B. . C. . D. . 27 27 9 9 3
Câu 22: Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M , N lần lượt là trung điểm các cạnh AD, BD sao cho DM DN 1 
 . Lấy điểm bất kỳ P trên cạnh AB (khác ,
A B ). Thể tích khối tứ diện PMNC bằng: DA DB 3 2 3 2 2 A. . B. . C. 3 2. D. . 2 2 4
Câu 23: Cho lăng trụ tam giác ABC.AB C
  có đáy là tam giác đều cạnh a . Độ dài cạnh bên bằng 4a . Mặt  phẳng  BCC B
  vuông góc với đáy và B B
C  30. Thể tích khối chóp . A CC B   là: 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 2 12 18 6
Câu 24: Cho lăng trụ ABC . D AB CD
  có đáy ABCD là hình chữ nhật với AB  6 , AD  3 , AC  3 và
mặt phẳng  AAC C
  vuông góc với mặt đáy. Biết hai mặt phẳng  AAC C
  ,  AAB B
  tạo với nhau góc  3 thỏa mãn tan 
. Thể tích khối lăng trụ ABC . D AB CD   bằng? 4 A. V  10 . B. V  12 . C. V  8 . D. V  6 .
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với đáy, mặt bên  SCD  hợp 3 a 3
với đáy một góc bằng 60 , M là trung điểm của BC . Biết thể tích khối chóp S.ABCD bằng . Khoảng 3
cách từ M đến mặt phẳng  SCD  bằng: a 3 a 3 a 3 A. . B. . C. . D. a 3 . 6 4 2
Câu 24: Cho lăng trụ ABC.A BC
  có đáy ABC là tam giác vuông tại A và góc  0
ABC  30 . Gọi M là trung
điểm của AB, tam giác MA C
 đều cạnh a và nằm trong mặt phẳng vuông góc với đáy ABC. Thể tích khối lăng trụ đã cho bằng 3 a 3 2a 3 3a 3 5a A. . B. . C. . D. . 7 7 7 7
Câu 6: Tổng diện tích tất cả các mặt của hình bát diện đều cạnh bằng a là A. 2 4a . B. 2 2a 3 . C. 2 4a 3 . D. 2 a 3 .
LỜI GIẢI CHI TIẾT Câu 1.
Khối chóp có diện tích đáy là B, chiều cao bằng h . Thể tích V khối chóp là: 1 1 1 A. B . h B. B . h C. B . h D. B . h 3 2 6 Lời giải Chọn A 1
Thể tích V của khối chóp có diện tích đáy là B , chiều cao bằng h là: V  . Bh 3 Câu 2.
Hình nào dưới đây không phải là hình đa diện? A. . B. C. D. Lời giải Chọn C
Giả sử ta đặt tên cho các cạnh như sau: A D C B E
Khi đó BC là cạnh chung của 3 tam giác ABC, BCD, BCE.
Như vậy không thỏa mãn định nghĩa của khối đa diện. Câu 3.
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a , SA   ABCD và
SA a 6 . Thể tích của khối chóp S.ABCD bằng 3 a 6 3 a 6 3 a 6 A. . B. 3 a 6 . C. . D. . 6 3 2 Lời giải Chọn C Trang 3/15 - WordToan
+ Diện tích hình vuông ABCD có cạnh bằng a là 2 Sa . ABCD
+ SA   ABCD  SA là chiều cao hình chóp, SA a 6
+ Thể tích khối chóp S.ABCD 3 1 1 a 6 2 V S
.SA  .a .a 6  . 3 ABCD 3 3 Câu 4.
Cho khối lăng trụ đứng có cạnh bên bằng 5 , đáy là hình vuông có cạnh bằng 4 . Tính thể tích khối lăng trụ. A. 100 . B. 20 . C. 64 . D. 80 . Lời giải Chọn D
Thể tích khối lăng trụ là 2 V  . B h  4 .5  80 . Câu 5. Cho khối chóp .
S ABC , trên ba cạnh SA, SB, SC lần lượt lấy ba điểm A , B , C sao cho 1 1 1 SA  SA , S
B SB , SC 
SC . Gọi V và V  lần lượt là thể tích của các khối chóp 2 3 4 V .
S ABC và S.  A B C . Khi đó tỉ số là: V 1 1 1 A. 24 B. . C. . D. . 24 12 8 Lời giải Chọn B
Trang 4/15 – Diễn đàn giáo viên Toán S C' A' B' A C B V
SASBSC 1 1 1 1  . .  . .  . V SA SB SC 2 3 4 24 Câu 6.
Cho khối chóp OABC có OA , OB , OC đôi một vuông góc tại O và OA  2 , OB  3 ,
OC  6 . Thể tích khối chóp bằng A. 12 . B. 6 . C. 24 . D. 36 . Lời giải Chọn B A O C B 1 1 VO . A . OB OC  .2.3.6  6 . OABC 6 6 Câu 7.
Cho hình chóp S.ABC có SA vuông góc với đáy, tam giác ABC vuông tại ,
A SA  4 AB  3, BC  5 . Tính thể tích khối chóp S.ABC A. 8 . B. 16 . C. 48 . D. 24 . Lời giải Chọn A
ABC vuông tại A 2 2  AC BC AB  25  9  4 . 1 1 1 1
Thể tích khối chóp là V  .S .SA  . .A . B AC.SA  .3.4.4  8 . 3 ABC 3 2 6 Câu 8.
Cho hình chóp đều S.ABCD có chiều cao bẳng a 2 và độ dài cạnh bên bẳng a 6 . Thể tích
khối chóp S.ABCD . 3 10a 2 3 8a 3 3 10a 3 3 8a 2 A. . B. . C. . D. . 3 3 3 3 Lời giải Trang 5/15 - WordToan Chọn D S D C O A B
Gọi O AC BD SO   ABCD . SAO vuông tại 2 2 2 2 O AO SA SO
6a  2a  2a AC  4a . 3 1 1 1 1 8a 2 Thể tích khối chóp là 2 2 V  .S
.SO  . .AC .SO  .16a .a 2  . 3 ABCD 3 2 6 3 Câu 9.
Cho hình hộp chữ nhật ABC . D AB CD
  có AB  2 cm, AD  3 cm, AA  7 cm. Tính thể
tích khối hộp ABC . D AB CD   . A. 12 3 cm . B. 42 3 cm . C. 24 3 cm . D. 36 3 cm . Lời giải Chọn B Ta có VA . B A . D AA  42 3 cm . ABCD.A BCD  
Câu 10. Cho khối lăng trụ đứng ABC.AB C
  có CC  2a , đáy ABC là tam giác vuông cân tại B và
AC a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a A. 3 V a . B. V  . C. 3 V  2a . D. V  . 2 3 Lời giải Chọn A
Trang 6/15 – Diễn đàn giáo viên Toán AC
Tam giác ABC vuông cân tại B AB   a . 2 1 Khi đó 2 V  .AB .AA 3  a .
ABC. AB C   2 Vậy 3 Va . ABC. A BC  
Câu 11. Cho khối lăng trụ tam giác ABC.AB C
  có thể tích bằng 1. Tính thể tích V của khối chóp . A AB C   ? 1 1 1 A. V  3 . B. V  . C. V  . D. V  . 4 3 2 Lời giải Chọn C
Chiều cao h của khối lăng trụ ABC.AB C
  chính bằng chiều cao của khối chóp . A AB C   . 1 Ta có: V  . h S  1  S  . ABC. A BC   ABC ABC h 1 1
Thể tích V của khối chóp . A AB C   là: V  . h S  .
ABC. AB C   3 ABC 3 A' C ' B' A C B Trang 7/15 - WordToan
Câu 12. Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và thể tích bằng 3
a . Tính chiều cao h
của khối chóp S.ABC ? 3a 3a 3a A. h  . B. h  . C. h  . D. h  3a . 6 2 3 Lời giải Chọn D 3
Diện tích tam giác ABC là: S  2a2 2 .  a 3 . 4 1 3.V Ta có: S . V  . ABC h Sh   a 3 . S .ABC 3 ABC S ABC
Câu 13. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a; SA vuông góc với mặt đáy; góc giữa
SC và mặt đáy của hình chóp bằng 0
60 . Thể tích khối chóp S.ABCD là 3 a 6 3 a 3 3 a 2 3 a A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn A
Ta có SA   ABCD gt   AC là hình chiếu của SC lên mặt phẳng  ABCD .
Khi đó SC ABCD  SC AC   0 ; ;  SCA  60 . Ta có 2 2 2 2 2 2
AC AB BC a a  2a AC a 2 . Xét SAC vuông tại A. SA 0 tan SCA
SA AC. tan 60  a 2. 3  a 6 . AC 3 1 1 a 6 2 VS .SA a .a 6  . S . ABCD 3 ABCD 3 3
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật; S
AB đều cạnh a nằm trong mặt
phẳng vuông góc với  ABCD . Biết SC tạo với  ABCD một góc bằng 0 30 . Tính thể tích
V của khối chóp S.ABCD . 3 a 6 3 a 6 3 a 3 3 a 3 A. V  . B. V  . C. V  . D. V  . 3 6 3 6 Lời giải Chọn B
Trang 8/15 – Diễn đàn giáo viên Toán
Gọi H là trung điểm của AB . Vì SA
B đều nên SH AB . Mà SA
B nằm trong mặt phẳng vuông góc với  ABCD và
SAB   ABCD  AB . Khi đó SH   ABCD .
Vì SH   ABCD  SH HC HC là hình chiếu của SC lên mặt phẳng  ABCD .
SC ABCD  SC HC   0 ; ;  SCH  30 . SH Xét S
HC vuông tại H ta có:  tan SCH    1 . HC a 3
Mà SH là đường cao trong tam giác đều cạnh a SH  . 2 a 3 SH 3a Từ   2 1  HC     . 1 tan SCH 2 3 Xét C
BH vuông tại B . 2 2 9a a 2 2 2 2 2 2
CH CB BH   CB
CB  2a CB a 2 . 4 4 2 SA . B BC  . a a 2  a 2 . ABCD 3 1 1 a 3 a 6 Vậy 2 V S .SH a 2.  . 3 ABCD 3 2 6 
Câu 15. Cho hình hộp đứng ABC . D AB CD
  có đáy ABCD là hình thoi cạnh a và BAD  60 , AC '
hợp với đáy  ABCD một góc 60 . Thể tích khối hộp là 3 a 3 3 3a 3 3 a 3 3 3a 3 A. V  . B. V  . C. V  . D. V  . 2 4 4 2 Lời giải Chọn D Trang 9/15 - WordToan
Gọi O là giao điểm của AC và BD , khi đó O là trung điểm của hai cạnh này.
Vì AC là hình chiếu của AC xuống mặt phẳng  ABCD nên ta có:
AC  ABCD   AC AC   0 , ',  CAC  60   1 Ta có: VS .CC  AC.B . D CC
ABCD. AB CD   ABCD 2 
Tam giác ABD cân tại A (vì AB AD a ) có BAD  60 nên là tam giác đều a 3
Suy ra: BD a và OA
. Mà AC  2OA AC a 3 2
Vì hình hộp này là hình hộp đứng nên các cạnh bên vuông góc với đáy, nghĩa là
CC   ABCD  CC  AC A
CC vuông tại C  Khi đó: 0
CC  AC.tan CAC  a 3. tan 60  3a 1 1 3a 3 Vậy VAC.B . D CC  .a 3. .3 a a  (đvtt) ABCD. A BCD   2 2 2
Câu 16. Cho lăng trụ đứng tam giác AB . C A BC
  có đáy ABC là tam giác vuông cân tại B với
BA BC a 2 . Gọi M là trung điểm A'C ', biết BM hợp với mặt phẳng  ABC  một góc 0
30 . Thể tích khối lăng trụ AB . C AB C   là: 3 a 3 3 2a 3 3 a 3 3 2a 3 A. . B. . C. . D. . 3 3 9 9 Lời giải Chọn A
Trang 10/15 – Diễn đàn giáo viên Toán
Gọi H AC sao cho HA HC MH   ABC
  BM ABC  MB BH  0 , ,    30 . do B
AC vuông cân tại B 2 0  S
a ; BH BAsin 45  . a ABC a 3
h MH BH tan  (do H
BM vuông cân tại H). 3 3 a 3  VhS  .
ABC .A' B 'C ' ABC 3
Câu 17. (Tự luận) Cho khối lăng trụ tam giác ABC.AB C
  . Tính tỉ số thể tích giữa khối đa diện A BCB
C và khối lăng trụ ABC.A BC   . Lời giải 1 Ta gọi V
V khi đó ta có VVVV . ABC.A BC   A .  ABC C .  AB B
C. ABC 3 2 V 2 2 Ta có VVV nên VV . Từ đó suy ra A BCBC   V :V  . AB CBCC .  A BBC .  ABC A BCBC  3 V 3 3 ABC. A BC  
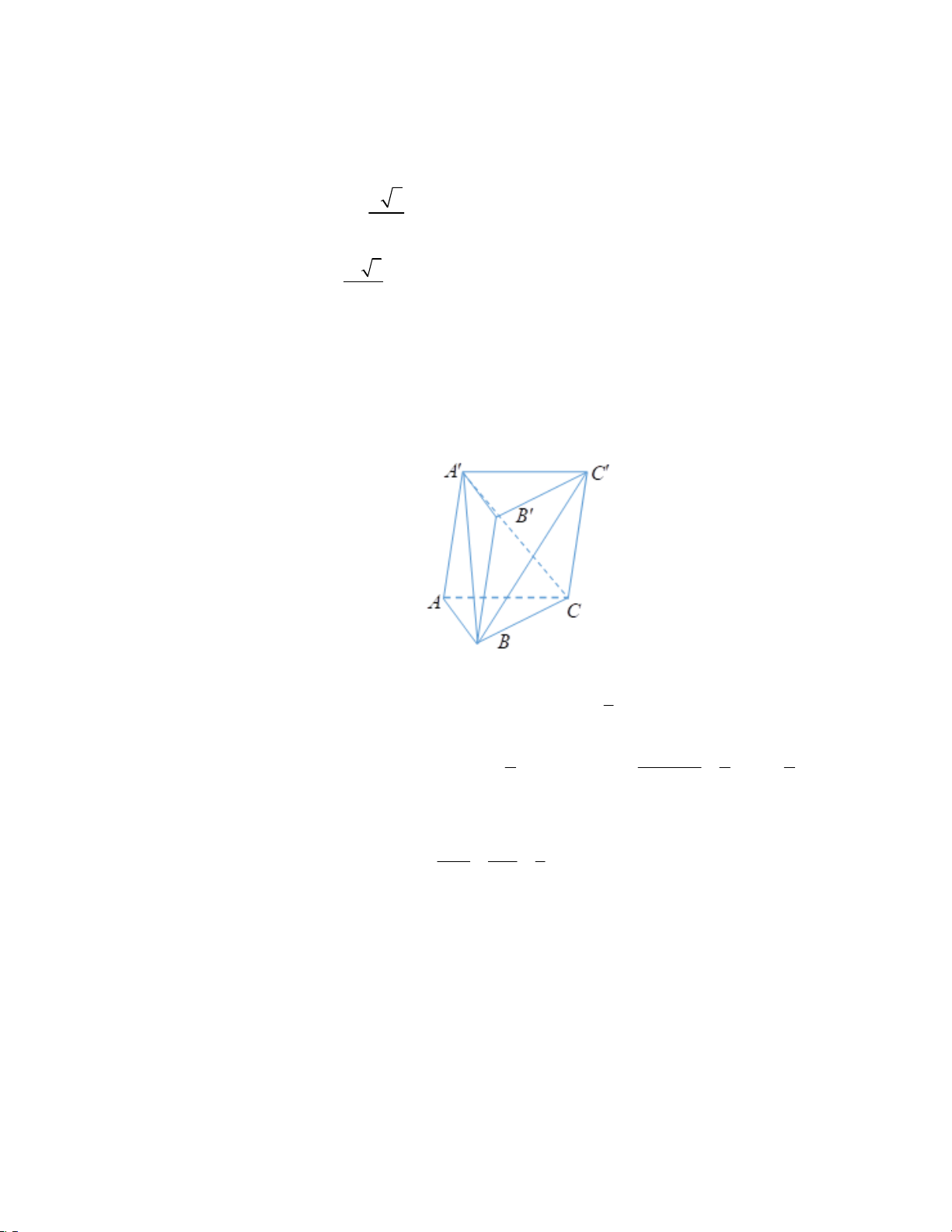
Câu 18. (Tự luận) Tự luận)Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M , N lần lượt là các điểm DM DN 1
thuộc các cạnh AD, BD sao cho 
 . Lấy điểm bất kỳ P trên cạnh AB ( khác DA DB 3
A , B ). Tính thể tích khối tứ diện PMNC. Lời giải Trang 11/15 - WordToan
Gọi I là tâm đường tròn ngoại tiếp tam giác ABD , E là trung điểm của AB . 2 2 Ta có: 0 DI DE B . D sin 60  3. 3 3
Vì ABCD là tứ diện đều nên 2 2
CI  ( ABD)  CI ID CI CD ID  6. 1 1 9 2 0 VCI.SCI.A . B A . D sin 60  . ABCD 3 ABD 6 4 DM DN 1 1 2 Tam giác ABD có 
 .  MN / / AB MN
AB và d (P, MN ) 
d (D, AB). DA DB 3 3 3 1 1 1 2 2 Do đó, S
MN.d (P, MN )  . .A . B
d (D, AB)  S . PMN 2 2 3 3 9 ABD 1 1 2 2 2 Vậy VCI.SCI. SV  . PMNC 3 PMN 3 9 ABD 9 ABCD 2
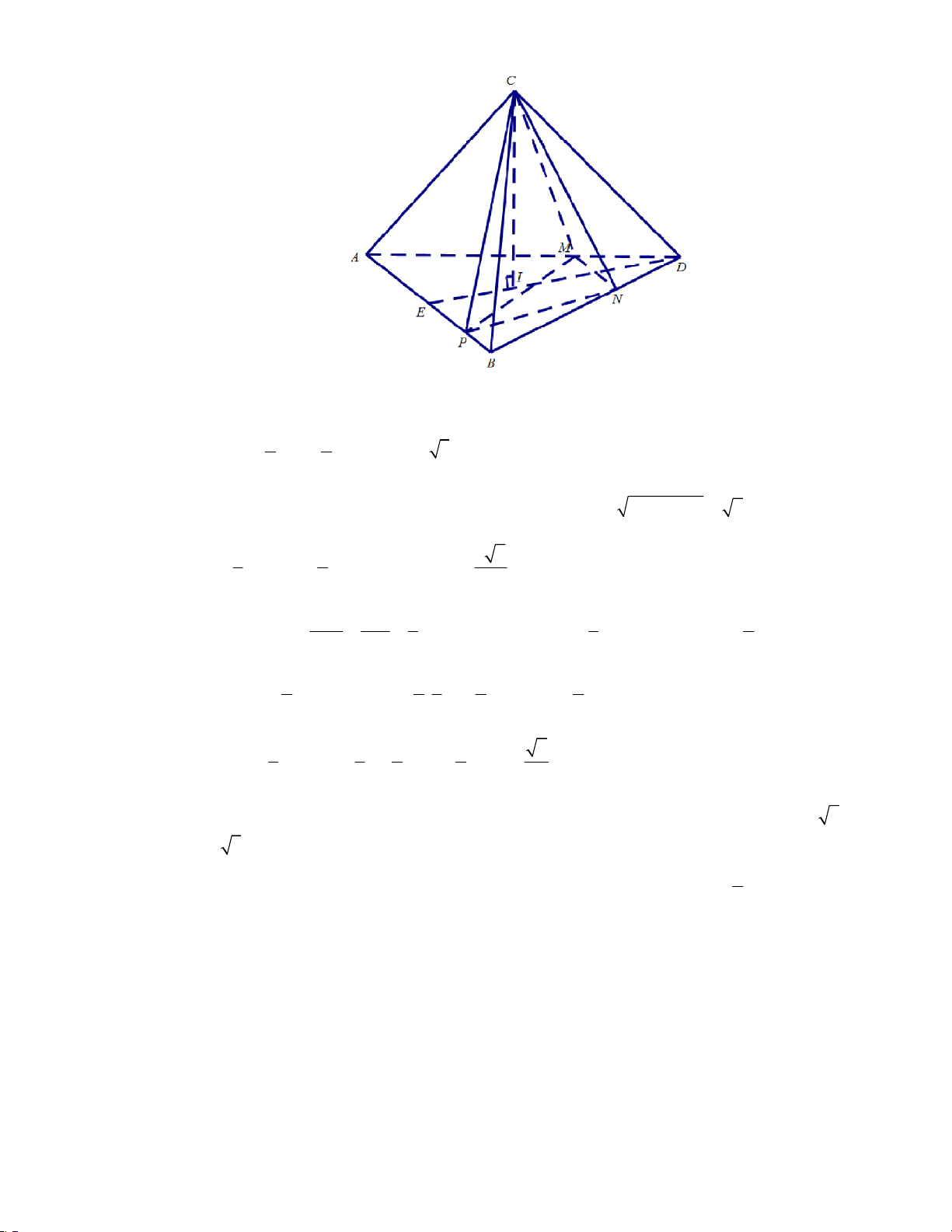
Câu 19. (Tự luận) Cho lăng trụ ABC . D AB CD
  có đáy ABCD là hình chữ nhật với AB  6 ,
AD  3 , AC  3 và mặt phẳng ( AA CC
 ) vuông góc với mặt phẳng đáy (ABCD) . Biết rằng 3
hai mặt phẳng ( AAC C  )  
và ( AA B B) tạo với nhau góc  thỏa mãn tan  . Tính thể tích 4 khối lăng trụ. Lời giải
Trang 12/15 – Diễn đàn giáo viên Toán
+ Ta có đáy ABCD là hình chữ nhật với AB  6 , AD  3 suy ra, diện tích đáy lăng trụ là: SA .
B AD  6. 3  3 2 . ABCD
+ Do mặt phẳng ( AAC C
 ) vuông góc với mặt phẳng đáy (ABCD) và ( ACC A  )
  (ABCD)  AC d ( A ; AC)  h là đường cao của hình bình hành và cũng là
đường cao của lăng trụ.Tính h  ?
Gọi H là hình chiếu của B lên ( AA CC
 ) thì điểm H nằm trên cạnh AC và
BH  ( ACC ' A')  BH AA ' (1) .
Ta có: ABCD là hình chữ nhật 2 2  AC
AB BC  3 ; B . A BC 6. 3
Trong tam giác ABC vuông tại B có BH    2 ; AC 3
Trong tam giác HBC vuông tại H có 2 2 HC
BC BH  1 ; AH AC CH  2 . Trong ( AAC C
 ) , kẻ HK AA',(K AA') (2) .
Từ (1) và (2)  AA'  (BHK )  AA'  BK . ( ABB A  )   ( ACC A  )   AA  Ta có,  
BK  ( ABB A  )
 , BK AA  (( ABB A  );  ( ACC A  )
 )  BKH   . HK  (ACC A  )
 , HK AA  BH 2 B
KH vuông tại H có  3 2 4 2 tan BKH     KH  ; 2 2 AK AH AK  . KH 4 KH 3 3
Xét tam giác ACA' cân tại C (do AC A'C  3 ). Kẻ CM AA thì M là trung điểm AA ' và CM AC
CM / /HK ACM  3 3 AHK     CM HK  2 2 . HK AH 2 2
Xét tam giác vuông CMA' (có CM AA ) 2 2 2 2  A M   A C
CM  3  (2 2)  1
AA  2AM  2 .
Ta có, diện tích hình bình hành ACC A   CM .AA 4 2 là: S
CM .AA  d ( A ;  AC).AC  . h AC h   . ACC A   AC 3 4 2 Vậy, V  . h S  .3 2  8 . ABCD.A BCD   ACC A   3
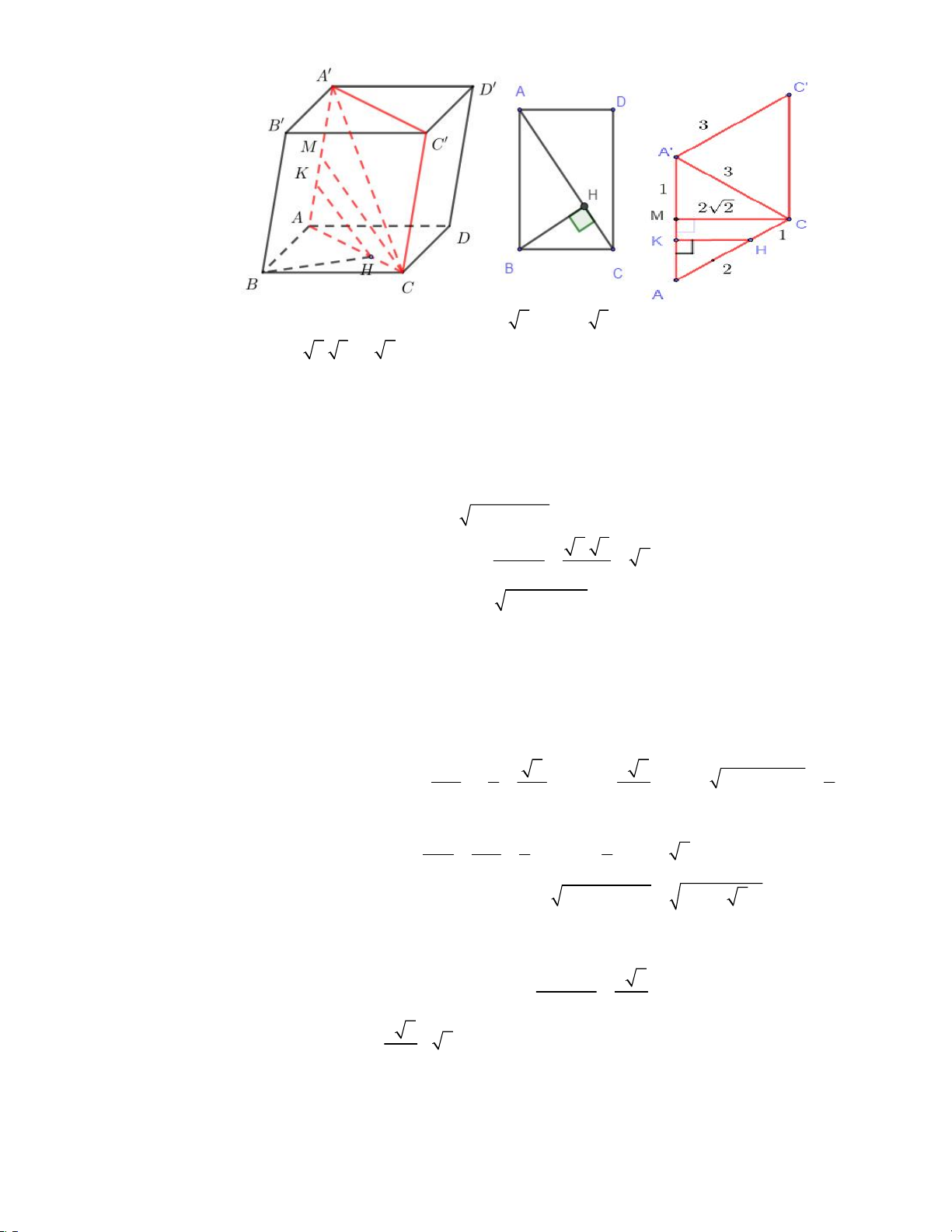
Câu 20. (Tự luận) Cho tam giác OAB đều cạnh a . Trên đường thẳng d qua O và vuông góc với mặt Trang 13/15 - WordToan
phẳng OAB lấy điểm M sao cho OM x . Gọi E, F lần lượt là hình chiếu vuông góc của
A trên MB và OB . Gọi N là giao điểm của EF và d (hình vẽ minh họa bên dưới). Tìm giá
trị của x theo a để thể tích khối tứ diện ABMN có giá trị nhỏ nhất. Lời giải Ta có:
AF OB mà tam giác ABC đều nên F là trung điểm cạnh OB . Mà AF OM .
Do đó, AF   MNB 1 Vậy, V  .S .AF . MNAB 3 MNB Mặt khác, ta có: a 3 AF  ; 2 1 1 SB . O MN  . a MN . MNB 2 2 2 1 a 3 Nên V  .S .AF  .MN . MNAB 3 MNB 12
Vậy, thể tích khối tứ diện ABMN có giá trị nhỏ nhất khi và chỉ khi độ dài MN nhỏ nhất. * Tính MN
Trang 14/15 – Diễn đàn giáo viên Toán Cách 1:
Ta có: AF  MNB  AF MB
Mà AE MB nên MB FE . Xét MEB , ta có: M . O FB M .
O FB FE.MB FE  . MB 2 2 MO .FB Mặt khác: 2 2 2 2 2 2
ME MF FE ME MO OF  . 2 MB MN ME ME
Ta lại có: MEN  MBO g g     MN  .MB . MB MO MO 2 2 2 2 ME MBMO .FB  2 2 2 2  MN  .MB  . MO OF  . 2 2  2  MO MO MB   2 2 2 OF a 1 a 2 2 2 2 2 2
MN MB
.MB FB x a  .  2 2 x a  . 2 2  MO 4 x 4 2 4 2 2 a 1  a a 2 2 2
MN x a  .  x   MN x  . 2   4 x 2x 2x   * Cách 2:
Ta có: AF  MNB  AF MB
Mà AE MB nên MB FE MB NE .
Mặt khác, ta có: OB MN .
Do đó, F là trực tâm MNB . NO OF MN MO OF
Ta có: NFO  MBO g g      . OB MO OB MO 2 MN x a a    MN x  . a 2x 2x 2 a
Áp dụng bất đẳng thức Cauchy cho 2 số x và , ta có: 2x 2 a x   a 2 . 2x 2 a 2 a a 2
Do đó, MN x
đạt giá trị nhỏ nhất là a 2 khi và chỉ khi x   x  . 2x 2x 2 a 2
Vậy, giá trị của x theo a là x  . 2 Trang 15/15 - WordToan
Document Outline

  • 5456
  • 1568179798_WT13-H12-KIỂM TRA 45 PHÚT-KHỐI ĐA DIỆN-H12-THỊ XÃ QUẢNG TRỊ-NĂM 2019