Đề kiểm tra 1 tiết Giải tích 12 chương 1 năm 2018 – 2019 trường THPT Tân Hiệp – Kiên Giang

Đề kiểm tra 1 tiết Giải tích 12 chương 1 năm 2018 – 2019 trường THPT Tân Hiệp – Kiên Giang mã đề 101 gồm 4 trang với 25 câu hỏi và bài tập trắc nghiệm khách quan về chủ đề hàm số và đồ thị, học sinh có 45 phút để làm bài, đề kiểm tra có đáp án.

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

21 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Trang 1/4
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT TÂN HIỆP
ĐỀ KIỂM TRA 1 TIẾT – NĂM HỌC 2018 - 2019
MÔN TOÁN LỚP 12
Thời gian làm bài : 45 Phút; (Đề có 25 câu)
(Đề có 5 trang)
Họ tên : ............................................................... Lớp : ...................
Câu 1: Giá trị nhỏ nhất của hàm số
1
1
yx
x
= −
+
trên đoạn
[ ]
1; 3
là
A.
1
2
B. 3 C.
7
4
D.
Câu 2: Tìm tất cả các giá trị thực của tham số
m
để đồ thị của hàm số
42
21y x mx
=−+
có
ba điểm cực trị là ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng
1
.
A.
15
2
m
−+
=
B.
1
m
=
C.
15
1;
2
mm
−−
= =
D.
15
1;
2
mm
−+
= =
Câu 3: Cho hàm số
()y fx=
có đồ thị như hình vẽ.
Tìm m để phương trình
( )
−=0fx m
có 9 nghiệm
phân biệt.
A.
1
m
=
. B.
13m<<
.
C.
01m
<<
. D.
3m =
.
Câu 4: Tiếp tuyến của đồ thị hàm số
32
32yx x
=−+
tại điểm
( )
1; 2M −−
có phương trình là:
A.
92
yx= −
B.
24 2yx= −
C.
24 22yx= +
D.
97yx= +
Câu 5: Cho hàm số
2
cos
()
cos 1
xm
y fx
x
+
= =
+
. Tìm tất cả giá trị của m để hàm số
( )
fx
đồng
biến trên khoảng
0;
2
π



.
A.
9m
≤
B.
3m ≥
C.
3m >
D.
9m <
Câu 6: Hàm số y = f(x) liên tục trên [-1;3] có bảng biến thiên:
Giá trị nhỏ nhất của hàm số trên đoạn [-1;3] là
A. 2 B. 1 C. -2. D. 0
Câu 7: Đồ thị hàm số
32
22
x
y
x
+
=
−
có
A. Tiệm cận đứng
2x = −
. B. Tiệm cận đứng
2x =
.
C. Tiệm cận ngang y = 1. D. Tiệm cận ngang
3
2
y =
.
Câu 8: Hàm số
3
3xyx
= −
nghịch biến trên khoảng nào dưới đây?
A.
( )
1; 3 .−
B.
( )
1; .− +∞
C.
( )
;1 .−∞
D.
( )
1;1 .−
Câu 9: Tổng số tất cả các đường tiệm cận đứng và ngang của đồ thị hai hàm số
Mã đề 101
Trang 2/4
2
2
21 3
56
−− + +
=
−+
x xx
y
xx
và
2
2
34
1
xx
y
x
−−
=
−
là :
A. 2. B. 4. C. 5. D. 3.
Câu 10: Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên như hình sau.
x
y'
y
−∞
1−
0
1
+∞
0
0
0
4
+
+
−
−
+∞
5
4
+∞
Khẳng định nào sau đây là khẳng định đúng ?.
A. Hàm số đồng biến trong khoảng
( )
1; +∞
.
B. Hàm số nghịch biến trên khoảng
(
)
1; 0−
.
C. Hàm số đồng biến trong các khoảng
(
)
;1−∞
và
( )
1; 0−
.
D. Hàm số nghịch biến trên khoảng
( )
1; +∞
.
Câu 11: Đường cong hình bên (H.2) là đồ thị của một trong
bốn hàm số dưới đây. Hàm số đó là hàm số nào?
A.
32
31yx x=−−
. B.
32
33yx x=−+
.
C.
32
31yx x
=−+ +
. D.
32
32
yx x=++
Câu 12: Đường cong sau (H.b) là đồ thị của hàm
số nào dưới đây?
A.
42
51yx x=−+ −
.
B.
42
231
yx x
=−−
.
C.
42
21
yx x=+−
.
D.
42
231yx x=−+
.
Câu 13: Số điểm cực tiểu của hàm số
42
2x 5yx=−+
là
A. 3. B. 1. C. 2. D. 0.
Câu 14: Tổng số điểm cực trị của 2 hàm số
3
51yx x
=−+
và
42
1y xx=−− +
là .
A. 2 B. 3 C. 5 D. 1
Câu 15: Đường cong trong hình vẽ bên là đồ thị của
một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi đó là hàm số
nào?
A.
22
1
x
y
x
−
=
−
. B.
21
1
x
y
x
−
=
+
.
C.
21
1
x
y
x
+
=
−
. D.
23
1
x
y
x
+
=
+
.
Câu 16: Cho hàm số
( )
y fx=
có bảng biến thiên
như sau:
Gọi
CĐ
y
,
CT
y
là giá trị cực đại
và giá trị cực tiểu của hàm số
đã cho. Tính
CĐ CT
yy+
.
Trang 3/4
A. 1 B. 2
C. 0 D. 3.
Câu 17: Tìm tất cả các giá trị của tham số m để đồ thị hàm số
3
2y x mx=−+
cắt trục hoành
tại 3 điểm phân biệt.
A.
3m >−
B.
3m
<−
C. Kết quả khác D.
3m >
Câu 18: Cho hàm số bậc ba:
32
y ax bx cx d= + ++
có bảng biến thiên như hình sau (H.6) .
Tính tổng
T abc=++
.
A.
9
8
−
. B.
3
8
. C.
7
8
. D.
11
8
−
.
Câu 19: Hàm số
( )
y fx=
có đồ thị là đường
cong trong hình vẽ bên.
Hàm
( )
y fx=
đạt cực tiểu tại điểm nào dưới đây?.
A. x = -2. B. x = 4.
C. x = 2. D. x = 0.
Câu 20: Hàm số nào trong các hàm số tương ứng ở
các phương án A, B, C, D có đồ thị là hình bên?
A.
1
1
x
y
x
−
=
+
.
B.
42
21
yx x=+−
.
C.
2
1
x
y
x
−
=
+
.
D.
1
1
x
y
x
+
=
−
.
Câu 21: Cho hàm số y = x
2
- 2x + 1. Tìm giá trị lớn nhất của hàm số đã cho trên [-2;3]
A. 9. B. 3. C. không tồn tại. D. 4.
Câu 22: Đường cong ở hình bên là đồ thị của một trong bốn
hàm số ở dưới đây. Hàm số đó là hàm số nào ?
A.
42
1yx x=−−
B.
42
2y xx
=−+ +
.
C.
42
2y xx=−−+
.
D.
42
22yx x=−+ −
.
Câu 23: Cho hàm số
2
3
1
x
y
x
+
=
+
. Mệnh đề nào dưới đây đúng?
A. Cực đại của hàm số bằng 2. B. Cực tiểu của hàm số bằng 1.
C. Cực đại của hàm số bằng -3. D. Cực đại của hàm số bằng -6.
Câu 24: Cho hàm số
1
1
x
y
x
+
=
−
. Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có tiệm cận đứng
1x = −
.
Trang 4/4
B. Đồ thị hàm số có tiệm cận ngang
1
y = −
.
C. Đồ thị hàm số có tiệm cận ngang
1
y =
.
D. Đồ thị hàm số có tiệm cận ngang
1x =
.
Câu 25: Cho hàm số y=f(x) xác định, liên tục trên
\ {0}R
và có bảng biến thiên :
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số nghịch biến trên khoảng
(
)
1; 0−
.
B. Hàm số đồng biến trong khoảng
( )
1; 0−
.
C. Hàm số đồng biến trong khoảng
( )
;1−∞
.
D. Hàm số đồng biến trên khoảng
( )
1; +∞
.
------ HẾT ------
1
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT TÂN HIỆP
KIỂM TRA 1 TIẾT MÔN TOÁN KHỐI 12 – NĂM HỌC
2018 - 2019
MÔN TOÁN LỚP 12
Thời gian làm bài : 45 Phút
Phần đáp án câu trắc nghiệm:
101
103
105
107
1
A
C
D
A
2
D
B
C
C
3
A
D
A
C
4
D
D
C
B
5
B
C
D
B
6
C
A
B
A
7
C
B
C
D
8
D
C
B
C
9
C
D
C
C
10
A
C
C
B
11
B
D
B
B
12
B
B
D
D
13
C
D
B
A
14
B
A
B
B
15
B
A
C
C
16
D
D
B
C
17
D
C
C
A
18
D
B
A
D
19
D
A
C
B
20
A
C
D
C
21
A
C
A
C
22
B
D
B
A
23
D
B
D
C
24
C
C
D
A
25
B
B
C
A
Tr
ang 1/16 - WordToan
SỞ
GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG THPT TÂN HIỆP-KIÊN GIANG
KIỂM-TRA-45 PHÚT-HK1
NĂM HỌC 2018 – 2019
Môn: Toán
Thời gian: 45 phút (Không kể thời gian phát đề)
Câu 1. Giá trị nhỏ nhất của hàm số
1
1
y x
x
trê
n đoạn
[1
;3]
là
A.
1
2
. B.
3
. C.
7
4
. D.
11
4
.
Câu 2. Tìm tất cả các giá trị thực của tham số
m
để đồ
thị hàm số
4 2
2 1y
x mx
có b
a điểm cực trị là
ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng
1
.
A.
1 5
2
m
. B.
1m
.
C.
1m
;
1 5
2
m
. D.
1m
;
1 5
2
m
.
Câu 3. Cho hàm số
y f
x
có
đồ thị như hình vẽ:
Tìm
m
để phương
trình
0f x
m
có
9
nghi
ệm phân biệt.
A.
1m
. B.
1 3m
. C.
0 1m
. D.
3m
.
Câu 4. Tiếp tuyến của đồ thị hàm số
3 2
3 2y
x x
tại điểm
1;
2M
có phương trình là
A.
9 2y x
. B.
24 2y x
. C.
24 22y x
. D.
9 7y x
.
Câu
5. Cho hàm số
2
cos
( )
cos 1
x m
y f x
x
. Tìm tất cả các giá trị của m để hàm số
f x
đồng biến
trên
khoảng
0;
2
.
A.
9m
B.
3m
C.
3m
. D.
9m
.
Câu
6. Hàm số
( )y
f x
liên tục trên
1;
3
có bảng biến thiên :
Tr
ang 2/16 – Diễn đàn giáo viên Toán
Giá
trị nhỏ nhất của hàm số trên đoạn
1;
3
là:
A. 2. B. 1. C. -2. D. 0
.
Câu 7. Đồ thị hàm số
3 2
2
2
x
y
x
có
A. Ti
ệm cận đứng
2x
. B. Tiệm
cận đứng
2x
. C
.
Tiệm cận ngang
1y
. D. Tiệm cận ngang
3
2
y
.
Câu 8. Hàm số
3
3y x
x nghịch biến trên khoảng nào dưới đây?
A.
1;
3
. B.
1;

. C.
;1
. D.
1;1
.
Câu
9. Tổng số các đường tiệm cận đứng và tiệm cận ngang của hai đồ thị hàm số
2
2
2x
1 3
5 6
x x
y
x x
và
2
2
3x 4
1
x
y
x
là
A. 2. B. 4. C. 5. D. 3.
Câu 10. Cho hàm số
y f
x
xác
định, liên tục trên
và c
ó bảng biến thiên như sau
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trong khoảng
1;
.
B. Hàm s
ố nghịch biến trong khoảng
1;0
.
C. Hàm
số đồng biến trong khoảng
;1
và
1;
0
.
D. Hàm số nghịch biến trong khoảng
1;
.
Câu
11. Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
Tr
ang 3/16 - WordToan
A.
3 2
3 1y x x
. B.
3 2
3 3y x x
. C.
3 2
3 1y x x
. D.
3 2
3 2y x x
.
Câu 12. Đường cong sau là đồ thị của hàm số nào dưới đây?
A.
4 2
5 1y
x x
. B.
4 2
2 3
1y x x
. C.
4 2
2 1y
x x
. D.
4 2
2 3
1y x x
.
Câu 13. Số điểm cực tiểu của hàm số
4 2
2 5y
x x
là
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 14. Tổng số điểm cực trị của hai hàm số
3
5 1y
x x
và
4 2
1y x
x
là
A.
2
. B.
3
. C.
5
. D.
1
.
Câu 15. Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào?
A.
2 2
.
1
x
y
x
B.
2 1
.
1
x
y
x
C.
2 1
.
1
x
y
x
D.
2 3
.
1
x
y
x
Câu
16. Cho hàm số
y f
x
có
bảng biến thiên như sau
Gọi ,
CD C
T
y y là giá trị cực đại và giá trị cực tiểu của hàm số đã cho. Tính .
CD
CT
y y
A.
1.
B.
2.
C.
0.
D.
3.
Câu 17. Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
3
2y x
mx
cắt trục hoành tại ba điểm
phân biệt.
A.
3m
. B.
3m
. C. Kết qu
ả khác. D.
3m
.
Câu
18. Cho hàm số bậc ba:
3 2
y ax
bx cx d
có bảng biến thiên như hình sau (H.6).
2
2
x
y '
y
0
0
3
0
Tran
g 4/16 – Diễn đàn giáo viên Toán
H.6
Tính tổng
T
a b c
.
A.
9
8
. B.
3
8
. C.
7
8
. D.
11
8
.
Câu 19
. Hàm số
y f x
có đồ
thị là đường cong trong hình vẽ bên. Hàm số
y f x
đạt cực
tiểu tại
điểm nào dưới đây.
A.
2x
. B.
4x
. C.
2x
. D.
0x
.
Câu 20
. Hàm số nào trong các hàm số tương ứng ở các phương án A, B, C, D có đồ thị là hình bên.
A.
1
1
x
y
x
. B.
4 2
2 1y x
x
.
C.
2
1
x
y
x
. D.
1
1
x
y
x
.
Câu 21. Cho hàm số
2
2 1y x
x
. Tì
m giá trị lớn nhất của hàm số đã cho trên
2;3
A.
9
. B.
3
. C. Không t
ồn tại. D.
4
.
Câu 22.
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
x
1
3
y
0
0
y
2
2
Tran
g 5/16 - WordToan
A.
4 2
1y x x
. B.
4 2
2y x x
. C.
4 2
2y x x
. D.
4 2
2 2y x x
.
Câu 23. Cho hàm số
2
3
1
x
y
x
. Mệnh
đề nào dưới đây đúng?
A. Cực đại của hàm số bằng 2. B. Cực tiểu của hàm số bằng 1.
C. Cực đại của hàm số bằng
3
. D. Cực đại của hàm số bằng
6
.
Câu 24. Cho hàm số
1
.
1
x
y
x
Khẳ
ng định nào sau đây đúng?
A. Đồ thị hàm số có tiệm cận đứng
1x
. B. Đồ thị hàm số có tiệm cận ngang
1y
.
C. Đồ thị hàm số có tiệm cận ngang
1y
. D. Đồ thị
hàm số có tiệm cận ngang
1x
.
Câu 25.
Cho hàm số
y f x
xác
định, liên tục trên
\ 0
và c
ó bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số nghịch biến trên khoảng
1;0
.
B. Hàm số
đồng biến trong khoảng
1;0
.
C. Hàm s
ố đồng biến trong khoảng
;1
.
D. Hàm s
ố đồng biến trong khoảng
1;
.
BẢNG ĐÁP Á
N
1.A 2.D 3.A 4.D 5.B 6.C 7.C 8.D 9.B 10.A
11.B 12.
B 13.C 14.B 15.B 16.D 17.D 18.D 21.A 22.B
23.D
24.C
25.B
LỜI GIẢI CHI
TIẾT
Câu 1. Giá trị nhỏ nhất của hàm số
1
1
y x
x
trên
đoạn
[1;
3]
là
A.
1
2
. B.
3
. C.
7
4
. D.
11
4
.
Lời giả
i
Chọn A
Tr
ang 6/16 – Diễn đàn giáo viên Toán
Ta
có:
2
1
1 0, 1
( 1)
y x
x
hàm số
1
1
y x
x
đồng
biến trên đoạn
[1;3]
.
Vậy,
[1
;3]
1 1
Min (1) 1
2 2
y y
.
Câu
2. Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
4 2
2 1y
x mx
có ba điểm cực trị là
ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng
1
.
A.
1 5
2
m
. B.
1m
.
C.
1m
;
1 5
2
m
. D.
1m
;
1 5
2
m
.
Lời
giải
Chọn D
+ Đ
ể hàm số có ba điểm cực trị
3 2
4 4
4 ( ) 0y x mx x x m
có ba nghiệm phân biệt
2
0x m
(*)
.
Khi đó, đồ thị hàm số có ba điểm cực trị
(0;1)A
,
2
( ;1
)B m m
,
2
( ;1
)C m m
.
+ Gọi
H
là trung
điểm
BC
, kh
i đó
2
(0;1 )H m
và
AH
là
đường cao của tam giác
AB
C
nê
n ta
có:
2 2
4
1 .
.
. 2 . . 4 .
2 4
AB AC BC
AH BC R AH AB AC R AH AB
R
(Vì
AB AC
)
2 4
4 4
2 4 2
2 4
0
2 ( )
4.1. ( ) 2 0 1
2
1 5
2
m
m m m
m m m m m m m
m m m
m
(**)
.
Từ
(*) và (**) suy ra:
1m
;
1 5
.
2
m
Câu
3. Cho hàm số
y f
x
có
đồ thị như hình vẽ:
Tìm
m
để phương
trình
0f x
m
có
9
nghi
ệm phân biệt.
A.
1m
. B.
1 3m
. C.
0 1m
. D.
3m
.
Lời
giải
Trang
7/16 - WordToan
Chọn A
Ta có:
0f x m f x m
. Phương
trình này có 9 nghiệm phân biệt khi và chỉ khi đồ thị
hàm số
y f x
cắt đường
thẳng
y m
tại 9 đi
ểm phân biệt.
Từ đồ thị hàm số
y f x
ta suy
ra đồ thị hàm số
y f x
như sa
u:
Từ đó ta suy ra đồ thị hàm số
y f x
như sau:
Dự
a vào đồ thị ta thấy đồ thị hàm số
y f x
cắt đường thẳng
1y
tại 9 điểm phân biệt.
Vậy
1m
.
Câu 4. Ti
ếp tuyến của đồ thị hàm số
3 2
3 2y x x
tại điểm
1; 2M
có phương trình là
A.
9 2y x
. B.
24 2y x
. C.
24 22y x
. D.
9 7y x
.
Lời giải
Chọn D
Ta có:
2
3 6y x x
. Suy ra
1 9y
.
Phương tr
ình tiếp tuyến của đồ thị hàm số tại
M
có phương
trình:
1 . 1 2y
y x
9. 1 2y
x
9 7y x
.
Tran
g 8/16 – Diễn đàn giáo viên Toán
Câu 5.
Cho hàm số
2
cos
( )
c
os 1
x m
y f x
x
. Tìm tất cả các giá trị của m để hàm số
f x
đồng
biế
n trên khoảng
0;
2
.
A.
9m
B.
3m
C.
3m
. D.
9m
.
Lời giải
Chọn B
Ta có
2
'
2
sin (
cos 2cos )
( )
(cos 1)
x x x m
f x
x
.
Hàm s
ố
f x
đồng biế
n trên khoảng
0;
2
'( )
0, 0;
2
f x x
2
cos 2cos
0, 0;
2
x x m x
2
2 , 0
; 1m t t t
, vớ
i cost x .
2
0;1
max
2m t t
3m
.
Câu 6.
Hàm số
( )y f
x
liên tục trên
1;3
có bảng biến thiên :
Giá trị nhỏ nhất của hàm số trên đoạn
1;3
là:
A. 2. B. 1
. C. -2. D. 0.
Lời giải
Chọn C
Dựa vào bảng biến thiên suy ra giá trị nhỏ nhất của hàm số trên
1;3
bằng -2.
Câu 7. Đồ thị hàm số
3 2
2 2
x
y
x
có
A. Tiệm cận đứng
2x
. B. Tiệm
cận đứng
2x
. C.
Tiệm cận
ngang
1y
. D. Tiệ
m cận ngang
3
2
y
.
Lời giả
i
Chọn C
Ta c
ó
3 2
lim lim 1
2 2
x x
x
y
x


hoặc
3 2
lim lim 1
2 2
x x
x
y
x


nên đồ
thị hàm số
3 2
2 2
x
y
x
có tiệm
c
ận ngang
1y
.
Câu 8. Hàm số
3
3y x x
nghịch biến trên khoảng nào dưới đây?
A.
1;3
. B.
1;
. C.
;1
. D.
1;1
.
Lời giả
i
Chọn D
Ta c
ó hàm số
3
3y x x
có tập xác định
D
,
2
3 3y x
. Ta
có
x
– ∞
-1
1
+
∞
y'
+
0
–
0
+
y
– ∞
2
-2
+
∞
T
rang 9/16 - WordToan
1
0
1
x
y
x
, từ đó ta có bảng biến thiên:
Vậy hàm số nghịch biến trên khoảng
1
;1
.
Câu
9. Tổng số các đường tiệm cận đứng và tiệm cận ngang của hai đồ thị hàm số
2
2
2
x 1 3
5 6
x x
y
x x
v
à
2
2
3x 4
1
x
y
x
là
A. 2. B. 4. C. 5. D. 3.
Lời
giải
Chọn
B.
Ta có:
2
2
1 1
4
1
3x 4
lim lim
1 1 1
x
x
x
x
x
x x x
T
CĐ:
1x
.
2
2
1
1 1
4
1
3x 4 4 5
lim lim lim
1 1 1 1 2
x x x
x
x
x x
x x x x
1x
khôn
g phải là TCĐ.
2
2
3x
4
lim 1
1
x
x
x
TCN:
1y
.
Ta c
ó:
2
2
3
2
x 1 3
lim
5 6
x
x
x
x x
TCĐ:
3x
.
2
2
2
2
2
2
1
2
2x 1 3 7
2 3
lim lim
5 6 2 5 6
x
x
x
x
x
x x
x x x
2x
khôn
g phải là TCĐ.
2
2
2x 1 3
lim 0
5 6
x
x x
x x

T
CN:
0y
.
2
2
2
2
2 2
6
3
2 2 2
2x 1 3
3 3 3 3
lim lim lim 0
5 6 5 6 3
x
x x
x
x x
x
x x
x x x x
x x x x x
  
T
CN:
0y
.
C
âu 10. Cho hàm số
y
f x
xá
c định, liên tục trên
v
à có bảng biến thiên như sau
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trong khoảng
1;
.
B. H
àm số nghịch biến trong khoảng
1
;0
.
C. Hàm
số đồng biến trong khoảng
;1
v
à
1
;0
.
T
rang 10/16 – Diễn đàn giáo viên Toán
D. Hàm
số nghịch biến trong khoảng
1
;
.
Lời
giải
Chọn
A.
Câu 11. Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
A.
3
2
3
1y x x . B.
3
2
3
3y x x . C.
3
2
3
1y x x . D.
3
2
3
2y x x .
Lờ
i giải
Chọn
B
Dựa vào đồ thị và đáp án, hàm số cần tìm có dạng
3
2
y ax bx c với
0a
. Loại C.
Đồ thị hàm số cắt trục tung tại
0
;c
với
0c
. Loại A.
2
3
2y ax bx
.
Hàm số cần tìm đạt cực đại tại 0
C
D
x v
à đạt cực tiểu tại 0
CT
x
d . Do đó
0y
h
ay
2
3 2 0ax bx
c
ó hai nghiệm là
0x
v
à
0x
d
.
+
Xét đáp án B:
2
3
6y x x
;
2
0
3 6 0 3 2 0
2
x
x x x x
x
(thỏa mãn).
+ Xét đáp án D:
2
3
6y x x
;
2
0
3
6 0 3 2 0
2
x
x x x x
x
(loại).
Vậy chọn B.
Câu 12. Đường cong sau là đồ thị của hàm số nào dưới đây?
A.
4 2
5 1y x x . B.
4 2
2 3 1y x x . C.
4 2
2 1y x x . D.
4 2
2 3 1y x x .
Lờ
i giải
Chọn
B
Dựa vào đồ thị và đáp án, hàm số cần tìm có dạng
4
2
y
ax bx c với
0a
.
Loại A.
Đồ thị hàm số cắt trục tung tại
0
;c
với
0c
.
Loại D.
Tra
ng 11/16 - WordToan
Hàm số
4 2
y ax
bx c
cần tìm có 2 cực tiểu và 1 cực đại khi
0
0
a
ab
.
+ Xét đáp án B:
2 0
6 0
a
ab
(thỏa mãn).
+ Xét đáp án C:
1 0
2 0
a
ab
(loại).
Vậy chọn B.
Câu 13. Số điểm cực tiểu của hàm số
4 2
2 5y x x
là
A.
3
. B.
1
. C.
2
. D.
0
.
Lời
giải
Chọn C
Ta có
3 2
4 4
4 1y x x x x
,
2
0
0 4
1 0
1
x
y x x
x
.
Bảng xét dấu
y
Dựa vào
xét ấu ta thấy hàm số có 2 điểm cực tiểu.
Làm trắc nghiệm: Hàm số bậc bốn trùng phương
4 2
y a
x bx c
thoản mãn
0
0
a
b
có 3 điểm
cực trị trong đó có 2 điểm cực tiểu, 1 điểm cực đại.
Câu 14. Tổng số điểm cực trị của hai hàm số
3
5 1y
x x
và
4 2
1y x
x
là
A
.
2
. B.
3
. C.
5
. D.
1
.
Lời
giải
Chọn
B
Hàm số
3
5 1y
x x
có
2
3 5y
x
,
0y
có
hai nghiệm đơn phân biệt nên hàm số có 2 điểm
cực trị.
Hàm số
4 2
1y x
x
có
3
4 2y
x x
,
0y
có
nghiệm đơn duy nhất nên hàm số có 1 điểm
cực trị.
Vậy tổng số điểm cực trị của hai hàm số
3
5 1y x x
và
4 2
1y x x
là
3
.
Câu
15. Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào?
Tr
ang 12/16 – Diễn đàn giáo viên Toán
A.
2 2
.
1
x
y
x
B.
2 1
.
1
x
y
x
C.
2 1
.
1
x
y
x
D.
2 3
.
1
x
y
x
Lời giải
Chọn
B
Từ đồ thị đã cho ta thấy đồ thị hàm số cần tìm có
- Tiệm cận ngang
2.y
- Ti
ệm cận đứng
1.x
- Gi
ao điểm với trục hoành:
1
;0
.
2
- Gi
ao điểm với trục tung:
0;
1 .
- Đồ thị là đường luôn đi lên từ trái sang phải nên hàm số đồng biến trên từng khoảng xác định.
Do đó ta có hàm số
2 1
1
x
y
x
th
ỏa mãn.
Câu 16. Cho hàm số
y f
x
có
bảng biến thiên như sau
Gọi ,
CD C
T
y y
là giá trị cực đại và giá trị cực tiểu của hàm số đã cho. Tính .
CD
CT
y y
A.
1.
B.
2.
C.
0.
D.
3.
Lời giả
i
Chọn
D
Từ bảng biến thiên ta có 3; 0
CD C
T
y y
nên 3.
CD C
T
y y
Câu 17. Tìm tất cả các giá trị của tham số
m
để
đồ thị hàm số
3
2y x
mx
cắt t
rục hoành tại ba điểm
phân biệt.
A.
3m
. B.
3m
. C. K
ết quả khác. D.
3m
.
Lời
giải
Chọn
D
Đồ thị hàm số
3
2y x
mx
cắt
trục hoành tại ba điểm phân biệt Đồ thị hàm số đó có hai
điểm cực trị nằm hai phía so với trục hoành.
2
2
x
y '
y
0
0
3
0
Tr
ang 13/16 - WordToan
Ta c
ó:
2
3y x m
2
0
3
m
y x
.
Hàm số c
ó hai điểm cực trị
0y
có hai nghiệm phân biệt
0m
1
.
Khi đó đồ thị hàm số có hai điểm cực trị là
2
2
; 2 , ; 2
3 3 3 3 3 3
m m m m m m
A B
.
A
và
B
nằm khác phía so với trục hoành
2 2
2 2 0
3 3 3 3
m m m m
3
4
4
0
27
m
3m
2
.
Kết
hợp
1
v
à
2
,
ta được
3m
.
Câu
18. Cho hàm số bậc ba:
3
2
y
ax bx cx d
c
ó bảng biến thiên như hình sau (H.6).
H.6
Tính tổng
T a b c
.
A.
9
8
. B.
3
8
. C
.
7
8
. D.
11
8
.
Lời giải
Chọn D
Ta có:
3
2
y f x ax bx cx d
2
3
2f x ax bx c
.
Dựa vào bảng biến thiên, ta thấy đồ thị hàm số có hai điểm cực trị
1
; 2A
v
à
3
; 2B
x
1
3
y
0
0
y
2
2
Tr
ang 14/16 – Diễn đàn giáo viên Toán

1
8
1 2
2
3
3 2
27 9 3 2
8
3 2 0 9
1 0
8
27 6 0
3 0
5
8
a
f
a b c d
b
f
a b c d
a b c
f
c
a b c
f
d
.
Vậy
11
8
T a b c
.
Câu
19 . Hàm số
y f x
có đ
ồ thị là đường cong trong hình vẽ bên. Hàm số
y f x
đạt
cực tiểu tại
điểm nào dưới đây.
A.
2x
. B.
4x
. C.
2x
. D.
0x
.
Lời
giải
Chọn D
D
ựa vào đồ thị hàm số ta thấy hàm số đạt cực tiểu tại
0x
.
Câu
20 . Hàm số nào trong các hàm số tương ứng ở các phương án A, B, C, D có đồ thị là hình bên.
A.
1
1
x
y
x
. B.
4 2
2 1y
x x .
C.
2
1
x
y
x
. D.
1
1
x
y
x
.
Lời
giải
Tra
ng 15/16 - WordToan
Chọn A
D
ựa vào đồ thị hàm số ta thấy đây là đồ thị của hàm phân thức dạng
ax b
y
cx
d
,
0ad
bc
,
nên
ta loại đáp án B.
Từ đồ thị hàm số ta thấy đồ thị hàm số có tiệm cận ngang là đường thằng
1y
và
tiệm cận đứng là
đường thẳng
1x
và đi qua điểm
0; 1M
nên đáp án cần tìm là A.
Câu 21. Cho hàm số
2
2 1y
x x
. T
ìm giá trị lớn nhất của hàm số đã cho trên
2;
3
A.
9
. B.
3
. C. K
hông tồn tại. D.
4
.
Lời giải
Chọn A
2
2 1y x x
Tập xác định
D
.
' 0
2 2 0 1 2;3y x x
.
2 9
; 3 4; 1 0f f f
.
Từ đó s
uy ra
2;
3
ma
x 9y
tại
2x
.
Câu
22. Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
A.
4 2
1y x
x
. B.
4 2
2y x
x
. C.
4 2
2y x
x
. D.
4 2
2 2y
x x
.
Lời
giải
Chọn
B
Quan sát đồ thị ta thấy:
Đồ thị hình trên là đồ thị của hàm số :
4 2
0y a
x bx c a
.
Nên loại A.
Hàm số có 3 điểm cực trị
. 0a
b
mà
0 0a
b
.
Nên loại C.
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên
0c
.
Nên loại D.
Câu 23. Cho hàm số
2
3
1
x
y
x
. M
ệnh đề nào dưới đây đúng?
A. Cực đại của hàm số bằng 2. B. Cực tiểu của hàm số bằng 1.
C. Cực đại của hàm số bằng
3
. D. Cực
đại của hàm số bằng
6
.
Lời
giải
Chọn
D
Hàm số đã cho có tập xác định
\{
1}.
Tr
ang 16/16 – Diễn đàn giáo viên Toán
Ta có
2
2
2 3
.
1
x
x
y
x
3
0
1
x
y
x
.
Bảng biến thiên
Dựa trên bảng biến thiên ta có cực đại của hàm số bằng
6
.
Câu 24. Cho hàm số
1
.
1
x
y
x
Kh
ẳng định nào sau đây đúng?
A. Đồ thị hàm số có tiệm cận đứng
1x
. B. Đồ
thị hàm số có tiệm cận ngang
1y
.
C. Đồ thị h
àm số có tiệm cận ngang
1y
. D. Đ
ồ thị hàm số có tiệm cận ngang
1x
.
Lời giải
Chọn
C
Tập xác định
\{1}.
Ta có
1
lim
1
1
x
x
x

nê
n đồ thị hàm số có tiệm cận ngang
1y
.
Câu
25. Cho hàm số
y f
x
xác định, liên tục trên
\ 0
và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số nghịch biến trên khoảng
1;0
.
B. Hàm số đồng biến trong khoảng
1;0
.
C. Hàm số đồng biến trong khoảng
;1
.
D. Hàm số đồng biến trong khoảng
1;
.
Lời
giải
Chọn
B
Từ bảng biến thiên ta thấy hàm số đồng biến trong khoảng
1;0
.
| 1/21
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT KIÊN GIANG
ĐỀ KIỂM TRA 1 TIẾT – NĂM HỌC 2018 - 2019 TRƯỜNG THPT TÂN HIỆP MÔN TOÁN LỚP 12
Thời gian làm bài : 45 Phút; (Đề có 25 câu)
(Đề có 5 trang)
Họ tên : ............................................................... Lớp : ................... Mã đề 101
Câu 1: Giá trị nhỏ nhất của hàm số 1 y = x − trên đoạn [1; ] 3 là x +1 A. 1 B. 3 C. 7 D. 11 2 4 4
Câu 2: Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số 4 2
y = x − 2mx +1 có
ba điểm cực trị là ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng 1. A. 1 5 m − + = B. m =1 C. 1 5 m 1;m − − = = D. 1 5 m 1;m − + = = 2 2 2
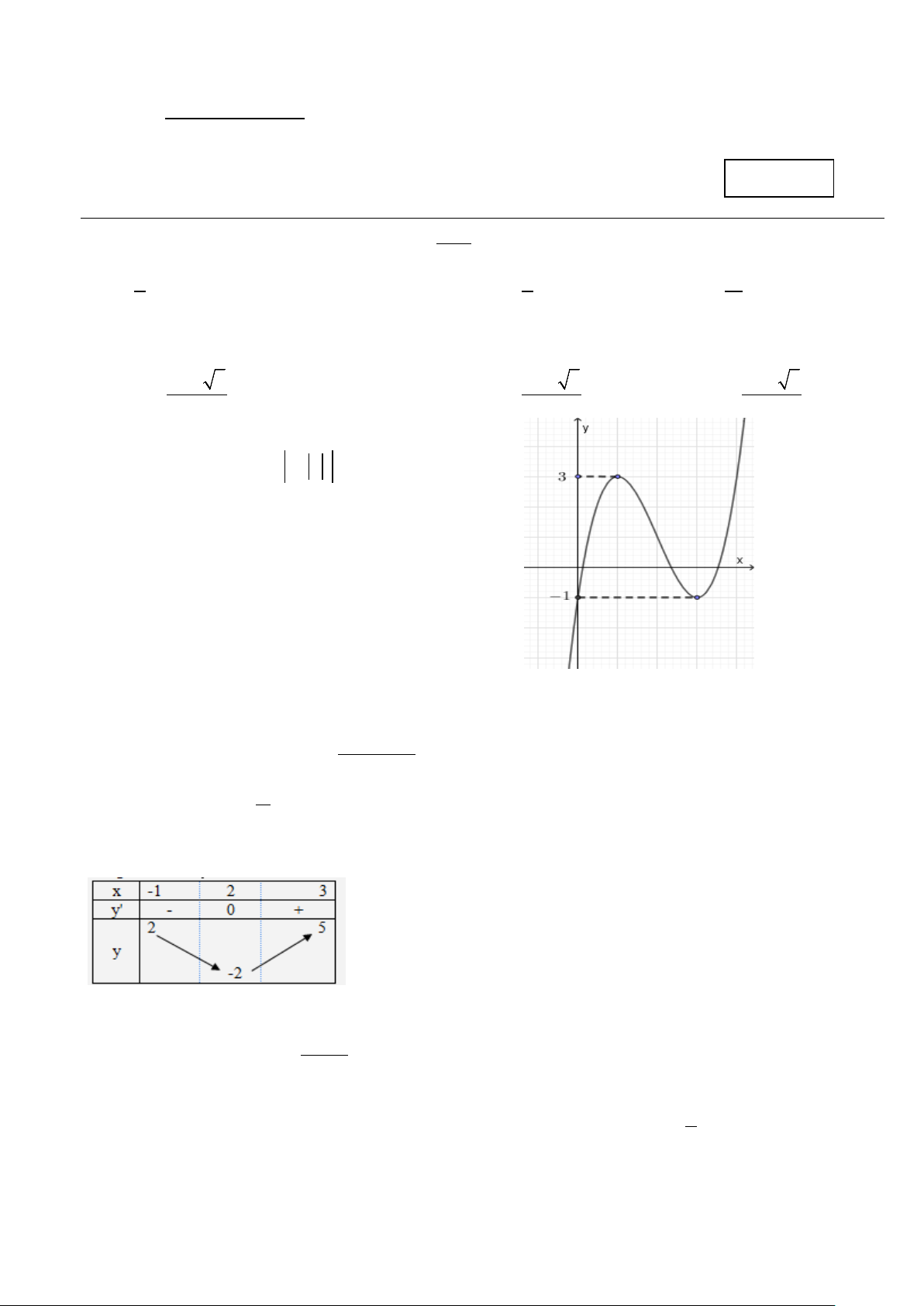
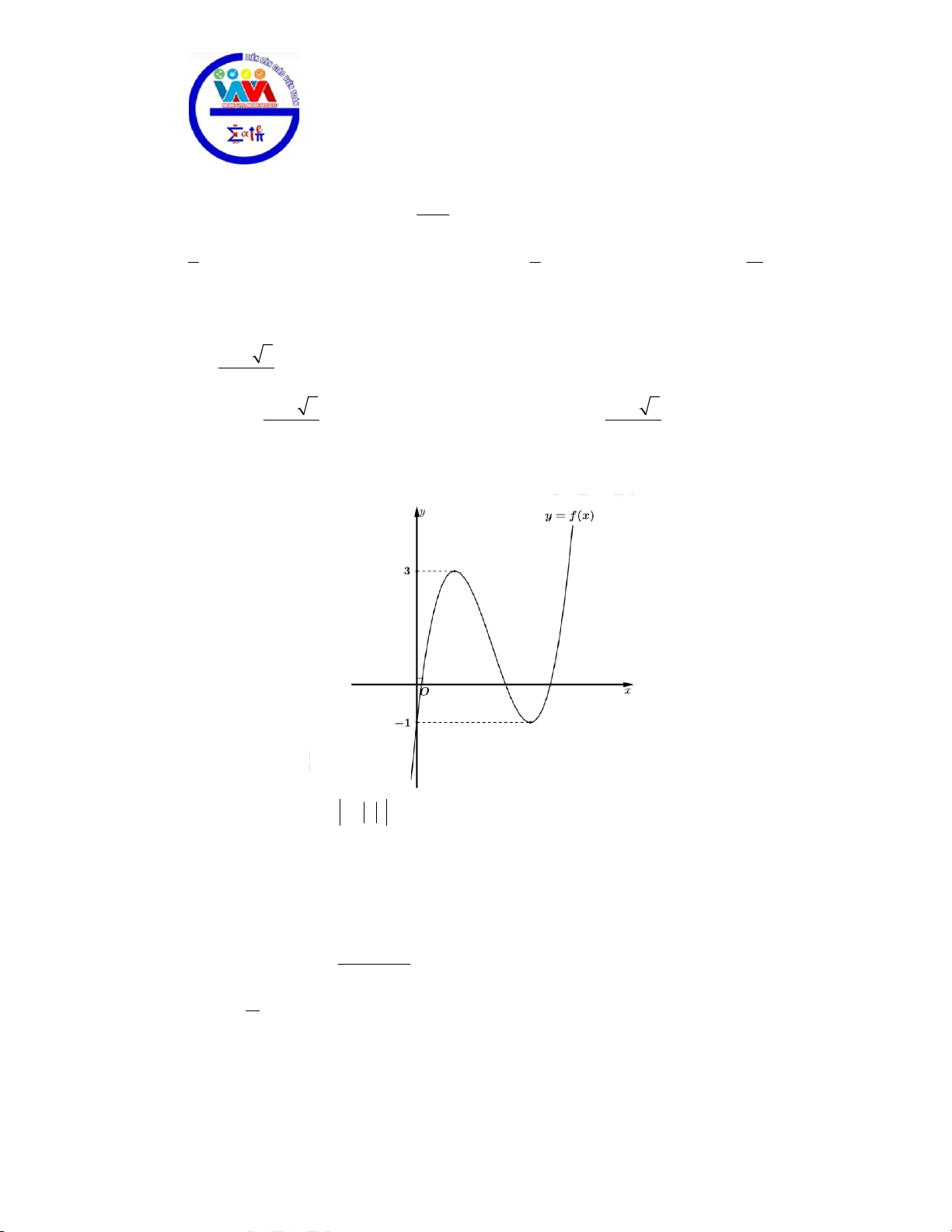
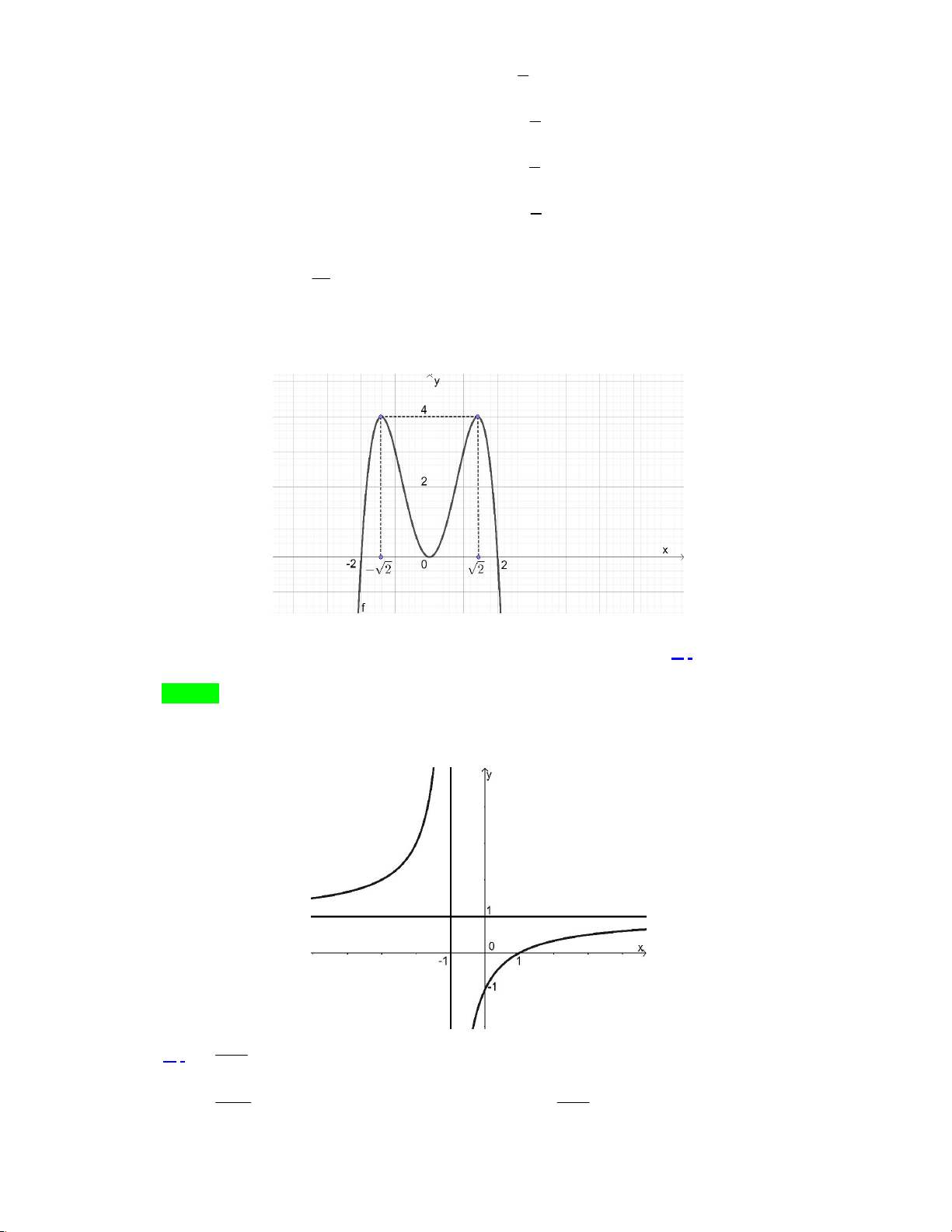
Câu 3: Cho hàm số y = f (x) có đồ thị như hình vẽ.
Tìm m để phương trình f ( x ) − m = 0 có 9 nghiệm phân biệt. A. m =1.
B. 1< m < 3.
C. 0 < m <1. D. m = 3.
Câu 4: Tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x + 2 tại điểm M ( 1; − 2
− ) có phương trình là:
A. y = 9x − 2
B. y = 24x − 2
C. y = 24x + 22
D. y = 9x + 7 2 Câu 5: Cho hàm số cos = ( ) x + m y f x =
. Tìm tất cả giá trị của m để hàm số f (x) đồng cos x +1 biến trên khoảng  π 0;   . 2    A. m ≤ 9 B. m ≥ 3 C. m > 3 D. m < 9
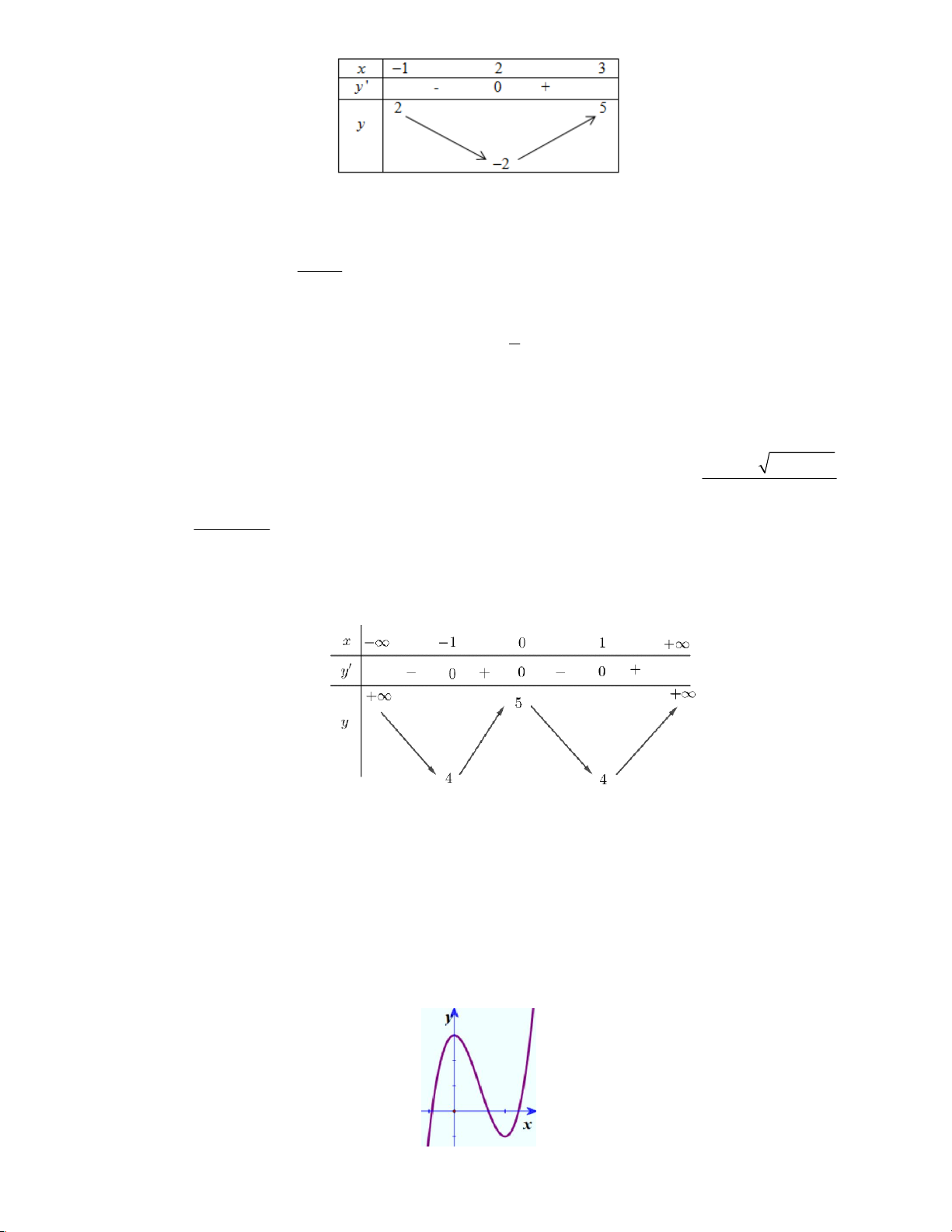
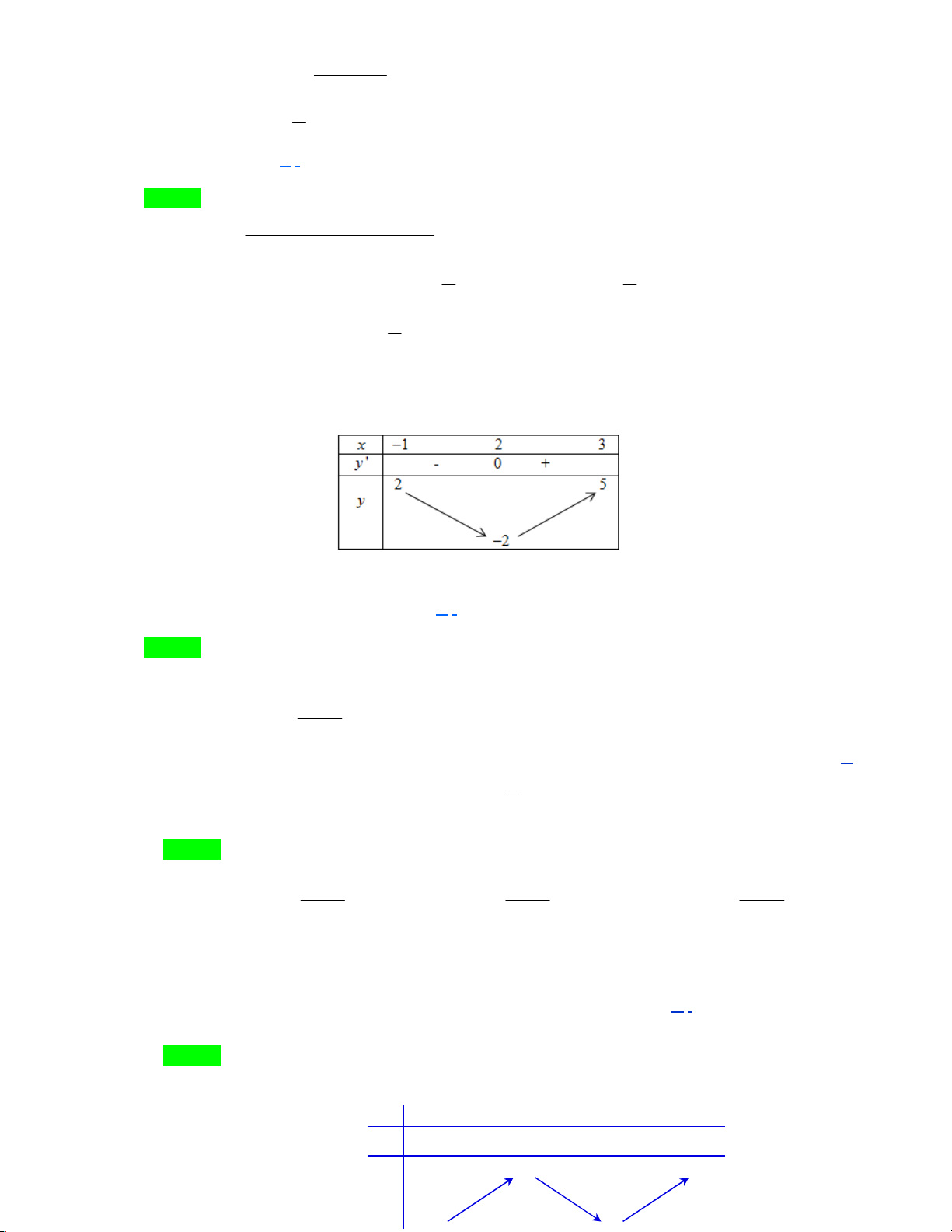
Câu 6: Hàm số y = f(x) liên tục trên [-1;3] có bảng biến thiên:
Giá trị nhỏ nhất của hàm số trên đoạn [-1;3] là A. 2 B. 1 C. -2. D. 0
Câu 7: Đồ thị hàm số 3+ 2x y = có 2x − 2
A. Tiệm cận đứng x = 2 − .
B. Tiệm cận đứng x = 2 .
C. Tiệm cận ngang y = 1. D. Tiệm cận ngang 3 y = . 2 Câu 8: Hàm số 3
y = x − 3x nghịch biến trên khoảng nào dưới đây? A. ( 1; − 3). B. ( 1; − +∞). C. (−∞ ) ;1 . D. ( 1; − ) 1 .
Câu 9: Tổng số tất cả các đường tiệm cận đứng và ngang của đồ thị hai hàm số Trang 1/4 2
2x −1− x + x + 3 2 − − y x 3x 4 = và y = là : 2 x − 5x + 6 2 x −1 A. 2. B. 4. C. 5. D. 3.
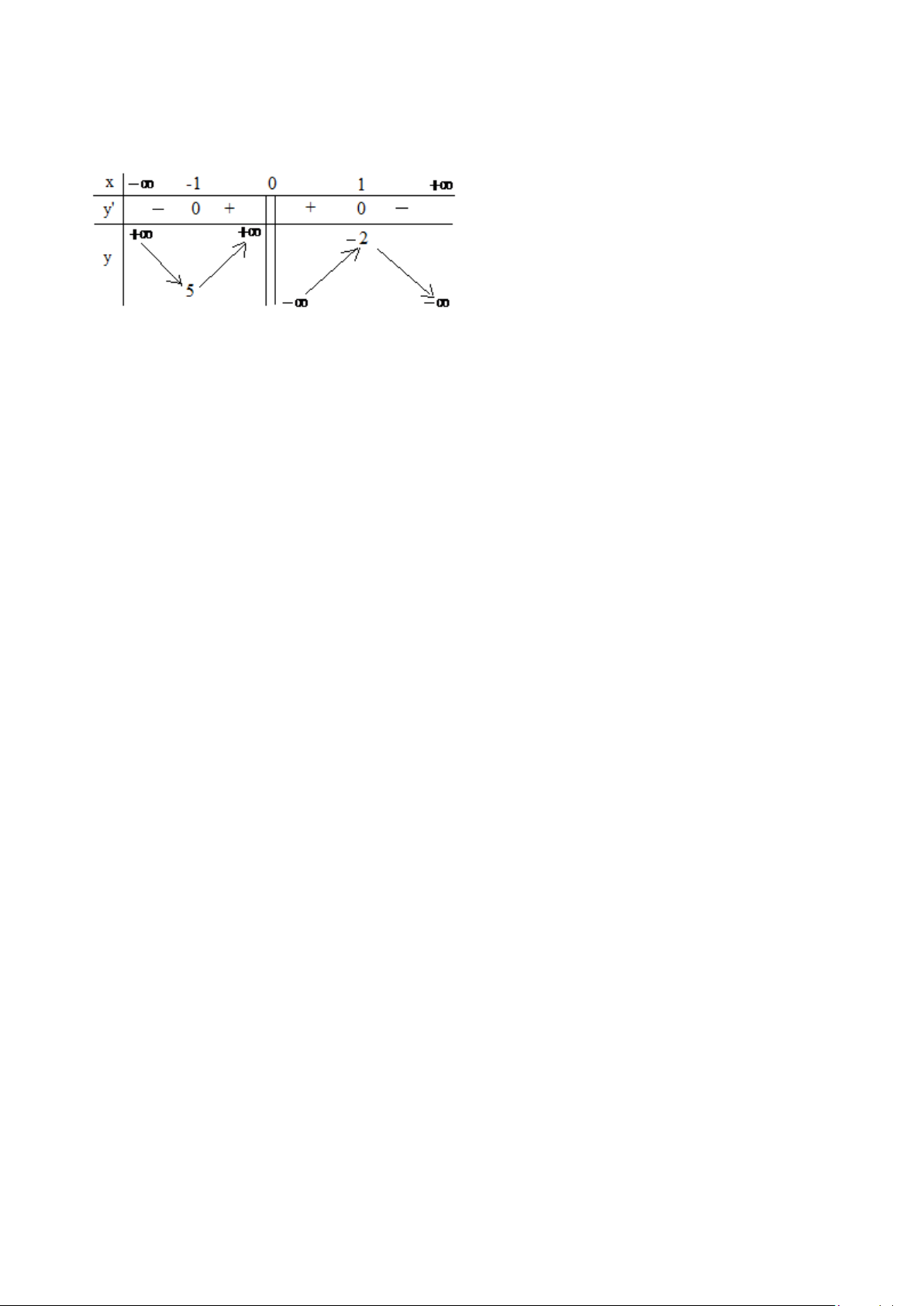
Câu 10: Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên như hình sau. x −∞ −1 0 1 +∞ y' 0 + 0 − − 0 + +∞ 5 +∞ y 4 4
Khẳng định nào sau đây là khẳng định đúng ?.
A. Hàm số đồng biến trong khoảng (1;+∞).
B. Hàm số nghịch biến trên khoảng( 1; − 0) .
C. Hàm số đồng biến trong các khoảng( ) ;1 −∞ và ( 1; − 0) .
D. Hàm số nghịch biến trên khoảng(1;+∞).
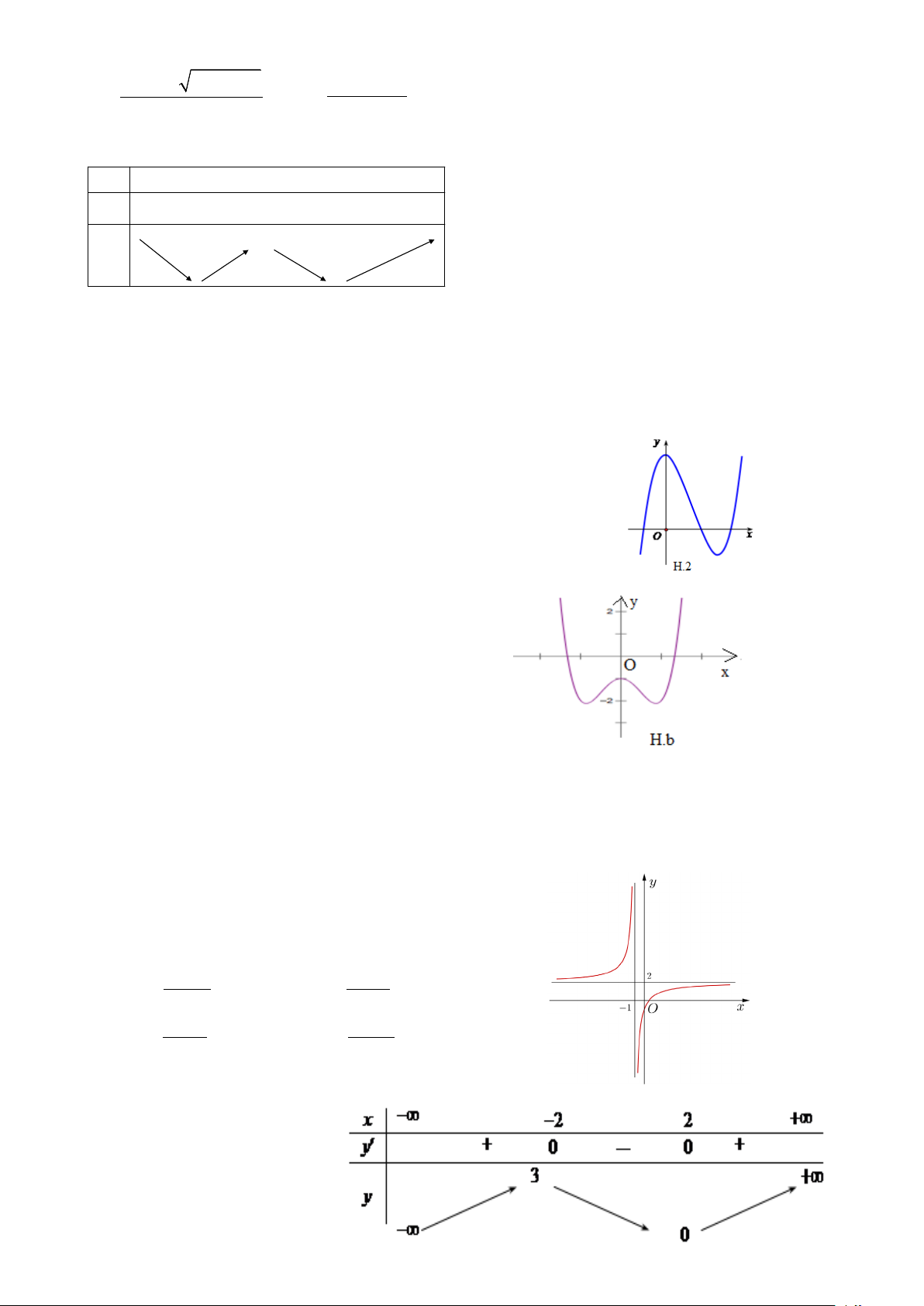
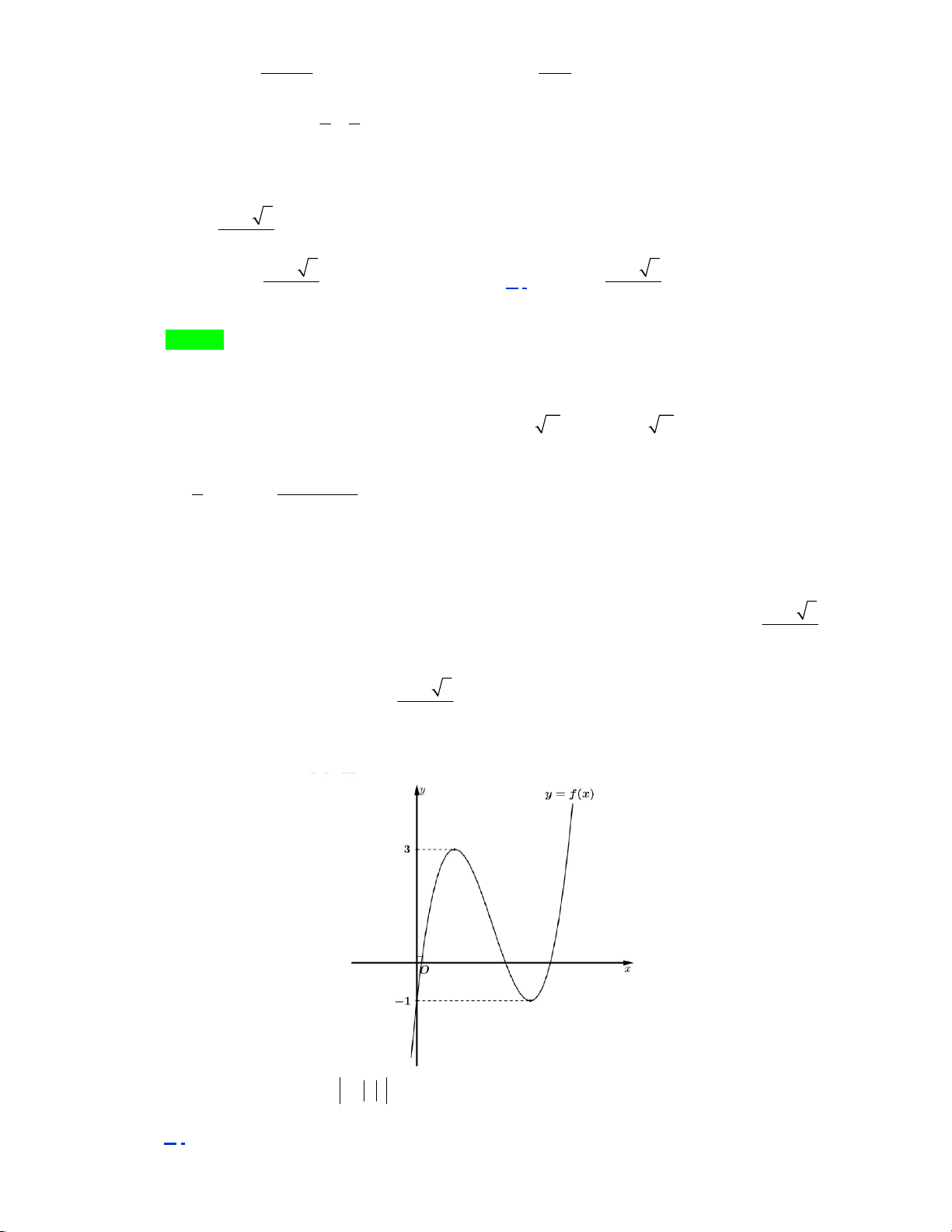
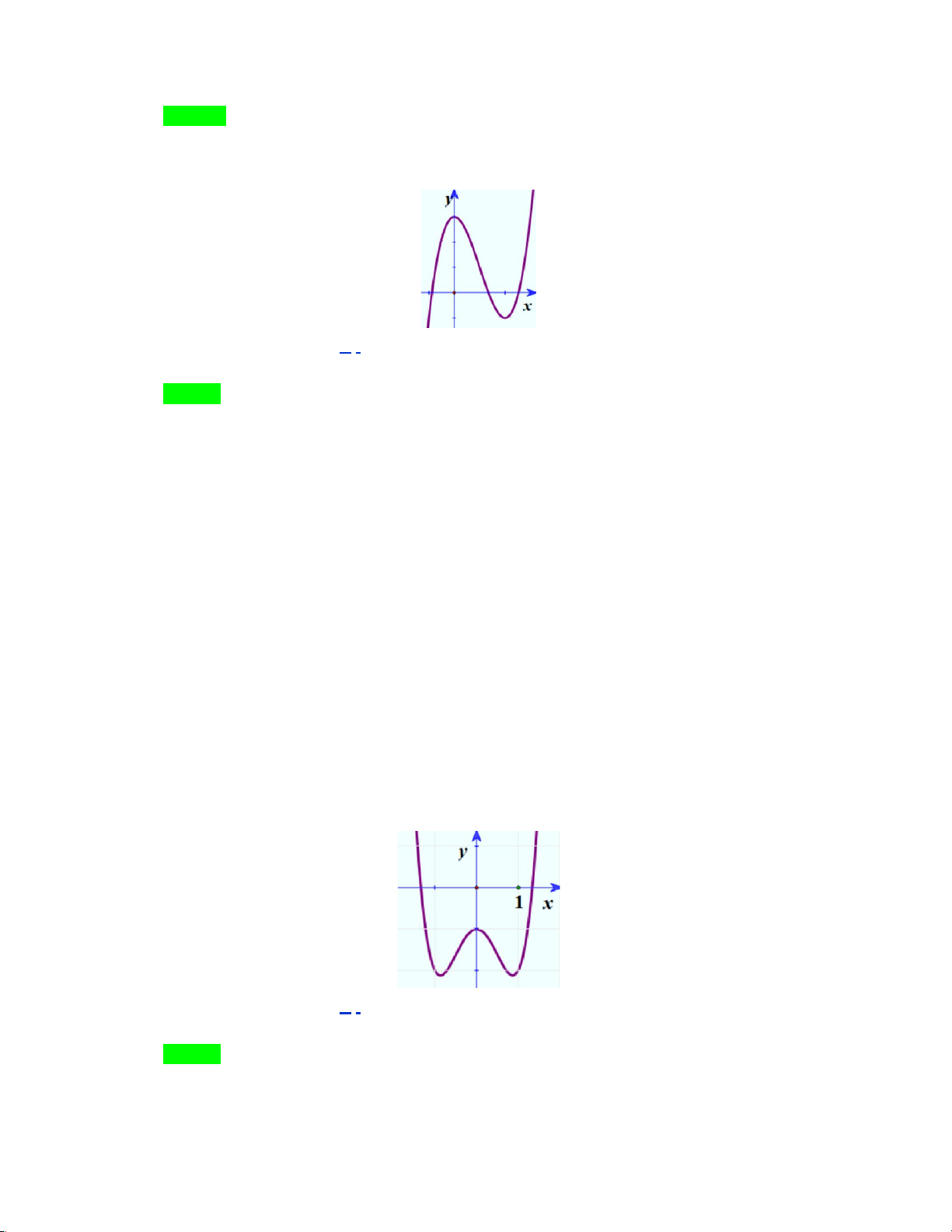
Câu 11: Đường cong hình bên (H.2) là đồ thị của một trong
bốn hàm số dưới đây. Hàm số đó là hàm số nào? A. 3 2
y = x − 3x −1. B. 3 2
y = x − 3x + 3 . C. 3 2
y = −x + 3x +1. D. 3 2
y = x + 3x + 2
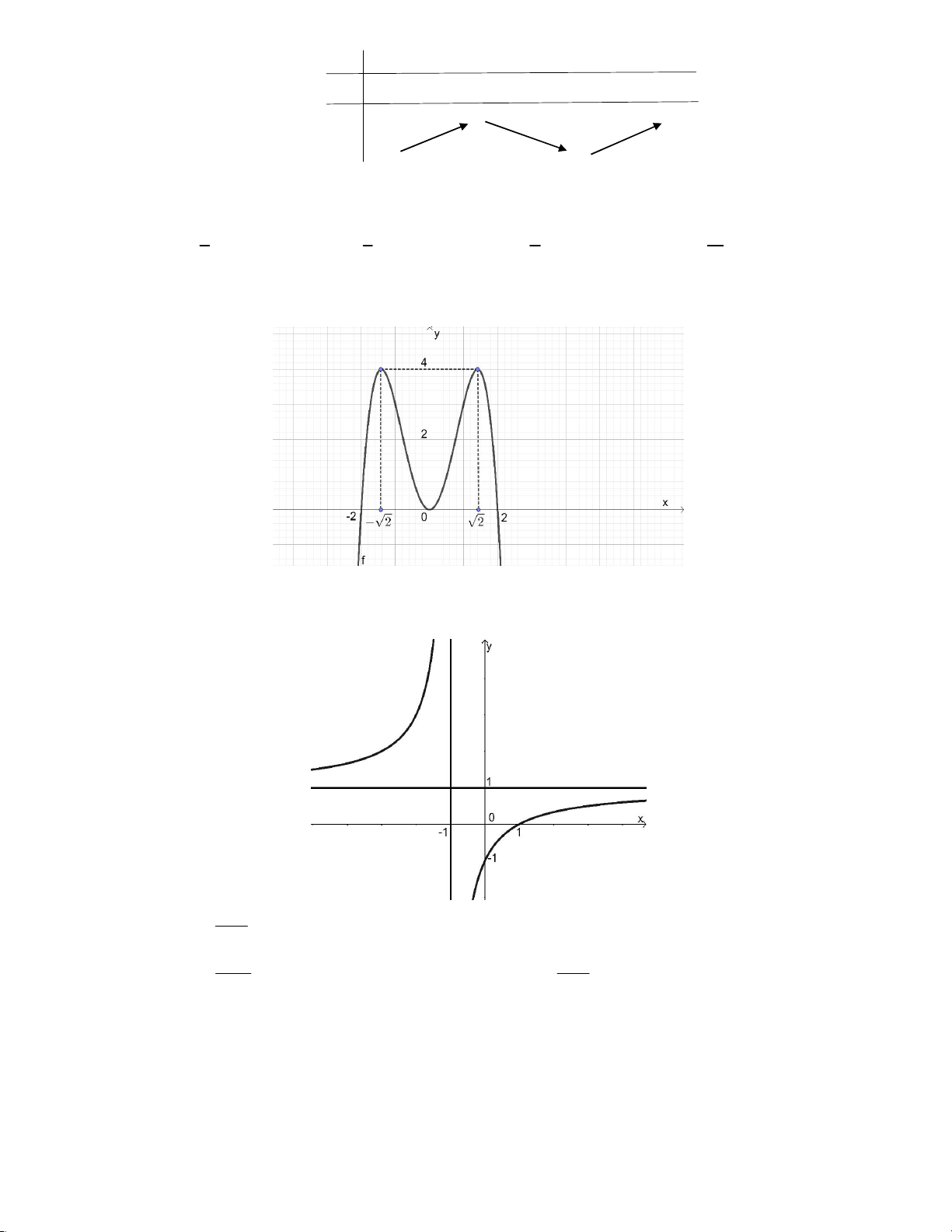
Câu 12: Đường cong sau (H.b) là đồ thị của hàm số nào dưới đây? A. 4 2
y = −x + 5x −1. B. 4 2
y = 2x − 3x −1 . C. 4 2
y = x + 2x −1. D. 4 2
y = 2x − 3x +1.
Câu 13: Số điểm cực tiểu của hàm số 4 2
y = x − 2x + 5 là A. 3. B. 1. C. 2. D. 0.
Câu 14: Tổng số điểm cực trị của 2 hàm số 3
y = x − 5x +1 và 4 2
y = −x − x +1 là . A. 2 B. 3 C. 5 D. 1
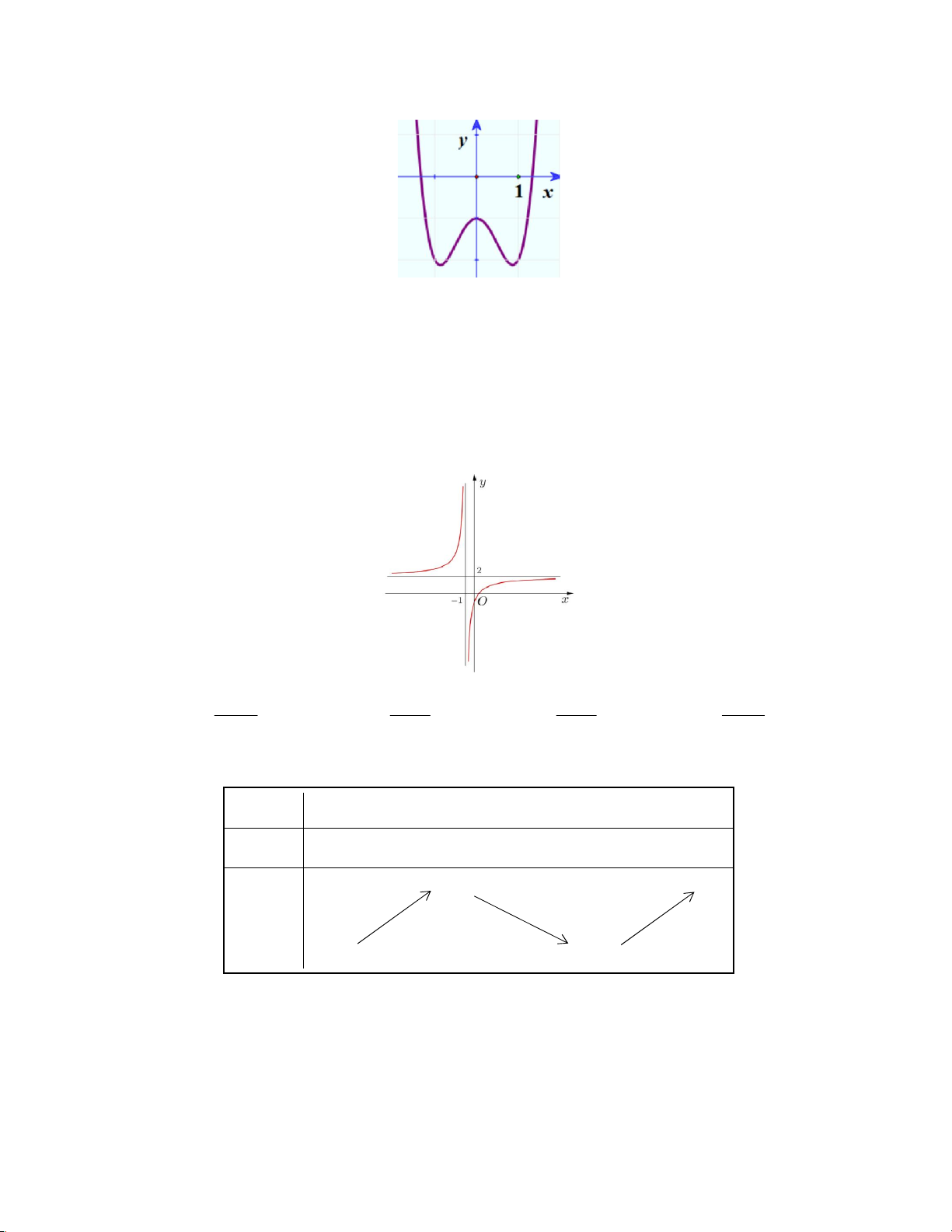
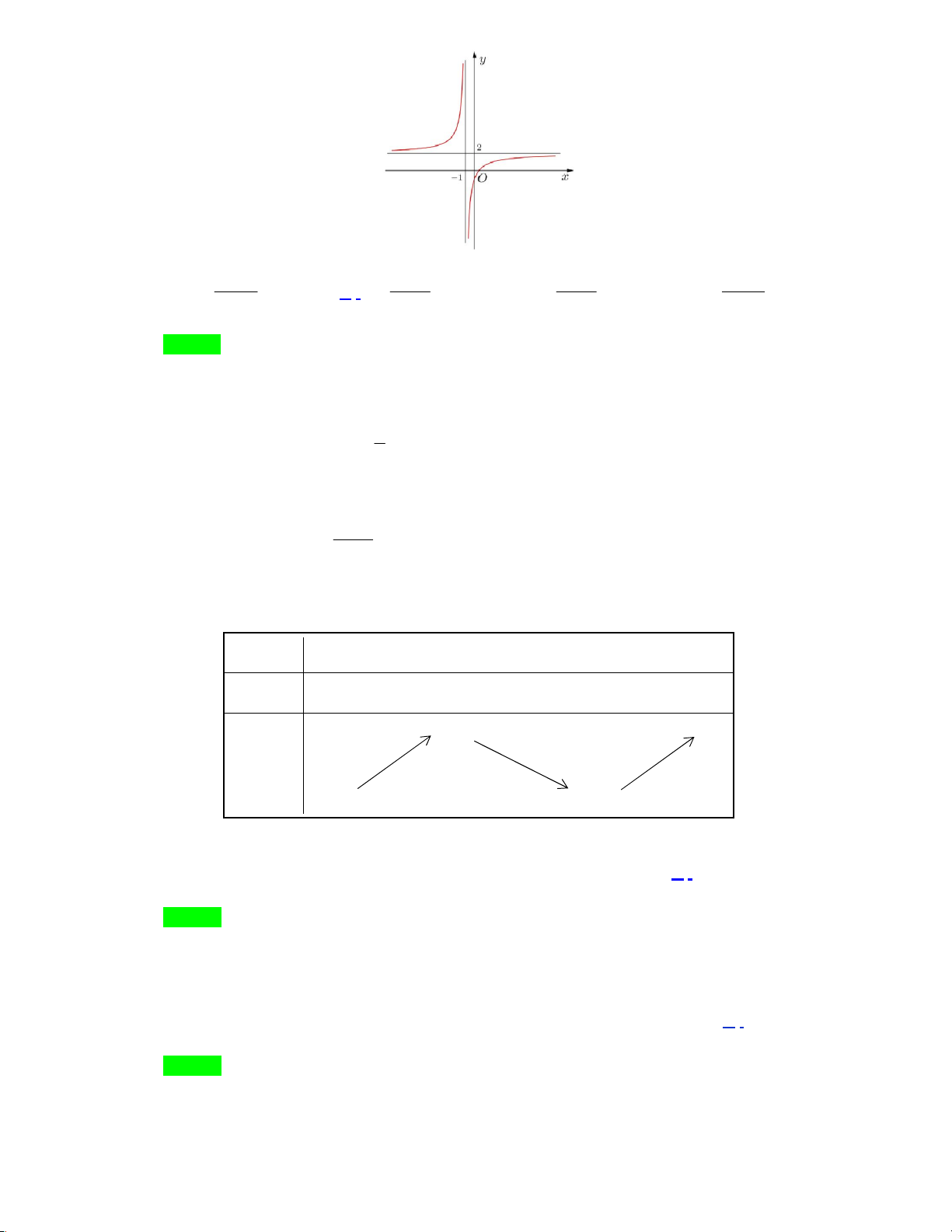
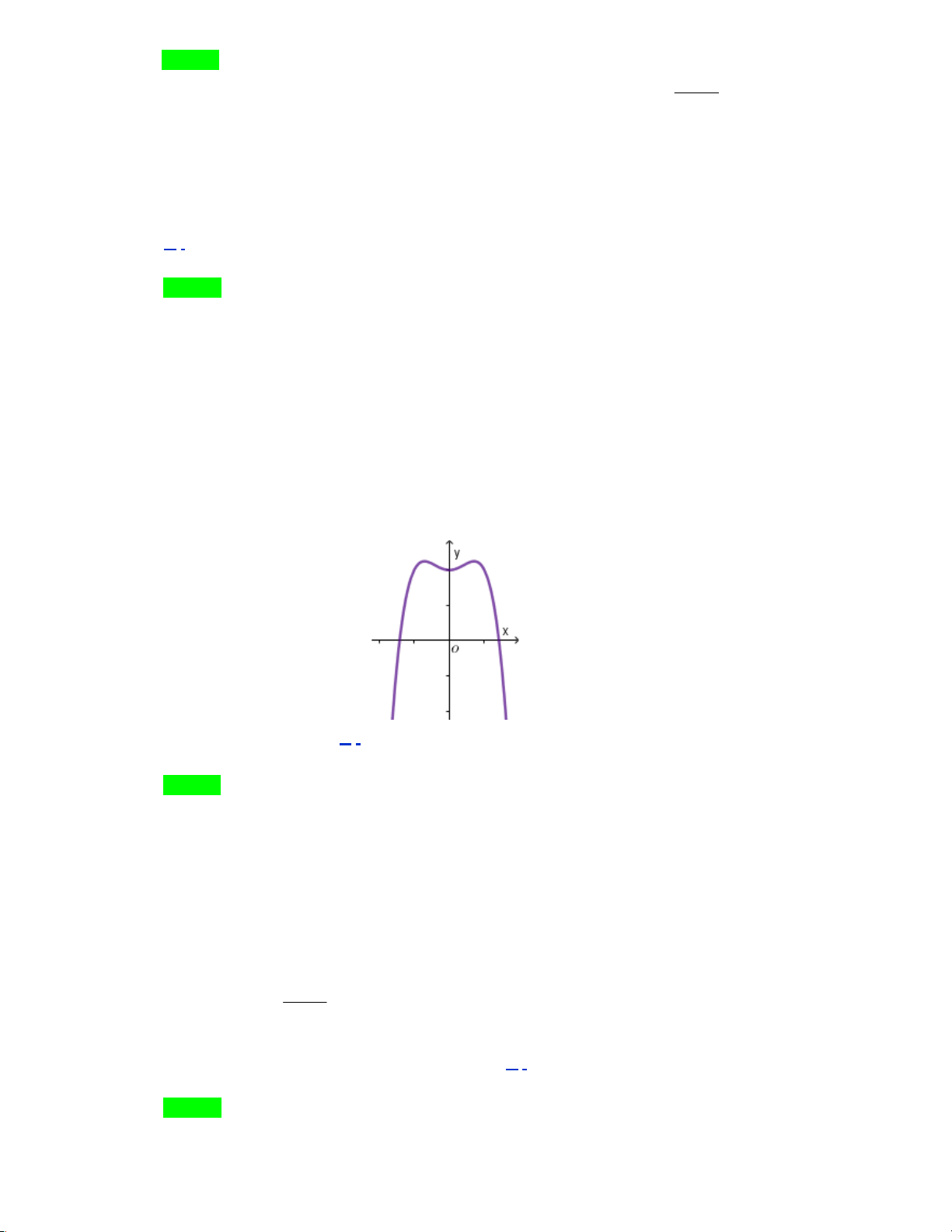
Câu 15: Đường cong trong hình vẽ bên là đồ thị của
một hàm số trong bốn hàm số được liệt kê ở bốn
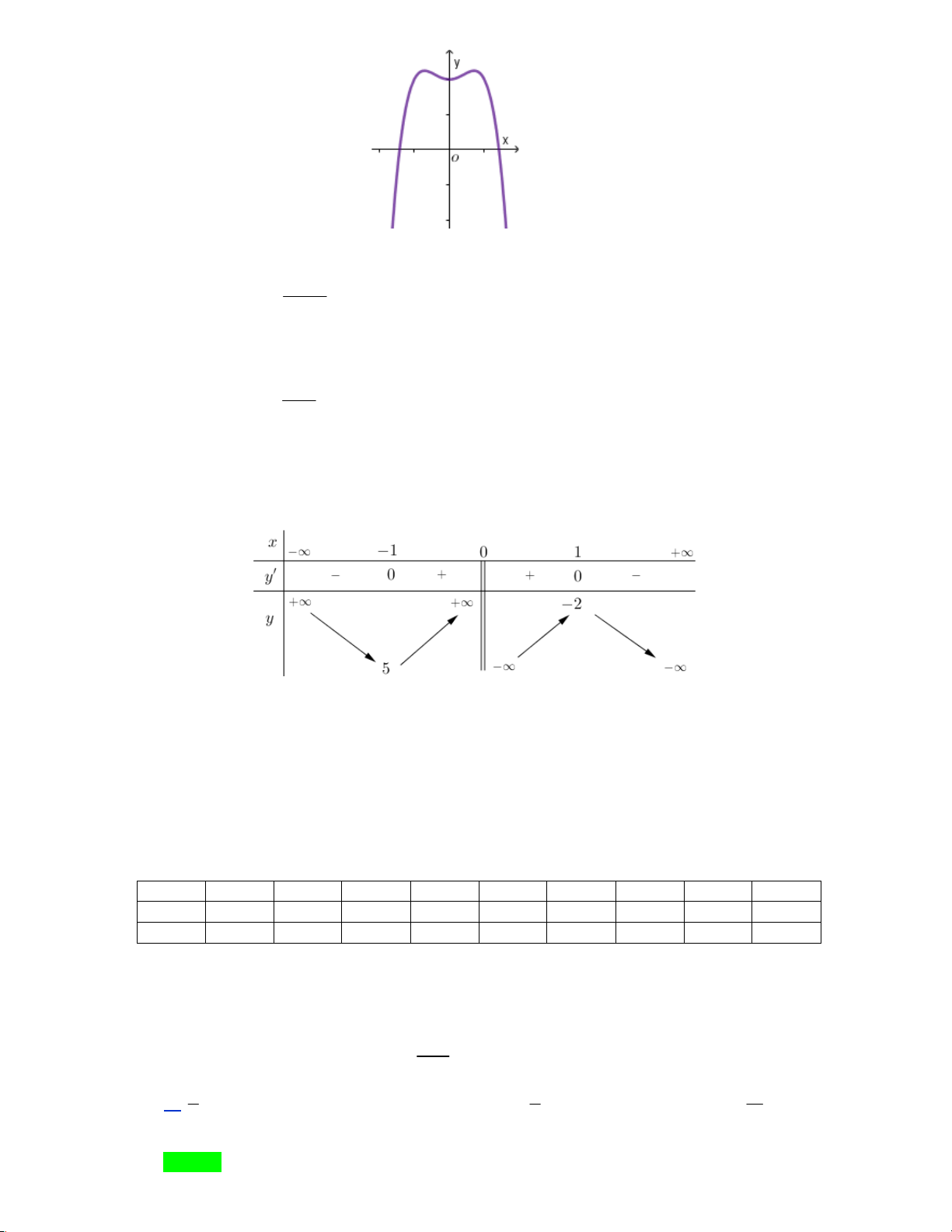
phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào? A. 2x − 2 y − = . B. 2x 1 y = . x −1 x +1 C. 2x +1 y + = . D. 2x 3 y = . x −1 x +1 Câu 16: Cho hàm số
y = f (x) có bảng biến thiên như sau:
Gọi y , y là giá trị cực đại CĐ CT
và giá trị cực tiểu của hàm số
đã cho. Tính y + y . CĐ CT Trang 2/4 A. 1 B. 2 C. 0 D. 3.
Câu 17: Tìm tất cả các giá trị của tham số m để đồ thị hàm số 3
y = x − mx + 2 cắt trục hoành tại 3 điểm phân biệt. A. m > 3 − B. m < 3 − C. Kết quả khác D. m > 3
Câu 18: Cho hàm số bậc ba: 3 2
y = ax + bx + cx + d có bảng biến thiên như hình sau (H.6) .
Tính tổng T = a + b + c . A. 9 − . B. 3 . C. 7 . D. 11 − . 8 8 8 8
Câu 19: Hàm số y = f (x) có đồ thị là đường cong trong hình vẽ bên.
Hàm y = f (x) đạt cực tiểu tại điểm nào dưới đây?. A. x = -2. B. x = 4. C. x = 2. D. x = 0.
Câu 20: Hàm số nào trong các hàm số tương ứng ở
các phương án A, B, C, D có đồ thị là hình bên? A. x −1 y = . x +1 B. 4 2
y = x + 2x −1. C. x − 2 y = . x +1 D. x +1 y = . x −1
Câu 21: Cho hàm số y = x2 - 2x + 1. Tìm giá trị lớn nhất của hàm số đã cho trên [-2;3] A. 9. B. 3. C. không tồn tại. D. 4.
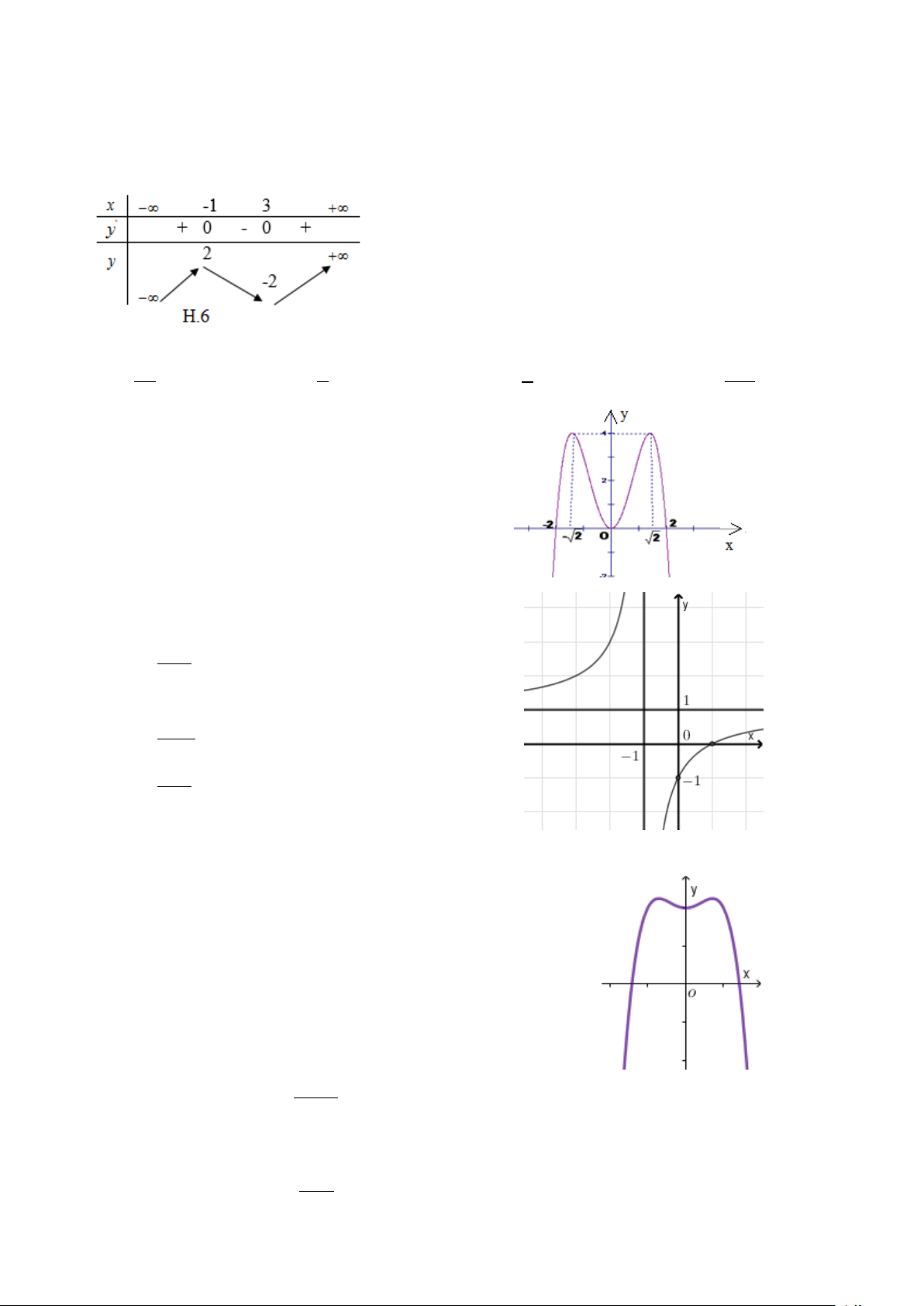
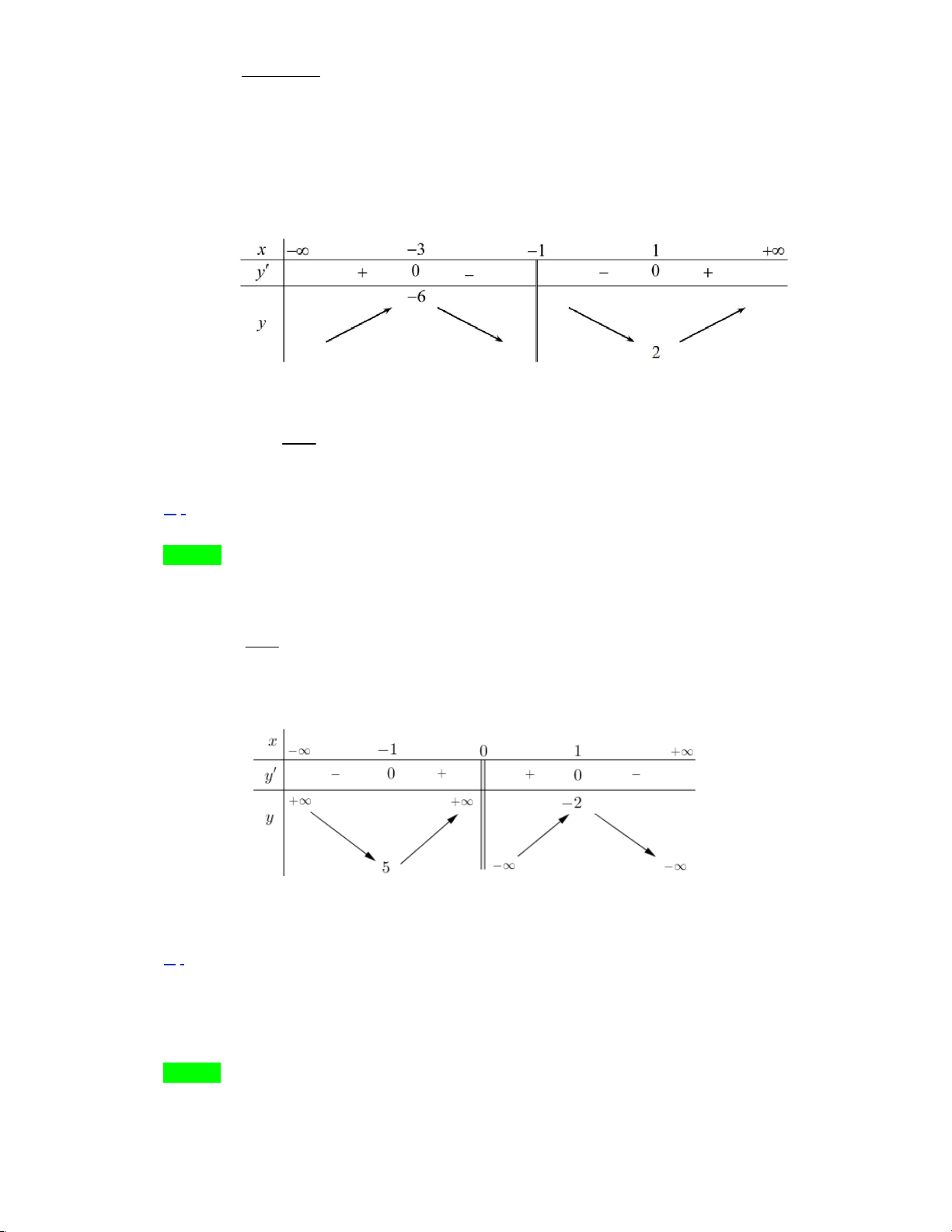
Câu 22: Đường cong ở hình bên là đồ thị của một trong bốn
hàm số ở dưới đây. Hàm số đó là hàm số nào ? A. 4 2
y = x − x −1 B. 4 2
y = −x + x + 2 . C. 4 2
y = −x − x + 2. D. 4 2
y = −x + 2x − 2 . 2 Câu 23: Cho hàm số x + 3 y =
. Mệnh đề nào dưới đây đúng? x +1
A. Cực đại của hàm số bằng 2.
B. Cực tiểu của hàm số bằng 1.
C. Cực đại của hàm số bằng -3.
D. Cực đại của hàm số bằng -6. Câu 24: Cho hàm số x +1 y =
. Khẳng định nào sau đây đúng? x −1
A. Đồ thị hàm số có tiệm cận đứng x = 1 − . Trang 3/4
B. Đồ thị hàm số có tiệm cận ngang y = 1 − .
C. Đồ thị hàm số có tiệm cận ngang y =1.
D. Đồ thị hàm số có tiệm cận ngang x =1.
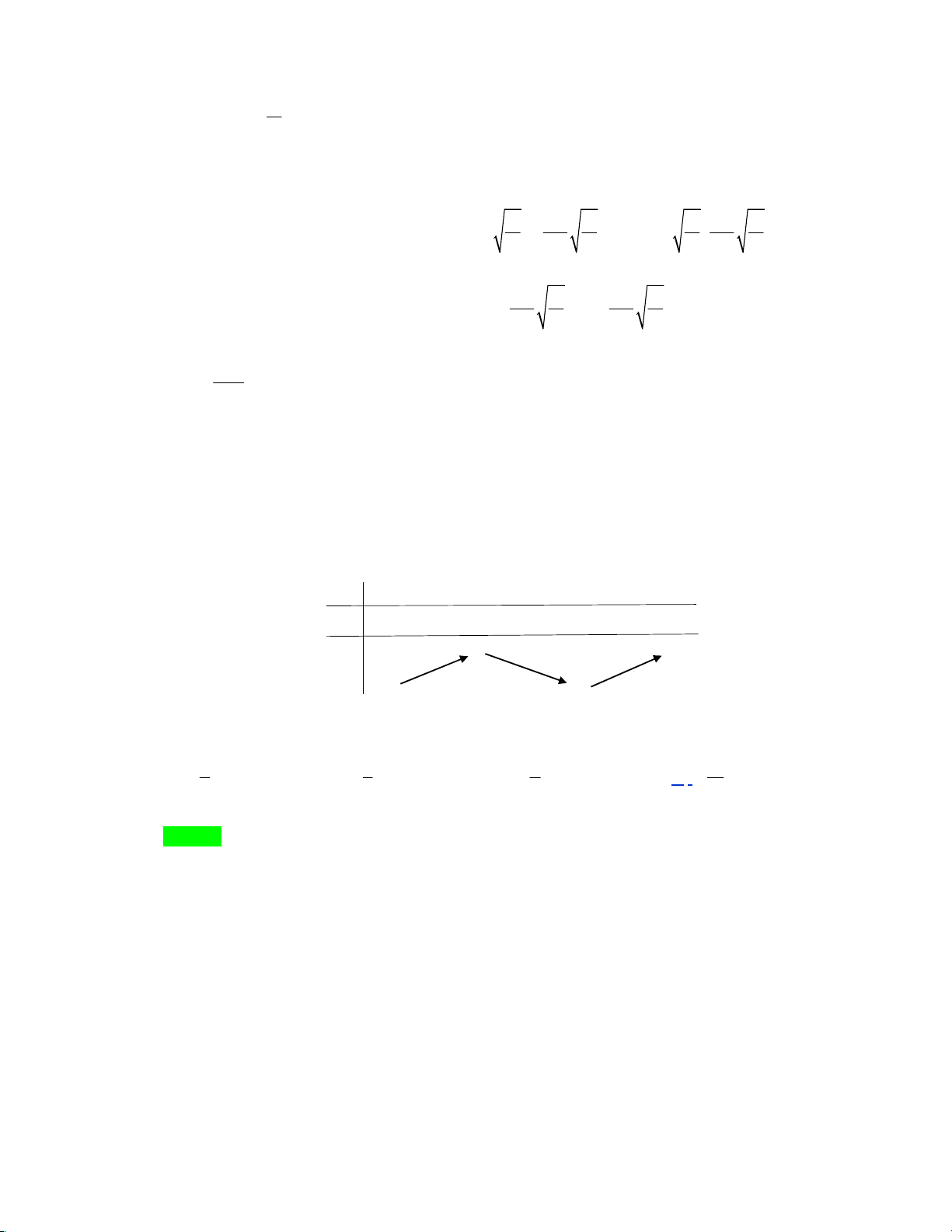
Câu 25: Cho hàm số y=f(x) xác định, liên tục trên R \{0} và có bảng biến thiên :
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số nghịch biến trên khoảng( 1; − 0) .
B. Hàm số đồng biến trong khoảng( 1; − 0) .
C. Hàm số đồng biến trong khoảng( ) ;1 −∞ .
D. Hàm số đồng biến trên khoảng(1;+∞).
------ HẾT ------ Trang 4/4
SỞ GD&ĐT KIÊN GIANG
KIỂM TRA 1 TIẾT MÔN TOÁN KHỐI 12 – NĂM HỌC TRƯỜNG THPT TÂN HIỆP 2018 - 2019 MÔN TOÁN LỚP 12
Thời gian làm bài : 45 Phút
Phần đáp án câu trắc nghiệm: 101 103 105 107 1 A C D A 2 D B C C 3 A D A C 4 D D C B 5 B C D B 6 C A B A 7 C B C D 8 D C B C 9 C D C C 10 A C C B 11 B D B B 12 B B D D 13 C D B A 14 B A B B 15 B A C C 16 D D B C 17 D C C A 18 D B A D 19 D A C B 20 A C D C 21 A C A C 22 B D B A 23 D B D C 24 C C D A 25 B B C A 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM-TRA-45 PHÚT-HK1
NĂM HỌC 2018 – 2019
TRƯỜNG THPT TÂN HIỆP-KIÊN GIANG Môn: Toán
Thời gian: 45 phút (Không kể thời gian phát đề) 1 Câu 1.
Giá trị nhỏ nhất của hàm số y x  trên đoạn [1;3] là x 1 1 7 11 A. . B. 3 . C. . D. . 2 4 4 Câu 2.
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 4 2
y x  2mx 1 có ba điểm cực trị là
ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng 1. 1   5 A. m  . B. m  1. 2 1   5 1 5
C. m  1; m  .
D. m  1; m  . 2 2 Câu 3.
Cho hàm số y f x có đồ thị như hình vẽ:
Tìm m để phương trình f x   m  0 có 9 nghiệm phân biệt. A. m  1.
B. 1  m  3 .
C. 0  m  1. D. m  3 . Câu 4.
Tiếp tuyến của đồ thị hàm số 3 2
y x  3x  2 tại điểm M  1  ; 2
  có phương trình là
A. y  9x  2 .
B. y  24x  2 .
C. y  24x  22 .
D. y  9x  7 . 2 cos x m Câu 5.
Cho hàm số y f (x) 
. Tìm tất cả các giá trị của m để hàm số f x đồng biến trên cos x 1    khoảng 0;   .  2  A. m  9 B. m  3 C. m  3 . D. m  9 .
Câu 6. Hàm số y f (x) liên tục trên  1  ;  3 có bảng biến thiên : Trang 1/16 - WordToan
Giá trị nhỏ nhất của hàm số trên đoạn  1  ;  3 là: A. 2. B. 1. C. -2. D. 0. 3  2x Câu 7.
Đồ thị hàm số y  có 2x  2
A. Tiệm cận đứng x  2  .
B. Tiệm cận đứng x  2 . C. 3
Tiệm cận ngang y  1. D. Tiệm cận ngang y  . 2 Câu 8. Hàm số 3
y x  3x nghịch biến trên khoảng nào dưới đây? A. 1;3 . B.  1  ;  . C.  ;   1 . D.  1   ;1 . 2
2x 1 x x  3 Câu 9.
Tổng số các đường tiệm cận đứng và tiệm cận ngang của hai đồ thị hàm số y  và 2 x  5x  6 2 x  3x  4 y  là 2 x 1 A. 2. B. 4. C. 5. D. 3.
Câu 10. Cho hàm số y f x xác định, liên tục trên  và có bảng biến thiên như sau
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trong khoảng 1;  .
B. Hàm số nghịch biến trong khoảng  1  ; 0 .
C. Hàm số đồng biến trong khoảng   ;1 và  1  ;0 .
D. Hàm số nghịch biến trong khoảng 1; .
Câu 11. Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
Trang 2/16 – Diễn đàn giáo viên Toán A. 3 2
y x  3x 1. B. 3 2
y x  3x  3 . C. 3 2
y  x  3x 1. D. 3 2
y x  3x  2 .
Câu 12. Đường cong sau là đồ thị của hàm số nào dưới đây? A. 4 2
y  x  5x 1 . B. 4 2
y  2x  3x 1 . C. 4 2
y x  2x 1. D. 4 2
y  2x  3x 1 .
Câu 13. Số điểm cực tiểu của hàm số 4 2
y x  2 x  5 là A. 3 . B. 1 . C. 2 . D. 0 .
Câu 14. Tổng số điểm cực trị của hai hàm số 3
y x  5x  1 và 4 2
y   x x  1 là A. 2 . B. 3 . C. 5 . D. 1 .
Câu 15. Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào? 2x  2 2x 1 2x 1 2x  3 A. y  . B. y  . C. y  . D. y  . x 1 x 1 x 1 x 1
Câu 16. Cho hàm số y f x có bảng biến thiên như sau x  2 2  y '  0  0   3 y 0  Gọi y , y
là giá trị cực đại và giá trị cực tiểu của hàm số đã cho. Tính yy . CD CT CD CT A. 1. B. 2. C. 0. D. 3.
Câu 17. Tìm tất cả các giá trị của tham số m để đồ thị hàm số y  3
x mx  2 cắt trục hoành tại ba điểm phân biệt. A. m  3  . B. m  3  . C. Kết quả khác. D. m  3 .
Câu 18. Cho hàm số bậc ba:  3  2 y ax
bx cx d có bảng biến thiên như hình sau ̣(H.6). Trang 3/16 - WordToan x  1 3   y  0  0  y 2   2 H.6
Tính tổng T a b c . 9 3 7 11 A.  . B. . C. . D.  . 8 8 8 8
Câu 19 . Hàm số y f x có đồ thị là đường cong trong hình vẽ bên. Hàm số y f x đạt cực tiểu tại điểm nào dưới đây. A. x  2  . B. x  4 . C. x  2 . D. x  0 .
Câu 20 . Hàm số nào trong các hàm số tương ứng ở các phương án A, B, C, D có đồ thị là hình bên. x 1 A. y  . B. 4 2
y x  2x 1. x 1 x  2 x 1 C. y  . D. y  . x 1 x 1 Câu 21. Cho hàm số 2
y x  2x 1. Tìm giá trị lớn nhất của hàm số đã cho trên  2  ;  3 A. 9 . B. 3 . C. Không tồn tại. D. 4 .
Câu 22. Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
Trang 4/16 – Diễn đàn giáo viên Toán A. 4 2
y x x 1 . B. 4 2
y   x x  2 . C. 4 2
y  x x  2 . D. 4 2
y   x  2 x  2 . 2 x  3
Câu 23. Cho hàm số y
. Mệnh đề nào dưới đây đúng? x  1
A. Cực đại của hàm số bằng 2.
B. Cực tiểu của hàm số bằng 1.
C. Cực đại của hàm số bằng 3 .
D. Cực đại của hàm số bằng 6 . x  1
Câu 24. Cho hàm số y
. Khẳng định nào sau đây đúng? x  1
A. Đồ thị hàm số có tiệm cận đứng x  1 .
B. Đồ thị hàm số có tiệm cận ngang y  1  .
C. Đồ thị hàm số có tiệm cận ngang y  1 .
D. Đồ thị hàm số có tiệm cận ngang x  1.
Câu 25. Cho hàm số y f x xác định, liên tục trên  \  
0 và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số nghịch biến trên khoảng  1;  0 .
B. Hàm số đồng biến trong khoảng  1;  0 .
C. Hàm số đồng biến trong khoảng ;  1 .
D. Hàm số đồng biến trong khoảng 1;   . BẢNG ĐÁP ÁN 1.A 2.D 3.A 4.D 5.B 6.C 7.C 8.D 9.B 10.A 11.B 12.B 13.C 14.B 15.B 16.D 17.D 18.D 21.A 22.B 23.D 24.C 25.B
LỜI GIẢI CHI TIẾT 1 Câu 1.
Giá trị nhỏ nhất của hàm số y x  trên đoạn [1;3] là x 1 1 7 11 A. . B. 3 . C. . D. . 2 4 4 Lời giải Chọn A Trang 5/16 - WordToan 1 1 Ta có: y  1  0, x   1
  hàm số y x
đồng biến trên đoạn [1;3] . 2 (x 1) x 1 1 1
Vậy, Min y y(1)  1  . [1;3] 2 2 Câu 2.
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 4 2
y x  2mx 1 có ba điểm cực trị là
ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng 1. 1   5 A. m  . B. m  1. 2 1   5 1 5
C. m  1; m  .
D. m  1; m  . 2 2 Lời giải Chọn D
+ Để hàm số có ba điểm cực trị 3 2
y  4x  4mx  4x(x  )
m  0 có ba nghiệm phân biệt 2
x m  0 (*) .
Khi đó, đồ thị hàm số có ba điểm cực trị ( A 0;1) , 2
B( m;1 m ) , 2
C ( m;1  m ) .
+ Gọi H là trung điểm BC , khi đó 2
H (0;1 m ) và AH là đường cao của tam giác ABC nên ta 1 . AB AC.BC có: 2 2 4 AH .BC   2 . R AH  .
AB AC  4R .AH AB (Vì 2 4R  m  0 2 4
2m  (m m )  AB AC ) 4 4 2 4 2
 4.1.m  (m m ) 
m  2m m  0   m  1 (**) . 2 4
2m m m   1 5 m   2 1 5
Từ (*) và (**) suy ra: m 1; m  . 2 Câu 3.
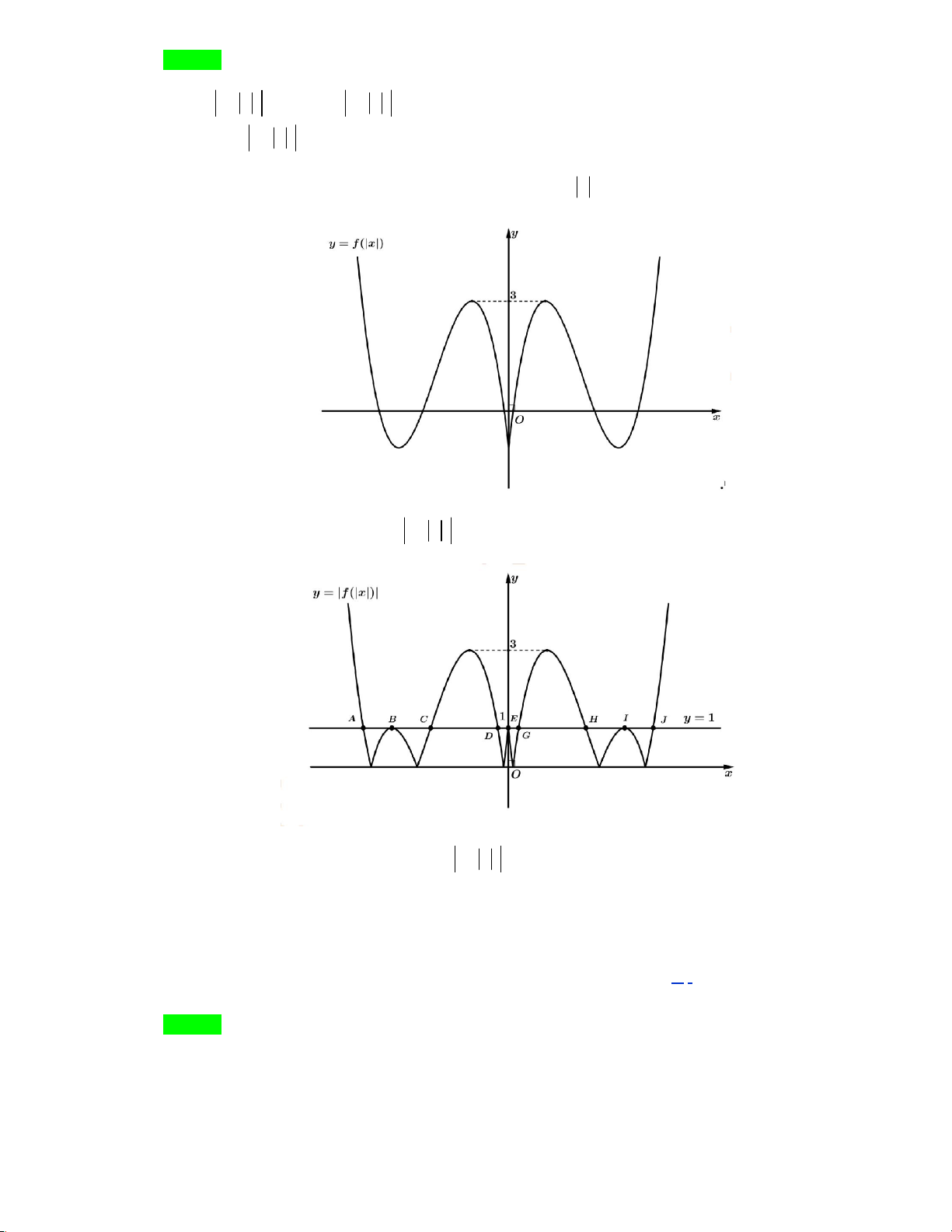
Cho hàm số y f x có đồ thị như hình vẽ:
Tìm m để phương trình f x   m  0 có 9 nghiệm phân biệt. A. m  1.
B. 1  m  3 .
C. 0  m  1. D. m  3 . Lời giải
Trang 6/16 – Diễn đàn giáo viên Toán Chọn A
Ta có: f x   m  0  f x   m . Phương trình này có 9 nghiệm phân biệt khi và chỉ khi đồ thị
hàm số y f x  cắt đường thẳng y m tại 9 điểm phân biệt.
Từ đồ thị hàm số y f x ta suy ra đồ thị hàm số y f x  như sau:
Từ đó ta suy ra đồ thị hàm số y f x  như sau:
Dựa vào đồ thị ta thấy đồ thị hàm số y f x  cắt đường thẳng y  1 tại 9 điểm phân biệt. Vậy m  1. Câu 4.
Tiếp tuyến của đồ thị hàm số 3 2
y x  3x  2 tại điểm M  1  ; 2
  có phương trình là
A. y  9x  2 .
B. y  24x  2 .
C. y  24x  22 .
D. y  9x  7 . Lời giải Chọn D Ta có: 2
y  3x  6x . Suy ra y  1  9 .
Phương trình tiếp tuyến của đồ thị hàm số tại M có phương trình:
y y  1 . x  
1  2  y  9. x  
1  2  y  9x  7 . Trang 7/16 - WordToan 2 cos x m
Câu 5. Cho hàm số y f (x) 
. Tìm tất cả các giá trị của m để hàm số f x đồng cos x 1    biến trên khoảng 0;   .  2  A. m  9 B. m  3 C. m  3 . D. m  9 . Lời giải Chọn B 2
 sin x(cos x  2 cos x m) Ta có ' f (x)  . 2 (cos x 1)      
Hàm số f x đồng biến trên khoảng 0; 
  f '(x)  0, x   0;    2   2     2 
cos x  2 cos x m  0, x   0; 2 
  m t  2t, t  0; 
1 , với t  cos x .  2   m  max  2
t  2t   m  3 . 0;  1
Câu 6. Hàm số y f (x) liên tục trên  1  ;  3 có bảng biến thiên :
Giá trị nhỏ nhất của hàm số trên đoạn  1  ;  3 là: A. 2. B. 1. C. -2. D. 0. Lời giải Chọn C
Dựa vào bảng biến thiên suy ra giá trị nhỏ nhất của hàm số trên  1  ;  3 bằng -2. 3  2x Câu 7.
Đồ thị hàm số y  có 2x  2
A. Tiệm cận đứng x  2  .
B. Tiệm cận đứng x  2 . C. 3
Tiệm cận ngang y  1. D. Tiệm cận ngang y  . 2 Lời giải Chọn C 3  2x 3  2x 3  2x Ta có lim y  lim
 1 hoặc lim y  lim
 1 nên đồ thị hàm số y  có tiệm x
x 2x  2 x
x 2x  2 2x  2 cận ngang y  1. Câu 8. Hàm số 3
y x  3x nghịch biến trên khoảng nào dưới đây? A. 1;3 . B.  1  ;  . C.  ;   1 . D.  1   ;1 . Lời giải Chọn D Ta có hàm số 3
y x  3x có tập xác định x – ∞ -1 1 + ∞ D   , 2
y  3x  3 . Ta có y' + 0 – 0 + 2 + ∞
Trang 8/16 – Diễn đàn giáo viên Toán y – ∞ -2 x  1  y  0  
, từ đó ta có bảng biến thiên: x  1 
Vậy hàm số nghịch biến trên khoảng  1  ;  1 . 2
2x 1 x x  3 Câu 9.
Tổng số các đường tiệm cận đứng và tiệm cận ngang của hai đồ thị hàm số y  và 2 x  5x  6 2 x  3x  4 y  là 2 x 1 A. 2. B. 4. C. 5. D. 3. Lời giải Chọn B. 2 x  3x  4
x  4 x   1 Ta có: lim  lim
   TCĐ: x  1 . 2 x 1  x 1 x 1   x   1  x   1 2 x  3x  4
x  4 x   1 x  4 5 lim  lim  lim   x  1  không phải là TCĐ. 2 x 1  x 1 x 1   x   1  x   x1 1 x 1 2 2 x  3x  4 lim  1  TCN: y  1. 2 x x 1 2
2x 1 x x  3 Ta có: lim
   TCĐ: x  3 . 2 x3 x  5x  6 2x 1 2  2 2
2x 1 x x  3 2 x x  3 7 lim  lim  
x  2 không phải là TCĐ. 2 x2 x2 x  5x  6 2x  5 6 2
2x 1 x x  3 lim
 0  TCN: y  0 . 2 x x  5x  6 2 x x  6 x  3 2 x  2  2  2 2 2
2x 1 x x  3
3  x x  3
3  x x  3 lim  lim  lim  0 2 2 x x  5x  6 x x  5x  6 x x  3  TCN: y  0 .
Câu 10. Cho hàm số y f x xác định, liên tục trên  và có bảng biến thiên như sau
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trong khoảng 1;  .
B. Hàm số nghịch biến trong khoảng  1  ; 0 .
C. Hàm số đồng biến trong khoảng   ;1 và  1  ;0 . Trang 9/16 - WordToan
D. Hàm số nghịch biến trong khoảng 1; . Lời giải Chọn A.
Câu 11. Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? A. 3 2
y x  3x 1. B. 3 2
y x  3x  3 . C. 3 2
y  x  3x 1. D. 3 2
y x  3x  2 . Lời giải Chọn B
Dựa vào đồ thị và đáp án, hàm số cần tìm có dạng 3 2
y ax bx c với a  0 . Loại C.
Đồ thị hàm số cắt trục tung tại 0;c với c  0 . Loại A. 2
y  3ax  2bx .
Hàm số cần tìm đạt cực đại tại x
 0 và đạt cực tiểu tại x
d  0 . Do đó y  0 hay CD CT 2
3ax  2bx  0 có hai nghiệm là x  0 và x d  0 .  x  0 + Xét đáp án B: 2
y  3x  6x ; 2
3x  6x  0  3x x  2  0   (thỏa mãn). x  2  x  0 + Xét đáp án D: 2
y  3x  6x ; 2
3x  6x  0  3x x  2  0   (loại). x  2  Vậy chọn B.
Câu 12. Đường cong sau là đồ thị của hàm số nào dưới đây? A. 4 2
y  x  5x 1 . B. 4 2
y  2x  3x 1 . C. 4 2
y x  2x 1. D. 4 2
y  2x  3x 1 . Lời giải Chọn B
Dựa vào đồ thị và đáp án, hàm số cần tìm có dạng 4 2
y ax bx c với a  0 . Loại A.
Đồ thị hàm số cắt trục tung tại 0;c với c  0 . Loại D.
Trang 10/16 – Diễn đàn giáo viên Toán a  0 Hàm số 4 2
y ax bx c cần tìm có 2 cực tiểu và 1 cực đại khi  . ab  0  a  2  0 + Xét đáp án B:  (thỏa mãn). ab  6  0  a  1  0 + Xét đáp án C:  (loại). ab  2  0  Vậy chọn B.
Câu 13. Số điểm cực tiểu của hàm số 4 2
y x  2 x  5 là A. 3 . B. 1 . C. 2 . D. 0 . Lời giải Chọn C x  0 Ta có 3
y  x x x  2 4 4 4 x  
1 , y  0  4x  2 x   1  0   . x  1  Bảng xét dấu y
Dựa vào xét ấu ta thấy hàm số có 2 điểm cực tiểu. a  0
Làm trắc nghiệm: Hàm số bậc bốn trùng phương 4 2
y ax bx c thoản mãn  có 3 điểm b  0 
cực trị trong đó có 2 điểm cực tiểu, 1 điểm cực đại.
Câu 14. Tổng số điểm cực trị của hai hàm số 3
y x  5x  1 và 4 2
y   x x  1 là A. 2 . B. 3 . C. 5 . D. 1 . Lời giải Chọn B Hàm số 3
y x  5 x  1 có 2
y  3x  5 , y  0 có hai nghiệm đơn phân biệt nên hàm số có 2 điểm cực trị. Hàm số 4 2
y   x x  1 có 3 y  4
x  2x , y  0 có nghiệm đơn duy nhất nên hàm số có 1 điểm cực trị.
Vậy tổng số điểm cực trị của hai hàm số 3
y x  5 x  1 và 4 2
y   x x  1 là 3 .
Câu 15. Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào? Trang 11/16 - WordToan 2x  2 2x 1 2x 1 2x  3 A. y  . B. y  . C. y  . D. y  . x 1 x 1 x 1 x 1 Lời giải Chọn B
Từ đồ thị đã cho ta thấy đồ thị hàm số cần tìm có
- Tiệm cận ngang y  2.
- Tiệm cận đứng x  1.  1 
- Giao điểm với trục hoành: ; 0 .    2 
- Giao điểm với trục tung: 0;   1 .
- Đồ thị là đường luôn đi lên từ trái sang phải nên hàm số đồng biến trên từng khoảng xác định. 2x 1
Do đó ta có hàm số y  thỏa mãn. x 1
Câu 16. Cho hàm số y f x có bảng biến thiên như sau x  2 2  y '  0  0   3 y 0  Gọi y , y
là giá trị cực đại và giá trị cực tiểu của hàm số đã cho. Tính yy . CD CT CD CT A. 1. B. 2. C. 0. D. 3. Lời giải Chọn D
Từ bảng biến thiên ta có y  3; y  0 nên yy  3. CD CT CD CT
Câu 17. Tìm tất cả các giá trị của tham số m để đồ thị hàm số y  3
x mx  2 cắt trục hoành tại ba điểm phân biệt. A. m  3  . B. m  3  . C. Kết quả khác. D. m  3 . Lời giải Chọn D
Đồ thị hàm số y  3
x mx  2 cắt trục hoành tại ba điểm phân biệt  Đồ thị hàm số đó có hai
điểm cực trị nằm hai phía so với trục hoành.
Trang 12/16 – Diễn đàn giáo viên Toán Ta có: 2
y  3x m m 2
y  0  x  . 3
Hàm số có hai điểm cực trị  y  0 có hai nghiệm phân biệt  m  0   1 .  m 2m m   m 2m m
Khi đó đồ thị hàm số có hai điểm cực trị là A ;   2 , B   ;  2 .  3 3 3   3 3 3       2m m   2m m
A và B nằm khác phía so với trục hoành     2   2   0  3 3   3 3      3 4m  4   0 27  m  3 2 . Kết hợp  
1 và 2 , ta được m  3 .
Câu 18. Cho hàm số bậc ba:  3  2 y ax
bx cx d có bảng biến thiên như hình sau ̣(H.6). x  1 3  y  0  0  y 2   2 H.6
Tính tổng T a b c . 9 3 7 11 A.  . B. . C. . D.  . 8 8 8 8 Lời giải Chọn D Ta có:     3  2 y f x ax
bx cx d
f x  2
3ax  2bx c .
Dựa vào bảng biến thiên, ta thấy đồ thị hàm số có hai điểm cực trị A 1; 2 và B3;  2 Trang 13/16 - WordToan  1 a    f  8 1  2 
a b c d  2   3 bf 3     2
27a  9b  3c d  2   8     . f   1   0
3a  2b c   0  9 c    f 3  
27a  6b c    0  0 8   5 d    8 11
Vậy T a b c   . 8
Câu 19 . Hàm số y f x có đồ thị là đường cong trong hình vẽ bên. Hàm số y f x đạt cực tiểu tại điểm nào dưới đây. A. x  2  . B. x  4 . C. x  2 . D. x  0 . Lời giải Chọn D
Dựa vào đồ thị hàm số ta thấy hàm số đạt cực tiểu tại x  0 .
Câu 20 . Hàm số nào trong các hàm số tương ứng ở các phương án A, B, C, D có đồ thị là hình bên. x 1 A. y  . B. 4 2
y x  2x 1. x 1 x  2 x 1 C. y  . D. y  . x 1 x 1 Lời giải
Trang 14/16 – Diễn đàn giáo viên Toán Chọn A ax b
Dựa vào đồ thị hàm số ta thấy đây là đồ thị của hàm phân thức dạng y
, ad bc  0 , cx d nên ta loại đáp án B.
Từ đồ thị hàm số ta thấy đồ thị hàm số có tiệm cận ngang là đường thằng y  1 và tiệm cận đứng là
đường thẳng x  1
 và đi qua điểm M 0;  
1 nên đáp án cần tìm là A. Câu 21. Cho hàm số 2
y x  2x 1. Tìm giá trị lớn nhất của hàm số đã cho trên  2  ;  3 A. 9 . B. 3 . C. Không tồn tại. D. 4 . Lời giải Chọn A 2
y x  2x 1 Tập xác định D   .
y '  0  2x  2  0  x  1 2  ;  3 . f  2
   9; f 3  4; f   1  0 .
Từ đó suy ra max y  9 tại x  2  .  2  ;  3
Câu 22. Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào? A. 4 2
y x x 1 . B. 4 2
y   x x  2 . C. 4 2
y  x x  2 . D. 4 2
y   x  2 x  2 . Lời giải Chọn B
Quan sát đồ thị ta thấy:
Đồ thị hình trên là đồ thị của hàm số : 4 2
y ax bx c a  0 . Nên loại A.
Hàm số có 3 điểm cực trị  .
a b  0 mà a  0  b  0 . Nên loại C.
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên c  0 . Nên loại D. 2 x  3
Câu 23. Cho hàm số y
. Mệnh đề nào dưới đây đúng? x  1
A. Cực đại của hàm số bằng 2.
B. Cực tiểu của hàm số bằng 1.
C. Cực đại của hàm số bằng 3 .
D. Cực đại của hàm số bằng 6 . Lời giải Chọn D
Hàm số đã cho có tập xác định  \ {  1}. Trang 15/16 - WordToan 2 x  2x  3 Ta có y  .  x  2 1  x  3 y  0   . x  1  Bảng biến thiên
Dựa trên bảng biến thiên ta có cực đại của hàm số bằng 6 . x  1
Câu 24. Cho hàm số y
. Khẳng định nào sau đây đúng? x  1
A. Đồ thị hàm số có tiệm cận đứng x  1 .
B. Đồ thị hàm số có tiệm cận ngang y  1  .
C. Đồ thị hàm số có tiệm cận ngang y  1 .
D. Đồ thị hàm số có tiệm cận ngang x  1. Lời giải Chọn C Tập xác định  \ {1}. x  1 Ta có lim
 1 nên đồ thị hàm số có tiệm cận ngang y  1 .
x x  1
Câu 25. Cho hàm số y f x xác định, liên tục trên  \  
0 và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số nghịch biến trên khoảng  1;  0 .
B. Hàm số đồng biến trong khoảng  1;  0 .
C. Hàm số đồng biến trong khoảng ;  1 .
D. Hàm số đồng biến trong khoảng 1;   . Lời giải Chọn B
Từ bảng biến thiên ta thấy hàm số đồng biến trong khoảng  1;  0 .
Trang 16/16 – Diễn đàn giáo viên Toán
Document Outline

  • 1132
    • de 101
    • Phieu soi dap an
  • 1567940758_WT06-GT12-C1-KIỂM-TRA-1-TIẾT-HÀM-SỐ-K12-THPT-TÂN-HIỆP-KIÊN-GIANG-NĂM-2019