Đề kiểm tra 1 tiết Giải tích 12 chương 3 năm 2017 – 2018 trường Phan Văn Đạt – Long An

Đề kiểm tra 1 tiết Giải tích 12 chương 3 năm học 2017 – 2018 trường THPT Phan Văn Đạt – Long An gồm 25 câu hỏi trắc nghiệm, thời gian làm bài 45 phút, nội dung kiểm tra thuộc chủ đề nguyên hàm – tích phân và ứng dụng, đề kiểm tra có ma trận đề, có đáp án và lời giải chi tiết.

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

15 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
SỞ GD-ĐT LONG AN ĐỀ KIỂM TRA 1 TIẾT – NĂM HỌC 2017-2018
TRƯỜNG THPT PHAN VĂN ĐẠT MÔN: TOÁN- Giải tích 12, CHƯƠNG 3.
Thời gian: 45 phút (không kể thời gian phát đề)
Hình thức: trắc nghiệm
Họ và tên:……………………………………….
Điểm:
Lớp:…………………………………………….
MA TRẬN ĐỀ KIỂM TRA
Cấp độ
Chủ đề
Nhận biết Thông hiểu
Vận dụng
Cộng
Cấp độ thấp Cấp độ cao
Nguyên hàm
Biết dựa vào
định nghĩa,tính
chất và bảng
nguyên hàm để
nhận biết
nguyên hàm của
các hàm số
Biết tìm nguyên
hàm của một số
hàm số đơn
giản
Biết sử dụng
các phương
pháp tìm
nguyên hàm
của các hàm số
Tìm một hàm
số cụ thể nhờ
xác định
nguyên hàm
Số câu:4
Số điểm:1.6
Số câu:2
Số điểm: 0.8
Số câu:2
Số điểm: 0.8
Số câu:1
Số điểm: 0.4
Số câu: 9
Số điểm:
3.6
Tích phân
Biết dựa vào
định nghĩa, tính
chất để tính các
tích phân đơn
giản
Biết tìm tích
phân của một số
hàm số đơn
giản
Biết sử dụng
các phương
pháp tính tích
phân để tính
tích phân của
một số hàm số
Biết sử dụng
tích phân để
giải quyết bài
toán thực tế
Số câu:2
Số điểm: 0.8
Số câu:3
Số điểm: 1.2
Số câu: 3
Số điểm: 1.2
Số câu:1
Số điểm:0.4
Số câu: 9
Số điểm:
3.6
Ứng dụng
Nhận biết được
công thức tính
diện tích, thể
tích
Tính được diện
tích, thể tích
của một số hình
giới hạn bởi các
hàm số đơn
giản
Tính được diện
tích, thể tích
một số hình
phải xác định
các cận
Tính được thể
tích một số hình
phải căn cứ vào
hình vẽ để xác
định
Số câu:2
Số điểm: 0.8
Số câu:2
Số điểm: 0.8
Số câu:2
Số điểm: 0.8
Số câu:1
Số điểm: 0.4
Số câu: 7
Số điểm:
2.8
Tổng
Số câu:8
Số điểm: 3.2
Số câu: 7
Số điểm: 2.8
Số câu: 7
Số điểm: 2.8
Số câu: 3
Số điểm: 1.2
Số câu:
25
Số điểm:
10
Câu 1: [2D3-1.1-1] Tìm họ nguyên hàm

F
x
của hàm số
2
() 3sinfx x
x

A.
() 3cos 2ln
F
xxxC
. B.
() 3cos 2ln
F
xxxC
.
C.
() 3cos 2lnFx x x C
. D.
() 3cos 2lnFx x x C
.
Câu 2: [2D3-1.1-1] Công thức nào sau đây sai?
A.
cos d sin
x
xxC
. B.
d
xx
ax a C
C.

2
11
d0xCx
x
x

. D.

2
1
dtan 0
cos
xx
x
CC
.
Câu 3:
[2D3-1.1-1] Trong các khẳng định sau, khẳng định nào là sai?
A. Nếu
,
f
xgx
là các hàm số liên tục trên R thì
   
f
x gx dx f xdx gxdx 


.
B. Nếu
Fx
và
Gx
đều là nguyên hàm của hàm số
f
x
thì
Fx Gx C
(với C là
hằng số).
C. Nếu các hàm số
,ux vx
liên tục và có đạo hàm trên R thì
() () () () ()()u x v x dx v x u x dx u x v x



.
D.
2
Fx x
là một nguyên hàm của

2
f
xx
.
Câu 4: [2D3-1.1-1] Tìm tất cả các nguyên hàm của hàm số
cos 2
f
xx
là
A.

1
sin2 .
2
Fx x C
B.

1
sin2 .
2
Fx x C
C.
sin2 .Fx x C
D.
sin2 .Fx x
Câu 5: [2D3-2.1-1] Tìm nguyên hàm

Fx của hàm số

2
13
x
x
fx e e

A.
3
3
xx
Fx e e C
 . B.
3
xx
Fx e e C
 .
C.
3
xx
F
xe e C

. D.
2
3
xx
F
xe e C

.
Câu 6: [2D3-2.1-1]Xét

f
x
là một hàm số liên tục trên đoạn

,ab
, (với
ab
) và

Fx
là một
nguyên hàm của hàm số

f
x
trên đoạn

,ab
. Mệnh đề nào dưới đây đúng?
A.
 
35d 35
b
b
a
a
fx xFx
. B.

1d
b
b
a
a
f
xxFx
.
C.


2d 2
b
a
f
xx Fb Fa
. D.

d
b
a
f
xxFb Fa
.
Câu 7: [2D3-3.1-1] Cắt một vật thể

T bởi hai mặt phẳng
P
và
Q vuông góc với trục Ox lần
lượt tại 1
x
và 2.x Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm
12xx cắt

T theo thiết diện có diện tích là
2
6.
x
Tính thể tích V của phần vật thể
T giới hạn bởi hai
mặt phẳng
P
và
.Q
A. 28 .V
B. 28.V C. 14 .V
D. 14.V
Câu 8: [2D3-3.1-1]Cho hàm số

yfx
liên tục trên đoạn

;ab
. Diện tích hình phẳng giới hạn bởi
đường cong
yfx
, trục hoành, các đường thẳng
x
a
,
x
b
là
A.

d
b
a
f
xx
. B.

d
b
a
f
xx
. C.

d
a
b
f
xx
. D.

d
b
a
f
xx
.
Câu 9: [2D3-1.4-2] Tìm
2
32
dx
x
x
A.
2
ln
1
x
C
x
. B.
1
ln
2
x
C
x
.
C.
ln( 2)( 1)
x
xC
. D.
11
ln ln
21
C
x
x


.
Câu 10: [2D3-1.6-2] Trong các hàm số
f
x
dưới đây, hàm số nào thỏa mãn đẳng thức
.sin d .cos .cos d


x
f
xxxfx x xx?
A.
ln .
x
f
xx
B.
.ln .

x
f
xx
C.

.
ln
x
fx D.

.
ln

x
fx
Câu 11: [2D3-2.1-2] Biết

4
2
1
dln5ln3,
21
xm n mn
x

. Tính
P
mn.
A.
3
2
P  .
B.
3
2
P .
C.
1
P

. D.
1
P
.
Câu 12: [2D3-2.1-2] Tính tích phân
1
2
0
2
d
4
Ix
x
bằng cách đặt
2sinxt
. Mệnh đề nào dưới đây
đúng?
A.
1
0
2d.It
B.
4
0
2d.It
C.
3
0
dIt
. D.
6
0
d.It
Câu 13: [2D3-2.6-2] Giá trị của tích phân
2
2
0
cos d
Ix xx
được biểu diễn dưới dạng
2
.
ab

, ab
.
Khi đó tích
.ab
bằng
A.
0
. B.
1
32
.
C.
1
16
.
D.
1
64
.
Câu 14: [2D3-3.1-2] Gọi
S
là hình phẳng giới hạn bởi đồ thị hàm số

1
:
1
x
Hy
x
và các trục tọa độ.
Khi đó giá trị của
S
bằng
A.
ln 2 1S đvdt
. B.
ln 4 1S đvdt
.
C.
ln 4 1S đvdt
. D.
ln 2 1S đvdt
.
Câu 15: [2D3-3.3-2] Thể tích của khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường có
phương trình
1
22
x
y
xe
, trục
Ox
,
1
x
,
2x
quay một vòng quanh trục
Ox
bằng:
A.
e
. B.
2
e
. C.
4
. D.
16
.
Câu 16: [2D3-1.1-3]Tìm hàm số
F
x
, biết rằng

2
1
sin
Fx
x
và đồ thị của hàm số

F
x
đi qua
điểm
;0
6



M
.
A.
cot 3Fx x . B.

1
3
sin
Fx
x
.
C.
cot 3 Fx x . D.
tan 3Fx x .
Câu 17: [2D3-1.5-3] Nguyên hàm
d
2tan 1
x
x
bằng
A.
2
ln 2sin cos
55
x
x
xC
. B.
21
ln 2sin cos
55
x
x
xC
.
C.
1
ln 2sin cos
55
x
x
xC
. D.
1
ln 2sin cos
55
x
x
xC
.
Câu 18: [2D3-2.1-3] Cho n là số tự nhiên sao cho

1
2
0
1
1d
20
n
xxx

. Tính tích phân
2
0
sin cos d
n
x
xx
A.
1
10
.
B.
1
15
.
C.
1
5
.
D.
1
20
.
Câu 19: [2D3-2.4-3] Tìm tất cả các số thực dương m để
2
0
d1
ln 2
12
m
xx
x

.
A.
2m
. B.
2m
. C.
3m
. D.
3m
.
Câu 20: [2D3-2.6-3] Biết



22
ln 1 d ln 1
x
x x ax bx c x mx nx p
, với
,,, ,,abcmn p
.
Tính
222
Sa b c
.
A.
1S
. B.
1
2
S
. C.
1
4
S
. D.
2S
.
Câu 21: [2D3-3.1-3]Gọi S là diện tíchhình phẳng giới hạn bởi đồ thị

21
:
1
x
Cy
x
, tiệm cận ngang
của
C
, trục tung và đường thẳng
0xaa
. Tìm
a
để
ln 2017S
.
A.
3
2017 1a . B.
2017
1
3
a 
. C.
2016a
. D. 2017 1a .
Câu 22: [2D3-3.7-3] Một ô tô đang chuyển động đều với vận tốc
12ms
thì người lái đạp phanh; từ
thời điểm đó ô tô chuyển động chậm dần đều với vận tốc
212 vt t ms
(trong đó t là
thời gian tính bằng giây, kể từ lúc đạp phanh). Hỏi trong thời gian 8 giây cuối (tính đến khi xe
dừng hẳn) thì ô tô đi được quãng đường bằng bao nhiêu?
A.
16m
. B.
60m
. C.
32m
. D.
100m
.
Câu 23: [2D3-3.6-4] Cho hàm số
y
fx
. Đồ thị của hàm số
y
fx
như hình bên. Đặt
cos
g
xfx x . Mệnh đề nào dưới đây đúng ?
A.

0
2
gg g




.
B.

0
2
ggg




.
C.

0
2
ggg




.
D.

0
2
ggg




.
Câu 24: [2D3-3.7-4] Một vật chuyển động trong 3 giờ với vận tốc v (km/h) phụ thuộc vào thời gian t
(h) có đồ thị vận tốc như hình bên. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển
động, đồ thị đó là một phần của đường parabol có đỉnh

2;5I và trục đối xứng song song với
trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính
quãng đường mà vật di chuyển được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm).
A.

33
3
km
. B.

15 km
. C.
12 km
. D.

35
3
km
.
Câu 25: [2D3-3.2-4] Xét hình phẳng
D
giới hạn bởi các đường

2
3, 0, 0.yx y x
Gọi
0;9 , ;0
A
Bb
30.b
Tìm b để đoạn thẳng
A
B chia
D
thành hai phần có diện tích
bằng nhau.
A. 2.b  B.
1
.
2
b  C. 1.b  D.
3
.
2
b 
BẢNG ĐÁP ÁN
1.A 2.B 3.C 4.B 5.B 6.D 7.C 8.A 9.A 10.C
11.A 12.C 13.D 14.B 15.B 16.C 17.A 18.A 19.B 20.B
21.A 22.B 23.B 24.A 25.C
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 26:
[2D3-1.1-1] Tìm họ nguyên hàm

F
x
của hàm số
2
() 3sin
fx x
x

A.
() 3cos 2lnFx x x C
. B.
() 3cos 2lnFx x x C
.
C.
() 3cos 2lnFx x x C
. D.
() 3cos 2lnFx x x C
.
Hướng dẫn giải
Chọn A.

21
3sin 3 sin 2 d 3cos 2ln





F
xxdxxdxxxxC
xx
.
Câu 27: [2D3-1.1-1] Công thức nào sau đây sai?
A. cos d sin
x
xxC
. B. d
xx
ax a C
C.

2
11
d0
xCx
xx

. D.

2
1
dtan 0
cos
xx
x
CC
.
Hướng dẫn giải
Chọn B.
d
ln
x
x
a
ax C
a

.
Câu 28: [2D3-1.1-1] Trong các khẳng định sau, khẳng định nào là sai?
A. Nếu
,
f
xgx
là các hàm số liên tục trên R thì
   
f
x gx dx f xdx gxdx



.
B. Nếu
Fx và
Gx đều là nguyên hàm của hàm số

f
x thì
Fx Gx C (với C là
hằng số).
C. Nếu các hàm số
,ux vx
liên tục và có đạo hàm trên R thì
() () () () ()()u x v x dx v x u x dx u x v x



.
D.
2
Fx x là một nguyên hàm của
2
f
xx .
Hướng dẫn giải
Chọn C.
Ta
có

() ()d () ()d () () () ()d ()()d ()() .uxv x x vxu x x uxv x vxu x x uxvx x uxvx C



.
Câu 29: [2D3-1.1-1] Tìm tất cả các nguyên hàm của hàm số
cos 2
f
xx
là
A.

1
sin2 .
2
Fx x C B.

1
sin2 .
2
Fx x C
C.
sin2 .Fx x C D.
sin2 .Fx x
Hướng dẫn giải
Chọn B.
Câu 30: [2D3-2.1-1] Tìm nguyên hàm
Fx của hàm số

2
13
x
x
fx e e

A.
3
3
xx
F
xe e C

. B.
3
xx
F
xe e C

.
C.
3
xx
Fx e e C
 . D.
2
3
xx
Fx e e C
 .
Hướng dẫn giải
Chọn B.
2
dx 1 3 dx 3 dx 3
xx xxxx
f
xee eeeeC



Câu 31: [2D3-2.1-1]Xét
f
x
là một hàm số liên tục trên đoạn

,ab
, (với
ab
) và
Fx
là một
nguyên hàm của hàm số
f
x
trên đoạn

,ab
. Mệnh đề nào dưới đây đúng?
A.
 
35d 35
b
b
a
a
fx xFx
. B.

1d
b
b
a
a
f
xxFx
.
C.


2d 2
b
a
f
xx Fb Fa
. D.

d
b
a
f
xxFb Fa
.
Lờigiải
Chọn D.
Theo định nghĩa Tích phân trong SGK trang 105 ta có:
  
d
b
b
a
a
f
xxFx Fb Fa
.
Câu 32: [2D3-3.1-1] Cắt một vật thể
T bởi hai mặt phẳng
P
và
Q vuông góc với trục
Ox lần lượt tại 1
x
và 2.x Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm
12xx
cắt

T
theo thiết diện có diện tích là
2
6.
x
Tính thể tích V của phần vật thể

T
giới hạn bởi hai
mặt phẳng
P
và
.Q
A. 28 .V
B. 28.V C. 14 .V
D. 14.V
Hướng dẫn giải
Chọn C.
Ta có:
2
2
23
1
1
6214Vxdxx


.
Câu 33: [2D3-3.1-1]Cho hàm số
yfx
liên tục trên đoạn

;ab
. Diện tích hình phẳng giới hạn
bởi đường cong

yfx
, trục hoành, các đường thẳng
x
a
,
x
b
là
A.

d
b
a
f
xx
. B.

d
b
a
f
xx
. C.

d
a
b
f
xx
. D.

d
b
a
f
xx
.
Hướng dẫn giải
Chọn A
Theo định nghĩa ta có

d
b
a
Sfxx
Câu 34: [2D3-1.4-2] Tìm
2
32
dx
xx
A.
2
ln
1
x
C
x
. B.
1
ln
2
x
C
x
.
C.
ln( 2)( 1)
x
xC
. D.
11
ln ln
21
C
x
x


.
Hướng dẫn giải
Chọn A.
2
(1)(2)
3 2 ( 1)( 2) ( 1)( 2)
dx dx x x dx
xx x x x x




11
()ln2ln1
21
dx x x C
x
x


2
ln
1
x
C
x

Câu 35: [2D3-1.6-2] Trong các hàm số
f
x
dưới đây, hàm số nào thỏa mãn đẳng thức
.sin d .cos .cos d


x
f
xxxfx x xx?
A.
ln .
x
f
xx
B.
.ln .

x
f
xx
C.

.
ln
x
fx D.

.
ln

x
fx
Hướng dẫn giải
Chọn C.
Đặt
 
dd
.
dsind cos






ufx ufxx
vxxv x
Khi đó
.sin d .cos .cos d


f
xxxfx xfx xx
Suy ra
 
d.
ln


x
xx
f
xfxxC
Câu 36: [2D3-2.1-2] Biết

4
2
1
dln5ln3,
21
xm n mn
x

. Tính
P
mn.
A.
3
2
P  .
B.
3
2
P .
C. 1
P
 . D. 1
P
.
Hướng dẫn giải
Chọn A.
Ta có



44
4
2
22
111 1 1 1
d d 2 1 ln 2 1 ln 9 ln 5 ln 5 ln 3
21 221 2 2 2
xxx
xx



Suy ra
1
; 1
2
mn . Do đó
3
2
Pmn.
Câu 37: [2D3-2.1-2] Tính tích phân
1
2
0
2
d
4
Ix
x
bằng cách đặt
2sinxt
. Mệnh đề nào dưới đây
đúng?
A.
1
0
2d.It
B.
4
0
2d.It
C.
3
0
dIt
. D.
6
0
d.It
Hướng dẫn giải
Chọn C.
Đặt:
2sin d 2cos dxtx tt
00
1
6
x
t
xt





666
6
0
2
000
22
2cos d 2cos d 2d 2
3
2cos
44sin
Itttttt
t
t
.
Câu 38: [2D3-2.6-2] Giá trị của tích phân
2
2
0
cos d
Ix xx
được biểu diễn dưới dạng
2
.
ab
, ab
.
Khi đó tích
.ab
bằng
A.
0
. B.
1
32
.
C.
1
16
.
D.
1
64
.
Hướng dẫn giải
Chọn D.
Đặt
2
1cos2
cos d d
2
d
x
vx
ux
xx
dd
11
sin 2
24

uv
vx x
Vậy
2
0
11 11
sin 2 sin 2 d
2
24 24
0




Ix x x x xx
2
2
11
cos 2
2
84 8
0




xx

22
11
11
8448





2
11
16 4

Theo giả thiết
2
.
Ia b
1
16
1
4

a
b
1
.
64
ab .
Câu 39: [2D3-3.1-2] Gọi
S
là hình phẳng giới hạn bởi đồ thị hàm số

1
:
1
x
Hy
x
và các trục tọa
độ. Khi đó giá trị của
S
bằng
A.
ln 2 1S đvdt
. B.
ln 4 1S đvdt
.
C.
ln 4 1S đvdt
. D.
ln 2 1S đvdt
.
Hướng dẫn giải
Chọn B.
Phương trình hoành độ giao điểm

H
và trục Ox là:
1
01
1
x
x
x

.
Giao điểm
H
và trục Oy là:

0; 1
.
Vậy diện tích hình phẳng giới hạn bởi đồ thị hàm số

1
:
1
x
Hy
x
và các trục tọa độ là:


11
1
0
00
12
d 1 d 2ln 1 2ln 2 1 ln 4 1
11
x
Sx xxx
xx






.
Câu 40: [2D3-3.3-2] Thể tích của khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường có
phương trình
1
22
x
y
xe
, trục
Ox
,
1
x
,
2x
quay một vòng quanh trục
Ox
bằng:
A.
e
. B.
2
e
. C.
4
. D.
16
.
Hướng dẫn giải
Chọn B.
Ta có

2
222 2
2
1
22
1
111 1
.










x
xxxx
V xedxxedxxde xe edx.
 
2
2222
1
22


x
ee e ee ee e
.
Câu 41: [2D3-1.1-3]Tìm hàm số

F
x
, biết rằng

2
1
sin
Fx
x
và đồ thị của hàm số
F
x
đi qua
điểm
;0
6



M
.
A.
cot 3Fx x . B.

1
3
sin
Fx
x
.
C.
cot 3 Fx x . D.
tan 3Fx x .
Hướng dẫn giải
Chọn C.
Theo giả thiết ta có

2
1
cot
sin

Fx dx x C
x
.
Mặt khác vì đồ thị hàm số
F
x
đi qua điểm
;0
6



M
nên
cot 0 3
6
CC
.
Vậy
cot 3 Fx x .
Câu 42: [2D3-1.5-3] Nguyên hàm
d
2tan 1
x
x
bằng
A.
2
ln 2sin cos
55
x
x
xC
. B.
21
ln 2sin cos
55
x
x
xC
.
C.
1
ln 2sin cos
55
x
x
xC
. D.
1
ln 2sin cos
55
x
x
xC
.
Hướng dẫn giải
Chọn A.
* Biến đổi
d
2tan 1
x
I
x
=
cos
d
2sin cos
x
x
x
x
=
12cos sin sin
d
22sincos
x
xx
x
x
x

=
1 2cos sin 1 sin
dd
22sin cos 22sin cos
J
xx x
x
x
x
xxx



=
11
ln 2sin cos
22
x
xJ
* Ta tính 2 1.d
J
IxxC
, suy ra

1
2
x
IC
* Thế kết quả trên trở lại đề:

11
ln 2sin cos
24
IxxxIC
41 1
ln 2sin cos
52 4
IxxxC




21
ln 2sin cos
55
IxxxC

Câu 43: [2D3-2.1-3] Cho n là số tự nhiên sao cho

1
2
0
1
1d
20
n
xxx

. Tính tích phân
2
0
sin cos d
n
x
xx
A.
1
10
.
B.
1
15
.
C.
1
5
.
D.
1
20
.
Hướng dẫn giải
Chọn A




0
10
1
2
01
1
1
111
1d d 9
20 2 2 1 2 1
n
n
n
n
t
xxxtt nn
nn






. (1)
1
1
1
2
00
0
1
sin cos d d
11
n
nn
t
Ixxxtt
nn






(2).
Từ (1) và (2) suy ra
2
0
1
sin cos d
10
n
xxx
.
Câu 44: [2D3-2.4-3] Tìm tất cả các số thực dương m để
2
0
d1
ln 2
12
m
xx
x

.
A.
2m
. B.
2m
. C.
3m
. D.
3m
.
Hướng dẫn giải
Chọn B.
Ta có
 
222
00
d1
1d ln1 ln1
112 2
0
mm
m
xx x m
Ixxxx mm
xx









Theo giả thiết
1
ln 2
2
I 

2
1
ln 1 ln 2
22
m
mm
2
1
22
12
m
m
m


1m .
Câu 45: [2D3-2.6-3] Biết



22
ln 1 d ln 1
x
x x ax bx c x mx nx p
, với
,,, ,,abcmn p
. Tính
222
Sa b c
.
A.
1S
. B.
1
2
S
. C.
1
4
S
. D.
2S
.
Hướng dẫn giải
Chọn B.
Đặt
ln 1
dd
ux
vxx

2
1
dd
1
1
2
ux
x
vx

ln 1 d
x
xx

2
2
11
ln 1 d
221
x
x
xx
x

=

2
111
ln 1 1 d
221
x
xx x
x




=
 
22
111
ln 1 ln 1
222
x
xxxxC




=

22
11 11
ln 1
22 44
x
xxxC




Do đó
11
;0;
22
abc. Vậy
222
1
2
abc.
Câu 46: [2D3-3.1-3]Gọi
S
là diện tíchhình phẳng giới hạn bởi đồ thị

21
:
1
x
Cy
x
, tiệm cận
ngang của
C
, trục tung và đường thẳng
0xaa
. Tìm
a
để
ln 2017S
.
A.
3
2017 1a . B.
2017
1
3
a 
. C. 2016a . D. 2017 1a .
Hướng dẫn giải
Chọn A.
Diện tíchhình phẳng giới hạn bởi đồ thị

21
:
1
x
Cy
x
, tiệm cận ngang: 2y , trục tung và
đường thẳng
0xaa
là:

0
000
21 3 1
2d d3 d3ln 1 3ln 1
111
aaa
a
x
Sxxxxa
xxx




.
Để
ln 2017S thì
3
3ln 1 ln 2017 2017 1aa
.
Câu 47: [2D3-3.7-3] Một ô tô đang chuyển động đều với vận tốc
12ms
thì người lái đạp phanh;
từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc
212 vt t ms
(trong đó
t là
thời gian tính bằng giây, kể từ lúc đạp phanh). Hỏi trong thời gian 8 giây cuối (tính đến khi xe
dừng hẳn) thì ô tô đi được quãng đường bằng bao nhiêu?
A.
16m
. B.
60m
. C.
32m
. D.
100m
.
Hướng dẫn giải
Chọn B.
Xe dừng hẳn khi
2120 6 vt t t
.
Vậy trong 8 giây cuối (Tính đến khi xe dừng hẳn) thì 2 giây đầu xe vẫn chuyển động đều được
quãng đường là
1
12.2 24
s
m .
Xe dừng hẳn trong 6 giây cuối với quãng đường

66
2
00
d212d36

s
vt t t t m
Vậy tổng quãng đường xe đi được là
60
s
m
.
Câu 48: [2D3-3.7-4] Cho hàm số
yfx . Đồ thị của hàm số
yfx
như hình bên. Đặt
cos
g
xfx x
. Mệnh đề nào dưới đây đúng ?
A.

0
2
gg g




.
B.

0
2
ggg




.
C.

0
2
ggg




.
D.

0
2
ggg




.
Hướng dẫn giải
Chọn C.
Ta có
''sin
g
xfx x

0
'0'sin
2
x
gx f x x x
x

Từ đồ thị của hàm
'yfx ta có bảng biến thiên. (Chú ý là hàm
g
x và
'
g
x )
Bảng biến thiên
x

0
2

y
0
0
0
y

0g
2
g
g

Suy ra
 
0,
22
ggg g
 

 
 
Kết hợp với đồ thị ta có:







22
00
22
sin ' ' sin ' '
x
fxdx fx xdx gxdx gxdx





Theo hình vẽ
 
 
2
0
2
00
22
gggg gg
gx gx

 

 
 
Vậy

0
2
ggg




.
Câu 49: [2D3-3.7-4] Một vật chuyển động trong 3 giờ với vận tốc v (km/h) phụ thuộc vào thời
gian t (h) có đồ thị vận tốc như hình bên. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển
động, đồ thị đó là một phần của đường parabol có đỉnh
2;5I và trục đối xứng song song với
trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng
đường mà vật di chuyển được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm).
A.

33
3
km
. B.
15 km
. C.
12 km
. D.

35
3
km
.
Hướng dẫn giải
Chọn A.
Gọi
2
vt at bt c
.
Khi đó đồ thị hàm số
vvt
là một parabol có đỉnh
2;5I
và đi qua điểm
0;1A
nên ta có
hệ phương trình sau:
2
2
2
.2 .2 5
1
b
a
abc
c


1; 4; 1abc .
Vậy
2
41vt t t
. Do đó phần parabol có phương trình
2
41vt t t
, còn phần
đường thẳng
A
B có phương trình là
4vt
.
Quãng đường mà vật đi được trong
3 h
là:


13
2
01
32
41 4
3
Stt dtkm

.
Câu 50: [2D3-3.2-3] Xét hình phẳng
D
giới hạn bởi các đường

2
3, 0, 0.yx y x
Gọi
0;9 , ;0
A
Bb
30.b
Tìm b để đoạn thẳng
A
B chia
D
thành hai phần có diện tích
bằng nhau.
A. 2.b  B.
1
.
2
b 
C. 1.b  D.
3
.
2
b 
Hướng dẫn giải
Chọn C.
Phương trình hoành độ giao điểm




3
0
0
22
3
3
3
30 3 3 9.
3
D
x
xxSxdx

Bài ra có

191 9
.991
222 2
OAB
D
S S OA OB b b
thỏa mãn
30.b
| 1/15
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD-ĐT LONG AN
ĐỀ KIỂM TRA 1 TIẾT – NĂM HỌC 2017-2018
TRƯỜNG THPT PHAN VĂN ĐẠT MÔN: TOÁN- Giải tích 12, CHƯƠNG 3.
Thời gian: 45 phút (không kể thời gian phát đề)
Hình thức: trắc nghiệm Điểm:
Họ và tên:……………………………………….
Lớp:…………………………………………….
MA TRẬN ĐỀ KIỂM TRA Vận dụng Cấp độ Nhận biết Thông hiểu Cộng Chủ đề
Cấp độ thấp Cấp độ cao
Biết dựa vào Biết tìm nguyên Biết sử dụng Tìm một hàm
định nghĩa,tính hàm của một số các
phương số cụ thể nhờ
chất và bảng hàm số đơn pháp tìm xác định
Nguyên hàm nguyên hàm để giản nguyên hàm nguyên hàm nhận biết của các hàm số nguyên hàm của các hàm số Số câu:4 Số câu:2 Số câu:2 Số câu:1 Số câu: 9 Số điểm:1.6 Số điểm: 0.8 Số điểm: 0.8 Số điểm: 0.4 Số điểm: 3.6 Biết dựa vào
Biết tìm tích Biết sử dụng Biết sử dụng
định nghĩa, tính phân của một số các phương tích phân để
chất để tính các hàm số đơn pháp tính tích giải quyết bài Tích phân tích phân đơn giản
phân để tính toán thực tế giản tích phân của một số hàm số Số câu:2 Số câu:3 Số câu: 3 Số câu:1 Số câu: 9 Số điểm: 0.8 Số điểm: 1.2 Số điểm: 1.2 Số điểm:0.4 Số điểm: 3.6
Nhận biết được Tính được diện Tính được diện Tính được thể
công thức tính tích, thể tích tích, thể tích tích một số hình diện tích, thể
của một số hình một số hình phải căn cứ vào Ứng dụng tích
giới hạn bởi các phải xác định hình vẽ để xác hàm số đơn các cận định giản Số câu:2 Số câu:2 Số câu:2 Số câu:1 Số câu: 7 Số điểm: 0.8 Số điểm: 0.8 Số điểm: 0.8 Số điểm: 0.4 Số điểm: 2.8 Số câu:8 Số câu: 7 Số câu: 7 Số câu: 3 Số câu: Số điểm: 3.2 Số điểm: 2.8 Số điểm: 2.8 Số điểm: 1.2 25 Tổng Số điểm: 10 2
Câu 1: [2D3-1.1-1] Tìm họ nguyên hàm F x  của hàm số f (x)  3sin x x
A. F (x)  3cos x  2ln x C .
B. F (x)  3cos x  2 ln x C .
C. F(x)  3
 cos x  2ln x C .
D. F(x)  3cos x  2ln x C .
Câu 2: [2D3-1.1-1] Công thức nào sau đây sai? A. cos d
x x  sin x C. B. xd x
a x a C 1 1  1 C. dx   C x  0  . D.
dx  tan x C C  0  . 2   2   x x cos x
Câu 3: [2D3-1.1-1] Trong các khẳng định sau, khẳng định nào là sai?
A. Nếu f x, g x là các hàm số liên tục trên R thì  f
 xgxdx f
 xdxg  xdx.
B. Nếu F x và G x đều là nguyên hàm của hàm số f x thì F x  G x  C (với C là hằng số).
C. Nếu các hàm số u x, v x liên tục và có đạo hàm trên R thì u(x)v (
x)dx v(x)u (x)dx u(x)v(x)   . D.   2
F x x là một nguyên hàm của f x  2x .
Câu 4: [2D3-1.1-1] Tìm tất cả các nguyên hàm của hàm số f x   cos 2x là
A. F x 1
 sin2x C. B. F x 1
  sin2x C. 2 2
C. F x  sin2x C. D. F x  sin2 . x
Câu 5: [2D3-2.1-1] Tìm nguyên hàm F x của hàm số   x  2 1 3 x f x e e    A.   x 3   3  x F x e eC . B.   x   3 x F x e e C . C.   x   3 x F x e
e C . D.   x 2   3 x F x e eC . f x a,bF x
Câu 6: [2D3-2.1-1]Xét
là một hàm số liên tục trên đoạn
, (với a b ) và là một f x a,b nguyên hàm của hàm số trên đoạn
. Mệnh đề nào dưới đây đúng? b b b b A. f
 3x5dx F 3x5 . B. f
 x 1dx F x . a a a a b b C. f
 2xdx  2F b F a. D. f
 xdx F b F a. a a
Câu 7: [2D3-3.1-1] Cắt một vật thể T  bởi hai mặt phẳng P và Q vuông góc với trục Ox lần
lượt tại x  1 và x  2. Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x 1  x  2 cắt
T  theo thiết diện có diện tích là 2
6x . Tính thể tích V của phần vật thể T  giới hạn bởi hai
mặt phẳng P và Q. A. V  28. B. V  28. C. V  14. D. V  14.
Câu 8: [2D3-3.1-1]Cho hàm số y f x liên tục trên đoạn  ;
a b . Diện tích hình phẳng giới hạn bởi
đường cong y f x , trục hoành, các đường thẳng x a , x b là b b a b
A. f xdx  . B. f  xdx .
C. f xdx  .
D. f xdx  . a a b a dx
Câu 9: [2D3-1.4-2] Tìm 2 x  3x  2 x  2 x 1 A. ln  C . B. ln  C . x 1 x  2 1 1
C. ln(x  2)(x 1)  C . D. ln  ln  C . x  2 x 1
Câu 10: [2D3-1.6-2] Trong các hàm số f x dưới đây, hàm số nào thỏa mãn đẳng thức
  .sin d    .cos   .cos d  x f x x x f x x x x ? xx
A.     x f x ln . x
B.     x f x .ln .
x C. f x  .
D. f x   . ln  ln  4 1
Câu 11: [2D3-2.1-2] Biết
dx m ln 5  n ln 3   ,
m n   . Tính P m n . 2x 1 2 3 3 A. P   . B. P  . C. P  1  . D. P  1 . 2 2 1
Câu 12: [2D3-2.1-2] Tính tích phân I   2 dx bằng cách đặt x  2sint . Mệnh đề nào dưới đây 4  2 0 x đúng?    1 4 3 6
A. I  2dt.
B. I  2dt.
C. I  dt .
D. I  dt. 0 0 0 0  2
Câu 13: [2D3-2.6-2] Giá trị của tích phân 2 I x cos d 
x x được biểu diễn dưới dạng 0 2 .
a   b a,b . Khi đó tích . a b bằng 1 1 1 A. 0 . B.  . C.  . D.  . 32 16 64 x
Câu 14: [2D3-3.1-2] Gọi S là hình phẳng giới hạn bởi đồ thị hàm số H  1 : y  và các trục tọa độ. x 1
Khi đó giá trị của S bằng
A. S  ln 2 1đvdt . B. S  ln 4 1đvdt .
C. S  ln 4 1đvdt . D. S  ln 2 1đvdt .
Câu 15: [2D3-3.3-2] Thể tích của khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường có 1 x phương trình 2 2
y x e , trục Ox , x 1, x  2 quay một vòng quanh trục Ox bằng: A. e. B. 2  e . C. 4 . D. 16 . 1
Câu 16: [2D3-1.1-3]Tìm hàm số F x, biết rằng F x 
và đồ thị của hàm số F x đi qua 2 sin x    điểm M ;0   .  6 
A. F x  cot x  3 . B. F x 1   3 . sin x
C. F x  cot x  3 . D. F x  tan x  3 . dx
Câu 17: [2D3-1.5-3] Nguyên hàm  bằng 2 tan x 1 x 2 2x 1
A.  ln 2sin x  cos x C . B.
 ln 2sin x  cos x C . 5 5 5 5 x 1 x 1
C.  ln 2sin x  cos x C .
D.  ln 2sin x  cos x C . 5 5 5 5  1 n 1  2
Câu 18: [2D3-2.1-3] Cho n là số tự nhiên sao cho  2 x   1 d x x  
. Tính tích phân sinn x cos d x x  20 0 0 1 1 1 1 A. . B. . C. . D. . 10 15 5 20 m 2 x dx 1
Câu 19: [2D3-2.4-3] Tìm tất cả các số thực dương m để  ln 2   . x 1 2 0 A. m  2 . B. m  2 . C. m  3 . D. m  3 .
Câu 20: [2D3-2.6-3] Biết x x   x   2
ax bx c  x   2 ln 1 d ln
1  mx nx p
, với a,b, c, m, n, p   . Tính 2 2 2
S a b c . 1 1 A. S  1 . B. S  . C. S  . D. S  2 . 2 4
Câu 21: [2D3-3.1-3]Gọi S là diện tíchhình phẳng giới hạn bởi đồ thị   C 2x 1 : y  , tiệm cận ngang x 1
của C , trục tung và đường thẳng x a a  0 . Tìm ađể S  ln 2017 . A. 3 a  2017 1 . B. 2017 a  1. C. a  2016 .
D. a  2017 1. 3
Câu 22: [2D3-3.7-3] Một ô tô đang chuyển động đều với vận tốc 12 m s thì người lái đạp phanh; từ
thời điểm đó ô tô chuyển động chậm dần đều với vận tốc vt  2
t 12m s (trong đó t là
thời gian tính bằng giây, kể từ lúc đạp phanh). Hỏi trong thời gian 8 giây cuối (tính đến khi xe
dừng hẳn) thì ô tô đi được quãng đường bằng bao nhiêu? A. 16 m . B. 60 m . C. 32 m . D. 100 m .
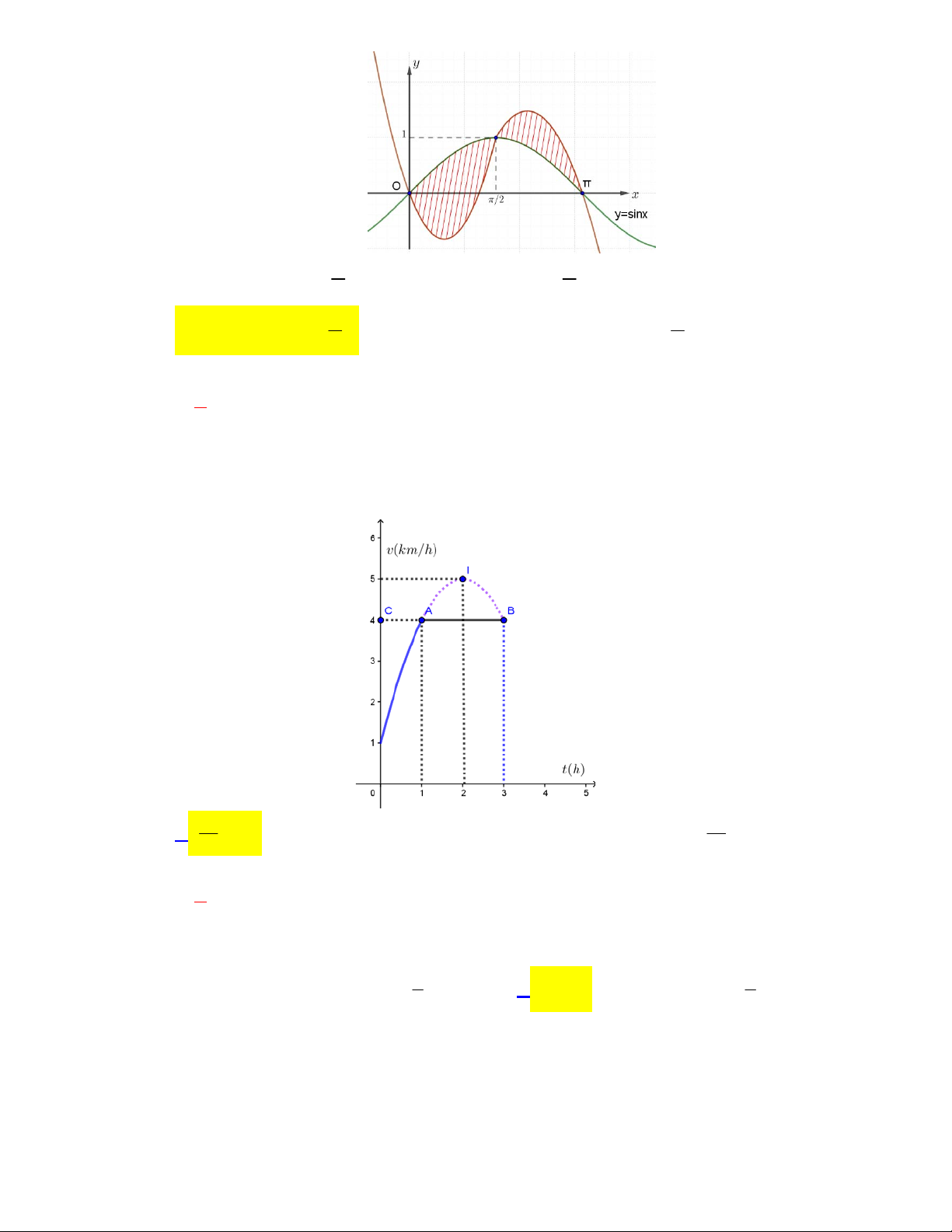
Câu 23: [2D3-3.6-4] Cho hàm số y f x . Đồ thị của hàm số y f  x như hình bên. Đặt
g x  f x  cos x . Mệnh đề nào dưới đây đúng ?      
A. g 0  g    g   . B. gg  
0  g   .  2   2       
C. g    g 0  g   .
D. g    g 0  g   .  2   2 
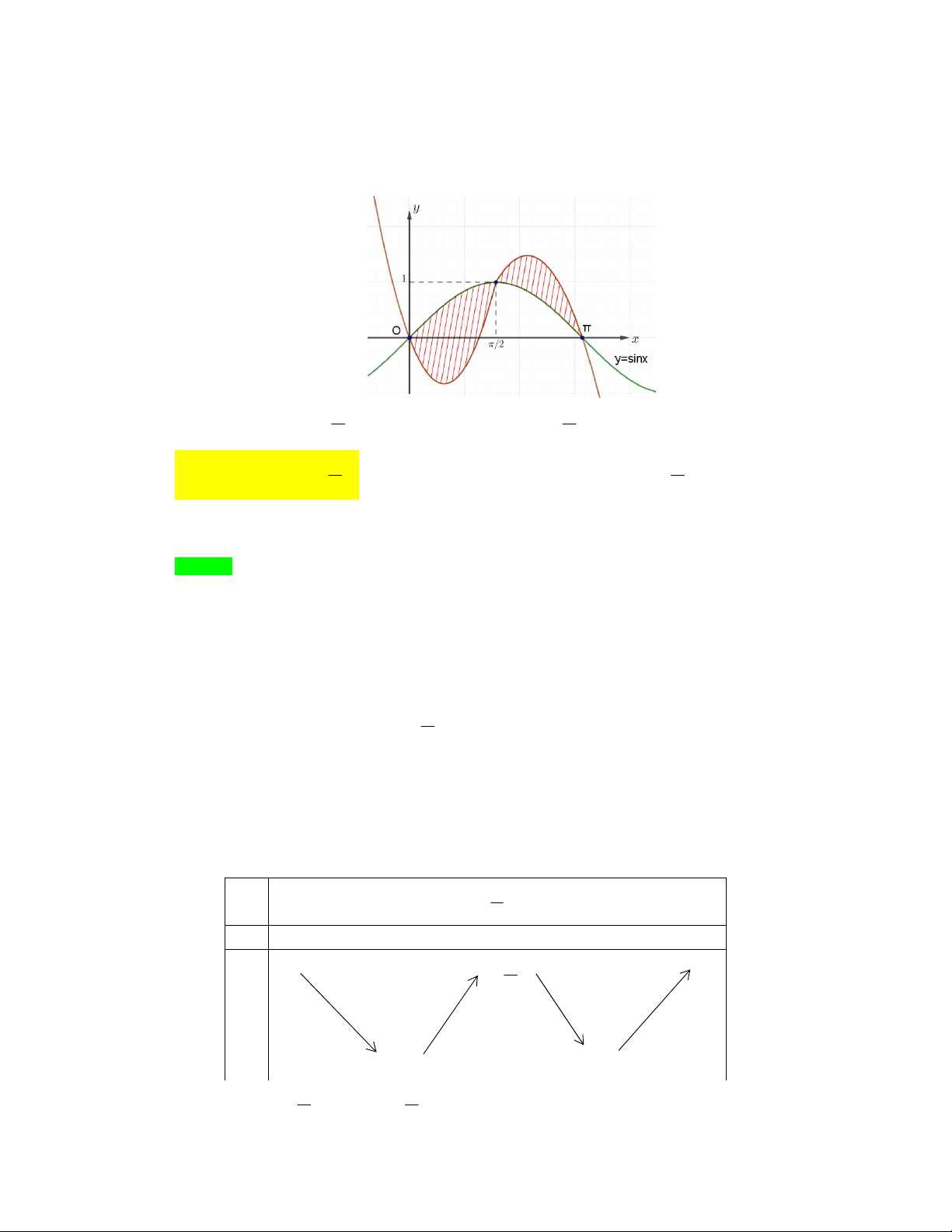
Câu 24: [2D3-3.7-4] Một vật chuyển động trong 3 giờ với vận tốc v (km/h) phụ thuộc vào thời gian t
(h) có đồ thị vận tốc như hình bên. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển
động, đồ thị đó là một phần của đường parabol có đỉnh I 2;5 và trục đối xứng song song với
trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính
quãng đường mà vật di chuyển được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm). 33 35 A. km . B. 15km . C. 12km . D. km . 3 3 D
y   x  2
3 , y  0, x  0.
Câu 25: [2D3-3.2-4] Xét hình phẳng
giới hạn bởi các đường Gọi
A0;9, B ; b 0  3   b  0. D
Tìm b để đoạn thẳng AB chia
thành hai phần có diện tích bằng nhau. 1 3 A. b  2.  B. b   . C. b  1.  D. b   . 2 2 BẢNG ĐÁP ÁN 1.A 2.B 3.C 4.B 5.B 6.D 7.C 8.A 9.A 10.C 11.A 12.C 13.D 14.B 15.B 16.C 17.A 18.A 19.B 20.B 21.A 22.B 23.B 24.A 25.C
HƯỚNG DẪN GIẢI CHI TIẾT 2
Câu 26: [2D3-1.1-1] Tìm họ nguyên hàm F x  của hàm số f (x)  3sin x x
A. F (x)  3
 cos x  2ln x C .
B. F (x)  3cos x  2 ln x C .
C. F (x)  3
 cos x  2ln x C .
D. F (x)  3cos x  2 ln x C . Hướng dẫn giải Chọn A. F x  2  1  3sin x
dx 3 sin xdx  2
d x   3cos x  2 ln x      C x x .
Câu 27: [2D3-1.1-1] Công thức nào sau đây sai? A. cos d
x x  sin x C. B. xd x
a x a C 1 1  1 C. dx   C x  0  . D.
dx  tan x C C  0  . 2   2   x x cos x Hướng dẫn giải Chọn B. x a x a dx   C  ln a .
Câu 28: [2D3-1.1-1] Trong các khẳng định sau, khẳng định nào là sai?
A. Nếu f x, g x là các hàm số liên tục trên R thì  f
 xgxdx f
 xdxg  xdx.
B. Nếu F x và G x đều là nguyên hàm của hàm số f x thì F x  G x  C (với C là hằng số).
C. Nếu các hàm số u x, v x liên tục và có đạo hàm trên R thì u(x)v (
x)dx v(x)u (x)dx u(x)v(x)   . D.   2
F x x là một nguyên hàm của f x  2x . Hướng dẫn giải Chọn C. Ta
có u(x)v (x)dx v(x)u (x)dx   
u(x)v (x)v(x)u (x)dx  u(x)v(x)    
dx u(x)v(x)  C. .
Câu 29: [2D3-1.1-1] Tìm tất cả các nguyên hàm của hàm số f x   cos 2x là
A. F x 1
 sin2x C. B. F x 1
  sin2x C. 2 2
C. F x  sin2x C. D. F x  sin2 . x Hướng dẫn giải Chọn B.
Câu 30: [2D3-2.1-1] Tìm nguyên hàm F x của hàm số   x  2 1 3 x f x e e    A.   x 3   3  x F x e eC . B.   x   3 x F x e e C . C.   x   3 x F x e
e C . D.   x 2   3 x F x e eC . Hướng dẫn giải Chọn B.    x    2 dx
1 3  x  dx   x 3 x dx  x 3 x f x e e e e e e C f x a,bF x
Câu 31: [2D3-2.1-1]Xét
là một hàm số liên tục trên đoạn
, (với a b ) và là một f x a,b nguyên hàm của hàm số trên đoạn
. Mệnh đề nào dưới đây đúng? b b b b A. f
 3x5dx F 3x5 . B. f
 x 1dx F x . a a a a b b C. f
 2xdx  2F b F a. D. f
 xdx F b F a. a a Lờigiải Chọn D. b b
Theo định nghĩa Tích phân trong SGK trang 105 ta có: f
 xdx F x  F b F a. a a
Câu 32: [2D3-3.1-1] Cắt một vật thể T  bởi hai mặt phẳng P và Q vuông góc với trục
Ox lần lượt tại x  1 và x  2. Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x 1  x  2
cắt T  theo thiết diện có diện tích là 2
6x . Tính thể tích V của phần vật thể T  giới hạn bởi hai
mặt phẳng P và Q. A. V  28. B. V  28. C. V  14. D. V  14. Hướng dẫn giải Chọn C. 2 2 Ta có: 2 3
V   6 x dx   2x  14  . 1 1
Câu 33: [2D3-3.1-1]Cho hàm số y f x liên tục trên đoạn  ;
a b . Diện tích hình phẳng giới hạn
bởi đường cong y f x , trục hoành, các đường thẳng x a , x b là b b a b
A. f xdx  . B. f  xdx .
C. f xdx  .
D. f xdx  . a a b a Hướng dẫn giải Chọn A b
Theo định nghĩa ta có S f  xdx a dx
Câu 34: [2D3-1.4-2] Tìm 2 x  3x  2 x  2 x 1 A. ln  C . B. ln  C . x 1 x  2 1 1
C. ln(x  2)(x 1)  C . D. ln  ln  C . x  2 x 1 Hướng dẫn giải Chọn A. dx dx
(x 1)  (x  2)dx      2 x  3x  2
(x 1)(x  2)
(x 1)(x  2) 1 1  x  ( 
)dx  ln x  2  ln x 1  C  2  ln  C x  2 x 1 x 1
Câu 35: [2D3-1.6-2] Trong các hàm số f x dưới đây, hàm số nào thỏa mãn đẳng thức
  .sin d    .cos   .cos d  x f x x x f x x x x ? xx
A.     x f x ln . x
B.     x f x .ln .
x C. f x  .
D. f x   . ln  ln Hướng dẫn giải Chọn C.
u f x
du f xdx Đặt    .
dv  sin xdx
v   cos x
Khi đó  f x.sin xdx   f x.cos x f
 x.cos xdx x xx
Suy ra f  x    f x   dx   C.  ln 4 1
Câu 36: [2D3-2.1-2] Biết
dx m ln 5  n ln 3   ,
m n   . Tính P m n . 2x 1 2 3 3 A. P   . B. P  . C. P  1  . D. P  1 . 2 2 Hướng dẫn giải Chọn A. 4 4 1 1 1 1 4 1 1 Ta có dx  d   2x  
1  ln 2x 1   ln 9  ln 5   ln 5  ln 3 2 2x 1 2 2x 1 2 2 2 2 2 1 3
Suy ra m   ; n  1. Do đó P m n   . 2 2 1
Câu 37: [2D3-2.1-2] Tính tích phân I   2 dx bằng cách đặt x  2sint . Mệnh đề nào dưới đây 4  2 0 x đúng?    1 4 3 6
A. I  2dt.
B. I  2dt.
C. I  dt .
D. I  dt. 0 0 0 0 Hướng dẫn giải Chọn C.
Đặt: x  2 sin t  dx  2 costdt
x  0  t  0 
x  1 t  6    6 6 6  2 2  I  2 cos d t t  2 cos d t t  2dt  6 2t     . 4  0 2 2 cost 3 0 4 sin t 0 0  2
Câu 38: [2D3-2.6-2] Giá trị của tích phân 2 I x cos d 
x x được biểu diễn dưới dạng 0 2 .
a   b a,b . Khi đó tích . a b bằng 1 1 1 A. 0 . B.  . C.  . D.  . 32 16 64 Hướng dẫn giải Chọn D. u x du  dv   Đặt  1 cos 2x   1 1 2 dv  cos d x x  d  x
v x  sin 2x  2  2 4   2  1 1   1 1  Vậy I x x  sin 2  x  2  x  sin 2x d   x  2 4   2 4  0 0  2   1 1 2    x  cos 2  x  2 8  4 8  0 2 2   1  1 1 1       1    1  2    8  4 4 8  16 4  1 a   1 Theo giả thiết 2 I  .
a   b  16   . a b   . 1  64 b    4 x
Câu 39: [2D3-3.1-2] Gọi S là hình phẳng giới hạn bởi đồ thị hàm số H  1 : y  và các trục tọa x 1
độ. Khi đó giá trị của S bằng
A. S  ln 2 1đvdt . B. S  ln 4 1đvdt .
C. S  ln 4 1đvdt . D. S  ln 2 1đvdt . Hướng dẫn giải Chọn B. x 1
Phương trình hoành độ giao điểm H  và trục Ox là:  0  x  1. x 1
Giao điểm H  và trục Oy là: 0;  1  . x
Vậy diện tích hình phẳng giới hạn bởi đồ thị hàm số H  1 : y
và các trục tọa độ là: x 1 1 1 x 1  2  S  dx  1 dx    
x 2lnx  11  2ln21 ln 41. 0 x 1  x 1 0 0
Câu 40: [2D3-3.3-2] Thể tích của khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường có 1 x phương trình 2 2
y x e , trục Ox , x  1, x  2 quay một vòng quanh trục Ox bằng: A. e. B. 2  e . C. 4 . D. 16 . Hướng dẫn giải Chọn B. 2 2 1 x 2 2 2 2     Ta có 2 2    .    x   
  x   x   x V x e dx xe dx xd e xe e dx    . 1   1 1  1 1    2   2 2  x e e e    2
2e e   2 e e 2  e . 1 1
Câu 41: [2D3-1.1-3]Tìm hàm số F x , biết rằng F x 
và đồ thị của hàm số F x đi qua 2 sin x    điểm M ;0   .  6 
A. F x  cot x  3 . B. F x 1   3 . sin x
C. F x  cot x  3 . D. F x  tan x  3 . Hướng dẫn giải Chọn C. 1
Theo giả thiết ta có F x 
dx  cot x   C . 2 sin x    
Mặt khác vì đồ thị hàm số F x đi qua điểm M ;0 
 nên cot  C  0  C  3 .  6  6
Vậy F x  cot x  3 . dx
Câu 42: [2D3-1.5-3] Nguyên hàm  bằng 2 tan x 1 x 2 2x 1
A.  ln 2sin x  cos x C . B.
 ln 2sin x  cos x C . 5 5 5 5 x 1 x 1
C.  ln 2sin x  cos x C .
D.  ln 2sin x  cos x C . 5 5 5 5 Hướng dẫn giải Chọn A. dx cos x
1 2cos x  sin x  sin x * Biến đổi I   = dx  = dx  2 tan x 1 2sin x  cos x 2 2sin x  cos x
1 2cos x  sin x 1 sin x 1 1 = dx  dx  
= ln 2sin x  cos x J
2 2sin x  cos x
2 2sin x  cos x    2 2 J 1
* Ta tính 2J I  1.dx x C
, suy ra   x I C  2 1 1
* Thế kết quả trên trở lại đề: I  ln 2sin x  cos x   x I C  2 4  4 1 1  I
ln 2sin x  cos x x C  2 1
I  ln 2sin x  cos x x C 5  2 4    5 5 1 n 1 
Câu 43: [2D3-2.1-3] Cho n là số tự nhiên sao cho
 2x  1 dxx   . Tính tích phân 20 0  2 sinn x cos d x x  0 1 1 1 1 A. . B. . C. . D. . 10 15 5 20 Hướng dẫn giải Chọn A 0 1 1 n        x   0 n 1 n 1 t n 1 1 2   1 d x x t dt     
n  9 n  . (1) 20 2 2  n 1 2 n 1 0 1      1   1 2 1 n 1 t    n n 1
I  sin x cos d
x x t dt       (2).  n 1 n 1 0 0 0  2 n 1
Từ (1) và (2) suy ra sin x cos d x x   . 10 0 m 2 x dx 1
Câu 44: [2D3-2.4-3] Tìm tất cả các số thực dương m để  ln 2   . x 1 2 0 A. m  2 . B. m  2 . C. m  3 . D. m  3 . Hướng dẫn giải Chọn B. m m 2 m 2 2 x dx  1   xm Ta có I   x 1 dx     
x  ln x   1  
m  ln m   1 x 1  x 1  2  2 0 0 0 1
Theo giả thiết I  ln 2  2 2  m 1
m  ln m   1  ln 2  2 2 2 m 1      m  2 2  m  1. m1 2
Câu 45: [2D3-2.6-3] Biết
x x   x   2
ax bx c  x   2 ln 1 d ln
1  mx nx p  , với
a,b, c, m, n, p   . Tính 2 2 2
S a b c . 1 1 A. S  1 . B. S  . C. S  . D. S  2 . 2 4 Hướng dẫn giải Chọn B.  1  u
  ln  x   1 du dx  Đặt    x 1  dv  d x x 1 2 v x  2 2 1 1 x 1 1  1  x lnx   1 dx   2
x ln  x   1  dx  = 2
x ln  x   1   x 1 dx 2 2 x 1 2 2  x 1 1 1  1   1 1  1 1 = 2
x ln  x   2
1   x x  ln  x   1   C = 2
x  ln  x   2
1  x x C 2 2  2   2 2  4 4 1 1 1
Do đó a  ; b  0; c   . Vậy 2 2 2
a b c  . 2 2 2
Câu 46: [2D3-3.1-3]Gọi S là diện tíchhình phẳng giới hạn bởi đồ thị   C 2x 1 : y  , tiệm cận x 1
ngang của C , trục tung và đường thẳng x a a  0 . Tìm ađể S  ln 2017 . A. 3 a  2017 1 . B. 2017 a  1. C. a  2016 .
D. a  2017 1. 3 Hướng dẫn giải Chọn A.
Diện tíchhình phẳng giới hạn bởi đồ thị   C 2x 1 : y
, tiệm cận ngang: y  2 , trục tung và x 1 đường thẳng
x a a  0là: a 2x 1 a 3 a  1 a S   2 dx  dx  3
dx  3ln x 1  3ln    a  1. 0 x 1 x 1 x 1 0 0 0
Để S  ln 2017 thì a   3 3ln
1  ln 2017  a  2017 1.
Câu 47: [2D3-3.7-3] Một ô tô đang chuyển động đều với vận tốc 12m s thì người lái đạp phanh;
từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc vt  2
t 12m s (trong đó t là
thời gian tính bằng giây, kể từ lúc đạp phanh). Hỏi trong thời gian 8 giây cuối (tính đến khi xe
dừng hẳn) thì ô tô đi được quãng đường bằng bao nhiêu? A. 16 m . B. 60 m . C. 32 m . D. 100 m . Hướng dẫn giải Chọn B.
Xe dừng hẳn khi vt  2
t 12  0  t  6 .
Vậy trong 8 giây cuối (Tính đến khi xe dừng hẳn) thì 2 giây đầu xe vẫn chuyển động đều được
quãng đường là s  12.2  24 m . 1 6 6
Xe dừng hẳn trong 6 giây cuối với quãng đường s v t dt
2t 12 dt  36 m 2      0 0
Vậy tổng quãng đường xe đi được là s  60 m . Câu 48:
[2D3-3.7-4] Cho hàm số y f x . Đồ thị của hàm số y f  x
như hình bên. Đặt g x  f x  cos x . Mệnh đề nào dưới đây đúng ?      
A. g 0  g    g   . B. gg  
0  g   .  2   2       
C. g    g 0  g   .
D. g    g 0  g   .  2   2  Hướng dẫn giải Chọn C.
Ta có g ' x  f ' x  sin x x  0  
g ' x  0  f ' x  sin x  x   2 x   
Từ đồ thị của hàm y f ' x ta có bảng biến thiên. (Chú ý là hàm g x và g ' x ) Bảng biến thiên  0    x 2 y  0  0  0       g  2  y g 0 g        
Suy ra g 0  g , g
     g    2   2    2  2 
Kết hợp với đồ thị ta có: sin x f 'xdx   f 'x sin xdx  g 'xdx g '  xdx 0  0  2 2        
Theo hình vẽ  gx 2  gx  gg  
0  g    gg  
0  g    0  2   2  2   
Vậy g    g 0  g   .  2 
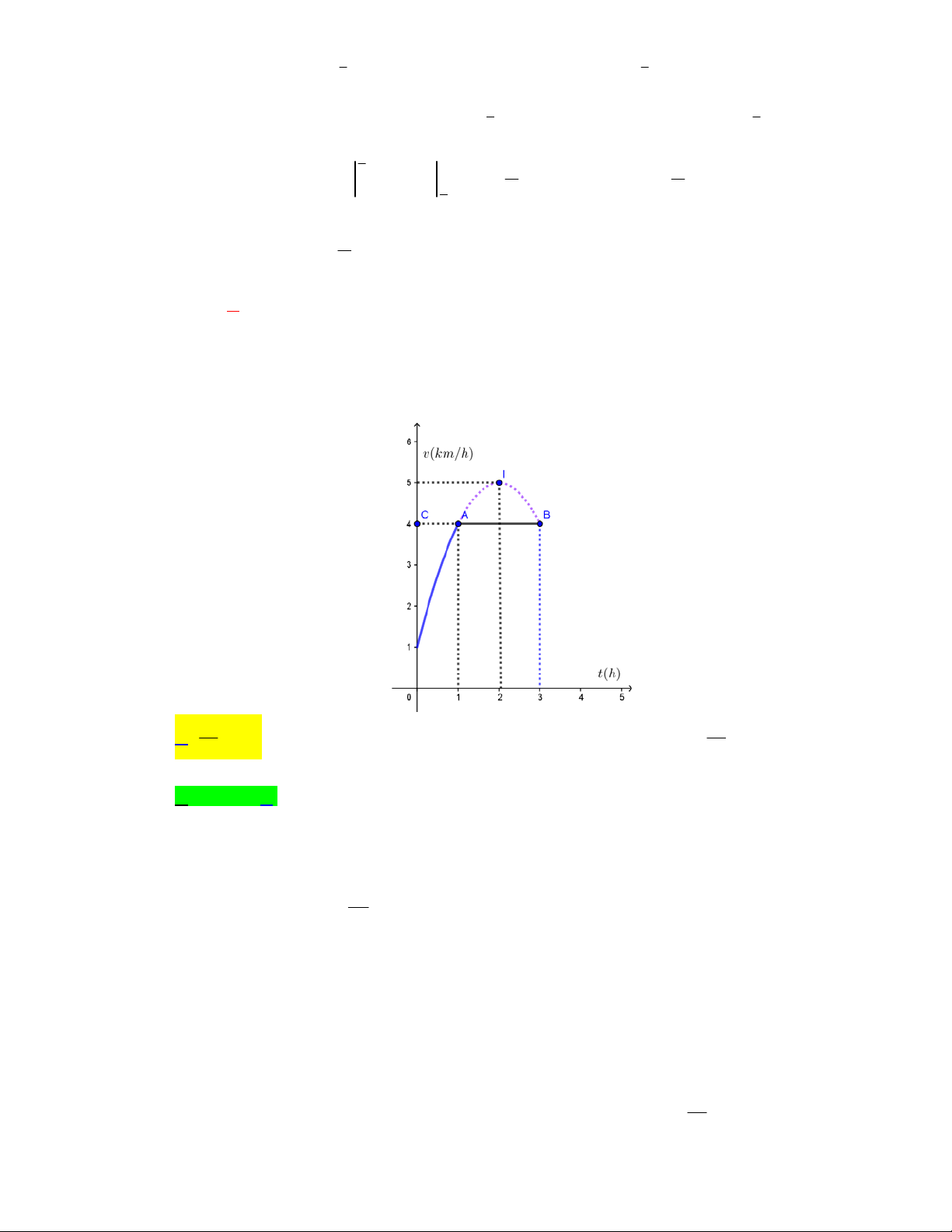
Câu 49: [2D3-3.7-4] Một vật chuyển động trong 3 giờ với vận tốc v (km/h) phụ thuộc vào thời
gian t (h) có đồ thị vận tốc như hình bên. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển
động, đồ thị đó là một phần của đường parabol có đỉnh I 2;5 và trục đối xứng song song với
trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng
đường mà vật di chuyển được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm). 33 35 A. km . B. 15km . C. 12km . D. km . 3 3 Hướng dẫn giải Chọn A. Gọi   2
v t at bt c .
Khi đó đồ thị hàm số v v t là một parabol có đỉnh I 2;5 và đi qua điểm A0;  1 nên ta có  b   2  2a  hệ phương trình sau: 2  .2 a  .
b 2  c  5  a  1;b  4;c  1 . c 1   Vậy v t 2  t
  4t 1. Do đó phần parabol có phương trình vt 2  t
  4t 1, còn phần
đường thẳng AB có phương trình là v t  4 . 1 3 32
Quãng đường mà vật đi được trong 3h là: S   2
t  4t   1  4dt    km. 3 0 1 D
y   x  2
3 , y  0, x  0.
Câu 50: [2D3-3.2-3] Xét hình phẳng
giới hạn bởi các đường Gọi
A0;9, B ; b 0  3   b  0. D
Tìm b để đoạn thẳng AB chia
thành hai phần có diện tích bằng nhau. 1 3 A. b  2.  B. b   . C. b  1.  D. b   . 2 2 Hướng dẫn giải Chọn C. x  3
Phương trình hoành độ giao điểm  x  3  0  x  3   Sx dx    D  3  3 0 0 2 2   9. 3 3  3  1 9 1 9 Bài ra có SS
  OA OB   b   b   thỏa mãn 3
  b  0. OABD . 9 9 1 2 2 2 2