Đề kiểm tra 1 tiết Giải tích 12 chương 3 năm 2017 – 2018 trường Phước Vĩnh – Bình Dương

Đề kiểm tra 1 tiết Giải tích 12 chương 3 năm học 2017 – 2018 trường THPT Phước Vĩnh – Bình Dương mã đề 302 gồm 4 trang với 25 câu hỏi trắc nghiệm thuộc chủ đề nguyên hàm, tích phân và ứng dụng, thời gian làm bài 45 phút (không kể thời gian phát đề), đây là bài kiểm tra số 1 giải đoạn HK2 Toán 12.

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
1/4 - Mã đề 302
SỞ GD&ĐT BÌNH DƯƠNG
TRƯỜNG THPT PHƯỚC VĨNH
(Đề thi có 04 tran
g
)
KIỂM TRA 1 TIẾT BÀI 1 HK II NĂM HỌC 2017 - 2018
MÔN TOÁN – Khối lớp 12
Thời gian làm bài : 45 phút
(không kể thời gian phát đề)
Họ và tên học sinh :..................................................... Số báo danh : ...................
Câu 1.
Tínhdiệntíchhìnhphẳnggiớihạnbởiđồthịhàm
s ố
y=2–x
2
vày=x.
A.
11
2
B. 7 C.
9
2
D. 5
Câu 2. Cho
2
2
1
ln 1
ln 2 ln 3
x
dx a b
x

,vớia,blàcácsốhữutỉ.Tính
4
P
ab
A.
0.P =
B.
1P =
. C.
3.P =-
D.
3.P =
Câu 3. Tính diện tích hình phẳng giới hạn bởi các đường ,0,1
x
y
xe
y
x.
A.
1
2
B. 1 C.
3
2
D.
3
2
Câu 4. Biếtmộtnguyênhàmcủahàmsố
yfx là
2
41Fx x x.Khiđó,giátrịcủahàmsố
yfx tại
3x
là
A.
330f . B.
310f . C.
322f . D.

36f .
Câu 5. Nếu
()
f
x
liên tục và
4
0
() 10fxdx
, thì
2
0
(2 )
f
xdx
bằng :
A. 19 B.
5
C.
9
D. 29
Câu 6. Tính tích phân
1
2
0
12
dx
xx
.
A.
19
ln
716
B.
9
ln
16
C.
19
ln
716
D.
19
ln
416
Câu 7. Cho hàm số
()
f
x
thỏa mãn
() 3 5sin
xx

và
(0) 7f
. Mệnh đề nào dưới đây là đúng?
A.
() 3 5cos 2fx x x
B.
() 3 5cos 2fx x x
C.
() 3 5cos 15fx x x
D.
() 3 5cos 5fx x x
Câu 8. Giảsửhàmsố
Fxlàmộtnguyênhàmcủahàmsố
fx
trên
K
.Khẳngđịnhnàosauđây
đúng.
A. Chỉcóduynhấthàmsố
()yFx
lànguyênhàmcủa
f
trên
.K
B. Vớimỗinguyênhàm
G
của
f
trên
K
thìtồntạimộthằngsố
C
saocho
() ()Gx Fx C
với x
thuộc
K
.
Mã đề 302
2/4 - Mã đề 302
C. Chỉcóduynhấtmộthằngsố
C
saochohàmsố
()yFx C
làmộtnguyênhàmcủahàm
f
trên
.K
D. Vớimỗinguyênhàm
G
của
f
trên
K
thì
() ()Gx Fx C
vớimọi x thuộc
K
và
C
bấtkỳ.
Câu 9. Cho
()dfx x=
ò
2
0
4
.Tínhtíchphân
(tan )
d.
cos
π
fx
Ix
x
=
ò
12
2
0
23
3
A.
.I =
1
3
B.
.I =
4
3
C.
.I =
2
3
D.
.I =
8
3
Câu 10. Tìmnguyênhàm
1
d
12
x
x
.
A.
1
dln12 .
12
xxC
x

B.
11
dln12.
12 2
xxC
x

C.
111
dln .
12 2 12
xC
xx


D.
11
dln .
12 12
xC
xx


Câu 11. Mộthìnhcầucóbánkính
dm,6
ngườitacắtbỏhaiphầnbằnghaimặtphẳngsongsongvà
cùngvuônggócvớiđườngkínhđểlàmmặtxungquanhcủamộtchiếcluchứanước(nhưhình
vẽ).
Tínhthểtích
V màchiếcluchứađượcbiếtmặtphẳngcáchtâmmặtcầu
dm.4
A.
V(dm).
3
288 B.
V(dm).
3
368
3
C.
V(dm).
3
192 D.
V(dm).
3
736
3
Câu 12. Biết
0
1
1
ln 1
2
x
b
dx a
x
c

. Khẳng định nào sau đây sai ?
A.
.3(1)ab c
B. 210ab c C. 3ac b D. 1ab c
Câu 13. Nếu
(1) 12, ( )
f
fx
liên tục và
4
1
() 17fxdx
, giá trị của
(4)
f
bằng:
A. 19 B. 29 C.
5
D.
9
Câu 14. Tìmnguyênhàmcủahàmsố
2
f(x) (x 1)
A.
3
2
x
F(x) x x C.
3

B.
32
F(x) x 3x 3x C. 
3/4 - Mã đề 302
C.
32
F(x) x x x C.
D.
3
2
x
F(x) x x C.
3

Câu 15. Cho () ()f x dx F x C
.Khiđóvới
0a
,tacó ()fax bdx
bằng:
A.
1
().Fax b C
a

B.
1
()
2
Fax b C
a

. C.
.( ) .aF ax b C
D.
().Fax b C
Câu 16. Gọi
S
là diện tích hình phẳng
H giới hạn bởi cácđường
,
y
fx trục hoành và hai
đườngthẳng
 1, 2xx
(nhưhìnhvẽ).
Đặt

0
1
,
afxdx

2
0
.bfxdxMệnhđềnàosauđâyđúng?
A. .Sba B.  .Sba C.  .Sba D. .Sba
Câu 17. Gọi
()
F
x
là một nguyên hàm của hàm
2
ln
ln 1.
x
yx
x

mà
1
(1)
3
F
. Giá trị
2
()Fe bằng:
A.
8
9
B.
1
9
. C.
1
3
. D.
8
3
Câu 18. Cho
2
2
1
21Ixxdx
. Khẳng định nào sau đây sai:
A.
3
2
3
0
2
3
It
B.
2
27
3
I
C. 33I D.
3
0
Iudu
Câu 19. Tìm nguyên hàm

cos 2 1 .
x
dx
. Chọn đáp án đúng:
A.

sin 2 1
x
C
B.

1
sin 2 1
2
x
C
C.

1
sin 2 1
2
x
C
D.

2sin 2 1
x
C
Câu 20. Chohàmsố
(
)
fxthỏamãn
2
0
(3)'() 50xfxdx
và
() ()
ff-=52 30 60.Tính.
2
0
()
f
xdx
A. I =10 . B. I = 8 . C. I =12 . D. I =-12 .
Câu 21. Nếu
9
0
() 37fxdx
và
9
0
() 16gxdx
thì

9
0
2() 3()
f
xgxdx
bằng :
A. 74 B. 48 C. 53 D. 122
4/4 - Mã đề 302
Câu 22. Tínhthểtích
V
củaphầnvậtthểgiớihạnbởihaimặtphẳng
x 0
và
x 3
,biếtrằngthiết
diệncủavậtthểcắtbởimặtphẳngvuônggócvớitrục
Ox
tạiđiểmcóhoànhđộ
x
(
x03
)là
mộthìnhchữnhậtcóhaikíchthướclà
x
và x
2
29 .
A.

Vxxdx
3
2
0
29
.
B.

Vx xdx
3
2
0
229
.
C.

Vx xdx
3
2
0
29
. D.


Vxdx
3
2
0
49
.
Câu 23. Cho hình phẳng

H
được giới hạn bởi các đường:
2
,0,1yxx x
và Ox. Tính thể tích khối
tròn xoay tạo thành khi hình
H quay quanh trục Ox.
A.
2
3
B.
4
C.
5
D.
3
Câu 24. Cho a, b là hai số nguyên thỏa mãn
3
1
31
ln
e
a
e
xxdx
b
. Khẳng định nào sau đây đúng ?
A.
12ab
B.
4ab
C.
.64ab
D.
.46ab
Câu 25. Cho hình phẳng (S) giới hạn bởi Ox và
2
1yx
. Thể tích của khối tròn xoay khi quay (S) quanh
Ox là
A.
3
2
B.
2
3
C.
3
4
D.
4
3
------ HẾT ------
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT BÌNH DƯƠNG
KIỂM TRA 1 TIẾT BÀI 1 HK II NĂM HỌC 2017 - 2018
TRƯỜNG THPT PHƯỚC VĨNH
MÔN TOÁN – Khối lớp 12
Thời gian làm bài : 45 phút
(không kể thời gian phát đề)
(Đề thi có 04 trang)
Họ và tên học sinh :..................................................... Số báo danh : ................... Mã đề 302
Câu 1. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 2 – x2 và y = x. A. 11 B. 7 C. 9 D. 5 2 2 2 ln  x   1 Câu 2. Cho
dx a ln 2  b ln 3 
, với a,b là các số hữu tỉ. Tính P a  4b 2 x 1
A. P = 0.
B. P = 1.
C. P = -3. D. P = 3.
Câu 3. Tính diện tích hình phẳng giới hạn bởi các đường x
y xe , y  0, x  1. 1 3 3 A. B. 1 C. D. 2 2 2
Câu 4. Biết một nguyên hàm của hàm số y f x là F x 2
x  4x 1. Khi đó, giá trị của hàm số
y f x tại x  3 là
A. f 3  30.
B. f 3  10 .
C. f 3  22 .
D. f 3  6 . 4 2
Câu 5. Nếu f (x) liên tục và f (x)dx  10 
, thì f (2x)dx  bằng : 0 0 A. 19 B. 5 C. 9 D. 29 1 dx
Câu 6. Tính tích phân  . 2 x x 12 0 1 9 9 1 9 1 9 A.  ln B. ln C. ln D. ln 7 16 16 7 16 4 16
Câu 7. Cho hàm số f (x) thỏa mãn f (x)  3  5sin x và f (0)  7 . Mệnh đề nào dưới đây là đúng?
A. f (x)  3x  5 cos x  2
B. f (x)  3x  5 cos x  2
C. f (x)  3x  5 cos x  15
D. f (x)  3x  5 cos x  5
Câu 8. Giả sử hàm số F x là một nguyên hàm của hàm số f x trên K . Khẳng định nào sau đây đúng.
A. Chỉ có duy nhất hàm số y F(x) là nguyên hàm của f trên . K
B. Với mỗi nguyên hàm G của f trên K thì tồn tại một hằng số C sao cho ( G ) x  ( F )
x C với x thuộc K . 1/4 - Mã đề 302
C. Chỉ có duy nhất một hằng số C sao cho hàm số y F( )
x C là một nguyên hàm của hàm f trên K.
D. Với mỗi nguyên hàm G của f trên K thì ( G ) x  ( F )
x C với mọi x thuộc K và C bất kỳ. π 2 12 2 3 Câu 9. f ( tan x) Cho f (x)dx = ò
4 . Tính tích phân I = d . x ò cos2 3x 0 0 1 4 2 8
A. I = .
B. I = .
C. I = . D. I = . 3 3 3 3 Câu 10. 1 Tìm nguyên hàm dx  . 1 2x A.
1 dx  ln 12x C.  B. 1 1
dx  ln 1 2x C.  1 2x 1 2x 2 C. 1 1 1 dx  ln  C.  D. 1 1 dx  ln  C.  1  2x 2 1  2x 1  2x 1  2x
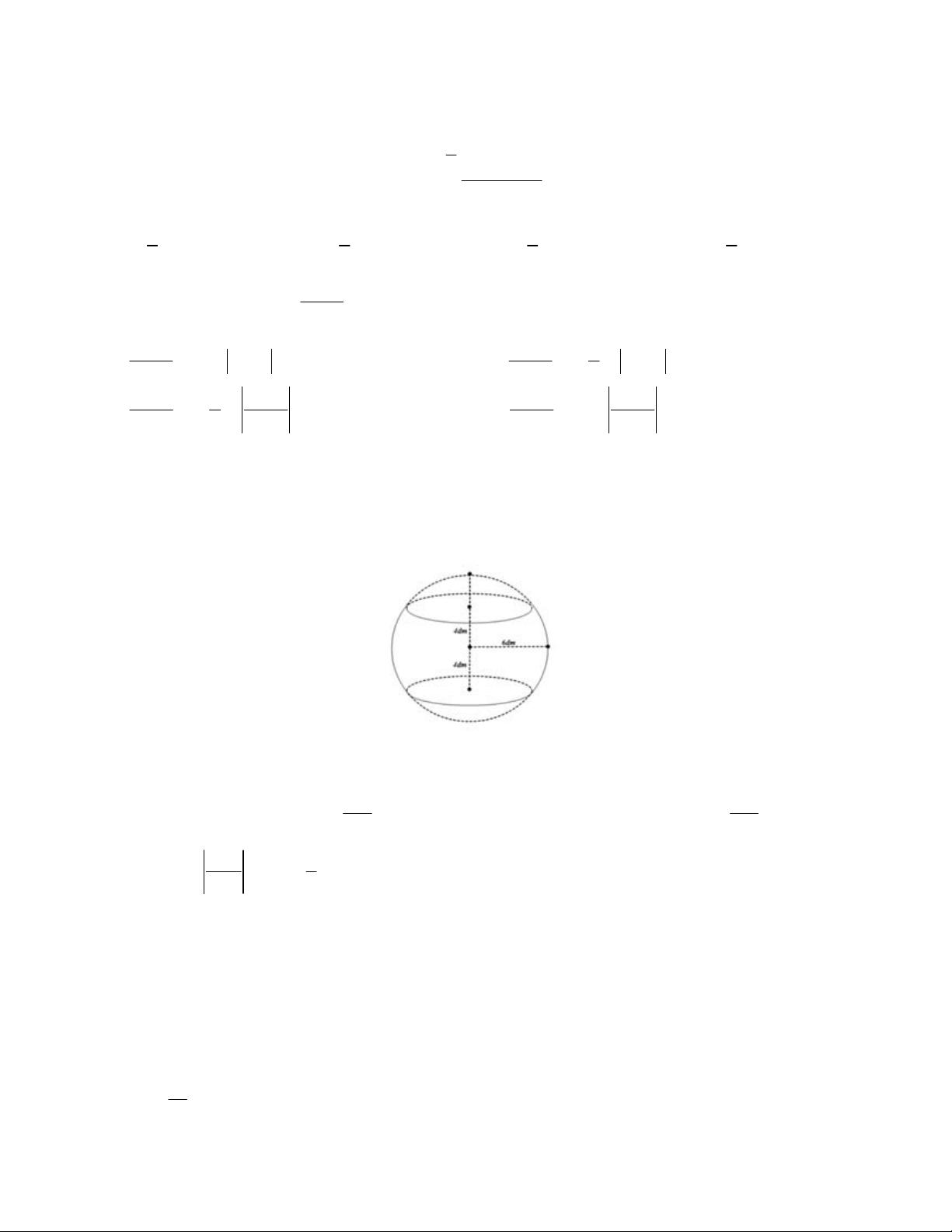
Câu 11. Một hình cầu có bán kính 6dm, người ta cắt bỏ hai phần bằng hai mặt phẳng song song và
cùng vuông góc với đường kính để làm mặt xung quanh của một chiếc lu chứa nước (như hình vẽ).
Tính thể tích V mà chiếc lu chứa được biết mặt phẳng cách tâm mặt cầu 4 dm. A. 368 736 V   (dm3 288 ). B. V
(dm3 ). C. V   (dm3 192 ). D. V   (dm3 ). 3 3 0 x 1 b Câu 12. Biết dx a ln 1 
. Khẳng định nào sau đây sai ? x  2 c 1  A. .
a b  3(c 1)
B. a b  2c 10
C. ac b  3
D. ab c 1 4
Câu 13. Nếu f (1)  12, f (
x) liên tục và f (x)dx  17 
, giá trị của f (4) bằng: 1 A. 19 B. 29 C. 5 D. 9
Câu 14. Tìm nguyên hàm của hàm số 2 f (x)  (x 1) 3 x A. 2 F(x)   x  x  C. B. 3 2
F(x)  x  3x  3x  C. 3 2/4 - Mã đề 302 3 x C. 3 2
F(x)  x  x  x  C. D. 2 F(x)   x  x  C. 3
Câu 15. Cho f (x)dx F(x)  C
. Khi đó với a  0 , ta có f (ax b)dx  bằng:
A. 1 F(ax  ) b  . C
B. 1 F(ax  )
b C . C. . a ( F ax  ) b  . C D. ( F ax  ) b  . C a 2a
Câu 16. Gọi S là diện tích hình phẳng H giới hạn bởi các đường y f x, trục hoành và hai
đường thẳng x  1,x  2 (như hình vẽ). 0 2
Đặt a   f xdx, b  f xd .x Mệnh đề nào sau đây đúng? 1 0
A. S b  . a
B. S  b  . a
C. S  b  . a
D. S b  . a x 1
Câu 17. Gọi F (x) là một nguyên hàm của hàm 2 ln y  ln x 1.
mà F (1)  . Giá trị 2 F (e) bằng: x 3 8 1 1 8 A. B. . C. . D. 9 9 3 3 2 Câu 18. Cho 2 I  2x x 1dx
. Khẳng định nào sau đây sai: 1 3 2 3 2 3 A. 2 I t B. I  27
C. I  3 3 D. I udu  3 0 3 0
Câu 19. Tìm nguyên hàm cos
 2x 1.dx . Chọn đáp án đúng: 1 1
A. sin 2x   1  C
B. sin 2x   1  C
C.  sin 2x   1  C D. 2s  in2x   1  C 2 2 2 2
Câu 20. Cho hàm số f (x) thỏa mãn (x  3) f '(x)dx  50  và 5 f ( ) 2 -3 f ( )
0 = 60 . Tính. f (x)dx 0 0
A. I =10 .
B. I = 8 .
C. I = 12 . D. I = -12 . 9 9 9
Câu 21. Nếu f (x)dx  37 
và g(x)dx  16 
thì 2 f (x) 3g(x)dx bằng : 0 0 0 A. 74 B. 48 C. 53 D. 122 3/4 - Mã đề 302
Câu 22. Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x  0 và x  3 , biết rằng thiết
diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ( 0  x  3 ) là
một hình chữ nhật có hai kích thước là x và  x2 2 9 . 3 3
A. V  2x 9   x2 dx .
B. V  2 x  2 9   x2 dx . 0 0 3 3
C. V  x  2 9  
x2 dx . D. V   4 9  x2 dx . 0 0
Câu 23. Cho hình phẳng H  được giới hạn bởi các đường: 2
y x , x  0, x  1 và Ox. Tính thể tích khối
tròn xoay tạo thành khi hình H  quay quanh trục Ox. 2    A. B. C. D. 3 4 5 3 e 3 a e 1
Câu 24. Cho a, b là hai số nguyên thỏa mãn 3 x ln xdx  
. Khẳng định nào sau đây đúng ? b 1
A. a b 12
B. a b  4 C. . a b  64 D. . a b  46
Câu 25. Cho hình phẳng (S) giới hạn bởi Ox và 2
y  1 x . Thể tích của khối tròn xoay khi quay (S) quanh Ox là 3 2 3 4 A. B. C. D.  2 3 4 3
------ HẾT ------ 4/4 - Mã đề 302