Đề kiểm tra 1 tiết Giải tích 12 chương 3 năm 2018 – 2019 trường THPT Thị xã Quảng Trị

Giới thiệu đến quý thầy, cô giáo cùng các em học sinh khối 12 đề kiểm tra 1 tiết Giải tích 12 chương 3 năm 2018 – 2019 trường THPT Thị xã Quảng Trị, kỳ kiểm tra được diễn ra vào tiết thứ 71 theo phân phối chương trình chuẩn môn Toán 12, nội dung kiểm tra thuộc chủ đề nguyên hàm, tích phân và ứng dụng.

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

19 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Tiết 71 : MA TRẬN ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG III - GIẢI TÍCH 12 NC
NĂM HỌC 2018 -2019
Chú ý: - 20 câu đầu trắc nghiệm A,B,C hay D.
- 5 câu cuối trắc nghiệm điền khuyết.
Chủ đề
Chuẩn kiến thức kĩ năng
Mức độ nhận thức Tổng
Nhận biết
Thông
hiểu
Vận dụng
thấp
Vận dụng
cao
Số câu Điểm
1. Nguyên hàm.
1 1 1 3 1,2
2. Phương pháp nguyên hàm.
1 1 1 1 4 1,6
3. Tích phân.
2 2 1 1 6 2,4
4. Ứng dụng tích phân (quảng
đường, vận tốc, gia tốc).
1 1 0,4
5. Phương pháp tích phân.
1 2 1 1 5 2,0
6. Ứng dụng tích phân tính diện tích
1 1 1 1 4 1,6
7. Ứng dụng tích phân tính thể tích
1 1 2 0,8
TỔNG
Số câu 7 8 6 4 25
Điểm 2,8 3,2 2,4 1,6
10
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
---------------------------------------------------------
Họ và tên học sinh: …………………..…………………………………….. Lớp: …………..
PHẦN ĐÁP ÁN
1
A B
C D
6
A B
C D
11
A B
C D
16
A B
C D
2
A B
C D
7
A B
C D
12
A B
C D
17
A B
C D
3
A B
C D
8
A B
C D
13
A B
C D
18
A B
C D
4
A B
C D
9
A B
C D
14
A B
C D
19
A B
C D
5
A B
C D
10
A B
C D
15
A B
C D
20
A B
C D
21
22
23
24
25
Chú ý: - Từ câu 1 đến câu 20 thí sinh tô đậm đáp án A, B, C hay D vào các ô tương ứng ở bảng trên.
- Từ câu 21 đến câu 25 thí sinh điền đáp án vào các ô tương ứng ở bảng trên.
Phần I: Trắc nghiệm A,B,C hay D
Câu 1: Tính
1
3
0
.de
x
I
x
.
A.
3
e1I 
. B.
e1I 
. C.
3
e1
3
. D.
3
1
e
2
I 
.
Câu 2: Họ nguyên hàm của hàm số

2sin2
f
xx x
là
A.
2
2cos2
x
xC
. B.
2
1
cos 2
2
x
xC
. C.
2
1
cos 2
2
x
xC
. D.
2
2cos2
x
xC
.
Câu 3: Cho hàm số

f
x
có đạo hàm liên tục trên đoạn

1; 3
thỏa mãn

12f
và
39f
. Tính

3
1
d
I
fxx
.
A.
11
I
. B.
7I
. C. 2
. D.
18I
.
Câu 4: Cho hai hàm số

f
x
và

gx
liên tục trên
K
,
,ab
K
. Khẳng định nào sau đây là khẳng định sai?
Mã đề 132
A.
 
dd
bb
aa
kfxxkfxx

. B.
   
dd.d
bbb
aaa
f
xgxx fxxgxx

.
C.
   
ddd
bbb
aaa
f
xgx x fxx gxx



. D.
   
ddd
bbb
aaa
f
xgx x fxx gxx



.
Câu 5: Cho tích phân
e
1
ln
d
x
I
x
x
. Nếu đặt
lntx
thì
A.
1
0
d
e
t
t
I
t
B.
1
2
0
d
I
tt
C.
1
0
d
I
tt
D.
e
1
d
I
tt
Câu 6: Diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số
2
y
x , trục hoành
Ox
, các đường thẳng
1
x
,
2x
là
A.
8
3
S
. B.
7
3
S
. C.
8S
. D.
7S
.
Câu 7: Cho hàm số

cos
f
xx
. Mệnh đề nào sau đây đúng
A.

dsin
f
xx xC
. B.

dcos
f
xx xC
.
C.

dcos
f
xx xC
. D.

dsin
f
xx xC
.
Câu 8: Cho hàm

yfx
liên tục và không âm trên

;ab
. Tính thể tích khối tròn xoay được tạo thành khi quay
hình phẳng

H
được giới hạn bởi các đường

yfx
, trục
Ox
và hai đường thẳng
x
a
,
x
b
,

ab
xung
quanh trục
Ox
.
A.

2
d
b
a
f
xx
. B.

2
2d
b
a
f
xx
. C.

2
d
b
a
f
xx
. D.

d
b
a
f
xx
.
Câu 9: Cho

2
12
I
xxdx
. Bằng cách đặt
2
1tx
, khẳng định nào sau đây đúng
A.
2
I
tdt
B.
1
2
I
tdt
C.

1
I
tdt
D.
I
tdt
Câu 10: Cho hàm số

f
x
liên tục trên

;ab
. Hãy chọn mệnh đề sai dưới đây:
A.
 
dd
ba
ab
f
xx fxx

.
B.
  
ddd
bcb
aac
f
xx fxx fxx

với
;cab
.
C.

d
b
a
kx kb a
,
k
.
D.
 
dd
ba
ab
f
xx fxx

.
Câu 11: Tính tích phân
π
0
cos d
I
xxx
bằng cách đặt
d cos d
ux
vxx
. Mệnh đề nào dưới đây đúng?
A.
π
π
0
0
sin sin d
I
xx xx
.
B.
π
π
0
0
sin sin d
I
xx xx
.
C.
π
π
0
0
sin cos d
I
xx xx
. D.
π
π
0
0
cos sin d
I
xx xx
.
Câu 12: Giả sử hàm số

yfx
liên tục trên và

5
3
d
f
xxa
,
a
. Tích phân

2
1
21d
I
fx x
có giá
trị là
A.
1
1
2
I
a
. B.
21Ia
. C.
2Ia
. D.
1
2
I
a
.
Câu 13: Goi

H
là hình phẳng giới hạn bởi đồ thị hàm số
x
y
e , trục
Ox
và hai đường thẳng
0,x
1
x
. Thể
tích của khối tròn xoay tạo thành khi quay

H
xung quanh trục
Ox
là
A.

2
1
2
e
. B.

2
1e
. C.

2
1
2
e
. D.

2
1e
.
Câu 14: Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số

yfx
, trục
Ox
và các đường
thẳng

,.
x
ax b a b
A.

b
a
f
xdx
. B.

b
a
f
xdx
. C.

2
b
a
f
xdx
. D.

b
a
f
xdx
.
Câu 15: Kết quả của
d
x
I
xe x
là
A.
xx
Ie xe C
. B.
xx
IxeeC
. C.
2
2
x
x
IeC
. D.
2
2
xx
x
IeeC
.
Câu 16: Một xe mô tô đang chạy với vận tốc
20m/s
thì người lái xe nhìn thấy một chướng ngại vật nên đạp phanh.
Từ thời điểm đó, mô tô chuyển động chậm dần với vận tốc

20 5vt t
, trong đó t là thời gian (được tính bằng
giây ) kể từ lúc đạp phanh. Quãng đường mà mô tô đi được từ khi người lái xe đạp phanh cho đến lúc mô tô dừng lại
là
A.
40m
B.
80m
C.
60m
D.
20m
Câu 17: Biết


e
1
ln 3
dln,,
ln 2 2
x
I
xa babQ
xx

. Mệnh đề nào sau đây đúng?
A.
1ab
. B.
21ab
. C.
20ab
. D.
22
4ab
.
Câu 18: Gọi

Fx
là một nguyên hàm của hàm số

e
x
f
xx
. Tính

Fx
biết

01F
.
A.

1e 2
x
Fx x

. B.

1e 2
x
Fx x

.
C.

1e 1
x
Fx x

. D.

1e 1
x
Fx x

.
Câu 19: Biết

Fx
là một nguyên hàm của

1
1
fx
x
và

02F
thì

1F
bằng.
A.
ln 2
. B.
3
. C.
4
. D.
2ln2
.
Câu 20: Giả sử
2
1
1
dln
21
a
x
x
b
với
a
,
*b
và
a
b
tối giản. Tính
22
M
ab
.
A.
28M
. B.
34M
. C.
14
M
. D.
8M
.
Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 21: Tính diện tích
S
của hình phẳng giới hạn bởi hai đồ thị hàm số
2
2
y
x và
52yx
.
Câu 22: Biết

Fx
là một nguyên hàm của hàm

ln 1fx x x
và

00,F

2lnFab
với
,ab
.
Tính
.Pab
Câu 23: Cho hàm số

f
x
có đạo hàm liên tục trên đoạn
0;1
và thỏa mãn
06f
,

1
0
22. d6xfxx

.
Tích phân

1
0
d
f
xx
.
Câu 24: Cho hàm số
()
=yfx
có đạo hàm liên tục trên
[
]
-2;4 .
Đồ thị của
hàm số
()
yfx
¢
=
được cho như hình bên. Diện tích hình phẳng giới hạn
bởi trục
Ox và đồ thị hàm số
()
yfx
¢
=
trên đoạn
[
]
2;1-
và
[
]
1; 4
lần lượt
bằng
9
và
12.
Cho
()
13.f =
Tính tổng
() ()
24.ff-+
Câu 25: Cho hàm số

f
x
thỏa mãn

1
2
5
f 
,
 
2
3
f
xxfx


và

0fx
với mọi
x
. Tính giá trị
của

1.f
----------- HẾT ----------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
---------------------------------------------------------
Họ và tên học sinh: …………………..……………………………………..Lớp: …………..
PHẦN ĐÁP ÁN
1
A B
C D
6
A B
C D
11
A B
C D
16
A B
C D
2
A B
C D
7
A B
C D
12
A B
C D
17
A B
C D
3
A B
C D
8
A B
C D
13
A B
C D
18
A B
C D
4
A B
C D
9
A B
C D
14
A B
C D
19
A B
C D
5
A B
C D
10
A B
C D
15
A B
C D
20
A B
C D
21
22
23
24
25
Chú ý: - Từ câu 1 đến câu 20 thí sinh tô đậm đáp án A, B, C hay D vào các ô tương ứng ở bảng trên.
- Từcâu 21 đến câu 25 thí sinh điền đáp án vào các ô tương ứng ở bảng trên.
Phần I: Trắc nghiệm A,B,C hay D
Câu 1: Cho hàm số

f
x
có đạo hàm liên tục trên đoạn

1; 3
thỏa mãn

12f
và

39f
. Tính

3
1
d
I
fxx
.
A.
2
. B.
18I
. C.
7I
. D. 11
I
.
Câu 2: Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số

yfx
, trục
Ox
và các đường
thẳng

,.
x
ax b a b
A.

b
a
f
xdx
. B.

2
b
a
f
xdx
. C.

b
a
f
xdx
. D.

b
a
f
xdx
.
Câu 3: Goi

H
là hình phẳng giới hạn bởi đồ thị hàm số
x
y
e , trục
Ox
và hai đường thẳng
0,x
1
x
. Thể tích
của khối tròn xoay tạo thành khi quay

H
xung quanh trục
Ox
là
A.

2
1
2
e
. B.

2
1e
. C.

2
1
2
e
. D.

2
1e
.
Mãđề209
Câu 4: Họ nguyên hàm của hàm số

2sin2
f
xx x
là
A.
2
1
cos 2
2
x
xC
. B.
2
2cos2
x
xC
. C.
2
1
cos 2
2
x
xC
. D.
2
2cos2
x
xC
.
Câu 5: Tính
1
3
0
.de
x
I
x
.
A.
3
e1I 
. B.
3
e1
3
. C.
e1I 
. D.
3
1
e
2
I 
.
Câu 6: Cho

2
12
I
xxdx
. Bằng cách đặt
2
1tx
, khẳng định nào sau đây đúng
A.
2
I
tdt
B.
1
2
I
tdt
C.

1
I
tdt
D.
I
tdt
Câu 7: Cho hàm số

cos
f
xx
. Mệnh đề nào sau đây đúng
A.

dcos
f
xx xC
. B.

dsin
f
xx xC
.
C.

dsin
f
xx xC
. D.

dcos
f
xx xC
.
Câu 8: Cho hai hàm số

f
x
và

gx
liên tục trên
K
,
,ab
K
. Khẳng định nào sau đây là khẳng định sai?
A.
   
dd.d
bbb
aaa
f
xgx x f x x gx x

. B.
 
dd
bb
aa
kfxxkfxx

.
C.
   
ddd
bbb
aaa
f
xgx x fxx gxx



. D.
   
ddd
bbb
aaa
f
xgx x fxx gxx



.
Câu 9: Cho tích phân
e
1
ln
d
x
I
x
x
. Nếu đặt
lntx
thì
A.
e
1
d
I
tt
B.
1
0
d
e
t
t
I
t
C.
1
0
d
I
tt
D.
1
2
0
d
I
tt
Câu 10: Diện tích
S của hình phẳng giới hạn bởi đồ thị hàm số
2
y
x , trục hoành
Ox
, các đường thẳng
1
x
,
2x
là
A.
7S
. B.
8S
. C.
7
3
S
. D.
8
3
S
.
Câu 11: Giả sử hàm số

yfx
liên tục trên
và

5
3
d
f
xxa
,

a
. Tích phân

2
1
21d
I
fx x
có giá
trị là
A.
1
1
2
I
a
. B.
21Ia
. C.
2Ia
. D.
1
2
I
a
.
Câu 12: Cho hàm

yfx
liên tục và không âm trên

;ab
. Tính thể tích khối tròn xoay được tạo thành khi quay
hình phẳng

H
được giới hạn bởi các đường

yfx
, trục
Ox
và hai đường thẳng
x
a
,
x
b
,

ab
xung
quanh trục
Ox
.
A.

2
d
b
a
f
xx
. B.

d
b
a
f
xx
. C.

2
2d
b
a
f
xx
. D.

2
d
b
a
f
xx
.
Câu 13: Kết quả của
d
x
I
xe x
là
A.
xx
Ie xe C
. B.
xx
IxeeC
. C.
2
2
x
x
IeC
. D.
2
2
xx
x
IeeC
.
Câu 14: Cho hàm số

f
x
liên tục trên

;ab
. Hãy chọn mệnh đề sai dưới đây:
A.
 
dd
ba
ab
f
xx fxx

.
B.

d
b
a
kx kb a
,
k
.
C.
  
ddd
bcb
aac
f
xx fxx fxx

với
;cab
.
D.
 
dd
ba
ab
f
xx fxx

.
Câu 15: Tính tích phân
π
0
cos d
I
xxx
bằng cách đặt
d cos d
ux
vxx
. Mệnh đề nào dưới đây đúng?
A.
π
π
0
0
sin sin d
I
xx xx
.
B.
π
π
0
0
sin sin d
I
xx xx
.
C.
π
π
0
0
sin cos d
I
xx xx
. D.
π
π
0
0
cos sin d
I
xx xx
.
Câu 16: Giả sử
2
1
1
dln
21
a
x
x
b
với
a
,
*b
và
a
b
tối giản. Tính
22
M
ab
.
A.
28M
. B.
34M
. C.
14
M
. D.
8M
.
Câu 17: Gọi

Fx
là một nguyên hàm của hàm số

e
x
f
xx
. Tính

Fx
biết

01F
.
A.

1e 1
x
Fx x

. B.

1e 2
x
Fx x

.
C.

1e 1
x
Fx x

. D.

1e 2
x
Fx x

.
Câu 18: Biết

Fx
là một nguyên hàm của

1
1
fx
x
và

02F
thì

1F
bằng.
A.
3
. B.
ln 2
. C.
2ln2
. D.
4
.
Câu 19: Biết


e
1
ln 3
dln,,
ln 2 2
x
I
xa babQ
xx

. Mệnh đề nào sau đây đúng?
A.
22
4ab
. B.
1ab
. C.
21ab
. D.
20ab
.
Câu 20: Một xe mô tô đang chạy với vận tốc
20m/s
thì người lái xe nhìn thấy một chướng ngại vật nên đạp phanh.
Từ thời điểm đó, mô tô chuyển động chậm dần với vận tốc

20 5vt t
, trong đó t là thời gian (được tính bằng
giây ) kể từ lúc đạp phanh. Quãng đường mà mô tô đi được từ khi người lái xe đạp phanh cho đến lúc mô tô dừng lại
là
A.
40m
B.
60m
C.
20m
D.
80m
Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 21: Tính diện tích
S
của hình phẳng giới hạn bởi hai đồ thị hàm số
2
y
x và
56yx
.
Câu 22: Biết

Fx
là một nguyên hàm của hàm

ln 1fx x x
và

22,F

3lnFabc
với
,,abc
. Tính
.Pabc
Câu 23: Cho hàm số

f
x
có đạo hàm liên tục trên đoạn
0;1
và thỏa mãn

08f
,

1
0
1. d 6xfxx

. Tích
phân

1
0
d
f
xx
.
Câu 24: Cho hàm số
()
=yfx
có đạo hàm liên tục trên
[
]
-2;4 .
Đồ thị của
hàm số
()
yfx
¢
=
được cho như hình bên. Diện tích hình phẳng giới hạn
bởi trục
Ox và đồ thị hàm số
()
yfx
¢
=
trên đoạn
[
]
2;1-
và
[
]
1; 4
lần lượt
bằng
8
và
11.
Cho
()
14.f =
Tính tổng
() ()
24.ff-+
Câu 25: Cho hàm số
f
x
thỏa mãn

1
2
25
f
,
 
2
3
4


f
xxfx
và

0fx
với mọi
x
. Tính giá
trị của
1.f
----------- HẾT ----------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
---------------------------------------------------------
Họ và tên học sinh: …………………..……………………………………..Lớp: …………..
PHẦN ĐÁP ÁN
1
A B
C D
6
A B
C D
11
A B
C D
16
A B
C D
2
A B
C D
7
A B
C D
12
A B
C D
17
A B
C D
3
A B
C D
8
A B
C D
13
A B
C D
18
A B
C D
4
A B
C D
9
A B
C D
14
A B
C D
19
A B
C D
5
A B
C D
10
A B
C D
15
A B
C D
20
A B
C D
21
22
23
24
25
Chú ý:
- Từ câu 1 đến câu 20 thí sinh tô đậm đáp án A, B, C hay D vào các ô tương ứng ở bảng trên.
- Từcâu 21 đến câu 25 thí sinh điền đáp án vào các ô tương ứng ở bảng trên.
Phần I: Trắc nghiệm A,B,C hay D
Câu 1: Goi

H
là hình phẳng giới hạn bởi đồ thị hàm số
x
y
e , trục
Ox
và hai đường thẳng
0,x
1
x
. Thể tích
của khối tròn xoay tạo thành khi quay

H
xung quanh trục
Ox
là
A.

2
1
2
e
. B.

2
1e
. C.

2
1
2
e
. D.

2
1e
.
Câu 2: Cho hàm số

f
x
liên tục trên

;ab
. Hãy chọn mệnh đề sai dưới đây:
A.
 
dd
ba
ab
f
xx fxx

.
B.
  
ddd
bcb
aac
f
xx fxx fxx

với
;cab
.
C.

d
b
a
kx kb a
,
k
.
D.
 
dd
ba
ab
f
xx fxx

.
Mãđề357
Câu 3: Cho hai hàm số

f
x
và

gx
liên tục trên
K
,
,ab
K
. Khẳng định nào sau đây là khẳng định sai?
A.
   
ddd
bbb
aaa
f
xgx x fxx gxx



. B.
   
dd.d
bbb
aaa
f
xgxx fxxgxx

.
C.
 
dd
bb
aa
kfxxkfxx

. D.
   
ddd
bbb
aaa
f
xgx x fxx gxx



.
Câu 4: Diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số
2
y
x , trục hoành
Ox
, các đường thẳng
1
x
,
2x
là
A.
8S
. B.
7S
. C.
7
3
S
. D.
8
3
S
.
Câu 5: Cho hàm số

f
x
có đạo hàm liên tục trên đoạn

1; 3
thỏa mãn

12f
và

39f
. Tính

3
1
d
I
fxx
.
A. 11
I
. B.
7I
. C. 2
. D.
18I
.
Câu 6: Tính
1
3
0
.de
x
I
x
.
A.
3
e1I 
. B.
3
1
e
2
I 
. C.
3
e1
3
. D.
e1I 
.
Câu 7: Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số

yfx
, trục
Ox
và các đường
thẳng

,.
x
ax b a b
A.

b
a
f
xdx
. B.

b
a
f
xdx
. C.

b
a
f
xdx
. D.

2
b
a
f
xdx
.
Câu 8: Họ nguyên hàm của hàm số

2sin2
f
xx x
là
A.
2
2cos2
x
xC
. B.
2
2cos2
x
xC
. C.
2
1
cos 2
2
x
xC
. D.
2
1
cos 2
2
x
xC
.
Câu 9: Tính tích phân
π
0
cos d
I
xxx
bằng cách đặt
dcosd
ux
vxx
. Mệnh đề nào dưới đây đúng?
A.
π
π
0
0
sin sin d
I
xx xx
.
B.
π
π
0
0
sin sin d
I
xx xx
.
C.
π
π
0
0
sin cos d
I
xx xx
. D.
π
π
0
0
cos sin d
I
xx xx
.
Câu 10: Giả sử hàm số

yfx
liên tục trên và

5
3
d
f
xxa
,

a
. Tích phân

2
1
21d
I
fx x
có giá
trị là
A.
1
1
2
I
a
. B.
21Ia
. C.
2Ia
. D.
1
2
I
a
.
Câu 11: Cho hàm

yfx
liên tục và không âm trên

;ab
. Tính thể tích khối tròn xoay được tạo thành khi quay
hình phẳng

H
được giới hạn bởi các đường

yfx
, trục
Ox
và hai đường thẳng
x
a
,
x
b
,

ab
xung
quanh trục
Ox
.
A.

2
d
b
a
f
xx
. B.

d
b
a
f
xx
. C.

2
2d
b
a
f
xx
. D.

2
d
b
a
f
xx
.
Câu 12: Kết quả của
d
x
I
xe x
là
A.
xx
Ie xe C
. B.
xx
IxeeC
. C.
2
2
x
x
IeC
. D.
2
2
xx
x
IeeC
.
Câu 13: Cho hàm số

cos
f
xx
. Mệnh đề nào sau đây đúng
A.

dsin
f
xx xC
. B.

dcos
f
xx xC
.
C.

dcos
f
xx xC
. D.

dsin
f
xx xC
.
Câu 14: Cho

2
12
I
xxdx
. Bằng cách đặt
2
1tx
, khẳng định nào sau đây đúng
A.
2
I
tdt
B.
1
2
I
tdt
C.

1
I
tdt
D.
I
tdt
Câu 15: Cho tích phân
e
1
ln
d
x
I
x
x
. Nếu đặt
lntx
thì
A.
1
0
d
I
tt
B.
1
0
d
e
t
t
I
t
C.
e
1
d
I
tt
D.
1
2
0
d
I
tt
Câu 16: Giả sử
2
1
1
dln
21
a
x
x
b
với
a
,
*b
và
a
b
tối giản. Tính
22
M
ab
.
A.
28M
. B.
34M
. C.
14
M
. D.
8M
.
Câu 17: Biết

Fx
là một nguyên hàm của

1
1
fx
x
và

02F
thì

1F
bằng.
A.
2ln2
. B.
ln 2
. C.
3
. D.
4
.
Câu 18: Một xe mô tô đang chạy với vận tốc
20m/s
thì người lái xe nhìn thấy một chướng ngại vật nên đạp phanh.
Từ thời điểm đó, mô tô chuyển động chậm dần với vận tốc

20 5vt t
, trong đó t là thời gian (được tính bằng
giây ) kể từ lúc đạp phanh. Quãng đường mà mô tô đi được từ khi người lái xe đạp phanh cho đến lúc mô tô dừng lại
là
A.
60m
B.
80m
C.
40m
D.
20m
Câu 19: Gọi

Fx
là một nguyên hàm của hàm số

e
x
f
xx
. Tính

Fx
biết

01F
.
A.

1e 1
x
Fx x

. B.

1e 2
x
Fx x

.
C.

1e 1
x
Fx x

. D.

1e 2
x
Fx x

.
Câu 20: Biết


e
1
ln 3
dln,,
ln 2 2
x
I
xa babQ
xx

. Mệnh đề nào sau đây đúng?
A.
22
4ab
. B.
1ab
. C.
21ab
. D.
20ab
.
Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 21: Tính diện tích
S
của hình phẳng giới hạn bởi hai đồ thị hàm số
2
y
x và
815yx
.
Câu 22: Biết

Fx
là một nguyên hàm của hàm

1
x
f
xxe
và

01,F

3
b
Faec
với
,,abc
.
Tính
.Pabc
Câu 23: Cho hàm số

f
x
có đạo hàm liên tục trên đoạn

0;1
và thỏa mãn

014f
,

1
0
1. d 10xfxx

.
Tích phân

1
0
d
f
xx
.
Câu 24:
Cho hàm số
()
=yfx
có đạo hàm liên tục trên
[
]
-2;4 .
Đồ thị của
hàm số
()
yfx
¢
=
được cho như hình bên. Diện tích hình phẳng giới hạn
bởi trục
Ox và đồ thị hàm số
()
yfx
¢
=
trên đoạn
[
]
2;1-
và
[
]
1; 4
lần lượt
bằng
5 và 7. Cho
()
14.f =
Tính tổng
() ()
24.ff-+
Câu 25: Cho hàm số
()
f
x
thỏa mãn
1
(2)
3
f 
,
2
() ()
f
xxfx
và

0fx
với mọi
.x
Tính giá trị
của
(1).
f
----------- HẾT ----------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
---------------------------------------------------------
Họ và tên học sinh: …………………..……………………………………..Lớp: …………..
PHẦN ĐÁP ÁN
1
A B
C D
6
A B
C D
11
A B
C D
16
A B
C D
2
A B
C D
7
A B
C D
12
A B
C D
17
A B
C D
3
A B
C D
8
A B
C D
13
A B
C D
18
A B
C D
4
A B
C D
9
A B
C D
14
A B
C D
19
A B
C D
5
A B
C D
10
A B
C D
15
A B
C D
20
A B
C D
21
22
23
24
25
Chú ý: - Từ câu 1 đến câu 20 thí sinh tô đậm đáp án A, B, C hay D vào các ô tương ứng ở bảng trên.
- Từcâu 21 đến câu 25 thí sinh điền đáp án vào các ô tương ứng ở bảng trên.
Phần I: Trắc nghiệm A,B,C hay D
Câu 1: Cho tích phân
e
1
ln
d
x
I
x
x
. Nếu đặt
lntx
thì
A.
1
0
d
I
tt
B.
1
2
0
d
I
tt
C.
1
0
d
e
t
t
I
t
D.
e
1
d
I
tt
Câu 2: Tính
1
3
0
.de
x
I
x
.
A.
3
e1I 
. B.
e1I 
. C.
3
e1
3
. D.
3
1
e
2
I 
.
Câu 3: Cho hai hàm số

f
x
và

gx
liên tục trên
K
,
,ab
K
. Khẳng định nào sau đây là khẳng định sai?
A.
   
ddd
bbb
aaa
f
xgx x fxx gxx



. B.
   
ddd
bbb
aaa
f
xgx x fxx gxx



.
C.
   
dd.d
bbb
aaa
f
xgx x f x x gx x

. D.
 
dd
bb
aa
kfxxkfxx

.
Mãđề485
Câu 4: Cho hàm số

f
x
liên tục trên

;ab
. Hãy chọn mệnh đề sai dưới đây:
A.
  
ddd
bcb
aac
f
xx fxx fxx

với
;cab
. B.
 
dd
ba
ab
f
xx fxx

.
C.

d
b
a
kx kb a
,
k
. D.
 
dd
ba
ab
f
xx fxx

.
Câu 5: Tính tích phân
π
0
cos d
I
xxx
bằng cách đặt
dcosd
ux
vxx
. Mệnh đề nào dưới đây đúng?
A.
π
π
0
0
sin sin d
I
xx xx
.
B.
π
π
0
0
sin sin d
I
xx xx
.
C.
π
π
0
0
sin cos d
I
xx xx
. D.
π
π
0
0
cos sin d
I
xx xx
.
Câu 6: Kết quả của d
x
I
xe x
là
A.
xx
Ie xe C
. B.
xx
IxeeC
. C.
2
2
x
x
IeC
. D.
2
2
xx
x
IeeC
.
Câu 7: Họ nguyên hàm của hàm số

2sin2
f
xx x
là
A.
2
2cos2
x
xC
. B.
2
2cos2
x
xC
. C.
2
1
cos 2
2
x
xC
. D.
2
1
cos 2
2
x
xC
.
Câu 8: Cho hàm số

f
x
có đạo hàm liên tục trên đoạn

1; 3
thỏa mãn

12f
và

39f
. Tính

3
1
d
I
fxx
.
A.
18I
. B. 2
. C. 11
I
. D.
7I
.
Câu 9: Goi

H
là hình phẳng giới hạn bởi đồ thị hàm số
x
y
e , trục
Ox
và hai đường thẳng
0,x
1
x
. Thể tích
của khối tròn xoay tạo thành khi quay

H
xung quanh trục
Ox
là
A.

2
1e
. B.

2
1e
. C.

2
1
2
e
. D.

2
1
2
e
.
Câu 10: Cho hàm

yfx
liên tục và không âm trên

;ab
. Tính thể tích khối tròn xoay được tạo thành khi quay
hình phẳng

H
được giới hạn bởi các đường

yfx
, trục
Ox
và hai đường thẳng
x
a
,
x
b
,

ab
xung
quanh trục
Ox
.
A.

2
d
b
a
f
xx
. B.

d
b
a
f
xx
. C.

2
2d
b
a
f
xx
. D.

2
d
b
a
f
xx
.
Câu 11: Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số

yfx
, trục
Ox
và các đường
thẳng

,.
x
ax b a b
A.

b
a
f
xdx
. B.

2
b
a
f
xdx
. C.

b
a
f
xdx
. D.

b
a
f
xdx
.
Câu 12: Cho hàm số

cos
f
xx
. Mệnh đề nào sau đây đúng
A.

dsin
f
xx xC
. B.

dcos
f
xx xC
.
C.

dcos
f
xx xC
. D.

dsin
f
xx xC
.
Câu 13: Cho

2
12
I
xxdx
. Bằng cách đặt
2
1tx
, khẳng định nào sau đây đúng
A.
2
I
tdt
B.
1
2
I
tdt
C.

1
I
tdt
D.
I
tdt
Câu 14: Giả sử hàm số

yfx
liên tục trên và

5
3
d
f
xxa
,

a
. Tích phân

2
1
21d
I
fx x
có giá
trị là
A.
1
1
2
I
a
. B.
21Ia
. C.
2Ia
. D.
1
2
I
a
.
Câu 15: Diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số
2
y
x , trục hoành
Ox
, các đường thẳng
1
x
,
2x
là
A.
7S
. B.
7
3
S
. C.
8
3
S
. D.
8S
.
Câu 16: Biết


e
1
ln 3
dln,,
ln 2 2
x
I
xa babQ
xx

. Mệnh đề nào sau đây đúng?
A.
1ab
. B.
22
4ab
. C.
21ab
. D.
20ab
.
Câu 17: Biết

Fx
là một nguyên hàm của

1
1
fx
x
và

02F
thì

1F
bằng.
A.
3
. B.
4
. C.
2ln2
. D.
ln 2
.
Câu 18: Gọi

Fx
là một nguyên hàm của hàm số

e
x
f
xx
. Tính

Fx
biết

01F
.
A.

1e 1
x
Fx x

. B.

1e 2
x
Fx x

.
C.

1e 1
x
Fx x

. D.

1e 2
x
Fx x

.
Câu 19: Một xe mô tô đang chạy với vận tốc
20m/s
thì người lái xe nhìn thấy một chướng ngại vật nên đạp phanh.
Từ thời điểm đó, mô tô chuyển động chậm dần với vận tốc

20 5vt t
, trong đó t là thời gian (được tính bằng
giây ) kể từ lúc đạp phanh. Quãng đường mà mô tô đi được từ khi người lái xe đạp phanh cho đến lúc mô tô dừng lại
là
A.
40m
B.
60m
C.
20m
D.
80m
Câu 20: Giả sử
2
1
1
dln
21
a
x
x
b
với
a
,
*b
và
a
b
tối giản. Tính
22
M
ab
.
A.
8M
. B.
34M
. C.
28M
. D. 14
M
.
Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 21: Tính diện tích
S
của hình phẳng giới hạn bởi hai đồ thị hàm số
2
y
x và
918yx
.
Câu 22: Biết

Fx
là một nguyên hàm của hàm

2
x
f
xxe
và

02,F

2
b
Faec
với
,,abc
.
Tính
.Pabc
Câu 23: Cho hàm số

f
x
có đạo hàm liên tục trên đoạn

0;1
và thỏa mãn

016f
,

1
0
1. d 10xfxx

.
Tích phân

1
0
d
f
xx
.
Câu 24:
Cho hàm số
()
=yfx
có đạo hàm liên tục trên
[
]
-2;4 .
Đồ thị của
hàm số
()
yfx
¢
=
được cho như hình bên. Diện tích hình phẳng giới hạn
bởi trục
Ox và đồ thị hàm số
()
yfx
¢
=
trên đoạn
[
]
2;1-
và
[
]
1; 4
lần lượt
bằng
14 và
18.
Cho
()
14.f =
Tính tổng
() ()
24ff-+
.
Câu 25:
Cho hàm số

f
x
thỏa mãn

1
2
5
f

,
 
2
3
f
xxfx


và

0fx
với mọi
x
. Tính giá trị
của

1.f
----------- HẾT ----------
ĐÁP ÁN ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3-GIẢI TÍCH 12-NH 2018-2019
MÃ ĐỀ 132:
1 C 6 B 11 B 16 A
2 C 7 D 12 D 17 C
3 B 8 C 13 A 18 B
4 B 9 D 14 A 19 D
5 C 10 A 15 B 20 B
21
9
8
22
9
2
23
3
24
3
25
4
5
MÃ ĐỀ 209:
1 C 6 D 11 D 16 B
2 D 7 B 12 A 17 D
3 A 8 A 13 B 18 C
4 A 9 C 14 A 19 D
5 B 10 C 15 B 20 A
21
1
6
22
25
4
23
2
24
5
25
1
10
MÃ ĐỀ 357:
1 A 6 C 11 A 16 B
2 A 7 C 12 B 17 A
3 B 8 C 13 D 18 C
4 C 9 B 14 D 19 D
5 B 10 D 15 A 20 D
21
4
3
22
7
23
4
24
6
25
2
3
MÃ ĐỀ 485:
1 A 6 B 11 A 16 D
2 C 7 C 12 D 17 C
3 C 8 D 13 D 18 D
4 D 9 C 14 D 19 A
5 B 10 A 15 B 20 B
21
9
2
22
6
23
6
24
4
25
4
5
ĐÁP ÁN CHI TIẾT CÁC CÂU 23-24-25 MÃ ĐỀ 132
(
Các mã đề còn lại tương tự)
Câu 23
: Ta có:
    
1111
1
0
0000
622' 22 2 6122 3.
|
x f x dx x f x f x dx f x dx f x dx

Câu 24: Theo giả thiết, ta có
()
1
2
d9fxx
-
¢
=-
ò
và
()
4
1
d 12.fxx
¢
=-
ò
•
() () () () ()
1
2
d 9 1 2 93 2 9 212.fxx f f f f
-
¢
=- - - =- - - =- ¾¾-=
ò
•
() () () () ()
4
1
d1241124312 49.fxx f f f f
¢
=- - =- - =- ¾¾=-
ò
Vậy
() () ()
241293.ff-+ = +-=
Câu 25: Ta có:
 




22
2
333
22
11
dd
fx fx
f
xxfx x x xx
fx fx





  

2
1
115 1115 4
1
4214 5
f
fx f f

 



.
| 1/19
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Tiết 71 : MA TRẬN ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG III - GIẢI TÍCH 12 NC NĂM HỌC 2018 -2019
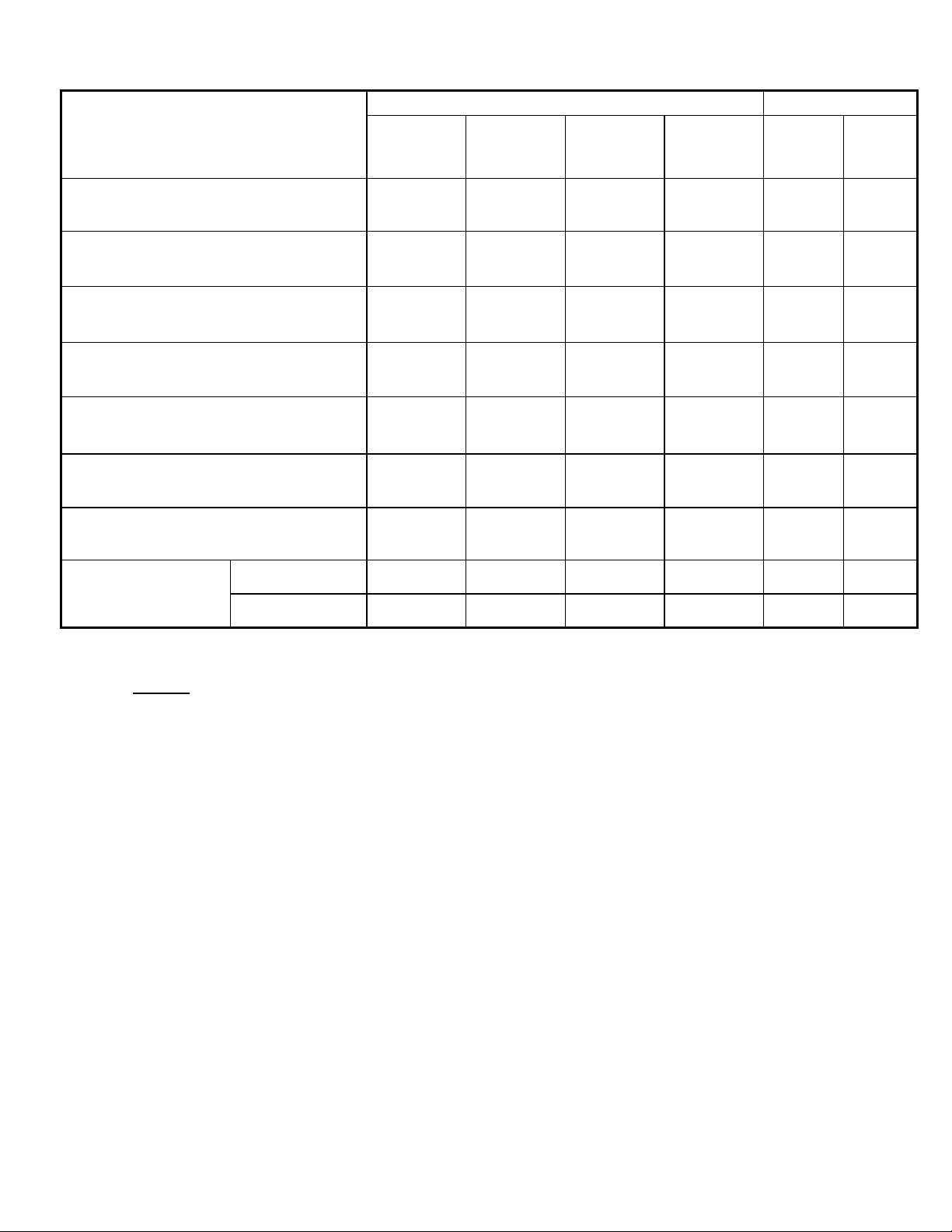
Mức độ nhận thức Tổng Chủ đề
Chuẩn kiến thức kĩ năng Thông Vận dụng Vận dụng Nhận biết Số câu Điểm hiểu thấp cao 1. Nguyên hàm. 1 1 1 3 1,2
2. Phương pháp nguyên hàm. 1 1 1 1 4 1,6 3. Tích phân. 2 2 1 1 6 2,4
4. Ứng dụng tích phân (quảng 1 1 0,4
đường, vận tốc, gia tốc).
5. Phương pháp tích phân. 1 2 1 1 5 2,0
6. Ứng dụng tích phân tính diện tích 1 1 1 1 4 1,6
7. Ứng dụng tích phân tính thể tích 1 1 2 0,8 Số câu 7 8 6 4 25 TỔNG Điểm 2,8 3,2 2,4 1,6 10
Chú ý: - 20 câu đầu trắc nghiệm A,B,C hay D.
- 5 câu cuối trắc nghiệm điền khuyết.
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
--------------------------------------------------------- Mã đề 132
Họ và tên học sinh: …………………..…………………………………….. Lớp: ………….. PHẦN ĐÁP ÁN 1 A B C D 6 11 16 A B C D A B C D A B C D 2 A B C D 7 12 17 A B C D A B C D A B C D 3 A B C D 8 13 18 A B C D A B C D A B C D 4 A B C D 9 14 19 A B C D A B C D A B C D 5 A B C D 10 15 20 A B C D A B C D A B C D 21 22 23 24 25
Chú ý: - Từ câu 1 đến câu 20 thí sinh tô đậm đáp án A, B, C hay D vào các ô tương ứng ở bảng trên. -
Từ câu 21 đến câu 25 thí sinh điền đáp án vào các ô tương ứng ở bảng trên.
Phần I: Trắc nghiệm A,B,C hay D 1 Câu 1: Tính 3  e x I .dx  . 0 3 e 1 1 A. 3 I  e 1 .
B. I  e 1. C. . D. 3 I  e  . 3 2
Câu 2: Họ nguyên hàm của hàm số f x  2x  sin 2x là 1 1 A. 2
x  2cos 2x C . B. 2
x  cos 2x C . C. 2
x  cos 2x C . D. 2
x  2 cos 2x C . 2 2
Câu 3: Cho hàm số f x có đạo hàm liên tục trên đoạn 1;  3 thỏa mãn f  
1  2 và f 3  9 . Tính 3 I f   xdx. 1 A. I  11. B. I  7 . C. I  2 . D. I  18 .
Câu 4: Cho hai hàm số f x và g x liên tục trên K , a, b K . Khẳng định nào sau đây là khẳng định sai? b b b b b A. kf
 xdx k f  xdx . B. f
 xgxdx f
 xd .x g  xdx . a a a a a b b b b b b C. f
 x gxdx f
 xdx g
 xdx. D. f
 x gxdx f
 xdx g  xdx . a a a a a a e ln x
Câu 5: Cho tích phân I  dx
. Nếu đặt t  ln x thì x 1 1 t 1 1 e A. I  dtB. 2
I t dt
C. I t dt
D. I t dt  et 0 0 0 1
Câu 6: Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y x , trục hoành Ox , các đường thẳng x  1, x  2 là 8 7 A. S  . B. S  . C. S  8 . D. S  7 . 3 3
Câu 7: Cho hàm số f x  cos x . Mệnh đề nào sau đây đúng A. f
 xdx  sin xC . B. f
 xdx  cosxC . C. f
 xdx  cosxC . D. f
 xdx  sin xC.
Câu 8: Cho hàm y f x liên tục và không âm trên  ;
a b . Tính thể tích khối tròn xoay được tạo thành khi quay
hình phẳng H  được giới hạn bởi các đường y f x , trục Ox và hai đường thẳng x a , x b , a b xung
quanh trục Ox . b b b b A. 2
f xdx  . B. 2 2 f  xdx . C. 2  f  xdx . D. f  xdx . a a a a
Câu 9: Cho I   2 x  
12xdx . Bằng cách đặt 2
t x 1, khẳng định nào sau đây đúng 1
A. I  2 tdtB. I tdt
C. I  t    1 dt
D. I tdt  2
Câu 10: Cho hàm số f x liên tục trên  ;
a b . Hãy chọn mệnh đề sai dưới đây: b a A. f
 xdx f  xdx. a b b c b B. f
 xdx f
 xdx f
 xdx với c ;ab. a a c b C. d k x k
b a, k    . a b a D. f
 xdx   f  xdx. a b π u x
Câu 11: Tính tích phân I x cos xdx  bằng cách đặt 
. Mệnh đề nào dưới đây đúng? dv  cos d x x 0 π π A. π
I x sin x  sin d x x π
I x sin x  sin d x x 0  . B. 0  . 0 0 π π C. π
I x sin x  cos xdx π
I x cos x  sin xdx 0  . D. 0  . 0 0 5 2
Câu 12: Giả sử hàm số y f x liên tục trên  và f
 xdx a, a . Tích phân I f 2x    1 dx có giá 3 1 trị là 1 1
A. I a 1 .
B. I  2a 1 .
C. I  2a .
D. I a . 2 2
Câu 13: Goi H  là hình phẳng giới hạn bởi đồ thị hàm số x
y e , trục Ox và hai đường thẳng x  0, x  1. Thể
tích của khối tròn xoay tạo thành khi quay H  xung quanh trụcOx là   A.  2e  1 . B.   2 e   1 . C.  2e  1. D.   2 e   1 . 2 2
Câu 14: Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y f x , trục Ox và các đường
thẳng x a, x b a b. b b b b A.
f xdx  . B. f  xdx. C. 2
f xdx  .
D. f xdx  . a a a a
Câu 15: Kết quả của x
I xe dx  là 2 x 2 x A. x x
I e xe C . B. x x
I xe e C . C. x I e C . D. x x I
e e C . 2 2
Câu 16: Một xe mô tô đang chạy với vận tốc 20 m/s thì người lái xe nhìn thấy một chướng ngại vật nên đạp phanh.
Từ thời điểm đó, mô tô chuyển động chậm dần với vận tốc vt  20  5t , trong đó t là thời gian (được tính bằng
giây ) kể từ lúc đạp phanh. Quãng đường mà mô tô đi được từ khi người lái xe đạp phanh cho đến lúc mô tô dừng lại là A. 40 m B. 80 m C. 60 m D. 20 m e ln x 3
Câu 17: Biết I
dx a ln  ,
b a,b Q
. Mệnh đề nào sau đây đúng? x ln x  2 2 1    
A. a b  1.
B. 2a b  1 .
C. a  2b  0 . D. 2 2 a b  4 .
Câu 18: Gọi F x là một nguyên hàm của hàm số   e x f x x  
. Tính F x biết F 0 1. A.    1e x F x x     2. B.    1e x F x x      2 . C.    1e x F x x     1. D.    1e x F x x    1.
Câu 19: Biết F x là một nguyên hàm của f x 1 
và F 0  2 thì F   1 bằng. x 1 A. ln 2 . B. 3 . C. 4 . D. 2  ln 2 . 2 1 a Câu 20: Giả sử d  ln  a x
với a , b* và tối giản. Tính 2 2
M a b . 2x 1 b b 1 A. M  28 . B. M  34 . C. M  14 . D. M  8 .
Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 21: Tính diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số 2
y  2x và y  5x  2 .
Câu 22: Biết F x là một nguyên hàm của hàm f x  x ln  x  
1 và F 0  0, F 2  a ln b với a,b   .
Tính P a  . b 1
Câu 23: Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 
1 và thỏa mãn f 0  6, 2x  2. f xdx  6 . 0 1 Tích phân
f xdx  . 0
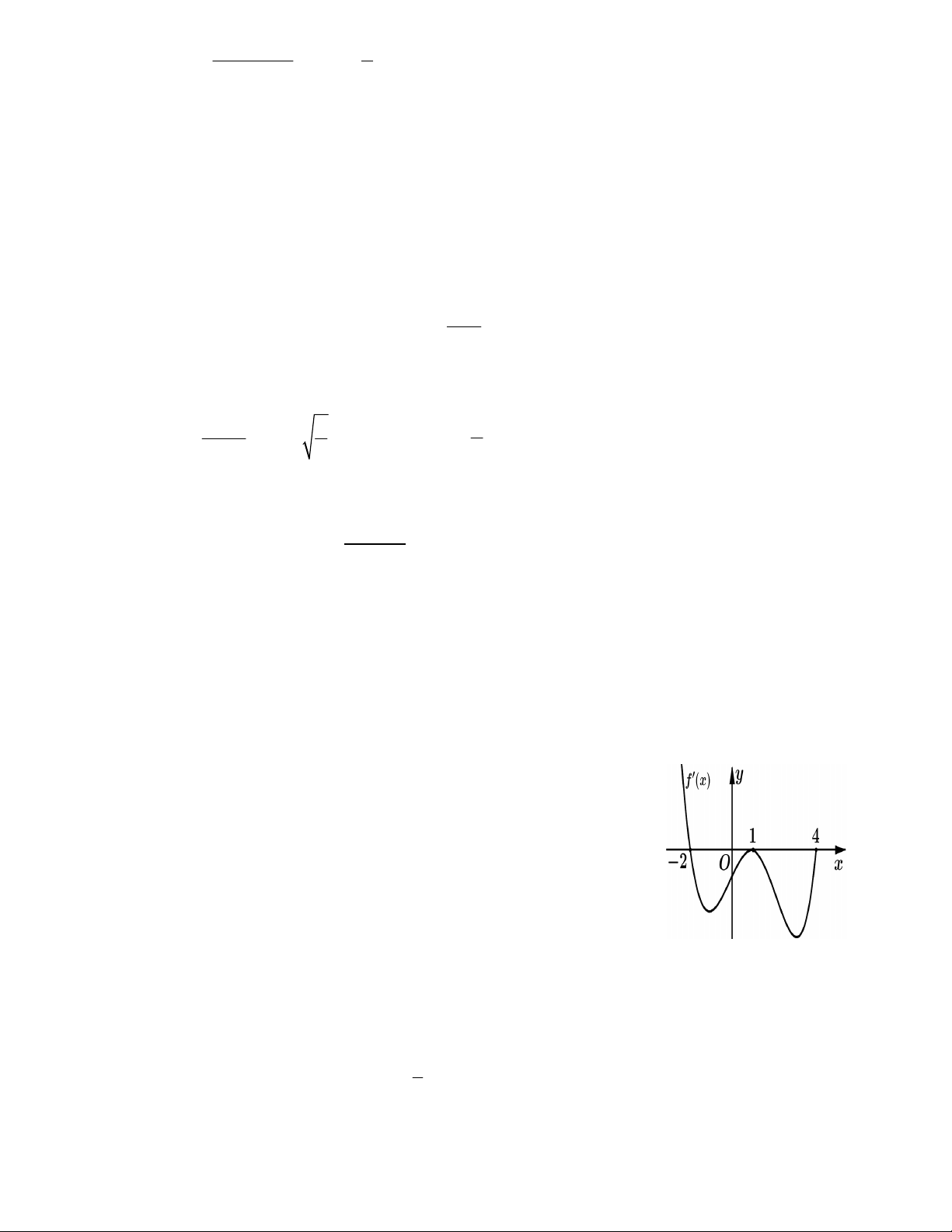
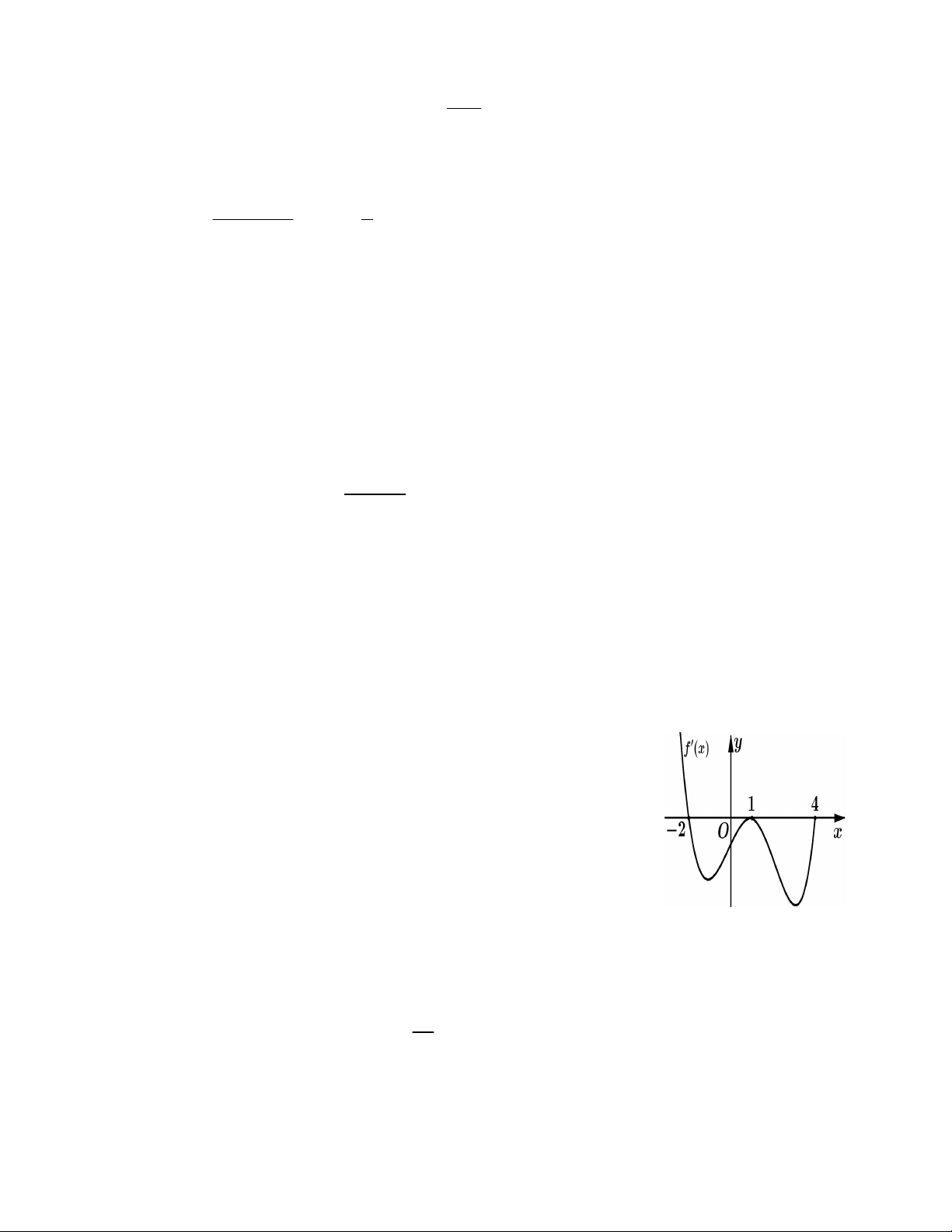
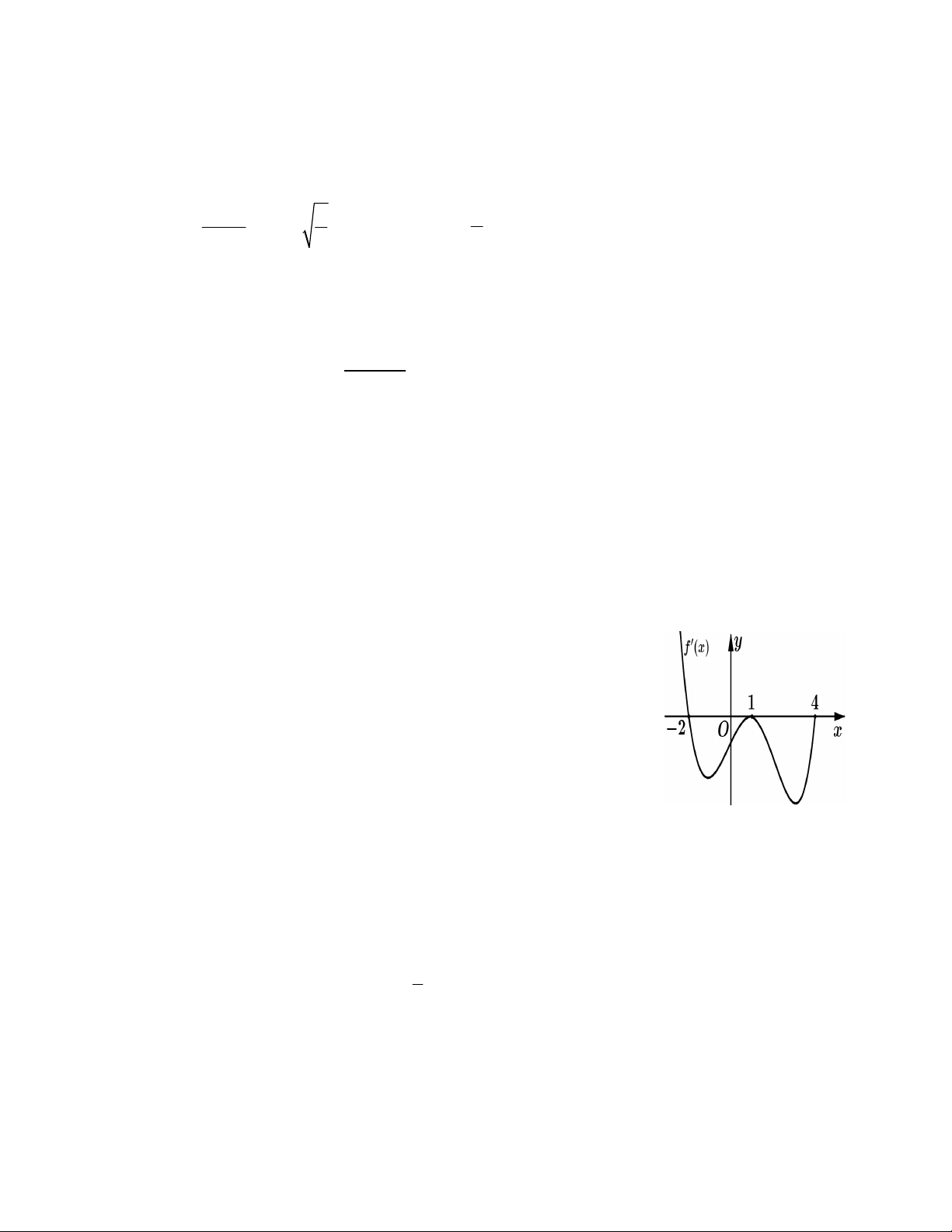
Câu 24: Cho hàm số y = f (x) có đạo hàm liên tục trên [-2;4]. Đồ thị của
hàm số y = f ¢(x) được cho như hình bên. Diện tích hình phẳng giới hạn
bởi trục Ox và đồ thị hàm số y = f ¢(x) trên đoạn [ ] 2;1 - và [1;4] lần lượt
bằng 9 và 12. Cho f ( )
1 = 3. Tính tổng f ( 2 - )+ f (4).
Câu 25: Cho hàm số f x thỏa mãn f   1
2   ,       2 3 f x x f x
f x  với mọi x   . Tính giá trị 5  và   0 của f   1 . ----------- HẾT ----------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
--------------------------------------------------------- Mã đề 209
Họ và tên học sinh: …………………..……………………………………..Lớp: ………….. PHẦN ĐÁP ÁN 1 A B C D 6 11 16 A B C D A B C D A B C D 2 A B C D 7 12 17 A B C D A B C D A B C D 3 A B C D 8 13 18 A B C D A B C D A B C D 4 A B C D 9 14 19 A B C D A B C D A B C D 5 A B C D 10 15 20 A B C D A B C D A B C D 21 22 23 24 25
Chú ý: - Từ câu 1 đến câu 20 thí sinh tô đậm đáp án A, B, C hay D vào các ô tương ứng ở bảng trên. -
Từcâu 21 đến câu 25 thí sinh điền đáp án vào các ô tương ứng ở bảng trên.
Phần I: Trắc nghiệm A,B,C hay D
Câu 1: Cho hàm số f x có đạo hàm liên tục trên đoạn 1;  3 thỏa mãn f  
1  2 và f 3  9 . Tính 3 I f   xdx. 1 A. I  2 . B. I  18 . C. I  7 . D. I  11.
Câu 2: Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y f x , trục Ox và các đường
thẳng x a, x b a b. b b b b A. f  xdx. B. 2
f xdx  .
C. f xdx  . D.
f xdx  . a a a a
Câu 3: Goi H  là hình phẳng giới hạn bởi đồ thị hàm số x
y e , trục Ox và hai đường thẳng x  0, x  1. Thể tích
của khối tròn xoay tạo thành khi quay H  xung quanh trục Ox là   A.  2e  1 . B.   2 e   1 . C.  2e  1. D.   2 e   1 . 2 2
Câu 4: Họ nguyên hàm của hàm số f x  2x  sin 2x là 1 1 A. 2
x  cos 2x C . B. 2
x  2 cos 2x C . C. 2
x  cos 2x C . D. 2
x  2cos 2x C . 2 2 1 Câu 5: Tính 3  e x I .dx  . 0 3 e 1 1 A. 3 I  e 1 . B. .
C. I  e 1. D. 3 I  e  . 3 2
Câu 6: Cho I   2 x  
12xdx . Bằng cách đặt 2
t x 1, khẳng định nào sau đây đúng 1
A. I  2 tdtB. I tdt
C. I  t    1 dt
D. I tdt  2
Câu 7: Cho hàm số f x  cos x . Mệnh đề nào sau đây đúng A. f
 xdx  cosxC . B. f
 xdx  sin xC. C. f
 xdx  sin xC . D. f
 xdx  cosxC .
Câu 8: Cho hai hàm số f x và g x liên tục trên K , a, b K . Khẳng định nào sau đây là khẳng định sai? b b b b b A. f
 xgxdx f
 xd .x g  xdx . B. kf
 xdx k f  xdx . a a a a a b b b b b b C. f
 x gxdx f
 xdx g
 xdx . D. f
 x gxdx f
 xdx g  xdx. a a a a a a e ln x
Câu 9: Cho tích phân I  dx
. Nếu đặt t  ln x thì x 1 e 1 t 1 1
A. I t dtB. I  dt
C. I t dtD. 2
I t dt  et 1 0 0 0
Câu 10: Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y x , trục hoành Ox , các đường thẳng x  1, x  2 là 7 8 A. S  7 . B. S  8 . C. S  . D. S  . 3 3 5 2
Câu 11: Giả sử hàm số y f x liên tục trên  và f
 xdx a, a . Tích phân I f 2x    1 dx có giá 3 1 trị là 1 1
A. I a 1 .
B. I  2a 1 .
C. I  2a .
D. I a . 2 2
Câu 12: Cho hàm y f x liên tục và không âm trên  ;
a b . Tính thể tích khối tròn xoay được tạo thành khi quay
hình phẳng H  được giới hạn bởi các đường y f x , trục Ox và hai đường thẳng x a , x b , a b xung
quanh trục Ox . b b b b A. 2  f  xdx . B. f  xdx . C. 2 2 f  xdx . D. 2
f xdx  . a a a a
Câu 13: Kết quả của x
I xe dx  là 2 x 2 x A. x x
I e xe C . B. x x
I xe e C . C. x I e C . D. x x I
e e C . 2 2
Câu 14: Cho hàm số f x liên tục trên  ;
a b . Hãy chọn mệnh đề sai dưới đây: b a A. f
 xdx f  xdx. a b b B. d k x k
b a, k    . a b c b C. f
 xdx f
 xdx f
 xdx với c ;ab. a a c b a D. f
 xdx   f  xdx. a b π u x
Câu 15: Tính tích phân I x cos d x x  bằng cách đặt 
. Mệnh đề nào dưới đây đúng? dv  cos d x x 0 π π A. π
I x sin x  sin d x x π
I x sin x  sin d x x 0  . B. 0  . 0 0 π π C. π
I x sin x  cos d x x π
I x cos x  sin d x x 0  . D. 0  . 0 0 2 1 a Câu 16: Giả sử d  ln  a x
với a , b* và tối giản. Tính 2 2
M a b . 2x 1 b b 1 A. M  28 . B. M  34 . C. M  14 . D. M  8 .
Câu 17: Gọi F x là một nguyên hàm của hàm số   e x f x x  
. Tính F x biết F 0 1. A.    1e x F x x    1. B.    1e x F x x     2. C.    1e x F x x     1. D.    1e x F x x      2 .
Câu 18: Biết F x là một nguyên hàm của f x 1 
và F 0  2 thì F   1 bằng. x 1 A. 3 . B. ln 2 . C. 2  ln 2 . D. 4 . e ln x 3
Câu 19: Biết I
dx a ln  ,
b a,b Q
. Mệnh đề nào sau đây đúng? x ln x  2 2 1     A. 2 2 a b  4 .
B. a b  1.
C. 2a b  1 .
D. a  2b  0 .
Câu 20: Một xe mô tô đang chạy với vận tốc 20 m/s thì người lái xe nhìn thấy một chướng ngại vật nên đạp phanh.
Từ thời điểm đó, mô tô chuyển động chậm dần với vận tốc vt  20  5t , trong đó t là thời gian (được tính bằng
giây ) kể từ lúc đạp phanh. Quãng đường mà mô tô đi được từ khi người lái xe đạp phanh cho đến lúc mô tô dừng lại là A. 40 m B. 60 m C. 20 m D. 80 m
Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 21: Tính diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số 2
y x và y  5x  6 .
Câu 22: Biết F x là một nguyên hàm của hàm f x  x ln  x  
1 và F 2  2, F 3  a ln b c với
a,b, c   . Tính P a b  . c 1
Câu 23: Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 
1 và thỏa mãn f 0  8 , x  
1 . f  xdx  6 . Tích 0 1 phân
f xdx  . 0
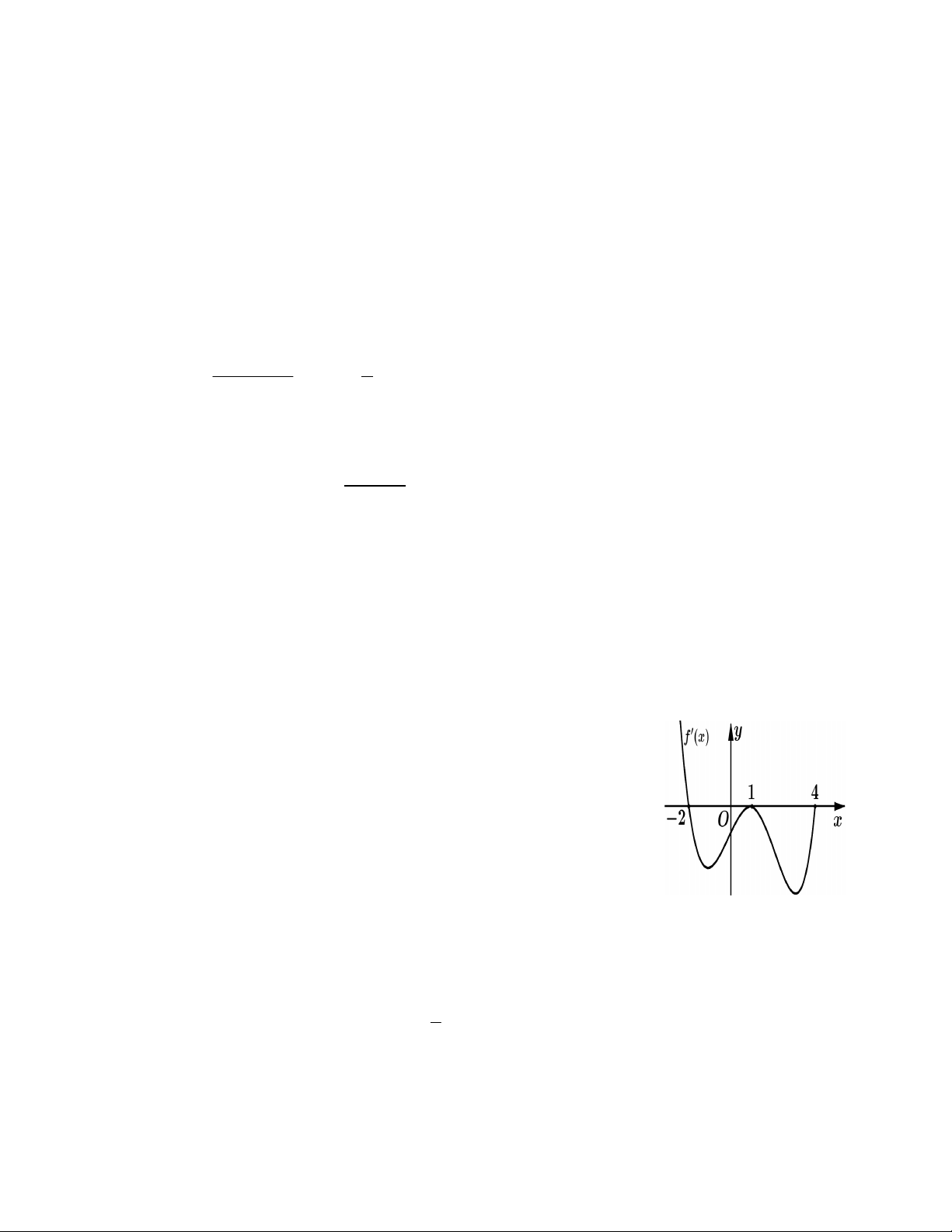
Câu 24: Cho hàm số y = f (x) có đạo hàm liên tục trên [-2;4]. Đồ thị của
hàm số y = f ¢(x) được cho như hình bên. Diện tích hình phẳng giới hạn
bởi trục Ox và đồ thị hàm số y = f ¢(x) trên đoạn [ ] 2;1 - và [1;4] lần lượt
bằng 8 và 11. Cho f ( )
1 = 4. Tính tổng f ( 2 - )+ f (4).
Câu 25: Cho hàm số f x thỏa mãn f   1 2  
, f  x  x  f x 2 3 4
 và f x  0 với mọi x. Tính giá 25  trị của f   1 . ----------- HẾT ----------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
--------------------------------------------------------- Mã đề 357
Họ và tên học sinh: …………………..……………………………………..Lớp: ………….. PHẦN ĐÁP ÁN 1 A B C D 6 11 16 A B C D A B C D A B C D 2 A B C D 7 12 17 A B C D A B C D A B C D 3 A B C D 8 13 18 A B C D A B C D A B C D 4 A B C D 9 14 19 A B C D A B C D A B C D 5 A B C D 10 15 20 A B C D A B C D A B C D 21 22 23 24 25
Chú ý: - Từ câu 1 đến câu 20 thí sinh tô đậm đáp án A, B, C hay D vào các ô tương ứng ở bảng trên. -
Từcâu 21 đến câu 25 thí sinh điền đáp án vào các ô tương ứng ở bảng trên.
Phần I: Trắc nghiệm A,B,C hay D
Câu 1: Goi H  là hình phẳng giới hạn bởi đồ thị hàm số x
y e , trục Ox và hai đường thẳng x  0, x  1. Thể tích
của khối tròn xoay tạo thành khi quay H  xung quanh trụcOx là   A.  2e  1 . B.   2 e   1 . C.  2e  1. D.   2 e   1 . 2 2
Câu 2: Cho hàm số f x liên tục trên  ;
a b . Hãy chọn mệnh đề sai dưới đây: b a A. f
 xdx f  xdx. a b b c b B. f
 xdx f
 xdx f
 xdx với c ;ab. a a c b C. d k x k
b a, k    . a b a D. f
 xdx   f  xdx. a b
Câu 3: Cho hai hàm số f x và g x liên tục trên K , a, b K . Khẳng định nào sau đây là khẳng định sai? b b b b b b A. f
 x gxdx f
 xdx g
 xdx. B. f
 xgxdx f
 xd .x g  xdx . a a a a a a b b b b b C. kf
 xdx k f  xdx . D. f
 x gxdx f
 xdx g  xdx . a a a a a
Câu 4: Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y x , trục hoành Ox , các đường thẳng x  1, x  2 là 7 8 A. S  8. B. S  7 . C. S  . D. S  . 3 3
Câu 5: Cho hàm số f x có đạo hàm liên tục trên đoạn 1;  3 thỏa mãn f  
1  2 và f 3  9 . Tính 3 I f   xdx. 1 A. I  11. B. I  7 . C. I  2 . D. I  18 . 1 Câu 6: Tính 3  e x I .dx  . 0 1 3 e 1 A. 3 I  e 1 . B. 3 I  e  . C. .
D. I  e 1. 2 3
Câu 7: Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y f x , trục Ox và các đường
thẳng x a, x b a b. b b b b A. f  xdx.
B. f xdx  . C.
f xdx  . D. 2
f xdx  . a a a a
Câu 8: Họ nguyên hàm của hàm số f x  2x  sin 2x là 1 1 A. 2
x  2 cos 2x C . B. 2
x  2cos 2x C . C. 2
x  cos 2x C . D. 2
x  cos 2x C . 2 2 π u x
Câu 9: Tính tích phân I x cos d x x  bằng cách đặt 
. Mệnh đề nào dưới đây đúng? dv  cos d x x 0 π π A. π
I x sin x  sin d x x π
I x sin x  sin d x x 0  . B. 0  . 0 0 π π C. π
I x sin x  cos d x x π
I x cos x  sin d x x 0  . D. 0  . 0 0 5 2
Câu 10: Giả sử hàm số y f x liên tục trên  và f
 xdx a, a . Tích phân I f 2x    1 dx có giá 3 1 trị là 1 1
A. I a 1 .
B. I  2a 1.
C. I  2a .
D. I a . 2 2
Câu 11: Cho hàm y f x liên tục và không âm trên  ;
a b . Tính thể tích khối tròn xoay được tạo thành khi quay
hình phẳng H  được giới hạn bởi các đường y f x , trục Ox và hai đường thẳng x a , x b , a b xung
quanh trục Ox . b b b b A. 2  f  xdx . B. f  xdx . C. 2 2 f  xdx . D. 2
f xdx  . a a a a
Câu 12: Kết quả của x
I xe dx  là 2 x 2 x A. x x
I e xe C . B. x x
I xe e C . C. x I e C . D. x x I
e e C . 2 2
Câu 13: Cho hàm số f x  cos x . Mệnh đề nào sau đây đúng A. f
 xdx  sin xC . B. f
 xdx  cosxC . C. f
 xdx  cosxC . D. f
 xdx  sin xC.
Câu 14: Cho I   2 x  
12xdx . Bằng cách đặt 2
t x 1, khẳng định nào sau đây đúng 1
A. I  2 tdtB. I tdt
C. I  t    1 dt
D. I tdt  2 e ln x
Câu 15: Cho tích phân I  dx
. Nếu đặt t  ln x thì x 1 1 1 t e 1
A. I t dtB. I  dt
C. I t dtD. 2
I t dt  et 0 0 1 0 2 1 a Câu 16: Giả sử d  ln  a x
với a , b* và tối giản. Tính 2 2
M a b . 2x 1 b b 1 A. M  28 . B. M  34 . C. M  14 . D. M  8 .
Câu 17: Biết F x là một nguyên hàm của f x 1 
và F 0  2 thì F   1 bằng. x 1 A. 2  ln 2 . B. ln 2 . C. 3 . D. 4 .
Câu 18: Một xe mô tô đang chạy với vận tốc 20 m/s thì người lái xe nhìn thấy một chướng ngại vật nên đạp phanh.
Từ thời điểm đó, mô tô chuyển động chậm dần với vận tốc vt  20  5t , trong đó t là thời gian (được tính bằng
giây ) kể từ lúc đạp phanh. Quãng đường mà mô tô đi được từ khi người lái xe đạp phanh cho đến lúc mô tô dừng lại là A. 60 m B. 80 m C. 40 m D. 20 m
Câu 19: Gọi F x là một nguyên hàm của hàm số   e x f x x  
. Tính F x biết F 0 1. A.    1e x F x x    1. B.    1e x F x x     2. C.    1e x F x x     1. D.    1e x F x x      2 . e ln x 3
Câu 20: Biết I
dx a ln  ,
b a,b Q
. Mệnh đề nào sau đây đúng? x ln x  2 2 1     A. 2 2 a b  4 .
B. a b  1.
C. 2a b  1 .
D. a  2b  0 .
Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 21: Tính diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số 2
y x và y  8x 15 .
Câu 22: Biết F x là một nguyên hàm của hàm       1 x f x x
e và F 0 1, 3 b F
ae c với a,b,c  .
Tính P a b  . c 1
Câu 23: Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 
1 và thỏa mãn f 0 14, x  
1 . f  xdx  10 . 0 1 Tích phân
f xdx  . 0
Câu 24: Cho hàm số y = f (x) có đạo hàm liên tục trên [-2;4]. Đồ thị của
hàm số y = f ¢(x) được cho như hình bên. Diện tích hình phẳng giới hạn
bởi trục Ox và đồ thị hàm số y = f ¢(x) trên đoạn [ ] 2;1 - và [1;4] lần lượt
bằng 5 và 7. Cho f ( )
1 = 4. Tính tổng f ( 2 - )+ f (4). 1
Câu 25: Cho hàm số f (x) thỏa mãn f (2)   , f x xf x 2 ( )
( ) và f x  0 với mọi x  . Tính giá trị 3 của f (1). ----------- HẾT ----------
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3
TỔ TOÁN Môn : Giải tích 12 NC . Thời gian làm bài : 45 phút
--------------------------------------------------------- Mã đề 485
Họ và tên học sinh: …………………..……………………………………..Lớp: ………….. PHẦN ĐÁP ÁN 1 A B C D 6 11 16 A B C D A B C D A B C D 2 A B C D 7 12 17 A B C D A B C D A B C D 3 A B C D 8 13 18 A B C D A B C D A B C D 4 A B C D 9 14 19 A B C D A B C D A B C D 5 A B C D 10 15 20 A B C D A B C D A B C D 21 22 23 24 25
Chú ý: - Từ câu 1 đến câu 20 thí sinh tô đậm đáp án A, B, C hay D vào các ô tương ứng ở bảng trên. -
Từcâu 21 đến câu 25 thí sinh điền đáp án vào các ô tương ứng ở bảng trên.
Phần I: Trắc nghiệm A,B,C hay D e ln x
Câu 1: Cho tích phân I  dx
. Nếu đặt t  ln x thì x 1 1 1 1 t e
A. I t dtB. 2
I t dtC. I  dt
D. I t dt  et 0 0 0 1 1 Câu 2: Tính 3  e x I .dx  . 0 3 e 1 1 A. 3 I  e 1 .
B. I  e 1. C. . D. 3 I  e  . 3 2
Câu 3: Cho hai hàm số f x và g x liên tục trên K , a, b K . Khẳng định nào sau đây là khẳng định sai? b b b b b b A. f
  x gxdx f
 xdx g
 xdx. B. f
  x gxdx f
 xdx g  xdx . a a a a a a b b b b b C. f
 xgxdx f
 xd .x g  xdx . D. kf
 xdx k f  xdx . a a a a a
Câu 4: Cho hàm số f x liên tục trên  ;
a b . Hãy chọn mệnh đề sai dưới đây: b c b b a A. f
 xdx f
 xdx f
 xdx với c ;ab. B. f
 xdx   f  xdx. a a c a b b b a C. d k x k
b a, k
   . D. f
 xdx f  xdx. a a b π u x
Câu 5: Tính tích phân I x cos d x x  bằng cách đặt 
. Mệnh đề nào dưới đây đúng? dv  cos d x x 0 π π A. π
I x sin x  sin d x x π
I x sin x  sin d x x 0  . B. 0  . 0 0 π π C. π
I x sin x  cos d x x π
I x cos x  sin d x x 0  . D. 0  . 0 0
Câu 6: Kết quả của x
I xe dx  là 2 x 2 x A. x x
I e xe C . B. x x
I xe e C . C. x I e C . D. x x I
e e C . 2 2
Câu 7: Họ nguyên hàm của hàm số f x  2x  sin 2x là 1 1 A. 2
x  2 cos 2x C . B. 2
x  2cos 2x C . C. 2
x  cos 2x C . D. 2
x  cos 2x C . 2 2
Câu 8: Cho hàm số f x có đạo hàm liên tục trên đoạn 1;  3 thỏa mãn f  
1  2 và f 3  9 . Tính 3 I f   xdx. 1 A. I  18 . B. I  2 . C. I  11. D. I  7 .
Câu 9: Goi H  là hình phẳng giới hạn bởi đồ thị hàm số x
y e , trục Ox và hai đường thẳng x  0, x  1. Thể tích
của khối tròn xoay tạo thành khi quay H  xung quanh trụcOx là   A.   2 e   1 . B.   2 e   1 . C.  2e  1 . D.  2e  1. 2 2
Câu 10: Cho hàm y f x liên tục và không âm trên  ;
a b . Tính thể tích khối tròn xoay được tạo thành khi quay
hình phẳng H  được giới hạn bởi các đường y f x , trục Ox và hai đường thẳng x a , x b , a b xung
quanh trục Ox . b b b b A. 2  f  xdx . B. f  xdx . C. 2 2 f  xdx . D. 2
f xdx  . a a a a
Câu 11: Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y f x , trục Ox và các đường
thẳng x a, x b a b. b b b b A.
f xdx  . B. 2
f xdx  .
C. f xdx  . D. f  xdx. a a a a
Câu 12: Cho hàm số f x  cos x . Mệnh đề nào sau đây đúng A. f
 xdx  sin xC . B. f
 xdx  cosxC . C. f
 xdx  cosxC . D. f
 xdx  sin xC.
Câu 13: Cho I   2 x  
12xdx . Bằng cách đặt 2
t x 1, khẳng định nào sau đây đúng 1
A. I  2 tdtB. I tdt
C. I  t    1 dt
D. I tdt  2 5 2
Câu 14: Giả sử hàm số y f x liên tục trên  và f
 xdx a, a . Tích phân I f 2x    1 dx có giá 3 1 trị là 1 1
A. I a 1 .
B. I  2a 1 .
C. I  2a .
D. I a . 2 2
Câu 15: Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 2
y x , trục hoành Ox , các đường thẳng x  1, x  2 là 7 8 A. S  7 . B. S  . C. S  . D. S  8 . 3 3 e ln x 3
Câu 16: Biết I
dx a ln  ,
b a,b Q
. Mệnh đề nào sau đây đúng? x ln x  2 2 1    
A. a b  1. B. 2 2 a b  4 .
C. 2a b  1 .
D. a  2b  0 .
Câu 17: Biết F x là một nguyên hàm của f x 1 
và F 0  2 thì F   1 bằng. x 1 A. 3 . B. 4 . C. 2  ln 2 . D. ln 2 .
Câu 18: Gọi F x là một nguyên hàm của hàm số   e x f x x  
. Tính F x biết F 0 1. A.    1e x F x x    1. B.    1e x F x x     2. C.    1e x F x x     1. D.    1e x F x x      2 .
Câu 19: Một xe mô tô đang chạy với vận tốc 20 m/s thì người lái xe nhìn thấy một chướng ngại vật nên đạp phanh.
Từ thời điểm đó, mô tô chuyển động chậm dần với vận tốc vt  20  5t , trong đó t là thời gian (được tính bằng
giây ) kể từ lúc đạp phanh. Quãng đường mà mô tô đi được từ khi người lái xe đạp phanh cho đến lúc mô tô dừng lại là A. 40 m B. 60 m C. 20 m D. 80 m 2 1 a Câu 20: Giả sử d  ln  a x
với a , b* và tối giản. Tính 2 2
M a b . 2x 1 b b 1 A. M  8 . B. M  34 . C. M  28 . D. M  14 .
Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 21: Tính diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số 2
y x và y  9x 18 .
Câu 22: Biết F x là một nguyên hàm của hàm      2 x f x x
e và F 0  2, 2 b F
ae c với a,b,c  .
Tính P a b  . c 1
Câu 23: Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 
1 và thỏa mãn f 0 16, x  
1 . f  xdx  10 . 0 1 Tích phân
f xdx  . 0
Câu 24: Cho hàm số y = f (x) có đạo hàm liên tục trên [-2;4]. Đồ thị của
hàm số y = f ¢(x) được cho như hình bên. Diện tích hình phẳng giới hạn
bởi trục Ox và đồ thị hàm số y = f ¢(x) trên đoạn [ ] 2;1 - và [1;4] lần lượt
bằng 14 và 18. Cho f ( )
1 = 4. Tính tổng f ( 2 - )+ f (4) .
Câu 25: Cho hàm số f x thỏa mãn f   1
2   ,       2 3 f x x f x
f x  với mọi x   . Tính giá trị 5  và   0 của f   1 . ----------- HẾT ----------
ĐÁP ÁN ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3-GIẢI TÍCH 12-NH 2018-2019 MÃ ĐỀ 132: 1 C 6 B 11 B 16 A 2 C 7 D 12 D 17 C 3 B 8 C 13 A 18 B 4 B 9 D 14 A 19 D 5 C 10 A 15 B 20 B 9 9 8 2 21 22 3 3 23 24 4  5 25 MÃ ĐỀ 209: 1 C 6 D 11 D 16 B 2 D 7 B 12 A 17 D 3 A 8 A 13 B 18 C 4 A 9 C 14 A 19 D 5 B 10 C 15 B 20 A 1 25 6 4 21 22 2 5 23 24 1  10 25 MÃ ĐỀ 357: 1 A 6 C 11 A 16 B 2 A 7 C 12 B 17 A 3 B 8 C 13 D 18 C 4 C 9 B 14 D 19 D 5 B 10 D 15 A 20 D 4 7 3 21 22 4 6 23 24 2  3 25 MÃ ĐỀ 485: 1 A 6 B 11 A 16 D 2 C 7 C 12 D 17 C 3 C 8 D 13 D 18 D 4 D 9 C 14 D 19 A 5 B 10 A 15 B 20 B 9 6 2 21 22 6 4 23 24 4  5 25
ĐÁP ÁN CHI TIẾT CÁC CÂU 23-24-25 MÃ ĐỀ 132
(Các mã đề còn lại tương tự) 1 1 1 1 1
Câu 23: Ta có: 6  2x  2 f 'xdx  2x  2 f x|  2 f
 xdx  6 122 f
 xdx f
 xdx  3. 0 0 0 0 0 1 4
Câu 24: Theo giả thiết, ta có
f ¢(x)dx = -9 ò và
f ¢(x)dx = 12. - ò -2 1 1 •
f ¢(x)dx = -9  f ( )
1 - f (-2) = -9  3- f (-2) = -9 ¾¾  f (-2) = 12. ò -2 4 •
f ¢(x)dx = -12  f (4)- f ( )
1 = -12  f (4)-3 = -12 ¾¾  f (4) = -9. ò 1 Vậy f ( 2 - )+ f (4) =12 +( 9 - ) = 3. 2 f x f x 3 3   2 2
Câu 25: Ta có: f  x  x f   x   3    x
dx x dx    2 f x 2 f x 1   1 2  1  15 1 1 15 4              . f  x  f    f   f   1 4 2 1 4 5 1