Đề kiểm tra 1 tiết Giải tích 12 chương 3 trường THPT Quốc Thái – An Giang

Đề kiểm tra 1 tiết Giải tích 12 chương 3 trường THPT Quốc Thái – An Giang gồm 3 trang với 20 câu hỏi trắc nghiệm, thời gian làm bài 45 phút, nội dung kiểm tra thuộc chủ đề nguyên hàm – tích phân và ứng dụng.

14 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

3 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
TRƯỜNG THPT QUỐC THÁI
TỔ TOÁN
KIỂM TRA 1 TIẾT MÔN TOÁN KHỐI 12
NGUYÊN HÀM – TÍCH PHÂN -ỨNG DỤNG.
Câu 1. Tìm nguyên hàm của hàm số
(
)
3x
f
xe=
A.
33
1
.
3
xx
edx e C=+
ò
B.
331
1
.
31
xx
edx e C
x
+
=+
+
ò
C.
33
.
xx
edx e C=+
ò
D.
33
3.
xx
edx e C=+
ò
Câu 2. Tìm nguyên hàm của hàm số
(
)
21.fx x=-
A.
() ()
d
2
2121 .
3
f
xx x x C=- -+
ò
B.
() ()
d
1
2121 .
3
f
xx x x C=- -+
ò
C.
()
d
1
21 .
3
f
xx x C=- - +
ò
D.
()
d
1
21 .
2
f
xx x C=-+
ò
Câu 3. Cho
()Fx là một nguyên hàm của hàm số () 2
x
f
xe x=+ thỏa mãn
3
(0)
2
F =
. Tìm ()Fx .
A.
2
3
() .
2
x
Fx e x=++ B.
2
1
() 2 .
2
x
Fx e x=+-
C.
2
5
() .
2
x
Fx e x=++ D.
2
1
() .
2
x
Fx e x=++
Câu 4. Tìm nguyên hàm
()Fx của hàm số thỏa mãn
2
2
F
p
æö
÷
ç
÷
=
ç
÷
ç
÷
ç
èø
.
A.
() cos sin 3.Fx x x=-+ B. () cos sin 3.Fx x x=- + +
C.
() cos sin 1.Fx x x=- + -
D.
() cos sin 1.Fx x x=- + +
Câu 5. Biết
()Fx là một nguyên hàm của của hàm số
1
()
1
fx
x
=
-
và (2) 1F = . Tính (3).F
A.
(3) ln 2 1.F =- B. (3) ln 2 1.F =+ C.
1
(3) .
2
F =
D.
7
(3) .
4
F =
Câu 6. Cho hàm số
()
f
x thỏa mãn
() 3 2sin
f
xx
¢
=-
và (0) 7.
= Tính
.
3
f
p
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
A.
6.
3
f
p
p
æö
÷
ç
÷
=+
ç
÷
ç
÷
ç
èø
B.
3.
3
f
p
p
æö
÷
ç
÷
=+
ç
÷
ç
÷
ç
èø
C.
1.
3
f
p
p
æö
÷
ç
÷
=+
ç
÷
ç
÷
ç
èø
D.
14.
3
f
p
p
æö
÷
ç
÷
=+
ç
÷
ç
÷
ç
èø
Câu 7. Cho hàm số
()
f
x có đạo hàm trên đoạn 1; 2
éù
êú
ëû
, (1) 7
= và 2(2)
f
= . Tính
2
1
'( )Ifxdx=
ò
.
A.
5.I =
B.
5.I =-
C.
9.I =
D.
7
.
2
I =
() sin cos
f
xxx
Câu 8. Cho
2
1
() 1.fx
-
=
ò
Tính
2
1
2() .Ixfxdx
-
éù
=+
êú
ëû
ò
A.
5
.
2
I =
B.
7
.
2
I =
C.
3
.
2
I =
D.
11
.
2
I =
Câu 9. Cho
6
0
() 12fxdx=
ò
. Tính
2
0
(3 )Ifxdx=
ò
.
A.
6.I = B. 36.I = C. 2.I = D. 4.I =
Câu 10. Tích phân
2
2
1
21.,Ixxdx=-
ò
bằng cách đặt
2
1.tx=-
Mệnh đề nào dưới đây đúng?
A.
3
0
2..Itdt=
ò
B.
2
1
..Itdt=
ò
C.
3
0
..Itdt=
ò
D.
2
1
1
..
2
Itdt=
ò
Câu 11. Tính tích phân
d
1
ln .
e
Ixxx=
ò
A.
1
.
2
I =
B.
2
2
.
2
e
I
-
=
C.
2
1
.
4
e
I
+
=
D.
2
1
.
4
e
I
-
=
Câu 12. Cho tích phân
()
d
1
0
23 . .
x
Ixexaeb=+ =+
ò
với
,abÎ
. Mệnh đề nào dưới đây là đúng?
A.
2ab-=. B.
33
28ab+=. C. 3.ab = D.
21.ab+=
Câu 13. Tính diện tích
S của hình phẳng giới hạn bởi đồ thị hàm số
,yx=
trục hoành và đường thẳng
4.x =-
A.
4.S = B. 6.S = C.
15
.
2
S =
D. 8.S =
Câu 14. Tính diện tích
S của hình phẳng giới hạn bởi đồ thị hàm số
3
yx x=-
và đồ thị hàm số
2
.yxx=-
A.
37
.
12
S =
B.
9
.
4
S =
C.
81
.
12
S =
D. 13.S =
Câu 15. Cho hàm số
(
)
32
32fx x x=- + + có đồ thị ()C như hình
vẽ. Tính diện tích
S
của hình phẳng (phần gạch sọc).
A. 10.S = B.
39
.
4
S =
C.
41
.
4
S =
D. 13.S =
Câu 16. Cho hình phẳng D giới hạn bởi đường cong
2
1yx
, trục hoành và các đường thẳng
0, 1.xx
Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ?
A.
4
.
3
V
p
=
B.
2.V p= C.
7
.
3
V
p
=
D.
2
.
3
V
p
=
Câu 17. Cho hình phẳng D giới hạn bởi đường cong
2
yx=
và đường thẳng
2.yx=
Khối tròn xoay tạo
thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ?
A.
51
.
7
V
p
=
B.
41
.
7
V
p
=
C.
64
.
15
V
p
=
D.
74
.
15
V
p
=
Câu 18. Cho đồ thị hàm số
()
yfx= như hình vẽ. Tìm diện tích S của
hình phẳng được giới hạn bởi đồ thị và trục
.Ox (Phần gạch sọc).
A.
()
d
3
2
Sfxx
-
=
ò
. B.
() ()
dd
13
21
.Sfxxfxx
-
=+
òò
C.
()
d
3
2
.Sfxx
-
=
ò
D.
() ()
dd
13
21
Sfxxfxx
-
=-
òò
Câu 19. Cho hàm số
()
yfx= liên tục trên và
,, .abcÎ
Mệnh đề
nào dưới đây sai?
A.
() () ()
.
bcb
aac
f
xdx f xdx f xdx=+
òòò
B.
() ()
.
bb
aa
f
xdx fxdx=
òò
C.
()
0
a
a
fxdx=
ò
D.
() ()
...
bb
aa
cf x dx c f x dx=
òò
Câu 20. Tìm thể tích
V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm
số
()
,yfx= trục Ox và hai đường thẳng
()
,,xaxbab==< xung quanh trục .Ox
A.
()
d
2
.
b
a
Vfxxp=
ò
B.
()
d
2
.
b
a
Vfxx=
ò
C.
()
d .
b
a
Vfxxp=
ò
D.
()
d .
b
a
Vfxx=
ò
| 1/3
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TRƯỜNG THPT QUỐC THÁI
KIỂM TRA 1 TIẾT MÔN TOÁN KHỐI 12 TỔ TOÁN
NGUYÊN HÀM – TÍCH PHÂN -ỨNG DỤNG.
Câu 1. Tìm nguyên hàm của hàm số ( ) 3x f x = e x 1 x 1 A. 3 3x
e dx = e +C. ò B. 3 3x 1 e dx e + = +C. ò 3 3x + 1 C. 3x 3x
e dx = e +C. ò D. 3x 3 = 3 x e dx e +C. ò
Câu 2. Tìm nguyên hàm của hàm số f (x) = 2x -1. 2 1 A. f
ò (x)dx = (2x - )1 2x -1 +C. B. f
ò (x)dx = (2x - )1 2x -1 +C. 3 3 1 1 C. f
ò (x)dx = - 2x -1 +C. D. f
ò (x)dx = 2x -1 +C. 3 2 3
Câu 3. Cho F(x) là một nguyên hàm của hàm số ( ) x
f x = e + 2x thỏa mãn F(0) = . Tìm F(x). 2 x 1 x 3 A. 2
F(x) = e + x + . B. 2
F(x) = 2e + x - . 2 2 x 1 x 5 C. 2
F(x) = e + x + . D. 2
F(x) = e + x + . 2 2 æpö
Câu 4. Tìm nguyên hàm F(x) của hàm số f (x)  sin x  cos x thỏa mãn F ç ÷ ç ÷ = 2 ç . çè2 ÷÷ø
A. F(x) = cos x - sin x + 3.
B. F(x) = - cos x + sin x + 3.
C. F(x) = -cos x + sin x -1.
D. F(x) = -cos x + sin x + 1. 1
Câu 5. Biết F(x) là một nguyên hàm của của hàm số f (x) =
và F(2) =1. Tính F(3). x -1 1 7
A. F(3) = ln 2 -1. B. F(3) = ln 2 + 1. C. F(3) = . D. F(3) = . 2 4 æpö
Câu 6. Cho hàm số f (x) thỏa mãn f (
¢ x) = 3 - 2 sin x và f (0) = 7. Tính f ç ÷ ç ÷. ç çè 3÷÷ø æpö æpö æpö æpö A. f ç ÷ ç ÷ = p + 6. ç ÷ ç ÷ ç ÷ ç
B. f ç ÷ = p + 3. C. f ç ÷ = p + 1.
D. f ç ÷ = p + 14. çè 3÷÷ø çè3÷÷ø çè3÷÷ø çè3÷÷ø 2
Câu 7. Cho hàm số f (x) có đạo hàm trên đoạn 1 é ;2ù ê = = = ë
úû , f(1) 7 và f(2) 2 . Tính I f '(x)dx ò . 1 7 A. I = 5. B. I =- 5. C. I = 9. D. I = . 2 2 2 Câu 8. Cho f (x) = 1. ò Tính I x é 2f (x)ù = + dx. ò êë úû -1 -1 5 7 3 11 A. I = . B. I = . C. I = . D. I = . 2 2 2 2 6 2 Câu 9. Cho
f (x)dx = 12 ò . Tính I = f (3x)dx ò . 0 0
A. I = 6.
B. I = 36.
C. I = 2. D. I = 4. 2 Câu 10. Tích phân 2 I = 2x x -1.dx, ò bằng cách đặt 2
t = x -1. Mệnh đề nào dưới đây đúng? 1 3 2 3 2 1 A. I = 2 t.dt. ò B. I = t .dt. ò C. I = t .dt. ò D. I = t.dt. ò 2 0 1 0 1 e
Câu 11. Tính tích phân I = x ln xdx. ò 1 1 2 e - 2 2 e + 1 2 e -1 A. I = . B. I = . C. I = . D. I = . 2 2 4 4 1
Câu 12. Cho tích phân = ò (2 + 3) x I x
e dx = a.e + .
b với a, b Î  . Mệnh đề nào dưới đây là đúng? 0
A. a -b = 2 . B. 3 3 a +b = 28 . C. ab = 3.
D.a + 2b = 1.
Câu 13. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = x, trục hoành và đường thẳng x = -4. 15 A. S = 4.
B. S = 6. C. S = . D. S = 8. 2
Câu 14. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 3
y = x - x và đồ thị hàm số 2
y = x - x . 37 9 A. S = . B. S = . 12 4 81 C. S = . D. S = 13. 12
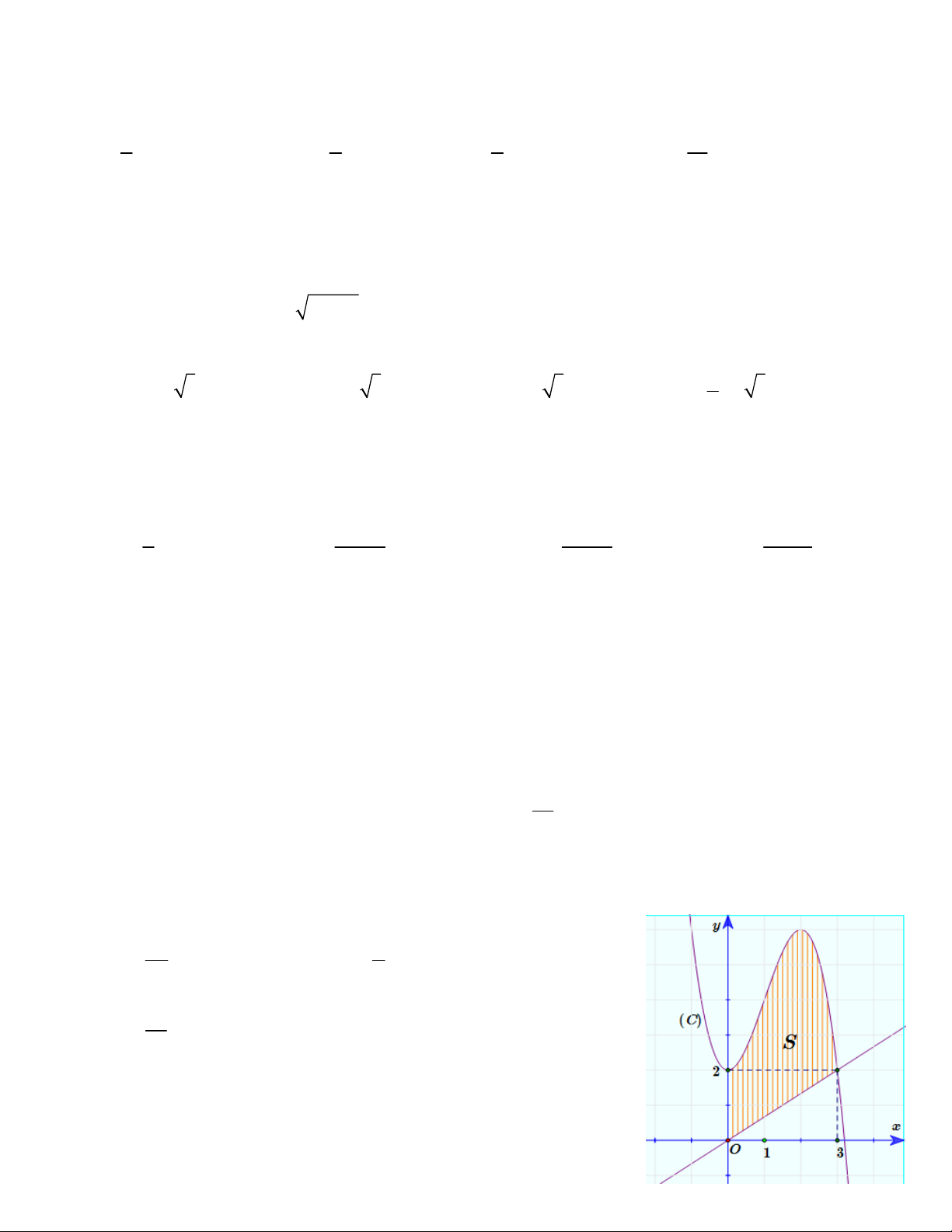
Câu 15. Cho hàm số f (x) 3 2 = x
- + 3x + 2 có đồ thị (C ) như hình
vẽ. Tính diện tích S của hình phẳng (phần gạch sọc). 39 41 A. S = 10. B. S = . C. S = . D. S = 13. 4 4
Câu 16. Cho hình phẳng D giới hạn bởi đường cong 2 y
x  1 , trục hoành và các đường thẳng
x  0, x  1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ? 4p 7p 2p A. V = .
B. V = p C. V = . V = . 3 2 . 3 D. 3
Câu 17. Cho hình phẳng D giới hạn bởi đường cong 2
y = x và đường thẳng y = 2x. Khối tròn xoay tạo
thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ? 51p 41p 64p 74p A. V = . B. V = . C. V = . V = . 7 7 15 D. 15
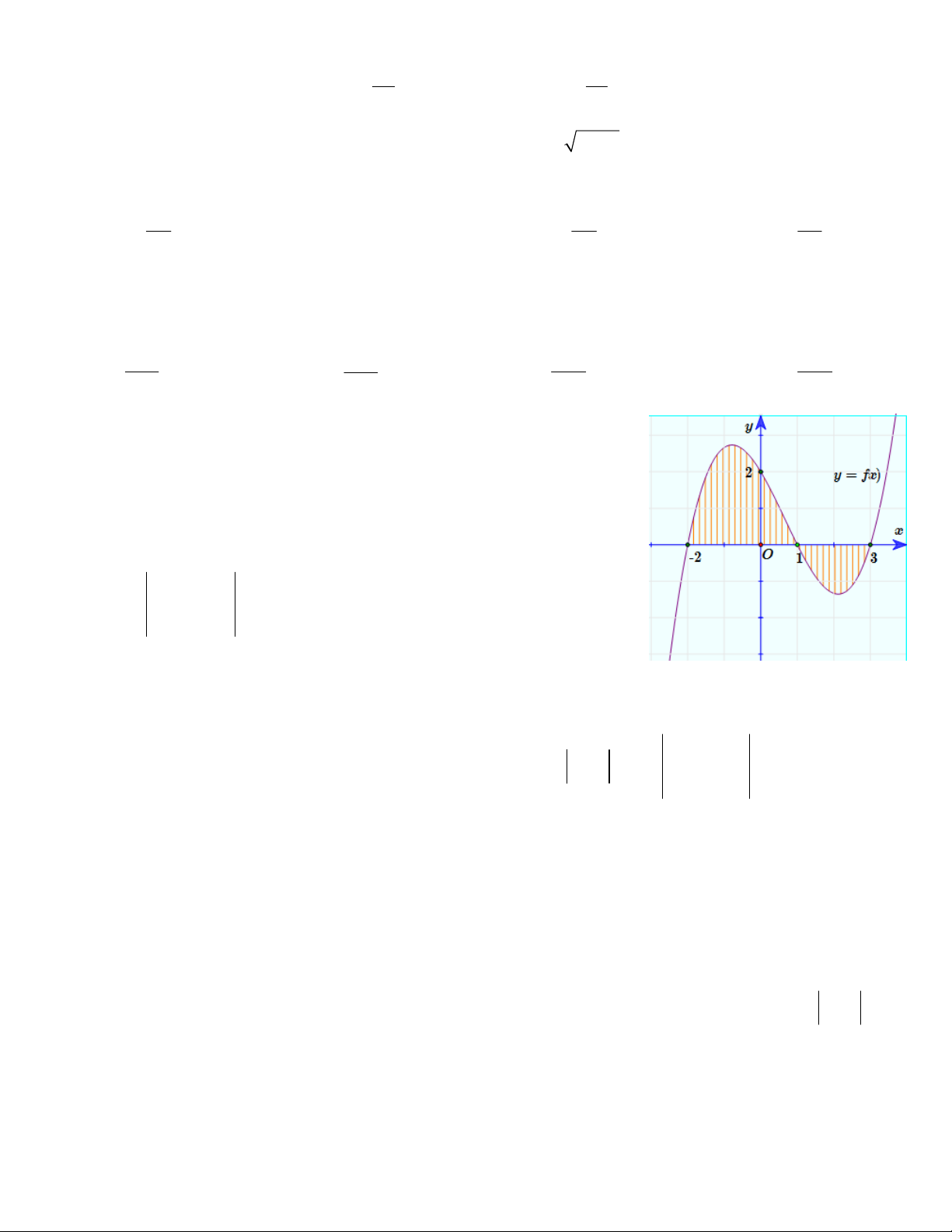
Câu 18. Cho đồ thị hàm số y = f (x) như hình vẽ. Tìm diện tích S của
hình phẳng được giới hạn bởi đồ thị và trục Ox. (Phần gạch sọc). 3 1 3 A. S = f
ò (x)dx . B. S = f
ò (x)dx + f ò (x)dx. -2 -2 1 3 1 3 C. S = f
ò (x)dx . D. S = f
ò (x)dx - f ò (x)dx -2 -2 1
Câu 19. Cho hàm số y = f (x) liên tục trên  và a, , b c Î .  Mệnh đề
nào dưới đây sai? b c b b b A. f
ò (x)dx = f
ò (x)dx + f ò (x)dx. B. f
ò (x) dx = f ò (x)dx . a a c a a a b b C. f ò (x)dx = 0 D. . c f
ò (x)dx = .c f ò (x)dx. a a a
Câu 20. Tìm thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm
số y = f (x), trục Ox và hai đường thẳng x = a, x = b (a < b), xung quanh trục Ox. b b b b A. 2 V = p f
ò (x)dx. B. 2 V = f
ò (x)dx. C. V = p f
ò (x)dx. D. V = f ò (x) dx. a a a a