Đề kiểm tra 1 tiết Hình học 12 chương 1 năm 2018 – 2019 trường THPT chuyên Hùng Vương – Gia Lai

Đề kiểm tra 1 tiết Hình học 12 chương 1 năm 2018 – 2019 trường THPT chuyên Hùng Vương – Gia Lai mã đề 001 được biên soạn nhằm kiển tra chủ đề kiến thức khối đa diện và thể tích khối đa diện, đề gồm 1 trang với 25 câu hỏi trắc nghiệm khách quan, học sinh làm bài trong 45 phút.

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

18 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Trang 1/(001)
SỞ GD & ĐT GIA LAI
TRƯỜNG THPT CHUYÊN HÙNG VƯƠNG
ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC 12 – (2018 – 2019)
MÔN TOÁN
Thời gian làm bài : 45 Phút; (Đề có 25 câu)
(Đề có 2 trang)
Họ tên : ............................................................... Số báo danh : ...................
Câu 1: Cho hình chóp S.ABCD có đáy ABCD hình chữ nhật,
,3,()
A
B SA a AD a SA ABCD . Tính góc giữa SD
và (SAB)?
A.
0
30
. B.
0
90
. C.
0
60
. D.
0
45
.
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
.SA ABC Gọi H là hình chiếu vuông góc của A
lên SB. Khẳng định nào dưới đây sai?
A.
BC SC . B. BC SB . C. BC AH . D. SC AH .
Câu 3: Tính theo a thể tích V của khối lập phương
.ABCD A B C D

biết .AC a
A.
3
33 .Va
B.
3
3
.
3
a
V
C.
3
.
27
a
V
D.
3
3
.
9
a
V
Câu 4: Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng ?
A.
4 mặt phẳng. B. 3 mặt phẳng. C. 1 mặt phẳng. D. 2 mặt phẳng.
Câu 5: Cho hình chóp
.SABCD có
SA ABCD
, đáy ABCD là hình chữ nhật. Tính thể tích khối chóp .SABCD biết
AB a , 2AD a , 3SA a .
A.
3
2a . B.
3
6a . C.
3
a . D.
3
3
a
Câu 6: Khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp 3 thì thể tích khối hộp tương ứng sẽ tăng
bao nhiêu lần?
A. tăng 18 lần. B. tăng 9 lần. C. tăng 6 lần. D. tăng 27 lần.
Câu 7: Cho hình chóp
.SABC có SA vuông góc mặt đáy, tam giác ABC vuông tại , 2ASA cm , 4, 3AB cm AC cm.
Tính thể tích khối chóp
.SABC.
A.
3
8cm . B.
3
12cm C.
3
24
5
cm
. D.
3
4cm .
Câu 8: Cho hình chóp
.SABC có
SA ABC
, đáy ABC là tam giác đều. Tính thể tích khối chóp .SABC biết AB a ,
SA a .
A.
3
3
12
a
. B.
3
3
a
. C.
3
a . D.
3
3
4
a
.
Câu 9: Phép đối xứng qua mặt phẳng (P) biến đường thẳng d thành chính nó khi:
A. d vuông góc với (P). B. d song song với (P).
C. d nằm trên (P) hoặc d vuông góc với (P). D. d nằm trên (P).
Câu 10: Tính thể tích
V của khối chóp có đáy là hình vuông cạnh 2a và chiều cao là 3a .
A.
3
2.Va B.
3
4
.
3
Va
C.
3
12 .Va D.
3
4.Va
Câu 11: Thể tích khối tam diện vuông
.OABC vuông tại O có , 2OA a OB OC a là
A.
3
2
a
B.
3
2a . C.
3
2
3
a
D.
3
6
a
Câu 12: Cho khối lăng trụ tam giác đều
.’’’ABC A B C có tất cả các cạnh đều bằng a . Thể tích khối tứ diện ’’’ABBC là
A.
3
3
6
a
B.
3
12
a
C.
3
3
4
a
D.
3
3
12
a
Câu 13: Tính thể tích của khối hộp chữ nhật
.ABCD A B C D

có 3AB , 4AD , 5AA
.
A. 12. B. 60. C. 10. D. 20.
Câu 14: Hình hộp đứng có đáy hình thoi ( không phải hình vuông) có bao nhiêu mặt phẳng đối xứng?
A. Bốn. B. Năm. C. Sáu. D. Ba.
Câu 15: Cho hình bát diện đều cạnh
a . Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề nào dưới đây
đúng?
A.
2
8Sa . B.
2
3Sa . C.
2
43Sa . D.
2
23Sa .
Mã đề 001
Trang 2/(001)
Câu 16: Cho khối tứ diện ABCD Gọi M, N, E lần lượt là trung điểm của AB, BD, DA. Tỉ
số thể tích của hai khối tứ diện MNEC và ABCD bằng :
A.
1
4
MNEC
ABCD
V
V
. B.
1
8
MNEC
ABCD
V
V
.
C.
1
2
MNEC
ABCD
V
V
. D.
1
3
MNEC
ABCD
V
V
.
Câu 17: Cho hình chóp
.SABC
có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần
và độ dài đường cao không đổi thì thể tích khối chóp
.SABC
tăng lên bao nhiêu lần?
A.
2 . B. 3 . C. 4 . D.
1
2
.
Câu 18: Cho hình chóp S.ABCD có đáy ABCD hình chữ nhật
,2,( )AB SA a BC a SA ABCD . Tính góc giữa hai
mặt phẳng
SBC
và
A
BCD
?
A.
0
30 . B.
0
90 . C.
0
60 . D.
0
45 .
Câu 19: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
a . Tính chiều cao h của hình chóp S.ABCD, biết
thể tích khối chóp S.ABCD là
3
a
.
A.
3ha
. B.
ha
. C.
4ha
. D.
2ha
.
Câu 20: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B có
3, 4AB BC
.
()SA ABC
và
5SA
. Gọi H
là hình chiếu vuông góc của A lên SB và K là trung điểm của SC. Khẳng định nào sau đây đúng?
A.
//
A
HK BC . B.
A
HK SBC . C.
A
HK SB . D.
HK SAB .
Câu 21: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau, OB OC . Gọi I là trung điểm của BC. Xác
định đoạn vuông góc chung của hai đường thẳng OA và BC?
A.
A
I
. B.
OI
. C.
OB
. D.
OC
.
Câu 22: Cho lăng trụ
.'' ' 'ABCD A B C D
có
ABCD
là hình thoi. Hình chiếu của
'
A
lên
A
BCD là trọng tâm của tam giác
A
BD
. Tính thể tích khối lăng trụ
.'' 'D'ABCD A B C biết AB a ,
0
120ABC , 'AA a .
A.
3
2
2
a
B.
3
2a .
C.
3
2
6
a
D.
3
2
3
a
Câu 23: Cho lăng trụ tam giác
.'' 'ABC A B C
có
'BB a , góc giữa đường thẳng 'BB
và
A
BC
bằng
60 , tam giác ABC
vuông tại
C
và góc
60BAC . Hình chiếu
vuông góc của điểm
'B lên
A
BC trùng với trọng tâm của ABC . Thể tích của
khối tứ diện
'.AABC
theo
a bằng:
A.
3
7
106
a
. B.
3
13
108
a
.
C.
3
15
108
a
. D.
3
9
208
a
.
Câu 24: Cho hình lăng trụ đứng
.'' 'ABC A B C , biết đáy ABC
là tam giác đều cạnh
a .
Khoảng cách từ tâm
O
của tam giác
ABC đến mặt phẳng
'
A
BC bằng
6
a
. Tính thể tích
khối lăng trụ
.'' 'ABC A B C .
A.
3
32
16
a
. B.
3
32
4
a
.
C.
3
32
28
a
. D.
3
32
8
a
.
Câu 25: Cho tứ diện ABCD có BCD tam giác đều cạnh
a
, ()AB BCD và AB a . Tính
khoảng cách từ điểm D đến (ABC)?
A.
3
4
a
. B.
3
2
a
.
C.
2a . D. 3a .
...hêt...
N
M
A
D
C
B
E
'A
'
B
'C
'
D
A
B
C
D
H
C'
A'
G
M
N
B
A
C
B'
O
H
A
'
A
C
C'
B
B'
M
Tr
ang 1/16 - WordToan
SỞ GIÁO
DỤC VÀ ĐÀO TẠO
TRƯỜNG THPT CHUYÊN HÙNG VƯƠNG-
GIA LAI
KIỂM-TRA-TẬP-TRUNG-LẦN-2-HK1
NĂM HỌC 2018 – 2019
Môn: Toán
Thời gian: 45 phút (Không kể thời gian phát đề)
Câu 1: Cho hình chóp
.S ABCD
có đáy
ABCD
hình chữ nhật
, 3
, ( )AB SA a AD a SA ABCD
.
Tính góc giữa
SD
và
SAB
?
A.
0
30
. B.
0
90
. C.
0
60
. D.
0
45
.
Câu 2: Cho
hình chóp
.S A
BC
có đáy
ABC
là
tam giác vuông tại
B
,
.SA A
BC
Gọi
H
là hình
chiếu vuông góc
của
A
lê
n
SB
. K
hẳng định nào dưới đây sai?
A.
BC SC
. B.
BC SB
. C.
BC AH
. D.
SC AH
.
Câu 3: Tính
theo
a
thể tích của khối lập phương
.ABCD A B C D
biết
AC a
.
A.
3
3 3V
a
. B.
3
3
3
a
V
. C.
3
27
a
V . D.
3
3
9
a
V
.
Câu 4: Hình
lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
A.
4
mặt
phẳng. B.
3
mặt
phẳng. C.
1
mặt
phẳng. D.
2
mặt
phẳng.
Câu 5: Cho hình chóp
.S ABCD
có
SA A
BCD
,
đáy
ABCD
là
hình chữ nhật. Tính thể tích khối
chóp
.S AB
CD
biết
AB a
,
2AD
a
,
3SA
a
.
A.
3
2a
. B.
3
6a
. C.
3
a
. D.
3
3
a
.
Câu 6: Khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp
3
thì thể tích khối hộp tương
ứng sẽ tăng bao nhiêu lần?
A. tăng
18
lần. B. tăng
9
lần. C. tăng
6
lần. D. tăng
27
lần.
Câu 7: Cho hình chóp
.S AB
C
có
SA
vuôn
g góc với mặt đáy, tam giác
AB
C
vuôn
g tại
A
2cm,SA 4cm, 3cm.AB AC
Tính
thể tích khối chóp
.S AB
C
.
A.
3
8c
m .
. B.
3
12
cm .
. C.
3
24
cm .
5
. D.
3
4cm
.
Câu 8: Cho hình chóp
.S ABC
có
SA AB
C
, đáy
ABC
là tam giác đều. Tính thể tích khối chóp
.S A
BC
biết
, .AB
a SA a
A.
3
3
.
12
a
. B.
3
.
3
a
. C.
3
.a
. D.
3
3
.
4
a
Câu 9: Ph
ép đối xứng qua mặt phẳng
P
biến đ
ường thẳng
d
thành
chính nó khi:
A.
d
vuông
góc với
P
.
B.
d
song
song với
P
.
C.
d
nằm t
rên
P
hoặc
d
vuông
góc với
P
.
D.
d
nằm t
rên
P
.
Câu 10: Tính
thể tích
V
của khối c
hóp có đáy là hình vuông cạnh
2a
và
chiều cao là
3a
.
T
rang 2/16 – Diễn đàn giáo viên Toán
A.
3
2V a
. B.
3
4
3
V
a
. C.
3
12V a
. D.
3
4V a
.
C
âu 11: Thể tích khối tam diện vuông
.
O
ABC
v
uông tại
O
c
ó
O
A a
,
2O
B OC a
l
à
A.
3
2
a
. B.
3
2a
. C.
3
2
3
a
. D.
3
6
a
.
C
âu 12: Cho khối lăng trụ tam giác đều
.
AB
C A B C
có
tất cả các cạnh đều bằng
.a
Thể
tích khối tứ
diện
A BB C
là
A.
3
3
6
a
. B.
3
.
12
a
. C.
3
3
4
a
. D.
3
3
12
a
.
C
âu 13: Tính thể tích của khối hộp chữ nhật
.
AB
CD A B C D
c
ó
3
AB
,
4A
D
,
5
AA
.
A
.
1
2
. B.
6
0
. C.
10
. D.
2
0
.
C
âu 14: Hình hộp đứng có đáy là hình thoi (không phải hình vuông) có bao nhiêu mặt phẳng đối xứng?
A
. Bốn
. B
. N
ăm. C. Sáu. D
. B
a.
Câu 15: Cho hình bát diện đều cạnh
a
.
Gọi
S
l
à tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề
nào dưới đây đúng?
A
.
2
8S a
. B.
2
3S
a
. C.
2
4
3S a
. D.
2
2
3S a
.
C
âu 16: Cho khối tứ diện ABCD. Gọi M, N, E lần lượt là trung điểm của AB, BD, DA. Tỉ số thể tích của
hai khối tứ diện MNEC và ABCD bằng
A.
1
4
M
NEC
ABCD
V
V
. B.
1
8
M
NEC
ABCD
V
V
. C.
1
2
M
NEC
ABCD
V
V
. D.
1
3
M
NEC
ABCD
V
V
.
C
âu 17: Cho hình chóp
.
S ABC
có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài
đường cao không đổi thì thể tích khối chóp
.
S
ABC
tă
ng lên bao nhiêu lần?
A
.
2
. B.
3
. C.
4
. D.
1
2
.
C
âu 18: Cho hình chóp S.ABCD có đáy
ABCD
hình
chữ nhật
AB SA a
,
2BC a
,
(
)SA ABCD
.
Tính góc giữa hai mặt phẳng
SBC
và
AB
CD
?
A
.
3
0
. B.
9
0
. C.
60
. D.
4
5
.
Câu 19: Cho hình chóp
.
S
ABCD
c
ó đáy là hình vuông cạnh
a
v
à thể tích bằng
3
a
.
Tính chiều cao
h
của
khối chóp
.
S
ABCD
?
A
.
3h
a
. B.
h
a
. C.
4h
a
. D.
2h
a
.
C
âu 20: Cho hình chóp
.
S ABC
có
đáy là tam giác vuông tại
B
có
3
, 4
A
B BC
.
S
A ABC
v
à
5
S
A
. Gọi
H
là hình chiếu vuông góc của
A
lên
S
B
và
K
là trung điểm của
S
C
. Khẳng
định nào sau đây đúng?
A
.
/
/AHK BC
. B.
AHK
SBC
. C.
AHK
SB
. D.
AH
K SAB
.
C
âu 21: Cho tứ diện
OA
BC
có
,
,OA OB OC
đôi một vuông góc với nhau,
O
B OC
. Gọi
I
là trung
điểm của
BC
.
Xác định đoạn vuông góc chung của hai đường thẳng
O
A
v
à
BC
?
A
.
A
I
. B.
OI
. C.
OB
. D.
OC
.
T
rang 3/16 - WordToan
Câu 22: Cho lăng trụ
.A
BCD A B C D
có
A
BCD
là hình thoi. Hình chiếu của
A
lên
(
)ABCD
là trọng
tâm của tam giác
A
BD
.
Tính thể tích khối lăng trụ
.AB
CD A B C D
biế
t
AB
a
,
0
1
20ABC ,
A
A a
.
A.
3
2
2
a
. B.
3
2a
. C.
3
2
6
a
. D.
3
2
3
a
.
Câu
23: Cho lăng trụ tam giác
.ABC
A B C
có
BB
a
, góc giữa đường thẳng
BB
và
ABC
bằng
0
60
,
tam giác
ABC
v
uông tại
C
v
à
0
60BAC
. Hình chiếu vuông góc của điểm
B
lê
n
A
BC
t
rùng với trọng tâm của
ABC
.
Thể tích khối tứ diện
.A ABC
th
eo a bằng:
A.
3
7
.
106
a
. B.
3
13
.
108
a
. C.
3
15
.
108
a
. D.
3
9
.
208
a
Câu 24: Cho hình lăng trụ đứng
.ABC
A B C
,
biết đáy
AB
C
là
tam giác đều cạnh a, Khoảng cách từ
tâm O của tam giác
A
BC
đến
mặt phẳng
A
BC
bằng
6
a
.
Tính thể tích khối lăng trụ
.ABC
A B C
.
A
.
3
3 2
.
16
a
. B.
3
3 2
.
4
a
. C.
3
3 2
.
28
a
. D.
3
3 2
.
8
a
Câu
25: Cho tứ diện
A
BCD
có
B
CD
là
tam giác đều cạnh
a
,
AB
BCD
v
à
AB
a
.
Tính khoảng
cách từ
D
đến
A
BC
?
A.
3
4
a
. B.
3
2
a
. C.
2a
. D. 3a .
BẢNG
ĐÁP ÁN
1.C 2.A 3.D 4.A 5.A 6.D 7.D 8.A 9.C 10.D
11.C 12.D 13.B 14.D 15.
D 16.A 17.C 18.D 19.A 20.B
21.B 22.A 23.
D 24.D 25.B
LỜI GIẢI CHI TIẾT
Câu 1. Cho hình chóp
.S
ABCD
có đáy
ABC
D
hình chữ
nhật,
,
3, ( )AB SA a AD a SA ABCD
. Tính
góc giữa
S
D
v
à
SAB
?
A
.
0
3
0
. B.
0
9
0
. C.
0
60
. D.
0
45
.
Lờ
i giải
Chọn C
Tran
g 4/16 – Diễn đàn giáo viên Toán
Ta có
.S SD
SAB
AD
SA
AD SAB
AD AB
A
là
hình chiếu vuông góc của
D
trên
.SAB
SA
là hì
nh chiếu vuông góc của
SD
tr
ên
.SAB
Góc
giữa
SD
và
SAB
là góc g
iữa
SD
và
SA
đó c
ũng chính là góc
.ASD
Trong
tam giác
ASD
vuông tại
A
có
3
tan 3.
A
D a
ASD
SA a
0
60 .A
SD
Góc giữa
SD
và
SAB
bằng
0
60
.
Câu 2. Cho hình chóp
.S A
BC
có đáy
ABC
là tam giác vuông tại
B
,
.SA ABC
Gọi
H
là hình
chiếu vuông góc
của
A
lê
n
SB
. K
hẳng định nào dưới đây sai?
A.
BC
SC
. B.
BC S
B
. C.
BC AH
. D.
SC
AH
.
Lời giải
Chọn A
T
rang 5/16 - WordToan
+ Ta có:
.
B
C AB
BC SAB BC SB
BC SA
( phương án B đúng )
Mà
A
H SAB
.BC
AH
( phư
ơng án C đúng )
+ T
a có:
.
A
H SB
AH SBC SC AH
AH BC
( phương án D đúng )
Phương án A sai.
Câu 3. Tính theo
a
thể
tích
V
của kh
ối lập phương
.AB
CD A B C D
biết
AC
a
.
A.
3
3 3V a . B.
3
3
3
a
V
. C.
3
27
a
V . D.
3
3
9
a
V
.
Lời giải
Chọn D
Công
thức tính độ dài đường chéo của hình lập phương là
3
.AC AB
Tr
ang 6/16 – Diễn đàn giáo viên Toán
Theo
bài ra ta có:
3
.
3
a
AC a AB a AB
Vậy
3
3
3
.
9
a
V
AB
.
Câu
4. Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
A.
4
mặt phẳng. B.
3
mặt
phẳng. C.
1
mặt
phẳng. D.
2
mặt
phẳng.
Lời giải
Chọn A
Hình lăng trụ tam giác đều
.A
BC A B C
có
4 mặt phẳng đối xứng là:
,
, , ,AHKA BB JF CC IE MNP
t
rong đó
,
, , , , , , , M N P I J K E F H
lần
lượt l
à
t
rung điểm của các cạnh
,
, , , , , , , .AA BB CC A B A C B C AB AC BC
.
Câu
5. Cho hình chóp
.S
ABCD
có
SA ABCD
, đáy
ABC
D
là hình chữ nhật. Tính thể tích khối
chóp
.S
ABCD
biế
t
AB
a
,
2A
D a
,
3S
A a
.
A.
3
2a
. B.
3
6a
. C.
3
a
. D.
3
3
a
.
Lời giải
Chọn A
Thể tí
ch khối chóp
.S
ABCD
l
à
3
1
3 .2 .
. 2
3 3
A
BCD
a
a a
V SA S a
.
Câu
6. Khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp
3
t
hì thể tích khối hộp tương
ứng sẽ tăng bao nhiêu lần?
D
B
C
A
S
Tra
ng 7/16 - WordToan
A. tăng
18
lần. B. tăng
9
lần. C. tăng
6
lần. D. tăng
27
lần.
Lời
giải
Chọn D
G
ọi
a
,
b
,
c
lần l
ượt là độ dài
3
cạnh c
ủa khối hộp chữ nhật.
Thể tích của khối hộp chữ nhật là
V a
bc
.
Sau khi tăng
độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp
3
thì th
ể tích khối hộp
tương ứng là
3 .3 .3 27 27V a b c abc V
.
Vậy sau khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp
3
thì
thể tích khối
hộp tương ứng sẽ tăng lên
27
lần.
Câu
7. Cho hình chóp
.
S ABC
có
SA
vuôn
g góc với mặt đáy, tam giác
ABC
vuôn
g tại
A
2c
m,
SA
4cm
, 3cm.
AB
AC
Tính thể tích khối chóp
.
S AB
C
.
A.
3
8cm
.
. B.
3
12
cm .
. C.
3
24
cm
.
5
. D.
3
4cm
.
Lời
giải
Chọn D
Ta
m giác
ABC
vuông
tại
A
nên
2
1 1
. .
.4.3 6cm .
2 2
ABC
S A
B AC
Thể tích
khối chóp
.
S A
BC
:
3
.
1 1
. .
.2.6 4cm .
3 3
S A
BC ABC
V SA
S
.
Câu
8. Cho hình chóp
.
S ABC
có
SA A
BC
, đá
y
ABC
là
tam giác đều. Tính thể tích khối chóp
.
S ABC
biết
, .A
B a SA a
A.
3
3
.
12
a
. B.
3
.
3
a
. C.
3
.a
. D.
3
3
.
4
a
Lời
giải
Chọn A
ABC
là tam giác đều có cạnh
AB a
nên
2
3
.
4
ABC
a
S
Thể tích
khối chóp
.
S A
BC
:
2 3
.
1 1
3 3
. . . . .
3 3 4 12
S AB
C ABC
a a
V
SA S a
.
Câu
9. Phép đối xứng qua mặt phẳng
P
biến
đường thẳng
d
thành
chính nó khi:
A.
d
vuông góc với
P
.
B.
d
song song với
P
.
C.
d
nằm
trên
P
hoặc
d
vuông
góc với
P
.
D.
d
nằm
trên
P
.
Lời
giải
Chọn C
Tran
g 8/16 – Diễn đàn giáo viên Toán
Phép
đối xứng qua mặt phẳng biến đường thẳng thành đường thẳng song song hoặc trùng với
nó. Để đường thẳng
d
biến
thành chính nó thì
d
nằm tr
ên
P
hoặc
d
vuông
góc với
P
.
Câu 10. Tính
thể tích
V
của khối c
hóp có đáy là hình vuông cạnh
2a
và
chiều cao là
3a
.
A.
3
2V a
. B.
3
4
3
V a
. C.
3
12V
a
. D.
3
4V a
.
Lời giả
i
Chọn D
Ta có:
2
3
1
2 .3 4
3
V a a a
.
Câu 11. Th
ể tích khối tam diện vuông
.O ABC
vuông
tại
O
có
OA a
,
2OB OC a
là
A.
3
2
a
. B.
3
2a
. C.
3
2
3
a
. D.
3
6
a
.
Lời giả
i
Chọn C
Thể
tích khối tam diện cần tìm là
3
1 1 1
2
. . . . . .2 .2 .
3 6 6 3
OBC
a
V OA
S OAOB OC a a a .
Câu 12. Cho khối lăng trụ tam giác đều
.ABC A
B C
có t
ất cả các cạnh đều bằng
.a
Thể tích
khối tứ
diện
A BB C
là
A.
3
3
6
a
. B.
3
.
12
a
. C
.
3
3
4
a
. D.
3
3
12
a
.
Lời giả
i
Chọn D
Ta có:
2
3
4
A B
C
a
S
(Diện
tích tam giác đều cạnh
a
).
T
rang 9/16 - WordToan
2
3
1
1 3 3
. . . . .
3 3 4 12
A
BB C A B C
a
a
V S BB a
.
Câu
13. Tính thể tích của khối hộp chữ nhật
.A
BCD A B C D
có
3AB
,
4A
D
,
5AA
.
A.
12
. B.
6
0
. C.
1
0
. D.
2
0
.
Lời
giải
Chọn B
Ta
có thể tích của khối hộp chữ nhật
.
.
. 3.4.5 60
AB
CD A B C D
V
AB AD AA
(đvtt).
Câu 14. Hình hộp đứng có đáy là hình thoi (không phải hình vuông) có bao nhiêu mặt phẳng đối xứng?
A. Bốn. B. Năm. C. Sáu. D. Ba.
Lời
giải
Chọn D
Ta
có hình hộp đứng có đáy là hình thoi (không phải hình vuông) có 3 mặt phẳng đối xứng.
Câu 15. Cho hình bát diện đều cạnh
a
.
Gọi
S
l
à tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề
nào dưới đây đúng?
A.
2
8S a
. B.
2
3S a . C.
2
4 3S a . D.
2
2 3S a .
Lời
giải
Chọn D
A
'
A
B'
B
C'
C
D'
D
Tr
ang 10/16 – Diễn đàn giáo viên Toán
Các
mặt của hình bát diện đều cạnh
a
l
à các tam giác đều có diện tích bằng
2
3
4
a
.
Hình
bát diện có
8
mặt.
Vậy
tổng diện tích tất cả các mặt của hình bát diện đó là
2
2
3
8.
2 3
4
a
S a
.
Câu 16. Cho khối tứ diện ABCD. Gọi M, N, E lần lượt là trung điểm của AB, BD, DA. Tỉ số thể tích của
hai khối tứ diện MNEC và ABCD bằng
A.
1
4
M
NEC
ABCD
V
V
. B.
1
8
M
NEC
ABCD
V
V
.
C.
1
2
MNEC
ABCD
V
V
. D.
1
3
MNEC
ABCD
V
V
.
Lời
giải
Chọn A
Theo
công thức tỷ số thể tích trong tứ diện ta có
1
1
.
4 4
AM
EC
AMEC ABCD
ABCD
V
A
M AE
V V
V AB AD
.
Do M,
N, E lần lượt là trung điểm của AB, BD, DA nên
1
4
A
MEC DNEC BMNC ABCD
V
V V V
.
K
hi đó ta có
1
3
4
M
NEC ABCD AMEC ABCD
V
V V V
.
Vậy
1
4
M
NEC
ABCD
V
V
.
T
rang 11/16 - WordToan
Kết
luận: Hàm số đã cho có
3
điể
m cực trị.
Câu 17. Cho hình chóp
.S
ABC
có
đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài
đường cao không đổi thì thể tích khối chóp
.S ABC
tăng
lên bao nhiêu lần?
A.
2
. B.
3
. C.
4
. D.
1
2
.
Lời
giải
Chọn C
Thể
tích khối chóp
.S
ABC
:
1
.
3
A
BC
V
S h
(
h
l
à độ dài đường cao hình chóp
.S
ABC
).
Diệ
n tích tam giác đều
A
BC
:
2
3
12
A
BC
AB
S
.
K
hi độ dài cạnh đáy tam giác đều
A
BC
tăng lên 2 lần thì diện tích tam giác
A
BC
tăng lên 4
lần.
Vậy, thể tích khối chóp
.S ABC
t
ăng lên 4 lần.
Câu 18. Cho hình chóp S.ABCD có đáy
A
BCD
hình
chữ nhật
A
B SA a
,
2B
C a
,
(
)SA ABCD
.
Tính
góc giữa hai mặt phẳng
SBC
và
AB
CD
?
A.
3
0
. B.
9
0
. C.
6
0
. D.
4
5
.
Lời giải
Chọn D
SA
ABCD SA BC
.
a
2
a
a
S
α
B
D
C
A
Tr
ang 12/16 – Diễn đàn giáo viên Toán
AB
CD
là hình chữ nhật
BC
AB
.
B
C SA
BC SAB
BC AB
.
SB
C ABCD BC
BC SAB
SAB SBC SB
SAB ABCD AB
Góc giữa mặt phẳng
SBC
và
A
BCD
là
SBA
.
SAB
v
uông tại
A
có
AB SA a
nên
SAB
v
uông cân tại
A
45
.
Vây
, góc giữa hai mặt phẳng
SBC
và
A
BCD
l
à
45
.
Câu
19. Cho hình chóp
.S
ABCD
có
đáy là hình vuông cạnh
a
v
à thể tích bằng
3
a
.
Tính chiều cao
h
của
khối chóp
.S
ABCD
?
A
.
3h
a
. B.
h
a
. C.
4h
a
. D.
2h
a
.
Lời giải
Chọn
A
Diện tích hình vuông
ABC
D
l
à:
2
S
a
.
Ta
có:
.
.
3
.
1
. 3
3
S
ABCD
S ABCD
V
V
h S h a
S
.
Câu 20. Cho hình chóp
.S
ABC
có
đáy là tam giác vuông tại
B
c
ó
3
, 4AB BC
.
SA
ABC
v
à
5S
A
.
Gọi
H
là
hình chiếu vuông góc của
A
l
ên
S
B
v
à
K
là
trung điểm của
S
C
.
Khẳng
định nào sau đây đúng?
A.
/
/AHK BC
. B.
AH
K SBC
. C
.
AH
K SB
. D.
AH
K SAB
.
Lời giải
Chọn
B
Ta có:
2
2
5AC AB BC a
.
Do đó,
S
AC
cân
tại
A
.
Suy
ra:
AK
SC
.
Ta có:
SA
ABC SA BC BC SAB BC AH
.
Ta
có:
A
H BC
AH SBC AHK SBC
AH SB
.
Tr
ang 13/16 - WordToan
Câu 21. Cho tứ diện
OABC
có
, ,O
A OB OC
đôi một vuông góc với nhau,
OB
OC
. Gọi
I
là trung
điểm của
BC
. X
ác định đoạn vuông góc chung của hai đường thẳng
OA
và
BC
?
A.
AI
. B.
OI
. C.
OB
. D.
OC
.
Lời giả
i
Chọn B
Ta có:
( )
OA OB
OA OBC
OA OC
mà
( )O
I OBC OA OI
(1
).
Lại có
:
OBC
cân
tại
O
do
có
OB
OC
và
I
là
trung điểm của
BC
OI BC
(2).
Từ
(1)
và
(2)
suy
ra
OI
là đoạn vuông góc chung của hai đường thẳng
OA
và
BC
.
Câu 22. Cho lăng trụ
.ABCD A B C D
có
ABCD
là
hình thoi. Hình chiếu của
A
lên
( )A
BCD
là
trọng
tâm của tam giác
ABD
. T
ính thể tích khối lăng trụ
.ABC
D A B C D
biết
AB a
,
0
120ABC ,
AA
a
.
A.
3
2
2
a
. B.
3
2a
. C.
3
2
6
a
. D.
3
2
3
a
.
Lời giải
Chọn A
Ta có
ABC
D
là
hình thoi biết
AB a
,
0
120 .A
BC
Suy ra,
 Diện tích đáy là:
2
0
3
. .
sin120
2
ABC
D
a
S B
A BC
.
 Góc
0
60BAD hay
tam giác
ABD
đều cạnh
a
có
H
là
trọng tâm (
H
là
hình chiếu của
A
lên
( )ABCD
) và
2 3
3
.
3 2 3
a a
AH
2
2 2
2
6
3 3
a a
A H AA AH a
là đường
cao của khối lăng trụ
.ABCD A B C D
.
Vậy, thể tích khối lăng trụ
.ABC
D A B C D
là:
2 3
.
6 3
2
. .
3 2 2
ABC
D A B C D ABCD
a a
a
V A H S
.
Tran
g 14/16 – Diễn đàn giáo viên Toán
Câu 23. Cho
lăng trụ tam giác
.ABC A B C
có
BB a
, g
óc giữa đường thẳng
BB
và
ABC
bằng
0
60
, t
am giác
AB
C
vuôn
g tại
C
và
0
60BAC . H
ình chiếu vuông góc của điểm
B
lên
ABC
trù
ng với trọng tâm của
AB
C
. Th
ể tích khối tứ diện
.A ABC
the
o a bằng:
A.
3
7
.
106
a
. B.
3
13
.
108
a
. C.
3
15
.
108
a
. D
.
3
9
.
208
a
Lời giả
i
Ch
ọn D
Gọi
G
là
trọng tâm
AB
C
;
M
là
trung điểm của
AC
.
Theo đề bài
.B G
ABC
Mà
0
; ; 60
.BB ABC B BB ABC BB BG B BG
Nên
3
.si
n
2
3 3
.cos
2 2 4
a
B G BB B BG
a a
BG BB B BG BM BG
Có
.t
an 3BC AC BAC AC
.
Mà
2 2
2 2 2 2 2
2 2
2
2 2
4
.
4 4 4
B
C BA AC BC BC AC AC
BC AC
BM
2 2 2
2
9 13 9
3 13 3 39
.
16 4 52 26 26
a AC a a a
AC AC BC
2 3
.
1 9
3 27
. . .
2 104 208
ABC AB
C A B C ABC
a a
S
CACB V S B G
Mà
3
. .
1 9
.
3
208
A AB
C ABC A B C
a
V V
.
Câu
24. Cho hình lăng trụ đứng
.ABC A B C
,
biết đáy
ABC
là tam
giác đều cạnh a, Khoảng cách từ
tâm O của tam giác
ABC
đến m
ặt phẳng
A BC
bằng
6
a
.
Tính thể tích khối lăng trụ
.ABC A
B C
.
A.
3
3 2
.
16
a
. B.
3
3 2
.
4
a
. C.
3
3 2
.
28
a
. D.
3
3 2
.
8
a
Lời giả
i
Chọn D
C'
A'
G
N
M
B
C
A
B'
M
B
C
A
Tr
ang 15/16 - WordToan
Vì
.ABC
A B C
là
lăng trụ đứng
AA
AB
AA ABC
AA AC
.
;A A
B A AC
vuông tại. A.
2 2
2 2 2 2
A B
A A AB A A AC A C A B A C A BC
cân
tại
A
.
Gọi
M
là t
rung điểm của
.
AM
BC
BC BC A AM
A M BC
A AM
A BC
theo
giao tuyến
A M
.
Hạ
; .
6
a
O
K A M OK A BC OK d O A BC
Vì
ABC
đều
3 1 3
2 3 6
a a
AM OM AM
.
Có
2
2
2 2
3 2
6
6 6
a a a
KM OM OK
.
Dễ d
àng chứng minh được
~
OK
KM
A AM OKM
AA AM
2 3
.
. 6 6
3 3 2
. .
2 2 4 8
ABC A B C ABC
OK
AM a a a a
AA V AA S
KM
.
Câu 25. Cho
tứ diện
ABCD
có
BCD
là t
am giác đều cạnh
a
,
AB BCD
và
AB a
. Tín
h khoảng
cách từ
D
đến
ABC
?
A.
3
4
a
. B.
3
2
a
. C.
2a
. D.
3a
.
Lời giả
i
Chọn B
C'
B'
O
N
M
A
C
B
A'
K
K
O
A'
A
M
Tr
ang 16/16 – Diễn đàn giáo viên Toán
Gọi
M
là
trung điểm cạnh
BC
.
Ta có:
DM BC
DM ABC
DM AB
hay
M
l
à hình chiếu của
D
lên
AB
C
.
Vậy
3
,
2
a
d
D ABC DM
.
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD & ĐT GIA LAI
ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC 12 – (2018 – 2019)
TRƯỜNG THPT CHUYÊN HÙNG VƯƠNG MÔN TOÁN
Thời gian làm bài : 45 Phút; (Đề có 25 câu)
(Đề có 2 trang)
Họ tên : ............................................................... Số báo danh : ................... Mã đề 001
Câu 1: Cho hình chóp S.ABCD có đáy ABCD hình chữ nhật, AB SA a, AD a 3, SA  (ABCD) . Tính góc giữa SD và (SAB)? A. 0 30 . B. 0 90 . C. 0 60 . D. 0 45 .
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA   ABC. Gọi H là hình chiếu vuông góc của A
lên SB. Khẳng định nào dưới đây sai?
A. BC SC . B. BC SB .
C. BC AH .
D. SC AH .
Câu 3: Tính theo a thể tích V của khối lập phương ABC . D AB CD
  biết AC  . a 3 3 3 A. 3a a 3a 3 V  3 3a . B. V  . C. V  . D. V  . 3 27 9
Câu 4: Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng ?
A. 4 mặt phẳng. B. 3 mặt phẳng. C. 1 mặt phẳng. D. 2 mặt phẳng.
Câu 5: Cho hình chóp S.ABCD có SA   ABCD , đáy ABCD là hình chữ nhật. Tính thể tích khối chóp S.ABCD biết
AB a , AD  2a , SA  3a . 3 A. a 3 2a . B. 3 6a . C. 3 a . D.  3
Câu 6: Khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp 3 thì thể tích khối hộp tương ứng sẽ tăng bao nhiêu lần?
A. tăng 18 lần. B. tăng 9 lần. C. tăng 6 lần. D. tăng 27 lần.
Câu 7: Cho hình chóp S.ABC có SA vuông góc mặt đáy, tam giác ABC vuông tại ,
A SA  2cm , AB  4c ,
m AC  3cm .
Tính thể tích khối chóp S.ABC . A. 24 3 8cm . B. 3 12cm C. 3 cm . D. 3 4cm . 5
Câu 8: Cho hình chóp S.ABC có SA   ABC , đáy ABC là tam giác đều. Tính thể tích khối chóp S.ABC biết AB a ,
SA a . 3 3 3 A. a 3 . B. a . C. a 3 3 a . D. . 12 3 4
Câu 9: Phép đối xứng qua mặt phẳng (P) biến đường thẳng d thành chính nó khi:
A. d vuông góc với (P).
B. d song song với (P).
C. d nằm trên (P) hoặc d vuông góc với (P).
D. d nằm trên (P).
Câu 10: Tính thể tích V của khối chóp có đáy là hình vuông cạnh 2a và chiều cao là 3a . A. 4 3 V  2a . B. 3 V   a . C. 3 V  12a . D. 3 V  4a . 3
Câu 11: Thể tích khối tam diện vuông .
O ABC vuông tại O có OA a, OB OC  2a là 3 3 3 A. a B. 2a a 3 2a . C. D.  2 3 6
Câu 12: Cho khối lăng trụ tam giác đều ABC. ’ A ’
B C’ có tất cả các cạnh đều bằng a . Thể tích khối tứ diện ’ A B ’ B C’ là 3 3 3 3 A. a 3  B. a C. a 3  D. a 3  6 12 4 12
Câu 13: Tính thể tích của khối hộp chữ nhật ABC . D AB CD
  có AB  3 , AD  4 , AA  5 . A. 12. B. 60. C. 10. D. 20.
Câu 14: Hình hộp đứng có đáy hình thoi ( không phải hình vuông) có bao nhiêu mặt phẳng đối xứng? A. Bốn. B. Năm. C. Sáu. D. Ba.
Câu 15: Cho hình bát diện đều cạnh a . Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề nào dưới đây đúng? A. 2 S  8a . B. 2 S  3a . C. 2 S  4 3a . D. 2 S  2 3a . Trang 1/(001)
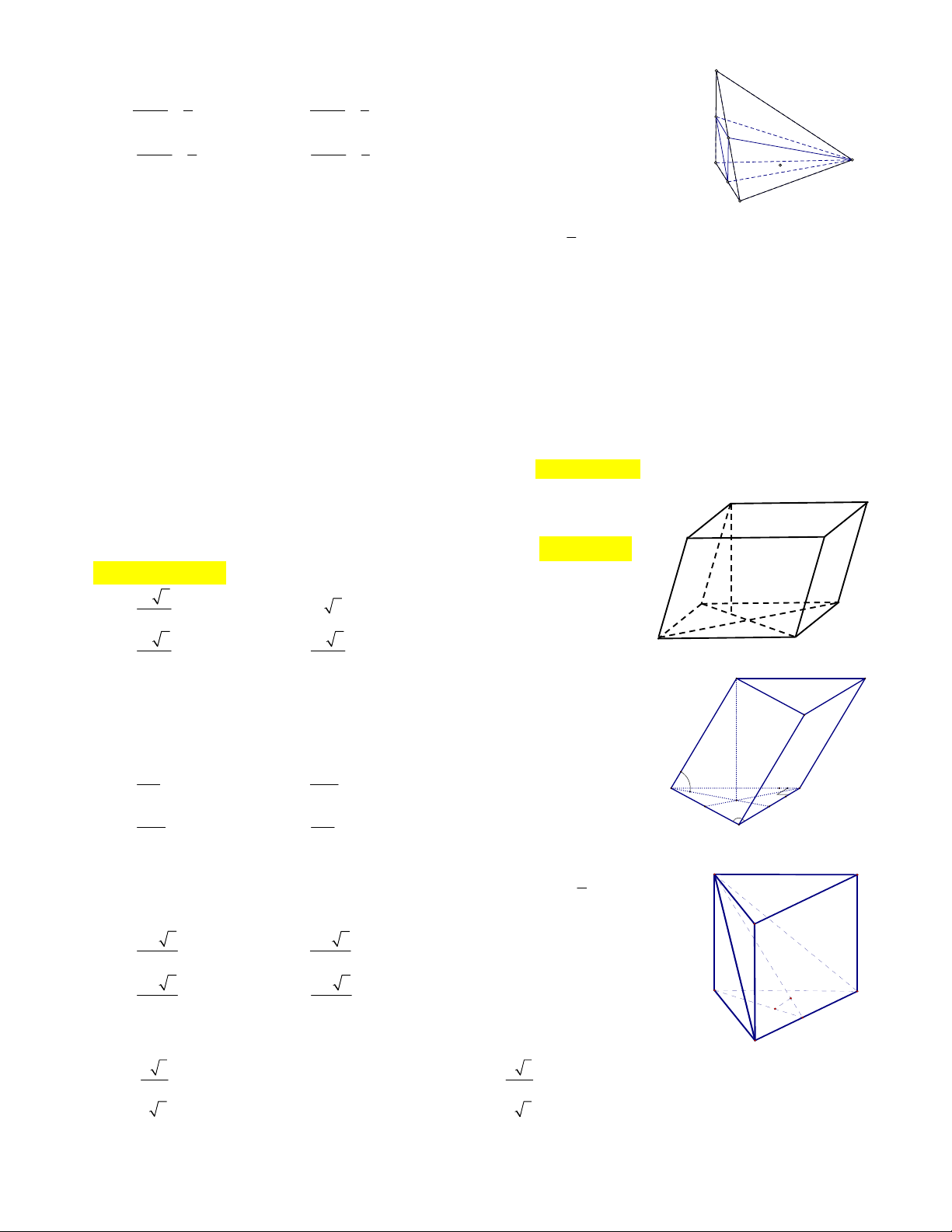
Câu 16: Cho khối tứ diện ABCD Gọi M, N, E lần lượt là trung điểm của AB, BD, DA. Tỉ A
số thể tích của hai khối tứ diện MNEC và ABCD bằng : V V A. 1 MNEC  . B. 1 MNEC  . V 4 V 8 M ABCD ABCD E V V C. 1 MNEC  . D. 1 MNEC  . V 2 V 3 B ABCD ABCD C
Câu 17: Cho hình chóp S.ABC có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần N
và độ dài đường cao không đổi thì thể tích khối chóp S.ABC tăng lên bao nhiêu lần? D A. 2 . B. 3 . C. 4 . D. 1 . 2
Câu 18: Cho hình chóp S.ABCD có đáy ABCD hình chữ nhật AB SA a, BC  2a, SA  (ABCD) . Tính góc giữa hai
mặt phẳng SBC và  ABCD ? A. 0 30 . B. 0 90 . C. 0 60 . D. 0 45 .
Câu 19: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Tính chiều cao h của hình chóp S.ABCD, biết
thể tích khối chóp S.ABCD là 3 a .
A. h  3a .
B. h a .
C. h  4a .
D. h  2a .
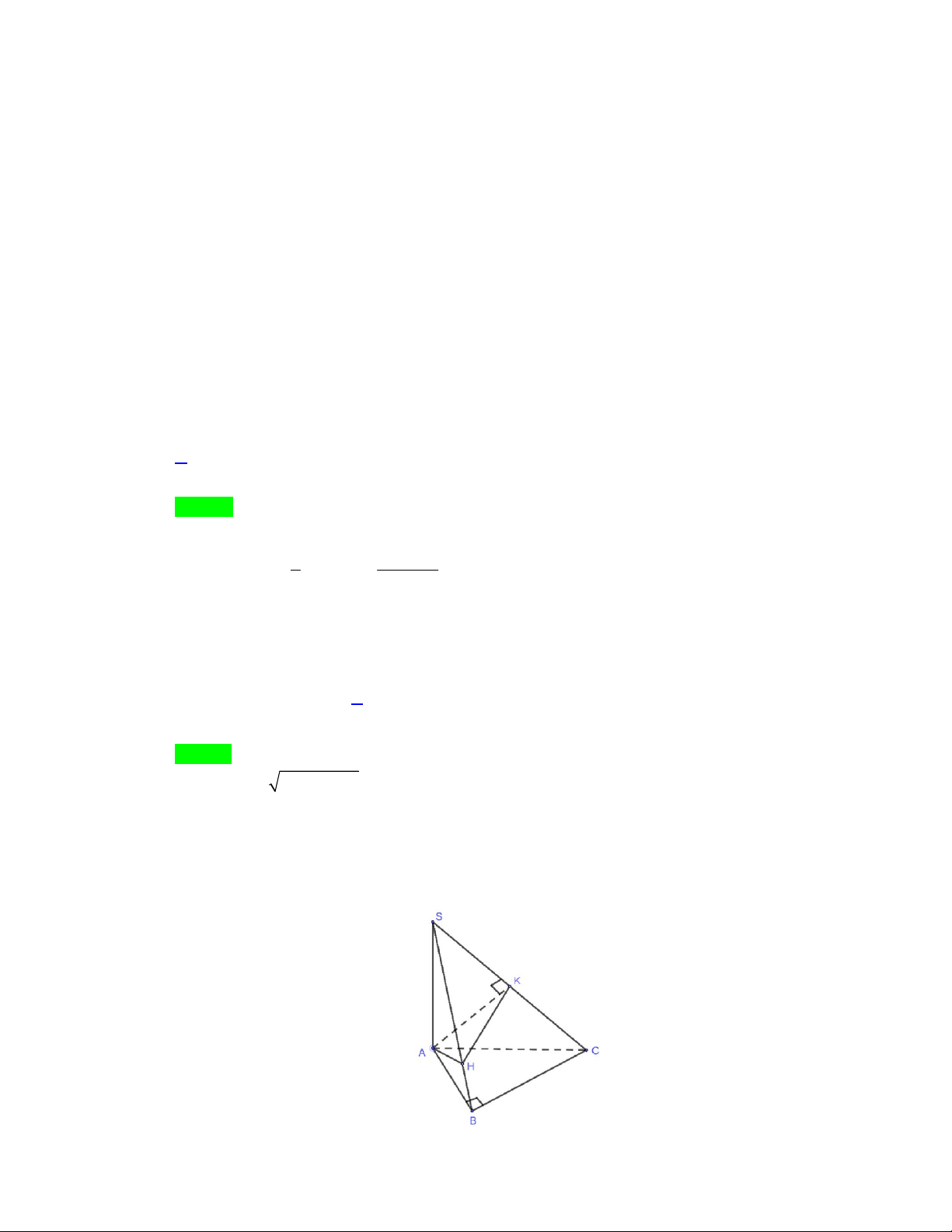
Câu 20: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B có AB  3, BC  4 . SA  (ABC) và SA  5 . Gọi H
là hình chiếu vuông góc của A lên SB và K là trung điểm của SC. Khẳng định nào sau đây đúng?
A. AHK  // BC . B. AHK   SBC . C. AHK   SB . D. AHK   SAB .
Câu 21: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau, OB OC . Gọi I là trung điểm của BC. Xác
định đoạn vuông góc chung của hai đường thẳng OA và BC? ' A A. AI .
B. OI . C. OB . D. OC . B'
Câu 22: Cho lăng trụ ABC .
D A' B 'C ' D ' có ABCD là hình thoi. Hình chiếu của A' C' D'
lên  ABCD là trọng tâm của tam giác ABD . Tính thể tích khối lăng trụ ABC .
D A' B 'C 'D' biết AB a ,  0
ABC  120 , AA'  a . 3 A A. a 2  B. 3 a 2 . B 2 H 3 a 2 3 a 2 D C C. D.  6 3 B' C'
Câu 23: Cho lăng trụ tam giác ABC.A' B 'C ' có BB'  a , góc giữa đường thẳng BB'
và  ABC bằng 60 , tam giác ABC vuông tại C và góc 
BAC  60 . Hình chiếu A'
vuông góc của điểm B ' lên  ABC trùng với trọng tâm của AB
C . Thể tích của
khối tứ diện A'.ABC theo a bằng: 3 3 A. 7a . B. 13a . B C 106 108 3 3 G M N C. 15a . D. 9a . 108 208 A
Câu 24: Cho hình lăng trụ đứng ABC.A' B 'C ' , biết đáy ABC là tam giác đều cạnh a . A' C' Khoảng cách từ tâm a
O của tam giác ABC đến mặt phẳng  A'BC bằng . Tính thể tích 6
khối lăng trụ ABC.A' B 'C ' . B' 3 3 A. 3a 2 . B. 3a 2 . 16 4 3 3 C. 3a 2 . D. 3a 2 . A H C 28 8 O
Câu 25: Cho tứ diện ABCD có BCD tam giác đều cạnh a , AB  (BCD) và AB a . Tính M
khoảng cách từ điểm D đến (ABC)? B A. a 3 . B. a 3 . 4 2 C. a 2 . D. a 3 . ...hêt... Trang 2/(001)
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM-TRA-TẬP-TRUNG-LẦN-2-HK1
TRƯỜNG THPT CHUYÊN HÙNG VƯƠNG-
NĂM HỌC 2018 – 2019 GIA LAI Môn: Toán
Thời gian: 45 phút (Không kể thời gian phát đề) Câu 1:
Cho hình chóp S.ABCD có đáy ABCD hình chữ nhật AB SA a , AD a 3 , SA  ( ABCD) .
Tính góc giữa SD và SAB ? A. 0 30 . B. 0 90 . C. 0 60 . D. 0 45 . Câu 2:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , SA   ABC . Gọi H là hình chiếu vuông góc
của A lên SB . Khẳng định nào dưới đây sai?
A. BC SC .
B. BC SB .
C. BC AH .
D. SC AH . Câu 3:
Tính theo a thể tích của khối lập phương ABC . D AB CD
  biết AC  a . 3 3a 3 a 3 3a A. 3 V  3 3a . B. V  . C. V  . D. V  . 3 27 9 Câu 4:
Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng? A. 4 mặt phẳng. B. 3 mặt phẳng. C. 1 mặt phẳng. D. 2 mặt phẳng. Câu 5:
Cho hình chóp S.ABCD có SA   ABCD , đáy ABCD là hình chữ nhật. Tính thể tích khối
chóp S.ABCD biết AB a , AD  2a , SA  3a . 3 a A. 3 2a . B. 3 6a . C. 3 a . D. . 3 Câu 6:
Khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp 3 thì thể tích khối hộp tương
ứng sẽ tăng bao nhiêu lần? A. tăng 18 lần. B. tăng 9 lần. C. tăng 6 lần. D. tăng 27 lần. Câu 7:
Cho hình chóp S.ABC có SA vuông góc với mặt đáy, tam giác ABC vuông tại
A SA  2cm, AB  4cm, AC  3cm. Tính thể tích khối chóp S.ABC . 24 A. 3 8cm .. B. 3 12cm . . C. 3 cm .. D. 3 4cm . 5 Câu 8:
Cho hình chóp S.ABC có SA   ABC  , đáy ABC là tam giác đều. Tính thể tích khối chóp
S.ABC biết AB a, SA  . a 3 a 3 3 a 3 a 3 A. .. B. . . C. 3 a . . D. . 12 3 4 Câu 9:
Phép đối xứng qua mặt phẳng  P biến đường thẳng d thành chính nó khi:
A. d vuông góc với  P .
B. d song song với  P .
C. d nằm trên  P hoặc d vuông góc với  P .
D. d nằm trên  P .
Câu 10: Tính thể tích V của khối chóp có đáy là hình vuông cạnh 2a và chiều cao là 3a . Trang 1/16 - WordToan 4 A. 3 V  2a . B. 3 V   a . C. 3 V  12a . D. 3 V  4a . 3
Câu 11: Thể tích khối tam diện vuông .
O ABC vuông tại O có OA a , OB OC  2a là 3 a 3 2a 3 a A. . B. 3 2a . C. . D. . 2 3 6
Câu 12: Cho khối lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh đều bằng .
a Thể tích khối tứ diện ABB C   là 3 a 3 3 a 3 a 3 3 a 3 A. . B. . . C. . D. . 6 12 4 12
Câu 13: Tính thể tích của khối hộp chữ nhật ABC . D A BCD
  có AB  3 , AD  4 , AA  5 . A. 12 . B. 60 . C. 10 . D. 20 .
Câu 14: Hình hộp đứng có đáy là hình thoi (không phải hình vuông) có bao nhiêu mặt phẳng đối xứng? A. Bốn. B. Năm. C. Sáu. D. Ba.
Câu 15: Cho hình bát diện đều cạnh a . Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề
nào dưới đây đúng? A. 2 S  8a . B. 2 S  3a . C. 2 S  4 3a . D. 2 S  2 3a .
Câu 16: Cho khối tứ diện ABCD. Gọi M, N, E lần lượt là trung điểm của AB, BD, DA. Tỉ số thể tích của
hai khối tứ diện MNEC và ABCD bằng V 1 V 1 V 1 V 1 A. MNEC  . B. MNEC  . C. MNEC  . D. MNEC  . V 4 V 8 V 2 V 3 ABCD ABCD ABCD ABCD
Câu 17: Cho hình chóp S.ABC có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài
đường cao không đổi thì thể tích khối chóp S.ABC tăng lên bao nhiêu lần? 1 A. 2 . B. 3 . C. 4 . D. . 2
Câu 18: Cho hình chóp S.ABCD có đáy ABCD hình chữ nhật AB SA a , BC  2a , SA  ( ABCD) .
Tính góc giữa hai mặt phẳng SBC  và  ABCD ? A. 30 . B. 90 . C. 60 . D. 45 .
Câu 19: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và thể tích bằng 3
a . Tính chiều cao h
của khối chóp S.ABCD ?
A. h  3a .
B. h a .
C. h  4a .
D. h  2a .
Câu 20: Cho hình chóp S.ABC có đáy là tam giác vuông tại B có AB  3, BC  4 . SA   ABC  và
SA  5 . Gọi H là hình chiếu vuông góc của A lên SB và K là trung điểm của SC . Khẳng
định nào sau đây đúng?
A. AHK  / /BC .
B. AHK    SBC  . C. AHK   SB .
D. AHK   SAB .
Câu 21: Cho tứ diện OABC có O ,
A OB,OC đôi một vuông góc với nhau, OB OC . Gọi I là trung
điểm của BC . Xác định đoạn vuông góc chung của hai đường thẳng OA và BC ? A. AI . B. OI . C. OB . D. OC .
Trang 2/16 – Diễn đàn giáo viên Toán
Câu 22: Cho lăng trụ ABC . D AB CD
  có ABCD là hình thoi. Hình chiếu của A lên ( ABCD) là trọng
tâm của tam giác ABD . Tính thể tích khối lăng trụ ABC . D AB CD
  biết AB a ,  0 ABC  120 , AA  a . 3 a 2 3 a 2 3 a 2 A. . B. 3 a 2 . C. . D. . 2 6 3
Câu 23: Cho lăng trụ tam giác ABC.AB C
  có BB  a , góc giữa đường thẳng BB và  ABC  bằng 0
60 , tam giác ABC vuông tại C và  0
BAC  60 . Hình chiếu vuông góc của điểm B lên
ABC  trùng với trọng tâm của ABC . Thể tích khối tứ diện A .ABC theo a bằng: 3 7a 3 13a 3 15a 3 9a A. . . B. .. C. . . D. . 106 108 108 208
Câu 24: Cho hình lăng trụ đứng ABC.AB C
  , biết đáy ABC là tam giác đều cạnh a, Khoảng cách từ a
tâm O của tam giác ABC đến mặt phẳng  ABC  bằng
. Tính thể tích khối lăng trụ 6
ABC.AB C   . 3 3a 2 3 3a 2 3 3a 2 3 3a 2 A. . . B. . . C. . . D. . 16 4 28 8
Câu 25: Cho tứ diện ABCD có BCD là tam giác đều cạnh a , AB   BCD và AB a . Tính khoảng
cách từ D đến  ABC  ? a 3 a 3 A. . B. . C. a 2 . D. a 3 . 4 2 BẢNG ĐÁP ÁN 1.C 2.A 3.D 4.A 5.A 6.D 7.D 8.A 9.C 10.D 11.C 12.D 13.B 14.D 15.D 16.A 17.C 18.D 19.A 20.B 21.B 22.A 23.D 24.D 25.B
LỜI GIẢI CHI TIẾT Câu 1. Cho hình chóp S.ABCD có đáy ABCD hình chữ
nhật, AB SA a , AD a 3 , SA  ( ABCD) . Tính góc giữa
SD và SAB ? A. 0 30 . B. 0 90 . C. 0 60 . D. 0 45 . Lời giải Chọn C Trang 3/16 - WordToan
Ta có S SD  SAB.
AD SA  AD  SAB  A là hình chiếu vuông góc của D trên SAB. AD AB
SA là hình chiếu vuông góc của SD trên  SAB.
 Góc giữa SD và  SAB là góc giữa SD và SA đó cũng chính là góc  A . SDAD a 3
Trong tam giác ASD vuông tại A có tan ASD    3. SA a   0 ASD  60 .
 Góc giữa SD và SAB bằng 0 60 . Câu 2.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , SA   ABC . Gọi H là hình chiếu vuông góc
của A lên SB . Khẳng định nào dưới đây sai?
A. BC SC .
B. BC SB .
C. BC AH .
D. SC AH . Lời giải Chọn A
Trang 4/16 – Diễn đàn giáo viên Toán + Ta có:
BC AB BC  SAB  BC  .
SB ( phương án B đúng ) BC SA
Mà AH  SAB  BC AH. ( phương án C đúng ) + Ta có: AH SB
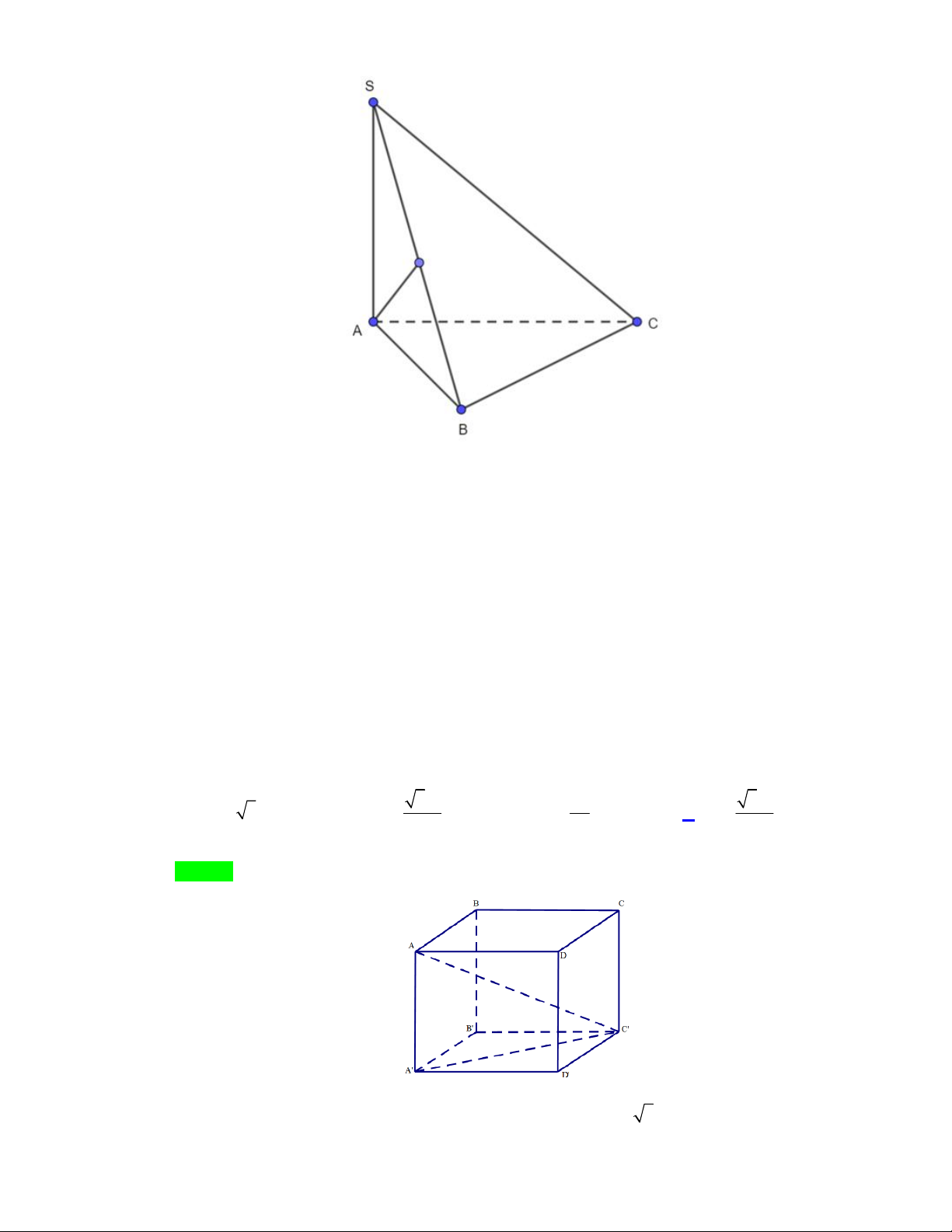
  AH   SBC   SC AH. ( phương án D đúng ) AH BC  Phương án A sai. Câu 3.
Tính theo a thể tích V của khối lập phương ABC . D AB CD
  biết AC  a . 3 3a 3 a 3 3a A. 3 V  3 3a . B. V  . C. V  . D. V  . 3 27 9 Lời giải Chọn D
Công thức tính độ dài đường chéo của hình lập phương là AC  3A . B Trang 5/16 - WordToan a
Theo bài ra ta có: AC  a  3AB a AB  . 3 3 3a Vậy 3 V AB  . . 9 Câu 4.
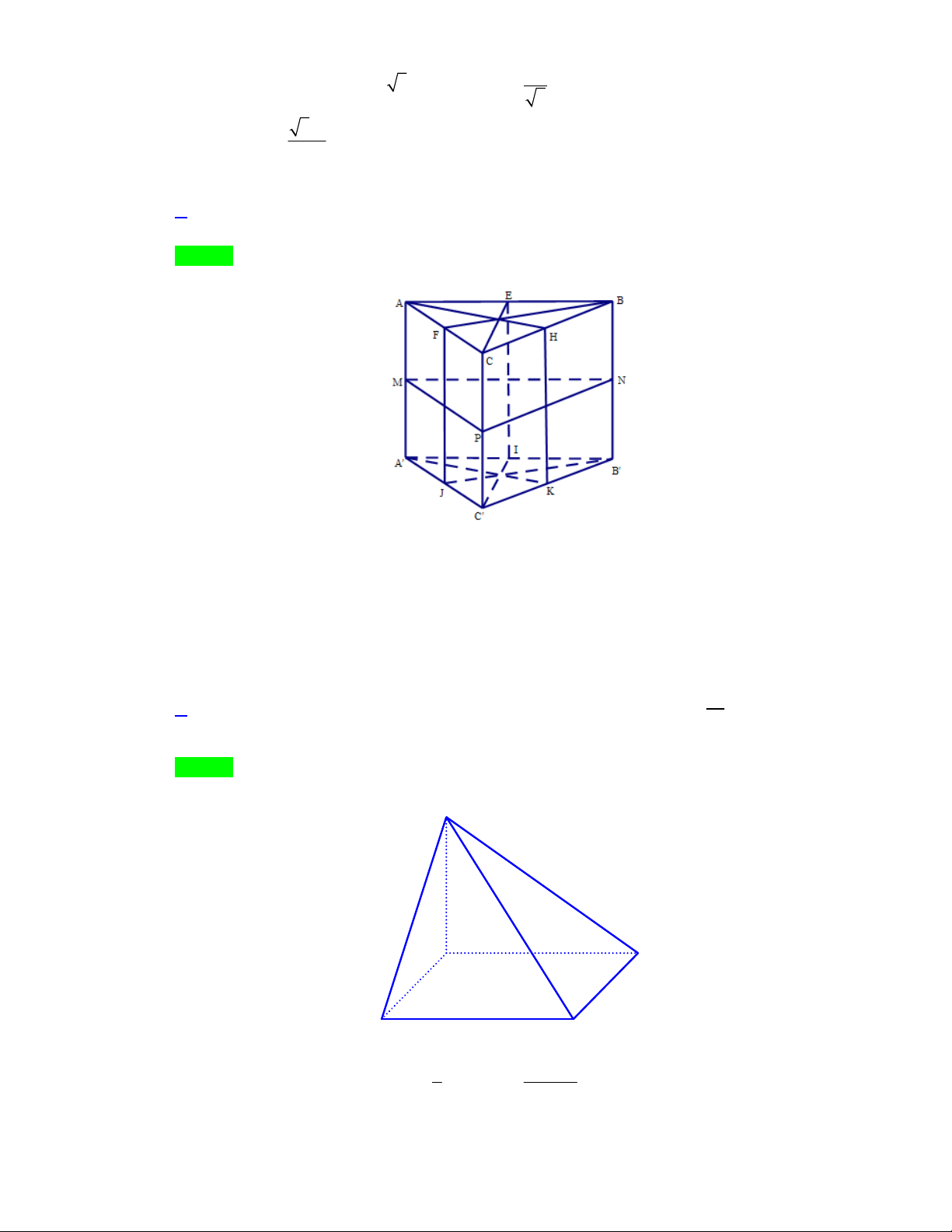
Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng? A. 4 mặt phẳng. B. 3 mặt phẳng. C. 1 mặt phẳng. D. 2 mặt phẳng. Lời giải Chọn A
Hình lăng trụ tam giác đều ABC.AB C
  có 4 mặt phẳng đối xứng là:
AHKA,  BB JF  , CC IE
, MNP, trong đó M , N, P, I, J, K, E, F, H lần lượt là
trung điểm của các cạnh AA ,
BB , CC , AB , A C  ,  B C
 , AB, AC, BC. . Câu 5.
Cho hình chóp S.ABCD có SA   ABCD , đáy ABCD là hình chữ nhật. Tính thể tích khối
chóp S.ABCD biết AB a , AD  2a , SA  3a . 3 a A. 3 2a . B. 3 6a . C. 3 a . D. . 3 Lời giải Chọn A S A D B C 1 3 . a 2 . a a
Thể tích khối chóp S.ABCD là 3 V  . SA S   2a . 3 ABCD 3 Câu 6.
Khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp 3 thì thể tích khối hộp tương
ứng sẽ tăng bao nhiêu lần?
Trang 6/16 – Diễn đàn giáo viên Toán A. tăng 18 lần. B. tăng 9 lần. C. tăng 6 lần. D. tăng 27 lần. Lời giải Chọn D
Gọi a , b , c lần lượt là độ dài 3 cạnh của khối hộp chữ nhật.
Thể tích của khối hộp chữ nhật là V abc .
Sau khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp 3 thì thể tích khối hộp
tương ứng là V   3 .3 a .3
b c  27abc  27V .
Vậy sau khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp 3 thì thể tích khối
hộp tương ứng sẽ tăng lên 27 lần. Câu 7.
Cho hình chóp S.ABC có SA vuông góc với mặt đáy, tam giác ABC vuông tại
A SA  2cm, AB  4cm, AC  3cm. Tính thể tích khối chóp S.ABC . 24 A. 3 8cm .. B. 3 12cm . . C. 3 cm .. D. 3 4cm . 5 Lời giải Chọn D 1 1
Tam giác ABC vuông tại A nên 2 S  .A . B AC  .4.3  6cm . ABC 2 2 1 1
Thể tích khối chóp S.ABC : 3 V  . . SA S  .2.6  4cm . . S . ABC 3 ABC 3 Câu 8.
Cho hình chóp S.ABC có SA   ABC  , đáy ABC là tam giác đều. Tính thể tích khối chóp
S.ABC biết AB a, SA  . a 3 a 3 3 a 3 a 3 A. .. B. . . C. 3 a . . D. . 12 3 4 Lời giải Chọn A 2 a 3
ABC là tam giác đều có cạnh AB a nên S  . ABC 4 2 3 1 1 a 3 a 3
Thể tích khối chóp S.ABC : V  . . SA S  . . a  . . S . ABC 3 ABC 3 4 12 Câu 9.
Phép đối xứng qua mặt phẳng  P biến đường thẳng d thành chính nó khi:
A. d vuông góc với  P .
B. d song song với  P .
C. d nằm trên  P hoặc d vuông góc với  P .
D. d nằm trên  P . Lời giải Chọn C Trang 7/16 - WordToan
Phép đối xứng qua mặt phẳng biến đường thẳng thành đường thẳng song song hoặc trùng với
nó. Để đường thẳng d biến thành chính nó thì d nằm trên  P hoặc d vuông góc với  P .
Câu 10. Tính thể tích V của khối chóp có đáy là hình vuông cạnh 2a và chiều cao là 3a . 4 A. 3 V  2a . B. 3 V   a . C. 3 V  12a . D. 3 V  4a . 3 Lời giải Chọn D 1 Ta có: V  2a2 3 .3a  4a . 3
Câu 11. Thể tích khối tam diện vuông .
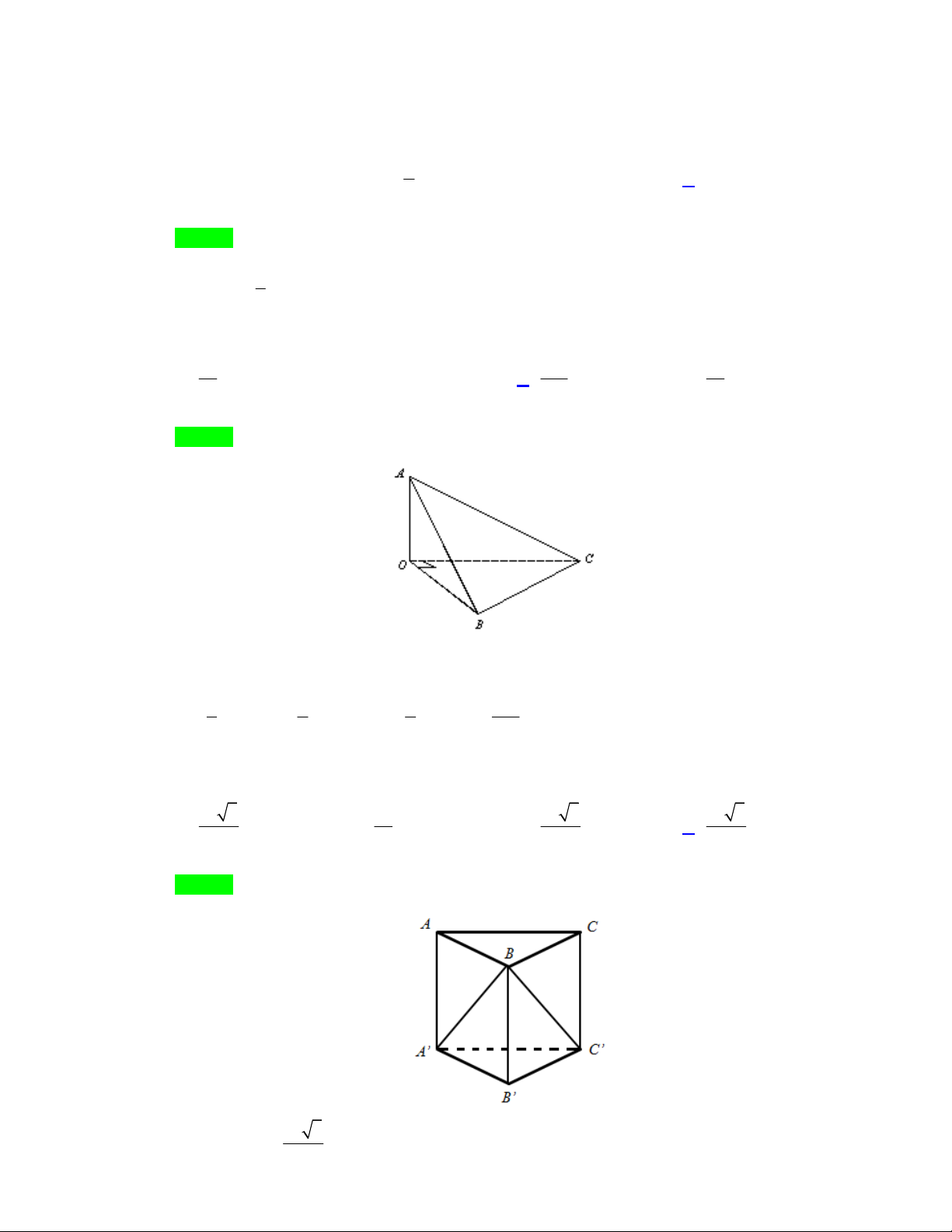
O ABC vuông tại O có OA a , OB OC  2a là 3 a 3 2a 3 a A. . B. 3 2a . C. . D. . 2 3 6 Lời giải Chọn C
Thể tích khối tam diện cần tìm là 3 1 1 1 2a V  . . OA S  . OA . OB OC  . .2 a .2 a a  . . 3 OBC 6 6 3
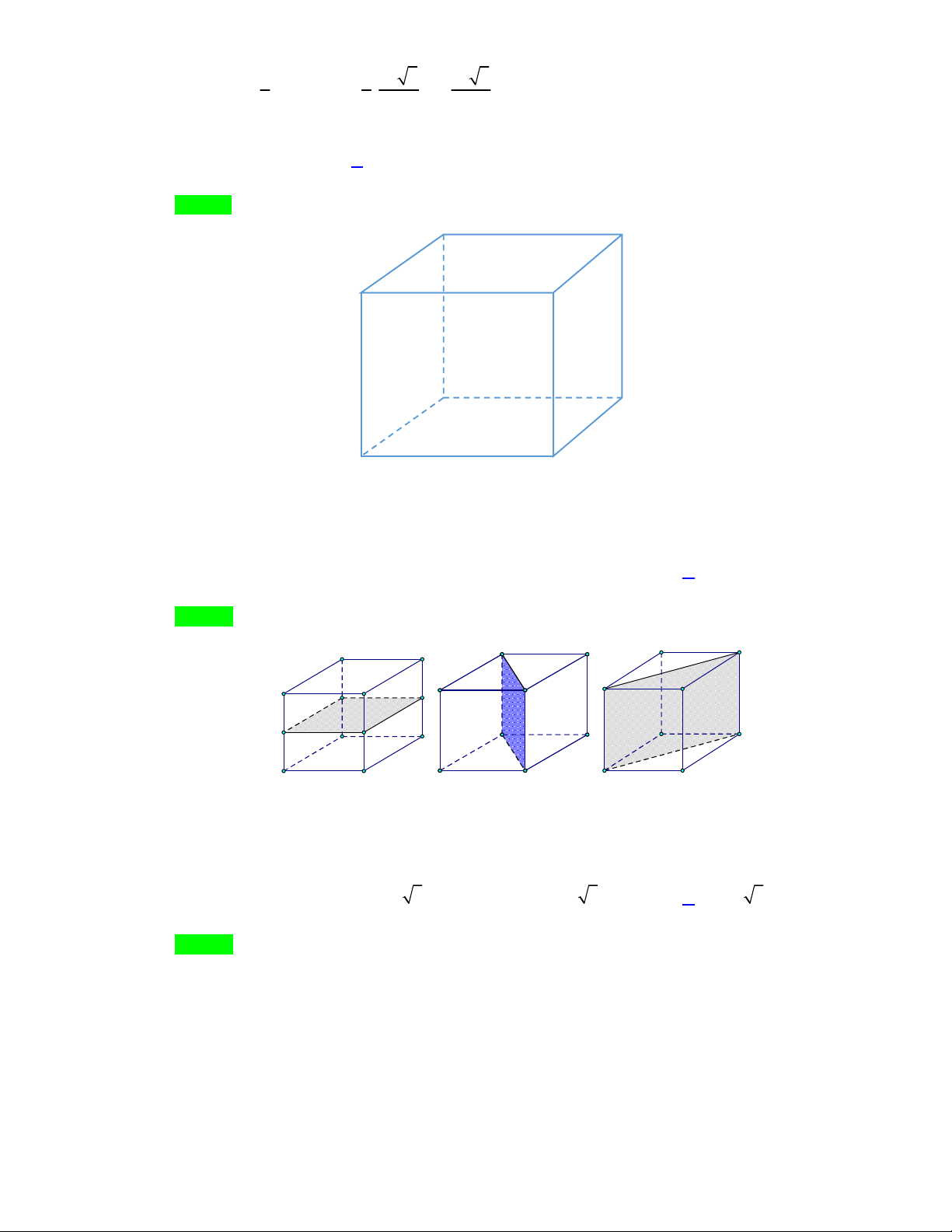
Câu 12. Cho khối lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh đều bằng .
a Thể tích khối tứ diện ABB C   là 3 a 3 3 a 3 a 3 3 a 3 A. . B. . . C. . D. . 6 12 4 12 Lời giải Chọn D 2 a 3 Ta có: S
(Diện tích tam giác đều cạnh a ). A BC   4
Trang 8/16 – Diễn đàn giáo viên Toán 2 3 1 1 a 3 a 3  V  .S .BB  . .a  . . ABB C      3 A B C 3 4 12
Câu 13. Tính thể tích của khối hộp chữ nhật ABC . D AB CD
  có AB  3 , AD  4 , AA  5 . A. 12 . B. 60 . C. 10 . D. 20 . Lời giải Chọn B A' D' Ta có thể tích của khối hộp chữ nhật B' C' A D B C VA . B A .
D AA  3.4.5  60 (đvtt).
ABCD. AB CD  
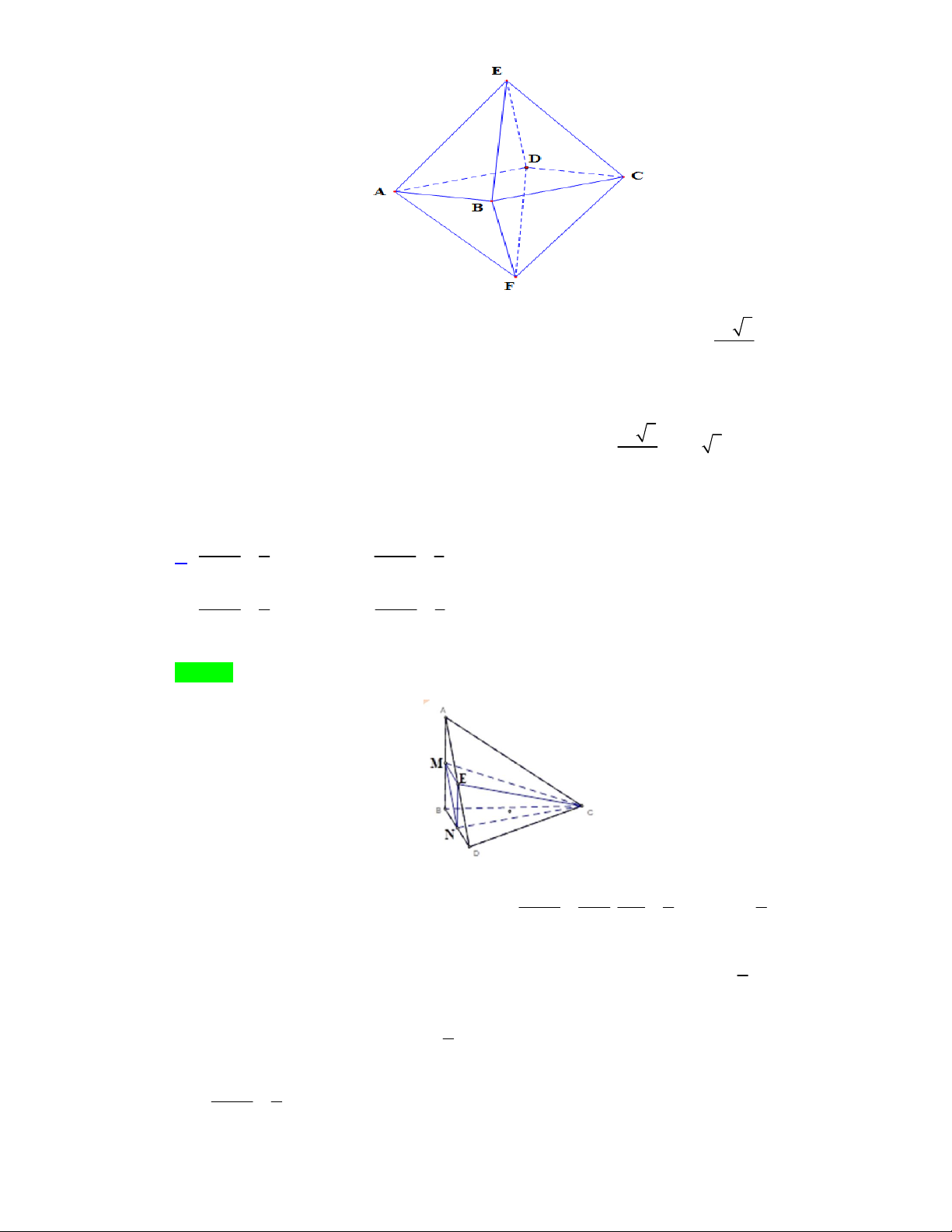
Câu 14. Hình hộp đứng có đáy là hình thoi (không phải hình vuông) có bao nhiêu mặt phẳng đối xứng? A. Bốn. B. Năm. C. Sáu. D. Ba. Lời giải Chọn D
Ta có hình hộp đứng có đáy là hình thoi (không phải hình vuông) có 3 mặt phẳng đối xứng.
Câu 15. Cho hình bát diện đều cạnh a . Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề
nào dưới đây đúng? A. 2 S  8a . B. 2 S  3a . C. 2 S  4 3a . D. 2 S  2 3a . Lời giải Chọn D Trang 9/16 - WordToan 2 a 3
Các mặt của hình bát diện đều cạnh a là các tam giác đều có diện tích bằng . 4
Hình bát diện có 8 mặt. 2 a 3
Vậy tổng diện tích tất cả các mặt của hình bát diện đó là 2 S  8.  2a 3 . 4
Câu 16. Cho khối tứ diện ABCD. Gọi M, N, E lần lượt là trung điểm của AB, BD, DA. Tỉ số thể tích của
hai khối tứ diện MNEC và ABCD bằng V 1 V 1 A. MNEC  . B. MNEC  . V 4 V 8 ABCD ABCD V 1 V 1 C. MNEC  . D. MNEC  . V 2 V 3 ABCD ABCD Lời giải Chọn A V AM AE 1 1
Theo công thức tỷ số thể tích trong tứ diện ta có AMEC  .   VV . V AB AD 4 AMEC 4 ABCD ABCD 1
Do M, N, E lần lượt là trung điểm của AB, BD, DA nên VVVV . AMEC DNEC BMNC 4 ABCD 1 Khi đó ta có VV  3VV . MNEC ABCD AMEC 4 ABCD V 1 Vậy MNEC  . V 4 ABCD
Trang 10/16 – Diễn đàn giáo viên Toán
Kết luận: Hàm số đã cho có 3 điểm cực trị.
Câu 17. Cho hình chóp S.ABC có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài
đường cao không đổi thì thể tích khối chóp S.ABC tăng lên bao nhiêu lần? 1 A. 2 . B. 3 . C. 4 . D. . 2 Lời giải Chọn C 1
Thể tích khối chóp S.ABC : V S
.h ( h là độ dài đường cao hình chóp S.ABC ). 3 ABC 2 AB 3
Diện tích tam giác đều ABC : S  . ABC 12
Khi độ dài cạnh đáy tam giác đều ABC tăng lên 2 lần thì diện tích tam giác ABC tăng lên 4 lần.
Vậy, thể tích khối chóp S.ABC tăng lên 4 lần.
Câu 18. Cho hình chóp S.ABCD có đáy ABCD hình chữ nhật AB SA a , BC  2a , SA  ( ABCD) .
Tính góc giữa hai mặt phẳng SBC  và  ABCD ? A. 30 . B. 90 . C. 60 . D. 45 . Lời giải Chọn D S a a α A B 2a D C
SA   ABCD  SA BC . Trang 11/16 - WordToan
ABCD là hình chữ nhật  BC AB . BC SA
BC  SAB . BC AB  
SBC    ABCD  BCBC   SAB 
 Góc giữa mặt phẳng SBC  và  ABCD là    SBA . SAB
  SBC  SB
SAB ABCD  ABS
AB vuông tại A có AB SA a nên S
AB vuông cân tại A    45 .
Vây, góc giữa hai mặt phẳng SBC  và  ABCD là 45 .
Câu 19. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và thể tích bằng 3
a . Tính chiều cao h
của khối chóp S.ABCD ?
A. h  3a .
B. h a .
C. h  4a .
D. h  2a . Lời giải Chọn A
Diện tích hình vuông ABCD là: 2 S a . 1 3.V Ta có: S . V  . ABCD h S h   3a . S . ABCD 3 S Câu 20.
Cho hình chóp S.ABC có đáy là tam giác vuông tại B có AB  3, BC  4 . SA   ABC
và SA  5 . Gọi H là hình chiếu vuông góc của A lên SB và K là trung điểm của SC . Khẳng
định nào sau đây đúng?
A. AHK  / /BC .
B. AHK    SBC  . C. AHK   SB .
D. AHK   SAB . Lời giải Chọn B Ta có: 2 2 AC
AB BC  5a . Do đó, SAC cân tại A .
Suy ra: AK SC .
Ta có: SA   ABC   SA BC BC  SAB  BC AH .  AH BC Ta có: 
AH   SBC    AHK   SBC  . AH SB
Trang 12/16 – Diễn đàn giáo viên Toán
Câu 21. Cho tứ diện OABC có O ,
A OB,OC đôi một vuông góc với nhau, OB OC . Gọi I là trung
điểm của BC . Xác định đoạn vuông góc chung của hai đường thẳng OA và BC ? A. AI . B. OI . C. OB . D. OC . Lời giải Chọn B OA   OB Ta có: 
OA  (OBC) mà OI  (OBC)  OA OI (1). OA OC
Lại có: OBC cân tại O do có OB OC và I là trung điểm của BC OI BC (2).
Từ (1) và (2) suy ra OI là đoạn vuông góc chung của hai đường thẳng OA và BC .
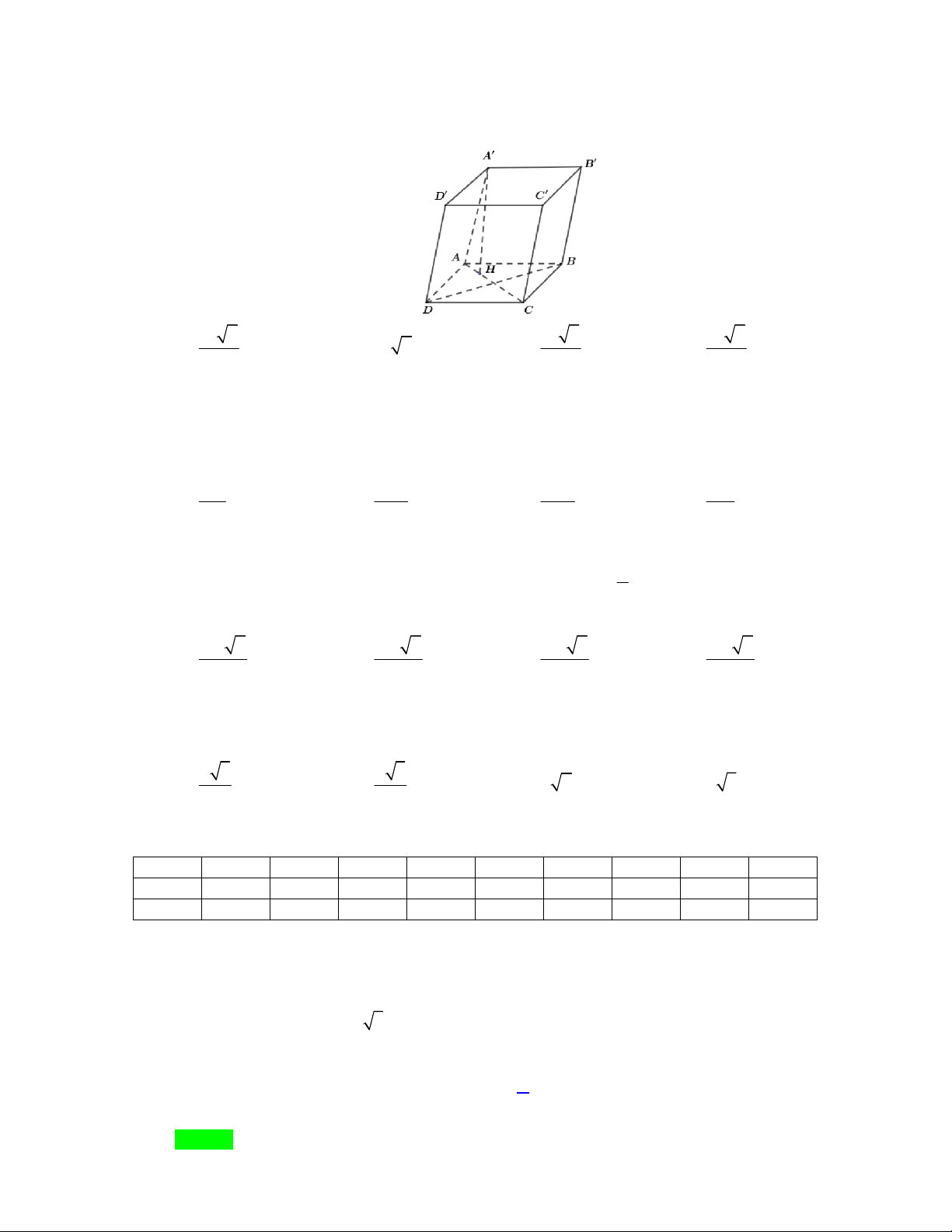
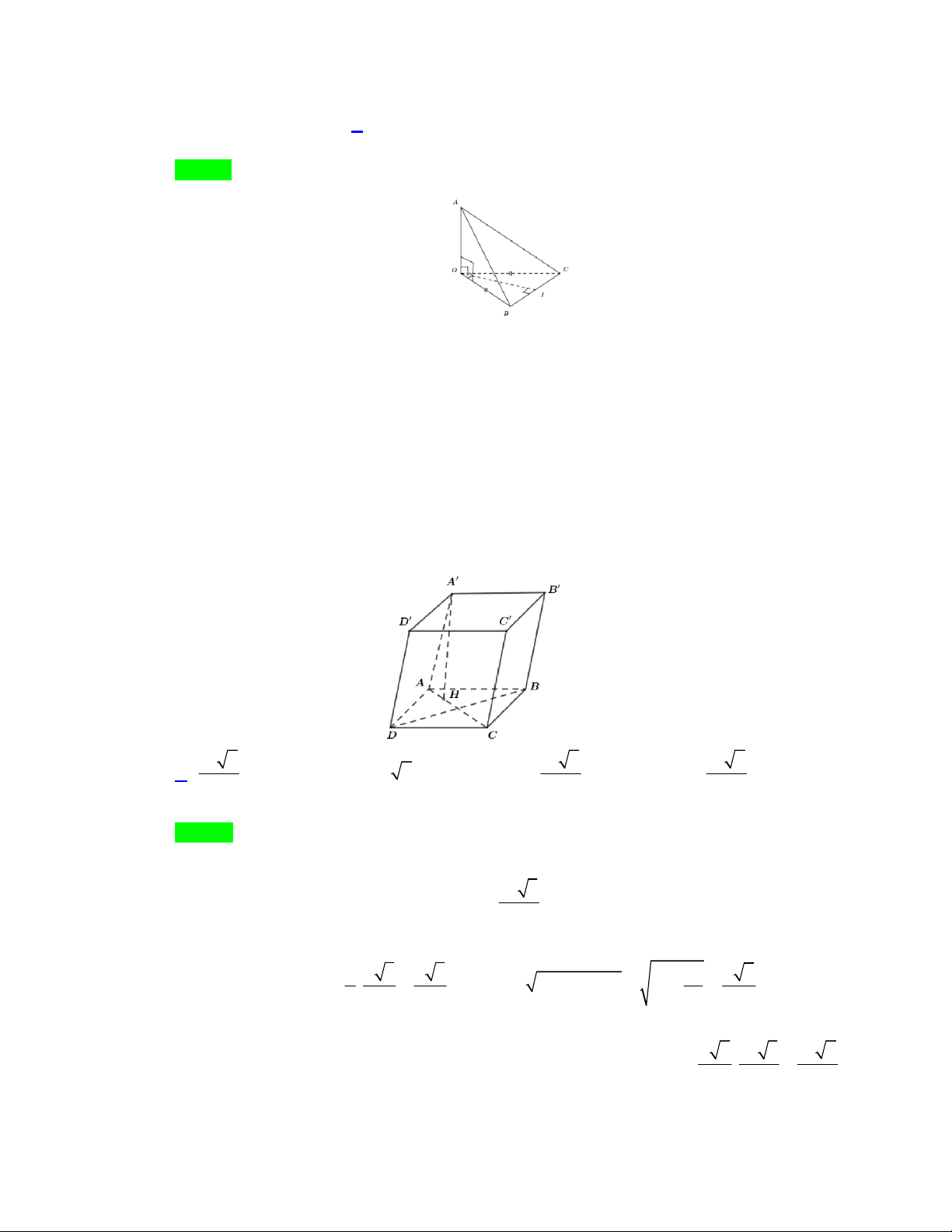
Câu 22. Cho lăng trụ ABC . D AB CD
  có ABCD là hình thoi. Hình chiếu của A lên ( ABCD) là trọng
tâm của tam giác ABD . Tính thể tích khối lăng trụ ABC . D AB CD
  biết AB a ,  0 ABC  120 , AA  a . 3 a 2 3 a 2 3 a 2 A. . B. 3 a 2 . C. . D. . 2 6 3 Lời giải Chọn A
Ta có ABCD là hình thoi biết AB a ,  0 ABC  120 . Suy ra, 2 a 3 Diện tích đáy là: 0 SB . A BC.sin120  . ABCD 2  Góc 0
BAD  60 hay tam giác ABD đều cạnh a có H là trọng tâm ( H là hình chiếu của A 2 a 3 a 3 2 a a 6
lên ( ABCD) ) và AH  .  2 2 2  A H  
AA  AH a   là đường 3 2 3 3 3
cao của khối lăng trụ ABC . D AB CD   . 2 3 a 6 a 3 a 2
Vậy, thể tích khối lăng trụ ABC . D AB CD   là: VA H  .S  .  . ABCD.A BCD   ABCD 3 2 2 Trang 13/16 - WordToan
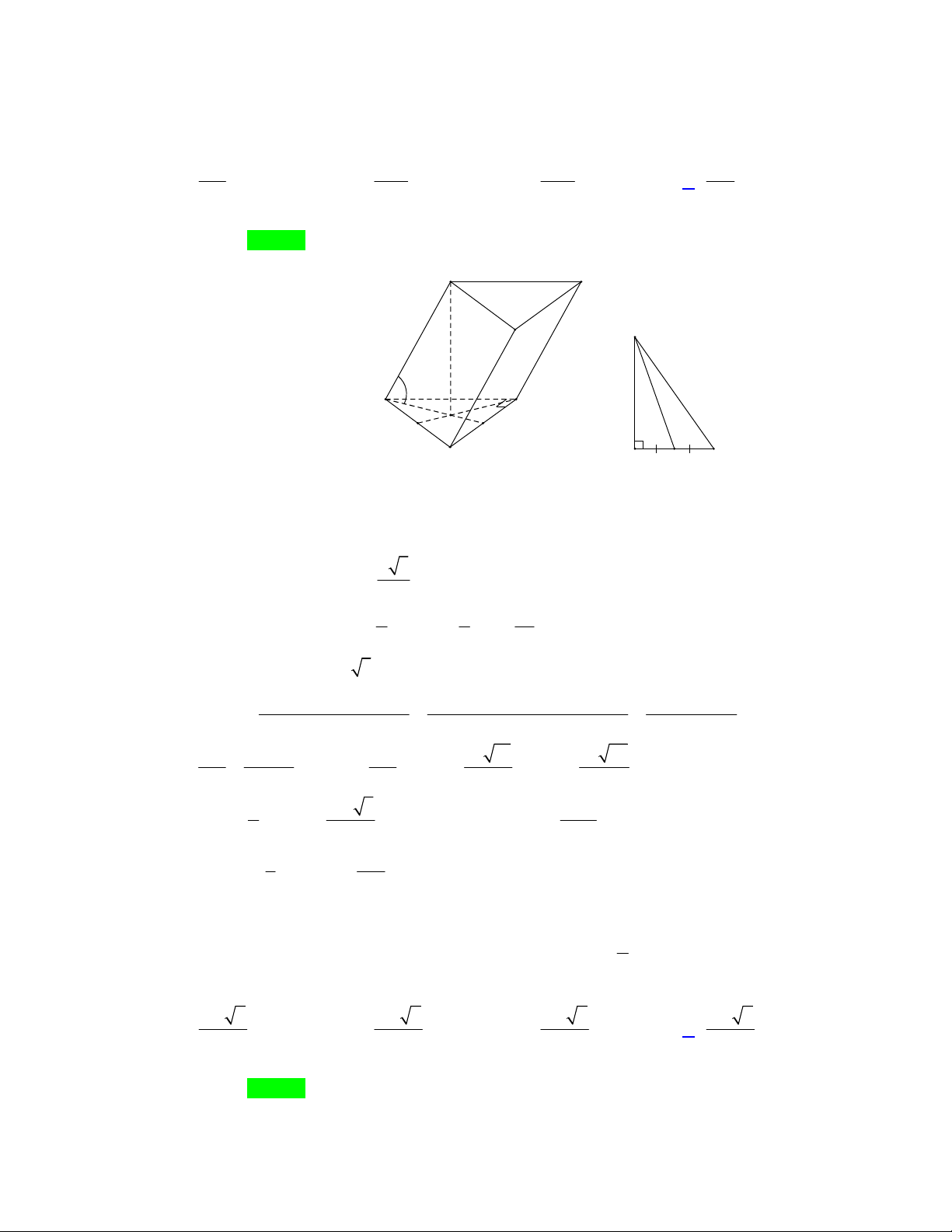
Câu 23. Cho lăng trụ tam giác ABC.AB C
  có BB  a , góc giữa đường thẳng BB và  ABC  bằng 0
60 , tam giác ABC vuông tại C và  0
BAC  60 . Hình chiếu vuông góc của điểm B lên
ABC  trùng với trọng tâm của ABC . Thể tích khối tứ diện A .ABC theo a bằng: 3 7a 3 13a 3 15a 3 9a A. . . B. .. C. . . D. . 106 108 108 208 Lời giải Chọn D B' C' B A' B C G N M A C M A
Gọi G là trọng tâm ABC ; M là trung điểm của AC . Theo đề bài B G    ABC .
Mà BB   ABC   B  BB  ABC 
  BBBG   0 ; ;  B BG   60 .   a 3 B G
BB .sin B BG     Nên 2    a 3 3a
BG BB .cos B BG   BM BG    2 2 4 
Có BC AC.tan BAC  3AC . 2 BC BAAC
2 BC BC ACAC 4BC AC 2  2 2  2  2 2 2  2 2 2 Mà BM    . 4 4 4 2 2 2 9a 13AC 9a 3a 13 3a 39 2    AC   AC   BC  . 16 4 52 26 26 2 3 1 9a 3 27aS  . CA CB   VS .B G   . ABC ABC.    2 104 A B C ABC 208 3 1 9a Mà VV  . . A .  ABC ABC. 3 A BC   208
Câu 24. Cho hình lăng trụ đứng ABC.AB C
  , biết đáy ABC là tam giác đều cạnh a, Khoảng cách từ a
tâm O của tam giác ABC đến mặt phẳng  ABC  bằng
. Tính thể tích khối lăng trụ 6 ABC.A BC   . 3 3a 2 3 3a 2 3 3a 2 3 3a 2 A. . . B. . . C. . . D. . 16 4 28 8 Lời giải Chọn D
Trang 14/16 – Diễn đàn giáo viên Toán A' C' B' A' K A C K O N M B A O MAA  AB
Vì ABC.AB C
  là lăng trụ đứng  AA   ABC    . AA  AC   A  AB ; A
 AC vuông tại.
A. 2 2 2 2 2 2
AB A A   AB A A
AC AC AB A C   A
 BC cân tại A .  AM BC
Gọi M là trung điểm của BC  
BC   A AM .
AM BC    A AM
   ABC  theo giao tuyến AM . a
Hạ OK AM OK   A BC
  OK d  ; O A BC    . 6 a 3 1 a 3
Vì ABC đều  AM   OM AM  . 2 3 6 2 2  a 3   a a 2 Có 2 2
KM OM OK        .  6   6  6   OK KM
Dễ dàng chứng minh được A  AM ~ OKM   AAAM 2 3 OK.AM a 6 a 6 a 3 3a 2  AA    VAA .S  .  . ABC.    KM 2 A B C ABC 2 4 8
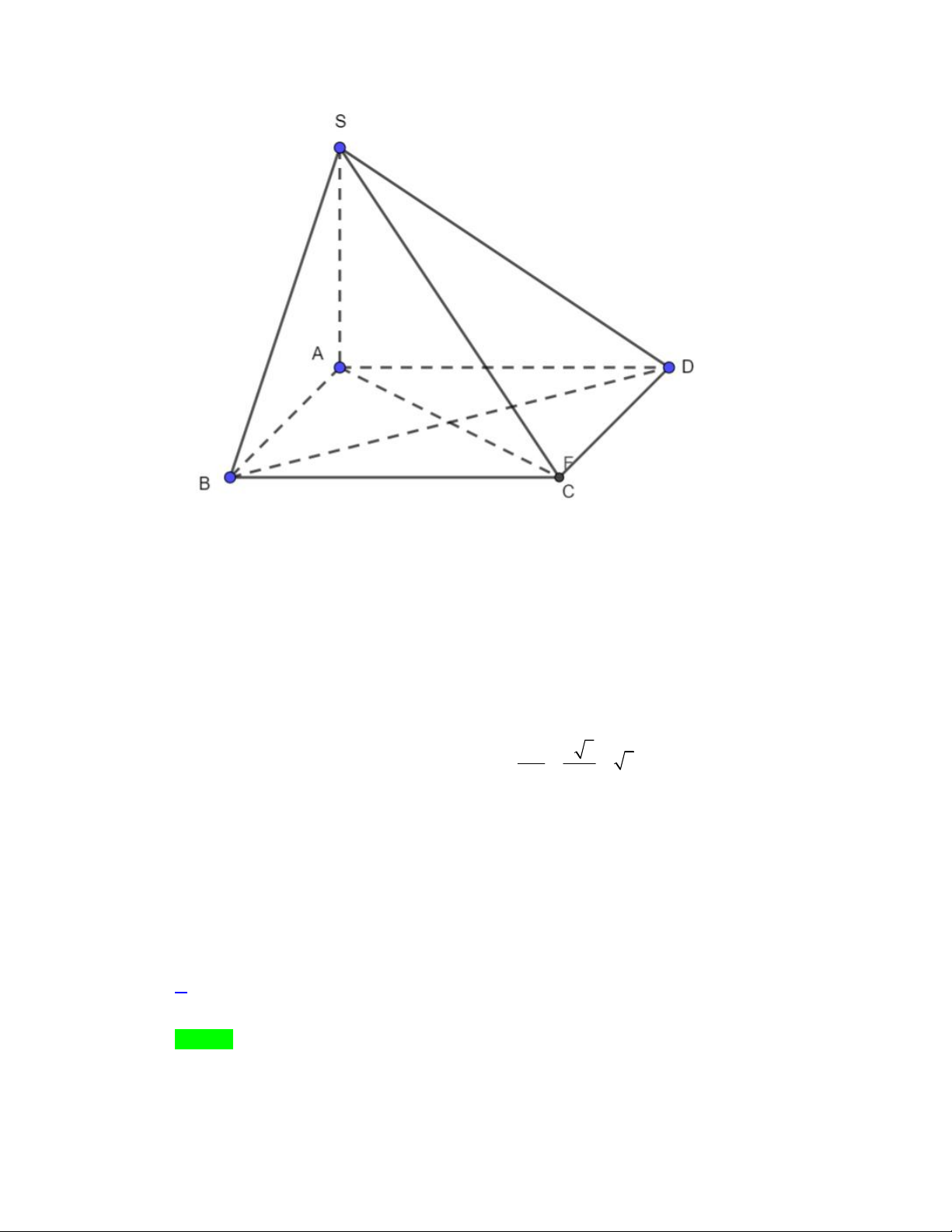
Câu 25. Cho tứ diện ABCD có BCD là tam giác đều cạnh a , AB   BCD và AB a . Tính khoảng
cách từ D đến  ABC  ? a 3 a 3 A. . B. . C. a 2 . D. a 3 . 4 2 Lời giải Chọn B Trang 15/16 - WordToan
Gọi M là trung điểm cạnh BC . DM BC Ta có: 
DM   ABC  hay M là hình chiếu của D lên  ABC  . DM ABa
Vậy d D ABC  3 ,  DM  . 2
Trang 16/16 – Diễn đàn giáo viên Toán
Document Outline

  • 545
  • 1568689351_WT14-H12-KIỂM TRA 45 PHÚT-KHỐI ĐA DIỆN-H12-THPT CHUYÊN HÙNG VƯƠNG-GIA LAI-NĂM 2019