Đề kiểm tra 45 phút Hình học 12 chương 1 năm 2018 – 2019 trường Ngô Sĩ Liên – Bắc Giang

Trường Ngô Sĩ Liên – Bắc Giang đã biên soạn đề kiểm tra 45 phút Hình học 12 chương 1 năm 2018 – 2019 và tổ chức kiểm tra tập trung tại trường, đề có mã đề 201 với 25 câu hỏi trắc nghiệm khách quan, học sinh làm bài trong vòng 1 tiết học để lấy điểm hệ số 2.

18 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

24 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Trang 1/3 - Mã đề thi 201
SỞ GD & ĐT BẮC GIANG
TRƯỜNG THPT NGÔ SĨ LIÊN
ĐỀ KIỂM TRA 45 PHÚT NĂM HỌC 2018 – 2019
MÔN : HÌNH HỌC 12
(25 câu trắc nghiệm)
Mã đề thi 201
Họ và tên học sinh:........................................................Lớp: …………………
Câu 1: Khối chóp tam giác đều
.S ABC
có cạnh đáy bằng
a
, cạnh bên bằng
3a
có thể tích bằng
A.
3
.
3
a
B.
3
2
.
6
a
C.
3
2
.
2
a
D.
3
6
.
2
a
Câu 2: Cho khối chóp .S ABC có đáy là tam giác đều cạnh a . Biết 3SC a , hai mặt phẳng
()SAB
và
()SAC
cùng vuông góc với đáy. Thể tích khối chóp .S ABC bằng
A.
3
3
.
2
a
B.
3
3
.
4
a
C.
3
26
.
9
a
D.
3
6
.
12
a
Câu 3: Số mặt phẳng đối xứng của hình lập phương là
A.
7 . B. 3. C. 6. D. 9 .
Câu 4: Số hình đa diện lồi trong các hình dưới đây là
A.
0
B.
1
C.
3
D.
2
Câu 5: Cho hình chóp
.SABCD
có đáy là hình vuông
cạnh
,a
SA
vuông góc với đáy,
SD
tạo với mặt
phẳng
A
BCD
một góc bằng
0
60 . Thể tích của khối chóp .SABCDbằng
A.
3
3
.
3
a
B.
3
.a
C.
3
3
.
9
a
D.
3
.
3
a
Câu 6: Cho hình hộp
.
A
BCDABCD

tất cả các cạnh đều bằng
0
, 60aBAD
, hình chiếu vuông góc
của
A
xuống
A
BCD trùng với trung điểm của
.AB
Thể tích khối hộp
.
A
BCDABCD

bằng
A.
3
3
12
a
.
B.
3
3
4
a
.
C.
3
3
2
a
.
D.
3
3
4
a
.
Câu 7: Số mặt đối xứng của hình chóp tứ giác đều là
A.
2.
B. 4 . C.
8
. D.
6
.
Câu 8: Cho khối chóp .SABCD có đáy là hình vuông cạnh a . Biết tam giác SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp
.S ABCD
bằng
A.
3
3
.
2
a
B.
3
.
3
a
C.
3
3
.
6
a
D.
3
.a
Câu 9: Cho khối chóp .S ABCD có đáy là hình chữ nhật. Biết 22
A
CABa, SA vuông góc với đáy,
2SA a . Thể tích khối chóp .S ABCD là
A.
3
5
.
3
a
B.
3
6.a
C.
3
6
.
3
a
D.
3
15
.
3
a
Câu 10: Số đỉnh của hình mười hai mặt đều là
A.
12. B.
30
. C.
20
. D.
16
.
Câu 11: Khối đa diện đều loại
4;3
là
Trang 2/3 - Mã đề thi 201
A. Khối chóp tứ giác đều. B. Khối bát diện đều.
C. Khối tứ diện đều. D. Khối lập phương.
Câu 12: Kim tự tháp Kê - ốp ở Ai cập được xây dựng khoảng năm 2500 trước công nguyên. Kim tự tháp
này là một khối chóp tứ giác đều có chiều cao
147m
, cạnh đáy là 230m . Thể tích của nó bằng
A.
3
2592100 .m
B.
3
2592100 .cm
C.
3
7776350 .m
D.
3
388150 .m
Câu 13: Tổng diện tích các mặt của hình tứ diện đều cạnh
a
bằng
A.
2
43a
.
B.
2
3
2
a
.
C.
2
23a
.
D.
2
3a
.
Câu 14: Cho tứ diện
BCD có cạnh
,,
A
BACAD
đôi một vuông góc và 
A
BACADa,
,,
M
NP
lần
lượt là trung điểm các cạnh
,,
B
CCDDB
. Thể tích của khối tứ diện
A
MNP bằng
A.
3
.
12
a
B.
3
.
24
a
C.
3
.
18
a
D.
3
.
4
a
Câu 15: Cho một mảnh giấy có hình dạng là tam giác nhọn
A
BC
có
10 cm, AB 16 cm,BC
14 cm.AC
Gọi
,,
M
NP
lần lượt là trung điểm của
,,.
A
BBCCA
Người ta
gấp mảnh giấy theo các đường
,,
M
NNPPM
sau đó dán trùng các cặp cạnh: AM và
;
B
M
BN
và
;CN
CP
và
AP
(các điểm
,,
A
BC
trùng nhau) để tạo thành một tứ diện (xem hình vẽ).
Thể tích của khối tứ diện nêu trên là
A.
3
20 11
cm .
3
B.
3
10 11
cm .
3
C.
3
280
cm .
3
D.
3
160 11
cm .
3
Câu 16: Cho khối chóp .S ABC có đáy là tam giác vuông tại .
B
Biết
3,BC a AB a
,
SA vuông góc
với đáy,
23SA a . Thể tích khối chóp
.SABC
là
A.
3
3.a B.
3
.a C.
3
3.a D.
3
3
.
3
a
Câu 17: Khối tứ diện đều thuộc loại
A.
3; 4
. B.
4;3
. C.
3; 3
. D.
3; 5
.
Câu 18: Có một khối gỗ có hình dạng là khối lăng trụ tam giác
.
A
BC A B C

. Khi đặt khối gỗ sao cho các
cạnh bên vuông góc với mặt bàn

P
, điểm
A
P
thì đoạn
BC
ở phía trên mặt bàn

P
và song song
với mặt bàn (xem hình vẽ).
Biết
100 cm, 40 cm, 30 cm, 60 .AA AB AC BC A AB


Người ta cắt, gọt khối gỗ trên bằng
các mặt phẳng vuông góc với các cạnh bên để thu được một lăng trụ đứng tam giác. Thể tích lớn nhất của
khối lăng đứng tạo thành gần với số nào sau đây nhất ?
Trang 3/3 - Mã đề thi 201
A.
3
37470 cm .
B.
3
35470 cm .
C.
3
36470 cm .
D.
3
38470 cm .
Câu 19: Cho khối lăng trụ .’’’
A
BC A B C có thể tích
V
. Điểm P thuộc cạnh
A
A' ,
Q
thuộc cạnh
B
B'
sao cho
1
4

PA QB'
PA' QB
và
R
là trung điểm của cạnh CC' . Thể tích khối chóp
R
.ABQP
theo V là
A.
4
3
V
. B.
2
3
V
. C.
1
2
V
. D.
1
3
V
.
Câu 20: Cho hình chóp tứ giác
.SABCD
có đáy
BCD
là hình vuông cạnh bằng
2a
. Tam giác
SAD
cân tại
S , mặt bên ( )SAD vuông góc với mặt phẳng đáy. Biết thể tích khối chóp .S ABCD bằng
3
4
3
a
,
điểm
N là trung điểm cạnh SB . Khoảng cách từ điểm N đến mặt phẳng
()SCD
bằng
A.
2
3
a
.
B.
4
3
a
.
C.
8
3
a
.
D.
3
4
a
.
Câu 21: Cho lăng trụ đứng
.
A
BC A B C

có đáy
A
BC là tam giác vuông cân tại
,2.CCB a
Biết rằng
góc giữa
BC
và
A
C
bằng
60
. Thể tích của khối lăng trụ đã cho bằng
A.
3
22 .a
B.
3
2.a
C.
3
2.a
D.
3
.a
Câu 22: Cho hình chóp .SABCD có đáy là hình chữ nhật,
,2.
A
BaAD a
Cạnh bên SA vuông góc
với đáy và
3.SA a
Điểm
P
là trung điểm của SC . Một mặt phẳng qua
A
P
cắt hai cạnh SB và SD lần
lượt tại
M
và
N
. Gọi
1
V là thể tích của khối chóp
.SAMPN
. Giá trị nhỏ nhất của
1
V bằng
A.
3
2
3
a
. B.
3
1
3
a
. C.
3
4
3
a
. D.
3
a
.
Câu 23: Cho lăng trụ tam giác .'' '
A
BC A B C có đáy
A
BC là tam giác vuông cân tại
A
, cạnh 22.AC
Biết
'
A
C tạo với mặt phẳng ( )
A
BC một góc
0
60 và '4AC . Thể tích khối chóp .''
B
ACC A bằng
A.
8
3
.
B.
83
3
.
C.
16 3
3
.
D.
16
3
.
Câu 24: Cho hình chóp tứ giác đều
.
SABCD
. Gọi
O
là tâm hình vuông
BCD
. Một mặt phẳng
()
bất
kì cắt các cạnh bên
,,,SA SB SC SD
và đoạn
SO
lần lượt tại các điểm
,,,,
M
NPQI
. Chọn đẳng thức đúng?
A.
1111
SM SP SN SQ
 . B.
11114
SM SP SN SQ SI
 .
C.
1111
SM SN SP SQ
. D.
1111
SM SQ SN SP
.
Câu 25: Cho lăng trụ tam giác .'' '
A
BC A B C . Một mặt phẳng ()
qua đường thẳng ''
A
B và trọng tâm
tam giác
A
BC , chia khối lăng trụ . ' ' '
A
BC A B C thành hai phần. Gọi
1
V là thể tích khối đa diện chứa đỉnh
C và
2
V là thể tích khối đa diện còn lại. Khi đó tỉ số
1
2
V
V
bằng
A.
1
2
17
10
V
V
. B.
1
2
19
8
V
V
. C.
1
2
10
17
V
V
. D.
1
2
8
19
V
V
.
-----------------------------------------------
----------- HẾT ----------
Tr
ang 1/21 - WordToan
SỞ GIÁO
DỤC VÀ ĐÀO TẠO
TRƯỜNG THPT NGỖ SỸ LIÊN-BẮC
GIANG
KIỂM-TRA-45 PHÚT-HK1
NĂM HỌC 2018 – 2019
Môn: Toán
Thời gian: 45 phút (Không kể thời gian phát đề)
Câu 1: Khối chóp tam giác đều
.S A
BC
có cạnh đáy bằng
a
, cạnh bên bằng 3a có thể tích bằng
A.
3
3
a
. B.
3
2
6
a
. C.
3
2
2
a
. D.
3
6
2
a
.
Câu 2: Cho
khối chóp
.S A
BC
có đáy là tam giác đều cạnh
a
. Biết 3SC a , hai mặt phẳng
( )S
AB
và
( )S
AC
cùng vuông góc với đáy. Thể tích khối chóp
.S A
BC
bằng
A.
3
3
2
a
. B.
3
3
4
a
. C.
3
2 6
9
a
. D.
3
6
12
a
.
Câu 3: S
ố mặt phẳng đối xứng của hình lập phương là
A.
7
. B.
3
. C.
6
. D.
9
.
Câu 4: S
ố hình đa diện lồi trong các hình dưới đây là
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 5: Cho hình chóp
.S ABCD
có đ
áy là hình vuông cạnh
a
,
SA
vuôn
g góc với đáy,
SD
tạo v
ới mặt
phẳng
ABC
D
một góc bẳng
60
. Thể tích của khối chóp
.S ABCD
bẳng
A.
3
3
3
a
. B.
3
a
. C.
3
3
9
a
. D.
3
3
a
.
Câu 6: Sô
 măt đôi xưng cua hinh chop tư giac đêu la
A.
2
. B.
4
. C.
8
. D.
6
.
Câu 7: Cho
khôi chop
.S A
BCD
co
đay la hinh vuông canh
a
. Biê
t tam giac
SA
B
đêu
va năm trong
măt phăng vuông goc vơi đay. Thê tich khôi chop
.S A
BCD
băn
g
A.
3
3
2
a
. B.
3
3
a
. C.
3
3
6
a
. D.
3
a
.
Câu 8: Cho
khối chóp
.S AB
CD
có đ
áy là hình chữ nhật. Biết
2 2A
C AB a
,
SA
vuôn
g góc với
đáy,
2SA a
. Thể tích khối chóp
.S A
BCD
là
A.
3
5
3
a
. B.
3
6a
. C.
3
6
3
a
. D.
3
15
3
a
.
Câu 9: Số đỉnh của hình mười hai mặt đều là
A.
12
. B.
30
. C.
20
. D.
16
.
Tran
g 2/21 – Diễn đàn giáo viên Toán
Câu 10: K
hối đa diện đều loại
4;3
là
A. Kh
ối chóp tứ giác đều. B. Khối bát diện đều.
C. Khối tứ diện đều. D. Khối lập phương.
Câu 11: Kim tự tháp Kê - ốp ở Ai cập được xây dựng khoảng năm 2500 trước công nguyên. Kim tự
tháp này là một khối chóp tứ giác đều có chiều cao
147 m
, c
ạnh đáy là
23
0 m
.
Thể tích của nó
bằng
A.
3
25921
00 .m B.
3
25921
00 .cm C.
3
777635
0 .m D.
3
388150
.m
Câu 12: Tổng diện tích các mặt của hình tứ diện đều cạnh
a
bằng
A.
2
4 3a . B.
2
3
2
a
. C.
2
2 3a . D.
2
3a .
Câu 13: Cho tứ diện
AB
CD
có c
ạnh
, ,A
B AC AD
đôi m
ột vuông góc và
AB
AC AD a
,
, ,M
N P
lần
lượt là trung điểm các cạnh
, ,BC CD DB
.
Thể tích của khối tứ diện
AM
NP
bằng
A.
3
.
12
a
B.
3
.
24
a
C.
3
.
18
a
D.
3
.
4
a
Câu 14: Cho một mảnh giấy có hình dạng là tam giác nhọn
ABC
có
10
cm, AB 16 cm,BC
14
cm.AC
Gọi
, ,M N P
lần
lượt là trung điểm của
, , .AB BC CA
Ng
ười ta gấp mảnh giấy theo
các đường
, ,MN
NP PM
sa
u đó dán trùng các cặp cạnh:
AM
và
;BM
BN
và
;CN
CP
và
AP
(các
điểm
, ,A
B C
trù
ng nhau) để tạo thành một tứ diện (xem hình vẽ).
Thể tích của khối tứ diện nêu trên là
A.
3
20 11
cm .
3
B.
3
10 1
1
cm .
3
C.
3
280
cm .
3
D.
3
160
11
cm .
3
Câu 15: Cho
khối chóp
.S A
BC
có
đáy là tam giác vuông tại
.B
Biết
3,B
C a AB a
,
SA
vuông
góc
với đáy,
2 3S
A a . Thể tích khối chóp
.S A
BC
là
A.
3
3 .a
B.
3
.a
C.
3
3.a D.
3
3
.
3
a
Câu 16: Khối tứ diện đều thuộc loại
A.
3;
4
. B.
4;
3
. C.
3;
3
. D.
3;
5
.
Câu 17: Có một khối gỗ có hình dạng là khối lăng trụ tam giác
.AB
C A B C
. K
hi đặt khối gỗ sao cho
các cạnh bên vuông góc với mặt bàn
P
, đi
ểm
A P
thì
đoạn
BC
ở phí
a trên mặt bàn
P
và
song song với mặt bàn (xem hình vẽ).
T
rang 3/21 - WordToan
Biết
100 cm, 40 cm, 30 cm, 60 .AA AB AC BC A AB
N
gười ta cắt, gọt khối gỗ tr
ên
bằ
ng các mặt phẳng vuông góc với các cạnh bên để thu được một lăng trụ đứng tam giác. Thể
tích lớn nhất của khối lăng đứng tạo thành gần với số nào sau đây nhất?
A.
3
37470 cm
. B.
3
35470 cm
. C.
3
36470 cm
. D.
3
38470 cm
.
Câu
18: Cho khối lăng trụ
.A
BC A B C
có thể tích
V
. Điểm
P
thuộc cạnh
A
A
,
Q
thuộc cạnh
BB
sao cho
1
4
PA
QB
PA QB
và
R
là trung điểm của cạnh
C
C
. Thể tích khối chóp
.R
ABQP
theo
V
l
à:
A.
4
3
V
. B.
2
3
V
. C
.
1
2
V
. D.
1
3
V
.
Câu
19: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng
2a
.
Tam giác SAD
cân tại S, mặt bên
S
AD
vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng
3
4
3
a
,
điểm N là trung điểm của cạnh SB. Khoảng cách từ điểm N đến mặt phẳng
S
CD
bằng
A.
2
3
a
. B.
4
3
a
. C.
8
3
a
. D.
3
4
a
.
Câu
20: Cho lăng trụ đứng
.A
BC A B C
c
ó đáy
ABC
l
à tam giác vuông cân tại
,
2 .C CB a
Biết
rằng
góc giữa
B
C
v
à
A
C
bằng
60
.
Thể tích của khối lăng trụ đã cho bằng
A.
3
2
2 .a
B.
3
2
.a
C
.
3
2
.a
D.
3
.a
Câu
21: Cho hình chóp
.S
ABCD
có
đáy là hình chữ nhật,
,
2 .AB a AD a
Cạnh
bên
S
A
v
uông góc
với đáy và
3
.SA a
Điểm
P
là
trung điểm của
S
C
.
Một mặt phẳng qua
A
P
cắt
hai cạnh
S
B
và
S
D
lần lượt tại
M
và
N
. Gọi
1
V là thể tích của khối chóp
.S
AMPN
. Giá trị nhỏ nhất của
1
V bằng
A.
3
2
3
a
. B.
3
1
3
a
. C.
3
4
3
a
. D.
3
a
.
Câu
22: Cho lăng trụ tam giác
.
' ' 'ABC A B C
có
đáy
A
BC
l
à tam giác vuông cân tại
A
,
cạnh
2
2.AC
Biết
'AC
tạ
o với mặt phẳng
(
)ABC
một
góc
0
6
0
v
à
' 4AC
.
Thể tích khối chóp
.
' 'B ACC A
bằ
ng
A.
8
3
. B.
8
3
3
. C.
1
6 3
3
. D.
1
6
3
.
Trang 4/
21 – Diễn đàn giáo viên Toán
Câu 23: Cho lăng trụ tam giác
. ' ' 'AB
C A B C
có đáy
ABC
là tam giác vuông cân tại
A
, cạnh
2 2.
AC Biết
'AC
tạo với
mặt phẳng
( )ABC
một góc
0
60
và
' 4
AC
. Th
ể tích khối chóp
. ' 'B A
CC A
bằng
A.
8
3
. B.
8 3
3
. C.
16 3
3
. D.
16
3
.
Câu 24: Cho hì
nh chóp tứ giác đều
.
S ABC
D
. Gọi
O
là tâm hì
nh vuông
ABCD
. Mộ
t mặt phẳng
( )
bất
kì cắ
t các cạnh bên
, , ,SA
SB SC SD
và đ
oạn
SO
lần lượ
t tại các điểm
, , , ,M
N P Q I
. Chọ
n đẳng
thức đúng?
A.
1 1 1 1
S
M SP SN SQ
. B.
1 1 1 1
4
SM SP SN SQ SI
.
C.
1 1 1 1
S
M SN SP SQ
. D.
1 1 1 1
S
M SQ SN SP
.
Câu 25: Cho lăng trụ tam giác
. ' ' 'ABC A B C
. Một
mặt phẳng
( )
qua đườ
ng thẳng
' 'A B
và tr
ọng tâm
tam giác
ABC
, chia
khối lăng trụ
. ' ' 'A
BC A B C
thành h
ai phần. Gọi
1
V
là t
hể tích khối đa diện
chứa đỉnh
C
và
2
V
là thể tí
ch khối đa diện còn lại. Khi đó tỉ số
1
2
V
V
bằng
A.
1
2
17
10
V
V
. B.
1
2
19
8
V
V
. C.
1
2
10
17
V
V
. D.
1
2
8
19
V
V
.
BẢNG ĐÁP ÁN
1.B 2.D
3.D 4.B 5.A 6.B 7.C 8.C 9.C 10.D
11.A 12.D
13.B 14.A 15.B 16.C 17.A 18.D 19.A 20.C
21.A 22.B 23.A
24.A 25.B
LỜI GIẢI CHI TIẾT
Câu 1. Khối chóp tam giác đều
.
S ABC
có c
ạnh đáy bằng
a
, cạnh bên
bằng
3a
có t
hể tích bằng
A.
3
3
a
. B.
3
2
6
a
. C.
3
2
2
a
. D.
3
6
2
a
.
Lời giải
Chọn B
Ta gọi
M
là trung
điểm
BC
,
H
là tr
ọng tâm tam giác
ABC
suy ra
H
là hình
chiếu vuông
góc của
S
trên
ABC
. Ta
có diện tích đáy khối chóp là
2
3
4
ABC
a
S
.
S
A
C
B
H
M
Tr
ang 5/21 - WordToan
Ta có
2 3
3
3
a
AH AM
suy
ra
2 2
SH SA AH
8
3
a
.
Do đó
1
.
3
SABC ABC
V SH
S
2 3
1 8
3 2
. .
3 3 4 6
a a
a
.
Câu 2. Cho khối chóp
.S A
BC
có đáy
là tam giác đều cạnh
a
. Bi
ết
3SC a ,
hai mặt phẳng
( )SAB
và
( )S
AC
cùng vuông
góc với đáy. Thể tích khối chóp
.S A
BC
bằng
A.
3
3
2
a
. B.
3
3
4
a
. C.
3
2 6
9
a
. D.
3
6
12
a
.
Lời giả
i
Chọn D
Ta có
diện tích đáy khối chóp
2
3
4
ABC
a
S
.
Vì mặt phẳng
( )S
AB
và
( )S
AC
cùng vuông
góc
với đáy
SA
ABC
suy ra
SA
là
đường cao của khối chóp và
2 2
SA SC AC
2a
.
Do đó
2 3
1 1 3 6
. . . 2.
3 3 4 12
SABC AB
C
a a
V SA S a
.
Câu 3.
Số mặt phẳng đối xứng của hình lập phương là
A.
7
. B.
3
. C.
6
. D.
9
.
Lời giả
i
Chọn D
Trang
6/21 – Diễn đàn giáo viên Toán
Câu 4. S
ố hình đa diện lồi trong các hình dưới đây là
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn B
Quan sát
bốn hình trên ta thấy chỉ có một hình thứ tư từ trái qua là hình đa diện lồi vì lấy bất kỳ
hai điểm nào thì đoạn thẳng nối hai điểm đó nằm trong khối đa diện.
Vậy chỉ có một đa diện lồi.
Câu 5. Cho hình chóp
.S AB
CD
có đá
y là hình vuông cạnh
a
,
SA
vuông
góc với đáy,
SD
tạo vớ
i mặt
phẳng
ABCD
một g
óc bẳng
60
. T
hể tích của khối chóp
.S AB
CD
bẳng
A.
3
3
3
a
. B.
3
a
. C.
3
3
9
a
. D.
3
3
a
.
Lời giải
Chọn A
T
rang 7/21 - WordToan
A
D
là
hình chiếu vuông góc của
SD
lên
mặt phẳng
ABCD
,
, 60SD ABCD SD AD SDA
.
.
tan 60 3SA AD a .
Thể tích là
3
2
1
3
. . 3
3 3
a
V a a
.
Câu
6. Sô măt đôi xưng cua hinh chop tư giac đêu la
A.
2
. B.
4
. C
.
8
. D.
6
.
Lơi
giai
Chon B
Hi
nh chop tư giac đêu co bôn măt phăng đôi xưng.
Câu 7. Cho khôi chop
.S
ABCD
co đay la hinh vuông canh
a
. Biêt tam giac
S
AB
đêu va năm trong
măt phăng vuông goc vơi đay. Thê tich khôi chop
.S
ABCD
bă
ng
A.
3
3
2
a
. B.
3
3
a
. C.
3
3
6
a
. D.
3
a
.
Lơi
giai
Cho
n C.
6
0°
A
B
D
C
S
Q
M
P
N
O
Q
M
P
N
O
Q
M
P
N
O
Q
M
P
N
O
A
B
D
C
S
S
C
D
B
A
S
C
D
B
A
S
C
D
B
A
A
D
B
C
S
H
Tran
g 8/21 – Diễn đàn giáo viên Toán
Ke
,SH AB
H AB SH ABCD
,
H
la
 trung điêm cua
AB
.
2 2
2 2 2 2
3
4 4
a
a
SH SA AH a
3
2
a
SH
.
2
ABC
D
S a
3
.
1 3
.
.
3 6
S ABC
D ABCD
a
V SH
S
.
Câu 8. Cho khối chóp
.S AB
CD
có đ
áy là hình chữ nhật. Biết
2 2A
C AB a
,
SA
vuôn
g góc với
đáy,
2SA a
. Th
ể tích khối chóp
.S A
BCD
là
A.
3
5
3
a
. B.
3
6a . C.
3
6
3
a
. D.
3
15
3
a
.
Lời giả
i
Chọn C
Ta có
2 2A
C AB a
2AC a
AB a
2 2
BC AC
AB
3a
.
Suy
ra
2
. 3
ABCD
S AB
BC a
.
Khi
đó
.
1
.
3
S ABCD ABCD
V SA
S
2
1
. 2. 3
3
a a
3
6
3
a
.
Vậy
3
.
6
3
S A
BCD
a
V
.
Câu 9.
Số đỉnh của hình mười hai mặt đều là
A.
12
. B.
30
. C.
20
. D.
16
.
Lời giả
i
Chọn C
Số đỉnh c
ủa hình mười hai mặt đều là 20 đỉnh.
Câu 10. Khối đa diện đều loại
4;
3
là
A. Kh
ối chóp tứ giác đều. B. Khối bát diện đều.
Tran
g 9/21 - WordToan
C. Khối
tứ diện đều. D. Khối lập phương.
Lời giải
Chọn D
Khố
i đa diện đều loại
4;3
là khối đa diện đều mà mỗi mặt là một đa giác đều có 4 cạnh và
mỗi đỉnh là đỉnh chung của đúng 3 cạnh chọn D.
Câu 11. Kim tự tháp Kê - ốp ở Ai cập được xây dựng khoảng năm 2500 trước công nguyên. Kim tự
tháp này là một khối chóp tứ giác đều có chiều cao
147 m
, cạnh
đáy là
230 m
. T
hể tích của nó
bằng
A.
3
2592100
.m
B.
3
2592100
.cm
C.
3
7776350
.m
D.
3
388150 .m
Lời giải
Chọn A
Giả sử kim tự tháp này là một khối chóp tứ giác đều
S.A
BCD
có chiều
cao
147SO m
, cạnh
đáy
là
230A
B m
2 2 3
1 1 1
.
. .147.230 2592100
3 3 3
V B h SO AB m
chọn
A.
Câu 12. Tổng diện tích các mặt của hình tứ diện đều cạnh
a
bằng
A.
2
4 3a
. B.
2
3
2
a
. C.
2
2 3a
. D.
2
3a
.
Lời giải
Chọn D
2
2
3
4 4. 3
4
ABC ACD
BCD ABD ABC
a
S S S
S S a
.
Câu 13. Cho
tứ diện
ABC
D
có cạnh
, ,AB
AC AD
đôi một
vuông góc và
AB A
C AD a
,
, ,M N
P
lần l
ượt là trung điểm các cạnh
, ,BC
CD DB
. T
hể tích của khối tứ diện
AMN
P
bằng
A.
3
.
12
a
B.
3
.
24
a
C.
3
.
18
a
D.
3
.
4
a
Lời giải
Chọn B
B
A
C
D
A
D
C
B
S
O
Trang
10/21 – Diễn đàn giáo viên Toán
3
1 1
. .
6 6
ABCD
V AB AC
AD a
.
MNP
DBC ∽
(do
1
2
MN NP
PM
DB BC CD
) theo tỉ số đồng dạng là
1
2
k
2
1
4
MNP
DBC
S
k
S
.
3
3
. .
1 1
. .
4 6 24
MNP
S MNP A B
CD
DBC
S
a
V V a
S
.
Câu 14. Cho một mảnh giấy có hình dạng là tam giác nhọn
ABC
có
10
cm, AB 16 cm,BC
14 cm.AC
Gọi
, ,M N
P
lần l
ượt là trung điểm của
, , .A
B BC CA
Ngư
ời ta gấp mảnh giấy theo
các đường
, ,MN NP PM
sau
đó dán trùng các cặp cạnh:
AM
và
;BM
BN
và
;CN
CP
và
AP
(các
điểm
, ,A B
C
trùng
nhau) để tạo thành một tứ diện (xem hình vẽ).
Thể tích của khối tứ diện nêu trên là
A.
3
20 11
cm
.
3
B.
3
10 11
cm .
3
C.
3
280
cm
.
3
D.
3
160 11
c
m .
3
Lời giải
Chọn A
Xét bài
toán: Cho tứ diện
ABC
D
, có
; ; AB CD a AD BC b AC BD c
. T
hể tích
của khối tứ diện
ABC
D
là
2 2 2
2 2 2 2 2 2
1
.
6 2
ABCD
V a b
c a b c a b c
A
P
N
M
D
C
B
T
rang 11/21 - WordToan
Dựng tứ diện
A
PRQ
sao cho
,
,B C D
lần lượt là trung điểm của đoạn
,
, .QR RP PQ
Ta có:
1
2
C
D AB QR AQR
v
uông tại A
2
2 2
4
.AQ AR a
Tươ
ng tự,
A
RP
vuôn
g tại A
2
2 2
4AR
AP b
;
APQ
v
uông tại A
2
2 2
4AP
AQ c
.
Xét
2
2 2
2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2
2 2 2
2( )
4 2( )
4 2( ) 2( )
4 2( )
2( )
AQ a b c
AQ AR a AQ a b c
AR AP b AR a b c AR a b c
AP AQ c AP a b c
AP a b c
Ta
có:
1
1 1
. . .
4 4 6
A
BCD AQRP
B
CD CBR QDB PDC V V AP AQ AR
2 2 2 2 2 2 2 2 2
1
6
2
ABC
D
V
a b c a b c a b c
.
Áp
dụng, ta có:
5
; 8 ; 7 .AM NP cm AN MP cm AP MN cm
2 2 2 2 2 2 2 2 2
1
20 11
.
3
6 2
AM
NP
V
a b c a b c a b c
Câu 15. Cho khối chóp
.S
ABC
có
đáy là tam giác vuông tại
.B
Biết
3,BC a AB a
,
S
A
v
uông góc
với đáy,
2 3SA a
. Thể tích khối chóp
.S
ABC
l
à
A.
3
3
.a
B.
3
.a
C
.
3
3
.a D.
3
3
.
3
a
Lời
giải
Chọn B
Ta
có:
2
3
.
2
BAC
a
B
S
Do
3
.
2
3 .
S ABC
S
A ABC h SA a V a
Câu
16. Khối tứ diện đều thuộc loại
Tr
ang 12/21 – Diễn đàn giáo viên Toán
A.
3;4
. B.
4;3
. C.
3;3
. D.
3;5
.
Lời gi
ải
Chọn
C
Câu 17. Có một khối gỗ có hình dạng là khối lăng trụ tam giác
.A
BC A B C
. Khi đặt khối gỗ sao cho
các cạnh bên vuông góc với mặt bàn
P
,
điểm
A
P
t
hì đoạn
B
C
ở
phía trên mặt bàn
P
v
à song song với mặt bàn (xem hình vẽ).
Biết
100 cm, 40 cm, 30 cm, 60 .AA AB AC BC A AB
N
gười ta cắt, gọt khối gỗ tr
ên
bằ
ng các mặt phẳng vuông góc với các cạnh bên để thu được một lăng trụ đứng tam giác. Thể
tích lớn nhất của khối lăng đứng tạo thành gần với số nào sau đây nhất?
A.
3
37470 cm
. B.
3
35470 cm
. C
.
3
36470 cm
. D.
3
38470 cm
.
Lời gi
ải
Chọn
A
Thể tích khối lăng trụ đứng sau khi cắt, gọt lớn nhất khi ta cắt bởi các mặt phẳng qua
A
,
B
v
à
vuông góc với
AA
, cắt
,
,BB CC AA
tại
1
1 1
,
,B C A .
Các tam giác
1
A
AB và
1
A
AC là các tam giác vuông bằng nhau.
Ta có:
1
1
.
sin 40.sin 60 20 3A B A C AB A AB
(cm)
1
.
cos60 20AA AB (cm).
Chiều cao khối lăng trụ (sau khi cắt, gọt):
1
100
20 80h AA AA
(cm).
Diện tích đáy lăng trụ (sau khi cắt, gọt):
1
75 39
A
BC
S S p p a p b p c
.
(
P
)
B
1
C
1
A
1
C'
B
'
A
B
C
A
'
T
rang 13/21 - WordToan
Thể
tích khối lăng trụ đứng:
8
0.75 39 6000 39 37469,98799V Sh
3
c
m
.
Câu
18. Cho khối lăng trụ
.A
BC A B C
có
thể tích
V
.
Điểm
P
thuộc
cạnh
A
A
,
Q
thuộc
cạnh
BB
sao
cho
1
4
PA
QB
PA QB
và
R
l
à trung điểm của cạnh
C
C
.
Thể tích khối chóp
.R
ABQP
theo
V
l
à:
A.
4
3
V
. B.
2
3
V
. C
.
1
2
V
. D.
1
3
V
.
Lời gi
ải
Chọn D
Ta có
.R
ABA B ABCR RA B C
V
V V V
.
Có
.
1
1 1 2
. .
2 3 6 3
RABC
RA B C R ABA B
V
V V V V V
.
Dễ dàng chứng minh được
A
BQP
v
à
A
B QP
là
hai tứ giác bằng nhau.
.
.ABQP A B QP R ABQP R A B QP
S
S V V
(2
khối chóp có cùng chiều cao, cùng diện tích đáy)
.
. .
1
1
2 3
R
ABQP R A B QP R ABA B
V
V V V
.
Câu
19. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng
2a
.
Tam giác SAD
cân tại S, mặt bên
SAD
v
uông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằ
ng
3
4
3
a
, điểm N là trung điểm của cạnh SB. Khoảng cách từ điểm N đến mặt phẳng
S
CD
bằng
A.
2
3
a
. B.
4
3
a
. C
.
8
3
a
. D.
3
4
a
.
Lời
giải
Chọn
A
R
P
Q
C'
A
'
A
C
B
B
'
Q
P
B'
A
B
A'
Tran
g 14/21 – Diễn đàn giáo viên Toán
Gọi H là
trung điểm của AD. Vì
SA
D
cân
tại
.S S
H AD
Ta có
.
.
3
ABC
D
S ABCD
SAD A
BCD AD
SH S
SH ABCD V
SAD ABCD
Câu 20. Cho lăng trụ đứng
.AB
C A B C
có
đáy
ABC
là
tam giác vuông cân tại
, 2 .C CB a
Biết rằ
ng
góc giữa
B C
và
AC
bằng
60
. Thể tích c
ủa khối lăng trụ đã cho bằng
A.
3
2 2
.a
B.
3
2 .a
C.
3
2 .a
D.
3
.a
Lời giả
i
Chọn C
Trong m
ặt phẳng
( )A
BC
, lấy điểm
D
sao cho
AC
BD
là hình vuông. Khi đó ta có
ADB
C
là
hình bình hành
AC D
B
góc giữa
B C
và
AC
bằng góc giữa
B C
và
DB
.
Xét hai tam giác vuông
B B
C
,
B B
D
ta có
BB
chung và
BD BC
suy ra
B BC
=
B B
D
Suy ra
B DC
là tam giác cân tại
B
.
Ta có
ABC
vuông
cân tại
C
,
2BC
a
su
y ra
2AC
a
và
2AB a
,
IA IB a
,
2DC a
Trường hợp 1:
0
120DB C
Khi đó
0
.t
an30
3
a
B I a
<
IB a
(vô lý)
N
H
C
A
B
D
S
K
I
D
C
B
B'
C'
A'
A
Tr
ang 15/21 - WordToan
Trường hợp 2:
0
60DB C
khi đó
B DC
đều cạnh
2a
.
Khi đó ta có
3B I
a
,
2 2
3 2B
B a a a
Thể tíc
h lăng trụ đã cho
2
3
.
1
2 2
3.
2
AB
C A B C
V a
a a
Câu 21.
Cho hình chóp
.S A
BCD
có đáy
là hình chữ nhật,
, 2 .AB a AD a
Cạnh b
ên
SA
vuôn
g góc
với đáy và
3 .S
A a
Điểm
P
là t
rung điểm của
SC
.
Một mặt phẳng qua
AP
cắt hai
cạnh
SB
và
SD
lần
lượt tại
M
và
N
. G
ọi
1
V là
thể tích của khối chóp
.S A
MPN
.
Giá trị nhỏ nhất của
1
V bằng
A.
3
2
3
a
. B.
3
1
3
a
. C.
3
4
3
a
. D.
3
a
.
Lời giả
i
Chọn A
Cách
xác định mặt phẳng qua
AP
cắt hai cạnh
SB
,
SD
như hình vẽ. Gọi
O
là giao điểm của
hai đường chéo hình chữ nhật
ABC
D
và
I
là
giao điểm
AP
và
MN
.
Ta có
3
.
1 1
.
. .3 . .2 2
3 3
S A
BCD
V AS AB AD a a a a
,
Áp d
ụng công thức tỉ số thể tích ta có
.
.
. .
1
.
. . 2
S AM
P
S ABC
V
SA SM
SP SM
V SA SB SC SC
;
.
.
. .
1
.
. . 2
S AN
P
S ADC
V
SA SN
SP SN
V SA SD SC SD
Suy ra
. .
.
4
S A
MP S ABCD
SM
V V
SB
,
. .
.
4
S A
NP S ABCD
SN
V V
SD
. Khi đó
3
1 . .
.
2
S A
MP S ANP
SM
SN a
V V V
SB SD
3a
a
2a
N
I
P
O
C
A
D
S
B
M
Tr
ang 16/21 – Diễn đàn giáo viên Toán
Ta
có
I
l
à trọng tâm tam giác
S
AC
n
ên
2
3
S
I
SO
Từ
,B
D
lầ
n lượt kẻ các đường thẳng song song với
M
N
cắ
t
SO
tại
,E
F
. K
hi đó hai tam giác
OED
OFB
(g.c.g) suy ra
OE
OF
Ta
có
SB SF SO OF
SM SI SI
;
SD SE SO OE
SN SI SI
Từ đó
suy ra
2
3
SB SD SO
SM SN SI
suy
ra
4
4
3
SM SN
SB SD
SB SD
SM SN
.
Dấu bằng xảy ra khi
SM
SN
MN BD
SB SD
.
Vậy
3
3
3
1
4
2
.
2 3 2 3
SM SN a a
V a
SB SD
.
Giá trị nhỏ nhất của
1
V bằng
3
2
3
a
.
Câu
22. Cho lăng trụ tam giác
.
' ' 'ABC A B C
có đáy
A
BC
là tam giác vuông cân tại
A
, cạnh
2
2.AC
Biết
'AC
tạ
o với mặt phẳng
( )ABC
một
góc
0
60
v
à
'
4AC
.
Thể tích khối chóp
.
' 'B ACC A
bằ
ng
A.
8
3
. B.
8
3
3
. C
.
1
6 3
3
. D.
1
6
3
.
Lời
giải
Chọn B
F
E
N
O
S
B
D
I
M
T
rang 17/21 - WordToan
Gọi
hình chiếu vuông góc của
'C
l
ên
AB
C
là
H
.
Suy
ra
0
'
, ', ' 60AC ABC AC AH HAC
.
Trong
'H
AC
vuông tại
H
và
0
' 60HAC suy ra
'
'
3 2 3
2
AC
C H
.
Diện tích
AB
C
l
à:
2
4
2
ABC
A
C
S
.
Thể
tích của hình chóp
.
' 'B ACC A
là
.
' ' '
. ' '
4.2
3 8 3
3 3 3
AB
C A B C
B ACC A
V
V
.
Câu 23. Cho lăng trụ tam giác
.
' ' 'ABC A B C
có
đáy
A
BC
l
à tam giác vuông cân tại
A
,
cạnh
2 2.AC
Biết
'AC
tạo với mặt phẳng
( )ABC
một góc
0
60
và
'
4AC
. Thể tích khối chóp
.
' 'B ACC A
bằ
ng
A.
8
3
. B.
8
3
3
. C
.
1
6 3
3
. D.
16
3
.
Lời giải
Chọn B
4
2 2
A'
B'
C
A
B
H
C'
Tr
ang 18/21 – Diễn đàn giáo viên Toán
Gọi
hình chiếu vuông góc của
'C
l
ên
AB
C
là
H
.
Suy
ra
0
'
, ', ' 60AC ABC AC AH HAC
.
Trong
'H
AC
vuông tại
H
và
0
' 60HAC suy ra
'
'
3 2 3
2
AC
C H
.
Diện tích
AB
C
l
à:
2
4
2
ABC
A
C
S
.
Thể
tích của hình chóp
.
' 'B ACC A
là
.
' ' '
. ' '
4.2
3 8 3
3 3 3
AB
C A B C
B ACC A
V
V
.
Câu 24: Cho hình chóp tứ giác đều
.S
ABCD
.
Gọi
O
l
à tâm hình vuông
A
BCD
. Một
mặt phẳng
(
)
bất
kì cắt các cạnh bên
,
, ,SA SB SC SD
v
à đoạn
S
O
lần
lượt tại các điểm
,
, , ,M N P Q I
.
Chọn đẳng
thức đúng?
A.
1
1 1 1
SM SP SN SQ
. B.
1
1 1 1 4
SM SP SN SQ SI
.
C.
1
1 1 1
SM SN SP SQ
. D.
1
1 1 1
SM SQ SN SP
.
Lời
giải
Chọn A
4
2 2
A'
B'
C
A
B
H
C'
T
rang 19/21 - WordToan
Theo
công thức tính tỉ lệ thể tích ta có:
DS
A SC SB S
SM SP SN SQ
.
*
Vì
.S
ABCD
l
à hình chóp tứ giác đều nên ta có
S
A SB SC SD
.
Do
đó
1 1 1 1
SM SP SN SQ
.
Chú ý: trong bài tập trên, thầy đã sử dụng công thức tỉ lệ thể tích của hình chóp tứ giác có đáy
l
à hình bình hành, khi tiến hành giải tự luận, các em cần chứng minh công thức
*
t
rước khi sử
dụng.
Câu 25. Cho lăng trụ tam giác
.
' ' 'ABC A B C
.
Một mặt phẳng
(
)
qua
đường thẳng
'
'A B
v
à trọng tâm
tam giác
A
BC
,
chia khối lăng trụ
.
' ' 'ABC A B C
t
hành hai phần. Gọi
1
V l
à thể tích khối đa diện
chứa đỉnh
C
v
à
2
V là thể tích khối đa diện còn lại. Khi đó tỉ số
1
2
V
V
bằng
A.
1
2
1
7
10
V
V
. B.
1
2
1
9
8
V
V
. C.
1
2
1
0
17
V
V
. D.
1
2
8
1
9
V
V
.
Lờ
i giải
Chọn
B
M
I
O
C
A
B
D
S
Q
P
N
Tr
ang 20/21 – Diễn đàn giáo viên Toán
Gọi
G
l
à trọng tâm của tam giác
ABC
.
Ta
có:
/
/
/ /
G ABC
AB A B
A B MN AB
AB ABC
ABC MN
.
Gọi
A M B N CC K
.
Gọi
,H
F
lần
lượt là hình chiếu vuông góc của
,M
K
tr
ên mp
ABC
.
Xét
:
Tam giác
A
BC
,
ta có:
2
/
/
3
CM CN MN
MN AB
CA CB AB
;
Ta
m giác
K
A B
,
ta có:
2
/
/
3
KM KN MN
MN A B
KA KB A B
v
ì
/
/ ,A B AB A B AB
;
Ta
m giác
K
A C
, ta có:
2
/
/
' 3
KM KC CM
CM A C
KA KC A C
vì
/
/ ,A C AC A C AC
;
Tam giác
K
A F
,
ta có:
1
/
/ 3
' 3
A M A H MH
MH KF KF MH
A K A F KF
.
Ta có:
.
.
2 2 2 8
. . . .
3 3 3 27
K MNC
K A B C
V
KM
KN KC
V KA KC KC
.
. .
8
.
27
K MNC K A B C
V
V
.
Gọi
.AB
C A B C
V
V
.
T
rang 21/21 - WordToan
Mặt
khác, ta có:
.
1
1
. . .3. .
3 3
K
A B C A B C A B C
V
KF S MH S V
. 1
8 8 19
. .
2
7 27 27
K MNC
V V V V V V
.
Do đó,
2
1
1
9 8
27 27
V V V V V V
.
Vậy
, ta có:
1
2
19
8
V
V
.
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD & ĐT BẮC GIANG
ĐỀ KIỂM TRA 45 PHÚT NĂM HỌC 2018 – 2019 TR
ƯỜNG THPT NGÔ SĨ LIÊN MÔN : HÌNH HỌC 12
(25 câu trắc nghiệm) Mã đề thi 201
Họ và tên học sinh:........................................................Lớp: …………………
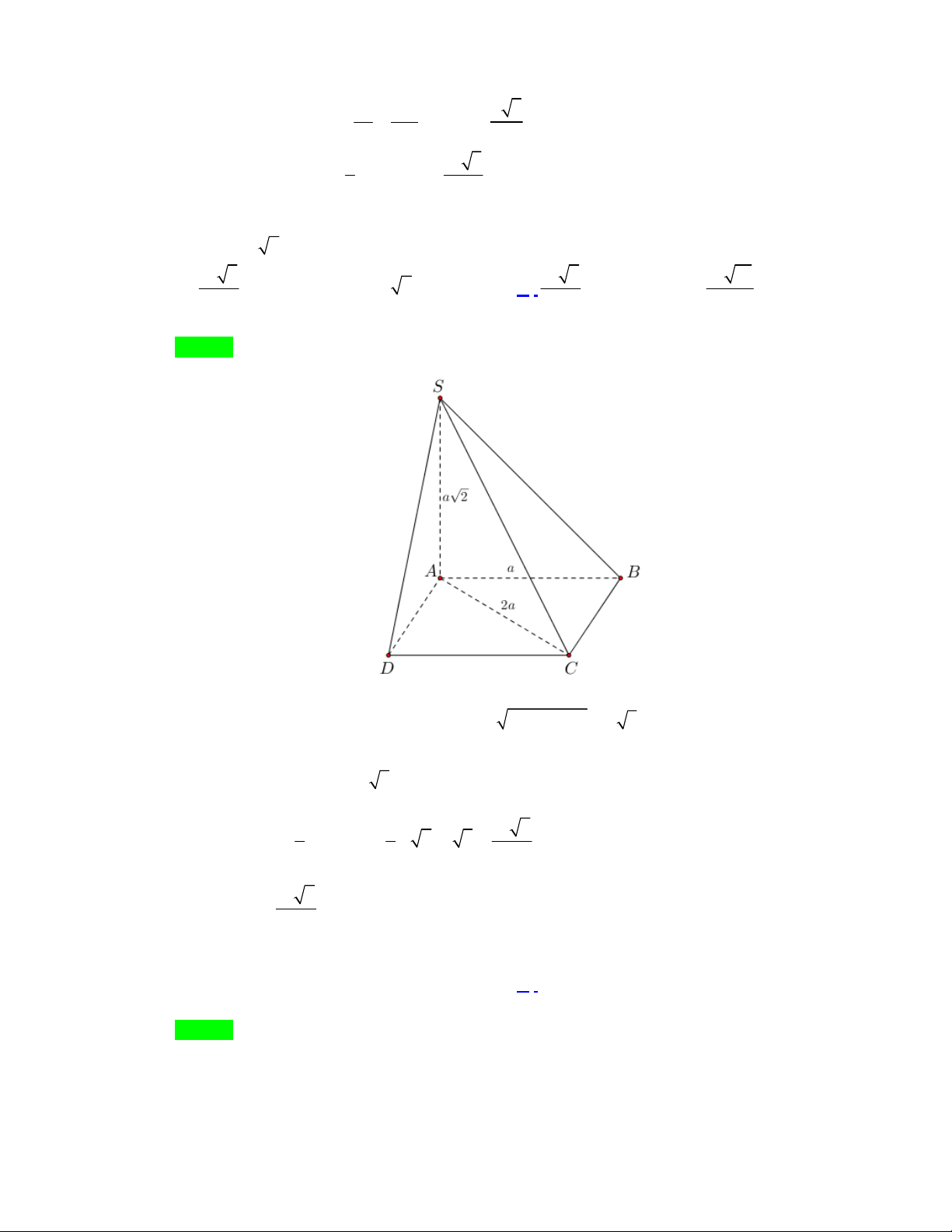
Câu 1: Khối chóp tam giác đều S.ABC có cạnh đáy bằng a , cạnh bên bằng a 3 có thể tích bằng 3 a 3 a 2 3 a 2 3 a 6 A. . B. . C. . D. . 3 6 2 2
Câu 2: Cho khối chóp S.ABC có đáy là tam giác đều cạnh a . Biết SC a 3 , hai mặt phẳng (SAB) và
(SAC) cùng vuông góc với đáy. Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 3 2a 6 3 a 6 A. . B. . C. . D. . 2 4 9 12
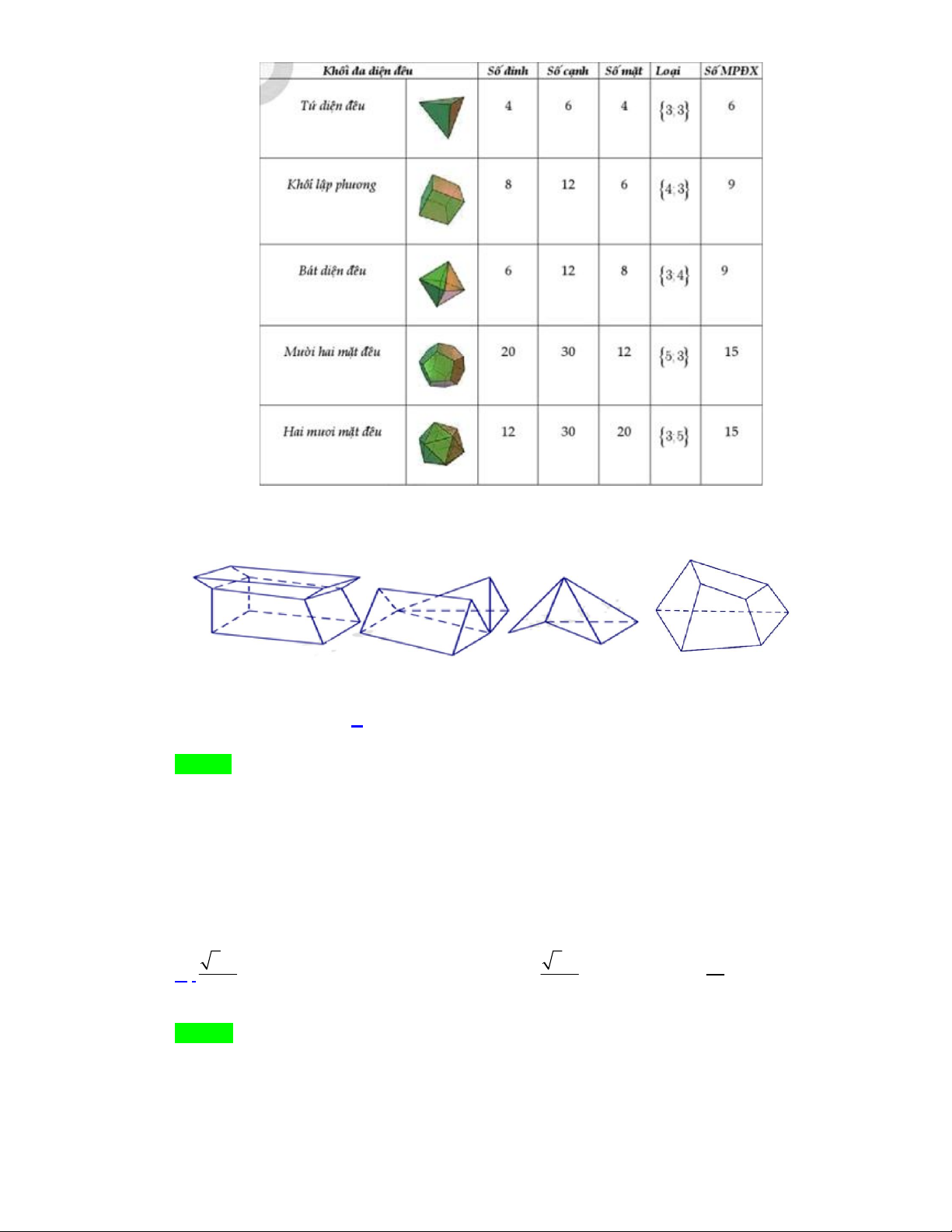
Câu 3: Số mặt phẳng đối xứng của hình lập phương là A. 7 . B. 3 . C. 6. D. 9 .
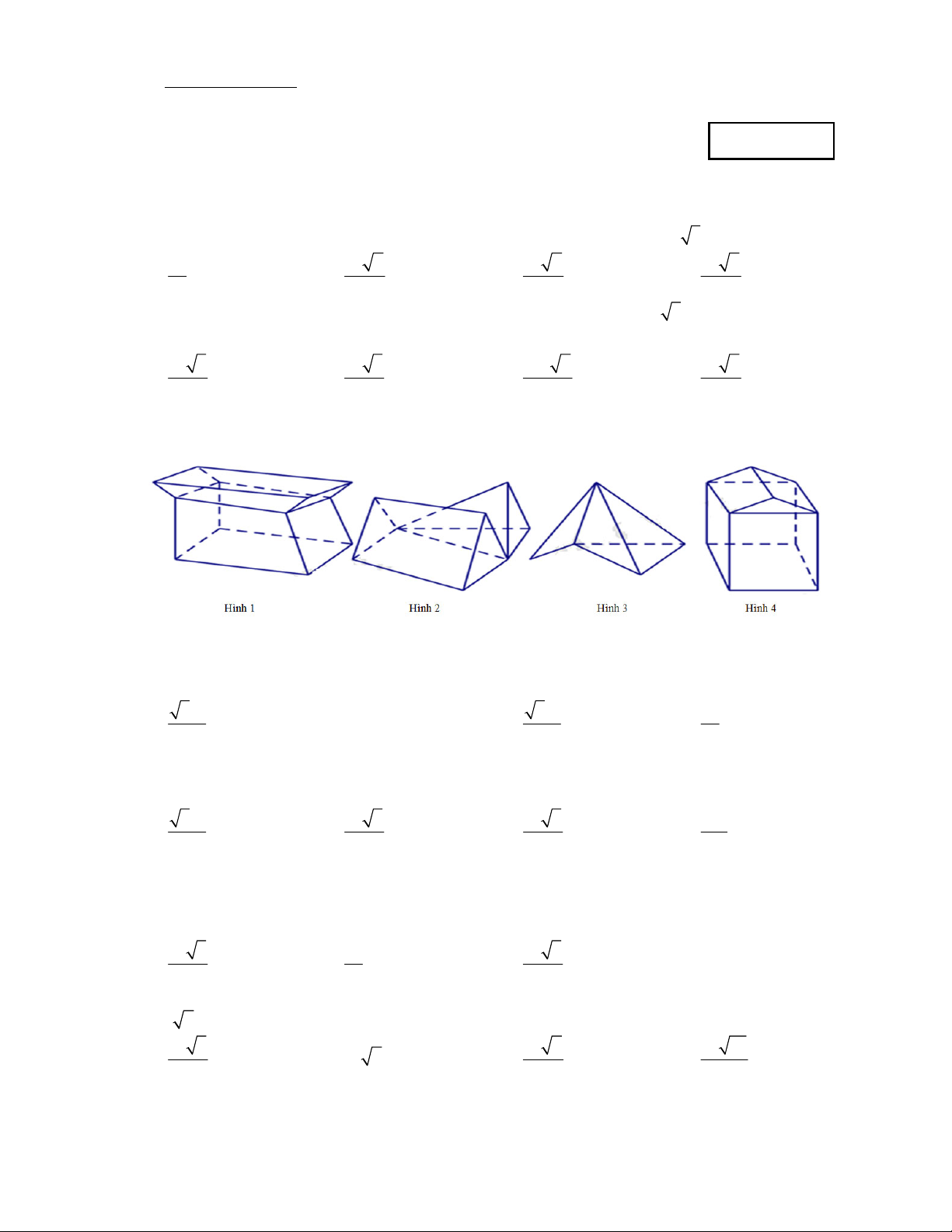
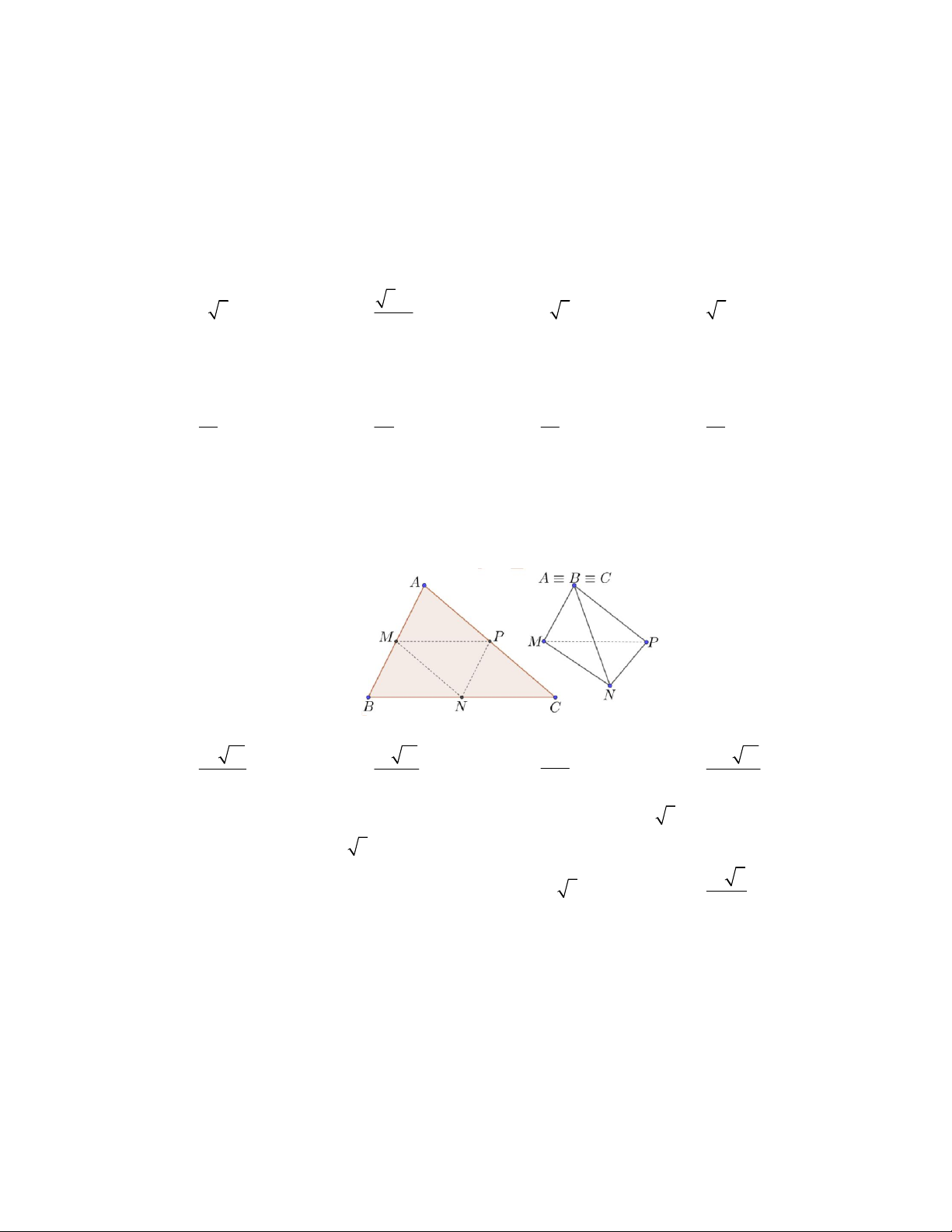
Câu 4: Số hình đa diện lồi trong các hình dưới đây là A. 0 B. 1 C. 3 D. 2
Câu 5: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SD tạo với mặt
phẳng  ABCD một góc bằng 0
60 . Thể tích của khối chóp S.ABCD bằng 3 3a 3 3a 3 a A. . B. 3 a . C. . D. . 3 9 3
Câu 6: Cho hình hộp ABC . D A BCD
  tất cả các cạnh đều bằng  0
a, BAD  60 , hình chiếu vuông góc
của A xuống  ABCD trùng với trung điểm của AB. Thể tích khối hộp ABC . D A BCD   bằng 3 3a 3 a 3 3 a 3 3 3a A. . B. . C. . D. . 12 4 2 4
Câu 7: Số mặt đối xứng của hình chóp tứ giác đều là A. 2. B. 4 . C. 8 . D. 6 .
Câu 8: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a . Biết tam giác SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp S.ABCD bằng 3 a 3 3 a 3 a 3 A. . B. . C. . D. 3 a . 2 3 6
Câu 9: Cho khối chóp S.ABCD có đáy là hình chữ nhật. Biết AC  2AB  2a , SA vuông góc với đáy,
SA a 2 . Thể tích khối chóp S.ABCD là 3 a 5 3 a 6 3 a 15 A. . B. 3 a 6. C. . D. . 3 3 3
Câu 10: Số đỉnh của hình mười hai mặt đều là A. 12 . B. 30 . C. 20 . D. 16 .
Câu 11: Khối đa diện đều loại 4;  3 là
Trang 1/3 - Mã đề thi 201
A. Khối chóp tứ giác đều.
B. Khối bát diện đều.
C. Khối tứ diện đều.
D. Khối lập phương.
Câu 12: Kim tự tháp Kê - ốp ở Ai cập được xây dựng khoảng năm 2500 trước công nguyên. Kim tự tháp
này là một khối chóp tứ giác đều có chiều cao 147m , cạnh đáy là 230m . Thể tích của nó bằng A. 3 2592100 m . B. 3 2592100 cm . C. 3 7776350 m . D. 3 388150 m .
Câu 13: Tổng diện tích các mặt của hình tứ diện đều cạnh a bằng 2 3a A. 2 4 3a . B. 2 . C. 2 2 3a . D. 2 3a .
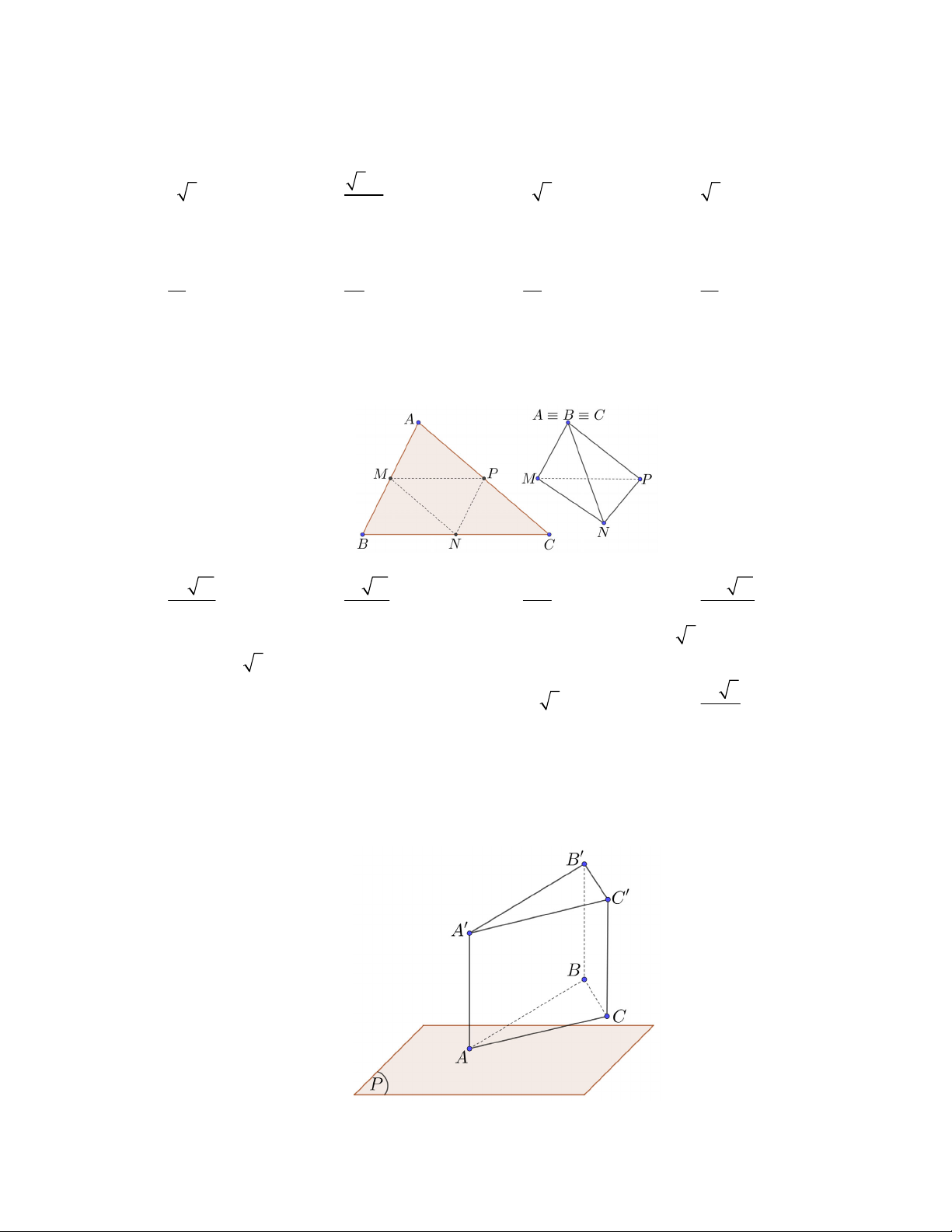
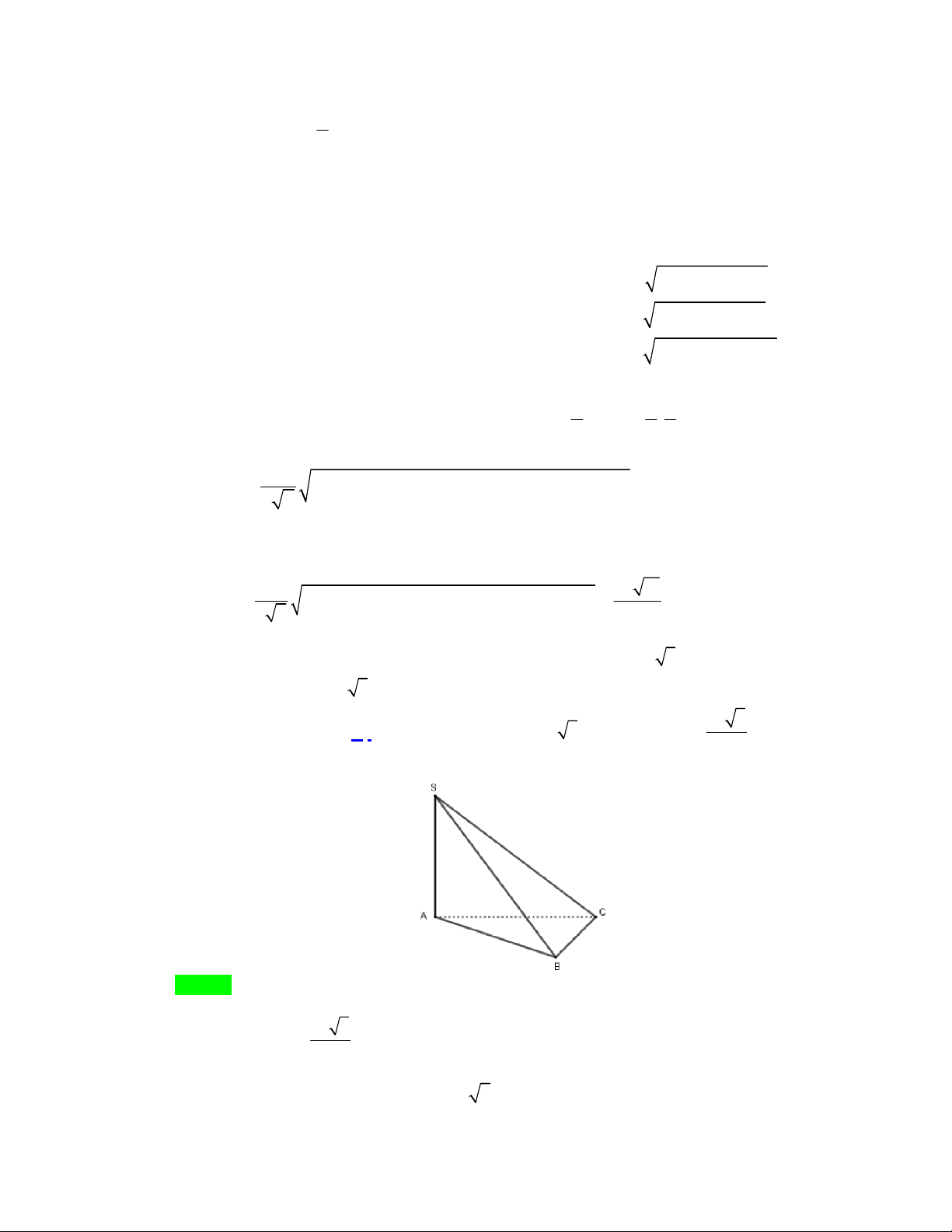
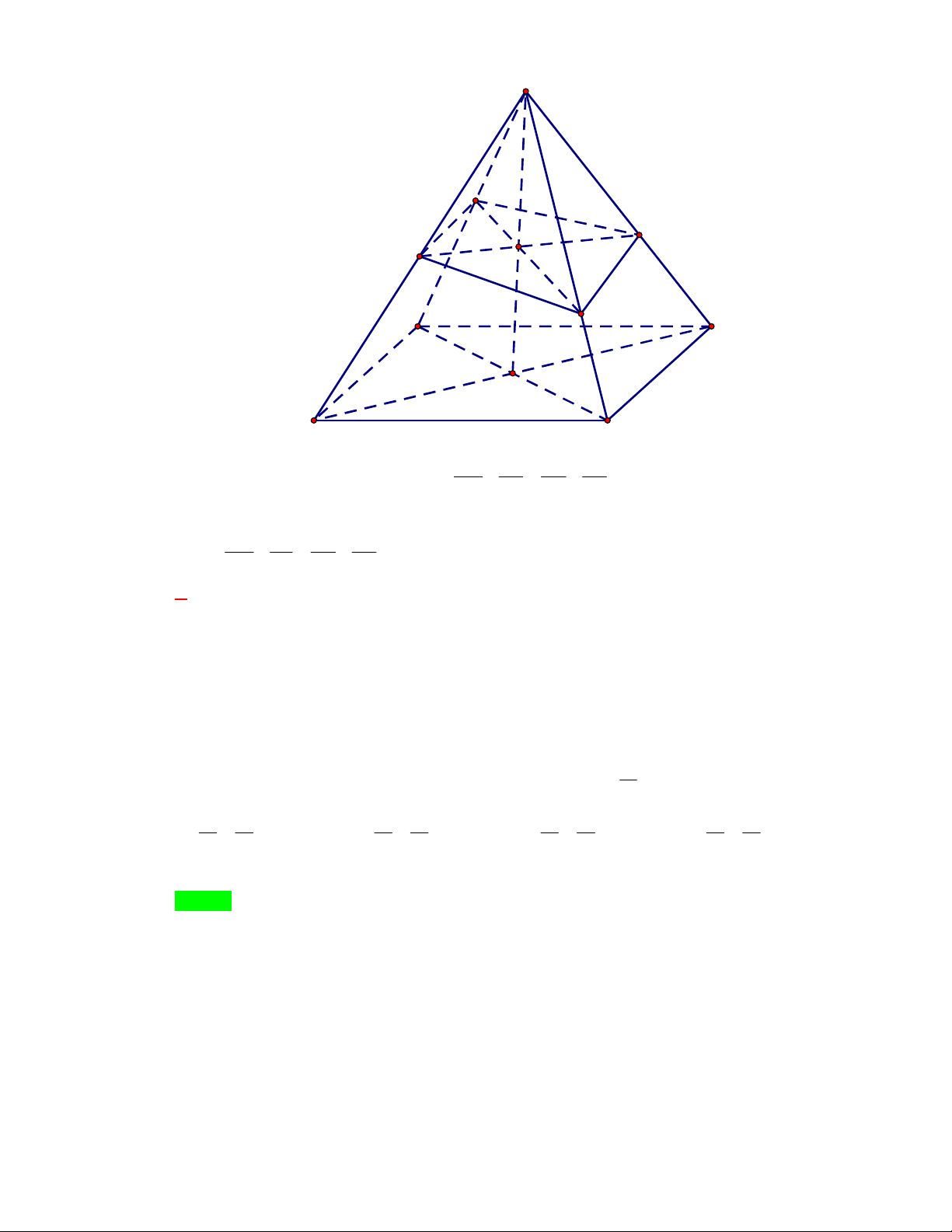
Câu 14: Cho tứ diện ABCD có cạnh A ,
B AC, AD đôi một vuông góc và AB AC AD a , M , N, P lần
lượt là trung điểm các cạnh BC,CD, DB . Thể tích của khối tứ diện AMNP bằng 3 a 3 a 3 a 3 a A. . B. . C. . D. . 12 24 18 4
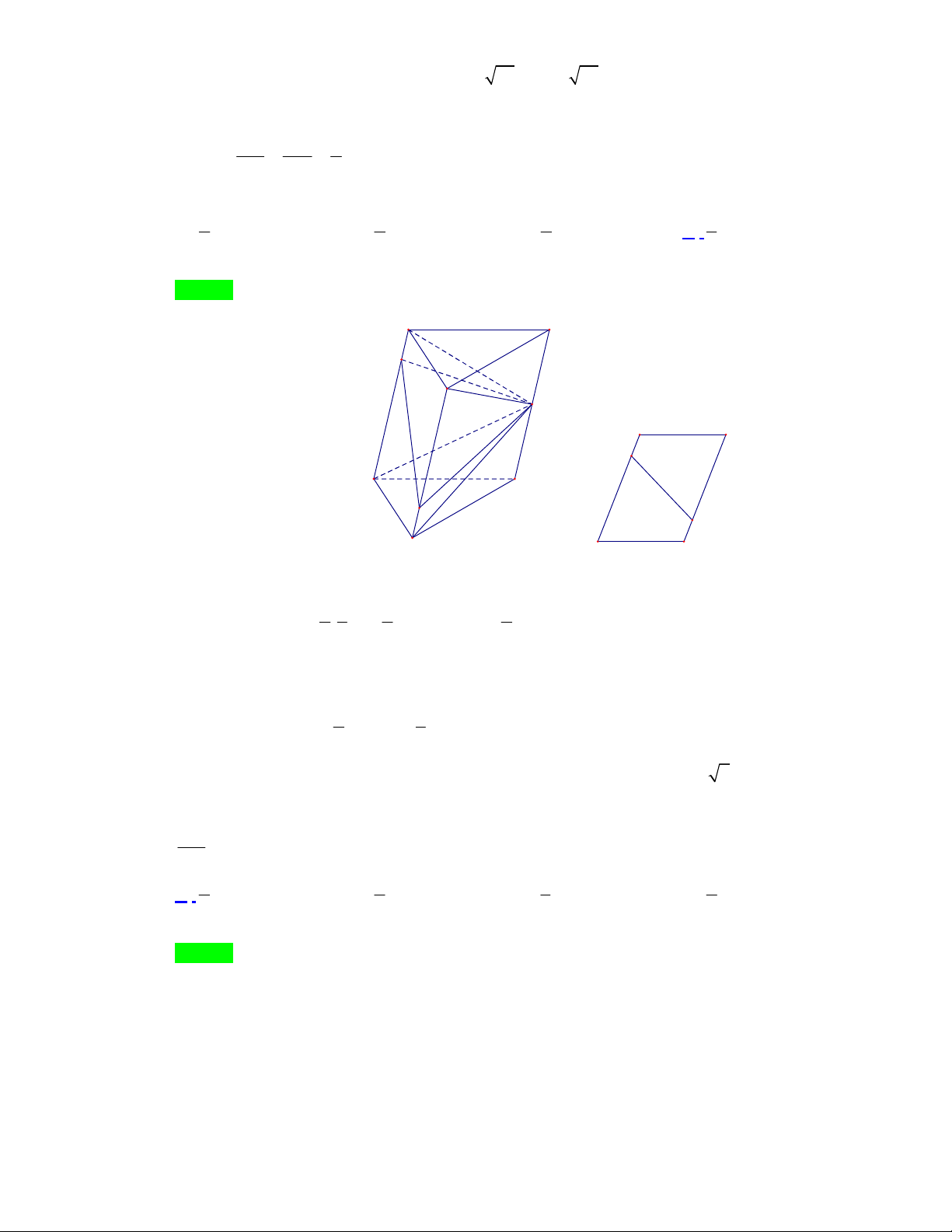
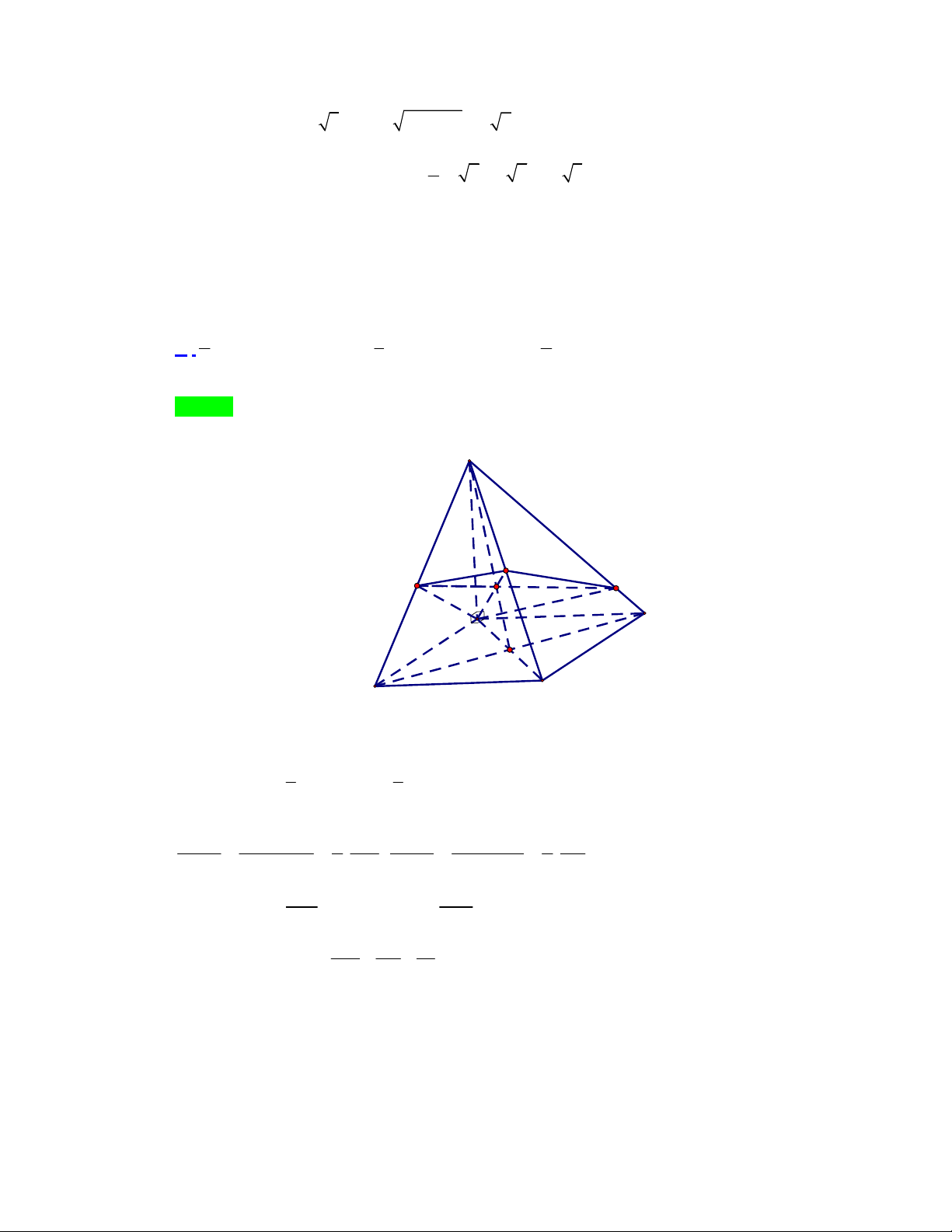
Câu 15: Cho một mảnh giấy có hình dạng là tam giác nhọn ABC có
AB  10 cm, BC  16 cm, AC 14 cm. Gọi M , N, P lần lượt là trung điểm của AB, BC,C . A Người ta
gấp mảnh giấy theo các đường MN , NP, PM sau đó dán trùng các cặp cạnh: AM và BM ; BN và
CN; CP và AP (các điểm ,
A B,C trùng nhau) để tạo thành một tứ diện (xem hình vẽ).
Thể tích của khối tứ diện nêu trên là 20 11 10 11 280 160 11 A. 3 cm . B. 3 cm . C. 3 cm . D. 3 cm . 3 3 3 3
Câu 16: Cho khối chóp S.ABC có đáy là tam giác vuông tại .
B Biết BC a 3, AB a , SA vuông góc
với đáy, SA  2a 3 . Thể tích khối chóp S.ABC là 3 a 3 A. 3 3a . B. 3 a . C. 3 a 3. D. . 3
Câu 17: Khối tứ diện đều thuộc loại A. 3;  4 . B. 4;  3 . C. 3;  3 . D. 3;  5 .
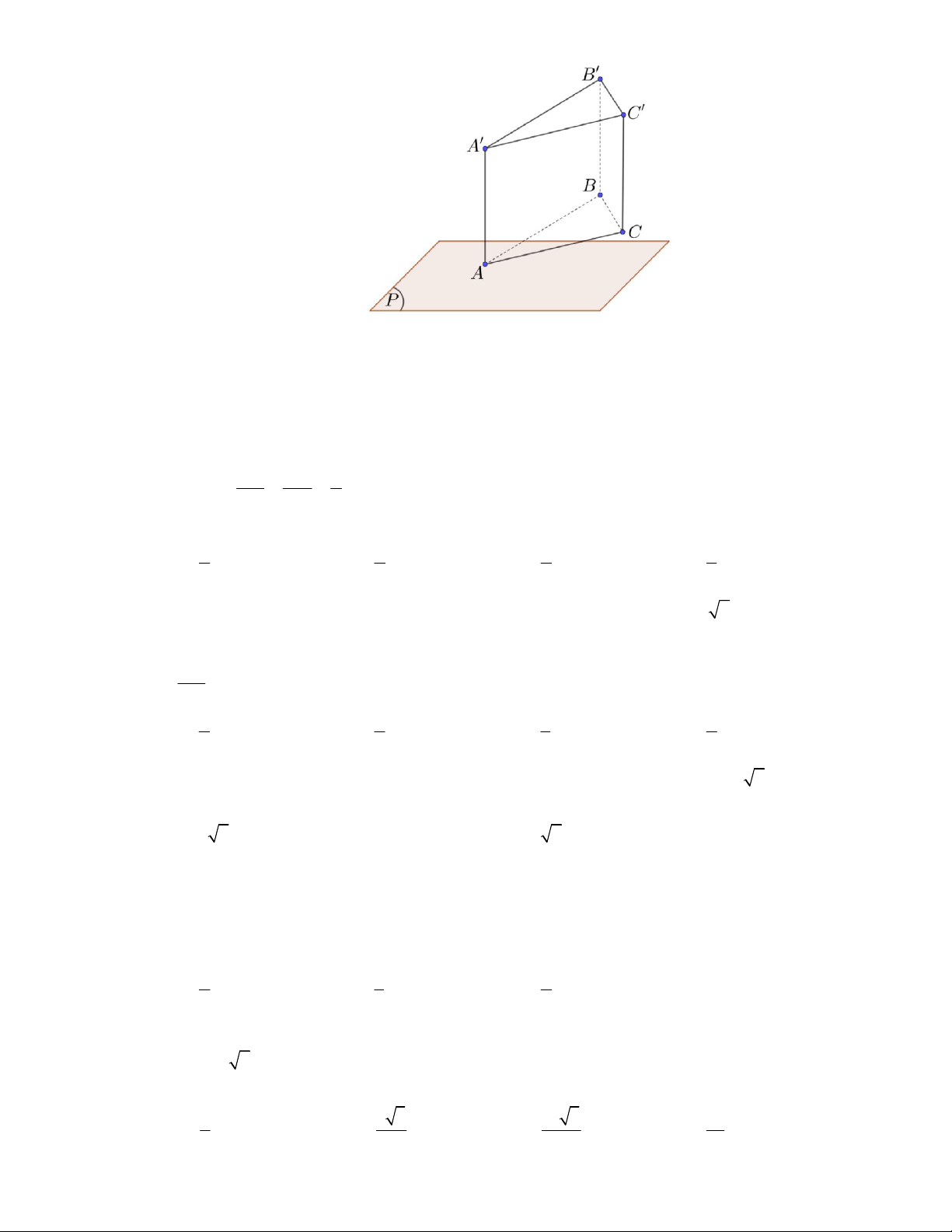
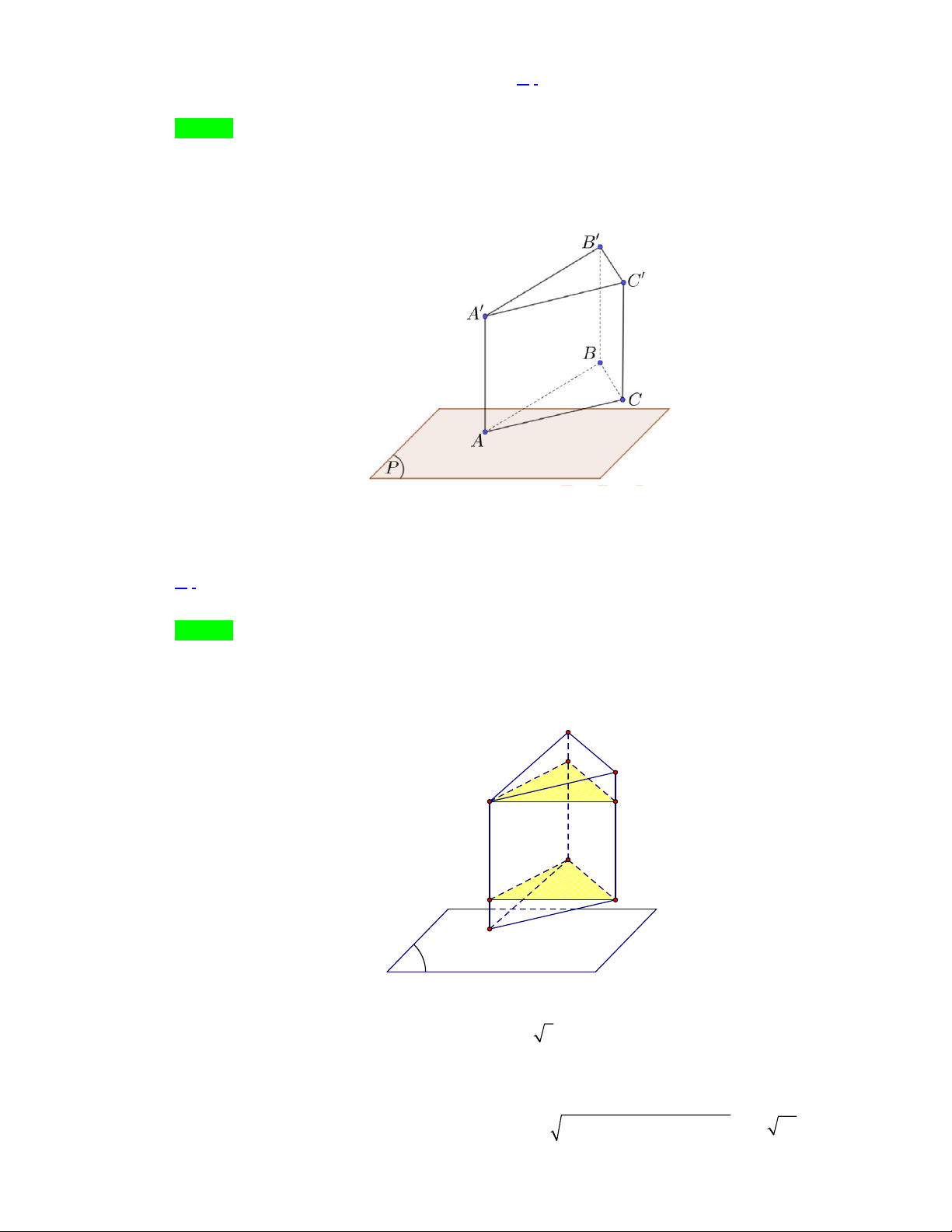
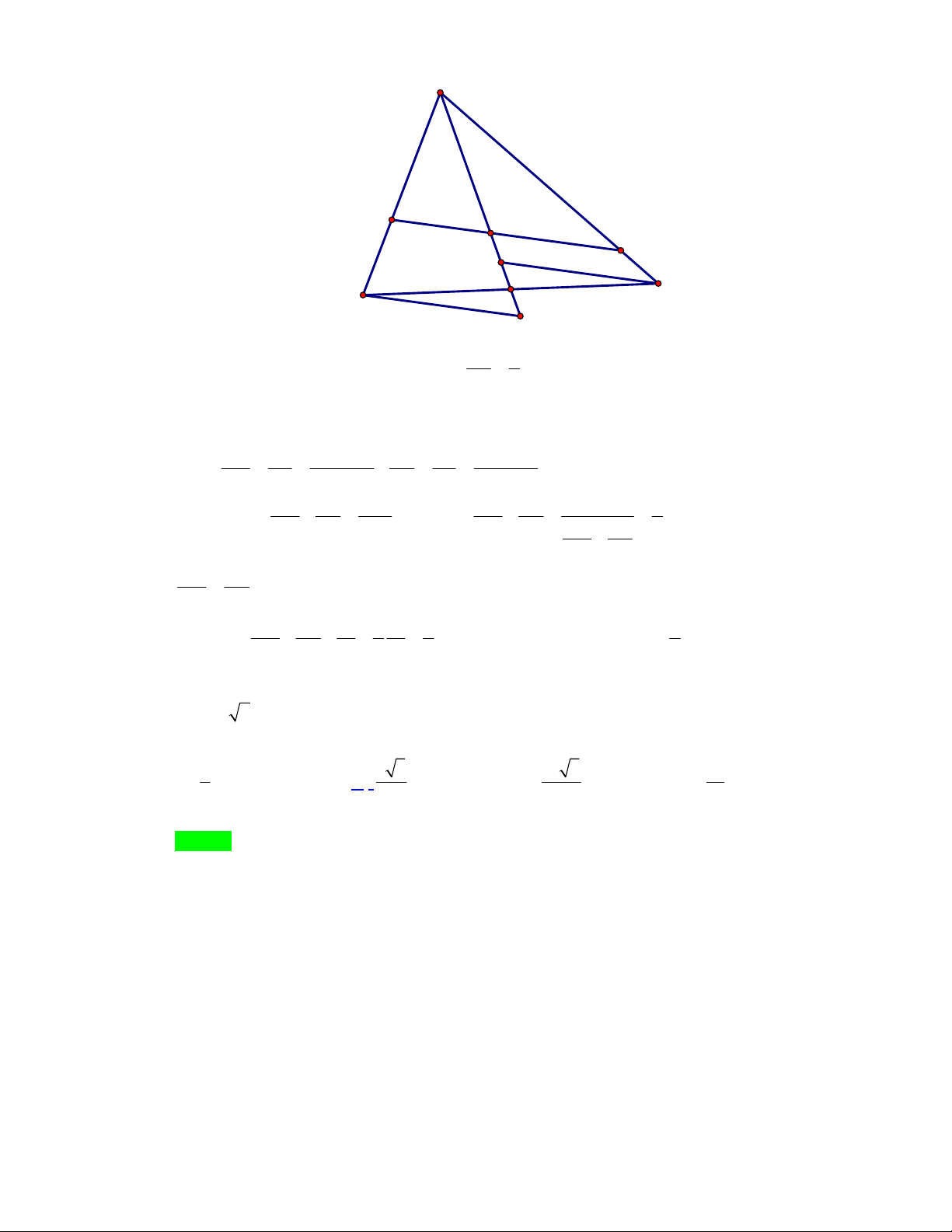
Câu 18: Có một khối gỗ có hình dạng là khối lăng trụ tam giác ABC.A BC
 . Khi đặt khối gỗ sao cho các
cạnh bên vuông góc với mặt bàn P , điểm AP thì đoạn BC ở phía trên mặt bàn P và song song
với mặt bàn (xem hình vẽ). Biết 
AA  100 cm, AB AC  40 cm, BC  30 cm, AAB  60 . Người ta cắt, gọt khối gỗ trên bằng
các mặt phẳng vuông góc với các cạnh bên để thu được một lăng trụ đứng tam giác. Thể tích lớn nhất của
khối lăng đứng tạo thành gần với số nào sau đây nhất ?
Trang 2/3 - Mã đề thi 201 A. 3 37470 cm . B. 3 35470 cm . C. 3 36470 cm . D. 3 38470 cm .
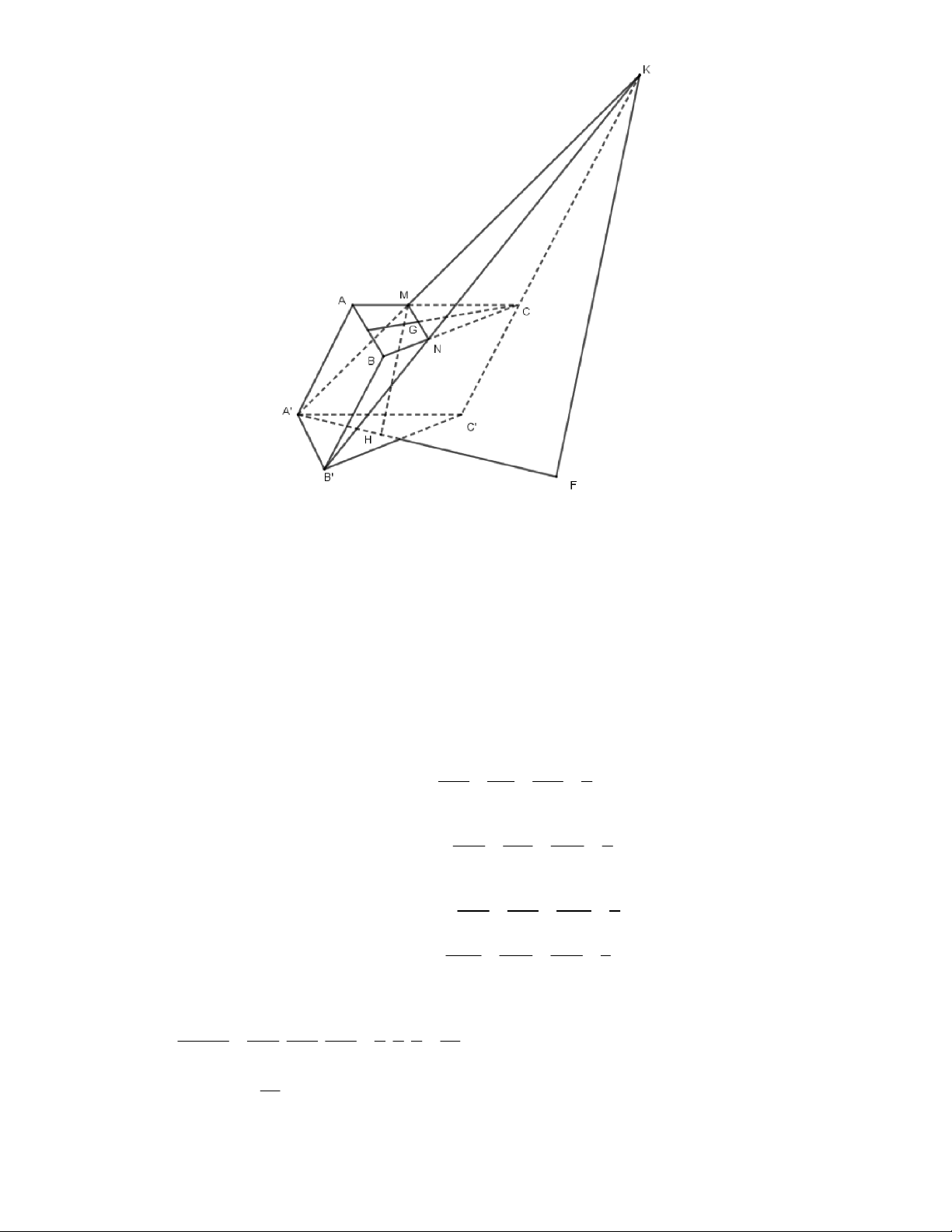
Câu 19: Cho khối lăng trụ ABC. ’ A ’
B C’ có thể tích V . Điểm P thuộc cạnh AA' , Q thuộc cạnh BB' PA QB' 1 sao cho 
 và R là trung điểm của cạnh CC' . Thể tích khối chóp R.ABQP theo V là PA' QB 4 4 2 1 1 A. V . B. V . C. V . D. V . 3 3 2 3
Câu 20: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a 2 . Tam giác SAD 3 4a
cân tại S , mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng , 3
điểm N là trung điểm cạnh SB . Khoảng cách từ điểm N đến mặt phẳng (SCD) bằng 2 4 8 3 A. a . B. a . C. a . D. a . 3 3 3 4
Câu 21: Cho lăng trụ đứng ABC.A BC
  có đáy ABC là tam giác vuông cân tại C,CB  2 . a Biết rằng góc giữa B C
 và AC bằng 60 . Thể tích của khối lăng trụ đã cho bằng A. 3 2 2a . B. 3 2a . C. 3 2a . D. 3 a .
Câu 22: Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB a, AD  2 .
a Cạnh bên SA vuông góc
với đáy và SA  3 .
a Điểm P là trung điểm của SC . Một mặt phẳng qua AP cắt hai cạnh SB và SD lần
lượt tại M và N . Gọi V là thể tích của khối chóp S.AMPN . Giá trị nhỏ nhất của V bằng 1 1 2 1 4 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 3 3 3
Câu 23: Cho lăng trụ tam giác ABC.A' B 'C ' có đáy ABC là tam giác vuông cân tại A , cạnh AC  2 2.
Biết AC ' tạo với mặt phẳng (ABC) một góc 0
60 và AC '  4 . Thể tích khối chóp .
B ACC ' A' bằng 8 8 3 16 3 16 A. . B. . C. . D. . 3 3 3 3
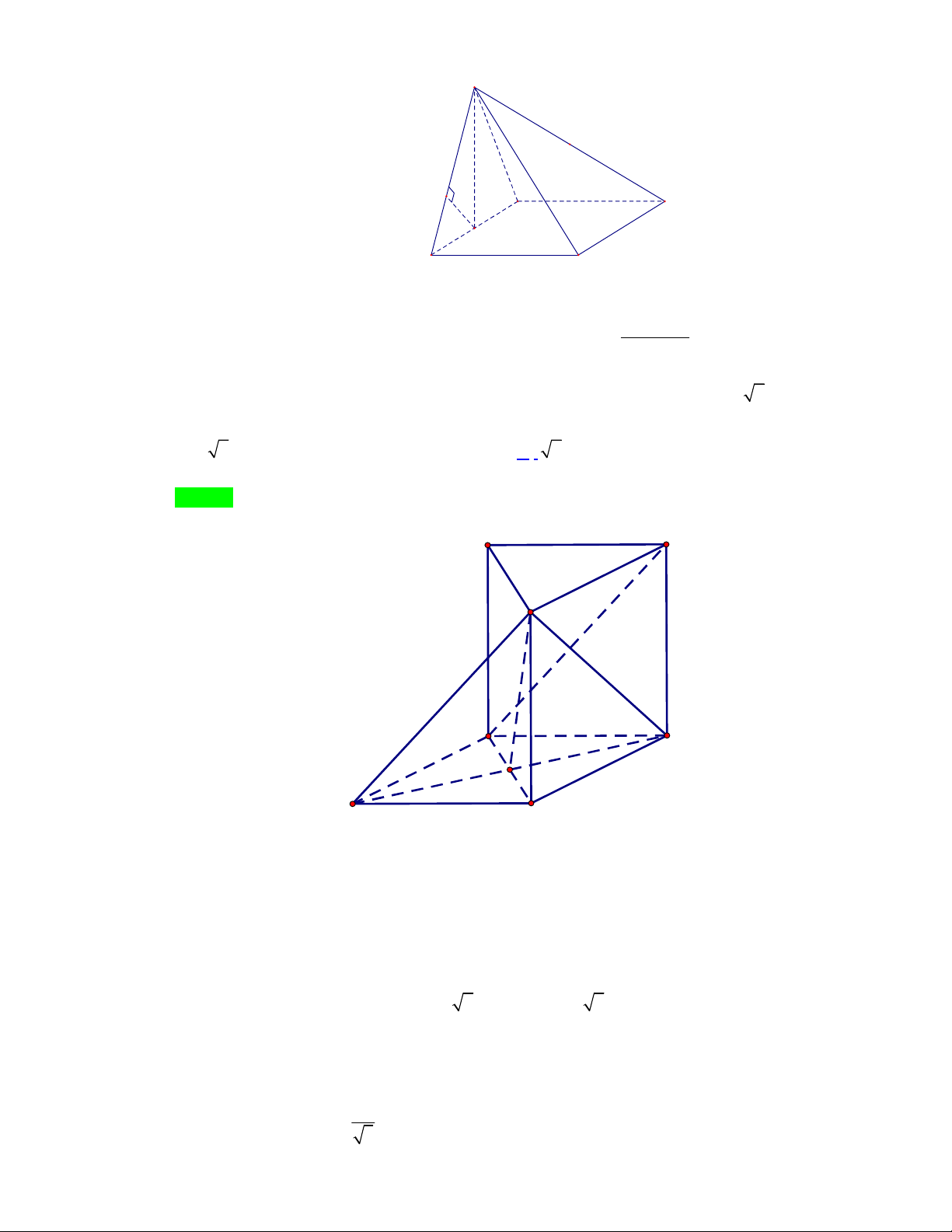
Câu 24: Cho hình chóp tứ giác đều S.ABCD . Gọi O là tâm hình vuông ABCD . Một mặt phẳng ( ) bất kì cắt các cạnh bên ,
SA SB, SC, SD và đoạn SO lần lượt tại các điểm M , N, P,Q, I . Chọn đẳng thức đúng? 1 1 1 1 1 1 1 1 4 A.    . B.     . SM SP SN SQ SM SP SN SQ SI 1 1 1 1 1 1 1 1 C.    . D.    . SM SN SP SQ SM SQ SN SP
Câu 25: Cho lăng trụ tam giác ABC.A' B 'C ' . Một mặt phẳng ( ) qua đường thẳng A' B ' và trọng tâm
tam giác ABC , chia khối lăng trụ ABC.A' B 'C ' thành hai phần. Gọi V là thể tích khối đa diện chứa đỉnh 1 V
C và V là thể tích khối đa diện còn lại. Khi đó tỉ số 1 bằng 2 V2 V 17 V 19 V 10 V 8 A. 1  . B. 1  . C. 1  . D. 1  . V 10 V 8 V 17 V 19 2 2 2 2
----------------------------------------------- ----------- HẾT ----------
Trang 3/3 - Mã đề thi 201
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM-TRA-45 PHÚT-HK1
TRƯỜNG THPT NGỖ SỸ LIÊN-BẮC
NĂM HỌC 2018 – 2019 GIANG Môn: Toán
Thời gian: 45 phút (Không kể thời gian phát đề) Câu 1:
Khối chóp tam giác đều S.ABC có cạnh đáy bằng a , cạnh bên bằng a 3 có thể tích bằng 3 a 3 a 2 3 a 2 3 a 6 A. . B. . C. . D. . 3 6 2 2 Câu 2:
Cho khối chóp S.ABC có đáy là tam giác đều cạnh a . Biết SC a 3 , hai mặt phẳng (SAB)
và (SAC ) cùng vuông góc với đáy. Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 3 2a 6 3 a 6 A. . B. . C. . D. . 2 4 9 12 Câu 3:
Số mặt phẳng đối xứng của hình lập phương là A. 7 . B. 3. C. 6. D. 9 . Câu 4:
Số hình đa diện lồi trong các hình dưới đây là A. 0 . B. 1. C. 3 . D. 2 . Câu 5:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy, SD tạo với mặt
phẳng  ABCD một góc bẳng 60 . Thể tích của khối chóp S.ABCD bẳng 3 3a 3 3a 3 a A. . B. 3 a . C. . D. . 3 9 3 Câu 6:
Số mặt đối xứng của hình chóp tứ giác đều là A. 2 . B. 4 . C. 8 . D. 6 . Câu 7:
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a . Biết tam giác SAB đều và nằm trong
mặt phẳng vuông góc với đáy. Thể tích khối chóp S.ABCD bằng 3 a 3 3 a 3 a 3 A. . B. . C. . D. 3 a . 2 3 6 Câu 8:
Cho khối chóp S.ABCD có đáy là hình chữ nhật. Biết AC  2AB  2a , SA vuông góc với
đáy, SA a 2 . Thể tích khối chóp S.ABCD là 3 a 5 3 a 6 3 a 15 A. . B. 3 a 6 . C. . D. . 3 3 3 Câu 9:
Số đỉnh của hình mười hai mặt đều là A. 12 . B. 30 . C. 20 . D. 16 . Trang 1/21 - WordToan
Câu 10: Khối đa diện đều loại 4;  3 là
A. Khối chóp tứ giác đều.
B. Khối bát diện đều.
C. Khối tứ diện đều.
D. Khối lập phương.
Câu 11: Kim tự tháp Kê - ốp ở Ai cập được xây dựng khoảng năm 2500 trước công nguyên. Kim tự
tháp này là một khối chóp tứ giác đều có chiều cao 147 m , cạnh đáy là 230 m . Thể tích của nó bằng A. 3 2592100 m . B. 3 2592100 cm . C. 3 7776350 m . D. 3 388150 m .
Câu 12: Tổng diện tích các mặt của hình tứ diện đều cạnh a bằng 2 3a A. 2 4 3a . B. . C. 2 2 3a . D. 2 3a . 2
Câu 13: Cho tứ diện ABCD có cạnh AB, AC, AD đôi một vuông góc và AB AC AD a , M , N , P
lần lượt là trung điểm các cạnh BC, CD, DB . Thể tích của khối tứ diện AMNP bằng 3 a 3 a 3 a 3 a A. . B. . C. . D. . 12 24 18 4
Câu 14: Cho một mảnh giấy có hình dạng là tam giác nhọn ABC có AB  10 cm, BC  16 cm,
AC  14 cm. Gọi M , N , P lần lượt là trung điểm của AB, BC, C .
A Người ta gấp mảnh giấy theo
các đường MN , NP, PM sau đó dán trùng các cặp cạnh: AM và BM ; BN và CN ; CP và AP (các điểm ,
A B, C trùng nhau) để tạo thành một tứ diện (xem hình vẽ).
Thể tích của khối tứ diện nêu trên là 20 11 10 11 280 160 11 A. 3 cm . B. 3 cm . C. 3 cm . D. 3 cm . 3 3 3 3
Câu 15: Cho khối chóp S.ABC có đáy là tam giác vuông tại .
B Biết BC a 3, AB a , SA vuông góc
với đáy, SA  2a 3 . Thể tích khối chóp S.ABC là 3 a 3 A. 3 3a . B. 3 a . C. 3 a 3. D. . 3
Câu 16: Khối tứ diện đều thuộc loại A. 3;  4 . B. 4;  3 . C. 3;  3 . D. 3;  5 .
Câu 17: Có một khối gỗ có hình dạng là khối lăng trụ tam giác ABC.A BC
  . Khi đặt khối gỗ sao cho
các cạnh bên vuông góc với mặt bàn  P , điểm A P thì đoạn BC ở phía trên mặt bàn  P
và song song với mặt bàn (xem hình vẽ).
Trang 2/21 – Diễn đàn giáo viên Toán
Biết AA  100 cm, AB AC  40 cm, BC  30 cm, A A
B  60 . Người ta cắt, gọt khối gỗ trên
bằng các mặt phẳng vuông góc với các cạnh bên để thu được một lăng trụ đứng tam giác. Thể
tích lớn nhất của khối lăng đứng tạo thành gần với số nào sau đây nhất? A. 3 37470 cm . B. 3 35470 cm . C. 3 36470 cm . D. 3 38470 cm .
Câu 18: Cho khối lăng trụ ABC.A BC
  có thể tích V . Điểm P thuộc cạnh AA , Q thuộc cạnh BBPA QB 1 sao cho  
và R là trung điểm của cạnh CC . Thể tích khối chóp . R ABQP theo PAQB 4 V là: 4 2 1 1 A. V . B. V . C. V . D. V . 3 3 2 3
Câu 19: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a 2 . Tam giác SAD
cân tại S, mặt bên  SAD vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng 3
4a , điểm N là trung điểm của cạnh SB. Khoảng cách từ điểm N đến mặt phẳng SCD bằng 3 2 4 8 3 A. a . B. a . C. a . D. a . 3 3 3 4
Câu 20: Cho lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông cân tại C,CB  2 . a Biết rằng góc giữa B C
 và AC bằng 60 . Thể tích của khối lăng trụ đã cho bằng A. 3 2 2a . B. 3 2a . C. 3 2a . D. 3 a .
Câu 21: Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB a, AD  2a. Cạnh bên SA vuông góc
với đáy và SA  3 .
a Điểm P là trung điểm của SC . Một mặt phẳng qua AP cắt hai cạnh SB
và SD lần lượt tại M và N . Gọi V là thể tích của khối chóp S.AMPN . Giá trị nhỏ nhất của 1 V bằng 1 2 1 4 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 3 3 3
Câu 22: Cho lăng trụ tam giác ABC.A ' B 'C ' có đáy ABC là tam giác vuông cân tại A , cạnh
AC  2 2. Biết AC ' tạo với mặt phẳng ( ABC) một góc 0
60 và AC '  4 . Thể tích khối chóp .
B ACC ' A ' bằng 8 8 3 16 3 16 A. . B. . C. . D. . 3 3 3 3 Trang 3/21 - WordToan
Câu 23: Cho lăng trụ tam giác ABC.A ' B 'C ' có đáy ABC là tam giác vuông cân tại A , cạnh
AC  2 2. Biết AC ' tạo với mặt phẳng ( ABC) một góc 0
60 và AC '  4 . Thể tích khối chóp .
B ACC ' A ' bằng 8 8 3 16 3 16 A. . B. . C. . D. . 3 3 3 3
Câu 24: Cho hình chóp tứ giác đều S.ABCD . Gọi O là tâm hình vuông ABCD . Một mặt phẳng ( ) bất
kì cắt các cạnh bên S ,
A SB, SC, SD và đoạn SO lần lượt tại các điểm M , N, P,Q, I . Chọn đẳng thức đúng? 1 1 1 1 1 1 1 1 4 A.    . B.     . SM SP SN SQ SM SP SN SQ SI 1 1 1 1 1 1 1 1 C.    . D.    . SM SN SP SQ SM SQ SN SP
Câu 25: Cho lăng trụ tam giác ABC.A' B 'C ' . Một mặt phẳng ( ) qua đường thẳng A ' B ' và trọng tâm
tam giác ABC , chia khối lăng trụ ABC.A' B 'C ' thành hai phần. Gọi V là thể tích khối đa diện 1 V
chứa đỉnh C và V là thể tích khối đa diện còn lại. Khi đó tỉ số 1 bằng 2 V2 V 17 V 19 V 10 V 8 A. 1  . B. 1  . C. 1  . D. 1  . V 10 V 8 V 17 V 19 2 2 2 2 BẢNG ĐÁP ÁN 1.B 2.D 3.D 4.B 5.A 6.B 7.C 8.C 9.C 10.D 11.A 12.D 13.B 14.A 15.B 16.C 17.A 18.D 19.A 20.C 21.A 22.B 23.A 24.A 25.B
LỜI GIẢI CHI TIẾT Câu 1.
Khối chóp tam giác đều S.ABC có cạnh đáy bằng a , cạnh bên bằng a 3 có thể tích bằng 3 a 3 a 2 3 a 2 3 a 6 A. . B. . C. . D. . 3 6 2 2 Lời giải Chọn B S A C H M
Ta gọi M là trung điểm BC , H là t B rọng tâm tam g
iác ABC suy ra H là hình chiếu vuông 2 a 3
góc của S trên  ABC  . Ta có diện tích đáy khối chóp là S  . ABC 4
Trang 4/21 – Diễn đàn giáo viên Toán 2 a 3 8 Ta có AH AM  suy ra 2 2
SH SA AHa . 3 3 3 1 2 3 1 8 a 3 a 2 Do đó VSH .S  .a .  . SABC 3 ABC 3 3 4 6 Câu 2.
Cho khối chóp S.ABC có đáy là tam giác đều cạnh a . Biết SC a 3 , hai mặt phẳng (SAB)
và (SAC ) cùng vuông góc với đáy. Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 3 2a 6 3 a 6 A. . B. . C. . D. . 2 4 9 12 Lời giải Chọn D 2 a 3
Ta có diện tích đáy khối chóp S
. Vì mặt phẳng (SAB) và (SAC) cùng vuông góc ABC 4
với đáy  SA   ABC  suy ra SA là đường cao của khối chóp và 2 2
SA SC AC a 2 . 2 3 1 1 a 3 a 6 Do đó V  . . SA S  .a 2.  . SABC 3 ABC 3 4 12 Câu 3.
Số mặt phẳng đối xứng của hình lập phương là A. 7 . B. 3. C. 6. D. 9 . Lời giải Chọn D Trang 5/21 - WordToan Câu 4.
Số hình đa diện lồi trong các hình dưới đây là A. 0 . B. 1. C. 3 . D. 2 . Lời giải Chọn B
Quan sát bốn hình trên ta thấy chỉ có một hình thứ tư từ trái qua là hình đa diện lồi vì lấy bất kỳ
hai điểm nào thì đoạn thẳng nối hai điểm đó nằm trong khối đa diện.
Vậy chỉ có một đa diện lồi. Câu 5.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy, SD tạo với mặt
phẳng  ABCD một góc bẳng 60 . Thể tích của khối chóp S.ABCD bẳng 3 3a 3 3a 3 a A. . B. 3 a . C. . D. . 3 9 3 Lời giải Chọn A
Trang 6/21 – Diễn đàn giáo viên Toán S 60° A D B C
AD là hình chiếu vuông góc của SD lên mặt phẳng  ABCD
SD ABCD      SD AD  , ,  SDA  60 . SA  .
AD tan 60  a 3 . 3 1 a 3 Thể tích là 2
V  .a .a 3  . 3 3 Câu 6.
Số mặt đối xứng của hình chóp tứ giác đều là A. 2 . B. 4 . C. 8 . D. 6 . Lời giải Chọn B
Hình chóp tứ giác đều có bốn mặt phẳng đối xứng. S S S S A A A A B B B B M M M M Q N Q N O O Q N O Q N O D P C D P C D P C D P C Câu 7.
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a . Biết tam giác SAB đều và nằm trong
mặt phẳng vuông góc với đáy. Thể tích khối chóp S.ABCD bằng 3 a 3 3 a 3 a 3 A. . B. . C. . D. 3 a . 2 3 6 Lời giải Chọn C. S D A H B C Trang 7/21 - WordToan
Kẻ SH AB, H AB SH   ABCD , H là trung điểm của AB . 2 2 a 3a a 3 2 2 2 2
SH SA AH a    SH  . 4 4 2 3 1 a 3 2 SaV  .SH.S  . ABCD S. ABCD 3 ABCD 6 Câu 8.
Cho khối chóp S.ABCD có đáy là hình chữ nhật. Biết AC  2AB  2a , SA vuông góc với
đáy, SA a 2 . Thể tích khối chóp S.ABCD là 3 a 5 3 a 6 3 a 15 A. . B. 3 a 6 . C. . D. . 3 3 3 Lời giải Chọn C AC  2a
Ta có AC  2AB  2a  2 2   BC
AC AB a 3 . AB a  Suy ra 2 S  . AB BC a 3 . ABCD 1 1 3 a 6 Khi đó V  . SA S 2  .a 2.a 3  . S . ABCD 3 ABCD 3 3 3 a 6 Vậy V  . S. ABCD 3 Câu 9.
Số đỉnh của hình mười hai mặt đều là A. 12 . B. 30 . C. 20 . D. 16 . Lời giải Chọn C
Số đỉnh của hình mười hai mặt đều là 20 đỉnh.
Câu 10. Khối đa diện đều loại 4;  3 là
A. Khối chóp tứ giác đều.
B. Khối bát diện đều.
Trang 8/21 – Diễn đàn giáo viên Toán
C. Khối tứ diện đều.
D. Khối lập phương. Lời giải Chọn D
Khối đa diện đều loại 4; 
3 là khối đa diện đều mà mỗi mặt là một đa giác đều có 4 cạnh và
mỗi đỉnh là đỉnh chung của đúng 3 cạnh  chọn D.
Câu 11. Kim tự tháp Kê - ốp ở Ai cập được xây dựng khoảng năm 2500 trước công nguyên. Kim tự
tháp này là một khối chóp tứ giác đều có chiều cao 147 m , cạnh đáy là 230 m . Thể tích của nó bằng A. 3 2592100 m . B. 3 2592100 cm . C. 3 7776350 m . D. 3 388150 m . Lời giải Chọn A S
Giả sử kim tự tháp này là một khối chóp tứ giác đều S.ABCD có chiều cao SO  147 m , cạnh
đáy là AB  230 m 1 1 1 2 2 3  V  . B h  .
SO AB  .147.230  2592100 m  chọn A. 3 3 3 A D
Câu 12. Tổng diện tích các mặt của hình tứ diện đều cạnh a bằng O 2 3a A. 2 4 3a . B. B. C. 2 2 C 3a . D. 2 3a . 2 Lời giải Chọn D A B D C 2 a 3 2 SSSS  4S  4.  a 3 . ABC ACDBCD ABD ABC 4
Câu 13. Cho tứ diện ABCD có cạnh AB, AC, AD đôi một vuông góc và AB AC AD a , M , N , P
lần lượt là trung điểm các cạnh BC, CD, DB . Thể tích của khối tứ diện AMNP bằng 3 a 3 a 3 a 3 a A. . B. . C. . D. . 12 24 18 4 Lời giải Chọn B Trang 9/21 - WordToan C N M A D P B 1 1 3 V  . AB AC.AD a . ABCD 6 6 MN NP PM 1 1 S 1 M
NP ∽ DBC (do   
) theo tỉ số đồng dạng là k   MNP 2  k  . DB BC CD 2 2 S 4 DBC 3 S 1 1 a MNP 3 V  .V  . a  . S .MNP . A BCD S 4 6 24 DBC
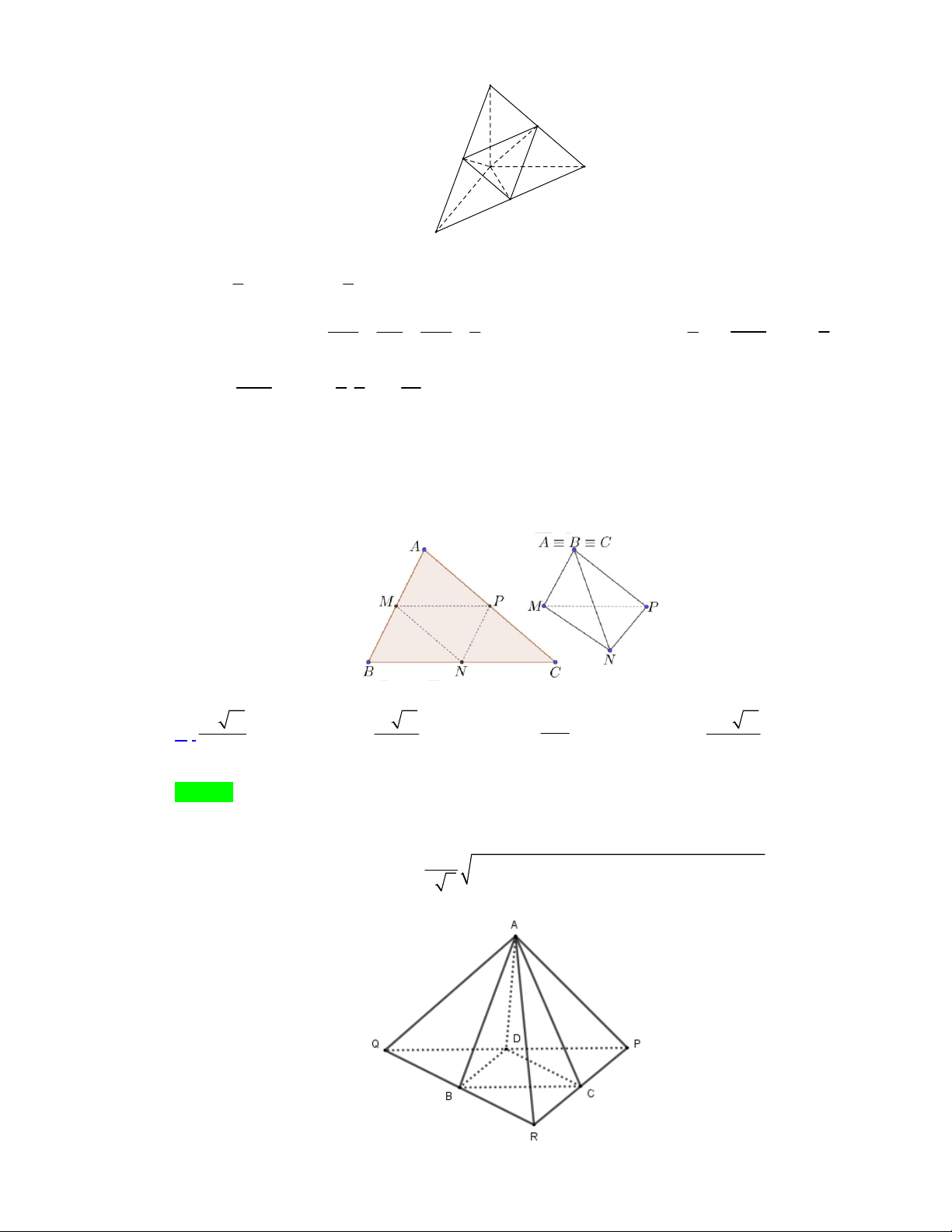
Câu 14. Cho một mảnh giấy có hình dạng là tam giác nhọn ABC có AB  10 cm, BC  16 cm,
AC  14 cm. Gọi M , N , P lần lượt là trung điểm của AB, BC, C .
A Người ta gấp mảnh giấy theo
các đường MN , NP, PM sau đó dán trùng các cặp cạnh: AM và BM ; BN và CN ; CP và AP (các điểm ,
A B, C trùng nhau) để tạo thành một tứ diện (xem hình vẽ).
Thể tích của khối tứ diện nêu trên là 20 11 10 11 280 160 11 A. 3 cm . B. 3 cm . C. 3 cm . D. 3 cm . 3 3 3 3 Lời giải Chọn A
Xét bài toán: Cho tứ diện ABCD , có AB CD a; AD BC  ;
b AC BD c . Thể tích 1
của khối tứ diện ABCD là V
a b c
a b c
a b c ABCD  2 2 2  2 2 2  2 2 2 . 6 2
Trang 10/21 – Diễn đàn giáo viên Toán
Dựng tứ diện APRQ sao cho B, C, D lần lượt là trung điểm của đoạn QR, RP, PQ. 1
Ta có: CD AB QR AQR vuông tại A 2 2 2
AQ AR  4a . 2 Tương tự, ARP vuông tại A 2 2 2
AR AP  4b ; APQ vuông tại A 2 2 2
AP AQ  4c . 2 2 2 2 2 2 2 2 2 2
AQ  2(a b c )
AQ AR  4a
AQ  2(a b c )     Xét 2 2 2 2 2 2 2 2 2 2
AR AP  4b   AR  2(a b c )   AR
2(a b c )  2 2 2  2 2 2 2  2 2 2
AP AQ  4c
AP  2(a b c )   AP
2(a b c )   1 1 1 Ta có: BCD CBR QDB PDC VV  . A . P A . Q AR ABCD 4 AQRP 4 6 1  V
a b c
a b c
a b c . ABCD  2 2 2  2 2 2  2 2 2  6 2
Áp dụng, ta có: AM NP  5c ;
m AN MP  8c ;
m AP MN  7c . m 1  V
a b c
a b c
a b cAMNP  20 11 2 2 2  2 2 2  2 2 2  . 6 2 3
Câu 15. Cho khối chóp S.ABC có đáy là tam giác vuông tại .
B Biết BC a 3, AB a , SA vuông góc
với đáy, SA  2a 3 . Thể tích khối chóp S.ABC là 3 a 3 A. 3 3a . B. 3 a . C. 3 a 3. D. . 3 Lời giải Chọn B 2 a 3 Ta có: B S  . BAC 2
Do SA   ABC  3
h SA  2a 3  Va . S . ABC
Câu 16. Khối tứ diện đều thuộc loại Trang 11/21 - WordToan A. 3;  4 . B. 4;  3 . C. 3;  3 . D. 3;  5 . Lời giải Chọn C
Câu 17. Có một khối gỗ có hình dạng là khối lăng trụ tam giác ABC.A BC
  . Khi đặt khối gỗ sao cho
các cạnh bên vuông góc với mặt bàn  P , điểm A P thì đoạn BC ở phía trên mặt bàn  P
và song song với mặt bàn (xem hình vẽ). 
Biết AA  100 cm, AB AC  40 cm, BC  30 cm, A A
B  60 . Người ta cắt, gọt khối gỗ trên
bằng các mặt phẳng vuông góc với các cạnh bên để thu được một lăng trụ đứng tam giác. Thể
tích lớn nhất của khối lăng đứng tạo thành gần với số nào sau đây nhất? A. 3 37470 cm . B. 3 35470 cm . C. 3 36470 cm . D. 3 38470 cm . Lời giải Chọn A
Thể tích khối lăng trụ đứng sau khi cắt, gọt lớn nhất khi ta cắt bởi các mặt phẳng qua A , B và
vuông góc với AA , cắt BB, CC ,
AA tại B ,C , A . 1 1 1 B' B1 C' A' C1 B A1 C A (P)
Các tam giác A AB và A AC là các tam giác vuông bằng nhau. 1 1 Ta có:  A B A C  .
AB sin AAB  40.sin 60  20 3 (cm) 1 1 AA  .
AB cos 60  20 (cm). 1
Chiều cao khối lăng trụ (sau khi cắt, gọt): h AA  AA  100  20  80 (cm). 1
Diện tích đáy lăng trụ (sau khi cắt, gọt): S Sp p a p b p c  . ABC     75 39 1
Trang 12/21 – Diễn đàn giáo viên Toán
Thể tích khối lăng trụ đứng: V Sh  80.75 39  6000 39  37469, 98799  3 cm  .
Câu 18. Cho khối lăng trụ ABC.A BC
  có thể tích V . Điểm P thuộc cạnh AA , Q thuộc cạnh BBPA QB 1 sao cho  
và R là trung điểm của cạnh CC . Thể tích khối chóp . R ABQP theo PAQB 4 V là: 4 2 1 1 A. V . B. V . C. V . D. V . 3 3 2 3 Lời giải Chọn D A C P B R A B P A' C' Q Q B' A' B' Ta có VV VV . R.ABA B   ABCR RA BC   1 1 1 2 Có VV  . .V V VV . RABC RA BC   R. 2 3 6 ABAB 3
Dễ dàng chứng minh được ABQP và AB Q
P là hai tứ giác bằng nhau.  SSVV
(2 khối chóp có cùng chiều cao, cùng diện tích đáy) ABQP A BQPR. ABQP R. A BQP  1 1  VVVV . R. ABQP R. A BQPR. 2 ABAB 3
Câu 19. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a 2 . Tam giác SAD
cân tại S, mặt bên  SAD vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng 3
4a , điểm N là trung điểm của cạnh SB. Khoảng cách từ điểm N đến mặt phẳng SCD bằng 3 2 4 8 3 A. a . B. a . C. a . D. a . 3 3 3 4 Lời giải Chọn A Trang 13/21 - WordToan S N K B A H D C
Gọi H là trung điểm của AD. Vì S
AD cân tại S SH A . D   SAD
   ABCD  AD SH.S Ta có 
SH   ABCDABCDV  SAD    ABCDS . ABCD 3 
Câu 20. Cho lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông cân tại C,CB  2 . a Biết rằng góc giữa B C
 và AC bằng 60 . Thể tích của khối lăng trụ đã cho bằng A. 3 2 2a . B. 3 2a . C. 3 2a . D. 3 a . Lời giải Chọn C A' C' B' A C I D B
Trong mặt phẳng ( ABC) , lấy điểm D sao cho ACBD là hình vuông. Khi đó ta có ADB C   là
hình bình hành  AC  DB  góc giữa B C
 và AC bằng góc giữa B C  và DB .
Xét hai tam giác vuông B BC , BB
D ta có BB chung và BD BC suy ra BBC  = BBD Suy ra B DC
là tam giác cân tại B .
Ta có ABC vuông cân tại C , BC a 2 suy ra AC a 2 và AB  2a , IA IB a , DC  2a Trường hợp 1:  0 DB C   120 a Khi đó 0 B I   . a tan 30 
< IB a (vô lý) 3
Trang 14/21 – Diễn đàn giáo viên Toán Trường hợp 2:  0 DB C
  60 khi đó B DC  đều cạnh 2a . Khi đó ta có B I   a 3 , 2 2
BB  3a a a 2 1
Thể tích lăng trụ đã cho Va aa ABC AB C    22 3 2 3. . 2
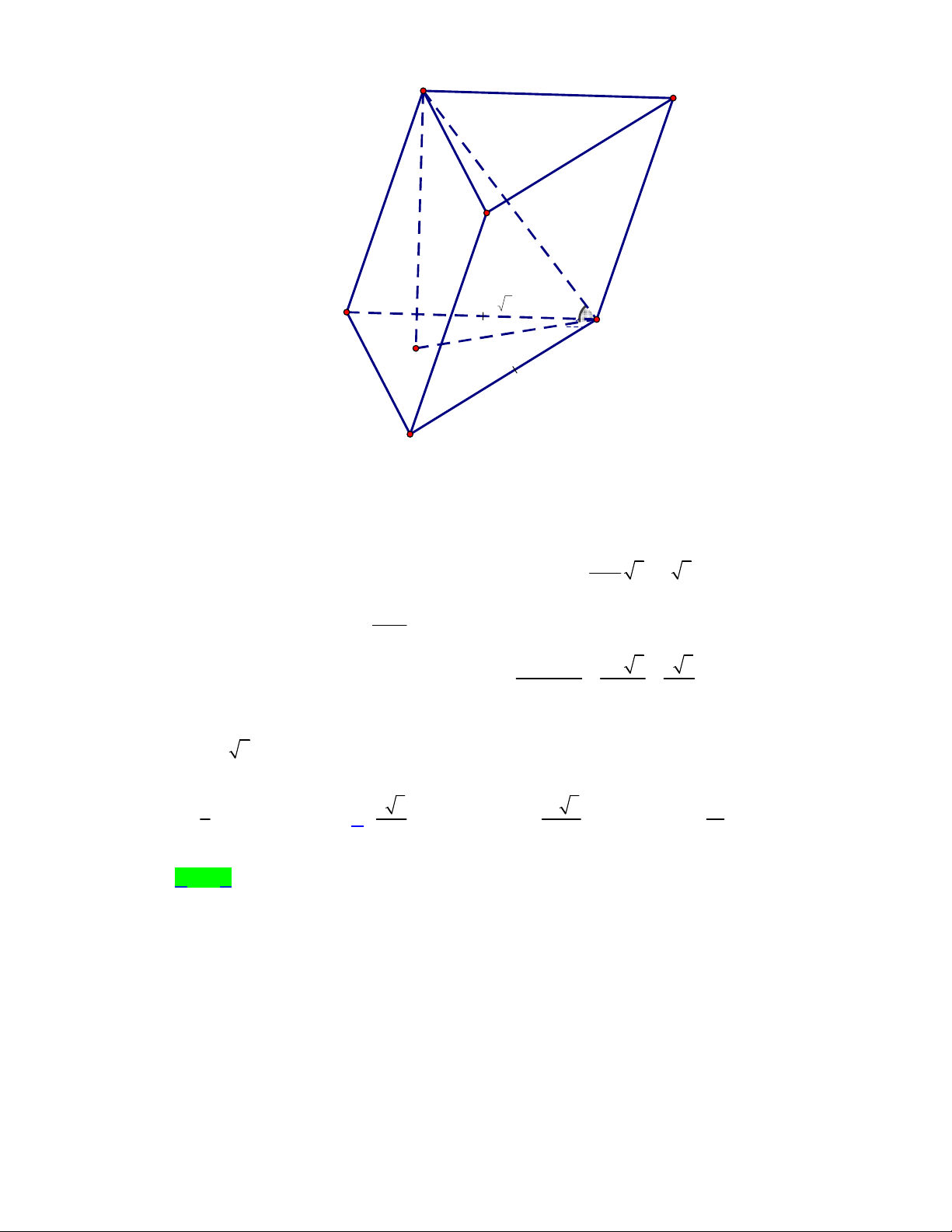
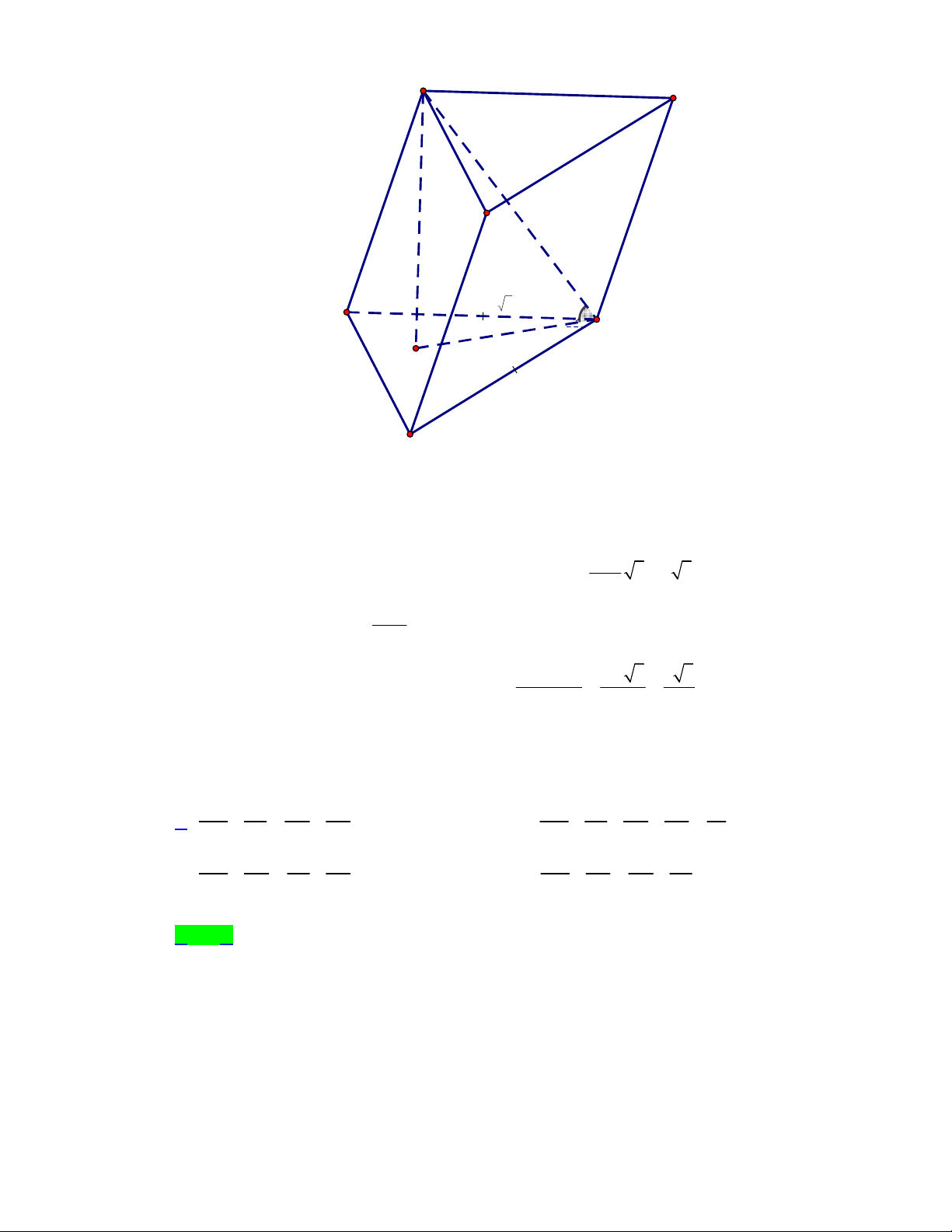
Câu 21. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB a, AD  2a. Cạnh bên SA vuông góc
với đáy và SA  3 .
a Điểm P là trung điểm của SC . Một mặt phẳng qua AP cắt hai cạnh SB
và SD lần lượt tại M và N . Gọi V là thể tích của khối chóp S.AMPN . Giá trị nhỏ nhất của 1 V bằng 1 2 1 4 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 3 3 3 Lời giải Chọn A S 3a P M N I A D a O 2a B C
Cách xác định mặt phẳng qua AP cắt hai cạnh SB , SD như hình vẽ. Gọi O là giao điểm của
hai đường chéo hình chữ nhật ABCD và I là giao điểm AP và MN . 1 1 Ta có 3 VAS.A . B AD  .3 . a .
a 2a  2a , S . ABCD 3 3
Áp dụng công thức tỉ số thể tích ta có V . SA SM .SP 1 SM V . SA SN.SP 1 SN S . AMP   . ; S.ANP   . V . SA . SB SC 2 SC V . SA . SD SC 2 SD S. ABC S . ADC SM SN Suy ra V  .V , V  .V . Khi đó S . AMP S . 4 ABCD SB S .ANP S . 4 ABCD SD 3  SM SN a V VV   . 1 S. AMP S. ANP    SB SD  2 Trang 15/21 - WordToan S M I N E D O B F SI 2
Ta có I là trọng tâm tam giác SAC nên  SO 3
Từ B, D lần lượt kẻ các đường thẳng song song với MN cắt SO tại E, F . Khi đó hai tam giác
OED  OFB (g.c.g) suy ra OE OF SB SF SO OF SD SE SO OE Ta có   ;   SM SI SI SN SI SI SB SD 2SO SM SN 4 4 Từ đó suy ra    3 suy ra    . Dấu bằng xảy ra khi SM SN SI SB SD SB SD 3  SM SN SM SN   MN BD . SB SD 3 3  SM SN a 4 a 2 2 Vậy 3 V   .  
a . Giá trị nhỏ nhất của V bằng 3 a . 1   1  SB SD  2 3 2 3 3
Câu 22. Cho lăng trụ tam giác ABC.A ' B 'C ' có đáy ABC là tam giác vuông cân tại A , cạnh
AC  2 2. Biết AC ' tạo với mặt phẳng ( ABC) một góc 0
60 và AC '  4 . Thể tích khối chóp .
B ACC ' A ' bằng 8 8 3 16 3 16 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn B
Trang 16/21 – Diễn đàn giáo viên Toán C' A' B' 4 2 2 C A H B
Gọi hình chiếu vuông góc của C ' lên  ABC  là H .
Suy ra  AC ABC    AC AH   0 ', ',  HAC '  60 . AC '
Trong HAC ' vuông tại H và  0
HAC '  60 suy ra C ' H  3  2 3 . 2 2 AC
Diện tích ABC là: S   4 . ABC 2 V 4.2 3 8 3
Thể tích của hình chóp . B ACC ' A ' là
ABC. A' B 'C ' V    .
B. ACC ' A' 3 3 3
Câu 23. Cho lăng trụ tam giác ABC.A ' B 'C ' có đáy ABC là tam giác vuông cân tại A , cạnh
AC  2 2. Biết AC ' tạo với mặt phẳng ( ABC) một góc 0
60 và AC '  4 . Thể tích khối chóp .
B ACC ' A ' bằng 8 8 3 16 3 16 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn B Trang 17/21 - WordToan C' A' B' 4 2 2 C A H B
Gọi hình chiếu vuông góc của C ' lên  ABC  là H .
Suy ra  AC ABC    AC AH   0 ', ',  HAC '  60 . AC '
Trong HAC ' vuông tại H và  0
HAC '  60 suy ra C ' H  3  2 3 . 2 2 AC
Diện tích ABC là: S   4 . ABC 2 V 4.2 3 8 3
Thể tích của hình chóp . B ACC ' A ' là
ABC. A' B 'C ' V    .
B. ACC ' A' 3 3 3
Câu 24: Cho hình chóp tứ giác đều S.ABCD . Gọi O là tâm hình vuông ABCD . Một mặt phẳng ( ) bất
kì cắt các cạnh bên S , A S ,
B SC, SD và đoạn SO lần lượt tại các điểm M , N, P,Q, I . Chọn đẳng thức đúng? 1 1 1 1 1 1 1 1 4 A.    . B.     . SM SP SN SQ SM SP SN SQ SI 1 1 1 1 1 1 1 1 C.    . D.    . SM SN SP SQ SM SQ SN SP Lời giải Chọn A
Trang 18/21 – Diễn đàn giáo viên Toán S M N I Q A P B O D C SA SC SB D S
Theo công thức tính tỉ lệ thể tích ta có:    . * SM SP SN SQ
Vì S.ABCD là hình chóp tứ giác đều nên ta có SA SB SC SD . 1 1 1 1 Do đó    . SM SP SN SQ
Chú ý: trong bài tập trên, thầy đã sử dụng công thức tỉ lệ thể tích của hình chóp tứ giác có đáy
là hình bình hành, khi tiến hành giải tự luận, các em cần chứng minh công thức * trước khi sử dụng.
Câu 25. Cho lăng trụ tam giác ABC.A' B 'C ' . Một mặt phẳng ( ) qua đường thẳng A ' B ' và trọng tâm
tam giác ABC , chia khối lăng trụ ABC.A' B 'C ' thành hai phần. Gọi V là thể tích khối đa diện 1 V
chứa đỉnh C và V là thể tích khối đa diện còn lại. Khi đó tỉ số 1 bằng 2 V2 V 17 V 19 V 10 V 8 A. 1  . B. 1  . C. 1  . D. 1  . V 10 V 8 V 17 V 19 2 2 2 2 Lời giải Chọn B Trang 19/21 - WordToan
Gọi G là trọng tâm của tam giác ABC . Ta có:
G      ABC  
AB / / AB  
AB   
  MN / / AB . 
AB   ABC  
   ABC MN     Gọi A M   B N
  CC  K .
Gọi H , F lần lượt là hình chiếu vuông góc của M , K trên mp  ABC . Xét: CM CN MN 2
Tam giác ABC , ta có: MN / / AB     ; CA CB AB 3 KM KN MN 2
Tam giác KAB , ta có: MN / / AB    
vì AB / / AB, AB  AB ; KAKBAB 3 KM KC CM 2
Tam giác KAC , ta có: CM / / AC    
vì AC / / AC, AC  AC ; KA ' KCAC 3 AM AH MH 1
Tam giác KAF , ta có: MH / / KF    
KF  3MH . A ' K AF KF 3 Ta có: V KM KN KC 2 2 2 8 K .MNC  . .  . .  . V
KAKCKC 3 3 3 27
K . AB C   8  V  .V . K .MNC K .    27 A B C Gọi VV .
ABC. AB C  
Trang 20/21 – Diễn đàn giáo viên Toán 1 1 Mặt khác, ta có: V  .KF.S  .3.MH .SV
K . AB C           3 A B C 3 A B C 8 8 19  V
.V V V  .V V . K .MNC 1 27 27 27 19 8
Do đó, V V V V V V . 2 1 27 27 V 19 Vậy, ta có: 1  . V 8 2 Trang 21/21 - WordToan
Document Outline

  • 6545
  • 1567941106_WT12-H12-C1-KIỂM TRA 45 PHÚT-KHỐI ĐA DIỆN-H12-THPT NGỖ SỸ LIÊN-BẮC GIANG-NĂM 2019