Đề kiểm tra 45 phút HK2 Toán 12 năm 2019 – 2020 trường THPT Phan Ngọc Hiển – Cà Mau

Đề kiểm tra 45 phút HK2 Toán 12 năm 2019 – 2020 trường THPT Phan Ngọc Hiển – Cà Mau mã đề 924 gồm 03 trang với 25 câu trắc nghiệm, nội dung kiểm tra thuộc chủ đề nguyên hàm, tích phân và ứng dụng, đề kiểm tra có đáp án và lời giải chi tiết.

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Trang 1/3 - Mã đề 924
SỞ GIÁO DỤC VÀ ĐÀO TẠO CÀ MAU
TRƯỜNG THPT PHAN NGỌC HIỂN
KIỂM TRA 45 PHÚT, HỌC KỲ II, NĂM HỌC 2019 - 2020
MÔN TOÁN 12
Thời gian làm bài : 45 phút; (Đề có 25 câu)
Câu 1: Họ nguyên hàm của hàm số
2
()
x
f x xe=
là
A.
2
1
() 2 .
2
x
Fx e x C

= −+


B.
( )
2
() 2 2 .
x
Fx e x C= −+
C.
( )
2
1
() 2 .
2
x
Fx e x C= −+
D.
2
11
() .
22
x
Fx e x C

= −+


Câu 2:
2
1
23
dx
x
+
∫
bằng
A.
. B.
7
ln
5
. C.
7
2 ln
5
. D.
1
ln 35
2
.
Câu 3: Tích phân
( )( )
1
0
3 1 3dxx x++
∫
bằng
A.
6
. B.
5
. C.
12
. D.
9
.
Câu 4: Trong các khẳng định sau, khẳng định nào sai?
A.
1
d ln 1
1
xxC
x
= ++
+
∫
( )
1x∀ ≠−
. B.
1
cos 2 d sin 2
2
xx x C= +
∫
.
C.
2
2
e
ed
2
x
x
xC= +
∫
. D.
2 d 2 ln 2
xx
xC= +
∫
.
Câu 5: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào
dưới đây?
A.
( )
2
1
22x dx
−
−+
∫
. B.
( )
2
1
22
x dx
−
−
∫
. C.
( )
2
2
1
2 24x x dx
−
− ++
∫
. D.
( )
2
2
1
2 24x x dx
−
−−
∫
.
Câu 6: Cho hàm số
( )
y fx=
xác định và liên tục trên đoạn
[
]
;ab
. Diện tích hình phẳng giới hạn
bởi đồ thị hàm số
( )
y fx=
, trục hoành và hai đường thẳng
,x ax b= =
được tính theo công thức
A.
( )
d
b
a
S fx x=
∫
. B.
( )
d
a
b
S fx x=
∫
. C.
( )
d
b
a
S fx x= −
∫
. D.
( )
d
b
a
S fx x=
∫
.
Câu 7: Biết
( )( )
2
1
d
ln 2 ln 3 ln 5
12 1
x
abc
xx
= ++
++
∫
. Khi đó giá trị
abc++
bằng
A.
1
. B.
0
. C.
2
. D.
3−
.
Câu 8: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
yx x
= −
và đồ thị hàm số
Mã đề 924
Trang 2/3 - Mã đề 924
2
.y xx= −
A.
37
12
B.
81
12
C.
13
D.
9
4
Câu 9: Tìm nguyên hàm của hàm số
( )
1
fx x
x
= +
A.
( )
2
1
ln
2
f x dx x x C=++
∫
. B.
( )
2
lnf x dx x x C= ++
∫
.
C.
( )
2
1
ln
2
f x dx x x C=++
∫
. D.
( )
2
lnf x dx x x C= ++
∫
.
Câu 10: Giả sử hàm số
(
)
y fx=
liên tục, nhận giá trị dương trên
(
)
0; +∞
và thỏa mãn
( )
11f =
,
( ) ( )
.3 1fx f x x
′
= +
, với mọi
0
x >
. Mệnh đề nào sau đây đúng?
A.
( )
3 54f<<
. B.
( )
2 53f<<
. C.
( )
1 52f<<
. D.
( )
4 55f<<
.
Câu 11: Cho hàm số
()y fx
=
có đạo hàm liên tục trên
và thỏa mãn
2
0
(2) 16, ( ) 4f f x dx
= =
∫
.
Tính
1
0
(2 )I xf x dx
′
=
∫
.
A.
13I
=
. B.
20I =
. C.
12I =
. D.
7
I
=
.
Câu 12: Nguyên hàm của hàm số
( )
1
22 1
fx
x
=
+
có dạng:
A.
( )
d 21fx x x C= ++
∫
. B.
( )
( )
1
d
2121
fx x C
xx
= +
++
∫
.
C.
( )
d 22 1fx x x C= ++
∫
. D.
( )
1
d 21
2
fx x x C= ++
∫
.
Câu 13: Tính tích phân
1
2 ln
d
2
e
x
Ix
x
+
=
∫
.
A.
33 22
3
+
. B.
32
3
+
. C.
32
3
−
. D.
33 22
3
−
.
Câu 14: Cho
1
0
()fx
∫
dx
1= −
;
3
0
()fx
∫
dx
5=
. Tính
3
1
()fx
∫
dx
A. 5. B. 4. C. 1. D. 6.
Câu 15: Cho biết
( )( )
2 13
dx ln 1 ln 2
12
x
ax bx C
xx
−
= ++ − +
+−
∫
.
Mệnh đề nào sau đây đúng?
A.
8ab−=
. B.
28ab−=
. C.
28ab+=
. D.
8ab+=
.
Câu 16: Tìm họ nguyên hàm của hàm số
( )
3 sinfx x x= −
.
A.
( )
2
3
d cos
2
x
fxx xC=++
∫
. B.
( )
d 3 cosfxx xC=++
∫
.
C.
( )
2
3
d cos
2
x
fxx xC=−+
∫
. D.
( )
2
d 3 cosfxx x xC=++
∫
.
Trang 3/3 - Mã đề 924
Câu 17: Cho
( )
Fx
là một nguyên hàm của hàm
( )
1
21
fx
x
=
+
; biết
( )
02F =
. Tính
( )
1F
.
A.
1
1 ln 3 2
2
F

. B.
1 ln 3 2F 
. C.
1 2 ln 3 2F 
. D.
1
1 ln 3 2
2
F 
.
Câu 18: Giá trị của
2
0
sin xdx
π
∫
bằng
A. 1. B. 0. C. -1. D.
2
π
.
Câu 19: Cho hàm số
( )
fx
thỏa mãn
(
)
x
f x xe
′
=
và
( )
02f =
.Tính
(
)
1
f
.
A.
( )
1 82fe= −
. B.
( )
1fe=
. C.
( )
13f =
. D.
( )
15fe= −
.
Câu 20: Tìm nguyên hàm của hàm số
(
)
1
12
fx
x
=
−
trên
1
;
2

−∞


.
A.
1
ln 2 1
2
xC
−+
. B.
( )
1
ln 1 2
2
xC−+
. C.
ln 2 1xC−+
. D.
1
ln 2 1
2
xC− −+
.
Câu 21: Cho hàm số
( )
fx
liên tục trên
[ ]
0;10
thỏa mãn
( )
10
0
7f x dx =
∫
,
( )
6
2
3f x dx =
∫
. Tính
( ) ( )
2 10
06
P f x dx f x dx= +
∫∫
.
A.
4P =
. B.
10P =
. C.
6P = −
. D.
7P =
.
Câu 22: Cho hàm số
( )
y fx=
. Đồ thị của hàm số
( )
y fx
′
=
như hình vẽ.
Đặt
( ) ( ) ( )
2
21gx f x x= −−
.
Mệnh đề nào dưới đây đúng?
A.
( ) ( )
( )
153
g gg−< <
. B.
( ) ( ) ( )
35 1ggg< <−
.
C.
( ) ( ) ( )
5 13
gg g< −<
. D.
( ) ( ) ( )
135g gg−< <
.
Câu 23: Tính diện tích S của hình phẳng (H) giới hạn bởi đồ thị hàm số
32
32yx x=−+ −
, hai trục
tọa độ và đường thẳng
2x =
.
A.
1
.
3
S =
B.
19
.
2
S =
C.
9
.
2
S
=
D.
5
.
2
S =
Câu 24: Tính tích phân
1
2
0
( 1) dIx x= +
∫
A.
1
2
I =
. B.
1
3
I =
. C.
7
3
I =
. D.
1
2
I = −
.
Câu 25: Nếu
2
3tx= +
thì tích phân
2
2
1
3I x x dx= +
∫
trở thành
A.
7
2
I tdt=
∫
. B.
7
2
2
I t dt=
∫
. C.
7
2
2
I t dt=
∫
. D.
7
3
2
I t dt=
∫
.
------ HẾT ------
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO CÀ MAU
TRƯỜNG THPT PHAN NGỌC HIỂN
KIỂM TRA 45 PHÚT – NĂM HỌC 2019 - 2020
CHƯƠNG III - MÔN TOÁN 12
Thời gian làm bài : 45 Phút; (Đề có 25 câu)
Phần đáp án câu trắc nghiệm:
Câu
651
742
833
924
1
D
A
B
D
2
D
D
B
A
3
C
A
B
D
4
B
B
A
D
5
A
D
C
C
6
A
C
A
D
7
D
A
D
B
8
B
A
C
A
9
B
C
B
C
10
D
D
D
A
11
B
C
D
D
12
A
C
C
D
13
C
B
C
D
14
C
D
D
D
15
D
B
D
A
16
B
A
C
A
17
A
D
A
A
18
C
C
C
A
19
A
B
A
C
20
B
C
D
D
21
D
C
C
A
22
B
B
B
A
23
D
B
D
D
24
D
A
B
C
25
A
D
B
C
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO CÀ MAU
KIỂM TRA 45 PHÚT, HỌC KỲ II, NĂM HỌC 2019 - 2020
TRƯỜNG THPT PHAN NGỌC HIỂN MÔN TOÁN 12 Mã đề 924
Thời gian làm bài : 45 phút; (Đề có 25 câu)
Câu 1: Họ nguyên hàm của hàm số 2 ( ) x f x = xe là A. 2x  1 F(x) 2e x  = − +   C. B. 2 ( ) = 2 x F x
e (x − 2) + C.  2  C. 1 2 ( ) x
F x = e (x − 2) + C. D. 1 2x  1 F(x) e x  = − +   C. 2 2  2  2 Câu 2: dx ∫ bằng 2x + 3 1 A. 1 7 ln . B. 7 ln . C. 7 2ln . D. 1 ln35 . 2 5 5 5 2 1
Câu 3: Tích phân ∫(3x+ )1(x+3)dx bằng 0 A. 6 . B. 5. C. 12. D. 9.
Câu 4: Trong các khẳng định sau, khẳng định nào sai?
A. 1 dx = ln x +1 + C ∫ ( x ∀ ≠ − ) 1 . B. 1 cos 2 d
x x = sin 2x + C x ∫ . +1 2 2x C. 2x e e dx = + C ∫ .
D. 2xd = 2x x ln 2 + C 2 ∫ .
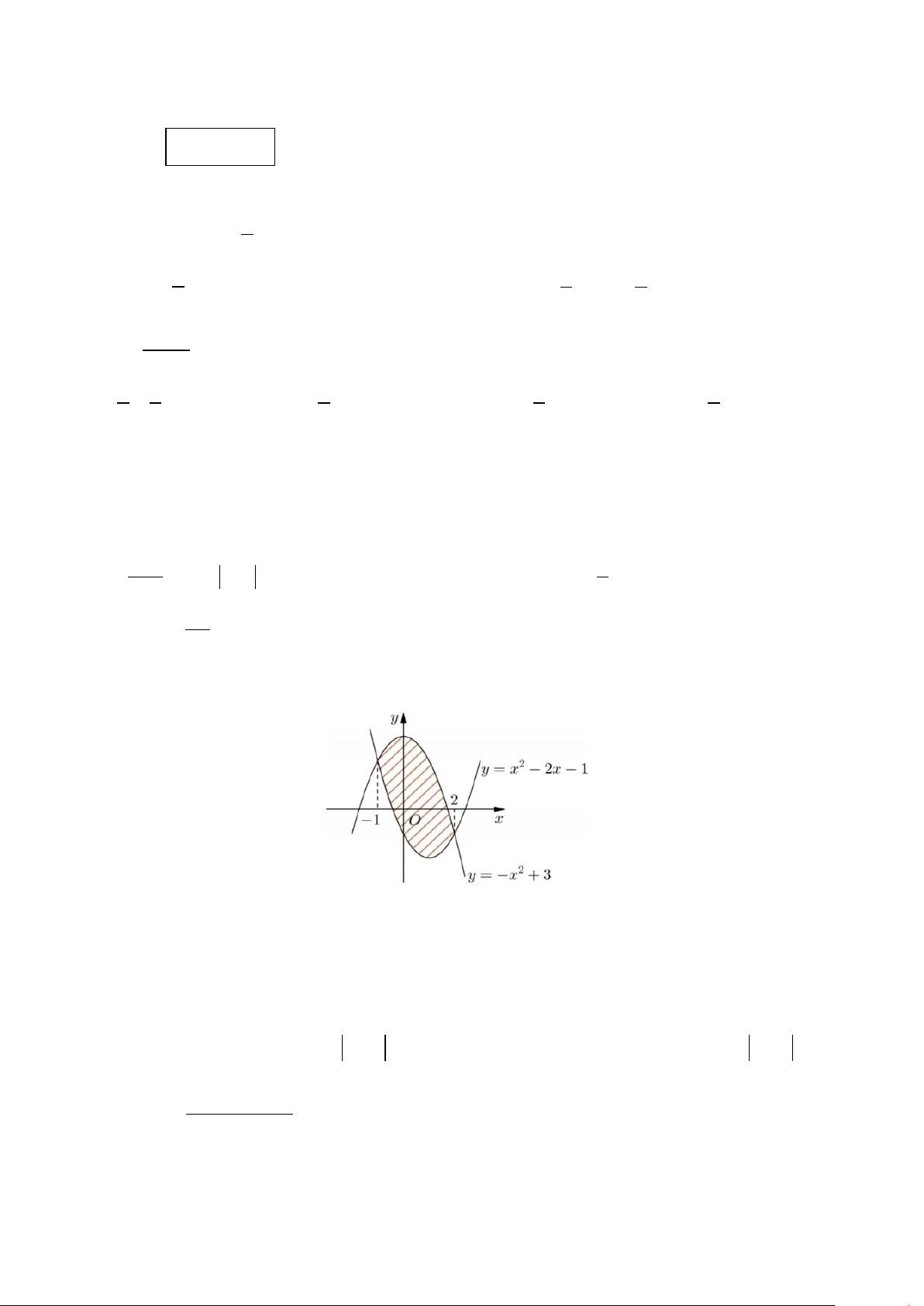
Câu 5: Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 2 2 2 2 A. ∫ ( 2 − x + 2)dx .
B. ∫ (2x −2)dx. C. ∫ ( 2 2
− x + 2x + 4)dx . D. ∫ ( 2
2x − 2x − 4)dx. 1 − 1 − 1 − 1 −
Câu 6: Cho hàm số y = f (x) xác định và liên tục trên đoạn [ ;ab]. Diện tích hình phẳng giới hạn
bởi đồ thị hàm số y = f (x) , trục hoành và hai đường thẳng x = a, x = b được tính theo công thức b a b b A. S = f
∫ (x)dx . B. S = f
∫ (x) dx.
C. S = − f
∫ (x)dx. D. S = f
∫ (x) dx. a b a a 2 Câu 7: Biết dx
= a ln 2 + bln 3+ c ln 5 ∫
. Khi đó giá trị a + b + c bằng x +1 2x +1 1 ( )( ) A. 1. B. 0 . C. 2 . D. 3 − .
Câu 8: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y = x − x và đồ thị hàm số Trang 1/3 - Mã đề 924 2
y = x − x . A. 37 B. 81 C. 13 D. 9 12 12 4
Câu 9: Tìm nguyên hàm của hàm số ( ) 1 f x = x + x A. f (x) 1 2
dx = ln x + x + ∫ C . B. f (x) 2
dx = ln x + x + ∫ C . 2 C. f (x) 1 2
dx = ln x + x + ∫ C . D. f (x) 2
dx = ln x + x + ∫ C . 2
Câu 10: Giả sử hàm số y = f (x) liên tục, nhận giá trị dương trên (0;+∞) và thỏa mãn f ( ) 1 =1,
f (x) = f ′(x). 3x +1, với mọi x > 0 . Mệnh đề nào sau đây đúng?
A. 3 < f (5) < 4.
B. 2 < f (5) < 3.
C. 1< f (5) < 2 .
D. 4 < f (5) < 5. 2
Câu 11: Cho hàm số y = f (x) có đạo hàm liên tục trên  và thỏa mãn f (2) =16, f (x)dx = 4 ∫ . 0 1 Tính I = xf (2 ′ x)dx ∫ . 0 A. I =13 . B. I = 20 . C. I =12. D. I = 7 .
Câu 12: Nguyên hàm của hàm số f (x) 1 = có dạng: 2 2x +1 A. 1 f
∫ (x)dx = 2x+1+C . B. f ∫ (x)dx = + . ( C 2x + ) 1 2x +1 C. f
∫ (x)dx = 2 2x+1+C . D. f ∫ (x) 1 dx = 2x +1 + C . 2 e
Câu 13: Tính tích phân 2 + ln x I = dx ∫ . 2x 1 A. 3 3 + 2 2 . B. 3 + 2 . C. 3 − 2 . D. 3 3 − 2 2 . 3 3 3 3 1 3 3
Câu 14: Cho f (x) ∫ dx = 1 − ; f (x) ∫
dx = 5. Tính f (x) ∫ dx 0 0 1 A. 5. B. 4. C. 1. D. 6. Câu 15: Cho biết 2x −13 ∫ ( )( = + + − + . +
x − )dx a ln x 1 bln x 2 C x 1 2
Mệnh đề nào sau đây đúng?
A. a −b = 8 .
B. 2a −b = 8 .
C. a + 2b = 8.
D. a + b = 8 .
Câu 16: Tìm họ nguyên hàm của hàm số f (x) = 3x −sin x . 2 A. ∫ ( ) 3 d x f x x = + cos x + C .
B. ∫ f (x)dx = 3+ cos x +C . 22 C. ∫ ( ) 3 d x f x x = − cos x + C .
D. ∫ f (x) 2
dx = 3x + cos x + C . 2 Trang 2/3 - Mã đề 924
Câu 17: Cho F (x) là một nguyên hàm của hàm f (x) 1 =
; biết F (0) = 2. Tính F ( ) 1 . 2x +1 A. F   1
1  ln 3  2 . B. F   1  ln 3  2 . C. F   1  2 ln 3  2 . D. F   1 1  ln 3  2 . 2 2 π 2
Câu 18: Giá trị của sin xdx ∫ bằng 0 A. 1. B. 0. C. -1. D. π . 2
Câu 19: Cho hàm số f (x) thỏa mãn ′( ) x
f x = xe và f (0) = 2 .Tính f ( ) 1 . A. f ( ) 1 = 8 − 2e . B. f ( ) 1 = e . C. f ( ) 1 = 3. D. f ( ) 1 = 5 − e .
Câu 20: Tìm nguyên hàm của hàm số f (x) 1 = trên  1  ;  −∞ . 1− 2x 2   
A. 1 ln 2x −1 + C .
B. 1 ln(1− 2x) + C .
C. ln 2x −1 + C . D. 1
− ln 2x −1 + C . 2 2 2 10 6
Câu 21: Cho hàm số f (x) liên tục trên [0;10] thỏa mãn f
∫ (x)dx = 7 , f
∫ (x)dx = 3. Tính 0 2 2 10 P = f
∫ (x)dx + f ∫ (x)dx. 0 6 A. P = 4 . B. P =10. C. P = 6 − . D. P = 7 .
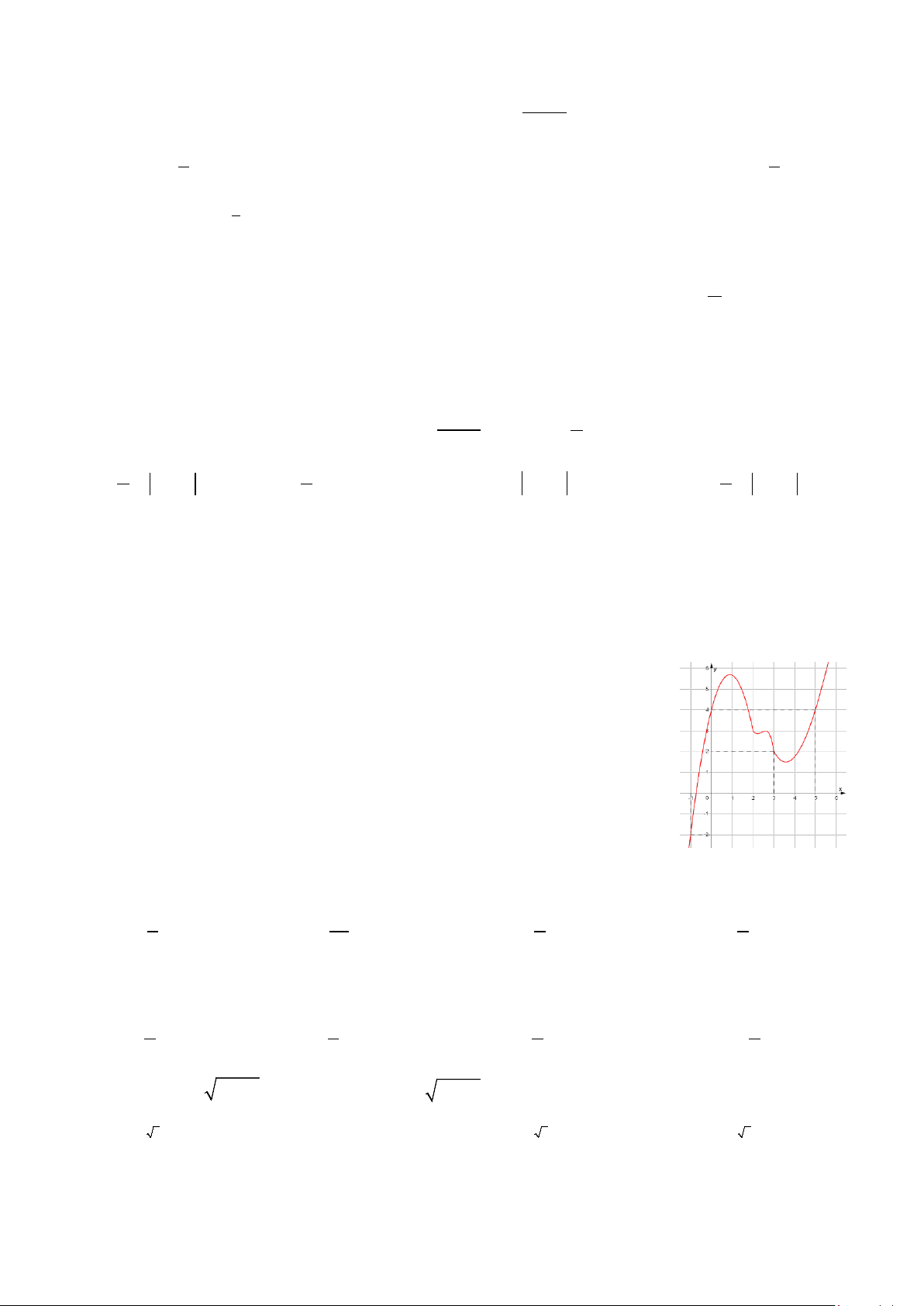
Câu 22: Cho hàm số y = f (x) . Đồ thị của hàm số y = f ′(x) như hình vẽ.
Đặt g (x) = f (x) −(x − )2 2 1 .
Mệnh đề nào dưới đây đúng? A. g (− )
1 < g (5) < g (3).
B. g (3) < g (5) < g (− ) 1 .
C. g (5) < g (− ) 1 < g (3). D. g (− )
1 < g (3) < g (5).
Câu 23: Tính diện tích S của hình phẳng (H) giới hạn bởi đồ thị hàm số 3 2
y = −x + 3x − 2, hai trục
tọa độ và đường thẳng x = 2 . A. 1 S = . B. 19 S = . C. 9 S = . D. 5 S = . 3 2 2 2 1
Câu 24: Tính tích phân 2
I = (x +1) dx ∫ 0 A. 1 I = . B. 1 I = . C. 7 I = . D. 1 I = − . 2 3 3 2 2 Câu 25: Nếu 2
t = x + 3 thì tích phân 2
I = x x + 3dx ∫ trở thành 1 7 7 7 7
A. I = ∫ tdt . B. 2 I = ∫t dt . C. 2 I = ∫ t dt . D. 3 I = ∫ t dt . 2 2 2 2
------ HẾT ------ Trang 3/3 - Mã đề 924
SỞ GIÁO DỤC VÀ ĐÀO TẠO CÀ MAU
KIỂM TRA 45 PHÚT – NĂM HỌC 2019 - 2020
TRƯỜNG THPT PHAN NGỌC HIỂN
CHƯƠNG III - MÔN TOÁN 12
Thời gian làm bài : 45 Phút; (Đề có 25 câu)
Phần đáp án câu trắc nghiệm: Câu 651 742 833 924 1 D A B D 2 D D B A 3 C A B D 4 B B A D 5 A D C C 6 A C A D 7 D A D B 8 B A C A 9 B C B C 10 D D D A 11 B C D D 12 A C C D 13 C B C D 14 C D D D 15 D B D A 16 B A C A 17 A D A A 18 C C C A 19 A B A C 20 B C D D 21 D C C A 22 B B B A 23 D B D D 24 D A B C 25 A D B C 1
Document Outline

  • de 924
  • Phieu soi dap an