Đề kiểm tra chất lượng Toán 9 tháng 5 năm 2024 phòng GD&ĐT Chương Mỹ – Hà Nội

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề kiểm tra chất lượng môn Toán 9 tháng 5 năm học 2023 – 2024 phòng Giáo dục và Đào tạo huyện Chương Mỹ, thành phố Hà Nội; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!

36 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 9

Môn: Toán 9

Thông tin:

8 trang 2 tháng trước

Tác giả:

Profile Lê Phương
ĐÁP ÁN – HƯỚNG DẪN CHẤM
Bài I (2,0 điểm)
Câu Nội dung Điểm
1)
(0,5 điểm)
Thay x = 25 (TMĐK) vào biểu thức A, ta được:
25 5 5
5 1 6
25 1
A
Vậy
5
6
A khi x = 25
0,25
0,25
2)
(1,0 điểm)
Với
0; 4
, ta có:
7 6 3 1
4
2 2
7 6 3 1
2 2
2 2
x x
B
x
x
x x
x
x x
x x
0,25
3
7 6 2
2 2
7 6 3 2 6 2
2
2
2 2 2 2
2
x
x x x
x
x x
x x
x x
x
x
x
x x
x
0,25
2
3 2
2
2 . 1
2
1
2
2
x x
x
x
x
x
x
x
x
x
0,25
Vậy B
1
2
x
x
với
0; 4
0,25
3)
(0,5 điểm)
+) Ta có:
1
.
2 2
1
.
x x
P AB
x
x
x
x
+) Với
0; 4
x x
, ta có:
0
0
P P
P P
P
0
2
x
x
0,25
Với
0; 4 0
x x x
Nên để
0 2 0
2
x
x
x
2 4
x x
+) Kết hợp ĐKXĐ, ta có:
0 4
x
Mà
x
là s
ố
nguyên
l
ớ
n nh
ấ
t
nên
3
x
(tmđk)
0,25
Bài II (2,0 điểm)
1
(1,5 điểm)
Gọi vận tốc xe của bạn Tú là x (km/h, x > 0)
Khi đó vận tốc xe của bạn Dũng là x +4 (km/h).
0,25
0,25
Thời gian bạn Tú đi hết quãng đường AB là:
28
x
(h)
Thời gian bạn Dũng đi hết quãng đường AB là:
28
4
x
(h)
0,25
Vì bạn Dũng đến B sớm hơn bạn Tú 10 phút tức là
1
6
h
nên
ta có phương trình:
2
1
6
28 28
4 672 0
4
x x
x x
0,25
Giải phương trình ta được
1
24
x
(TMĐK);
2
28
x
(Loại)
0,25
Vận tốc xe của Tú là 24 km/h, vận tốc xe của Dũng là 28 km/h.
Như vậy thì bạn Tú đi đúng vận tốc quy định, còn bạn Dũng đi
không đúng v
ậ
n t
ố
c quy đ
ị
nh.
0,25
2
(0,5 điểm)
Ký hiệu độ dài đường sinh của hình nón là
15
l
cm, bán kính đáy
nón
là
9
R
cm, chi
ề
u cao là h
Chiều cao của hình nón bằng
2 2 2 2
15 9 12
h l R
cm.
0,25
Thể tích của hình nón bằng :
2 2 3
1 1
. .9 .12 324 1017,36
3 3
V R h cm
0,25
Bài III (2,5 điểm)
Câu Nội dung Điểm
1
(1,0 điểm)
1
3 1 2
3 4
3
5 1 4
3 4
y
x
y
x
Điều kiện:
4
; 1
3
x y
Đặt
1
; 1 0; 0 .
3 4
a b y a b
x
0,25
Hệ phương trình trở thành
1
2 3
3 2 2 3
2
3 2 3 5 4
3 5 4 4 2 1
2
a
a b
a b a b
b b
a b b
b
(thỏa mãn).
Trở lại ẩn cũ:
2
1 1
3 4 2
3 4 2 (tm)
2
3 4 2
3 4 2
3
1
1
1
1
3
4
2
4
x
x
x
x
x
x
y
y
y tm
0,25
Vậy Hệ phương trình có 2 nghiệm (x ; y) là
3 2 3
2; ; ;
4 3 4
0,25
2)
(1,5 điểm)
a) Xét phương trình hoành độ giao điểm của
( )
d
và
( )
P
:
2 22 2
(2 1) 2 (2 1) 2 0 1
x xm x m m x m
Tính được:
2
2 2 2
2 1 4 2 4 4 1 4 8 4 7
m m m m m m
0,25
0,25
Để
( )
d
cắt
( )
P
tại hai điểm phân biệt
Khi pt (1) có 2 nghiệm phân biệt
7
0 4 7 0 (*)
4
m m
0,25
Gọi
1 2
;
x x
là hai nghiệm của phương trình (1)
Theo định lý Viete, ta có:
1 2
2
1 2
2 1 (2)
. 2 (3)
x x m
x x m
Mà
2
1 2 1 2
(2 1) 2 7 (4)
x m x x x
Thay (2) vào (4) ta được:
2
1 1 2 2 1 2
( ) 2 7
x x x x x x
0,25
2 2
1 2 1 2 1 2
2
1 2 1 2
2 7
7
( ) 3
x x x x x x
x x x x
2
2 2
2
2
2 1 7
4 4 1 3 6 7 0
4 12 0
2 6 0
3 2m
m m m
m m
m m
m
2
6
m TM
m L
V
ậ
y
2
m
là giá tr
ị
c
ầ
n tìm.
0,25
0,25
Bài IV (3,0 điểm)
Câu Nội dung Điểm
Hình vẽ
0,25
1)
(0,75
đi
ể
m)
+)
l
ậ
p lu
ậ
n
:
0
90
ABO
0,25
+)
l
ậ
p lu
ậ
n
:
0
90
ACO
0,25
+) Chứng minh: Tứ giác
ABOC
nội tiếp 0,25
2)
(1,5 điểm)
+) Chứng minh:
ABD
AEB ( g.g)
+
ch
ỉ
ra :
2
.
AD AE AB
(1)
0,25
+) lập luận
AO
là đường trung trực của
BC
AO BC
tại H
+) Chỉ ra:
2
.AH AO AB
(HTL trong tam giác vuông) (2)
T
ừ
(1) và (2) s
uy ra:
. .
AH AO AD AE
0,25
0,25
+) Từ
. .AH AO AD AE
Suy ra:
AH AD
AE AO
mà
DAH
chung
+) Ch
ứ
ng minh:
AHD
AEO( c.g.c)
0,25
+ chỉ ta
AHD AEO
hay
AHD EDO
(do
DEO EDO
vì
ODE
cân tại O)
Chứng minh tứ giác:
DHOE
nội tiếp
EDO EHO
( 2 góc nội tiếp cùng chắn cung
EO
)
0,25
+ chỉ ra
AHD EHO
+) chứng minh được
DHB EHB
( cùng phụ với 2 góc bằng nhau)
Do dó
HB
là tia phân giác của
DHE
0,25
3)
(0,5 điểm)
0,25
+ Ta có
AHD EDO
(cmt) hay
XHD DEO
+ Chứng minh được tứ giác
DXYH
nội tiếp ( do
0
90 )
DXH DYH
suy ra
XYD XHD
+ Chứng minh được tứ giác
DYZE
nội tiếp suy ra
EYZ EDZ
Khi đó
0
90
XYZ XYD DYE EYZ XHD EDZ
0
90
DEO EDZ
Mà
DEZ
vuông tại Z nên
0
90
DEO EDZ
Nên
0
180
XYZ
vậy 3 điểm
, ,
X Y Z
thẳng hàng ( đpcm)
0,25
0,25
Bài V (0,5 điểm)
Ta có :
2
1 2 1 2 0 3 2
x x x x x
2
2 3 2 3 0 5 6
y y y y y
Khi đó
(2 5)(3 2 ) 6 10 4 15
P x y x y xy
2 2
2
2 3 5 2 15 2 2 8 15
2 1 1
x y xy x xy y
x y
0,25
Dấu “ = ” xảy ra khi
2
2
1 2 0
3 2
5 6 2 3 0 2( )
x x
x x
y y y y x y tmdk
x y
x y
Vậy
P
đạt giá trị nhỏ nhất bằng
1
khi
2
x y
.
0,25
Chú ý: Các cách giải khác đúng vẫn cho điểm tối đa
| 1/8
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


ĐÁP ÁN – HƯỚNG DẪN CHẤM Bài I (2,0 điểm) Câu Nội dung Điểm
Thay x = 25 (TMĐK) vào biểu thức A, ta được: 1) A  25  5  5 0,25 25  1 5  1 6 (0,5 điểm) 0,25 Vậy A  5 khi x = 25 6
Với x  0; x  4 , ta có: 7 x  6 x  3 1 B    x  4 x  2 2  x 0,25 7 x  6 x  3 1     x  2 x  2 x  2 x  2 x   x 3 7 6  x 2 x  2    
x  2 x  2  x  2 x  2  x  2 x  2 0,25 2)
7 x  6  x  3 x  2 x  6  x  2   x 2 x 2 (1,0 điểm) x  3 x  2   x 2 x 2  x 2. x  1   0,25 x  2 x  2 x 1  x 2  Vậy B x 1  với x  0; x  4 0,25 x  2 +) Ta có: x  1  .  . x x P AB  x  1 x  2 x  2 3)
+) Với x  0; x  4 , ta có:   (0,5 điểm) P P 0  P  P   P  0 x   0 0,25 x  2
Với x  0; x  4  x  0 Nên để x  0  x  2  0 x  2  x  2  x  4
+) Kết hợp ĐKXĐ, ta có: 0  x  4 0,25
Mà x là số nguyên lớn nhất nên x  3 (tmđk) Bài II (2,0 điểm)
Gọi vận tốc xe của bạn Tú là x (km/h, x > 0) 0,25
Khi đó vận tốc xe của bạn Dũng là x +4 (km/h). 0,25 28
Thời gian bạn Tú đi hết quãng đường AB là: (h) x 28 0,25
Thời gian bạn Dũng đi hết quãng đường AB là: (h) x  4 1 (1,5 điểm) 1
Vì bạn Dũng đến B sớm hơn bạn Tú 10 phút tức là h nên 6 28 28 0,25 ta có phương trình: 1 2 
  x  4x  672  0 x x  4 6
Giải phương trình ta được x  24 (TMĐK); x  2  8 (Loại) 1 2 0,25
Vận tốc xe của Tú là 24 km/h, vận tốc xe của Dũng là 28 km/h.
Như vậy thì bạn Tú đi đúng vận tốc quy định, còn bạn Dũng đi 0,25
không đúng vận tốc quy định.
Ký hiệu độ dài đường sinh của hình nón là l 15 cm, bán kính đáy
nón là R  9 cm, chiều cao là h 2
Chiều cao của hình nón bằng 2 2 2 2
h  l  R  15  9 12 cm. 0,25
(0,5 điểm) Thể tích của hình nón bằng : 1 1 2 2
V   R h  . .9 .12  324  1017,36 3 cm  0,25 3 3 Bài III (2,5 điểm) Câu Nội dung Điểm  1  3 y 1  2  3x  4   3  1  5 y 1  4  3x  4  0,25
(1,0 điểm) Điều kiện: x  4;y  1 3 1 Đặt a 
; b  y 1 a  0;b  0. 3x  4
Hệ phương trình trở thành  1  a  3b  2   2  3  a  2  3 a a b b  2        (thỏa mãn). 3  a  5b  4 3
 2  3b  5b  4  4  b  2 1 b    2 Trở lại ẩn cũ:  x  2  1 1 3x  4  2   3x  4  2      2 (tm)  3x  4 2  3x  4  2  x     1    3 0,25  1 y 1  y 1     4 3   2 y  tm  4  3    2 3 0,25
Vậy Hệ phương trình có 2 nghiệm (x ; y) là 2;     ; ;    4     3 4 
a) Xét phương trình hoành độ giao điểm của (d)và (P): 2 2 2 2
x  (2m 1)x  m  2  x  (2m 1)x  m  2  0   1 0,25 Tính được:
   m  2   2 m    2 m  m   2 2 1 4 2 4 4 1 4m  8  4m  7 0,25
Để (d) cắt (P) tại hai điểm phân biệt
Khi pt (1) có 2 nghiệm phân biệt 0,25
    m    m  7 0 4 7 0 (*) 4
Gọi x ;x là hai nghiệm của phương trình (1) 1 2 x  x  2m 1 (2)
Theo định lý Viete, ta có: 1 2  x .x  2 m  2 (3) 2)  1 2 Mà 2
x  (2m 1)x  2x x  7 (4) 1 2 1 2 0,25
(1,5 điểm) Thay (2) vào (4) ta được: 2
x  (x  x )x  2x x  7 1 1 2 2 1 2 2 2
 x  x  x x  2x x  7 1 2 1 2 1 2 2  (x  x )  3x x  7 1 2 1 2   m  2  3 2 2 1 m  2  7 0,25  2 4m  4m  1 2 3m  6  7  0  2 m  4m 12  0
 m 2m  6  0 m   2 TM   0,25 m    6 L
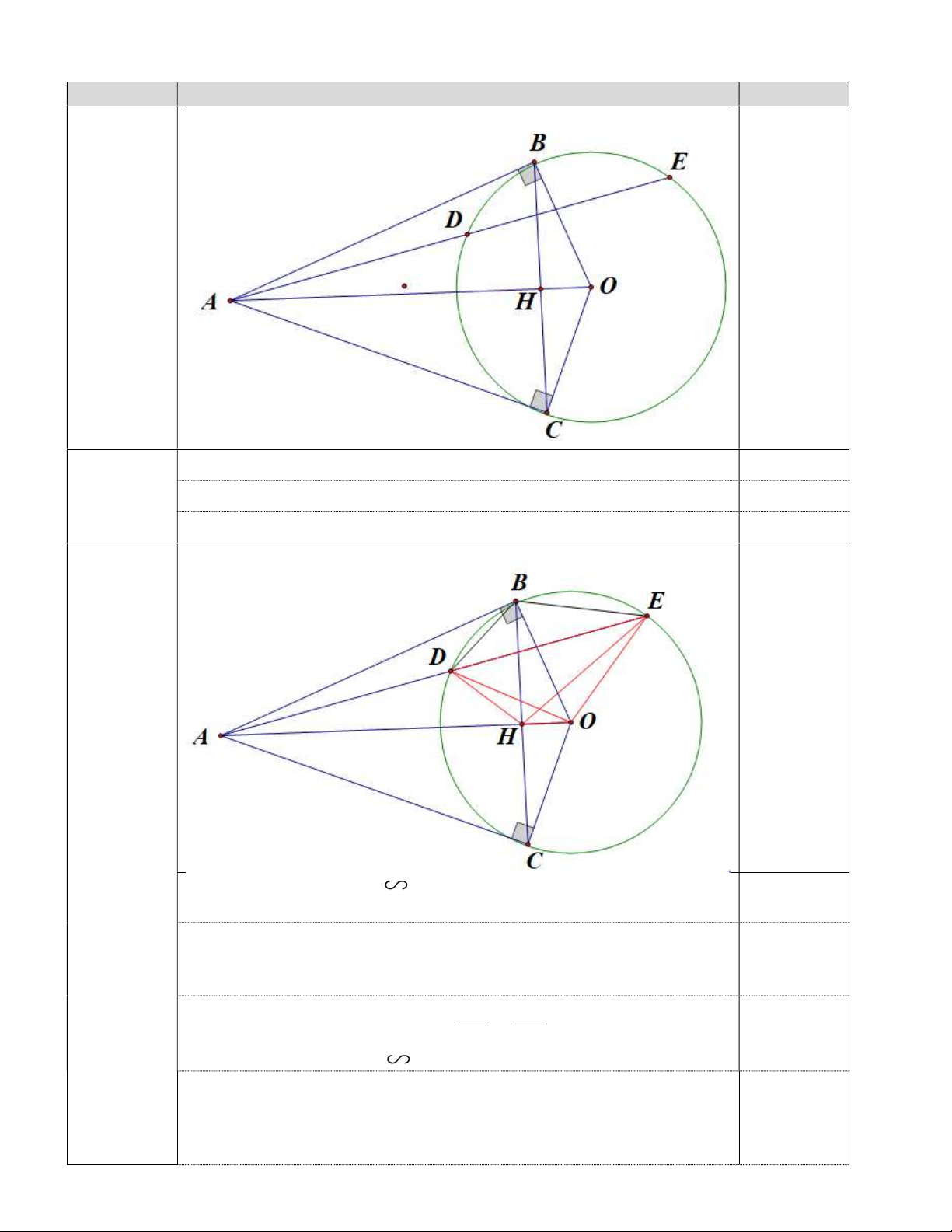
Vậy m  2 là giá trị cần tìm. Bài IV (3,0 điểm) Câu Nội dung Điểm Hình vẽ 0,25 1) +) lập luận :  0 ABO  90 0,25 (0,75 +) lập luận:  0 ACO  90 0,25 điểm)
+) Chứng minh: Tứ giác ABOC nội tiếp 0,25 2) (1,5 điểm) +) Chứng minh:  ABD  AEB ( g.g) 0,25 + chỉ ra : 2 AD.AE  AB (1)
+) lập luận AO là đường trung trực của BC  AO  BC tại H 0,25 +) Chỉ ra: 2
AH.AO  AB (HTL trong tam giác vuông) (2) 0,25 T
ừ (1) và (2) suy ra: AH.AO  AD.AE
+) Từ AH.AO  AD.AE Suy ra: AH AD  mà  DAH chung AE AO + ) Chứng minh:  AHD  AEO( c.g.c) 0,25 + chỉ ta   AHD  AEO hay   AHD  EDO (do   DEO  EDO vì ODE cân tại O)
Chứng minh tứ giác: DHOE nội tiếp  
 EDO  EHO ( 2 góc nội tiếp cùng chắn cung EO ) 0,25 + chỉ ra   AHD  EHO +) chứng minh được  
DHB  EHB ( cùng phụ với 2 góc bằng nhau) 0,25
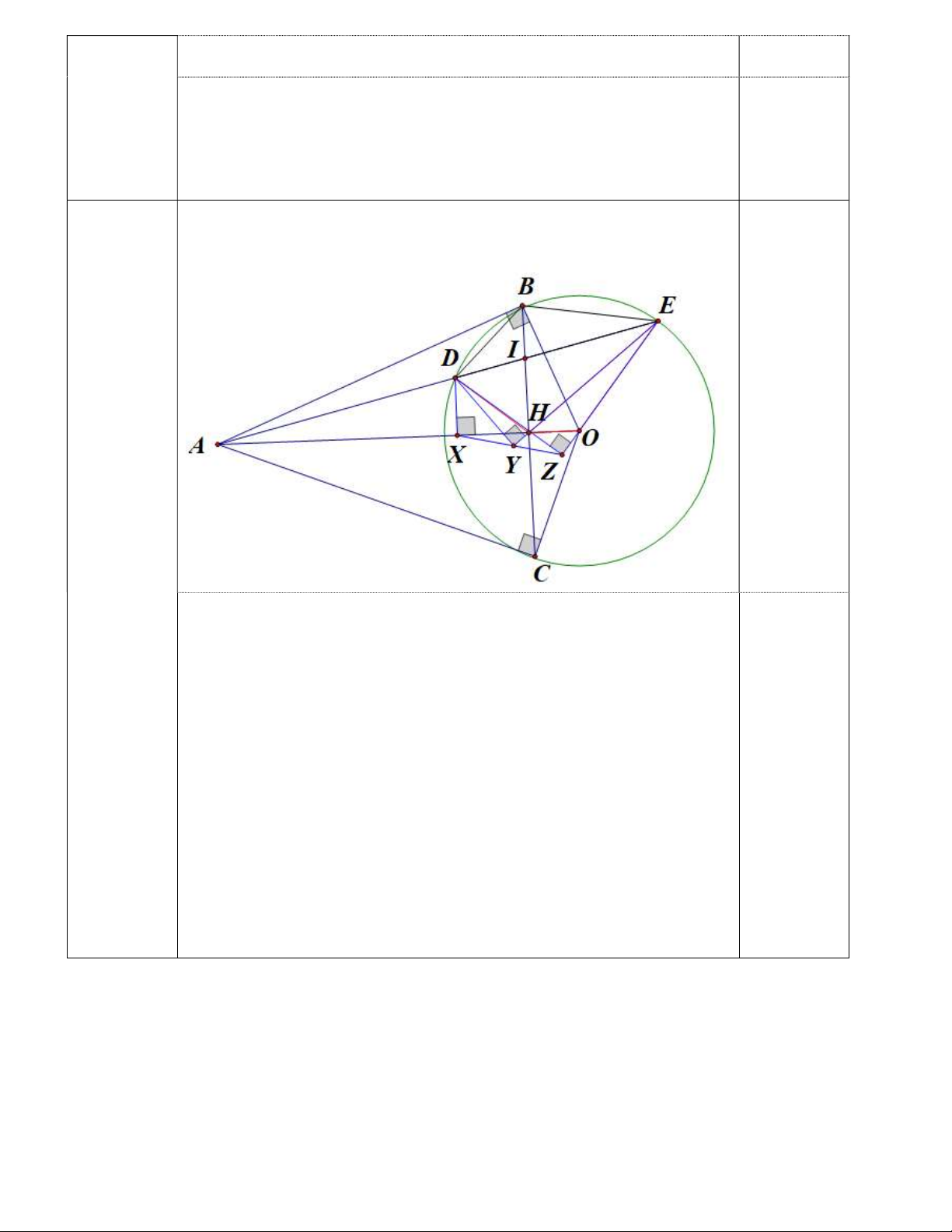
Do dó HB là tia phân giác của  DHE 0,25 3) (0,5 điểm) + Ta có   AHD  EDO (cmt) hay   XHD  DEO
+ Chứng minh được tứ giác DXYH nội tiếp ( do   DXH  DYH  0 90 )suy ra   XYD  XHD
+ Chứng minh được tứ giác DYZE nội tiếp suy ra   EYZ  EDZ 0,25 Khi đó      0 
XYZ  XYD  DYE  EYZ  XHD  90  EDZ    DEO  EDZ  0 90
Mà DEZ vuông tại Z nên   DEO  EDZ  0 90 0,25 Nên  XYZ  0
180 vậy 3 điểm X,Y,Z thẳng hàng ( đpcm) Bài V (0,5 điểm)
Ta có :  x   x  x   2 1 2 1 2  0  3x  x  2
 y    y   y   2 2 3 2 3  0  5y  y  6
Khi đó P  (2x  5)(3 2y)  6x 10y  4xy 15
 23x  5y  2xy 15  2 2 2
x  2xy  y  8 15 0,25  2x  y2 11 2 3  x  x  2   x   1 x  2  0   Dấu “ = ” xảy ra khi 2 5  y  y  6  
 y  2 y  3  0  x  y  2(tmdk)  x y   x  y   0,25
Vậy P đạt giá trị nhỏ nhất bằng 1 khi x  y  2 .
Chú ý: Các cách giải khác đúng vẫn cho điểm tối đa
Document Outline

  • chương my
  • Đáp án