Đề kiểm tra chung Hình học 10 chương 1 trường THPT Thanh Miện – Hải Dương

TRƯỜNG THPT THANH MIỆN
ĐỀ KIỂM TRA CHUNG 45 PHÚT MÔN: TOÁN
Thời gian làm bài: 45 phút;
(25 câu trắc nghiệm) Mã đề thi 132
Câu 1: Cho tam giác ABC, gọi điểm M trên cạnh BC sao cho MB = 2MC. Phân tích véctơ AM theo hai véctơ AB và .
AC Khẳng định nào sau đây đúng? 2 2 2 1 A. AM  AB  AC . B. AM  AB  AC . 3 3 3 3 1 2 1 1 C. AM  AB  AC . D. AM  AB  AC . 3 3 3 3
Câu 2: Cho tam giác ABC, có thể xác định được bao nhiêu vectơ (khác vectơ không) có điểm đầu
và điểm cuối là các đỉnh của tam giác đã cho? A. 4 B. 5 C. 3 D. 6
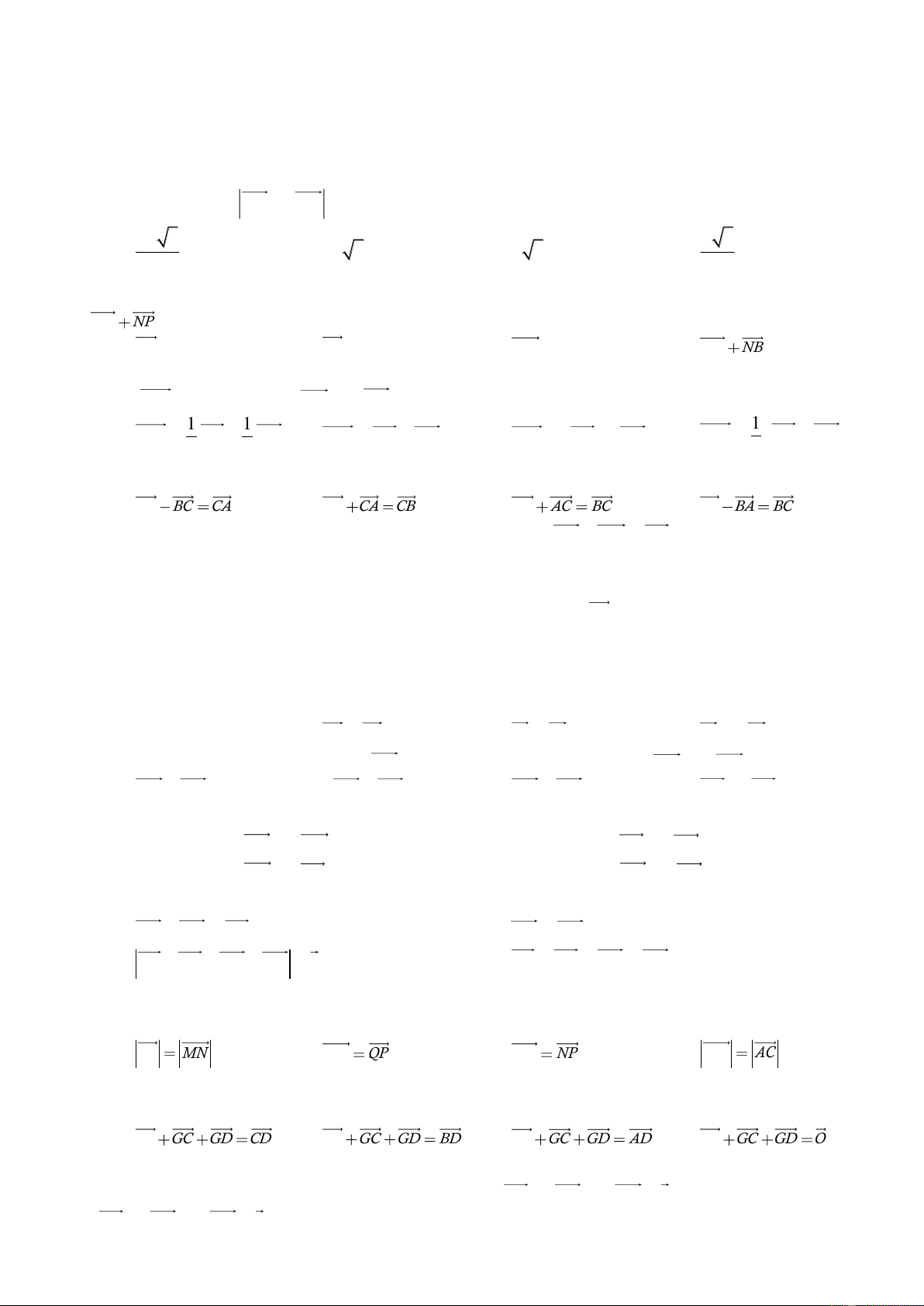
Câu 3: Trên đường thẳng MN lấy điểm P sao cho MN  3  M .
P Điểm P được xác định đúng
trong hình vẽ nào sau đây: A. Hình 3. B. Hình 4. C. Hình 2. D. Hình 1.
Câu 4: Cho ba điểm , A ,
B C phân biệt. Đẳng thức nào sau đây là đẳng thức sai?
A. BA  AC  BC
B. AB  BC  AC
C. AB  AC  C . B
D. CA  AB  BC
Câu 5: Cho hình bình hành ABCD tâm O. Đẳng thức nào sau đây sai? A. OA OB OC OD 0 . B. AC AB AD . C. BA BC DA DC . D. AB CD AB CB .
Câu 6: Cho tam giác ABC nội tiếp trong đường tròn tâm .
O Gọi H là trực tâm của tam giác.
Trong các khẳng định sau, khẳng định nào đúng ?
A. OH  4OG
B. OH  3OG
C. OH  2OG
D. 3OH  OG
Câu 7: Cho tam giác ABC với các cạnh AB  , c CB  , a AC  .
b Gọi I là tâm đường tròn nội tiếp tam giác .
ABC Đẳng thức nào sau đây đúng? 1 1 1
A. bIA  cIB  aIC  0 B. IA  IB  IC  0 a b c
C. aIA  bIB  cIC  0
D. aIA  bIB  cIC  0
Câu 8: Cho  ABC, nếu điểm M thỏa mãn MA  MB  MC  0 thì ta có:
A. ABMC là hình bình hành
B. ABCM là hình bình hành
C. M là trung điểm BC
D. M là trung điểm AB
Câu 10. Cho tam giác đều ABC cạnh a (a
0). Tính độ dài vecto u biết u AB AC ? 3 A. 2a . B. a 3 . C. a . D. a . 2
Câu 9: Cho tứ giác ABC ,
D có bao nhiêu vectơ khác vectơ không có điểm đầu và cuối là các đỉnh của tứ giác? A. 12 . B. 6 . C. 4 . D. 8 . Trang 1/28 - Mã đề thi 132
Câu 10: Chọn khẳng định đúng?
A. Hai vecto bằng nhau nếu độ dài của chúng bằng nhau.
B. Hai vecto bằng nhau nếu chúng cùng hướng và có cùng độ dài.
C. Hai vecto bằng nhau nếu hai véc tơ cùng hướng
D. Hai vecto bằng nhau nếu hai véc tơ cùng phương
Câu 11: Cho  ABC đều cạnh a, (d) là đường thẳng qua A và song song BC; khi M di động trên (d) thì
giá trị nhỏ nhất của MA  2MB là: 2a 3 a 3 A. B. 2a 3 C. a 3 D. 3 2
Câu 12: Cho M, N, P lần lượt là trung điểm các cạnh A ,
B BC, CA của tam giác ABC. Hỏi vectơ MP
NP bằng vectơ nào? A. AP B. BP C. MN D. MB NB .
Câu 13: Cho tam giác ABC có M là trung điểm của BC. Hãy chọn kết quả đúng khi phân tích
vectơ AM theo hai véctơ AB và AC ? 1 1 1 A. AM  AB 
AC B. AM  AB  AC
C. AM  2AB  3AC D. AM  AB AC 2 2 3
Câu 14: Cho ba điểm phân biệt , A ,
B C. Đẳng thức nào sau đây đúng? A. AB BC CA B. AB CA CB C. AB AC BC D. CA BA BC
Câu 15: Cho hình bình hành ABCD , điểm M thoả mãn: MA  MC  AB . Khi đó M là trung điểm của: A. AB B. BC C. AD D. CD
Câu 16: Cho lục giác đều ABCDEF tâm O. Số các vectơ bằng OC có điểm đầu và điểm cuối là các
đỉnh của lục giác đã cho là: A. 4 B. 2 C. 6 D. 3
Câu 17: Cho hai điểm phân biệt A và .
B Điều kiện để điểm I là trung điểm của đoạn thẳng AB là:
A. IA  IB
B. AI  BI
C. IA  IB
D. IA  IB .
Câu 18: Cho tam giác ABC. Vectơ AB được phân tích theo hai vectơ AC và BC bằng
A. AC  BC
B. AC  BC
C. AC  BC
D. AC  2BC .
Câu 19: Cho lục giác đều ABCDEF tâm .
O Khẳng định đúng là:
A. Vectơ đối của AF là DC
B. Vectơ đối của EF là CB
C. Vectơ đối của AO là FE
D. Vectơ đối của AB là ED
Câu 20: Cho hình chữ nhật ABCD , gọi O là giao điểm của AC và BD , phát biểu nào là đúng?
A. AC  AD  AB .
B. AC  BD.
C. OA  OB  OC  OD  0
D. OA  OB  OC  OD
Câu 21: Cho tứ giác ABC .
D Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, . DA Khẳng
định nào sau đây là sai? A. QP MN . B. MN QP . C. MQ NP . D. MN AC .
Câu 22: Cho hình bình hành ABC .
D Gọi G là trọng tâm của tam giác ABC. Mệnh đề nào sau đây đúng? A. GA GC GD
CD . B. GA GC GD
BD . C. GA GC GD
AD . D. GA GC GD O .
Câu 23: Cho tam giác ABC, gọi M là trung điểm của AB và N thuộc cạnh AC sao cho
NC  2NA . Hãy xác định điểm K thỏa mãn: 3AB  2AC 12AK  0 và điểm D thỏa mãn:
3AB  4AC 12KD  0 .
Trang 2/28 - Mã đề thi 132
A. K là trung điểm của MN và D là trung điểm của BC .
B. K là trung điểm của BC và D là trung điểm của MN .
C. K là trung điểm của MN và D là trung điểm của AB .
D. K là trung điểm của MN và D là trung điểm của AC . Câu 24: Cho ABC 
có trung tuyến AM và trọng tâm G . Khẳng định nào sau đây đúng: 2
A. AG   AB  AC.
B. AM  3MG 3 1
C. MG  MA MB  MC
D. AM  AB  AC 3
Câu 25: Gọi M , N lần lượt là trung điểm của các cạnh A ,
B AC của tam giác đều ABC. Đẳng thức nào sau đây đúng? A. MA MB . B. AB AC . C. MN BC . D. BC 2 MN . ----------- HẾT -----------
Trang 3/28 - Mã đề thi 132
TRƯỜNG THPT THANH MIỆN
ĐỀ KIỂM TRA CHUNG 45 PHÚT MÔN: TOÁN
Thời gian làm bài: 45 phút;
(25 câu trắc nghiệm) Mã đề thi 134
Câu 1: Cho tam giác ABC , số điểm M thoả mãn: MA  MB  MC  1 là: A. 0 điểm B. 2 điểm C. 1 điểm D. vô số điểm
Câu 2: Hai véc tơ có cùng độ dài và ngược hướng gọi là:
A. Hai véc tơ đối nhau.
B. Hai véc tơ cùng hướng.
C. Hai véc tơ bằng nhau.
D. Hai véc tơ cùng phương.
Câu 3: Cho hai vectơ a và b không cùng phương. Hai vectơ nào sau đây cùng phương? 1 1 A. 3
 ab và  a  6b B. 
a  b và 2a  b 2 2 1 1 1 C.
a  b và a  2b . D.
a  b và  a  b 2 2 2
Câu 4: Cho hình bình hành ABC .
D Đẳng thức nào sau đây đúng?
A. BA  AD  AC
B. BC  BA  BD
C. AB  AD  CA
D. AB  BC  CA
Câu 5: Cho ABC với G là trọng tâm. Đặt CA  a, CB  .
b Khi đó, AG được biểu diễn theo hai
vectơ a và b là : 1 2 2 1 2 1 2 1 A. AG 
a  b . B. AG 
a  b . C. AG 
a  b . D. AG   a  b . 3 3 3 3 3 3 3 3
Câu 6: Cho hình chữ nhật ABCD và I là giao điểm của hai đường chéo. Tập hợp các điểm M thỏa mãn MA MB MC MD là :
A. Trung trực của đoạn thẳng . AB
B. Trung trực của đoạn thẳng . AD AC AB BC
C. Đường tròn tâm I , bán kính .
D. Đường tròn tâm I , bán kính . 2 2
Câu 7: Cho tam giác ABC với M là một điểm nằm trong tam giác. Gọi S , S , S lần lượt là diện a b c
tích các tam giác MBC, MAC,MAB. Đẳng thức nào sau đây đúng? 1 1 1
A. S MA  S MB  S MC  0 B. MA  MB  MC  0 a b c S S S a b c
C. S MA  S MB  S MC  0
D. S MA  S MB  S MC  0 b c a a b c
Câu 8: Ba trung tuyến AM , BN, CP của tam giác ABC đồng quy tại .
G Hỏi vectơ AM  BN  CP bằng vectơ nào? 3 1 A.
GAGBCG. B. 3MGNGGP. C. ABBC AC. D. 0. 2 2
Câu 9: Cho lục giác đều ABCDEF. Số các vectơ ( khác vecto không ) có điểm đầu và điểm cuối
thuộc các đỉnh của lục giác đã cho là: A. 30 . B. 36 . C. 6 . D. 12
Câu 10: Cho tứ giác ABC .
D Có thể xác định được bao nhiêu vectơ (khác 0 ) có điểm đầu và điểm cuối là các điểm , A , B , C D? A. 4 B. 12 . C. 10 . D. 8 .
Câu 11: Cho tam giác ABC nội tiếp trong đường tròn tâm O . Gọi H là trực tâm của tam giác.
Trong các khẳng định sau, khẳng định nào đúng?
Trang 4/28 - Mã đề thi 134 2
A. OH  2OG
B. 3OH  OG
C. OH  4OG D. HG  HO 3
Câu 12: Cho tam giác ABC, điểm M thuộc cạnh AB sao cho 3 AM
AB và N là trung điểm của
AC. Biểu diễn MN theo AB và AC ? 1 1 1 1 1 1 1 1 A. MN AC A . B B. MN AC A . B C. MN AB AC. D. MN AC A . B 2 3 2 3 2 3 3 2
Câu 13: Cho tam giác đều ABC và điểm I thỏa mãn IA 2I .
B Mệnh đề nào sau đây đúng ? CA 2CB 1 2 CA 2CB A. CI CA 2C . B B. CI . C. CI CA CB D. CI . 3 3 3 3
Câu 14: Cho tam giác ABC. Khẳng định nào sau đây đúng? A. AA BB AB .
B. CA BA CB . C. AC BA BC . D. AB AC BC .
Câu 15: Cho tam giác ABC với trực tâm H , D là điểm đối xứng với B qua tâm O của đường
tròn ngoại tiếp tam giác .
ABC Khẳng định nào sau đây là đúng?
A. HA  CD và AD  CH
B. HA  CD và DA  HC
C. HA  CD và AD  HC
D. HA  CD và AD  HC và OB  OD .
Câu 16: Cho hình bình hành ABC .
D Trong các khẳng định sau hãy tìm khẳng định sai?
A. AB  DC
B. AD  CB .
C. AB  CD .
D. AD  CB
Câu 17: Cho hai điểm A và B phân biệt, điều kiện nào dưới đây là điều kiện cần và đủ để điểm O
là trung điểm của đoạn AB?
A. AO  BO
B. OA  OB
C. OA  OB  0
D. OA  OB
Câu 18: Cho tam giác MNP . Vectơ MN được phân tích theo hai vectơ MP và NP bằng:
A. MP  NP
B. MP  NP
C. MP  NP
D. MP  2N . P
Câu 19: Cho 4 điểm O,A,B,C phân biệt. Chọn đẳng thức đúng:
A. BC  AB  CA
B. OC  OA  CA
C. AB  CB  AC
D. BA  CA  BC
Câu 20: Cho hình chữ nhật ABCD , gọi O là giao điểm của AC và ,
BD phát biểu nào là đúng?
A. AC  AD  AB .
B. AC  BD.
C. OA  OB  OC  OD  0
D. OA  OB  OC  OD
Câu 21: Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào sau đây đúng? A. BC EF AD . B. OA OC OE 0 . C. OA OC OB EB . D. AB CD EF 0
Câu 22: Cho O là tâm hình bình hành ABC .
D Hỏi vectơ AO DO bằng vectơ nào? A. BC . B. BA . C. AC . D. DC .
Câu 23: Cho tam giác ABC và đường thẳng d. Gọi O là điểm thỏa mãn hệ thức
OA  OB  2OC  0 . Tìm điểm M trên đường thẳng d sao cho vectơ v  MA  MB  2MC có độ dài nhỏ nhất?
A. Điểm M là hình chiếu vuông góc của O trên d .
B. Điểm M là hình chiếu vuông góc của A trên d .
C. Điểm M là hình chiếu vuông góc của B trên d .
D. Điểm M là giao điểm của AB và d .
Câu 24: Cho tam giác ABC có M thỏa mãn điều kiện MA MB MC
0. Xác định vị trí điểm M ?
A. M là trung điểm của đoạn thẳng AB .
B. M trùng C .
C. M là trọng tâm tam giác ABC .
D. M là điểm thứ tư của hình bình hành ACBM .
Trang 5/28 - Mã đề thi 134
Câu 25: Cho hình chữ nhật ABCD biết AB  4a và AD  3 .
a Tìm AB  AD ? A. 7a B. 6a
C. 2a 3 . D. 5a .
----------- HẾT -----------
Trang 6/28 - Mã đề thi 134 made cautron dapan made cautron dapan 132 1 C 134 1 D 132 2 D 134 2 A 132 3 A 134 3 D 132 4 D 134 4 B 132 5 D 134 5 D 132 6 B 134 6 B 132 7 C 134 7 A 132 8 A 134 8 D 132 9 A 134 9 A 132 10 B 134 10 B 132 11 C 134 11 D 132 12 B 134 12 B 132 13 A 134 13 A 132 14 B 134 14 C 132 15 C 134 15 C 132 16 B 134 16 B 132 17 D 134 17 C 132 18 C 134 18 B 132 19 A 134 19 C 132 20 A 134 20 A 132 21 D 134 21 C 132 22 B 134 22 A 132 23 A 134 23 A 132 24 C 134 24 C 132 25 D 134 25 D