Đề kiểm tra cuối kì 1 Toán 10 năm 2020 – 2021 trường THPT Tân Túc – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề kiểm tra cuối kì 1 Toán 10 năm học 2020 – 2021 trường THPT Tân Túc, thành phố Hồ Chí Minh; đề thi có lời giải chi tiết, mời bạn đọc đón xem

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GD&ĐT TP. HỒ CHÍ MINH ĐỀ KIỂM TRA CUỐI KÌ I - NĂM HỌC 2020 – 2021
TRƯỜNG THPT TÂN TÚC Môn: Toán; Lớp 10
Thời gian làm bài: 90 phút, không kể thời gian phát đề
ĐỀ CHÍNH THỨC
(Đề kiểm tra có 01 trang)
Câu 1 (1,0 điểm). Tìm tập xác định của hàm số
153yx x

.
Câu 2 (1,5 điểm). Cho hàm số
2
23
y
xx
có đồ thị là parabol (P).
a) Lập bảng biến thiên và vẽ đồ thị hàm số đã cho.
b) Tìm tọa độ giao điểm của đồ thị (P) và đường thẳng
9.yx
Câu 3 (2,0 điểm). Giải các phương trình sau:
a)
2
541
1.
1
xx
x
x


b)
3223.xx

Câu 4 (0,75 điểm). Xác định parabol
2
y
ax bx c
 biết parabol đó đi qua điểm
1; 8A và
có đỉnh

1; 4 .I
Câu 5 (1,0 điểm). Giải hệ phương trình
2
4
(, ).
2250
xy
xy
xxy


Câu 6 (2,5 điểm). Trong mặt phẳng Oxy, cho tam giác ABC có

2; 1 , 1; 4 , 3;0 .ABC
a) Chứng minh tam giác ABC cân tại A.
b) Gọi M là trung điểm của cạnh BC. Tính độ dài AM, từ đó suy ra diện tích của tam
giác ABC.
c) Tìm tọa độ trực tâm H của tam giác ABC.
Câu 7 (0,75 điểm). Tìm tất cả các giá trị của tham số m đề phương trình
22
210xmxmm
có hai nghiệm phân biệt
12
,
x
x sao cho
12 12
7.
x
xxx

Câu 7 (0,5 điểm). Trong mặt phẳng
Oxy
, cho điểm A(2;1). Gọi B là điểm thuộc trục hoành có
hoành độ dương, gọi C là điểm thuộc trục tung có tung độ âm sao cho tam giác ABC vuông
tại A. Tìm toạ độ điểm B và C để tam giác ABC có diện tích bằng 5.
----------HẾT----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:…………………………; Số báo danh:.………….; Lớp:……..
SỞ GD & ĐT TP HỒ CHÍ MINH
TRƯỜNG THPT TÂN TÚC
ĐÁP ÁN MÔN TOÁN ĐỀ THI HỌC KÌ 1 KHỐI 10
NĂM HỌC 2020-2021
Câu Nội dung Điểm
Câu 1
(1 đ)
Điều kiện xác định
10
53 0
x
x


1
5
3
x
x

5
1
3
x

Vậy tập xác định là
5
1;
3
D




.
0.25
0.25
0.25
0.25
Câu 2
(1.5đ)
a) Khảo sát sự biến thiên và vẽ
TXĐ: D=
Đỉnh
1; 4I 
Trục đối xứng
1x 
Bảng biến thiên
Vẽ đồ thị:
x
-1
y
-4
0.25
0,25
0.25
0.25
b
) Tìm tọa độ giao điểm
Phương trình hoành độ giao điểm:
22
4
23 9 120
3
x
xx x xx
x


Với
4495xy 
ta được giao điểm
4;5A
Với
33912xy 
ta được giao điểm
3;12B .
0.25
0.25
Câu 3
(2đ)
Giải phương trình
a)
2
541
1
1
xx
x
x


ĐK: 1
x
0.25
2
22
2
541
1
1
541 1
440
0(n)
1( )
{0}
xx
x
x
xx x
xx
x
xl
S




0.25
0.25
0.25
b)
3232
x
x
3223
x
x
2
230
32(23)
x
xx


2
3
2
415110
x
xx

3
2
1()
11
()
4
x
x
l
x
n
Vậy
11
{}
4
S
0.25
0.25
0.25
0.25
Câu 4
(0.75 đ)
Thay lần lượt tọa độ điểm
1; 8A ,
1; 4I vào
P
và do hoành độ đỉnh bằng
1, ta có hệ phương trình:
8
4
1
2
8
4
20
1
2
5
abc
abc
b
a
abc
abc
ab
a
b
c






Vậy

2
:25
P
yx x
.
0.25
0.25
0.25
Câu 5
(1.0đ)
Giải hệ phương trình
2
4 (1)
2250 (2)
xy
xxy


(1) 4yx
( Hoặc
4
x
y
)
Thay
4yx
vào (2) ta được
2
430xx

31
13
x
y
xy


0.25
0.25
0.25
0.25
Vậy nghiệm của hệ
(1; 3); 3;1
Câu 6.
(2.5đ)
a) Chứng minh
ABC
cân tại A.


15 26
51 26




;
;
AB AB
AC AC
Suy ra
26AB AC
.
Vậy
ABC
cân tại
A
.
0.25
0.25
0.25
b)
M
là trung điểm của
BC
Suy ra

12;M . ( Có thể dùng định lý Pitago để tính độ dài AM)
32AM .
42BC
Vậy
1
12
2
..
ABC
SAMBC
0.25
0.25
0.25
c
) Tìm tọa độ trực tâm
H
tam giác
ABC
.
Gọi

;Hxy
là trực tâm của tam giác ABC.
Tính đúng các tọa độ của các vecto:
Để
H
là trực tâm của
ABC

 
AH BC
BH AC
0
0
 
 
.
.
AH BC
BH AC


42410
51 40
1
3
2
3



xy
xy
x
y
Vậy
12
33



;H
.
0.25
0.25
0.25
0.25
Câu 7
(0.75đ)
Cho phương trình
22
x2mxmm10
Để pt có 2 nghiệm phân biệt
12
x,x
a0
0
m1
Điều kiện
12 12
xx 7xx
2
2m 7 (m m 1)

m2 (n)
m3 (l)

Vậy m = 2
0.25
0.25
0.25
Câu 8
(0.5đ)
Cho điểm A(2; 1). Lấy điểm
B
nằm trên trục hoành ,có hoành độ dương và
điểm
C
trên trục tung, có tung độ âm sao cho tam giác
ABC
vuông tại
A
.
Tìm toạ độ
,
B
C để tam giác ABC có diện tích bằng 5 ( đvdt).
Gọi

;0 , 0;
B
xCy
với 0x , 0y
.
Suy ra

2; 1 , 2; 1AB x AC y


Theo giả thiết ta có tam giác
ABC
vuông tại
A
nên

.0 221.10 25AB AC x y y x 

Ta có
22 2
11
.(2)1.2(1)
22
ABC
SABACx y

2
45
x
x

Mà
5
ABC
S
nên
0( )
4( )
x
l
x
n
3y
Vậy
4;0 , 0; 3BC
0.25
0,25
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT TP. HỒ CHÍ MINH ĐỀ KIỂM TRA CUỐI KÌ I - NĂM HỌC 2020 – 2021 TRƯỜNG THPT TÂN TÚC Môn: Toán; Lớp 10
Thời gian làm bài: 90 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC
(Đề kiểm tra có 01 trang)
Câu 1 (1,0 điểm). Tìm tập xác định của hàm số y x 1  5  3x .
Câu 2 (1,5 điểm). Cho hàm số 2
y x  2x  3 có đồ thị là parabol (P). a)
Lập bảng biến thiên và vẽ đồ thị hàm số đã cho. b) Tìm
tọa độ giao điểm của đồ thị (P) và đường thẳng y x  9.
Câu 3 (2,0 điểm). Giải các phương trình sau: 2 5x  4x 1 a)  x 1.
b) 3x  2  2x  3. x 1
Câu 4 (0,75 điểm). Xác định parabol 2
y ax bx c biết parabol đó đi qua điểm A 1  ;8 và
có đỉnh I 1;4. x y  4
Câu 5 (1,0 điểm). Giải hệ phương trình  (x, y  ). 2
x  2x  2y  5  0
Câu 6 (2,5 điểm). Trong mặt phẳng Oxy, cho tam giác ABC có A 2;    1 , B  1  ;4,C 3;0.
a) Chứng minh tam giác ABC cân tại A.
b) Gọi M là trung điểm của cạnh BC. Tính độ dài AM, từ đó suy ra diện tích của tam giác ABC.
c) Tìm tọa độ trực tâm H của tam giác ABC.
Câu 7 (0,75 điểm). Tìm tất cả các giá trị của tham số m đề phương trình 2 2
x  2mx m m 1  0 có hai nghiệm phân biệt x , x sao cho x x  7  x x . 1 2 1 2 1 2
Câu 7 (0,5 điểm). Trong mặt phẳng Oxy , cho điểm A(2;1). Gọi B là điểm thuộc trục hoành có
hoành độ dương, gọi C là điểm thuộc trục tung có tung độ âm sao cho tam giác ABC vuông
tại A. Tìm toạ độ điểm B và C để tam giác ABC có diện tích bằng 5.
----------HẾT----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:…………………………; Số báo danh:.………….; Lớp:……..
SỞ GD & ĐT TP HỒ CHÍ MINH
ĐÁP ÁN MÔN TOÁN ĐỀ THI HỌC KÌ 1 KHỐI 10
TRƯỜNG THPT TÂN TÚC NĂM HỌC 2020-2021 Câu Nội dung Điểm Câu 1 x  1 0.25 (1 đ) x 1  0 
Điều kiện xác định    5 5  1  x 0.25 5  3x  0 x   3 0.25  3  5
Vậy tập xác định là D  1  ;  . 3   0.25
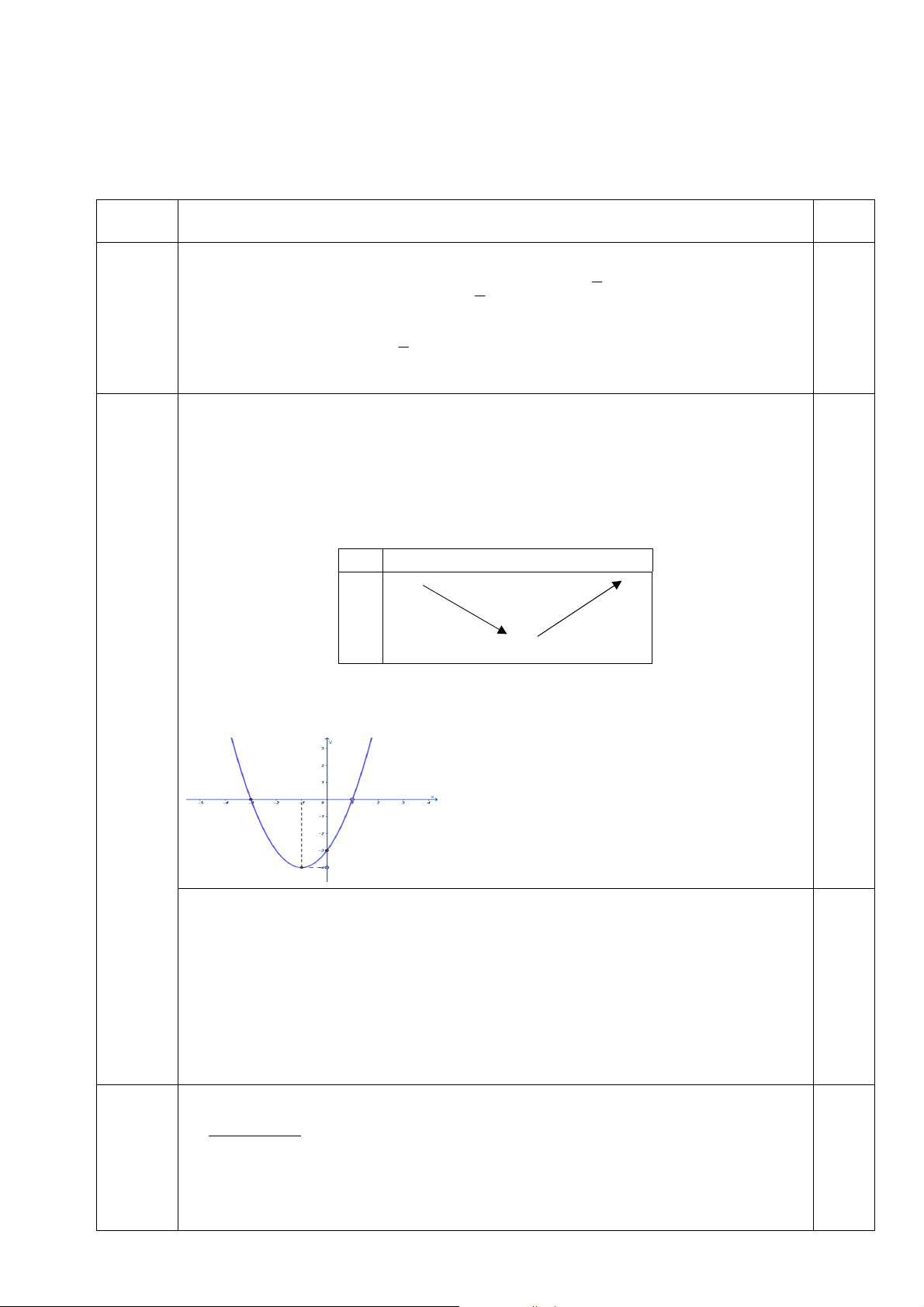
a) Khảo sát sự biến thiên và vẽ TXĐ: D= 0.25 Đỉnh I  1  ; 4   0,25
Trục đối xứng x  1 Bảng biến thiên x  -1    y 0.25 -4 Câu 2 Vẽ đồ thị: 0.25 (1.5đ)
b) Tìm tọa độ giao điểm x  4 
Phương trình hoành độ giao điểm: 2 2
x  2x  3  x  9  x x 12  0   0.25 x  3
Với x  4  y  4  9  5 ta được giao điểm A 4;  5 0.25
Với x  3  y  3  9  12 ta được giao điểm B3;12 . Giải phương trình 2 5x  4x 1 a)  x 1 Câu 3 x 1 0.25 (2đ) ĐK: x  1 2 5x  4x 1 x 1 x 1 2 2
 5x  4x 1  x 1 0.25 2
 4x  4x  0 x  0(n)  0.25  x  1(l) S  {0} 0.25
b) 3x  2  3  2x
3x  2  2x  3 2x  3  0   0.25 2 3
x  2  (2x  3)  3 x   2 0.25 2
4x 15x 11 0  3 x   2 0.25
  x 1 (l)  11 x  (n)  4 11 0.25 Vậy S  { } 4
Thay lần lượt tọa độ điểm A 1
 ;8 , I 1;4 vào P và do hoành độ đỉnh bằng
1, ta có hệ phương trình:
a b c  8 
a b c  4 0.25 b  1 2a Câu 4
a b c  8 (0.75 đ)
 a b c  4 2a b  0  0.25 a 1   b   2  c   5  0.25 Vậy P 2
: y x  2x  5 .
x y  4 (1)
Giải hệ phương trình  2
x  2x  2y  5  0 ( 2) 0.25
(1)  y  4  x ( Hoặc x  4  y ) Câu 5 (1.0đ)
Thay y  4  x vào (2) ta được 2
x  4x  3  0 0.25
x  3  y  1 0.25  
x  1 y  3 0.25
Vậy nghiệm của hệ (1;3);3;  1 a) Chứng minh ABC cân tại A. 
AB  1;5  AB  26  0.25 AC  5;  1  AC  26 0.25
Suy ra AB AC  26 . Vậy ABC  cân tại A. 0.25
b) M là trung điểm của BC
Suy ra M 1; 2 . ( Có thể dùng định lý Pitago để tính độ dài AM) AM  3 2 . 0.25 BC  4 2 0.25 1 Vậy S
AM.BC  12. ABC 2 0.25
Câu 6. c) Tìm tọa độ trực tâm H tam giác ABC . (2.5đ)
Gọi H x;y là trực tâm của tam giác ABC.
Tính đúng các tọa độ của các vecto: 0.25      AH BC
AH.BC  0
Để H là trực tâm của ABC  
    0.25 BH   ACBH.AC  0 
4 x  2  4 y  1  0 0.25  5
 x  1  y  4  0  1 x    3   0.25 2 y   3  1 2  Vậy H   ; . 3 3   Cho phương trình 2 2
x  2mx  m  m 1  0 a  0
Để pt có 2 nghiệm phân biệt x , x   m  1 0.25 1 2    0 Câu 7 (0.75đ) m  2 (n)
Điều kiện x  x  7  x x 2
 2m  7  (m  m 1)  0.25 1 2 1 2  m   3 (l) Vậy m = 2 0.25
Cho điểm A(2; 1). Lấy điểm B nằm trên trục hoành ,có hoành độ dương và
điểm C trên trục tung, có tung độ âm sao cho tam giác ABC vuông tại A .
Tìm toạ độ B, C để tam giác ABC có diện tích bằng 5 ( đvdt). Gọi B  ;0
x , C 0; y với x  0 , 0 y  .  
Suy ra AB x  2;  1 , AC  2  ; y   1 Câu 8
Theo giả thiết ta có tam giác ABC vuông tại A nên   (0.5đ) .
AB AC  0   x  2 2
  1. y  
1  0  y  2x  5 0.25 1 1 Ta có 2 2 2 SA . B AC
(x  2) 1. 2  ( y 1) ABC 2 2 2
x  4x  5 x  0(l) Mà S  5 nên  y  3
 Vậy B4;0,C 0; 3   0,25 ABC  x  4(n)
Document Outline

  • toan10-hk1-2020-2021_1112021213243
  • da-toan10-hk1-2020-2021_1112021213345