ĐỀ KIỂM TRA ĐIỀU KIỆN MÔN TOÁN RỜI RẠC

Câu 1: Hỏi giá trị của k sẽ là bao nhiêu sau khi đoạn chương trình PASCAL sau được thực hiện?

A. 24000 . B. 90 . C. 900 . D. 240 .

Câu 2: Có bao nhiêu tên biến trong PASCAL có độ dài 11 chỉ chứa hai chữ cái A, B, khởi đầu bởi AAA hoặc BBB.

A. 1024 . B. 36 . C. 512. D. 514 .

Câu 3: Số điện thoại di động của một hãng viễn thông là một dãy có 10 chữ số dạng 09.A.B.XXX.XXX, trong đó miền xác định của các chữ số A, B, X như sau:

• A có giá trị từ 2 đến 8;
• B có giá trị từ 0 đến 5;
• X có giá trị từ 0 đến 9.

Bạn hãy cho biết hãng viễn thông có thể phát hành được bao nhiêu số điện thoại?

A. 30000000. B. 3000000 . C. 42000000 . D. 4200000 .

Câu 4: Có bao nhiêu hoán vị của các chữ cái trong xâu ABCDEFGH mà trong đó có chứa xâu con DEF.

A. 1440 . B. 5040 . C. 720 . D. 360 .

Câu 5: Tính số dãy nhị phân có độ dài bằng 15, trong đó có chứa 5 chữ số 0 và không có hai chữ số 0 nào đứng cạnh nhau.

A. 252 . B. 55440 . C. 126 .D. 462 .

Câu 6: Có bao nhiêu xâu nhị phân có độ dài 11 hoặc là bắt đầu bởi 00 hoặc là kết thúc bởi 11?

A. 1024 . B. 896 . C. 2048 . D. 968 .

Câu 7: Trong tập 1, 2,3, 4,5,...,1000 có bao nhiêu số không chia hết cho bất cứ số nào trong các số 2, 3, 5?

A. 299 . B. 265 . C. 266 . D. 300 .

a_n 

a  5a

 6a

a  4, a

 9.

Câu 8: Cho dãy số Chọn khẳng định đúng:

n0

thỏa mãn

n2

n1

n với mọi số tự nhiên n, đồng thời 0 1

A. a  3ⁿ  3 2ⁿ.

n

B. a  33ⁿ  2ⁿ.

C. a  3ⁿ  3.2ⁿ

. D.

a  3^n1  2ⁿ .

n

n

n

Câu 9: Trên mặt phẳng cho 12 đường thẳng sao cho không có 2 đường thẳng nào song song và không có 3 đường thẳng nào đồng quy. Hỏi mặt phẳng được chia thành bao nhiêu miền?

A. 157 . B. 156 . C. 78 . D. 79 .

Câu 10: Một nhóm gồm 4 người đàn ông, 5 người phụ nữ và 1 đứa trẻ được xếp vào 1 bàn tròn có 10 ghế, mỗi người ngồi vào 1 ghế. Hỏi có bao nhiêu cách xếp đứa trẻ ngồi giữa hai người phụ nữ? Biết rằng hai cách xếp không coi là khác nhau nếu chúng có thể thu được từ nhau bởi một phép quay bàn tròn.

A. 30240 . B. 10!. C. 50400 . D. 100800 .

Câu 11: Cho hàm

f (n)  1²  2²  3²  ...  n²

. Khẳng định nào đúng?

A. f (n)  O(1) . B.

f (n)  O(n) . C.

f (n)  O(n³ ) . D.

f (n)  O(n² ) .

Câu 12: Cho đồ thị bánh xe Wn có 200 cạnh. Hỏi đồ thị đó có bao nhiêu đỉnh?

A. 101. B. 201. C. 100 .D. 99 .

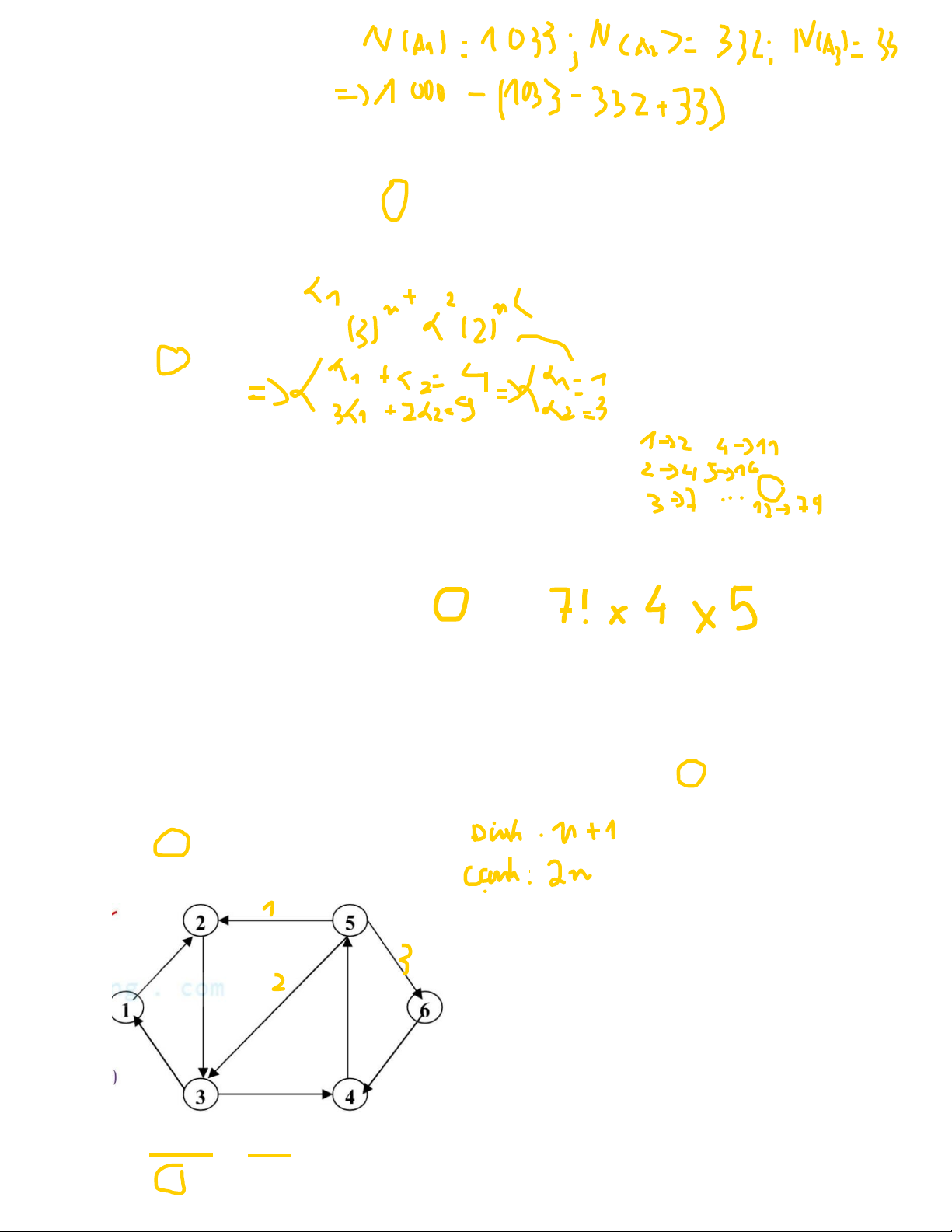
Câu 13:

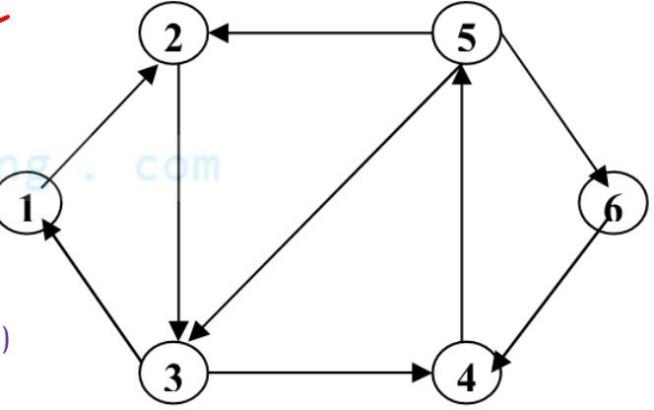
Tìm bán bậc ra của đỉnh 5 của đồ thị trên.

A. 3 . B. 1. C. 4 . D. 2 .

Câu 14:

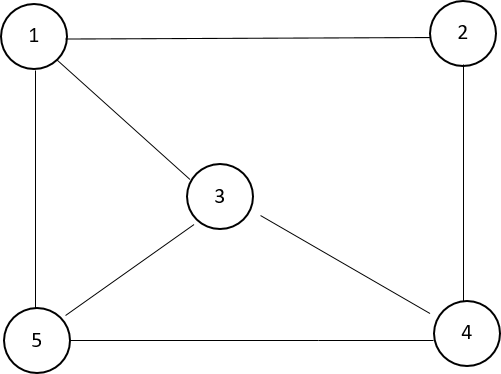
Ma trận kề của đồ thị trên là



A.



B.

 0 1 1 0 1

1 0 0 1 0

 

1 0 0 1 1

 

0 1 1 0 1 

C. 1 0 1 1 0 .



D.

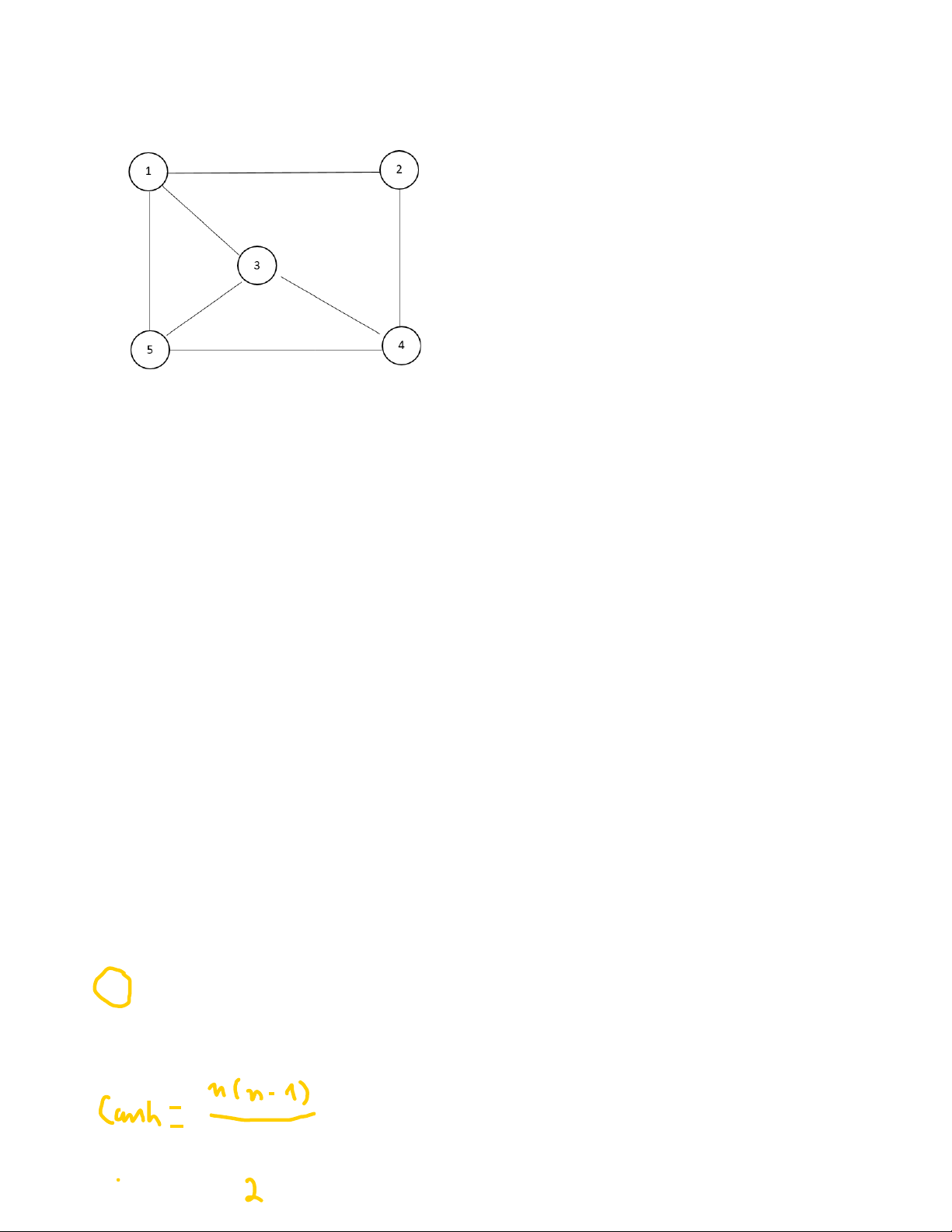
Câu 15: Cho G là đồ thị đầy đủ có 190 cạnh. Tìm số đỉnh của đồ thị G.

A. 19 .

B. 20.

C. 18.

D. 21.

Câu 16: Cho G là đơn đồ thị vô hướng có tập các đỉnh là V (G)  1, 2,3, 4,5,6,7. Cho G có biểu diễn bởi danh sách cạnh như sau

Chọn khẳng định đúng:

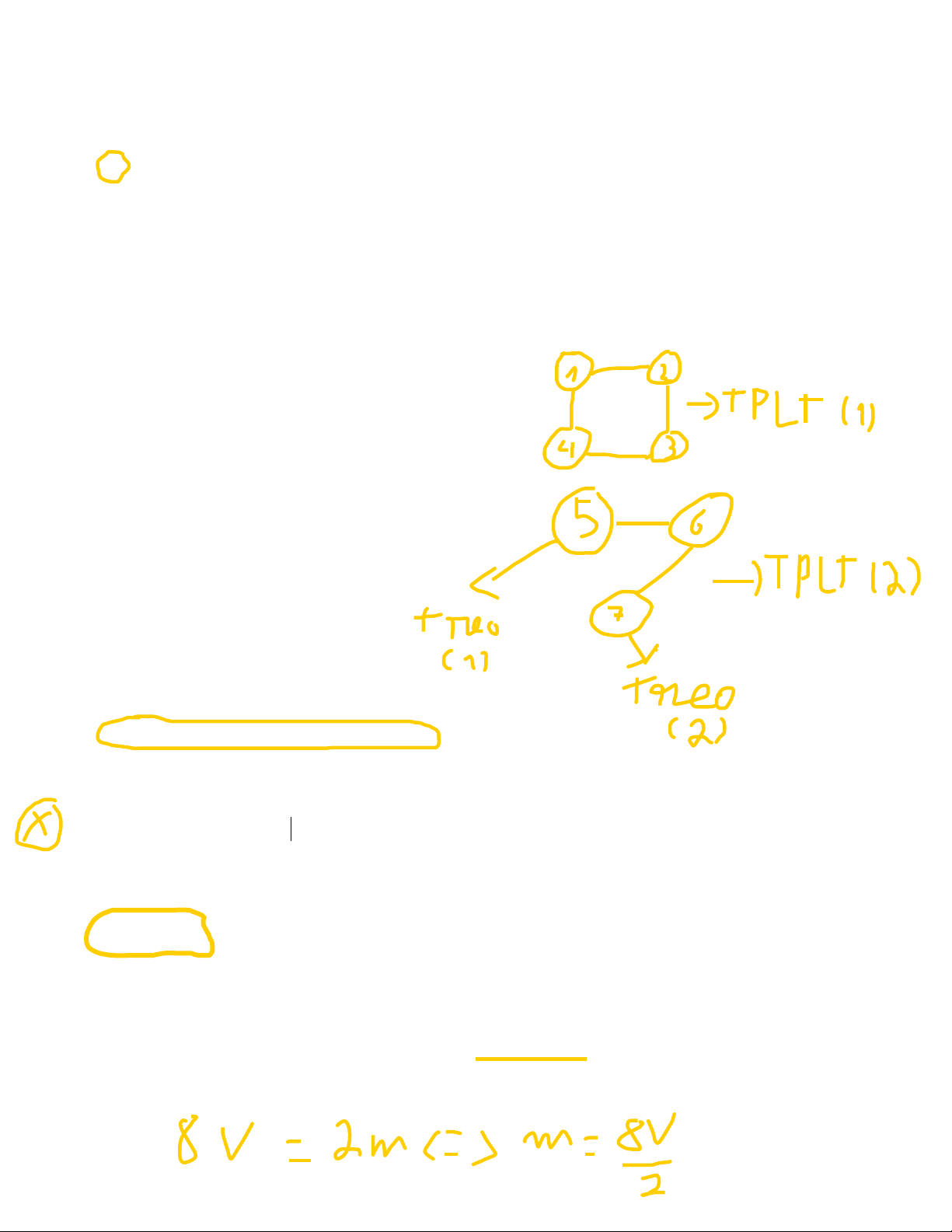
G là đồ thị liên thông có 6 cạnh.

G có 2 thành phần liên thông và có 2 đỉnh cô lập. G có 2 đỉnh treo và có 2 thành phần liên thông. G là đồ thị có 7 đỉnh và có 2 đỉnh cô lập.

Câu 17: Cho G là đơn đồ thị vô hướng có 5 đỉnh, có 9 cạnh và không có đỉnh nào có bậc 3. Kí hiệu

δ G   mindegG (u) u V (G)

. Chọn khẳng định đúng:

δ G  2 . δ G  1. δ G  0. δ G  4 .

Câu 18: Cho G là đơn đồ thị vô hướng có tất cả các đỉnh đều có bậc 8. Gọi m là số cạnh của đồ thị G. Chọn khẳng định đúng:

m chia hết cho 4. m chia 4 dư 1.

m chia 4 dư 2.

m chia 4 dư 3.

Câu 19: Cho G là đơn đồ thị với tập các đỉnh là V (G)  1, 2,3, 4,5,6,7. Danh sách lân cận kề của đồ thị G như sau:

Ke(1)  3,5 , Ke(2)  5,6 , Ke(3)  1,5 ,

Ke(4)  5,7 , Ke(5)  1, 2,3, 4,6,7, Ke(6)  2,5,7 , Ke(7)  4,5,6 .

Tìm một đường đi của đồ thị G. 4, 7, 6, 2, 3, 5.

1, 3, 5, 2, 7, 4.

5, 2, 6, 7, 1, 3.

3, 1, 5, 4, 7, 6.

Câu 20: Cho G là đơn đồ thị vô hướng, liên thông và có 20 cạnh. Chọn khẳng định đúng: G có 2 thành phần liên thông.

G có ít nhất 23 đỉnh.

G có nhiều nhất 21 đỉnh. G có đỉnh cô lập.