Đề kiểm tra định kì lần 1 Toán 10 năm 2021 – 2022 trường THPT chuyên Bắc Ninh

TRƯỜNG THPT CHUYÊN BẮC NINH
ĐỀ KIỂM TRA ĐỊNH KÌ LẦN 1 TỔ TOÁN - TIN NĂM HỌC 2021 - 2022
(Đề thi gồm 01 trang) Môn thi: TOÁN
Dành cho các lớp 10: Lí – Hoá - Tin
Thời gian: 120 phút (không kể thời gian giao đề)
Câu 1 (2,0 điểm). Cho hàm số 2
y = (4 − m )x + 9 . Gọi A là tập hợp tất cả giá trị của tham số m
đề hàm số đồng biến và tập hợp B =m 1m  3 .
a) Xác định các tập hợp A và A  B .
b) Tìm tất cả giá trị của tham số m để đồ thị hàm số đã cho đi qua điểm M (1; 3 − ) .
Câu 2 (2,0 điểm). Cho hình bình hành ABCD tâm O , M là một điểm bất kì trong mặt phẳng. Chứng minh rằng
a) BA + DA + AC = 0 và OA + OB + OC + OD = 0 .
b) MA + MC = MB + MD .
Câu 3 (2,0 điểm). Cho phương trình 2
x − 3x + m = 0 ( )
1 (với m là tham số). a) Giải phương trình ( ) 1 khi m = 2 .
b) Tìm tất cả giá trị của tham số m để phương trình ( )
1 có hai nghiệm x , x thỏa mãn 1 2 3 3 2 2
x x + x x − 2x x = 5 . 1 2 1 2 1 2
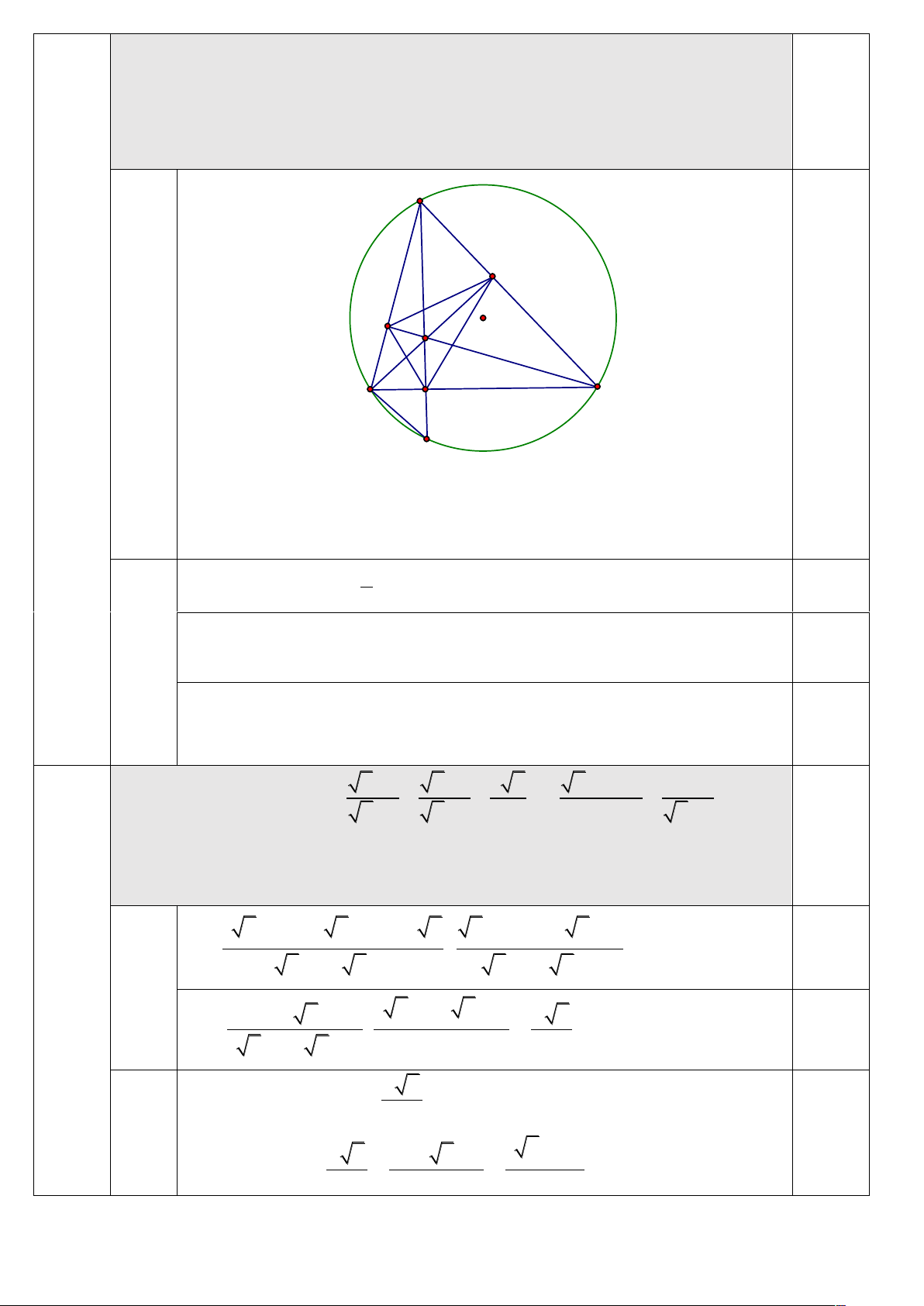
Câu 4 (1,5 điểm). Cho tam giác ABC nhọn, nội tiếp đường tròn (O) và có trực tâm H . Gọi ,
D E, F theo thứ tự là chân các đường cao hạ từ các đỉnh ,
A B,C xuống các cạnh BC,C , A AB của tam giác ABC .
a) Chứng minh rằng đường tròn ngoại tiếp các tam giác AEF, BF ,
D CDE cùng đi qua một điểm.
b) Đường thẳng AH cắt đường tròn (O) tại điểm thứ hai là A . Chứng minh rằng hai điểm
H và A đối xứng nhau qua đường thẳng BC .
Câu 5 (1,5 điểm ). Cho biểu thức  x +1 x −1 8 x   x − x − 3 1  P =  − −  :  −
 (với x  0, x 1). x −1 x +1 x −1 x −1 x −1     a) Rút gọn biểu thức . P
b) Tìm tất cả các số thực x để biểu thức P nhận giá trị nguyên.
Câu 6 (1,0 điểm ). Cho ba số ,
x y, z  0 thỏa mãn xyz = 1. Chứng minh rằng: 1 1 1 1 + +  2 2 2 2 2 2 x + 2 y + 3 y + 2z + 3 z + 2x + . 3 2
-------------- HẾT --------------
(Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh: ............................................................... Số báo danh: ..............................
MÔN: TOÁN 10 (DÀNH CHO 10 LÍ – HOÁ - TIN)
ĐÁP ÁN, THANG ĐIỂM Câu Ý Nội dung trình bày Điểm Cho hàm số 2
y = (4 − m )x + 9 . Gọi A là tập hợp tất cả giá trị của tham số m đề
hàm số đồng biến và tập hợp B =m 1m  3 .
a) Xác định các tập hợp A và A  B . 2,0
b) Tìm tất cả giá trị của tham số m để đồ thị hàm số đã cho đi qua điểm Câu 1 M (1; 3 − ) . A =  2
m | 4 − m   0 = m | 2 −  m   2 = ( 2 − ;2) ; 1,0 a A = ( 2
− ;2) , B = (1;3)  A B = (1;2). 0,5
Đồ thị hàm số đi qua điểm M (1; 3 − ) b − = ( 2 − 0,5 m ) 2 3 4 1+ 9  3
− =13− m  m = 4 
Cho hình bình hành ABCD tâm O , M là một điểm bất kì trong mặt phẳng. Chứng minh rằng 2,0
a) BA + DA + AC = 0 và OA + OB + OC + OD = 0 .
b) MA + MC = MB + MD . Câu 2
Hình bình hành ABCD tâm O  BC = AD và O là trung điểm của AC, BD . 0,5
BA + DA + AC = (BA+ AC) + = + = a DA BC DA 0
OA + OB + OC + OD = (OA + OC) + (OB + OD) = 0 + 0 = 0. 0,5
Vì O là trung điểm của AC, BD nên với mọi điểm M ta có: b 1,0
MA + MC = 2M ;
O MB + MD = 2MO  MA + MC = MB + MD .
Cho phương trình 2
x − 3x + m = 0 ( )
1 (với m là tham số).
a) Giải phương trình ( )
1 khi m = 2 . 2,0
b) Tìm tất cả giá trị của tham số m để phương trình ( )
1 có hai nghiệm
x , x thỏa mãn 3 3 2 2
x x + x x − 2x x = 5 . 1 2 1 2 1 2 1 2 x =1 a
Với m = 2 , ta có phương trình 2
x − 3x + 2 = 0   . 0,5 x =2
Phương trình (1) có hai nghiệm x , x 1 2 9    0,5
0  9 − 4m  0  m  ( ) * 4 Câu 3  + = x x 3 Theo ĐL Viet ta có 1 2  0,25 x x = m  1 2 3 3 2 2
x x + x x − 2x x = 5 1 2 1 2 1 2 b
 x x (x + x ) − 2(x x )2 2 2 = 5 1 2 1 2 1 2 0,5
 x x (x + x )2 − 2x x  − 2(x x )2 = 5 1 2 1 2 1 2 1 2    m( − m) 2 9 2 − 2m = 5 m=1 0,25 2 4m 9m 5 0   − + =  5  (thoả mãn (*)). m =  4
Cho tam giác ABC nhọn, nội tiếp đường tròn (O) và có trực tâm H . Gọi Câu 4 1,5 ,
D E, F theo thứ tự là chân các đường cao hạ từ các đỉnh ,
A B,C xuống các
cạnh BC,C ,
A AB của tam giác ABC .
a) Chứng minh rằng đường tròn ngoại tiếp các tam giác AEF, BF , D CDE
cùng đi qua một điểm.
b) Đường thẳng AH cắt đường tròn (O) tại điểm thứ hai là A . Chứng
minh rằng hai điểm H và A đối xứng nhau qua đường thẳng BC . A E O F H a 0,5 C B D A'
Ta chứng minh các tứ giác AEHF, BFH ,
D CDHE nội tiếp. Từ đó suy ra
đường tròn ngoại tiếp các tam giác AEF, BF ,
D CDE cùng đi qua điểm H 1 Ta có A B  C = A A  C = sd A C  ( ) 1 0,25 2
Xét tam giác DHB và tam giác EHA có 0
BDH = AEH =90 và 0,5 b
DHB = EHA (hai góc đối đỉnh). Suy ra DBH = EAH =CAA (2) Từ ( ) 1 ,(2) suy ra A B
 D= HBD . Do đó BHA cân tại B ( BD vừa là
đường cao vừa là phân giác), suy ra BC là đường trung trực đoạn thăng 0,25
HA hay H và A đối xứng nhau qua đường thẳng BC .  x +1 x −1 8 x   x − x − 3 1  Cho biểu thức P =  − −  :  −  (với x −1 x +1 x −1 x −1 x −1    
x  0, x  1). 1,5
a) Rút gọn biểu thức . P
b) Tìm tất cả các số thực x để P nhận giá trị nguyên.
( x + )2 −( x − )2 1 1 − 8 x
x − x − 3 − ( x + ) 1 P = ( 0,5 x − )( x + ) : 1 1
( x − )1( x + ) Câu 5 1 a ( x − )1( x + − x )1 4 4 x = (  = 0,5 x − ) 1 ( x + ) . 1 −x − 4 x + 4 4 x
Vì x  0, x  1 nên P =  0. x + 4 b 0,25 − + ( x − x x x )2 2 4 4 4 Ta có: 1− P = 1− = =  0 P  x + 4 x + 4 x + suy ra 1. 4
Do đó 0  P  1 mà P  nên P = 0 hoặc P = 1.
Với P = 0 thì x = 0 (thỏa mãn). 0,25
Với P = 1 thì x − 2 = 0  x = 4 (thỏa mãn).
Vậy x = 0; x = 4 thì P nhận giá trị nguyên. Cho ,
x y, z  0 thỏa mãn xyz = 1. Chứng minh rằng: 1 1 1 1 + +  1,0 2 2 2 2 2 2 x + 2 y + 3 y + 2z + 3 z + 2x + 3 2 Ta có: 2 2 2
x + y  2x ; y y +1  2 y 2 2
 x + 2y +3  2(xy + y + ) 1  0 . 1 1 Suy ra  2 2 x + 2 y + 3 2 ( xy + y + ) 1 Tương tự 1 1 1 1 :  ;  . 2 2 y + 2z + 3 2 ( yz + z + ) 1 2 2 z + 2x + 3 2 ( zx + x + ) 1 0,5 Câu 6 Suy ra: 1 1 1 1 1 1 + +  + + 2 2 2 2 2 2 x + 2 y + 3 y + 2z + 3 z + 2x + 3 2 ( xy + y + ) 1 2 ( yz + z + ) 1 2 ( zx + x + ) 1 Mặt khác: 1 1 1 1 xy y + + = + + =1 2 xy + y +1 yz + z +1 zx + x +1 xy + y +1
xy z + xyz + xy
yzx + xy + y . 0,5 1 1 1 1 Suy ra: + +  . 2 2 2 2 2 2 x + 2 y + 3 y + 2z + 3 z + 2x + 3 2
Dấu bằng xảy ra: x = y = z =1
========================= HẾT=====================
TRƯỜNG THPT CHUYÊN BẮC NINH
ĐỀ KIỂM TRA ĐỊNH KÌ LẦN 1 TỔ TOÁN - TIN NĂM HỌC 2021 - 2022
(Đề thi gồm 01 trang) Môn thi: TOÁN
Dành cho các lớp 10: Văn, Anh, Sinh
Thời gian: 120 phút (không kể thời gian giao đề)
Câu 1 (2,0 điểm). Cho hàm số 2
y = (4 − m )x + 9 . Gọi A là tập hợp tất cả giá trị của tham số m
đề hàm số đồng biến và tập hợp B =m 1m  3 .
a) Xác định các tập hợp A và A  B .
b) Tìm tất cả giá trị của tham số m để đồ thị hàm số đã cho đi qua điểm M (1; 3 − ) .
Câu 2 (2,0 điểm). Cho hình bình hành ABCD tâm O , M là một điểm bất kì trong mặt phẳng. Chứng minh rằng
a) BA + DA + AC = 0 và OA + OB + OC + OD = 0 .
b) MA + MC = MB + MD .
Câu 3 (2,0 điểm). Cho phương trình 2
x − 3x + m = 0 ( )
1 (với m là tham số). a) Giải phương trình ( ) 1 khi m = 2 .
b) Tìm tất cả giá trị của tham số m để phương trình ( )
1 có hai nghiệm x , x thỏa mãn 1 2 3 3 2 2
x x + x x − 2x x = 5 . 1 2 1 2 1 2
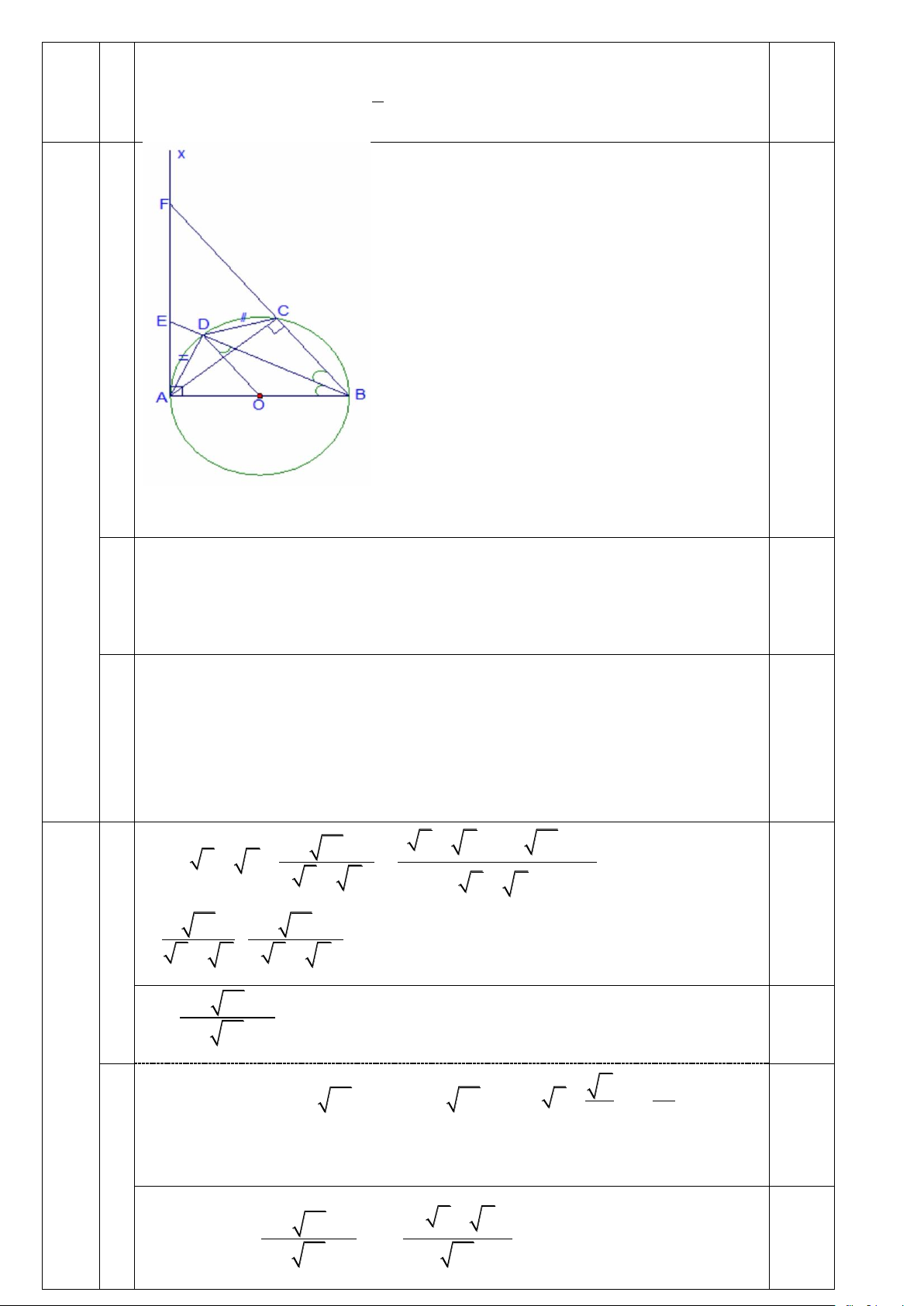
Câu 4 (1,5 điểm). Cho đường tròn tâm O đường kính AB và tia Ax là tiếp tuyến tại A của
đường tròn. Trên Ax lấy điểm F , BF cắt đường tròn (O) tại điểm C (khác B ). Đường phân
giác của góc ABF cắt Ax tại điểm E và cắt đường tròn (O) tại điểm D (khác B ).
a) Chứng minh: OD song song BC . b) Chứng minh: B .
D BE = BC.BF .
Câu 5 (1,5 điểm ). Cho biểu thức:  x − y x x − y y  x x + y y A =  −  :  
với x  0, y  0, x  y . x − y x − y
x + y + 2 xy  
a) Rút gọn biểu thức A .
b) Chứng minh: 0  A  1.
Câu 6 (1,0 điểm ). Cho , a ,
b c  0 thỏa mãn abc =1. Chứng minh rằng: 1 1 1 1 + +  . 2 2 2 2 2 2 a + 2b + 3 b + 2c + 3 c + 2a + 3 2
-------------- HẾT --------------
(Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh: ............................................................... Số báo danh: ..............................
TRƯỜNG THPT CHUYÊN BẮC NINH
ĐỀ KIỂM TRA ĐỊNH KÌ LẦN 1 TỔ TOÁN - TIN NĂM HỌC 2021 - 2022
(Đề thi gồm 01 trang) Môn thi: TOÁN
Dành cho các lớp 10: Văn, Anh, Sinh
Thời gian: 120 phút (không kể thời gian giao đề) ĐÁP ÁN Câu ý Nội dung Điểm 1 a A =  2 m  | 4 − m   0 = m  | 2 −  m   2 = ( 2 − ;2) ; 1,0 A = ( 2 − ;2), B = (1; )
3  A  B = (1;2) . 0,5
b Để đồ thị hàm số đi qua điểm M (1; 3 − ) thì 0,5 − = ( 2 − m ) 2 3 4 1+ 9  3
− =13 − m  m = 4  2
a Hình bình hành ABCD tâm O  BC = AD và O là trung điểm của 0,5 AC, BD .
BA + DA + AC = (BA+ AC) + DA = BC + DA = 0
OA + OB + OC + OD = (OA+ OC) + (OB + OD) = 0 + 0 = 0. 0,5
b Vì O là trung điểm của AC, BD nên với mọi điểm M ta có: 1,0
MA + MC = 2M ;
O MB + MD = 2MO  MA + MC = MB + MD . 3 a x =1 0,5
Với m = 2 , ta có phương trình 2
x − 3x + 2 = 0   . x =2 b 0,5
Phương trình (1) có hai nghiệ 9
m x , x    0  9 − m  0  m  ( ) * 1 2 4 x + x = 3 0,25 Theo ĐL Viet ta có 1 2 
x  x = m  1 2 3 3 2 2
x x + x x − 2x x = 5 0,5 1 2 1 2 1 2
 x x (x + x ) − 2(x x )2 2 2 = 5 1 2 1 2 1 2
 x x (x + x )2 − 2x x  − 2(x x )2 = 5 1 2 1 2 1 2 1 2    m( − m) 2 9 2 − 2m = 5 0,25 m=1 2 4m 9m 5 0   − + =  5  (thoả mãn (*)). m =  4 4
Vẽ hình sai trừ 0,25đ
a Tam giác BOD cân tại O (do OB = OD = R ) suy ra OBD = ODB . 0,5 Mà OBD = CB (
D gt) nên CBD = ODB . Hai góc này ở vị trí so le trong nên OD / /BC . b Ta có: ,
D C thuộc đường tròn đường kính AB nên ADB = ACB = 90 . 1,0 Xét E
 AB vuông tại A, AD ⊥ BE 2  AB = B . D BE (1). Xét F
 AB vuông tại A, AC ⊥ BF 2
 AB = BC.BF (2). Từ (1) (2) suy ra B .
D BE = BC.BF . a  +
+  ( x + y )(x − xy + y 0,5 x xy y )
A =  x + y −  :   x + y   ( x + y)2 xy x − xy + y = : 5 x + y x + y xy 0,5 A =
, với x  0, y  0, x  y x − xy + y b 2  0,25 y  3y
+) Vì x  0, y  0  xy  0 và x − xy + y =  x −  +  0  . 2  4   Suy ra A  0 . 0,25 −( x − y xy )2 +) Xét A −1 = −1 =
 0 với x  0, y  0, x  y.
x − xy + y
x − xy + y Suy ra A  1. Vậy 0  A  1. Ta có: 2 2 2
a + b  2a ; b b +1  2b 2 2
 a + 2b + 3  2(ab +b + ) 1  0 . 0,5 1 1 Suy ra  2 2 a + 2b + 3 2(ab + b + ) 1 Tương tự 1 1 1 1 :  ;  . 2 2 b + 2c + 3 2(bc + c + ) 1 2 2 c + 2a + 3 2(ca + a + ) 1 Suy ra: 1 1 1 1 1 1 + +  + + 2 2 2 2 2 2 a + 2b + 3 b + 2c + 3 c + 2a + 3 2(ab + b + ) 1 2(bc + c + ) 1 2(ca + a + ) 1 6 Mặt khác: 1 1 1 1 ab b + + = + + =0,5 1 2 ab + b +1 bc + c +1 ca + a +1 ab + b +1
ab c + abc + ab
bca + ab + b . 1 1 1 1 Suy ra: + +  . 2 2 2 2 2 2 a + 2b + 3 b + 2c + 3 c + 2a + 3 2
Dấu bằng xảy ra: a = b = c =1
-----------------------------------------HẾT--------------------------------------------
Document Outline

• 1_De_Toan_10_L_H_T_bce6dea8ce
• 1_DA_Toan_10_L_H_T_f43f4ea8ce
• 2__De_Toan_10_S_V_A_8b89df0ebe
• 2__DA_Toan_10_S_V_A_fe206f0ebe