Đề kiểm tra định kỳ HK1 Toán 12 năm 2019 – 2020 trường Tô Hiệu – Hà Nội

Đề kiểm tra định kỳ học kỳ 1 môn Toán 12 năm học 2019 – 2020 trường THPT Tô Hiệu – Thường Tín – Hà Nội là đề kiểm tra một tiết Giải tích 12 chương 1: ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số, đề gồm 25 câu hỏi và bài tập dạng trắc nghiệm 04 đáp án

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

20 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Trang 1/20 - Mã đề 104
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
TỔ TOÁN
KIỂM TRA ĐỊNH KỲ - HỌC KỲ I
NĂM HỌC 2019 – 2020
Môn: Toán - Lớp 12 - Chương trình chuẩn
ĐỀ CHÍNH THỨC Thời gian: 45 phút (Không kể thời gian phát đề)
Mã đề thi
104 Họ và tên:
………………………………….
Lớp:
…………….......……..………
Câu 1. Cho hàm số
3
2 1
x
y
x
. Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên
. B. Hàm số nghịch biến trên
1
;
2

.
C. Hàm số đồng biến trên
0;
. D. Hàm số đồng biến trên
1
;
2

.
Câu 2. Cho hàm số
( )f x
xác định, liên tục trên
và có bảng xét dấu
'( )f x
như sau:
Hàm số
( )f x
có bao nhiêu điểm cực đại ?
A. 0. B. 3. C. 2. D. 1.
Câu 3. Cho hàm số có bảng biến thiên sau:
Giá trị cực tiểu của hàm số đã cho bằng :
A. . B. . C.
3.
D. .
Câu 4. Cho hàm số
y f x
có bảng biến thiên trên
3;5
như sau :
Mệnh đề nào dưới đây là đúng?
A.
3;5
min 3
f x
. B.
3;5
max 7
f x
. C.
3;5
min 5
f x
. D.
3;5
max 2
f x
.
y f x
4
2
2
x
– 3
-1
2
5
y'
+
0
–
0
+
y
- 5
2
-3
7
Trang 2/20 - Mã đề 104
Câu 5. Đồ thị của hàm số nào dưới đây có dạng như đường cong hình vẽ.
A.
3
3 2y x x
. B.
4 2
2 3y x x
.
C.
3
3 3y x x
. D.
3 2
2 2y x x
.
Câu 6. Tiệm cận đứng của đồ thị hàm số
x 1
y
3x 2
là?
A.
2
y
3
B.
1
y
3
C.
1
x
3
D.
2
x
3
Câu 7. Cho hàm số
( )y f x
có bảng biến thiên
như hình vẽ. Hàm số
( )y f x
nghịch biến trên
khoảng:
A.
( ; 2)
. B. . C.
(1; )
. D.
( 2 ; 2)
.
Câu 8. Bảng biến thiên dưới đây là của hàm số nào sau đây?
A.
2
1
x
y
x
. B.
2
1
x
y
x
. C.
2
1
x
y
x
. D.
3
1
x
y
x
.
Câu 9. Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm của phương trình
7 2 0f x
là:
A.
3
. B.
1
.
C.
2
. D.
0
.
Câu 10. Gọi M,m là giá trị lớn nhất và nhỏ nhất của hàm số
3
1
7
3
y x x
trên đoạn
3;0
. Tổng
3M m
bằng: A.
24
. B.
7
. C.
8
. D.
23
3
.
Câu 11. Cho hàm số có đạo hàm . Số điểm cực trị của hàm số
đã cho là:
A. 6. B. 1. C. 3.
D.
2
.
1;

f x
2 3
1 2 2 3 ,f x x x x x
Trang 3/20 - Mã đề 104
Câu 12. Cho hàm số
y f x
có đạo hàm
3 2
4 ,f x x x
. Hàm số
y f x
nghịch biến trên
khoảng:
A.
0;2
. B.
2; 
. C.
; 2
. D.
2;0
.
Câu 13. Cho hàm số
y f x
có đồ thị như hình vẽ dưới đây. Tìm
m
để phương trình
f x m
có hai nghiệm phân biệt.
A.
4m
và
3m
. B.
4 3m
.
C.
4 3m
. D.
4m
.
Câu 14. Điểm cực tiểu của đồ thị hàm số
4 2
y x 2x 6 là:
A.
1;5
B.
x 1
C.
0;6
D.
x 1
Câu 15. Cho hàm số
y f x
có bảng biến thiên như hình vẽ dưới đây
Đường tiệm cận ngang của đồ thị hàm số đã cho có phương trình là:
A.
3x
. B.
1x
. C.
1y
. D.
3y
.
Câu 16. Hàm số
3 2
2 1y x x x nghịch biến trên khoảng nào dưới đây ?
A.
1
;
3

. B.
1
;1
3
. C.
1
;1
3
. D.
1;
.
Câu 17. Cho hàm số
y f x
liên tục trên
có đồ thị như hình vẽ.
Phương trình
1 1f f x
có tất cả bao nhiêu nghiệm thực phân biệt?
A.
4
. B.
3
.
C.
5
. D.
6
.
Câu 18. Tìm tất cả các giá trị thực của tham số m để hàm số
mx 4
y
x m
nghịch biến trên khoảng
0;
.
A.
0 m 2.
B.
0 m 2.
C.
0 m 2.
D.
2 m 2.
Câu 19. Cho hàm số
( )y f x
có bảng biến thiên như hình vẽ.
Trang 4/20 - Mã đề 104
Hàm số
(1 )y f x
nghịch biến trên khoảng nào?
A.
. B.
( 2 ; 0)
.
C.
( 3 ; 2)
. D.
( 1;3)
.
Câu 20. Số các giá trị nguyên của m để hàm số
3 2 2
3 – 4 3
3
m
y x m x x m
đạt cực tiểu tại
1x
là:
A.
5
. B.
2
. C.
0
. D.
1
.
Câu 21. Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
2
x 1
y
x 2mx 3
có ba đường tiệm cận?
A.
m 3
. B.
3 m 2
. C.
3 m 2
. D.
2 m 5
.
Câu 22. Cho hàm số
1
1
x m
y
x
(
m
là tham số thực) thỏa mãn
[2;4]
min 3.
y
Mệnh đề nào dưới đây đúng?
A.
4m
. B.
1m
. C.
3 4m
. D.
1 3m
.
Câu 23. Cho hàm số
y f x
có bảng biến thiên như hình bên.
Có bao nhiêu số nguyên dương của m để bất phương trình
1
1
3 2
x
f x m
có nghiệm
2, 2
x
.
A. 9. B. 4. C. 8. D. 6.
Câu 24. Cho hàm số
f x
có đồ thị hàm số
y f x
được
cho như hình vẽ bên.
Hàm số
2
1
1 1
2
y f x x f
có nhiều nhất bao nhiêu
điểm cực tiểu trong khoảng
3;5
?
A.
2
. B.
1
.
C.
5
. D.
3
.
Câu 25. Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
10;10
để hàm số
3 2
3 3 2019
y x x mx nghịch biến trên khoảng
1;2
?
A.
11
. B.
10
. C.
21
. D.
20
.
------------- HẾT -------------
Mã đề [104]
Trang 5/20 - Mã đề 104
1 2 3 4
5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D D D
B
A
D
C
A
A
A D D A A D C A A B D B A B A A
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
TỔ TOÁN
KIỂM TRA ĐỊNH KỲ - HỌC KỲ I
NĂM HỌC 2019 – 2020
Môn: Toán - Lớp 12 - Chương trình chuẩn
ĐỀ CHÍNH THỨC Thời gian: 45 phút (Không kể thời gian phát đề)
Mã đề thi
105 Họ và tên:
………………………………….
Lớp:
…………….......……..………
Câu 1. Hàm số nào trong bốn hàm số sau có bảng biến thiên như hình vẽ sau?
A.
3 2
3 1.y x x B.
3 2
3 2.y x x C.
3 2
3 1.y x x D.
3
3 2.y x x
Câu 2. Cho hàm số
3 2
y ax bx cx d
, , ,a b c d
. Đồ thị
hàm số
y f x
như hình vẽ dưới đây.
Giá trị cực tiểu của hàm số bằng:
A.
0
. B.
1
.
C.
2
. D.
2
.
Câu 3. Hàm số nào trong bốn hàm số sau có đồ thị như hình vẽ
bên.
A.
2
.
2 1
y
x
B.
2
2 1
x
y
x
C.
3
3 2y x x D.
4 2
2 2y x x .
x
1
2
1
2
y
O
-2
-2
Câu 4. Hàm số
1 2
2
x
y
x
có bao nhiêu cực trị ?
A. 3. B.
1
. C. 0 . D.
2
.
Câu 5. Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như hình dưới đây
Trang 6/20 - Mã đề 104
Khẳng định nào sau đây là sai?
A. Hàm số nghịch biến trên khoảng
; 1
. B. Hàm số đồng biến trên khoảng
1;3
.
C. Hàm số đồng biến trên khoảng
1;1
. D. Hàm số nghịch biến trên khoảng
1;

.
Câu 6. Cho hàm số
2 1
2
x
y
x
. Khẳng định nào sao đây là khẳng đinh đúng?
A. Hàm số nghịch biến trên các khoảng
;2
và
2;

.
B. Hàm số nghịch biến trên
;2 2; . 
C. Hàm số đồng biến trên các khoảng
;2
và
2;

.
D. Hàm số đồng biến trên
;2 2; . 
Câu 7. Hàm số nào sau đây nhận đường thẳng
5
x
làm một tiệm cận?
A.
5
1
y
x
. B.
2 5
1
x
y
x
. C.
2
5
y
x
. D.
5 3
2
x
y
x
.
Câu 8. Hàm số
y f x
liên tục trên R và có bảng biến thiên trên khoảng
3;5
như sau
Gọi
,m
M
là giá trị lớn nhất,nhỏ nhất của hàm số
y f x
trên khoảng
3;5
. Tìm mệnh đề đúng ?
A.
5
M
. B.
0
M
. C.
5
m
. D.
3
m
.
Câu 9. Hàm số nào sau đây đồng biến trên khoảng
( ; ). 
A.
4
1
y x
B.
2
1
x
y
x
C.
3
2 3 1
y x x
D.
3
2 1
y x x
Câu 10. Cho hàm số
y f x
liên tục trên
có đồ thị như
hình vẽ. Tìm tất cả các giá trị m để phương trình
f x m
có
một nghiệm âm và hai nghiệm dương phân biệt?
A.
0 4
m m
. B.
0 2
m
.
C.
2 4
m
. D.
0 4
m
.
Câu 11. Tìm giá trị thực của tham số
m
để hàm số
4 3
4 1
y x mx m
đạt cực tiểu tại điểm
3
x
.
A.
1
m
. B.
0
m
. C.
2
m
. D.
m
.
Câu 12. Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
2 3
x x
y
x
là:
A. 1. B. 2. C. 3 . D. 0.
Trang 7/20 - Mã đề 104
Câu 13. Cho hàm số
y f x
có đạo hàm trên
và
2
' 1 2 3 ,f x x x x x
. Số điểm cực trị
của hàm số đã cho là
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 14. Cho hàm số
( )y f x
có đạo hàm
2
( ) 5 6,f x x x x R
. Hàm số
5 ( )y f x
nghịch biến
trên khoảng nào sau đây?
A.
2;
B.
2;3
C.
; 2
và
3;
D.
;3
Câu 15. Cho hàm số
4 2
0f x ax bx c a
xác định, liên tục trên
và có bảng biến thiên như hình
vẽ:
Tìm tất cả các giá trị thực
m
để phương trình
f x m
có bốn nghiệm phân biệt.
A. 1 3m m . B. 1 3m . C. 1 3m . D. 3m .
Câu 16. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 2
3 9 35y x x x
trên đoạn
4;4
. Khi đó tổng
M m
bằng bao nhiêu?
A. 48. B.
1
. C. 55 D. 11.
Câu 17. Cho hàm số
y f x
. Biết rằng hàm số
f x
có đạo hàm
là
'f x
và hàm số
'y f x
có đồ thị như hình vẽ bên.
Hàm số
1y f x
đồng biến trên khoảng:
A.
;0
và
3;
. B.
3;
.
C.
1;
. D.
2;1
.
Câu 18. Xác định m để đồ thị hàm số
3 1x x
y
x m
có hai đường tiệm cận tạo với hai trục tọa độ một hình
chữ nhật có diện tích bằng
6
.
A.
2m
. B.
1m
. C.
2m
. D.
1m
.
Câu 19. Cho hàm số
y f x
có bảng biến
thiên như sau:
Có bao nhiêu giá trị nguyên của tham số m để phương trình
0f x m
có 4 nghiệm phân biệt .
A.
4.
B.
6.
C.
5
. D.
8.
Trang 8/20 - Mã đề 104
Câu 20. Tìm tham số
m
để hàm số
x
y
x m
nghịch biến trên khoảng
1; 2
.
A.
1 2
m
. B.
0
m
. C.
0
m
. D.
0 1 2
m m
.
Câu 21. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình bên.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất hàm số
4 1
y f x
trên đoạn
0;2
. Mệnh đề nào dưới đây đúng?
A.
3M m
. B.
7
M m
.
C.
4
M m
. D.
5M m
.
Câu 22. Cho hàm số
4 2 2
2 1 1
y x m m x m
với
m
là tham số thực. Giá trị của
m
để đồ thị hàm số
có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất là
A.
1
2
m
. B.
3
2
m
. C.
3
2
m
. D.
1
2
m
.
Câu 23. Cho hàm số
y f x
liên tục trên
. Hàm số
y f x
có đồ
thị như hình bên.
Xác định tất cả các giá trị m để phương trình
3 2
3 3 4
f x x x m
có nghiệm
1;3
x
.
A.
3 3 4 3 1
f m f
B.
3 1
m f
.
C.
3 3
m f
. D.
3 3 3 1 2
f m f
.
Câu 24. Cho hàm số
y f x
liên tục trên
1;3
và
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của
m
để phương trình
2
1
4 5
m
f x
x x
có nghiệm trên khoảng
1;2
.
A.
10.
B.
0.
C.
4.
D.
5
.
Câu 25. Cho hàm số
f x
có đạo hàm
2
2
1 2f x x x x
với mọi
.
x
Hỏi số thực nào dưới đây
thuộc khoảng đồng biến của hàm số
2
2 2
g x f x x
?
A.
3
.
2
B.
3.
C.
1.
D.
2.
------------- HẾT -------------
Mã đề [105]
1
2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B
C
B
C
B
C
C
A
D
B A D A B B B B A A D B D A C B
Trang 9/20 - Mã đề 104
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
TỔ TOÁN
KIỂM TRA ĐỊNH KỲ - HỌC KỲ I
NĂM HỌC 2019 – 2020
Môn: Toán - Lớp 12 - Chương trình chuẩn
ĐỀ CHÍNH THỨC Thời gian: 45 phút (Không kể thời gian phát đề)
Mã đề thi
106 Họ và tên:
………………………………….
Lớp:
…………….......……..………
Câu 1. Cho hàm số
( )y f x
có bảng xét dấu
( )f x
như sau:
Hàm số đồng biến trên khoảng:
A.
; 0
. B.
; 3
và
3;
. C.
; 3
và
0;3
. D.
0;
.
Câu 2. Cho hàm số
y f x
có bảng biến thiên như hình
vẽ. Bảng biến thiên trên có thể là của hàm số nào trong các
hàm số sau?
A.
2 5
2
x
y
x
. B.
2 3
2
x
y
x
. C.
2 1
2
x
y
x
. D.
3
1
x
y
x
.
Câu 3. Cho hàm số
y f x
xác định trên đoạn
0;5
và có bảng biến thiên như sau:
Giá trị cực đại của hàm số
y f x
là:
A.
4
y
. B.
1x
. C.
3
y
. D.
3
x
.
Câu 4. Cho hàm số
y f x
xác định trên
\ 7
D
và
lim ( ) 2
x
f x

,
7
lim ( )
x
f x

. Trong các
mệnh đề sau, mệnh đề nào đúng?
A. Đồ thị hàm số có đúng hai tiệm cận ngang
7, 2y y
.
B. Đồ thị hàm số có một tiệm cận đứng
7x
và một tiệm cận ngang
.
C. Đồ thị hàm số có đúng một đường tiệm cận.
D. Đồ thị hàm số có hai tiệm cận đứng và không có tiệm cận ngang.
Câu 5. Đường cong dưới đây là đồ thị của một trong các hàm số đã cho, hỏi
đó là hàm số nào?
A.
4 2
2y x x
. B.
4 2
y x x
.
C.
4 2
y x x
. D.
4 2
2y x x
.
2
2
∞
+∞
2
∞
+∞
y
y'
x
x
y
O
1
Trang 10/20 - Mã đề 104
Câu 6. Cho hàm số
3 1
1
x
y
x
. Mệnh đề nào dưới đây là đúng?
A. Hàm số luôn đồng biến trên
\ 1
.
B. Hàm số nghịch biến trên
;1 1;
 
.
C. Hàm số đồng biến trên các khoảng
;1
và
1;

.
D. Hàm số nghịch biến trên các khoảng
;1
và
1;

.
Câu 7. Giá trị lớn nhất của hàm số
3 2
2y x x
trên đoạn
1;3
bằng:
A.
9
. B.
32
27
. C.
3
. D.
0
.
Câu 8. Cho hàm số
y f x
có bảng biến
thiên như bên. Hàm số đạt cực tiểu tại điểm:
A.
0
x
. B.
1
x
.
C.
4
x
. D.
1.
x
Câu 9. Cho hàm số
y f x
có đồ thị như hình vẽ.
Hàm số đồng biến trên khoảng nào sau đây?
A.
2;

. B.
1;1
.
C.
0;
. D.

.
Câu 10. Cho hàm số
y f x
xác định trên
và có đạo hàm
2
1
f x x x
, với
x
.
Khẳng định nào sau đây là đúng?
A. Hàm số đã cho nghịch biến trên khoảng
;1
. B. Hàm số đã cho đồng biến trên khoảng
0;
.
C. Hàm số đã cho đồng biến trên
. D. Hàm số đã cho nghịch biến trên khoảng
0;
.
Câu 11. Cho hàm số
3
2
x 2
y 2x 3x
3 3
. Điểm cực đại của đồ thị hàm số là:
A.
1.
x
B. (1;2) C. (3;
2
3
) D.
2.
y
Câu 12. Cho hàm số
y f x
có đồ thị như hình vẽ.
Tìm tất cả các giá trị thực
m
để phương trình
1
f x m
có ba nghiệm
phân biệt.
A.
1 5
m
. B.
0 4
m
.
C.
0 5
m
. D.
1 4
m
.
O
x
y
2
2
1
2
Trang 11/20 - Mã đề 104
Câu 13. Cho hàm số
y f x
có đạo hàm trên
và
2 3
' 1 2 3 ,f x x x x x
. Số điểm cực
trị của hàm số đã cho là
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 14. Đồ thị hàm số
2
2
9
3 4
x
y
x x
có bao nhiêu đường tiệm cận?
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 15. Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm phương trình
2 3 0
f x
là:
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 16. Giá trị lớn nhất của hàm số
3 2
2y x x
trên đoạn
1;3
bằng:
A.
3
. B.
32
27
. C.
9
. D.
0
.
Câu 17. Với giá trị nào của m thì hàm số
3 2
1
2 3
3
y x mx m x
có hai điểm cực trị có hoành độ
dương? A.
0
m
. B.
2 1
m
. C.
1 2
m m
. D.
2
m
.
Câu 18. Cho hàm số
3 2
f x ax bx cx d
có đồ thị là hình vẽ bên.
Phương trình
2 0
f f x
có bao nhiêu nghiệm phân biệt?
A. 6. B. 4.
C. 5. D. 7.
Câu 19. Có tất cả bao nhiêu giá trị nguyên của tham số để hàm số nghịch biến trên khoảng
0;2
. A. . B. . C. . D. .
Câu 20. Cho hàm số
( )y f x
có bảng biến thiên như hình vẽ.
Hàm số
(1 )y f x
đồng biến trên khoảng nào?
A.
. B.
( 2 ; 0)
. C.
(1; 2019)
. D.
(2 ; )
.
m
10
2
mx
y
x m
6
5
4
9
Trang 12/20 - Mã đề 104
Câu 21. Hàm số
y f x
liên tục và có bảng biến
thiên trong đoạn
2;4
như sau:
Gọi
,m M
lần lượt là giá trị nhỏ nhất, lớn nhất của
hàm số
2
4
y f x x
trên đoạn
0;4
. Tìm
mệnh đề đúng ?
A.
32
M
. B.
1M
C.
1
m
D.
3M m
Câu 22. Tìm tất cả các giá trị thực của m để đồ thị hàm số
2
x 1
y
m x 1 4
có hai tiệm cận đứng:
A.
m 0
B.
m 1
C.
m 0
D.
m 0,m 1
Câu 23. Cho hàm số
f x
có đồ thị hàm số
y f x
được cho như hình vẽ bên.
Hàm số
2
1
1 1
2
y f x x f
có nhiều nhất
bao nhiêu điểm cực trị trong khoảng
5;5
?
A.
1
. B.
3
. C.
5
. D.
5
.
Câu 24. Cho hàm số
y f x
thỏa mãn
2
1 4 2
f x x x x x m
. Gọi S là tập hợp tất cả các giá trị
nguyên
10;10
m
để hàm số
2
1
y f x
đồng biến trên
0;1
. Tổng các phần tử của S bằng:
A.
52.
. B.
110
. C.
0
. D.
45
.
Câu 25. Cho hàm số
y f x
có bảng biến thiên như hình bên.
Tìm tất cả các giá trị của m để phương trình
1
1
3 2
x
f x m
có nghiệm
2,6
x
.
A.
4 6
m
. B.
4 2
m
. C.
4 2
m
. D.
6
m
.
------------- HẾT -------------
Mã đề [106]
1
2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B
C
C
B
D
D
A
B
C
A B A D C A C D B A A B D D A C
Trang 13/20 - Mã đề 104
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
TỔ TOÁN
KIỂM TRA ĐỊNH KỲ - HỌC KỲ I
NĂM HỌC 2019 – 2020
Môn: Toán - Lớp 12 - Chương trình chuẩn
ĐỀ CHÍNH THỨC Thời gian: 45 phút (Không kể thời gian phát đề)
Mã đề thi
107 Họ và tên:
………………………………….
Lớp:
…………….......……..………
Câu 1. Cho hàm số
y f x
có bảng xét dấu đạo hàm như hình vẽ.
Hỏi hàm số
y f x
có bao nhiêu cực trị ?
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 2. Cho hàm số
y f x
xác định trên
và
lim ( ) 5
x
f x

,
lim ( ) 5
x
f x

. Trong các mệnh đề sau,
mệnh đề nào đúng?
A. Đồ thị hàm số có đúng hai tiệm cận ngang
5, 5y y
.
B. Đồ thị hàm số có hai tiệm cận đứng và không có tiệm cận ngang.
C. Đồ thị hàm số có đúng hai tiệm cận đứng
5, 5x x
.
D. Đồ thị hàm số có đúng một tiệm cận đứng
5x
và một tiệm cận ngang
5y
.
Câu 3. Hàm số
4 2
2 3y x x
đồng biến trên khoảng nào sau đây?
A.
1;0
. B.
0;2
. C.
1;1
. D.
0;1
.
Câu 4. Hàm số
y f x
liên tục và có bảng biến thiên trong đoạn
2;4
như sau
Gọi
m
là giá trị nhỏ nhất của hàm số
y f x
trên đoạn
2;4
. Tìm mệnh đề đúng ?
A.
0m f
. B.
3m
. C.
3m f
. D.
1m
.
Câu 5. Bảng biến thiên trong hình vẽ bên là của hàm số nào sau đây?
A.
4 2
2 5y x x
. B.
4 2
2 1y x x
. C.
4 2
2 5y x x
. D.
4 2
2 5y x x
.
Trang 14/20 - Mã đề 104
Câu 6. Đường cong ở hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án
A,B,C, D
dưới đây. Hỏi hàm số đó là hàm số nào?
A.
1
1
x
y
x
. B.
3 2
3 1y x x .
C.
3
1
x
y
x
. D.
4 2
2 1y x x .
Câu 7. Cho hàm số
y f x
có bảng biến thiên như sau:
Mệnh đề nào sau đây đúng ?
A. Hàm số đạt cực tiểu tại
2x
.
B. Hàm số không có cực trị.
C. Hàm số đạt cực đại tại
2x
.
D. Hàm số đạt cực đại tại
3x
.
Câu 8. Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số
y f x
nghịch biến trên khoảng nào dưới đây?
A.
1; 3
. B.
; 2
. C.
0;
. D.
2;0
.
Câu 9. Cho hàm số
2
3y x x
. Hàm số đạt cực đại tại điểm có hoành độ:
A.
0x
. B.
1x
. C.
3x
. D.
3y
.
Câu 10. Cho hàm số
3 2
y ax bx cx d
, , ,a b c d
. Đồ thị hàm số
y f x
như hình vẽ bên.Số nghiệm thực của phương trình
5 2 0
f x
là
A.
3
. B.
2
.
C.
4
. D.
0
.
Câu 11. Cho hàm số
f x
có đạo hàm
2
3
1 2f x x x x
. Hỏi hàm số có bao nhiêu điểm cực đại ?
A.
0
. B.
1
. C.
3
. D.
2
.
Trang 15/20 - Mã đề 104
y
x
O
Câu 12. Hàm số nào sau đây nghịch biến trên
?
A.
1
1
x
y
x
. B.
1y x
. C.
4 2
1
y x x
. D.
3 2
3 9 4
y x x x
.
Câu 13. Cho hàm số có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A.
0, 0, 0
b c d
B.
0, 0, 0
b c d
C.
0, 0, 0
b c d
D.
0, 0, 0
b c d
Câu 14. Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số
2
2
4 3
x
y
x x
là :
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 15. Khoảng nghịch biến của hàm số
2
4 3
y x x
là
A.
;1
. B.
;2

. C.
2;

. D.
3;
.
Câu 16. Gọi m là giá trị nhỏ nhất của hàm số
2
1
x
f x
x
trên
1;5
. Trong các mệnh đề sau, mệnh đề nào
đúng? A.
4
m
. B.
m
. C.
5
m f
. D.
1m f
.
Câu 17. Biết đồ thị hàm số
2
2
2 3
1
x x
y
x mx
có đúng 2 đường tiệm cận. Mệnh đề nào dưới đây đúng?
A.
3;5
m
. B.
5; .
m
C.
; 4 .
m

D.
4;3 .
m
Câu 18. Tìm tất cả các giá trị của tham số
m
để hàm số
4 2
1 1 2y mx m x m
có đúng một điểm cực
trị.
A.
0
m
. B.
0 1
m
. C.
0
m
hay
1
m
. D.
0
m
hay
1
m
.
Câu 19. Hỏi có bao nhiêu giá trị nguyên
m
để hàm số
2 3 2
1 1 4y m x m x x
nghịch biến trên
khoảng
;
 
?
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 20. Tìm tất cả các giá trị của
m
để hàm số
1mx
y
x m
đồng biến trên từng khoảng xác định của nó là
A.
–1m
hoặc
1m
. B.
–1m
hoặc
1m
.
C.
–1 1m
D.
–1m
hoặc
1m
.
( 0)
ax b
y a
cx d
Trang 16/20 - Mã đề 104
Câu 21. Cho hàm số
y f x
có đồ thị như hình vẽ:
Hàm số
cos 1
y f x
đạt giá trị lớn nhất và nhỏ nhất lần
lượt là
M
và
m
. Mệnh đề nào dưới đây sai?
A.
2 5
M m
. B.
4
M m
.
C.
2 2
10
M m
. D.
2
M m
.
Câu 22. Cho hàm số
( )y f x
ax b
cx d
có đồ thị hàm số
f x
như trong hình vẽ dưới đây:
Biết rằng đồ thị hàm số
( )f x
đi qua điểm
0;4
A
. Khẳng
định nào dưới đây là đúng?
A.
1 6
f
. B.
11
1
2
f
.
C.
7
1
2
f
. D.
1 2
f
.
Câu 23. Cho hàm số
( )y f x
có đạo hàm
2 2
'( ) 1 4 3
f x x x x
. Hỏi hàm số
2
( ) (2 )g x f x x
có
bao nhiêu điểm cực đại?
A.
3.
B.
5
C.
2
D.
0
Câu 24. Biết hàm số
3 2
1
( ) 1 ( 1) 1
3
f x x m x m x
đồng biến trên khoảng
;1

khi
; 1;0
b
m a
c
, (
*
, , ,
a b c
,
b
c
tối giản). Giá trị
T a b c
bằng:
A.
7
. B.
5
. C.
9
. D.
13
.
Câu 25. Cho
f x
mà hàm số
y f x
có bảng
biến thiên như hình bên. Tất cả các giá trị của tham
số
m
để bất phương trình
2 3
1
3
m x f x x
có
nghiệm
0;3
x
là :
A.
2
1
3
m f
. B.
0
m f
. C.
3
m f
. D.
0
m f
.
------------- HẾT -------------
Mã đề [107]
1 2 3 4 5 6 7 8 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
A
A
B
C
A
C
D
B
C B D C B A A D C C B A B A C C
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
TỔ TOÁN
KIỂM TRA ĐỊNH KỲ - HỌC KỲ I
NĂM HỌC 2019 – 2020
Trang 17/20 - Mã đề 104
Môn: Toán - Lớp 12 - Chương trình chuẩn
ĐỀ CHÍNH THỨC Thời gian: 45 phút (Không kể thời gian phát đề)
Mã đề thi
108 Họ và tên:
………………………………….
Lớp:
…………….......……..………
Câu 1. Cho hàm số
( )y f x
có bảng biến thiên như sau:
Hàm số đồng biến trên khoảng
A.
(2; )
. B.
( ;0)
. C.
(0;2)
. D.
(1;5)
.
Câu 2. Giá trị lớn nhất của hàm số
1
1
x
y
x
trên
2;
bằng:
A. 3. B. 4 C. 2. D. 1.
Câu 3. Hàm số nào sau đây nhận đường thẳng
2y
làm một tiệm cận?
A.
3
2
y
x
. B.
2 3
1
x
y
x
. C.
2
1
x
y
x
. D.
2
2
y
x
.
Câu 4. Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào dưới đây?
A.
2 1
1
x
y
x
. B.
3
1.y x
. C.
4 2
y 2 1x x
. D.
2 3
1
x
y
x
.
Câu 5. Đường cong trong hình vẽ bên dưới là đồ thị của một hàm số nào?
A.
4 2
2 3y x x . B.
4 2
3 2y x x .
C.
2
1y x x . D.
3 2
2y x x .
Câu 6. Cho hàm số
f x
xác định trên
và có bảng xét dấu
f x
như hình bên. Khẳng định nào sau đây
sai ?
Trang 18/20 - Mã đề 104
A.
1x
là điểm cực đại của hàm số. B. Hàm số có hai điểm cực trị.
C. Hàm số đạt cực tiểu tại
2x
. D. Hàm số đạt cực đại tại
3x
.
Câu 7. Tìm điểm cực tiểu của đồ thị hàm số
3
3 4y x x .
A.
1;2
. B.
1;6
. C.
1x
. D.
1x
.
Câu 8. Các khoảng nghịch biến của hàm số
2 1
1
x
y
x
là
A.
;1
.
B.
;1
và
1;
.
C.
1;
. D.
\ 1
.
Câu 9. Cho hàm số
3 2
y ax bx cx d
, , ,a b c d
. Đồ thị hàm số
y f x
như hình vẽ dưới đây.
Số nghiệm thực của phương trình
5 9 0f x
là
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 10. Giá trị nhỏ nhất của hàm số
4 2
2 1y x x
trên
1;1
A.
1
. B. 2 C. 1. D. 0.
Câu 11. Biết đồ thị hàm số
3 2
3 1y ax x a
có một điểm cực trị là
1; 2A
. Giá trị của
3 12a
bằng:
A.
6
. B.
1
. C.
18
. D.
6
.
Câu 12. Cho hàm số
y f x
có đạo hàm trên
và
2
' 1 2 3f x x x x
. Số điểm cực trị của
hàm số đã cho là
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 13. Cho hàm số
4 2
0f x ax bx c a
xác định, liên tục trên
và có bảng biến thiên như hình
vẽ:
Tìm
m
để phương trình
f x m
có hai nghiệm phân biệt.
Trang 19/20 - Mã đề 104
A.
1 3
m
. B.
3
1
m
m
. C.
3
m
. D.
3
1
m
m
.
Câu 14. Cho hàm số
3 2
3 2019
y x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
0;2
. B. Hàm số nghịch biến trên khoảng
2;
.
C. Hàm số đồng biến trên khoảng
0;2
. D. Hàm số nghịch biến trên khoảng
;0

.
Câu 15. Tổng số tiệm cận đứng và tiệm cận ngang của hàm số
2
2
2 3
x x
y
x x
là bao nhiêu?
A. 3 . B. 2. C. 0. D. 1.
Câu 16. Hàm số
y f x
có đạo hàm
2
( 6)
y x x
. Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên
(0; )
. B. Hàm số nghịch biến trên
.
C. Hàm số đồng biến trên
6; .
D. Hàm số nghịch biến trên
;0

và
6; .
Câu 17. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
3
2
6 2
3
x
y mx mx
nghịch biến trên
.
A.
6
. B.
5
. C. vô số. D.
7
Câu 18. Cho hàm số y =
f x
có bảng biến thiên như sau:
Hỏi phương trình
1
f x
có bao nhiêu nghiệm?
A. 5. B. 6. C. 4. D. 2.
Câu 19. Gọi
T
là tập hợp tất cả các giá trị của tham số
m
để hàm số
2
1mx
y
x m
có giá trị nhỏ nhất trên đoạn
1;5
bằng
1
. Số phần tử của
T
là:
A.
2.
B.
4.
C.
0.
D.
3.
Câu 20. Cho hàm số
( )y f x
liên tục trên từng khoảng xác định và có bảng biến thiên như hình vẽ.
Tổng số tiệm cận đứng và ngang của đồ thị hàm số
1
( ) 2
g x
f x
là:
A. 4. B. 3. C. 5. D. 2.
Trang 20/20 - Mã đề 104
Câu 21. Biết
0
m
là giá trị của tham số
m
để hàm số
3 2
3 1y x x mx
có hai điểm cực trị
1
x
,
2
x
sao cho
2 2
1 2 1 2
13
x x x x
. Mệnh đề nào dưới đây đúng?
A.
0
7; 1
m
. B.
0
9; 1
m
. C.
0
15; 7
m
. D.
0
7;10
m
.
Câu 22. Cho hàm số
y f x
có đạo hàm liên tục trên
, dấu của đạo hàm được cho bởi bảng dưới đây
Hàm số
2 2
y f x
nghịch biến trong khoảng nào?
A.
1;1
. B.
1;2
. C.
2;
. D.
; 1
.
Câu 23. Cho hàm số
y f x
có bảng biến thiên như hình bên.
Gọi
M
là giá trị lớn nhất của hàm số
1
1
3 2
x
y f x
trên đoạn
2, 2
x
. Trong các mệnh đề sau,
mệnh đề nào đúng?
A.
6;m

. B.
4;2
m
. C.
; 5
m

. D.
2;6
m
.
Câu 24. Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
3 2
6 1 y x mx m x
đồng biến
trên khoảng
2;

?
A.
3
B.
0
. C.
2
. D.
4
.
Câu 25. Cho hàm số
f x
có đạo hàm trên
là
1 3
f x x x
. Gọi T là tập hợp các giá trị nguyên
của tham số
10;20
m
để hàm số
2
2
y f x x m
có 3 điểm cực trị. Tính tổng các phần tử của T.
A.
4
. B.
6
. C.
0
. D.
2
.
------------- HẾT -------------
Mã đề [108]
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C
A
B
A
A
D
A
B
C
A D B B A B C D A A C C B D A D
| 1/20
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
KIỂM TRA ĐỊNH KỲ - HỌC KỲ I TỔ TOÁN NĂM HỌC 2019 – 2020
Môn: Toán - Lớp 12 - Chương trình chuẩn ĐỀ CHÍNH THỨC
Thời gian: 45 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên:………………………………….Lớp:…………….......……..……… 104 x  3
Câu 1. Cho hàm số y
. Mệnh đề nào dưới đây đúng ? 2x 1  1 
A. Hàm số nghịch biến trên .
B. Hàm số nghịch biến trên  ;    .  2   1 
C. Hàm số đồng biến trên 0;  .
D. Hàm số đồng biến trên ;    .  2 
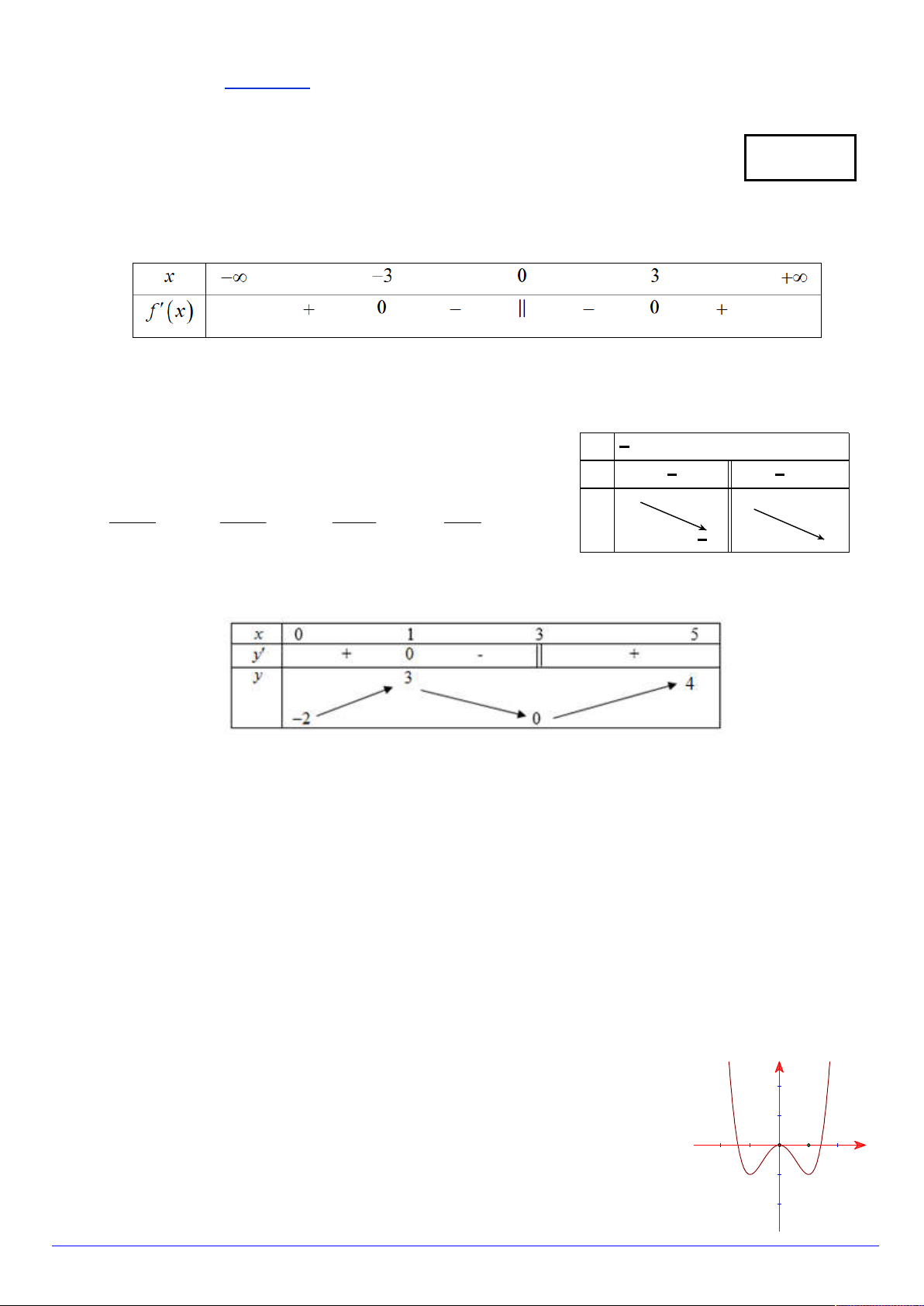
Câu 2. Cho hàm số f (x) xác định, liên tục trên  và có bảng xét dấu f '(x) như sau:
Hàm số f (x) có bao nhiêu điểm cực đại ? A. 0. B. 3. C. 2. D. 1.
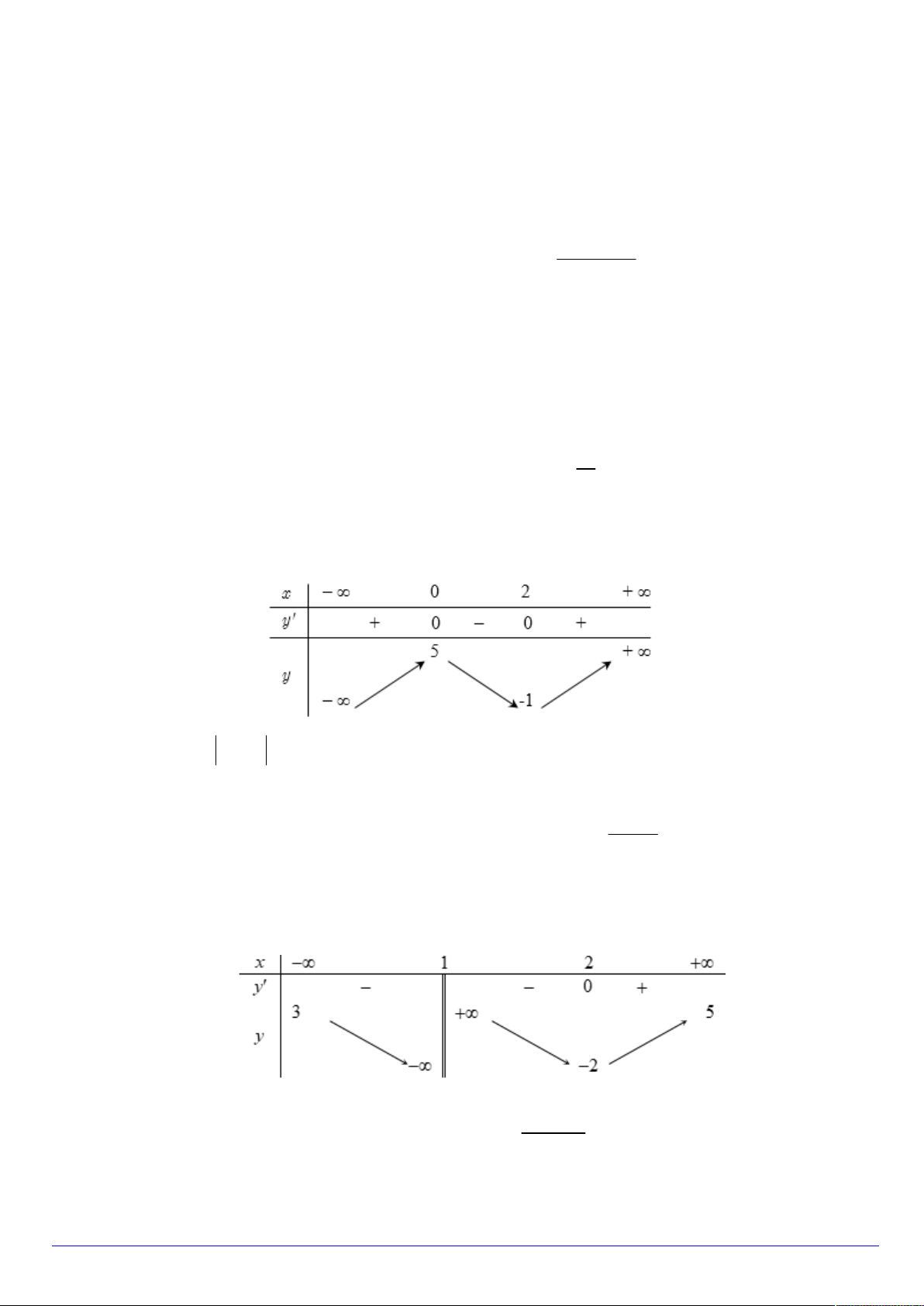
Câu 3. Cho hàm số y f x có bảng biến thiên sau:
Giá trị cực tiểu của hàm số đã cho bằng : A. 4 . B. 2 . C. 3. D. 2 .
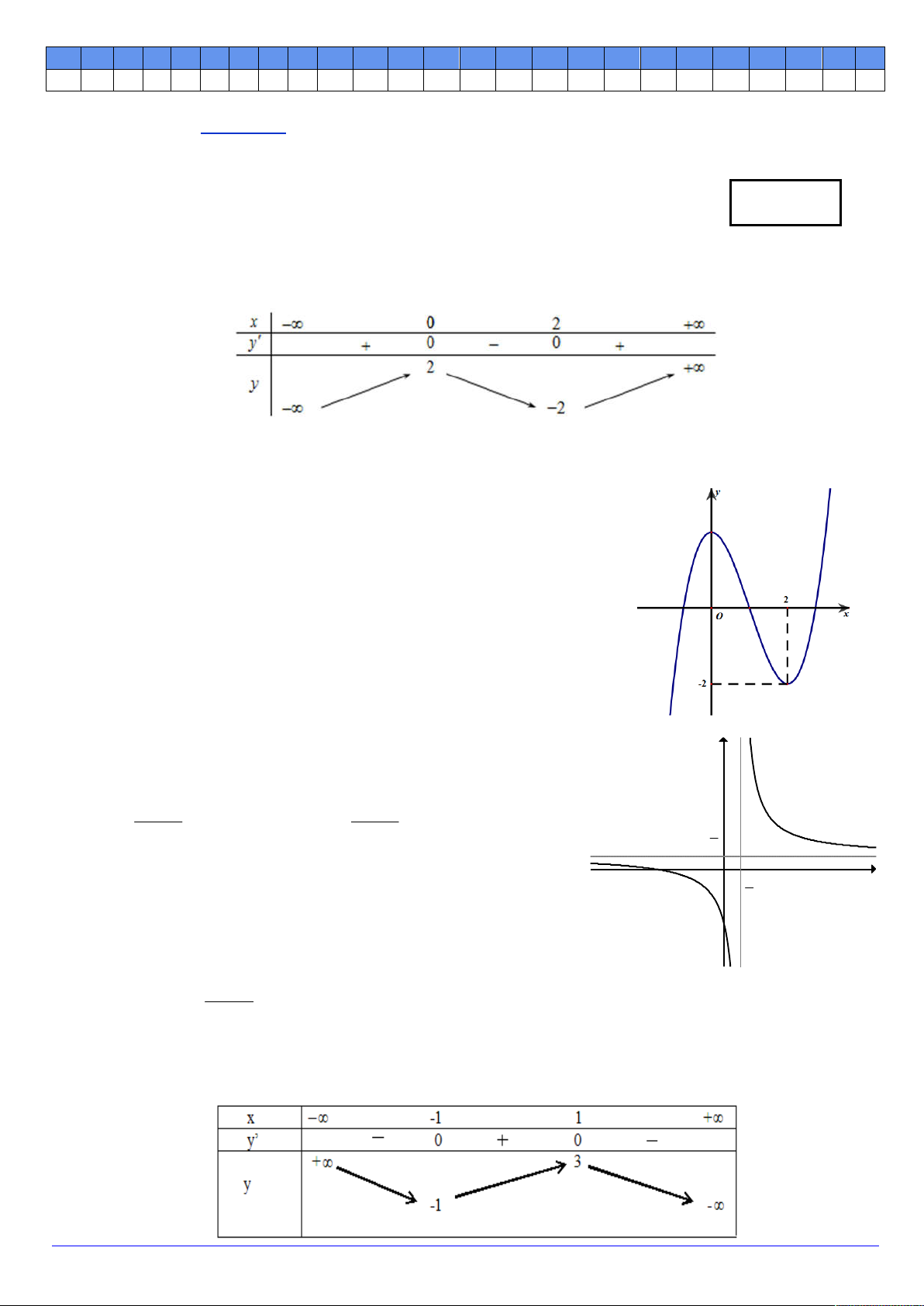
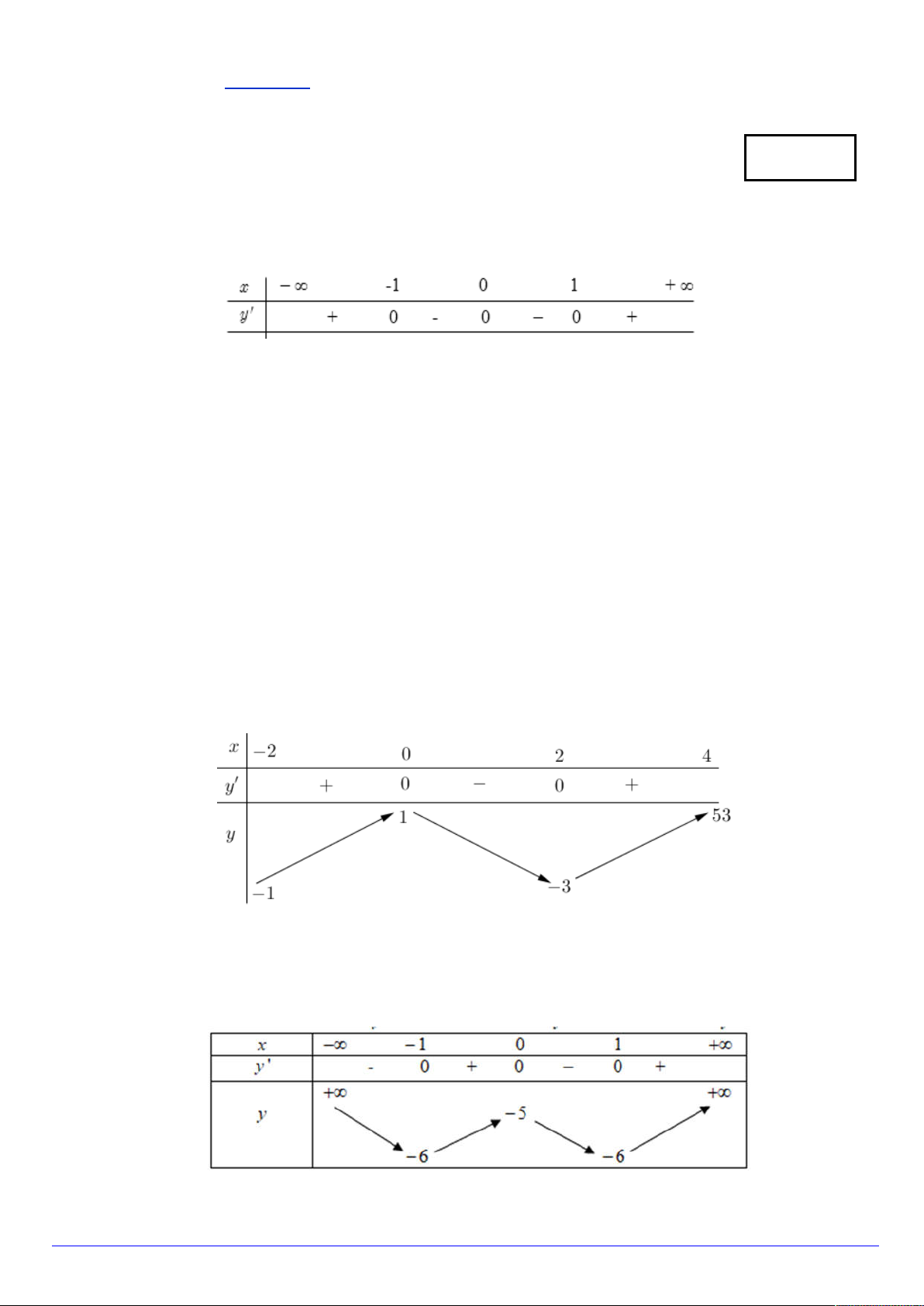
Câu 4. Cho hàm số y f x có bảng biến thiên trên  3  ;  5 như sau : x – 3 -1 2 5 y' + 0 – 0 + 2 7 y - 5 -3
Mệnh đề nào dưới đây là đúng?
A. min f x  3 .
B. max f x  7 .
C. min f x  5 .
D. max f x  2 . 3;5  3;  5 3;5  3;  5 Trang 1/20 - Mã đề 104
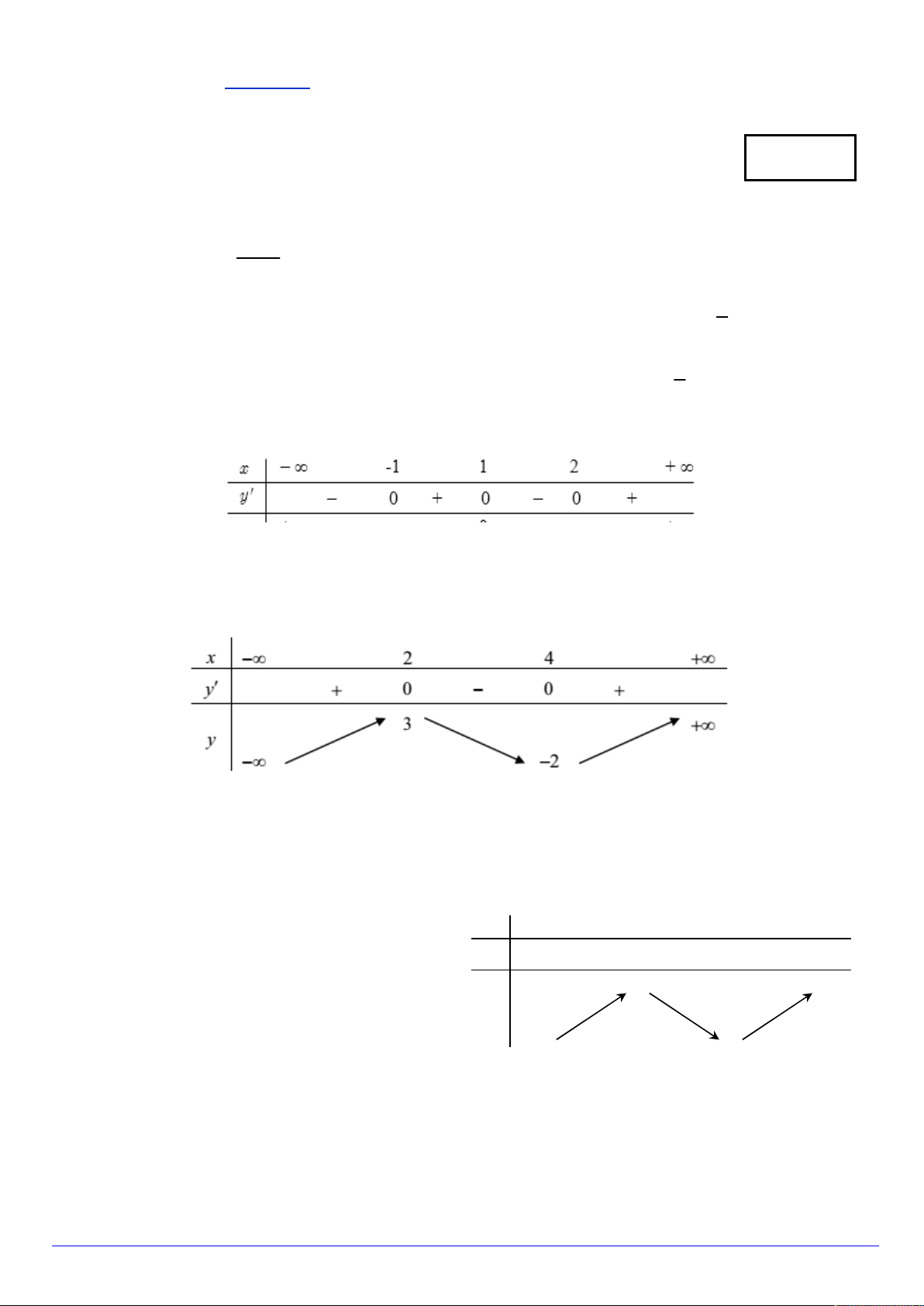
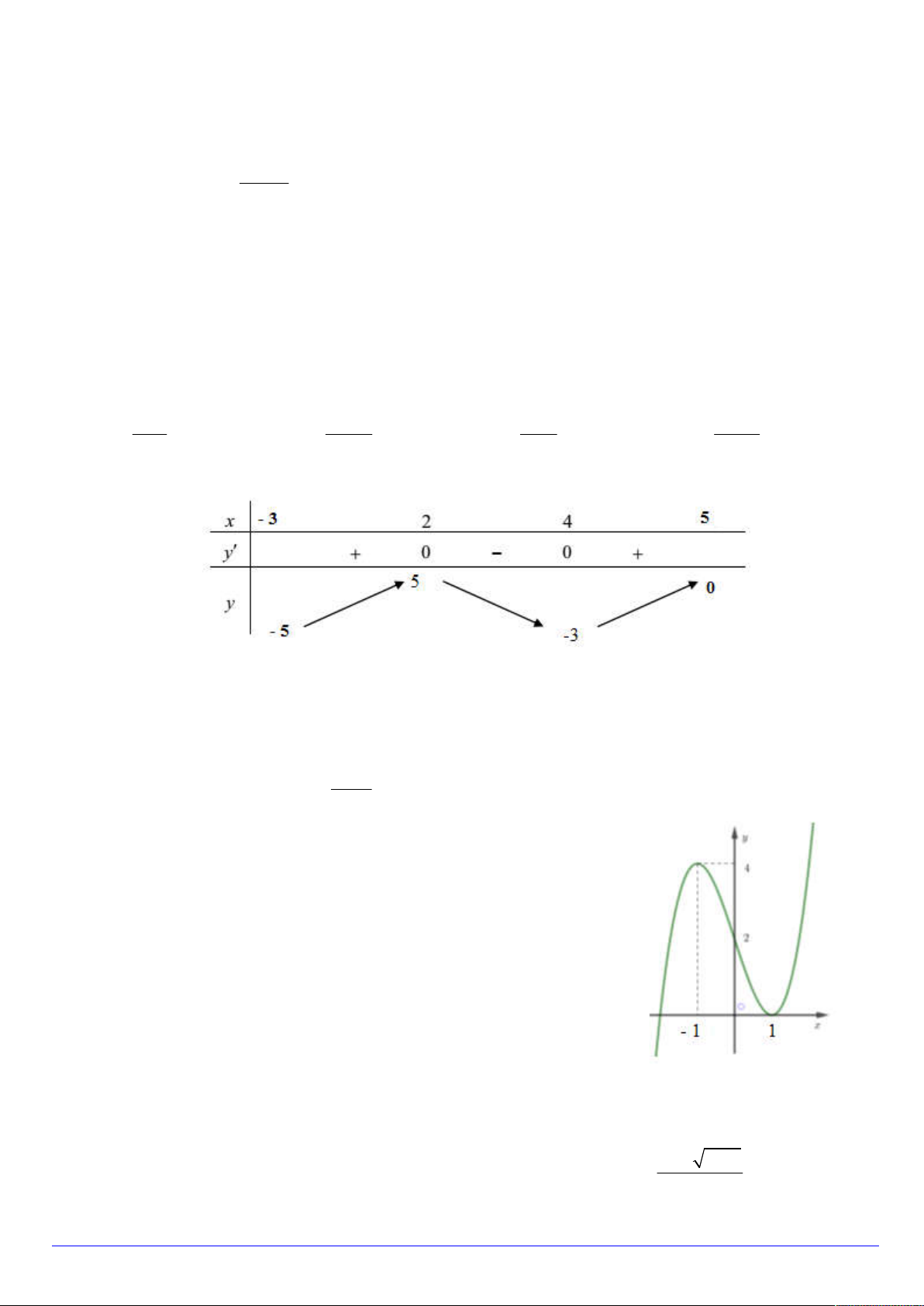
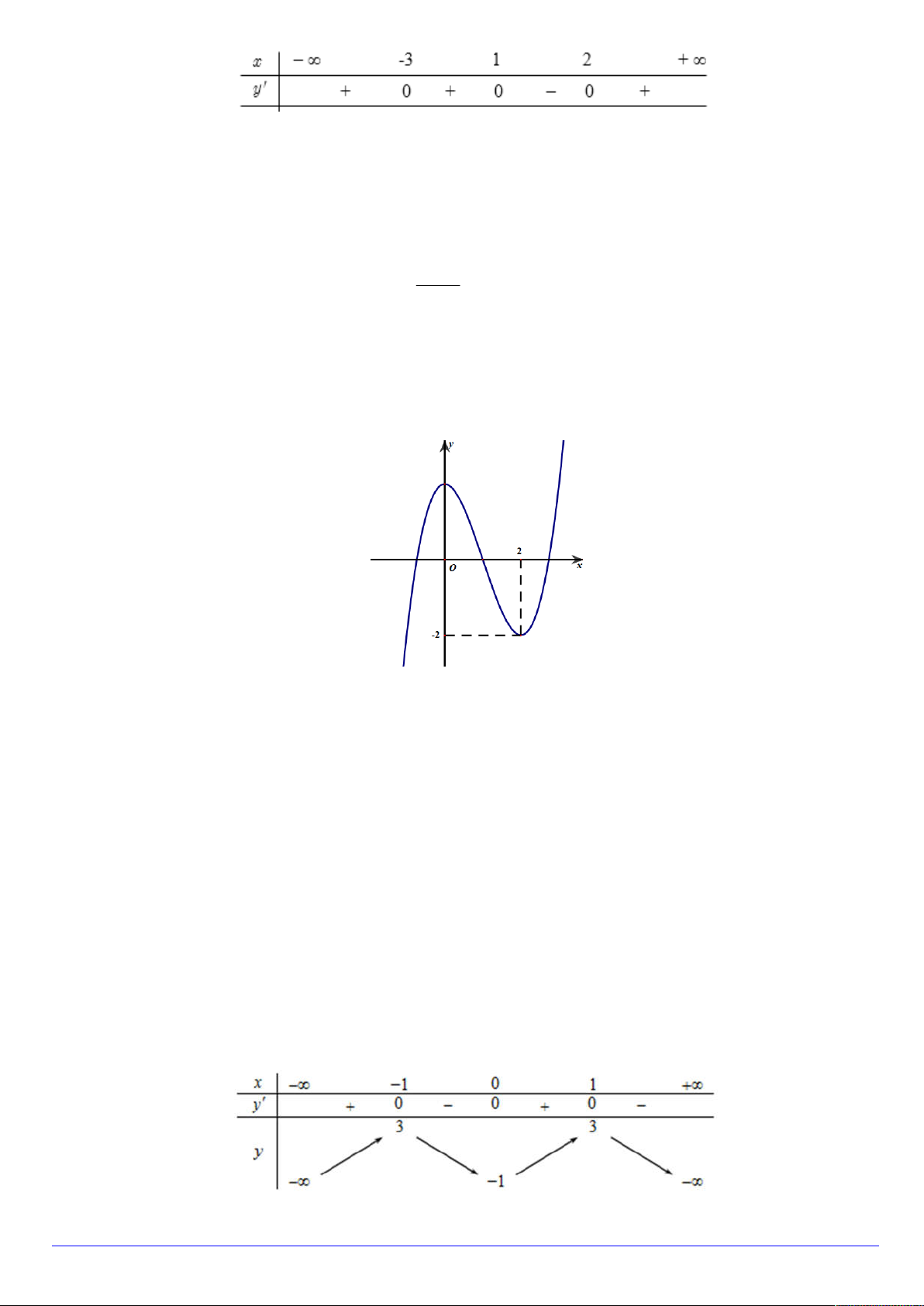
Câu 5. Đồ thị của hàm số nào dưới đây có dạng như đường cong hình vẽ. A. 3
y x  3x  2 . B. 4 2
y x  2x  3 . C. 3
y x  3x  3 . D. 3 2
y x  2x  2 . x 1
Câu 6. Tiệm cận đứng của đồ thị hàm số y  là? 3x   2 2 1 1 2 A. y  B. y   C. x   D. x  3 3 3 3
Câu 7. Cho hàm số y f (x) có bảng biến thiên
như hình vẽ. Hàm số y f (x) nghịch biến trên khoảng: A. ( ;  2) . B.  1  ;  . C. (1;  ) . D. ( 2  ; 2) .
Câu 8. Bảng biến thiên dưới đây là của hàm số nào sau đây? x  2 x  2 x  2 x  3 A. y  . B. y  . C. y  . D. y  . x 1 x 1 x 1 x 1
Câu 9. Cho hàm số y f x có bảng biến thiên như sau:
Số nghiệm của phương trình 7 f x  2  0 là: A. 3 . B. 1 . C. 2 . D. 0 . 1
Câu 10. Gọi M,m là giá trị lớn nhất và nhỏ nhất của hàm số 3 y
x x  7 trên đoạn  3
 ; 0 . Tổng 3M m 3 23 bằng: A. 24 . B. 7 . C. 8 . D. . 3 2 3
Câu 11. Cho hàm số f x có đạo hàm f  x   x  
1  x  2 2x  3, x
   . Số điểm cực trị của hàm số đã cho là: A. 6. B. 1. C. 3. D. 2 . Trang 2/20 - Mã đề 104
Câu 12. Cho hàm số y f x có đạo hàm f  x 3  x  2
4  x ,  . Hàm số y f x nghịch biến trên khoảng: A. 0; 2 . B.  2  ;  . C.  ;  2   . D.  2  ;0 .
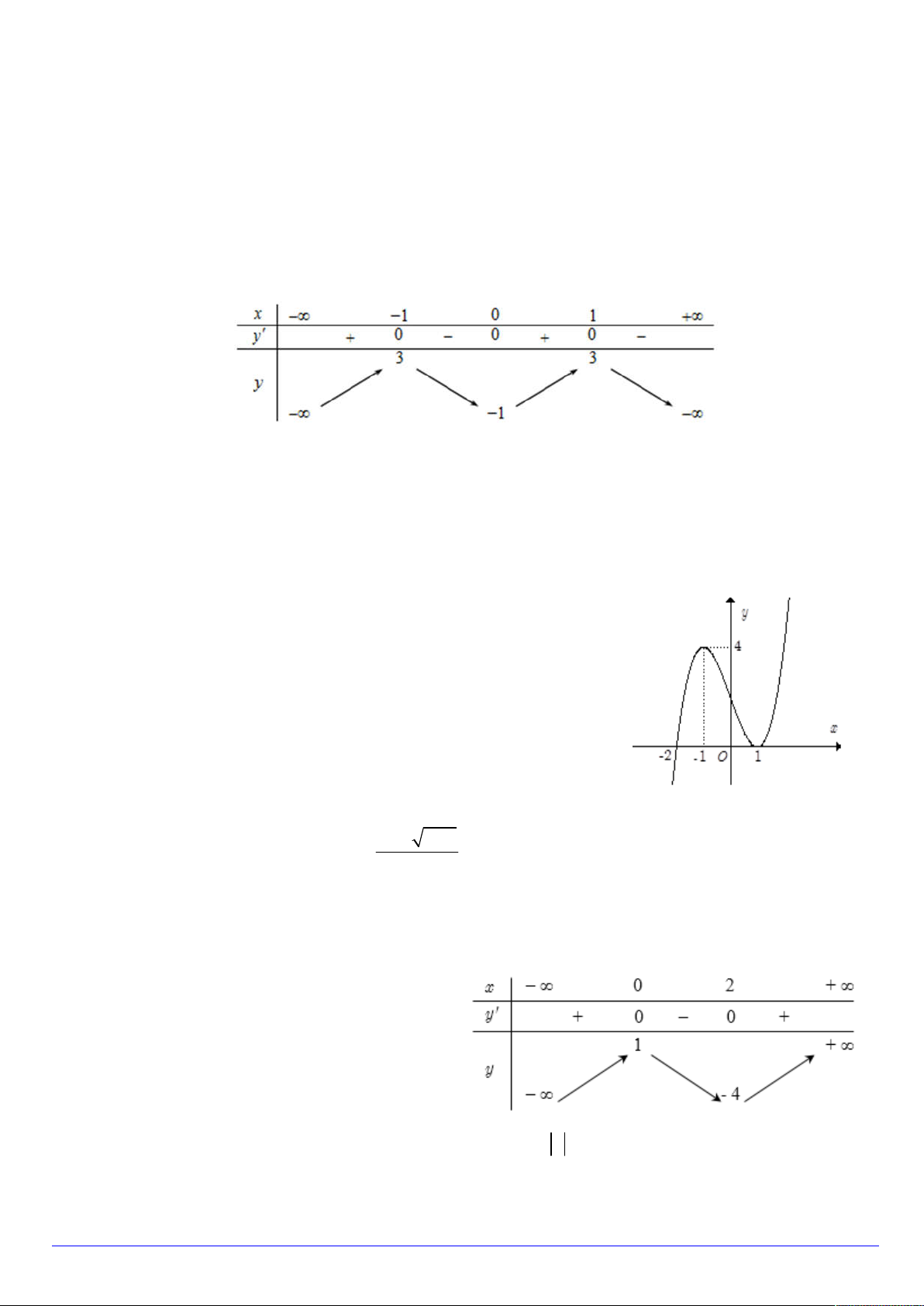
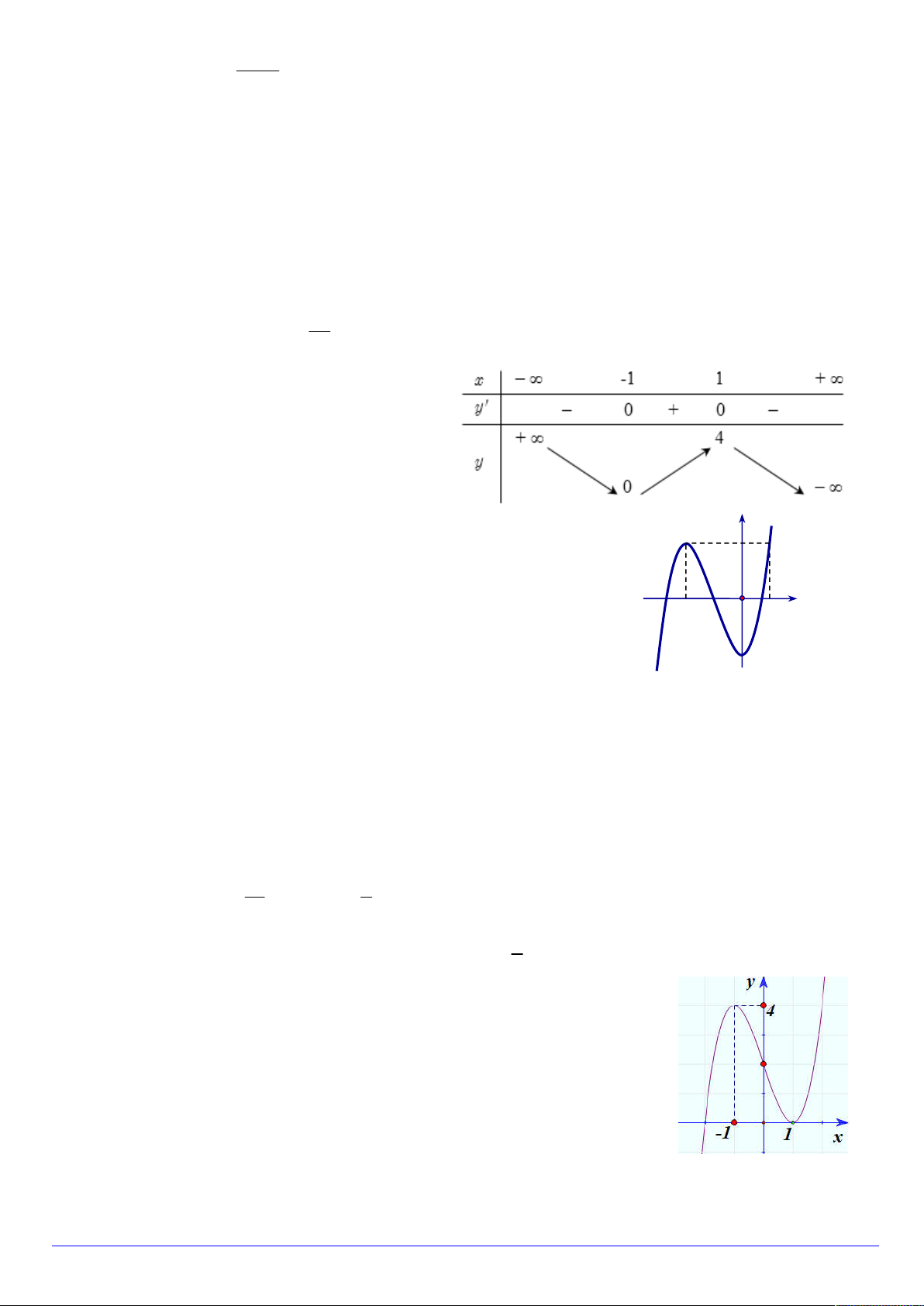
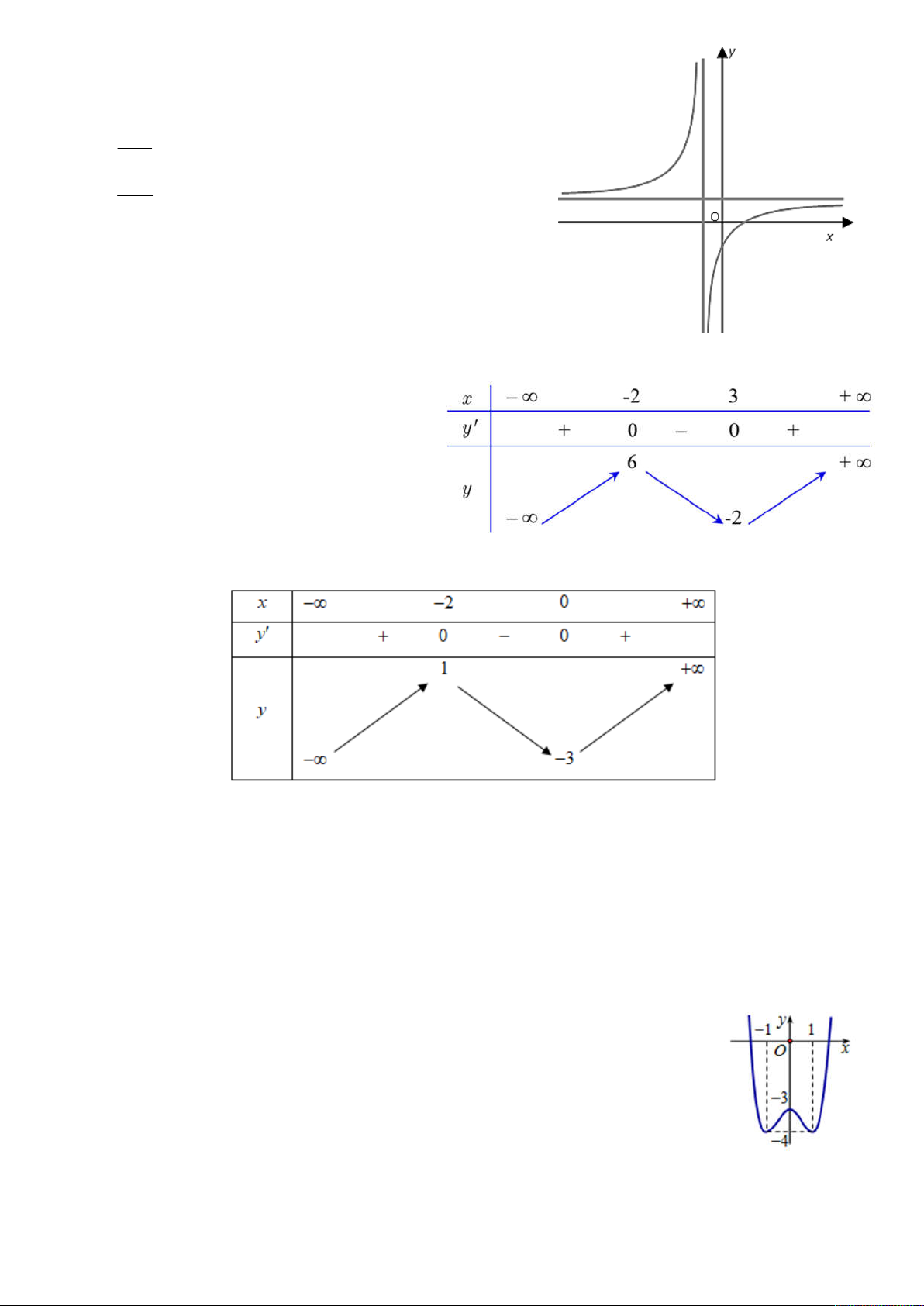
Câu 13. Cho hàm số y f x có đồ thị như hình vẽ dưới đây. Tìm
m để phương trình f x  m có hai nghiệm phân biệt. A. m  4  và m  3  . B. 4   m  3  . C. 4   m  3  . D. m  4  .
Câu 14. Điểm cực tiểu của đồ thị hàm số 4 2 y  x  2x  6 là: A. 1;5 B. x  1 C. 0;6 D. x  1
Câu 15. Cho hàm số y f x có bảng biến thiên như hình vẽ dưới đây
Đường tiệm cận ngang của đồ thị hàm số đã cho có phương trình là: A. x  3 . B. x  1 . C. y  1. D. y  3. Câu 16. Hàm số 3 2
y x  2x x 1 nghịch biến trên khoảng nào dưới đây ?  1   1   1  A.  ;   . B.  ;1   . C. ;1   . D. 1;   .  3   3   3 
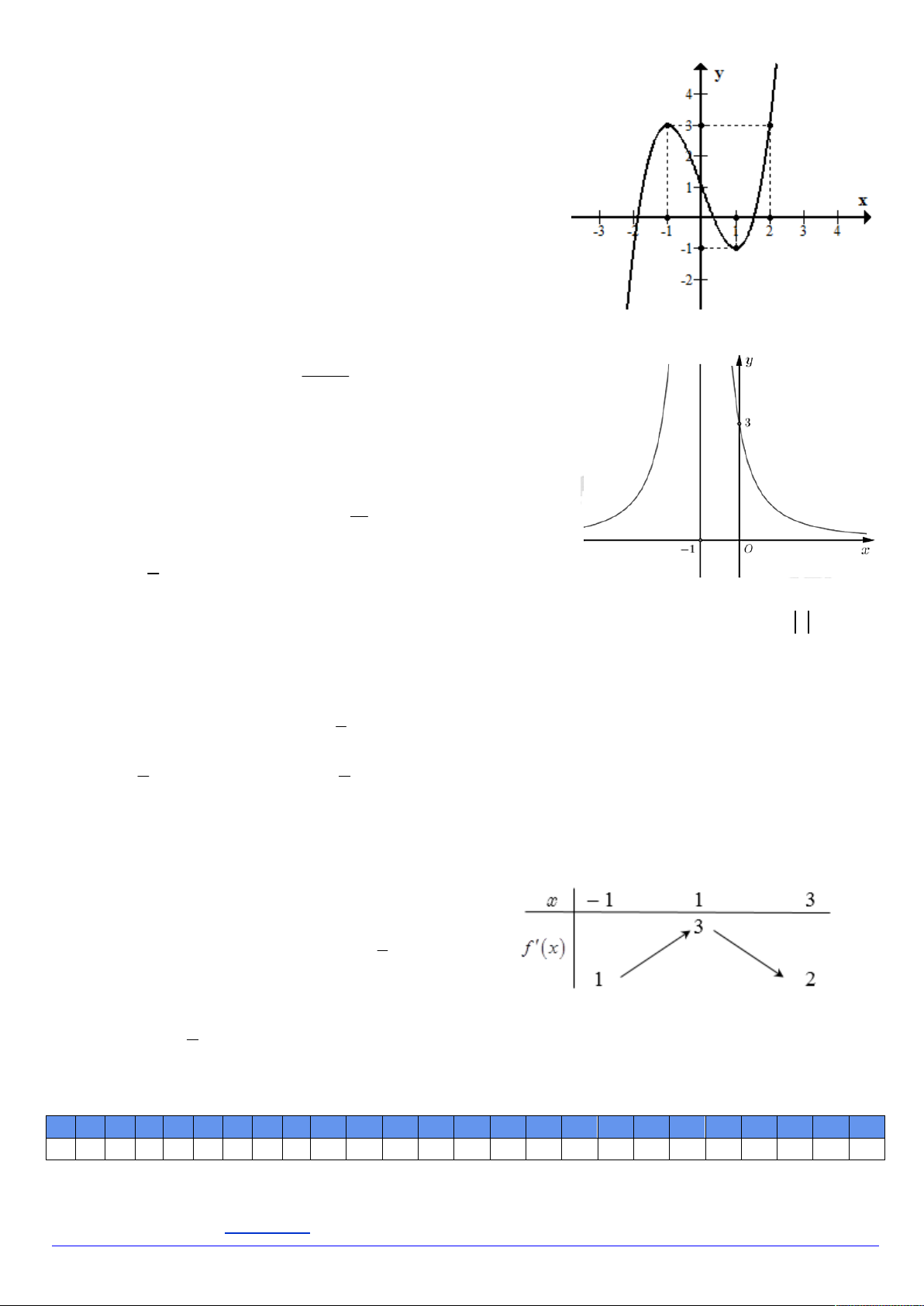
Câu 17. Cho hàm số y f x liên tục trên  có đồ thị như hình vẽ.
Phương trình f 1 f x  1 có tất cả bao nhiêu nghiệm thực phân biệt? A. 4 . B. 3 . C. 5 . D. 6 . mx  4
Câu 18. Tìm tất cả các giá trị thực của tham số m để hàm số y 
nghịch biến trên khoảng 0;  . x  m A. 0  m  2. B. 0  m  2. C. 0  m  2. D. 2   m  2.
Câu 19. Cho hàm số yf (x) có bảng biến thiên như hình vẽ. Trang 3/20 - Mã đề 104
Hàm số y f (1 x) nghịch biến trên khoảng nào? A. ( 1  ; 1) . B. ( 2  ; 0) . C. ( 3  ; 2) . D. ( 1  ;3) . m
Câu 20. Số các giá trị nguyên của m để hàm số 3 2 2 y
x m x  3x – 4m  3 đạt cực tiểu tại x  1 là: 3 A. 5 . B. 2 . C. 0 . D. 1. x 1
Câu 21. Tìm tất cả các giá trị của tham số m để đồ thị hàm số y 
có ba đường tiệm cận? 2 x  2mx  3 A. m  3 . B. 3  m  2 . C. 3  m  2 . D. 2  m  5 . x m  1
Câu 22. Cho hàm số y
( m là tham số thực) thỏa mãn min y  3. Mệnh đề nào dưới đây đúng? x  1 [2;4] A. m  4. B. m  1. C. 3  m  4 . D. 1  m  3 .
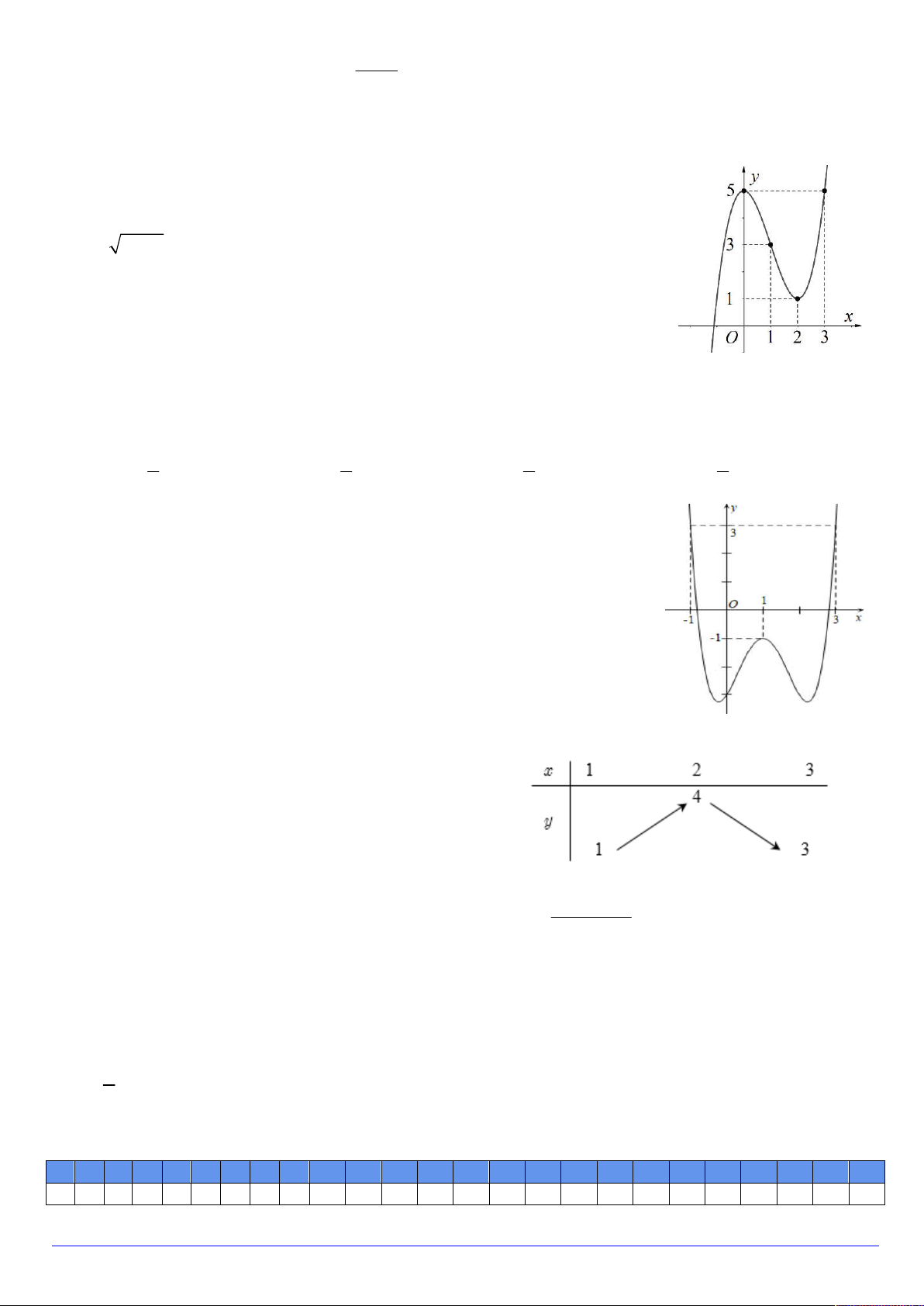
Câu 23. Cho hàm số y f x có bảng biến thiên như hình bên. 1  x
Có bao nhiêu số nguyên dương của m để bất phương trình f 1  x m  
có nghiệm x  2  , 2 . 3  2  A. 9. B. 4. C. 8. D. 6.
Câu 24. Cho hàm số f x có đồ thị hàm số y f  x được cho như hình vẽ bên. 1 2
Hàm số y f x   x   1  f  
1 có nhiều nhất bao nhiêu 2
điểm cực tiểu trong khoảng  3  ;5 ? A. 2 . B. 1. C. 5 . D. 3 .
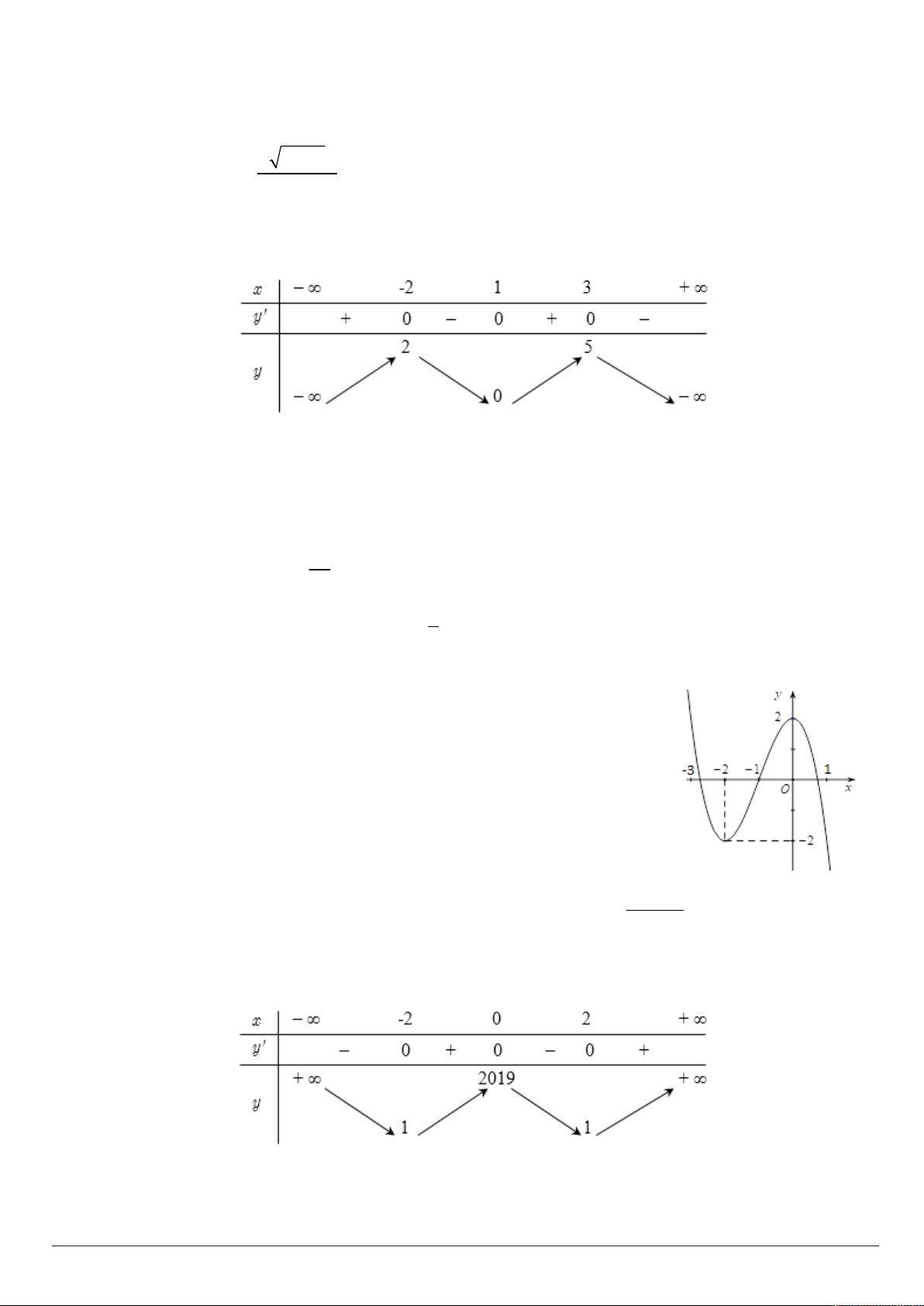
Câu 25. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn  1  0;10 để hàm số 3 2
y x  3x  3mx  2019 nghịch biến trên khoảng 1; 2 ? A. 11. B. 10 . C. 21 . D. 20 .
------------- HẾT ------------- Mã đề [104] Trang 4/20 - Mã đề 104 1 2
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 D D D B A D C A A A D D A A D C A A B D B A B A A
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
KIỂM TRA ĐỊNH KỲ - HỌC KỲ I TỔ TOÁN NĂM HỌC 2019 – 2020
Môn: Toán - Lớp 12 - Chương trình chuẩn ĐỀ CHÍNH THỨC
Thời gian: 45 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên:………………………………….Lớp:…………….......……..……… 105
Câu 1. Hàm số nào trong bốn hàm số sau có bảng biến thiên như hình vẽ sau? A. 3 2
y  x  3x 1. B. 3 2
y x  3x  2. C. 3 2
y x  3x 1. D. 3
y x  3x  2. Câu 2. Cho hàm số 3 2
y ax bx cx d a, , b ,
c d   . Đồ thị
hàm số y f x như hình vẽ dưới đây.
Giá trị cực tiểu của hàm số bằng: A. 0 . B. 1. C. 2 . D. 2 . y
Câu 3. Hàm số nào trong bốn hàm số sau có đồ thị như hình vẽ bên. 2 x  2 A. y  . B. y  2x 1 2x 1 1 2 C. 3
y x  3x  2 D. 4 2
y x  2x  2 . -2 O 1 x 2 -2 1 2x Câu 4. Hàm số y  có bao nhiêu cực trị ? x  2 A. 3 . B. 1. C. 0 . D. 2 .
Câu 5. Cho hàm số y f x  liên tục trên  và có bảng biến thiên như hình dưới đây Trang 5/20 - Mã đề 104
Khẳng định nào sau đây là sai?
A. Hàm số nghịch biến trên khoảng  ;    1 .
B. Hàm số đồng biến trên khoảng  1  ;  3 .
C. Hàm số đồng biến trên khoảng  1   ;1 .
D. Hàm số nghịch biến trên khoảng 1;   . 2x 1
Câu 6. Cho hàm số y
. Khẳng định nào sao đây là khẳng đinh đúng? 2  x
A. Hàm số nghịch biến trên các khoảng  ;  2 và 2;   .
B. Hàm số nghịch biến trên  ;  22;   .
C. Hàm số đồng biến trên các khoảng  ;  2 và 2;   .
D. Hàm số đồng biến trên  ;  22;   .
Câu 7. Hàm số nào sau đây nhận đường thẳng x  5 làm một tiệm cận? 5 2  5x 2 5x  3 A. y  . B. y  . C. y  . D. y  . x 1 1  x x  5 x  2
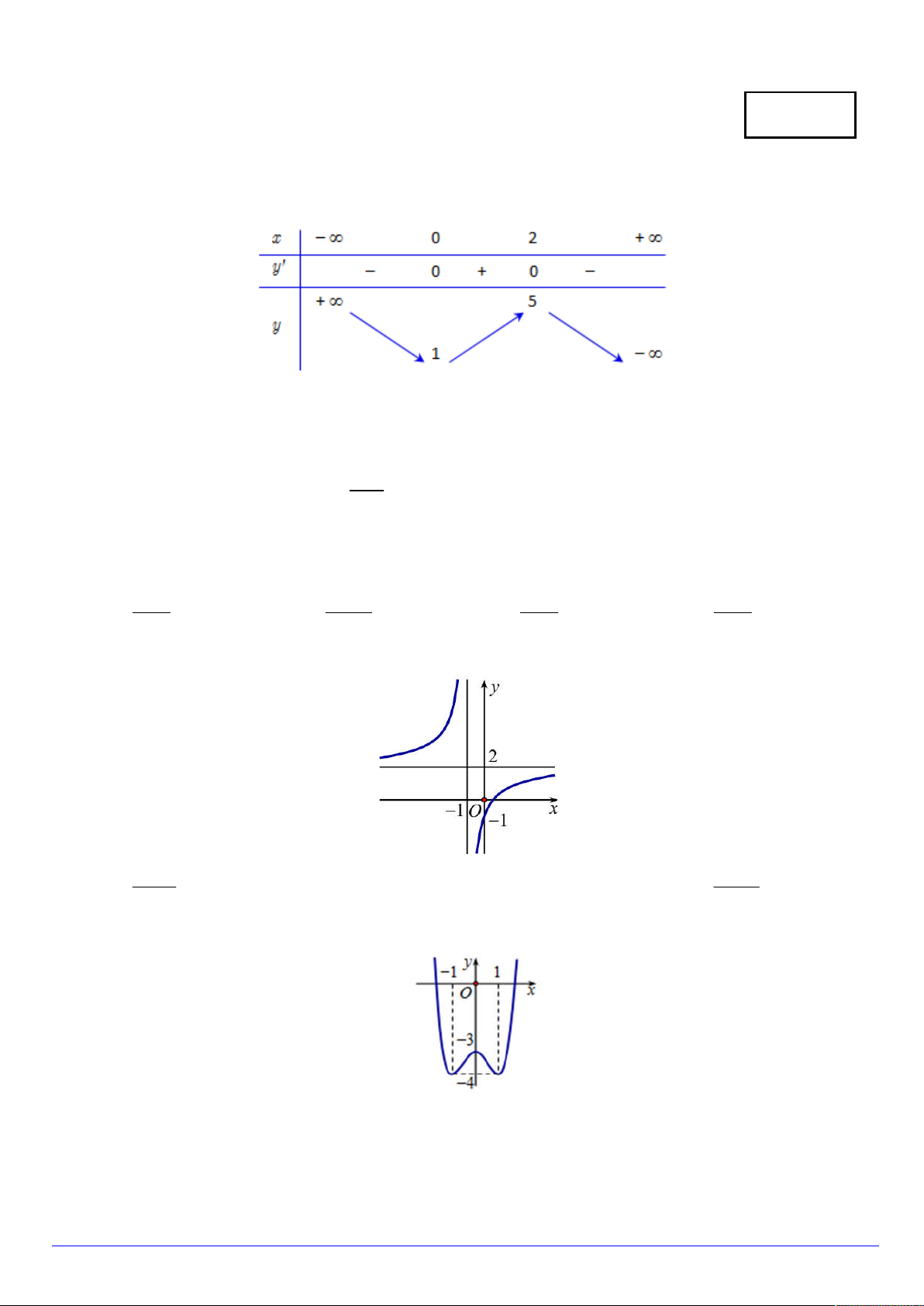
Câu 8. Hàm số y f x liên tục trên R và có bảng biến thiên trên khoảng  3  ;5 như sau
Gọi M , m là giá trị lớn nhất,nhỏ nhất của hàm số y f x trên khoảng  3
 ;5. Tìm mệnh đề đúng ? A. M  5 . B. M  0 . C. m  5  . D. m  3  .
Câu 9. Hàm số nào sau đây đồng biến trên khoảng ( ;  ). x  2 A. 4 y x 1 B. y  C. 3
y  2x 3x 1 D. 3
y  2x x 1 x 1
Câu 10. Cho hàm số y f x liên tục trên  có đồ thị như
hình vẽ. Tìm tất cả các giá trị m để phương trình f x  m có
một nghiệm âm và hai nghiệm dương phân biệt?
A. m  0  m  4 . B. 0  m  2 .
C. 2  m  4 . D. 0  m  4 .
Câu 11. Tìm giá trị thực của tham số m để hàm số 4 3
y x  4mx m 1 đạt cực tiểu tại điểm x  3 . A. m  1. B. m  0 . C. m  2 . D. m  . 2 x x  2
Câu 12. Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  là: 2x  3 A. 1. B. 2. C. 3 . D. 0. Trang 6/20 - Mã đề 104 2
Câu 13. Cho hàm số y f x có đạo hàm trên  và f ' x   x  
1  x  2  x  3,x . Số điểm cực trị của hàm số đã cho là A. 2 . B. 0 . C. 1. D. 3 .
Câu 14. Cho hàm số y f (x ) có đạo hàm 2
f (x )  x  5x  6, x R . Hàm số y  5 f (x ) nghịch biến
trên khoảng nào sau đây? A. 2;   B. 2 ;3
C. ;2 và 3;   D. ;  3
Câu 15. Cho hàm số f x 4 2
ax bx c a  0 xác định, liên tục trên  và có bảng biến thiên như hình vẽ:
Tìm tất cả các giá trị thực m để phương trình f x  m có bốn nghiệm phân biệt. A. m  1   m  3 . B. 1   m  3 . C. 1   m  3 . D. m  3 .
Câu 16. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
y x  3x  9x  35 trên đoạn
4;4. Khi đó tổng M m bằng bao nhiêu? A. 48. B. 1  . C. 55 D. 11.
Câu 17. Cho hàm số y f x  . Biết rằng hàm số f x  có đạo hàm
là f 'x  và hàm số y f 'x  có đồ thị như hình vẽ bên.
Hàm số y f 1 x  đồng biến trên khoảng: A.  ;
 0 và 3;  . B. 3;   . C. 1;   . D.   2;1  . 3x  1 x
Câu 18. Xác định m để đồ thị hàm số y
có hai đường tiệm cận tạo với hai trục tọa độ một hình x m
chữ nhật có diện tích bằng 6 . A. m  2 . B. m  1. C. m  2 . D. m  1.
Câu 19. Cho hàm số y f x có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x   m  0 có 4 nghiệm phân biệt . A. 4. B. 6. C. 5 . D. 8. Trang 7/20 - Mã đề 104 x
Câu 20. Tìm tham số m để hàm số y
nghịch biến trên khoảng 1; 2 . x m A. 1  m  2 . B. m  0 . C. m  0 .
D. 0  m  1 m  2 .
Câu 21. Cho hàm số y f x liên tục trên  và có đồ thị như hình bên.
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất hàm số
y f  4x 1 trên đoạn 0;2. Mệnh đề nào dưới đây đúng? A. M  3m .
B. M m  7 .
C. M m  4 . D. M  5m . Câu 22. Cho hàm số 4
y x   2
m m   2 2
1 x m 1 với m là tham số thực. Giá trị của m để đồ thị hàm số
có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất là 1 3 3 1 A. m   . B. m   . C. m  . D. m  . 2 2 2 2
Câu 23. Cho hàm số y f x liên tục trên  . Hàm số y f  x có đồ thị như hình bên.
Xác định tất cả các giá trị m để phương trình f x 3 2 3
x  3x m  4 có nghiệm x  1  ;3 .
A. 3 f 3  4  m  3 f  
1 B. m  3 f   1 .
C. m  3 f 3 . D. 3 f 3  m  3 f   1  2 .
Câu 24. Cho hàm số y f x liên tục trên 1;  3 và
có bảng biến thiên như sau: m
Có bao nhiêu giá trị nguyên của m để phương trình f x   1 
có nghiệm trên khoảng 1; 2 . 2 x  4x  5 A. 10. B. 0. C. 4. D. 5 . 2
Câu 25. Cho hàm số f x  có đạo hàm f x   x    2 1
x 2x với mọi x  .
 Hỏi số thực nào dưới đây
thuộc khoảng đồng biến của hàm số gx   f  2
x  2x  2 ? 3 A. . B. 3. C. 1.  D. 2.  2
------------- HẾT ------------- Mã đề [105]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 B C B C B C C A D B A D A B B B B A A D B D A C B Trang 8/20 - Mã đề 104
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
KIỂM TRA ĐỊNH KỲ - HỌC KỲ I TỔ TOÁN NĂM HỌC 2019 – 2020
Môn: Toán - Lớp 12 - Chương trình chuẩn ĐỀ CHÍNH THỨC
Thời gian: 45 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên:………………………………….Lớp:…………….......……..……… 106
Câu 1. Cho hàm số y f (x) có bảng xét dấu f (  x) như sau:
Hàm số đồng biến trên khoảng: A.  ;  0   . B.  ;  3
  và 3;   . C.  ;  3   và 0;3 . D. 0;   .
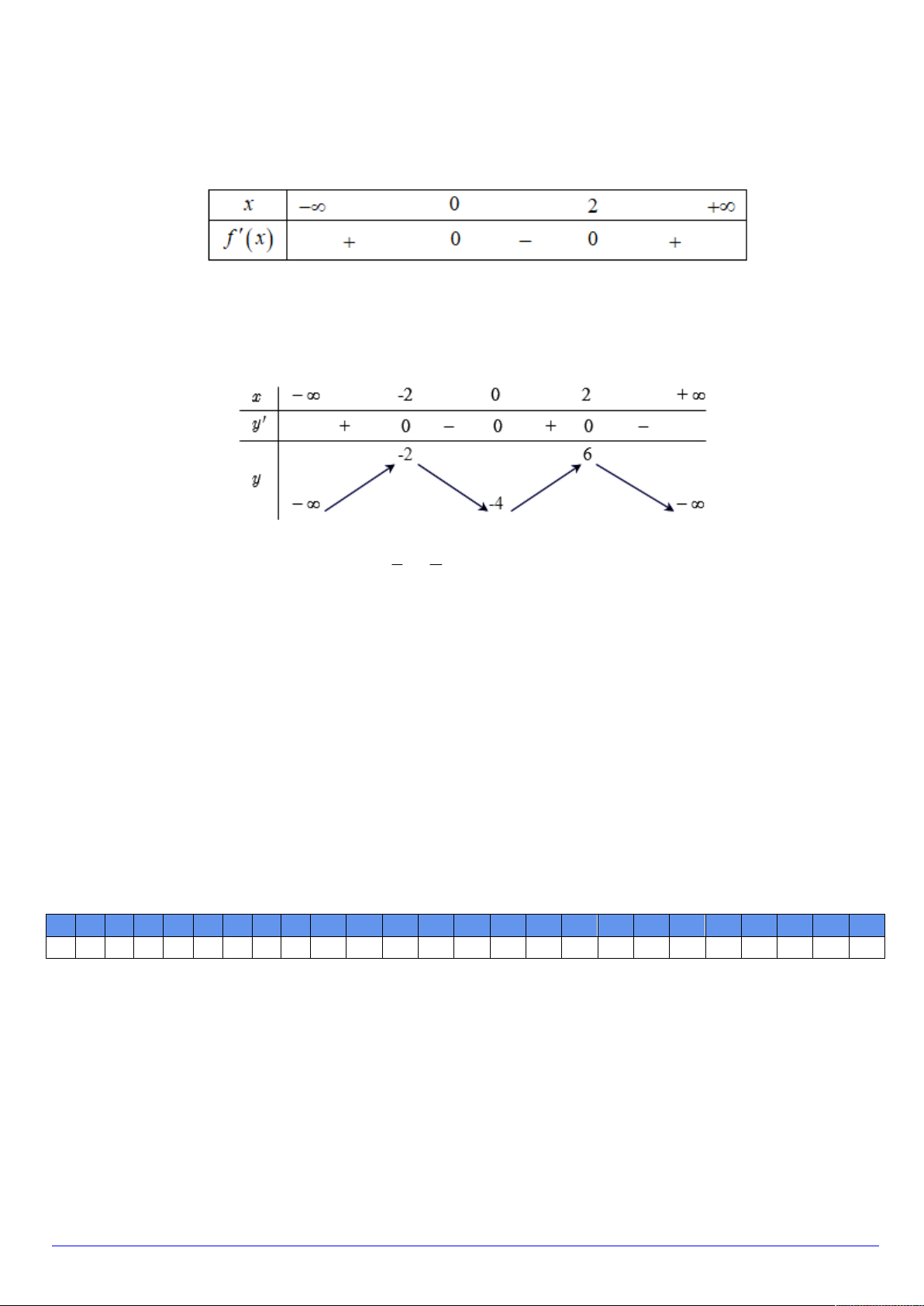
Câu 2. Cho hàm số y f x có bảng biến thiên như hình ∞ x 2 +∞
vẽ. Bảng biến thiên trên có thể là của hàm số nào trong các y' hàm số sau? 2 +∞ 2x  5 2x  3 2x 1 x  3 A. y  . B. y  . C. y  . D. y  . y x  2 x  2 x  2 x 1 ∞ 2
Câu 3. Cho hàm số y f x xác định trên đoạn 0;5 và có bảng biến thiên như sau:
Giá trị cực đại của hàm số y f x là: A. y  4 . B. x  1 . C. y  3 . D. x  3 .
Câu 4. Cho hàm số y f x xác định trên D   \  
7 và lim f (x)  2 , lim f (x)   . Trong các x x 7 
mệnh đề sau, mệnh đề nào đúng?
A. Đồ thị hàm số có đúng hai tiệm cận ngang y  7, y  2  .
B. Đồ thị hàm số có một tiệm cận đứng x  7 và một tiệm cận ngang y  2 .
C. Đồ thị hàm số có đúng một đường tiệm cận.
D. Đồ thị hàm số có hai tiệm cận đứng và không có tiệm cận ngang.
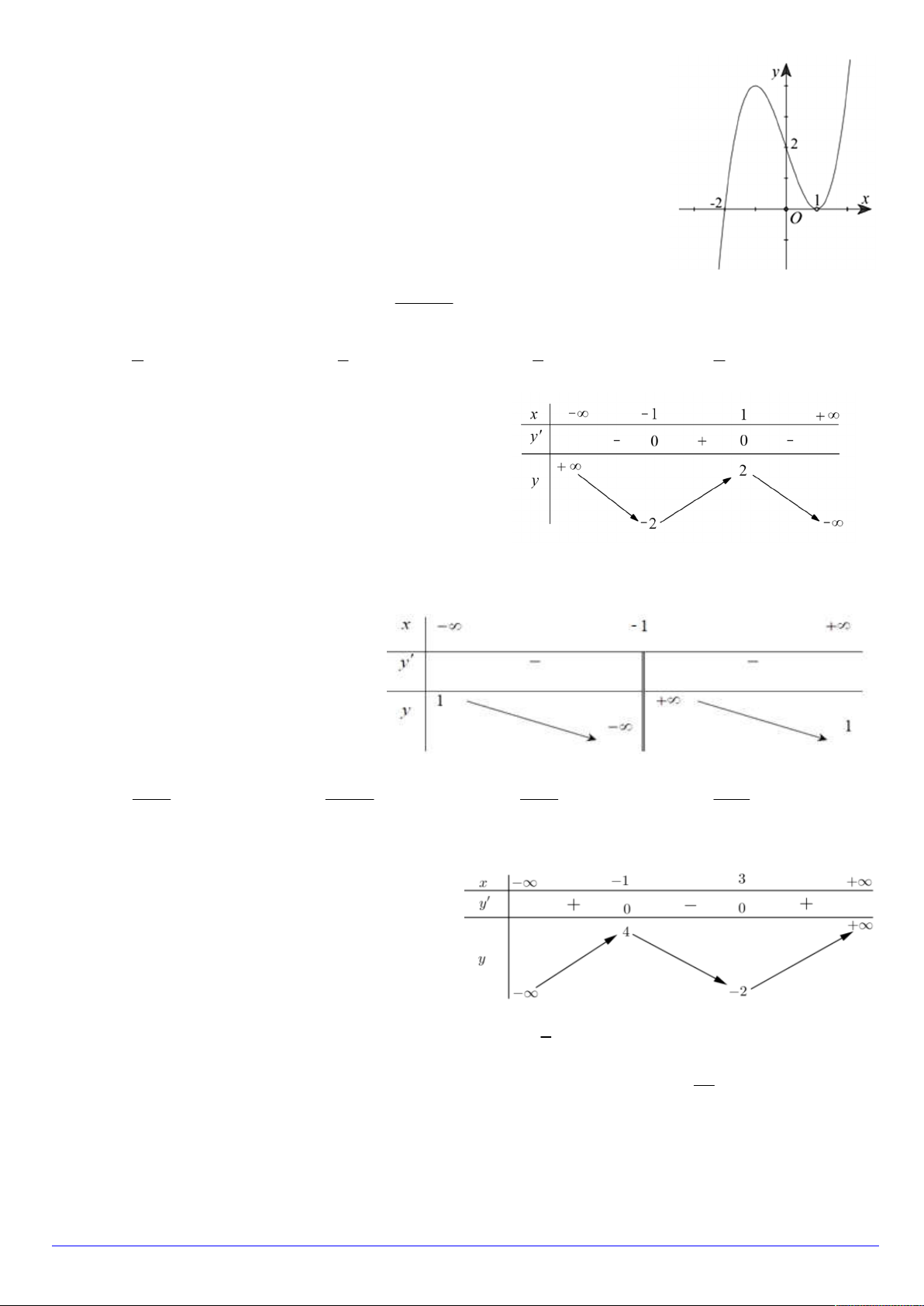
Câu 5. Đường cong dưới đây là đồ thị của một trong các hàm số đã cho, hỏi y đó là hàm số nào? A. 4 2
y  x  2x . B. 4 2
y  x x . C. 4 2
y x x . D. 4 2
y x  2x . x O 1 Trang 9/20 - Mã đề 104 3x 1
Câu 6. Cho hàm số y
. Mệnh đề nào dưới đây là đúng? x 1
A. Hàm số luôn đồng biến trên  \   1 .
B. Hàm số nghịch biến trên   ;1  1;  .
C. Hàm số đồng biến trên các khoảng  ;   1 và 1;  .
D. Hàm số nghịch biến trên các khoảng  ;   1 và 1;  .
Câu 7. Giá trị lớn nhất của hàm số 3 2
y x  2x trên đoạn  1  ;  3 bằng: 32 A. 9 . B.  . C. 3  . D. 0 . 27
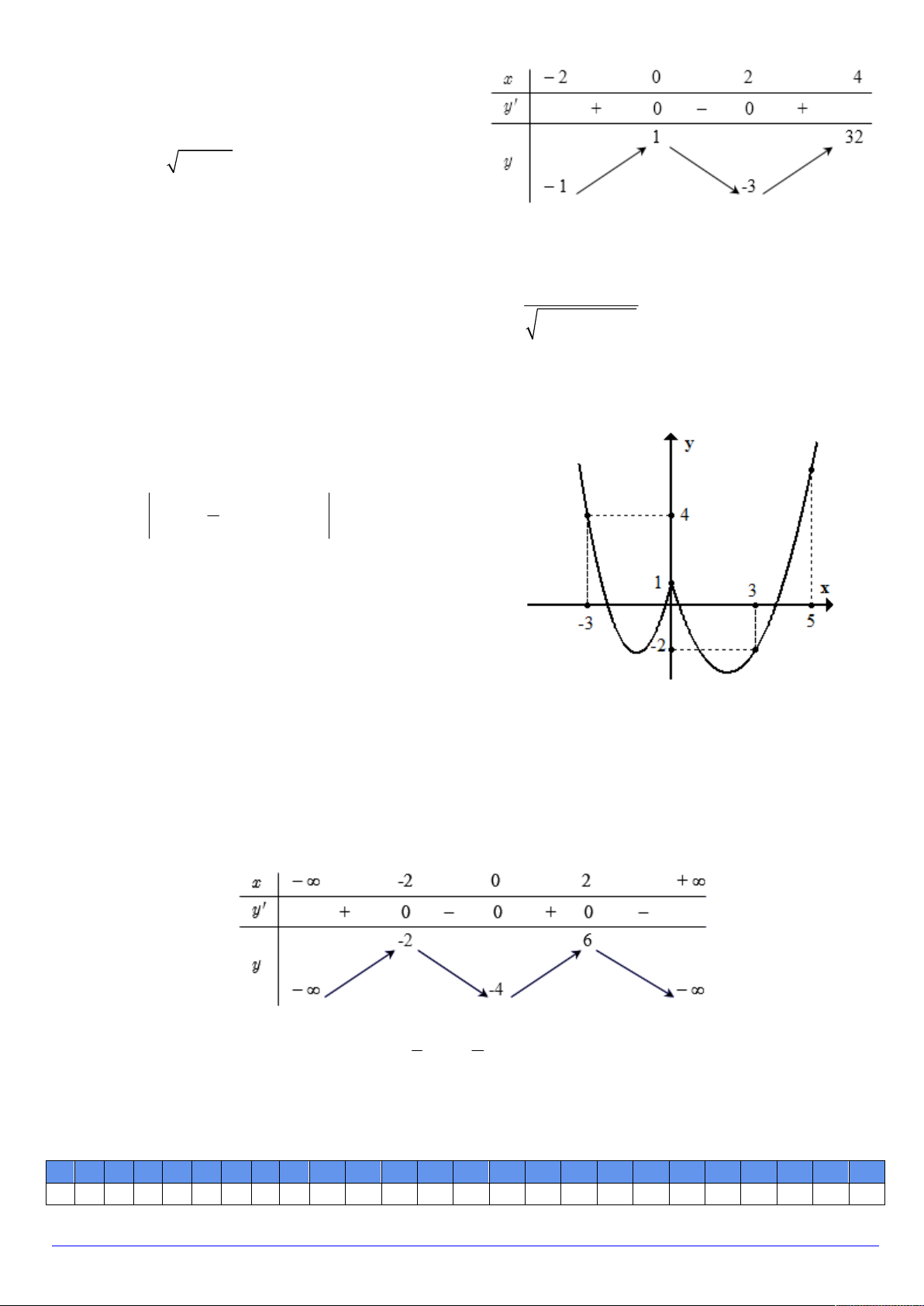
Câu 8. Cho hàm số y  f  x có bảng biến
thiên như bên. Hàm số đạt cực tiểu tại điểm: A. x  0 . B. x  1  . C. x  4 . D. x  1. y
Câu 9. Cho hàm số y f x có đồ thị như hình vẽ. 2
Hàm số đồng biến trên khoảng nào sau đây? A.  2  ;  . B.  1   ;1 . 2 O 1 x C. 0;  . D.  ;  0 . 2
Câu 10. Cho hàm số y f x xác định trên và có đạo hàm f  x 2
x x  
1 , với x .
Khẳng định nào sau đây là đúng?
A. Hàm số đã cho nghịch biến trên khoảng  
;1 . B. Hàm số đã cho đồng biến trên khoảng 0;  .
C. Hàm số đã cho đồng biến trên .
D. Hàm số đã cho nghịch biến trên khoảng 0;  . 3 x 2 Câu 11. Cho hàm số 2 y   2x  3x 
. Điểm cực đại của đồ thị hàm số là: 3 3 2 A. x  1. B. (1;2) C. (3; ) D. y  2. 3
Câu 12. Cho hàm số y f x có đồ thị như hình vẽ.
Tìm tất cả các giá trị thực m để phương trình f x 1  m có ba nghiệm phân biệt.
A. 1  m  5 . B. 0  m  4 . C. 0  m  5 . D. 1   m  4 . Trang 10/20 - Mã đề 104 2 3
Câu 13. Cho hàm số y f x có đạo hàm trên  và f ' x   x  
1  x  2  x  3 , x
  . Số điểm cực
trị của hàm số đã cho là A. 0 . B. 1. C. 3 . D. 2 . 2 9  x
Câu 14. Đồ thị hàm số y
có bao nhiêu đường tiệm cận? 2 x  3x  4 A. 2 . B. 3 . C. 1. D. 4 .
Câu 15. Cho hàm số y f x có bảng biến thiên như sau:
Số nghiệm phương trình 2 f x  3  0 là: A. 4 . B. 3 . C. 1. D. 2 .
Câu 16. Giá trị lớn nhất của hàm số 3 2
y x  2x trên đoạn  1  ;  3 bằng: 32 A. 3  . B.  . C. 9 . D. 0 . 27 1
Câu 17. Với giá trị nào của m thì hàm số 3 2 y
x mx  m  2 x  3 có hai điểm cực trị có hoành độ 3 dương? A. m  0 . B. 2   m  1  . C. m  1
  m  2 . D. m  2 . Câu 18. Cho hàm số   3 2
f x ax bx cx d có đồ thị là hình vẽ bên.
Phương trình f 2  f x  0 có bao nhiêu nghiệm phân biệt? A. 6. B. 4. C. 5. D. 7. mx 10
Câu 19. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y
nghịch biến trên khoảng 2x m 0;2 . A. 6 . B. 5 . C. 4 . D. 9 .
Câu 20. Cho hàm số yf (x) có bảng biến thiên như hình vẽ.
Hàm số y f (1 x) đồng biến trên khoảng nào? A. ( 1  ; 1) . B. ( 2  ; 0) . C. (1 ; 2019) . D. (2 ;  ) . Trang 11/20 - Mã đề 104
Câu 21. Hàm số y f x liên tục và có bảng biến thiên trong đoạn  2  ; 4 như sau: Gọi ,
m M lần lượt là giá trị nhỏ nhất, lớn nhất của
hàm số y f  2
4x x  trên đoạn0;4 . Tìm mệnh đề đúng ? A. M  32 . B. M 1 C. m  1  D. M  3m x 1
Câu 22. Tìm tất cả các giá trị thực của m để đồ thị hàm số y 
có hai tiệm cận đứng: m x  2 1  4 A. m  0 B. m  1 C. m  0 D. m  0, m  1
Câu 23. Cho hàm số f x có đồ thị hàm số
y f  x được cho như hình vẽ bên. 1 2
Hàm số y f x   x   1  f   1 có nhiều nhất 2
bao nhiêu điểm cực trị trong khoảng  5  ;5 ? A. 1. B. 3 . C. 5 . D. 5 .
Câu 24. Cho hàm số y f x thỏa mãn f  x  x x   2
1 x  4x m  2 . Gọi S là tập hợp tất cả các giá trị nguyên m  1
 0;10 để hàm số y f  2 x  
1 đồng biến trên 0 
;1 . Tổng các phần tử của S bằng: A. 52. . B. 1  10 . C. 0 . D. 45 .
Câu 25. Cho hàm số y f x có bảng biến thiên như hình bên. 1  x
Tìm tất cả các giá trị của m để phương trình f 1  x m  
có nghiệm x 2,6 . 3  2  A. 4   m  6 . B. 4   m  2  . C. 4   m  2  . D. m  6 .
------------- HẾT ------------- Mã đề [106]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 B C C B D D A B C A B A D C A C D B A A B D D A C Trang 12/20 - Mã đề 104
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
KIỂM TRA ĐỊNH KỲ - HỌC KỲ I TỔ TOÁN NĂM HỌC 2019 – 2020
Môn: Toán - Lớp 12 - Chương trình chuẩn ĐỀ CHÍNH THỨC
Thời gian: 45 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên:………………………………….Lớp:…………….......……..……… 107
Câu 1. Cho hàm số y f x có bảng xét dấu đạo hàm như hình vẽ.
Hỏi hàm số y f x có bao nhiêu cực trị ? A. 2 . B. 0 . C. 1. D. 3 .
Câu 2. Cho hàm số y f x xác định trên  và lim f (x)  5 , lim f (x)  5 . Trong các mệnh đề sau, x x mệnh đề nào đúng?
A. Đồ thị hàm số có đúng hai tiệm cận ngang y  5, y  5  .
B. Đồ thị hàm số có hai tiệm cận đứng và không có tiệm cận ngang.
C. Đồ thị hàm số có đúng hai tiệm cận đứng x  5, x  5  .
D. Đồ thị hàm số có đúng một tiệm cận đứng x  5 và một tiệm cận ngang y  5 . Câu 3. Hàm số 4 2
y x  2x  3 đồng biến trên khoảng nào sau đây? A.  1  ; 0 . B. 0; 2 . C.  1   ;1 . D. 0  ;1 .
Câu 4. Hàm số y f x liên tục và có bảng biến thiên trong đoạn  2  ; 4 như sau
Gọi m là giá trị nhỏ nhất của hàm số y f x trên đoạn 2
 ; 4 . Tìm mệnh đề đúng ?
A. m f 0 . B. m  3  . C. m f  3   . D. m  1  .
Câu 5. Bảng biến thiên trong hình vẽ bên là của hàm số nào sau đây? A. 4 2
y  x  2x  5 . B. 4 2
y x  2x 1 . C. 4 2
y x  2x  5 . D. 4 2
y x  2x  5 . Trang 13/20 - Mã đề 104
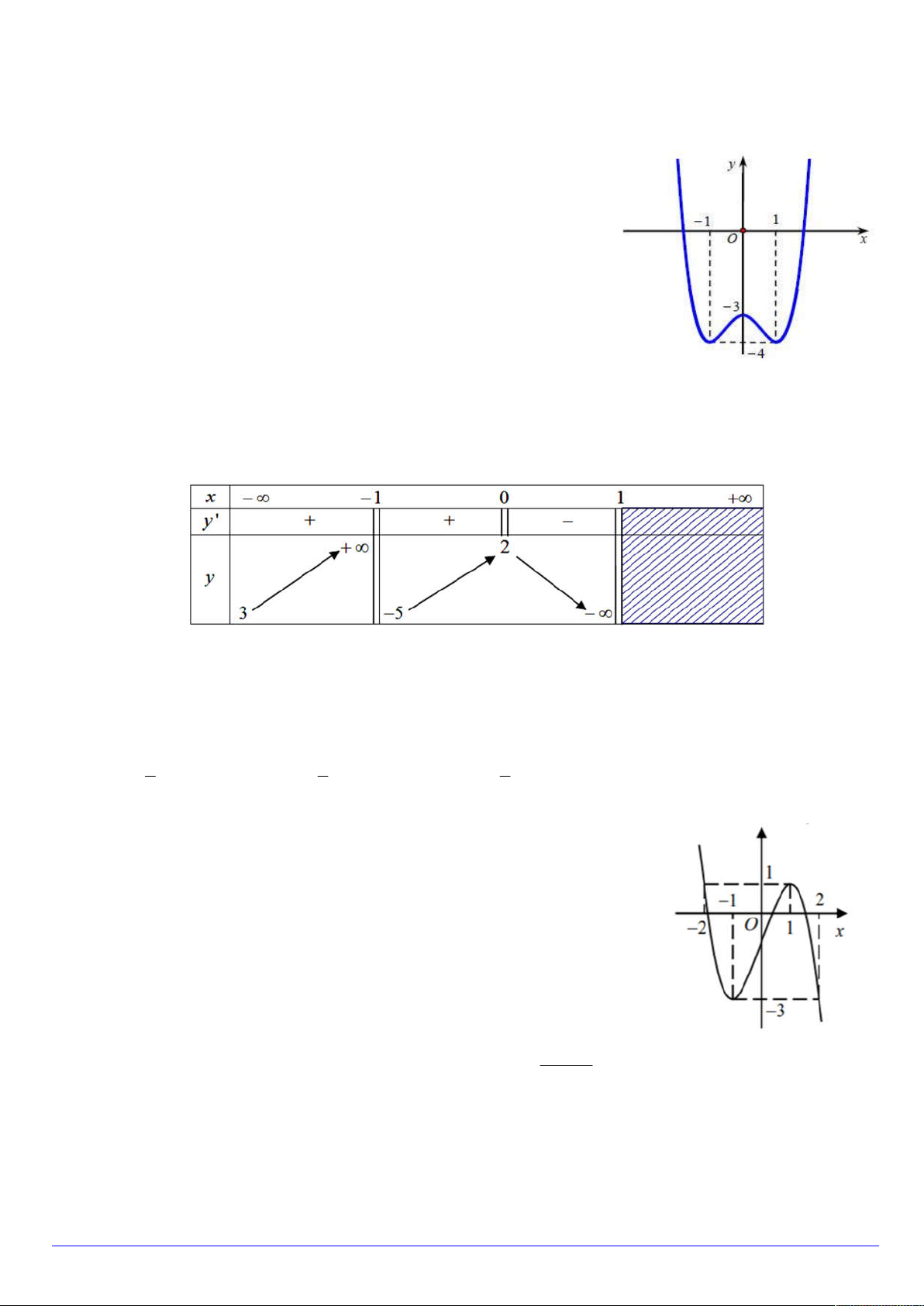
Câu 6. Đường cong ở hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án
A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? x 1 A. y  . B. 3 2
y x  3x 1. x 1 x  3 C. y  . D. 4 2
y  x  2x 1. x 1
Câu 7. Cho hàm số y f x có bảng biến thiên như sau:
Mệnh đề nào sau đây đúng ?
A. Hàm số đạt cực tiểu tại x  2  .
B. Hàm số không có cực trị.
C. Hàm số đạt cực đại tại x  2  .
D. Hàm số đạt cực đại tại x  3 .
Câu 8. Cho hàm số y f x có bảng biến thiên như sau
Hàm số y f x nghịch biến trên khoảng nào dưới đây? A. 1;  3 . B. ;  2 . C. 0;   . D.  2  ;0 .
Câu 9. Cho hàm số y x x  2
3 . Hàm số đạt cực đại tại điểm có hoành độ: A. x  0 . B. x  1 . C. x  3 . D. y  3 . Câu 10. Cho hàm số 3 2
y ax bx cx d a, , b ,
c d   . Đồ thị hàm số
y f x như hình vẽ bên.Số nghiệm thực của phương trình 5 f x  2  0 là A. 3 . B. 2 . C. 4 . D. 0 .
Câu 11. Cho hàm số f x có đạo hàm f  x  x x   x  2 3 1
2 . Hỏi hàm số có bao nhiêu điểm cực đại ? A. 0 . B. 1. C. 3 . D. 2 . Trang 14/20 - Mã đề 104
Câu 12. Hàm số nào sau đây nghịch biến trên  ? x 1 A. y  .
B. y  1 x . C. 4 2
y  x x 1. D. 3 2
y  x  3x  9x  4 . x 1 ax b y
Câu 13. Cho hàm số y
(a  0) có đồ thị như hình vẽ bên. cx d
Mệnh đề nào dưới đây đúng?
A. b  0, c  0, d  0 B. b  0, c  0, d  0
C. b  0, c  0, d  0 D. b  0, c  0, d  0 O x 2  x
Câu 14. Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số y  là : 2
x  4x  3 A. 2 . B. 3. C. 0 . D. 1 .
Câu 15. Khoảng nghịch biến của hàm số 2 y
x  4x  3 là A.  ;   1 . B.  ;  2 . C. 2;   . D. 3;  . 2 x
Câu 16. Gọi m là giá trị nhỏ nhất của hàm số f x 
trên 1;5 . Trong các mệnh đề sau, mệnh đề nào x 1 25 đúng? A. m  4 . B. m  .
C. m f 5 .
D. m f   1 . 4 2 x  2x  3
Câu 17. Biết đồ thị hàm số y
có đúng 2 đường tiệm cận. Mệnh đề nào dưới đây đúng? 2 x mx 1 A. m 3;5 .
B. m 5; . C. m   ;  4  . D. m  4  ;3.
Câu 18. Tìm tất cả các giá trị của tham số m để hàm số 4
y mx  m   2
1 x 1 2m có đúng một điểm cực trị. A. m  0 . B. 0  m  1.
C. m  0 hay m  1.
D. m  0 hay m  1.
Câu 19. Hỏi có bao nhiêu giá trị nguyên m để hàm số y   2 m   3
x  m   2 1
1 x x  4 nghịch biến trên khoảng  ;   ? A. 1. B. 3 . C. 2 . D. 0 . mx 1
Câu 20. Tìm tất cả các giá trị của m để hàm số y
đồng biến trên từng khoảng xác định của nó là x m
A. m  –1 hoặc m  1 .
B. m  –1 hoặc m  1 . C. –1  m  1
D. m  –1 hoặc m  1 . Trang 15/20 - Mã đề 104
Câu 21. Cho hàm số y f x có đồ thị như hình vẽ:
Hàm số y f cos x  
1 đạt giá trị lớn nhất và nhỏ nhất lần
lượt là M và m . Mệnh đề nào dưới đây sai?
A. M  2m  5 .
B. M m  4 . C. 2 2
M m  10 .
D. M m  2 . ax b
Câu 22. Cho hàm số y f (x) 
có đồ thị hàm số f  xcx d
như trong hình vẽ dưới đây:
Biết rằng đồ thị hàm số f (x) đi qua điểm A0; 4 . Khẳng
định nào dưới đây là đúng? 11 A. f   1  6 . B. f   1  . 2 7 C. f   1  . D. f   1  2 . 2
Câu 23. Cho hàm số y f (x) có đạo hàm f x   2 x   2 '( )
1 x  4x  3 . Hỏi hàm số 2
g(x)  f (2 x x ) có
bao nhiêu điểm cực đại? A. 3. B. 5 C. 2 D. 0 1 Câu 24. Biết hàm số 3 f (x) 
x  m   2
1 x  (m 1)x 1 đồng biến trên khoảng   ;1 khi 3  b b m  a;      1  ; 0 , ( * a, , b c , ,
tối giản). Giá trị T a b c bằng:  c c A. 7 . B. 5 . C. 9 . D. 13 .
Câu 25. Cho f x mà hàm số y f  x có bảng
biến thiên như hình bên. Tất cả các giá trị của tham 1
số m để bất phương trình 2
m x f x 3  x có 3
nghiệm x 0;3 là : 2
A. m f   1  .
B. m f 0 .
C. m f 3 .
D. m f 0 . 3
------------- HẾT ------------- Mã đề [107]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 D A A B C A C D B C B D C B A A D C C B A B A C C
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
KIỂM TRA ĐỊNH KỲ - HỌC KỲ I TỔ TOÁN NĂM HỌC 2019 – 2020 Trang 16/20 - Mã đề 104
Môn: Toán - Lớp 12 - Chương trình chuẩn ĐỀ CHÍNH THỨC
Thời gian: 45 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên:………………………………….Lớp:…………….......……..……… 108
Câu 1. Cho hàm số y f (x) có bảng biến thiên như sau:
Hàm số đồng biến trên khoảng A. (2; ) . B. ( ;  0) . C. (0; 2) . D. (1;5) . x 1
Câu 2. Giá trị lớn nhất của hàm số y
trên 2;  bằng: x 1 A. 3. B. 4 C. 2. D. 1.
Câu 3. Hàm số nào sau đây nhận đường thẳng y  2 làm một tiệm cận? 3 2x  3 2  x 2 A. y  . B. y  . C. y  . D. y  . x  2 x 1 1 x x  2
Câu 4. Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào dưới đây? 2x 1 2x  3 A. y  . B. 3 y x 1. . C. 4 2
y  x  2x 1 . D. y  . x  1 x  1
Câu 5. Đường cong trong hình vẽ bên dưới là đồ thị của một hàm số nào? A. 4 2
y x  2x  3 . B. 4 2
y  x  3x  2 . C. 2
y  x x 1. D. 3 2
y  x x  2 .
Câu 6. Cho hàm số f x xác định trên  và có bảng xét dấu f  x như hình bên. Khẳng định nào sau đây sai ? Trang 17/20 - Mã đề 104
A. x  1 là điểm cực đại của hàm số.
B. Hàm số có hai điểm cực trị.
C. Hàm số đạt cực tiểu tại x  2 .
D. Hàm số đạt cực đại tại x  3  .
Câu 7. Tìm điểm cực tiểu của đồ thị hàm số 3
y  x  3x  4 . A.  1  ; 2 . B. 1;6 . C. x  1  . D. x  1 . 2x  1
Câu 8. Các khoảng nghịch biến của hàm số y  là x 1 A.  ;   1 .  ;   B. 1 và 1;. C. 1;  . D.  \   1 . Câu 9. Cho hàm số 3 2
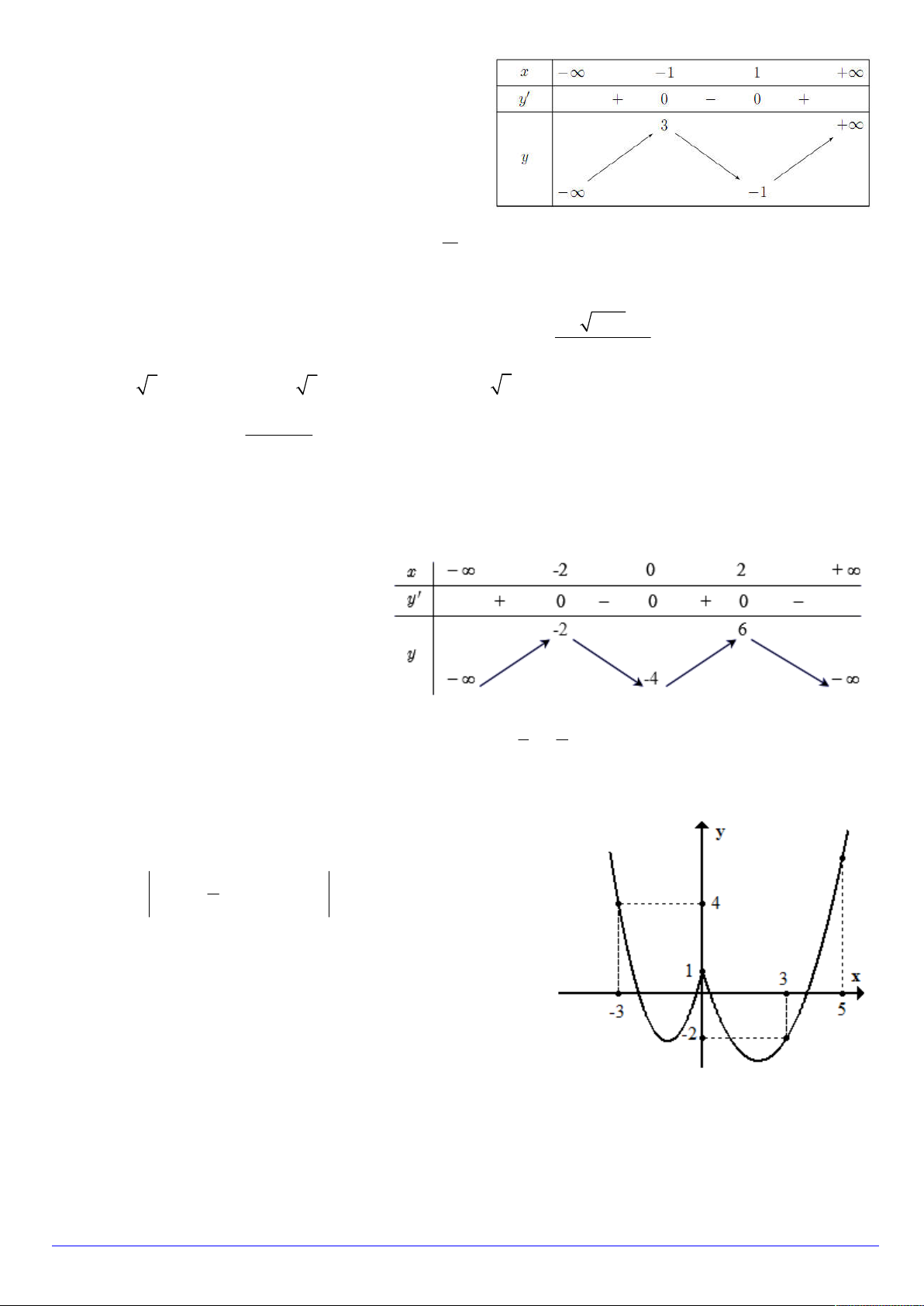
y ax bx cx d a, , b ,
c d   . Đồ thị hàm số y f x như hình vẽ dưới đây.
Số nghiệm thực của phương trình 5 f x  9  0 là A. 1. B. 0 . C. 3 . D. 2 .
Câu 10. Giá trị nhỏ nhất của hàm số 4 2
y x  2x 1 trên  1  ;  1 A. 1  . B. 2 C. 1. D. 0.
Câu 11. Biết đồ thị hàm số 3 2
y ax  3x 1a   có một điểm cực trị là A1; 2
  . Giá trị của 3a 12 bằng: A. 6 . B. 1. C. 1  8 . D. 6  . 2
Câu 12. Cho hàm số y f x có đạo hàm trên  và f ' x   x  
1  x  2  x  3 . Số điểm cực trị của hàm số đã cho là A. 0 . B. 2 . C. 1. D. 3 .
Câu 13. Cho hàm số f x 4 2
ax bx c a  0 xác định, liên tục trên  và có bảng biến thiên như hình vẽ:
Tìm m để phương trình f x  m có hai nghiệm phân biệt. Trang 18/20 - Mã đề 104 m  3 m  3 A. 1   m  3 . B.  . C. m  3 . D.  . m  1   m  1   Câu 14. Cho hàm số 3 2
y x  3x  2019 . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng 0; 2 .
B. Hàm số nghịch biến trên khoảng 2;   .
C. Hàm số đồng biến trên khoảng 0; 2 .
D. Hàm số nghịch biến trên khoảng  ; 0 . 2 x x
Câu 15. Tổng số tiệm cận đứng và tiệm cận ngang của hàm số y  là bao nhiêu? 2 x  2x  3 A. 3 . B. 2. C. 0. D. 1.
Câu 16. Hàm số y f x có đạo hàm 2
y  x (x  6) . Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên (0; ) .
B. Hàm số nghịch biến trên  .
C. Hàm số đồng biến trên 6; .
D. Hàm số nghịch biến trên  ;  0 và 6;. 3 x
Câu 17. Có bao nhiêu giá trị nguyên của tham số m để hàm số 2 y  
mx  6mx  2 nghịch biến trên  . 3 A. 6 . B. 5 . C. vô số. D. 7
Câu 18. Cho hàm số y = f x có bảng biến thiên như sau:
Hỏi phương trình f x  1 có bao nhiêu nghiệm? A. 5. B. 6. C. 4. D. 2. mx 1
Câu 19. Gọi T là tập hợp tất cả các giá trị của tham số m để hàm số y
có giá trị nhỏ nhất trên đoạn 2 x m 1; 
5 bằng 1. Số phần tử của T là: A. 2. B. 4. C. 0. D. 3.
Câu 20. Cho hàm số y f (x) liên tục trên từng khoảng xác định và có bảng biến thiên như hình vẽ. 1
Tổng số tiệm cận đứng và ngang của đồ thị hàm số g x  là: f (x)  2 A. 4. B. 3. C. 5. D. 2. Trang 19/20 - Mã đề 104
Câu 21. Biết m là giá trị của tham số m để hàm số 3 2
y x  3x mx 1 có hai điểm cực trị x , x sao cho 0 1 2 2 2
x x x x  13 . Mệnh đề nào dưới đây đúng? 1 2 1 2 A. m  7  ; 1  . B. m  9  ; 1  . C. m  1  5; 7  . D. m  7;10 . 0   0   0   0  
Câu 22. Cho hàm số y f x có đạo hàm liên tục trên  , dấu của đạo hàm được cho bởi bảng dưới đây
Hàm số y f 2x  2 nghịch biến trong khoảng nào? A.  1  ;  1 . B. 1; 2 . C. 2;  . D.  ;    1 .
Câu 23. Cho hàm số y f x có bảng biến thiên như hình bên. 1  x
Gọi M là giá trị lớn nhất của hàm số y f 1  x  
trên đoạn x  2
 , 2 . Trong các mệnh đề sau, 3  2  mệnh đề nào đúng?
A. m  6;  . B. m   4  ; 2 . C. m   ;  5   . D. m   2  ; 6 .
Câu 24. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 3 2
y x mx  m  6 x 1 đồng biến trên khoảng  2  ;  ? A. 3 B. 0 . C. 2 . D. 4 .
Câu 25. Cho hàm số f x có đạo hàm trên  là f  x   x  
1  x  3 . Gọi T là tập hợp các giá trị nguyên
của tham số m  1
 0; 20 để hàm số y f  2
x  2x m có 3 điểm cực trị. Tính tổng các phần tử của T. A. 4 . B. 6 . C. 0 . D. 2 .
------------- HẾT ------------- Mã đề [108]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 C A B A A D A B C A D B B A B C D A A C C B D A D Trang 20/20 - Mã đề 104