SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM
ĐỀ KIỂM TRA ĐỊNH KÌ THÁNG 9
TRƯỜNG THCS – THPT KHAI MINH Năm học 2017 - 2018 Môn thi: TOÁN 10
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Bài 1: (1 điểm) Giả sử ABC là một tam giác đã cho. Lập mệnh đề P  Q và Q  P , rồi xét tính
đúng sai của chúng với: P : “Góc A bằng 0 90 ” và Q: “ 2 2 2
BC  AB  AC ”.
Bài 2: (1 điểm) Phát biểu mệnh đề phủ định của mỗi mệnh đề sau và giải thích mệnh đề phủ định đó đúng hay sai? a) 2
x  R:x  5  b) 2
 x  R: x  2x  8  0
Bài 3: (2 điểm) Cho các tập hợp:
A  xZ   x  
B  x R  2 2 2
x  5x  6x  4x 5   0
Xác định các tập hợp: A  B ; A B ; A \ B ; B \ A ?
Bài 4: (2 điểm) Cho các tập hợp: A  5;1 
1 và B  2;18 .
Xác định các tập hợp: A  B ; A B ; A \ B ; B \ A và biểu diễn chúng lên trục số?
Bài 5: (0,5 điểm) Tìm tất cả các tập hợp X sau cho:
a;b  X  1;a;3;b     Bài 6: (1 điểm) a) Cho A
 BC có trọng tâm G và M là một điểm tùy ý trong mặt phẳng. Chứng minh rằng:
   
MA  MB  MC  3MG
b) Cho hình bình hành ABCD có tâm O và M là một điểm tùy ý trong mặt phẳng. Chứng minh
    
rằng: MA  MB  MC  MD  4MO .
Bài 7: (1,5 điểm) Cho sáu điểm A, B, C, D, E và F. Tính:
   
a) AB  DC  BD  CA     b) AB + CD  CB+ ED
    
c) AD  EB  CF  AE  FB
Bài 8: (1 điểm) Cho hình vuông ABCD có cạnh bằng 5cm . Tính độ dài các vectơ sau:   a) AB  AD   b) AC  BC ------HẾT------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:………………………………Số báo danh:………………
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM
ĐÁP ÁN ĐỀ KIỂM TRA ĐỊNH KÌ THÁNG 9
TRƯỜNG THCS – THPT KHAI MINH Năm học 2017 - 2018 Môn thi: TOÁN 10 Bài Đáp Án Điểm
P  Q : “ Nếu Góc A bằng 0 90 thì 2 2 2
BC  AB  AC ”. 0,25
P  Q là mệnh đề đúng. 0,25 Bài 1 0,25
Q  P : “ Nếu 2 2 2
BC  AB  AC thì Góc A bằng 0 90 ”. 0,25
Q  P là mệnh đề đúng.
a) Mệnh đề phủ định là: 2
 x  R:x  5  0,25
Đây là mệnh đề đúng vì: 2
 x  R:x  0 0,25 Bài 2
b) Mệnh đề phủ định là: 2
x R:x  2x 8  0 0,25
Đây là mệnh đề sai vì:   4  4.1.8  0 0,25 Ta có:
A    2, 1, 0 , 1 ,  2 0,5
B  xR  2
x  5x  6x  4x 5   0 Ta có:  2
x  5x  6x  4x  5  0 x  2 2  0,25
x  5x  6  0   x  3  x  4  0    x  4 Bài 3 x 5  0   x  5 0,25
Suy ra: B  2,3, 4,  5 Ta có:
A  B  2, 1,0,1, 2,3, 4,  5 0,25 A  B   2  0,25 A \ B  2, 1,0,  1 0,25 0,25 B \ A  3, 4,  5 Ta có: A  B  5,18 0,5 0,5 A  B  2,1  1 Bài 4 0,5 A \ B  5, 2 0,5 B \ A  11,18
Trong đó vẽ đúng trục số mỗi câu được 0,25 điểm
X có thể là các tập hợp sau: Bài 5 a,  b ; a , b,  1 ;a , b,  3 ;1,a ,3,  b 0,5 a) ta có:
        
MA  MB  MC  MG  GA  MG  GB  MC  GC 0,25
  
      Bài 6  
MG  MG  MG  GA GB  GC  3MG  0  3MG
   
Vậy : MA  MB  MC  3MG 0,25 b) ta có:
           
MA  MB  MC  MD  MO  OA  MO  OB  MO  OC  MO  OD
        0,25
 MO  MO  MO  MOOAOC OB OD    
 4MO  0  0  4MO
    
Vậy MA  MB  MC  MD  4MO 0,25 a) ta có:
       
AB  DC  BD  CA   AB  BD  DC CA 0,25    
 AD  DA  AA 0 0,25 b) ta có:    
   
AB + CD  CB+ ED  AB+ CD CB ED
    0,25  AB + CD  BC + DE    
 AB BCCD  DE Bài 7    AC  CE   AE 0,25 c) ta có:
         
AD  EB  CF  AE  FB  AD  BE  CF  EA  FB      0,25
 CF  FBBE  EA AD
   
CB  BA  AD   
 CA  AD  CD 0,25 5cm A B C D F
a) Vì ABCD là hình vuông nên ABCD cũng là hình bình hành;
  
ta có: AB  AD  AC ( quy tắc hình bình hành)  Bài 8
Xét ABC vuông tại B, ta có: 2 2 2
AC  AB  BC ( Định lí Pytago) 0,25
 AC  5 2 cm   
Ta có: AB  AD  AC  AC  5 2 cm 0,25
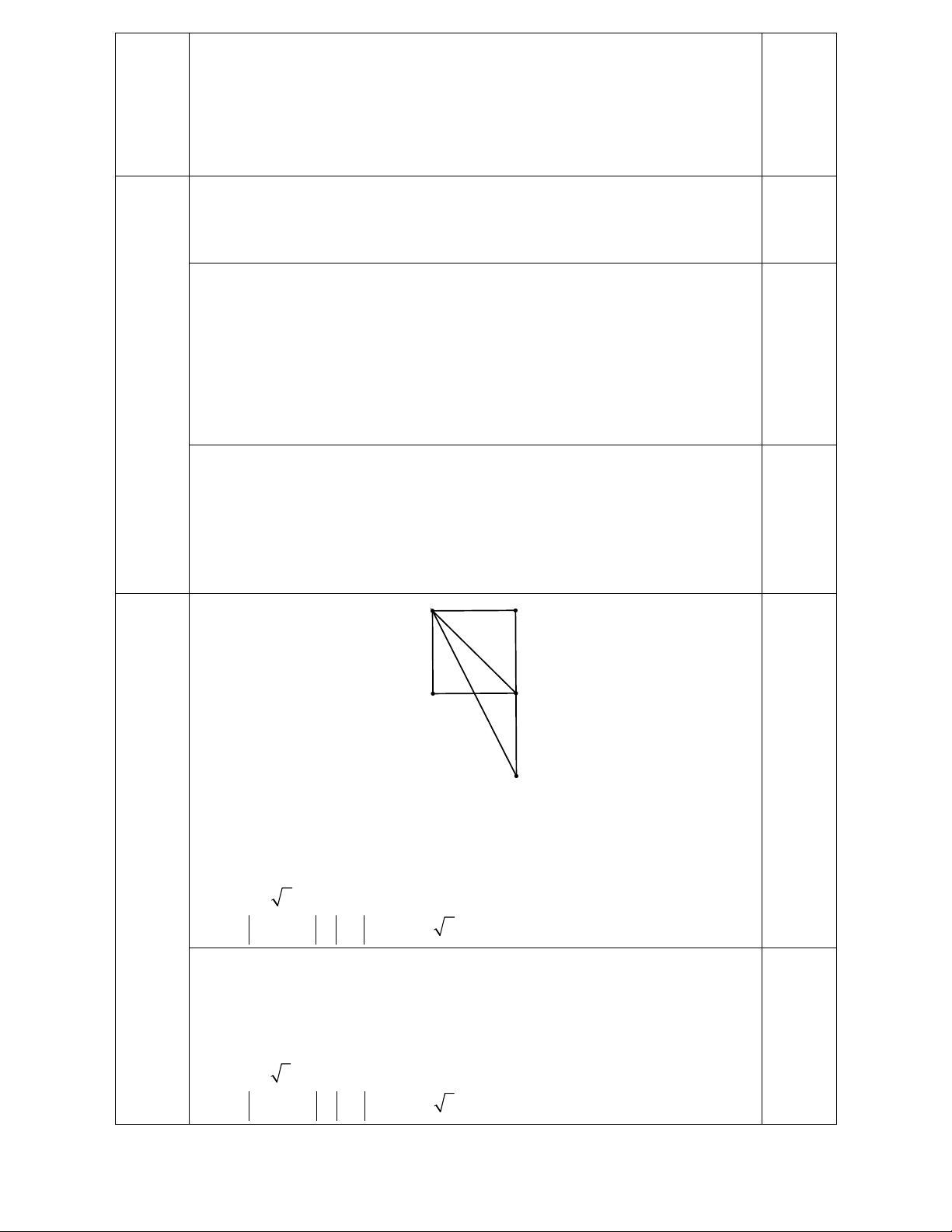
b) Gọi điểm F sao cho tứ giác ACFD là hình bình hành.
    
Ta có: AC  BC  AC  AD  AF 0,25
Độ dài BF: BF  BC  CF  5  5 10cm
Xét ABF vuông tại B, ta có: 2 2 2
AF  AB  BF ( Định lí Pytago)
 AF  5 5 cm    0,25
Ta có: AC  BC  AF  AF  5 5 cm