Đề kiểm tra đội tuyển HSG Toán năm 2021 – 2022 trường chuyên Vị Thanh – Hậu Giang

SỞ GD & ĐT TỈNH HẬU GIANG KIỂM TRA ĐÔI TUYỂN HỌC SINH GIỎI
TRƯỜNG THPT CHUYÊN VỊ THANH KHÓA NGÀY 01/03/2022 MÔN TOÁN ĐỀ CHÍNH THỨC
(Đề thi gồm 01 trang)
Thời gian làm bài: 180 phút (không kể thời gian phát đề) Câu I: (5,0 điểm) 1) Giải phương trình 2
(x -1) x +1 - x 5 - x = 3x - 4x -1 trên tập số thực. 3 3
x  y  9
2) Giải hệ phương trình  (với , x y Î ). 2 2
x  2y  x  4y Câu II: (3,0 điểm) Cho hàm số 3 2
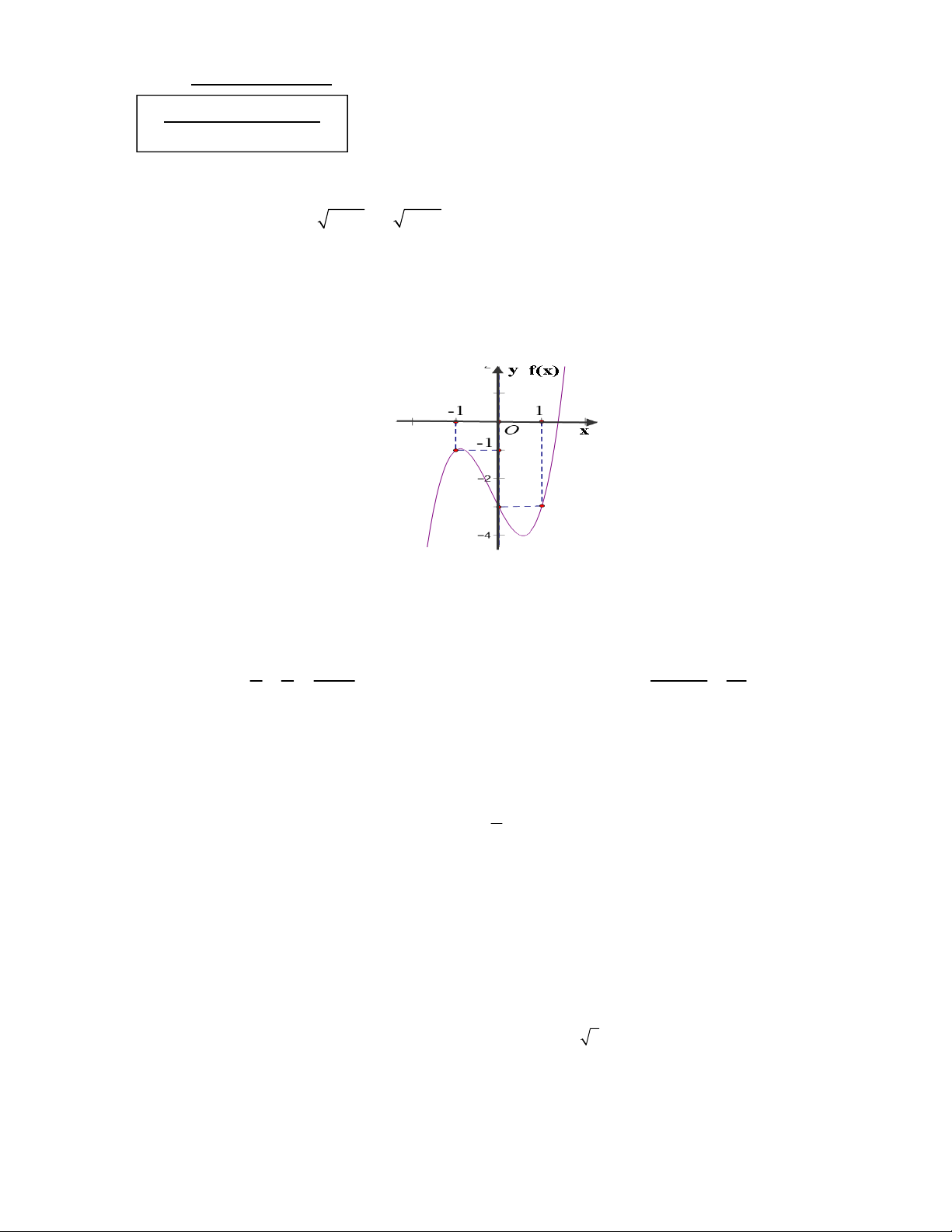
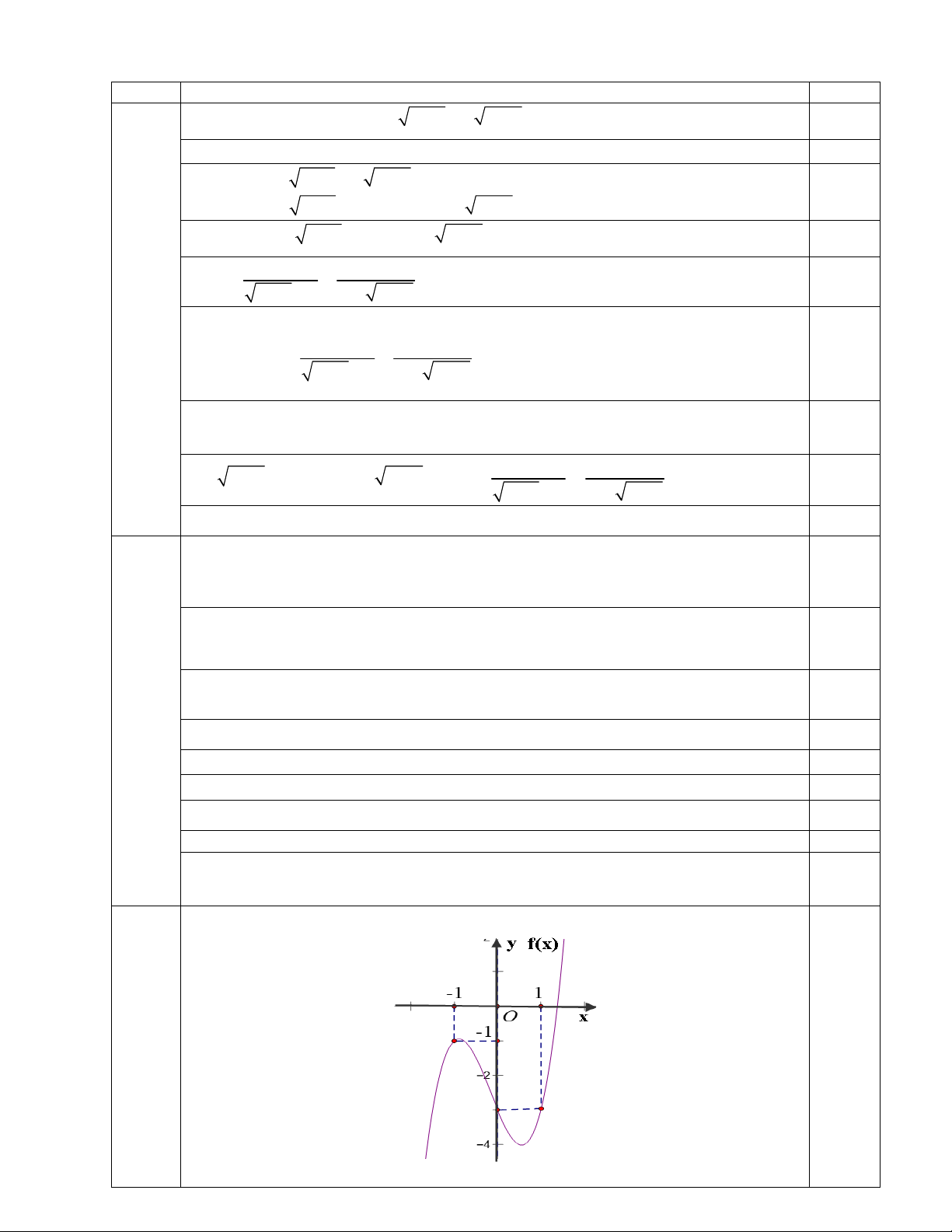
f (x)  ax  bx  3x  d (với a,b, c, d   ) có đồ thị như hình vẽ
1) Tìm hàm số f (x). 2) Phương trình 2
f (x  2x)  2 có tất cả bao nhiêu nghiệm thực. Câu III: (4,0 điểm)
1) Cho hai số thực dương x, y thỏa mãn điều kiện x + y £1. 1 1 4 1 1 Chứng minh rằng + ³
. Tìm giá trị nhỏ nhất của biểu thức P = + + 4xy. x y x + y 2 2 x + y xy
2) Cho dãy số (u ) được xác định như sau u = 4;u = 5 và 2 u
= u - (n +1)u , với n Î , n ³1. n 1 2 n+2 n n 1 +
Tính u và u . Tìm số hạng tổng quát u của dãy số trên. 3 4 n Câu IV: (3,0 điểm) 10  1 
1) Tìm số hạng không chứa x trong khai triển ? 2 x  1    x 
2) Có 30 tấm thẻ đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 10 tấm thẻ. Tính xác suất để có 5 tấm thẻ mang
số lẻ, 5 tấm thẻ mang số chẵn trong đó chỉ có đúng 1 tấm chia hết cho 10? Câu V: (5,0 điểm)
1). Trong mặt phẳng Oxy, biết một cạnh tam giác có trung điểm là M  1  ; 
1 ; hai cạnh kia nằm trên các x  2  t
đường thẳng 2x  6y  3  0 và 
t  . Hãy viết phương trình tham số của cạnh thứ ba của tam y  t giác đó?
2). Cho hình chóp S.ABCD có đáy là hình chữ nhật với AD  a 3 ,AB  2a . Tam giác SAB cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Góc giữa SD và mặt phẳng (ABCD) bằng 0 45 .Tính khoảng
cách giữa hai đường thẳng SD và BC .
...........................HẾT...........................
Thí sinh không được sử dụng tài liệu và máy tính cầm tay
Giám thị coi thi không giải thích gì thêm
Đáp án và thang điểm Câu Nội dung Điểm
1) Giải phương trình 2
(x -1) x +1 - x 5 - x = 3x - 4x -1 trên tập số thực. 2,0 Điều kiện: 1   x  5. 0,25 Ta có 2
(x -1) x +1 - x 5- x = 3x - 4x -1 0,25 2
 (x -1) x +1 - (x -1) + 2x - x 5 - x = 3x -3x 2
 (x -1)( x +1 -1) + x(2 - 5- x) -3x + 3x = 0 0,25 x (x -1) x(x -1)  + -3x(x -1) = 0 Câu 0,25 x +1 +1 2 + 5- x I.1
é f (x) = x(x -1) = 0 (2,0 ê điểm)  ê 1 1 ê ( g x) = + -3 = 0 0,25 ê x +1 +1 2 + 5- ë x x  0
Ta có f (x)  0   (nhận). 0,25 x  1 1 1
Do x +1 +1³1 và 2 + 5- x ³ 2 nên + < 2. 0,25 x +1 +1 2 + 5- x
Do đó g(x)  0, x   1
 ;5. Do đó, phương trình g(x)  0 vô nghiệm. 0,25 3 3
x  y  9
2) Giải hệ phương trình  (với , x y Î ). 2 2 3,0
x  2y  x  4y 3 3 3 3
x  y  9 (1)
x  y  9  0 Ta có    . 0,25 2 2 2 2
x  2y  x  y 4 (2) 3
 x  6y  3x 12y  0
Lấy phương trình thứ nhất trừ cho phương trình thứ hai theo vế, ta được: Câu 0,25 I.2 3 2 3 2
x  3x  3x 1 y  6y 12y  8  0 (3,0 3 3
 (x 1)  (y  2)  0 0,5 điểm)
 x 1  2  y 0,25
 y  3  x 0,25
Thay y  3  x vào (2), ta có 2
x  3x  2  0 0,5
 x  1 hoặc x  2 (nhận). 0,5 x 1 x  2
Vậy nghiệm của hệ phương trình là  hoặc  . 0,5 y  2 y 1 Cho hàm số 3 2
f (x)  ax  bx  3x  d (với a,b, c, d   ) có đồ thị như hình vẽ Câu II.1 1,25 (1,25 điểm)
1) Tìm hàm số f (x).
Dựa vào hình vẽ  Đồ thị đi qua 3 điểm: (-1; -1), (0; -3) và (1; -3) 0,25
a  b  3  d  1 Ta có hệ : d  3 0,5 a  b  3  d    3 a  2 Suy ra b  1 0,25 d    3 Vậy 3 2
f (x)  2x  x  3x  3 0,25 2) Phương trình 2
f (x  2x)  2 có tất cả bao nhiêu nghiệm thực. 1,75
Hoành độ giao điểm 2 đồ thị 2
y  f (x  2x) và y  2 là nghiệm của phương trình :  2
x  2x  a 2;    1 Câu 2 0,5
f (x  2x)  2   2
x  2x  b 1;0 (*) II.2   2 x  2x  c 1; 2 (1,75 
điểm) Xét: 2    2 x 2x m
x  2x  m  0 có nghiệm khi ʹ  0  1  m  0  m  1 0,5
Từ (*)  Phương trình có 4 nghiệm phân biệt. 0,5 Vậy 2
f (x  2x)  2 có 4 nghiệm phân biệt. 0,25
1) Cho hai số thực dương x, y thỏa mãn điều kiện x + y £1. 1 1 4
Chứng minh rằng + ³ . x y x + y 2,0 1 1
Tìm giá trị nhỏ nhất của biểu thức P = + + 4xy. 2 2 x + y xy 1 1 2 Ta có + ³
và x + y ³ 2 xy. x y 0,5 xy æ1 1ö 1 1 4 Câu Khi đó ç ÷
ç + ÷(x + y) ³ 4  + ³ . ç ÷ ç 0,5 III.1 è x yø x y x + y (2,0 Ta có 1 1 1 1 P = + + + + 4xy điểm) 2 2 x + y 2xy 4xy 4xy 4 1 ³ + + 2 0,25 2 2 2
x + y + 2xy æ x + yö 4ç ÷ ç ÷ ç ÷ è 2 ø 4 1 ³ + + 2 ³ 7. 2 2 0,25 (x + y) (x + y) 1
Ta có P  7  x  y  . 0,25 2 Vậy P
 7 là giá trị nhỏ nhất của biểu thức. 0,25 min
2) Cho dãy số (u ) được xác định như sau u = 4;u = 5 và 2 u
= u -(n +1)u , n 1 2 n 2 + n n 1 + 2,0
với n Î , n ³1. Tính u và u . Tìm số hạng tổng quát u của dãy số trên. Câu 3 4 n III.2 Ta có 2 2
u = u -2u = 4 -2.5 = 6
u = u -3u = 5 -3.6 = 7. 1,0 3 1 2 và 2 2 4 2 3 (2,0
Từ u = 4;u = 5;u = 6 và u = 7, ta dự đoán *
u = n +3; n " Î  . 0,25 điểm) 1 2 3 4 n
Ta chứng minh bằng quy nạp *
u = n +3; n " Î  . n 0,25
Thật vậy, ta có u = 4 =1+3;u = 5 = 2+3;u = 6 = 3+3 (đúng). 1 2 3
Giả sử với n  k  3. Ta có u = k +3. Khi đó k 1 2. k u k    Ta có 2 2 u 0,25 1  u 
1  k.u  (k  2)  k (k  3)  k  4  (k  1)  3. k k  k
Vậy, mệnh đề đúng với n  k 1. Do đó, ta có *
u = n +3; n " Î  . 0,25 n 10  1 
1) Tìm số hạng không chứa x trong khai triển 2 x  1   1,5  x 
Từ lý thuyết ta có công thức tổng quát như sau: Với 0  q  p  n thì số 10  1 
hạng tổng quát khi khai triển tam thức là 2 x  1    x  0,5 Câu pq IV.1  p  1  T  C C x 1 q   C C 1 q p q p q q p  x p 10 p  10 2     10 p   20 3 (1,5  x 
điểm) Số hạng không chứa x trong khai triển ứng với .
20  q  3 p  0  3 p  q  20 0,25
Mà 0  q  p  n và q, p, n   nên  p;q   7 
;1 ,8; 49;7,10;10 0,25
Lúc này số hạng không chứa x trong khai triển là 1 4 10 7 7 1 8 4 10 10 9 7 0,25  
1 C C  1 C C  1 C C  1  C C  1951 10 7
  10 8   10 10   10 9 10  1 
Vậy Số hạng không chứa x trong khai triển l 2 x  1 à 1951 0,25    x 
2) Có 30 tấm thẻ đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 10 tấm thẻ. Tính xác
suất để có 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn trong đó chỉ có đúng 1 1,5
tấm chia hết cho 10? Gọi biến cố : A “Lấy 5 tấm thẻ mang số lẻ,
5 tấm thẻ mang số chẵn, trong đó chỉ có đúng
1 tấm thẻ mang số chia hết cho 10 ” 0,25
Số cách lấy ngẫu nhiên 10 tấm thẻ trong 30 tấm thẻ: 10 C 10    C . 30 cách 30 Trong
30 tấm thẻ có 15 tấm thẻ mang số lẻ, t
15 ấm thẻ mang số chẵn, 3 tấm thẻ mang Câu
số chia hết cho 10 (chú ý là các thẻ chia hết cho 10 đều là số chẵn) IV.2 Số cách chọn 5 tấm thẻ mang số lẻ: 5 C  3003 15 cách. (1,5 0,75
điểm) Số cách chọn
1 tấm thẻ mang số chia hết cho 10 1 C  3 3 cách Số cách chọn
4 tấm thẻ mang số chẵn không chia hết cho 4 10 : C  495 12 cách Số cách lấy 5 tấm thẻ mang số lẻ,
5 tấm thẻ mang số chẵn trong đó chỉ có đúng 1 tấm
thẻ chia hết cho 10 : 3003.3.495  4459455 cách. 0,25    4459455 A A 4459455 99 Vậy P( ) A    . 10 0,25  C 667 30
1). Trong mặt phẳng Oxy, biết một cạnh tam giác có trung điểm là M  1  ;  1 ; hai x  2  t
cạnh kia nằm trên các đường thẳng 2x  6y  3  0 và 
t  . Hãy viết 2,5 y  t Câu
phương trình tham số của cạnh thứ ba của tam giác đó? V.1 (2,5 A điểm) 0,5 B M C x  2  t
Giả sử AB : 2x  6y  3  0, AC :  và M  1  ; 
1 là trung điểm của cạnh BC . y  t x  x  2  Do M  1  ; 
1 là trung điểm cạnh BC nên ta có: B C  (1) . y  y  2  B C
Điểm B  AB  2x  6 y  3  0 (2) . 0,25 B B x  2  t Điểm C C  AC   (3) . 0,25 y  t  C
x  2  t  2  x  4   t Thế 3 vào   1 ta được: B B    4 0,25 y  t  2 y  2  t  B  B
Thế 4 vào 2 ta được:   t    t 7 2 4 6 2
 3  0  t  . 0,25 4  1 7 
Từ đây ta tìm được: C ;   . 0,25  4 4    5 3 
Đường thẳng chứa cạnh BC đi qua M  1  ;  1 nhận MC  ;   làm vtcp 0,25  4 4  x  1   5t
nên có phương trình tham số là: BC :  t . 0,25 y 1 3t x  1   5t
Vậy phương trình tham số là: BC :  t . 0,25 y 1 3t
2). Cho hình chóp S.ABCD có đáy là hình chữ nhật với AD  a 3 ,AB  2a . Tam
giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa SD và 2,5
mặt phẳng (ABCD) bằng 0
45 .Tính khoảng cách giữa hai đường thẳng SD và BC. S 0,25 A D H Câu B C V.1
+ Gọi H là trung điểm AB. (2,5 SAB  ABCD điểm) 
+ SAB  ABCD  AB  SH  ABCD 0,25 SH   AB
+ Hình chiếu của SD lên mp (ABCD) là DH  Góc giữa SD và mặt phẳng (ABCD) bằng 0 45  0,25   0 SDH 45
+ Xét tam giác AHD vuông tại A   2  2 DH AD AH  2a 0,25
+ Xét tam giác SDH vuông tại H và có   0 SDH 45  DH = SH = 2a. 0,25
+ d(SD,BC)  d(BC,SAD)  dB,SAD  2.dH,SAD 0,5 1 1 1 1 1 5 2 d H,SAD      2 2 2 2 2 SH AH 4a a 4a 0,5 2  2     4a      2 5a d H, SAD d H, SAD 5 5  4 5 d(SD, BC) a 0,25 5 - - Hết - -