Đề kiểm tra Giải tích 12 chương 1 trường THPT Trần Văn Kỷ – Thừa Thiên Huế

TRƯỜNG THPT TRẦN VĂN KỶ
KIỂM TRA ĐỊNH KỲ, NĂM HỌC 2012  2013 TỔ TOÁN
MÔN: GIẢI TÍCH _ 12 _CHƯƠNG I Thời gia n là m bài: 45 phút ĐỀ CHÍNH THỨC
MA TRẬN ĐỀ KIỂM TRA MỨC ĐỘ NHẬN THỨC Vận Vận TỔNG NỘI DUNG – CHỦ ĐỀ Nhận Thông dụng dụng SỐ biết hiểu (1) (2) Sự đồng biến, nghịch Chương 1: 1a 1 biến của hàm số Ứng dụng 2 2
đạo hàm Cực trị của hàm số 1b 4b 1(2) để khảo 2 2 2(4)
Giá trị lớn nhất và giá sát và vẽ 2a 2b 4a 3(2)
trị nhỏ nhất của hàm số đồ thị hàm 1 1 2 4(2) số 3 1 Đường tiệm cận 2 2 TỔNG SỐ 2 2 1 1(1) 6 4 3 1 2(2) 10 Chú thích:
a) Đề được thiết kế với tỉ lệ: 40% nhận biết + 30% thông hiểu + 10% vận dụng (1) + 20% vận dụng
(2) (tất cả các câu đều tự luận). b) Cấu trúc bài: 4 câu
c) Cấu trúc câu hỏi: Số lượng câu hỏi (ý) là 6. d) Dự kiến câu hỏi:
Câu 1: Xét tính đơn điệu của một hàm số thường gặp. Tìm các điểm cực trị của một hàm số thường gặp.
Câu 2: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số thường gặp.
Câu 3: Tìm các đường tiệm cận của một hàm số thường gặp.
Câu 4: Vận dụng giá trị lớn nhất, giá trị nhỏ nhất của hàm số, cực trị, tính đơn điệu của hàm số vào giải toán.
TRƯỜNG THPT TRẦN VĂN KỶ
KIỂM TRA ĐỊNH KỲ, NĂM HỌC 2012  2013 TỔ TOÁN
MÔN: GIẢI TÍCH _ 12 _CHƯƠNG I Thời gian là m bài: 45 p hút ĐỀ SỐ 1
A. PHẦN CHUNG: (8 điểm) (Dành cho tất cả các lớp 12)
Câu 1: (4 điểm) 2x 1
a/ Xét sự đồng biến, nghịch biến của hàm số y  . x  1
b/ Tìm cực trị của hàm số 4 2
y  x  2x  2.
Câu 2: (2 điểm) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số a/ 3 2
y  x  3x  2 trên đoạn [ 3  ; ] 1 ; 1 x b/ y 
trên nửa khoảng  ;  0 . 2 x  2 x Câu 1
3: (2 điểm) Tìm các đường tiệm cận của đồ thị hàm số  y . 2 x 2x3
B. PHẦN RIÊNG: (2 điểm) (Học sinh chỉ được làm phần dành riêng cho lớp mình)
Phần 1 (Dành cho lớp 12/1)
Câu 4a: (2 điểm) Xác định tất cả các giá trị của m để phương trình 5  x  1 x  m có nghiệm.
Phần 2 (Dành cho lớp 12/2  12/9)
Câu 4b: (2 điểm) Tìm m để đồ thị hàm số 3 2
y  x  x   2 4 m  
1 x 1 có hai điểm cực trị nằm về
hai phía so với trục tung. Hết
Học sinh không được sử dụng tài liệu. Giáo viên coi thi không giải thích gì thêm.
Họ và tên học sinh:…………………………………………………………………..
TRƯỜNG THPT TRẦN VĂN KỶ
KIỂM TRA ĐỊNH KỲ, NĂM HỌC 2012  2013 TỔ TOÁN
MÔN: GIẢI TÍCH _ 12 _CHƯƠNG I Thời gian là m bài: 45 p hút ĐỀ SỐ 2
A. PHẦN CHUNG: (8 điểm) (Dành cho tất cả các lớp 12)
Câu 1: (4 điểm) 3  x 1
a/ Xét sự đồng biến, nghịch biến của hàm số y  . x  2
b/ Tìm cực trị của hàm số 4 2
y  x  8x 1.
Câu 2: (2 điểm) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số a/ 3
y  x  3x 1trên đoạn [ 3  ; ] 0 ; 2  x b/ y 
trên nửa khoảng  ;  1 . 2 x  4 x  3
Câu 3: (2 điểm) Tìm các đường tiệm cận của đồ thị hàm số . 2 x  3x  2
B. PHẦN RIÊNG: (2 điểm) (Học sinh chỉ được làm phần dành riêng cho lớp mình)
Phần 1 (Dành cho lớp 12/1)
Câu 4a: (2 điểm) Xác định tất cả các giá trị của m để phương trình 3  x  2  x  m có nghiệm.
Phần 2 (Dành cho lớp 12/2  12/9)
Câu 4b: (2 điểm) Tìm m để đồ thị hàm số 3 2
y  x  x   2 2
1 m  x 1 có hai điểm cực trị nằm về
hai phía so với trục tung. Hết
Học sinh không được sử dụng tài liệu. Giáo viên coi thi không giải thích gì thêm.
Họ và tên học sinh:…………………………………………………………………..
TRƯỜNG THPT TRẦN VĂN KỶ
KIỂM TRA ĐỊNH KỲ, NĂM HỌC 2012  2013 TỔ TOÁN
MÔN: GIẢI TÍCH _ 12 _CHƯƠNG I Thời gian là m bài: 45 phút ĐỀ SỐ 1
ĐÁP ÁN VÀ THANG ĐIỂM
(Đáp án và thang điểm này gồm 02 trang) Câu Ý Đáp án Điểm a 2
Tập xác định: D  \ { 1}. 0,5 3 y '  . 2 (x  0,5 1)
y '  0 với mọi x  . D 0,5
Vậy hàm số đồng biến trên mỗi khoảng ( ; 1  ) vµ ( 1  ; ). 0,5 b 2,0
Tập xác định: D  . 3 0,5
y '  4x  4 . x 1
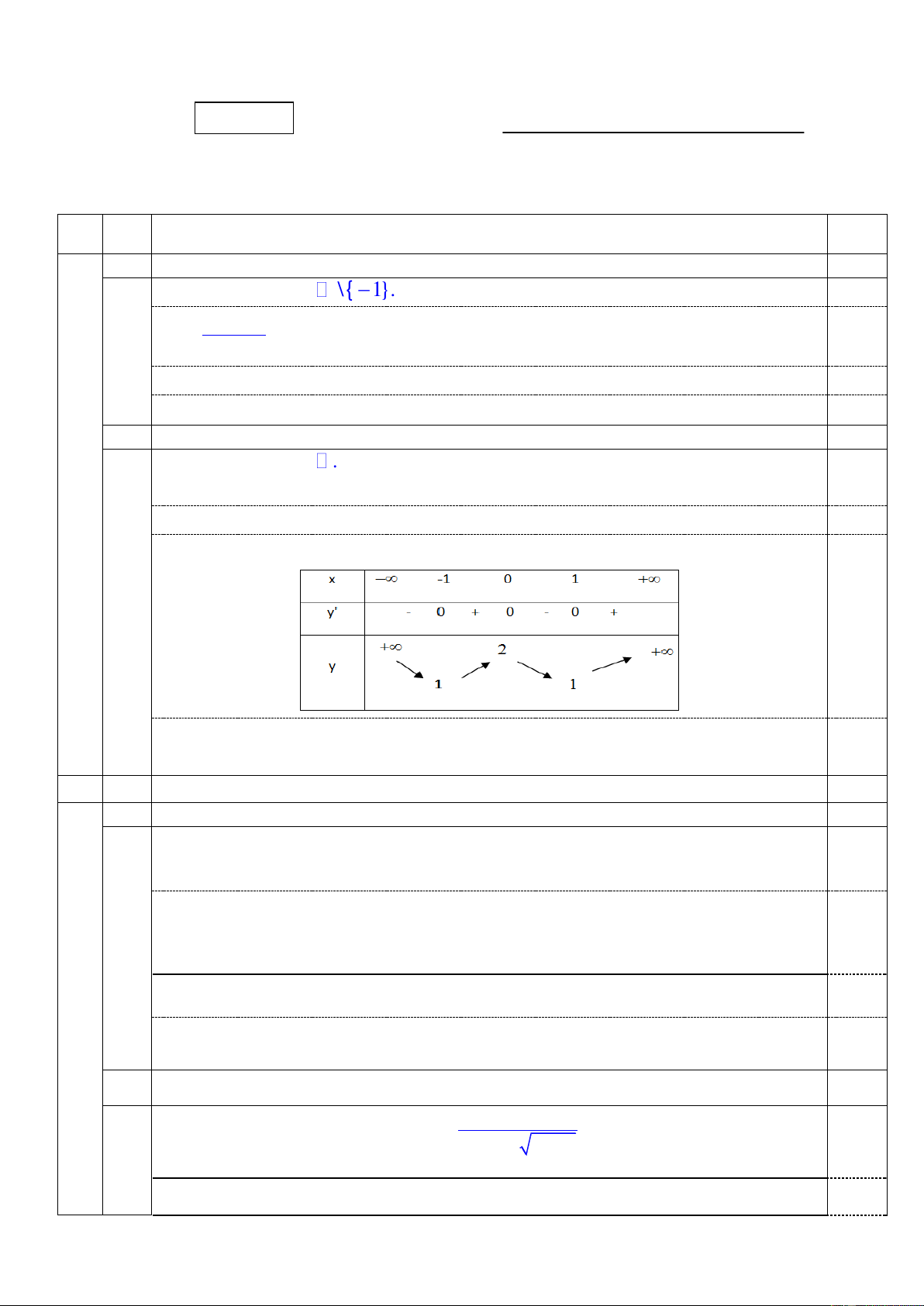
y '  0  x  0 hoÆ c x  1  . 0,5 Bảng biến thiên 0,5
Vậy, hàm số đạt cực đại tại x  0, giá trị cực đại y(0)  2. Hàm số đạt cực tiểu tại các điểm 0,5 x  1
 , giá trị cực tiểu y( 1  ) 1. 2 2,0 a 1,0
Hàm số liên tục trên đoạn [ 3  ; ] 1 0,25 Ta có: 2 y '  3  x  6 . x x  0 y '  0   x  2  lo¹i. 0,25 y  3
   56, y 
1  4, y 0  2 0,25
Vậy, max y  y 3
   56 vµ min y  y0  2. x [  3  ; ] 1 x [  3  ; ] 1 0,25 b 1,0   Trên nửa khoảng  2 x ;  0 , ta có y '   , 2 x  2 2 x  2 0,25
y '  0  x  2  0,25 BBT 0,25 3 1
Vậy max y  y  2   
vµ min y  y0  . 0,25 x (  ; ] 0 x (  ; ] 6 0 2 3 2,0
Tập xác định: D  \ 1,   3 . x 1 x 1 0,5 Ta có: lim y  lim
 , lim y  lim     2   2 x 1  x 1    x 3  x 3 x 2x 3  x  2x  3
Do đó, hai đường thẳng x 1, x  3
 là hai tiệm cận đứng của đồ thị hàm số. 0,5 x 1
Mặt khác: lim y  lim  0. 0,5 2 x
x x  2x  3
Suy ra, đường thẳng y  0 là tiệm cận ngang của đồ thị hàm số. 0,5 4 4a/4b 2,0
Xét hàm số f (x)  5  x  1 x
Tập xác định: D   1  ;5
Hàm số liên tục trên đoạn [ 1  ;5]. 0,5
Bài toán trở thành, tìm m để phương trình f (x)  m có nghiệm thuộc [ 1  ;5]
 min f (x)  m  max f (x) [ 1  ;5] [ 1  ;5] 4a Ta có: 1 1 f '(x)     0, x  ( 1  ;5) 2 5  x 2 1 x 0,5
Suy ra, hàm số nghịch biến trên khoảng ( 1  ;5) .
Suy ra: max f (x)  f ( 1
 )  6; min f (x)  f (5)   6. 0,5 [ 1  ;5] [ 1  ;5]
Vậy:  6  m  6 . 0,5
Tập xác định: D  . 2 2
y '  3x  8x  m 1. 0,5
Đồ thị hàm số có hai điểm cực trị nằm về hai phía so với trục tung k.v.c.k phương trình 2 2
y '  3x  8x  m 1  0 có hai nghiệm phân biệt x , x thỏa 1 2 0,5 4b x  0  x 1 2 2 m 1   0 0,5 3  1
  m 1. Vậy m 1  ;  1 0,5
Lưu ý: Nếu học sinh làm bài không theo cách nêu trong đáp án mà vẫn đúng thì cho đủ điểm
từng phần tương ứng. Hết
TRƯỜNG THPT TRẦN VĂN KỶ
KIỂM TRA ĐỊNH KỲ, NĂM HỌC 2012  2013 TỔ TOÁN
MÔN: GIẢI TÍCH _ 12 _CHƯƠNG I Thời gian là m bài: 45 phút ĐỀ SỐ 2
ĐÁP ÁN VÀ THANG ĐIỂM
(Đáp án và thang điểm này gồm 02 trang) Câu Ý Đáp án Điểm 1 2
Tập xác định: D  \   2 . 0,5 7 y '  . 2 (x  0,5 2)
y '  0 với mọi x  . D 0,5
Vậy hàm số nghịch biến trên mỗi khoảng ( ; 2  ) vµ ( 2  ; ). 0,5 2 2,0
Tập xác định: D  . 3 0,5
y '  4x 16 . x
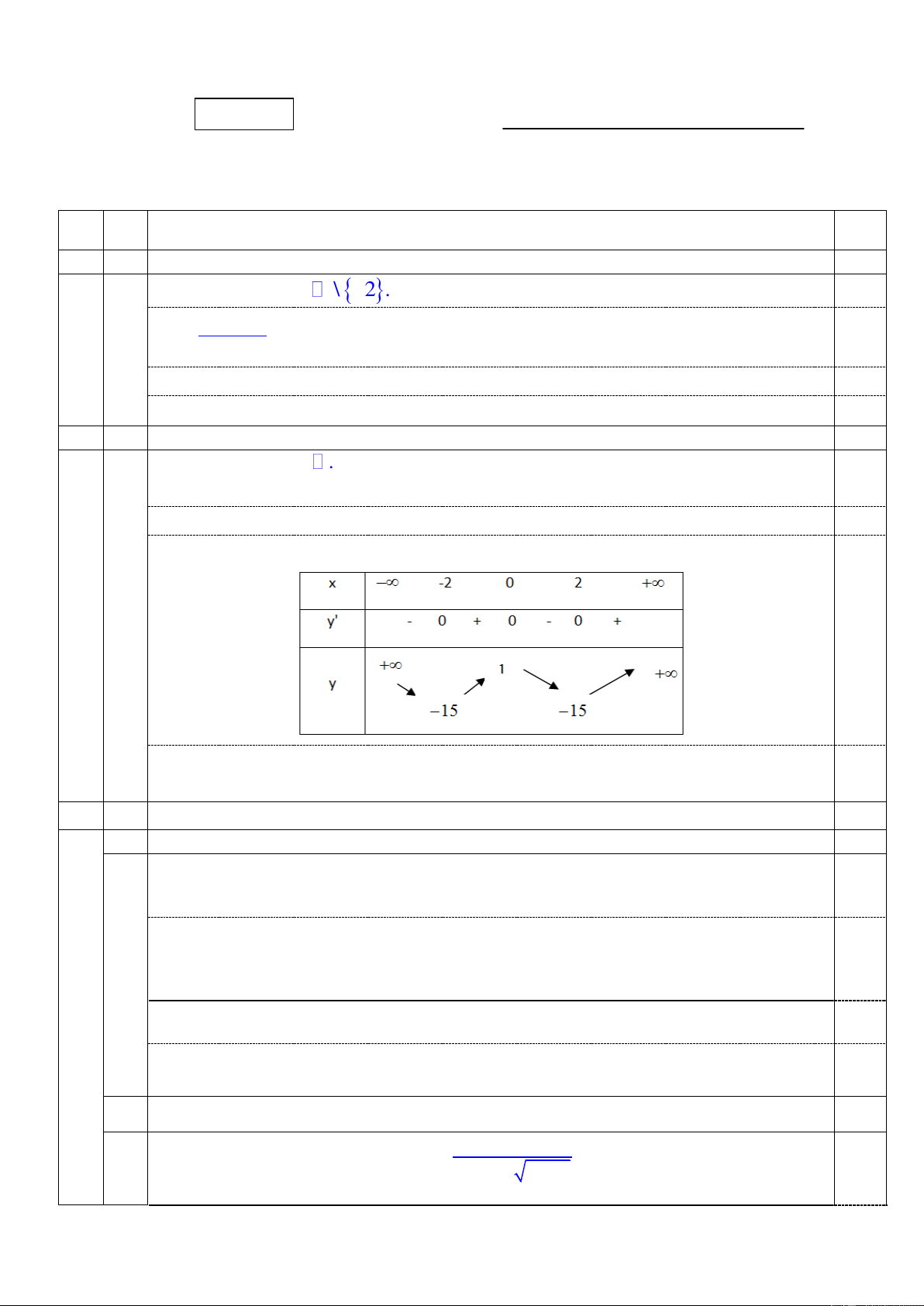
y '  0  x  0 hoÆ c x  2  . 0,5 Bảng biến thiên 0,5
Vậy, hàm số đạt cực đại tại x  0, giá trị cực đại y(0) 1. Hàm số đạt cực tiểu tại các điểm 0,5 x  2,
 giá trị cực tiểu y( 2  )  1  5. 3 2,0 a 1,0
Hàm số liên tục trên đoạn [ 3  ; ] 0 0,25 Ta có: 2 y '  3  x  3. x   1 lo¹ i  y '  0   .    0,25 x 1 y  3
  17, y  1  3  , y 0  1  0,25
Vậy, max y  y 
3 17 vµ min y  y  1  3  . x [  3  ;0] x [  3  ;0] 0,25 b 1,0   Trên nửa khoảng  4 2x ;  1 , ta có y '  ,
 2x 4 2x 4 0,25
y '  0  x  2  0,25 BBT 0,25 4 1
Vậy max y  y  2   
vµ min y  y  1  . 0,25 x (  ; ] 1 x (  ; ] 8 1 5 4 2,0
Tập xác định: D  \ 1,  2 . x  3 x  3 0,5 Ta có: lim y  lim   ,  lim y  lim     2   2 x 1  x 1    x2 x2 x 3x 2 x  3x  2
Do đó, hai đường thẳng x 1, x  2 là hai tiệm cận đứng của đồ thị hàm số. 0,5 x  3
Mặt khác: lim y  lim  0. 0,5 2 x
x x  3x  2
Suy ra, đường thẳng y  0 là tiệm cận ngang của đồ thị hàm số. 0,5 5 2,0
Xét hàm số f (x)  3 x  2  x . Tập xác định: D   3  ;2
Hàm số liên tục trên đoạn [ 3  ;2]. Bài toán trở thành, tìm 0,5
m để phương trình f (x)  m có nghiệm thuộc [ 3  ;2]
 min f (x)  m  max f (x) [ 3  ;2] [ 3  ;2] 5a Ta có: 1 1 f '(x)    0, x  ( 3  ;2) 2 3  x 2 2  x 0,5
Suy ra, hàm số đồng biến trên khoảng ( 3  ;2) .
Suy ra: max f (x)  f (2)  5; min f (x)  f ( 3  )   5. 0,5 [ 3  ;2] [ 3  ;2]
Vậy:  5  m  5 . 0,5
Tập xác định: D  . 2 2
y '  6x  2x 1 m . 0,5
Đồ thị hàm số có hai điểm cực trị nằm về hai phía so với trục tung k.v.c.k phương trình 0,5 2 2
y '  6x  2x 1 m .  0 có hai nghiệm phân biệt x , x thỏa x  0  x 1 2 1 2 5b 2 1  m   0 0,5 6 m  1    . Vậy m ;    1  1;. m 1 0,5
Lưu ý:Nếu học sinh làm bài không theo cách nêu trong đáp án mà vẫn đúng thì cho đủ điểm
từng phần tương ứng. Hết