Đề kiểm tra Giải tích 12 chương 2 (Mũ – Logarit) trường THPT chuyên Huỳnh Mẫn Đạt – Kiên Giang

Đề kiểm tra Giải tích 12 chương 2 trường THPT chuyên Huỳnh Mẫn Đạt – Kiên Giang gồm 6 mã đề, mỗi mã đề gồm 30 câu trắc nghiệm, nội dung kiểm tra thuộc chương lũy thừa, mũ và logarit.

18 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

24 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Mã đề thi 197 - Trang số : 1
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT CHUYÊN HUỲNH MẪN ĐẠT
---------------
KIỂM TRA TOÁN 12
BÀI THI: TOÁN 12 CH, CB, NC
(Th
ờ
i gian làm bài: 45 phút)
MÃ ĐỀ THI: 197
Họ tên thí sinh:.................................................SBD:.........................
Câu 1: Quan sát đồ thị, cho biết đồ thị đó có thể là của hàm nào sau đây:
A.
(1)
x
ya a
B.
(0 1)
x
ya a
C.
log ( 1)
b
yxb
D.
log (0 1)
b
yxb
Câu 2: Cho số thực
x
thỏa mãn
2016log 2016x
. Vậy giá trị
x
là:
A. 1 B. 5 C. 10 D. 0
Câu 3: Đặt ln 2a và ln 5b . Hãy biểu diễn ln 200 theo a và b .
A.
32ba
B.
32ab
C.
6ab
D.
32ab
Câu 4: Hãy chọn mệnh đề đúng:
A.
2
; 2 , log 4 log( 2) log( 2).xxxx
B. Với mọi
0x
,
22
93 33
1
log 3log 2 0 log 3log 2 0
2
xx xx .
C. Cho số
a
dương khác 1 và
0x
:
log ( 2 ) log 2 log ( )
aaa
x
x
.
D. Với mọi
x
thỏa
2
(1)0x  , ta có:
2
4444
log ( 1) 2log 5 log ( 1) log 5 1 5 6xxxx .
Câu 5: Thu gọn biểu thức:
32
.?xx
A.
5
x
B.
5
x
C.
5
x
D.
x
Câu 6: Cho các mệnh đề sau
i. Với
12
,0xx thì

2
12 12
1
5log 5log 5 log log 5log
x
xx xx
 .
ii. Cho
123
,, 0xxx
và
01a
, ta có:
123 1 2 3
log ( ) log .log .log
aaaa
x
xx x x x .
iii.
2
66
(2 .3)
11
log 12 log 12 (1 log 2)
22

iv. Cho các số thực dương
,ab
, với
1a
, ta có:
2
11
log ( ) log
22
a
a
ab b .
Số mệnh đề sai là:
A. 4 B. 1 C. 2 D. 3
Mã đề thi 197 - Trang số : 2
Câu 7: Đạo hàm của hàm số
2
cos
() 2
x
fx
là hàm nào sau đây:
A.
2
cos
sin(2 ).2 .ln 2
x
x
B.
2
cos
sin(2 ).2 .ln 2
x
x
C.
2
cos
sin(2 ).2
x
x
D.
2
cos 1
sin(2 ).2
x
x
Câu 8: Đạo hàm của hàm số
2
()
2
x
x
fx
là hàm nào sau đây:
A.
2
2.2 2.ln2
2
xx
x
xx
B.
31
2
2.2 2
2
xx
x
xx
C.
(2 ln 2)
2
x
xx
D. Đáp án khác
Câu 9: Hãy cho biết giá trị của
/
(2)g
nếu
2
() ln 1gx x
:
A.
2
5
B.
0,8
C.
2
3
D.
0,65
Câu 10: Cho hai số thực
a
và
b
, với
01ab
. Khẳng định nào dưới đây là khẳng định đúng?
A.
log 1 log
ab
ba
B.
1log log
ab
ba
C.
1log log
ba
ab
D. log 1 log
ba
ab
Câu 11: Cho biết tập xác định của hàm số
5
2
() 4fx x
 .
A.
(;2)(2;) 
B.
\2
C.
2; 2
D.
Câu 12: Tìm điều kiện của
x
để hàm số
2
2
log ( 2)yx
xác định.
A.
2x
B.
2x
C.
x
D.
2x
Câu 13: Tìm điều kiện của
x
để hàm số
2
2
log
x
y
x
xác định.
A.
1
0,
2
xx
B.
0, 2xx
C.
2x
D.
02x
Câu 14: Viết dạng lũy thừa số mũ hữu tỉ biểu thức
3
aa
với
0a
.
A.
5
6
a
B.
1
6
a
C.
1
12
a
D.
2
3
a
Câu 15: Thu gọn biểu thức,
3
4
2
(0)
a
Aa
a

.
A.
5
4
a
B.
5
2
a
C.
3
8
a
D.
11
4
a
Câu 16: Cho 0, 1aa. Đơn giản biểu thức
23
4
log
a
B
aa .
A.
11
4
a
B.
3
2
a
C.
11
4
D.
3
2
Câu 17: Số nghiệm của phương trình
33
log (2 1) log ( 3) 1xx
là:
A. Vô nghiệm. B. Một. C. Hai. D. Ba.
Câu 18: Gọi
0
x
là nghiệm của phương trình
1
52.515
xx

. Hãy chọn nhận xét đúng.
A.
0
0x
B.
0
01x
C.
0
(1; 2)x
D.
0
1
2
x
Câu 19: Giải phương trình
345
x
xx

.
Mã đề thi 197 - Trang số : 3
A.
2.x
B.
3.x
C.
0.x
D.
2x 
.
Câu 20: Gọi
0
x
là nghiệm của phương trình

42
1
log 1 2log
2
x . Hãy chọn nhận xét đúng.
A.
0
x
là số tự nhiên. B.
0
x
là số vô tỷ. C.
0
x
là số nguyên âm. D.
0
x
là số hữu tỷ dương.
Câu 21: Giá trị lớn nhất của hàm số
() ln(1 2)
x
f
xe x
trên đoạn
0; 2
bằng:
A.
0.
B.
ln 3e
C.
2
ln 5e
D.
2
ln 6e
Câu 22: Hãy cho biết số nghiệm của phương trình
2
3
3
log ( 1) log (2 1) 0xx
.
A. Vô nghiệm. B. Một. C. Hai. D. Bốn
Câu 23: Tìm tất cả những giá trị
m
để phương trình
2
2
2
log 8log 8 4 0xxm
vô nghiệm trên đoạn
1; 4
.
A.
0m
hoặc
1
2
m
B.
0m
hoặc
1
2
m
C.
0m
D.
1
2
m 
hoặc
1
2
m
Câu 24: Cho phương trình
222
2
log 9 log log 3
.3
x
xx x
. Với điều kiện
x
thỏa mãn, một trong những cách giải
phương trình trên là bước đầu đặt
2
logtx
, thay vào phương trình ban đầu, trở thành phương trình theo
ẩn
t
hoàn toàn. Hãy giải phương trình tìm
t
.
A.
1
2
t
B.
0t
C.
1.t
D.
4t
Câu 25: Giá trị nhỏ nhất của hàm số
2
() 4ln(1 )
f
xx x
trên đoạn

3; 0
là giá trị nào sau đây?
A.
14ln2.
B. 0. C.
94ln4
D.
14ln3
Câu 26: Một chiếc ô tô mới mua năm 2016 với giá
900
triệu đồng. Cứ sau mỗi năm, giá chiếc ô tô này bị
giảm
10%
.Hỏi đến năm 2020, giá chiếc ô tô này là bao nhiêu?
A.
590.490.000
đồng B.
656.100.000
đồng C.
864.536409
đồng D.
531.441.000
đồng
Câu 27: Số vi khuẩn trong ống nghiệm ban đầu có 100 con, chỉ sau hai giờ đã là 4000 con. Biết số lượng
vi khuẩn tăng trong mỗi giờ theo một tỷ lệ không đổi. Hãy ước lượng sau năm giờ (tính từ ban đầu có 100
con) số vi khuẩn sẽ có, gấp khoảng bao nhiêu lần số vi khuẩn ban đầu (chọn đáp án gần đúng nhất).
A. Gấp khoảng 9.000 lần . B. Gấp khoảng 11.000 lần.
C. Gấp khoảng 12.000 lần. D. Gấp khoảng 10.000 lần.
Mã đề thi 197 - Trang số : 4
Câu 28: Quan sát đồ thị, cho biết đồ thị đó có thể biểu diễn cho hàm số nào?
A.
1
2
x
y
B.
31
x
y 
C.
21
x
y 
D.
2
2yx
.
Câu 29: Trong các mệnh đề sau, cho biết có bao nhiêu mệnh đề sai:
i. Đồ thị của hai hàm số
x
ya
và
log
a
yx
(với
01a
) đối xứng nhau qua đường thẳng
yx
.
ii. Với
1a
, ta có đồ thị hai hàm số
x
ya
và
1
x
y
a
đối xứng nhau qua trục tung.
iii. Một tiệm cận của đồ thị hàm số
log (0 1)
a
yxa
có phương trình là
0
y
.
iv. Đồ thị hàm số
lnyx
có 2 nhánh đối xứng nhau qua trục tung.
A. Một. B. Hai. C. Ba. D. Bốn.
Câu 30: Đồ thị ở hình vẽ biểu diễn cho hàm số nào sau đây:
A.
2
1logyx
B.
2
1logyx
C.
2
log ( 1)yx
D.
1
2
4
x
y

.
----------------- Hết -----------------
Mã đề thi 320 - Trang số : 1
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT CHUYÊN HUỲNH MẪN ĐẠT
---------------
KIỂM TRA TOÁN 12
BÀI THI: TOÁN 12 CH, CB, NC
(Th
ờ
i gian làm bài: 45 phút)
MÃ ĐỀ THI: 320
Họ tên thí sinh:.................................................SBD:.........................
Câu 1: Quan sát đồ thị, cho biết đồ thị đó có thể biểu diễn cho hàm số nào?
A.
1
2
x
y
B.
21
x
y 
C.
31
x
y 
D.
2
2yx
.
Câu 2: Thu gọn biểu thức:
32
.?xx
A.
5
x
B.
5
x
C.
x
D.
5
x
Câu 3: Đặt ln 2a và ln 5b . Hãy biểu diễn ln 200 theo a và b .
A.
32ba B.32ab C. 6ab D. 32ab
Câu 4: Trong các mệnh đề sau, cho biết có bao nhiêu mệnh đề sai:
i. Đồ thị của hai hàm số
x
ya
và
log
a
yx
(với
01
a
) đối xứng nhau qua đường thẳng
yx
.
ii. Với
1a
, ta có đồ thị hai hàm số
x
ya và
1
x
y
a
đối xứng nhau qua trục tung.
iii. Một tiệm cận của đồ thị hàm số log (0 1)
a
yxa có phương trình là 0y .
iv. Đồ thị hàm số
lnyx
có 2 nhánh đối xứng nhau qua trục tung.
A. Ba. B. Bốn. C. Một. D. Hai.
Câu 5: Hãy cho biết giá trị của
/
(2)g
nếu
2
() ln 1gx x
:
A.
0,8
B.
0,65
C.
2
3
D.
2
5
Câu 6: Viết dạng lũy thừa số mũ hữu tỉ biểu thức
3
aa
với
0
a
.
A.
1
6
a
B.
2
3
a
C.
1
12
a
D.
5
6
a
Câu 7: Cho phương trình
222
2
log 9 log log 3
.3
x
xx x
. Với điều kiện
x
thỏa mãn, một trong những cách giải
phương trình trên là bước đầu đặt
2
logtx
, thay vào phương trình ban đầu, trở thành phương trình theo
ẩn
t
hoàn toàn. Hãy giải phương trình tìm
t
.
Mã đề thi 320 - Trang số : 2
A.
4t
B.
1
2
t
C.
0t
D.
1.t
Câu 8: Gọi
0
x
là nghiệm của phương trình
1
52.515
xx

. Hãy chọn nhận xét đúng.
A.
0
0x
B.
0
1
2
x
C.
0
(1; 2)x
D.
0
01x
Câu 9: Đồ thị ở hình vẽ biểu diễn cho hàm số nào sau đây:
A.
2
1logyx
B.
1
2
4
x
y

. C.
2
1logyx
D.
2
log ( 1)yx
Câu 10: Thu gọn biểu thức
3
4
2
a
A
a
,
(0)a
.
A.
5
4
a
B.
11
4
a
C.
5
2
a
D.
3
8
a
Câu 11: Tìm điều kiện của
x
để hàm số
2
2
log ( 2)yx
xác định.
A.
2x
B.
x
C.
2x
D.
2x
Câu 12: Cho 0, 1aa. Đơn giản biểu thức
23
4
log
a
Baa
A.
11
4
a
B.
11
4
C.
3
2
a
D.
3
2
Câu 13: Đạo hàm của hàm số
2
()
2
x
x
fx là hàm nào sau đây:
A.
2
2.2 2.ln2
2
xx
x
xx
B.
31
2
2.2 2
2
xx
x
xx
C.
(2 ln 2)
2
x
xx
D. Đáp án khác
Câu 14: Tìm điều kiện của
x
để hàm số
2
2
log
x
y
x xác định.
A.
2x
B.
02x
C.
1
0,
2
xx D.
0, 2xx
Câu 15: Cho biết tập xác định của hàm số
5
2
() 4fx x
 .
A.
\2
B.
C.
2; 2
D.
(;2)(2;) 
Mã đề thi 320 - Trang số : 3
Câu 16: Cho các mệnh đề sau
i. Với
12
,0xx
thì

2
12 12
1
5log 5log 5 log log 5log
x
xx xx

ii. Cho
123
,, 0xxx
và
01a
, ta có:
123 1 2 3
log ( ) log .log .log
aaaa
x
xx x x x
iii.
2
66
(2 .3)
11
log 12 log 12 (1 log 2)
22

.
iv. Cho các số thực dương
,
ab
với
1a
, ta có:
2
11
log ( ) log
22
a
a
ab b
.
Số mệnh đề sai là:
A. 1 B. 3 C. 2 D. 4
Câu 17: Đạo hàm của hàm số
2
cos
() 2
x
fx
là hàm nào sau đây:
A.
2
cos
sin(2 ).2
x
x
B.
2
cos
sin(2 ).2 .ln 2
x
x
C.
2
cos 1
sin(2 ).2
x
x
D.
2
cos
sin(2 ).2 .ln 2
x
x
Câu 18: Hãy chọn mệnh đề đúng:
A. Cho số
a
dương khác 1 và
0x
:
log ( 2 ) log 2 log ( )
aaa
x
x
.
B. Với mọi
0x
,
22
93 33
1
log 3log 2 0 log 3log 2 0
2
xx xx 
C.
2
; 2 , log 4 log( 2) log( 2).xxxx
D. Với mọi
x
thỏa
2
(1)0x 
, ta có:
2
4444
log ( 1) 2log 5 log ( 1) log 5 1 5 6xxxx
.
Câu 19: Giải phương trình
345
x
xx

.
A.
2x 
. B.
2.x
C.
3.x
D.
0.x
Câu 20: Số vi khuẩn trong ống nghiệm ban đầu có 100 con, chỉ sau hai giờ đã là 4000 con. Biết số lượng
vi khuẩn tăng trong mỗi giờ theo một tỷ lệ không đổi. Hãy ước lượng sau năm giờ (tính từ ban đầu có 100
con) số vi khuẩn sẽ có, gấp khoảng bao nhiêu lần số vi khuẩn ban đầu (chọn đáp án gần đúng nhất).
A. Gấp khoảng 11.000 lần. B. Gấp khoảng 12.000 lần.
C. Gấp khoảng 10.000 lần. D. Gấp khoảng 9.000 lần .
Câu 21: Cho hai số thực
a
và
b
, với
01ab
. Khẳng định nào dưới đây là khẳng định đúng?
A.
1log log
ab
ba
B.
1log log
ba
ab
C. log 1 log
ba
ab D.
log 1 log
ab
ba
Câu 22: Hãy cho biết số nghiệm của phương trình
2
3
3
log ( 1) log (2 1) 0xx
.
A. Vô nghiệm. B. Hai. C. Một. D. Bốn
Câu 23: Một chiếc ô tô mới mua năm 2016 với giá
900
triệu đồng. Cứ sau mỗi năm, giá chiếc ô tô này bị
giảm
10%
.Hỏi đến năm 2020, giá chiếc ô tô này là bao nhiêu?
A.
864.536409
đồng B.
656.100.000
đồng C. 531.441.000 đồng D.
590.490.000
đồng
Câu 24: Cho số thực
x
thỏa mãn
2016log 2016x
. Vậy giá trị
x
là:
A. 5 B. 1 C. 0 D. 10
Câu 25:
Gọi
0
x
là nghiệm của phương trình

42
1
log 1 2log
2
x
. Hãy chọn nhận xét đúng.
A.
0
x
là số vô tỷ. B.
0
x
là số tự nhiên. C.
0
x
là số hữu tỷ dương. D.
0
x
là số nguyên âm.
Mã đề thi 320 - Trang số : 4
Câu 26: Số nghiệm của phương trình
33
log (2 1) log ( 3) 1xx
là:
A. Vô nghiệm. B. Hai. C. Ba. D. Một.
Câu 27: Giá trị lớn nhất của hàm số
() ln(1 2)
x
f
xe x
trên đoạn
0; 2
bằng:
A.
2
ln 5e
B.
ln 3e
C.
0.
D.
2
ln 6e
Câu 28: Giá trị nhỏ nhất của hàm số
2
() 4ln(1 )
f
xx x
trên đoạn

3; 0
là giá trị nào sau đây?
A.
94ln4
B. 0. C.
14ln2.
D.
14ln3
Câu 29: Tìm tất cả những giá trị
m
để phương trình
2
2
2
log 8log 8 4 0xxm
vô nghiệm trên đoạn
1; 4
.
A.
1
2
m 
hoặc
1
2
m
B.
0m
hoặc
1
2
m
C.
0m
hoặc
1
2
m
D.
0m
Câu 30: Quan sát đồ thị, cho biết đồ thị đó có thể là của hàm nào sau đây:
A.
(0 1)
x
ya a
B.
log ( 1)
b
yxb
C.
(1)
x
ya a
D.
log (0 1)
b
yxb
----------------- Hết -----------------
Mã đề thi 443 - Trang số : 1
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT CHUYÊN HUỲNH MẪN ĐẠT
---------------
KIỂM TRA TOÁN 12
BÀI THI: TOÁN 12 CH, CB, NC
(Th
ờ
i gian làm bài: 45 phút)
MÃ ĐỀ THI: 443
Họ tên thí sinh:.................................................SBD:.........................
Câu 1: Quan sát đồ thị, cho biết đồ thị đó có thể là của hàm nào sau đây:
A.
(1)
x
ya a
B.
(0 1)
x
ya a
C.
log ( 1)
b
yxb
D.
log (0 1)
b
yxb
Câu 2: Số vi khuẩn trong ống nghiệm ban đầu có 100 con, chỉ sau hai giờ đã là 4000 con. Biết số lượng vi
khuẩn tăng trong mỗi giờ theo một tỷ lệ không đổi. Hãy ước lượng sau năm giờ (tính từ ban đầu có 100
con) số vi khuẩn sẽ có, gấp khoảng bao nhiêu lần số vi khuẩn ban đầu (chọn đáp án gần đúng nhất).
A. Gấp khoảng 9.000 lần . B. Gấp khoảng 12.000 lần.
C. Gấp khoảng 10.000 lần. D. Gấp khoảng 11.000 lần.
Câu 3: Số nghiệm của phương trình
33
log (2 1) log ( 3) 1xx
là:
A. Một. B. Ba. C. Hai. D. Vô nghiệm.
Câu 4: Quan sát đồ thị, cho biết đồ thị đó có thể biểu diễn cho hàm số nào?
A.
31
x
y 
B.
2
2yx
. C.
21
x
y 
D.
1
2
x
y
Câu 5: Viết dạng lũy thừa số mũ hữu tỉ biểu thức
3
aa
với
0a
.
A.
2
3
a
B.
5
6
a
C.
1
6
a
D.
1
12
a
Câu 6: Một chiếc ô tô mới mua năm 2016 với giá
900
triệu đồng. Cứ sau mỗi năm, giá chiếc ô tô này bị
Mã đề thi 443 - Trang số : 2
giảm
10%
.Hỏi đến năm 2020, giá chiếc ô tô này là bao nhiêu?
A.
590.490.000
đồng B. 531.441.000 đồng C.
864.536409
đồng D.
656.100.000
đồng
Câu 7: Giá trị lớn nhất của hàm số
() ln(1 2)
x
f
xe x
trên đoạn
0; 2
bằng:
A.
0.
B.
2
ln 6e
C.
2
ln 5e
D.
ln 3e
Câu 8: Cho số thực
x
thỏa mãn
2016log 2016
x
. Vậy giá trị
x
là:
A. 0 B. 1 C. 5 D. 10
Câu 9: Gọi
0
x
là nghiệm của phương trình

42
1
log 1 2log
2
x . Hãy chọn nhận xét đúng.
A.
0
x
là số vô tỷ. B.
0
x
là số nguyên âm. C.
0
x
là số hữu tỷ dương. D.
0
x
là số tự nhiên.
Câu 10: Thu gọn biểu thức:
32
.?xx
A.
5
x
B.
5
x
C.
5
x
D.
x
Câu 11: Thu gọn biểu thức
3
4
2
a
A
a
,
(0)
a
.
A.
5
4
a
B.
5
2
a
C.
3
8
a
D.
11
4
a
Câu 12: Hãy chọn mệnh đề đúng:
A.
2
; 2 , log 4 log( 2) log( 2).xxxx
B. Cho số
a
dương khác 1 và 0x : log ( 2 ) log 2 log ( )
aaa
x
x .
C. Với mọi
x
thỏa
2
(1)0x , ta có:
2
4444
log ( 1) 2log 5 log ( 1) log 5 1 5 6xxxx .
D. Với mọi
0x
,
22
93 33
1
log 3log 2 0 log 3log 2 0
2
xx xx .
Câu 13: Tìm điều kiện của
x
để hàm số
2
2
log
x
yx xác định.
A.
0, 2xx
B.
02x
C.
2x
D.
1
0,
2
xx
Câu 14: Gọi
0
x
là nghiệm của phương trình
1
52.515
xx

. Hãy chọn nhận xét đúng.
A.
0
0x
B.
0
(1; 2)x
C.
0
1
2
x
D.
0
01x
Câu 15: Giá trị nhỏ nhất của hàm số
2
() 4ln(1 )
f
xx x
trên đoạn

3; 0
là giá trị nào sau đây?
A.
14ln2.
B.
94ln4
C.
14ln3
D. 0.
Câu 16: Hãy cho biết giá trị của
/
(2)g
nếu
2
() ln 1gx x
:
A.
2
3
B.
0,8
C.
2
5
D.
0,65
Câu 17: Đặt ln 2a và ln5b . Hãy biểu diễn ln 200 theo a và b .
A.
32ba B. 32ab C. 6ab D.32ab
Câu 18: Cho phương trình
222
2
log 9 log log 3
.3
x
xx x
. Với điều kiện
x
thỏa mãn, một trong những cách giải
phương trình trên là bước đầu đặt
2
logtx
, thay vào phương trình ban đầu, trở thành phương trình theo
Mã đề thi 443 - Trang số : 3
ẩn
t
hoàn toàn. Hãy giải phương trình tìm
t
.
A.
0t
B.
1.t
C.
4t
D.
1
2
t
Câu 19: Cho các mệnh đề sau
i. Với
12
,0xx thì

2
12 12
1
5log 5log 5 log log 5log
x
xx xx
 .
ii. Cho
123
,, 0xxx
và
01a
, ta có:
123 1 2 3
log ( ) log .log .log
aaaa
x
xx x x x
iii.
2
66
(2 .3)
11
log 12 log 12 (1 log 2)
22

iv. Cho các số thực dương
,ab
, với
1a
, ta có:
2
11
log ( ) log
22
a
a
ab b .
Số mệnh đề sai là:
A. 1 B. 2 C. 3 D. 4
Câu 20: Tìm tất cả những giá trị
m
để phương trình
2
2
2
log 8log 8 4 0xxm
vô nghiệm trên đoạn
1; 4
.
A.
0m
hoặc
1
2
m
B.
0m
hoặc
1
2
m
C.
0m
D.
1
2
m 
hoặc
1
2
m
Câu 21: Hãy cho biết số nghiệm của phương trình
2
3
3
log ( 1) log (2 1) 0xx
.
A. Hai. B. Bốn C. Một. D. Vô nghiệm.
Câu 22: Cho biết tập xác định của hàm số
5
2
() 4fx x

.
A.

2; 2
B.
C.
\2
D.
(;2)(2;) 
Câu 23: Giải phương trình
345
x
xx

.
A.
3.x
B.
2x 
. C.
2.x
D.
0.x
Câu 24: Đạo hàm của hàm số
2
cos
() 2
x
fx
là hàm nào sau đây:
A.
2
cos
sin(2 ).2 .ln 2
x
x
B.
2
cos
sin(2 ).2
x
x
C.
2
cos 1
sin(2 ).2
x
x
D.
2
cos
sin(2 ).2 .ln 2
x
x
Câu 25: Cho 0, 1aa. Đơn giản biểu thức
23
4
log
a
Baa .
A.
11
4
B.
3
2
a
C.
11
4
a
D.
3
2
Câu 26: Đạo hàm của hàm số
2
()
2
x
x
fx
là hàm nào sau đây:
A.
2
2.2 2.ln2
2
xx
x
xx
B.
31
2
2.2 2
2
xx
x
xx
C.
(2 ln 2)
2
x
xx
D. Đáp án khác
Câu 27: Cho hai số thực
a
và
b
, với
01ab
. Khẳng định nào dưới đây là khẳng định đúng?
A. log 1 log
ba
ab B.
log 1 log
ab
ba
C.
1log log
ab
ba
D.
1log log
ba
ab
Câu 28: Tìm điều kiện của
x
để hàm số
2
2
log ( 2)yx
xác định.
Mã đề thi 443 - Trang số : 4
A.
x
B.
2x
C.
2x
D.
2x
Câu 29: Trong các mệnh đề sau, cho biết có bao nhiêu mệnh đề sai:
i. Đồ thị của hai hàm số
x
ya
và
log
a
yx
(với
01a
) đối xứng nhau qua đường thẳng
y
x
.
ii. Với
1a
, ta có đồ thị hai hàm số
x
ya và
1
x
y
a
đối xứng nhau qua trục tung.
iii. Một tiệm cận của đồ thị hàm số
log (0 1)
a
yxa
có phương trình là
0y
.
iv. Đồ thị hàm số
lnyx
có 2 nhánh đối xứng nhau qua trục tung.
A. Một. B. Bốn. C. Ba. D. Hai.
Câu 30: Đồ thị ở hình vẽ biểu diễn cho hàm số nào sau đây:
A.
2
log ( 1)yx
B.
1
2
4
x
y

. C.
2
1logyx
D.
2
1logyx
----------------- Hết -----------------
Mã đề thi 566 - Trang số : 1
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT CHUYÊN HUỲNH MẪN ĐẠT
---------------
KIỂM TRA TOÁN 12
BÀI THI: TOÁN 12 CH, CB, NC
(Th
ờ
i gian làm bài: 45 phút)
MÃ ĐỀ THI: 566
Họ tên thí sinh:.................................................SBD:.........................
Câu 1: Cho các mệnh đề sau
i. Với
12
,0xx thì

2
12 12
1
5log 5log 5 log log 5log
x
xx xx
 .
ii. Cho
123
,, 0xxx
và
01a
, ta có:
123 1 2 3
log ( ) log .log .log
aaaa
x
xx x x x
iii.
2
66
(2 .3)
11
log 12 log 12 (1 log 2)
22

iv. Cho các số thực dương
,ab
, với
1a
, ta có:
2
11
log ( ) log
22
a
a
ab b
.
Số mệnh đề sai là:
A. 4 B. 2 C. 3 D. 1
Câu 2: Số vi khuẩn trong ống nghiệm ban đầu có 100 con, chỉ sau hai giờ đã là 4000 con. Biết số lượng vi
khuẩn tăng trong mỗi giờ theo một tỷ lệ không đổi. Hãy ước lượng sau năm giờ (tính từ ban đầu có 100
con) số vi khuẩn sẽ có, gấp khoảng bao nhiêu lần số vi khuẩn ban đầu (chọn đáp án gần đúng nhất).
A. Gấp khoảng 9.000 lần . B. Gấp khoảng 12.000 lần.
C. Gấp khoảng 10.000 lần. D. Gấp khoảng 11.000 lần.
Câu 3: Tìm điều kiện của
x
để hàm số
2
2
log ( 2)yx
xác định.
A.
2x
B.
2x
C.
x
D.
2x
Câu 4: Viết dạng lũy thừa số mũ hữu tỉ biểu thức
3
aa
với
0a
.
A.
5
6
a
B.
2
3
a
C.
1
6
a
D.
1
12
a
Câu 5: Trong các mệnh đề sau, cho biết có bao nhiêu mệnh đề sai:
i. Đồ thị của hai hàm số
x
ya
và
log
a
yx
(với
01a
) đối xứng nhau qua đường thẳng
yx
.
ii. Với
1a
, ta có đồ thị hai hàm số
x
ya
và
1
x
y
a
đối xứng nhau qua trục tung.
iii. Một tiệm cận của đồ thị hàm số log (0 1)
a
yxa có phương trình là 0y .
iv. Đồ thị hàm số
lnyx
có 2 nhánh đối xứng nhau qua trục tung.
A. Bốn. B. Ba. C. Một. D. Hai.
Câu 6: Cho phương trình
222
2
log 9 log log 3
.3
x
xx x
. Với điều kiện
x
thỏa mãn, một trong những cách giải
phương trình trên là bước đầu đặt
2
logtx
, thay vào phương trình ban đầu, trở thành phương trình theo
ẩn
t
hoàn toàn. Hãy giải phương trình tìm
t
.
A.
4t
B.
1.t
C.
1
2
t
D.
0t
Câu 7: Cho 0, 1aa. Đơn giản biểu thức
23
4
log
a
B
aa .
Mã đề thi 566 - Trang số : 2
A.
3
2
a
B.
11
4
a
C.
3
2
D.
11
4
Câu 8: Giải phương trình
345
x
xx

.
A.
0.x
B.
2x 
. C.
3.x
D.
2.x
Câu 9: Gọi
0
x
là nghiệm của phương trình
1
52.515
xx

. Hãy chọn nhận xét đúng.
A.
0
0x
B.
0
01x
C.
0
(1; 2)x
D.
0
1
2
x
Câu 10: Tìm điều kiện của
x
để hàm số
2
2
log
x
yx xác định.
A.
2x
B.
1
0,
2
xx C.
02x
D.
0, 2xx
Câu 11: Quan sát đồ thị, cho biết đồ thị đó có thể biểu diễn cho hàm số nào?
A.
21
x
y 
B.
1
2
x
y
C.
2
2yx
. D.
31
x
y 
Câu 12: Giá trị nhỏ nhất của hàm số
2
() 4ln(1 )
f
xx x
trên đoạn

3; 0
là giá trị nào sau đây?
A.
14ln2.
B.
94ln4
C.
14ln3
D. 0.
Câu 13: Số nghiệm của phương trình
33
log (2 1) log ( 3) 1xx
là:
A. Hai. B. Một. C. Vô nghiệm. D. Ba.
Câu 14: Đạo hàm của hàm số
2
cos
() 2
x
fx
là hàm nào sau đây:
A.
2
cos
sin(2 ).2
x
x
B.
2
cos
sin(2 ).2 .ln 2
x
x
C.
2
cos
sin(2 ).2 .ln 2
x
x
D.
2
cos 1
sin(2 ).2
x
x
Câu 15: Hãy chọn mệnh đề đúng:
A. Với mọi
0x
,
22
93 33
1
log 3log 2 0 log 3log 2 0
2
xx xx 
.
B.
2
; 2 , log 4 log( 2) log( 2).xxxx
C. Với mọi
x
thỏa
2
(1)0x
, ta có:
2
4444
log ( 1) 2log 5 log ( 1) log 5 1 5 6xxxx
.
D. Cho số a
dương khác 1 và 0x : log ( 2 ) log 2 log ( )
aaa
x
x .
Mã đề thi 566 - Trang số : 3
Câu 16: Cho hai số thực
a
và
b
, với
01ab
. Khẳng định nào dưới đây là khẳng định đúng?
A. log 1 log
ba
ab B.
1log log
ba
ab
C.
1log log
ab
ba
D.
log 1 log
ab
ba
Câu 17: Đặt
ln 2a
và
ln 5b
. Hãy biểu diễn
ln 200
theo
a
và
b
.
A.
32ba B.32ab C. 6ab D.32ab
Câu 18: Cho biết tập xác định của hàm số
5
2
() 4fx x
 .
A.

2; 2
B.
C.
\2
D.
(;2)(2;) 
Câu 19: Hãy cho biết giá trị của
/
(2)g
nếu
2
() ln 1gx x
:
A.
2
3
B.
0,65
C.
0,8
D.
2
5
Câu 20: Đồ thị ở hình vẽ biểu diễn cho hàm số nào sau đây:
A.
2
1logyx
B.
1
2
4
x
y

. C.
2
1logyx
D.
2
log ( 1)yx
Câu 21: Cho số thực
x
thỏa mãn
2016log 2016x
. Vậy giá trị
x
là:
A. 1 B. 10 C. 0 D. 5
Câu 22: Quan sát đồ thị, cho biết đồ thị đó có thể là của hàm nào sau đây:
A.
(0 1)
x
ya a
B.
log ( 1)
b
yxb
C.
(1)
x
ya a
D.
log (0 1)
b
yxb
Câu 23: Đạo hàm của hàm số
2
()
2
x
x
fx
là hàm nào sau đây:
Mã đề thi 566 - Trang số : 4
A.
2
2.2 2.ln2
2
xx
x
xx
B.
31
2
2.2 2
2
xx
x
xx
C.
(2 ln 2)
2
x
xx
D. Đáp án khác
Câu 24: Gọi
0
x
là nghiệm của phương trình

42
1
log 1 2log
2
x
. Hãy chọn nhận xét đúng.
A.
0
x
là số tự nhiên. B.
0
x
là số hữu tỷ dương. C.
0
x
là số vô tỷ. D.
0
x
là số nguyên âm.
Câu 25: Giá trị lớn nhất của hàm số
() ln(1 2)
x
f
xe x
trên đoạn
0; 2
bằng:
A.
0.
B.
2
ln 5e
C.
ln 3
e
D.
2
ln 6e
Câu 26: Thu gọn biểu thức:
32
.?xx
A.
5
x
B.
x
C.
5
x
D.
5
x
Câu 27: Hãy cho biết số nghiệm của phương trình
2
3
3
log ( 1) log (2 1) 0xx
.
A. Hai. B. Bốn C. Vô nghiệm. D. Một.
Câu 28: Thu gọn biểu thức
3
4
2
a
A
a
,
(0)
a
.
A.
3
8
a
B.
11
4
a
C.
5
2
a
D.
5
4
a
Câu 29: Tìm tất cả những giá trị
m
để phương trình
2
2
2
log 8log 8 4 0xxm
vô nghiệm trên đoạn

1; 4
.
A.
1
2
m 
hoặc
1
2
m
B.
0
m
hoặc
1
2
m
C.
0
m
hoặc
1
2
m
D.
0
m
Câu 30: Một chiếc ô tô mới mua năm 2016 với giá
900
triệu đồng. Cứ sau mỗi năm, giá chiếc ô tô này bị
giảm
10%
.Hỏi đến năm 2020, giá chiếc ô tô này là bao nhiêu?
A.
531.441.000
đồng B.
656.100.000
đồng C.
590.490.000
đồng D.
864.536409
đồng
----------------- Hết -----------------
Mã đề thi 689 - Trang số : 1
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT CHUYÊN HUỲNH MẪN ĐẠT
---------------
KIỂM TRA TOÁN 12
BÀI THI: TOÁN 12 CH, CB, NC
(Th
ờ
i gian làm bài: 45 phút)
MÃ ĐỀ THI: 689
Họ tên thí sinh:.................................................SBD:.........................
Câu 1: Thu gọn biểu thức:
32
.?xx
A.
5
x
B.
5
x
C.
5
x
D.
x
Câu 2: Cho
0a
. Đơn giản biểu thức
23
4
log
a
Baa
A.
11
4
B.
11
4
a
C.
3
2
D.
3
2
a
Câu 3: Quan sát đồ thị, cho biết đồ thị đó có thể biểu diễn cho hàm số nào?
A.
21
x
y 
B.
31
x
y 
C.
2
2yx
. D.
1
2
x
y
Câu 4: Cho phương trình
222
2
log 9 log log 3
.3
x
xx x
. Với điều kiện
x
thỏa mãn, một trong những cách giải
phương trình trên là bước đầu đặt
2
logtx
, thay vào phương trình ban đầu, trở thành phương trình theo
ẩn
t
hoàn toàn. Hãy giải phương trình tìm
t
.
A.
1
2
t
B.
0t
C.
4t
D.
1.t
Câu 5: Tìm điều kiện của
x
để hàm số
2
2
log
x
y
x xác định.
A.
02x
B.
2x
C.
1
0,
2
xx D.
0, 2xx
Câu 6: Hãy cho biết số nghiệm của phương trình
2
3
3
log ( 1) log (2 1) 0xx .
A. Bốn B. Hai. C. Vô nghiệm. D. Một.
Câu 7: Viết dạng lũy thừa số mũ hữu tỉ biểu thức
3
aa
với
0a
.
A.
1
6
a
B.
5
6
a
C.
2
3
a
D.
1
12
a
Câu 8:
Hãy chọn mệnh đề đúng:
Mã đề thi 689 - Trang số : 2
A. Với mọi
x
thỏa
2
(1)0x 
, ta có:
2
4444
log ( 1) 2log 5 log ( 1) log 5 1 5 6xxxx
.
B. Cho số
a
dương khác 1 và
0x
:
log ( 2 ) log 2 log ( )
aaa
x
x
.
C. Với mọi
0x
,
22
93 33
1
log 3log 2 0 log 3log 2 0
2
xx xx 
.
D.
2
; 2 , log 4 log( 2) log( 2).xxxx
Câu 9: Đạo hàm của hàm số
2
()
2
x
x
fx là hàm nào sau đây:
A.
2
2.2 2.ln2
2
xx
x
xx
B.
31
2
2.2 2
2
xx
x
xx
C.
(2 ln 2)
2
x
xx
D. Đáp án khác
Câu 10: Hãy cho biết giá trị của
/
(2)g
nếu
2
() ln 1gx x
:
A.
0,8
B.
2
5
C.
2
3
D.
0,65
Câu 11: Cho số thực
x
thỏa mãn
2016log 2016
x
. Vậy giá trị
x
là:
A. 0 B. 5 C. 10 D. 1
Câu 12: Số nghiệm của phương trình
33
log (2 1) log ( 3) 1xx
là:
A. Vô nghiệm. B. Ba. C. Hai. D. Một.
Câu 13: Trong các mệnh đề sau, cho biết có bao nhiêu mệnh đề sai:
i. Đồ thị của hai hàm số
x
ya
và
log
a
yx
(với
01a
) đối xứng nhau qua đường thẳng
yx
.
ii. Với
1a
, ta có đồ thị hai hàm số
x
ya và
1
x
y
a
đối xứng nhau qua trục tung.
iii. Một tiệm cận của đồ thị hàm số log (0 1)
a
yxa có phương trình là
0y
.
iv. Đồ thị hàm số
lnyx có 2 nhánh đối xứng nhau qua trục tung.
A. Ba. B. Một. C. Hai. D. Bốn.
Câu 14: Đồ thị ở hình vẽ biểu diễn cho hàm số nào sau đây:
A.
2
log ( 1)yx
B.
2
1logyx
C.
2
1logyx
D.
1
2
4
x
y

.
Mã đề thi 689 - Trang số : 3
Câu 15: Một chiếc ô tô mới mua năm 2016 với giá
900
triệu đồng. Cứ sau mỗi năm, giá chiếc ô tô này bị
giảm
10%
.Hỏi đến năm 2020, giá chiếc ô tô này là bao nhiêu?
A.
590.490.000
đồng B.
656.100.000
đồng C.
531.441.000
đồng D.
864.536409
đồng
Câu 16: Đặt ln 2a và ln 5b . Hãy biểu diễn ln 200 theo a và b .
A.
32ba
B.
32ab
C.
6ab
D.
32ab
.
Câu 17: Giá trị nhỏ nhất của hàm số
2
() 4ln(1 )
f
xx x
trên đoạn

3; 0
là giá trị nào sau đây?
A.
14ln3
B.
94ln4
C. 0. D.
14ln2.
Câu 18: Giá trị lớn nhất của hàm số
() ln(1 2)
x
f
xe x
trên đoạn
0; 2
bằng:
A.
ln 3e
B.
0.
C.
2
ln 5e
D.
2
ln 6e
Câu 19: Gọi
0
x
là nghiệm của phương trình
1
52.515
xx

. Hãy chọn nhận xét đúng.
A.
0
(1; 2)x
B.
0
1
2
x
C.
0
01x
D.
0
0x
Câu 20: Tìm tất cả những giá trị
m
để phương trình
2
2
2
log 8log 8 4 0xxm
vô nghiệm trên đoạn
1; 4
.
A.
1
2
m 
hoặc
1
2
m
B.
0m
hoặc
1
2
m
C.
0m
hoặc
1
2
m
D.
0m
Câu 21: Cho các mệnh đề sau
i. Với
12
,0xx
thì

2
12 12
1
5log 5log 5 log log 5log
x
xx xx
 .
ii. Cho
123
,, 0xxx
và
01
a
, ta có:
123 1 2 3
log ( ) log .log .log
aaaa
x
xx x x x .
iii.
2
66
(2 .3)
11
log 12 log 12 (1 log 2)
22
.
iv. Cho các số thực dương
,ab
, với
1
a
, ta có:
2
11
log ( ) log
22
a
a
ab b
.
Số mệnh đề sai là:
A. 3 B. 1 C. 4 D. 2
Câu 22: Giải phương trình
345
x
xx

.
A.
0.x
B.
2.x
C.
2x 
. D.
3.x
Câu 23: Gọi
0
x
là nghiệm của phương trình

42
1
log 1 2log
2
x . Hãy chọn nhận xét đúng.
A.
0
x
là số nguyên âm. B.
0
x
là số tự nhiên. C.
0
x
là số vô tỷ. D.
0
x
là số hữu tỷ dương.
Câu 24:
Quan sát đồ thị, cho biết đồ thị đó có thể là của hàm nào sau đây:
Mã đề thi 689 - Trang số : 4
A.
log ( 1)
b
yxb
B.
(1)
x
ya a
C.
(0 1)
x
ya a
D.
log (0 1)
b
yxb
Câu 25: Cho biết tập xác định của hàm số
5
2
() 4fx x

.
A.
(;2)(2;) 
B.

2; 2
C.
\2
D.
Câu 26: Thu gọn biểu thức
3
4
2
a
A
a
, (0)a .
A.
5
4
a
B.
3
8
a
C.
5
2
a
D.
11
4
a
Câu 27: Cho hai số thực
a
và
b
, với
01ab
. Khẳng định nào dưới đây là khẳng định đúng?
A. log 1 log
ba
ab B.
1log log
ba
ab
C.
log 1 log
ab
ba
D.
1log log
ab
ba
Câu 28: Tìm điều kiện của
x
để hàm số
2
2
log ( 2)yx
xác định.
A.
2x
B.
x
C.
2x
D.
2x
Câu 29: Đạo hàm của hàm số
2
cos
() 2
x
fx
là hàm nào sau đây:
A.
2
cos 1
sin(2 ).2
x
x
B.
2
cos
sin(2 ).2
x
x
C.
2
cos
sin(2 ).2 .ln 2
x
x
D.
2
cos
sin(2 ).2 .ln 2
x
x
Câu 30: Số vi khuẩn trong ống nghiệm ban đầu có 100 con, chỉ sau hai giờ đã là 4000 con. Biết số lượng
vi khuẩn tăng trong mỗi giờ theo một tỷ lệ không đổi. Hãy ước lượng sau năm giờ (tính từ ban đầu có 100
con) số vi khuẩn sẽ có, gấp khoảng bao nhiêu lần số vi khuẩn ban đầu
(chọn đáp án gần đúng nhất).
A. Gấp khoảng 10.000 lần. B. Gấp khoảng 11.000 lần.
C. Gấp khoảng 9.000 lần . D. Gấp khoảng 12.000 lần.
----------------- Hết -----------------
Mã đề thi 812 - Trang số : 1
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT CHUYÊN HUỲNH MẪN ĐẠT
---------------
KIỂM TRA TOÁN 12
BÀI THI: TOÁN 12 CH, CB, NC
(Th
ờ
i gian làm bài: 45 phút)
MÃ ĐỀ THI: 812
Họ tên thí sinh:.................................................SBD:.........................
Câu 1: Cho phương trình
222
2
log 9 log log 3
.3
x
xx x
. Với điều kiện
x
thỏa mãn, một trong những cách giải
phương trình trên là bước đầu đặt
2
logtx
, thay vào phương trình ban đầu, trở thành phương trình theo
ẩn
t
hoàn toàn. Hãy giải phương trình tìm
t
.
A.
4
t
B.
1
2
t
C.
1.
t
D.
0t
Câu 2: Trong các mệnh đề sau, cho biết có bao nhiêu mệnh đề sai:
i. Đồ thị của hai hàm số
x
ya và log
a
yx (với 01a ) đối xứng nhau qua đường thẳng yx .
ii. Với
1a
, ta có đồ thị hai hàm số
x
ya và
1
x
y
a
đối xứng nhau qua trục tung.
iii. Một tiệm cận của đồ thị hàm số
log (0 1)
a
yxa
có phương trình là
0y
.
iv. Đồ thị hàm số
lnyx có 2 nhánh đối xứng nhau qua trục tung.
A. Ba. B. Hai. C. Bốn. D. Một.
Câu 3: Cho biết tập xác định của hàm số
5
2
() 4fx x

.
A.
(;2)(2;) 
B.
\2
C.
D.

2; 2
Câu 4: Đồ thị ở hình vẽ biểu diễn cho hàm số nào sau đây:
A.
2
1logyx
B.
2
1logyx
C.
1
2
4
x
y
 . D.
2
log ( 1)yx
Câu 5: Viết dạng lũy thừa số mũ hữu tỉ biểu thức
3
aa
với
0a
.
A.
2
3
a
B.
1
12
a
C.
5
6
a
D.
1
6
a
Câu 6:
Quan sát đồ thị, cho biết đồ thị đó có thể biểu diễn cho hàm số nào?
Mã đề thi 812 - Trang số : 2
A.
1
2
x
y
B.
31
x
y 
C.
2
2yx
. D.
21
x
y 
Câu 7: Đạo hàm của hàm số
2
cos
() 2
x
fx
là hàm nào sau đây:
A.
2
cos 1
sin(2 ).2
x
x
B.
2
cos
sin(2 ).2
x
x
C.
2
cos
sin(2 ).2 .ln 2
x
x
D.
2
cos
sin(2 ).2 .ln 2
x
x
Câu 8: Một chiếc ô tô mới mua năm 2016 với giá
900
triệu đồng. Cứ sau mỗi năm, giá chiếc ô tô này bị
giảm
10%
.Hỏi đến năm 2020, giá chiếc ô tô này là bao nhiêu?
A.
656.100.000 đồng B. 590.490.000 đồng C. 864.536409 đồng D. 531.441.000 đồng
Câu 9: Quan sát đồ thị, cho biết đồ thị đó có thể là của hàm nào sau đây:
A.
(0 1)
x
ya a
B.
(1)
x
ya a
C.
log ( 1)
b
yxb
D.
log (0 1)
b
yxb
Câu 10: Số vi khuẩn trong ống nghiệm ban đầu có 100 con, chỉ sau hai giờ đã là 4000 con. Biết số lượng
vi khuẩn tăng trong mỗi giờ theo một tỷ lệ không đổi. Hãy ước lượng sau năm giờ (tính từ ban đầu có 100
con) số vi khuẩn sẽ có, gấp khoảng bao nhiêu lần số vi khuẩn ban đầu (chọn đáp án gần đúng nhất).
A. Gấp khoảng 10.000 lần. B. Gấp khoảng 9.000 lần .
C. Gấp khoảng 12.000 lần. D. Gấp khoảng 11.000 lần.
Câu 11: Tìm điều kiện của
x
để hàm số
2
2
log
x
y
x
xác định.
A.
2x
B.
0, 2xx
C.
02x
D.
1
0,
2
xx
Câu 12:
Giá trị lớn nhất của hàm số
() ln(1 2)
x
f
xe x
trên đoạn
0; 2
bằng:
A.
2
ln 5e
B.
ln 3e
C.
2
ln 6e
D.
0.
Mã đề thi 812 - Trang số : 3
Câu 13: Thu gọn biểu thức:
32
.?xx
A.
x
B.
5
x
C.
5
x
D.
5
x
Câu 14: Số nghiệm của phương trình
33
log (2 1) log ( 3) 1xx
là:
A. Hai. B. Vô nghiệm. C. Một. D. Ba.
Câu 15: Đạo hàm của hàm số
2
()
2
x
x
fx là hàm nào sau đây:
A.
2
2.2 2.ln2
2
xx
x
xx
B.
31
2
2.2 2
2
xx
x
xx
C.
(2 ln 2)
2
x
xx
D. Đáp án khác
Câu 16: Gọi
0
x
là nghiệm của phương trình
1
52.515
xx

. Hãy chọn nhận xét đúng.
A.
0
0x
B.
0
01x
C.
0
1
2
x
D.
0
(1; 2)x
Câu 17: Giá trị nhỏ nhất của hàm số
2
() 4ln(1 )
f
xx x
trên đoạn

3; 0
là giá trị nào sau đây?
A.
14ln3
B.
94ln4
C. 0. D.
14ln2.
Câu 18: Giải phương trình
345
x
xx

.
A.
3.x
B.
2.x
C.
0.x
D.
2x 
.
Câu 19: Gọi
0
x
là nghiệm của phương trình

42
1
log 1 2log
2
x . Hãy chọn nhận xét đúng.
A.
0
x
là số vô tỷ. B.
0
x
là số tự nhiên. C.
0
x
là số nguyên âm. D.
0
x
là số hữu tỷ dương.
Câu 20: Cho 0, 1aa. Đơn giản biểu thức
23
4
log
a
B
aa .
A.
3
2
B.
11
4
C.
3
2
a
D.
11
4
a
Câu 21: Cho các mệnh đề sau
i. Với
12
,0xx
thì

2
12 12
1
5log 5log 5 log log 5log
x
xx xx
 .
ii. Cho
123
,, 0xxx
và
01a
, ta có:
123 1 2 3
log ( ) log .log .log
aaaa
x
xx x x x .
iii.
2
66
(2 .3)
11
log 12 log 12 (1 log 2)
22
.
iv. Cho các số thực dương
,
ab
, với
1a
, ta có:
2
11
log ( ) log
22
a
a
ab b .
Số mệnh đề sai là:
A. 4 B. 3 C. 1 D. 2
Câu 22: Cho hai số thực
a
và
b
, với
01ab
. Khẳng định nào dưới đây là khẳng định đúng?
A. log 1 log
ba
ab B.
log 1 log
ab
ba
C.
1log log
ba
ab
D.
1log log
ab
ba
Câu 23: Cho số thực
x
thỏa mãn
2016log 2016x
. Vậy giá trị
x
là:
A. 0 B. 1 C. 10 D. 5
Câu 24: Đặt ln 2a và ln 5b . Hãy biểu diễn ln 200 theo a và b .
A.
32ba B. 32ab C. 6ab D.32ab .
Mã đề thi 812 - Trang số : 4
Câu 25: Tìm điều kiện của
x
để hàm số
2
2
log ( 2)yx xác định.
A.
2x
B.
2x
C.
2x
D.
x
Câu 26: Tìm tất cả những giá trị
m
để phương trình
2
2
2
log 8log 8 4 0xxm vô nghiệm trên đoạn

1; 4
.
A.
0m
hoặc
1
2
m
B.
0m
hoặc
1
2
m
C.
1
2
m 
hoặc
1
2
m
D.
0m
Câu 27: Hãy cho biết số nghiệm của phương trình
2
3
3
log ( 1) log (2 1) 0xx .
A. Hai. B. Vô nghiệm. C. Một. D. Bốn
Câu 28: Thu gọn biểu thức
3
4
2
a
A
a
,
(0)a
.
A.
11
4
a
B.
3
8
a
C.
5
4
a
D.
5
2
a
Câu 29: Hãy cho biết giá trị của
/
(2)g
nếu
2
() ln 1gx x
:
A.
0,65
B.
2
3
C.
0,8
D.
2
5
Câu 30: Hãy chọn mệnh đề đúng:
A. Với mọi
x
thỏa
2
(1)0x 
, ta có:
2
4444
log ( 1) 2log 5 log ( 1) log 5 1 5 6xxxx
.
B. Cho số
a
dương khác 1 và 0x : log ( 2 ) log 2 log ( )
aaa
x
x .
C. Với mọi
0x
,
22
93 33
1
log 3log 2 0 log 3log 2 0
2
xx xx .
D.
2
; 2 , log 4 log( 2) log( 2).xxxx
----------------- Hết -----------------
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT KIÊN GIANG KIỂM TRA TOÁN 12
TRƯỜNG THPT CHUYÊN HUỲNH MẪN ĐẠT BÀI THI: TOÁN 12 CH, CB, NC ---------------
(Thời gian làm bài: 45 phút) MÃ ĐỀ THI: 197
Họ tên thí sinh:.................................................SBD:.........................
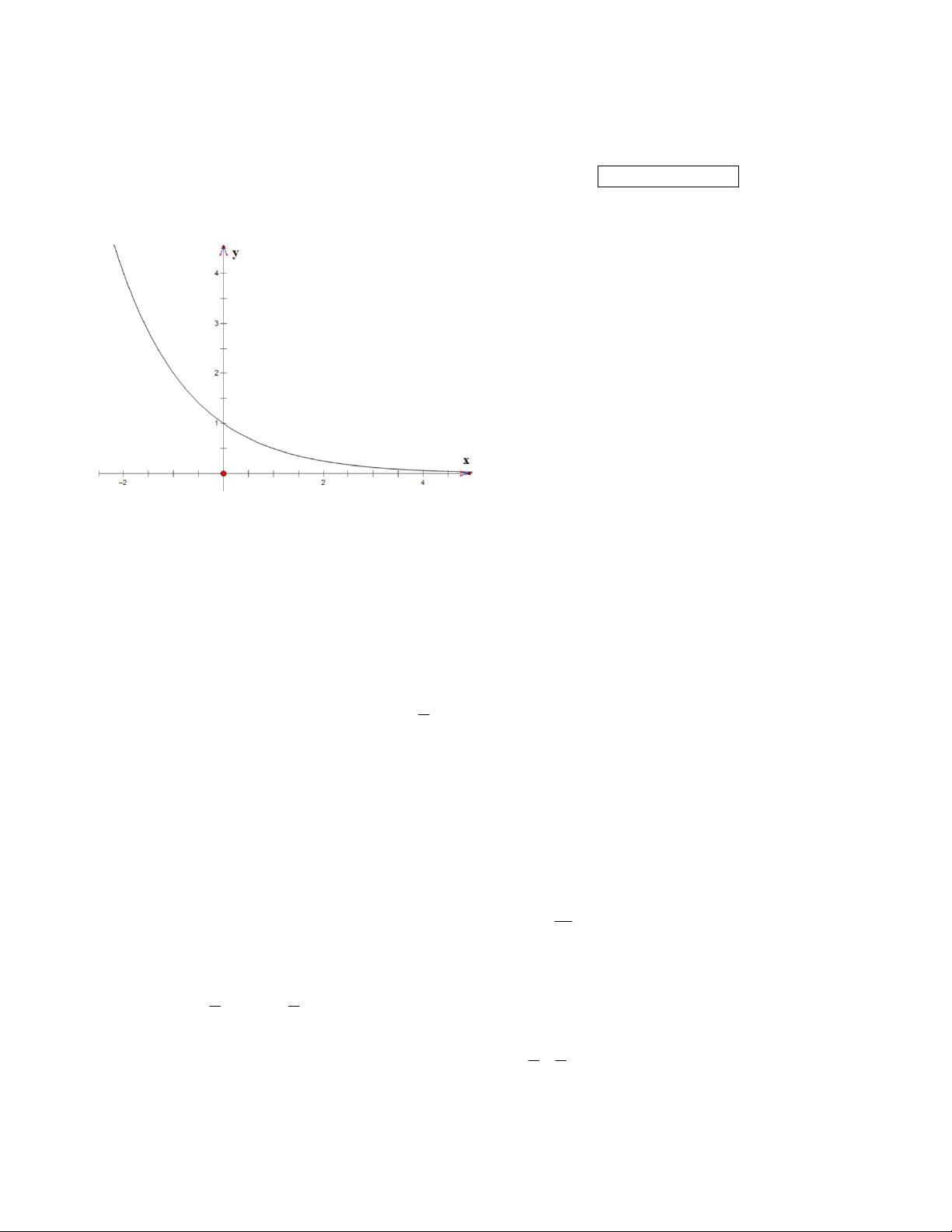
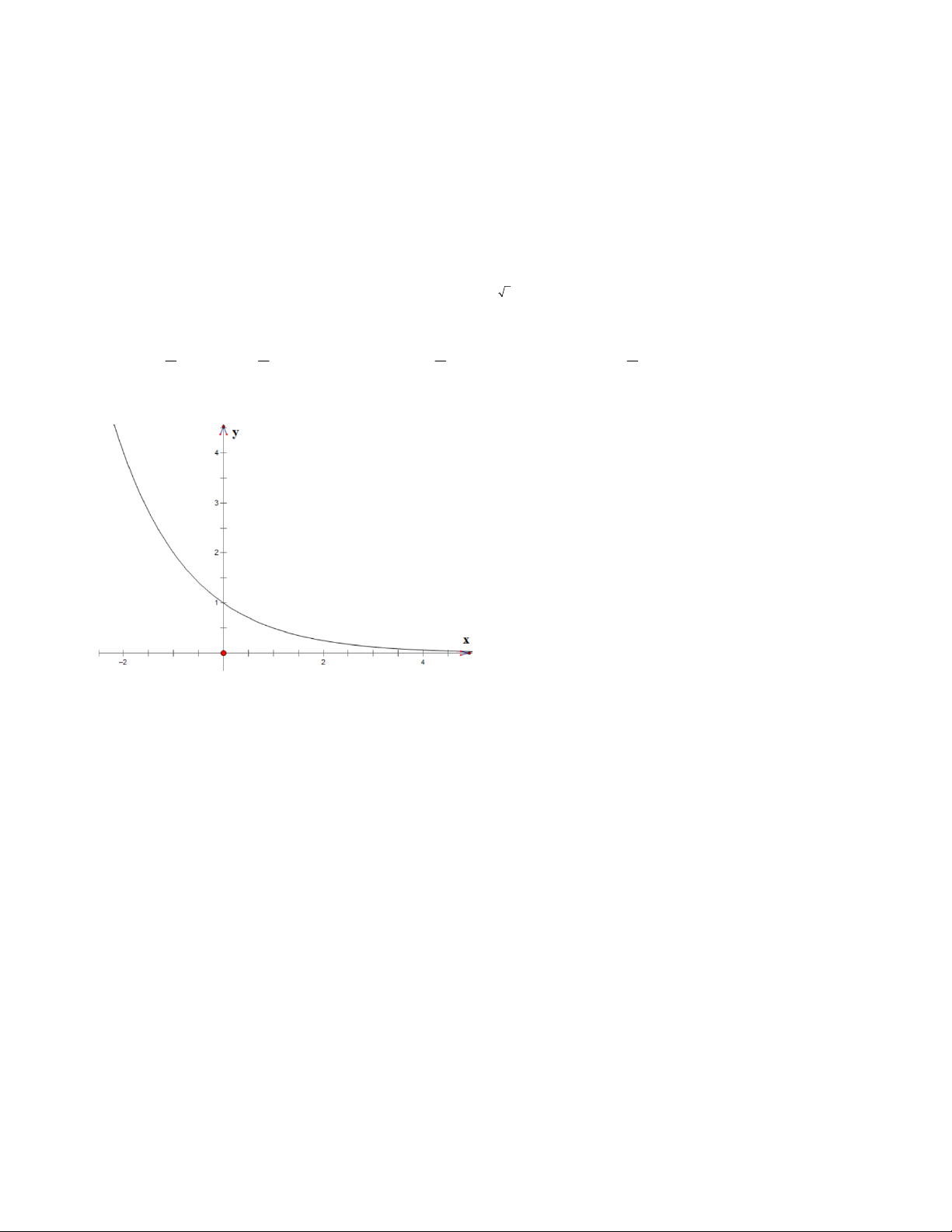
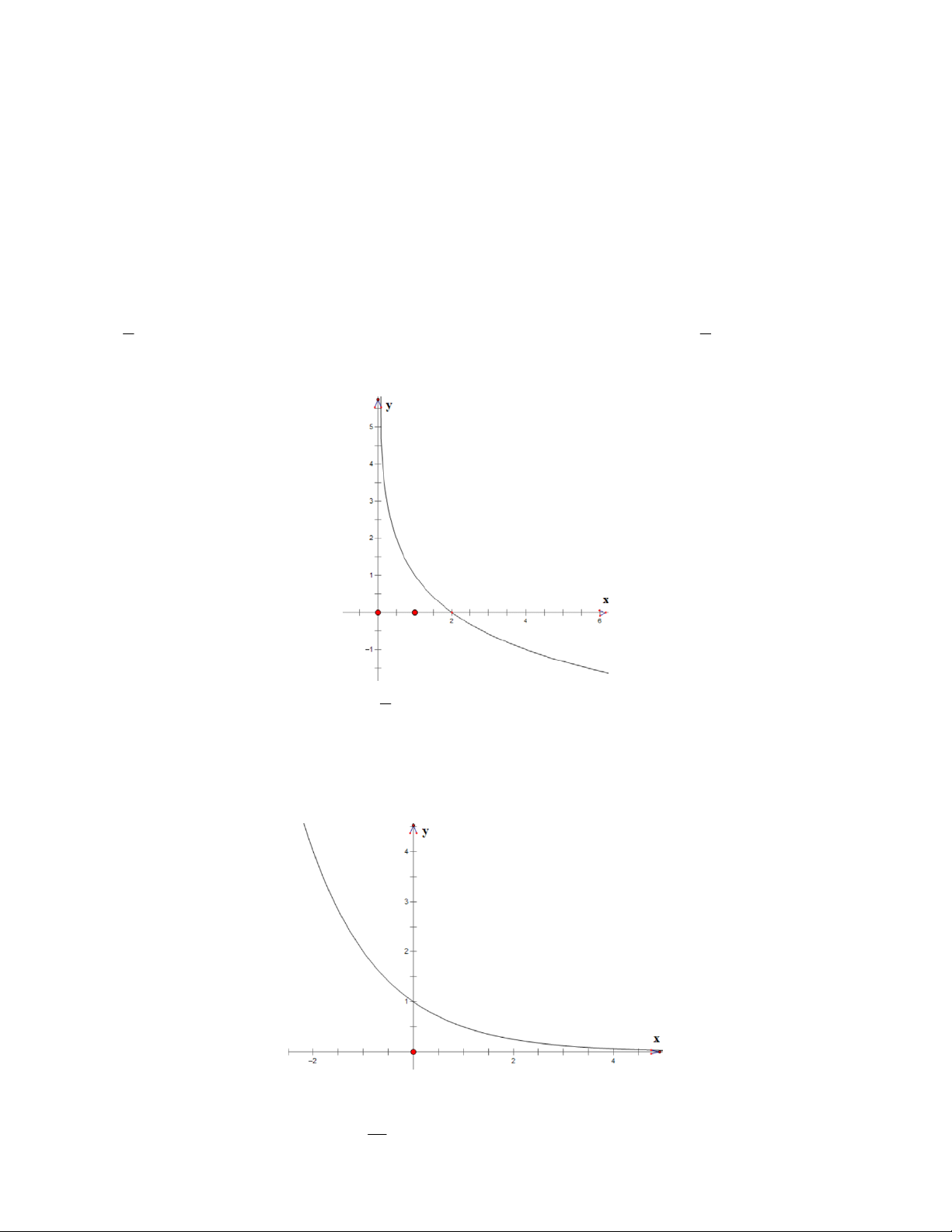
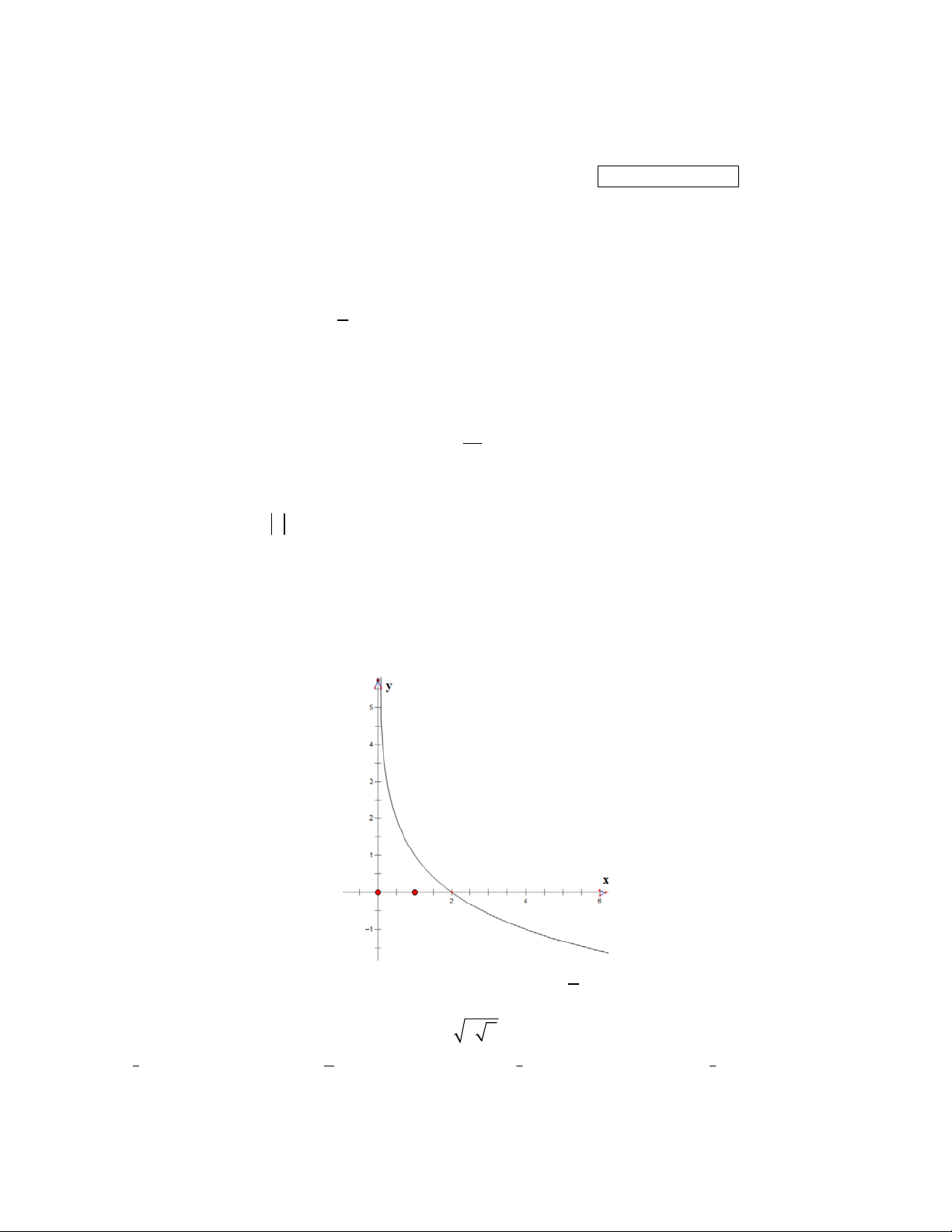
Câu 1: Quan sát đồ thị, cho biết đồ thị đó có thể là của hàm nào sau đây: x x
A. y a (a  1)
B. y a (0  a  1)
C. y  log x (b  1) y xb b D. log (0 1) b
Câu 2: Cho số thực x thỏa mãn 2016log x  2016 . Vậy giá trị x là: A. 1 B. 5 C. 10 D. 0
Câu 3: Đặt a  ln 2 và b  ln 5 . Hãy biểu diễn ln 200 theo a và b . A. 3b  2a B. 3a  2b C. 6ab D. 3a  2b
Câu 4: Hãy chọn mệnh đề đúng: A. x      2
; 2 , log x  4  log(x  2)  log(x  2). 1
B. Với mọi x  0 , 2 2
log x  3log x  2  0  log x  3log x  2  0 . 9 3 3 3 2    
C. Cho số a dương khác 1 và x  0 : log ( 2x) log 2 log ( x) a a a .
D. Với mọi x thỏa 2
(x 1)  0 , ta có: 2
log (x 1)  2 log 5  log (x 1)  log 5  x 1  5  x  6 . 4 4 4 4 3 2
Câu 5: Thu gọn biểu thức: x .x  ? 5 5 A. x B. x C. 5x D. x
Câu 6: Cho các mệnh đề sau
i. Với x , x  0 thì 5log x  5log x  5 log x  log x  5log x . 1 2  1 2  2 1 2 1 x
ii. Cho x , x , x  0 1 2 3
và 0  a  1, ta có: log (x x x )  log x .log x .log x . a 1 2 3 a 1 a 2 a 3 1 1 iii. log
12  log 12  (1 log 2) 2 6 6 (2 .3) 2 2 1 1
iv. Cho các số thực dương a,b , với a  1 , ta có: log (ab)   log . 2 b 2 2 a a Số mệnh đề sai là: A. 4 B. 1 C. 2 D. 3
Mã đề thi 197 - Trang số : 1 2 cos
Câu 7: Đạo hàm của hàm số ( ) 2 x f x  là hàm nào sau đây: 2 cos 2 2 2 x cos x cos cos 1 A.  sin(2x).2 .ln 2 B. sin(2x).2 .ln 2 C.  sin(2 ).2 x x D. sin(2 ).2 x x   2 ( ) x f x
Câu 8: Đạo hàm của hàm số
2x là hàm nào sau đây: x 2 2 . x 2  x 2 . x ln 2 x 3 x 1 2 . x 2 x 2   x(2  x ln 2) A. 2x B. 2 2 x C. 2x D. Đáp án khác / g x   2 ( ) ln x   1
Câu 9: Hãy cho biết giá trị của g (2) nếu : 2 2 A. 5 B. 0,8 C. 3 D. 0,65
Câu 10: Cho hai số thực a và b , với 0  a b  1. Khẳng định nào dưới đây là khẳng định đúng?       A. log b 1 log a b a a b a b B. 1 log log a b C. 1 log log b a
D. log a  1  log b b a
Câu 11: Cho biết tập xác định của hàm số f x  x   5 2 ( ) 4 .  \   2  2;  2 A. ( ;  2  )  (2;) B. C. D.  2
y  log (x  2)
Câu 12: Tìm điều kiện của x để hàm số 2 xác định. A. x  2 B. x  2 C. x   D. x  2
Câu 13: Tìm điều kiện của x để hàm số y  log xác định. 2 x x 2 1 x  0, x  A. 2
B. x  0, x  2 C. x  2 D. 0  x  2 3
Câu 14: Viết dạng lũy thừa số mũ hữu tỉ biểu thức a a với a  0 . 5 1 1 2 A. 6 a B. 6 a C. 12 a D. 3 a 3 4
Câu 15: Thu gọn biểu thức, a A  (a  0) . 2 a 5  5  3 11 A. 4 a B. 2 a C. 8 a D. 4 a
Câu 16: Cho a  0, a  1 . Đơn giản biểu thức B  log a a . a  2 4 3  11 3 11 3 A. 4 a B. 2 a C. 4 D. 2     
Câu 17: Số nghiệm của phương trình log (2x 1) log (x 3) 1 3 3 là: A. Vô nghiệm. B. Một. C. Hai. D. Ba. x 1  Câu 18: Gọi x 0
x là nghiệm của phương trình 5  2.5 15. Hãy chọn nhận xét đúng. 1   0 x  A. x  0 0 x 1 x  (1; 2) 0 B. 0 C. 0 D. 2
Câu 19: Giải phương trình 3x 4x 5x   .
Mã đề thi 197 - Trang số : 2 A. x  2. B. x  3. C. x  0. D. x  2 . 1 Câu 20: Gọi 0
x là nghiệm của phương trình log 1 2log
 . Hãy chọn nhận xét đúng. 4  2 x  2 A. 0
x là số tự nhiên. B. 0 x là số vô tỷ. C. 0
x là số nguyên âm. D. 0
x là số hữu tỷ dương. x 0;2
Câu 21: Giá trị lớn nhất của hàm số f (x)  e ln(1 2x) trên đoạn bằng: 2 2 A. 0. B. e ln 3 C. e ln 5 D. e ln 6 2
log (x 1)  log (2x 1)  0
Câu 22: Hãy cho biết số nghiệm của phương trình 3 3 . A. Vô nghiệm. B. Một. C. Hai. D. Bốn 2
log x  8log x  8m  4  0
Câu 23: Tìm tất cả những giá trị m để phương trình 2 2 vô nghiệm trên đoạn 1;4. 1 1 1 1 m m m   m  A. m  0 hoặc 2 B. m  0 hoặc 2 C. m  0 D. 2 hoặc 2 log 9 2 log log 3
Câu 24: Cho phương trình 2 2 2  .3 x x xx
. Với điều kiện x thỏa mãn, một trong những cách giải 
phương trình trên là bước đầu đặt t log2 x , thay vào phương trình ban đầu, trở thành phương trình theo
ẩn t hoàn toàn. Hãy giải phương trình tìm t . 1 t  A. 2 B. t  0 C. t  1. D. t  4 2 3;0
Câu 25: Giá trị nhỏ nhất của hàm số f (x)  x  4 ln(1 x) trên đoạn
là giá trị nào sau đây? A. 1 4ln 2. B. 0. C. 9  4ln 4 D. 1 4 ln 3
Câu 26: Một chiếc ô tô mới mua năm 2016 với giá 900 triệu đồng. Cứ sau mỗi năm, giá chiếc ô tô này bị
giảm 10% .Hỏi đến năm 2020, giá chiếc ô tô này là bao nhiêu? A. 590.490.000 đồng B. 656.100.000 đồng C. 864.536409 đồng D. 531.441.000 đồng
Câu 27: Số vi khuẩn trong ống nghiệm ban đầu có 100 con, chỉ sau hai giờ đã là 4000 con. Biết số lượng
vi khuẩn tăng trong mỗi giờ theo một tỷ lệ không đổi. Hãy ước lượng sau năm giờ (tính từ ban đầu có 100
con) số vi khuẩn sẽ có, gấp khoảng bao nhiêu lần số vi khuẩn ban đầu (chọn đáp án gần đúng nhất).
A. Gấp khoảng 9.000 lần .
B. Gấp khoảng 11.000 lần.
C. Gấp khoảng 12.000 lần.
D. Gấp khoảng 10.000 lần.
Mã đề thi 197 - Trang số : 3
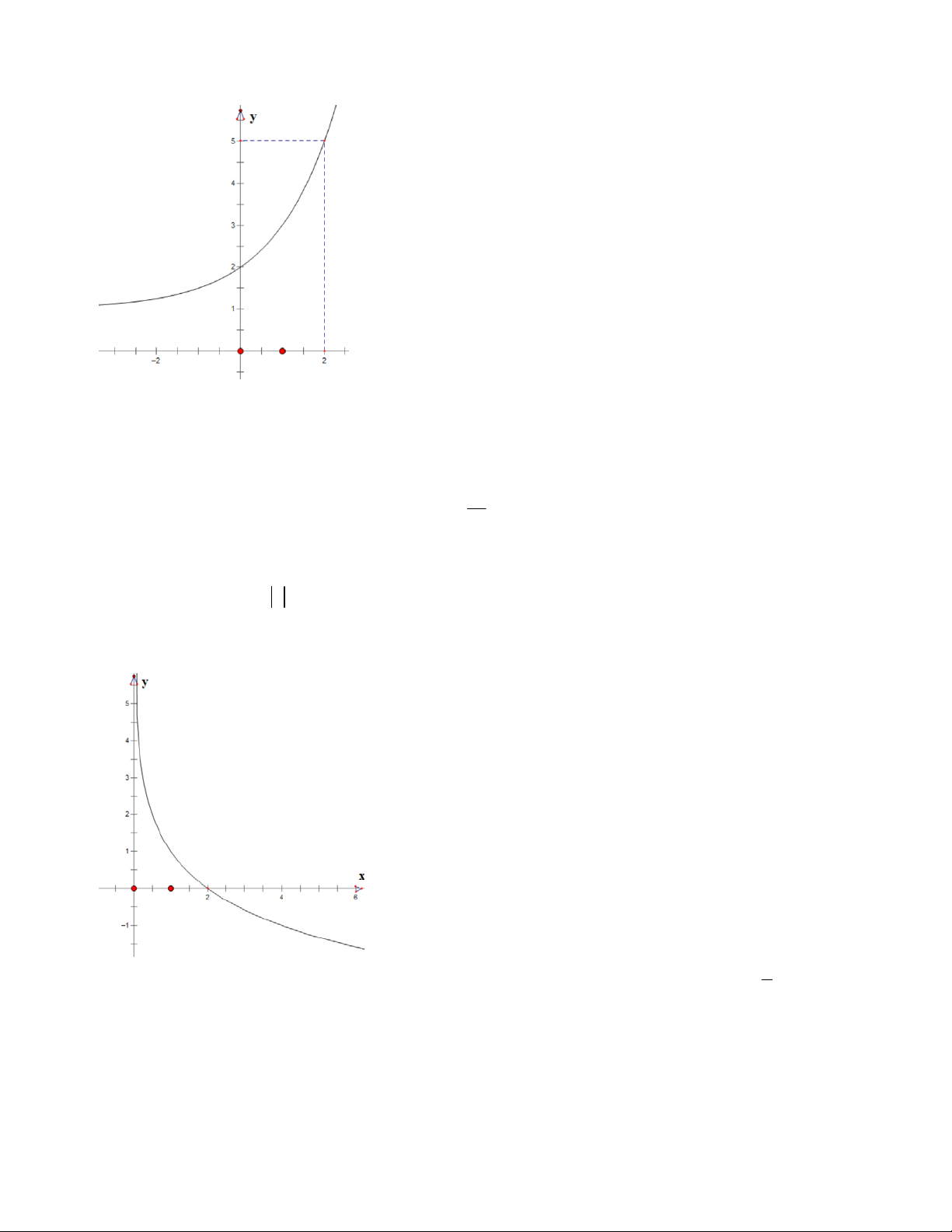
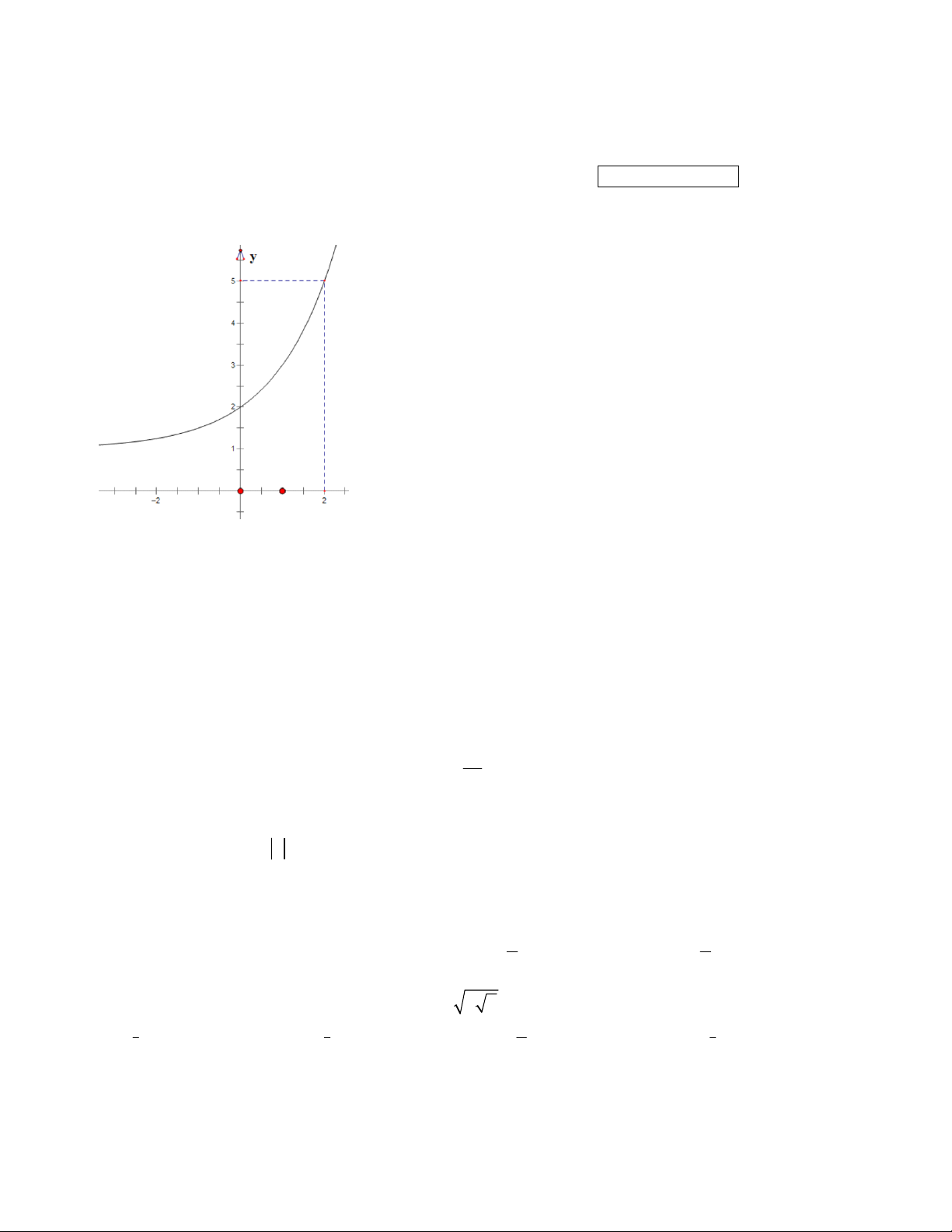
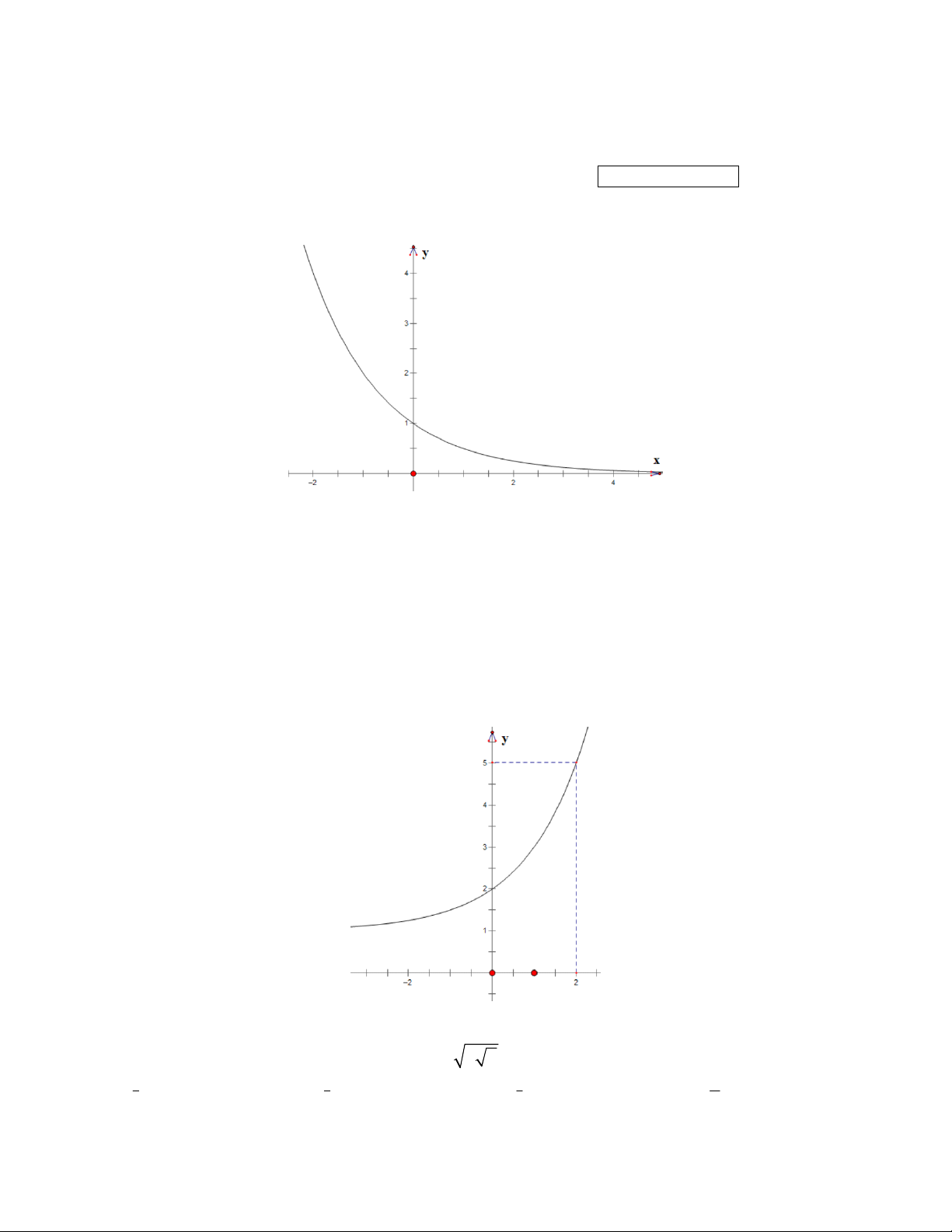
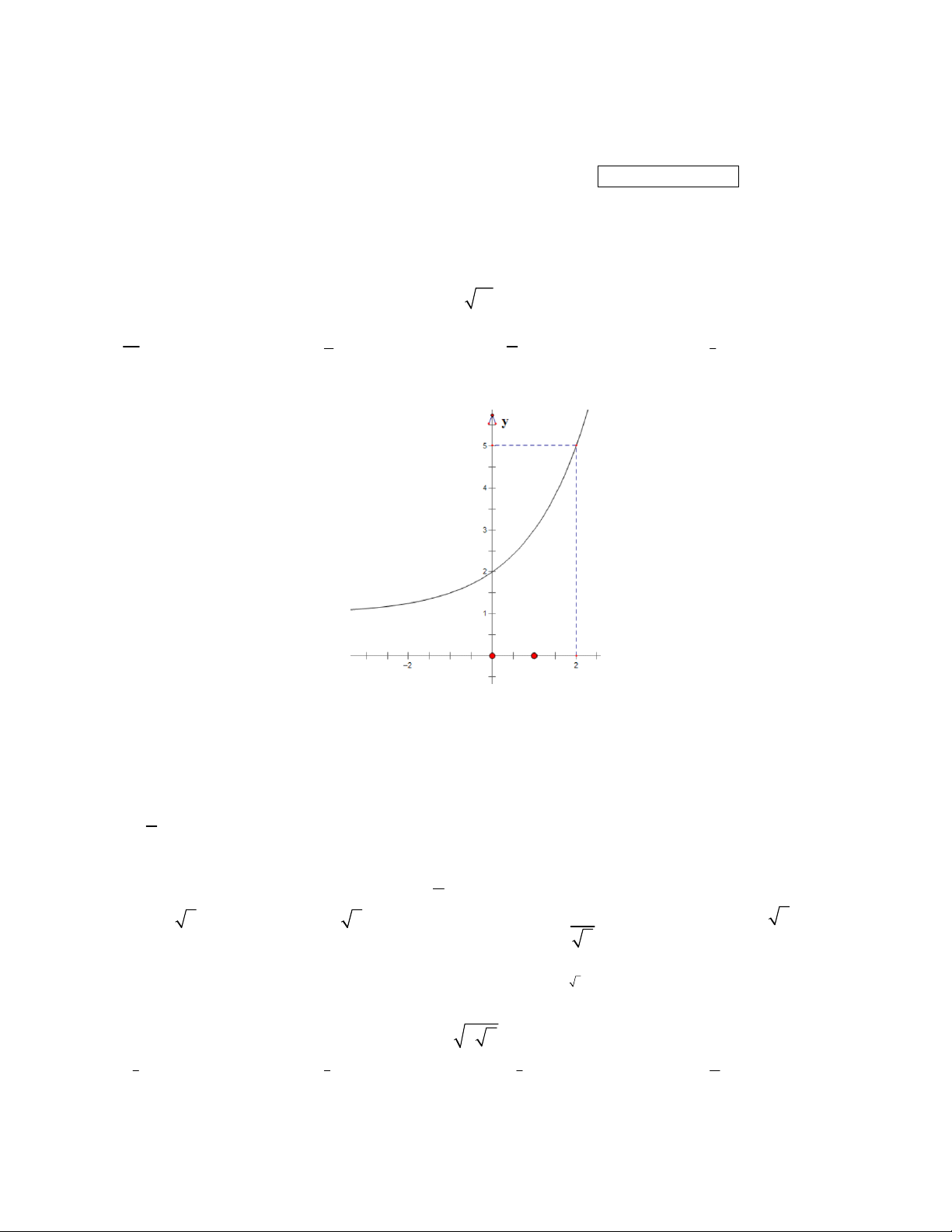
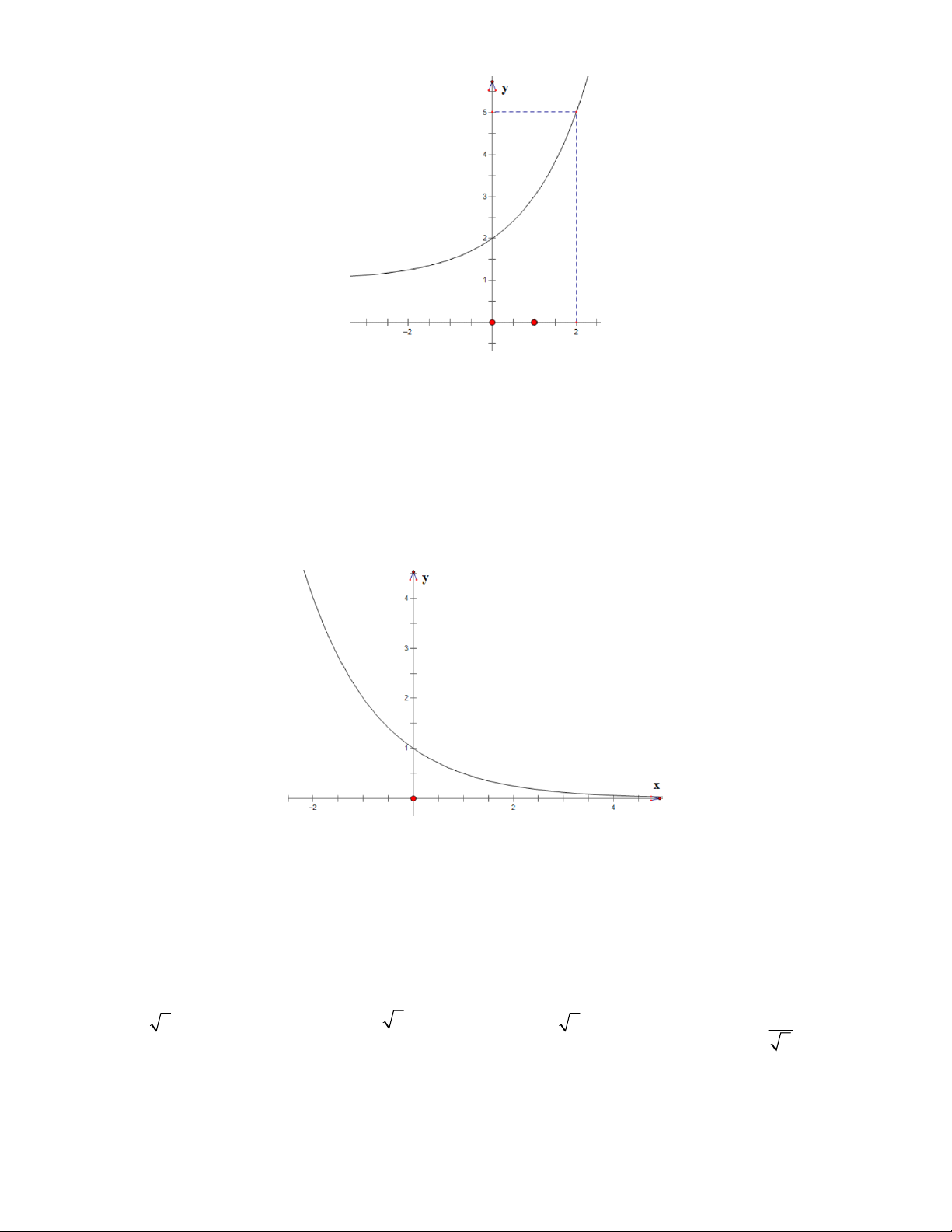
Câu 28: Quan sát đồ thị, cho biết đồ thị đó có thể biểu diễn cho hàm số nào? 1 x x 2 A. 2x y   B. y  3 1 C. y  2 1
D. y x  2 .
Câu 29: Trong các mệnh đề sau, cho biết có bao nhiêu mệnh đề sai: x
i. Đồ thị của hai hàm số y a và y log x    a
(với 0 a 1) đối xứng nhau qua đường thẳng y x . 1  x y
ii. Với a  1, ta có đồ thị hai hàm số y a và x
a đối xứng nhau qua trục tung.   
iii. Một tiệm cận của đồ thị hàm số y log x (0 a 1) y a có phương trình là 0 . y  ln iv. Đồ thị hàm số
x có 2 nhánh đối xứng nhau qua trục tung. A. Một. B. Hai. C. Ba. D. Bốn.
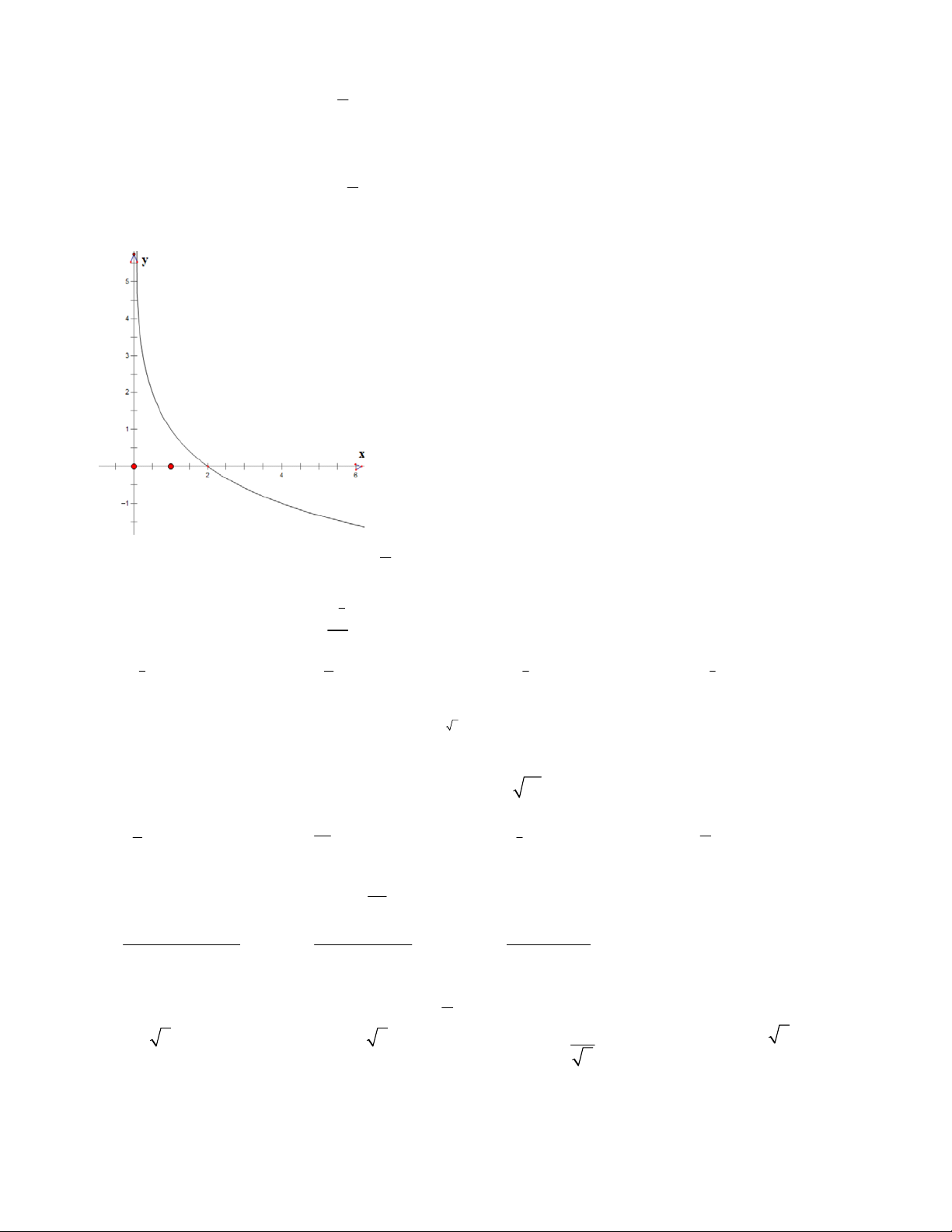
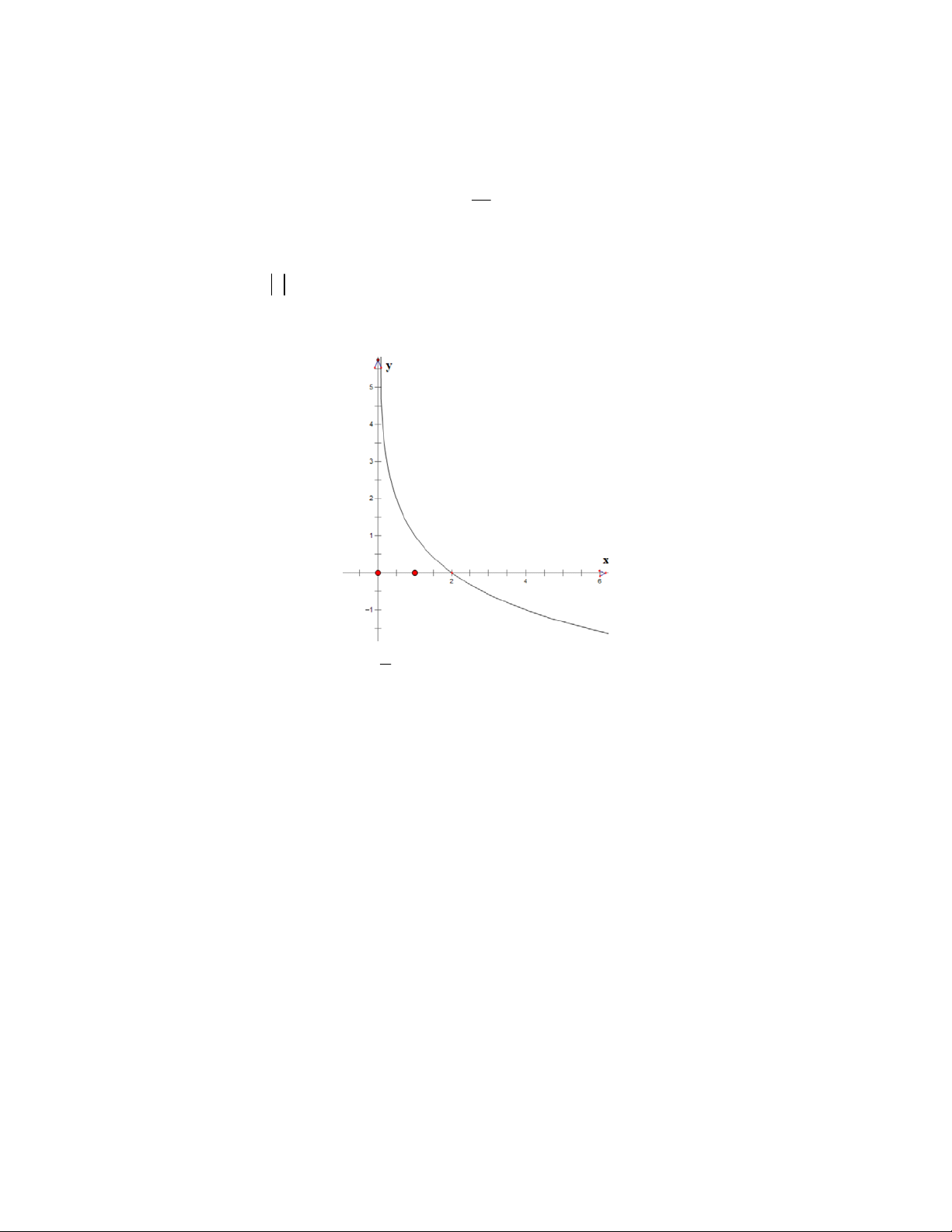
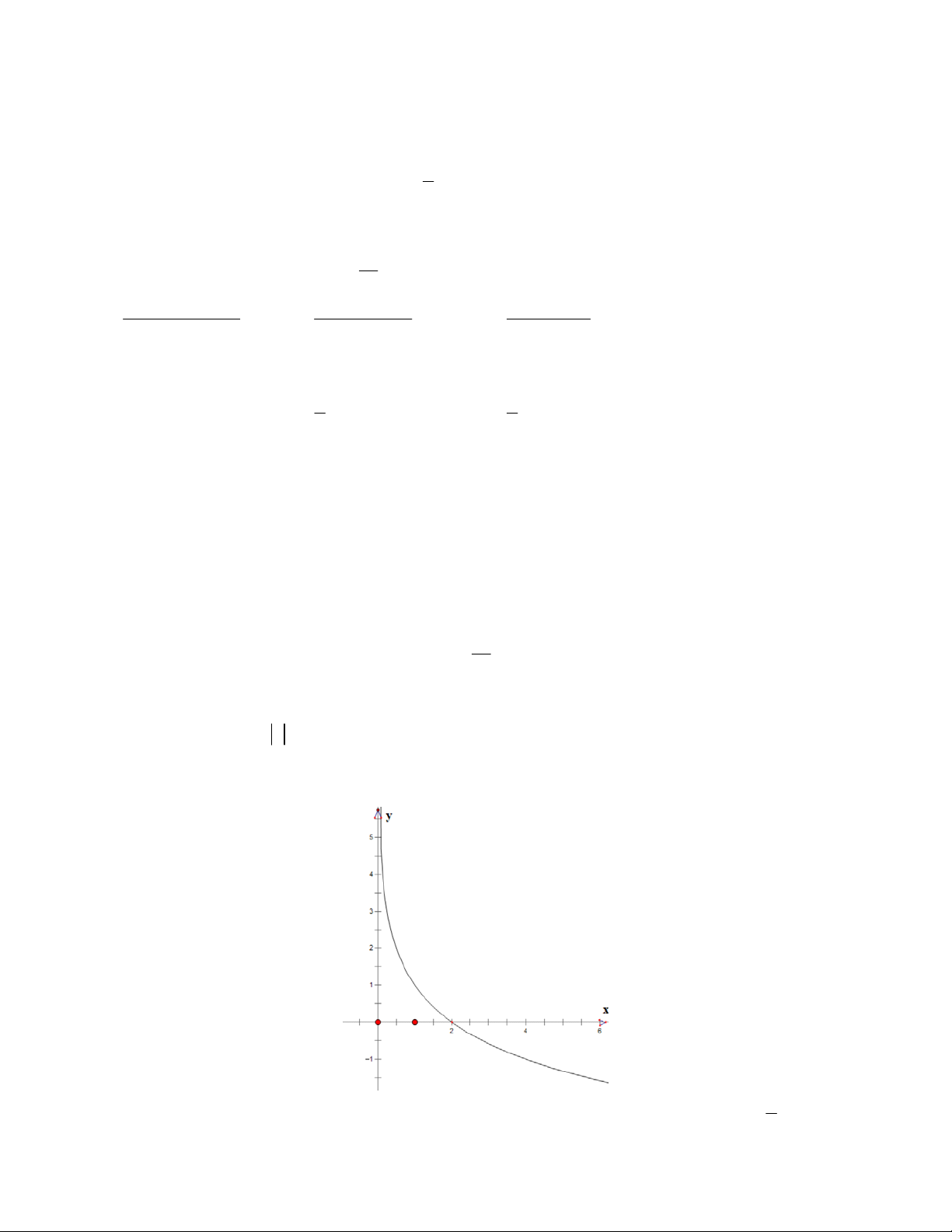
Câu 30: Đồ thị ở hình vẽ biểu diễn cho hàm số nào sau đây:         x 1 A. y 1 log y 1 log y log (x 1) 2 x B. 2 x C. 2 D. y  2  . 4
----------------- Hết -----------------
Mã đề thi 197 - Trang số : 4 SỞ GD&ĐT KIÊN GIANG KIỂM TRA TOÁN 12
TRƯỜNG THPT CHUYÊN HUỲNH MẪN ĐẠT BÀI THI: TOÁN 12 CH, CB, NC ---------------
(Thời gian làm bài: 45 phút) MÃ ĐỀ THI: 320
Họ tên thí sinh:.................................................SBD:.........................
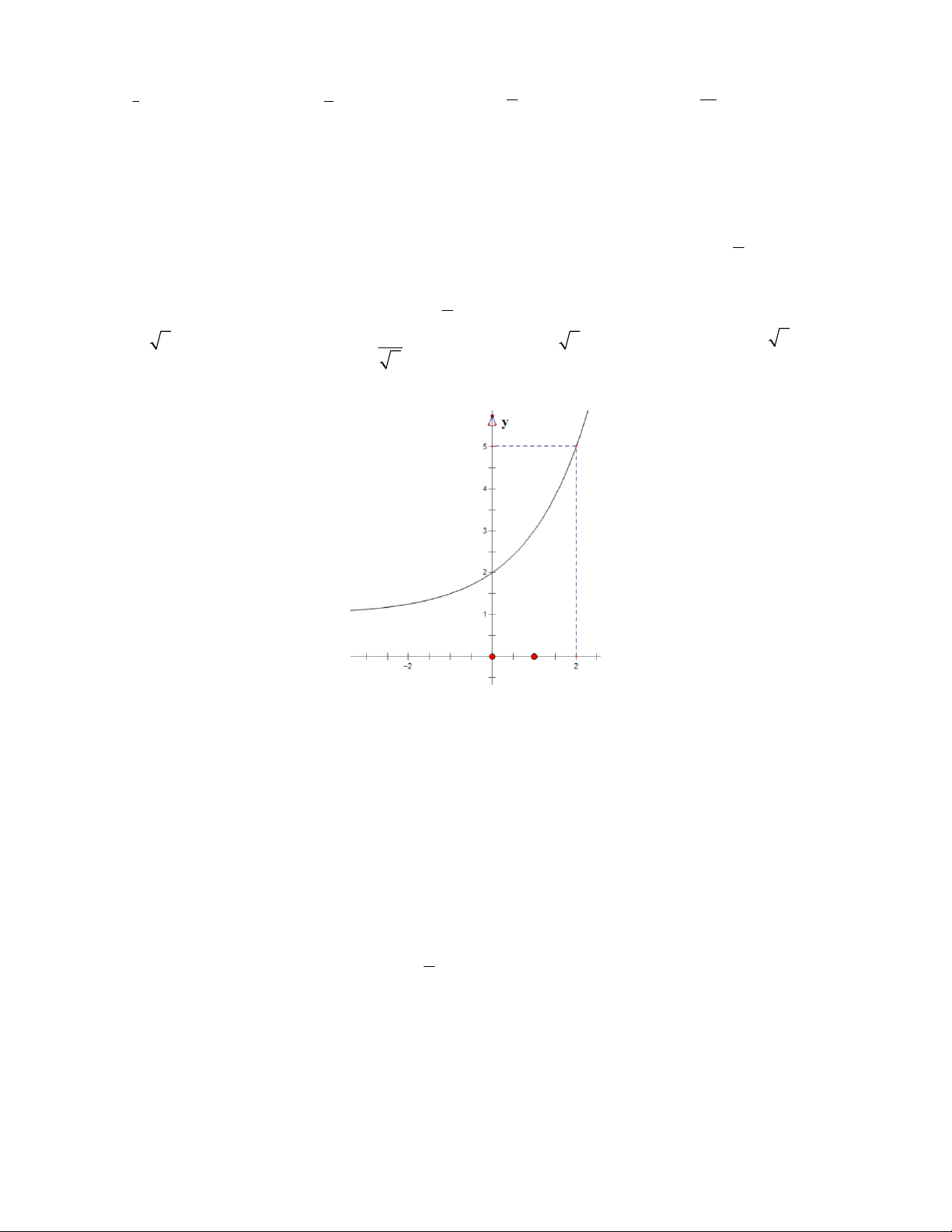
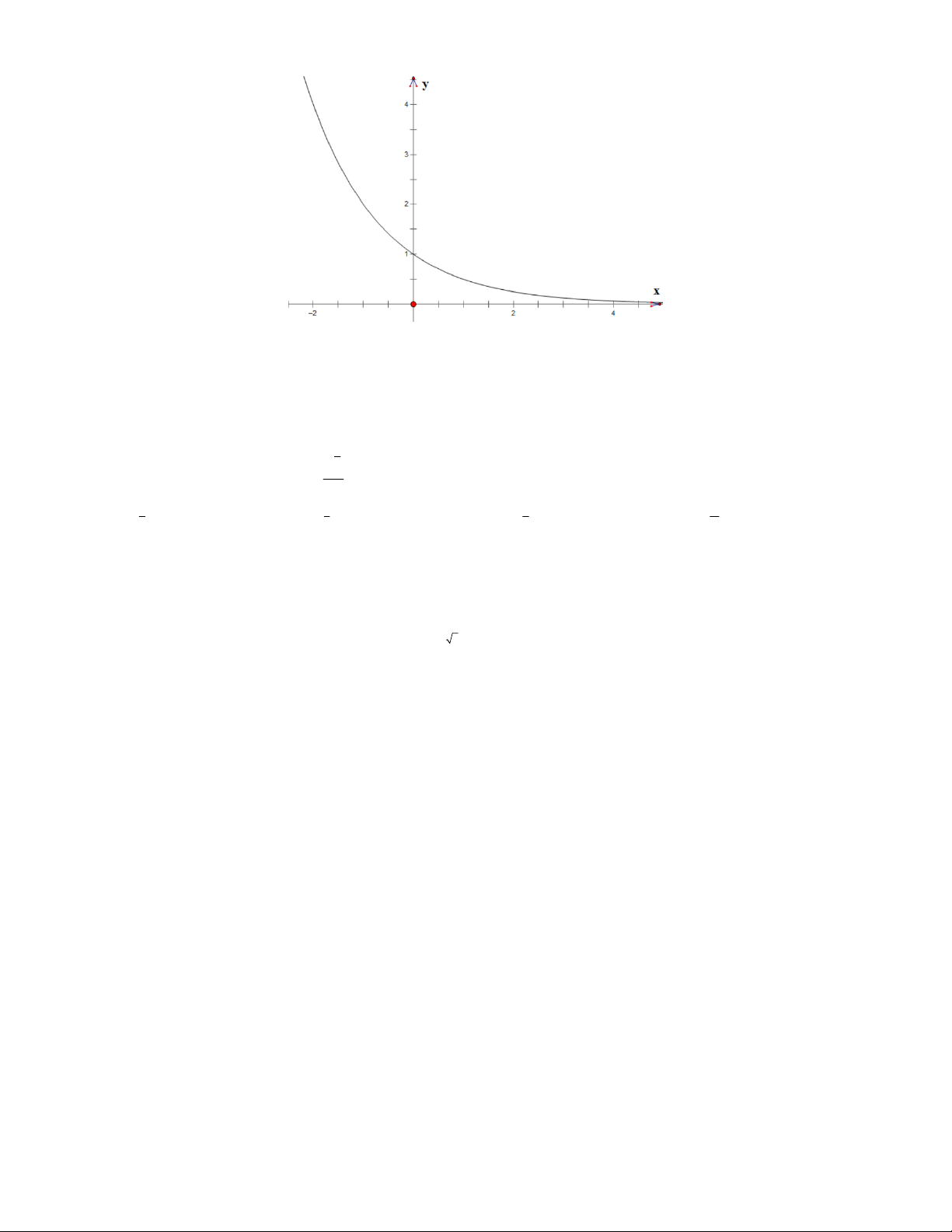
Câu 1: Quan sát đồ thị, cho biết đồ thị đó có thể biểu diễn cho hàm số nào? 1 x x 2 A. 2x y   B. y  2 1 C. y  3 1
D. y x  2 . 3 2
Câu 2: Thu gọn biểu thức: x .x  ? 5 5 A. x B. x C. x D. 5x
Câu 3: Đặt a  ln 2 và b  ln 5 . Hãy biểu diễn ln 200 theo a và b . A. 3b  2a B. 3a  2b C. 6ab D. 3a  2b
Câu 4: Trong các mệnh đề sau, cho biết có bao nhiêu mệnh đề sai: x
i. Đồ thị của hai hàm số y a và y  log x    a
(với 0 a 1) đối xứng nhau qua đường thẳng y x . 1
ii. Với a  1, ta có đồ thị hai hàm số x
y a và y
đối xứng nhau qua trục tung. x a
iii. Một tiệm cận của đồ thị hàm số y  log x (0  a  1) có phương trình là y  0 . a
iv. Đồ thị hàm số y  ln x có 2 nhánh đối xứng nhau qua trục tung. A. Ba. B. Bốn. C. Một. D. Hai. / g x   2 ( ) ln x   1
Câu 5: Hãy cho biết giá trị của g (2) nếu : 2 2 A. 0,8 B. 0,65 C. 3 D. 5 3
Câu 6: Viết dạng lũy thừa số mũ hữu tỉ biểu thức a a với a  0 . 1 2 1 5 A. 6 a B. 3 a C. 12 a D. 6 a log 9 log log 3 Câu 7: 2 Cho phương trình 2 2 2  .3 x x xx
. Với điều kiện x thỏa mãn, một trong những cách giải 
phương trình trên là bước đầu đặt t log2 x , thay vào phương trình ban đầu, trở thành phương trình theo
ẩn t hoàn toàn. Hãy giải phương trình tìm t .
Mã đề thi 320 - Trang số : 1 1 t  A. t  4 B. 2 C. t  0 D. t  1. x 1  Câu 8: Gọi x 0
x là nghiệm của phương trình 5  2.5 15. Hãy chọn nhận xét đúng. 1 0 x    A. x  0 x  (1; 2) 0 x 1 0 B. 2 C. 0 D. 0
Câu 9: Đồ thị ở hình vẽ biểu diễn cho hàm số nào sau đây:  x 1    y  2      A. y 1 log y 1 log y log (x 1) 2 x B. 4 . C. 2 x D. 2 3 4 a A
Câu 10: Thu gọn biểu thức 2 a , (a  0) . 5  11 5  3 A. 4 a B. 4 a C. 2 a D. 8 a 2
y  log (x  2)
Câu 11: Tìm điều kiện của x để hàm số 2 xác định. A. x  2 B. x   C. x  2 D. x  2
Câu 12: Cho a  0, a  1 . Đơn giản biểu thức B  log a a a  2 4 3  11 3 11 3 A. 4 a B. 4 C. 2 a D. 2 2
Câu 13: Đạo hàm của hàm số ( ) x f x  là hàm nào sau đây: 2x x 2 2 . x 2  x 2 . x ln 2 x 3 x 1 2 . x 2 x 2   x(2  x ln 2) A. 2x B. 2 2 x C. 2x D. Đáp án khác
Câu 14: Tìm điều kiện của x để hàm số y  log xác định. 2 x x 2 1 A. x  2 B. 0  x  2 C.   x  0, x  D. x 0, x 2 2 
Câu 15: Cho biết tập xác định của hàm số f x  x   5 2 ( ) 4 .  \   2   2;  2 A. B.  C. D. ( ;  2  )  (2;)
Mã đề thi 320 - Trang số : 2
Câu 16: Cho các mệnh đề sau
i. Với x , x  0 thì 5log x  5log x  5 log x  log x  5log x 1 2  1 2  2 1 2 1 x   
ii. Cho x , x , x  0 log (x x x )
log x .log x .log 1 2 3
và 0  a  1, ta có: x a 1 2 3 a 1 a 2 a 3 1 1 iii. log
12  log 12  (1 log 2) . 2 6 6 (2 .3) 2 2 1 1
iv. Cho các số thực dương a,b với a  1 , ta có: log (ab)   log . 2 b 2 2 a a Số mệnh đề sai là: A. 1 B. 3 C. 2 D. 4 2 cos
Câu 17: Đạo hàm của hàm số ( ) 2 x f x  là hàm nào sau đây: 2 cos 2 cos 2 2 x cos 1 cos x A. sin(2 ).2 x x B. sin(2x).2 .ln 2 C. sin(2 ).2 x x   D. sin(2x).2 .ln 2
Câu 18: Hãy chọn mệnh đề đúng:
A. Cho số a dương khác 1 và x  0 : log ( 2
x)  log 2  log (x) a a a . 1 2 2
log x  3log x  2  0  log x  3log x  2  0 9 3 3 3
B. Với mọi x  0 , 2 x      2
; 2 , log x  4  log(x  2)  log(x  2). C. 2 2          
D. Với mọi x thỏa (x 1)  0 , ta có: log (x 1) 2 log 5 log (x 1) log 5 x 1 5 x 6 4 4 4 4 .
Câu 19: Giải phương trình 3x 4x 5x   . A. x  2  . B. x  2. C. x  3. D. x  0.
Câu 20: Số vi khuẩn trong ống nghiệm ban đầu có 100 con, chỉ sau hai giờ đã là 4000 con. Biết số lượng
vi khuẩn tăng trong mỗi giờ theo một tỷ lệ không đổi. Hãy ước lượng sau năm giờ (tính từ ban đầu có 100
con) số vi khuẩn sẽ có, gấp khoảng bao nhiêu lần số vi khuẩn ban đầu (chọn đáp án gần đúng nhất).
A. Gấp khoảng 11.000 lần.
B. Gấp khoảng 12.000 lần.
C. Gấp khoảng 10.000 lần.
D. Gấp khoảng 9.000 lần .
Câu 21: Cho hai số thực a và b , với 0  a b  1. Khẳng định nào dưới đây là khẳng định đúng?       A. 1 log b log a a b b a a b B. 1 log log b a
C. log a  1  log b D. log 1 log a b b a 2
log (x 1)  log (2x 1)  0
Câu 22: Hãy cho biết số nghiệm của phương trình 3 3 . A. Vô nghiệm. B. Hai. C. Một. D. Bốn
Câu 23: Một chiếc ô tô mới mua năm 2016 với giá 900 triệu đồng. Cứ sau mỗi năm, giá chiếc ô tô này bị
giảm 10% .Hỏi đến năm 2020, giá chiếc ô tô này là bao nhiêu? A. 864.536409 đồng B. 656.100.000 đồng C. 531.441.000 đồng D. 590.490.000 đồng
Câu 24: Cho số thực x thỏa mãn 2016log x  2016 . Vậy giá trị x là: A. 5 B. 1 C. 0 D. 10 1 log 1 2 log  4  2 x Câu 25: Gọi 0
x là nghiệm của phương trình
2 . Hãy chọn nhận xét đúng. A. 0 x là số vô tỷ. B. 0
x là số tự nhiên. C. 0
x là số hữu tỷ dương. D. 0
x là số nguyên âm.
Mã đề thi 320 - Trang số : 3     
Câu 26: Số nghiệm của phương trình log (2x 1) log (x 3) 1 3 3 là: A. Vô nghiệm. B. Hai. C. Ba. D. Một. x 0;2
Câu 27: Giá trị lớn nhất của hàm số f (x)  e ln(1 2x) trên đoạn bằng: 2 2 A. e ln 5 B. e ln 3 C. 0. D. e ln 6 2  3;  0
Câu 28: Giá trị nhỏ nhất của hàm số f (x)  x  4 ln(1 x) trên đoạn
là giá trị nào sau đây? A. 9   4ln 4 B. 0. C. 1 4ln 2. D. 1 4 ln 3 2
log x  8log x  8m  4  0
Câu 29: Tìm tất cả những giá trị m để phương trình 2 2 vô nghiệm trên đoạn 1;4. 1 1 1 1 m   m m m  A. 2 hoặc 2 B. m  0 hoặc 2 C. m  0 hoặc 2 D. m  0
Câu 30: Quan sát đồ thị, cho biết đồ thị đó có thể là của hàm nào sau đây: x x
A. y a (0  a  1)
B. y  log x (b  1) y a a y xb b C. ( 1) D. log (0 1) b
----------------- Hết -----------------
Mã đề thi 320 - Trang số : 4 SỞ GD&ĐT KIÊN GIANG KIỂM TRA TOÁN 12
TRƯỜNG THPT CHUYÊN HUỲNH MẪN ĐẠT BÀI THI: TOÁN 12 CH, CB, NC ---------------
(Thời gian làm bài: 45 phút) MÃ ĐỀ THI: 443
Họ tên thí sinh:.................................................SBD:.........................
Câu 1: Quan sát đồ thị, cho biết đồ thị đó có thể là của hàm nào sau đây: x x
A. y a (a  1)
B. y a (0  a  1)
C. y  log x (b  1) y xb b D. log (0 1) b
Câu 2: Số vi khuẩn trong ống nghiệm ban đầu có 100 con, chỉ sau hai giờ đã là 4000 con. Biết số lượng vi
khuẩn tăng trong mỗi giờ theo một tỷ lệ không đổi. Hãy ước lượng sau năm giờ (tính từ ban đầu có 100
con) số vi khuẩn sẽ có, gấp khoảng bao nhiêu lần số vi khuẩn ban đầu (chọn đáp án gần đúng nhất).
A. Gấp khoảng 9.000 lần .
B. Gấp khoảng 12.000 lần.
C. Gấp khoảng 10.000 lần.
D. Gấp khoảng 11.000 lần.     
Câu 3: Số nghiệm của phương trình log (2x 1) log (x 3) 1 3 3 là: A. Một. B. Ba. C. Hai. D. Vô nghiệm.
Câu 4: Quan sát đồ thị, cho biết đồ thị đó có thể biểu diễn cho hàm số nào? x 2 x 1 A. y  3 1
B. y x  2 . C. y  2 1 D. 2x y   3
Câu 5: Viết dạng lũy thừa số mũ hữu tỉ biểu thức a a với a  0 . 2 5 1 1 A. 3 a B. 6 a C. 6 a D. 12 a
Câu 6: Một chiếc ô tô mới mua năm 2016 với giá 900 triệu đồng. Cứ sau mỗi năm, giá chiếc ô tô này bị
Mã đề thi 443 - Trang số : 1
giảm 10% .Hỏi đến năm 2020, giá chiếc ô tô này là bao nhiêu? A. 590.490.000 đồng B. 531.441.000 đồng C. 864.536409 đồng D. 656.100.000 đồng x 0;2
Câu 7: Giá trị lớn nhất của hàm số f (x)  e ln(1 2x) trên đoạn bằng: 2 2 A. 0. B. e ln 6 C. e ln 5 D. e ln 3
Câu 8: Cho số thực x thỏa mãn 2016log x  2016 . Vậy giá trị x là: A. 0 B. 1 C. 5 D. 10 1 Câu 9: Gọi 0
x là nghiệm của phương trình log 1 2log
 . Hãy chọn nhận xét đúng. 4  2 x  2 A. 0 x là số vô tỷ. B. 0
x là số nguyên âm. C. 0
x là số hữu tỷ dương. D. 0
x là số tự nhiên. 3 2
Câu 10: Thu gọn biểu thức: x .x  ? 5 5 A. x B. x C. 5x D. x 3 4 a A
Câu 11: Thu gọn biểu thức 2 a , (a  0) . 5  5  3 11 A. 4 a B. 2 a C. 8 a D. 4 a
Câu 12: Hãy chọn mệnh đề đúng: A. x      2
; 2 , log x  4  log(x  2)  log(x  2).
B. Cho số a dương khác 1 và x  0 : log ( 2
x)  log 2  log (x) . a a a
C. Với mọi x thỏa 2
(x 1)  0 , ta có: 2
log (x 1)  2 log 5  log (x 1)  log 5  x 1  5  x  6 . 4 4 4 4 1
D. Với mọi x  0 , 2 2
log x  3log x  2  0  log x  3log x  2  0 . 9 3 3 3 2
Câu 13: Tìm điều kiện của x để hàm số y  log xác định. 2 x x 2 1
A. x  0, x  2 B. 0  x  2 C. x  2
D. x  0, x  2  Câu 14: Gọi x x 0
x là nghiệm của phương trình 1 5
 2.5 15 . Hãy chọn nhận xét đúng. 1 0 x    A. x  0 x  (1; 2) 0 x 1 0 B. 0 C. 2 D. 0 2  3;  0
Câu 15: Giá trị nhỏ nhất của hàm số f (x)  x  4 ln(1 x) trên đoạn
là giá trị nào sau đây? A. 1 4ln 2. B. 9   4ln 4 C. 1 4ln 3 D. 0. / g x   2 ( ) ln x   1
Câu 16: Hãy cho biết giá trị của g (2) nếu : 2 2 A. 3 B. 0,8 C. 5 D. 0,65
Câu 17: Đặt a  ln 2 và b  ln 5 . Hãy biểu diễn ln 200 theo a và b . A. 3b  2a B. 3a  2b C. 6ab D. 3a  2b log 9 2 log log 3
Câu 18: Cho phương trình 2 2 2  .3 x x xx
. Với điều kiện x thỏa mãn, một trong những cách giải 
phương trình trên là bước đầu đặt t log2 x , thay vào phương trình ban đầu, trở thành phương trình theo
Mã đề thi 443 - Trang số : 2
ẩn t hoàn toàn. Hãy giải phương trình tìm t . 1 t  A. t  0 B. t  1. C. t  4 D. 2
Câu 19: Cho các mệnh đề sau
i. Với x , x  0 thì 5log x  5log x  5 log x  log x  5log x . 1 2  1 2  2 1 2 1 x
ii. Cho x , x , x  0
log (x x x )  log x .log x .log 1 2 3
và 0  a  1, ta có: x a 1 2 3 a 1 a 2 a 3 1 1 iii. log
12  log 12  (1 log 2) 2 6 6 (2 .3) 2 2 1 1
iv. Cho các số thực dương a,b , với a  1 , ta có: log (ab)   log . 2 b 2 2 a a Số mệnh đề sai là: A. 1 B. 2 C. 3 D. 4 2
log x  8log x  8m  4  0
Câu 20: Tìm tất cả những giá trị m để phương trình 2 2 vô nghiệm trên đoạn 1;4. 1 1 1 1 m m m   m  A. m  0 hoặc 2 B. m  0 hoặc 2 C. m  0 D. 2 hoặc 2 2
log (x 1)  log (2x 1)  0
Câu 21: Hãy cho biết số nghiệm của phương trình 3 3 . A. Hai. B. Bốn C. Một. D. Vô nghiệm. 
f x   x   5 2 ( ) 4
Câu 22: Cho biết tập xác định của hàm số .  2;  2  \  2  A. B.  C. D. ( ;  2  )  (2;)
Câu 23: Giải phương trình 3x 4x 5x   . A. x  3. B. x  2  . C. x  2. D. x  0. 2 cos
Câu 24: Đạo hàm của hàm số ( ) 2 x f x  là hàm nào sau đây: 2 cos 2 2 2 x cos cos 1 cos x A.  sin(2x).2 .ln 2 B. sin(2 ).2 x x C. sin(2 ).2 x x   D. sin(2x).2 .ln 2
Câu 25: Cho a  0, a  1 . Đơn giản biểu thức B  log a a . a  2 4 3  11 3 3 11 A. 4 B. 2 a C. 4 a D. 2 2 ( ) x f x
Câu 26: Đạo hàm của hàm số
2x là hàm nào sau đây: x 2 2 . x 2  x 2 . x ln 2 x 3 x 1 2 . x 2 x 2   x(2  x ln 2) A. 2x B. 2 2 x C. 2x D. Đáp án khác
Câu 27: Cho hai số thực a và b , với 0  a b  1. Khẳng định nào dưới đây là khẳng định đúng?       A. log b a b a a b
a  1  log b B. log 1 log a b C. 1 log log a b D. 1 log log b a b a 2
y  log (x  2)
Câu 28: Tìm điều kiện của x để hàm số 2 xác định.
Mã đề thi 443 - Trang số : 3 A. x   B. x  2 C. x  2 D. x  2
Câu 29: Trong các mệnh đề sau, cho biết có bao nhiêu mệnh đề sai: x
i. Đồ thị của hai hàm số y a và y  log x    a
(với 0 a 1) đối xứng nhau qua đường thẳng y x . 1
ii. Với a  1, ta có đồ thị hai hàm số x
y a và y
đối xứng nhau qua trục tung. x a
iii. Một tiệm cận của đồ thị hàm số y  log x (0  a  1) y a có phương trình là 0 .
iv. Đồ thị hàm số y  ln x có 2 nhánh đối xứng nhau qua trục tung. A. Một. B. Bốn. C. Ba. D. Hai.
Câu 30: Đồ thị ở hình vẽ biểu diễn cho hàm số nào sau đây:  x 1   y  2       A. y log (x 1) y 1 log y 1 log 2 B. 4 . C. 2 x D. 2 x
----------------- Hết -----------------
Mã đề thi 443 - Trang số : 4 SỞ GD&ĐT KIÊN GIANG KIỂM TRA TOÁN 12
TRƯỜNG THPT CHUYÊN HUỲNH MẪN ĐẠT BÀI THI: TOÁN 12 CH, CB, NC ---------------
(Thời gian làm bài: 45 phút) MÃ ĐỀ THI: 566
Họ tên thí sinh:.................................................SBD:.........................
Câu 1: Cho các mệnh đề sau
i. Với x , x  0 thì 5log x  5log x  5 log x  log x  5log x . 1 2  1 2  2 1 2 1 x   
ii. Cho x , x , x  0 log (x x x )
log x .log x .log 1 2 3
và 0  a  1, ta có: x a 1 2 3 a 1 a 2 a 3 1 1 iii. log
12  log 12  (1 log 2) 2 6 6 (2 .3) 2 2 1 1
iv. Cho các số thực dương a,b , với a  1 , ta có: log (ab)   log . 2 b 2 2 a a Số mệnh đề sai là: A. 4 B. 2 C. 3 D. 1
Câu 2: Số vi khuẩn trong ống nghiệm ban đầu có 100 con, chỉ sau hai giờ đã là 4000 con. Biết số lượng vi
khuẩn tăng trong mỗi giờ theo một tỷ lệ không đổi. Hãy ước lượng sau năm giờ (tính từ ban đầu có 100
con) số vi khuẩn sẽ có, gấp khoảng bao nhiêu lần số vi khuẩn ban đầu (chọn đáp án gần đúng nhất).
A. Gấp khoảng 9.000 lần .
B. Gấp khoảng 12.000 lần.
C. Gấp khoảng 10.000 lần.
D. Gấp khoảng 11.000 lần. 2
y  log (x  2)
Câu 3: Tìm điều kiện của x để hàm số 2 xác định. A. x  2 B. x  2 C. x   D. x  2 3
Câu 4: Viết dạng lũy thừa số mũ hữu tỉ biểu thức a a với a  0 . 5 2 1 1 A. 6 a B. 3 a C. 6 a D. 12 a
Câu 5: Trong các mệnh đề sau, cho biết có bao nhiêu mệnh đề sai: x
i. Đồ thị của hai hàm số y a và y log x    a
(với 0 a 1) đối xứng nhau qua đường thẳng y x . 1  x y
ii. Với a  1, ta có đồ thị hai hàm số y a và x
a đối xứng nhau qua trục tung.
iii. Một tiệm cận của đồ thị hàm số y  log x (0  a  1) có phương trình là y  0 . a
iv. Đồ thị hàm số y  ln x có 2 nhánh đối xứng nhau qua trục tung. A. Bốn. B. Ba. C. Một. D. Hai. log 9 2 log log 3
Câu 6: Cho phương trình 2 2 2  .3 x x xx
. Với điều kiện x thỏa mãn, một trong những cách giải 
phương trình trên là bước đầu đặt t log2 x , thay vào phương trình ban đầu, trở thành phương trình theo
ẩn t hoàn toàn. Hãy giải phương trình tìm t . 1 t  A. t  4 B. t  1. C. 2 D. t  0
Câu 7: Cho a  0, a  1. Đơn giản biểu thức B  log a a . a  2 4 3 
Mã đề thi 566 - Trang số : 1 3 11 3 11 A. 2 a B. 4 a C. 2 D. 4
Câu 8: Giải phương trình 3x 4x 5x   . A. x  0. B. x  2 . C. x  3. D. x  2. x 1  Câu 9: Gọi x 0
x là nghiệm của phương trình 5  2.5 15. Hãy chọn nhận xét đúng. 1   0 x  A. x  0 0 x 1 x  (1; 2) 0 B. 0 C. 0 D. 2
Câu 10: Tìm điều kiện của x để hàm số y  log xác định. 2 x x 2 1 A. x  2 B.   x  0, x  C. 0  x  2 D. x 0, x 2 2
Câu 11: Quan sát đồ thị, cho biết đồ thị đó có thể biểu diễn cho hàm số nào? x 1 2 x A. y  2 1 B. 2x y  
C. y x  2 . D. y  3 1 2  3;  0
Câu 12: Giá trị nhỏ nhất của hàm số f (x)  x  4ln(1 x) trên đoạn
là giá trị nào sau đây? A. 1 4ln 2. B. 9  4 ln 4 C. 1 4ln 3 D. 0.     
Câu 13: Số nghiệm của phương trình log (2x 1) log (x 3) 1 3 3 là: A. Hai. B. Một. C. Vô nghiệm. D. Ba. 2 cos
Câu 14: Đạo hàm của hàm số ( ) 2 x f x  là hàm nào sau đây: 2 cos 2 cos 2 2 x cos x cos 1 A.  sin(2 ).2 x x B. sin(2x).2 .ln 2 C.  sin(2x).2 .ln 2 D. sin(2 ).2 x x  
Câu 15: Hãy chọn mệnh đề đúng: 1
A. Với mọi x  0 , 2 2
log x  3log x  2  0  log x  3log x  2  0 . 9 3 3 3 2 B. x      2
; 2 , log x  4  log(x  2)  log(x  2). 2
C. Với mọi x thỏa (x 1)  0 , ta có: 2
log (x 1)  2log 5  log (x 1)  log 5  x 1  5  x  6 . 4 4 4 4
D. Cho số a dương khác 1 và x  0 : log ( 2
x)  log 2  log (x) . a a a
Mã đề thi 566 - Trang số : 2
Câu 16: Cho hai số thực a và b , với 0  a b  1. Khẳng định nào dưới đây là khẳng định đúng?       A. log a b b a b a
a  1  log b B. 1 log log b a C. 1 log log a b D. log 1 log a b b a
Câu 17: Đặt a  ln 2 và b  ln 5 . Hãy biểu diễn ln 200 theo a và b . A. 3b  2a B. 3a  2b C. 6ab D. 3a  2b
Câu 18: Cho biết tập xác định của hàm số f x  x   5 2 ( ) 4 .  2;  2  \  2  A. B.  C. D. ( ;  2  )  (2;) / g x   2 ( ) ln x   1
Câu 19: Hãy cho biết giá trị của g (2) nếu : 2 2 A. 3 B. 0,65 C. 0,8 D. 5
Câu 20: Đồ thị ở hình vẽ biểu diễn cho hàm số nào sau đây:  x 1   y  2       A. y 1 log y 1 log y log (x 1) 2 x B. 4 . C. 2 x D. 2
Câu 21: Cho số thực x thỏa mãn 2016log x  2016 . Vậy giá trị x là: A. 1 B. 10 C. 0 D. 5
Câu 22: Quan sát đồ thị, cho biết đồ thị đó có thể là của hàm nào sau đây: x   x   
A. y a (0  a  1)
B. y log x (b 1) y a a y x b b C. ( 1) D. log (0 1) b 2 ( ) x f x
Câu 23: Đạo hàm của hàm số
2x là hàm nào sau đây:
Mã đề thi 566 - Trang số : 3 x 2 2 . x 2  x 2 . x ln 2 x 3 x 1 2 . x 2 x 2   x(2  x ln 2) A. 2x B. 2 2 x C. 2x D. Đáp án khác 1 log 1 2log  4  2 x Câu 24: Gọi 0
x là nghiệm của phương trình
2 . Hãy chọn nhận xét đúng. A. 0
x là số tự nhiên. B. 0
x là số hữu tỷ dương. C. 0 x là số vô tỷ. D. 0
x là số nguyên âm. x 0;2
Câu 25: Giá trị lớn nhất của hàm số f (x)  e ln(1 2x) trên đoạn bằng: A. 0. B. 2 e ln 5 C. e ln 3 D. 2 e ln 6 3 2
Câu 26: Thu gọn biểu thức: x .x  ? A. 5x B. x C. 5 x D. 5 x 2
log (x 1)  log (2x 1)  0
Câu 27: Hãy cho biết số nghiệm của phương trình 3 3 . A. Hai. B. Bốn C. Vô nghiệm. D. Một. 3 4 a A
Câu 28: Thu gọn biểu thức 2 a , (a  0) . 3 11 5  5  A. 8 a B. 4 a C. 2 a D. 4 a 2
log x  8log x  8m  4  0
Câu 29: Tìm tất cả những giá trị m để phương trình 2 2 vô nghiệm trên đoạn 1;4. 1 1 1 1 m   m m m  A. 2 hoặc 2 B. m  0 hoặc 2 C. m  0 hoặc 2 D. m  0
Câu 30: Một chiếc ô tô mới mua năm 2016 với giá 900 triệu đồng. Cứ sau mỗi năm, giá chiếc ô tô này bị
giảm 10% .Hỏi đến năm 2020, giá chiếc ô tô này là bao nhiêu? A. 531.441.000 đồng B. 656.100.000 đồng C. 590.490.000 đồng D. 864.536409 đồng
----------------- Hết -----------------
Mã đề thi 566 - Trang số : 4 SỞ GD&ĐT KIÊN GIANG KIỂM TRA TOÁN 12
TRƯỜNG THPT CHUYÊN HUỲNH MẪN ĐẠT BÀI THI: TOÁN 12 CH, CB, NC ---------------
(Thời gian làm bài: 45 phút) MÃ ĐỀ THI: 689
Họ tên thí sinh:.................................................SBD:......................... 3 2
Câu 1: Thu gọn biểu thức: x .x  ? 5 5 A. x B. x C. 5x D. x
Câu 2: Cho a  0 . Đơn giản biểu thức B  log a a a  2 4 3  11 3 11 3 A. 4 B. 4 a C. 2 D. 2 a
Câu 3: Quan sát đồ thị, cho biết đồ thị đó có thể biểu diễn cho hàm số nào? x x 2 1 A. y  2 1 B. y  3 1
C. y x  2 . D. 2x y   log 9 2 log log 3
Câu 4: Cho phương trình 2 2 2  .3 x x xx
. Với điều kiện x thỏa mãn, một trong những cách giải 
phương trình trên là bước đầu đặt t log2 x , thay vào phương trình ban đầu, trở thành phương trình theo
ẩn t hoàn toàn. Hãy giải phương trình tìm t . 1 t  A. 2 B. t  0 C. t  4 D. t  1.
Câu 5: Tìm điều kiện của x để hàm số y  log xác định. 2 x x 2 1 A. 0  x  2 B. x  2 C.   x  0, x  D. x 0, x 2 2
Câu 6: Hãy cho biết số nghiệm của phương trình 2
log (x 1)  log (2x 1)  0 . 3 3 A. Bốn B. Hai. C. Vô nghiệm. D. Một. 3
Câu 7: Viết dạng lũy thừa số mũ hữu tỉ biểu thức a a với a  0 . 1 5 2 1 A. 6 a B. 6 a C. 3 a D. 12 a
Câu 8: Hãy chọn mệnh đề đúng:
Mã đề thi 689 - Trang số : 1 2 2          
A. Với mọi x thỏa (x 1)  0 , ta có: log (x 1) 2log 5 log (x 1) log 5 x 1 5 x 6 4 4 4 4 .    
B. Cho số a dương khác 1 và x  0 : log ( 2x) log 2 log ( x) a a a . 1
C. Với mọi x  0 , 2 2
log x  3log x  2  0  log x  3log x  2  0 . 9 3 3 3 2 D. x      2
; 2 , log x  4  log(x  2)  log(x  2). 2
Câu 9: Đạo hàm của hàm số ( ) x f x  là hàm nào sau đây: 2x x 2 2 . x 2  x 2 . x ln 2 x 3 x 1 2 . x 2 x 2   x(2  x ln 2) A. 2x B. 2 2 x C. 2x D. Đáp án khác / g x   2 ( ) ln x   1
Câu 10: Hãy cho biết giá trị của g (2) nếu : 2 2 A. 0,8 B. 5 C. 3 D. 0,65
Câu 11: Cho số thực x thỏa mãn 2016log x  2016 . Vậy giá trị x là: A. 0 B. 5 C. 10 D. 1     
Câu 12: Số nghiệm của phương trình log (2x 1) log (x 3) 1 3 3 là: A. Vô nghiệm. B. Ba. C. Hai. D. Một.
Câu 13: Trong các mệnh đề sau, cho biết có bao nhiêu mệnh đề sai: x
i. Đồ thị của hai hàm số y a và y  log xa
(với 0  a  1) đối xứng nhau qua đường thẳng y x . 1
ii. Với a  1, ta có đồ thị hai hàm số x
y a và y
đối xứng nhau qua trục tung. x a
iii. Một tiệm cận của đồ thị hàm số y  log x (0  a  1) có phương trình là y  0 . a
iv. Đồ thị hàm số y  ln x có 2 nhánh đối xứng nhau qua trục tung. A. Ba. B. Một. C. Hai. D. Bốn.
Câu 14: Đồ thị ở hình vẽ biểu diễn cho hàm số nào sau đây:  x 1        y  2  A. y log (x 1) y 1 log y 1 log 2 B. 2 x C. 2 x D. 4 .
Mã đề thi 689 - Trang số : 2
Câu 15: Một chiếc ô tô mới mua năm 2016 với giá 900 triệu đồng. Cứ sau mỗi năm, giá chiếc ô tô này bị
giảm 10% .Hỏi đến năm 2020, giá chiếc ô tô này là bao nhiêu? A. 590.490.000 đồng B. 656.100.000 đồng C. 531.441.000 đồng D. 864.536409 đồng
Câu 16: Đặt a  ln 2 và b  ln 5 . Hãy biểu diễn ln 200 theo a và b . A. 3b  2a B. 3a  2b C. 6ab D. 3a  2b . 2  3;  0
Câu 17: Giá trị nhỏ nhất của hàm số f (x)  x  4ln(1 x) trên đoạn
là giá trị nào sau đây? A. 1 4ln 3 B. 9   4ln 4 C. 0. D. 1 4 ln 2. x 0;2
Câu 18: Giá trị lớn nhất của hàm số f (x)  e ln(1 2x) trên đoạn bằng: A. e ln 3 B. 0. C. 2 e ln 5 D. 2 e ln 6  Câu 19: Gọi x x 0
x là nghiệm của phương trình 1 5
 2.5 15 . Hãy chọn nhận xét đúng. 1 0 x  A. x  (1;2) 0  x  1 x  0 0 B. 2 C. 0 D. 0 2
log x  8log x  8m  4  0
Câu 20: Tìm tất cả những giá trị m để phương trình 2 2 vô nghiệm trên đoạn 1;4. 1 1 1 1 m   m m m  A. 2 hoặc 2 B. m  0 hoặc 2 C. m  0 hoặc 2 D. m  0
Câu 21: Cho các mệnh đề sau
i. Với x , x  0 1 2
thì 5log x  5log x  5log x  log x  2  5log x . 1 2 1 2 1 x
ii. Cho x , x , x  0 1 2 3
và 0  a  1, ta có: log (x x x )  log x .log x .log x . a 1 2 3 a 1 a 2 a 3 1 1 iii. log
12  log 12  (1 log 2) . 2 6 6 (2 .3) 2 2 1 1
iv. Cho các số thực dương a,b , với a  1 , ta có: log (ab)   log . 2 b 2 2 a a Số mệnh đề sai là: A. 3 B. 1 C. 4 D. 2
Câu 22: Giải phương trình 3x 4x 5x   . A. x  0. B. x  2. C. x  2  . D. x  3. 1 Câu 23: Gọi 0
x là nghiệm của phương trình log 1 2log
 . Hãy chọn nhận xét đúng. 4  2 x  2 A. 0
x là số nguyên âm. B. 0
x là số tự nhiên. C. 0 x là số vô tỷ. D. 0
x là số hữu tỷ dương.
Câu 24: Quan sát đồ thị, cho biết đồ thị đó có thể là của hàm nào sau đây:
Mã đề thi 689 - Trang số : 3 x x
A. y  log x (b  1) y a a y aa y xb b B. ( 1) C. (0 1) D. log (0 1) b
f x   x   5 2 ( ) 4
Câu 25: Cho biết tập xác định của hàm số .  2;  2  \  2  A. ( ;  2  )  (2;) B. C. D.  3 4
Câu 26: Thu gọn biểu thức a A  , (a  0) . 2 a 5  3 5  11 A. 4 a B. 8 a C. 2 a D. 4 a
Câu 27: Cho hai số thực a và b , với 0  a b  1. Khẳng định nào dưới đây là khẳng định đúng?       A. log a b b a b a
a  1  log b B. 1 log log b a C. log 1 log a b D. 1 log log a b b a 2
y  log (x  2)
Câu 28: Tìm điều kiện của x để hàm số 2 xác định. A. x  2 B. x   C. x  2 D. x  2 2 cos
Câu 29: Đạo hàm của hàm số ( ) 2 x f x  là hàm nào sau đây: 2 cos 1 2 cos 2 cos 2 x cos x A. sin(2 ).2 x x   B. sin(2 ).2 x x C. sin(2x).2 .ln 2 D. sin(2x).2 .ln 2
Câu 30: Số vi khuẩn trong ống nghiệm ban đầu có 100 con, chỉ sau hai giờ đã là 4000 con. Biết số lượng
vi khuẩn tăng trong mỗi giờ theo một tỷ lệ không đổi. Hãy ước lượng sau năm giờ (tính từ ban đầu có 100
con) số vi khuẩn sẽ có, gấp khoảng bao nhiêu lần số vi khuẩn ban đầu (chọn đáp án gần đúng nhất).
A. Gấp khoảng 10.000 lần.
B. Gấp khoảng 11.000 lần.
C. Gấp khoảng 9.000 lần .
D. Gấp khoảng 12.000 lần.
----------------- Hết -----------------
Mã đề thi 689 - Trang số : 4 SỞ GD&ĐT KIÊN GIANG KIỂM TRA TOÁN 12
TRƯỜNG THPT CHUYÊN HUỲNH MẪN ĐẠT BÀI THI: TOÁN 12 CH, CB, NC ---------------
(Thời gian làm bài: 45 phút) MÃ ĐỀ THI: 812
Họ tên thí sinh:.................................................SBD:......................... log 9 2 log log 3
Câu 1: Cho phương trình 2 2 2  .3 x x xx
. Với điều kiện x thỏa mãn, một trong những cách giải 
phương trình trên là bước đầu đặt t log2 x , thay vào phương trình ban đầu, trở thành phương trình theo
ẩn t hoàn toàn. Hãy giải phương trình tìm t . 1 t  A. t  4 B. 2 C. t  1. D. t  0
Câu 2: Trong các mệnh đề sau, cho biết có bao nhiêu mệnh đề sai:
i. Đồ thị của hai hàm số x
y a và y  log x (với 0  a  1 ) đối xứng nhau qua đường thẳng y x . a 1
ii. Với a  1, ta có đồ thị hai hàm số x
y a và y
đối xứng nhau qua trục tung. x a
iii. Một tiệm cận của đồ thị hàm số y  log x (0  a  1) có phương trình là y  0 . a
iv. Đồ thị hàm số y  ln x có 2 nhánh đối xứng nhau qua trục tung. A. Ba. B. Hai. C. Bốn. D. Một. 
f x   x   5 2 ( ) 4
Câu 3: Cho biết tập xác định của hàm số .  \   2  2;  2 A. ( ;  2  )  (2;) B. C.  D.
Câu 4: Đồ thị ở hình vẽ biểu diễn cho hàm số nào sau đây:         x 1 A. y 1 log y 1 log y log (x 1) 2 x B. 2 x C. y  2  . D. 2 4 3
Câu 5: Viết dạng lũy thừa số mũ hữu tỉ biểu thức a a với a  0 . 2 1 5 1 A. 3 a B. 12 a C. 6 a D. 6 a
Câu 6: Quan sát đồ thị, cho biết đồ thị đó có thể biểu diễn cho hàm số nào?
Mã đề thi 812 - Trang số : 1 1 x 2 x A. 2x y   B. y  3 1
C. y x  2 . D. y  2 1 2 cos
Câu 7: Đạo hàm của hàm số ( ) 2 x f x  là hàm nào sau đây: 2 cos 1 2 cos 2 cos 2 x cos x A. sin(2 ).2 x x   B. sin(2 ).2 x x C. sin(2x).2 .ln 2 D. sin(2x).2 .ln 2
Câu 8: Một chiếc ô tô mới mua năm 2016 với giá 900 triệu đồng. Cứ sau mỗi năm, giá chiếc ô tô này bị
giảm 10% .Hỏi đến năm 2020, giá chiếc ô tô này là bao nhiêu? A. 656.100.000 đồng B. 590.490.000 đồng C. 864.536409 đồng D. 531.441.000 đồng
Câu 9: Quan sát đồ thị, cho biết đồ thị đó có thể là của hàm nào sau đây: x x     
A. y a (0  a  1)
B. y a (a  1)
C. y log x (b 1) y x b b D. log (0 1) b
Câu 10: Số vi khuẩn trong ống nghiệm ban đầu có 100 con, chỉ sau hai giờ đã là 4000 con. Biết số lượng
vi khuẩn tăng trong mỗi giờ theo một tỷ lệ không đổi. Hãy ước lượng sau năm giờ (tính từ ban đầu có 100
con) số vi khuẩn sẽ có, gấp khoảng bao nhiêu lần số vi khuẩn ban đầu (chọn đáp án gần đúng nhất).
A. Gấp khoảng 10.000 lần.
B. Gấp khoảng 9.000 lần .
C. Gấp khoảng 12.000 lần.
D. Gấp khoảng 11.000 lần.
Câu 11: Tìm điều kiện của x để hàm số y  log xác định. 2 x x 2 1 A. x  2
B. x  0, x  2 C. 0  x  2
D. x  0, x  2 x 0;2
Câu 12: Giá trị lớn nhất của hàm số f (x)  e ln(1 2x) trên đoạn bằng: A. 2 e ln 5 B. e ln 3 C. 2 e ln 6 D. 0.
Mã đề thi 812 - Trang số : 2 3 2
Câu 13: Thu gọn biểu thức: x .x  ? 5 5 A. x B. x C. 5x D. x     
Câu 14: Số nghiệm của phương trình log (2x 1) log (x 3) 1 3 3 là: A. Hai. B. Vô nghiệm. C. Một. D. Ba. 2
Câu 15: Đạo hàm của hàm số ( ) x f x  là hàm nào sau đây: 2x x 2 2 . x 2  x 2 . x ln 2 x 3 x 1 2 . x 2 x 2   x(2  x ln 2) A. 2x B. 2 2 x C. 2x D. Đáp án khác x 1  Câu 16: Gọi x 0
x là nghiệm của phương trình 5  2.5 15. Hãy chọn nhận xét đúng. 1   0 x  A. x  0 0 x 1 x  (1; 2) 0 B. 0 C. 2 D. 0 2  3;  0
Câu 17: Giá trị nhỏ nhất của hàm số f (x)  x  4ln(1 x) trên đoạn
là giá trị nào sau đây? A. 1 4ln 3 B. 9  4 ln 4 C. 0. D. 1 4 ln 2.
Câu 18: Giải phương trình 3x 4x 5x   . A. x  3. B. x  2. C. x  0. D. x  2 . 1 Câu 19: Gọi 0
x là nghiệm của phương trình log 1 2log
 . Hãy chọn nhận xét đúng. 4  2 x  2 A. 0 x là số vô tỷ. B. 0
x là số tự nhiên. C. 0
x là số nguyên âm. D. 0
x là số hữu tỷ dương.
Câu 20: Cho a  0, a  1 . Đơn giản biểu thức B  log a a . a  2 4 3  3 11 3 11 A. 2 B. 4 C. 2 a D. 4 a
Câu 21: Cho các mệnh đề sau
i. Với x , x  0 1 2
thì 5log x  5log x  5log x  log x  2  5log x . 1 2 1 2 1 x
ii. Cho x , x , x  0 1 2 3
và 0  a  1, ta có: log (x x x )  log x .log x .log x . a 1 2 3 a 1 a 2 a 3 1 1 iii. log
12  log 12  (1 log 2) . 2 6 6 (2 .3) 2 2 1 1
iv. Cho các số thực dương a,b , với a  1 , ta có: log (ab)   log . 2 b 2 2 a a Số mệnh đề sai là: A. 4 B. 3 C. 1 D. 2
Câu 22: Cho hai số thực a và b , với 0  a b  1. Khẳng định nào dưới đây là khẳng định đúng?       A. log b a a b b a
a  1  log b B. log 1 log a b C. 1 log log b a D. 1 log log a b b a
Câu 23: Cho số thực x thỏa mãn 2016log x  2016 . Vậy giá trị x là: A. 0 B. 1 C. 10 D. 5
Câu 24: Đặt a  ln 2 và b  ln 5 . Hãy biểu diễn ln 200 theo a và b . A. 3b  2a B. 3a  2b C. 6ab D. 3a  2b .
Mã đề thi 812 - Trang số : 3
Câu 25: Tìm điều kiện của x để hàm số 2
y  log (x  2) xác định. 2 A. x  2 B. x  2 C. x  2 D. x  
Câu 26: Tìm tất cả những giá trị m để phương trình 2
log x  8log x  8m  4  0 vô nghiệm trên đoạn 2 2 1;4. 1 1 1 1 m m m   m  A. m  0 hoặc 2 B. m  0 hoặc 2 C. 2 hoặc 2 D. m  0
Câu 27: Hãy cho biết số nghiệm của phương trình 2
log (x 1)  log (2x 1)  0 . 3 3 A. Hai. B. Vô nghiệm. C. Một. D. Bốn 3 4 a A
Câu 28: Thu gọn biểu thức 2 a , (a  0) . 11 3 5  5  A. 4 a B. 8 a C. 4 a D. 2 a / g x   2 ( ) ln x   1
Câu 29: Hãy cho biết giá trị của g (2) nếu : 2 2 A. 0, 65 B. 3 C. 0,8 D. 5
Câu 30: Hãy chọn mệnh đề đúng: 2 2          
A. Với mọi x thỏa (x 1)  0 , ta có: log (x 1) 2log 5 log (x 1) log 5 x 1 5 x 6 4 4 4 4 .
B. Cho số a dương khác 1 và x  0 : log ( 2
x)  log 2  log (x) . a a a 1
C. Với mọi x  0 , 2 2
log x  3log x  2  0  log x  3log x  2  0 . 9 3 3 3 2 D. x      2
; 2 , log x  4  log(x  2)  log(x  2).
----------------- Hết -----------------
Mã đề thi 812 - Trang số : 4