Đề kiểm tra Giải tích 12 chương 3 trường THPT Y JUT – Đăk Lăk

Đề kiểm tra Giải tích 12 chương 3 trường THPT Y JUT – Đăk Lăk theo hình thức tự luận, nội dung kiểm tra thuộc chương nguyên hàm – tích phân và ứng dụng, đề kiểm tra có lời giải chi tiết.

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
ĐỀ KIỂM TRA GIẢI TÍCH 12 CHƯƠNG III
Thời gian làm bài: 45 phút (Không kể giao đề)
ĐỀ 1
TRƯỜNG THPT Y JUT
TỔ TOÁN
Câu 1: (4,5 điểm) 
a)
21
1
x
dx
x
b)
2
7 10
dx
xx
Câu 2: (4,0 điểm :
a)
1
1
2 ln
e
x xdx
b)
2
4
sin .sin
4
dx
xx



Câu 3: (1,5 điểm)

12y
x x x

ĐỀ 2
Câu 1: (4 điểm) m:
a)
32
2 3 1x x x
dx
x
b)
3
tan xdx
.
Câu 2: (4,5 điểm) 
a)
2
0
( 1)cosx xdx
b)
2
2
ln 9
e
e
dx
xx
Câu 3: (1,5 điểm) 
,
2x

Ox
.
ĐỀ 3
Câu 1: 
a.
2
3
2
1
21x
I dx
x
, b.
32
1
ln ln
e
xx
J dx
x
c.
2
0
1 2 cos2K x xdx

, d.
2
3
1 sin
1 cos
x
x
L e dx
x
Câu 2: 
4
2
xy

2 xy
Câu 3: 
0
2
2
y
xxy

Bài 4: 
1
2
1
4
1x
dx
I
ĐỀ 4
I. PHÂ
N CHUNG CHO TÂ
T CA
THI
SINH
Câu 1 (2 điê
m). Ch
ng minh r ng h
m s
2
( ) ln( 4)F x x
l

m c
a h
m s
2
2
()
4
x
fx
x
 R.
Câu 2 (3 điê
m). Cho h
m s
3
8
()
21
x
fx
x
a. T
m h

m c
a h
m s
()fx
.
b. T
m m

m
()Fx
c
a h
m s
()fx
sao cho
2012)1( F
.
Câu 3 (3 điê
m). T
nh c
c t

a.
4
4
2
0
1
sin2
cos
x
e x dx
x




b.
2
0
cos1
.2sin
x
dxx
II. PHÂ
N RIÊNG CHO TƯ
NG BAN
A. Phâ
n riêng cho ban KHTN
Câu 4A (2 điê
m ). T
nh t

4
2
0
cos
x
dx
x
B. Phâ
n riêng cho ban cơ ba
n A + D
Câu 4B (2 điê
m ). T
nh t

4
0
.2cos).32(
dxxx
®Ò 5
C©u 1: T×m c¸c nguyªn hµm cña c¸c hµm sè sau:
a/ f(x) = x
3
+
3
12
xx
b) f(x) = sin3x + cos5x -2e
2x
C©u 2: TÝnh c¸c tÝch ph©n sau:
a)
2
0
2
3011xx
dx
I
b)
3
1
.ln).1( dxxx
c)
4
0
1
dx
cosx
C©u 3: 
3
- -2

ĐÁP ÁN ĐỀ 1


Câu 1:
a (2,5 điểm)
2 1 3
2
11
x
dx dx
xx






1
2 3 2 3ln | 1|
1
dx dx x x C
x


 x 3
b.(2,0 điểm)
2
52
7 10
dx dx
xx
xx



1 1 1
3 5 2
dx
xx





1 1 1 1
3 5 3 2
dx dx
xx



11
ln 5 ln 2
33
x x C
15
ln
32
x
C
x



0,7

Câu 2:
a.(2,0 điểm)
1
1
2 ln
e
I x xdx

2
1
ln
12
du dx
ux
x
dv x dx
v x x



2
1
11
1
2 ln ln 1
ee
e
I x xdx x x x x dx

22
2
1
1
3
ln
22
e
e
xe
x x x x






0,5
b.(2,0 điểm)
2
4
sin .sin
4
dx
J
xx




cos
cos
4
cot cot
4 sin
sin
4
x
x
xx
x
x









sin .cos cos sin
44
sin .si n
4
x x x x
xx




11
.
2
sin .sin
4
xx




2
4
2 cot cot
4
J x x dx






22
44
2 cot 2 cot
4
xdx x dx






2
2
4
4
2ln sin 2ln sin 2ln2
4
xx






0,7
0,2


Câu 3:
(1,5 điểm)

0
1 2 0 1
2
x
x x x x
x

22
32
00
1 2 3 2S x x x dx x x x dx


32
32
32
3 2 0 1
32
3 2 1 2
x x x khi x
x x x
x x x khi x

12
3 2 3 2
01
3 2 3 2S x x x dx x x x dx

12
44
3 2 3 2
01
1
4 4 2
xx
x x x x






| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT Y JUT
ĐỀ KIỂM TRA GIẢI TÍCH 12 CHƯƠNG III TỔ TOÁN
Thời gian làm bài: 45 phút (Không kể giao đề) ĐỀ 1
Câu 1: (4,5 điểm) Tìm các họ nguyên hàm: 2x  1 dx a) dx  b)  x 1 2 x  7x 10
Câu 2: (4,0 điểm) Tính các tích phân:  e 2 dx a)
1 2xln xdx  b)      1  sin . x sin x    4  4
Câu 3: (1,5 điểm)
Tính diện tích của hình phẳng giới hạn bởi đồ thị hàm số y xx  
1  x  2 và trục hoành. ĐỀ 2
Câu 1: (4 điểm) Tìm các họ nguyên hàm: 3 2
x  2x  3x 1 a) dxx b) 3 tan xdx  .
Câu 2: (4,5 điểm) Tính các tích phân:  2 2 e dx a) (x 1) cos xdx  b)  x x e  2 ln 9 0
Câu 3: (1,5 điểm) Tính diện tích hình phẳng giới hạn bởi các đường: y  ln x , x  2 và trục Ox . ĐỀ 3
Câu 1: (4,5 điểm) Tính các tích phân sau 2 3 2x 1 e 3 2 ln x  ln x a. I dx  , b. J dx  2 x x 1 1   2 2 1 sin x
c. K  1 2xcos2xdx , d. x L e dx 1cosx 0 3
Câu 2: (1,5 điểm) Tính diện tích hình phẳng (S) giới hạn bởi: 2
y x  4 và y x  2
Câu 3: (2 điểm) Cho hình phẳng (S) giới hạn bởi:
y  2x  2 x
. Tính thể tích do hình phẳng (S) quay quanh trục 0x y  0 1 Bài 4: dx
(2 điểm)Tính các tích phân sau: I   4 x 1 1 2 ĐỀ 4
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH
Câu 1 (2 điểm). Chứng minh rằng hàm số 2
F(x)  ln(x  4) là nguyên hàm của hàm số 2x f (x)  2 x  trên R. 4 3 8x
Câu 2 (3 điểm). Cho hàm số f (x)  2x 1
a. Tìm ho ̣ nguyên hàm của hàm số f (x) .
b. Tìm mô ̣t nguyên hàm F (x) của hàm số f (x) sao cho F ) 1 (  2012 .
Câu 3 (3 điểm). Tính các tích phân sau.   4   2 x 1 sin 2 . x dx a. 4 e  sin 2x dx   b.  2  cos x  1  cos x 0 0
II. PHẦN RIÊNG CHO TỪNG BAN
A. Phần riêng cho ban KHTN  4 x
Câu 4A (2 điểm ). Tính tích phân sau. dx  2 cos x 0
B. Phần riêng cho ban cơ bản A + D  4
Câu 4B (2 điểm ). Tính tích phân sau. (2x  ). 3 cos2 . x dx 0 ®Ò 5
C©u 1: T×m c¸c nguyªn hµm cña c¸c hµm sè sau: 1 2 a/ f(x) = x3 +  b) f(x) = sin3x + cos5x -2e2x 3 x x
C©u 2: TÝnh c¸c tÝch ph©n sau:  2 dx 3 4 1 a) I   b) (x  ). 1 ln . x dx c) dx  2 x  11x  30 cosx 0 1 0
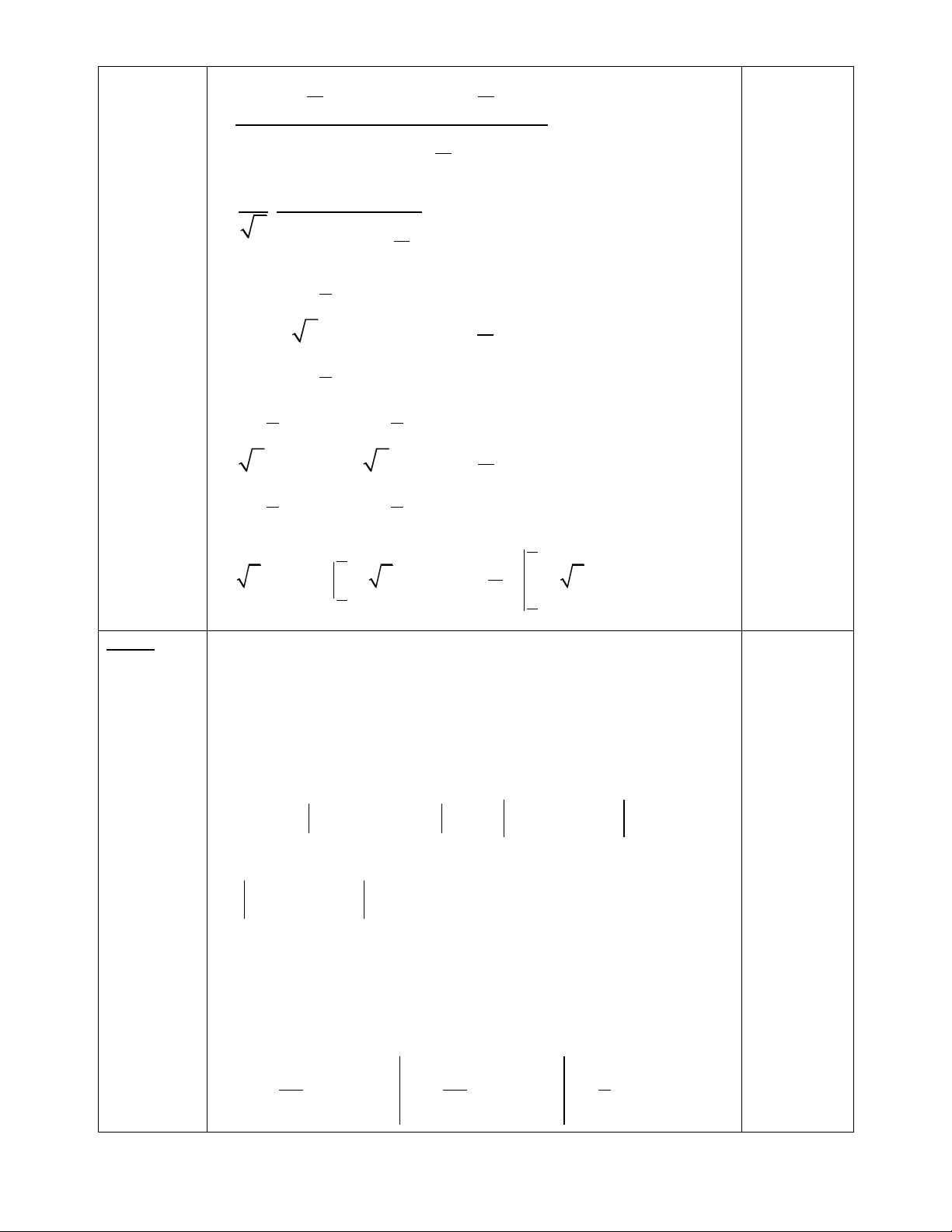
C©u 3: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x3 - 4x , trục hoành , đường thẳng x = -2 và đường thẳng x = 4 ĐÁP ÁN ĐỀ 1 Đáp án Biểu điểm Câu 1: 2x 1  3  a (2,5 điểm) dx  2  dx     1,0đ x 1  x 1 1  2dx  3
dx  2x  3ln | x 1| C   0,5đ x 3 x 1 b.(2,0 điểm) dx dx    2 0,5đ x  7x 10
x 5x  2 1  1 1    dx    0,5đ 3  x  5 x  2  1 1 1 1  dx dx   1 1
 ln x  5  ln x  2  C 0,75đ 3 x  5 3 x  2 3 3 1 x  5  ln  C 3 x  2 0,25đ Câu 2: e a.(2,0 điểm)
I  1 2xln xdx 1  1 u   ln x du dx  Đặt       x dv 1 2xdx  1,0đ 2
v x x e e    e I
1  2xln xdx    2
x x ln x  1 xdx  0,5đ 1 1 1      x x e 2 2 e 2 x e 3
ln x   x      0,5đ 1 2 2  1 b.(2,0 điểm)  2 dx J       sin . x sin x     4  4 Ta có    cos x       cos x  4 
cot x  cot x       4  sin x    sin x     4        sin x
.cos x  cos x  sin x      4   4      sin . x sin x     4  1 1  . 0,75đ 2    sin . x sin x     4   2     Nên J  2
cot x  cot x dx    0,25đ   4   4   2 2   
 2 cot xdx  2 cot x dx      4 0,5đ   4 4        2 lnsin x 2 2  2 ln sin x   2 ln 2     0,5đ   4    4 4 Câu 3: (1,5 điểm) x  0 
Ta có xx  
1  x  2  0  x 1  0,25đ x  2 
Diện tích hình phẳng cần tìm là 2 2 S xx   1  x  2 3 2 dx
x  3x  2x dx   0,5đ 0 0 3 2
x 3x  2x khi 0  x 1 Vì 3 2
x  3x  2x   0,25đ 3 2
x  3x  2x khi 1 x  2 Nên 1
S  x 3x  2x 2 3 2 dx   3 2
x  3x  2xdx 0,25đ 0 1 1 2 4 4  x    3 2 x 3 2 1 
x x   
x x    (đvdt) 0,25đ 4   4  2     0 1