Đề kiểm tra giữa kỳ 1 năm 2018 Toán 12 trường THPT chuyên Lê Hồng Phong – Nam Định

Đề kiểm tra giữa kỳ 1 năm 2018 Toán 12 trường THPT chuyên Lê Hồng Phong – Nam Định mã đề 843 được biên soạn nhằm kiểm tra các kiến thức Toán 12 đã học, đề gồm 6 trang với 50 câu hỏi và bài toán trắc nghiệm khách quan, đề có thời gian làm bài 90 phút, đề thi có đáp án và lời giải chi tiết.Mời bạn đọc đón xem,

40 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

36 trang 8 tháng trước

Tác giả:

Profile Lan Tường
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
Hãythamgia GroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang1Mãđề843
SỞ GD&ĐT NAM ĐỊNH KIỂM TRA GIỮA HKI NĂM 2018 - 2019
THPT CHUYÊN LÊ HỒNG PHONG MÔN TOÁN – LỚP 12 KHỐI ABCD
Thời gian làm bài: 90 phút
(50 câu hỏi trắc nghiệm)
MÃ ĐỀ THI: 843
(Thí sinh không được sử dụng tài liệu)
Họ và tên thí sinh: …………………………………...…………… SBD: ………………..…….
Câu 1. Cho
với
m
,
p
, và là các phân số tối giản. Giá trị
bằng
A.
10
. B.
6
. C.
22
3
. D.
8
.
Câu 2. Trong không gian
Oxyz
, cho mặt cầu
()( ) ( ) ( )
222
:3 1 14Sx y z-+++-=
. Tâm của
()
S
có
tọa độ là
A.
()
3;1; 1--
. B.
()
3; 1;1-
. C.
()
3; 1; 1--
. D.
()
3;1; 1-
.
Câu 3. Cho các số thực dương
,,abc
với
a
và
b
khác
1
. Khẳng định nào sau đây là đúng?
A.
2
log .log log
aa
b
bcc
. B.
2
1
log .log log
4
aa
b
bc c
.
C.
2
log .log 4 log
aa
b
bc c
. D.
2
log .log 2log
aa
b
bc c
.
Câu 4. Khẳng định nào sau đây là đúng?
A.
11
3
3
11
ddxx xx


. B.

2018 2018
42 42
11
1d 1 dxx x xx x

 

.
C.
 
33
22
1d 1d
xx
ex x ex x



. D.
2
22
22
1cos d sindxx xx





.
Câu 7. Đồ thị sau đây là của hàm số nào ?
A.
32
34yx x
. B.
32
34yx x
. C.
32
34yx x
. D.
32
34yx x
.
Câu 8. Cho hàm số
42
23yx x
có đồ thị hàm số như hình bên dưới. Với giá trị nào của tham số
m
phương trình
42
2324xx m
có hai nghiệm phân biệt ?
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
Hãythamgia GroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang2Mãđề843
A.
0
1
2
m
m
. B.
1
0
2
m
. C.
0
1
2
m
m
. D.
1
2
m
.
Câu 9. Trong các khẳng định sau, khẳng định nào sai ?
A.
2d 2ln2
xx
xC
. B.
2
2
e
ed
2
x
x
xC
.
C.
1
cos 2 d sin 2
2
xx x C
. D.
1
dln 1
1
xxC
x


1x

.
Câu 10. Tìm hàm số

Fx
biết

3
4
d
1
x
Fx x
x
và

01F
.
A.


4
ln 1 1Fx x
. B.


4
13
ln 1
44
Fx x
.
C.


4
1
ln 1 1
4
Fx x
. D.


4
4ln 1 1Fx x
.
Câu 11. Trong không gian
Oxyz
, mặt phẳng
():2 1 0Pxz
có một vectơ pháp tuyến là:
A.

3
2;1;0n

. B.

2
0;2;1n

. C.

1
2;1; 1n 

. D.

4
2;0;1n

.
Câu 12. Cho hàm số
()yfx
liên tục trên
và có bảng xét dấu đạo hàm như hình vẽ. Hàm số đã
cho có bao nhiêu cực tr
A. 1. B. 3. C. 4. D. 2.
Câu 13. Trong không gian
Oxyz
, cho hai điểm

2; 4;3A
và

2; 2;9B
. Trung điểm của đoạn
AB
có
tọa độ là
A.

0;3;3
. B.

4; 2;12
. C.

2; 1;6
. D.
33
0; ;
22



.
Câu 14. Trong các mệnh đề sau

I
.
 

2
2
fxdx fxdx


II
.
 
fxdx fx C


III
.
 
kf x dx k f x dx

với mọi
k

IV
.



fxdx fx
x

-2 0 2 4

'( )
f
x
+ - || + 0 + 0 -
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang3Mãđề843
Số mệnh đề đúng là
A. 2. B. 4. C. 1. D. 3.
Câu 15. Cho

2
1
421
f
xxdx

. Khi đó

2
1
f
xdx
bằng :
A.
1. B.
3
. C.
3
. D. 1 .
Câu 16. Thể tích của khối lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3a bằng:
A.
3
27 3
.
4
a
B.
3
93
.
4
a
C.
3
27 3
.
2
a
D.
3
93
.
2
a
Câu 17. Tìm tất cả các giá trị thực của tham số
m để hàm số
422
1yx m x m
đạt cực tiểu tại
0x
A.
1m . B. 1m . C. m . D. 1m .
Câu 18. Giá trị nhỏ nhất của hàm số
ln
x
y
x
trên đoạn
2;3
bằng
A.
ln 2
2
. B.
ln 3
3
. C.
2
3
e
. D.
1
e
.
Câu 19. Một hình trụ có diện tích xung quanh bằng
2
4 a
và bán kính đáy là a . Tính độ dài đường cao
của hình trụ đó.
A.
a . B.
2a
. C.
3a
. D.
4a
.
Câu 20. Cho hình lăng trụ đứng
.
A
BCABC

có đáy
A
BC
là tam giác vuông với
A
BACa
, góc
giữa
B
C
và

A
BC
bằng
45
. Tính thể tích khối lăng trụ.
A.
3
2
2
a
. B.
3
a
. C.
3
6
a
. D.
3
2
a
.
Câu 21: Trong không gian
Oxyz
, cho 2 điểm
(5; 4;2)A
và
B(1;2;4)
. Mặt phẳng đi qua
A
và vuông
góc với đường thẳng
A
B là?
A.
33250xy z
B.
23 80xyz
C.
33130xy z
D.
23 200xyz
Câu 22: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Đồ thị của hàm số
2
x
y
và
2
logyx
đối xứng với nhau qua đường thẳng
y
x .
B. Đồ thị của hai hàm số
x
ye
và
lnyx
đối xứng với nhau qua đường thẳng
y
x .
C. Đồ thị của hai hàm số
2
x
y
và hàm số
1
2
x
y
đối xứng với nhau qua trục hoành.
D. Đồ thị của hai hàm số
2
logyx
và
2
1
logy
x
đối xứng với nhau qua trục tung.
Câu 23: Tính đạo hàm của hàm số
2
2
x
y
.
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang4Mãđề843
A.
2
1
2
'
ln2
x
x
y
. B.
2
'2ln4
x
yx
. C.
2
21
'2
x
yx
. D.
2
'2ln2
x
yx
.
Câu 24: Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng BA’ và B’D’ bằng
A.
0
45
. B.
0
90
. C.
0
30
. D.
0
60
.
Câu 25. Cho hàm số
4
2
23
()
x
fx
x
. Khẳng định nào sau đây là đúng?
A.
3
23
()
32
x
f
xdx C
x

. B.
3
23
()
3
x
f
xdx C
x

.
C.
3
23
()
3
x
f
xdx C
x

. D.
3
3
() 2
f
xdx x C
x

.
Câu 26. Hình tứ diện đều có bao nhiêu trục đối xứng?
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 27. Tìm tập xác định của hàm số:

x
yx2log3
A.
0;

. B.
0; 3
. C.

;3
. D.
0; 3
.
Câu 28. Tìm tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số:
x
y
x
x
2
11
3

A. 3. B. 2. C. 4. D. 1.
Câu 29. Trong không gian với hệ tọa độ
Oxyz
, cho điểm

2; 4;1 ; 1;1;3AB
và mặt phẳng
:3250Px y z
. Một mặt phẳng

Q
đi qua hai điểm
,
A
B
và vuông góc với mặt
phẳng

P
có dạng
11 0ax by cz
. Khẳng định nào sau đây là đúng?
A.
5abc
. B.
15abc
. C.
5abc
. D.
15abc
.
Câu 30. Cho

2
1
ln
ln 3 ln 2
3
ln 2
e
x
c
Idxab
xx

, với
,,abc
. Khẳng định nào sau đâu đúng.
A.
222
1abc
. B.
222
11abc
. C.
222
9abc
. D.
222
3abc
.
Câu 31. Cho tam giác
A
BC
vuông tại
A
có 3
A
Ba= và
2
B
Ca=
. Tính thể tích khối nón tròn xoay
khi quay tam giác
A
BC
quanh trục
A
B
A.
3
3Vap=
. B.
3
2Vap=
. C.
3
2
3
a
V
p
=
. D.
3
3
3
a
V
p
=
.
Câu 32. Cho hình chóp .S ABCD có đáy là hình vuông cạnh a , tam giác SAB đều và nằm trong mặt
phẳng vuông góc với đáy. Khoảng cách giữa hai đường thẳng
SA
và
B
C
bằng
A.
a . B.
5
2
a
.
C.
3
2
a
.
D.
2a
.
Câu 33. Tìm tất cả các nguyên hàm của hàm số


2
31.ln
f
xx x
.
A.


3
2
1ln
3
x
f
xdx xx x C
. B.

3
3
ln
3
x
f
xdx x x C
.
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang5Mãđề843
C.


3
2
1ln
3
x
f
xdx xx x x C
. D.

3
3
ln
3
x
f
xdx x x x C
.
Câu 34. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
:20Pxyz
và hai điểm

3; 4;1 ; 7; 4; 3AB
. Điểm

;; 2Mabc a
thuộc

P
sao cho tam giác
A
BM vuông tại
M
và có diện tích nhỏ nhất. Khi đó giá trị biểu thức
T abc
bằng:
A.
6T
. B.
8T
. C. 4T . D.
0T
.
Câu 35. Cho hàm số
yfx
liên tục trên

0; 
thỏa mãn
2
2' 3
x
fx fx x x
. Biết

1
1
2
f
.
Tính
4f
?
A.
24 . B.14. C.4 . D.
16
.
Câu 36. Cho hàm số
3
62yx x
có đồ thị là

C
và đường thẳng
:2dy mx m
. Tìm giá trị của
tham số
m
để
d
cắt

C
tại ba điểm phân biệt
,,
A
BC
sao cho tổng các hệ số góc của các tiếp
tuyến của đồ thị

C
tại
,,
A
BC
bằng
6
.
A.
1m 
. B.
m 
. C.
2m
. D.
1m
.
Câu 37. Biết

2
1
1
2
1
p
x
q
x
x
edxme n

, trong đó ,, ,mn pq là các số nguyên dương và
p
q
là phân số tối
giản. Tính
Tmnpq
.
A.
11T . B.
10T
. C.
7T
. D.
8T
.
Câu 38. Cho hình chóp
.S ABCD
có đáy
A
BCD
là hình vuông cạnh a , tam giác
SAB
đều và nằm trong
mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích
V
của khối cầu ngoại tiếp hình chóp đã
cho.
A.
3
721
54
a
V
. B.
3
721
18
a
V
. C.
3
43
81
a
V
. D.
3
43
27
a
V
.
Câu 39. Cho hình lập phương
.
A
BCDABCD

có cạnh a . Một khối nón có đỉnh là tâm của hình vuông
A
BCD
và đáy là hình tròn nội tiếp hình vuông
A
BCD

. Diện tích toàn phần của khối nón đó
là
A.

2
32
2
tp
a
S

. B.

2
51
4
tp
a
S

. C.

2
52
4
tp
a
S

. D.

2
31
2
tp
a
S

.
Câu 40. Tổng tất cả các giá trị nguyên của tham số m để hàm số
432
38624yx x x xm
có
7
điểm cực trị bằng
A.
63
. B. 42 . C.
55
. D.
30
.
Câu 41. Một chiếc ô tô đang chạy với vận tốc
15m/s
thì người lái xe hãm phanh. Sau khi hãm phanh, ô
tô chuyển động chậm dần đều với vận tốc
315m/svt t
, trong đó t (giây). Hỏi từ lúc
hãm phanh đến khi dừng hẳn, ô tô di chuyển được bao nhiêu mét?
A.
38m. B. 37,2m. C. 37,5m. D. 37m.
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
Hãythamgia GroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang6Mãđề843
Câu 42. Tổng các nghiệm của phương trình
 
2
3
3
log 2 log 4 0xx
là
2Sab
(với
,ab
là
các số nguyên). Giá trị của biểu thức
.Qab
bằng
A. 0. B. 3. C. 9. D. 6.
Câu 43. Cho hình chóp
.SABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA a
và
SA
vuông góc với
đáy. Gọi
M
là trung điểm
SB
và
N
là điểm thuộc cạnh
SD
sao cho
2SN ND
. Tính thể tích
khối tứ diện
ACMN
.
A.
3
1
12
Va
. B.
3
1
8
Va
. C.
3
1
6
Va
. D.
3
1
36
Va
.
Câu 44. Biết

4
1
5fxdx
và

5
4
20fxdx
. Tính


2ln2
22
10
43
xx
fx dx feedx

.
A.
15
4
I
. B.
15I
. C.
5
2
I
. D.
25I
.
Câu 45. Có bao nhiêu giá trị nguyên
m
trên

1; 5
để hàm số
2xm
y
xm
đồng biến trên khoảng

;3

?
A. 2. B. 6. C. 5. D. 3.
Câu 46. Cho hàm số

'yfx
có đồ thị như hình vẽ
Hàm số

2
2yf x
đồng biến trên khoảng nào dưới đây
A.

;0

. B.

0;1
. C.

1; 2
. D.

0;

.
Câu 47. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng

:2230Px y z

và mặt cầu

S
tâm

5; 3;5I
, bán kính
25R
. Từ một điểm
A
thuộc mặt phẳng

P
kẻ một đường
thẳng tiếp xúc với mặt cầu

S
tại
B
. Tính
OA
biết
4AB
.
A.
11OA
. B.
5OA
. C.
3OA
. D.
6OA
.
Câu 48. Cho hình chóp tứ giác đều
.S ABCD
cạnh đáy bằng
2a
, góc giữa hai mặt phẳng

SAB
và

ABCD
bằng
0
45
;
,,MNP
lần lượt là trung điểm của
,SA SB
và
AB
. Tính thể tích
V
khối tứ diện
DMNP
A.
3
6
a
. B.
3
4
a
. C.
3
2
a
. D.
3
12
a
.
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang7Mãđề843
Câu 49. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
2
():2x2yzm 3 0Pm
và
mặt cầu

222
(): 1 1 1 9Sx y z
. Tìm tất cả các giá trị của
m
để
()P
tiếp xúc với
()S
.
A.
2
5
m
m

.
B.
2
5
m
m

.
C.
2m
. D.
5m 
.
Câu 50. Cho hai số thực
1, 1ab
. Biết phương trình
2
1
1
xx
ab
có hai nghiệm phân biệt
12
,
x
x
. Tìm
giá trị nhỏ nhất của biểu thức

2
12
12
12
4
xx
Sxx
xx




.
A.
3
34
. B.4 C.
3
32
. D.
3
4
.
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang8Mãđề843
BẢNG ĐÁP ÁN
1‐C. 2‐B. 3‐C. 4‐B. 5‐C. 6‐A. 7‐D. 8‐A. 9‐A. 10‐C.
11‐D. 12‐B. 13‐C. 14‐A. 15‐A. 16‐A. 17‐B. 18‐A. 19‐B. 20‐A.
21‐D. 22‐B. 23‐B. 24‐D. 25‐B. 26‐C. 27‐D. 28‐B. 29‐A. 30‐D.
31‐D. 32‐C. 33‐C. 34‐D. 35‐D. 36‐C. 37‐B. 38‐A. 39‐B. 40‐B.
41‐C. 42‐D. 43‐A. 44‐A. 45‐D. 46‐B. 47‐A. 48‐A. 49‐B. 50‐A.
LỜI GIẢI CHI TIẾT
Phamquoctoan87@gmail.com
Câu 1.
Cho với
m
,
p
, và là các phân số tối giản. Giá trị
bằng
A.
10
. B.
6
. C.
22
3
. D.
8
.
Lời giải
Tác giả: Phạm Quốc Toàn, FB: Phạm Quốc Toàn
Chọn C.
Ta có
()
2
31 5 2
1
11
33
x
eee
-
=⋅ = -
. Suy ra
1
3
m =
,
5p =
và
2q =
.
Vậy
122
52
33
mpq++=++=
.
Câu 2. Trong không gian
Oxyz
, cho mặt cầu
(
)
(
)
(
)
(
)
222
:3 1 14Sx y z-+++-=
. Tâm của
()
S
có
tọa độ là
A.
()
3;1; 1--
. B.
()
3; 1;1-
. C.
()
3; 1; 1--
. D.
()
3;1; 1-
.
Lời giải
Tác giả: Phạm Quốc Toàn, FB: Phạm Quốc Toàn
Chọn B.
Tâm của
()
S
có tọa độ là
()
3; 1;1-
.
Tuonganh0209@gmail.com
Câu 3.
Cho các số thực dương
,,abc
với a và
b
khác
1
. Khẳng định nào sau đây là đúng?
A.
2
log .log log
aa
b
bcc
. B.
2
1
log .log log
4
aa
b
bc c
.
C.
2
log .log 4log
aa
b
bc c
. D.
2
log .log 2log
aa
b
bc c
.
Lời giải
Tác giả: Nguyễn Ngọc Thảo, FB: Nguyễn Ngọc Thảo
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang9Mãđề843
Chọn C.
Ta có:
1
2
2
log .log 2log .log
aa
b
b
bc bc
2log .2log
ab
bc 4log .log
ab
bc 4log
a
c
.
Tuonganh0209@gmail.com
Câu 4.
Khẳng định nào sau đây là đúng?
A.
11
3
3
11
dd
x
xxx


. B.

2018 2018
42 42
11
1d 1 d
x
xx xx x

 

.
C.
 
33
22
1d 1d
xx
ex x ex x



. D.
2
22
22
1cos d sind
x
xxx





.
Lời giải
Tác giả: Nguyễn Ngọc Thảo, FB: Nguyễn Ngọc Thảo
Chọn B
Ta có:
42 4 2
113
12..
244
xx x x
2
2
13
0,
24
xx




.
Do đó:

2018 2018
42 42
11
1d 1 d
x
xx xx x

 

.
bichngock36@gmail.com
Câu 5 .
Tích phân
1
0
1
d
1
Ix
x
có giá trị bằng
A.
ln 2 1
. B.
ln 2
. C.
ln 2
. D.
1ln2
.
Lời giải
Tác giả : Nguyễn Mạnh Dũng, FB: dungmanhnguyen
Chọn C
Cách 1: Ta có:
11
1
0
00
1d(1)
dln1ln2ln1ln2
11
x
Ix x
xx



. Chọn đáp án C.
Cách 2 : Sử dụng MTCT.
Câu 6 . Hàm số
22
(4)yx x
nghịch biến trong khoảng nào dưới đây ?
A.
(2;4)
. B.
(1;2)
. C.
(0;2)
. D.
(0;4)
.
Lời giải
Tác giả : Nguyễn Mạnh Dũng, FB: dungmanhnguyen
Chọn A
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
Hãythamgia GroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang10Mãđề843
Xét hàm số
22
(4)yx x
TXĐ:
D
,
'2
2.( 4 )(2 4)yxxx
.
Khi đó:
'
0
02
4
x
yx
x

. Ta có bảng biến thiên sau:
x

0
2
4

'y
0
0
0
y
Từ BBT ta có hàm số đã cho nghịch biến trên

2; 4
. Chọn đáp án A.
quynhvanyka@gmail.com
Câu 7. Đồ thị sau đây là của hàm số nào ?
A.
32
34yx x
. B.
32
34yx x
. C.
32
34yx x
. D.
32
34yx x
.
Lời giải
Tác giả : Mai Quỳnh Vân, FB: Van Mai
Chọn D
Quan sát đồ thị hàm số ta thấy nhánh cuối cùng bên phải của đồ thị đi xuống nên hệ số
0a
.
Loại đáp án A, C.
Mặt khác hàm số có hai điểm cực trị
0
CT
x
và
2
CĐ
x
nên phương trình
0y
có hai
nghiệm phân biệt là 0 và 2. Loại đáp án B, chọn đáp án D.
(Hoặc do điểm uốn của đồ thị hàm số là:

1; 2
nên loại đáp án B, chọn D)
Câu 8. Cho hàm số
42
23yx x
có đồ thị hàm số như hình bên dưới. Với giá trị nào của tham số
m
phương trình
42
2324xx m
có hai nghiệm phân biệt ?
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
Hãythamgia GroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang11Mãđề843
A.
0
1
2
m
m
. B.
1
0
2
m
. C.
0
1
2
m
m
. D.
1
2
m
.
Lời giải
Tác giả : Mai Quỳnh Vân, FB: Van Mai
Chọn A
Số nghiệm của phương trình
42
2324xx m
bằng số giao điểm của đường thẳng
24ym
và đồ thị hàm số
42
23yx x
.
Dựa vào đồ thị ta có phương trình
42
2324xx m
có hai nghiệm phân biệt khi và chỉ khi
0
244
1
243
2
m
m
m
m


. Chọn đáp án A.
Email: buinguyenphuong1991@gmail.com
Câu 9. Trong các khẳng định sau, khẳng định nào sai ?
A.
2d 2ln2
xx
xC
. B.
2
2
e
ed
2
x
x
xC
.
C.
1
cos 2 d sin 2
2
xx x C
. D.
1
dln 1
1
xxC
x


1x

.
Lời giải
Tác giả: Bùi Nguyên Phương. Facebook: Bùi Nguyên Phương
Chọn A
Ta có:
2
2d
ln 2
x
x
xC
.
Câu 10. Tìm hàm số

Fx
biết

3
4
d
1
x
Fx x
x
và

01F
.
A.


4
ln 1 1Fx x
. B.


4
13
ln 1
44
Fx x
.
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang12Mãđề843
C.


4
1
ln 1 1
4
Fx x
. D.
4
4ln 1 1Fx x
.
Lời giải
Tác giả: Bùi Nguyên Phương. Facebook: Bùi Nguyên Phương
Chọn C
Ta có:

 
44
4
11 1
d1ln1
41 4
Fx x x C
x

.
Do
01F nên

1
ln 0 1 1 1
4
CC
.
Vậy:


4
1
ln 1 1
4
Fx x
.
dotrang1008@gmail.com
Câu 11.
Trong không gian
Oxyz
, mặt phẳng
():2 1 0
P
xz
có một vectơ pháp tuyến là:
A.
3
2;1;0n

. B.
2
0;2;1n

. C.
1
2;1; 1n 

. D.
4
2;0;1n

.
Lời giải
Tác giả: Đỗ thị Huyền Trang, FB: Trang Đỗ
Chọn D
Lý thuyết: Phương trình của mặt phẳng
()
P
có dạng :
0
A
xByCzD
, khi đó
()
P
có vectơ pháp tuyến là:
()
;;
P
nABC
Áp dụng: Mặt phẳng
():2 1 0
P
xz
có một vectơ pháp tuyến là
4
2;0;1n

.
Câu 12. Cho hàm số
()yfx
liên tục trên
và có bảng xét dấu đạo hàm như hình vẽ. Hàm số đã
cho có bao nhiêu cực trị
A. 1. B. 3. C. 4. D. 2.
Lời giải
Tác giả: Đỗ thị Huyền Trang, FB: Trang Đỗ
Chọn B
x

-2 0 2 4

'( )
f
x
+ - || + 0 + 0 -
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang13Mãđề843
x

-2 0 2 4

()
f
x
+ - || + + -
()
f
x
Từ bảng biến thiên ta thấy hàm số có 3 cực trị.
tongthuyqn@gmail.com
Câu 13. Trong không gian
Oxyz
, cho hai điểm
2; 4;3A và

2; 2;9B . Trung điểm của đoạn
A
B
có
tọa độ là
A.

0;3;3
. B.

4; 2;12
. C.
2; 1;6
. D.
33
0; ;
22



.
Lời giải
Tác giả : Tống Thị Thúy, FB: Thuy tong
Chọn C
Gọi
I
là trung điểm của đoạn
A
B
. Ta có
22
2
22
42
1
22
39
6
22
AB
I
AB
I
AB
I
xx
x
yy
y
zz
z






2; 1;6I.
Câu 14. Trong các mệnh đề sau

I
.
 
2
2
f
xdx f xdx

I
I
.
f
xdx f x C

I
II
.
kf x dx k f x dx

với mọi
k

I
V
.



f
xdx f x
Số mệnh đề đúng là
A. 2. B. 4. C. 1. D. 3.
Lời giải
Tác giả : Tống Thị Thúy, FB: Thuy tong
Chọn A
Mệnh đề

I
: Cho

1,fx x
,

1.VT I dx x C
,


2
2
22
1. 2VP I dx x C x x C
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang14Mãđề843
VT I VP I , mệnh đề

I
sai.
Mệnh đề

I
I đúng theo tính chất nguyên hàm.
Mệnh đề
I
II sai khi
0k
.
Mệnh đề

I
V
đúng . Gọi
Fx
là một nguyên hàm của
f
x
.


VT IV F x C

Fx C



f
xVPIV
phuongthu081980@gmail.com
Câu 15.
Cho

2
1
421
f
xxdx


. Khi đó

2
1
f
xdx
bằng :
A.
1
. B.
3
. C.
3
. D.
1
.
Lời giải
Tác giả :Nguyễn Thị Phương Thu, FB: Nguyễn Phương Thu
Chọn A
  
 
2
2222
2
1111
1
22
11
4214 214 2.1
2
44 1
x
fx xdx fxdx xdx fxdx
fxdx fxdx
 




Câu 16. Thể tích của khối lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3a bằng:
A.
3
27 3
.
4
a
B.
3
93
.
4
a
C.
3
27 3
.
2
a
D.
3
93
.
2
a
Lời giải
Tác giả :Nguyễn Thị Phương Thu, FB: Nguyễn Phương Thu
Chọn A

2
3
3.3
27 3
.3.
44
a
a
VhB a
trichinhsp@gmail.com
Câu 17.
Tìm tất cả các giá trị thực của tham số m để hàm số
422
1yx m x m
đạt cực tiểu tại
0x
A.
1m
. B.
1m
. C.
m
. D.
1m
.
Lời giải
Tác giả : Nguyễn Trí Chính, FB: Nguyễn trí Chính
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang15Mãđề843
Chọn B
422
1yfx x m x m

/3
42 1yx mx ,


/
2
0
0
21
x
y
x
m
TH1: Nếu
1m
thì phương trình
/
0y
có một nghiệm đơn duy nhất
0x
Có
10a
. Nên hàm số luôn đạt cực tiểu tại
0x
. Suy ra
1m
nhận
Hoặc ta vẽ BBT:
TH2: Nếu
1m
thì phương trình
/
0y
có 3 nghiệm đơn


123
11
0
22
mm
xxx
Có
10a
. Nên hàm số luôn đạt cực đại tại
0x
. Suy ra
1m
loại
Hoặc ta vẽ BBT:
Kết luận:
Qua 2 trường hợp ta có
1m
.
Câu 18.
Giá trị nhỏ nhất của hàm số
ln
x
y
x
trên đoạn
2;3
bằng
A.
ln 2
2
. B.
ln 3
3
. C.
2
3
e
. D.
1
e
.
Lời giải
Tác giả : Nguyễn Trí Chính, FB: Nguyễn trí Chính
+
0
x
y
/
y
+∞- ∞
_
m
2
0
+∞+∞
+
0
_
00
+
_
+∞
1-m
2
0
-
1-m
2
- ∞
y
y
/
x
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang16Mãđề843
Chọn A
Xét

ln
x
yfx
x

. Hàm số
yfx
liên tục trên đoạn
2;3
/
2
1ln
x
y
x
;
/
0y

2
1ln
0
x
x



2; 3xe
Có


ln2
20,3466
2
f
;


1
0,3679fe
e
;


ln3
30,366
3
f
,
Suy ra



2;3
ln2
2
x
Min f x
.
Vậy giá trị nhỏ nhất của hàm số
ln
x
y
x
trên đoạn
2;3
bằng
ln 2
2
.
lehongphivts@gmail.com
Câu 19.
Một hình trụ có diện tích xung quanh bằng
2
4 a
và bán kính đáy là
a
. Tính độ dài đường cao
của hình trụ đó.
A.
a
. B.
2a
. C.
3a
. D.
4a
.
Lời giải
Người giải: Lê Hồng Phi, FB: Lê Hồng Phi
Chọn B
Diện tích xung quanh của hình trụ có bán kính đáy
a và chiều cao
h
là
2
xq
xq
S
4
S2 2
22
a
ah h a
aa

.
Vậy độ dài đường cao của hình trụ đó là
2ha
.
Câu 20. Cho hình lăng trụ đứng
.
A
BCABC

có đáy
A
BC
là tam giác vuông với
A
BACa
, góc
giữa
B
C
và

A
BC
bằng
45
. Tính thể tích khối lăng trụ.
A.
3
2
2
a
. B.
3
a
. C.
3
6
a
. D.
3
2
a
.
Lời giải
Người giải: Lê Hồng Phi, FB: Lê Hồng Phi
Chọn A
C'
B'
A
C
A'
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang17Mãđề843
Tam giác
ABC
vuông và có
AB AC a
nên
90A
. Như thế thì
2
S
2
ABC
a
.
Từ

BC ABC B
và
CC ABC
suy ra góc giữa
B
C
và

A
BC
là
45CBC
.
Do đó
2222
2CC BC AB AC a a a

.
Vậy thể tích của khối lăng trụ là
23
2
V=S . 2
22
ABC
aa
CC a

.
Email: Ninhtldh@gmail.com
Câu 21:
Trong không gian
Oxyz
, cho 2 điểm
(5; 4;2)A
và
B(1;2;4)
. Mặt phẳng đi qua
A
và vuông
góc với đường thẳng
A
B
là?
A.
33250xy z
B.
23 80xyz
C.
33130xy z
D.
23 200xyz
Lời giải
Tác giả: Hứa Chí Ninh
Chọn D.
Mặt phẳng vuông góc với đường thẳng
A
B
nên nhận AB

làm vectơ pháp tuyến,
(4;6;2)AB 

Mặt phẳng đi qua
(5; 4;2)A
và có vectơ pháp tuyến,
(4;6;2)AB 

có phương trình
4( 5) 6(y 4) 2(z 2) 0x
hay
23yz200x 
. Vậy chọn D.
Câu 22: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Đồ thị của hàm số
2
x
y
và
2
logyx
đối xứng với nhau qua đường thẳng
yx
.
B. Đồ thị của hai hàm số
x
ye
và
lnyx
đối xứng với nhau qua đường thẳng
yx
.
C. Đồ thị của hai hàm số
2
x
y
và hàm số
1
2
x
y
đối xứng với nhau qua trục hoành.
D. Đồ thị của hai hàm số
2
logyx
và
2
1
logy
x
đối xứng với nhau qua trục tung.
Lời giải
Tác giả: Hứa Chí Ninh
Chọn B.
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang18Mãđề843
Đồ thị hàm số
x
ya
và đồ thị hàm số
log
a
yx
đối xứng với nhau qua đường phân giác góc
phần tư thứ nhất (
yx
), suy ra chọn B.
kimoanh0102@gmail.com
Câu 23:
Tính đạo hàm của hàm số
2
2
x
y
.
A.
2
1
2
'
ln2
x
x
y
. B.
2
'2ln4
x
yx . C.
2
21
'2
x
yx
. D.
2
'2ln2
x
yx .
Lời giải
Tác giả: Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh
Chọn B
2222
2
2 ' '.2 ln2 2 .2 .ln2 2 ln4
xxxx
yyx x x
.
Câu 24: Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng BA’ và B’D’ bằng
A.
0
45
. B.
0
90
. C.
0
30
. D.
0
60
.
Lời giải
Tác giả: Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh
Chọn D
Vì
// ' 'BD B D
nên góc giữa hai đường thẳng BA’ và B’D’ bằng góc giữa hai đường thẳng BA’
và BD.
Ta có ABCD.A’B’C’D’ là hình lập phương nên tam giác A’BD là tam giác đều.
Khi đó góc giữa hai đường thẳng BA’ và BD bằng
0
60ABD
.
Vậy góc giữa hai đường thẳng BA’ và B’D’ bằng
0
60
.
chauhieu2013@gmail.com
Câu 25.
Cho hàm số
4
2
23
()
x
fx
x
. Khẳng định nào sau đây là đúng?
A.
3
23
()
32
x
f
xdx C
x

. B.
3
23
()
3
x
f
xdx C
x

.
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang19Mãđề843
C.
3
23
()
3
x
f
xdx C
x

. D.
3
3
() 2
f
xdx x C
x

.
Họ và tên tác giả :Trần Văn Hiếu Tên FB: Hieu Tran
Lời giải
Chọn B
Ta có
43
2
22
23 3 2 3
() 2
3
xx
f
xdx dx x dx C
xxx





Câu 26. Hình tứ diện đều có bao nhiêu trục đối xứng?
A.
0
.B.
1
. C.
3
. D.
2
.
Họ và tên tác giả :Trần Văn Hiếu Tên FB: Hieu Tran
Lời giải
Chọn C
Gọi
S
là tập hợp các đỉnh của khối tứ diện đều
A
BCD
. Giả sử
d
là trục đối xứng của tứ diện
đã cho, phép đối xứng trục
d
biến
S
thành chính
S
nên
d
phải là trung trực của ít nhất một
đoạn thẳng nối hai đỉnh bất kỳ của tứ diện .
Vậy tứ diện đều có 3 trục đối xứng là các đường thẳng nối trung điểm của các cặp cạnh đối
diện.
tuenhi210510@gmail.com
Câu 27.
Tìm tập xác định của hàm số:

x
yx2log3
A.
0;

. B.
0; 3
. C.

;3
. D.
0; 3
.
Lời giải
Tác giả : Lê Khánh Vân, FB: khanhvan le
Chọn D
Điều kiện xác định:
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang20Mãđề843
xx
D
xx
00
0; 3
30 3






Câu 28. Tìm tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số:
x
y
x
x
2
11
3

A. 3. B. 2. C. 4. D. 1.
Lời giải
Tác giả : Lê Khánh Vân, FB: khanhvan le
Chọn B
Điều kiện xác định:
2
10
1
3
30
x
x
x
xx



xx x
x
xx x
y
xx
x
34 2
2
111
11
lim lim lim 0
3
3
1
  



x
x
x
x
2
3
11
lim
3


vì

3
2
3
lim 1 1 2 1
lim 3 0
x
x
x
xx


2
30 3(x3)0x30xxx x

x
x
x
x
2
3
11
lim
3


vì


3
2
3
lim 1 1 2 1
lim 3 0
x
x
x
xx


2
33(x3)0x30xxx x
 
Đường thẳng
y 0
là tiệm cận ngang của đồ thị hàm số.
Đường thẳng
x 3
là tiệm cận đứng của đồ thị hàm số.
(tien.vuviet@yahoo.com)
Câu 29.
Trong không gian với hệ tọa độ
Oxyz
, cho điểm

2; 4;1 ; 1;1;3AB
và mặt phẳng
:3250Px y z
. Một mặt phẳng

Q
đi qua hai điểm
,AB
và vuông góc với mặt phẳng

P
có dạng
11 0ax by cz
. Khẳng định nào sau đây là đúng?
A.
5abc
. B.
15abc
. C.
5abc
. D.
15abc
.
Lời giải
Tác giả : Vũ Việt Tiến, FB: Vũ Việt Tiến
Chọn A
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang21Mãđề843
Vì

Q vuông góc với

P
nên
Q nhận vtpt

1; 3; 2n 
của

P
làm vtcp
Mặt khác

Q đi qua
A
và
B
nên

Q nhận
3; 3; 2AB 

làm vtcp

Q
nhận

,0;8;12
Q
nnAB



 
làm vtpt
Vậy phương trình mặt phẳng
: 0( 1) 8( 1) 12( 3) 0xy zQ  
, hay

:2 3 11 0yzQ 
Vậy
5abc
. Chọn A.
(tien.vuviet@yahoo.com)
Câu 30. Cho

2
1
ln
ln 3 ln 2
3
ln 2
e
x
c
Idxab
xx

, với
,,abc
. Khẳng định nào sau đâu đúng.
A.
222
1abc
. B.
222
11abc
. C.
222
9abc
. D.
222
3abc
.
Lời giải
Tác giả : Vũ Việt Tiến, FB: Vũ Việt Tiến
Chọn D
Ta có

2
1
ln
ln 2
e
x
Idx
xx
, đặt
ln 2
dx
x
tdt
x

333
33
22
22
222
21 1 2 22 1
2 ln ln 3 ln 2 ln 3 ln 2
32 3
t
Idtdtdtt
ttt t


Suy ra
1; 1; 1ab c
, vậy
222
3abc
. Chọn D.
Email: trandongphong.c3lehongphong@lamdong.edu.vn.
Câu 31. Cho tam giác
A
BC
vuông tại
A
có
3
A
Ba=
và
2
B
Ca=
. Tính thể tích khối nón tròn xoay
khi quay tam giác
A
BC
quanh trục
A
B
A.
3
3Vap=
. B.
3
2Vap=
. C.
3
2
3
a
V
p
=
. D.
3
3
3
a
V
p
=
.
Lời giải
Họ và tên tác giả: Trần Đông Phong FB: Phong Do
Chọn D
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang22Mãđề843
Xét tam giác
A
BC
vuông tại
A
có
3
A
Ba=
và
2
B
Ca=
, suy ra:
A
Ca=
Quay tam giác
A
BC
quanh trục
A
B
tạo thành khối nón tròn xoay
Biết chiều cao
3BA a=
, bán kính đường tròn đáy
R
AC a==
Thể tích khối nón
3
2
13
33
a
VRh
p
p==
.
Email: trandongphong.c3lehongphong@lamdong.edu.vn.
Câu 32. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh a , tam giác
SAB
đều và nằm trong mặt
phẳng vuông góc với đáy. Khoảng cách giữa hai đường thẳng
SA
và
B
C
bằng
A. a . B.
5
2
a
.
C.
3
2
a
.
D.
2a
.
Lời giải
Họ và tên tác giả: Trần Đông Phong FB: Phong Do
Chọn C
Ta có
()
1
Trong mặt phẳng
(
)
SAB
, dựng
B
KSA^
tại
K
()
2
Từ
(
)
(
)
1,2
suy ra:
B
K là đoạn vuông góc chung của
SA
và
B
C
Vậy
()
3
,
2
a
dSABC BK
==
tuluc0201@gmail.com
Câu 33.
Tìm tất cả các nguyên hàm của hàm số
2
31.ln
f
xx x
.
A.


3
2
1ln
3
x
f
xdx xx x C
. B.

3
3
ln
3
x
f
xdx x x C
.
C.


3
2
1ln
3
x
f
xdx xx x x C
. D.

3
3
ln
3
x
f
xdx x x x C
.
Lời giải
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang23Mãđề843
Tác giả :Võ Tự Lực, FB: Võ Tự Lực
Chọn C.
Ta có

2
31lnIx xdx
Đặt


2
23
1
ln
31
31
u x du dx
x
dv x dx
vxdxxx





.
    
3
33 222
1
ln 1ln 1 1ln
3
x
I x x x x x dx x x x x dx x x x x C
x


.
Câu 34. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
:20Pxyz
và hai điểm
3; 4;1 ; 7; 4; 3AB
. Điểm

;; 2Mabc a
thuộc

P
sao cho tam giác
A
BM vuông tại
M
và có diện tích nhỏ nhất. Khi đó giá trị biểu thức
T abc
bằng:
A.
6T
. B.
8T
. C. 4T . D.
0T
.
Lời giải
Tác giả : Võ Tự Lực, FB: Võ Tự Lực
Chọn D.
Ta có:
1
.
2
ABM
SABMH
với H là hình chiếu vuông góc của
M
lên AB.
Do
A
B không đổi nên
A
BM
S
nhỏ nhất khi
M
H nhỏ nhất.


4; 8; 4
. 0 //( )
1;1; 1
P
P
AB
A
Bn AB P
n






M
H nhỏ nhất khi
M
nằm trên giao tuyến của mặt phẳng
Q
và

P
;
với
Q
là mặt phẳng chứa
A
B và vuông góc với mp

P
.



4; 8; 4
3; 0; 3
1; 1; 1
Q
P
AB
n
n






phương trình mp
Q
là 40xz.
M
nằm trên giao tuyến của mặt phẳng
Q
và

P
nên tọa độ
M
là nghiệm của hệ phương
trình

40
22 ;22;4
20
4
xt
xz
ytMttt
xyz
zt





với
2t
.
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang24Mãđề843
Ta có
3; 2 2 ; 3 ; 7; 6 2 ; 7
A
Mt t tBMt t t 

.
Tam giác
A
BM
vuông tại
M
nên
. 0 3 7 22 62 3 7 0AM BM t t t t t t

 

3
372310 3350
5
3
tn
tt tt t t
tl
 
.
+
33;4;1 3410t M abc  .
Chọn
D
nguyentuanblog1010@gmail.com
Câu 35. Cho hàm số
yfx
liên tục trên

0; 
thỏa mãn
 
2
2' 3
x
fx fx x x
. Biết

1
1
2
f
.
Tính

4f
?
A.24 . B.14. C. 4 . D.
16
.
Lời giải
Tác giả:Phạm Chí Tuân, FB: Tuân Chí Phạm
Chọn D
Trên khoảng

0; 
ta có:
  
22
13
2' 3 '
2
2
x
fx fx x x xfx x
x

.


''
22
33
..
22
x
fx x xfx dx xdx

.

3
1
.
2
xf
xxC
.
Mà

1
1
2
f
nên từ
có:

3
111
1. 1 .1 0
222
fCCC

2
2
x
x
fx
 .
Vậy

2
44
416
2
f 
.
Câu 36.
Cho hàm số
3
62yx x
có đồ thị là

C và đường thẳng
:2dy mx m
. Tìm giá trị của
tham số
m
để
d
cắt

C
tại ba điểm phân biệt
,,ABC
sao cho tổng các hệ số góc của các tiếp
tuyến của đồ thị

C
tại
,,ABC
bằng
6
.
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang25Mãđề843
A.
1m 
. B.
m 
. C.
2m
. D.
1m
.
Lời giải
Tác giả:Phạm Chí Tuân, FB: Tuân Chí Phạm
Chọn C
Phương trình hoành độ giao điểm của

C
và
d
:

33
62 2 6 0xx mxm xmxm 

1
Điều kiện cần:
Giả sử
d
cắt

C
tại ba điểm phân biệt
,,ABC
thì phương trình

1
có ba nghiệm phân biệt.
Gọi ba nghiệm của

1 là
,,
A
BC
x
xx
, theo viet ta có:
0
6
ABC
AB BC C A
xxx
xx xx xx m



i
hàm số
3
62yx x
có đồ thị là

C
. Ta có
2
'3 6yx
Gọi
12
,kk
,
3
k
lần lượt là hệ số góc của các tiếp tuyến của đồ thị

C
tại ba điểm
,AB
và
C
.
Ta có:
2
1
36
A
kx
;
2
2
36
B
kx
và
2
3
36
C
kx
Theo bài:

222 222
123
63 186 8
ABC ABC
kkk xxx xxx

2
82
A
BC ABBCCA
x
xx xxxxxx

2
Thay
i
vào

2
ta có:

082 6 2mm
.
Điều kiện đủ: Với
2m
ta có

1
trở thành
3
420xx
.
Xét hàm số
3
34fx x x
. Do

f
x
là hàm đa thức nên xác định và liên tục trên .
Ta có:

22f 
;

11f 
;
02f 
;
2f
.
Vì:
+
2. 1 0ff
phương trình
0fx
có ít nhất một nghiệm thuộc
2; 1
.
+
1. 0 0ff
phương trình
0fx
có ít nhất một nghiệm thuộc
1; 0
.
+
0. 2 0ff
phương trình
0fx
có ít nhất một nghiệm thuộc

0; 2
.
Mặt khác vì
f
x
là đa thức bậc ba nên phương trình
0fx
chỉ có tối đa ba nghiệm.
Vậy phương trình
0fx
có ba nghiệm phân biệt.
Do đó
2m
là giá trị cần tìm.
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang26Mãđề843
Phản biện: lanhoang0254@gmail.com
(phunghang10ph5s@gmail.com)
Câu 37. Biết

2
1
1
2
1
p
x
q
x
x
edxme n

, trong đó ,, ,mn pq là các số nguyên dương và
p
q
là phân số tối
giản. Tính
Tmnpq
.
A.
11T
. B.
10T
. C.
7T
. D.
8T
.
Lời giải
Tác giả : Phùng Hằng, FB: Hằng Phùng
Chọn B
Ta có:


11
22
11
2
2
2
11
2
2
1 1
12112
xxxx
xxxx
I x e dx x x e dx x e dx xe dx



Xét

1
22 2 2
1
11 1
11 1
2
2
1
222
2
1
1.. .
1
xx x x
x
xx x
x
I x edxxe dxxed xx
x
de
x








22
22
11
11
1
1
2
1
1
22
2
xx x x
xx x x
x
eedxxe xedx

 

11
22
2
1
1
11
1
3
22
2
241
xx x
xx x
Ixedxxe Ixe e


Do

2
1
1
2
1
p
x
q
x
x
edxme n

, trong đó
,, ,mnpq
và
p
q
là phân số tối giản
4
1
3
2
m
n
p
q
Khi đó,
413210Tmnpq
.
Câu 38. Cho hình chóp
.S ABCD
có đáy
A
BCD
là hình vuông cạnh a , tam giác
SAB
đều và nằm trong
mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích
V
của khối cầu ngoại tiếp hình chóp đã
cho.
A.
3
721
54
a
V
. B.
3
721
18
a
V
. C.
3
43
81
a
V
. D.
3
43
27
a
V
.
Lời giải
Tác giả : Phùng Hằng, FB: Hằng Phùng
Chọn A
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang27Mãđề843
*) Xác định tâm mặt cầu ngoại tiếp hình chóp
.S ABCD
:
Gọi
G
là trọng tâm tam giác
SAB
,
O
là tâm của hình vuông
A
BCD
,
M
là trung điểm của
A
B .
Do
SAB
đều
SM AB
Mà
SAB ABCD SM ABCD SM OM
OM
là đường trung bình của
// ( )ABC OM AD OM AB do AD AB
OM SAB
.
Dựng các đường thẳng qua
,GO
lần lượt song song với
,
M
OSM
, hai đường thẳng này cắt
nhau tại
I
Ta có:
// ,
I
O SM SM ABCD IO ABCD
, mà
O
là tâm của hình vuông
A
BCD
IA IB IC ID
(1)
Ta có:
// ,GI OM MO SAB GI SAB
, mà
G
là trọng tâm tam giác đều
SAB
IS IA IB
(2)
Từ (1), (2) suy ra:
I
là tâm mặt cầu ngoại tiếp hình chóp
.SABCD
.
*) Tính bán kính, thể tích khối cầu ngoại tiếp hình chóp
.SABCD
:
Ta có:
1
22 2
aa
OM AD GI OM
(do tứ giácOMIG là hình chữ nhật)
SAB
đều cạnh bằng a có
G
là trọng tâm
23 3
.
32 3
aa
BG

Do
GI SAB GI BG BGI
vuông tại
G
2
2
22
22
37
23 4312
aa aa
IB IG GB a








SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
Hãythamgia GroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang28Mãđề843
Bán kính khối cầu ngoại tiếp hình chóp
.SABCD
là:
7
12
RIBa
Thể tích khối cầu ngoại tiếp hình chóp
.SABCD
là:
3
3
3
447721
.
3 3 12 54
a
VR a






.
hoangthihonghanhc3ln@gmail.com
Câu 39. Cho hình lập phương
.ABCDABCD

có cạnh
a
. Một khối nón có đỉnh là tâm của hình vuông
ABCD
và đáy là hình tròn nội tiếp hình vuông
ABCD

. Diện tích toàn phần của khối nón đó
là
A.

2
32
2
tp
a
S

. B.

2
51
4
tp
a
S

. C.

2
52
4
tp
a
S

. D.

2
31
2
tp
a
S

.
Lời giải
Tác giả :Hoàng Thị Hồng Hạnh, FB: Hoàng Thị Hồng Hạnh
Chọn B
Bán kính của đường tròn đáy là
2
a
r
.
Diện tích đáy nón là:
2
2
1
4
a
Sr

.
Độ dài đường sinh là
22
5
2
a
lar
.
Diện tích xung quanh của khối nón là:
2
2
5
4
a
Srl

.
Vây, diện tích toàn phần của khối nón đó là:

2
12
51
4
tp
a
SSS

.
Câu 40. Tổng tất cả các giá trị nguyên của tham số
m
để hàm số
432
38624yx x x xm
có
7
điểm cực trị bằng
A
B
C
D
O
A
B
C
D
O
a
a
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang29Mãđề843
A.
63
. B.
42
. C.
55
. D.
30
.
Lời giải
Tác giả :Hoàng Thị Hồng Hạnh, FB: Hoàng Thị Hồng Hạnh
Chọn B
Đặt
432
() 3 8 6 24
f
xxxx xm
32
( ) 12 24 12 24fx x x x

2
() 0 1
1
x
fx x
x


Bảng biến thiên của
()
f
x
()
f
x
luôn có
3
điểm cực trị, để hàm số
()yfx
có
7
điểm cực trị thì đồ thị hàm số
()
f
x
cắt trục hoành tại
4 điểm phân biệt (số điểm cực trị của hàm
()yfx
bằng số điểm cực trị
của hàm
()
f
x
cộng với số giao điểm của đồ thị hàm số
()
f
x
với trục hoành).
8013 813mmm
.
Mà
m nguyên nên
9;10;11;12m
.
Vậy, tổng tất cả các giá trị nguyên của tham số
m bằng
9101112 42
.
thaygiaothaogiay@gmail.com
Câu 41.
Một chiếc ô tô đang chạy với vận tốc
15m/s
thì người lái xe hãm phanh. Sau khi hãm phanh, ô
tô chuyển động chậm dần đều với vận tốc
315m/svt t
, trong đó t (giây). Hỏi từ lúc
hãm phanh đến khi dừng hẳn, ô tô di chuyển được bao nhiêu mét?
A. 38m. B. 37,2m. C. 37,5m. D. 37m.
Lời giải
Tác giả : Đinh Phước Tân, FB: Tân Độc
Chọn C
Khi xe dừng hẳn thì
05vt t
.
Khi đó quảng đường xe đi được tính từ lúc bắt đầu hãm phanh đến khi dừng hẳn là:
()
f
x
'( )
f
x
x

2
1
1

0
0
0

8 m
13 m
19 m

SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang30Mãđề843

5
5
2
0
0
3
315 15 37,5
2
d
t
Stt t




m
Vậy ta chọn đáp án C.
Câu 42. Tổng các nghiệm của phương trình
 
2
3
3
log 2 log 4 0xx là 2Sab (với
,ab
là
các số nguyên). Giá trị của biểu thức
.Qab
bằng
A. 0. B. 3. C. 9. D. 6.
Lời giải
Tác giả : Đinh Phước Tân, FB: Tân Độc
Chọn D
Điều kiện:
24x
.
Với điều kiện trên, phương trình đã cho tương đương
33 3
2log 2 2log 4 0 log 2 4 0 2 4 1xx xxxx   

2
2
241
670
32
241
3
690
xx
xx
x
xx
x
xx






So lại điều kiện, ta nhận hai nghiệm
12
32; 3xx
Ta được:
12
62 6;1Sxx a b
. Vậy
.6Qab
.
(tanbaobg@gmail.com)
Câu 43.
Cho hình chóp
.SABCD
có đáy
A
BCD
là hình vuông cạnh
a
,
SA a
và
SA
vuông góc với
đáy. Gọi
M
là trung điểm
SB
và
N
là điểm thuộc cạnh
SD
sao cho
2SN ND
. Tính thể tích
khối tứ diện
A
CMN
.
A.
3
1
12
Va
. B.
3
1
8
Va
. C.
3
1
6
Va
. D.
3
1
36
Va
.
Lời giải
Tác giả : Đỗ Tấn Bảo, FB: Đỗ Tấn Bảo
Chọn A
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang31Mãđề843
Cách 1. Đặt hệ trục tọa độ như hình vẽ.
Ta có




0;0; 0
;0;0
;0;
22
;;0
2
0; ;
0; ;0
33
0;0;
A
aa
Ba
M
Caa
aa
N
Da
Sa









.
Suy ra

222
;0;
22
,;;
222
;;0
2
0; ;
2
0; ;
33
33
aa
AM
aaa
AM AC
AC a a
aa
AN
aa
AN





















 



.
Do đó
3
11
,.
612
ACMN
VAMACANa



 
(đvtt)
Cách 2.( Dành cho hsg giải tự luận)
Đặt
SN k SD

và
SK xSI

với
;;0;1kx kx
.
Gọi I là tâm của hình vuông
A
BCD
và
K
MN SI
.
Ta có

11 1
1
22 2
1
2
M
K SK SM xSI SB x SB xSD
MN SN SM k SD SB


 
 
.
Vì
,,
M
KN
thẳng hàng nên

2
21
12
k
kxxx
k

.
Suy ra
21
12 12
k
SK SI KI SI
kk


.
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang32Mãđề843
Do đó
 

2
12
,.,
12 2 212
AKC
IK a a
dKAC SA S ACdKAC
SI k k


.
Hơn nữa ta có




12 22
,;,
24 33
aa
d M AKC BO d N AKC BO
 
.
Vậy





1
,,
3
ACMN MACK NACK AKC
VVV SdMACKdNACK
 
23
12 22 7
..
3 2 1 2 4 3 3.12 1 2
aaa a
kk






(đvtt).
Thay
2
3
k
ta được
3
1
12
Va
(đvtt).
Câu 44. Biết

4
1
5fxdx
và

5
4
20fxdx
. Tính


2ln2
22
10
43
xx
f
xdx feedx

.
A.
15
4
I
. B.
15I
. C.
5
2
I
. D.
25I
.
Lời giải
Tác giả : Đỗ Tấn Bảo, FB: Đỗ Tấn Bảo
Chọn A
Đặt
43 4tx dtdx
thì
    
2545
1114
11 125
43 520
44 44
f x dx f t dt f t dt f t dt





.
Đặt
22
2
xx
ue du edx
thì


ln 2 4
22
01
15
22
xx
fe edx fudu

.
Vậy
25 5 15
424
I 
.
Tuan.nt81@gmail.com
Câu 45.
Có bao nhiêu giá trị nguyên m trên

1; 5
để hàm số
2
x
m
y
x
m
đồng biến trên khoảng
;3
?
A. 2. B. 6. C. 5. D. 3.
Lời giải
Tác giả : Tuyetnguyen, FB: tuyet nguyen
Chọn D
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
Hãythamgia GroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang33Mãđề843
Ta có

2
'
m
y
xm
Hàm số đồng biến trên khoảng

;3



0
'0, ;3 0 3
;3
m
yx m
m


Do đó có 3 giá trị của
m
thỏa mãn điều kiện đề bài.
Câu 46. Cho hàm số

'yfx
có đồ thị như hình vẽ
Hàm số

2
2yf x
đồng biến trên khoảng nào dưới đây
A.

;0

. B.

0;1
. C.

1; 2
. D.

0;

.
Lời giải
Chọn B
Hàm số

2
2yf x
có

2
'2.'2yxfx

2
2
2
2
0
0
12 2
11
01
0
'2.'2 0
0
1
1
21
1
22
x
x
x
x
x
x
yxfx
x
x
x
x
x
x











Do đó hàm số đồng biến trên

0;1
.
Mar.nang@gmail.com
Câu 47. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng

:2230Px y z

và mặt cầu

S
tâm

5; 3;5I
, bán kính
25R
. Từ một điểm
A
thuộc mặt phẳng

P
kẻ một đường
thẳng tiếp xúc với mặt cầu

S
tại
B
. Tính
OA
biết
4AB
.
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang34Mãđề843
A.
11OA
. B.
5OA
. C.
3OA
. D.
6OA
.
Lời giải
Tác giả : Lê Đình Năng FB: Lê Năng
Chọn A
Khoảng cách từ điểm I đến mp(P) là:

222
52.(3)2.53
;( ) 6
1(2)2
dI P



.
AB
tiếp xúc với
()S
tại
B
nên tam giác
AIB
vuông tại B, do đó ta có:


2
22 22 2
25 4 6 ;()IA IB AB R AB d I P
A
là hình chiếu của I lên (P)
Đường thẳng IA đi qua
5; 3;5I có VTCP
()
1; 2; 2
P
un

có phương trình
5
32
52
x
t
yt
zt



Có
()
A
IA P
5 2( 3 2 ) 2(5 2 ) 3 0 2 (3;1;1)ttt tA
11OA
.
Câu 48. Cho hình chóp tứ giác đều .SABCD cạnh đáy bằng 2a , góc giữa hai mặt phẳng
SAB
và
A
BCD bằng
0
45
;
,,
M
NP
lần lượt là trung điểm của
,SA SB
và
A
B
. Tính thể tích
V
khối tứ diện
DMNP
A.
3
6
a
. B.
3
4
a
. C.
3
2
a
. D.
3
12
a
.
Lời giải
Tác giả : Lê Đình Năng FB: Lê Năng
Chọn A
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang35Mãđề843
Gọi điểm O là tâm của đáy, theo giả thiết suy ra:

SO ABCD tại O
Góc giữa mặt phẳng
SAB và
A
BCD bằng
0
45
nên suy ra góc
SPO
bằng
0
45
.
Ta có
OP a
suy ra
0
tan 45SO OP a
; 2SP a .
2
111 2
.. .
442 4
MNP SAB
a
SS ABSP


.
Tứ diện
DMNP
có chiều cao
,( ) 2 ( ,( ))hdDMNP dOSAB
Trong (SPO) kẻ OH vuông góc với SP tại H thì OH là khoảng cách từ O đến (SAB)
Áp dụng hệ thức lượng trong tam giác vuông SPO tại O, đường cao OH ta có
2222
1112
OH OP SO a

2
2
a
OH h a
Thể tích khối chóp D.MNP là
23
12
..2
34 6
aa
Va
hungvn1985@gmail.com
Câu 49.
Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
2
():2x2yzm 3 0Pm
và
mặt cầu

222
(): 1 1 1 9Sx y z. Tìm tất cả các giá trị của m để
()P
tiếp xúc với
()S
.
A.
2
5
m
m

. B.
2
5
m
m

. C.
2m
. D.
5m 
.
Lời giải
Tác giả : Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng
Chọn B
Ta có
1; 1; 1
():
3
I
S
R
.
Để
()P
tiếp xúc với
()S
thì


2
2
2
13
3100 2
;3
5
3
380
mm
mm m
dI P R
m
mm





.
Câu 50. Cho hai số thực
1, 1ab
. Biết phương trình
2
1
1
xx
ab
có hai nghiệm phân biệt
12
,
x
x
. Tìm
giá trị nhỏ nhất của biểu thức

2
12
12
12
4
xx
Sxx
xx




.
A.
3
34
. B. 4 C.
3
32
. D.
3
4
.
SảnphẩmcủaGroup:TEAMTOÁNVD–VDCĐềGiữaHK1Lớp12ChuyênLêHồngPhong–NamĐịnh18‐19
HãythamgiaGroupSTRONGTEAMTOÁNVD‐VDC.‐GroupchỉdànhchocácGv,Svtoán!Trang36Mãđề843
Lời giải
Tác giả : Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng
Chọn A
Ta có

2
12 2
1 1 log 0 log log 0
xx
aa a
ab x x b b x x b

Do phương trình có hai nghiệm
12
,
x
x
nên theo định lý Viet ta có:
12
12
1
log
log
1
b
a
x
xa
b
xx


Khi đó
2
1
4log
log
b
b
Sa
a

Đặt
log
b
ta
, do
1, 1 0ab t
. Khi đó
3
22
11
42234Sttt
tt

.
Đẳng thức xảy ra khi
2
3
11
2
2
tt
t

. Vậy
3
min 3 4S
=== STRONG TEAM TOÁN VD-VDC===
| 1/36
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19
SỞ GD&ĐT NAM ĐỊNH KIỂM TRA GIỮA HKI NĂM 2018 - 2019
THPT CHUYÊN LÊ HỒNG PHONG MÔN TOÁN – LỚP 12 KHỐI ABCD
Thời gian làm bài: 90 phút
(50 câu hỏi trắc nghiệm) MÃ ĐỀ THI: 843
(Thí sinh không được sử dụng tài liệu)
Họ và tên thí sinh: …………………………………...…………… SBD: ………………..……. Câu 1. Cho với m , p ,
và là các phân số tối giản. Giá trị bằng 22 A. 10 . B. 6 . C. . D. 8 . 3
Câu 2. Trong không gian Oxyz , cho mặt cầu (S) (x- )2 +( y + )2 +(z - )2 : 3 1
1 = 4 . Tâm của (S) có tọa độ là A. ( 3; - 1;- ) 1 . B. (3; 1 - ; ) 1 . C. (3; 1 - ;- ) 1 . D. (3;1; ) 1 - .
Câu 3. Cho các số thực dương a,b,c với a và b khác 1. Khẳng định nào sau đây là đúng? 1 A. 2
log b .log c  log c . B. 2
log b .log c  log c . a b a a b 4 a C. 2
log b .log c  4 log c . D. 2
log b .log c  2 log c . a b a a b a
Câu 4. Khẳng định nào sau đây là đúng? 1 1 2018 2018 A. 3 3 x dx x dx   . B. 4 2
x x 1 dx   4 2 x x    1dx. 1 1 1  1    3 3 C. x    1 d x e x x e x    1dx . D. 2 2 2 1 cos xdx  sin d x x   . 2  2      2 2
Câu 7. Đồ thị sau đây là của hàm số nào ? A. 3 2
y x  3x  4. B. 3 2
y  x  3x  4 . C. 3 2
y x  3x  4 . D. 3 2
y  x  3x  4 . Câu 8. Cho hàm số 4 2
y x  2x  3 có đồ thị hàm số như hình bên dưới. Với giá trị nào của tham số m phương trình 4 2
x  2x  3  2m  4 có hai nghiệm phân biệt ?
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 1 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 m  0   1 m 0 1 A.  1 .
B. 0  m  . C.  1 . D. m  . m  m   2 2 2  2
Câu 9. Trong các khẳng định sau, khẳng định nào sai ? 2 x e x
A. 2x d  2x x ln 2  C  . B. 2 e dx   C  . 2 1 1 C. cos 2 d
x x  sin 2x C  . D.
dx  ln x 1  C   x     1 . 2 x 1 3 x
Câu 10. Tìm hàm số F x biết F x  dx
và F 0 1. 4 x 1 1 3
A. F x   4 ln x   1 1.
B. F x  ln 4 x   1  . 4 4 1
C. F x  ln 4 x   1 1.
D. F x   4 4ln x   1 1. 4
Câu 11. Trong không gian Oxyz , mặt phẳng (P) : 2x z 1  0 có một vectơ pháp tuyến là:    
A. n  2;1;0 .
B. n  0; 2;1 . C. n  2;1; 1
 . D. n  2;0;1 . 4   1   2   3  
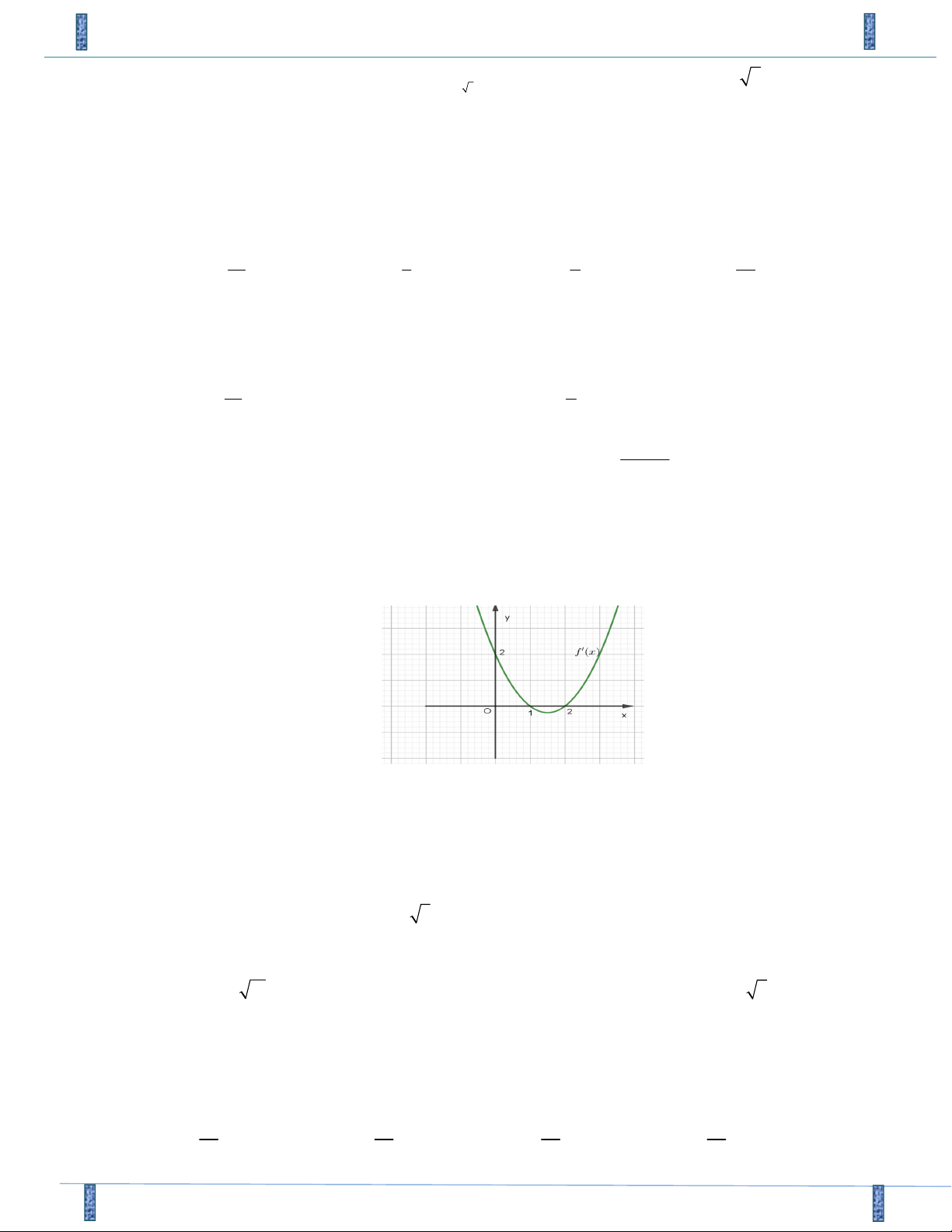
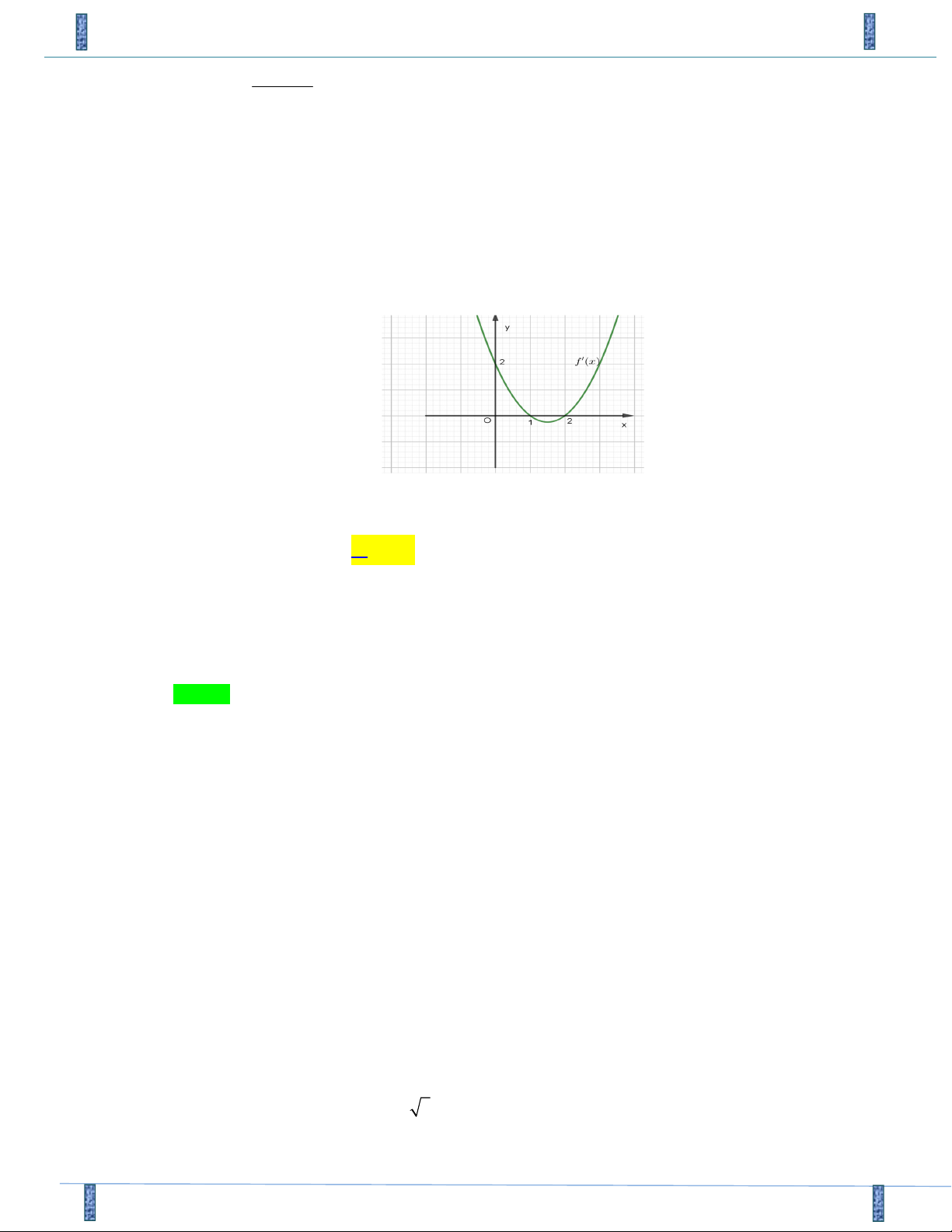
Câu 12. Cho hàm số y f (x) liên tục trên  và có bảng xét dấu đạo hàm như hình vẽ. Hàm số đã cho có bao nhiêu cực tr x  -2 0 2 4  f '(x) + - | + 0 + 0 - A. 1. B. 3. C. 4. D. 2.
Câu 13. Trong không gian Oxyz , cho hai điểm A2; 4;
 3 và B2;2;9 . Trung điểm của đoạn AB có tọa độ là  3 3 
A. 0;3;3 . B. 4; 2  ;12 .
C. 2;1;6 . D. 0; ;   .  2 2 
Câu 14. Trong các mệnh đề sau I .        2 2 f x dx f x dx II . f
 xdx f xC  III  . kf
 xdx k f
 xdx với mọi k  IV .  f
 xdx  f x
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 2 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19
Số mệnh đề đúng là A. 2. B. 4. C. 1. D. 3. 2 2
Câu 15. Cho 4 f
 x2xdx 1 
. Khi đó f xdx  bằng : 1 1 A.1. B. 3  . C. 3 . D. 1.
Câu 16. Thể tích của khối lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3a bằng: 3 27 3a 3 9 3a 3 3 9 3a A. . B. .
C. 27 3a . D. . 4 4 2 2
Câu 17. Tìm tất cả các giá trị thực của tham số m để hàm số 4
y x  m   2 2
1 x m đạt cực tiểu tại x  0
A. m  1.
B. m  1.
C. m   . D. m  1. ln x
Câu 18. Giá trị nhỏ nhất của hàm số y  trên đoạn 2;  3 bằng x ln 2 ln 3 3 1 A. . B. . C. . D. . 2 3 2 e e
Câu 19. Một hình trụ có diện tích xung quanh bằng 2
4 a và bán kính đáy là a . Tính độ dài đường cao
của hình trụ đó. A. a . B. 2a . C. 3a . D. 4a .
Câu 20. Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông với AB AC a , góc
giữa BC và  ABC bằng 45 . Tính thể tích khối lăng trụ. 3 a 2 3 a 3 A. . B. 3 a a . C. . D. . 2 6 2
Câu 21: Trong không gian Oxyz , cho 2 điểm (5
A ; 4; 2) và B(1; 2; 4) . Mặt phẳng đi qua A và vuông
góc với đường thẳng AB là?
A. 3x y  3z  25  0
B. 2x  3y z  8  0
C. 3x y  3z 13  0
D. 2x  3y z  20  0
Câu 22: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Đồ thị của hàm số 2x y
và y  log x đối xứng với nhau qua đường thẳng y  x . 2
B. Đồ thị của hai hàm số x
y e và y  ln x đối xứng với nhau qua đường thẳng y x . 1
C. Đồ thị của hai hàm số 2x y  và hàm số y
đối xứng với nhau qua trục hoành. 2x 1
D. Đồ thị của hai hàm số y  log x và y  log
đối xứng với nhau qua trục tung. 2 2 x
Câu 23: Tính đạo hàm của hàm số 2 2x y  .
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 3 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 2 1 2 x x A. y'  . B. 2 '  2x y x ln4 . C. 2 2 1 ' 2 x y x   . D. 2 '  2x y x ln2 . ln2
Câu 24: Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng BA’ và B’D’ bằng A. 0 45 . B. 0 90 . C. 0 30 . D. 0 60 . 4 2x  3
Câu 25. Cho hàm số f (x) 
. Khẳng định nào sau đây là đúng? 2 x 3 2x 3 3 2x 3
A. f (x)dx    C  .
B. f (x)dx    C  . 3 2x 3 x 3 2x 3 3
C. f (x)dx    C  . D. 3
f (x)dx  2x   C  . 3 x x
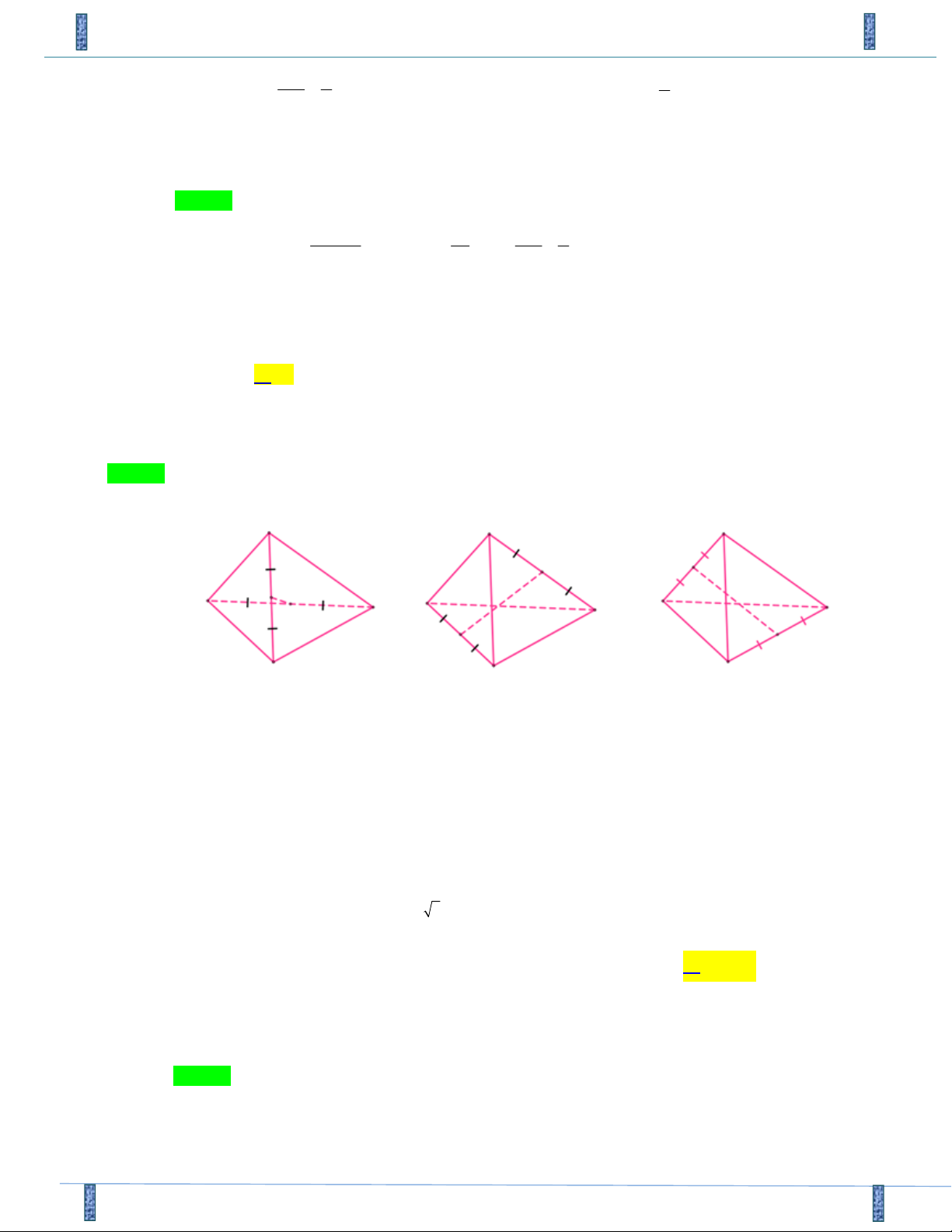
Câu 26. Hình tứ diện đều có bao nhiêu trục đối xứng? A. 0 . B. 1. C. 3 . D. 2 .
Câu 27. Tìm tập xác định của hàm số: x y  2
 log3 x A. 0;   . B. 0;  3 . C.   ;3  . D. 0;  3 . x 1 1
Câu 28. Tìm tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số: y x2  x 3 A. 3. B. 2. C. 4. D. 1.
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho điểm A2;4;  1 ; B  1  ;1;3 và mặt phẳng
P: x 3y  2z 5  0 . Một mặt phẳng Q đi qua hai điểm ,
A B và vuông góc với mặt
phẳng P có dạng ax by cz 11  0 . Khẳng định nào sau đây là đúng?
A. a b c  5 .
B. a b c  15 .
C. a b c  5 .
D. a b c  15  . e ln x c
Câu 30. Cho I
dx a ln 3  b ln 2  
, với a,b,c   . Khẳng định nào sau đâu đúng.
x ln x  22 3 1 A. 2 2 2
a b c  1. B. 2 2 2
a b c  11 . C. 2 2 2
a b c  9 . D. 2 2 2
a b c  3 .
Câu 31. Cho tam giác ABC vuông tại A có AB = a 3 và BC = 2a . Tính thể tích khối nón tròn xoay
khi quay tam giác ABC quanh trục AB 3 2pa 3 pa 3 A. 3
V = pa 3 . B. 3
V = 2pa . C. V = . D. V = . 3 3
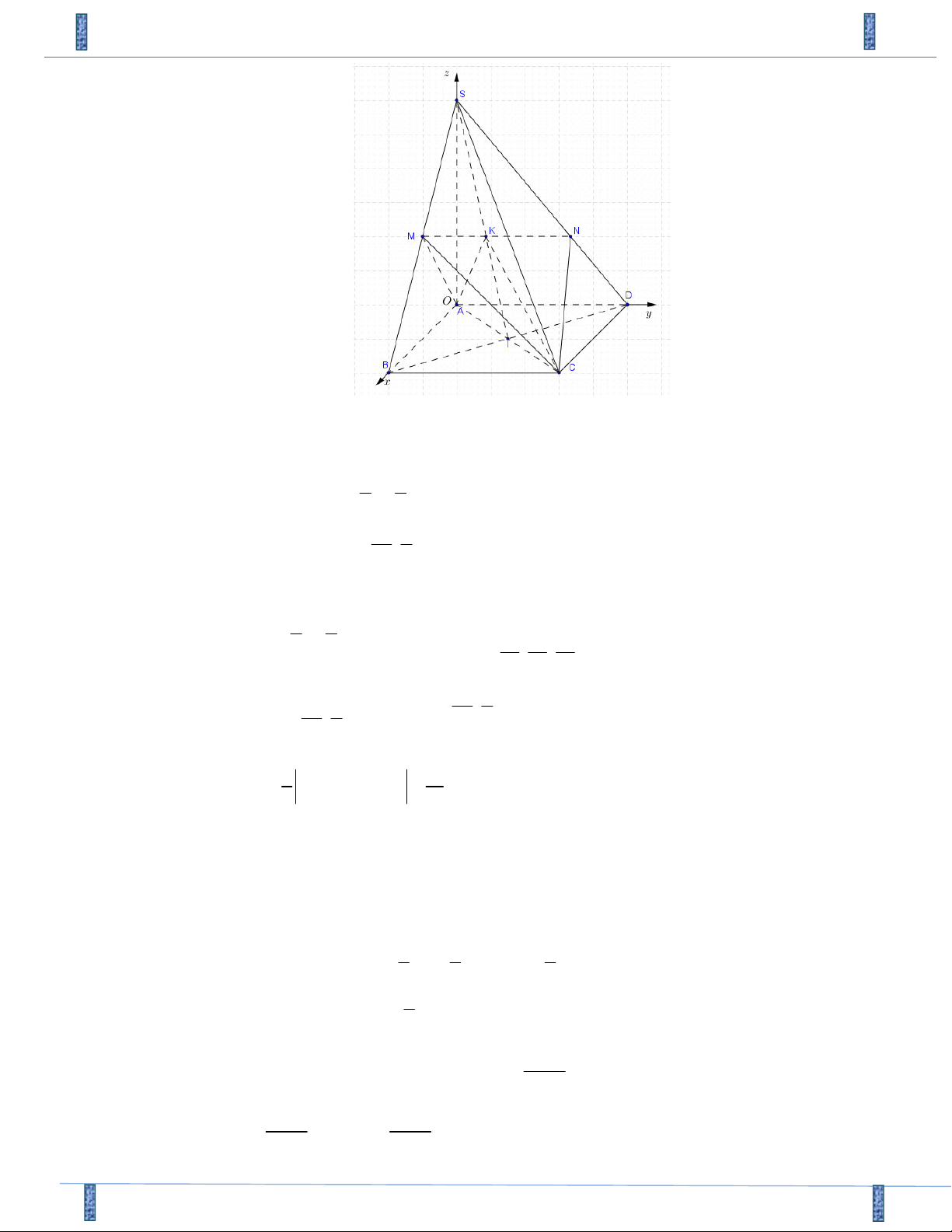
Câu 32. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , tam giác SAB đều và nằm trong mặt
phẳng vuông góc với đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng a 5 a 3 A. a . B. . C. . D. a 2 . 2 2
Câu 33. Tìm tất cả các nguyên hàm của hàm số f x   2 3x   1 .ln x . x 3 x A. f
 xdx xx   3 2 1 ln x   C . B. f  x 3
dx x ln x   C . 3 3
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 4 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 x 3 x C. f
 xdx xx   3 2 1 ln x
x C . D. f  x 3
dx x ln x   x C . 3 3
Câu 34. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P :x y z  2  0 và hai điểm A3;4;  1 ; B 7; 4;  3
  . Điểm M  ; a ;
b ca  2 thuộc P sao cho tam giác ABM vuông tại
M và có diện tích nhỏ nhất. Khi đó giá trị biểu thức T a b c bằng:
A.T  6 .
B.T  8. C. T  4 . D.T  0 .
Câu 35. Cho hàm số y f x liên tục trên 0; thỏa mãn xf x  f x 2 2 '  3x
x . Biết f   1 1  . 2
Tính f 4 ? A. 24 . B.14 . C. 4 . D.16 . Câu 36. Cho hàm số 3
y  x  6x  2 có đồ thị là C và đường thẳng d : y mx m  2 . Tìm giá trị của
tham số m để d cắt C tại ba điểm phân biệt ,
A B,C sao cho tổng các hệ số góc của các tiếp
tuyến của đồ thị C tại , A B,C bằng 6  .
A. m  1.
B. m  .
C. m  2 . D. m  1 . 2 1 p xp
Câu 37. Biết x  2 1 x q e
dx me n , trong đó , m ,
n p, q là các số nguyên dương và là phân số tối q 1
giản. Tính T m n p q .
A. T  11.
B. T  10 .
C. T  7 . D. T  8.
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tam giác SAB đều và nằm trong
mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho. 3 7 21 a 3 7 21 a 3 4 3 a 3 4 3 a A. V  . B. V  . C. V  . D. V  . 54 18 81 27
Câu 39. Cho hình lập phương ABC . D AB CD
  có cạnh a . Một khối nón có đỉnh là tâm của hình vuông
ABCD và đáy là hình tròn nội tiếp hình vuông AB CD
  . Diện tích toàn phần của khối nón đó là 2  2  2  2  A. a a a a S   . B. S   . C. S   . D. S   . tp  3 1 tp  5 2 tp  5 1 tp  3 2 2 4 4 2
Câu 40. Tổng tất cả các giá trị nguyên của tham số m để hàm số 4 3 2
y  3x  8x  6 x  24 x m có 7
điểm cực trị bằng A. 63 . B. 42 . C. 55 . D. 30 .
Câu 41. Một chiếc ô tô đang chạy với vận tốc 15m/s thì người lái xe hãm phanh. Sau khi hãm phanh, ô
tô chuyển động chậm dần đều với vận tốc v t  3  t 15m/ 
s , trong đó t (giây). Hỏi từ lúc
hãm phanh đến khi dừng hẳn, ô tô di chuyển được bao nhiêu mét? A. 38m. B. 37,2m. C. 37,5m. D. 37m.
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 5 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19
Câu 42. Tổng các nghiệm của phương trình log  x  2  log  x  42  0 là S a b 2 (với a,b là 3 3
các số nguyên). Giá trị của biểu thức Q  . a b bằng A. 0. B. 3. C. 9. D. 6.
Câu 43. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA a và SA vuông góc với
đáy. Gọi M là trung điểm SB và N là điểm thuộc cạnh SD sao cho SN  2ND . Tính thể tích
khối tứ diện ACMN . 1 1 1 1 A. 3 V a . B. 3
V a . C. 3
V a . D. 3 V a . 12 8 6 36 4 5 2 ln 2
Câu 44. Biết f
 xdx  5 và f
 xdx  20. Tính 4 3     2x 2x f x dx f e e dx . 1 4 1 0 15 5 A. I  .
B. I  15 .
C. I  . D. I  25. 4 2 2x m
Câu 45. Có bao nhiêu giá trị nguyên m trên  1; 
5 để hàm số y
đồng biến trên khoảng x m  ;  3   ? A. 2. B. 6. C. 5. D. 3.
Câu 46. Cho hàm số y f ' x có đồ thị như hình vẽ
Hàm số y f  2
2  x  đồng biến trên khoảng nào dưới đây A.  ;0  . B. 0;  1 . C. 1;2 . D. 0;.
Câu 47. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : x  2y  2z  3  0 và mặt cầu S  tâm I 5; 3
 ;5 , bán kính R  2 5 . Từ một điểm A thuộc mặt phẳng P kẻ một đường
thẳng tiếp xúc với mặt cầu S  tại B . Tính OA biết AB  4 .
A. OA  11 .
B. OA  5 .
C. OA  3. D. OA  6 .
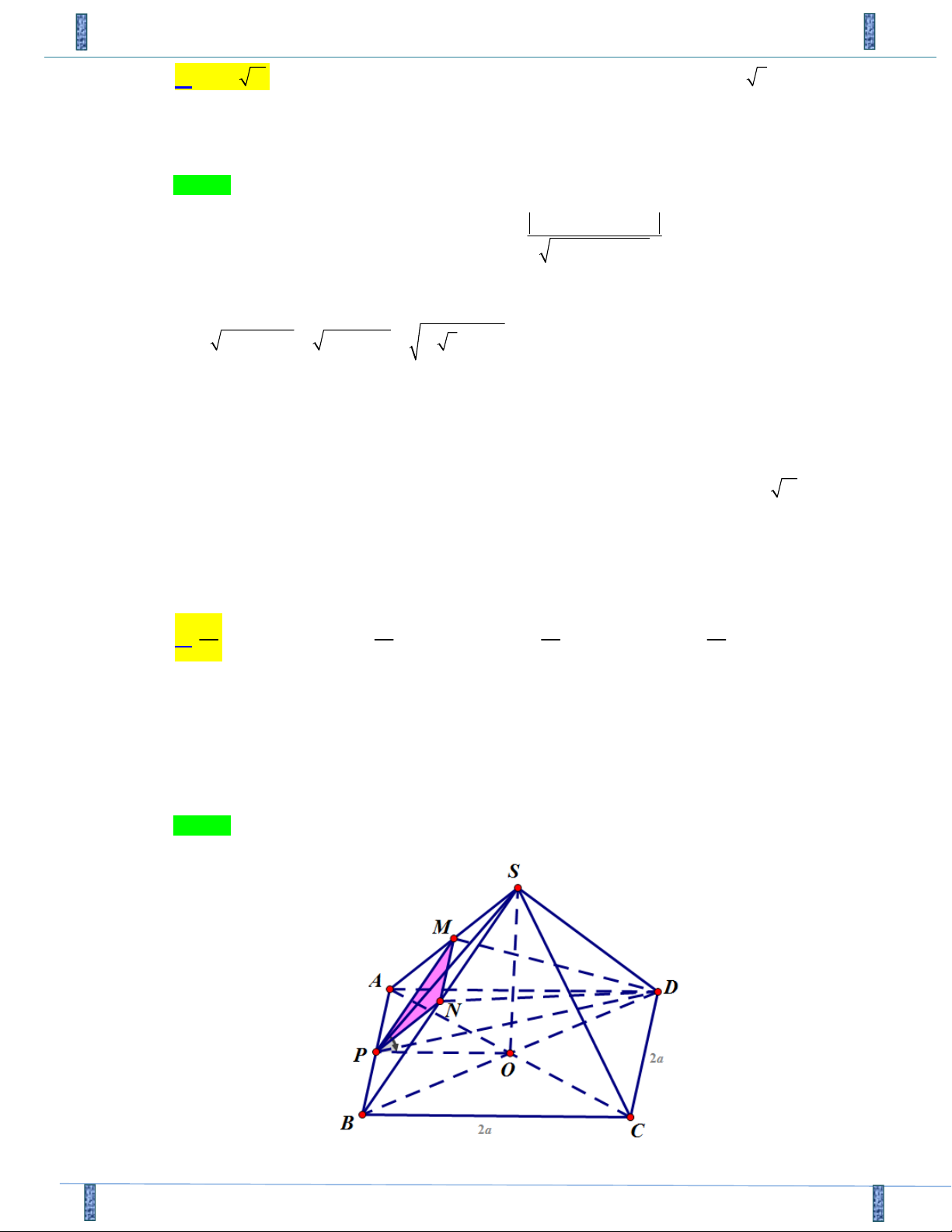
Câu 48. Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng 2a , góc giữa hai mặt phẳng SAB và ABCD bằng 0
45 ; M , N, P lần lượt là trung điểm của ,
SA SB và AB . Tính thể tích V
khối tứ diện DMNP 3 a 3 a 3 a 3 a A. . B. . C. . D. . 6 4 2 12
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 6 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19
Câu 49. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng 2
(P) : 2 x 2 y z m  3m  0 và
mặt cầu S x  2   y  2   z  2 ( ) : 1 1
1  9 . Tìm tất cả các giá trị của m để (P) tiếp xúc với (S) . m  2 m  2 A.  . B.  .
C. m  2 . D. m  5 . m  5 m  5
Câu 50. Cho hai số thực a  1,b  1. Biết phương trình 2 x x 1
a b   1 có hai nghiệm phân biệt x , x . Tìm 1 2 2  x x
giá trị nhỏ nhất của biểu thức 1 2 S  
  4 x x . 1 2  x x  1 2  A. 3 3 4 . B. 4 C. 3 3 2 . D. 3 4 .
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 7 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 BẢNG ĐÁP ÁN 1‐C. 2‐B. 3‐C. 4‐B. 5‐C. 6‐A. 7‐D. 8‐A. 9‐A. 10‐C. 11‐D. 12‐B. 13‐C. 14‐A. 15‐A. 16‐A. 17‐B. 18‐A. 19‐B. 20‐A. 21‐D. 22‐B. 23‐B. 24‐D. 25‐B. 26‐C. 27‐D. 28‐B. 29‐A. 30‐D. 31‐D. 32‐C. 33‐C. 34‐D. 35‐D. 36‐C. 37‐B. 38‐A. 39‐B. 40‐B. 41‐C. 42‐D. 43‐A. 44‐A. 45‐D. 46‐B. 47‐A. 48‐A. 49‐B. 50‐A.
LỜI GIẢI CHI TIẾT
Phamquoctoan87@gmail.com Câu 1. Cho với m , p ,
và là các phân số tối giản. Giá trị bằng 22 A. 10 . B. 6 . C. . D. 8 . 3 Lời giải
Tác giả: Phạm Quốc Toàn, FB: Phạm Quốc Toàn Chọn C. 1 1 x- 1 Ta có 2 3 1 = ⋅e = ( 5 2
e - e . Suy ra m = , p = 5 và q = 2 . 1 ) 3 3 3 1 22
Vậy m + p + q = + 5 + 2 = . 3 3
Câu 2. Trong không gian Oxyz , cho mặt cầu (S ) (x - )2 +(y + )2 +(z - )2 : 3 1
1 = 4 . Tâm của (S) có tọa độ là A. ( 3; - 1;- ) 1 . B. (3; 1 - ; ) 1 . C. (3; 1 - ;- ) 1 . D. (3;1; ) 1 - . Lời giải
Tác giả: Phạm Quốc Toàn, FB: Phạm Quốc Toàn Chọn B.
Tâm của (S) có tọa độ là (3; 1 - ; ) 1 .
Tuonganh0209@gmail.com
Câu 3. Cho các số thực dương a, ,
b c với a và b khác 1. Khẳng định nào sau đây là đúng? 1 A. 2
log b .log c  log c . B. 2
log b .log c  log c . a b a a b 4 a C. 2
log b .log c  4 log c . D. 2
log b .log c  2 log c . a b a a b a Lời giải
Tác giả: Nguyễn Ngọc Thảo, FB: Nguyễn Ngọc Thảo
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 8 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 Chọn C. Ta có: 2
log b .log c  2log .
b log c  2log .
b 2log c  4log .
b log c  4log c . 1 a b a a b a b a 2 b
Tuonganh0209@gmail.com
Câu 4. Khẳng định nào sau đây là đúng? 1 1 2018 2018 A. 3 3 x dx x dx   . B. 4 2
x x 1 dx   4 2 x x    1dx. 1 1 1  1    3 3 C. x    1 d x e x x e x    1dx. D. 2 2 2
1  cos xdx  sin d x x   . 2  2      2 2 Lời giải
Tác giả: Nguyễn Ngọc Thảo, FB: Nguyễn Ngọc Thảo Chọn B 1 1 3 2   Ta có: 4 2 4 2
x x  1  x  2.x .   2 1 3  x    0, x     . 2 4 4  2  4 2018 2018 Do đó: 4 2
x x 1 dx   4 2 x x    1dx . 1  1 
bichngock36@gmail.com 1 1
Câu 5 . Tích phân I  dx  có giá trị bằng x 1 0 A. ln 2 1 . B.  ln 2 . C. ln 2 . D. 1  ln 2 . Lời giải
Tác giả : Nguyễn Mạnh Dũng, FB: dungmanhnguyen Chọn C 1 1 1 d(x 1) Cách 1: Ta có: 1 I  dx
 ln x 1  ln 2  ln1  ln 2   . Chọn đáp án C. 0 x 1 x 1 0 0 Cách 2 : Sử dụng MTCT. Câu 6 . Hàm số 2 2
y  (x  4x) nghịch biến trong khoảng nào dưới đây ? A. (2;4). B. ( 1  ;2) . C. (0;2) . D. (0;4) . Lời giải
Tác giả : Nguyễn Mạnh Dũng, FB: dungmanhnguyen Chọn A
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 9 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 Xét hàm số 2 2
y  (x  4x) TXĐ: D   , ' 2
y  2.(x  4x)(2x  4) . x  0 Khi đó: ' y 0    x  2 
. Ta có bảng biến thiên sau: x  4  x  0 2 4  y'  0  0  0  y
Từ BBT ta có hàm số đã cho nghịch biến trên 2;4 . Chọn đáp án A.
quynhvanyka@gmail.com
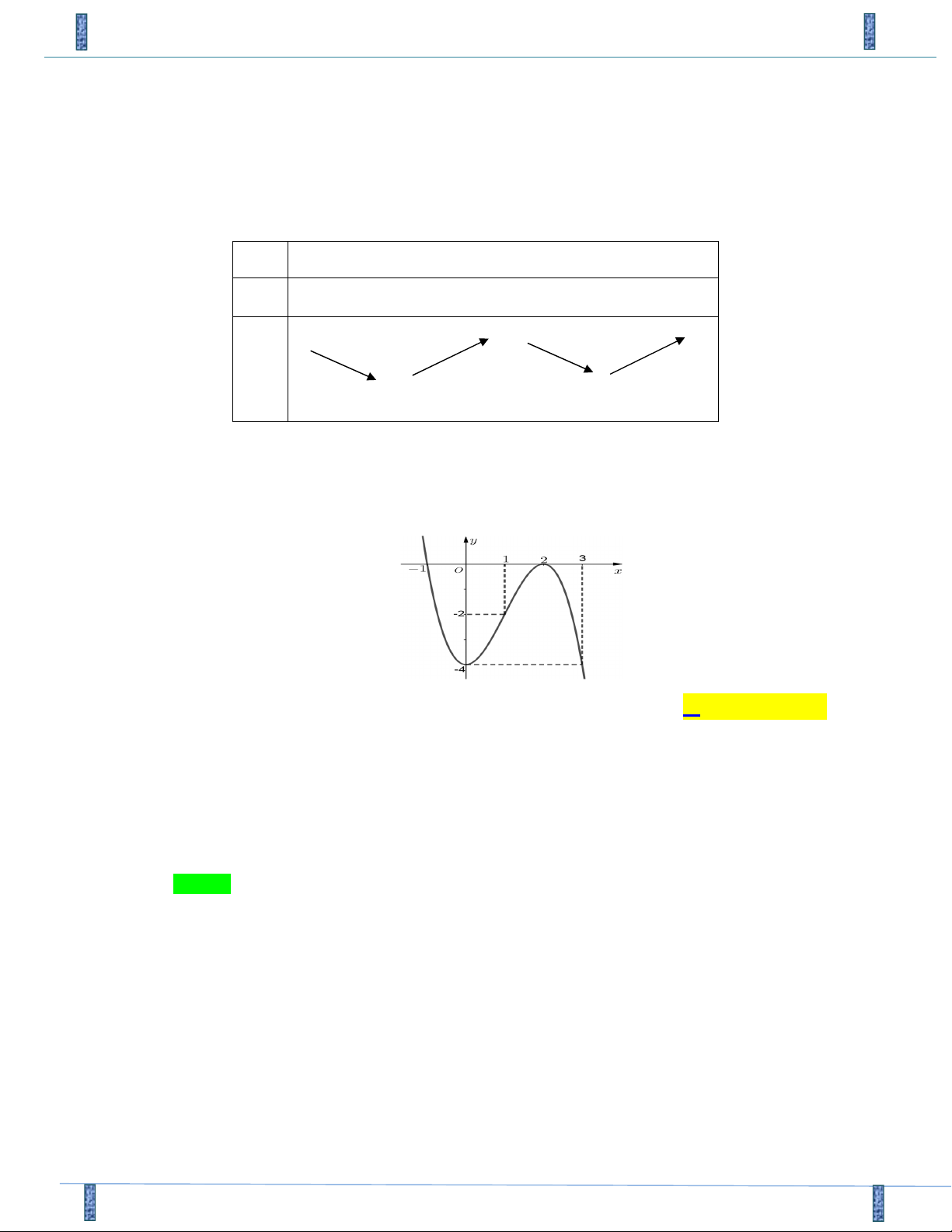
Câu 7. Đồ thị sau đây là của hàm số nào ? A. 3 2
y x  3x  4 . B. 3 2
y  x  3x  4 . C. 3 2
y x  3x  4 . D. 3 2
y  x  3x  4 . Lời giải
Tác giả : Mai Quỳnh Vân, FB: Van Mai Chọn D
Quan sát đồ thị hàm số ta thấy nhánh cuối cùng bên phải của đồ thị đi xuống nên hệ số a  0 . Loại đáp án A, C.
Mặt khác hàm số có hai điểm cực trị x  0 và x  2 nên phương trình y  0 có hai CT CĐ
nghiệm phân biệt là 0 và 2. Loại đáp án B, chọn đáp án D.
(Hoặc do điểm uốn của đồ thị hàm số là: 1; 2
  nên loại đáp án B, chọn D) Câu 8. Cho hàm số 4 2
y x  2x  3 có đồ thị hàm số như hình bên dưới. Với giá trị nào của tham số m phương trình 4 2
x  2x  3  2m  4 có hai nghiệm phân biệt ?
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 10 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 m  0 m  0 1 1 A.  1 .
B. 0  m  . C.  1 . D. m  . m  m   2 2 2  2 Lời giải
Tác giả : Mai Quỳnh Vân, FB: Van Mai Chọn A
Số nghiệm của phương trình 4 2
x  2x  3  2m  4 bằng số giao điểm của đường thẳng
y  2m  4 và đồ thị hàm số 4 2
y x  2x  3 .
Dựa vào đồ thị ta có phương trình 4 2
x  2x  3  2m  4 có hai nghiệm phân biệt khi và chỉ khi m  0 2m  4  4    1  . Chọn đáp án A. 2m  4  3  m   2
Email: buinguyenphuong1991@gmail.com
Câu 9. Trong các khẳng định sau, khẳng định nào sai ? 2 x e x
A. 2x d  2x x ln 2  C  . B. 2 e dx   C  . 2 1 1 C. cos 2 d
x x  sin 2x C  . D.
dx  ln x 1  C   x     1 . 2 x 1 Lời giải
Tác giả: Bùi Nguyên Phương. Facebook: Bùi Nguyên Phương Chọn A x 2x Ta có: 2 dx   C  . ln 2 3 x
Câu 10. Tìm hàm số F x biết F x  dx  và F 0 1. 4 x 1 1 3
A. F x   4 ln x   1 1.
B. F x  ln 4 x   1  . 4 4
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 11 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 1
C. F x  ln 4 x   1 1.
D. F x   4 4ln x   1 1. 4 Lời giải
Tác giả: Bùi Nguyên Phương. Facebook: Bùi Nguyên Phương Chọn C 1 1 1
Ta có: F x  d 
 4x  1  ln 4x 1 C. 4  4 x 1 4 1
Do F 0 1 nên ln 0  
1  C 1  C 1. 4 1
Vậy: F x  ln 4 x   1 1. 4
dotrang1008@gmail.com
Câu 11. Trong không gian Oxyz , mặt phẳng (P) : 2x z 1  0 có một vectơ pháp tuyến là:    
A. n  2;1;0 .
B. n  0; 2;1 . C. n  2;1; 1
 . D. n  2;0;1 . 4   1   2   3   Lời giải
Tác giả: Đỗ thị Huyền Trang, FB: Trang Đỗ Chọn D
Lý thuyết: Phương trình của mặt phẳng (P) có dạng : Ax By Cz D  0 , khi đó (P) 
có vectơ pháp tuyến là: n(P)   ; A ; B C  
Áp dụng: Mặt phẳng (P) : 2x z 1  0 có một vectơ pháp tuyến là n  2;0;1 . 4  
Câu 12. Cho hàm số y f (x) liên tục trên  và có bảng xét dấu đạo hàm như hình vẽ. Hàm số đã
cho có bao nhiêu cực trị x  -2 0 2 4  f '(x) + - || + 0 + 0 - A. 1. B. 3. C. 4. D. 2. Lời giải
Tác giả: Đỗ thị Huyền Trang, FB: Trang Đỗ Chọn B
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 12 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 x  -2 0 2 4  f (x) + - | + + - f (x)
Từ bảng biến thiên ta thấy hàm số có 3 cực trị.
tongthuyqn@gmail.com
Câu 13. Trong không gian Oxyz , cho hai điểm A2; 4;
 3 và B2;2;9 . Trung điểm của đoạn AB có tọa độ là  3 3  A. 0;3;3 . B. 4; 2  ;12 . C. 2;1;6 . D. 0; ;   .  2 2  Lời giải
Tác giả : Tống Thị Thúy, FB: Thuy tong Chọn C x x 2  2 A B x    2  I 2 2   y y 4   2
Gọi I là trung điểm của đoạn AB . Ta có A By    1   I 2; 1  ;6 . I 2 2   z z 3  9 A B z    6  I  2 2
Câu 14. Trong các mệnh đề sau I .        2 2 f x dx f x dx
II  . f
 xdx f xC  III  . kf
 xdx k f
 xdx với mọi k IV .  f
 xdx  f x Số mệnh đề đúng là A. 2. B. 4. C. 1. D. 3. Lời giải
Tác giả : Tống Thị Thúy, FB: Thuy tong Chọn A
Mệnh đề I  : Cho f x 1, x    , 2
VT I   1.dx x C
, VPI    dx
   xC2 2 2 1.
x  2x C
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 13 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19
VT I   VPI  , mệnh đề I  sai.
Mệnh đề II  đúng theo tính chất nguyên hàm.
Mệnh đề III  sai khi k  0 .
Mệnh đề IV  đúng . Gọi F x là một nguyên hàm của f x .
VT IV  F xC  
Fx  C  f x VPIV
phuongthu081980@gmail.com 2 2
Câu 15. Cho 4 f
  x2xdx 1 
. Khi đó f xdx  bằng : 1 1 A.1. B. 3  . C. 3 . D. 1 . Lời giải
Tác giả :Nguyễn Thị Phương Thu, FB: Nguyễn Phương Thu Chọn A 2 2 2 2 2 2 x 4 f
 x2xdx 1 4 f
 xdx2 xdx 1 4 f
 xdx2. 1 2 1 1 1 1 1 2 2  4 f
 xdx  4  f
 xdx 1 1 1
Câu 16. Thể tích của khối lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3a bằng: 3 27 3a 3 9 3a 3 27 3a 3 9 3a . . . . A. 4 B. 4 C. 2 D. 2 Lời giải
Tác giả :Nguyễn Thị Phương Thu, FB: Nguyễn Phương Thu Chọn A a2 3 3 . 3 27 3a V  . h B  3 . a  4 4
trichinhsp@gmail.com
Câu 17. Tìm tất cả các giá trị thực của tham số m để hàm số 4
y x  m   2 2
1 x m đạt cực tiểu tại x  0 A. m 1. B. m 1. C. m . D. m 1. Lời giải
Tác giả : Nguyễn Trí Chính, FB: Nguyễn trí Chính
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 14 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 Chọn B
y f x 4
x  m   2 2 1 x m x  0 / 3
y  4x  2m   1 x , / y  0    2 2x  1 m
TH1: Nếu m 1thì phương trình /
y  0 có một nghiệm đơn duy nhất x  0
Có a 1 0. Nên hàm số luôn đạt cực tiểu tại x  0. Suy ra m 1nhận Hoặc ta vẽ BBT: x - ∞ 0 +∞ _ y / 0 + +∞ +∞ y m2
TH2: Nếu m 1 thì phương trình /
y  0 có 3 nghiệm đơn 1 m 1     m x x 0  x  1 2 3 2 2
Có a 1 0. Nên hàm số luôn đạt cực đại tại x  0. Suy ra m 1loại Hoặc ta vẽ BBT: 1-m 1-m x - ∞ - 0 2 +∞ 2 _ 0 0 _ y / + 0 + y
Kết luận: Qua 2 trường hợp ta có m 1. ln x
Câu 18. Giá trị nhỏ nhất của hàm số y  trên đoạn 2;  3 bằng x ln 2 ln 3 3 1 A. . B. . C. . D. . 2 3 2 e e Lời giải
Tác giả : Nguyễn Trí Chính, FB: Nguyễn trí Chính
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 15 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 Chọn A Xét    ln x y f x
. Hàm số y f x liên tục trên đoạn 2;  3 x 1 ln x 1 ln x /  y  ; / y  0 
 0  x e 2;  3 2 x 2 x   ln2 1 ln3 Có f 2   0,3466 ; f  
e   0,3679; f   3   0,366 , 2 e 3 ln2
Suy ra Min f x  . x   2;    3 2 ln x ln 2
Vậy giá trị nhỏ nhất của hàm số y  trên đoạn 2;  3 bằng . x 2
lehongphivts@gmail.com
Câu 19. Một hình trụ có diện tích xung quanh bằng 2
4 a và bán kính đáy là a . Tính độ dài đường cao của hình trụ đó. A. a . B. 2a . C. 3a . D. 4a . Lời giải
Người giải: Lê Hồng Phi, FB: Lê Hồng Phi Chọn B
Diện tích xung quanh của hình trụ có bán kính đáy a và chiều cao h là 2 S  xq 4 a
S  2 ah h    2a . xq 2 a 2 a
Vậy độ dài đường cao của hình trụ đó là h  2a .
Câu 20. Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông với AB AC a , góc
giữa BC và  ABC bằng 45 . Tính thể tích khối lăng trụ. 3 a 2 3 a 3 a A. . B. 3 a . C. . D. . 2 6 2 Lời giải
Người giải: Lê Hồng Phi, FB: Lê Hồng Phi Chọn A A' C' B'
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 16 Mã đề 843 A C
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 2 a
Tam giác ABC vuông và có AB AC a nên A 90  . Như thế thì S  . ABC 2
Từ BC   ABC  B và CC   ABC suy ra góc giữa BC và  ABC là  C BC 45   . Do đó 2 2 2 2
CC  BC AB AC a a a 2 . 2 3 a a 2
Vậy thể tích của khối lăng trụ là V=S .CC   a 2  . ABC 2 2
Email: Ninhtldh@gmail.com
Câu 21: Trong không gian Oxyz , cho 2 điểm A(5; 4; 2) và B(1; 2; 4) . Mặt phẳng đi qua A và vuông
góc với đường thẳng AB là?
A. 3x y  3z  25  0
B. 2x  3y z  8  0
C. 3x y  3z 13  0
D. 2x  3y z  20  0 Lời giải
Tác giả: Hứa Chí Ninh Chọn D. 
Mặt phẳng vuông góc với đường thẳng AB nên nhận AB làm vectơ pháp tuyến,  AB  (4; 6; 2)  Mặt phẳng đi qua (5
A ; 4; 2) và có vectơ pháp tuyến, AB  (4;6; 2) có phương trình
4(x  5)  6(y 4)  2(z 2)  0 hay 2x  3 y z 20  0 . Vậy chọn D.
Câu 22: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Đồ thị của hàm số 2x y
và y  log x đối xứng với nhau qua đường thẳng y   x . 2
B. Đồ thị của hai hàm số x
y e và y  ln x đối xứng với nhau qua đường thẳng y x . 1
C. Đồ thị của hai hàm số 2x y  và hàm số y
đối xứng với nhau qua trục hoành. 2x 1
D. Đồ thị của hai hàm số y  log x và y  log
đối xứng với nhau qua trục tung. 2 2 x Lời giải
Tác giả: Hứa Chí Ninh Chọn B.
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 17 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 Đồ thị hàm số x
y a và đồ thị hàm số y  log x đối xứng với nhau qua đường phân giác góc a
phần tư thứ nhất ( y x ), suy ra chọn B.
kimoanh0102@gmail.com
Câu 23: Tính đạo hàm của hàm số 2 2x y  . 2 1 2 x x A. y'  . B. 2 '  2x y x ln4 . C. 2 2 1 ' 2 x y x   . D. 2 '  2x y x ln2 . ln2 Lời giải
Tác giả: Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh Chọn B 2 x      2 2 2 2 2 '
'.2x ln2  2 .2x .ln2  2x y y x x x ln4 .
Câu 24: Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng BA’ và B’D’ bằng A. 0 45 . B. 0 90 . C. 0 30 . D. 0 60 . Lời giải
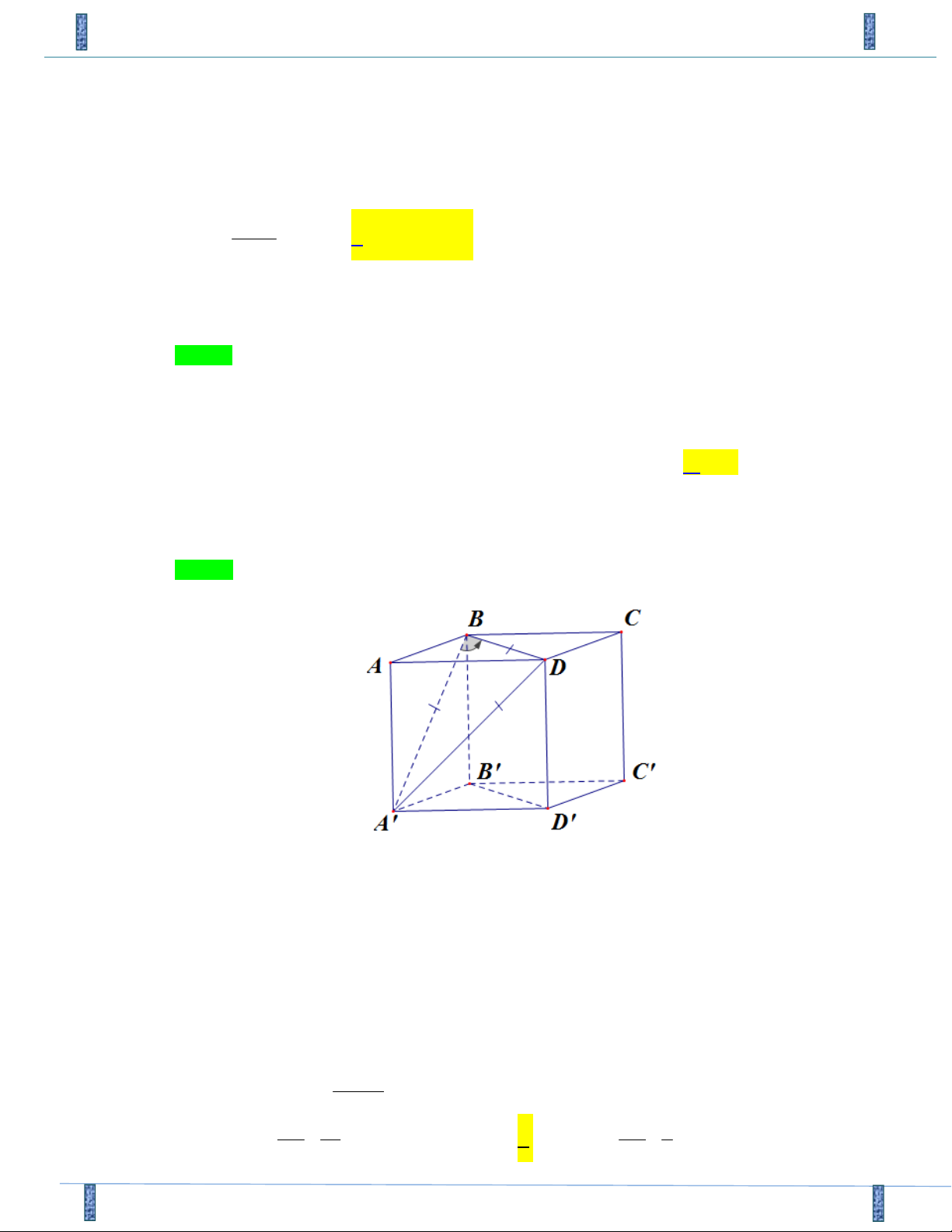
Tác giả: Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh Chọn D
Vì BD // B' D ' nên góc giữa hai đường thẳng BA’ và B’D’ bằng góc giữa hai đường thẳng BA’ và BD.
Ta có ABCD.A’B’C’D’ là hình lập phương nên tam giác A’BD là tam giác đều.
Khi đó góc giữa hai đường thẳng BA’ và BD bằng  0 ABD  60 .
Vậy góc giữa hai đường thẳng BA’ và B’D’ bằng 0 60 .
chauhieu2013@gmail.com 4 2x  3
Câu 25. Cho hàm số f (x) 
. Khẳng định nào sau đây là đúng? 2 x 3 2x 3 3 2x 3
A. f (x)dx    C  .
B. f (x)dx    C  . 3 2x 3 x
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 18 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 3 2x 3 3
C. f (x)dx    C  . D. 3
f (x)dx  2x   C  . 3 x x
Họ và tên tác giả :Trần Văn Hiếu Tên FB: Hieu Tran Lời giải Chọn B 4 3 2x  3  3  2x 3 Ta có 2
f (x)dx dx  2x dx    C    2  2  xx  3 x
Câu 26. Hình tứ diện đều có bao nhiêu trục đối xứng?
A. 0 .B. 1. C. 3 . D. 2 .
Họ và tên tác giả :Trần Văn Hiếu Tên FB: Hieu Tran Lời giải Chọn C
Gọi S là tập hợp các đỉnh của khối tứ diện đều ABCD . Giả sử d là trục đối xứng của tứ diện
đã cho, phép đối xứng trục d biến S thành chính S nên d phải là trung trực của ít nhất một
đoạn thẳng nối hai đỉnh bất kỳ của tứ diện .
Vậy tứ diện đều có 3 trục đối xứng là các đường thẳng nối trung điểm của các cặp cạnh đối diện.
tuenhi210510@gmail.com
Câu 27. Tìm tập xác định của hàm số: x y  2  log3 xA. 0;    . B. 0;3 . C.  ;3   . D. 0;3   . Lời giải
Tác giả : Lê Khánh Vân, FB: khanhvan le Chọn D Điều kiện xác định:
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 19 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19x  0 x  0     D  0;  3 3   x  0 x  3 x 1 1
Câu 28. Tìm tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số: y x2  x 3 A. 3. B. 2. C. 4. D. 1. Lời giải
Tác giả : Lê Khánh Vân, FB: khanhvan le Chọn B x 1 0 x  1
Điều kiện xác định:    2
x  3x  0 x  3 1 1 1   x 1 1 x3 x4 x2 lim y  lim  lim  0 x x 2  x x x  3 3 1 x  lim        x 1 1 2 1 x 1 1 lim
  vì x 3   x   x2 3  x 3  lim     2 x 3x 0 x 3   2
x  3  0  x  3  x(x 3)  0  x  3x  0  lim        x 1 1 2 1 x 1 1 lim   vì x 3   x   x2 3  x 3  lim     2 x 3x 0 x 3   2
x  3  x  3  x(x 3)  0  x  3x  0
Đường thẳng y  0 là tiệm cận ngang của đồ thị hàm số.
Đường thẳng x  3 là tiệm cận đứng của đồ thị hàm số.
(tien.vuviet@yahoo.com)
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho điểm A2;4;  1 ; B  1  ;1;3 và mặt phẳng
P: x 3y  2z 5  0. Một mặt phẳng Q đi qua hai điểm ,
A B và vuông góc với mặt phẳng
P có dạng ax by cz 11 0 . Khẳng định nào sau đây là đúng?
A. a b c  5.
B. a b c 15.
C. a b c  5  .
D. a b c  15  . Lời giải
Tác giả : Vũ Việt Tiến, FB: Vũ Việt Tiến Chọn A
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 20 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19
Vì Q vuông góc với P nên Q nhận vtpt n  1; 3;2 của P làm vtcp 
Mặt khác Q đi qua A và B nên Q nhận AB  3;3;2 làm vtcp    
Q nhận n   ,
n AB  0;8;12 làm vtpt Q   
Vậy phương trình mặt phẳng Q : 0(x 1)  8(y 1) 12(z  3)  0 , hay Q : 2y  3z 11  0
Vậy a b c  5. Chọn A.
(tien.vuviet@yahoo.com) e ln x c
Câu 30. Cho I
dx a ln 3  b ln 2  
, với a,b,c   . Khẳng định nào sau đâu đúng.
x ln x  22 3 1 A. 2 2 2
a b c  1. B. 2 2 2
a b c  11 . C. 2 2 2
a b c  9 . D. 2 2 2
a b c  3 . Lời giải
Tác giả : Vũ Việt Tiến, FB: Vũ Việt Tiến Chọn D e ln x dx Ta có I dx
, đặt ln x  2  t   dt
x ln x  22 x 1 3 3 3 3 3 t  2 1 1 2 2 2 1 I dt dt  2 dt  ln t
 ln 3 ln 2    ln 3 ln 2     2 2 t t t t 3 2 3 2 2 2 2 2
Suy ra a  1;b  1;c  1 , vậy 2 2 2
a b c  3. Chọn D.
Email: trandongphong.c3lehongphong@lamdong.edu.vn.
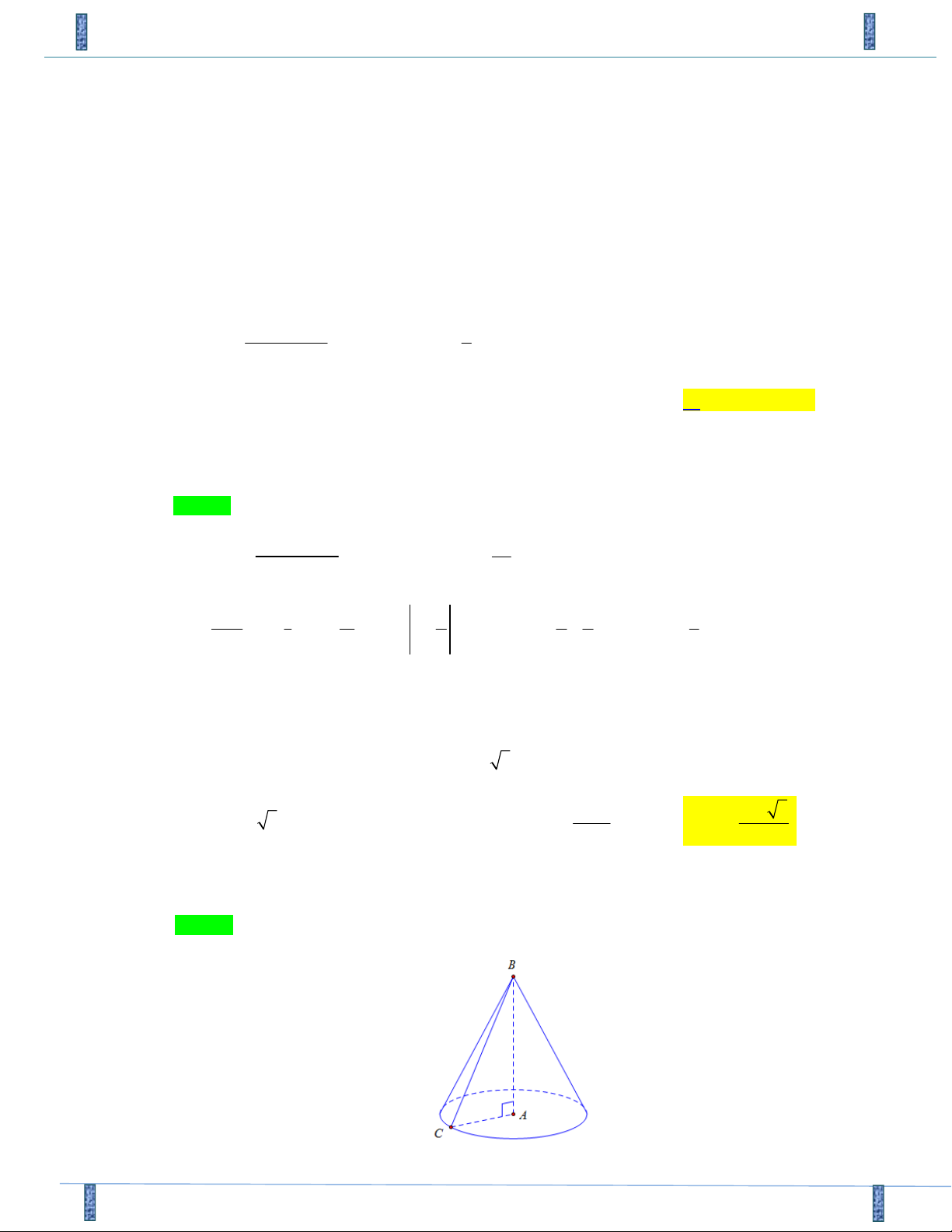
Câu 31. Cho tam giác ABC vuông tại A có AB = a 3 và BC = 2a . Tính thể tích khối nón tròn xoay
khi quay tam giác ABC quanh trục AB 3 2pa 3 pa 3 A. 3 V = a p 3 . B. 3 V = 2pa . C. V = . D. V = . 3 3 Lời giải
Họ và tên tác giả: Trần Đông Phong FB: Phong Do Chọn D
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 21 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19
Xét tam giác ABC vuông tại A có AB = a 3 và BC = 2a , suy ra: AC = a
Quay tam giác ABC quanh trục AB tạo thành khối nón tròn xoay
Biết chiều cao BA = a 3 , bán kính đường tròn đáy R = AC = a 3 1 pa 3 Thể tích khối nón 2 V = pR h = . 3 3
Email: trandongphong.c3lehongphong@lamdong.edu.vn.
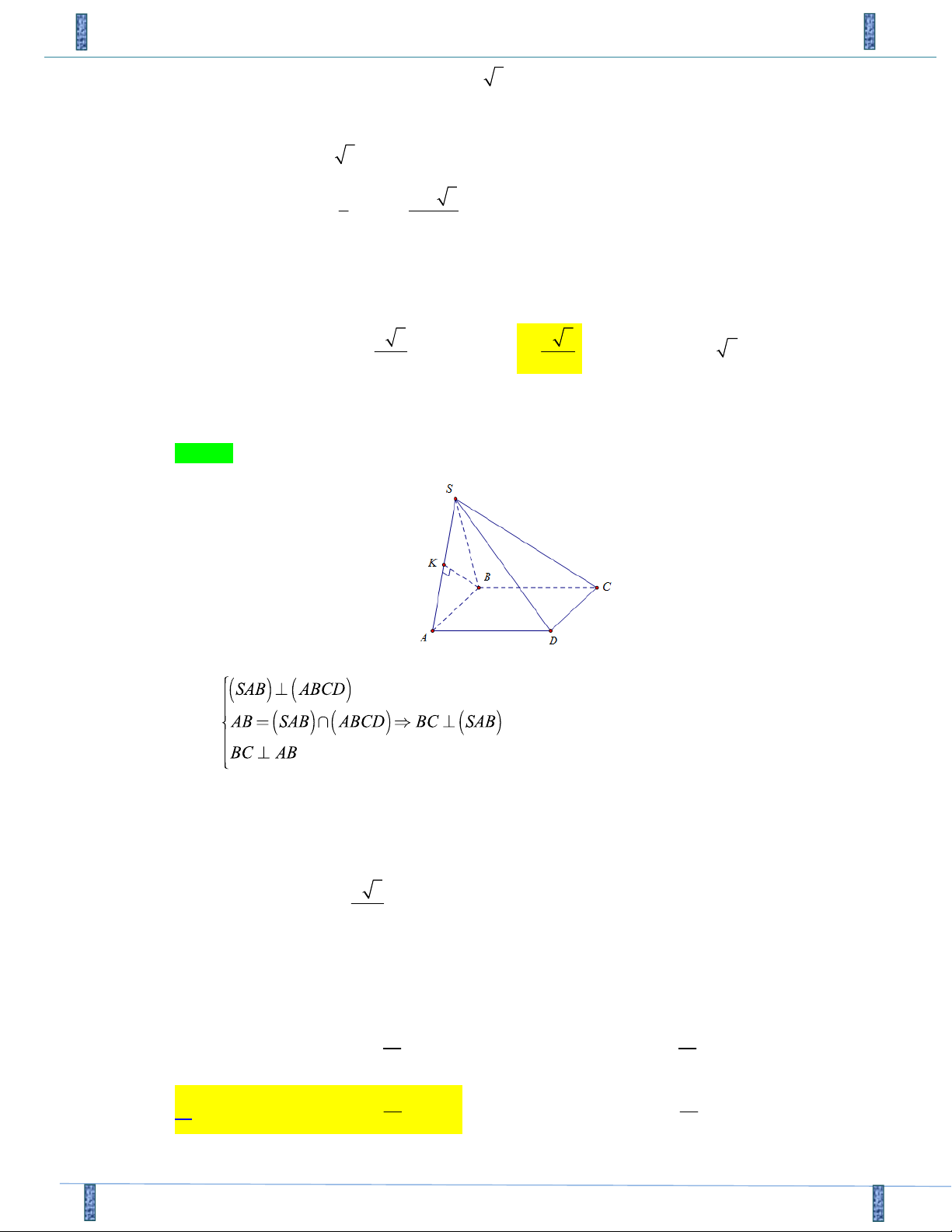
Câu 32. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , tam giác SAB đều và nằm trong mặt
phẳng vuông góc với đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng a 5 a 3 A. a . B. . C. . D. a 2 . 2 2 Lời giải
Họ và tên tác giả: Trần Đông Phong FB: Phong Do Chọn C Ta có ( ) 1
Trong mặt phẳng (SAB), dựng BK ^ SA tại K (2) Từ ( )
1 ,(2) suy ra: BK là đoạn vuông góc chung của SA và BC a Vậy d (SA BC) 3 , = BK = 2
tuluc0201@gmail.com
Câu 33. Tìm tất cả các nguyên hàm của hàm số f x   2 3x   1 .ln x . x 3 x A. f
 xdx xx   3 2 1 ln x   C . B. f  x 3
dx x ln x   C . 3 3 x 3 x C. f
 xdx xx   3 2 1 ln x   x C . D. f  x 3
dx x ln x   x C . 3 3 Lời giải
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 22 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19
Tác giả :Võ Tự Lực, FB: Võ Tự Lực Chọn C. Ta có I   2 3x   1ln xdx  1 u   ln x du dx   Đặt    . dv    x 2 3x  
1dx v   2 3x   3
1 dx x x  
     x  x x 1 x I x x ln
dx x x  
1 ln x  x   1 dx x  x   3 3 3 2 2 2 1 ln x   x C . x 3
Câu 34. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P :x y z  2  0 và hai điểm A3;4;  1 ; B 7; 4;  3
  . Điểm M  ; a ;
b ca  2 thuộc P sao cho tam giác ABM vuông tại
M và có diện tích nhỏ nhất. Khi đó giá trị biểu thức T a b c bằng: A.T  6 . B.T  8. C. T  4 . D.T  0 . Lời giải
Tác giả : Võ Tự Lực, FB: Võ Tự Lực Chọn D. 1 Ta có: SA .
B MH với H là hình chiếu vuông góc của M lên AB. ABM 2
Do AB không đổi nên S
nhỏ nhất khi MH nhỏ nhất. ABM  AB  4; 8  ; 4        A .
B n  0  AB //(P) n    P P 1;1; 1
MH nhỏ nhất khi M nằm trên giao tuyến của mặt phẳng Q và P ;
với Q là mặt phẳng chứa AB và vuông góc với mpP .  AB  4; 8  ; 4       n
 phương trình mp Q là x z  4  0 . Q 3;0;3 n    P 1;1;  1
M nằm trên giao tuyến của mặt phẳng Q và P nên tọa độ M là nghiệm của hệ phương x t
x z  4  0  trình 
 y  2  2t M t;2  2t;4 t với t  2.
x y z  2  0 z  4t
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 23 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19  
Ta có AM  t  3;2  2t;3  t; BM  t  7;6  2t;7  t .
Tam giác ABM vuông tại M nên
 
AM .BM  0  t  3t  7  2  2t 6  2t   3  t 7  t   0
t  3 n
t 3t 7 2t 3t 1 0 t 33t 5 0              5  . t  l  3
+ t  3  M 3; 4  ; 
1  a b c  3  4 1  0 . Chọn D
nguyentuanblog1010@gmail.com
Câu 35. Cho hàm số y f x liên tục trên 0; thỏa mãn xf x  f x 2 2 '  3x
x . Biết f   1 1  . 2 Tính f 4 ? A. 24 . B.14 . C. 4 . D.16 . Lời giải
Tác giả:Phạm Chí Tuân, FB: Tuân Chí Phạm Chọn D 1 3
Trên khoảng 0; ta có: 2xf ' x  f x 2
 3x x x f 'x 2   x . 2 x 2
  x.f x' 3
x   x.f x' 3 2 2 dx x dx  . 2 2
x. f x 1 3
x C .  2 1 1 1 2 x x Mà f   1
1  nên từ  có: 1. f   3
1  .1  C    C C  0  f x  . 2 2 2 2 2 2 4 4 Vậy f 4  16 . 2 Câu 36. Cho hàm số 3
y  x  6x  2 có đồ thị là Cvà đường thẳng d : y mx m  2 . Tìm giá trị của
tham số m để d cắt C tại ba điểm phân biệt ,
A B,C sao cho tổng các hệ số góc của các tiếp
tuyến của đồ thị C tại , A B,C bằng 6  .
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 24 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 A. m  1. B. m  . C. m  2 . D. m  1 . Lời giải
Tác giả:Phạm Chí Tuân, FB: Tuân Chí Phạm Chọn C
Phương trình hoành độ giao điểm của C và d : 3 3
x  6x  2  mx m  2  x  m  6 x m  0   1 Điều kiện cần:
Giả sử d cắt C tại ba điểm phân biệt ,
A B,C thì phương trình  
1 có ba nghiệm phân biệt.
x x x  0
Gọi ba nghiệm của  
1 là x , x , x , theo viet ta có: A B CiA B C
x x x x x x m6  A B B C C A hàm số 3
y  x  6x  2 có đồ thị là C 2 y '  3  x  6 . Ta có
Gọi k , k , k lần lượt là hệ số góc của các tiếp tuyến của đồ thị C tại ba điểm , A B và C . 1 2 3 Ta có: 2
k  3x  6 ; 2
k  3x  6 và 2
k  3x  6 1 A 2 B 3 C
Theo bài: k k k  6   3   2 2 2
x x x
   x x x A B C  2 2 2 18 6 8 1 2 3 A B C
 x x x 2  8  2 x x x x x x 2 A B CA B B C C A
Thay i vào 2 ta có: 0  8  2m  6  m  2 .
Điều kiện đủ: Với m  2 ta có   1 trở thành 3
x  4x  2  0 .
Xét hàm số f x 3
x  3x  4 . Do f x là hàm đa thức nên xác định và liên tục trên  . Ta có: f  2    2  ; f  
1  1 ; f 0  2  ; f  2  . Vì: + f  2  . f  
1  0  phương trình f x  0 có ít nhất một nghiệm thuộc  2;    1 . + f  
1 . f 0  0  phương trình f x  0 có ít nhất một nghiệm thuộc  1;  0 .
+ f 0. f 2  0  phương trình f x  0 có ít nhất một nghiệm thuộc 0;2 .
Mặt khác vì f x là đa thức bậc ba nên phương trình f x  0 chỉ có tối đa ba nghiệm.
Vậy phương trình f x  0 có ba nghiệm phân biệt.
Do đó m  2 là giá trị cần tìm.
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 25 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19
Phản biện: lanhoang0254@gmail.com
(phunghang10ph5s@gmail.com) 2 1 p xp
Câu 37. Biết x  2 1 x q e
dx me n , trong đó , m ,
n p, q là các số nguyên dương và là phân số tối q 1
giản. Tính T m n p q . A. T  11. B. T  10 . C. T  7 . D. T  8. Lời giải
Tác giả : Phùng Hằng, FB: Hằng Phùng Chọn B 2 1 2 1 2 1 2 1 xxxx Ta có:    2 1 x
 2  2  1 x  2  1 x  2 x I x e dx x x e dx x e dx xe dx  1 1 1 1 2 2 1 2 2 1 2 1 xxx 1 x  1   x  Xét 2 2 2 2 I x 1 x e dx x . x e . dx x . x x e d x   x d        e 1   1  2 xx  1 1 1 1   2 2 1 2 1 xx       2  1 2 1 2 2 x x x x x   2 x x e e d x x e xe dx  1 1 1 1 1 1 2 2 2 1 3 x   2 x 2 x x x x 2
I  2xe dx x eI x e  4e 1 1  1 1 1 m  4 2 1 pxpn  1 Do x  2 1 x q e
dx me n , trong đó m, n, p, q
  và là phân số tối giản   q p  3 1  q  2
Khi đó, T m n p q  4 1 3  2  10 .
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tam giác SAB đều và nằm trong
mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho. 3 7 21 a 3 7 21 a 3 4 3 a 3 4 3 a A. V  . B. V  . C. V  . D. V  . 54 18 81 27 Lời giải
Tác giả : Phùng Hằng, FB: Hằng Phùng Chọn A
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 26 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19
*) Xác định tâm mặt cầu ngoại tiếp hình chóp S.ABCD :
Gọi G là trọng tâm tam giác SAB , O là tâm của hình vuông ABCD , M là trung điểm của AB .
Do SAB đều  SM AB
Mà SAB   ABCD  SM   ABCD  SM OM
OM là đường trung bình của ABC OM //AD OM AB (do AD AB)
OM  SAB .
Dựng các đường thẳng qua G, O lần lượt song song với MO, SM , hai đường thẳng này cắt nhau tại I
IO//SM , SM   ABCD  IO   ABCD Ta có:
, mà O là tâm của hình vuông ABCD
IA IB IC ID (1)
GI //OM , MO  SAB  GI  SAB Ta có:
, mà G là trọng tâm tam giác đều SAB
IS IA IB (2)
Từ (1), (2) suy ra: I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD .
*) Tính bán kính, thể tích khối cầu ngoại tiếp hình chóp S.ABCD : 1 a a
Ta có: OM AD
GI OM  (do tứ giácOMIG là hình chữ nhật) 2 2 2  2 a 3 a 3
SAB đều cạnh bằng a có G là trọng tâm  BG  .  3 2 3
Do GI  SAB  GI BG B
GI vuông tại G 2 2 2 2  a   a 3  a a 7 2 2
IB IG GB          a 2  3    4 3 12  
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 27 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 7
Bán kính khối cầu ngoại tiếp hình chóp S.ABCD là: R IB a 12
Thể tích khối cầu ngoại tiếp hình chóp S.ABCD là: 3 3 4 4  7  7 21 a 3
V   R  . a   . 3 3  12  54  
hoangthihonghanhc3ln@gmail.com
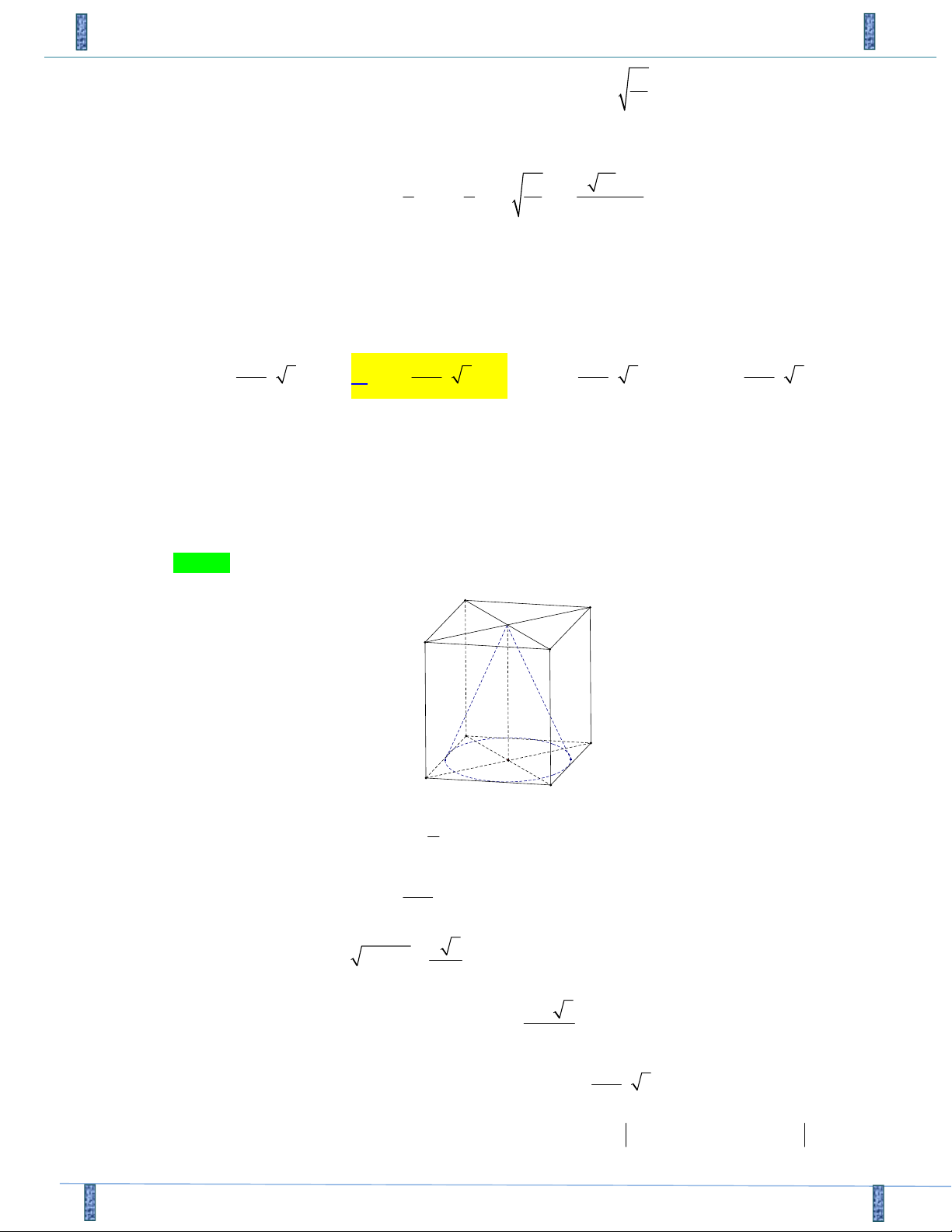
Câu 39. Cho hình lập phương ABC . D AB CD
  có cạnh a . Một khối nón có đỉnh là tâm của hình vuông
ABCD và đáy là hình tròn nội tiếp hình vuông AB CD
  . Diện tích toàn phần của khối nón đó là 2  2  2  2  A. a a a a S   . B. S   . C. S   . D. S   . tp  3 1 tp  5 2 tp  5 1 tp  3 2 2 4 4 2 Lời giải
Tác giả :Hoàng Thị Hồng Hạnh, FB: Hoàng Thị Hồng Hạnh Chọn B A D O B C a ADBOa C
Bán kính của đường tròn đáy là a r  . 2 2  Diện tích đáy nón là: a 2 S   r  . 1 4 a 5 Độ dài đường sinh là 2 2
l a r  . 2 2  a 5
Diện tích xung quanh của khối nón là: S   rl  . 2 4 2 
Vây, diện tích toàn phần của khối nón đó là: a
S S S  5 1 . tp 1 2   4
Câu 40. Tổng tất cả các giá trị nguyên của tham số m để hàm số 4 3 2
y  3x  8x  6 x  24x m có 7 điểm cực trị bằng
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 28 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 A. 63 . B. 42 . C. 55 . D. 30 . Lời giải
Tác giả :Hoàng Thị Hồng Hạnh, FB: Hoàng Thị Hồng Hạnh Chọn B Đặt 4 3 2
f (x)  3x  8x  6x  24x m 3 2 f (
x) 12x  24x 12x  24 x  2 f (x) 0     x  1  x  1 
Bảng biến thiên của f (x) x  2 1 1  f '(x)  0  0  0    f (x) 13 m  8  m 19  m
f (x) luôn có 3 điểm cực trị, để hàm số y f (x) có 7 điểm cực trị thì đồ thị hàm số f (x)
cắt trục hoành tại 4 điểm phân biệt (số điểm cực trị của hàm y f (x) bằng số điểm cực trị
của hàm f (x) cộng với số giao điểm của đồ thị hàm số f (x) với trục hoành).
 8  m  0  13  m  8  m  13 .
Mà m nguyên nên m 9;10;11;  12 .
Vậy, tổng tất cả các giá trị nguyên của tham số m bằng 9 10 1112  42 .
thaygiaothaogiay@gmail.com
Câu 41. Một chiếc ô tô đang chạy với vận tốc 15m/s thì người lái xe hãm phanh. Sau khi hãm phanh, ô
tô chuyển động chậm dần đều với vận tốc v t  3  t 15m/ 
s , trong đó t (giây). Hỏi từ lúc
hãm phanh đến khi dừng hẳn, ô tô di chuyển được bao nhiêu mét? A. 38m. B. 37,2m. C. 37,5m. D. 37m. Lời giải
Tác giả : Đinh Phước Tân, FB: Tân Độc Chọn C
Khi xe dừng hẳn thì v t  0  t  5.
Khi đó quảng đường xe đi được tính từ lúc bắt đầu hãm phanh đến khi dừng hẳn là:
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 29 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 5 5 2      t   3t S 3 15 dt   15t  37,5   m  2 0  0 Vậy ta chọn đáp án C.
Câu 42. Tổng các nghiệm của phương trình log  x  2  log  x  42  0 là S a b 2 (với a,b là 3 3
các số nguyên). Giá trị của biểu thức Q  . a b bằng A. 0. B. 3. C. 9. D. 6. Lời giải
Tác giả : Đinh Phước Tân, FB: Tân Độc Chọn D
Điều kiện: 2  x  4 .
Với điều kiện trên, phương trình đã cho tương đương
2log x  2  2log x  4  0  log x  2 x  4  0  x  2 x  4  1 3   3 3    
x  2x  4 2 1
x  6x  7  0 x  3 2       
x  2 x  4 2  1 
x  6x  9  0 x  3
So lại điều kiện, ta nhận hai nghiệm x  3  2; x  3 1 2
Ta được: S x x  6  2  a  6;b  1. Vậy Q  . a b  6 . 1 2
(tanbaobg@gmail.com)
Câu 43. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA a và SA vuông góc với
đáy. Gọi M là trung điểm SB và N là điểm thuộc cạnh SD sao cho SN  2ND . Tính thể tích
khối tứ diện ACMN . 1 1 1 1 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 V a . 12 8 6 36 Lời giải
Tác giả : Đỗ Tấn Bảo, FB: Đỗ Tấn Bảo Chọn A
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 30 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19
Cách 1. Đặt hệ trục tọa độ như hình vẽ. A0;0;0
  ;0;0   a a B a   M ;0;       2 2  Ta có C
 a;a;0   .     D a a 0; a;0 2 N 0; ;      3 3  S  0;0;a   a a AM  ;0; 2 2 2       2 2   a a a    
AM , AC    ; ;        2 2 2 Suy ra AC  ; a ; a 0     . 
  2a a
  2a a AN  0; ; AN  0; ;        3 3    3 3  
1    1 Do đó 3 V
 AM , AC.AN a (đvtt) ACMN 6   12
Cách 2.( Dành cho hsg giải tự luận)    
Đặt SN kSD và SK xSI với k; x  ;0  k; x  1.
Gọi I là tâm của hình vuông ABCD và K MN SI .
    1  1  
MK SK SM xSI SB   x   1 1 SB xSD  Ta có 2 2 2
    1   .
MN SN SM k SD SB  2 k
Vì M , K , N thẳng hàng nên k   x 2 2 1  x x  . 1 2k 2k 1 Suy ra SK SI KI SI . 1 2k 1 2k
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 31 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 2 IK a 1 a 2
Do đó d K, AC   SA   S
AC.d K AC  . AKC  ,  SI 1 2k 2 2 1 2k  1 a 2 2 a 2
Hơn nữa ta có d M, AKC  BO
;d N, AKC  BO  . 2 4 3 3 1 Vậy VVVS
d M ACK d N ACK ACMN MACK NACK AKC   ,   ,  3 2 3 1 a 2  a 2 a 2  7a  .      (đvtt). k  . 3 2 1 2  4 3   3.12   1 2k 2 1 Thay k  ta được 3 V a (đvtt). 3 12 4 5 2 ln 2
Câu 44. Biết f
 xdx  5 và f
 xdx  20. Tính 4 3     2x 2x f x dx f e e dx . 1 4 1 0 15 5 A. I  . B. I  15 . C. I  . D. I  25. 4 2 Lời giải
Tác giả : Đỗ Tấn Bảo, FB: Đỗ Tấn Bảo Chọn A
Đặt t  4x  3  dt  4dx thì 2 5 4 5 1 1   1 25 f
 4x 3dx f
 tdt   f
 tdt f
 tdt  5 20  . 4 4 4 4 1 1  1 4  Đặt 2 x 2    2 x u e du e dx thì ln 2 4 x x 1 5 f  2 e  2 e dx
f udu    . 2 2 0 1 25 5 15 Vậy I    . 4 2 4
Tuan.nt81@gmail.com 2x m
Câu 45. Có bao nhiêu giá trị nguyên m trên  1
 ;5 để hàm số y
đồng biến trên khoảng x m  ;  3   ? A. 2. B. 6. C. 5. D. 3. Lời giải
Tác giả : Tuyetnguyen, FB: tuyet nguyen Chọn D
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 32 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 m Ta có y '  x m2
Hàm số đồng biến trên khoảng  ;  3       y x     m 0 ' 0, ; 3      m     0 m 3 ; 3
Do đó có 3 giá trị của m thỏa mãn điều kiện đề bài.
Câu 46. Cho hàm số y f ' x có đồ thị như hình vẽ
Hàm số y f  2
2  x  đồng biến trên khoảng nào dưới đây A.  ;0  . B. 0;  1 . C. 1;2 . D. 0;. Lời giải Chọn B
Hàm số y f  2
2  x  có y   x f  2 ' 2 . ' 2  x  x  0 x  0  2  1
  2  x  2  1   x 1    x y '  2  . x f ' 0 1 2
2  x   0  x  0   x  0       x  1  2 2 x 1 x  1    2
2  x  2 x 1
Do đó hàm số đồng biến trên 0;  1 .
Mar.nang@gmail.com
Câu 47. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : x  2y  2z  3  0 và mặt cầu S  tâm I 5; 3
 ;5 , bán kính R  2 5 . Từ một điểm A thuộc mặt phẳng P kẻ một đường
thẳng tiếp xúc với mặt cầu S  tại B . Tính OA biết AB  4 .
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 33 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 A. OA  11 . B. OA  5 . C. OA  3. D. OA  6 . Lời giải
Tác giả : Lê Đình Năng FB: Lê Năng Chọn A 5  2.( 3  )  2.5  3
Khoảng cách từ điểm I đến mp(P) là: d I;(P)   6 . 2 2 2 1  ( 2  )  2
AB tiếp xúc với (S) tại B nên tam giác AIB vuông tại B, do đó ta có:
IA IB AB R AB   2 2 2 2 2 2
2 5  4  6  d I;(P)  A là hình chiếu của I lên (P) x  5  t   
Đường thẳng IA đi qua I 5; 3
 ;5 có VTCP u n  1;2;2 có phương trình y  3 2t ( P)   z  5 2t
Có A IA  (P)  5  t  2(3  2t)  2(5  2t)  3  0  t  2  (3
A ;1;1)  OA  11 .
Câu 48. Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng 2a , góc giữa hai mặt phẳng SAB và ABCD bằng 0
45 ; M , N, P lần lượt là trung điểm của ,
SA SB và AB . Tính thể tích V
khối tứ diện DMNP 3 a 3 a 3 a 3 a A. . B. . C. . D. . 6 4 2 12 Lời giải
Tác giả : Lê Đình Năng FB: Lê Năng Chọn A
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 34 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19
Gọi điểm O là tâm của đáy, theo giả thiết suy ra: SO   ABCD tại O
Góc giữa mặt phẳng SAB và  ABCD bằng 0
45 nên suy ra góc SPO bằng 0 45 .
Ta có OP a suy ra 0
SO OP tan 45  a ; SP a 2 . 2 1 1 1 a 2 SS  . .A . B SP  . MNP 4 SAB 4 2 4
Tứ diện DMNP có chiều cao h d D,(MNP)  2d(O,(SAB))
Trong (SPO) kẻ OH vuông góc với SP tại H thì OH là khoảng cách từ O đến (SAB)
Áp dụng hệ thức lượng trong tam giác vuông SPO tại O, đường cao OH ta có 1 1 1 2    aOH   h a 2 2 2 2 2 OH OP SO a 2 2 3 1 a 2 a
Thể tích khối chóp D.MNP là V  . .a 2  3 4 6
hungvn1985@gmail.com
Câu 49. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng 2
(P) : 2 x 2 y z m  3m  0 và
mặt cầu S x  2   y  2   z  2 ( ) : 1 1
1  9 . Tìm tất cả các giá trị của m để (P) tiếp xúc với (S) . m  2 m  2 A.  . B.  . C. m  2 . D. m  5 . m  5 m  5 Lời giải
Tác giả : Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng Chọn B I 1; 1  ;  1 Ta có (S) :  . R  3 2 2 1 m  3m
m  3m 10  0 m  2
Để (P) tiếp xúc với (S) thì d I;P  R   3     2 3
m  3m  8  0 m  5 .
Câu 50. Cho hai số thực a  1,b  1. Biết phương trình 2 x x 1
a b   1 có hai nghiệm phân biệt x , x . Tìm 1 2 2  x x
giá trị nhỏ nhất của biểu thức 1 2 S  
  4 x x . 1 2  x x  1 2  A. 3 3 4 . B. 4 C. 3 3 2 . D. 3 4 .
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 35 Mã đề 843
Sản phẩm của Group: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên Lê Hồng Phong – Nam Định 18‐19 Lời giải
Tác giả : Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng Chọn A Ta có 2 x x 1
a b    x   2 x   b   b x x b aa  2 1 1 log 0 log log 0 a  1  x x   log a
Do phương trình có hai nghiệm x , x nên theo định lý Viet ta có: 1 2  log b b 1 2 ax x  1   1 2 1 Khi đó S   4log a 2 log b a b 1 1
Đặt t  log a , do a  1,b  1  t  0 . Khi đó 3 S   4t
 2t  2t  3 4 . b 2 2 t t 1 1 Đẳng thức xảy ra khi  2t t  . Vậy 3 min S  3 4 2 3 t 2
=== STRONG TEAM TOÁN VD-VDC===
Hãy tham gia Group STRONG TEAM TOÁN VD‐VDC.‐ Group chỉ dành cho các Gv, Sv toán! Trang 36 Mã đề 843