




Preview text:
Tr˜Ìng THPT Ngô Quy∑n KIöM TRA GI⁄A K› I N´m hÂc 2020 – 2021 ( ∑ gÁm có 5 trang) Môn: Toán – KhËi: 12
ThÌi gian làm bài: 75 phút(không k∫ phát ∑) Mã ∑ 101
Tên:.............................................................LÓp:.................
Câu 1. Tìm hàm sË mÙ trong các hàm sË sau. 1 A y = 5x. B y = x⇡. C y = . D y = x5. x5 Câu 2.
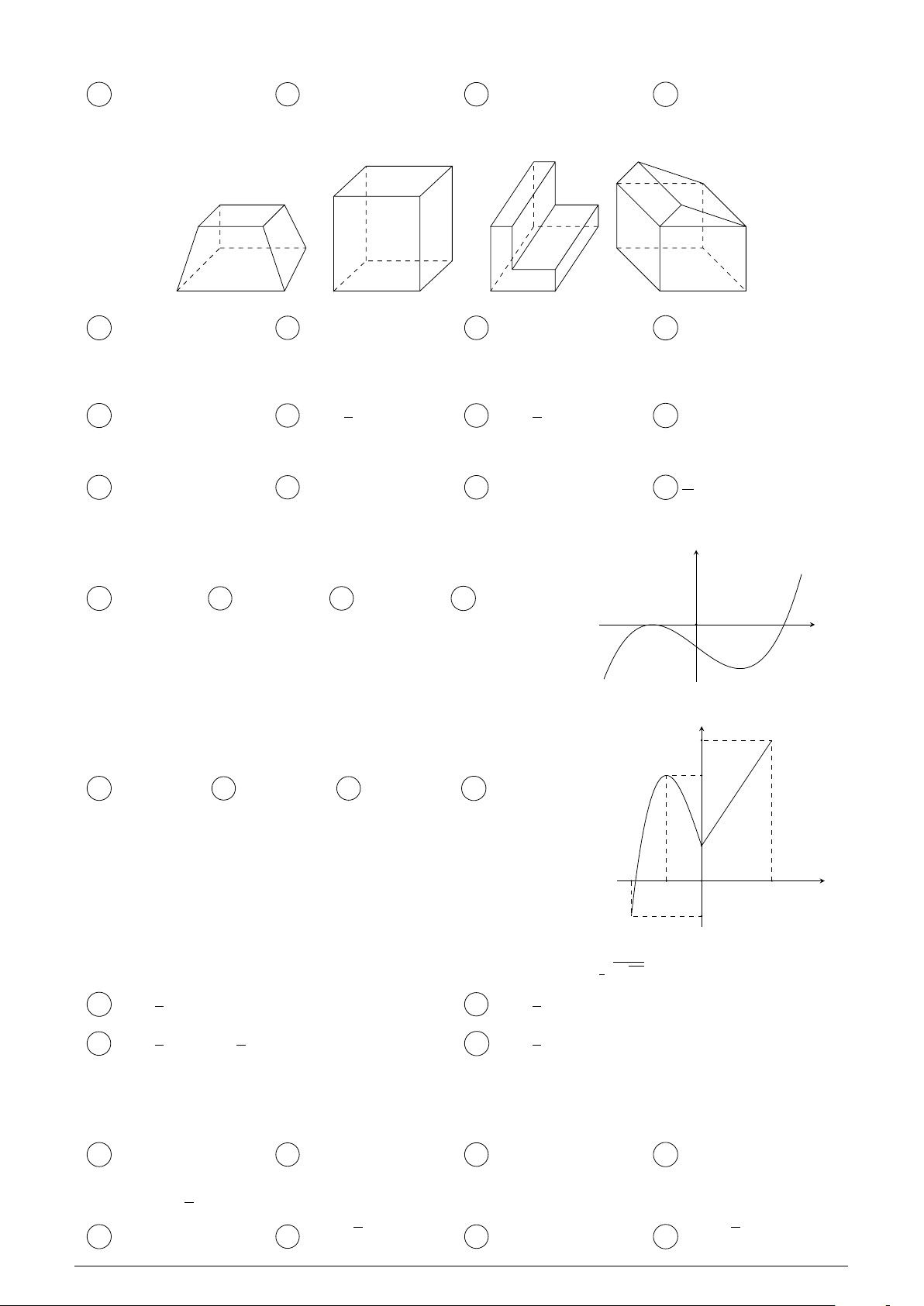
Cho Á th‡ hàm sË y = f (x) có Á th‡ nh˜ hình bên. Hàm sË y = f (x) y )
ngh‡ch bi∏n trên kho£ng nào sau ây? (xf A (0; 4). B (1; 4). C ( 1; 0). D (0; 1). = 1 1 y 4 O x
Câu 3. Tìm kho£ng Áng bi∏n cıa hàm sË y = x3 3x. A ( 1; 1). B ( 1; 0). C (0; +1). D (1; +1) . 2x Câu 4.
˜Ìng tiªm c™n ngang cıa Á th‡ hàm sË y = là 1 x2 A x = 1 và x = 1. B y = 2. C x = 1. D y = 0. Câu 5.
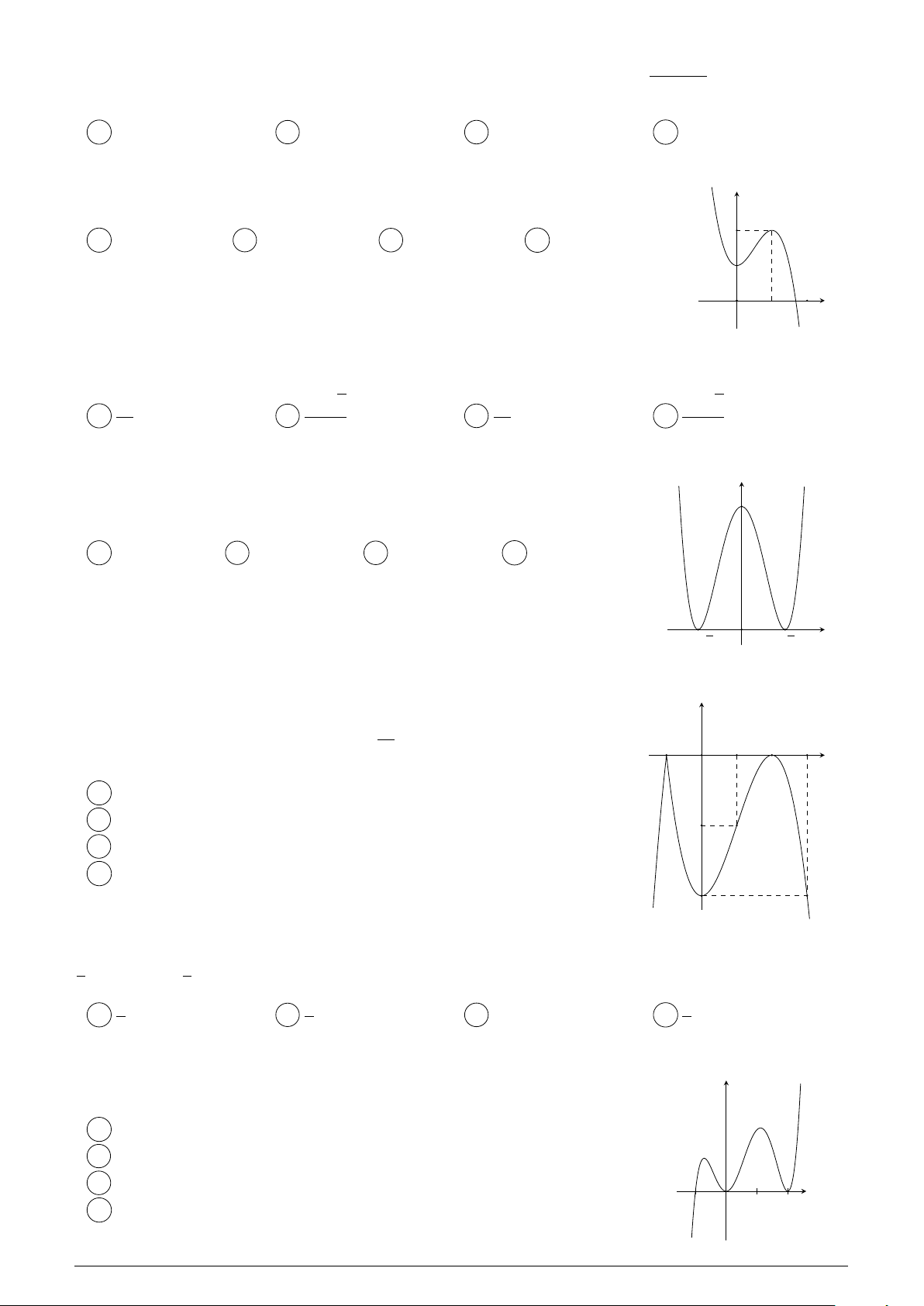
Á th‡ hình bên là cıa hàm sË nào sau ây? y 1 1 A y = x3 x + 1 . B y = x3 3x2 + 9x + 1 . 4 4 1 1 C y = x3 + x + 1 . D y = x4 2x2 + 1 . 4 4 O x y = f (x)
Câu 6. Tính th∫ tích khËi t˘ diªn ABCD có AB = a, AC = 2a, AD = 3a ôi mÎt vuông vÓi nhau. a3 a3 A 3a3. B . C a3. D . 6 3
Câu 7. Mªnh ∑ nào sau ây sai? ✓ ◆ ✓ ◆ 1 2021 1 2020 A 22020 < 22021. B > . ⇡ ⇡ ✓ ◆ ✓ ◆ ✓ ◆ 1 2020 p 2020 2021 2020 1 1 C p = 2 + 1 . D > . 2 1 2 2
Câu 8. Cho sË th¸c ↵ th‰a mãn 3↵ = 7. Tìm ↵. A ↵ = 3log 3 7 . B ↵ = log 7. C ↵ = log 3. D ↵ = 73. 3 7 a
Câu 9. KhËi l´ng trˆ ˘ng ABC.A0B0C0 có c§nh bên b¨ng
và áy là tam giác vuông t§i A, 2
AB = 2a và AC = a. Tính th∫ tích cıa khËi l´ng trˆ ABC.A0B0C0. a3 a3 a3 A . B . C . D a3. 6 2 2 a
Câu 10. Cho sË th¸c d˜Ïng a. Vi∏t bi∫u th˘c P = p v∑ d§ng lÙy th¯a vÓi sË mÙ h˙u t . 3 a Trang 1/5 – Mã ∑ 101 3 3 2 1 A P = a 2 . B P = a2 . C P = a3 . D P = a4 .
Câu 11. Cho hàm sË f (x) = x4 8x2 + 1. Tìm max p f (x). [1; 5] A 6 . B 15. C 14. D 1. Câu 12.
Á th‡ hình bên là cıa hàm sË nào sau ây? y A y = x2 + x 1. B y = x4 + 2x2 + 1. x + 1 C y = x3 + 3x + 1. D y = . x 1 O x Câu 13. Cho log a =
1. Tính giá tr‡ bi∫u th˘c 2 log a6. 2 8 2 A . B 4. C 48 . D 4. 3
Câu 14. Tìm khØng ‡nh sai? p 1 A 1 2 = 1. B 100 = 1. C 00 = 1. D 5 2 = . 52
Câu 15. Cho sË th¸c d˜Ïng a. Mªnh ∑ nào sau ây sai? p 1 p 3 p 1 A 3 a 3 = . B 4 a3 = a4 . C a = a2 . D (a3)2 = a9. a Câu 16.
Hình a diªn trong hình v≥ bên có bao nhiêu c§nh? A 15. B 17. C 18. D 16. x + 1 Câu 17.
˜Ìng tiªm c™n ˘ng cıa Á th‡ hàm sË y = là 2x 4 A x = 4. B y = 2. C y = 2. D x = 2.
Câu 18. Tìm t™p xác ‡nh cıa hàm sË y = log (1 3x). 2 ✓ ◆ ⇢ ✓ ◆ ✓ ◆ 1 1 1 1 A D = 1; . B D = R \ . C D = ; +1 . D D = 1; . 3 3 3 3
Câu 19. Cho hàm sË y = f (x) liên tˆc trên R và có b£ng xét dßu cıa §o hàm nh˜ hình bên d˜Ói x 1 3 2 1 +1 f 0(x) + 0 0 + 0
Hàm sË y = f (x) có i∫m c¸c §i là A x = 1. B x = 2. C y = 0. D x = 0. p
Câu 20. Cho khËi chóp (H ) có chi∑u cao b¨ng a 3 và áy là tam giác ∑u c§nh a. Tính th∫ tích cıa (H ). p a3 3a3 a3 3a3 3 A . B . C . D . 12 4 4 4
Câu 21. Cho hàm sË y = f (x) liên tˆc trên R và có b£ng xét dßu cıa §o hàm f0(x) nh˜ hình v≥ bên d˜Ói x 1 2 3 +1 f 0(x) 0 + 0 Trang 2/5 – Mã ∑ 101
Hàm sË y = f (x) ngh‡ch bi∏n trên kho£ng nào sau ây? A ( 2; +1). B (1; 4). C ( 1; 2). D ( 2; 3).
Câu 22. Trong các hình bên d˜Ói, có bao nhiêu hình bi∫u diπn khËi a diªn lÁi? A 3. B 2. C 1. D 4.
Câu 23. KhËi chóp có diªn tích m∞t áy B và chi∑u cao h. Th∫ tích khËi chóp ˜Òc tính theo công th˘c 1 1 A V = B · h. B V = B · h . C V = B · h. D V = 3B · h. 3 2
Câu 24. Tính §o hàm cıa hàm sË y = x⇡ t§i i∫m xo = 1. 1 A ⇡. B ⇡ 1. C 1 ⇡. D . ⇡ Câu 25. GÂi x y 1, x2 là 2
i∫m c¸c tr‡ cıa hàm sË y = f (x) có Á th‡ nh˜ y = f (x)
hình bên. KhØng ‡nh nào sau ây úng?
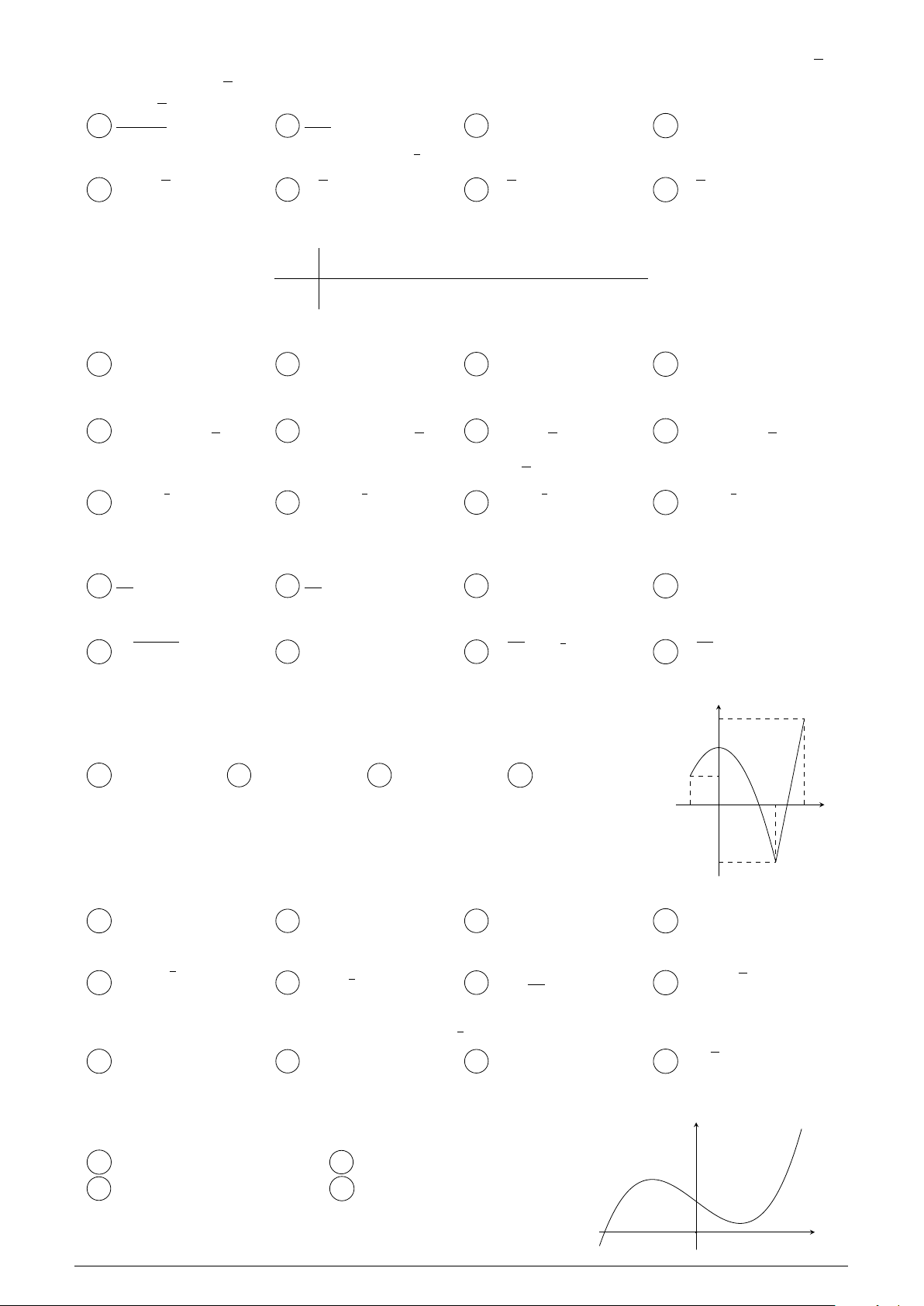
A x1 · x2 = 0. B x1 · x2 < 0. C x1 · x2 = 1. D x1 · x2 > 0. O x Câu 26.
Cho hàm sË y = f (x) liên tˆc trên o§n [ 2; 2] và có Á th‡ nh˜ y 4
hình v≥ bên. Tìm min f (x). [ 2;2] 3 A 1. B 2. C 3. D 1 . 1 2 O x 1 2 1 a2
Câu 27. Cho 2 sË th¸c d˜Ïng a và b. Rút gÂn bi∫u th˘c P = log p . 1 3 3 b2 2 2 A P = log b 2 log a. B P = log b + 2 log a. 3 3 3 3 3 3 1 2 1 C P = log a + log b. D P = log b 2 log a. 2 3 3 3 3 3 3
Câu 28. MÎt ng˜Ìi g˚i ti∏t kiªm 200 triªu Áng vào mÎt ngân hàng vÓi lãi sußt 7% mÎt n´m.
Bi∏t r¨ng n∏u không rút ti∑n ra kh‰i ngân hàng thì c˘ sau mÈi n´m, sË ti∑n lãi s≥ ˜Òc nh™p vào
vËn ban ¶u. Sau 5 n´m mÓi rút lãi thì ng˜Ìi ó thu ˜Òc sË ti∑n lãi là A 50, 2 triªu Áng. B 62, 16 triªu Áng. C 80, 51 triªu Áng. D 72, 3 triªu Áng.
Câu 29. Cho khËi l™p ph˜Ïng ABCD.A0B0C0D0 có kho£ng cách gi˙a hai ˜Ìng thØng AA0 và p
BD0 b¨ng a 2. Tính th∫ tích cıa ABCD.A0B0C0D0. p p A 8a3. B 54a3 2. C 64a3. D 16a3 2. Trang 3/5 – Mã ∑ 101 mx + 1
Câu 30. Có bao nhiêu giá tr‡ nguyên cıa tham sË m ∫ hàm sË y = ngh‡ch bi∏n trên 9x + m
t¯ng kho£ng cıa t™p xác ‡nh? A 0. B 3. C 5. D 9. Câu 31.
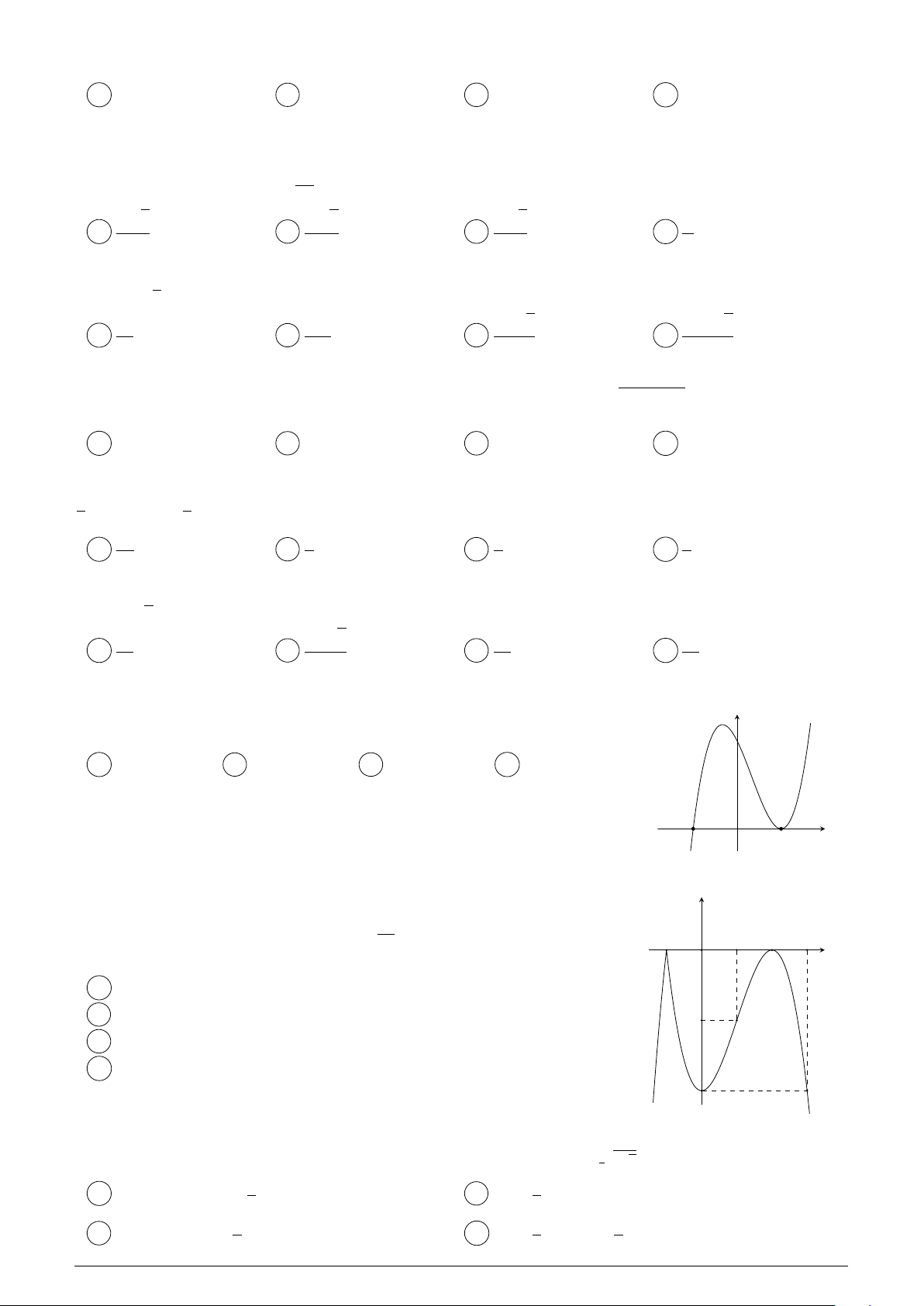
Cho hàm sË b™c ba y = f (x) có Á th‡ nh˜ hình bên. Ph˜Ïng trình f 2(x) 2 = y 0 có bao nhiêu nghiªm? 2 A 4. B 3. C 2. D 1. 1 O 2 x
Câu 32. Cho khËi chóp S.ABCD có áy ABCD là hình thoi c§nh a, \ BAD = 60 , c§nh bên SA
b¨ng 2a và t§o vÓi m∞t áy mÎt góc b¨ng 30 . Tính th∫ tích khËi chóp S.ABCD. p p a3 a3 3 a3 a3 3 A . B . C . D . 2 2 3 6 Câu 33.
Cho hàm sË f (x) = ax4 + bx2 + c (a, b, c 2 R) có Á th‡ nh˜ hình v≥ bên. y
Có bao nhiêu giá tr‡ nguyên cıa tham sË m ∫ ph˜Ïng trình f (x)+m = 0 4 có 4 nghiªm? A 3. B 2. C 1. D 0. O x p p 2 2 Câu 34.
Cho hàm sË y = f (x) có §o hàm liên tˆc trên R và Á th‡ y = f0(x) y x2 nh˜ hình v≥ bên. ∞t hàm sË g(x) = + x + f (x). KhØng ‡nh nào 1 2 1 2 3 x sau ây úng? O
A Hàm sË g(x) ngh‡ch bi∏n trên ( 1; 2).
B Hàm sË g(x) §t c¸c §i t§i x = 1. 2
C Hàm sË g(x) ngh‡ch bi∏n trên (1; +1).
D Hàm sË g(x) có 3 i∫m c¸c tr‡. 4
Câu 35. Cho khËi chóp S.ABC. GÂi B0, C0 l¶n l˜Òt là các i∫m trên c§nh SB, SC sao cho SB0 = 1 1
SB, SC0 = SC. Tính t sË th∫ tích V 2 3 S.AB0C0 và VS.ABC . 1 1 1 A . B . C 0. D . 9 6 8 Câu 36.
Cho hàm sË y = f (x) có §o hàm trên R và Á th‡ cıa y = f0(x) nh˜ hình y
bên. Mªnh ∑ nào sau ây úng?
A Hàm sË y = f (x) có 4 c¸c tr‡.
B Hàm sË y = f (x) §t c¸c ti∫u t§i x = 1.
C Ph˜Ïng trình f 0(x) = 0 có 2 nghiªm. x O
D Hàm sË y = f (x) §t c¸c §i t§i x = 1. 1 1 2 Trang 4/5 – Mã ∑ 101
Câu 37. MÎt sÒi dây không dãn dài 1 mét ˜Òc c≠t thành hai o§n. o§n th˘ nhßt ˜Òc cuËn
thành tam giác ∑u có diªn tích S1, o§n th˘ hai ˜Òc cuËn thành ˜Ìng tròn có diªn tích S2. Khi S S 1 1 + S2 §t nh‰ nhßt, tính . S2 p p p 2 3 9 3 3 3 3 A . B . C . D . ⇡ ⇡ ⇡ ⇡ ln x Câu 38. Cho hàm sË y = . Mªnh ∑ nào sau ây úng? x x e 1 A x2 · y0 = ln . B x2 · y0 = ln . C x2 · y0 = ln . D x2 · y0 = 1 x. e x x Câu 39.
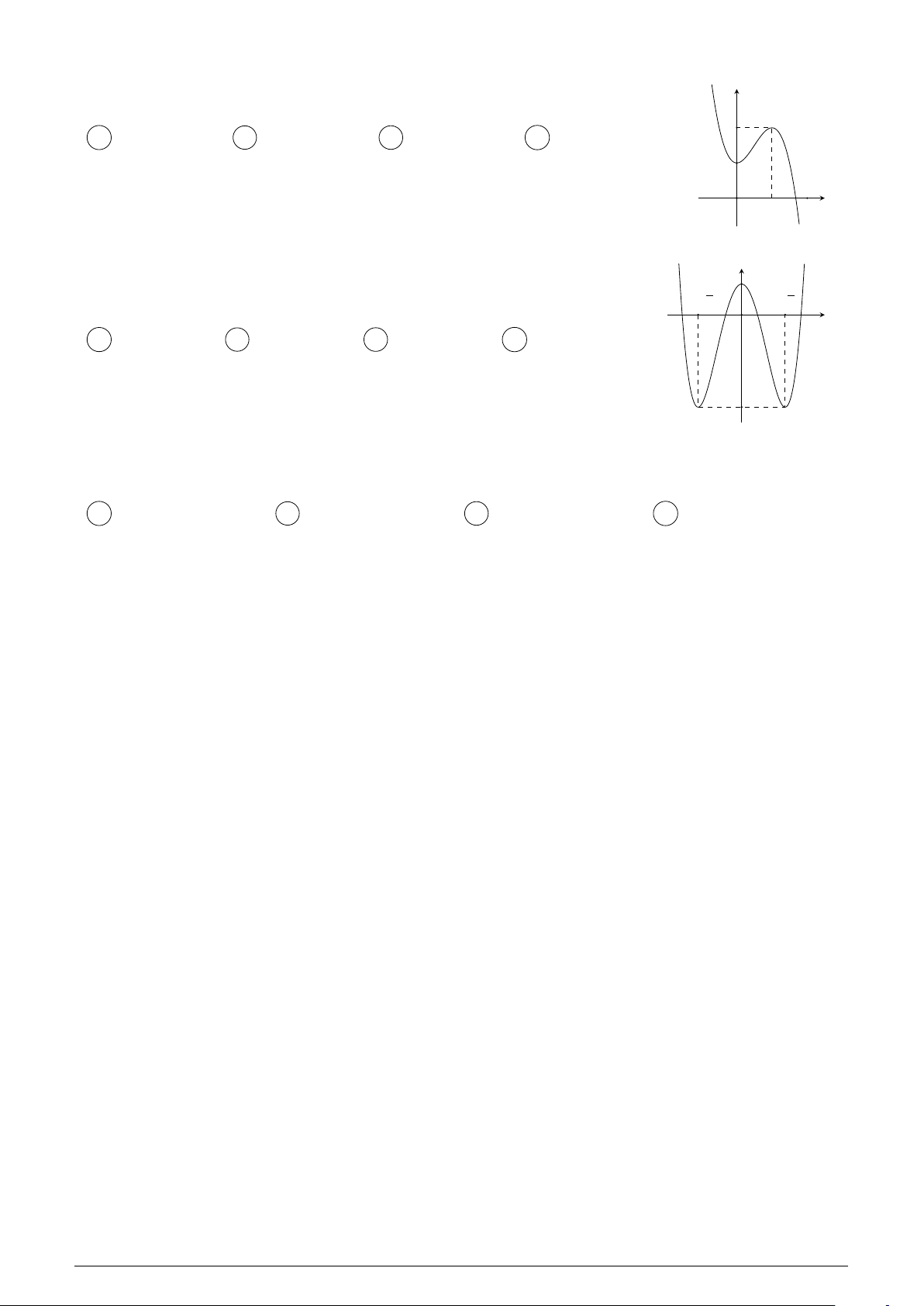
Cho hàm sË b™c bËn y = f (x) có Á th‡ y = f 0(x) nh˜ hình v≥ bên. y Hàm sË g(x) = f (x2 + x
1) có bao nhiêu i∫m c¸c tr‡? A 6. B 4. C 5. D 3. O x 1 1 p
Câu 40. Cho khËi l´ng trˆ ˘ng ABC.A0B0C0 có [
BAC = 60 , AB = a 3, AC = a và Î dài cıa p
c§nh bên b¨ng a 3. Tính th∫ tích cıa khËi l´ng trˆ ABC.A0B0C0. p p p 3a3 3 3a3 3 3a3 a3 3 A . B . C . D . 2 4 4 4
- - - - - - - - - - HòT- - - - - - - - - - Trang 5/5 – Mã ∑ 101 Tr˜Ìng THPT Ngô Quy∑n KIöM TRA GI⁄A K› I N´m hÂc 2020 – 2021 ( ∑ gÁm có 5 trang) Môn: Toán – KhËi: 12
ThÌi gian làm bài: 75 phút(không k∫ phát ∑) Mã ∑ 102
Tên:............................................................. LÓp:.................
Câu 1. Cho hàm sË y = f (x) liên tˆc trên R và có b£ng xét dßu cıa §o hàm f0(x) nh˜ hình v≥ bên d˜Ói x 1 2 3 +1 f 0(x) + 0 0 +
Hàm sË y = f (x) Áng bi∏n trên kho£ng nào sau ây? A (3; +1). B (1; 4). C ( 2; 3). D ( 1; 0). Câu 2.
Á th‡ hình bên là cıa hàm sË nào sau ây? y y = f (x) A y = x4 2x2 1. B y = x3 + 3x2 9x 1 . 1 1 1 1 O C y = x3 x 1. D y = x3 + x 1. x 4 4 4 4 Câu 3.
Hình a diªn trong hình v≥ bên có bao nhiêu c§nh? A 17. B 14. C 16. D 15.
Câu 4. – các hình bên d˜Ói, có bao nhiêu hình là hình bi∫u diπn cıa khËi a diªn lÁi? A 0. B 3. C 3. D 1. x + 1 Câu 5.
˜Ìng tiªm c™n ngang cıa Á th‡ hàm sË y = là 2x 1 1 1 A x = 1. B y = . C y = 2. D x = . 2 2 Câu 6.
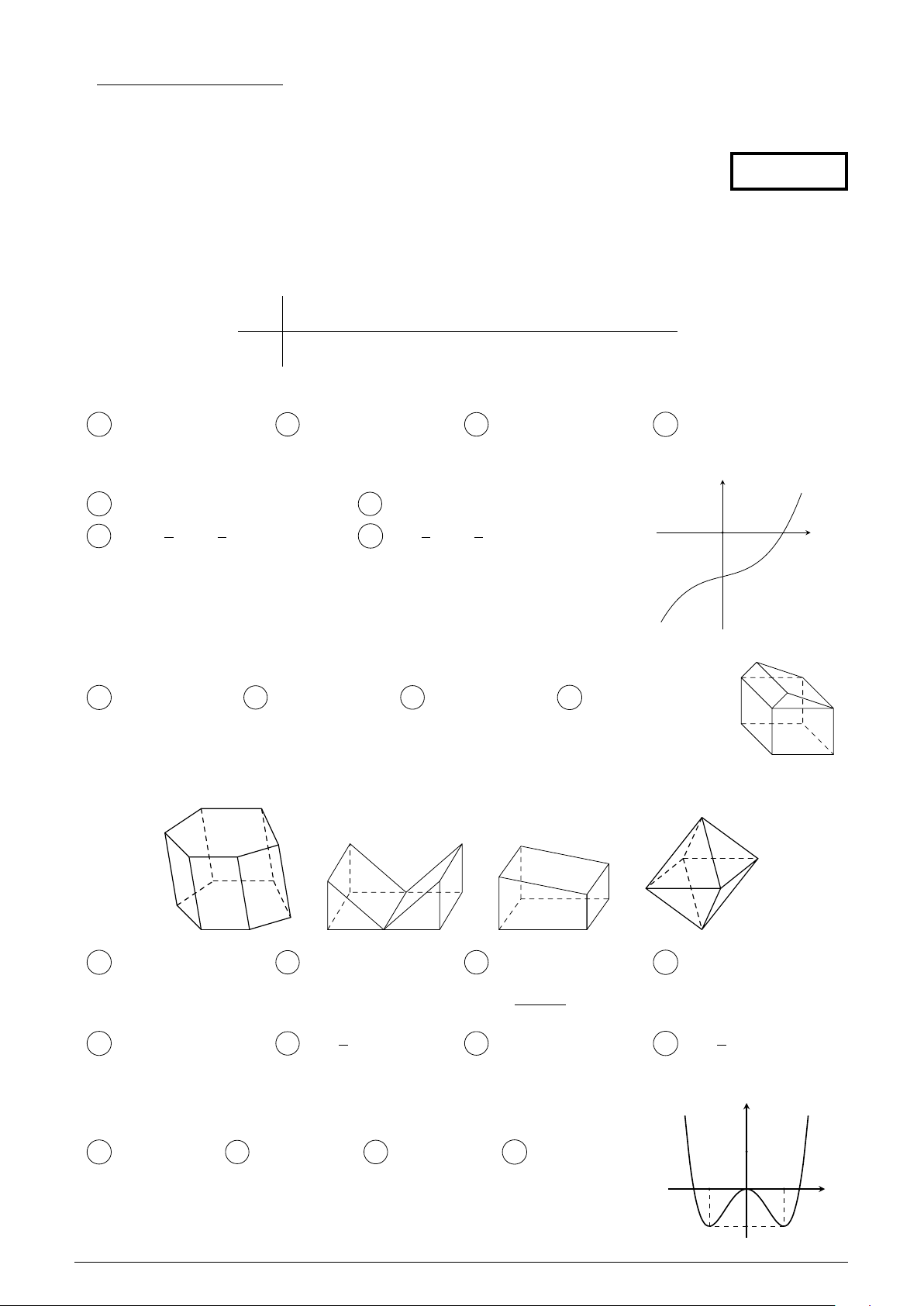
Cho Á th‡ hàm sË y = f (x) có Á th‡ nh˜ hình bên. Hàm sË y = f (x) y
Áng bi∏n trên kho£ng nào sau ây? A ( 1; 0). B (0; 1). C ( 1; 1). D (0; 2). 1 1 O 1 x 1 Trang 1/5 – Mã ∑ 102 p
Câu 7. Cho khËi chóp S.ABCD có áy ABCD là hình ch˙ nh™t có AB = 2a, AD = a 3 và p
chi∑u cao b¨ng a 3. Tính th∫ tích cıa khËi chóp S.ABCD. p 2a3 3 2a3 A . B . C 2a3. D a3. 3 3 p
Câu 8. Tính §o hàm cıa hàm sË y = x 2+1 t§i i∫m xo = 1. p p p p A 1 2. B 2 1. C 2. D 2 + 1.
Câu 9. Cho hàm sË y = f (x) liên tˆc trên R và có b£ng xét dßu cıa §o hàm nh˜ hình bên d˜Ói x 1 3 2 1 +1 f 0(x) + 0 0 + 0
Hàm sË y = f (x) có i∫m c¸c ti∫u là A x = 3. B x = 2. C y = 0. D x = 1.
Câu 10. Tìm t™p xác ‡nh cıa hàm sË y = log ( 2x + 3). 2 ✓ ◆ ✓ ◆ ✓ ◆ ⇢ 3 3 3 2 A D = 1; . B D = 1; . C D = ; +1 . D D = R \ . 2 2 2 3 p
Câu 11. Cho sË th¸c d˜Ïng a. Vi∏t bi∫u th˘c P = a · 3 a v∑ d§ng lÙy th¯a vÓi sË mÙ h˙u t . 1 2 2 4 A P = a2 . B P = a 3 . C P = a3 . D P = a3 .
Câu 12. Tính th∫ tích khËi t˘ diªn ABCD có AB = 2a, AC = 3a, AD = 3a ôi mÎt vuông vÓi nhau.a3 a3 A . B . C 3a3. D a3. 6 3
Câu 13. Cho sË th¸c d˜Ïng a. Mªnh ∑ nào sau ây sai? p p 4 p A 4 ( a)4 = a. B (a4)2 = a8. C 3 a4 = a3 . D 3 a3 = a. Câu 14.
Cho hàm sË y = f (x) liên tˆc trên o§n [ 1; 3] và có Á th‡ nh˜ hình v≥. y 3
GÂi M là giá tr‡ lÓn nhßt cıa hàm sË ã cho trên o§n [ 1; 3]. Giá tr‡ cıa M b¨ng A 1. B 2. C 2. D 3. 1 2 1 O x 3 2
Câu 15. Tìm kho£ng ngh‡ch bi∏n cıa hàm sË y = x3 + 3x 1. A ( 1; 1). B (0; +1). C ( 1; 1). D ( 2; +1) .
Câu 16. Tìm hàm sË mÙ trong các hàm sË sau. p 1 1 p x A y = x 2. B y = x 2 . C y = . D y = 3 . x2
Câu 17. Cho hàm sË f (x) = x4 8x2. Tìm min p f (x). [ 5; 1] p A 0. B 16. C 15. D 5. Câu 18.
GÂi y1, y2 là 2 c¸c tr‡ cıa hàm sË y = f (x) có Á th‡ nh˜ hình y y = f (x)
bên. KhØng ‡nh nào sau ây úng? A y1 · y2 > 0. B y1 · y2 < 0. C y1 · y2 = 0. D y1 · y2 = 1. O x Trang 2/5 – Mã ∑ 102 Câu 19. Cho log a =
2. Tính giá tr‡ bi∫u th˘c 2 log (8a2). 2 2 A 12. B 2 . C 32. D 3 .
Câu 20. KhËi l´ng trˆ có diªn tích m∞t áy B và chi∑u cao h. Th∫ tích khËi l´ng trˆ ˜Òc tính theo công th˘c 1 1 A V = 3B · h. B V = B · h . C V = B · h. D V = B · h. 3 2 p
Câu 21. Cho khËi l´ng trˆ ˘ng (H ) có chi∑u cao b¨ng a 2 và áy là tam giác ∑u c§nh a. Tính th∫ tích cıa (H ). p p 3a3 p a3 2 a3 6 A . B a3 2. C . D . 4 3 4
Câu 22. Mªnh ∑ nào sau ây sai? ✓ ◆ ✓ ◆ ✓ ◆ 1 2020 1 2021 1 2020 p 2020 A > . B p > 2 1 . 2 2 2 + 1 ✓ ◆ ✓ ◆ 2 2020 2 2021 C 32021 > 32020. D p < p . 3 3 2 x Câu 23.
˜Ìng tiªm c™n ngang cıa Á th‡ hàm sË y = là 1 x2 A y = 1. B x = 1 và x = 1. C y = 0. D y = 2.
Câu 24. Tìm khØng ‡nh sai? ✓ ◆ 1 2 p 0 A = 9. B 1⇡ = 1. C 0 2 = 1. D 2 = 1. 3 Câu 25.
Hàm sË nào d˜Ói ây có Á th‡ d§ng nh˜ ˜Ìng cong trong hình bên? y A y = x4 2x2 + 1. B y = x + 1. 2x + 1 C y = . D y = x3 3x + 1. x + 1 O x
Câu 26. Cho sË th¸c ↵ th‰a mãn 4↵ = 5. Tìm ↵. A ↵ = log 5. B ↵ = 45. C ↵ = log 4. D ↵ = 5log 3 4 . 4 5
Câu 27. Cho khËi l´ng trˆ ∑u ABC.A0B0C0 có các c§nh ∑u b¨ng nhau và kho£ng cách gi˙a hai p
˜Ìng thØng AA0 và BC b¨ng a 3. Tính th∫ tích cıa khËi l´ng trˆ ABC.A0B0C0. p p p 2a3 3 A a3. B 2a3 3. C a3 3. D . 3
Câu 28. Cho hàm sË y = x · ln x. Mªnh ∑ nào sau ây úng? y0 ⇣x⌘ y0 A = ln . B y0 = ln(ex). C = 1. D y0 = ln x + e. x e x
Câu 29. Cho hàm sË y = f (x) có §o hàm trên R và có b£ng bi∏n thiên cıa §o hàm f0(x) nh˜ sau x 1 1 +1 +1 +1 f 0(x) 2 Trang 3/5 – Mã ∑ 102
. Khi ó hàm sË y = f (x) có bao nhiêu i∫m c¸c tr‡? A 2. B 0. C 1. D 3.
Câu 30. MÎt sÒi dây không dãn dài 1 mét ˜Òc c≠t thành hai o§n. o§n th˘ nhßt ˜Òc cuËn
thành tam giác ∑u có diªn tích S1, o§n th˘ hai ˜Òc cuËn thành ˜Ìng tròn có diªn tích S2. Khi S S 1 1 + S2 §t nh‰ nhßt, tính . S2 p p p 3 3 2 3 9 3 3 A . B . C . D . ⇡ ⇡ ⇡ ⇡ Câu 31. Cho khËi l´ng trˆ
˘ng ABC.A0B0C0 có tam giác ABC vuông t§i A, [ ABC = 60 , p
AB = a 3 và Î dài cıa c§nh bên b¨ng a. Tính th∫ tích cıa khËi l´ng trˆ ABC.A0B0C0. p p a3 3a3 a3 3 3a3 3 A . B . C . D . 4 4 12 2 mx 2
Câu 32. Có bao nhiêu giá tr‡ nguyên cıa tham sË m ∫ hàm sË y = Áng bi∏n trên t¯ng 4x 2m kho£ng cıa t™p xác ‡nh? A 3. B 2. C 1. D 0.
Câu 33. Cho khËi chóp S.ABC. GÂi B0, C0 l¶n l˜Òt là các i∫m trên c§nh SB, SC sao cho SB0 = 1 1
SB, SC0 = SC. Tính t sË th∫ tích V 3 4 S.AB0C0 và VS.ABC . 1 1 1 1 A . B . C . D . 12 9 6 7
Câu 34. Cho khËi chóp S.ABCD có áy là hình thoi, tam giác ABC ∑u c§nh a, c§nh bên SA p
b¨ng a 3 và t§o vÓi m∞t áy mÎt góc b¨ng 30 . Tính th∫ tích khËi chóp S.ABCD. p a3 a3 3 a3 a3 A . B . C . D . 6 2 4 2 Câu 35.
Cho hàm sË b™c bËn y = f (x) có Á th‡ y = f 0(x) nh˜ hình v≥ bên. y Hàm sË g(x) = f (x2
1) có bao nhiêu i∫m c¸c tr‡? A 3. B 0. C 1. D 2. O x 1 1 Câu 36.
Cho hàm sË y = f (x) có §o hàm liên tˆc trên R và Á th‡ y = f0(x) y x2 nh˜ hình v≥ bên. ∞t hàm sË g(x) = + x + f (x). KhØng ‡nh nào 1 2 1 2 3 x sau ây úng? O
A Hàm sË g(x) ngh‡ch bi∏n trên (1; +1).
B Hàm sË g(x) có 3 i∫m c¸c tr‡. 2
C Hàm sË g(x) ngh‡ch bi∏n trên ( 1; 2).
D Hàm sË g(x) §t c¸c §i t§i x = 1. 4 a3
Câu 37. Cho 2 sË th¸c d˜Ïng a và b. Rút gÂn bi∫u th˘c P = log p . 1 3 2 b 1 1 A P = 3 log a + log b. B P = log a + 3 log b. 2 3 2 2 2 2 1 3 2 C P = 3 log a log b. D P = log a log b. 2 3 2 2 2 3 2 Trang 4/5 – Mã ∑ 102 Câu 38.
Cho hàm sË b™c ba y = f (x) có Á th‡ nh˜ hình bên. Ph˜Ïng trình f 2(x) 5 = y 0 có bao nhiêu nghiªm? 2 A 1. B 4. C 3. D 2. 1 O 2 x Câu 39.
Cho hàm sË f (x) = ax4+bx2+c (a, b, c 2 R) có Á th‡ nh˜ hình v≥ bên. Có y 1
bao nhiêu giá tr‡ nguyên cıa tham sË m ∫ ph˜Ïng trình f (x)+m 1 = 0 p p 2 2 x có 4 nghiªm? O A 1. B 3. C 2. D 4. 3
Câu 40. MÎt ng˜Ìi g˚i ti∏t kiªm 350 triªu Áng vào mÎt ngân hàng vÓi lãi sußt 7% mÎt n´m.
Bi∏t r¨ng n∏u không rút ti∑n ra kh‰i ngân hàng thì c˘ sau mÈi n´m, sË ti∑n lãi s≥ ˜Òc nh™p vào
vËn ban ¶u. Sau 5 n´m mÓi rút lãi thì ng˜Ìi ó thu ˜Òc sË ti∑n lãi là A 140, 89 triªu Áng. B 105, 30 triªu Áng. C 108, 78 triªu Áng. D 90, 16 triªu Áng.
- - - - - - - - - - HòT- - - - - - - - - - Trang 5/5 – Mã ∑ 102 ÁP ÁN BÉNG ÁP ÁN CÁC MÃ ó Mã ∑ thi 101 1. A 2. D 3. D 4. D 5. A 6. C 7. B 8. B 9. C 10. C 11. A 12. B 13. B 14. C 15. D 16. C 17. D 18. A 19. A 20. C 21. C 22. A 23. B 24. A 25. B 26. D 27. A 28. C 29. A 30. C 31. A 32. D 33. A 34. A 35. B 36. B 37. D 38. B 39. D 40. B Mã ∑ thi 103 1. C 2. C 3. A 4. A 5. A 6. D 7. A 8. D 9. B 10. C 11. D 12. B 13. C 14. C 15. B 16. A 17. A 18. B 19. D 20. A 21. C 22. C 23. B 24. C 25. D 26. B 27. D 28. A 29. D 30. C 31. C 32. B 33. A 34. A 35. B 36. C 37. A 38. D 39. C 40. B Mã ∑ thi 105 1. B 2. D 3. D 4. D 5. C 6. A 7. B 8. D 9. B 10. A 11. A 12. C 13. B 14. A 15. B 16. C 17. A 18. C 19. A 20. B 21. B 22. D 23. C 24. A 25. C 26. A 27. A 28. A 29. C 30. C 31. C 32. B 33. C 34. C 35. D 36. B 37. D 38. B 39. A 40. D Mã ∑ thi 107 1. B 2. D 3. C 4. A 5. B 6. B 7. B 8. C 9. A 10. A 11. D 12. B 13. B 14. C 15. C 16. A 17. D 18. A 19. C 20. B 21. D 22. B 23. C 24. B 25. C 26. D 27. D 28. D 29. B 30. B 31. A 32. A 33. A 34. A 35. A 36. B 37. A 38. B 39. A 40. B 1 ÁP ÁN BÉNG ÁP ÁN CÁC MÃ ó Mã ∑ thi 102 1. A 2. D 3. A 4. B 5. B 6. A 7. C 8. D 9. B 10. A 11. D 12. C 13. A 14. D 15. C 16. D 17. B 18. A 19. B 20. C 21. D 22. B 23. C 24. C 25. D 26. A 27. B 28. B 29. A 30. A 31. D 32. A 33. A 34. C 35. C 36. C 37. A 38. D 39. B 40. A Mã ∑ thi 104 1. D 2. C 3. C 4. D 5. C 6. C 7. A 8. D 9. A 10. C 11. B 12. C 13. B 14. D 15. C 16. C 17. D 18. A 19. C 20. A 21. A 22. D 23. B 24. D 25. B 26. C 27. A 28. A 29. D 30. D 31. A 32. A 33. A 34. B 35. B 36. D 37. A 38. C 39. C 40. B Mã ∑ thi 106 1. A 2. C 3. D 4. B 5. D 6. C 7. C 8. D 9. C 10. B 11. D 12. D 13. C 14. C 15. D 16. B 17. B 18. C 19. C 20. A 21. D 22. A 23. C 24. C 25. D 26. B 27. A 28. C 29. B 30. A 31. B 32. C 33. A 34. B 35. D 36. C 37. C 38. B 39. C 40. A Mã ∑ thi 108 1. C 2. B 3. A 4. D 5. D 6. C 7. D 8. C 9. A 10. D 11. A 12. D 13. D 14. D 15. C 16. C 17. D 18. D 19. D 20. D 21. A 22. C 23. A 24. A 25. D 26. C 27. A 28. B 29. B 30. A 31. B 32. D 33. B 34. D 35. B 36. B 37. C 38. A 39. B 40. C 1




