
Preview text:
TRƯỜNG THPT NGUYỄN BỈNH KHIÊM
ĐỀ KIỂM TRA MỘT TIẾT CHƢƠNG I TỔ TOÁN - TIN
Môn: Hình học Lớp 10 ĐỀ CHÍNH THỨC
I. PHẦN CHUNG CHO TẤT CẢ HỌC SINH (7.0 điểm)
Câu 1. (3.0 điểm)
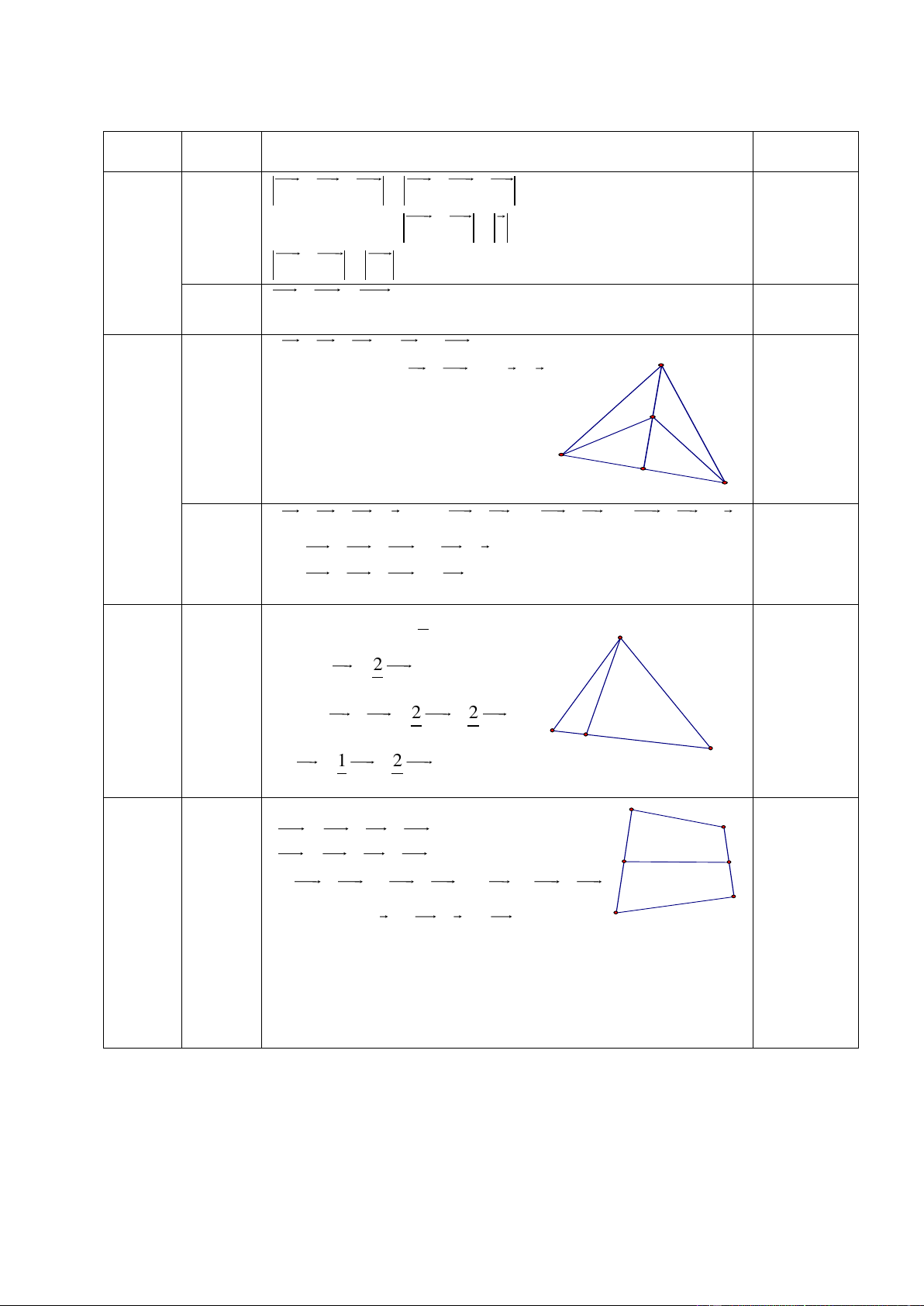
Cho tam giác ABC đều cạnh a.
1) Tính độ dài các vectơ: AB CA BC , AB AC
2) Xác định điểm M sao cho: AB AC AM .
Câu 2. (3.0 điểm)
Cho tam giác ABC, gọi M là trung điểm của BC và I là trung điểm của AM.
1) Chứng minh rằng: 2IA IB IC 0 .
2) Với điểm O bất kỳ. Chứng minh: 2OA OB OC 4OI .
Câu 3. (1.0 điểm)
Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho 2CI = 3BI. Hãy phân tích AI
theo hai vectơ AB và AC .
II. PHẦN RIÊNG (3.0 điểm)
Học sinh học chương trình nào thì chỉ được làm phần dành riêng cho chương trình đó
(Phần 1 hoặc phần 2)
Phần 1. Dành cho chƣơng trình Chuẩn.
Câu 4.a. (3.0 điểm)
1) Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB và CD. Chứng minh
rằng AD BC 2EF .
2) Tam giác ABC có trọng tâm G. Gọi M, N là các điểm xác định bởi AM 2AB , 2 AN
AC . Chứng minh rằng: M, N, G thẳng hàng. 5
Phần 2. Dành cho chƣơng trình Nâng cao.
Câu 4.b. (3.0 điểm)
Trong mặt phẳng toạ độ Oxy cho A( 2; 1), B( 1; 1), C( 3; 4).
1) Chứng minh A, B, C không thẳng hàng. Xác định điểm D sao cho tứ giác ABCD là hình bình hành.
2) Xác định điểm N trên trục Oy sao cho | NA NB 4NC | đạt giá trị nhỏ nhất.
…………………..HẾT………………….
Họ và tên học sinh:………………………………….SBD:…………. ĐÁP ÁN Câu Ý Nội dung Điểm
AB CA BC AB BC CA 0.5 1) 1 (2.0đ) AC CA 0 0 0.5 (3đ)
AB AC CB CB a 0.5+0.5 2)
AB AC AM 1.0
(1.0đ) M là đỉnh của hình bình hành ABMC.
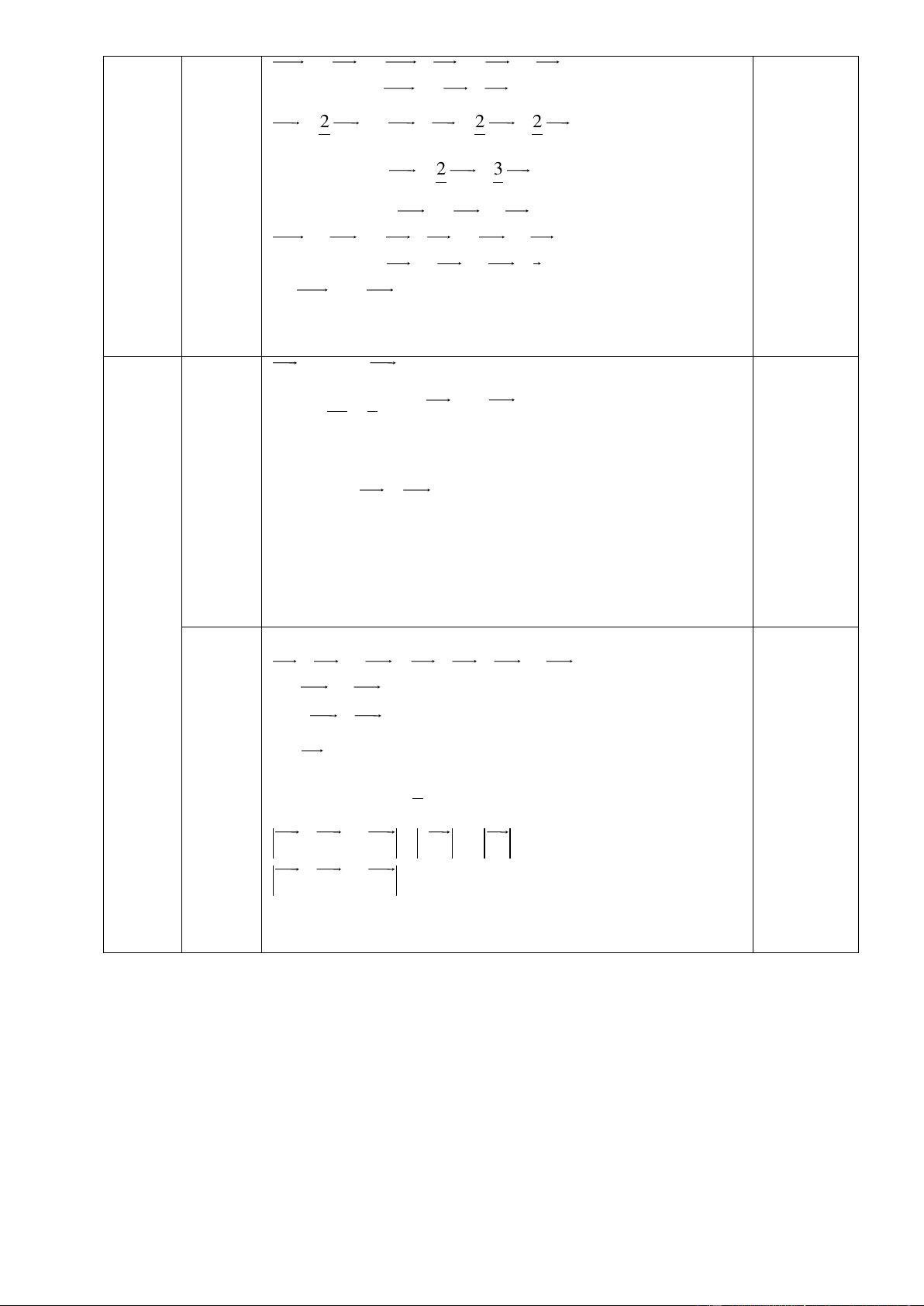
2IA IB IC 2IA 2IM 0.5 A 1)
2IA IM 2.0 0 0.5+0.5 (1.5đ) I 2 B (3đ) M C
2IA IB IC 0 2OAOI OB OI OC OI 0 0.75 2) 0.5
2OA OB OC 4OI 0 (1.5đ) 0.25 2OA OB OC 4OI 2
2CI 3BI BI BC A 3 0.25 2 Ta có: BI BC 3 0.25 2 2
AI AB AC AB 0.25 3 3 3 B I C (1đ) 1 2
AI AB AC . 0.25 3 3 A D
AD AE EF FD 0.5
BC BE EF FC E F 0.5
AD BC AE BE 2EFFD FC 0.25 C B 0.25 0 2EF 0 2EF 1) 4a (1.5đ) (3đ)
AM 2AB GM GA 2GB 2GA
GM 2GB GA 0.5 2 2 2 AN
AC GN GA GC GA 5 5 5 2) 2 3
GN GC GA (1.5đ) 5 5
5GN 2GC 3GA 0.5
GM 5GN 2GB GA + 2GC 3GA
= 2GA 2GB + 2GC = 0 GM 5 GN . 0.25 Vậy G, M, N thẳng hàng. 0.25 AB ( 1 ;0), AC (1;3) 0.25 1 0 Ta có
nên AB và AC không cùng phương. 1 3 0.25
Vậy A, B, C không thẳng hàng. 0.25 1)
Giả sử D(x; y). Vì ABCD là hình bình hành nên ta có:
(1.5đ) AB DC 0.25 3 x 1
1;0 3 ;x4 y 4 y 0 0.25 x 4 . Vậy D(4; 4). 0.25 y 4 4b
N Oy N(0; y ) 0.25 N (3đ)
NA NB 4NC NA NB NC 3NC
3NG 3NC (với G là trọng tâm ABC )
3NG NC 2)
(1.5đ) 6NI ( với I là trung điểm của GC). 0.5 Ta có G 5 2; 2 , I ;3 . 0.25 2
NA NB 4NC = 6NI 6 NI NI . 0.25
NA NB 4NC nhỏ nhất khi NI nhỏ nhất
N là hình chiếu của I trên Oy. N (0; 3). 0.25đ




