
Preview text:
Trường THPT: HAI Bµ TR¦NG KiÓm tra GI÷A Kú I (TP HuÕ) TO¸N 10 CB – H×nh (25 câu trắc nghiệm) Thêi gian: 45 phót
Họ và tên: ………………………………………..
Câu 1. Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của CD và BC. Phân
tích AC theo hai vectơ AM và AN . 2 1 1 1
A. AC AM AN 3 3 . B. AC AM AN 2 2 . 2 2 1 2
C. AC AM AN 3 3 . D. AC AM AN 3 3 .
Câu 2. Cho a,b là các vectơ khác 0 , a và b đối nhau. Mệnh đề nào sau đây sai ?
A. a,b cùng phương và ngược hướng.
B. a,b có độ dài bằng nhau.
C. a,b có giá trùng nhau.
D. a b 0 . 3
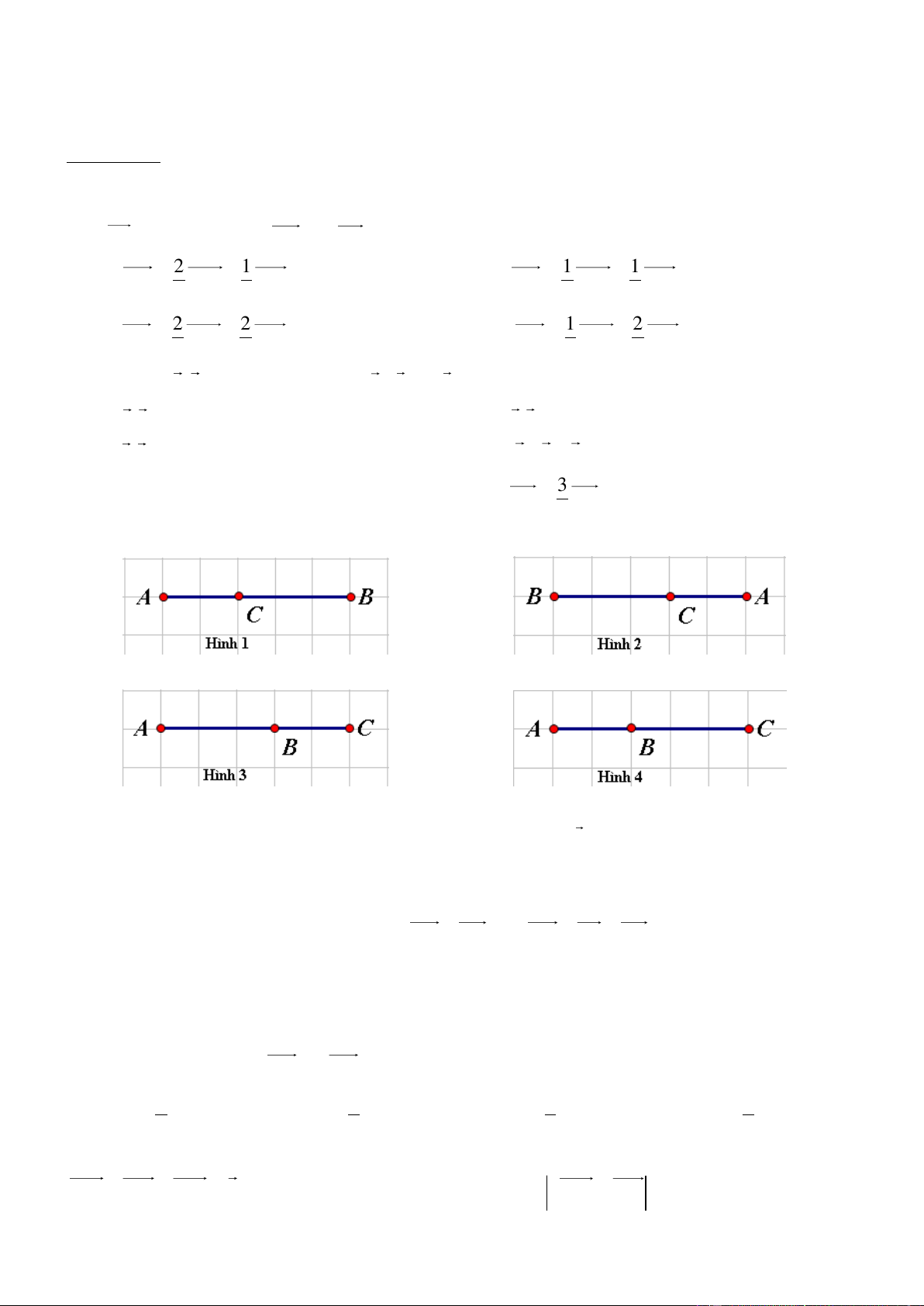
Câu 3. Cho ba điểm phân biệt A, B, C thỏa mãn BC AB 2
. Hình nào sau đây vẽ đúng vị trí ba điểm A, B, C. A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 4. Cho tam giác ABC có bao nhiêu vectơ khác vectơ 0 có điểm đầu và điểm cuối là các đỉnh của tam giác ABC. A. 9 . B. 3 . C. 12 . D. 6 .
Câu 5. Cho tứ giác ABCD. Đẳng thức AC CD k DC CB BA xảy ra khi và chỉ khi giá trị của k là : A. k 1 . B. k 1. C. k 1. D. k tùy ý.
Câu 6. Cho tam giác ABC với trọng tâm G và I là trung điểm của AG. Gọi K là điểm nằm
trên đoạn AC sao cho AK xAC . Tìm x để ba điểm B, I, K thẳng hàng. 2 1 1 1 A. x 5. B. x 3 . C. x 5 . D. x 6 .
Câu 7. Cho tam giác ABC vuông tại B có AB = 3a và BC = 4a. Gọi M là điểm thỏa mãn
MA MB MC 0 và N là trung điểm của AC. Tính 2MA MB theo a . a 3 17 a 1201 A. a 3 17 . B. 2 . C. a. 13 D. 5 .
Câu 8. Cho hình thang cân ABCD có đáy AB = 2a và CD = a. Trong các khẳng định sau,
khẳng định nào đúng?
A. AD 2 CB
B. AB DC
C. DA CB
D. AC BD
Câu 9. Cho hình bình hành ABCD tâm O. Đẳng thức nào sau đây sai ?
A. DA DB DC
B. COOB BA
C. AB BC DB
D. AB AD AC
Câu 10. Trong các mệnh đề sau, mệnh đề nào sai ?
A. Vectơ là một đoạn thẳng có hướng.
B. Ba điểm A, B, C thẳng hàng khi và chỉ khi AB, AC không cùng phương.
C. Độ dài vectơ là khoảng cách từ điểm đầu đến điểm cuối của vectơ đó.
D. Vectơ 0 là vectơ có điểm đầu và điểm cuối trùng nhau.
Câu 11. Cho tam giác ABC có trọng tâm G, I là trung điểm BC. Khẳng định nào sau đây sai ?
A. AI I 3 G 0
B. AB AC 3GB GC 2 1
C. AG AI 0 3 D. GI GA 2
Câu 12. Cho tam giác ABC. Gọi M, N, P lần luwọt là trung điểm của BC, CA, AB. Vectơ
MN cùng hướng với vectơ nào trong các vectơ sau? A. AB B. BP C. AP D. NM
Câu 13. Cho tam giác ABC vuông tại A, I là trung điểm BC, 3 3; 30o AC C .
Tính CB CA BI : A. 3 3 B. 3 C. 9 3 D. 6
Câu 14. Cho tam giá ABC có trọng tâm G, biết AG CG GB CB . Kết luận nào sau đây đúng?
A. ABC vuông tại B.
B. ABC cân tại C.
C. ABC cân tại B.
D. ABC cân tại A.
Câu 15. Cho ba điểm A, B, C phân biệt. Trong các khẳng định sau, khẳng định nào đúng?
A. Ba điểm A,B,C thẳng hàng khi và chỉ khi tồn tại một số k 0 để AB k B . C .
B. Ba điểm A,B,C thẳng hàng khi và chỉ khi tồn tại một số k 0 để AB k BC . .
C. Ba điểm A,B,C thẳng hàng khi và chỉ khi tồn tại một số k 0 để AB k B . C .
D. Ba điểm A,B,C thẳng hàng khi và chỉ khi tồn tại một số k 0 để AB k BC . .
Câu 16. Trong các mệnh đề sau, mệnh đề nào sai?
A. Có một vectơ cùng phương với mọi vectơ.
B. Hai vectơ cùng phương với một vectơ thứ ba thì cùng phương.
C. Hai vectơ bằng nhau nếu chúng cùng hướng và cùng cùng độ dài.
D. Hai vectơ bằng nhau thì chúng có độ dài bằng nhau.
Câu 17. Cho bốn điểm A, B, C, D phân biệt sao cho AB DC . Trong các mệnh đề sau, mệnh đề nào sai?
A. ABCD là hình bình hành.
B. AD BC .
C. AB CD .
D. AB,DC cùng hướng.
Câu 18. Cho điểm M, N là hai điểm phân biệt, điều kiện cần và đủ để O là trung điểm của đoạn MN là ?
A. OM ON .
B. OM ON O .
C. OM ON .
D.OM NO .
Câu 19. Cho các điểm M, N, P, Q phân biệt. Tổng NP PQ QM MN bằng vectơ nào đưới đây. A. O B. QN C. MQ D. MP
Câu 20. Cho bốn điểm phân biệt A, B, C, D. Khẳng định nào sau đây sai?:
A. AB BD AC CD .
B. AC BD AD BC .
C. AB AD CB CD .
D. AC BD AD BC .
Câu 21. Cho hai vectơ a,b là các vectơ khác 0 và số thực k 0 . Trong các khẳng định sau,
khẳng định nào sai?
A. b và kb cùng phương.
B. a và 3a ngược hướng.
C. ka k a .
D. k a b ka kb
Câu 22. Cho hình vuông ABCD tâm O. Trong các khẳng định sau, khẳng định nào sai ? 1
A. AB BO CA 2 2 . B. BA BC BO . 1
C. AC DB 2AB .
D.OA OB 2 DA.
Câu 23. Cho tam giác ABC, điểm M thỏa mãn MA 2MB CB . Khi đó điểm M là:
A. Đỉnh thứ tư của hình bình hành ACBM.
B. Trọng tâm tam giác ABC.
C. Tâm đường tròn ngoại tiếp tam giác ABC.
D. Đỉnh thứ tư hình bình hành ABCM.
Câu 24. Cho tam giác ABC vuông tại A có AB = 6, BC = 10. Tính BC BA : A. 8 . B. 6 . C. 4 . D. 16 .
Câu 25. Cho tam giác ABC với trọng tâm G, I là trung điểm của đoạn thẳng AB và M là
một điểm bất kỳ. Đẳng thức nào sau đây đúng ?
A. MA MB MC O .
B. MA MB 2MG . 1 1
C. IM MA MB 2 . D. MG MA MB MC 3 .
-------------- HẾT -----------------




