Đề kiểm tra Hình học 12 chương 1 năm 2019 – 2020 trường Nguyễn Bỉnh Khiêm – Gia Lai

Đề kiểm tra Hình học 12 chương 1 năm 2019 – 2020 trường Nguyễn Bỉnh Khiêm – Gia Lai có mã đề 178, đề kiểm tra gồm 03 trang với 25 câu hỏi và bài toán dạng trắc nghiệm khách quan, thời gian kiểm tra là 45 phút, đề kiểm tra có đáp án và lời giải chi tiết.

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

11 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Trang 1/3 - Mã đề 178 - https://toanmath.com/
TRƯỜNG THPT NGUYỄN BỈNH KHIÊM
TỔ TOÁN
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA 1 T
IẾT HÌNH HỌC CHƯƠNG 1
NĂM HỌC 2019 – 2020
Môn: Toán 12
Thời gian: 45 phút (không kể thời gian phát đề)
Mã đề thi
178
Họ và tên: …………………………………………………………. Lớp: ……………
Câu 1. Hình nào dưới đây không phải là hình đa diện?
Hình nào dưới đây không phải là hình đa diện?
A.Hình 1. B.Hình 2. C.Hình 3. D.Hình 4.
Câu 2. Cho một hình đa diện. Trong các khẳng định sau, khẳng định nào sai?
A.Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh. B.Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
C.Mỗi mặt có ít nhất ba cạnh. D.Mỗi cạnh là cạnh chung của ít nhất ba mặt.
Câu 3. Cho hình chóp có đáy là hình vuông. Cạnh bên vuông góc với . Phép
đối xứng qua mặt phẳng biến khối chóp thành khối chóp nào?
A. . B. . C. . D. .
Câu 4. Số mặt phẳng đối xứng của hình hộp chữ nhật mà không có mặt nào là hình vuông là:
A.
3
. B.
12
. C.
9
. D.
6
.
Câu 5. Số mặt phẳng đối xứng của hình chóp tứ giác đều là:
A.. B.. C.. D..
Câu 6. Cho các hình khối sau:
Hình 1 Hình 2 Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số khối đa diện lồi là:
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 7. Khối hai mươi mặt đều là khối đa diện đều loại:
A. . B. . C.. D..
Câu 8. Khẳng định nào sau đây sai?
A.Số cạnh của một khối đa diện đều luôn là số chẵn.
B.Tồn tại một khối đa diện đều có số cạnh là số lẻ.
C.Số mặt của một khối đa diện đều luôn là số chẵn.
D.Số đỉnh của một khối đa diện đều luôn là số chẵn.
Câu 9. Nếu không sử dụng thêm điểm nào khác ngoài các đỉnh của hình lập phương thì có thể chia hình lập
phương thành
A.Bốn tứ diện đều và một hình chóp tam giác đều.
B.Năm hình chóp tam giác đều, không có tứ diện đều.
C.Một tứ diện đều và bốn hình chóp tam giác đều.
D.Năm tứ diện đều.
.S ABCD
A
BCD SA

ABCD
SAC
.SABC
.SCBD .S ABC .SADC .SABD
24
86
35;
24;
43;
53;
Trang 2/3 - Mã đề 178 - https://toanmath.com/
Câu 10. Cho khối chóp tứ giác đều
.SABCD
có cạnh đáy bằng
a
, cạnh bên hợp với đáy một góc
60
. Gọi
M
là điểm đối xứng với
C
qua
D
,
N
là trung điểm
SC
. Mặt phẳng

B
MN
chia khối chóp
.SABCD
thành hai khối đa diện. Tính thể tích
V
của khối đa diện chứa đỉnh
C
.
A.
3
76
36
a
V
. B.
3
76
72
a
V
. C.
3
56
72
a
V
. D.
3
56
36
a
V
.
Câu 11. Khối chóp có một nửa diện tích đáy là
S
, chiều cao là
2h
thì có thể tích là:
A.
4
.
3
VSh
. B.
1
.
3
VSh
. C.
.VSh
. D.
1
.
2
VSh
.
Câu 12. Tính thể tích của khối lăng trụ biết diện tích đáy là và chiều cao là .
A. . B. . C. . D. .
Câu 13. Cho hình hộp chữ nhật có cm, cm, cm. Tính thể tích khối
hộp .
A. . B. . C. . D. .
Câu 14. Cho hình chóp có là trung điểm của cạnh . Khi đó bằng:
A. . B. . C. . D. .
Câu 15. Tính thể tích của khối tứ diện đều có tất cả các cạnh đều bằng
1
.
A.
2
12
. B.
3
12
. C.
2
4
. D.
3
4
.
Câu 16. Cho hình chóp tam giác đều có diện tích đáy bằng
2
3
4
a
, chiều cao hình chóp gấp đôi độ dài cạnh
đáy . Tính thể tích
V
của khối chóp.
A.
3
4
a
V . B.
3
3
6
a
V
. C.
3
3
12
a
V
. D.
3
12
a
V .
Câu 17. Tính thể tích
V
của lập phương
.
A
BCD A B C D

, biết 3AC a
.
A.
3
33Va . B.
3
Va
. C.
3
36
4
a
V
. D.
3
3
a
V .
Câu 18. Cho một khối lăng trụ có thể tích là
3
3a , đáy là tam giác đều cạnh
a
. Tính chiều cao
h
của khối
lăng trụ.
A.
4ha
. B.
3ha
. C.
2ha
. D.
ha
.
Câu 19. Cho hình chóp có và mặt bên là tam giác đều cạnh Khoảng cách từ
đến bằng:
A. B. C. D.
Câu 20. Cho lăng trụ đứng có đáy là tam giác vuông cân tại , . Biết tạo
với đáy góc . Thể tích khối lăng trụ là
A. B. . C. D.
Câu 21. Cho hình lăng trụ . Gọi , lần lượt là trung điểm của và . Mặt phẳng
chia khối lăng trụ thành phần có thể tích và như hình vẽ. Tính .
2
2a
3a
3
2
3
Va
3
3Va
3
2Va
3
6Va
.
A
BCD A B C D

2
B 3AD 7AA
.
A
BCD A B C D

12
3
cm
42
3
cm
24
3
cm
36
3
cm
.SABC
M
SC
SABM
CABM
V
V
1
3
1
1
2
2
.SABC
3
.
2
36
SABC
a
V
SBC
.a
A
SBC
2
.
9
a 6
.
3
a 6
.
9
a 6
.
27
a
.
A
BC A B C

A
2AB AC a
A
B
60
3
5
.
3
a
3
33
2
a
3
46.a
3
6.a
.
A
BC A B C

E
FBB
CC

AEF
2
1
V
2
V
1
2
V
V
Trang 3/3 - Mã đề 178 - https://toanmath.com/
A. . B. . C. . D. .
Câu 22. Cho hình chóp
.S ABCD
có đáy
A
BCD
là hình vuông cạnh bằng
a
. Cạnh
SA
vuông góc với đáy và
SA y
. Trên cạnh
A
D
lấy điểm
M
sao cho
A
Mx
.
Biết rằng
222
x
ya. Tìm giá trị lớn nhất của thể tích khối chóp
.S ABCM
.
A.
3
3
2
a
. B.
3
8
a
. C.
3
3
8
a
. D.
3
3
4
a
.
Câu 23. Cho hình chóp
.S ABCD
có đáy
A
BCD
là hình thang cân,
2222
A
DABBCCDa
. Hai mặt
phẳng

SAB
và
SAD
cùng vuông góc với mặt phẳng

ABCD
. Gọi
,
M
N
lần lượt là trung điểm của
SB
và
CD
. Tính cosin góc giữa
M
N
và
SAC
, biết thể tích khối chóp
.S ABCD
bằng
3
3
4
a
.
A.
3310
20
. B.
310
20
. C.
5
10
. D.
35
10
.
Câu 24. Cho hình lăng trụ
.

A
BC A B C
có đáy
A
BC
là tam giác vuông tại
A
, cạnh
2BC a
và
60
ABC .
Biết tứ giác

BCC B
là hình thoi có
B
BC nhọn. Biết

BCC B
vuông góc với
ABC
và


ABB A
tạo với
ABC
góc
45
. Thể tích của khối lăng trụ
.

A
BC A B C
bằng
A.
3
6
7
a
. B.
3
7
a
. C.
3
37
a
. D.
3
3
7
a
.
Câu 25. Cho hình chóp có đáy là tam giác đều cạnh , tam giác vuông tại , tam giác
vuông tại . Biết góc giữa hai mặt phẳng và bằng . Tính thể tích khối chóp
theo .
A. . B. . C. . D. .
------------- HẾT -------------
1
1
4
1
3
1
2
.SABC
A
BC
a
SBA
B
SAC C

SAB

ABC
60
.SABC
a
3
3
8
a
3
3
12
a
3
3
6
a
3
3
4
a
Trang 1/8 - Mã đề 178 - https://toanmath.com/
TRƯỜNG THPT NGUYỄN BỈNH KHIÊM
TỔ TOÁN
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA 1 T
IẾT HÌNH HỌC CHƯƠNG 1
NĂM HỌC 2019 – 2020
Môn: Toán 12
Thời gian: 45 phút (không kể thời gian phát đề)
Mã đề thi
178
Họ và tên: …………………………………………………………. Lớp: ……………
Câu 1. Hình nào dưới đây không phải là hình đa diện?
Hình nào dưới đây không phải là hình đa diện?
A.Hình 1. B.Hình 2. C. Hình 3. D.Hình 4.
Câu 2. Cho một hình đa diện. Trong các khẳng định sau, khẳng định nào sai?
A.Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh. B.Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
C.Mỗi mặt có ít nhất ba cạnh. D. Mỗi cạnh là cạnh chung của ít nhất ba mặt.
Câu 3. Cho hình chóp có đáy là hình vuông. Cạnh bên vuông góc với . Phép
đối xứng qua mặt phẳng biến khối chóp thành khối chóp nào?
A. . B. . C. . D. .
Câu 4. Số mặt phẳng đối xứng của hình hộp chữ nhật mà không có mặt nào là hình vuông là:
A.
3
. B.
12
. C.
9
. D.
6
.
Câu 5. Số mặt phẳng đối xứng của hình chóp tứ giác đều là:
A.. B. . C.. D..
Câu 6. Cho các hình khối sau:
Hình 1 Hình 2 Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số khối đa diện lồi là:
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 7. Khối hai mươi mặt đều là khối đa diện đều loại:
A. . B. . C.. D..
Câu 8. Khẳng định nào sau đây sai?
A.Số cạnh của một khối đa diện đều luôn là số chẵn.
B. Tồn tại một khối đa diện đều có số cạnh là số lẻ.
C.Số mặt của một khối đa diện đều luôn là số chẵn.
D.Số đỉnh của một khối đa diện đều luôn là số chẵn.
Câu 9. Nếu không sử dụng thêm điểm nào khác ngoài các đỉnh của hình lập phương thì có thể chia hình lập
phương thành
A.Bốn tứ diện đều và một hình chóp tam giác đều.
B.Năm hình chóp tam giác đều, không có tứ diện đều.
C. Một tứ diện đều và bốn hình chóp tam giác đều.
D.Năm tứ diện đều.
Lời giải
.S ABCD
A
BCD SA

ABCD
SAC
.SABC
.SCBD .S ABC .SADC .SABD
24
86
35;
24;
43;
53;
Trang 2/8 - Mã đề 178 - https://toanmath.com/
Chọn C
Hình tứ diện đều là
A
CB D

.
Bốn hình chóp tam giác đều là
.
D
ACD
,
.CCBD

,
.BACB
.
A
AB D

.
Câu 10. Cho khối chóp tứ giác đều
.SABCD
có cạnh đáy bằng
a
, cạnh bên hợp với đáy một góc
60
. Gọi
M
là điểm đối xứng với
C
qua
D
,
N
là trung điểm
SC
. Mặt phẳng

B
MN
chia khối chóp
.SABCD
thành hai khối đa diện. Tính thể tích
V
của khối đa diện chứa đỉnh
C
.
A.
3
76
36
a
V
. B.
3
76
72
a
V
. C.
3
56
72
a
V
. D.
3
56
36
a
V
.
Lời giải
Chọn C
Gọi
PMN SD
,
QBM AD
. Suy ra
BNPQ
là thiết diện của

B
MN
với hình chóp
.SABCD
. Gọi
H
là tâm của đáy, ta có:

26
.tan60 . 3
22
aa
SH ABCD SH AH 
.
Ta có:
..CDPQBN N BCDQ N DPQ
VVV
.
Do
N
là trung điểm của
SC
, suy ra


1
,
2
dN BCDQ SH
.
Ta lại có:
M
là điểm đối xứng với
C
qua
D
, suy ra
Q
là trung điểm của
A
D
.
nên

2
.
.
3
2
224
BCDQ
a
aa
BC DQ CD
a
S



,
23
.
116336
.. . .
662448
N BCDQ BCDQ
aa a
VSHS
.
Ta có:




,,dN DPQ dH SAD
.
Trang 3/8 - Mã đề 178 - https://toanmath.com/
Mà
HQ AD
, kẻ
H
ISQ I


,dH SAD HI
.
222222
1112414
33HI SH HQ a a a

3
.
14
HI a
.
Xét
SCM
, có
N
và
D
là trung điểm của
SC
và
CM
suy ra
P
là trọng tâm
SCM
.
1
3
DP SD
. Kẻ
PK DQ K
,
22
22
3
7
24
33 36
aa
SH HQ
SQ a
PK

.
Suy ra:
2
1177
...
222624
DPQ
aa a
SDQPK
,
23
.
13 7 6
...
3 14 24 144
NDPQ
aa
Va
.
Vậy
33 3
36 6 5 6
48 144 72
CDPQBN
aa a
V 
.
Câu 11. Khối chóp có một nửa diện tích đáy là
S
, chiều cao là
2h
thì có thể tích là:
A.
4
.
3
VSh
. B.
1
.
3
VSh
. C.
.VSh
. D.
1
.
2
VSh
.
Câu 12. Tính thể tích của khối lăng trụ biết diện tích đáy là và chiều cao là .
A. . B. . C. . D. .
Câu 13. Cho hình hộp chữ nhật có cm, cm, cm. Tính thể tích khối
hộp .
A. . B. . C. . D. .
Câu 14. Cho hình chóp có là trung điểm của cạnh . Khi đó bằng:
A. . B. . C. . D. .
Câu 15. Tính thể tích của khối tứ diện đều có tất cả các cạnh đều bằng
1
.
A.
2
12
. B.
3
12
. C.
2
4
. D.
3
4
.
Câu 16. Cho hình chóp tam giác đều có diện tích đáy bằng
2
3
4
a
, chiều cao hình chóp gấp đôi độ dài cạnh
đáy . Tính thể tích
V
của khối chóp.
A.
3
4
a
V . B.
3
3
6
a
V
. C.
3
3
12
a
V
. D.
3
12
a
V .
Câu 17. Tính thể tích
V
của lập phương
.
A
BCD A B C D

, biết 3AC a
.
A.
3
33Va . B.
3
Va
. C.
3
36
4
a
V
. D.
3
3
a
V .
Câu 18. Cho một khối lăng trụ có thể tích là
3
3a , đáy là tam giác đều cạnh
a
. Tính chiều cao
h
của khối
lăng trụ.
A.
4ha
. B.
3ha
. C.
2ha
. D.
ha
.
Câu 19. Cho hình chóp có và mặt bên là tam giác đều cạnh Khoảng cách từ
đến bằng:
A. B. C. D.
Câu 20. Cho lăng trụ đứng có đáy là tam giác vuông cân tại , . Biết tạo
với đáy góc . Thể tích khối lăng trụ là
2
2a
3a
3
2
3
Va
3
3Va
3
2Va
3
6Va
.
A
BCD A B C D

2
B 3AD 7AA
.
A
BCD A B C D

12
3
cm
42
3
cm
24
3
cm
36
3
cm
.SABC
M
SC
SABM
CABM
V
V
1
3
1
1
2
2
.SABC
3
.
2
36
SABC
a
V
SBC
.a
A
SBC
2
.
9
a 6
.
3
a 6
.
9
a 6
.
27
a
.
A
BC A B C

A
2AB AC a
A
B
60
Trang 4/8 - Mã đề 178 - https://toanmath.com/
A. B. . C. D.
Câu 21. Cho hình lăng trụ . Gọi , lần lượt là trung điểm của và . Mặt phẳng
chia khối lăng trụ thành phần có thể tích và như hình vẽ. Tính .
A. . B. . C. . D. .
Lời giải
Chọn D
Gọi
V
là thể tích khối lăng trụ
.
A
BC A B C

.
Ta có:

1. .
11 11121
.
22 23233
ABCBC AABC
VV VV VV VV
 




21
12
33
VVVV V V
.
Do đó:
1
2
12 1
:
33 2
V
VV
V

.
Câu 22. Cho hình chóp
.S ABCD
có đáy
A
BCD
là hình vuông cạnh bằng
a
. Cạnh
SA
vuông góc với đáy và
SA y
. Trên cạnh
A
D
lấy điểm
M
sao cho
A
Mx
.
Biết rằng
222
x
ya. Tìm giá trị lớn nhất của thể tích khối chóp
.S ABCM
.
A.
3
3
2
a
. B.
3
8
a
. C.
3
3
8
a
. D.
3
3
4
a
.
Lời giải
Chọn A.
3
5
.
3
a
3
33
2
a
3
46.a
3
6.a
.
A
BC A B C

E
FBB
CC

AEF
2
1
V
2
V
1
2
V
V
1
1
4
1
3
1
2
Trang 5/8 - Mã đề 178 - https://toanmath.com/
Ta có
22
ABCM
A
MBC ax
SABa


.
Thể tích khối chóp
.S ABCM
là

1
.
36
ABCM
a
VSAS yax
.
Do
222
x
ya
22
y
ax ,suy ra
 

2
22 22
66
aa
Vaxax axax
.
Xét hàm số


2
22
f
xaxax
với
0
x
a
.
Ta có


 

2
22 2 2
2222
f
x axa x xax ax x axa


0fx
2
a
x
x
a

Bảng biến thiên
Từ bảng biến thiên suy ra
3
max
3
8
a
V
.
Câu 23. Cho hình chóp
.S ABCD
có đáy
A
BCD
là hình thang cân,
2222
A
DABBCCDa
. Hai mặt
phẳng

SAB
và
SAD
cùng vuông góc với mặt phẳng

ABCD
. Gọi
,
M
N
lần lượt là trung điểm của
SB
và
CD
. Tính cosin góc giữa
M
N
và
SAC
, biết thể tích khối chóp
.S ABCD
bằng
3
3
4
a
.
A.
3310
20
. B.
310
20
. C.
5
10
. D.
35
10
.
Lời giải
Chọn B
S
A
D
C
B
M
x
y
Trang 6/8 - Mã đề 178 - https://toanmath.com/
Gọi

là mp đi qua
M
N
và song song với mp
SAD
. Khi đó

cắt
A
B
tại
P
, cắt
SC
tại
Q
,
cắt
A
C
tại
K
. Gọi
I
là giao điểm của
M
N
và
QK

I
SAC
.
Suy ra:
P
,
Q
,
K
lần lượt là trung điểm của
A
B
,
SC
và
A
C
.
Lại có:
A
BCD
là hình thang cân có
2222
A
DABBCCDa
2;
A
DaABBCCDa
3
2
a
CH
;
2
2333
.
22 4
ABCD
aaa a
S

.
Nên
23
133 3
..
34 4
ABCD
aa
VSA
SA a
1
22
a
MP SA
và
3
2
a
NP
.
Xét tam giác
M
NP
vuông tại P:
22
310
22 2
aaa
MN




,
M
PKQ
lần lượt là đường trung bình của tam giác
,SAB SAC
// //
M
PKQSA
K
N
là đường trung bình của tam giác
1
2
A
CD KN AD a
.
Xét tam giác
A
HC
vuông tại H:
2
2
33
3
22
aa
A
Ca








3
2
a
KC
Suy ra: tam giác
K
NC
vuông tại
C
C
là hình chiếu vuông góc của
N
lên
SAC
.
góc giữa
M
N
và
SAC
là góc
NIC
Khi đó:
2221010
..
33323
IN KN a a
IN MN
M
NNP

Xét tam giác
NIC
vuông tại
C
:
10
;
23
aa
NC IN
2
2
10 31
326
aaa
IC








31 10 310
cos :
63 20
IC a a
NIC
I
N

.
Câu 24. Cho hình lăng trụ
.

A
BC A B C
có đáy
A
BC
là tam giác vuông tại
A
, cạnh
2BC a
và
60
ABC .
Biết tứ giác

BCC B
là hình thoi có
B
BC nhọn. Biết

BCC B
vuông góc với
ABC
và


ABB A
tạo với
ABC
góc
45
. Thể tích của khối lăng trụ
.

A
BC A B C
bằng
A.
3
6
7
a
. B.
3
7
a
. C.
3
37
a
. D.
3
3
7
a
.
A
B
C
D
S
M
Q
N
K
I
H
Trang 7/8 - Mã đề 178 - https://toanmath.com/
Lời giải
Chọn B
Do
A
BC
là tam giác vuông tại
,
A
cạnh
2BC a
và
60ABC
nên
A
Ba
,
3
A
Ca
.
Gọi
H
là hình chiếu vuông góc của
B
lên
BC
H
thuộc đoạn
BC
(do
BBC
nhọn)

B
HABC
(do

B
CC B
vuông góc với

A
BC
).
Kẻ
H
K
song song
A
C
K
AB

H
KAB
(do
A
BC
là tam giác vuông tại
A
).

, 45 (1)




ABB A ABC B KH B H KH
Ta có
BB H
vuông tại
H
22
4 (2)
 BH a B H
Mặt khác
H
K
song song
A
C

B
HHK
B
CAC
.2
(3)
3

HK a
BH
a
Từ (1), (2) và (3) suy ra
22
.2
4
3

B
Ha
aBH
a
12
7
BH a
.
Vậy
3
.''
13
...
2
7


ABC A B C ABC
a
V S B H AB AC B H
.
Câu 25.
Cho hình chóp có đáy là tam giác đều cạnh , tam giác vuông tại , tam giác
vuông tại . Biết góc giữa hai mặt phẳng và bằng . Tính thể tích khối chóp
theo .
A. . B. . C. . D. .
Lời giải
Chọn B
60
2a
2a
K
H
C'
B'
A'
C
B
A
.SABC
A
BC
a
SBA
B
SAC C

SAB

ABC
60
.SABC
a
3
3
8
a
3
3
12
a
3
3
6
a
3
3
4
a
Trang 8/8 - Mã đề 178 - https://toanmath.com/
Gọi
D
là hình chiếu của
S
lên mặt phẳng

A
BC
, suy ra

SD ABC
.
Ta có
SD AB
và
()SB AB
g
t
, suy ra

A
B SBD BA BD
.
Tương tự có
A
CDC
hay tam giác
A
CD
vuông ở
C
.
Dễ thấy
SBA SCA
(cạnh huyền và cạnh góc vuông), suy ra
SB SC
. Từ đó ta chứng minh
được
SBD SCD
nên cũng có
D
BDC
.
Vậy
D
A
là đường trung trực của
BC
, nên cũng là đường phân giác của góc
B
AC .
Ta có
30DAC , suy ra
3
a
DC
. Ngoài ra góc giữa hai mặt phẳng

SAB
và

A
BC
là
60SBD , suy ra
tan tan . 3
3
SD a
SBD SD BD SBD a
BD
 .
Vậy
23
.
1133
.. . .
33412
S ABC ABC
aa
VSSD a

.
------------- HẾT -------------
S
D
B
A
C
| 1/11
| | Tải xuống

Có thể bạn quan tâm:

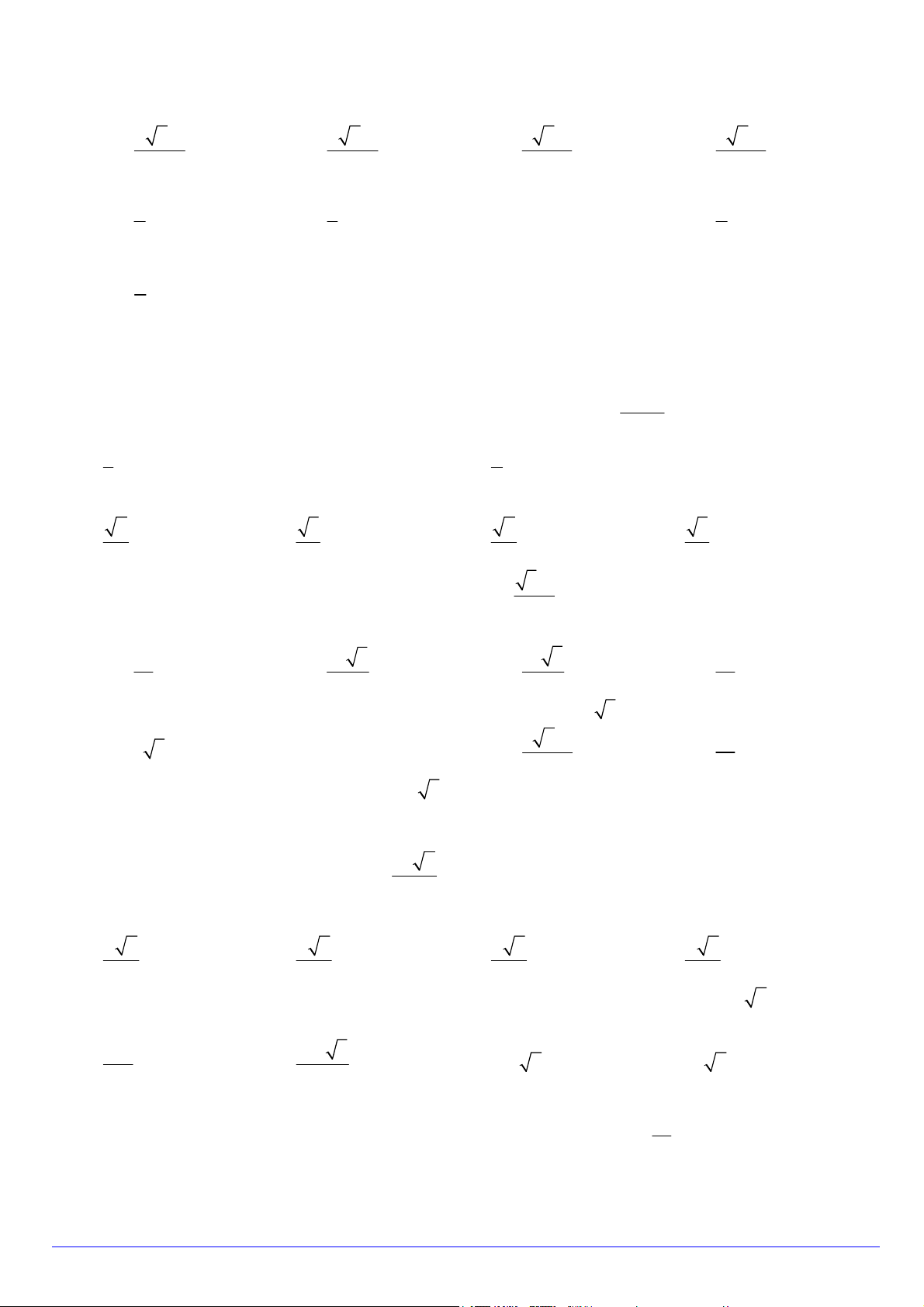
Preview text:

TRƯỜNG THPT NGUYỄN BỈNH KHIÊM
ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC CHƯƠNG 1 TỔ TOÁN
NĂM HỌC 2019 – 2020 Môn: Toán 12 ĐỀ CHÍNH THỨC
Thời gian: 45 phút (không kể thời gian phát đề) Mã đề thi 178
Họ và tên: …………………………………………………………. Lớp: ……………
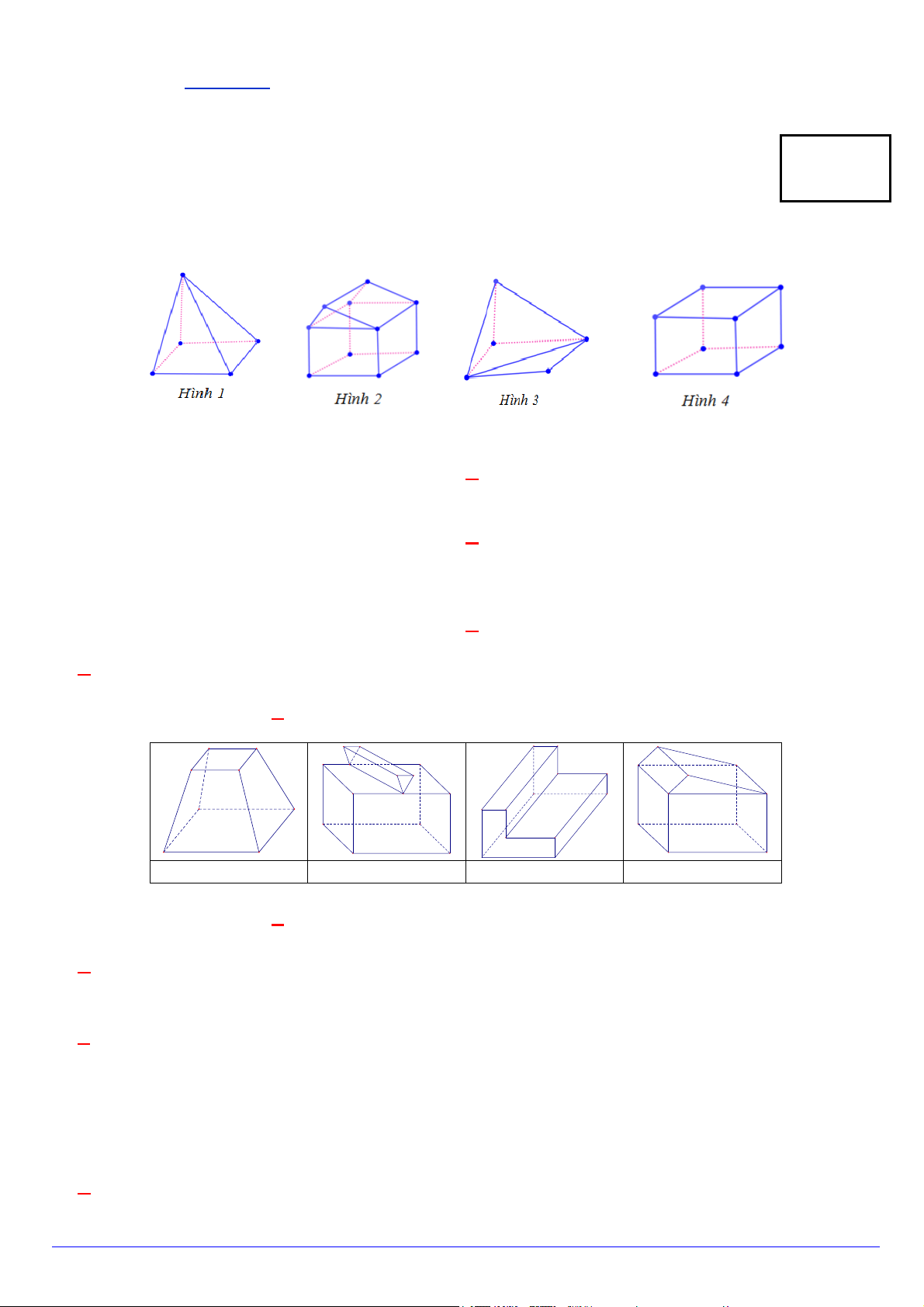
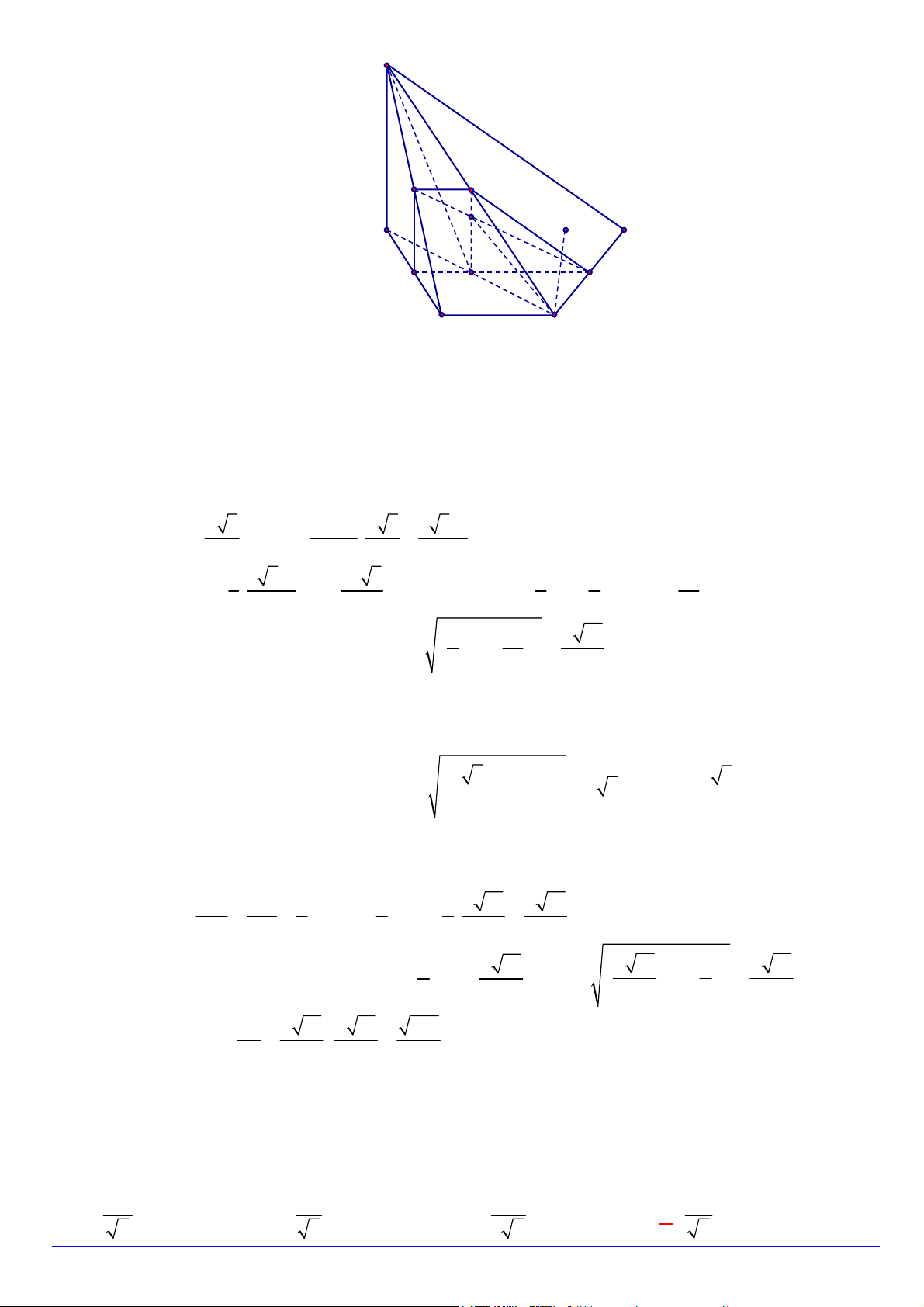
Câu 1. Hình nào dưới đây không phải là hình đa diện?
Hình nào dưới đây không phải là hình đa diện? A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 2. Cho một hình đa diện. Trong các khẳng định sau, khẳng định nào sai?
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.
B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
C. Mỗi mặt có ít nhất ba cạnh.
D. Mỗi cạnh là cạnh chung của ít nhất ba mặt.
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Cạnh bên SA vuông góc với  ABCD . Phép
đối xứng qua mặt phẳng SAC biến khối chóp S.ABC thành khối chóp nào?
A. S.CBD .
B. S.ABC .
C. S.ADC .
D. S.ABD .
Câu 4. Số mặt phẳng đối xứng của hình hộp chữ nhật mà không có mặt nào là hình vuông là: A. 3 . B. 12 . C. 9 . D. 6 .
Câu 5. Số mặt phẳng đối xứng của hình chóp tứ giác đều là: A. 2 . B. 4 . C. 8 . D. 6 .
Câu 6. Cho các hình khối sau: Hình 1 Hình 2 Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số khối đa diện lồi là: A. 4 . B. 2 . C. 1. D. 3 .
Câu 7. Khối hai mươi mặt đều là khối đa diện đều loại: A. 3;  5 . B. 2;  4 . C. 4;  3 . D. 5;  3 .
Câu 8. Khẳng định nào sau đây sai?
A. Số cạnh của một khối đa diện đều luôn là số chẵn.
B. Tồn tại một khối đa diện đều có số cạnh là số lẻ.
C. Số mặt của một khối đa diện đều luôn là số chẵn.
D. Số đỉnh của một khối đa diện đều luôn là số chẵn.
Câu 9. Nếu không sử dụng thêm điểm nào khác ngoài các đỉnh của hình lập phương thì có thể chia hình lập phương thành
A. Bốn tứ diện đều và một hình chóp tam giác đều.
B. Năm hình chóp tam giác đều, không có tứ diện đều.
C. Một tứ diện đều và bốn hình chóp tam giác đều.
D. Năm tứ diện đều.
Trang 1/3 - Mã đề 178 - https://toanmath.com/
Câu 10. Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với đáy một góc 60 . Gọi
M là điểm đối xứng với C qua D , N là trung điểm SC . Mặt phẳng BMN  chia khối chóp S.ABCD
thành hai khối đa diện. Tính thể tích V của khối đa diện chứa đỉnh C . 3 7 6a 3 7 6a 3 5 6a 3 5 6a A. V  . B. V  . C. V  . D. V  . 36 72 72 36
Câu 11. Khối chóp có một nửa diện tích đáy là S , chiều cao là 2h thì có thể tích là: 4 1 1
A. V S.h .
B. V S.h .
C. V S.h .
D. V S.h . 3 3 2
Câu 12. Tính thể tích của khối lăng trụ biết diện tích đáy là 2
2a và chiều cao là 3a . 2 A. 3
V a . B. 3
V  3a . C. 3
V  2a . D. 3
V  6a . 3
Câu 13. Cho hình hộp chữ nhật ABC . D AB CD
  có AB  2 cm, AD  3 cm, AA  7 cm. Tính thể tích khối hộp ABC . D AB CD   . A. 12 3 cm . B. 42 3 cm . C. 24 3 cm . D. 36 3 cm . V
Câu 14. Cho hình chóp S.ABC có M là trung điểm của cạnh SC . Khi đó SABM bằng: VCABM 1 1 A. . B. . 1 C. . D. 2 . 3 2
Câu 15. Tính thể tích của khối tứ diện đều có tất cả các cạnh đều bằng 1. 2 3 2 3 A. . B. . C. . D. . 12 12 4 4 2 3a
Câu 16. Cho hình chóp tam giác đều có diện tích đáy bằng
, chiều cao hình chóp gấp đôi độ dài cạnh 4
đáy . Tính thể tích V của khối chóp. 3 a 3 a 3 3 a 3 3 a A. V  . B. V  . C. V  . D. V  . 4 6 12 12
Câu 17. Tính thể tích V của lập phương ABCD.AB CD
 , biết AC a 3 . 3 3 6a 3 a A. 3
V  3 3a . B. 3
V a . C. V  . D. V  . 4 3
Câu 18. Cho một khối lăng trụ có thể tích là 3
a 3 , đáy là tam giác đều cạnh a . Tính chiều cao h của khối lăng trụ.
A. h  4a .
B. h  3a .
C. h  2a .
D. h a . 3 a 2
Câu 19. Cho hình chóp S.ABC có V
và mặt bên SBC là tam giác đều cạnh . a Khoảng cách từ S.ABC 36
A đến SBC bằng: a 2 a 6 a 6 a 6 A. . B. . C. . D. . 9 3 9 27
Câu 20. Cho lăng trụ đứng ABC.A BC
  có đáy là tam giác vuông cân tại A , AB AC a 2 . Biết AB tạo
với đáy góc 60 . Thể tích khối lăng trụ là 3 5a 3 3a 3 A. . B. . C. 3 4a 6. D. 3 a 6. 3 2
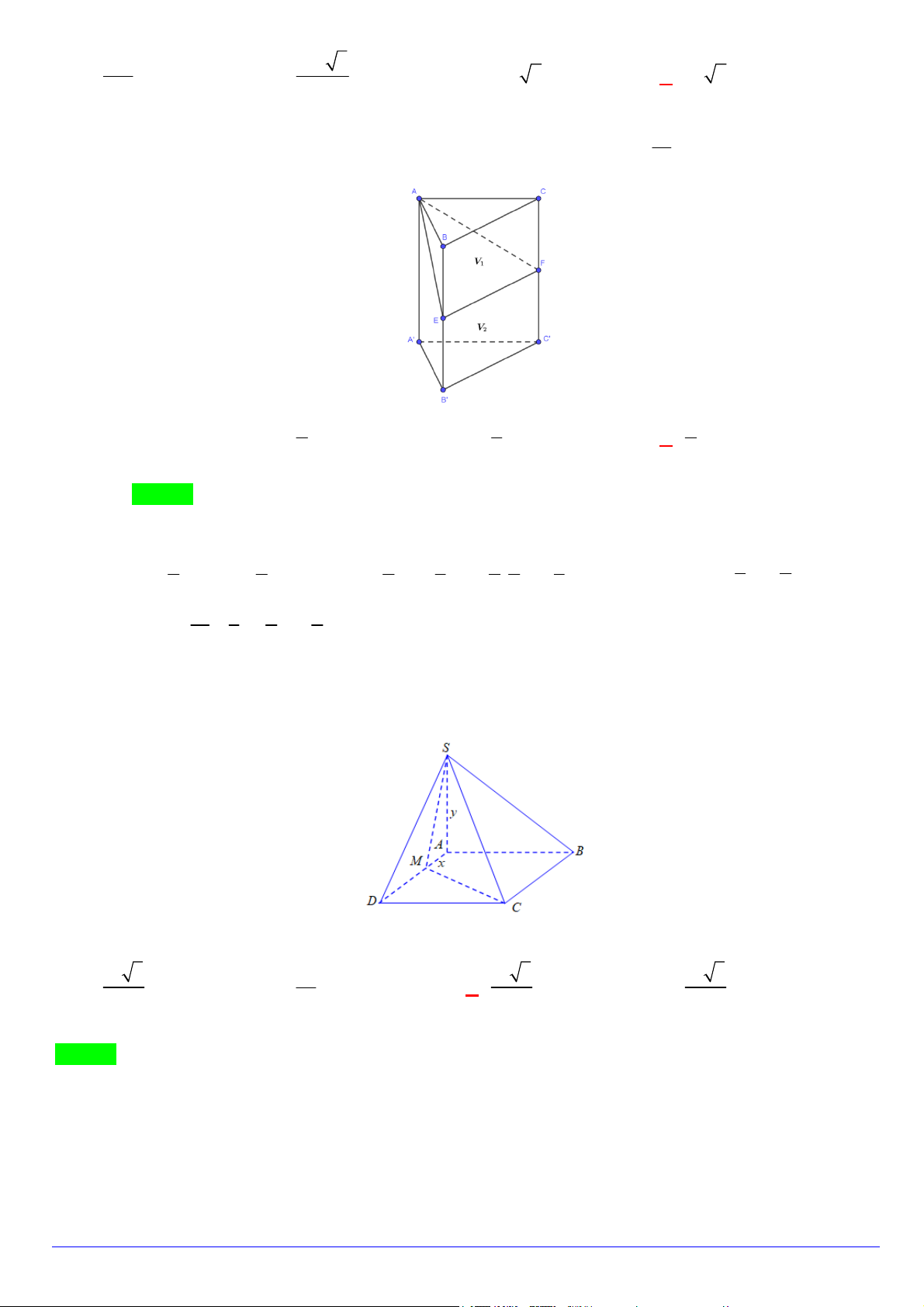
Câu 21. Cho hình lăng trụ ABC.AB C
  . Gọi E , F lần lượt là trung điểm của BB và CC . Mặt phẳng AEFV
chia khối lăng trụ thành 2 phần có thể tích V và V như hình vẽ. Tính 1 . 1 2 V2
Trang 2/3 - Mã đề 178 - https://toanmath.com/ 1 1 1 A. . 1 B. . C. . D. . 4 3 2
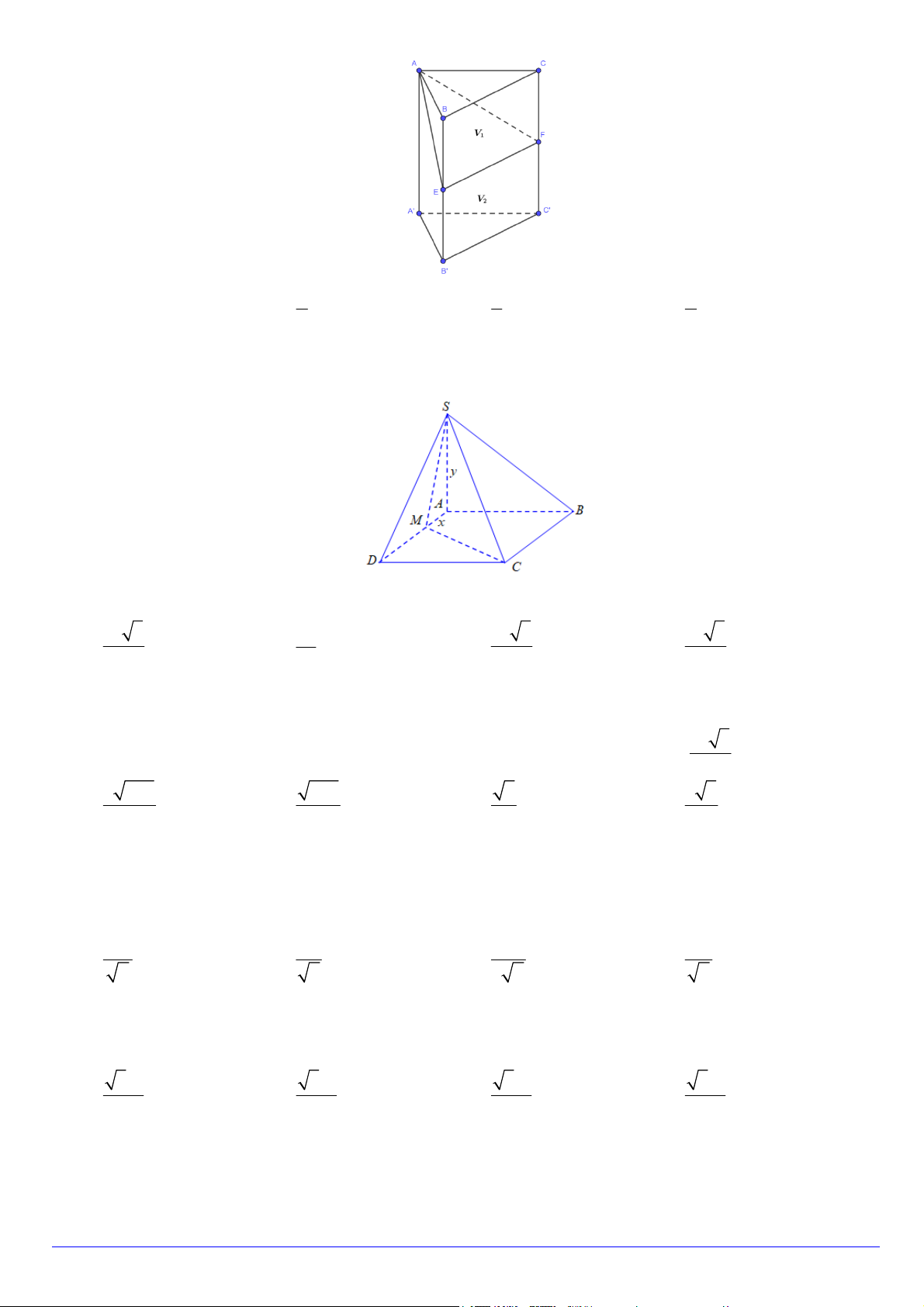
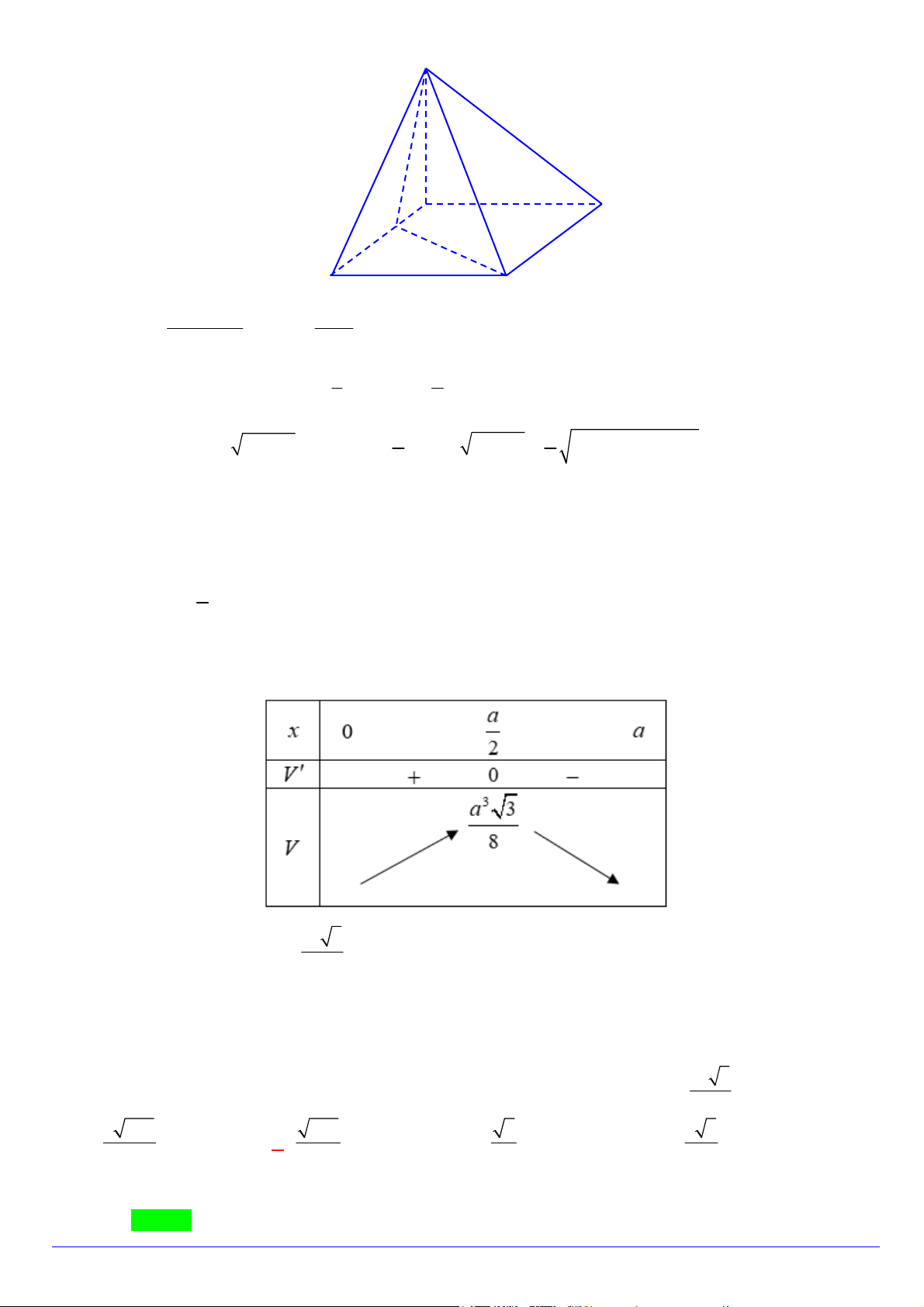
Câu 22. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a . Cạnh SA vuông góc với đáy và
SA y . Trên cạnh AD lấy điểm M sao cho AM x . Biết rằng 2 2 2
x y a . Tìm giá trị lớn nhất của thể tích khối chóp S.ABCM . 3 a 3 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 2 8 8 4
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD  2AB  2BC  2CD  2a . Hai mặt
phẳng SAB và SAD cùng vuông góc với mặt phẳng  ABCD . Gọi M, N lần lượt là trung điểm của SB 3 a 3
và CD . Tính cosin góc giữa MN và SAC , biết thể tích khối chóp S.ABCD bằng . 4 3 310 310 5 3 5 A. . B. . C. . D. . 20 20 10 10 
Câu 24. Cho hình lăng trụ ABC. 
A BC có đáy ABC là tam giác vuông tại A , cạnh BC  2a và ABC 60  . 
Biết tứ giác BCC 
B là hình thoi có BBC nhọn. Biết BCCB vuông góc với  ABC và   ABB A  tạo với
ABC góc 45 . Thể tích của khối lăng trụ ABC. 
A BCbằng 3 6a 3 a 3 a 3 3a A. . B. . C. . D. . 7 7 3 7 7
Câu 25. Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a , tam giác SBA vuông tại B , tam giác
SAC vuông tại C . Biết góc giữa hai mặt phẳng SAB và  ABC bằng 60 . Tính thể tích khối chóp
S.ABC theo a . 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 8 12 6 4
------------- HẾT -------------
Trang 3/3 - Mã đề 178 - https://toanmath.com/
TRƯỜNG THPT NGUYỄN BỈNH KHIÊM
ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC CHƯƠNG 1 TỔ TOÁN
NĂM HỌC 2019 – 2020 Môn: Toán 12 ĐỀ CHÍNH THỨC
Thời gian: 45 phút (không kể thời gian phát đề) Mã đề thi 178
Họ và tên: …………………………………………………………. Lớp: ……………
Câu 1. Hình nào dưới đây không phải là hình đa diện?
Hình nào dưới đây không phải là hình đa diện? A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 2. Cho một hình đa diện. Trong các khẳng định sau, khẳng định nào sai?
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.
B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
C. Mỗi mặt có ít nhất ba cạnh.
D. Mỗi cạnh là cạnh chung của ít nhất ba mặt.
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Cạnh bên SA vuông góc với  ABCD . Phép
đối xứng qua mặt phẳng SAC biến khối chóp S.ABC thành khối chóp nào?
A. S.CBD .
B. S.ABC .
C. S.ADC .
D. S.ABD .
Câu 4. Số mặt phẳng đối xứng của hình hộp chữ nhật mà không có mặt nào là hình vuông là: A. 3 . B. 12 . C. 9 . D. 6 .
Câu 5. Số mặt phẳng đối xứng của hình chóp tứ giác đều là: A. 2 . B. 4 . C. 8 . D. 6 .
Câu 6. Cho các hình khối sau: Hình 1 Hình 2 Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số khối đa diện lồi là: A. 4 . B. 2 . C. 1. D. 3 .
Câu 7. Khối hai mươi mặt đều là khối đa diện đều loại: A. 3;  5 . B. 2;  4 . C. 4;  3 . D. 5;  3 .
Câu 8. Khẳng định nào sau đây sai?
A. Số cạnh của một khối đa diện đều luôn là số chẵn.
B. Tồn tại một khối đa diện đều có số cạnh là số lẻ.
C. Số mặt của một khối đa diện đều luôn là số chẵn.
D. Số đỉnh của một khối đa diện đều luôn là số chẵn.
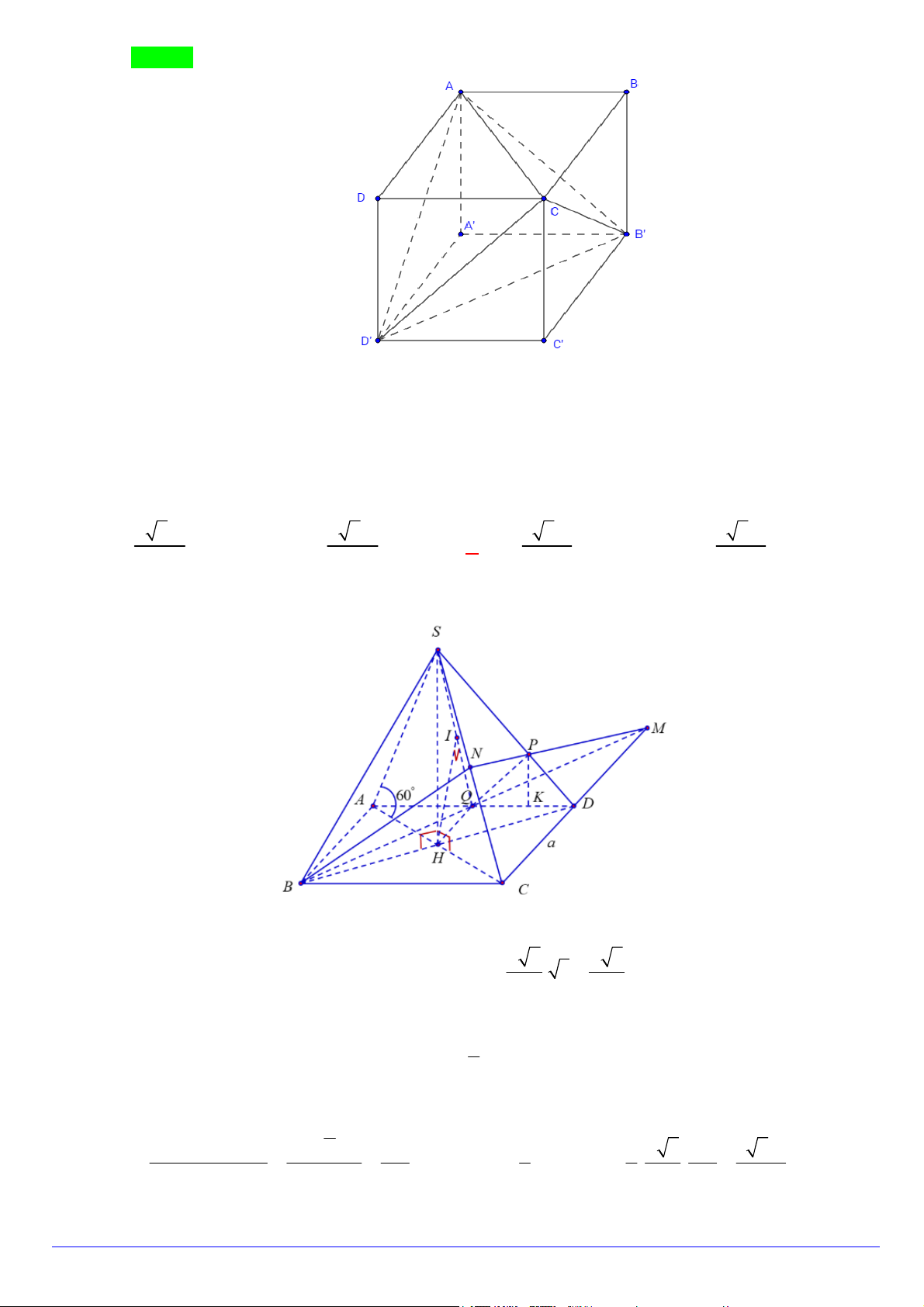
Câu 9. Nếu không sử dụng thêm điểm nào khác ngoài các đỉnh của hình lập phương thì có thể chia hình lập phương thành
A. Bốn tứ diện đều và một hình chóp tam giác đều.
B. Năm hình chóp tam giác đều, không có tứ diện đều.
C. Một tứ diện đều và bốn hình chóp tam giác đều.
D. Năm tứ diện đều. Lời giải
Trang 1/8 - Mã đề 178 - https://toanmath.com/ Chọn C
Hình tứ diện đều là ACB D   .
Bốn hình chóp tam giác đều là .
D ACD , C .CB D   , .
B ACBA .AB D  .
Câu 10. Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với đáy một góc 60 . Gọi
M là điểm đối xứng với C qua D , N là trung điểm SC . Mặt phẳng BMN  chia khối chóp S.ABCD
thành hai khối đa diện. Tính thể tích V của khối đa diện chứa đỉnh C . 3 7 6a 3 7 6a 3 5 6a 3 5 6a A. V  . B. V  . C. V  . D. V  . 36 72 72 36 Lời giải Chọn C
Gọi P MN SD , Q BM AD . Suy ra BNPQ là thiết diện của BMN  với hình chóp S.ABCD . Gọi H a a
là tâm của đáy, ta có: SH   ABCD 2 6
SH AH.tan 60  . 3  . 2 2 Ta có: VVV . CDPQBN N .BCDQ N .DPQ
Do N là trung điểm của SC , suy ra d N BCDQ 1 ,  SH . 2
Ta lại có: M là điểm đối xứng với C qua D , suy ra Q là trung điểm của AD .  a    BC DQa .a   2 .CD  2  3a 2 3 1 1 a 6 3a 3 6a nên S    ,  V  .SH.S  . .  . BCDQ 2 2 4 N .BCDQ 6 BCDQ 6 2 4 48
Ta có: d N,DPQ  d H,SAD .
Trang 2/8 - Mã đề 178 - https://toanmath.com/
Mà HQ AD , kẻ HI SQ  I  d H,SAD  HI . 1 1 1 2 4 14      3  HI  .a . 2 2 2 2 2 2 HI SH HQ 3a a 3a 14
Xét SCM , có N và D là trung điểm của SC và CM suy ra P là trọng tâm SCM . 2 2 3a a  1 2 2   SQ SH HQ 2 4 a 7
DP SD . Kẻ PK DQ  K, PK     . 3 3 3 3 6 2 1 1 a a 7 a 7 2 3 1 3 a 7 a 6 Suy ra: SD . Q PK  . .  ,  V  . . . a  . DPQ 2 2 2 6 24 N .DPQ 3 14 24 144 3 3 3 3 6a a 6 5a 6 Vậy V    . CDPQBN 48 144 72
Câu 11. Khối chóp có một nửa diện tích đáy là S , chiều cao là 2h thì có thể tích là: 4 1 1
A. V S.h .
B. V S.h .
C. V S.h .
D. V S.h . 3 3 2
Câu 12. Tính thể tích của khối lăng trụ biết diện tích đáy là 2
2a và chiều cao là 3a . 2 A. 3
V a . B. 3
V  3a . C. 3
V  2a . D. 3
V  6a . 3
Câu 13. Cho hình hộp chữ nhật ABC . D AB CD
  có AB  2 cm, AD  3 cm, AA  7 cm. Tính thể tích khối hộp ABC . D AB CD   . A. 12 3 cm . B. 42 3 cm . C. 24 3 cm . D. 36 3 cm . V
Câu 14. Cho hình chóp S.ABC có M là trung điểm của cạnh SC . Khi đó SABM bằng: VCABM 1 1 A. . B. . 1 C. . D. 2 . 3 2
Câu 15. Tính thể tích của khối tứ diện đều có tất cả các cạnh đều bằng 1. 2 3 2 3 A. . B. . C. . D. . 12 12 4 4 2 3a
Câu 16. Cho hình chóp tam giác đều có diện tích đáy bằng
, chiều cao hình chóp gấp đôi độ dài cạnh 4
đáy . Tính thể tích V của khối chóp. 3 a 3 a 3 3 a 3 3 a A. V  . B. V  . C. V  . D. V  . 4 6 12 12
Câu 17. Tính thể tích V của lập phương ABCD.AB CD
 , biết AC a 3 . 3 3 6a 3 a A. 3
V  3 3a . B. 3
V a . C. V  . D. V  . 4 3
Câu 18. Cho một khối lăng trụ có thể tích là 3
a 3 , đáy là tam giác đều cạnh a . Tính chiều cao h của khối lăng trụ.
A. h  4a .
B. h  3a .
C. h  2a .
D. h a . 3 a 2
Câu 19. Cho hình chóp S.ABC có V
và mặt bên SBC là tam giác đều cạnh . a Khoảng cách từ S.ABC 36
A đến SBC bằng: a 2 a 6 a 6 a 6 A. . B. . C. . D. . 9 3 9 27
Câu 20. Cho lăng trụ đứng ABC.A BC
  có đáy là tam giác vuông cân tại A , AB AC a 2 . Biết AB tạo
với đáy góc 60 . Thể tích khối lăng trụ là
Trang 3/8 - Mã đề 178 - https://toanmath.com/ 3 5a 3 3a 3 A. . B. . C. 3 4a 6. D. 3 a 6. 3 2
Câu 21. Cho hình lăng trụ ABC.AB C
  . Gọi E , F lần lượt là trung điểm của BB và CC . Mặt phẳng AEFV
chia khối lăng trụ thành 2 phần có thể tích V và V như hình vẽ. Tính 1 . 1 2 V2 1 1 1 A. . 1 B. . C. . D. . 4 3 2 Lời giải Chọn D
Gọi V là thể tích khối lăng trụ ABC.AB C  . Ta có: 1 1 1  1  1 2 1 1 2 V V      
V V V V V V   V V    V V . V V . 1 A.BCB CA.A B C    2 2 2  3  2 3 3 2 1 3 3 V 1 2 1
Do đó: 1  V : V  . V 3 3 2 2
Câu 22. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a . Cạnh SA vuông góc với đáy và
SA y . Trên cạnh AD lấy điểm M sao cho AM x . Biết rằng 2 2 2
x y a . Tìm giá trị lớn nhất của thể tích khối chóp S.ABCM . 3 a 3 3 a 3 a 3 3 a 3 A. . B. . C. . D. . 2 8 8 4 Lời giải Chọn A.
Trang 4/8 - Mã đề 178 - https://toanmath.com/ S y A B M x D C AM BC a x Ta có S   AB a  . ABCM 2 2 1 a
Thể tích khối chóp S.ABCM là V S . A Sy a x . ABCM   3 6 a a Do 2 2 2
x y a  2 2
y a x ,suy ra V  a xa x  a x2 2 2  2 2 a x  . 6 6
Xét hàm số      2  2 2 f x a x
a x  với 0  x a .
Ta có f  x  a xa x   xa x2 2 2
  a x 2 2 2 2 2
2x ax a   a x
f  x  0   2  x  a Bảng biến thiên 3 a 3
Từ bảng biến thiên suy ra V  . max 8
Câu 23. Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD  2AB  2BC  2CD  2a . Hai mặt
phẳng SAB và SAD cùng vuông góc với mặt phẳng  ABCD . Gọi M, N lần lượt là trung điểm của SB 3 a 3
và CD . Tính cosin góc giữa MN và SAC , biết thể tích khối chóp S.ABCD bằng . 4 3 310 310 5 3 5 A. . B. . C. . D. . 20 20 10 10 Lời giải Chọn B
Trang 5/8 - Mã đề 178 - https://toanmath.com/ S M Q A I H D N K B C
Gọi   là mp đi qua MN và song song với mp SAD . Khi đó   cắt AB tại P , cắt SC tại Q ,
cắt AC tại K . Gọi I là giao điểm của MN và QK I SAC  .
Suy ra: P , Q , K lần lượt là trung điểm của AB , SC và AC .
Lại có: ABCD là hình thang cân có AD  2AB  2BC  2CD  2a AD  2 ;
a AB BC CD a 2  a 3 a  2a a 3 3 3a CH  ; S  .  . 2 ABCD 2 2 4 2 3 1 3 3a a 3 a 3a Nên V  . .SA   SA  1
a MP SA  và NP  . ABCD 3 4 4 2 2 2 2 2  a   3a a 10
Xét tam giác MNP vuông tại P: MN         2   2  2 M ,
P KQ lần lượt là đường trung bình của tam giác SA  , B S
AC MP//KQ//SA 1
KN là đường trung bình của tam giác ACD KN AD a . 2 2 2
a 3   3a a 3
Xét tam giác AHC vuông tại H: AC      a 3      KC  2    2  2
Suy ra: tam giác KNC vuông tại C C là hình chiếu vuông góc của N lên SAC.
 góc giữa MN và SAC là góc  NIC IN KN 2 2 2 a 10 a 10 Khi đó: 
  IN  .MN  .  MN NP 3 3 3 2 3 2 a a 10 2
a 10   a a 31
Xét tam giác NIC vuông tại C : NC  ; IN   IC          2 3 3    2  6   IC a 31 a 10 310 cos NIC   :  . IN 6 3 20
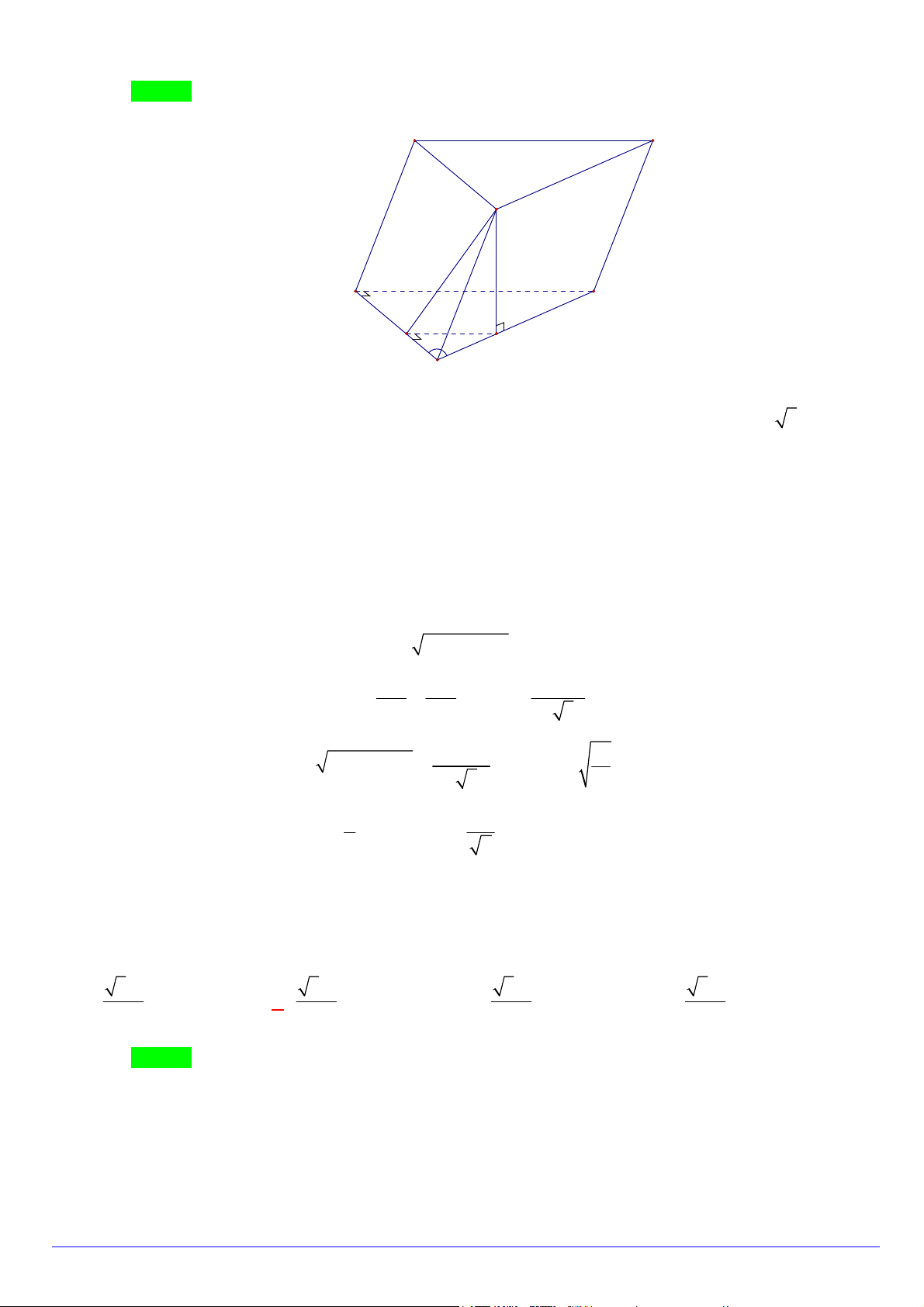
Câu 24. Cho hình lăng trụ ABC. 
A BC có đáy ABC là tam giác vuông tại A , cạnh BC  2a và ABC 60  . 
Biết tứ giác BCC 
B là hình thoi có BBC nhọn. Biết BCCB vuông góc với  ABC và   ABB A  tạo với
ABC góc 45 . Thể tích của khối lăng trụ ABC. 
A BCbằng 3 6a 3 a 3 a 3 3a A. . B. . C. . D. . 7 7 3 7 7
Trang 6/8 - Mã đề 178 - https://toanmath.com/ Lời giải Chọn B A' C' B' A 2a C 2a K 60 H B
Do ABC là tam giác vuông tại ,
A cạnh BC  2a và 
ABC  60 nên AB a , AC a 3 .
Gọi H là hình chiếu vuông góc của B lên BC H thuộc đoạn BC (do   B BC nhọn)
BH   ABC (do BCCB vuông góc với  ABC ).
Kẻ HK song song AC K AB  HK AB (do ABC là tam giác vuông tại A ).    ABB 
A   ABC    ,
BKH  45  BH KH (1)  
Ta có BBH vuông tại H 2 2
BH  4a BH (2) BH HK .2
Mặt khác HK song song AC     HK a BH (3) BC AC a 3  .2 12 Từ (1), (2) và (3) suy ra 2 2 4    B H a a B H
BH a . a 3 7 3 1 3a Vậy VS
BH AB AC BH  . ABC A B C . . . . ' ' ABC 2 7
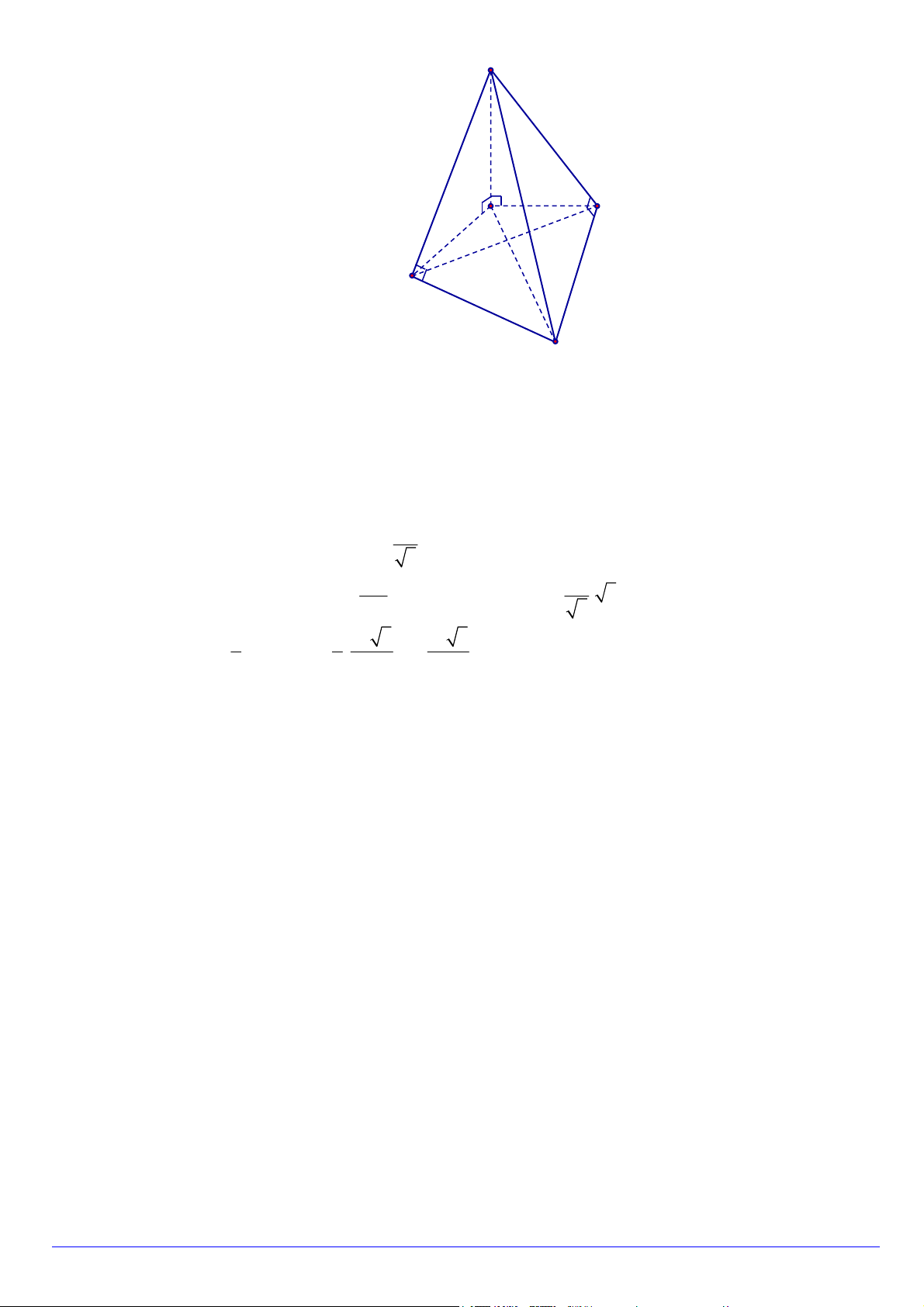
Câu 25. Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a , tam giác SBA vuông tại B , tam giác
SAC vuông tại C . Biết góc giữa hai mặt phẳng SAB và  ABC bằng 60 . Tính thể tích khối chóp
S.ABC theo a . 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 8 12 6 4 Lời giải Chọn B
Trang 7/8 - Mã đề 178 - https://toanmath.com/ S D C B A
Gọi D là hình chiếu của S lên mặt phẳng  ABC  , suy ra SD   ABC  .
Ta có SD AB và SB AB (gt) , suy ra AB  SBD  BA BD .
Tương tự có AC DC hay tam giác ACD vuông ở C . Dễ thấy SBA   S
CA (cạnh huyền và cạnh góc vuông), suy ra SB SC . Từ đó ta chứng minh được SBD S
CD nên cũng có DB DC .
Vậy DA là đường trung trực của BC , nên cũng là đường phân giác của góc  BAC . a Ta có 
DAC  30 , suy ra DC
. Ngoài ra góc giữa hai mặt phẳng SAB và  ABC  là 3  SD a SBD  60 , suy ra   tan SBD
SD BD tan SBD  . 3  a . BD 3 2 3 1 1 a 3 a 3 Vậy V  .S .SD  . .a  . S.ABC 3 ABC 3 4 12
------------- HẾT -------------
Trang 8/8 - Mã đề 178 - https://toanmath.com/
Document Outline

  • aaĐề gốc có lời giải chi tiết
  • Đề gốc có lời giải chi tiết