Đề kiểm tra học kì 1 Toán 9 năm 2022 – 2023 phòng GD&ĐT Gia Lâm – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề kiểm tra chất lượng cuối học kì 1 môn Toán 9 năm học 2022 – 2023 phòng Giáo dục và Đào tạo huyện Gia Lâm. Mời bạn đọc đón xem.
Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KÌ I LỚP 9 HUYỆN G IA LÂM NĂM HỌC 2022-2023 MÔN: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút x 8 2 x 8
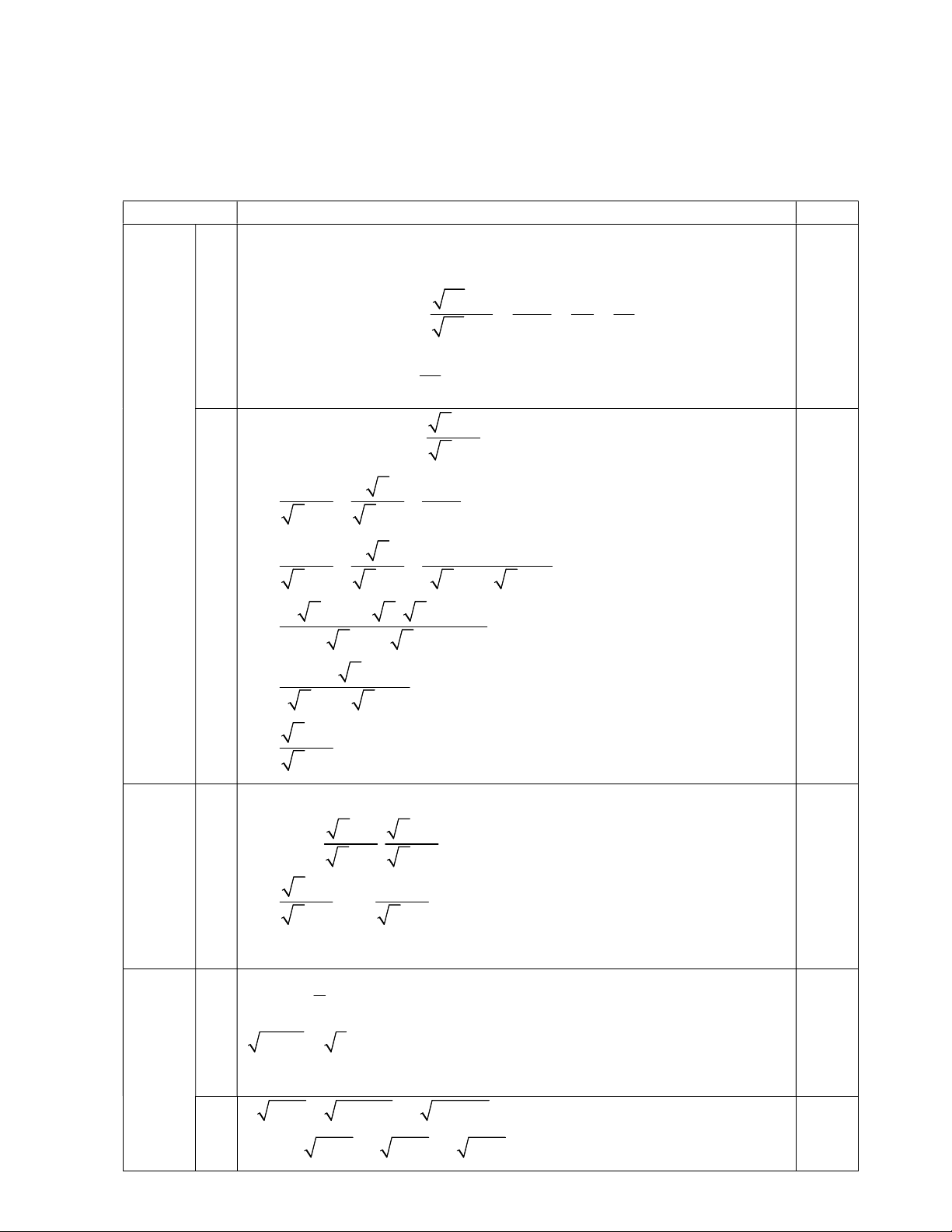
Bài I (2,0 điểm). Cho 2 biểu thức: A và B với x 0; x 4 . x 2 x 2 x 2 4 x
a) Tính giá trị của A tại x 36; x 2 b) Chứng minh rằng B ; x 2 c) Cho P .
A B . Tìm giá trị nguyên của x để P nhận giá trị nguyên.
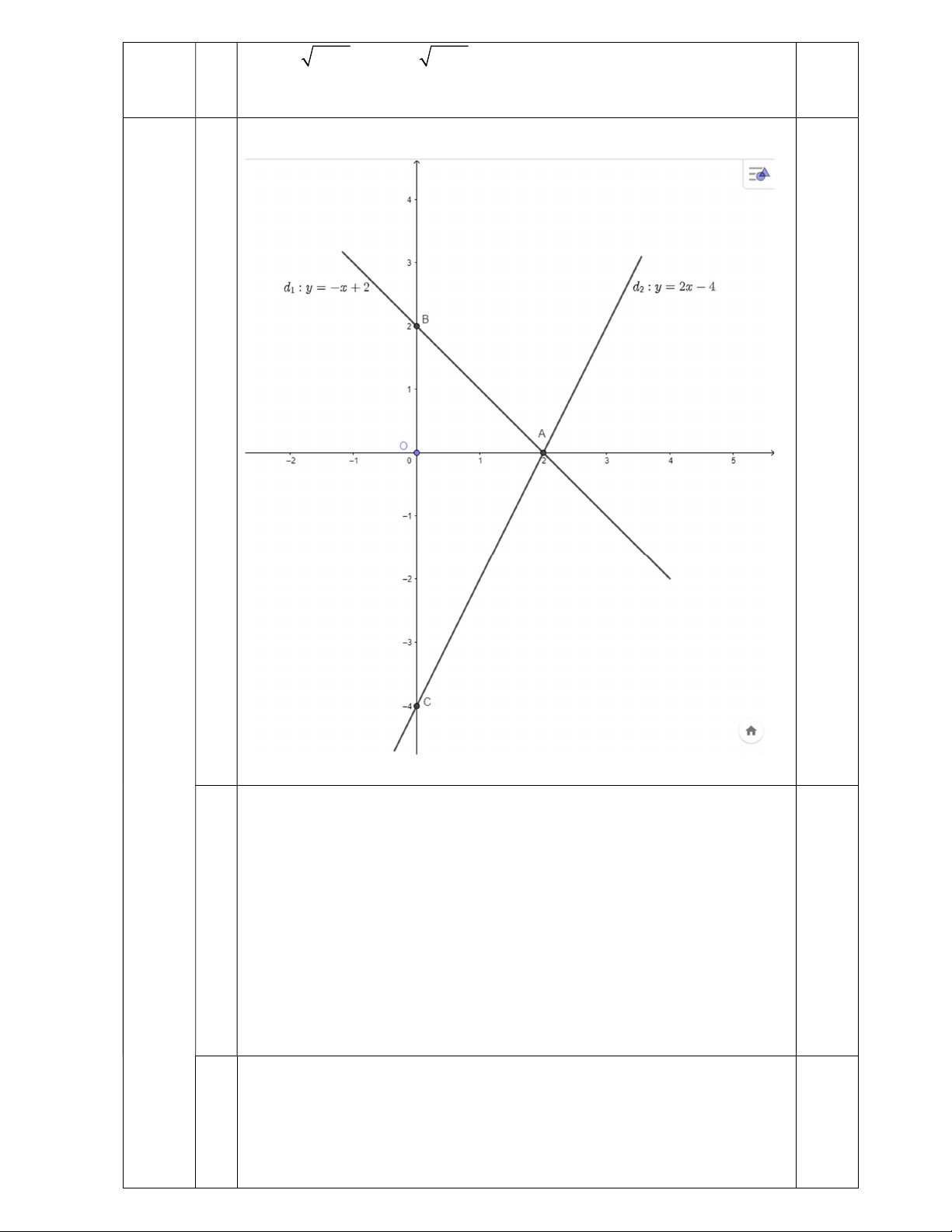
Bài II (1,5 điểm). Giải phương trình: a) 2x 1 5 ;
b) 6 x 5 9x 45 2 4x 20 25 .
Bài III (2,5 điểm). Cho đường thẳng 1
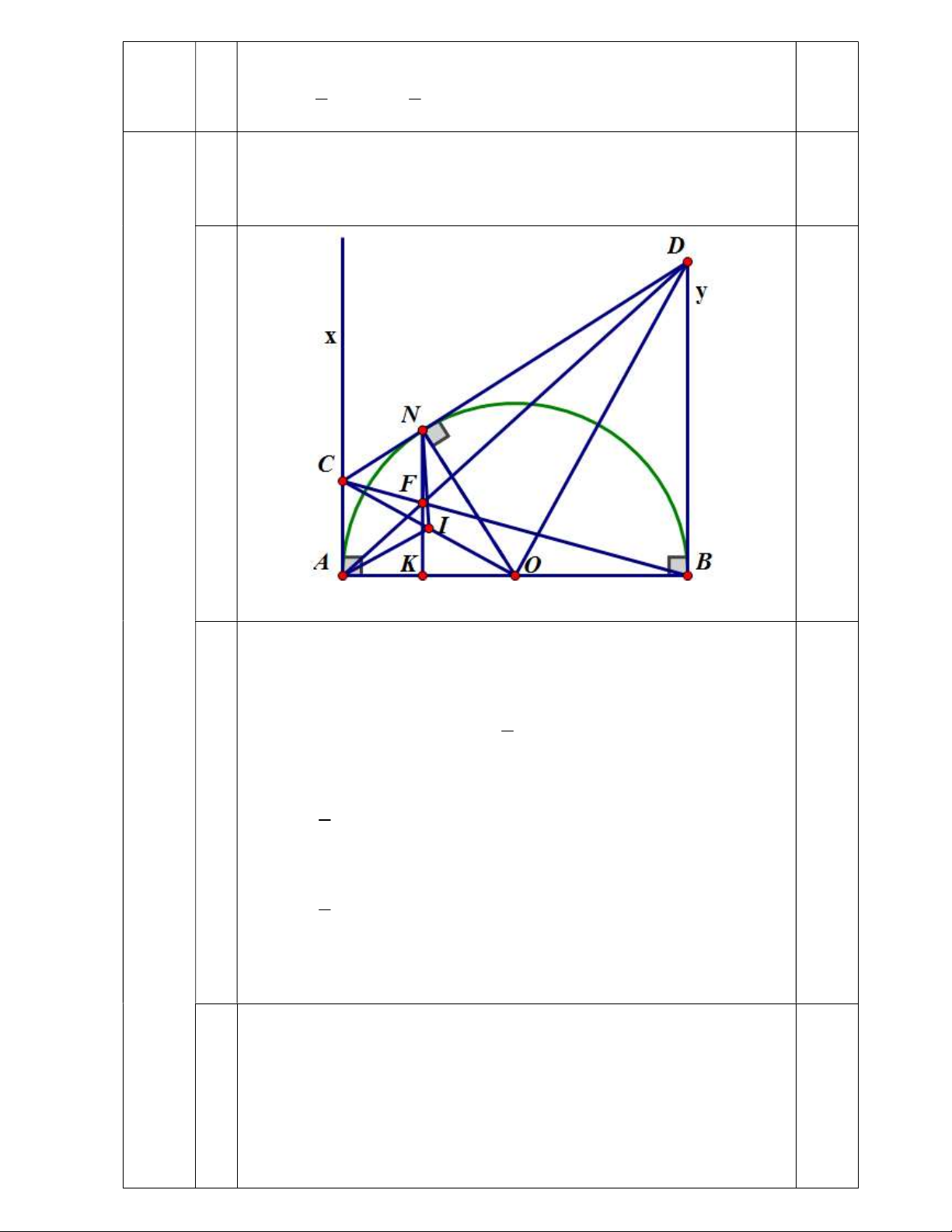
d : y x 2 và d : y 2x 4 . 2
a) Vẽ hai đường thẳng d , d trên cùng một mặt phẳng tọa độ; 2 1
b) Tìm toạ độ giao điểm A của hai đường thẳng trên;
c) Gọi B là giao điểm của đường thẳng 1
d với trục tung, C là giao điểm của đường thẳng
d2với trục tung. Tính diện tích ABC (đơn vị trên các trục tọa độ là centimet). Bài IV (3,5 điểm).
1) Hãy tính chiều cao của tháp Eiffel mà không cần
lên tận đỉnh tháp khi biết góc tạo bởi tia nắng mặt
trời với mặt đất là 62o và bóng của tháp trên mặt
đất là 172 m (làm tròn kết quả đến chữ số thập phân thứ nhất).
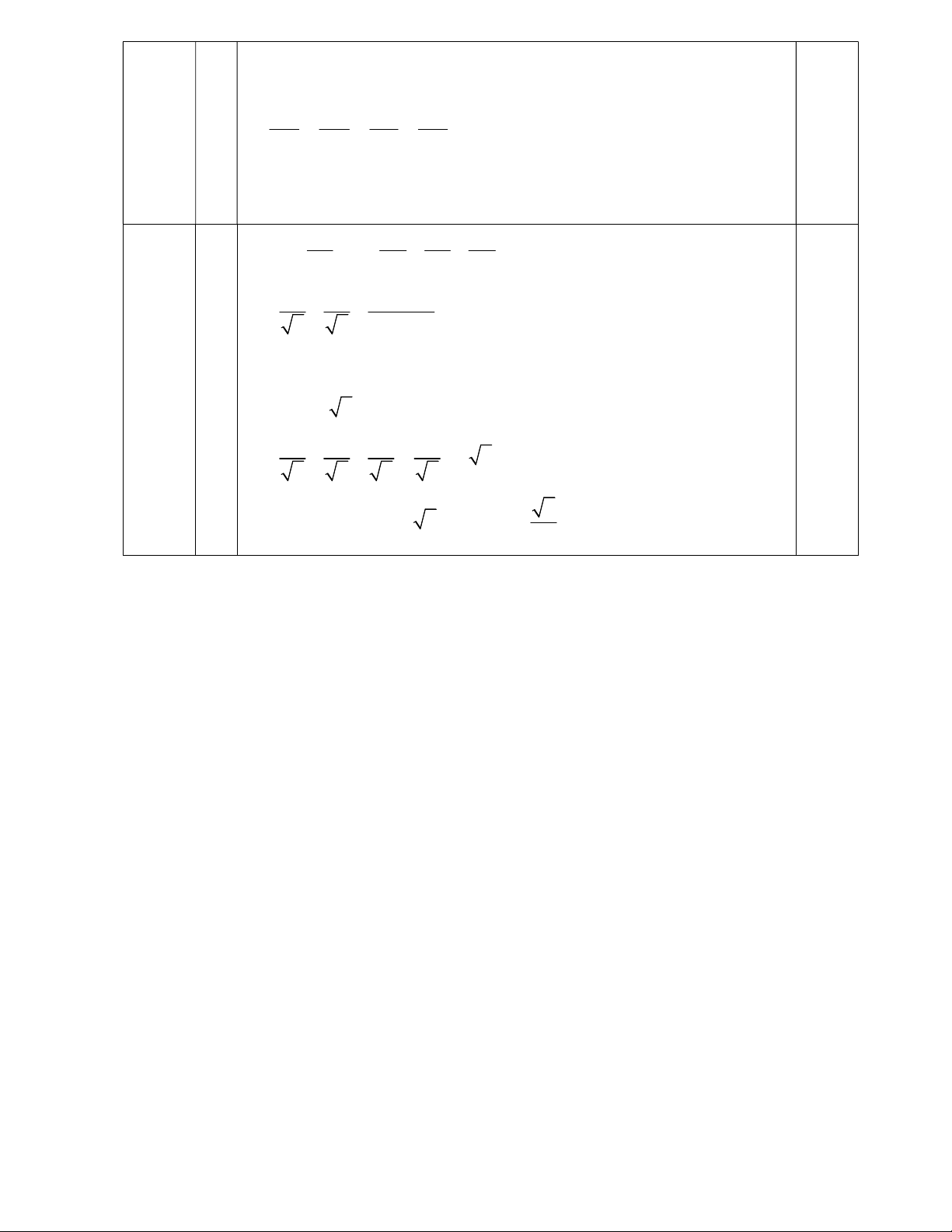
2) Cho điểm N thuộc nửa đường tròn (O; R) đường kính AB. Trên nửa mặt phẳng bờ AB chứa
điểm N, kẻ các tia tiếp tuyến Ax, By với nửa đường tròn. Tiếp tuyến tại N của nửa đường tròn cắt tia Ax tại C.
a) Chứng minh rằng 4 điểm A, C, O, N cùng thuộc một đường tròn. Chỉ rõ tâm đường đó;
b) Tiếp tuyến tại N cắt tia By tại D. Chứng minh AC + BD = CD và ∆COD vuông tại O;
c) Gọi F là giao điểm của AD và BC, K là giao điểm của NF và AB. Chứng minh rằng F là trung điểm NK.
Bài V (0,5 điểm). Cho x, y dương thỏa mãn 2 2
x y 1. Tìm giá trị nhỏ nhất của biểu thức: 1 1 P x y . x y
..........................................HẾT..........................................
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN VÀ BIỂU ĐIỂM CHẤM HUYỆN GIA LÂM
ĐỀ KIỂM TRA HỌC KÌ I LỚP 9 Môn: Toán NĂM HỌC 2022-2023
Thời gian làm bài: 90 phút Bài Đáp án Điểm I
Tính giá trị của A tại x = 36. (2,0đ)
Thay x = 36 (TM ĐKXĐ) vào biểu thức A ta có: 0,25 36 8 6 8 2 1 a A 36 2 6 2 8 4 1 Vậy với x = 36 thì A . 0,25 4 x 2 Chứng minh rằng B . x 2 2 x 8 B x 2 x 2 4 x 2 x 8 0,25 B x 2 x 2 ( x 2)( x 2) b 0,25
2( x 2) x( x 2) 8 B ( x 2)( x 2) 0,25 x 4 x 4 B ( x 2)( x 2) x 2 0,25 B x 2
Cho P = A. B. Tìm giá trị nguyên của x để P nhận giá trị nguyên. x 8 x 2 P AB . x 2 x 2 c 0,25 x 8 6 P 1 x 2 x 2
Lập luận được P nguyên khi x ∈ {0; 1; 9; 16; 25; 64}. 0,25 II 1 (1,5đ) ĐK: x 2 0,25 a
2x 1 5 2x 1 5 x 3 Kết hợp ĐK: x 3. 0,25
6 x 5 9x 45 2 4x 20 25 (*) (Điều kiện: x 5) 0,25 b
(*) 6 x 5 3 x 5 4 x 5 25 0,25
5 x 5 25 x 5 5 x 5 25 x 30(nhận) 0,25
Vậy tập nghiệm phương trình: S 3 0 . 0,25 III
Vẽ hai đường thẳng d , d trên cùng một mặt phẳng tọa độ. 2 1 (2,5đ) a Vẽ 2 đồ thị đúng 1,0
Xác định tọa độ giao điểm A của d2 1 d và
Xét phương trình hoành độ giao điểm của 1 d và d2 : x 2 2x 4 x 2x 4 2 b 3x 6 x 2 0,25 Thay x 2 vào 1
d ta có y 2 2 0 0,25
Vậy tọa độ giao điểm của 2 đường thẳng là A2;0 . c Tính diện tích ABC
Xác định tọa độ A2;0, B0;2, C 0; 4 0,5
Tính được cạnh BC 6, AO 2 0,25
Tính được diện tích tam giác ABC : 1 1 S .A . O BC .2.6 6 ABC 2 cm . 0,25 2 2 IV
Lập luận dẫn đến BH = AH. tan62o (3,5đ) 0,25
1 Tính được BH = 172.tan62o 323,5 m 0,25 Kết luận. 2 0,25
Vẽ hình đúng đến câu 1
Chứng minh rằng 4 điểm A, C, O, N cùng thuộc một đường tròn.
Chỉ rõ tâm đường đó.
Chứng minh ∆CNO, ∆CAO vuông lần lượt tại N, A 0,5 1
I là trung điểm CO => IC = IO = OC 0,25 2
+) ∆CNO vuông tại N có đường trung tuyến NI 2a 1 0,25 => NI = OC 2
+) ∆CAO vuông tại A có đường trung tuyến AI 0,25 1 => AI = OC 2 0,25
=> IC = IO = IA = IN. => 4 điểm C, O, A, N thuộc (I) Kết luận.
Chứng minh AC + BD = CD và ∆COD vuông tại O
Nêu tính chất 2 tiếp tuyến cắt nhau CA, CN; DN,DB 0,25 Chứng minh được: 2b +) AC + BD = CD 0,25
+) góc COD = 90° ∆COD vuông tại O 0,25 Kết luận.
Chứng minh rằng F là trung điểm NK +) NK // AC // BD 0,25 NF DF FB FK 2c +) AC AD BC AC 0,25 NE = FK, F thuộc NK F là trung điểm NK. V 1 1 1 1 (0,5đ) P x y 2.x 2.y 2.x 2.y 2 2 4 P 0,25 2 2 2 x y 2 2
2 x y x y2 x y 2 2 2 2 6 P 3 2 0,25 2 2 2 2 2
Vậy GTNN của P 3 2 tại x y . 2