Đề Kiểm Tra Kiến Thức Toán Lớp 12 Năm 2022 Chuyên Đại Học KHTN Hà Nội Có Lời Giải Chi Tiết

Đề kiểm tra kiến thức Toán lớp 12 năm học 2022 chuyên Đại học KHTN Hà Nội được biên soạn dưới dạng file PDF gồm 25 trang. Tài liệu là toàn bộ kiến thức môn Toán chuyên Đại học KHTN năm học 2022.  Đề thi có sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

25 trang 8 tháng trước

Tác giả:

Profile ha phan
Trang1
TRƯỜNG ĐẠI HỌC KHOA HỌC TỰ NHIÊN
TRƯỜNG THPT CHUYÊN KHTN-HÀ NỘI
ĐỀ KIỂM TRA KIẾN THỨC LỚP 12
NĂM HỌC 2021 – 2022
Câu 1: Tìm
2
sin 2 dxx
A.
sin 4
8
x
C
. B.
sin 4
28
xx
C
. C.
3
cos 3
3
x
C
. D.
sin 4
28
xx
C
.
Câu 2: Có bao nhiêu giá trị nguyên của
m
để hàm số
đồng biến trên
1; 
A.
1
. B.
2
. C.
4
. D.
3
.
Câu 3: Trên mặt phẳng tọa độ
,Oxy
điểm biểu diễn số phức
( )
3
1zi=+
là
A.
( )
2;2-
. B.
( )
2; 2-
. C.
( )
2;2
. D.
( )
2;4-
.
Câu 4: Có bao nhiêu số tự nhiên chẵn gồm 3 chữ số đôi một khác nhau và không có chữ số nào lớn
hơn 5.
A.
75
. B.
90
. C.
52
. D.
60
.
Câu 5: Tính thể tích khối chóp tứ giác đều có cạnh đáy bằng
2a
và có mặt bên tạo với đáy một góc
bằng
60°
.
A.
3
4
3
a
. B.
3
43
3
a
C.
3
4
33
a
. D.
3
43a
.
Câu 6: Tìm
3
23
2 1 dx x x
A.
4
3
21
24
x
C
. B.
4
3
21
24
x
C
. C.
4
3
21
24
x
C
. D.
4
3
21
24
x
C
.
Câu 7: Tổng tất cả các nghiệm của phương trình
2
22
log 1 2 logx x x
bằng?
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 8: Biết rằng phương trình
3
1
1
2
22
x
x



có một nghiệm thực duy nhất. Nghiệm đó thuộc
khoảng nào dưới đây?
A.
6; 5
. B.
0;1
. C.
2; 1
. D.
1;0
.
Câu 9: Cho
1
2
0
2 3 d 1x x f x x
. Tính
1
0
df x x
.
A.
1
3
. B.
5
3
. C.
1
9
. D.
5
9
.
Câu 10: Cho hai số phức
12zi
và
34wi
. Tính
.wz
.
A.
125
. B.
5
. C.
5
. D.
55
.
Câu 11: Viết phương trình mặt cầu tâm
1; 2;0I
và tiếp xúc với mặt phẳng
: 2 2 1 0P x y z
A.
22
2
1 2 4x y z
. B.
22
2
1 2 4x y z
.
C.
22
2
1 2 2x y z
. D.
22
2
1 2 2x y z
.
Trang2
Câu 12: Trong không gian với hệ trục tọa độ
Oxyz
, cho tứ diện
ABCD
với
1;0;0A
,
0;2;0B
,
0;0;3C
,
1;2;3D
. Tìm tọa độ trọng tâm
G
của tứ diện
ABCD
.
A.
1 1 3
;;
424
G



. B.
13
;1;
22
G



. C.
24
; ;2
33
G



. D.
2;4;6G
.
Câu 13: Tính
2
2
0
2 1dx x x
.
A.
1
2
. B.
2
. C.
5
2
. D.
1
.
Câu 14: Cho hàm số
3
12 1y x x
. Điểm cực tiểu của hàm số là
A.
2
. B.
15
. C.
13
. D.
2
.
Câu 15: Số nghiệm nguyên dương của bất phưng trình
15
11
2 16
x



là
A.
15
. B.
8
. C.
16
. D.
9
.
Câu 16: Số phức liên hợp của số phức
4
1
z
i
là
A.
22i
. B.
22i
. C.
22i
. D.
22i
.
Câu 17: Một lớp học sinh có 15 học sinh nữ và 25 học sinh nam. Giáo viên chủ nhiệm cần chọn ban cán
sự lớp gồm 3 học sinh. Tính xác suất để ban cán sự có cả nam và nữ.
A.
251
1976
. B.
2625
9880
. C.
1425
1976
. D.
450
988
.
Câu 18: Cho hàm số
3
31y x x
. Viết phương trình tiếp tuyến với đồ thị tại giao điểm của đồ thị
hàm số với trục tung.
A.
1y
. B.
31yx
. C.
31yx
. D.
31yx
.
Câu 19: Thể tích của khối trụ có bán kính đáy bằng
2
, độ dài đường sinh bằng
22
A.
8
. B.
4
. C.
42
. D.
82
.
Câu 20: Viết phương trình đường thẳng đi qua hai điểm
2;1; 3A
,
3;0;1B
A.
4
1
54
xt
yt
zt



. B.
2
1
34
xt
yt
zt


. C.
3
14
xt
yt
zt


. D.
4
1
54
xt
yt
zt


.
Câu 21: Có bao nhiêu giá trị nguyên của
m
để phương trình sau là phương trình mặt cầu:
2 2 2 2
2 4 6 10 0x y z x z m m
.
A.
5
. B.
0
. C.
2
. D.
3
.
Câu 22: Người thợ làm một bể cá hai ngăn không nắp với thể tích
3
1296 dm
. Người thợ này cắt các tấm
kính ghép lại một bể cá dạng hình hộp chữ nhật với ba kích thước
,,abc
(mét) để đỡ tốn kính
nhất như hình vẽ và giả thiết rằng độ dày của kính không đáng kể. Tính
abc
Trang3
A.
3,3
. B.
3,6
. C.
4,8
. D.
3,9
.
Câu 23: Biết
1
1
d6f x x
, tích phân
1
0
2 1 df x x
bằng
A. 3. B. 6. C. 12. D. 2.
Câu 24: Cho số phức
4
1zi
. Tìm phần ảo của số phức
w iz
A.
4
. B.
4
. C.
4i
. D.
4i
.
Câu 25: Đồ thị hàm số nào sau đây không cắt trục hoành?
A.
3
52y x x
. B.
42
33y x x
. C.
1
2
x
y
x
. D.
3
31y x x
.
Câu 26: Hàm số
2
2lny x x
đồng biến trên khoảng nào dưới đây?
A.
1;0
. B.
0;1
. C.
1;2
. D.
1;1
Câu 27: Viết phương trình đường thẳng đi qua
1; 2;0A
và vuông góc với mặt phẳng
: 2 2 1 0P x y z
A.
2 2 3 0x y z
. B.
12
1 2 2
x y z

. C.
12
1 2 2
x y z

. D.
2 2 5 0x y z
Câu 28: Cho hình chóp
.S ABC
có
; 3 ; 2 ; 2AB a BC a CA a SA SB SC a
. Tính thể tích khối
chóp
.S ABC
A.
3
26
24
a
. B.
3
26
12
a
. C.
3
26
4
a
. D.
3
26
8
a
Câu 29: Cho cấp số cộng
n
u
thỏa mãn
2 9 4 6
3; 1u u u u
. Tìm công sai của cấp số cộng
n
u
A.
4
. B.
2
. C.
2
. D.
3
Câu 30: Biết rằng
3
4 2 2
a
. Giá trị của
a
bằng
A.
5
6
. B.
15
2
. C.
1
2
. D.
5
2
Câu 31: Cho
a
là số thực dương. Khi đó
3
4
log 8a
bằng
A.
2
3
log
2
a
. B.
2
33
log
22
a
. C. . D.
2
6 6log a
.
Câu 32: Viết phương trình mặt phẳng đi qua ba điểm
0,2,0 ; 3,0,0 ; 0,0,4A B C
A.
0
2 3 4
x y z
. B.
0
3 2 4
x y z
. C.
1
3 2 4
x y z
. D.
1
2 3 4
x y z
.
Câu 33: Hàm số
2
2
43
x
y
xx

có bao nhiêu đường tiệm cận?
A.
2
. B.
1
. C.
0
. D.
3
.
b
c
a
Trang4
Câu 34: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2a
, mặt bên
SAB
là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ
A
đến mặt phẳng
SCD
A.
2 21
7
a
. B.
14
6
a
. C.
3 14
7
a
. D.
21
6
a
.
Câu 35: Tính thể tích khối lập phương nội tiếp mặt cầu có bán kính bằng 3.
A.
18 3.
B.
12 2.
C.
24 3.
D.
54 2.
Câu 36: Cho hàm số
2 3 4
1 2 3y x x x x
. Hàm số có bao nhiêu điểm cực trị?
A.
3.
B.
4.
C.
1.
D.
2.
Câu 37: Đạo hàm của hàm số
1
2
3
x
x
y
bằng
A.
1
2
ln2 ln3 .
3
x
x
B.
1
1 .2
.
.3
x
x
x
x
C.
1
2 ln 2
.
3 ln3
x
x
D.
2
ln2 ln3 .
3
x
x
Câu 38: Cho tam giác vuông tại
A
có
3, 4AB AC
. Tính diện tích xung quanh khối nón sinh
ra khi cho tam giác
ABC
quay quanh trục
AB
.
A.
20
. B.
15
. C.
12
. D.
60
.
Câu 39: Gọi
,Mm
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
16y x x
. Tính
Mm
.
A.
88
. B.
8
. C. 0. D. 8.
Câu 40: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
2SA a
và
SA
vuông góc với đáy.
Tính
cos
với
là góc giữa hai mặt phẳng
SCD
và
ABCD
.
A.
1
5
. B.
2
5
. C.
2
3
. D.
1
3
.
Câu 41: Cho hàm số
y f x
có đồ thị như hình vẽ. Hỏi hàm số
1
2022
f f x
y
có bao nhiêu điểm
cực trị
?
A.
9
. B.
5
. C.
3
. D.
7
.
Câu 42: Cho số phức
z
thỏa mãn
1z
. Tìm giá trị lớn nhất của biểu thức
A.
8 4 2
. B.
2
. C.
2 2 2
. D.
22
.
Câu 43: Cho hàm số
fx
liên tục trên
và có đồ thị như hình vẽ. Giả sử
m
là tham số thự C. Hỏi
phương trình
f f x m
có nhiều nhất bao nhiêu nghiệm thực?
Trang5
A. 5. B. 10. C. 7. D. 12.
Câu 44: Có bao nhiêu số thực
c
để hình phẳng giới hạn bởi đồ thị hàm số
2
4y x x c
, trục hoành
và các đường thẳng
2; 4xx
có diện tích bằng
3
.
A.
3
B.
0
C.
1
D.
2
Câu 45: Cho hàm số
y f x
là hàm đa thức bậc 4. Biết hàm số
'y f x
có đồ thị
C
như hình vẽ
và diện tích của hình phẳng giới hạn bởi đò thị
C
và trục hoành bằng 9. Gọi
,Mm
lần lượt là
giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y f x
trên đoạn
3;2
. Tính
Mm
A.
16
3
. B.
32
3
. C.
27
3
D.
5
3
.
Câu 46: Trong không gian
Oxyz
cho hai đường thẳng
1
12
:;
1 2 1
x y z
d


2
2 1 1
:
2 1 1
x y z
d

và
mặt phẳng
: 2 5 0P x y z
. Lập phương trình đường thẳng
d
song song với mặt phẳng
P
và cắt
12
,dd
lần lượt tại
,AB
sao cho độ dài đoạn
AB
đạt giá trị nhỏ nhất.
A.
1 2 2
1 1 1
x y z


. B.
1 2 2
1 1 1
x y z

.
C.
1 2 2
1 1 1
x y z

. D.
1 2 2
1 1 1
x y z

.
Câu 47: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
(1; 1;3)A
và hai đurờng thã
ng :
12
4 2 1 2 1 1
: , :
1 4 2 1 1 1
x y z x y z
dd

. Viết phương trình đường thẳng
d
đi qua
điểm
A
, vuông góc với đuờng thẳng
1
d
và cắt đường thẳng
2
d
.
A.
1 1 3
2 1 1
x y z

B.
1 1 3
2 1 1
x y z

C.
1 1 3
2 1 1
x y z

D.
1 1 3
2 1 1
x y z


Câu 48: Biết rằng có đúng một số phức
z
thòa mãn
| 2 | | 2 4 |z i z i
vả
zi
zi
là số thuần ảo. Tính
tổng phần thực và phần ảo của
z
A.
4.
B.
4
. C.
1
. D.
1
.
Câu 49: Cho hàm số
()fx
có đạo hàm trên
và thỏa mãn
32
( 3 ) 2f x x x
với mọi số thực
x
.
Tính
4
2
0
. ( )dx f x x
Trang6
A.
27
4
. B.
219
8
. C.
357
4
. D.
27
8
.
Câu 50: Có bao nhiêu số nguyên dương
a
để phương trình sau có ít nhất một nghiệm thực
log
log log
1 2 2
a
xx
a a x
A.
8
. B.
1
. C. . D.
9
.
------------------------------Hết-----------------------------
BẢNG ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
D
A
C
B
B
D
D
D
D
B
B
D
A
A
C
C
B
C
D
D
B
A
A
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
C
B
B
C
A
B
C
A
A
C
_
A
A
C
A
A
C
B
A
B
B
D
C
A
D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Tìm
2
sin 2 dxx
A.
sin 4
8
x
C
. B.
sin 4
28
xx
C
. C.
3
cos 3
3
x
C
. D.
sin 4
28
xx
C
.
Lời giải
Chọn D
2
1 1 sin4
sin 2 d cos4 d
2 2 2 8
xx
x x x x C




Câu 2: Có bao nhiêu giá trị nguyên của
m
để hàm số
đồng biến trên
1; 
A.
1
. B.
2
. C.
4
. D.
3
.
Lời giải
Chọn D
2
24m
y
mx
Để hàm số đồng biến trên
1; 
thì
0y
với mọi
1;x 
.
2 4 0
21
1
m
m
m

.
Mà
1;0;1mm
Câu 3: Trên mặt phẳng tọa độ
,Oxy
điểm biểu diễn số phức
( )
3
1zi=+
là
A.
( )
2;2-
. B.
( )
2; 2-
. C.
( )
2;2
. D.
( )
2;4-
.
Lời giải
ChọnA.
Ta có:
( ) ( ) ( )
( )
( ) ( )( )
32
2
1 1 1 1 2 1 2 1 2 2 .z i i i i i i i i i= + = + + = + + + = + = - +
Vậy điểm biểu diễn số phức
z
là
( )
2;2-
.
Trang7
Câu 4: Có bao nhiêu số tự nhiên chẵn gồm 3 chữ số đôi một khác nhau và không có chữ số nào lớn
hơn 5.
A.
75
. B. . C.
52
. D.
60
.
Lời giải
Chọn C
Gọi số cần tìm có dạng
abc
Trường hợp 1: Nếu
0c =
Chọn a: 5 cách
Chọn b: 4 cách
Khi đó thành lập đc
5.4=
20
số.
Trường hợp 2: Nếu
0c ¹
Chọn
:c
có 2 cách.
Chọn
a
: 4 cách.
Chọn
b
:
4
cách.
Khi đó thành lập được
2.4.4 32=
số.
Vậy thành lập được tất cả
20 32 52+=
số.
Câu 5: Tính thể tích khối chóp tứ giác đều có cạnh đáy bằng
2a
và có mặt bên tạo với đáy một góc
bằng
60°
.
A.
3
4
3
a
. B.
3
43
3
a
C.
3
4
33
a
. D.
3
43a
.
Lời giải
Chọn B
Gọi
M
là trung điểm
.DC OM DCÞ^
Ta có:
( )
;DC OM DC SO DC SOM^ ^ Þ ^
.
( ) ( )
( )
( )
·
;;SDC ABCD SM OM SMOÞ = =
60=°
.
.tan60 3.SO OM aÞ = ° =
( )
2
2
24
ABCD
S a a==
Trang8
Vậy thể tích chóp
3
2
1 1 4 3
. .4 . 3
3 3 3
ABCD
a
V S SO a a= = =
Câu 6: Tìm
3
23
2 1 dx x x
A.
4
3
21
24
x
C
. B.
4
3
21
24
x
C
. C.
4
3
21
24
x
C
. D.
4
3
21
24
x
C
.
Lời giải
Chọn B
Đặt
3 2 2
2 1 6
6
dt
t x dt x dx x dx
Ta có
4
3
4
3
2 3 3
21
1
21
6 24 24
x
t
x x dx t dt C C

Câu 7: Tổng tất cả các nghiệm của phương trình
2
22
log 1 2 logx x x
bằng?
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn D
ĐKXĐ:
2
10
0
0
xx
x
x

Ta có
Tổng tất cả các nghiệm của phương trình
2
22
log 1 2 logx x x
bằng
3
Câu 8: Biết rằng phương trình
3
1
1
2
22
x
x



có một nghiệm thực duy nhất. Nghiệm đó thuộc
khoảng nào dưới đây?
A.
6; 5
. B.
0;1
. C.
2; 1
. D.
1;0
.
Lời giải
Chọn D
Ta có
1
3
3
1
3
2
1 3 1 2
2 2 2 1;0
2 3 11
22
x
x
x
x
xx
x



Câu 9: Cho
1
2
0
2 3 d 1x x f x x
. Tính
1
0
df x x
.
A.
1
3
. B.
5
3
. C.
1
9
. D.
5
9
.
Lời giải
Trang9
Chọn D
Ta có
1 1 1 1
22
0 0 0 0
2
2 3 1 2 3 1 3 1
3
x x f x dx x x dx f x dx f x dx
1
0
5
d
9
f x x 
Câu 10: Cho hai số phức
12zi
và
34wi
. Tính
.wz
.
A.
125
. B.
5
. C.
5
. D.
55
.
Lời giải
Chọn B
Ta có
. 1 2 3 4 11 2 5 5z w i i i
Câu 11: Viết phương trình mặt cầu tâm
1; 2;0I
và tiếp xúc với mặt phẳng
: 2 2 1 0P x y z
A.
22
2
1 2 4x y z
. B.
22
2
1 2 4x y z
.
C.
22
2
1 2 2x y z
. D.
22
2
1 2 2x y z
.
Lời giải
Chọn B
Vì mặt cầu tiếp xúc với mặt phẳng
P
nên
2
22
1 4 0 1
;2
1 2 2
R d I P
.
Vậy phương trình mặt cầu cần tìm là
22
2
1 2 4x y z
.
Câu 12: Trong không gian với hệ trục tọa độ
Oxyz
, cho tứ diện
ABCD
với ,
0;2;0B
,
0;0;3C
,
1;2;3D
. Tìm tọa độ trọng tâm
G
của tứ diện
ABCD
.
A.
1 1 3
;;
424
G



. B.
13
;1;
22
G



. C.
24
; ;2
33
G



. D.
2;4;6G
.
Lời giải
Chọn B
Ta có:
1 0 0 1 1
4 4 2
0 2 0 2 1 3
1 ;1;
4 4 2 2
0 0 3 3 3
4 4 2
A B C D
G
A B C D
G
A B C D
G
x x x x
x
y y y y
yG
z z z z
z



.
Câu 13: Tính
2
2
0
2 1dx x x
.
A.
1
2
. B.
2
. C.
5
2
. D.
1
.
Lời giải
Chọn D
Trang10
Ta có
2 2 2 1 2
2
2
0 0 0 0 1
2 1d 1 d 1d 1 d 1 dx x x x x x x x x x x
12
22
01
11
1
2 2 2 2
xx
xx
.
Câu 14: Cho hàm số
3
12 1y x x
. Điểm cực tiểu của hàm số là
A.
2
. B.
15
. C.
13
. D.
2
.
Lời giải
Chọn A
Ta có:
3
2
3 12; 0
2
x
y x y
x
.
Điểm cực tiểu của hàm số là
2x
Câu 15: Số nghiệm nguyên dương của bất phưng trình
15
11
2 16
x



là
A.
15
. B.
8
. C.
16
. D.
9
.
Lời giải
ChọnA.
Điều kiện xác định
15 0 15xx
.
Khi đó
15 15 4
1 1 1 1
15 4 15 16 1
2 16 2 2
xx
x x x

.
Kết hợp với điều kiện ta được
1 15x
mà
; 0 1;2;3;4;......;14;15x x x
.
Câu 16: Số phức liên hợp của số phức
4
1
z
i
là
A.
22i
. B.
22i
. C.
22i
. D.
22i
.
Lời giải
Chọn C
Ta có:
4
2 2 2 2
1
z i z i
i
Câu 17: Một lớp học sinh có 15 học sinh nữ và 25 học sinh nam. Giáo viên chủ nhiệm cần chọn ban
cán sự lớp gồm 3 học sinh. Tính xác suất để ban cán sự có cả nam và nữ.
A.
251
1976
. B.
2625
9880
. C.
1425
1976
. D.
450
988
.
Lời giải
Trang11
Chọn C
Tổng số học sinh của lớp là:
15 25 40
.
Chọn 3 học sinh bất kì có số cách chọn là:
3
40
9880C
.
Chọn 3 học sinh trong đó có 2 nam và 1 nữ có số cách chọn là:
12
15 25
. 4500CC
.
Chọn 3 học sinh trong đó có 1 nam và 2 nữ có số cách chọn là:
21
15 25
. 2625CC
.
Chọn 3 học sinh trong đó cả nam và nữ có số cách chọn là:
12
15 25
.CC
21
15 25
. 7125CC
.
Vậy xác suất để ban cán sự có cả nam và nữ là:
7125 75 1425
9880 104 1976
P
.
Câu 18: Cho hàm số
3
31y x x
. Viết phương trình tiếp tuyến với đồ thị tại giao điểm của đồ thị
hàm số với trục tung.
A.
1y
. B.
31yx
. C.
31yx
. D.
31yx
.
Lời giải
Chọn B
Đồ thị hàm số giao với trục tung tại
0;1M
.
Ta có:
2
3 3 0 3y x y

.
Phương trình tiếp tuyến của đồ thị hàm số tại
0;1M
là:
3 0 1 3 1y x x
.
Câu 19: Thể tích của khối trụ có bán kính đáy bằng
2
, độ dài đường sinh bằng
22
A.
8
. B.
4
. C.
42
. D.
82
.
Lời giải
Chọn C
Thể tích của khối trụ là:
2
.2.2 2 4 2V r h
.
Câu 20: Viết phương trình đường thẳng đi qua hai điểm
2;1; 3A
,
3;0;1B
A.
4
1
54
xt
yt
zt



. B.
2
1
34
xt
yt
zt


. C.
3
14
xt
yt
zt


. D.
4
1
54
xt
yt
zt


.
Lời giải
Chọn D
Ta có:
1; 1;4AB
.
Đường thẳng đi qua hai điểm
2;1; 3A
,
3;0;1B
nhận
1; 1;4AB
làm vectơ chỉ phương có
phương trình là:
2
1
34
xt
yt
zt


.
Ta thấy điểm
4; 1;5M AB
và đường thẳng
4
1
54
xt
yt
zt


và đường thẳng
AB
cùng vectơ chỉ
phương nên chúng trùng nhau chọn đáp án D.
Câu 21: Có bao nhiêu giá trị nguyên của
m
để phương trình sau là phương trình mặt cầu:
2 2 2 2
2 4 6 10 0x y z x z m m
.
Trang12
A.
5
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn D
Phương trình
2 2 2
2 2 2 0x y z ax by cz d
với
2 2 2
0a b c d
là phương trình của
một mặt cầu.
Từ đó ta có:
22
1
2
2
6 10
21
20
4
60
0
2
aa
b
dmm
cc
m
b
d m









Để phương trình đã cho là phương trình mặt cầu ta phải có
22 2 2
01 610 4 00a b c d mm
2
6 5 0 1 5m m m 
Do
m
nên có
3
giá trị tìm được
2;3;4m
.
Câu 22: Người thợ làm một bể cá hai ngăn không nắp với thể tích
3
1296 dm
. Người thợ này cắt các tấm
kính ghép lại một bể cá dạng hình hộp chữ nhật với ba kích thước
,,abc
(mét) để đỡ tốn kính
nhất như hình vẽ và giả thiết rằng độ dày của kính không đáng kể. Tính
abc
A.
3,3
. B.
3,6
. C.
4,8
. D.
3,9
.
Lời giải
Chọn B
Ta có
33
1296 1,296dm m
Diện tích đáy bể cá là:
ab
Diện tích các mặt bên bể cá là:
23ac bc
Diện tích kính cần dùng là:
23S ab ac bc
Theo bất đẳng thức Côsi áp dụng với 3 số dương ta có
22
3
33
2 3 3 .2 .3 3 6 3 6 1,296S ab ac bc ab ac bc abc
Dấu bằng xảy ra khi
2
2
23
3
23
2
bc
ab ac
ab ac bc
ac bc
ab

Thay vào
1,296abc
ta được
3
6 1,296 0,6; 1,2; 1,8c c b a
Vậy
0,6 1,2 1,8 3,6abc
Câu 23: Biết
1
1
d6f x x
, tích phân
1
0
2 1 df x x
bằng
A. 3. B. 6. C. 12. D. 2.
Lời giải
b
c
a
Trang13
Chọn A
Ta có
1 1 1
0 0 1
1 1 1
2 1 d 2 1 d 2 1 d .6 3
2 2 2
f x x f x x f t t
.
Câu 24: Cho số phức
4
1zi
. Tìm phần ảo của số phức
w iz
A.
4
. B.
4
. C.
4i
. D.
4i
.
Lời giải
Chọn A
Ta có
4 2 2
1 1 1 2 2 4z i i i i i
Do đó
w 4 4iz i i
.
Vậy phần ảo là: -4
Câu 25: Đồ thị hàm số nào sau đây không cắt trục hoành?
A.
3
52y x x
. B.
42
33y x x
. C.
1
2
x
y
x
. D.
3
31y x x
.
Lời giải
Chọn B
Xét phương trình hoành độ giao điểm của đồ thị hàm số ở bốn phương án
Phương trình
3
5 2 0xx
có
1
nghiệm (Sử dụng máy tính cầm tay CASIO)
Phương trình
42
3 3 0xx
vô nghiệm (Sử dụng máy tính cầm tay CASIO)
Phương trình
1
0
2
x
x
có nghiệm
1x
(Sử dụng máy tính cầm tay CASIO)
Phương trình
3
3 1 0xx
có
3
nghiệm (Sử dụng máy tính cầm tay CASIO)
Câu 26: Hàm số
2
2lny x x
đồng biến trên khoảng nào dưới đây?
A.
1;0
. B.
0;1
. C.
1;2
. D.
1;1
Lời giải
Chọn C
ĐK:
0x
và
2
2yx
x

2
1
0 2 2 0
1
x
yx
x

Bảng xét dấu
Vậy hàm số đồng biến trên
1;2
Câu 27: Viết phương trình đường thẳng đi qua
1; 2;0A
và vuông góc với mặt phẳng
: 2 2 1 0P x y z
A.
2 2 3 0x y z
. B.
12
1 2 2
x y z

. C.
12
1 2 2
x y z

. D.
2 2 5 0x y z
Lời giải
Chọn B
Đường thẳng
d
P
d
có một vtcp là
1; 2;2u 
Trang14
Phương trình đường thẳng
12
:
1 2 2
x y z
d


Câu 28: Cho hình chóp
.S ABC
có
; 3 ; 2 ; 2AB a BC a CA a SA SB SC a
. Tính thể tích khối
chóp
.S ABC
A.
3
26
24
a
. B.
3
26
12
a
. C.
3
26
4
a
. D.
3
26
8
a
Lời giải
Chọn B
Xét
ABC
có
2 2 2
BC AB AC
ABC
vuông tại
A
SA SB SC
hình chiếu của
S
lên
ABC
trùng với tâm đường tròn ngoại tiếp
ABC
Gọi
H
là trung điểm của
BC
SH ABC
* Diện tích tam giác
ABC
là
2
1 1 2
. . . . 2
2 2 2
a
S AB AC a a
*
2
2
2
2
3 13
2
2 2 2
BC a a
SH SC a







Thể tích khối chóp
.S ABC
là
23
1 1 13 2 26
. . . .
3 3 2 2 12
ABC
a a a
V SH S
Câu 29: Cho cấp số cộng
n
u
thỏa mãn
2 9 4 6
3; 1u u u u
. Tìm công sai của cấp số cộng
n
u
A.
4
. B.
2
. C.
2
. D.
3
Lời giải
Chọn C
Có
29
1 1 1
4 6 1 1 1
3
8 3 2 9 3
2
1 3 5 1 2 8 1
uu
u d u d u d
d
u u u d u d u d



Câu 30: Biết rằng
3
4 2 2
a
. Giá trị của
a
bằng
A.
5
6
. B.
15
2
. C.
1
2
. D.
5
2
Lời giải
Chọn A
Có
11
5
2.
33
2
23
6
4 2 2 . 2 2 2



Trang15
Câu 31: Cho
a
là số thực dương. Khi đó
3
4
log 8a
bằng
A.
2
3
log
2
a
. B.
2
33
log
22
a
. C.
2
2 3log a
. D.
2
6 6log a
.
Lời giải
Chọn B
Ta có
33
4 4 4 2 2 2
3 3 3 3
log 8 log 8 log log 2 log log
2 2 2 2
a a a a
.
Câu 32: Viết phương trình mặt phẳng đi qua ba điểm
0,2,0 ; 3,0,0 ; 0,0,4A B C
A.
0
2 3 4
x y z
. B.
0
3 2 4
x y z
. C.
1
3 2 4
x y z
. D.
1
2 3 4
x y z
.
Lời giải
Chọn C
Phương trình mặt phẳng đi qua ba điểm
0,2,0 ; 3,0,0 ; 0,0,4A B C
là
1
3 2 4
x y z
.
Câu 33: Hàm số
2
2
43
x
y
xx

có bao nhiêu đường tiệm cận?
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Chọn A
Tập xác định của hàm số
;2 \ 1D 
.
Ta có:
2
2
lim lim 0 0
43
xx
x
yy
xx
 





là TCN
Ta có:
2
1
4 3 0
3
x
xx
x
Vì
2
11
2
lim lim
43
xx
x
y
xx








;
2
11
2
lim lim
43
xx
x
y
xx








.
Suy ra
1x
là TCĐ
2
33
2
lim lim
43
xx
x
y
xx






không xác định.Vì
3xD
Vậy hàm số có 2 đường tiệm cận.
Câu 34: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2a
, mặt bên
SAB
là tam giác đều và
nằmtrong mặt phẳng vuông góc với đáy. Tính khoảng cách từ
A
đến mặt phẳng
SCD
A.
2 21
7
a
. B.
14
6
a
. C.
3 14
7
a
. D.
21
6
a
.
Lời giải
Chọn A
Trang16
Gọi
,MH
lần lượt là trung điểm của
,CD AB
. Do mặt bên
SAB
là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy nên
3SH ABCD SH a
và
CD HM CD SMH
.
Kẻ
HK SM HK SCD
.
Do đó
;;d A SCD d H SCD HK
Xét tam giác
SMH
vuông tại
H
có
2 2 2
2 2 2
2
1 1 1 . 2 . 3 2 21
7
23
HS HM a a a
HK
HK HS HM
HS HM
aa
.
Vậy
2 21
;
7
a
d A SC D HK
.
Câu 35: Tính thể tích khối lập phương nội tiếp mặt cầu có bán kính bằng 3.
A.
18 3.
B.
12 2.
C.
24 3.
D.
54 2.
Lời giải
Chọn C
Đặt
AB a
. Suy ra mặt cầu ngoại tiếp hình lập phương có bán kính
3
3 2 3
2
a
Ra
.
Trang17
Vậy thể tích khối lập phương cần tìm:
3
24 3.Va
Câu 36: Cho hàm số
2 3 4
1 2 3y x x x x
. Hàm số có bao nhiêu điểm cực trị?
A.
3.
B.
4.
C.
1.
D.
2.
Lời giải
Chọn?
2 3 4 3 4 2 2 4 2 3 3
23
23
32
1 2 3 2 1 2 3 3 1 2 3 4 1 2 3
1 2 3 1 2 3 2 2 3 3 1 3 4 1 2
1 2 3 10 40 40 6
y x x x x x x x x x x x x x x x
x x x x x x x x x x x x x x x
x x x x x x


1
2 .
3
0
2,49
0,18
1,33
x
x ng kép
x
y
x
x
x







Vậy hàm số đã cho có 5 điểm cực trị.
Câu 37: Đạo hàm của hàm số
1
2
3
x
x
y
bằng
A.
1
2
ln2 ln3 .
3
x
x
B.
1
1 .2
.
.3
x
x
x
x
C.
1
2 ln 2
.
3 ln3
x
x
D.
2
ln2 ln3 .
3
x
x
Lời giải
Chọn A
11
2 2 2 2 2
2 2. .ln ln2 ln3 .
3 3 3 3 3
xx
xx
xx
y








Câu 38: Cho tam giác
ABC
vuông tại
A
có
3, 4AB AC
. Tính diện tích xung quanh khối nón sinh
ra khi cho tam giác
ABC
quay quanh trục
AB
.
A.
20
. B.
15
. C.
12
. D.
60
.
Lời giải
Chọn A
Trang18
Khối nón sinh ra có bán kính đáy là
4R AC
, đường sinh
22
5l BC AB AC
.
Vậy diện tích xung quanh khối nón bằng:
20Rl

.
Câu 39: Gọi
,Mm
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
16y x x
. Tính
Mm
.
A.
88
. B.
8
. C. 0. D. 8.
Lời giải
ChọnC
Xét hàm số:
2
16y x x
TXĐ:
4;4
.
Hàm số liên tục trên
4;4
.
22
2
22
16 2
16 , 4;4
16 16
xx
y x x
xx

;
0 2 2yx
.
40y 
,
2 2 8y
,
2 2 8y
.
Vậy
8, 8Mm
.
Câu 40: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
2SA a
và
SA
vuông góc với đáy.
Tính
cos
với
là góc giữa hai mặt phẳng
SCD
và
ABCD
.
A.
1
5
. B.
2
5
. C.
2
3
. D.
1
3
.
Lời giải
ChọnA
Ta có
SCD ABCD CD
và
,CD AD SA
CD SAD
. Suy ra
SDA
.
Xét tam giác
SAD
vuông tại
A
có
2SA a
,
22
5SD SA AD a
.
Vậy
1
cos
5
AD
SD

.
Câu 41: Cho hàm số
y f x
có đồ thị như hình vẽ. Hỏi hàm số
1
2022
f f x
y
có bao nhiêu điểm
cực trị
?
A.
9
. B.
5
. C.
3
. D.
7
.
Trang19
Lời giải
ChọnA.
Có
11
2022 1 2022 ln2022 0
f f x f f x
y y f x f f x

10f x f f x

0
2; 0; 1
1; 1; 2.
10
fx
x x x
f x f x f x
f f x


Dựa vào đồ thị, ta có:
1fx
có hai nghiệm đơn;
1fx
có hai nghiệm đơn;
2fx
có hai nghiệm đơn;
Vậy hàm số trên có
9
điểm cực trị.
Câu 42: Cho số phức
z
thỏa mãn
1z
. Tìm giá trị lớn nhất của biểu thức
1P z z i
A.
8 4 2
. B.
2
. C.
2 2 2
. D.
22
.
Lời giải
Chọn C
Trang20
Gọi
A
là điểm biểu diễn số phức
z
, suy ra tập hợp
A
là đường tròn
C
tâm
O
, bán kính
bằng
1
.
Gọi
B
,
C
lần lượt là hai điểm biểu diễn số phức
1
,
i
; ta có
1OB OC
.
Gọi
I
là trung điểm
BC
suy ra
2
2
OI
.
Khi đó
22
2
2
22
2 2 1 2 2 2
22
P AB AC IB IO R
.
Câu 43: Cho hàm số
fx
liên tục trên
và có đồ thị như hình vẽ. Giả sử
m
là tham số thự C. Hỏi
phương trình
f f x m
có nhiều nhất bao nhiêu nghiệm thực?
A. 5. B. 10. C. 7. D. 12.
Lời giải
Chọn B
Trang21
Xét
f f x m
(1), đặt
,0f x t t
Phương trình (1) trở thành
f t m
(2)
Ta thấy với mỗi
0;1t
thì (1) có 6 nghiệm phân biệt.
Nếu
0t
hoặc với mỗi
1;3t
thì (1) có có 4 nghiệm phân biệt.
Nếu
1t
thì (1) có 5 nghiệm.
Để (1) có nhiều nghiệm
x
nhất thì (2) có nhiều nghiệm dương nhất.
Từ đồ thị suy ra phương trình (2) có nhiều nhất là 2 nghiệm dương
12
,tt
với
12
0;1 , 1;3tt
Khi đó với
1
f x t
có 6 nghiệm
x
; với
2
f x t
có 4 nghiệm
x
.
Vậy phương trình (1) có nhiều nhất 10 nghiệm.
Câu 44: Có bao nhiêu số thực
c
để hình phẳng giới hạn bởi đồ thị hàm số
2
4y x x c
, trục hoành
và các đường thẳng
2; 4xx
có diện tích bằng
3
.
A.
3
B.
0
C.
1
D.
2
Lời giải
Chọn A
Xét phương trình
2
40x x c
(1)
Xét hàm số
2
4y x x c
trên
2;4
, có BBT
TH1: Phương trình (1) không có nghiệm trên đoạn
4 0 4
2;4
00
cc
cc





.
Trang22
Khi đó diện tích hình phẳng là:
4
44
3
2 2 2
22
2
25
16
6
4 d 4 d 2 2 3
7
33
6
c TM
x
S x x c x x x c x x cx c
cL




.
TH2: Phương trình (1) có nghiệm
2;4 0;4ac
.
Ta có
22
4 0 4a a c c a a
.
Khi đó diện tích hình phẳng là:
4
4
33
2 2 2 2
2
2
4 d 4 d 2 2
33
a
a
a
a
xx
S x x c x x x c x x cx x cx

3 3 3
2 2 2
16 32 2
2 2 4 2 4 2 16 6
3 3 3 3 3
a a a
a ca c c a ca a ca c
3
2 2 2 3 2
24
4 2 4 16 6 4 10 24 16
33
a
a a a a a a a a a
.
Ta có
32
15
3
4
4
3 10 24 16 3
2
3
3
3
c TM
a
S a a a
c TM
a
.
Vậy có 3 giá trị
c
thoả mãn.
.
Câu 45: Cho hàm số
y f x
là hàm đa thức bậc 4. Biết hàm số
'y f x
có đồ thị
C
như hình vẽ
và diện tích của hình phẳng giới hạn bởi đò thị
C
và trục hoành bằng 9. Gọi
,Mm
lần lượt là
giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y f x
trên đoạn
3;2
. Tính
Mm
A.
16
3
. B.
32
3
. C.
27
3
D.
5
3
.
Lời giải
Chọn B
+ Từ đồ thị
C
ta có
2
' . 2 . 1f x a x x
.
+ Do diện tích của hình phẳng giới hạn bởi đồ thị
C
và trục hoành bằng 9
Câu 1. x
Câu 2. y
Trang23
1
22
2
44
. 2 . 1 9 ' . 2 . 1
33
a x x dx a f x x x
+ Ta có
2
'0
1
x
fx
x


4
2
2
48
' . 2 . 1 2
3 3 3
x
f x dx x x dx f x x x c

+
8
3 1, 2 , 2 8, 1 1
3
f c f c f c f c
8 32
,8
33
M c m c M m
Câu 46: Trong không gian
Oxyz
cho hai đường thẳng
1
12
:;
1 2 1
x y z
d


2
2 1 1
:
2 1 1
x y z
d

và
mặt phẳng
: 2 5 0P x y z
. Lập phương trình đường thẳng
d
song song với mặt phẳng
P
và cắt
12
,dd
lần lượt tại
,AB
sao cho độ dài đoạn
AB
đạt giá trị nhỏ nhất.
A.
1 2 2
1 1 1
x y z


. B.
1 2 2
1 1 1
x y z

.
C.
1 2 2
1 1 1
x y z

. D.
1 2 2
1 1 1
x y z

.
Lời giải
Chọn B
Do
1
1 ; 2 2 ;A d A t t t
; do
2
2 2 ;1 ;1B d B u u u
3 2 ;3 2 ;1AB u t u t u t
+ Mặt phẳng
P
có véc tơ pháp tuyến
1;1; 2n 
. Do
/ / . 0 4d P AB n u t
2
2 8 35 3 3AB t t
. Suy ra độ dài đoạn
AB
nhỏ nhất bằng
33
khi
2t
.
Khi đó
3; 3; 3AB d
đi qua điểm
1;2;2A
và có véc tơ chỉ phương
1;1;1u
Suy ra phương trình
1 2 2
:
1 1 1
x y z
d

. Chọn B
Câu 47: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
(1; 1;3)A
và hai đurờng thã
ng :
12
4 2 1 2 1 1
: , :
1 4 2 1 1 1
x y z x y z
dd

. Viết phương trình đường thẳng
d
đi qua
điểm
A
, vuông góc với đuờng thẳng
1
d
và cắt đường thẳng
2
d
.
A.
1 1 3
2 1 1
x y z

B.
1 1 3
2 1 1
x y z

C.
1 1 3
2 1 1
x y z

D.
1 1 3
2 1 1
x y z


Lời giải
Chọn D
Giả sử
2
2 ; 1 ;1 1 ; ; 2d d M M t t t AM t t t
.
1
d
có véc tơ chỉ phương
1
1;4; 2u 

. Do
1 1 1
. 1 4 2 2 0 1 2; 1; 1d d AM u AM u t t t t AM
là véc tơ
chỉ phương của
d
. Phương trình chính tắc của
d
:
1 1 3
2 1 1
x y z


.
Trang24
Câu 48: Biết rằng có đúng một số phức
z
thòa mãn
| 2 | | 2 4 |z i z i
vả
zi
zi
là số thuần ảo. Tính
tổng phần thực và phần ảo của
z
A.
4.
B.
4
. C.
1
. D.
1
.
Lời giải
Chọn C
Giả sử
,,z x yi x y
.
2 2 2
2
| 2 | | 2 4 | 2 2 4 2 2 4z i z i x y i x y i x y x y
2 2 2 2
4 4 4 4 8 16 4x y y x x y y x y
(1).
22
22
22
11
1
21
1
11
x y i x y i
x y i
z i x y y
mi
x y i
zi
x y x y

.
( Điều kiện
2
2
10xy
).
Do
zi
zi
là số thuần ảo
22
22
2
2
21
0 2 1 0
1
x y y
x y y
xy

(2).
Thay (1) vào (2) ta được phương trình:
2
2
5
4 2 1 0 6 15 0
2
y y y y y
.
Thay
5
2
y
vào (1) ta được
3 3 5
1
2 2 2
x x y

.
Câu 49: Cho hàm số
()fx
có đạo hàm trên
và thỏa mãn
32
( 3 ) 2f x x x
với mọi số thực
x
.
Tính
4
2
0
. ( )dx f x x
A.
27
4
. B.
219
8
. C.
357
4
. D.
27
8
.
Lời giải
ChọnA.
Đặt
4
2
0
. ( )dI x f x x
Đặt
2
d 2 d
()
d ( )d
u x x
ux
v f x
v f x x

.
Khi đó
44
4
2
0
00
( ) 2 ( )d 16 (4) 2 . ( )dI x f x f x x f x f x x

.
Xét
44
00
. ( )d . ( )dK x f x x t f t t

.
Đặt
2
3
2
( ) 2
3
d (3 +3)d
f t x
t x x
t x x

.
0 0; 4 1t x t x
.
Do đó
1
3 2 2
0
165
( 3 )( 2).(3 +3)d
8
K x x x x x
.
1 (4) 3.xf
Trang25
Vậy
4
2
0
165 27
. ( )d 16.3 2.
84
I x f x x
.
Câu 50: Có bao nhiêu số nguyên dương
a
để phương trình sau có ít nhất một nghiệm thực
log
log log
1 2 2
a
xx
a a x
A.
8
. B.
1
. C.
0
. D.
9
.
Lời giải
Chọn D
Điều kiện
a
,
0x
Phương trình ban đầu tương đương
log
log log
1 2 2
a
aa
x x x
(*)
Đặt
log
1
a
tx
(1)
Suy ra
log
1
a
xt
Phương trình (*) trở thành
log log
1 2 1 2
aa
t t x t t x
(2)
Lấy (1) + (2) ta được
log log
22
aa
t t x x
Xét hàm số
log
2
a
f u u u
với
0u
và
a
ta có
log 1
.log 2 0
a
f u u a
với mọi
a
Từ đó suy ra hàm số
fu
đồng biến trên
0;
Mà
f t f x
suy ra
tx
log log
11
ax
x x a x
+ Nếu
1x
thay lại ta có
log2 log
1 2 1 log 0 1
a
a a a
(thỏa)
Suy ra nhận
1a
+ Nếu
1x
, khi đó
log log log
ln 1
1 1 ln ln 1 log 1
ln
x a a
x
a x x x x x a
x
Từ đó suy ra
log 1 0 10aa
Mà
a
suy ra
1;2;3;...;9a
Kết hợp 2 TH suy ra
1;2;3;...;9a
| 1/25
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TRƯỜNG ĐẠI HỌC KHOA HỌC TỰ NHIÊN
ĐỀ KIỂM TRA KIẾN THỨC LỚP 12
NĂM HỌC 2021 – 2022
TRƯỜNG THPT CHUYÊN KHTN-HÀ NỘI Câu 1: Tìm 2 sin 2 d x x sin 4x x sin 4x 3 cos 3x x sin 4x A. C . B.   C . C.   C . D.   C . 8 2 8 3 2 8 x Câu 2:
Có bao nhiêu giá trị nguyên của m để hàm số 2 4 y
đồng biến trên 1;  m x A. 1. B. 2 . C. 4 . D. 3 . Câu 3:
Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức z = ( + i)3 1 là A. (- 2; 2). B. (2;- 2). C. (2; ) 2 . D. (- 2; 4). Câu 4:
Có bao nhiêu số tự nhiên chẵn gồm 3 chữ số đôi một khác nhau và không có chữ số nào lớn hơn 5. A. 75. B. 90 . C. 52 . D. 60 . Câu 5:
Tính thể tích khối chóp tứ giác đều có cạnh đáy bằng 2a và có mặt bên tạo với đáy một góc bằng 60°. 4 4 3 4 A. 3 a . B. 3 a C. 3 a . D. 3 4 3a . 3 3 3 3 3 Câu 6: Tìm 2 x  3 2x   1 dxx  4 3 2 1  x  4 3 2 1  x  4 3 2 1  x  4 3 2 1 A. C . B. C . C. C . D. C . 24 24 24 24 Câu 7:
Tổng tất cả các nghiệm của phương trình log  2
x x 1  2 log x bằng? 2  2 A. 1. B. 4 . C. 2 . D. 3 . x  1  Câu 8: Biết rằng phương trình 3 x 1 
  2  có một nghiệm thực duy nhất. Nghiệm đó thuộc  2 2 
khoảng nào dưới đây? A.  6  ;  5 . B. 0;  1 . C.  2  ;  1 . D.  1  ;0 . 1   1 2
x  2x  3 f xdx  1
f x dxCâu 9: Cho 0 . Tính 0 . 1 5 1 5 A. . B. . C. . D.  . 3 3 9 9
Câu 10: Cho hai số phức z 1 2i và w  3  4i . Tính .w z . A. 125 . B. 5 . C. 5 . D. 5 5 .
Câu 11: Viết phương trình mặt cầu tâm I 1; 2
 ;0 và tiếp xúc với mặt phẳng P: x  2y  2z 1 0 2 2 2 2
A. x     y   2 1 2  z  4 .
B. x     y   2 1 2  z  4 . 2 2 2 2
C. x     y   2 1 2  z  2 .
D. x     y   2 1 2  z  2 . Trang1
Câu 12: Trong không gian với hệ trục tọa độ Oxyz , cho tứ diện ABCD với A1;0;0 , B 0; 2;0 , C 0;0; 
3 , D 1; 2;3 . Tìm tọa độ trọng tâm G của tứ diện ABCD .  1 1 3   1 3   2 4  A. G ; ;   . B. G ;1;  . C. G ; ; 2   .
D. G 2; 4;6 .  4 2 4   2 2   3 3  2 2
x  2x 1 dxCâu 13: Tính 0 . 1 5 A. . B. 2 . C. . D. 1. 2 2 Câu 14: Cho hàm số 3
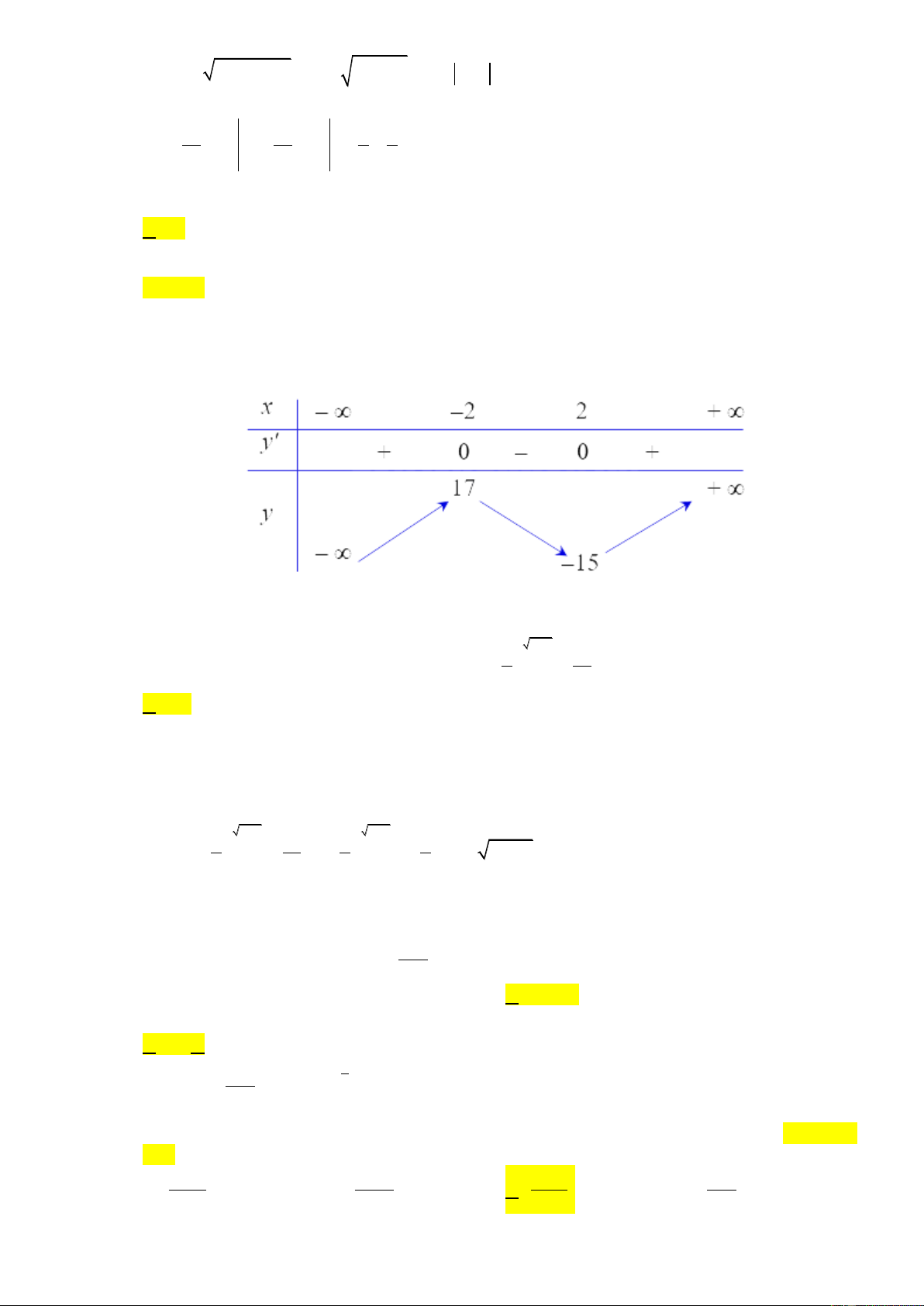
y x 12x 1. Điểm cực tiểu của hàm số là A. 2 . B. 15  . C. 13 . D. 2  . 15x  1  1
Câu 15: Số nghiệm nguyên dương của bất phưng trình    là  2  16 A. 15 . B. 8 . C. 16 . D. 9 . 4
Câu 16: Số phức liên hợp của số phức z  là 1 i
A. 2  2i . B. 2  2i .
C. 2  2i . D. 2   2i .
Câu 17: Một lớp học sinh có 15 học sinh nữ và 25 học sinh nam. Giáo viên chủ nhiệm cần chọn ban cán
sự lớp gồm 3 học sinh. Tính xác suất để ban cán sự có cả nam và nữ. 251 2625 1425 450 A. . B. . C. . D. . 1976 9880 1976 988 Câu 18: Cho hàm số 3
y x  3x 1. Viết phương trình tiếp tuyến với đồ thị tại giao điểm của đồ thị
hàm số với trục tung. A. y  1. B. y  3  x 1 .
C. y  3x 1 .
D. y  3x 1.
Câu 19: Thể tích của khối trụ có bán kính đáy bằng 2 , độ dài đường sinh bằng 2 2 A. 8 . B. 4 . C. 4 2 . D. 8 2 .
Câu 20: Viết phương trình đường thẳng đi qua hai điểm A2;1; 3   , B3;0;  1 x  4  tx  2  tx  3 tx  4  t    
A. y  1 t .
B. y  1 t .
C. y t . D. y  1   t .     z  5  4tz  3   4tz  1 4tz  5  4t
Câu 21: Có bao nhiêu giá trị nguyên của m để phương trình sau là phương trình mặt cầu: 2 2 2 2
x y z  2x  4z m  6m 10  0 . A. 5 . B. 0 . C. 2 . D. 3 .
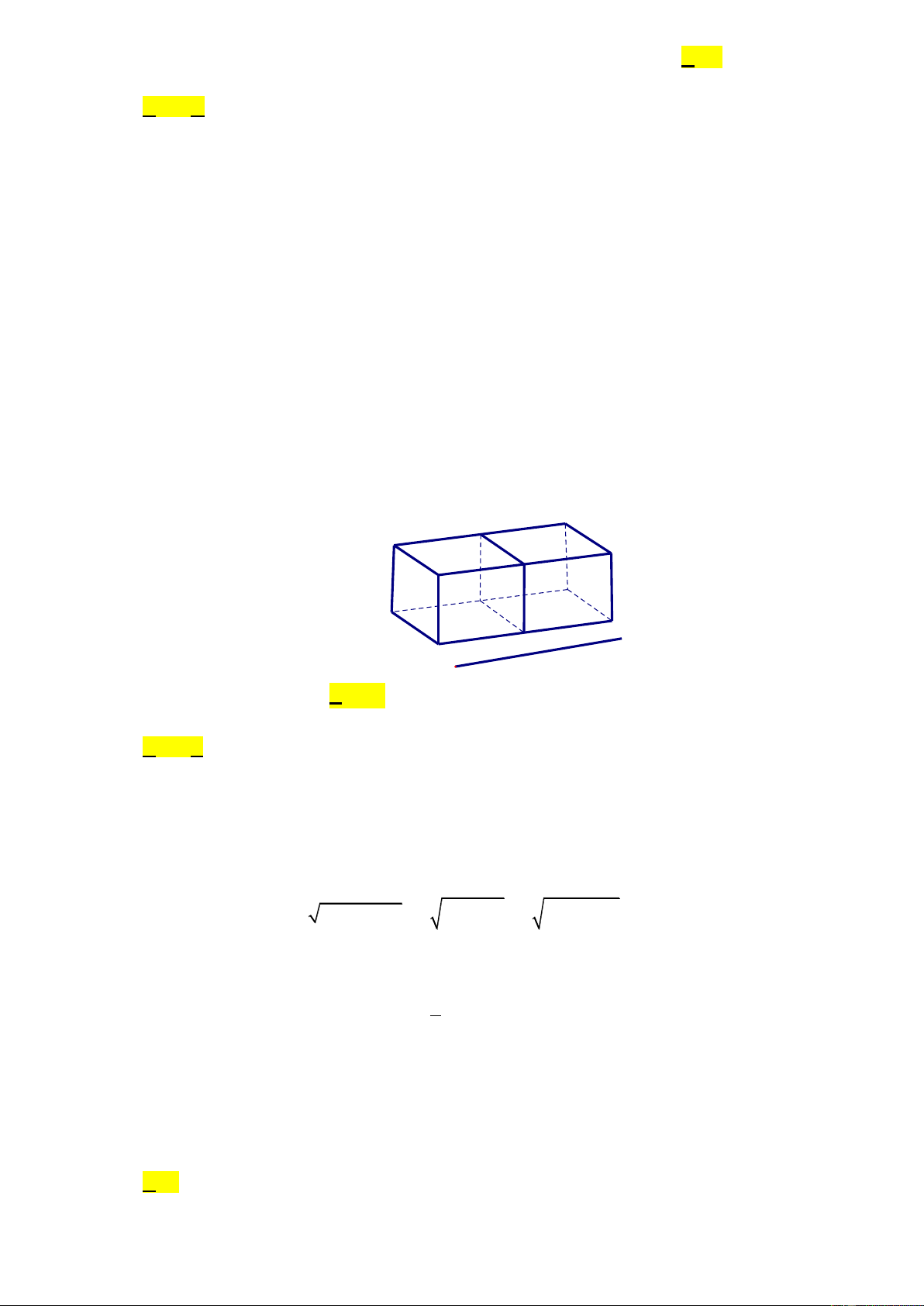
Câu 22: Người thợ làm một bể cá hai ngăn không nắp với thể tích 3
1296 dm . Người thợ này cắt các tấm
kính ghép lại một bể cá dạng hình hộp chữ nhật với ba kích thước a , b , c (mét) để đỡ tốn kính
nhất như hình vẽ và giả thiết rằng độ dày của kính không đáng kể. Tính a b c Trang2 c b a A. 3, 3 . B. 3, 6 . C. 4, 8 . D. 3, 9 . 1 1 Câu 23: Biết f
 xdx  6, tích phân f 2x  1dxbằng 1  0 A. 3. B. 6. C. 12. D. 2.
Câu 24: Cho số phức z    i4 1
. Tìm phần ảo của số phức w iz A. 4  . B. 4 . C. 4i . D. 4  i .
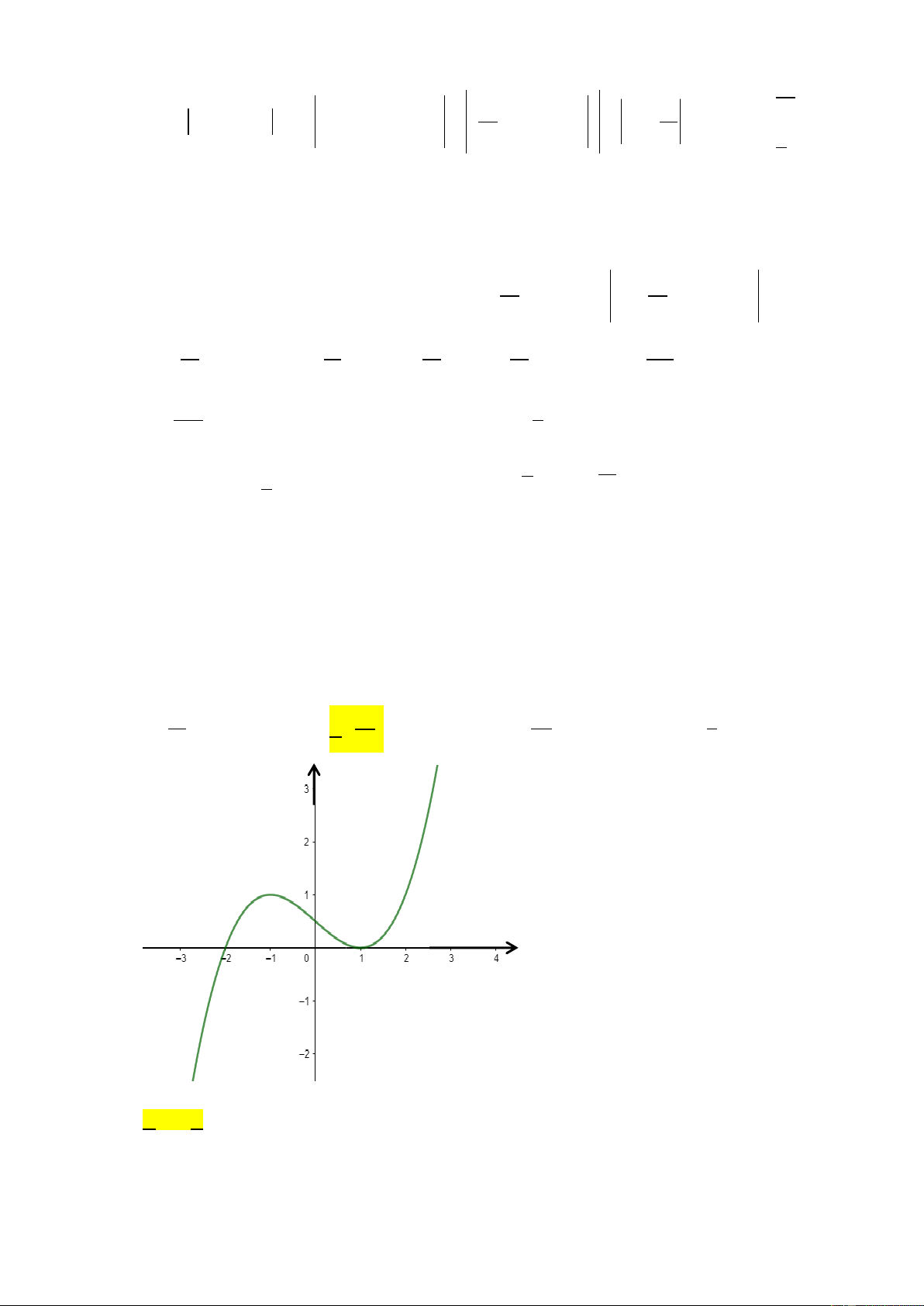
Câu 25: Đồ thị hàm số nào sau đây không cắt trục hoành? x 1 A. 3
y x  5x  2 . B. 4 2
y x  3x  3 . C. y  . D. 3
y x  3x 1. 2  x Câu 26: Hàm số 2
y x  2 ln x đồng biến trên khoảng nào dưới đây? A.  1  ;0 . B. 0;  1 . C. 1; 2 . D.  1   ;1
Câu 27: Viết phương trình đường thẳng đi qua A1; 2
 ;0 và vuông góc với mặt phẳng
P: x 2y  2z 1 0 x 1 y  2 z x 1 y  2 z
A. x  2 y  2z  3  0 . B.   . C.
 . D. x  2y  2z  5  0 1 2  2 1 2  2
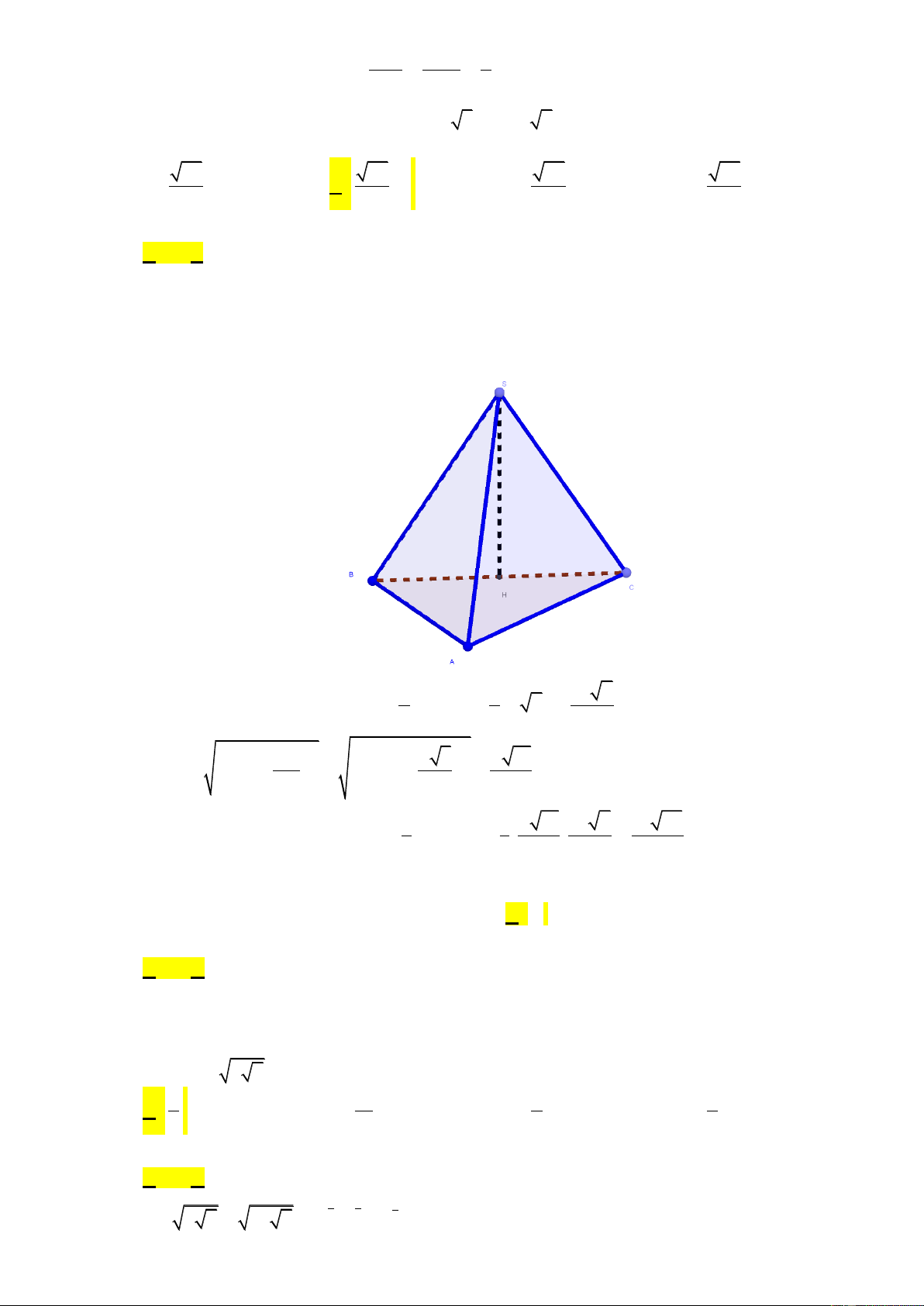
Câu 28: Cho hình chóp S.ABC có AB  ; a BC  3 ; a CA  2 ;
a SA SB SC  2a . Tính thể tích khối chóp S.ABC 26 26 26 26 A. 3 a . B. 3 a . C. 3 a . D. 3 a 24 12 4 8
Câu 29: Cho cấp số cộng u thỏa mãn u u  3;u u  1. Tìm công sai của cấp số cộng u n n  2 9 4 6 A. 4 . B. 2  . C. 2 . D. 3
Câu 30: Biết rằng 3 4 2 2a
. Giá trị của a bằng 5 15 1 5 A. . B. . C. . D. 6 2 2 2
Câu 31: Cho a là số thực dương. Khi đó 3 log 8a bằng 4 3 3 3 A.  log a . B.  log a . C. .
D. 6  6 log a . 2 2 2 2 2 2
Câu 32: Viết phương trình mặt phẳng đi qua ba điểm A0, 2, 0; B 3, 0, 0;C 0, 0, 4 x y z x y z x y z x y z A.    0 . B.    0 . C.    1 . D.    1 . 2 3 4 3 2 4 3 2 4 2 3 4 2  x
Câu 33: Hàm số y
có bao nhiêu đường tiệm cận? 2 x  4x  3 A. 2 . B. 1. C. 0 . D. 3 . Trang3
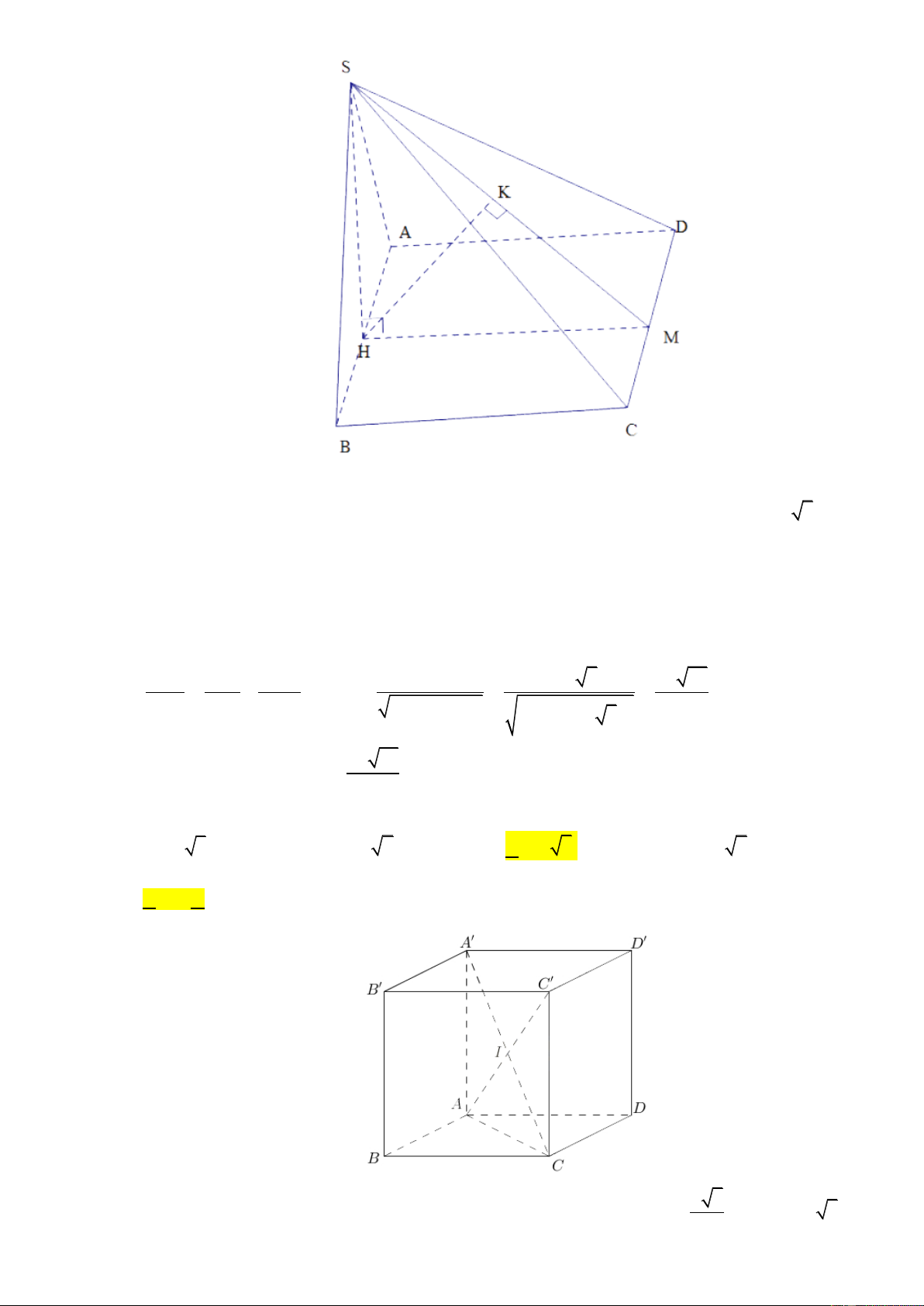
Câu 34: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a , mặt bên S AB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ A đến mặt phẳng SCD 2a 21 a 14 3a 14 a 21 A. . B. . C. . D. . 7 6 7 6
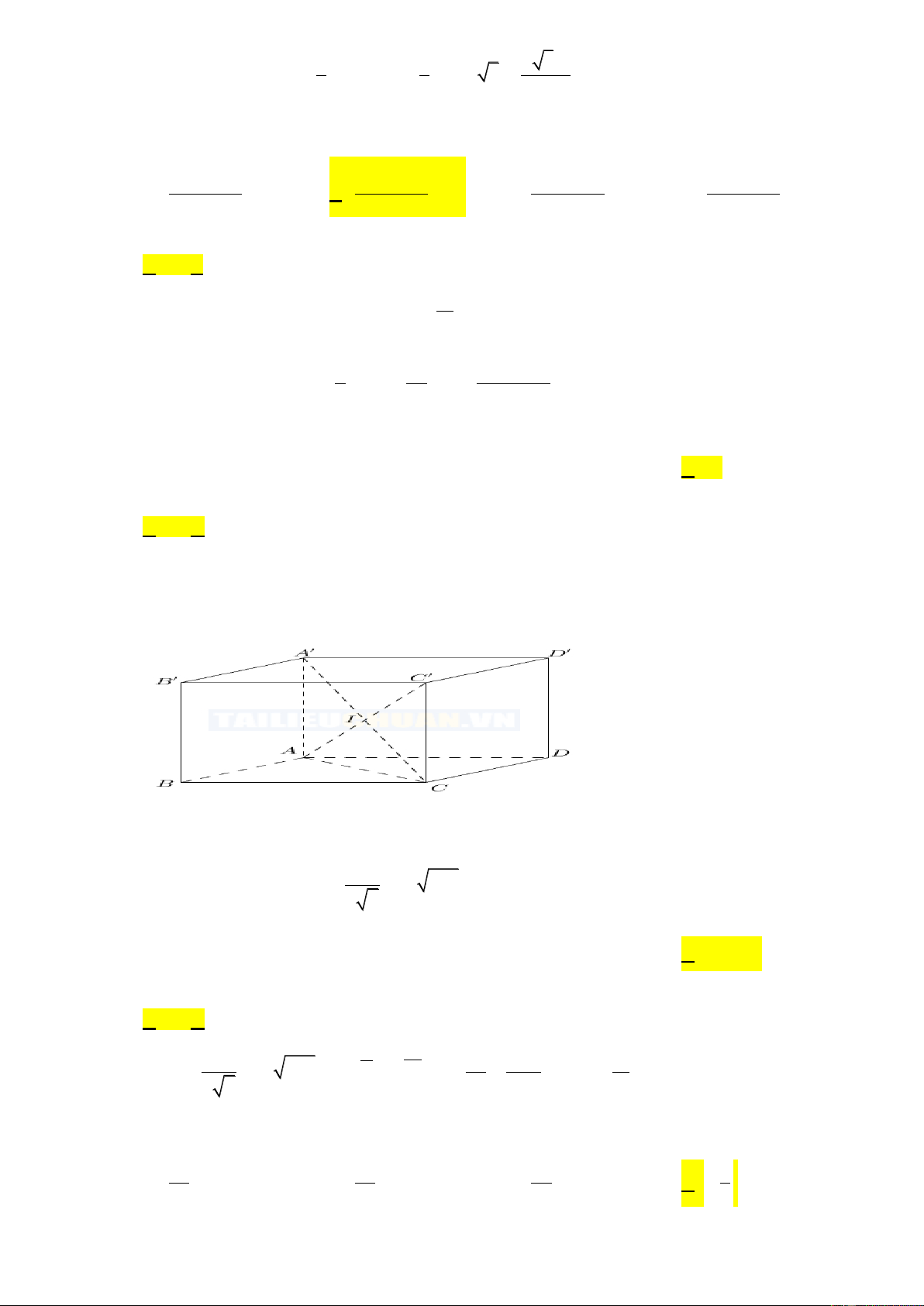
Câu 35: Tính thể tích khối lập phương nội tiếp mặt cầu có bán kính bằng 3. A. 18 3. B. 12 2. C. 24 3. D. 54 2. 2 3 4
Câu 36: Cho hàm số y x x  
1  x  2  x  3 . Hàm số có bao nhiêu điểm cực trị? A. 3. B. 4. C. 1. D. 2. x 1 2 
Câu 37: Đạo hàm của hàm số y  bằng 3x x 1 2  x  1.2x x 1 2  ln 2 2x A. B. . C. . D. x  ln 2 ln 3. x ln 2 ln3. 3 x 1 .3 x  3x ln 3 3 Câu 38: Cho tam giác
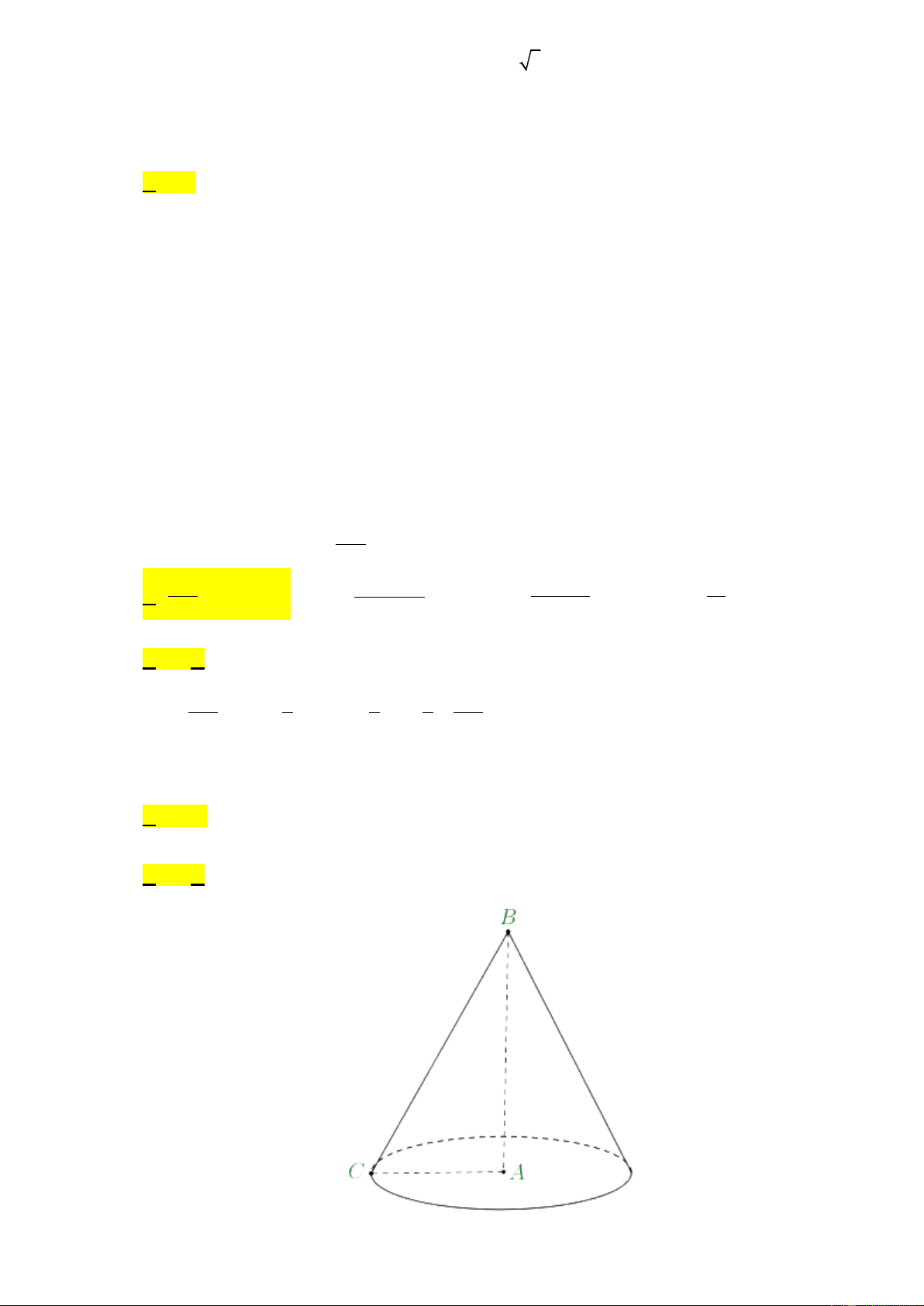
vuông tại A có AB  3, AC  4 . Tính diện tích xung quanh khối nón sinh
ra khi cho tam giác ABC quay quanh trục AB . A. 20 . B. 15 . C. 12 . D. 60 .
Câu 39: Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2
y x 16  x . Tính M m. A. 8  8 . B. 8 . C. 0. D. 8.
Câu 40: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA  2a và SA vuông góc với đáy.
Tính cos với  là góc giữa hai mặt phẳng SCD và  ABCD . 1 2 2 1 A. . B. . C. . D. . 5 5 3 3   
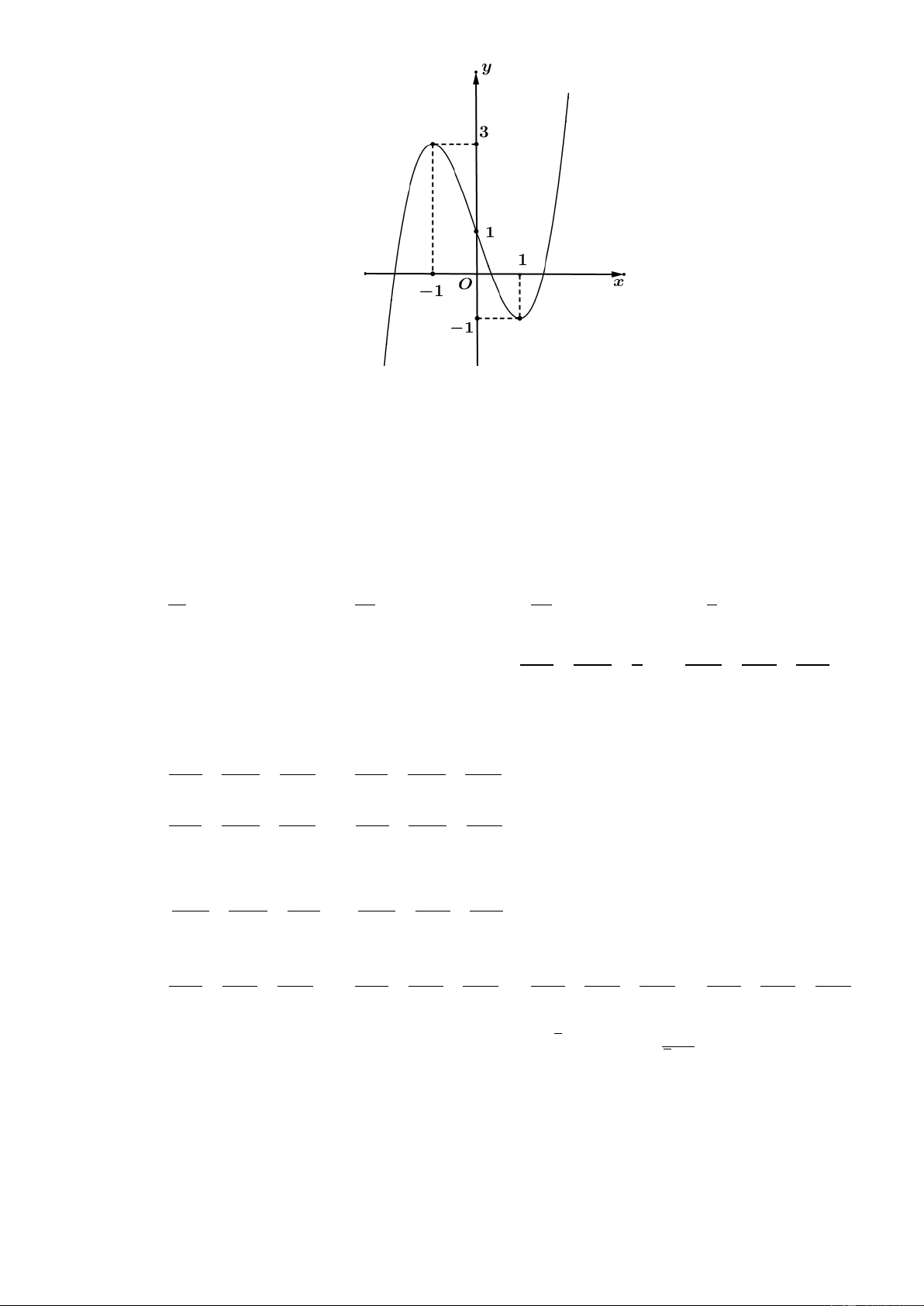
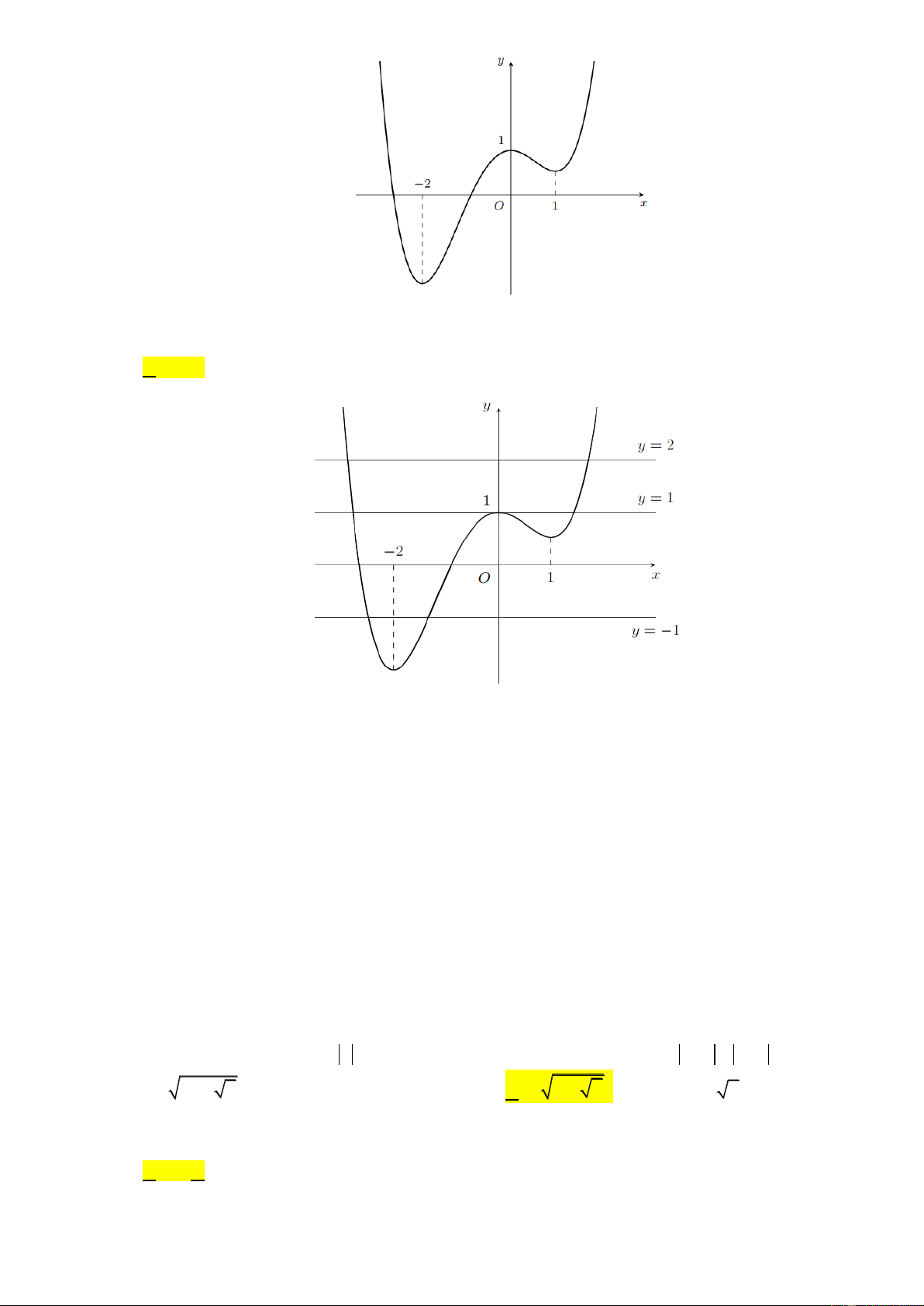
Câu 41: Cho hàm số y f x có đồ thị như hình vẽ. Hỏi hàm số   1  2022f f x y có bao nhiêu điểm cực trị ? A. 9 . B. 5 . C. 3 . D. 7 .
Câu 42: Cho số phức z thỏa mãn z  1. Tìm giá trị lớn nhất của biểu thức A. 8  4 2 . B. 2 . C. 2 2  2 . D. 2 2 .
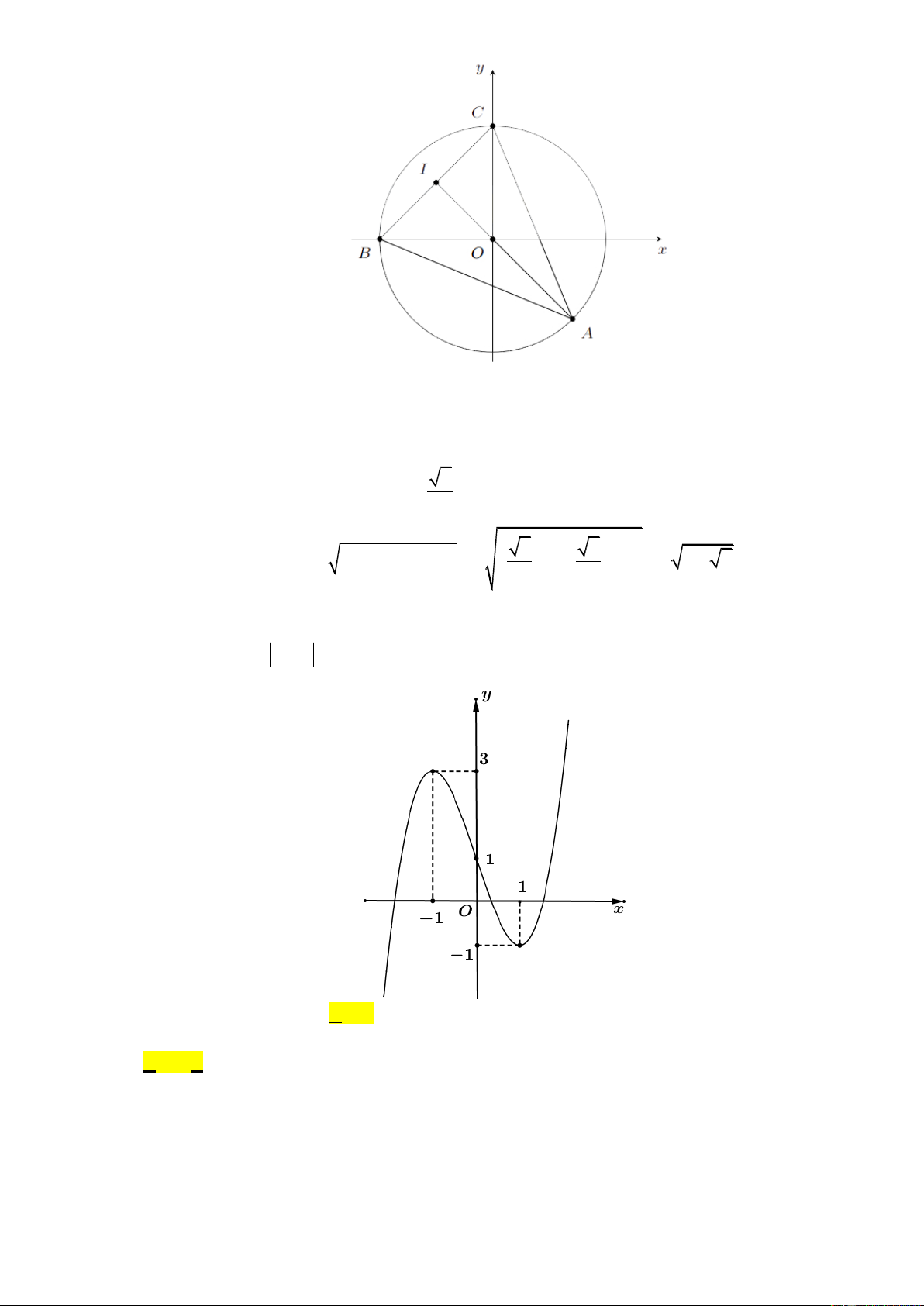
Câu 43: Cho hàm số f x liên tục trên  và có đồ thị như hình vẽ. Giả sử m là tham số thự C. Hỏi
phương trình f f x   m có nhiều nhất bao nhiêu nghiệm thực? Trang4 A. 5. B. 10. C. 7. D. 12.
Câu 44: Có bao nhiêu số thực c để hình phẳng giới hạn bởi đồ thị hàm số 2
y x  4x c , trục hoành
và các đường thẳng x  2; x  4 có diện tích bằng 3 . A. 3 B. 0 C. 1 D. 2
Câu 45: Cho hàm số y f x là hàm đa thức bậc 4. Biết hàm số y f ' x có đồ thị C như hình vẽ
và diện tích của hình phẳng giới hạn bởi đò thị C và trục hoành bằng 9. Gọi M , m lần lượt là
giá trị lớn nhất, giá trị nhỏ nhất của hàm số y f x trên đoạn  3
 ;2. Tính M m 16 32 27 5 A. . B. . C. D. . 3 3 3 3 x 1 y  2 z x  2 y 1 z 1
Câu 46: Trong không gian Oxyz cho hai đường thẳng d :   ; d :   và 1 1 2 1 2 2 1 1
mặt phẳng  P : x y  2z  5  0 . Lập phương trình đường thẳng d song song với mặt phẳng
P và cắt d ,d lần lượt tại ,
A B sao cho độ dài đoạn AB đạt giá trị nhỏ nhất. 1 2 x 1 y  2 z  2 x 1 y  2 z  2 A.   . B.   . 1 1 1  1 1 1 x 1 y  2 z  2 x 1 y  2 z  2 C.   . D.   . 1 1 1 1 1 1
Câu 47: Trong không gian với hệ tọa độ Oxyz , cho điểm (
A 1; 1; 3) và hai đurờng thã̉ng : x  4 y  2 z 1 x  2 y 1 z 1 d :   , d :  
. Viết phương trình đường thẳng d đi qua 1 2 1 4 2  1 1  1
điểm A , vuông góc với đuờng thẳng d và cắt đường thẳng d . 1 2 x 1 y 1 z  3 x 1 y 1 z  3 x 1 y 1 z  3 x 1 y 1 z  3 A.   B.   C.   D.   2 1 1 2 1 1 2 1 1 2 1 1 z i
Câu 48: Biết rằng có đúng một số phức z thòa mãn | z  2i | |
z  2  4i | vả là số thuần ảo. Tính z i
tổng phần thực và phần ảo của z A. 4. B. 4  . C. 1. D. 1.
Câu 49: Cho hàm số f (x) có đạo hàm trên  và thỏa mãn 3 2
f (x  3x)  x  2 với mọi số thực x . 4 Tính 2 x . f (  x)dx 0 Trang5 27 219 357 27 A. . B. . C. . D. . 4 8 4 8
Câu 50: Có bao nhiêu số nguyên dương a để phương trình sau có ít nhất một nghiệm thực
x  loga log log 1 x aa  2x  2 A. 8 . B. 1. C. . D. 9 .
------------------------------Hết----------------------------- BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 D D A C B B D D D D B B D A A C C B C D D B A A B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 C B B C A B C A A C _ A A C A A C B A B B D C A D
HƯỚNG DẪN GIẢI CHI TIẾT 2 sin 2 d x xCâu 1: Tìm sin 4x x sin 4x 3 cos 3x x sin 4x A. C . B.   C . C.   C . D.   C . 8 2 8 3 2 8 Lời giải Chọn D  1 1  x sin 4x 2 sin 2 d x x
 cos 4x dx    C     2 2  2 8 x Câu 2:
Có bao nhiêu giá trị nguyên của m để hàm số 2 4 y
đồng biến trên 1;  m x A. 1. B. 2 . C. 4 . D. 3 . Lời giải Chọn D 2m  4 y   m x2
Để hàm số đồng biến trên 1; thì y  0 với mọi x 1; . 2m  4  0    2   m 1. m 1
Mà m    m  1  ;0  ;1 Câu 3:
Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức z = ( + i)3 1 là A. (- 2; 2). B. (2;- 2). C. (2; ) 2 . D. (- 2; 4). Lời giải ChọnA. 3 2
Ta có: z = ( + i) = ( + i) ( + i)= ( 2 1 1 1
1+ 2i + i )(1+ i)= (2i)(1+ i)= - 2 + 2 .i
Vậy điểm biểu diễn số phức z là (- 2;2). Trang6 Câu 4:
Có bao nhiêu số tự nhiên chẵn gồm 3 chữ số đôi một khác nhau và không có chữ số nào lớn hơn 5. A. 75. B. . C. 52 . D. 60 . Lời giải Chọn C
Gọi số cần tìm có dạng abc
Trường hợp 1: Nếu c = 0 Chọn a: 5 cách Chọn b: 4 cách
Khi đó thành lập đc 5.4 = 20 số.
Trường hợp 2: Nếu c ¹ 0
Chọn c : có 2 cách. Chọn a : 4 cách. Chọn b : 4 cách.
Khi đó thành lập được 2.4.4 = 32 số.
Vậy thành lập được tất cả 20+ 32 = 52 số. Câu 5:
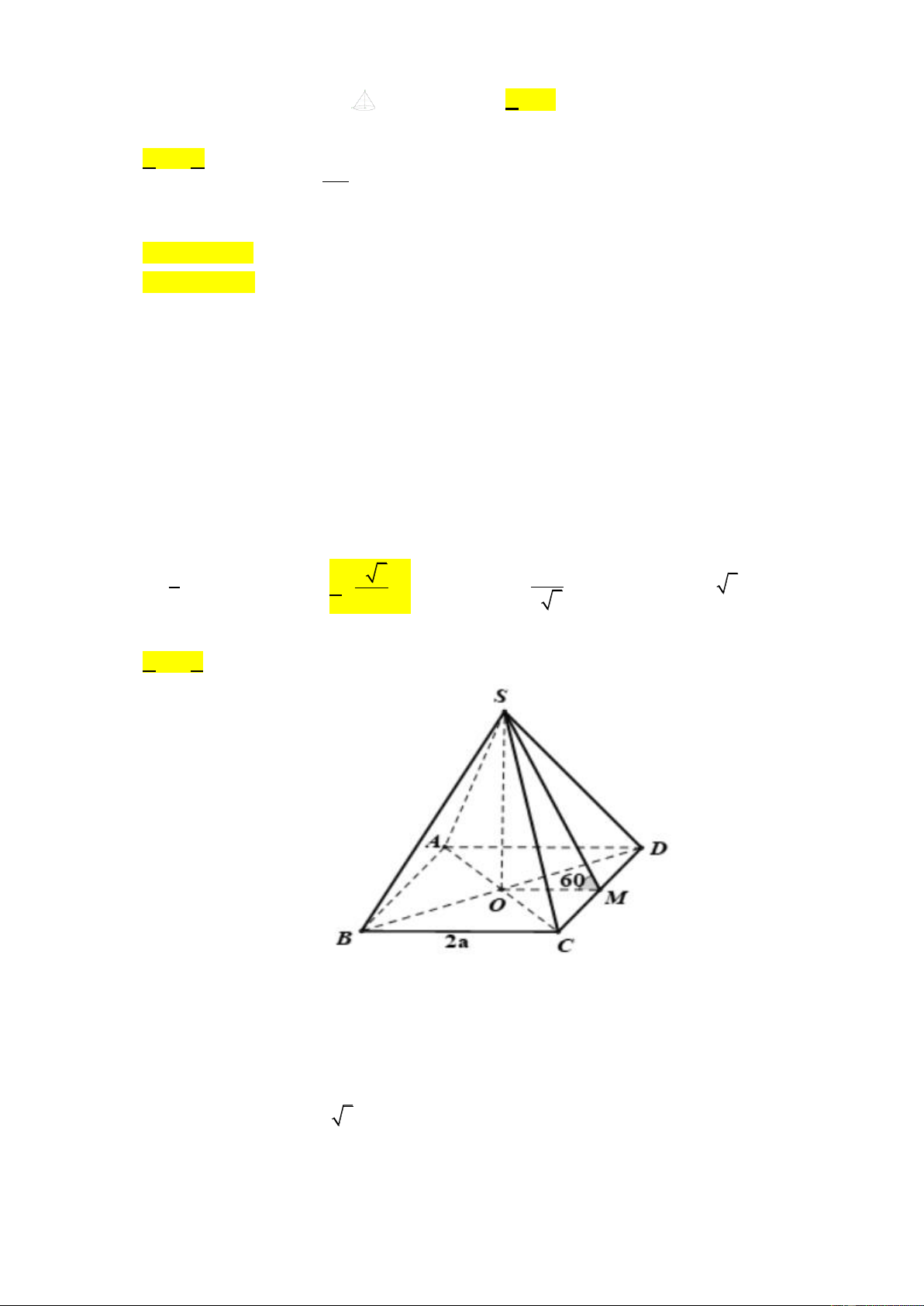
Tính thể tích khối chóp tứ giác đều có cạnh đáy bằng 2a và có mặt bên tạo với đáy một góc bằng 60°. 4 4 3 4 A. 3 a . B. 3 a C. 3 a . D. 3 4 3a . 3 3 3 3 Lời giải Chọn B
Gọi M là trung điểm DC Þ OM ^ D . C
Ta có: DC ^ OM ; DC ^ SO Þ DC ^ (SOM ). Þ (
( SDC) (ABCD))= (SM OM ) · ; ; = SMO = 60°.
Þ SO = OM.tan 60° = a 3. S = ( a)2 2 2 = 4a ABCD Trang7 3 Vậy thể tích chóp 1 1 4 3a 2 V = S .SO = .4a .a 3 = 3 ABCD 3 3 x x   3 2 3 2 1 dx Câu 6: Tìm  x  4 3 2 1  x  4 3 2 1  x  4 3 2 1  x  4 3 2 1 A. C . B. C . C. C . D. C . 24 24 24 24 Lời giải Chọn B dt Đặt 3 2 2
t  2x 1 dt  6x dx x dx  6 2x 1 1 t Ta có x  2x    4 3 4 3 2 3 3 1 dx t dt  C  C  6 24 24 Câu 7:
Tổng tất cả các nghiệm của phương trình log  2
x x 1  2 log x bằng? 2  2 A. 1. B. 4 . C. 2 . D. 3 . Lời giải Chọn D 2
x x 1 0 ĐKXĐ:   x  0 x  0 Ta có
Tổng tất cả các nghiệm của phương trình log  2
x x 1  2 log x bằng 3 2  2 x  1   Câu 8: Biết rằng phương trình 3 x 1 
  2 có một nghiệm thực duy nhất. Nghiệm đó thuộc  2 2 
khoảng nào dưới đây? A.  6  ;  5 . B. 0;  1 . C.  2  ;  1 . D.  1  ;0 . Lời giải Chọn D x 3x x 1   1    x x x 3 1 2 Ta có 3 1 2 3    2  2  2     x    1  ;  0 2 3 11  2 2  1   1 2
x  2x  3 f xdx  1
f x dxCâu 9: Cho 0 . Tính 0 . 1 5 1 5 A. . B. . C. . D.  . 3 3 9 9 Lời giải Trang8 Chọn D 1 1 1 1 2 Ta có   2
x  2x  3 f x dx  1    2
x  2xdx  3 f
 xdx 1  3 f
 xdx 1 0 0 0 0 3 1 f x 5 dx    0 9
Câu 10: Cho hai số phức z 1 2i và w  3  4i . Tính .w z . A. 125 . B. 5 . C. 5 . D. 5 5 . Lời giải Chọn B Ta có .
z w  1 2i3 4i  11 2i  5 5
Câu 11: Viết phương trình mặt cầu tâm I 1; 2
 ;0 và tiếp xúc với mặt phẳng P: x  2y  2z 1 0 2 2 2 2
A. x     y   2 1 2  z  4 .
B. x     y   2 1 2  z  4 . 2 2 2 2
C. x     y   2 1 2  z  2 .
D. x     y   2 1 2  z  2 . Lời giải Chọn B 1 4  0 1
Vì mặt cầu tiếp xúc với mặt phẳng P nên R d I;P   2 . 1   2  2 2 2  2
Vậy phương trình mặt cầu cần tìm là x  2   y  2 2 1 2  z  4 .
Câu 12: Trong không gian với hệ trục tọa độ Oxyz , cho tứ diện ABCD với , B 0; 2;0 , C 0;0; 
3 , D 1; 2;3 . Tìm tọa độ trọng tâm G của tứ diện ABCD .  1 1 3   1 3   2 4  A. G ; ;   . B. G ;1;  . C. G ; ; 2   .
D. G 2; 4;6 .  4 2 4   2 2   3 3  Lời giải Chọn B Ta có: 
x x x x 1 0  0 1 1 A B C D x     G 4 4 2  
y y y y 0  2  0  2  1 3  A B C Dy   1 G ;1; . G   4 4   2 2  
z z z z 0  0  3  3 3 A B C D z     G  4 4 2 2 2
x  2x 1 dxCâu 13: Tính 0 . 1 5 A. . B. 2 . C. . D. 1. 2 2 Lời giải Chọn D Trang9 2 2 2 1 2 2 Ta có 2
x  2x 1dx  x   1 dx
x 1dx   x  
1 dx   x        1 dx 0 0 0 0 1 1 2 2 2  x   x  1 1
   x   x   1.  2   2  2 2 0 1 Câu 14: Cho hàm số 3
y x 12x 1. Điểm cực tiểu của hàm số là A. 2 . B. 15  . C. 13 . D. 2  . Lời giải Chọn A x  2 Ta có: 3
y  3x 12; y  0   . x  2 
Điểm cực tiểu của hàm số là x  2 15x  1  1
Câu 15: Số nghiệm nguyên dương của bất phưng trình    là  2  16 A. 15 . B. 8 . C. 16 . D. 9 . Lời giải ChọnA.
Điều kiện xác định 15 x  0  x 15. 15x 15x 4       Khi đó 1 1 1 1   
 15  x  4  15  x  16  x  1       .  2  16  2   2 
Kết hợp với điều kiện ta được 1
  x 15 mà x ; x  0  x1;2;3;4;......;14;1  5 . 4
Câu 16: Số phức liên hợp của số phức z  là 1 i
A. 2  2i . B. 2  2i .
C. 2  2i . D. 2   2i . Lời giải Chọn C 4 Ta có: z
 2  2i z  2  2i 1 i
Câu 17: Một lớp học sinh có 15 học sinh nữ và 25 học sinh nam. Giáo viên chủ nhiệm cần chọn ban
cán sự lớp gồm 3 học sinh. Tính xác suất để ban cán sự có cả nam và nữ. 251 2625 1425 450 A. . B. . C. . D. . 1976 9880 1976 988 Lời giải Trang10 Chọn C
Tổng số học sinh của lớp là: 15  25  40 .
Chọn 3 học sinh bất kì có số cách chọn là: 3 C  9880 . 40
Chọn 3 học sinh trong đó có 2 nam và 1 nữ có số cách chọn là: 1 2 C .C  4500 . 15 25
Chọn 3 học sinh trong đó có 1 nam và 2 nữ có số cách chọn là: 2 1 C .C  2625 . 15 25
Chọn 3 học sinh trong đó cả nam và nữ có số cách chọn là: 1 2 C .C  2 1 C .C  7125. 15 25 15 25 7125 75 1425
Vậy xác suất để ban cán sự có cả nam và nữ là: P    . 9880 104 1976 Câu 18: Cho hàm số 3
y x  3x 1. Viết phương trình tiếp tuyến với đồ thị tại giao điểm của đồ thị
hàm số với trục tung. A. y  1. B. y  3  x 1 .
C. y  3x 1 .
D. y  3x 1. Lời giải Chọn B
Đồ thị hàm số giao với trục tung tại M 0  ;1 . Ta có: 2
y  3x  3  y0  3  .
Phương trình tiếp tuyến của đồ thị hàm số tại M 0  ;1 là: y  3
 x  0 1 3  x 1.
Câu 19: Thể tích của khối trụ có bán kính đáy bằng 2 , độ dài đường sinh bằng 2 2 A. 8 . B. 4 . C. 4 2 . D. 8 2 . Lời giải Chọn C
Thể tích của khối trụ là: 2
V   r h  .2.2 2  4 2 .
Câu 20: Viết phương trình đường thẳng đi qua hai điểm A2;1; 3   , B3;0;  1 x  4  tx  2  tx  3 tx  4  t    
A. y  1 t .
B. y  1 t .
C. y t . D. y  1   t .     z  5  4tz  3   4tz  1 4tz  5  4tLời giải Chọn D 
Ta có: AB 1; 1; 4 . 
Đường thẳng đi qua hai điểm A2;1; 3   , B3;0; 
1 nhận AB 1; 1; 4 làm vectơ chỉ phương có x  2  t
phương trình là: y 1 t . z  3   4t  x  4  t
Ta thấy điểm M 4; 1
 ;5 AB và đường thẳng y  1
  t và đường thẳng AB cùng vectơ chỉ z  5 4t
phương nên chúng trùng nhau chọn đáp án D.
Câu 21: Có bao nhiêu giá trị nguyên của m để phương trình sau là phương trình mặt cầu: 2 2 2 2
x y z  2x  4z m  6m 10  0 . Trang11 A. 5 . B. 0 . C. 2 . D. 3 . Lời giải Chọn D Phương trình 2 2 2
x y z  2ax  2by  2cz d  0 với 2 2 2
a b c d  0 là phương trình của một mặt cầu. 2a  2  a  1    2b  0 b   0 Từ đó ta có:    2c  4 c  2   2 2
d m 6m10 d m 6m10
Để phương trình đã cho là phương trình mặt cầu ta phải có 2 2 2
a b c d  0  1 0  4   2
m  6m 10  0 2
 m  6m  5  0  1  m  5
Do m nên có 3 giá trị tìm được m  2;3;  4 .
Câu 22: Người thợ làm một bể cá hai ngăn không nắp với thể tích 3
1296 dm . Người thợ này cắt các tấm
kính ghép lại một bể cá dạng hình hộp chữ nhật với ba kích thước a , b , c (mét) để đỡ tốn kính
nhất như hình vẽ và giả thiết rằng độ dày của kính không đáng kể. Tính a b c c b a A. 3, 3 . B. 3, 6 . C. 4, 8 . D. 3, 9 . Lời giải Chọn B Ta có 3 3
1296 dm  1, 296 m
Diện tích đáy bể cá là: ab
Diện tích các mặt bên bể cá là: 2ac  3bc
Diện tích kính cần dùng là: S ab  2ac  3bc
Theo bất đẳng thức Côsi áp dụng với 3 số dương ta có
S ab ac bc ab ac bc  abc2   2 3 3 3 2 3 3 .2 .3 3 6 3 6 1, 296 Dấu bằng xảy ra khi b   2cab  2ac
ab  2ac  3bc     3 2ac  3bc a b  2
Thay vào abc  1, 296 ta được 3
6c  1, 296  c  0, 6; b 1, 2; a 1,8
Vậy a b c  0,6 1, 2 1  ,8 3,6 1 1 Câu 23: Biết f
 xdx  6, tích phân f 2x  1dxbằng 1  0 A. 3. B. 6. C. 12. D. 2. Lời giải Trang12 Chọn A 1 1 1 1 1 1 Ta có f
 2x 1dx f
 2x 1d2x 1  f
 tdt  .6  3. 2 2 2 0 0 1 
Câu 24: Cho số phức z    i4 1
. Tìm phần ảo của số phức w iz A. 4  . B. 4 . C. 4i . D. 4  i . Lời giải Chọn A 4 2 2
Ta có z  1 i  1 i 1 i   2  i 2  i  4 
Do đó w  iz i  4    4  i . Vậy phần ảo là: -4
Câu 25: Đồ thị hàm số nào sau đây không cắt trục hoành? x 1 A. 3
y x  5x  2 . B. 4 2
y x  3x  3 . C. y  . D. 3
y x  3x 1. 2  x Lời giải Chọn B
Xét phương trình hoành độ giao điểm của đồ thị hàm số ở bốn phương án Phương trình 3
x  5x  2  0 có 1 nghiệm (Sử dụng máy tính cầm tay CASIO) Phương trình 4 2
x  3x  3  0 vô nghiệm (Sử dụng máy tính cầm tay CASIO) 
Phương trình x 1  0 có nghiệm x 1 (Sử dụng máy tính cầm tay CASIO) 2  x Phương trình 3
x  3x 1  0 có 3 nghiệm (Sử dụng máy tính cầm tay CASIO) Câu 26: Hàm số 2
y x  2 ln x đồng biến trên khoảng nào dưới đây? A.  1  ;0 . B. 0;  1 . C. 1; 2 . D.  1   ;1 Lời giải Chọn C ĐK: 2
x  0 và y  2x xx  1  2
y  0  2x  2  0   x 1 Bảng xét dấu
Vậy hàm số đồng biến trên 1; 2
Câu 27: Viết phương trình đường thẳng đi qua A1; 2
 ;0 và vuông góc với mặt phẳng
P: x 2y  2z 1 0 x 1 y  2 z x 1 y  2 z
A. x  2 y  2z  3  0 . B.   . C.
 . D. x  2y  2z  5  0 1 2  2 1 2  2 Lời giải Chọn B
Đường thẳng d  P  d có một vtcp là u  1;2;2 Trang13   Phương trình đườ x 1 y 2 z ng thẳng d :   1 2  2
Câu 28: Cho hình chóp S.ABC có AB  ; a BC  3 ; a CA  2 ;
a SA SB SC  2a . Tính thể tích khối chóp S.ABC 26 26 26 26 A. 3 a . B. 3 a . C. 3 a . D. 3 a 24 12 4 8 Lời giải Chọn B Xét ABC  có 2 2 2
BC AB AC ABC  vuông tại A
SA SB SC  hình chiếu của S lên  ABC  trùng với tâm đường tròn ngoại tiếp ABC
Gọi H là trung điểm của BC SH   ABC  2 1 1 a 2
* Diện tích tam giác ABC là S  .A . B AC  . . a 2a  2 2 2 2 2  BC    2 a 3 a 13 * 2 SH SC     2a       2  2 2   2 3 1 1 a 13 a 2 a 26
Thể tích khối chóp S.ABC là V  .SH.S  . .  3 ABC 3 2 2 12
Câu 29: Cho cấp số cộng u thỏa mãn u u  3;u u  1. Tìm công sai của cấp số cộng u n n  2 9 4 6 A. 4 . B. 2  . C. 2 . D. 3 Lời giải Chọn C u   u  3 u
  d u  8d  3
2u  9d  3 Có 2 9 1 1 1       d  2 u u  1
u  3d u  5d  1 2u  8d  1    4 6 1 1 1
Câu 30: Biết rằng 3 4 2 2a
. Giá trị của a bằng 5 15 1 5 A. . B. . C. . D. 6 2 2 2 Lời giải Chọn A  1  1 5 2 .   Có 3 3 2  2  3 6 4 2  2 . 2  2  2 Trang14
Câu 31: Cho a là số thực dương. Khi đó 3 log 8a bằng 4 3 3 3 A.  log a . B.  log a .
C. 2  3log a .
D. 6  6 log a . 2 2 2 2 2 2 2 Lời giải Chọn B 3 3 3 3 Ta có 3 3
log 8a  log 8  log a  log 2  log a   log a . 4 4 4 2 2 2 2 2 2 2
Câu 32: Viết phương trình mặt phẳng đi qua ba điểm A0, 2, 0; B 3, 0, 0;C 0, 0, 4 x y z x y z x y z x y z A.    0 . B.    0 . C.    1 . D.    1 . 2 3 4 3 2 4 3 2 4 2 3 4 Lời giải Chọn C x y z
Phương trình mặt phẳng đi qua ba điểm A0,2,0; B3,0,0;C 0,0,4 là    1 . 3 2 4 2  x
Câu 33: Hàm số y
có bao nhiêu đường tiệm cận? 2 x  4x  3 A. 2 . B. 1. C. 0 . D. 3 . Lời giải Chọn A
Tập xác định của hàm số D   ;  2\  1 .  2  x
Ta có: lim y  lim    0  y  0  là TCN 2  x x x  4x  3    x 1 Ta có: 2
x  4x  3  0   x  3  2  x   2  x  Vì lim y  lim 
   ; lim y  lim     .    2     2  x 1  x 1  x  4x  3   x 1  x 1  x  4x  3   Suy ra x 1là TCĐ  2  x  lim y  lim   
không xác định.Vì x  3 D 2  x 3  x 3  x  4x  3  
Vậy hàm số có 2 đường tiệm cận.
Câu 34: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a , mặt bên S AB là tam giác đều và
nằmtrong mặt phẳng vuông góc với đáy. Tính khoảng cách từ A đến mặt phẳng SCD 2a 21 a 14 3a 14 a 21 A. . B. . C. . D. . 7 6 7 6 Lời giải Chọn A Trang15
Gọi M , H lần lượt là trung điểm của CD, AB . Do mặt bên S AB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy nên
SH   ABCD  SH a 3 và
CD HM CD  SMH  .
Kẻ HK SM HK  SCD . Do đó d  ;
A SCD  d H;SCD  HK Xét tam giác SMH vuông tại H có 1 1 1 HS.HM 2 . a a 3 2a 21    HK    . 2 2 2 2 2 HK HS HM HS HM
a a 2 2 7 2 3 a
Vậy d A SCD  2 21 ;  HK  . 7
Câu 35: Tính thể tích khối lập phương nội tiếp mặt cầu có bán kính bằng 3. A. 18 3. B. 12 2. C. 24 3. D. 54 2. Lời giải Chọn C Đặ a
t AB a . Suy ra mặt cầu ngoại tiếp hình lập phương có bán kính 3 R   3  a  2 3 . 2 Trang16
Vậy thể tích khối lập phương cần tìm: 3
V a  24 3. 2 3 4
Câu 36: Cho hàm số y x x  
1  x  2  x  3 . Hàm số có bao nhiêu điểm cực trị? A. 3. B. 4. C. 1. D. 2. Lời giải Chọn?
y   x  2
1  x  23  x  34  2xx  
1  x  23  x  34  3x x  2
1  x  22  x  34  4x x  2
1 x  23 x  33  x  
1  x  22  x  33  x  
1  x  2 x  3  2x x  2 x  3  3x x  
1 x  3  4x x   1 x  2    x  
1  x  22  x  33  3 2
10x  40x  40x  6 x  1  x  2
 ng.kép  x  3  y  0   x  2  , 49 x  0  ,18  x  1  ,33
Vậy hàm số đã cho có 5 điểm cực trị. x 1 2 
Câu 37: Đạo hàm của hàm số y  bằng 3x x 1 2  x  1.2x x 1 2  ln 2 2x A. B. . C. . D. x  ln 2 ln 3. x ln 2 ln3. 3 x 1 .3 x  3x ln 3 3 Lời giải Chọn A   1 x x xx 1  2   2    2  2 2  y     2    2. .ln     x x ln2 ln3.  3   3     3  3 3  
Câu 38: Cho tam giác ABC vuông tại A có AB  3, AC  4 . Tính diện tích xung quanh khối nón sinh
ra khi cho tam giác ABC quay quanh trục AB . A. 20 . B. 15 . C. 12 . D. 60 . Lời giải Chọn A Trang17
Khối nón sinh ra có bán kính đáy là R AC  4 , đường sinh 2 2 l BC
AB AC  5 .
Vậy diện tích xung quanh khối nón bằng:  Rl  20 .
Câu 39: Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2
y x 16  x . Tính M m. A. 8  8 . B. 8 . C. 0. D. 8. Lời giải ChọnC Xét hàm số: 2
y x 16  x TXĐ:  4  ;4 .
Hàm số liên tục trên  4  ;4 . 2 2 x 16  2x 2
y  16  x   , x   4
 ;4 ; y  0  x  2  2 . 2 2 16  x 16  x y  4
   0 , y2 2  8, y 2  2  8  .
Vậy M  8, m  8  .
Câu 40: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA  2a và SA vuông góc với đáy.
Tính cos với  là góc giữa hai mặt phẳng SCD và  ABCD . 1 2 2 1 A. . B. . C. . D. . 5 5 3 3 Lời giải ChọnA
Ta có SCD   ABCD  CD và CD AD, SA CD  SAD . Suy ra   SDA .
Xét tam giác SAD vuông tại A có SA  2a , 2 2 SD
SA AD a 5 . AD 1 Vậy cos   . SD 5   
Câu 41: Cho hàm số y f x có đồ thị như hình vẽ. Hỏi hàm số   1  2022f f x y có bao nhiêu điểm cực trị ? A. 9 . B. 5 . C. 3 . D. 7 . Trang18 Lời giải ChọnA.
f f x  1
f f x   1 Có y  2022
y  f xf  f x    1 2022 ln 2022  0
f xf  f x   1  0
f x  0 x  2
 ; x  0; x 1      f
  f x   1  0 f  x  1
 ; f x 1; f x  2.
Dựa vào đồ thị, ta có: f x  1  có hai nghiệm đơn;
f x  1 có hai nghiệm đơn;
f x  2 có hai nghiệm đơn;
Vậy hàm số trên có 9 điểm cực trị.
Câu 42: Cho số phức z thỏa mãn z  1. Tìm giá trị lớn nhất của biểu thức P z 1  z i A. 8  4 2 . B. 2 . C. 2 2  2 . D. 2 2 . Lời giải Chọn C Trang19
Gọi A là điểm biểu diễn số phức z , suy ra tập hợp A là đường tròn C tâm O , bán kính bằng 1.
Gọi B , C lần lượt là hai điểm biểu diễn số phức 1, i ; ta có OB OC 1. Gọi 2
I là trung điểm BC suy ra OI  . 2 2 2    
Khi đó P AB AC  2 IB  IO R2 2 2 2  2     1  2 2 2     . 2 2    
Câu 43: Cho hàm số f x liên tục trên  và có đồ thị như hình vẽ. Giả sử m là tham số thự C. Hỏi
phương trình f f x   m có nhiều nhất bao nhiêu nghiệm thực? A. 5. B. 10. C. 7. D. 12. Lời giải Chọn B Trang20
Xét f f x   m (1), đặt f x  t,t  0
Phương trình (1) trở thành f t  m (2)
Ta thấy với mỗi t  0 
;1 thì (1) có 6 nghiệm phân biệt.
Nếu t  0 hoặc với mỗi t 1;3 thì (1) có có 4 nghiệm phân biệt.
Nếu t 1 thì (1) có 5 nghiệm.
Để (1) có nhiều nghiệm x nhất thì (2) có nhiều nghiệm dương nhất.
Từ đồ thị suy ra phương trình (2) có nhiều nhất là 2 nghiệm dương t , t với t  0;1 ,t  1;3 1   2   1 2
Khi đó với f x  t có 6 nghiệm x ; với f x  t có 4 nghiệm x . 1 2
Vậy phương trình (1) có nhiều nhất 10 nghiệm.
Câu 44: Có bao nhiêu số thực c để hình phẳng giới hạn bởi đồ thị hàm số 2
y x  4x c , trục hoành
và các đường thẳng x  2; x  4 có diện tích bằng 3 . A. 3 B. 0 C. 1 D. 2 Lời giải Chọn A Xét phương trình 2
x  4x c  0 (1) Xét hàm số 2
y x  4x c trên 2;4 , có BBT c   c
TH1: Phương trình (1) không có nghiệm trên đoạn   4 0 4 2; 4     . c  0 c  0 Trang21 Khi đó diện tích hình phẳng là:  25 4  4 4 c TM 3    x  16  2 S
x x c x  
 2x x c 2 6 4 d 4 dx  
 2x cx  2c   3   .  3  3 7  2 2 2 c  L  6
TH2: Phương trình (1) có nghiệm a 2;4  c 0;4. Ta có 2 2
a  4a c  0  c  a  4a . Khi đó diện tích hình phẳng là: a 4 a    x   xS
x  4x c 4
dx  x  4x c 3 3 2 2 2 2 dx   
 2x cx    2x cx  3   3  2 a 2 a 3 3 3  a   16   32   a  2a 2 2 2
   2a ca    2c    4c      
 2a ca  
 4a  2ca 16  6c  3   3   3   3  3 3 2a 4 2  
 4a  2a 2
a  4a 16  6 2 a  4a 3 2
a 10a  24a 16 . 3 3  3  15 4 a c  TM    Ta có 3 2 S  3 
a 10a  24a 16  3  2  4 . 3   a  3 c  3  TM
Vậy có 3 giá trị c thoả mãn. .
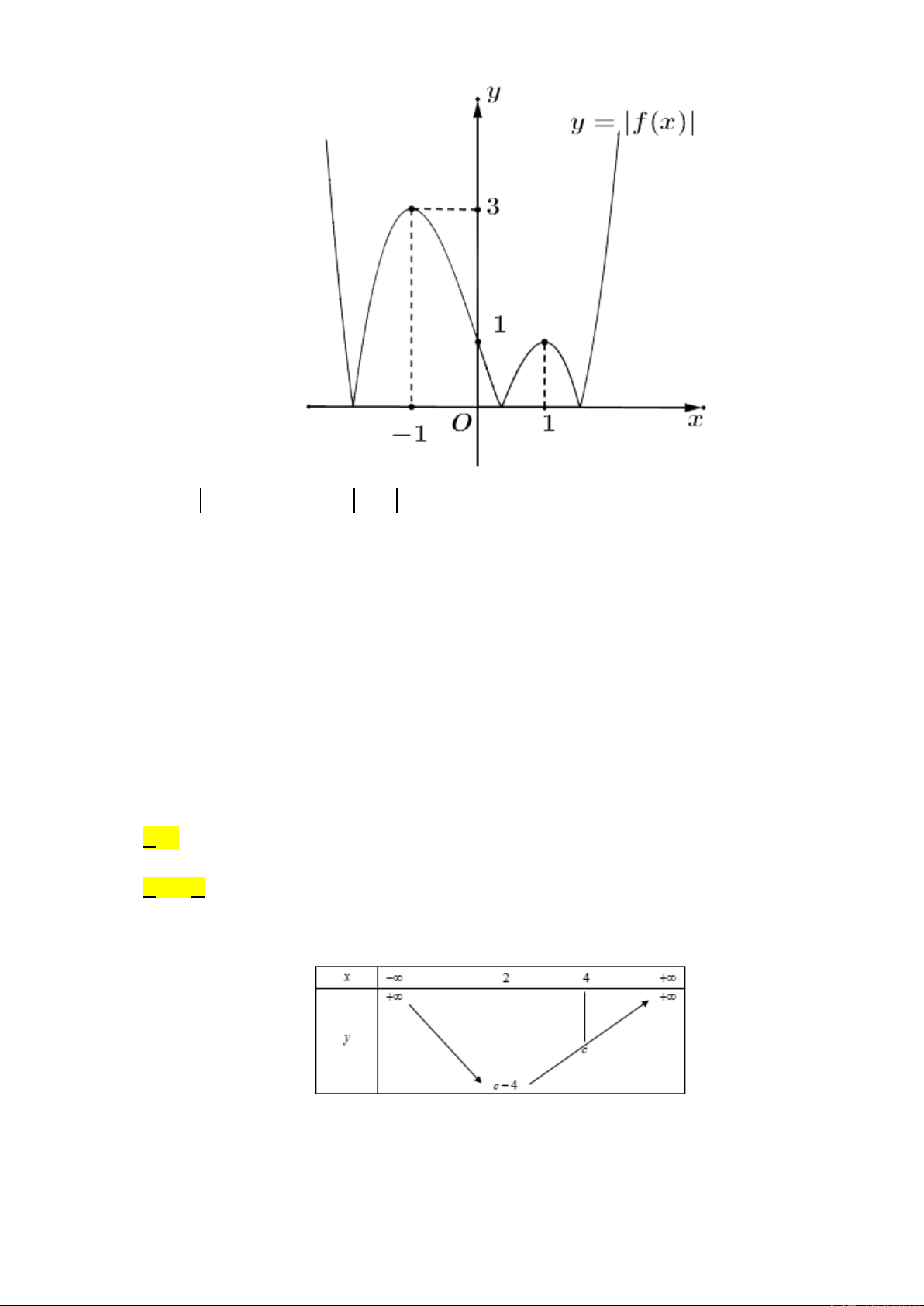
Câu 45: Cho hàm số y f x là hàm đa thức bậc 4. Biết hàm số y f ' x có đồ thị C như hình vẽ
và diện tích của hình phẳng giới hạn bởi đò thị C và trục hoành bằng 9. Gọi M , m lần lượt là
giá trị lớn nhất, giá trị nhỏ nhất của hàm số y f x trên đoạn  3
 ;2. Tính M m 16 32 27 5 A. . B. . C. D. . 3 3 3 3 Câu 2. y Câu 1. x Lời giải Chọn B
+ Từ đồ thị C ta có f x  a x    x  2 ' . 2 . 1 .
+ Do diện tích của hình phẳng giới hạn bởi đồ thị C và trục hoành bằng 9 Trang22 1
a x   x  2 4 dx   a   f x 4 . 2 . 1 9 '
 .x  2.x   2 1 3 3 2  x  
+ Ta có f x 2 '  0   x 1 x f '  x 4 dx  .
 x2.x 1 dx f x 4 2 8 2 
 2x x c 3 3 3 8
+ f 3  c 1, f 2  c  , f 2  c  8, f   1  c  8 32
1  M c  , m c  8  M m  3 3 3 x 1 y  2 z x  2 y 1 z 1
Câu 46: Trong không gian Oxyz cho hai đường thẳng d :   ; d :   và 1 1 2 1 2 2 1 1
mặt phẳng  P : x y  2z  5  0 . Lập phương trình đường thẳng d song song với mặt phẳng
P và cắt d ,d lần lượt tại ,
A B sao cho độ dài đoạn AB đạt giá trị nhỏ nhất. 1 2 x 1 y  2 z  2 x 1 y  2 z  2 A.   . B.   . 1 1 1  1 1 1 x 1 y  2 z  2 x 1 y  2 z  2 C.   . D.   . 1 1 1 1 1 1 Lời giải Chọn B
Do Ad A 1   t; 2
  2t;t ; do Bd B 2  2u;1 u;1 u 2   1   
AB  3 2u t;3 u  2t;1 u t   
+ Mặt phẳng  P có véc tơ pháp tuyến n  1;1; 2 . Do d / /  P  .
AB n  0  u t  4 2
AB  2t 8t  35  3 3 . Suy ra độ dài đoạn AB nhỏ nhất bằng 3 3 khi t  2.   Khi đó AB   3
 ;3;3  d đi qua điểm A1;2;2 và có véc tơ chỉ phương u  1;1  ;1    Suy ra phương trình x 1 y 2 z 2 d :   . Chọn B 1 1 1
Câu 47: Trong không gian với hệ tọa độ Oxyz , cho điểm (
A 1; 1; 3) và hai đurờng thã̉ng : x  4 y  2 z 1 x  2 y 1 z 1 d :   , d :  
. Viết phương trình đường thẳng d đi qua 1 2 1 4 2  1 1  1
điểm A , vuông góc với đuờng thẳng d và cắt đường thẳng d . 1 2 x 1 y 1 z  3 x 1 y 1 z  3 x 1 y 1 z  3 x 1 y 1 z  3 A.   B.   C.   D.   2 1 1 2 1 1 2 1 1 2 1 1 Lời giải Chọn D Giả sử 
d d M M 2  t; 1
  t;1 t AM  1 t; t  ;t  2 . 2      d có véc tơ chỉ phương u  1; 4; 2  . Do 1   1     
d d AM u AM .u  1 t  4t  2 t  2  0  t  1  AM  2; 1; 1 là véc tơ 1 1 1     x 1 y 1 z  3
chỉ phương của d . Phương trình chính tắc của d :   2 1  . 1 Trang23 z i
Câu 48: Biết rằng có đúng một số phức z thòa mãn | z  2i | |
z  2  4i | vả là số thuần ảo. Tính z i
tổng phần thực và phần ảo của z A. 4. B. 4  . C. 1. D. 1. Lời giải Chọn C
Giả sử z x yi,  , x y    .
z i z   i x   y  i x    y  i x   y  2   x  2   y  2 2 | 2 | | 2 4 | 2 2 4 2 2 4 2 2 2 2
x y  4y  4  x  4x  4  y  8y 16  x y  4 (1). z i
x   y   1 ix    y   1 i x    y   2 2
1 i x y  2y 1     . z i     mi x y 1 i
x   y  2 1
x   y  2 2 2 1
( Điều kiện x  y  2 2 1  0 ). z i 2 2
x y  2 y 1 Do là số thuần ảo 2 2 
 0  x y  2y 1  0(2). z i
x   y  2 2 1
Thay (1) vào (2) ta được phương trình:  y  42 5 2
y  2y 1  0  6y 15  0  y  . 2 5 3 3  5 Thay y
vào (1) ta được x   x y    1. 2 2 2 2
Câu 49: Cho hàm số f (x) có đạo hàm trên  và thỏa mãn 3 2
f (x  3x)  x  2 với mọi số thực x . 4 Tính 2 x . f (  x)dx 0 27 219 357 27 A. . B. . C. . D. . 4 8 4 8 Lời giải ChọnA. 4 Đặt 2
I x . f (  x)dx 0 2 u   x du  2 d x x Đặt    .
dv f (x)dx
v f (x) 4 4 Khi đó 4 2
I x f (x)  2 f (x)dx  16 f (4)  2 . x f (x)dx   . 0 0 0 4 4 Xét K  .
x f (x)dx t. f (t)dt   . 0 0 2
 f (t)  x  2 Đặt 3
t x  3x   . 2
dt  (3x +3)dx
t  0  x  0; t  4  x  1 . 1 Do đó 165 3 2 2
K  (x  3x)(x  2).(3x +3)dx   . 8 0
x  1  f (4)  3. Trang24 4 Vậy 165 27 2
I x . f (
x)dx 16.3 2.   . 8 4 0
Câu 50: Có bao nhiêu số nguyên dương a để phương trình sau có ít nhất một nghiệm thực
x  loga log log 1 x aa  2x  2 A. 8 . B. 1. C. 0 . D. 9 . Lời giải Chọn D Điều kiện a    , x  0
Phương trình ban đầu tương đương
a  loga log log 1 a xx  2x  2 (*) Đặt log a t x 1 (1) Suy ra loga xt 1
Phương trình (*) trở thành log a log  1  2 1 a t t xt
t  2x (2) Lấy (1) + (2) ta được log a log  2 a t t x  2x Xét hàm số   log a f u u
 2u với u  0 và a    ta có f u log a 1 u   
.log a  2  0 với mọi a   
Từ đó suy ra hàm số f u đồng biến trên 0;
Mà f t   f x suy ra t x log a log  1 x xx ax 1
+ Nếu x 1 thay lại ta có log2 log 1  2 a a
1  log a  0  a 1 (thỏa) Suy ra nhận a 1
+ Nếu x 1, khi đó ln x 1 log x log a log ax 1  xx 1  ln a x  ln x     1  log a  1 ln x
Từ đó suy ra log a  1  0  a  10 Mà a
  suy ra a 1;2;3;...;  9
Kết hợp 2 TH suy ra a 1;2;3;...;  9 Trang25