Đề kiểm tra một tiết chương 1 Đại số 10 NC trường THPT Thị xã Quảng Trị

Đề kiểm tra một tiết chương 1 Đại số 10 NC trường THPT Thị xã Quảng Trị gồm 2 mã đề, mỗi đề gồm 5 bài toán tự luận thuộc chủ đề mệnh đề và tập hợp, đề kiểm tra có lời giải chi tiết, mời các bạn đón xem

14 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 10

Môn: Toán 10

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Tiết 13: MA TRẬN ĐỀ KIỂM TRA MỘT TIẾT CHƯƠNG I
MÔN: ĐS 10 NC
Mạch kiến
thức
Mức độ nhận thức
Cộng
1 2 3
4
Mệnh đề-
phản chứng
1
2
1
1
2
3
Sai số
1
1
1
1
Tập hợp và
các phép toán
1
2
1
2
2
4
Tổng hợp
2
2
2
2
Tổng
1
2
2
3
2
3
2
2
7
10
MÔ TẢ TIÊU CHÍ NỘI DUNG KIỂM TRA
Câu 1 (2 điểm): Mệnh đề chứa biến (ký hiệu
,
): Xét đúng-sai và lập mệnh đề phủ định.
Câu 2 (2 điểm): a) Chứng minh bằng phản chứng.
b) Sai số (quy tròn số).
Câu 3 (1 điểm): Viết tập hợp dưới dạng liệt kê.
Câu 4 (4 điểm): a) Viết tập hợp dưới dạng khoảng hoặc nửa khoảng hoặc đoạn.
b) Tìm: giao, hợp, hiệu (phần bù).
c) Tổng hợp.
Câu 5 (1 điểm): Tổng hợp.
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA MỘT TIẾT CHƯƠNG I
Tổ: Toán Môn: ĐẠI SỐ 10 NC. Thời gian: 45 phút
ĐỀ 1
Câu 1 (2 điểm): Cho mệnh đề: “
,
x
R
30x 
” (1). Hãy xét tính đúng-sai (có giải thích) và
lập mệnh đề phủ định của mệnh đề (1).
Câu 2(2 điểm): a) Chứng minh định lý sau bằng phản chứng: “ Với mọi số tự nhiên
n
, nếu
53n
chia hết cho 3 thì
n
chia hết cho 3.”
b) Hãy quy tròn số gần đúng của
10 đến hàng phần nghìn.
Câu 3(1 điểm): Hãy viết tập hợp sau dưới dạng liệt kê các phần tử.
32
|x 7 2 16 0AxR x x
Câu 4 (4 điểm): Cho các tập hợp
|3Bx x
;
|2 4Cx x
a) Hãy viết các tập hợp B, C dưới dạng khoảng hoặc nửa khoảng hoặc đoạn.
b) Tìm
BC
,
BC
,
\BC
, CC
.
c) Cho tập hợp
|| 2 | 1ExRx
. Tìm

ECC
.
Câu 5 (1 điểm): Cho tập hợp
2
|x 2 1 2( 3)Dx x x . Hãy viết tập hợp D dưới dạng
liệt kê các phần tử.
TRƯỜNG THPT TX QUẢNG TRỊ
ĐỀ KIỂM TRA MỘT TIẾT CHƯƠNG I
Tổ: Toán Môn: ĐẠI SỐ 10 NC. Thời gian: 45 phút
ĐỀ 2
Câu 1 (2 điểm): Cho mệnh đề: “
,
x
R
2
20xx
” (1). Hãy xét tính đúng-sai (có giải thích)
và lập mệnh đề phủ định của mệnh đề (1).
Câu 2(2 điểm): a) Chứng minh định lý sau bằng phản chứng: “ Với mọi số tự nhiên
n
, nếu
76n
chia hết cho 3 thì
n
chia hết cho 3.”
b) Hãy quy tròn số gần đúng của
5 đến hàng phần trăm.
Câu 3(1 điểm): Hãy viết tập hợp sau dưới dạng liệt kê các phần tử.
32
|x 7 10 0AxR x x 
Câu 4 (4 điểm): Cho các tập hợp
|x 1Bx
;
|4 6Cx x
a) Hãy viết các tập hợp B, C dưới dạng khoảng hoặc nửa khoảng hoặc đoạn.
b) Tìm
BC
,
BC
,
B
\
C
,CC
.
c) Cho tập hợp
|| 1| 2ExRx
. Tìm

ECC
.
Câu 5 (1 điểm): Cho tập hợp
2
|x 2 1 2( 3)Dx x x . Hãy viết tập hợp D dưới dạng
liệt kê các phần tử.
HƯỚNG DẪN CHẤM ĐỀ 1
Câu NỘI DUNG ĐIỂM
Câu
1
- Xét được tính đúng-sai (có giải thích)
- Lập được mệnh đề phủ định
1
1
Câu
2
a) Giả sử tồn tại số tự nhiên n sao cho 5n+3chia hết cho 3 nhưng n
không chia hết cho 3.
Khi đó n = 3k+1 hoặc n = 3k+2 với
k
+Với n = 3k+1 ta có 5n+3 = 5(3k+1)+3 = 15k+8 không chia hết cho 3
(mâu thuẫn).
+Với n = 3k+2 ta có 5n+3 = 5(3k+2)+3 = 15k+13 không chia hết cho 3
(mâu thuẫn).
b) Quy tròn đúng: 3,162
0,5
0,5
1
Câu
3
+)
32 2
x7 2 160 ( 2)( 5 8)0xx x xx
+)Viết đúng tập hợp
565565
2, ,
22
A






0,5
0,5
Câu
4
a) Viết đúng
;3B 
,
2; 4C 
b) Tìm đúng
2;3BC

;4 ,B\ ; 2 , ( ; 2) (4; )
R
BC C CC
c)
21 1
21
2 1 3
xx
x
xx






Do đó
(;1)(3;)E 
Suy ra
[2;1) (3;4]EC
. Vậy
( ) ( ; 2) [1;3] (4; )
R
CE C .
0,5+0,5
Mỗi ý
đúng 0,5
0,5
0,5
Câu
5
Giải phương trình:
2
x212(3)xx
(1)
Điều kiện:
1
2
x
(*)
pt(1)
2
2 1 3 2 13 15xxx
210 2
(5)(23)(x5) 230
213 213
5
2
2 3 (2)
213
x
xx x
xx
x
x
x



 



(2) (2 3)( 2 1 3) 2xx
0,5
Đặt 2 1, t 0tx pt trở thành
2
(2)(3)2tt
2( )
117
()
2
117
2
tloai
t loai
t




Với
117
2
t

ta có
117
21
2
x


917 1117
21
24
xx


Vậy
11 17
5;
4
E





0,5
HƯỚNG DẪN CHẤM ĐỀ 2
Câu NỘI DUNG ĐIỂM
Câu 1 - Xét được tính đúng-sai (có giải thích)
- Lập được mệnh đề phủ định
1
1
Câu 2 a) Giả sử tồn tại số tự nhiên n sao cho 7n+6 chia hết cho 3 nhưng n không
chia hết cho 3.
Khi đó n = 3k+1 hoặc n = 3k+2 với
k
+Với n = 3k+1 ta có 7n+6 = 7(3k+1)+6 = 21k+13 không chia hết cho 3
(mâu thuẫn).
+Với n = 3k+2 ta có 7n+6 = 7(3k+2)+6 = 21k+20 không chia hết cho 3
(mâu thuẫn).
b) Quy tròn đúng: 2,24
0,5
0,5
1
Câu 3
+)
32 2
x7100(2)( 5)0xx x xx
+)Viết đúng tập hợp
121121
2, ,
22
A







0,5
0,5
Câu 4
a) Viết đúng
(1; )B 
,
(4;6)C 
b) Tìm đúng
(1; 6)BC
,
( 4; ), B\ [6; ), C ( ; 4] [6; )
R
BC C C
c)
12 1
12
2 2 4
xx
x
xx






Do đó
(;1][4;)E 
Suy ra
(4;1] [4;6)EC
. Vậy
( ) ( ; 4] ( 1;4) [6; )
R
CE C .
0,5+0,5
Mỗi ý
đúng 0,5
0,5
0,5
Câu 5
Giải phương trình:
2
x212(3)xx
(1)
Điều kiện:
1
2
x
(*)
pt(1)
2
2 1 3 2 13 15xxx
210 2
(5)(23)(x5) 230
213 213
5
2
2 3 (2)
213
x
xx x
xx
x
x
x



 



(2) (2 3)( 2 1 3) 2xx
Đặt
2 1, t 0tx
pt trở thành
2
(2)(3)2tt
2( )
117
()
2
117
2
t loai
t loai
t




Với
117
2
t

ta có
117
21
2
x


917 1117
21
24
xx


Vậy
11 17
5;
4
E





0,5
0,5
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Tiết 13: MA TRẬN ĐỀ KIỂM TRA MỘT TIẾT CHƯƠNG I MÔN: ĐS 10 NC Mạch kiến
Mức độ nhận thức Cộng thức 1 2 3 4 Mệnh đề- 1 1 2 phản chứng 2 1 3 1 1 Sai số 1 1 Tập hợp và 1 1 2 các phép toán 2 2 4 Tổng hợp 2 2 2 2 1 2 2 2 7 Tổng 2 3 3 2 10
MÔ TẢ TIÊU CHÍ NỘI DUNG KIỂM TRA
Câu 1 (2 điểm): Mệnh đề chứa biến (ký hiệu ,
  ): Xét đúng-sai và lập mệnh đề phủ định.
Câu 2 (2 điểm): a) Chứng minh bằng phản chứng. b) Sai số (quy tròn số).
Câu 3 (1 điểm): Viết tập hợp dưới dạng liệt kê.
Câu 4 (4 điểm): a) Viết tập hợp dưới dạng khoảng hoặc nửa khoảng hoặc đoạn.
b) Tìm: giao, hợp, hiệu (phần bù). c) Tổng hợp.
Câu 5 (1 điểm): Tổng hợp.
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA MỘT TIẾT CHƯƠNG I
Tổ: Toán Môn: ĐẠI SỐ 10 NC. Thời gian: 45 phút ĐỀ 1
Câu 1 (2 điểm): Cho mệnh đề: “x R, x  3  0 ” (1). Hãy xét tính đúng-sai (có giải thích) và
lập mệnh đề phủ định của mệnh đề (1).
Câu 2(2 điểm): a) Chứng minh định lý sau bằng phản chứng: “ Với mọi số tự nhiên n , nếu
5n  3chia hết cho 3 thì n chia hết cho 3.”
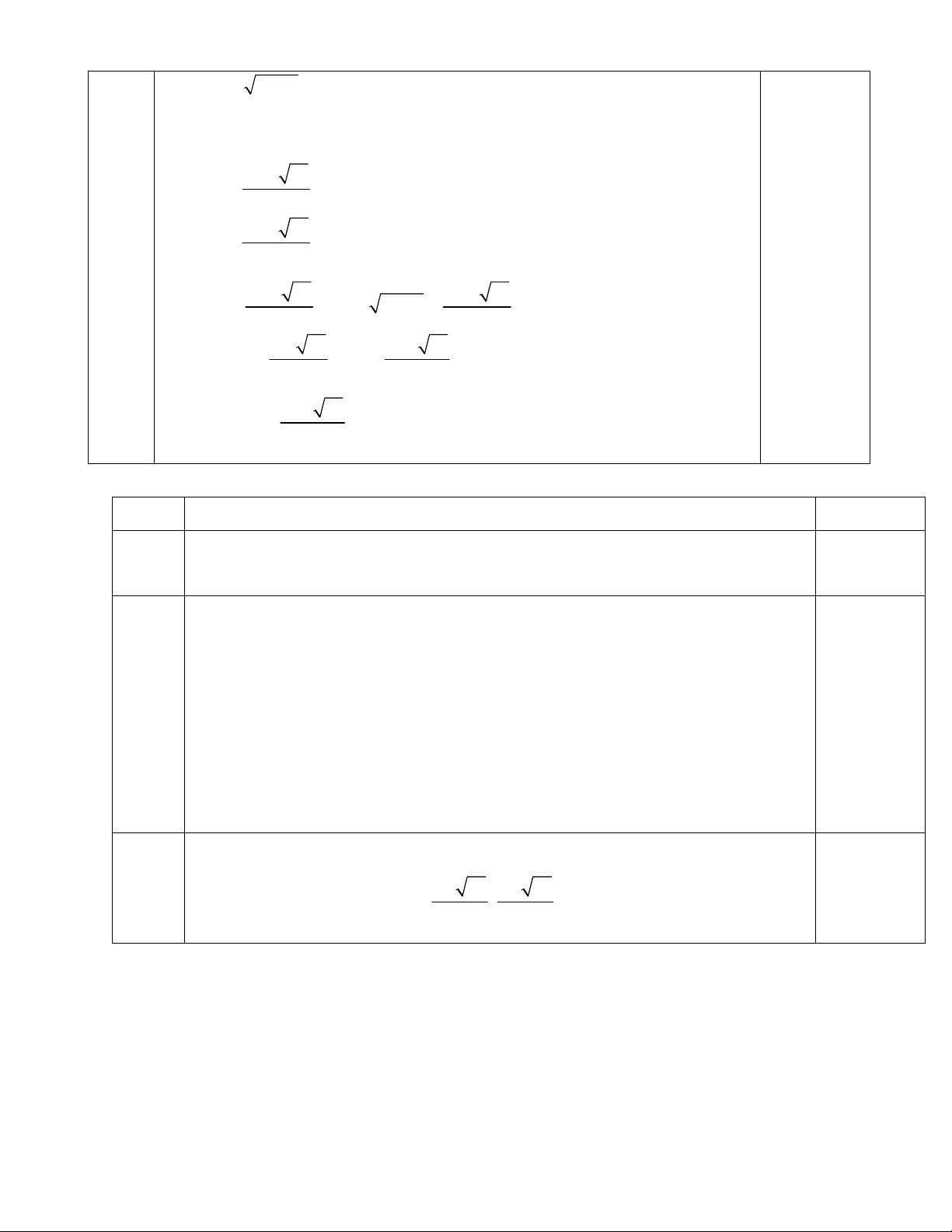
b) Hãy quy tròn số gần đúng của 10 đến hàng phần nghìn.
Câu 3(1 điểm): Hãy viết tập hợp sau dưới dạng liệt kê các phần tử. A   3 2
x R | x  7x  2x 16   0
Câu 4 (4 điểm): Cho các tập hợp B  x | x  
3 ; C  x  | 2   x   4
a) Hãy viết các tập hợp B, C dưới dạng khoảng hoặc nửa khoảng hoặc đoạn.
b) Tìm B C , B C , B \ C , C C .
c) Cho tập hợp E  xR || x  2 |  1 . Tìm C .   E C
Câu 5 (1 điểm): Cho tập hợp D   2
x   | x 2x 1  2(x  3)  . Hãy viết tập hợp D dưới dạng liệt kê các phần tử.
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ KIỂM TRA MỘT TIẾT CHƯƠNG I
Tổ: Toán Môn: ĐẠI SỐ 10 NC. Thời gian: 45 phút ĐỀ 2
Câu 1 (2 điểm): Cho mệnh đề: “ x R, 2
x  2x  0 ” (1). Hãy xét tính đúng-sai (có giải thích)
và lập mệnh đề phủ định của mệnh đề (1).
Câu 2(2 điểm): a) Chứng minh định lý sau bằng phản chứng: “ Với mọi số tự nhiên n , nếu
7n  6 chia hết cho 3 thì n chia hết cho 3.”
b) Hãy quy tròn số gần đúng của 5 đến hàng phần trăm.
Câu 3(1 điểm): Hãy viết tập hợp sau dưới dạng liệt kê các phần tử. A   3 2
x R | x  x  7x 10   0
Câu 4 (4 điểm): Cho các tập hợp B  x | x  
1 ; C  x  | 4   x   6
a) Hãy viết các tập hợp B, C dưới dạng khoảng hoặc nửa khoảng hoặc đoạn.
b) Tìm B C , B C , B \C ,C C .
c) Cho tập hợp E  x R || x 1|  2 . Tìm C .   E C
Câu 5 (1 điểm): Cho tập hợp D   2
x   | x 2x 1  2(x  3)  . Hãy viết tập hợp D dưới dạng liệt kê các phần tử.
HƯỚNG DẪN CHẤM ĐỀ 1 Câu NỘI DUNG ĐIỂM Câu
- Xét được tính đúng-sai (có giải thích) 1 1
- Lập được mệnh đề phủ định 1 Câu
a) Giả sử tồn tại số tự nhiên n sao cho 5n+3chia hết cho 3 nhưng n 2 không chia hết cho 3.
Khi đó n = 3k+1 hoặc n = 3k+2 với k  0,5
+Với n = 3k+1 ta có 5n+3 = 5(3k+1)+3 = 15k+8 không chia hết cho 3 (mâu thuẫn).
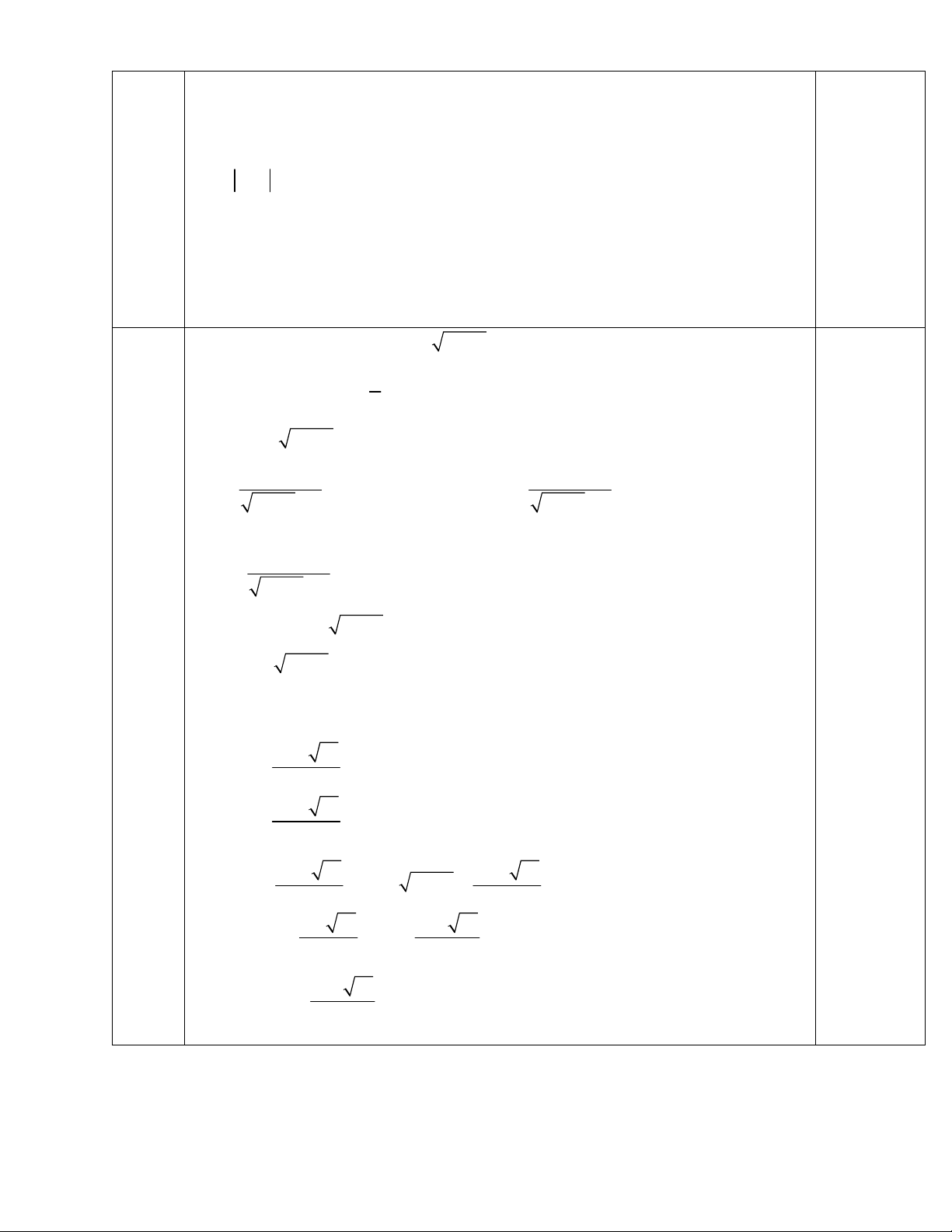
+Với n = 3k+2 ta có 5n+3 = 5(3k+2)+3 = 15k+13 không chia hết cho 3 (mâu thuẫn). 0,5 b) Quy tròn đúng: 3,162 1 Câu +) 3 2 2
x  7x  2x 16  0  (x  2)(x  5x  8)  0 0,5 3  5  65 5  65 
+)Viết đúng tập hợp A  2, ,   2 2   0,5 Câu
a) Viết đúng B    ;3 , C   2;  4 0,5+0,5 4
b) Tìm đúng B C   2;  3 Mỗi ý
B C   ;4
 ,B\ C   ;  2  ,C C  ( ;  2  )  (4;) đúng 0,5 Rx  2  1   x 1 c) x  2  1    x 2 1    x  3 0,5 Do đó E  ( ;  1)  (3;)
Suy ra E C  [2;1)  (3; 4]. Vậy 0,5
C (E C)  ( ;  2)  [1;3] (4;) . R Câu Giải phương trình: 2
x 2x 1  2(x  3) (1) 5 1
Điều kiện: x  (*) 2 pt(1) 2
 2x 1  3  2x 13x 15 2x 10  2 
 (x  5)(2x  3)  (x 5)  2x  3  0   2x 1  3  2x 1  3  x  5 0,5   2   2x  3 (2)  2x 1  3
(2)  (2x  3)( 2x 1  3)  2
Đặt t  2x 1, t  0 pt trở thành 2
(t  2)(t  3)  2
t  2(loai)   1 17  t  (loai)  2   1   17 t   2     Với 1 17 t  ta có 1 17 2x 1  2 2 0,5 9  17 11 17  2x 1   x  2 4    Vậy 11 17  E  5;    4  
HƯỚNG DẪN CHẤM ĐỀ 2 Câu NỘI DUNG ĐIỂM Câu 1
- Xét được tính đúng-sai (có giải thích) 1
- Lập được mệnh đề phủ định 1
Câu 2 a) Giả sử tồn tại số tự nhiên n sao cho 7n+6 chia hết cho 3 nhưng n không 0,5 chia hết cho 3.
Khi đó n = 3k+1 hoặc n = 3k+2 với k 
+Với n = 3k+1 ta có 7n+6 = 7(3k+1)+6 = 21k+13 không chia hết cho 3 (mâu thuẫn). 0,5
+Với n = 3k+2 ta có 7n+6 = 7(3k+2)+6 = 21k+20 không chia hết cho 3 (mâu thuẫn). b) Quy tròn đúng: 2,24 1 Câu 3 +) 3 2 2
x  x  7x 10  0  (x  2)(x x  5)  0 0,5  1 21 1 21 
+)Viết đúng tập hợp A   2,  ,   2 2   0,5 Câu 4
a) Viết đúng B  (1; )  , C  ( 4  ;6) 0,5+0,5
b) Tìm đúng B C  (1;6) , Mỗi ý B C  ( 4
 ;), B\ C  [6;),C C  ( ;  4][6;) R đúng 0,5 x 1  2 x  1  c) x 1  2    x 2 2     x  4 0,5 Do đó E  ( ;  1][4;) Suy ra
E C  (4; 1] [4;6) . Vậy
C (E C)  ( ;  4]   ( 1  ;4) [6;) . 0,5 R Câu 5 Giải phương trình: 2
x 2x 1  2(x  3) (1) 1
Điều kiện: x  (*) 2 pt(1) 2
 2x 1  3  2x 13x 15 2x 10  2 
 (x  5)(2x  3)  (x 5)  2x  3  0   2x 1  3  2x 1  3  x  5 0,5   2   2x  3 (2)  2x 1  3
(2)  (2x  3)( 2x 1  3)  2
Đặt t  2x 1, t  0 pt trở thành 2
(t  2)(t  3)  2 t  2(  loai)   1 17  t  (loai)  2   1 17 t   2     Với 1 17 t  ta có 1 17 2x 1  2 2 9  17 11 17  2x 1   x 2 4    Vậy 11 17  E  5;   0,5  4  