Đề kiểm tra một tiết Giải tích 12 chương 1 (Hàm số) trường THPT chuyên Lê Quý Đôn – Khánh Hòa

TRƯỜNG THPT CHUYÊN BÀI KIỂM TRA MỘT TIẾT LÊ QUÝ ĐÔN MÔN GIẢI TÍCH LỚP 12 TỔ TOÁN
Thời gian làm bài: 45 phút;
(25 câu trắc nghiệm) Mã đề thi 134
Họ và tên học sinh:.......................................................................... Lớp ……………………….
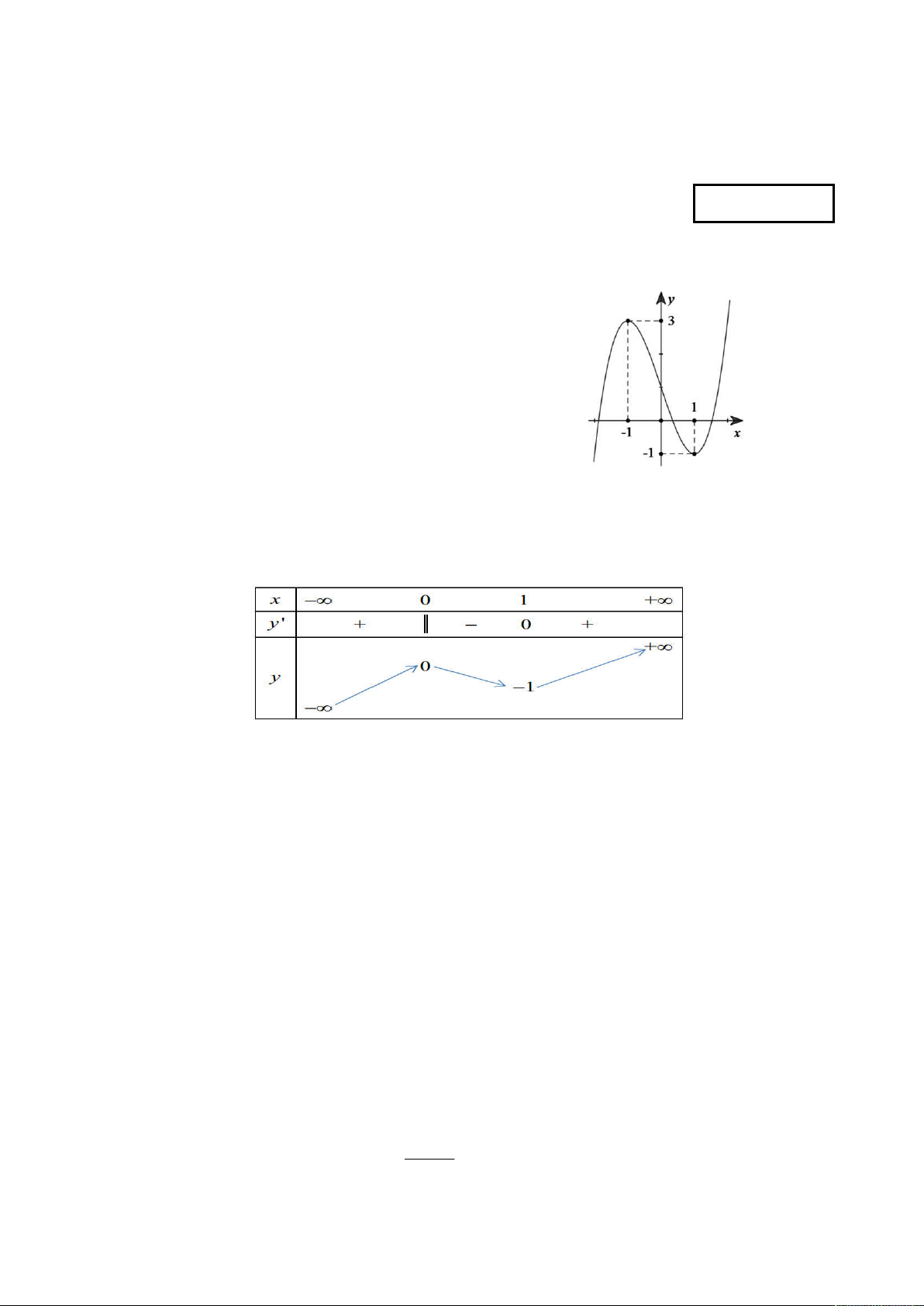
Câu 1: Đồ thị trong hình bên dưới là đồ thị của hàm số nào ? A. / 3
y  2x  6x 1 B. / 3 2
y  2x  3x 1 C. / 3
y  x  3x 1 D. / 3
y  x  3x 1 Phương án D.
Câu 2: Cho hàm số y  f (x) xác định và liên tục trên  có bảng biến thiên như hình bên dưới. Hãy
chọn khẳng định đúng
A. / Hàm số có giá trị cực tiểu bằng 1.
B. / Hàm số có giá trị lớn nhất bằng 0 và giá trị bé nhất bằng -1.
C. / Hàm số có đúng một cực trị.
D. / Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1.
Đạo hàm cấp 1 đổi dấu từ dương sang âm khi x vượt qua điểm x1 =0 và đạo hàm cấp 1 đổi dấu từ âm sang
dương khi x vượt qua điểm x2 =1. Phương án D. Câu 3: Cho hàm số 3
y  f (x)  x  ax  b ( a ≠ b ). Biết rằng tiếp tuyến với đồ thị tại các điểm có hoành
độ x  a và x  b song song với nhau. Khi đó giá trị f (1) bằng : A. / f (1)  1
B. / f (1)  a  b C. / f (1)  1
D. / f (1)  a  b f  x 2 '
 3x  a . Với giả thiết ta có 
 f ' a  f 'b 2 2 3
 a  a  3b  a     a  b a  b a  b   .  f  x 3
 x  ax  a  f   1  1 Chọn phương án A mx  4
Câu 4: Giá trị của tham số m để hàm số y 
nghịch biến trong khoảng  ;   1 là x  m A. / -2 < m  -1 B. / -2  m  2 C. / -1  m < 2 D. / -2 < m < 2
TXĐ D   \   m
Trang 1/6 – Bài giải mã đề 134 2 m  4 2 m  4  0 2  m  2 y ' 
. Hàm số nghịch biến trong khoảng  ;   1      2   m  1  .  x  m2 m  1 m  1   Phương án A.
Câu 5: Số giao điểm của đồ thị hàm số 3
y  x  4x với trục hoành là A. / 0 B. /1 C. /2 D. /3
Phương trình hoành độ giao điểm của đồ thị với trục hoành 3 x  x   x  2 4 0
x  4  0  x  0 Phương án B 2x 1
Câu 6: Hệ số góc tiếp tuyến của đồ thị hàm số y 
tại giao điểm của đồ thị với trục tung bằng x 1 A. / 1 B. / -1 C. / 2 D. / -2 2x 1 1 y   y '  . x 1  x  2 1
x  0  y  1 y '0  1 Phương án A.
Câu 7: Đường thẳng có phương trình y  2 là tiệm cận ngang của đồ thị hàm số nào bên dưới ? 2 1 2x 2 2x 1 x 1 2x 1 A. / y  B. / y  C. / y  D. / y  2 1 x  x 2 1 x  x 2x 1 1 x 2 1 2x Vì lim  2 .Phương án A. 2
x 1 x  x Câu 8: Hàm số 3 2 2016
y  2x  3(m  2)x  6(m 1)x  m
 2017 đồng biến trong khoảng 5;  thì tham
số m thoả điều kiện A. / m  4 B. / m  4 C. / m  4 D. m  4 3 2 2016
y  2x  3(m  2)x  6(m 1)x  m  2017 2 2
y '  6x  6(m  2)x  6(m 1)  6  x  m  2 x  m 1  
  m  22  4m   2 1  m  0; m    x  1 y '  0  
.Hàm số đồng biến trong khoảng 5;   m 1  5  m  4 . x  m 1  Phương án C
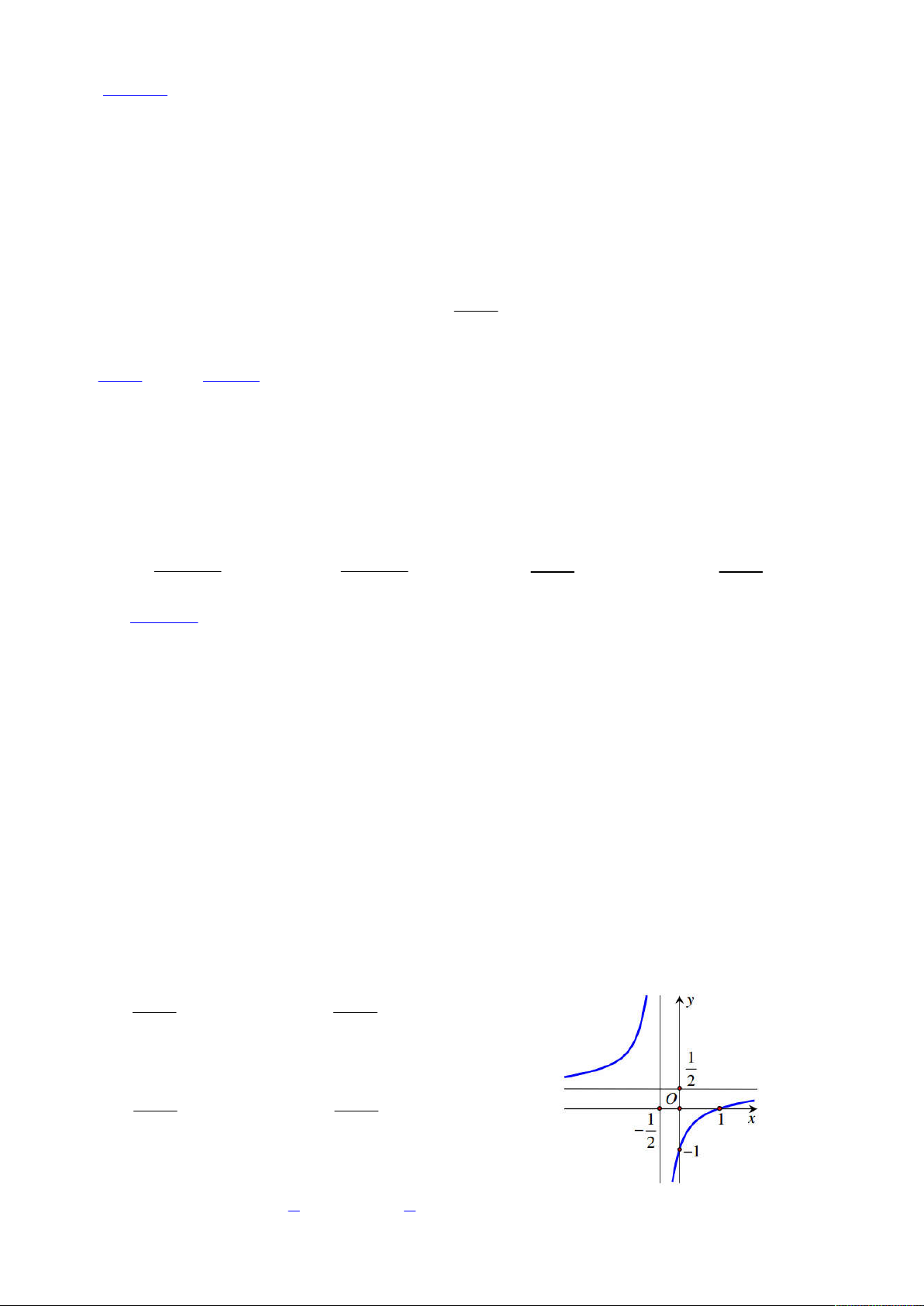
Câu 9: Đồ thị trong hình bên cạnh là đồ thị của hàm số nào bên dưới ? x 1 x 1 A. / y  B. / y  1 2x 2x 1 x 1 x 1 C. / y  D. / y  2x 1 2x 1 1 1
Đồ thị hàm số có TCĐ x   và TCN y 
và đi qua 2 điểm (1;0), (0;-1). Phương án D 2 2
Trang 2/6 – Bài giải mã đề 134
Câu 10: Cho hàm số y  f (x) có tập xác định D ( D   ) đạt cực tiểu tại x . Hãy chọn khẳng định 0 đúng
A. /Hàm số đã cho có giá trị bé nhất bằng f (x ) . 0
B. / Nếu hàm số có đạo hàm tại x thì tiếp tuyến với đồ thị tại điểm M  x ; f (x ) song song với trục 0 0  0 hoành.
C. / Nếu hàm số có đạo hàm tại x thì tiếp tuyến với đồ thị tại điểm M  x ; f (x ) song song với trục 0 0  0 tung.
D. / Hàm số có đạo hàm cấp một tại x và f '(x )  0 . 0 0
Phương án B. ( Điều kiện cần cực trị ).
Câu 11: Biết rằng hàm số y  f (x) đạt cực đại tại điểm x . Hãy chọn khẳng định đúng 0
A. / Đạo hàm f '(x) đổi dấu từ âm sang dương khi x đi qua x . 0
B. / Đạo hàm f '(x) đổi dấu từ dương sang âm khi x đi qua x . 0
C. / f '(x )  0 0
D. / f ' (x )  0 0
Phương án B. Đây là chỉ là một câu hỏi lý thuyết thôi !
Câu 12: Giá trị lớn nhất của hàm số 2
y  x  1 x bằng 2 A. / B. / 2 C. / 1 D. / 2 2 TXĐ D  1  ;1
Hàm số liên tục trên đoạn  1   ;1 2 x 1 x  x 2
y  x  1 x  y '  1  2 2 1 x 1 x  2 2 2 1   x  x x   2 2
y '  0  1 x  x  0     2  x  x  0 2  x  0   2  2 2 y   1  1; y   1  1; y      2 .GTLN bằng 2 .  2  2 2   Phương án B. Câu 13: Hàm số 3 2
y  x  3x  2016x  2017 có 2 điểm cực trị là x ; x thì tích x .x có giá trị bằng 1 2 1 2 A. / 2016 B. / 672 C. / - 672 D. / - 2016 3 2
y  x  3x  2016x  2017 2 2
 y '  3x  6x  2016 .
Vì a= 3 và c =-2016 trái dấu nên 2 2
y '  0  3x  6x  2016  0 luôn có 2 nghiệm x , x với 1 2 c 2016 x .x     672 .Phương án C. 1 2 a 3
Câu 14: Số điểm cực trị của hàm số 2
y  sin x  cos x trên đoạn 0;  là A. / 3 B. / 2 C. /1 D. / 0
y '  sin 2x  sin x
Trang 3/6 – Bài giải mã đề 134
y '  0  sin 2x  sin x  0  sin 2x  sin(x)  2k
2x  x  2k x     3 
.Vậy hàm số có 1 cực trị trên đoạn 0;  .Phương án C.
2x    x  2k  
x    2k   2 
x 0;   x  0; ;   3  x  2
Câu 15: Giá trị bé nhất của hàm số y  trên đoạn  8  ; 4   bằng x  3 A. / 2 B. / 6 C. / -2 D. / -6 x  2 5 y  ; y '   0; x
  D   \ 3 2   x  3  x  3
Hàm số đồng biến và liên tục trên đoạn  8  ; 4   . y  8    2 ; y  4
   6 .Miny = 2.Phương án A. Câu 16: Cho hàm số 3 2
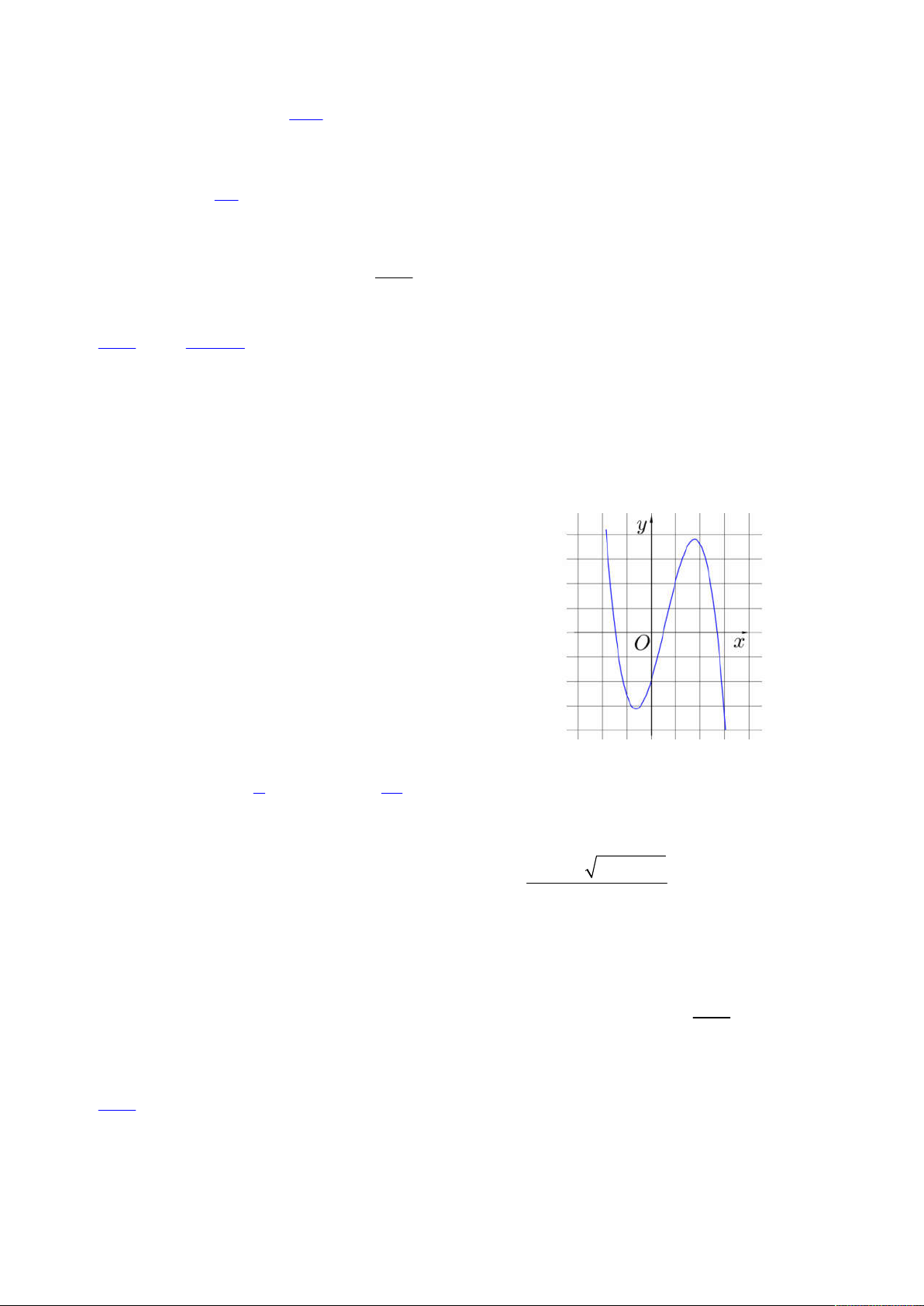
y  ax  bx  cx  d có đồ thị như hình bên dưới. Hãy chọn khẳng định đúng
A. / a  0;b  0; c  0; d  0
B. / a  0;b  0; c  0; d  0
C. / a  0;b  0; c  0; d  0
D. / a  0;b  0; c  0; d  0 Do x  x  a  0 CT CD 1 2b Do 2
y '  3ax  2bx  c ;  x  x    CT CD  0 2 3a
Do a  0  b  0 .Do y 0  d  0 .Do x  0  x
 y '(0)  c  0 .Phương án D. CT CD 2
2x 1 x  x  3
Câu 17: Tìm tất cả các tiệm cận đứng của đồ thị hàm số y  2 x  5x  6 A. / x  3  và x  2  B. / x  2 C. / x  3
D. / x  3 và x  2
Vì lim y   nên x = 2 không phải là tiệm cận đứng và vì lim y   nên x = 3 là tiệm cận đứng x2 x3 Phương án C x 1
Câu 18: Trong mặt phẳng toạ độ Oxy các đường tiệm cận của đồ thị hàm số y  tạo với các trục x  2
toạ độ một đa giác có diện tích bằng (đơn vị diện tích) A. / 1 B. / 3 C. / 2 D. / 4 x 1 y  x  2
TCĐ : x  2 ; TCN : y  1
Vậy các đường tiệm cận của đồ thị cùng với các trục tọa độ tạo thành HCN có 2 kích thước là 1 và 2.
Nên diện tích HCN bằng 2 (đvdt). Phương án C.
Trang 4/6 – Bài giải mã đề 134 2x 1
Câu 19: Phương trình tiếp tuyến với đồ thị hàm số y 
tại giao điểm của đồ thị với trục tung có x 1 phương trình là
A. / y  3x 1
B. / y  3x  2
C. / y  3x  2
D. / y  3x 1 2x 1 3 y   y  x 1  x  2 1
x  0  y  1
 .PTTT y  3x 1 .Phương án D. y '(0)  3 Câu 20: Hàm số 3 y 
x  x  2  x là hàm số đồng biến trên khoảng A. /  1  ;0 B. /  1  ;  C. / 0  ;1 D. / 1; 
TXĐ D  1;  2 3x 1 3 y 
x  x  2  x ; y '  1 > 0 x   1 2  x   1  2 x  x  2
Vậy hàm số đồng biến trên 1;  .Phương án D. 1 Câu 21: Hàm số 3 2 2 5 y 
x  mx  (m  m 1)x  m đạt cực đại tại điểm x  1 thì giá trị của tham số m 3 bằng m  0 A. / m = 0 B. /  C. / m = 3 D. / m = -3 m  3  1 3 2 2 5 y 
x  mx  (m  m 1)x  m 3 2 2
y '  x  2mx  (m  m 1)
y '  2x  2m
Hàm số đạt cực đại tại điểm x  1 2  y '(1)  0 1
  2m  m  m 1  0     y ' (1)  0  2  2m  0  Phương án C. 2
m  3m  0
m  0, m  3      m  3 1 m  0 1  m  
Câu 22: Với giá trị nào của tham số m thì đồ thị hàm số 3 2 2 2016
y  x  (m  m  2)x  (m  2017)x  2018
có 2 điểm cực trị cách đều trục tung ? m  1 A. / m = 1 B. /  C. / m = 2 D. / m = -1 m  2  3 2 2 2016
y  x  (m  m  2)x  (m  2017)x  2018 2
y  x   2 m  m   2016 ' 3 2 2 x  (m  2017) 2 
m  m  2  0
Để 2 điểm cực trị cách đều trục tung thì 
 m  1. Phương án D. 2016 m  2017  0 
Câu 23: Số điểm cực tiểu của hàm số 2016 y  16  x là A. /0 B. /1 C. / 2016 D. / 2015
Trang 5/6 – Bài giải mã đề 134 2016 y  16  x . Hàm số xác định khi 2016 16  x  0 2015 1008x y '  2016 16  x
y '  0  x  0
Đạo hàm đổi dấu từ dương sang âm khi vượt qua x = 0. Vậy x = 0 là điểm cực tiểu duy nhất của hàm số. Phương án A.
Câu 24: Đồ thị hàm số 3 2
y  x  3x  ax  b có điểm cực tiểu (
A 2; 2) thì tổng (a+b) có giá trị bằng A. / -2 B. /2 C. / -3 D. / 3 2
y '  3x  6x  a y '  6x  6  y '  2  0 12  12  a  0
Hàm số đạt CT tại điểm ( A 2; 2)      a  0 y '  2  0 6  0   Khi đó 3 2
y  x  3x  b Vì y 2  2
  8 12  b  2
  b  2  a  b  2 .Phương án B.
Câu 25: Biết rằng đồ thị hàm số 3 2
y  x  3x  4 cắt đường thằng có phương trình y  7  x tại một
điểm duy nhất. Tung độ giao điểm y đó là 0 A. / y  3 B. / y  4 C. / y  5 D. / y  6 0 0 0 0
Phương trình hoành độ giao điểm : 3 2 3 2 2
x  3x  4  7  x  x  3x  x  3  0  x  x  3  x  3  0   x  3 2 x   1  0  x  3
y  y 3  7  3  4 0   Phương án B. ĐÁP ÁN MÃ ĐỀ 134
1 { | } ) 6 ) | } ~ 11 { ) } ~ 16 { | } ) 21 { | ) ~
2 { | } ) 7 ) | } ~ 12 { ) } ~ 17 { | ) ~ 22 { | } )
3 ) | } ~ 8 { | ) ~ 13 { | ) ~ 18 { | ) ~ 23 ) | } ~
4 ) | } ~ 9 { | } ) 14 { | ) ~ 19 { | } ) 24 { ) } ~
5 { ) } ~ 10 { ) } ~ 15 ) | } ~ 20 { | } ) 25 { ) } ~
Trang 6/6 – Bài giải mã đề 134