Đề kiểm tra số 3 Toán 10 năm 2018 – 2019 trường THPT Đoàn Thượng – Hải Dương

Đề kiểm tra số 3 Toán 10 năm 2018 – 2019 trường THPT Đoàn Thượng – Hải Dương gồm 2 mã đề thi chẵn và lẻ, đề được biên soạn theo hình thức tự luận với 4 bài toán thuộc chủ đề hàm số bậc nhất và hàm số bậc hai thuộc chương trình Đại số 10 chương 2

12 6 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 10

Môn: Toán 10

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GD VÀ ĐT HẢI DƯƠNG
TRƯỜNG THPT ĐOÀN THƯỢNG
ĐỀ KIỂM TRA SỐ 3, NĂM HỌC 2018-2019
Môn: TOÁN 10
Thời gian làm bài: 45 phút (không tính thời gian giao đề)
- Họ và tên thí sinh: .................................................... – Số báo danh : .......................................
Câu 1. (3,0 điểm). Tìm tập xác định của các hàm số sau:
a)
2
3
6 8
y
x x
b)
5
3
2 4
y x
x
Câu 2. (3,0 điểm).
a) Cho
hàm số
2
2 2 3
khi 2
1
2 khi 2
x
x
f x
x
x x
. Tính giá trị biểu thức
2 2
P f f
.
b) Xác định parabol
P
:
2
y ax bx c
,
0,
a
biết
P
cắt trục tung tại điểm có tung độ
bằng
và có đỉnh
2;5 .
I
Câu 3 (2,0 điểm). Lập bảng biến thiên và vẽ đồ thị hàm số
2
2 3y x x
. Từ đó vẽ đồ thị hàm số
2
2 3.
y x x
Câu 4 (2,0 điểm).
a) Hàm số
f
xác định trên đoạn
1;5
có đồ thị như hình vẽ sau. Hãy cho biết sự biến thiên
của hàm số
f
trên đoạn
1;5
.
b) Gọi
1 2
,x x
là các nghiệm của phương trình:
2 2
2 1 0x mx m m
. Tìm các giá trị của m
để tổng
2 2
1 2
S x x
đạt giá trị nhỏ nhất.
-----------------------------HẾT-----------------------------
MÃ ĐỀ THI: LẺ
O
1
1
2
3
4
5
x
y
1
1
2
SỞ GD VÀ ĐT HẢI DƯƠNG
TRƯỜNG THPT ĐOÀN THƯỢNG
ĐỀ KIỂM TRA SỐ 3, NĂM HỌC 2018-2019
Môn: TOÁN 10
Thời gian làm bài: 45 phút (không tính thời gian giao đề)
- Họ và tên thí sinh: .................................................... – Số báo danh : .......................................
Câu 1. (3,0 điểm). Tìm tập xác định của các hàm số sau:
a)
2
5
4 3
y
x x
b)
5
3
2 4
y x
x
Câu 2. (3,0 điểm).
a) Cho
hàm số
2
2 1 3
khi 1
2
2 1 khi 1
x
x
f x
x
x x
. Tính giá trị biểu thức
1 1
P f f
.
b) Xác định parabol
P
:
2
y ax bx c
,
0,
a
biết
P
cắt trục tung tại điểm có tung độ
bằng
và có đỉnh
2; 3 .
I
Câu 3 (2,0 điểm). Lập bảng biến thiên và vẽ đồ thị hàm số
2
2 3y x x
. Từ đó vẽ đồ thị hàm số
2
2 3.
y x x
Câu 4 (2,0 điểm).
a) Hàm số
f
xác định trên đoạn
1;5
có đồ thị như hình vẽ sau. Hãy cho biết sự biến thiên
của hàm số
f
trên đoạn
1;5
.
b) Gọi
1 2
,x x
là các nghiệm của phương trình:
2 2
2 1 0x mx m m
. Tìm các giá trị của m
để tổng
2 2
1 2
S x x
đạt giá trị nhỏ nhất.
-----------------------------HẾT-----------------------------
MÃ ĐỀ THI: CHẴN
O
1
1
2
3
4
5
x
y
1
1
2
ĐÁP ÁN BIỂU ĐIỂM BÀI KIỂM TRA TOÁN 10- SỐ 3
Câu
ĐỀ LẺ Điểm
Câu 1
3đ
a) ĐK:
2
6 8 0
x x
0,5
2
4
x
x
(nếu hs viết
2
4
x
x
thì trừ 0,25 điểm)
0,5
Vậy tập xđ của hs là
/ 2;4
D
0,5
b) ĐK:
3 0
2 4 0
x
x
0,5
3
3
2
x
x
x
0,5
Vậy tập xđ của hs là
3;D

0,5
Câu 2
3đ
a) Ta có:
2
2 2 2 3
2 2 2 2
2 1
f f
3
P
.
1,0
b) Ta có
P
cắt trục tung tại điểm có tung độ bằng
: Khi
0
x
thì
1y
1c
.
0,5
Do parabol có đỉnh
2;5
I
nên ta có:
2
2
2 5
b
a
y
0,5
4
4 2 1 5
b a
a b
0,5
4 1
4 8 4 4
b a a
a a b
Vậy
P
:
2
4 1y x x
.
0,5
Câu 3
2đ
TXĐ:
0,25
1 0
a
, đỉnh
1;4
I
0,25
BBT đúng 0,25
Giao với các trục
0;3 , 1;0 , 3;0
0,25
Đồ thị
0,5
+ Do hàm số
2
2 3
y x x
là hàm số chẵn nên đồ thị nhận trục Oy làm trục đối xứng
Với
2
0 2 3x y x x
Giữ nguyên phần đồ thị bên phải trục Oy của hs đã vẽ, lấy đối xứng phần đồ thị đó qua
trục Oy ta được đths cần tìm.
0,25
Vẽ đúng đồ thị
(HS có thể vẽ hai đồ thị trên cùng một hình)
0,25
Câu 4
2đ
a) Hàm số đồng biến trên các khoảng
1;1
và
2;3
0,25
Hàm số nghịch biến trên các khoảng
1;2
và
3;5
(Nếu hs viết
1;1 2;3
thì cả bài trừ 0,25 điểm)
0,5
b)
2 2
2 1 0 1
x mx m m
Phương trình (1) có nghiệm
1 2
,x x
khi và chỉ khi
' 1 0 1
m m
0,25
Theo Viet:
1 2
2
1 2
2
. 1
x x m
x x m m
2
2 2 2
1 2 1 2 1 2
2 2 2 2
S x x x x x x m m
0,25
Lập BBT của hs
2
2 2 2
f m m m
trên
1;

0,25
Tìm được GTNN của S bằng 2 đạt được tại m = 1
0,25
Câu
ĐỀ CHẴN Điểm
Câu 1
3đ
a) ĐK:
2
4 3 0
x x
0,5
1
3
x
x
0,5
Vậy tập xđ của hs là
/ 1;3
D
0,5
b) ĐK:
3 0
2 4 0
x
x
0,5
3
2
2
x
x
x
0,5
Vậy tập xđ của hs là
2;D

0,5
Câu 2
3đ
a) Ta có:
2 2 2
f f
.
1,0
b) Ta có
P
cắt trục tung tại điểm có tung độ bằng
: Khi
0
x
thì
1y
1c
.
0,5
Do parabol có đỉnh
2; 3
I
nên ta có:
2
2
2 3
b
a
y
0,5
4
4 2 1 3
b a
a b
0,5
4 1
4 8 4 4
b a a
a a b
Vậy
P
:
2
4 1y x x
.
0,5
Câu 3
2đ
TXĐ:
2
2 3y x x
0,25
1 0
a
, đỉnh
1; 4
I
0,25
BBT đúng 0,25
Giao với các trục
0; 3 , 1;0 , 3;0
0,25
Đồ thị
0,5
+ Do hàm số
2
2 3
y x x
là hàm số chẵn nên đồ thị nhận trục Oy làm trục đối xứng
Với
2
0 2 3x y x x
Giữ nguyên phần đồ thị bên phải trục Oy của hs đã vẽ, lấy đối xứng phần đồ thị đó qua
trục Oy ta được đths cần tìm.
0,25
Vẽ đúng đồ thị
(HS có thể vẽ hai đồ thị trên cùng một hình)
0,25
Câu 4
2đ
a) Hàm số đồng biến trên các khoảng
1;1
và
2;3
0,25
Hàm số nghịch biến trên các khoảng
1;2
và
3;5
(Nếu hs viết
1;1 2;3
thì cả bài trừ 0,25 điểm)
0,5
b)
2 2
2 1 0 1
x mx m m
Phương trình (1) có nghiệm
1 2
,x x
khi và chỉ khi
' 1 0 1
m m
0,25
Theo Viet:
1 2
2
1 2
2
. 1
x x m
x x m m
2
2 2 2
1 2 1 2 1 2
2 2 2 2
S x x x x x x m m
0,25
Lập BBT của hs
2
2 2 2
f m m m
trên
1;

0,25
Tìm được GTNN của S bằng 2 đạt được tại m = 1
0,25
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD VÀ ĐT HẢI DƯƠNG
ĐỀ KIỂM TRA SỐ 3, NĂM HỌC 2018-2019
TRƯỜNG THPT ĐOÀN THƯỢNG Môn: TOÁN 10 MÃ ĐỀ THI: LẺ
Thời gian làm bài: 45 phút (không tính thời gian giao đề)
- Họ và tên thí sinh: .................................................... – Số báo danh : .......................................
Câu 1. (3,0 điểm). Tìm tập xác định của các hàm số sau: 3 5 a) y y x  3  2 x  6x  8 b) 2x  4 Câu 2. (3,0 điểm). a) Cho  2 x  2  3  khi x  2
hàm số f x   x 1
. Tính giá trị biểu thức P f 2  f  2   . 2 x  2 khi x  2  b)
Xác định parabol  P : 2
y ax bx c , a  0, biết  P cắt trục tung tại điểm có tung độ
bằng 1 và có đỉnh I 2;5.
Câu 3 (2,0 điểm). Lập bảng biến thiên và vẽ đồ thị hàm số 2
y  x  2x  3 . Từ đó vẽ đồ thị hàm số 2
y  x  2 x  3. Câu 4 (2,0 điểm).
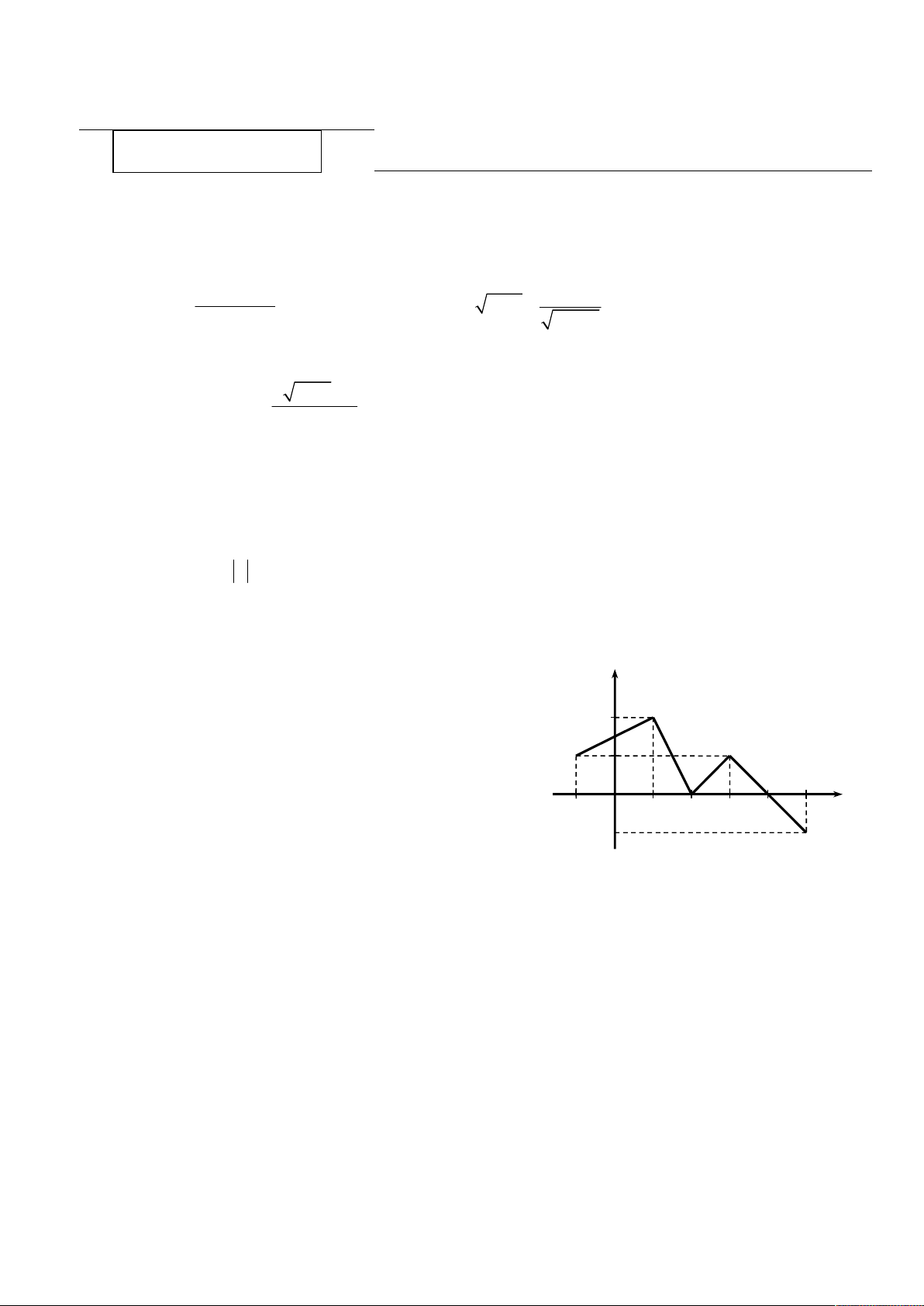
a) Hàm số f xác định trên đoạn  1  ; 
5 có đồ thị như hình vẽ sau. Hãy cho biết sự biến thiên
của hàm số f trên đoạn  1  ;  5 . y 2 1 x O 1  1 2 3 4 5 1 
b) Gọi x , x là các nghiệm của phương trình: 2 2
x  2mx m m 1  0 . Tìm các giá trị của m 1 2 để tổng 2 2
S x x đạt giá trị nhỏ nhất. 1 2
-----------------------------HẾT----------------------------- SỞ GD VÀ ĐT HẢI DƯƠNG
ĐỀ KIỂM TRA SỐ 3, NĂM HỌC 2018-2019
TRƯỜNG THPT ĐOÀN THƯỢNG Môn: TOÁN 10 MÃ ĐỀ THI: CHẴN
Thời gian làm bài: 45 phút (không tính thời gian giao đề)
- Họ và tên thí sinh: .................................................... – Số báo danh : .......................................
Câu 1. (3,0 điểm). Tìm tập xác định của các hàm số sau: 5 5 a) y y x  3  2 x  4x  3 b) 2x  4 Câu 2. (3,0 điểm). a) Cho  2 x 1  3  khi x  1
hàm số f x   x  2
. Tính giá trị biểu thức P f   1  f   1 . 2 2x 1 khi x  1  b)
Xác định parabol  P : 2
y ax bx c , a  0, biết  P cắt trục tung tại điểm có tung độ
bằng 1 và có đỉnh I 2; 3  .
Câu 3 (2,0 điểm). Lập bảng biến thiên và vẽ đồ thị hàm số 2
y x  2x  3 . Từ đó vẽ đồ thị hàm số 2
y x  2 x  3. Câu 4 (2,0 điểm).
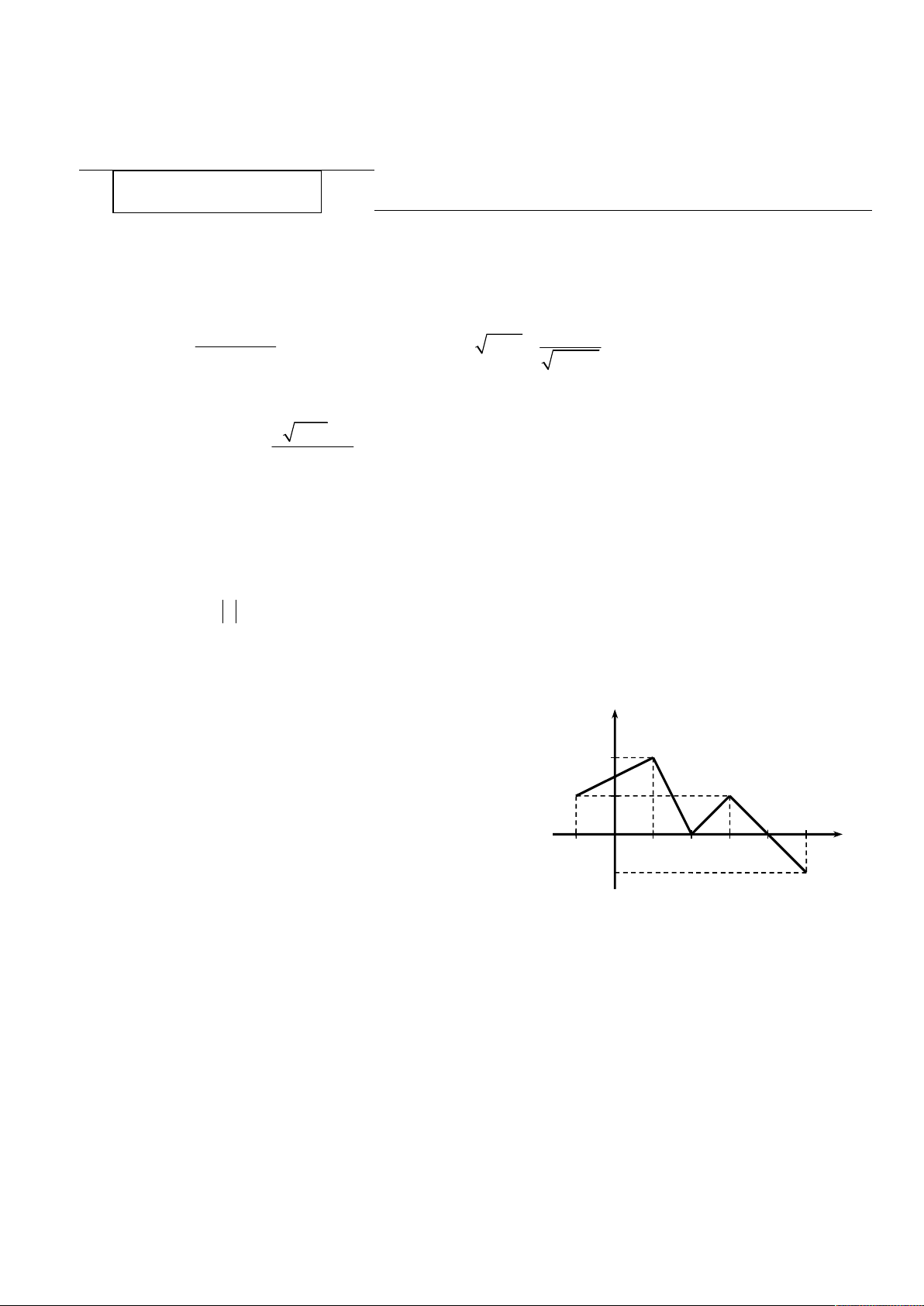
a) Hàm số f xác định trên đoạn  1  ; 
5 có đồ thị như hình vẽ sau. Hãy cho biết sự biến thiên
của hàm số f trên đoạn  1  ;  5 . y 2 1 x O 1  1 2 3 4 5 1 
b) Gọi x , x là các nghiệm của phương trình: 2 2
x  2mx m m 1  0 . Tìm các giá trị của m 1 2 để tổng 2 2
S x x đạt giá trị nhỏ nhất. 1 2
-----------------------------HẾT-----------------------------
ĐÁP ÁN BIỂU ĐIỂM BÀI KIỂM TRA TOÁN 10- SỐ 3 Câu ĐỀ LẺ Điểm Câu 1 a) ĐK: 2
x  6x  8  0 0,5 3đ x  2 x  2  
(nếu hs viết  
thì trừ 0,25 điểm) 0,5 x  4  x  4 
Vậy tập xđ của hs là D   / 2;  4 0,5 x  3  0 b) ĐK:  0,5 2x  4  0  x  3    x  3 0,5 x  2 
Vậy tập xđ của hs là D  3;  0,5 2 2  2  3
a) Ta có: f 2  f  2      2
 2  2  P  3. 1,0 2 1
b) Ta có  P cắt trục tung tại điểm có tung độ bằng 1: Khi x  0 thì y  1  c  1. 0,5  b   2 
Do parabol có đỉnh I 2;5 nên ta có: 2a  0,5 Câu 2  y 2  5  3đ b   4a  0,5
4a  2b 1  5  b   4  aa  1     4a  8a  4 b  4   0,5 Vậy  P : 2
y  x  4x 1. Câu 3 TXĐ:  0,25
a  1  0 , đỉnh I  1  ; 4 0,25 2đ BBT đúng 0,25
Giao với các trục 0;3,1;0, 3  ;0 0,25 Đồ thị 0,5 + Do hàm số 2
y  x  2 x  3 là hàm số chẵn nên đồ thị nhận trục Oy làm trục đối xứng Với 2
x  0  y  x  2x  3 0,25
Giữ nguyên phần đồ thị bên phải trục Oy của hs đã vẽ, lấy đối xứng phần đồ thị đó qua
trục Oy ta được đths cần tìm. Vẽ đúng đồ thị 0,25
(HS có thể vẽ hai đồ thị trên cùng một hình)
Câu 4 a) Hàm số đồng biến trên các khoảng  1   ;1 và 2;3 0,25 2đ
Hàm số nghịch biến trên các khoảng 1; 2 và 3;5 0,5 (Nếu hs viết  1  
;1  2;3 thì cả bài trừ 0,25 điểm) 2 2
b) x  2mx m m 1  0   1 0,25
Phương trình (1) có nghiệm x , x khi và chỉ khi  '  m 1  0  m  1 1 2
x x  2m Theo Viet: 1 2  2
x .x m m 1  1 2 0,25
S x x   x x 2 2 2 2
 2x x  2m  2m  2 1 2 1 2 1 2
Lập BBT của hs f m 2
 2m  2m  2 trên 1; 0,25
Tìm được GTNN của S bằng 2 đạt được tại m = 1 0,25 Câu ĐỀ CHẴN Điểm Câu 1 a) ĐK: 2
x  4x  3  0 0,5 3đ x  1   0,5 x  3 
Vậy tập xđ của hs là D   / 1;  3 0,5 x  3  0 b) ĐK:  0,5 2x  4  0  x  3    x  2 0,5 x  2 
Vậy tập xđ của hs là D  2;  0,5
a) Ta có: f 2  f  2    2 . 1,0
b) Ta có  P cắt trục tung tại điểm có tung độ bằng 1: Khi x  0 thì y  1  c  1. 0,5  b   2 
Do parabol có đỉnh I 2; 3   nên ta có: 2a  0,5  Câu 2 y 2  3  3đ b   4  a  0,5
4a  2b 1  3  b   4  aa  1    4a  8a  4  b  4    0,5 Vậy  P : 2
y x  4x 1 . Câu 3 TXĐ:  2
y x  2x  3 0,25
a  1  0 , đỉnh I  1  ; 4   0,25 2đ BBT đúng 0,25 Giao với các trục 0; 3  ,1;0, 3  ;0 0,25 Đồ thị 0,5 + Do hàm số 2
y x  2 x  3 là hàm số chẵn nên đồ thị nhận trục Oy làm trục đối xứng Với 2
x  0  y x  2x  3 0,25
Giữ nguyên phần đồ thị bên phải trục Oy của hs đã vẽ, lấy đối xứng phần đồ thị đó qua
trục Oy ta được đths cần tìm. Vẽ đúng đồ thị 0,25
(HS có thể vẽ hai đồ thị trên cùng một hình)
Câu 4 a) Hàm số đồng biến trên các khoảng  1   ;1 và 2;3 0,25 2đ
Hàm số nghịch biến trên các khoảng 1; 2 và 3;5 0,5 (Nếu hs viết  1  
;1  2;3 thì cả bài trừ 0,25 điểm) b) 2 2
x  2mx m m 1  0   1 0,25
Phương trình (1) có nghiệm x , x khi và chỉ khi  '  m 1  0  m  1 1 2
x x  2m Theo Viet: 1 2  2
x .x m m 1  1 2 0,25
S x x   x x 2 2 2 2
 2x x  2m  2m  2 1 2 1 2 1 2
Lập BBT của hs f m 2
 2m  2m  2 trên 1; 0,25
Tìm được GTNN của S bằng 2 đạt được tại m = 1 0,25