












Preview text:
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC ƠNG V GIỚI HẠN HÀM SỐ LIÊN TỤC CHƯ
BÀI: GIỚI HẠN CỦA DÃY SỐ ĐỀ TEST SỐ 01
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án. Câu 1: Tìm 9 lim 2 + ? n→+∞ 1945n A. −∞ B. 1. C. 2 . D. +∞ .
Câu 2: Cho lim u =
v = − . Trong các mệnh đề sau, mệnh đề nào sai? n 3, lim n 1 n→+∞ n→+∞ A. lim (u u − v = .
B. lim (u + v = . C. lim (u v = − . D. lim n = 3 − . n. n ) 3 n n ) 2 n n ) 2 n→+∞ n→+∞ n→+∞ n→+∞ vn 2 Câu 3: Tìm 7n + 5n +1954 lim ? 2 n→+∞ n +1 A. +∞ B. 5. C. 1954. D. 7 .
Câu 4: Cho hai dãy số (u và (v thỏa mãn u ≥ v < n ∀ . Biết = = . Trong các n 0, n 0, lim u a v b n , lim n ) n ) n n→+∞ n→+∞
mệnh đề sau, mệnh đề nào đúng?
A. lim u = a .
B. lim u = a .
C. lim v = b .
D. lim v = b . n n→+∞ n n→+∞ n n→+∞ n n→+∞
Câu 5: Cho hai dãy số không âm (u và (v thỏa mãn lim u =
v = . Trong các mệnh đề sau, n 4, lim n 3 n ) n ) n→+∞ n→+∞ mệnh đề nào sai? A. lim u = .
B. lim u + v = . n 7 n 5 n 2 n→+∞ n→+∞
C. lim u + v = + . D. lim v = . n 3 n 7 n 2 21 n→+∞ n→+∞ 2 Câu 6: Tính 30n + 4n +1975 lim . n→+∞ n +1 A. 2 . B. 30 . C. +∞ . D. 0 .
Câu 7: Tìm công bội của cấp số nhân lùi vô hạn, biết S = 6; − 3 u = − . 1 A. 1 . B. 1 . C. 1 − . D. 1 − . 2 3 2 3
Câu 8: Tính tổng sau: 1 1 S = 1− + + .... 2 4 A. 1 . B. 3 . C. 2 . D. 1. 2 2 3 Page 1
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC
Câu 9: Cho cấp số nhân lùi vô hạn (un) với 3
un = . Tổng của cấp số nhân này bằng 4n A. 3. B. 2. C. 1. D. 6. Câu 10: Giới hạn ( 4
lim −n −5n +1 ) 1 bằng A. −∞ . B. +∞ . C. 1. D. 1 − .
Câu 11: Giới hạn lim(2n 5n − ) bằng A. +∞ . B. 2 . C. 2 − . D. −∞ . n 1 − Câu 12: Tính tổng 1 1 1 1 S 1 ... = − + − + + − + ... 5 25 125 5 A. 6 . B. 4 . C. 5 . D. 5 . 5 5 6 4
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời câu hỏi. Trong mỗi ý a), b), c), d) ở mỗi câu, thí
sinh chọn đúng hoặc sai.
Câu 1: Cho hai dãy số (u và (v với: 2
u = n + n + v = − n . Xét tính đúng sai của các mệnh đề n 1; n 1 n ) n ) sau. a) lim u = +∞ n . n→+∞ b) lim v = +∞ n . n→+∞ c) lim u v = −∞ n. n . n→+∞ d) lim vn = 0. n→+∞ un 2 − + 2
Câu 2: Cho hai dãy số ( 2n 4n 7 4n + 5
u và (v với u = , v = . n ) n ) n 2
8n + 3n +1 n 8n 1 a) lim u = n n→+∞ 2 b) 1 lim v − = n 0 n→+∞ 4
c) lim (2u − v = n 4 n ) 0 n→+∞ d) lim un =1 n→+∞ 2vn Page 2
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC
Câu 3: Xét quá trình tạo ra hình vuông như sau:
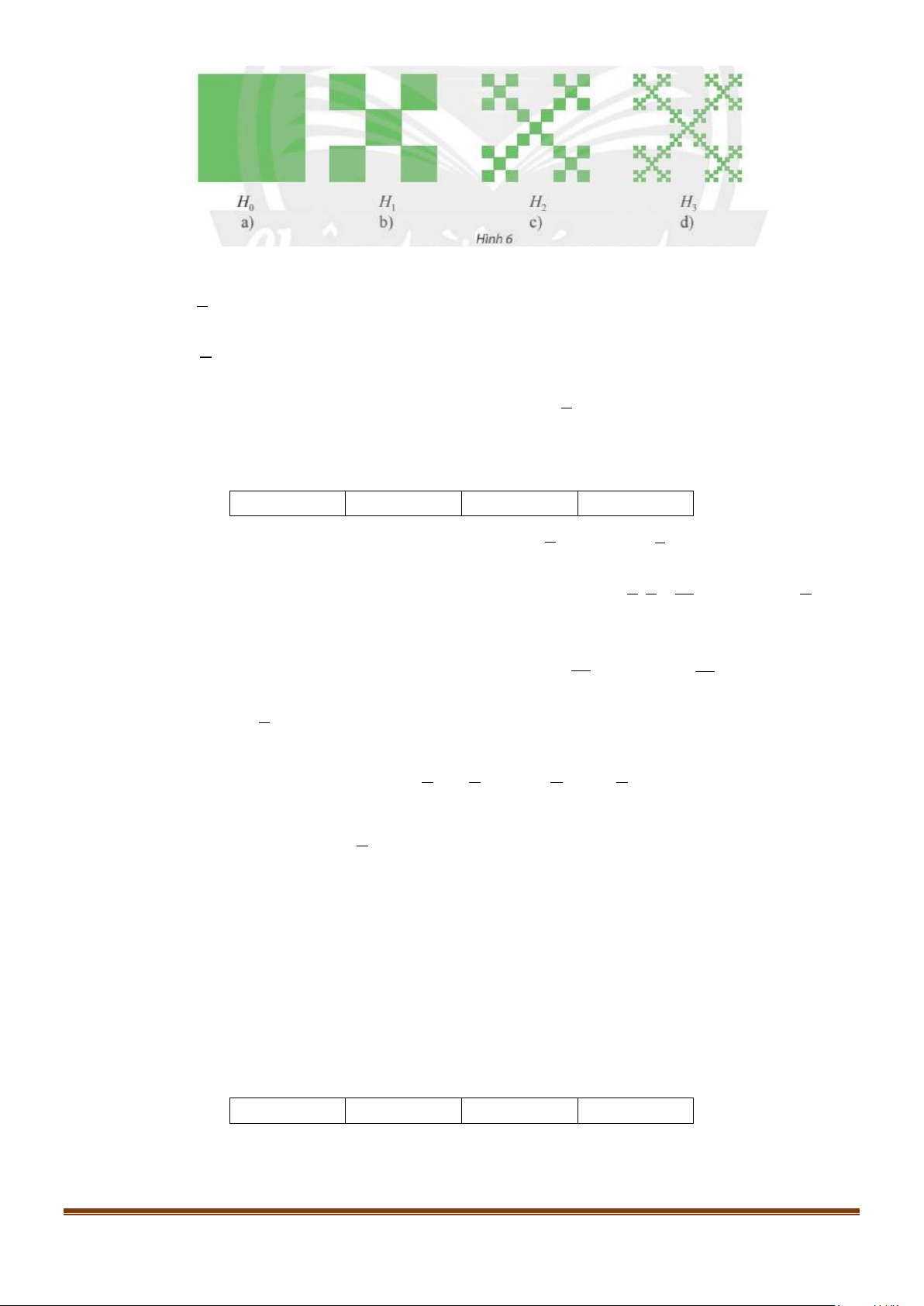
Bắt đầu hằng một hình vuông H0 cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông H H
0 thành chín hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình 1 (xem Hình 6b).
Tiếp theo, chia mỗi hình vuông của H1 thành chín hình vuông rồi bỏ đi bốn hình vuông, nhận
được hình H2(xem Hình 6c). Tiếp tục quá trình này, ta nhận được một dãy hình H n = . n ( 1,2,3,...)
Xét u là cạnh của mỗi hình vuông tương ứng với hình H n = . n ( 1,2,3,...) n a) 1 u = 1 3 b) 1 u = 2 2
c) u lập thành cấp số nhân lùi vô hạn với công bội 1 q = n 3
d) Gọi S là tổng diện tích tất cả các hình vuông ở hình H . Khi đó limS = n 0 n n
Câu 4: Một bệnh nhân hàng ngày phải uống một viên thuốc 100mg . Sau ngày đầu, trước mỗi lần uống,
hàm lượng thuốc cũ trong cơ thể vẫn còn tồn dư 5%. Xét tính đúng sai của các khẳng định sau
a) Ngay trước khi uống viên thuốc ngày thứ 2, hàm lượng thuốc trong cơ thể là 100mg .
b) Ngay sau khi uống viên thuốc ngày thứ 2, hàm lượng thuốc trong cơ thể là 105mg .
c) Hàm lượng thuốc trong cơ thể sau khi uống viên thuốc ngày thứ 4 là 105,2625mg .
d) Nếu sử dụng thuốc lâu ngày thì hàm lượng thuốc trong cơ thể hằng ngày được ước tính theo
công thức 100(1+ 5%)mg .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Tính giới hạn sau: + −
+ (kết quả làm tròn đến hàng phần trăm) →+∞ ( 2 2 lim 2n n 2n 1 n ) n
Câu 2: Biết giới hạn của 9 +1 lim
= a ( a,b tối giản). Giá trị của P = 2a + b là 2.3n −1 b
Câu 3: Bạn đang chuẩn bị làm một chiếc bánh nhiều lớp. Để phủ đều các lớp bánh, bạn sử dụng một loại
bột mịn. Lượng bột phủ cho lớp bánh đầu tiên là 100g. Ở mỗi lớp tiếp theo, lượng bột cần thiết
sẽ giảm đi 20% so với lớp trước đó do diện tích cần phủ giảm dần. Hãy tính tổng lượng bột bạn
cần sử dụng nếu bạn muốn phủ vô hạn lớp bánh theo quy tắc này.
Câu 4: Cho số a = 3,13131313...là số thập phân vô hạn tuần hoàn có chu kì là 13, số a được biểu diễn
dưới dạng phân số tối giản dạng x
a = , trong đó x và y là các số nguyên dương. Tìm tổng x + y y . Page 3
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC
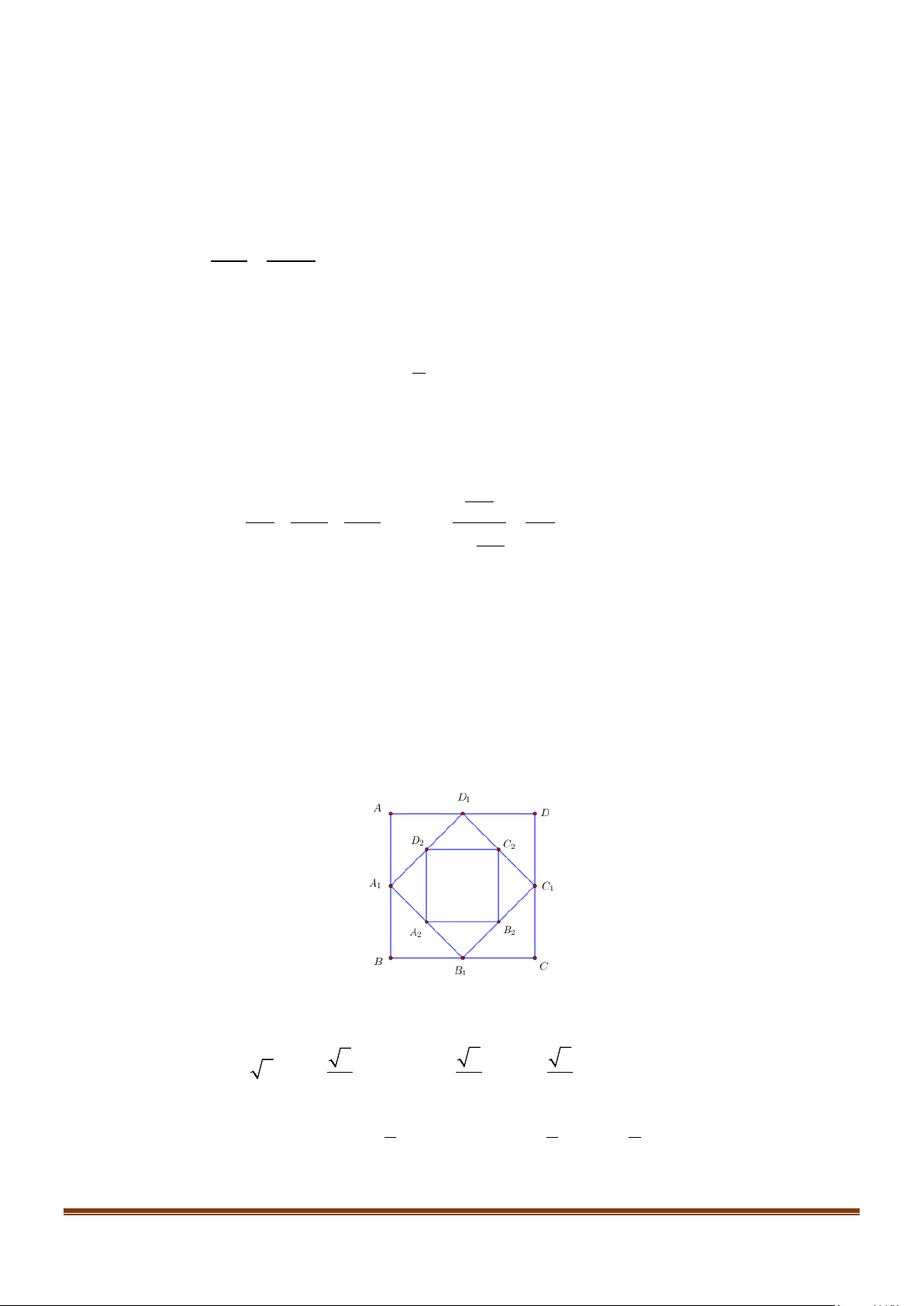
Câu 5: Cho hình vuông ABCD có cạnh bằng a và có diện tích S . Nối 4 trung điểm A , B , C , D 1 1 1 1 1 1
theo thứ tự của 4 cạnh AB, BC , CD , DA ta được hình vuông thứ hai có diện tích S2. Tiếp
tục làm như thế, ta được hình vuông thứ ba là A B C D S 2 2 2
2 có diện tích 3 , …và cứ tiếp tục làm
như thế. Giả sử quá trình trên kéo dài vô hạn. Tính tổng diện tích các hình vuông được tạo thành nếu a = 4cm . 1
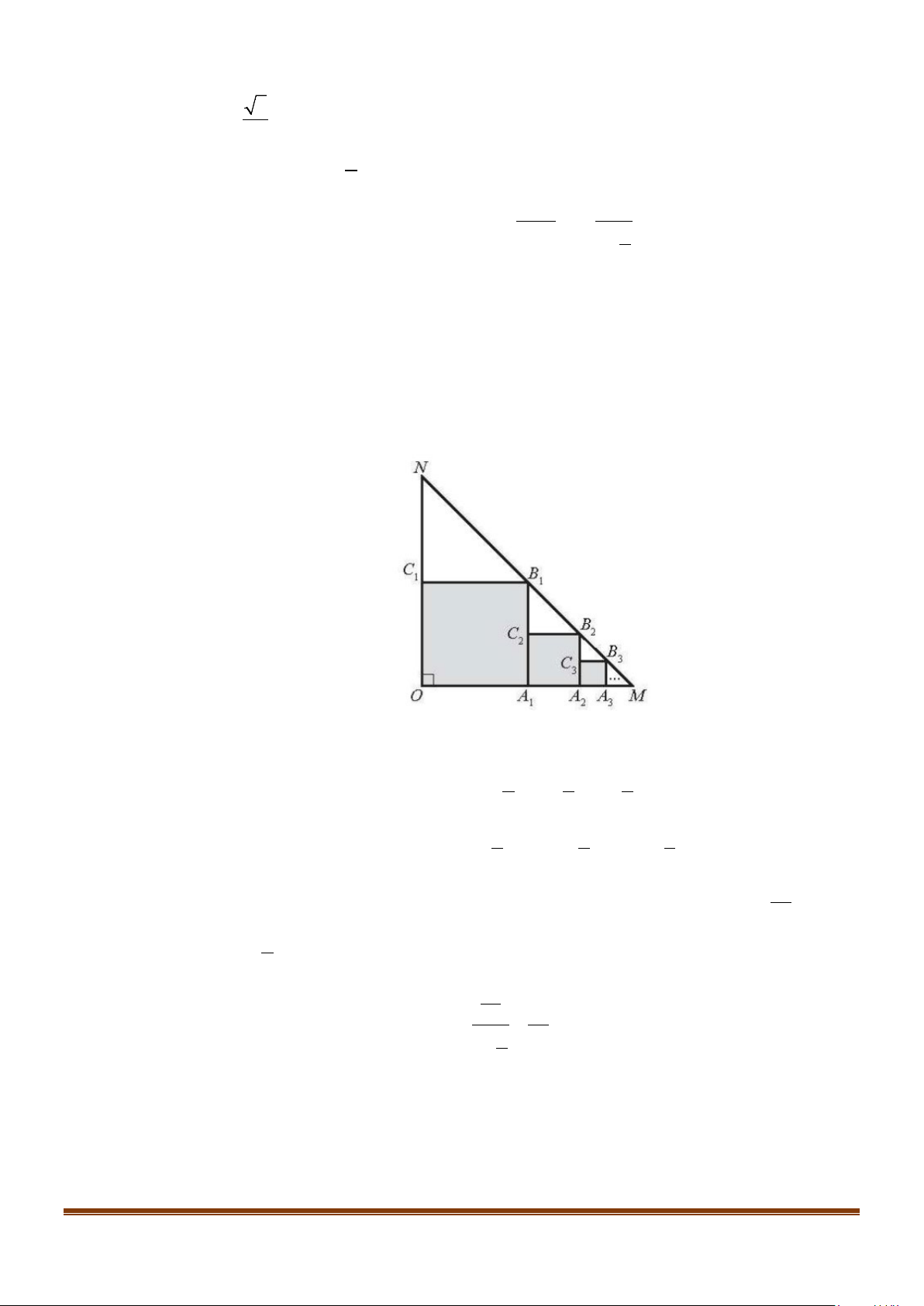
Câu 6: Cho tam giác OMN vuông cân tại O , OM = ON = 5. Trong tam giác OMN , vẽ hình vuông
OA B C sao cho các đỉnh A , B ,C lần lượt nằm trên các cạnh 1 1 1 1 1 1
OM , MN,ON . Trong tam giác
A MB , vẽ hình vuông A A B C sao cho các đỉnh A , B ,C lần lượt nằm trên các cạnh 1 1 1 2 2 2 2 2 2
A M , MB , A B . Tiếp tục quá trình đó mãi mãi, ta được một dãy các hình vuông (tham khảo 1 1 1 1
hình vẽ dưới đây). Tính tổng diện tích các hình vuông này.
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án. Câu 1: Tìm 9 lim 2 + ? n→+∞ 1945n A. −∞ B. 1. C. 2 . D. +∞ . Lời giải 9 9 1 9 lim 2 + = lim 2 + . = 2 + .0 = 2 . n→+∞ 1945 n n →+∞ 1945 n 1945
Câu 2: Cho lim u =
v = − . Trong các mệnh đề sau, mệnh đề nào sai? n 3, lim n 1 n→+∞ n→+∞ A. lim (u u − v = .
B. lim (u + v = . C. lim (u v = − . D. lim n = 3 − . n. n ) 3 n n ) 2 n n ) 2 n→+∞ n→+∞ n→+∞ n→+∞ vn Lời giải + lim (u − v = u − v = − − = . n n )
lim n lim n 3 ( ) 1 4 n→+∞ n→+∞ n→+∞ + lim (u + v = u + v = + − = . n n )
lim n lim n 3 ( ) 1 2 n→+∞ n→+∞ n→+∞ + lim (u v = u v = − = − . n. n )
lim n. lim n 3.( ) 1 3 n→+∞ n→+∞ n→+∞ lim u u n n n→+∞ 3 + Có lim = = = 3 − . n→+∞ v v − n lim n 1 n→+∞ 2 Câu 3: Tìm 7n + 5n +1954 lim ? 2 n→+∞ n +1 A. +∞ B. 5. C. 1954. D. 7 . Lời giải 5 1954 2 7 + + 2 7n + 5n +1954 n n 7 lim = lim = = 7 . 2 n→+∞ n +1 n→+∞ 1 1 1+ 2 n
Câu 4: Cho hai dãy số (u và (v thỏa mãn u ≥ v < n ∀ . Biết = = . Trong các n 0, n 0, lim u a v b n , lim n ) n ) n n→+∞ n→+∞
mệnh đề sau, mệnh đề nào đúng?
A. lim u = a .
B. lim u = a .
C. lim v = b .
D. lim v = b . n n→+∞ n n→+∞ n n→+∞ n n→+∞ Lời giải Có u ≥ và lim = nên = . n 0 u a lim u a n n→+∞ n n→+∞
Câu 5: Cho hai dãy số không âm (u và (v thỏa mãn lim u =
v = . Trong các mệnh đề sau, n 4, lim n 3 n ) n ) n→+∞ n→+∞ mệnh đề nào sai? A. lim u = .
B. lim u + v = . n 7 n 5 n 2 n→+∞ n→+∞
C. lim u + v = + . D. lim v = . n 3 n 7 n 2 21 n→+∞ n→+∞ Lời giải Có u ≥ và = nên = = . n 0 lim u lim un 4 2 n 4 n→+∞ n→+∞ Page 5
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC
Có v ≥ và lim u = nên lim v = . n 3 n 3 n 0 n→+∞ n→+∞ Có lim (u + v = + = = . n 7 n ) 4 7.3 25 5 n→+∞ 2 Câu 6: Tính 30n + 4n +1975 lim . n→+∞ n +1 A. 2 . B. 30 . C. +∞ . D. 0 . Lời giải 30 1975 2 + 4 + 2 + + Ta có 30n 4n 1975 n n 4 lim = lim = = 2 . n→+∞ n +1 1 1 1+ n
Câu 7: Tìm công bội của cấp số nhân lùi vô hạn, biết S = 6; − 3 u = − . 1 A. 1 . B. 1 . C. 1 − . D. 1 − . 2 3 2 3 Lời giải − + Ta có: u 3 1 1 S = ( q < )1 ⇒ 6 − = ⇒ q = . 1− q 1− q 2
Câu 8: Tính tổng sau: 1 1 S = 1− + + .... 2 4 A. 1 . B. 3 . C. 2 . D. 1. 2 2 3 Lời giải
+ Do các số hạng của vế phải của tổng S lập thành một cấp số nhân lùi vô hạn có số hạng đầu 1 1 u =1,q = − . 2 + Áp dụng công thức: u1 S = . 1− q + Ta được: 1 1 1 2 S = 1− + + .... = 1. = . 2 4 1 3 1+ 2
Câu 9: Cho cấp số nhân lùi vô hạn (un) với 3
un = . Tổng của cấp số nhân này bằng 4n A. 3. B. 2. C. 1. D. 6. Lời giải
Gọi q là công bội của cấp số nhân (un). Ta có n un 1+ 3 3 3 4 1 un 1 = ⇒ = = = ⇔ = + unq q : . q . n 1 u 4 + 4n 4.4n n 3 4 Số hạng đầu tiên 3 u 1
u = . Suy ra tổng của cấp số nhân lùi vô hạn này là 1 3 3 S = = : =1. 4 1− q 4 4 Câu 10: Giới hạn ( 4
lim −n −5n +1 ) 1 bằng A. −∞ . B. +∞ . C. 1. D. 1 − . Lời giải Ta có Page 6
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC ( 4n n ) 4 5 11 lim 5 11 lim n 1 − − + = − − + = . −∞ 3 4 n n 5 11 Vì 4 lim n ; lim 1 = +∞ − − + = 1 − 3 4 n n
Câu 11: Giới hạn lim(2n 5n − ) bằng A. +∞ . B. 2 . C. 2 − . D. −∞ . Lời giải ( n n ) n 2 n lim 2 5 lim5 − = − 1 = −∞ . 5 n Vì n 2 lim5 ; lim = +∞ − 1 = 1 − . 5 n 1 − Câu 12: Tính tổng 1 1 1 1 S 1 ... = − + − + + − + ... 5 25 125 5 A. 6 . B. 4 . C. 5 . D. 5 . 5 5 6 4 Lời giải
Các số hạng của tổng lập thành cấp số nhân lùi vô hạn với u =1, 1 q = − . 1 5
Tổng của n số hạng đầu của cấp số nhân có u =1, 1 q = − bằng: 1 5 n 1 1 1 1 1 − 1 n − q S = − + − + + − = u . n 1 ... .1 5 25 125 5 1− q Vì: q <1, do đó: n 1 1 1 1 1 − u 1 5 1 S =1− + − +...+ − + ... = lim S = = = . 5 25 125 5 n 1− q 1 6 1− − 5 Vậy 5 S = . 6
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời câu hỏi. Trong mỗi ý a), b), c), d) ở mỗi câu, thí
sinh chọn đúng hoặc sai.
Câu 1: Cho hai dãy số (u và (v với: 2
u = n + n + v = − n . Xét tính đúng sai của các mệnh đề n 1; n 1 n ) n ) sau. a) lim u = +∞ n . n→+∞ b) lim v = +∞ n . n→+∞ c) lim u v = −∞ n. n . n→+∞ d) lim vn = 0. n→+∞ un Lời giải a) Đúng b) Sai c) Đúng d) Đúng Page 7
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC a) Đúng 2 2 1 1 lim u = n + n + = n + + = + ∞ . n lim ( 1) lim (1 ) 2 n→+∞ n→+∞ n→+∞ n n b) Sai 1 lim v = − n = n − − = − ∞ . n lim (1 ) lim ( 1 ) n→+∞ n→+∞ n→+∞ n c) Đúng 2 3 lim u v = n + n + − n = − n = −∞ . n. n lim ( 1)(1 ) lim (1 ) n→+∞ n→+∞ n→+∞ d) Đúng v − n n 1 lim = lim = 0. 2 n→+∞ n u →+∞ n + n + n 1 2 − + 2
Câu 2: Cho hai dãy số ( 2n 4n 7 4n + 5
u và (v với u = , v = . n ) n ) n 2
8n + 3n +1 n 8n 1 a) lim u = n n→+∞ 2 b) 1 lim v − = n 0 n→+∞ 4
c) lim (2u − v = n 4 n ) 0 n→+∞ d) lim un =1 n→+∞ 2vn Lời giải a) Sai b) Đúng c) Sai d) Sai 4 7 2 2 − + a) 2 2n − 4n + 7 n n 2 1 lim u = = = = Sai n lim lim 2 n→+∞
n→+∞ 8n + 3n +1 n→+∞ 3 1 8 4 8 + + 2 n n 5 2 4 + 2 b) 4n + 5 n 2 1 lim v = = = = 1 lim v ⇒ − = n 0 Đúng n lim lim n→+∞ n→+∞ 8 n n →+∞ 8 8 4 n→+∞ 4 c) ( u −v = u − v = − = n n ) 1 1 3 lim 4 4 lim n lim n 4. Sai n→+∞ n→+∞ n→+∞ 4 4 4 1 lim u d) u n n n→+∞ 4 1 lim = = = Sai n→+∞ 2v v n 2.lim 1 n 2 2. n→+∞ 4
Câu 3: Xét quá trình tạo ra hình vuông như sau:
Bắt đầu hằng một hình vuông H0 cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông H H
0 thành chín hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình 1 (xem Hình 6b).
Tiếp theo, chia mỗi hình vuông của H1 thành chín hình vuông rồi bỏ đi bốn hình vuông, nhận
được hình H2(xem Hình 6c). Tiếp tục quá trình này, ta nhận được một dãy hình H n = . n ( 1,2,3,...) Page 8
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC
Xét u là cạnh của mỗi hình vuông tương ứng với hình H n = . n ( 1,2,3,...) n a) 1 u = 1 3 b) 1 u = 2 2
c) u lập thành cấp số nhân lùi vô hạn với công bội 1 q = n 3
d) Gọi S là tổng diện tích tất cả các hình vuông ở hình H . Khi đó limS = n 0 n n Lời giải a) Đúng b) Sai c) Đúng d) Đúng 1 a) H 1 u =
1 có 5 hình vuông, mỗi hình vuông có cạnh bằng . Do đó . Vậy mệnh đề đúng. 3 1 3 b) H = 1 1 1 = 1 u = 2 có 2
5.5 5 hình vuông, mỗi hình vuông có cạnh bằng . . Do đó . Vậy 2 3 3 3 2 9 mệnh đề sai. 1 c) H . Do đó 1 u = là cấp số nhân lùi
n có 5n hình vuông, mỗi hình vuông có cạnh bằng 3n n 3n vô hạn với 1
q = . Vậy mệnh đề đúng 3 n n 2n n
d) Diện tích S của H là: n 1 1 n 1 5 = = = n n S 5 . . 5 . n 3 3 3 9 n Khi đó 5 lim S =
= . Vậy mệnh đề đúng. n lim 0 9
Câu 4: Một bệnh nhân hàng ngày phải uống một viên thuốc 100mg . Sau ngày đầu, trước mỗi lần uống,
hàm lượng thuốc cũ trong cơ thể vẫn còn tồn dư 5%. Xét tính đúng sai của các khẳng định sau
a) Ngay trước khi uống viên thuốc ngày thứ 2, hàm lượng thuốc trong cơ thể là 100mg .
b) Ngay sau khi uống viên thuốc ngày thứ 2, hàm lượng thuốc trong cơ thể là 105mg .
c) Hàm lượng thuốc trong cơ thể sau khi uống viên thuốc ngày thứ 4 là 105,2625mg .
d) Nếu sử dụng thuốc lâu ngày thì hàm lượng thuốc trong cơ thể hằng ngày được ước tính theo
công thức 100(1+ 5%)mg . Lời giải a) Sai b) Đúng c) Đúng d) Sai a) Sai.
Ngay trước khi uống viên thuốc ngày thứ 2, hàm lượng thuốc trong cơ thể là % 100.5 = 5mg . b) Đúng. Page 9
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC
Ngay sau khi uống viên thuốc ngày thứ 2, hàm lượng thuốc trong cơ thể là 100 + 5 =105mg . c) Đúng.
Sau khi uống viên thuốc ngày thứ 1, hàm lượng thuốc trong cơ thể là u =100mg . Sau khi 1
uống viên thuốc ngày thứ 2, hàm lượng thuốc trong cơ thể là 5 1 1 u u 100 100 100 1001 = + = ⋅ + = +
mg . Sau khi uống viên thuốc ngày thứ 3, hàm 2 1 100 20 20 2
lượng thuốc trong cơ thể là 1 1 1 u u 100 1001 = + = + +
mg . Sau khi uống viên 3 2 20 20 20
thuốc ngày thứ 4, hàm lượng thuốc trong cơ thể là 2 3 1 1 1 1 u u 100 1001 = + = + + +
= 105, 2625mg . 4 3 20 20 20 20 d) Sai. n − n Đặt 1 r r = , ta có 2 1 − 1
1+ r + r +...+ r =
, n ≥ 2, n∈ . 20 1− r
Nếu sử dụng thuốc lâu ngày thì hàm lượng thuốc trong cơ thể hằng ngày là n = n n r u r r r . n n n ( 1− −2 + + + + ) 1− 100 lim lim 100 ... 1 = lim100⋅ = →∞ →+∞ n→∞ 1− r 1− r
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Tính giới hạn sau: + −
+ (kết quả làm tròn đến hàng phần trăm) →+∞ ( 2 2 lim 2n n 2n 1 n ) Lời giải Trả lời: 0,35 2 2 2 2
2n + n − 2n +1
2n + n + 2n +1 Ta có: lim( 2 2
2n + n − 2n +1) ( )( ) = lim . 2 2
2n + n + 2n +1 1 1 n1− 1 n −1 − n n 2 = lim = lim = lim = . 2 2
2n + n + 2n +1 1 1 1 1 4 n 2 + + 2 + 2 + + 2 + 2 2 n n n n n
Câu 2: Biết giới hạn của 9 +1 lim
= a ( a,b tối giản). Giá trị của P = 2a + b là 2.3n −1 b Lời giải Trả lời: 4 n n + + 9n +1 ( )2 1 1 + 3 1 1 3 1 n n Ta có: 3 3 1 im l = im l = im l = lim = . 2.3n −1 2.3n −1 n 1 1 2 3 2 − 2 − 3n 3n
Do đó a = 1, b = 2 . Suy ra P = 2a + b = 2.1+ 2 = 4.
Câu 3: Bạn đang chuẩn bị làm một chiếc bánh nhiều lớp. Để phủ đều các lớp bánh, bạn sử dụng một loại
bột mịn. Lượng bột phủ cho lớp bánh đầu tiên là 100g. Ở mỗi lớp tiếp theo, lượng bột cần thiết
sẽ giảm đi 20% so với lớp trước đó do diện tích cần phủ giảm dần. Hãy tính tổng lượng bột bạn
cần sử dụng nếu bạn muốn phủ vô hạn lớp bánh theo quy tắc này. Page 10
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC Lời giải Trả lời: 500.
Lượng bột cần cho lớp đầu tiên: u = 100 g. 1
Do mỗi lớp tiếp theo lớp bột cần giảm đi 20% nên ta có: q = 1− 0,2 = 0,8 .
Khối lượng bột ở từng lớp lập thành một cấp số nhân với u = 100 và q = 0,8. 1
Tổng lượng bột cần dùng cho các lớp bánh là tổng của một cấp số nhân lùi vô hạn: u1 100 S = = = 500 1− q 1− 0.8
Vậy, tổng lượng bột cần để phủ vô hạn lớp bánh là 500 g.
Câu 4: Cho số a = 3,13131313...là số thập phân vô hạn tuần hoàn có chu kì là 13, số a được biểu diễn
dưới dạng phân số tối giản dạng x
a = , trong đó x và y là các số nguyên dương. Tìm tổng x + y y . Lời giải
Trả lời: 409 13 Ta có 13 13 13 100 310 a = 3+ + + + ... = 3+ = . 2 3 100 100 100 1 99 1− 100 x = 310 Suy ra
⇒ x + y = 409. y = 99
Câu 5: Cho hình vuông ABCD có cạnh bằng a và có diện tích S . Nối 4 trung điểm A , B , C , D 1 1 1 1 1 1
theo thứ tự của 4 cạnh AB, BC , CD , DA ta được hình vuông thứ hai có diện tích S2. Tiếp
tục làm như thế, ta được hình vuông thứ ba là A B C D S 2 2 2
2 có diện tích 3 , …và cứ tiếp tục làm
như thế. Giả sử quá trình trên kéo dài vô hạn. Tính tổng diện tích các hình vuông được tạo thành nếu a = 4cm . 1 Lời giải Trả lời: 32 2 Ta có: 2 2 2 A D = 2.AD = AD , C D = A D = AD ,… 1 1 1 2 2 2 1 1 2 2 2 Khi đó: 2 1 1 S 1 = AD , 2 2
S = A D = AD , 2 2 2
S = C D = A D = AD ,… 1 2 1 1 2 3 2 2 1 1 2 2 Page 11
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC
Cứ như vậy ta thấy cạnh của các hình vuông lập thành 1 cấp số nhân với số hạng đầu là AD và công bội 2 q =
, còn diện tích các hình vuông lập thành 1 cấp số nhân lùi vô hạn với số hạng 2
đầu là S và công bội 1 = . 1 q ' 2
Do đó tổng diện tích các hình vuông sẽ là: 1 1 S = S . = S . = 2S . 1 1 1 1− q ' 1 1− 2 Khi 2
a = 4 ⇒ S =16cm 2 ⇒ S = 32cm . 1 1
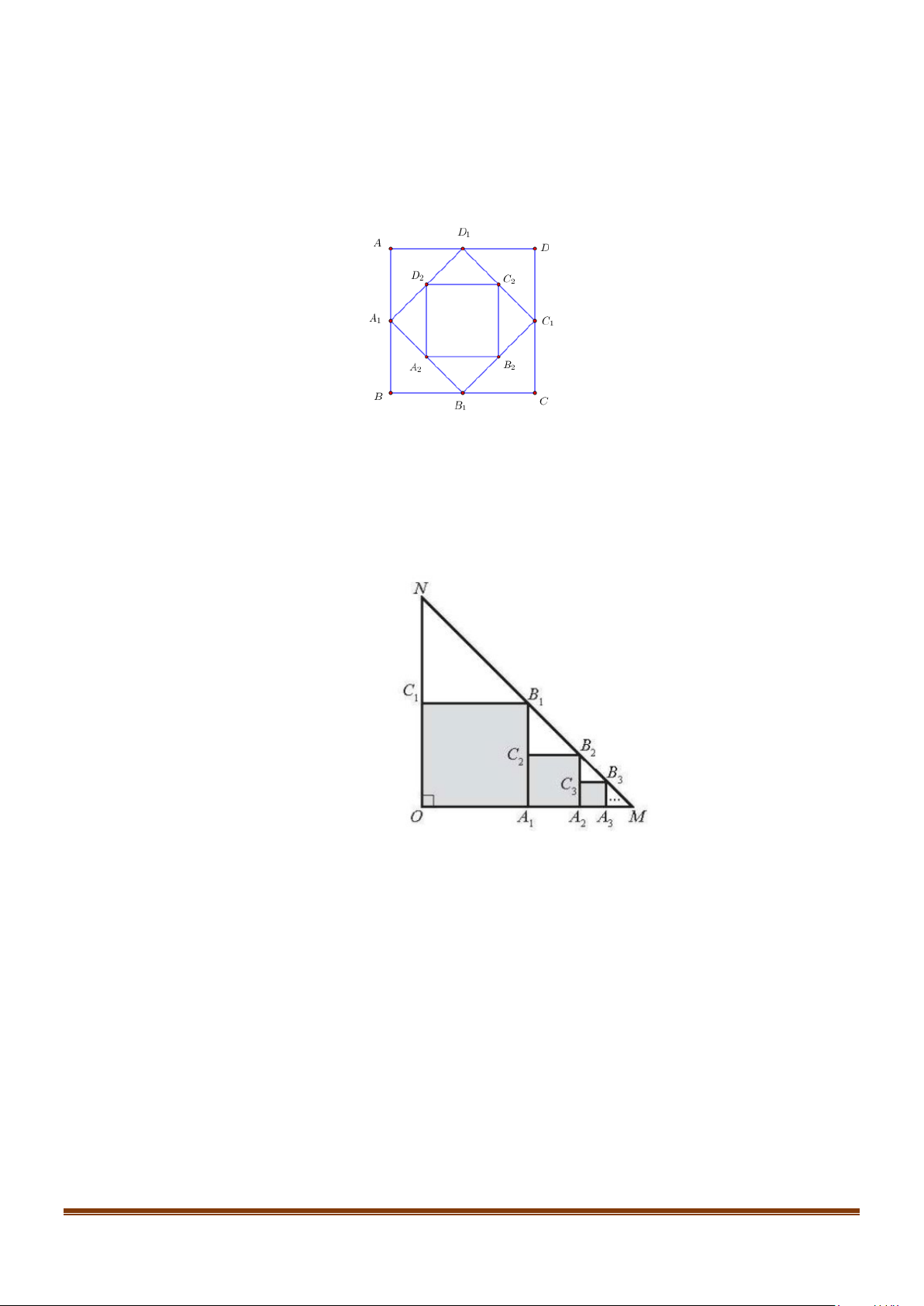
Câu 6: Cho tam giác OMN vuông cân tại O , OM = ON = 5. Trong tam giác OMN , vẽ hình vuông
OA B C sao cho các đỉnh A , B ,C lần lượt nằm trên các cạnh 1 1 1 1 1 1
OM , MN,ON . Trong tam giác
A MB , vẽ hình vuông A A B C sao cho các đỉnh A , B ,C lần lượt nằm trên các cạnh 1 1 1 2 2 2 2 2 2
A M , MB , A B . Tiếp tục quá trình đó mãi mãi, ta được một dãy các hình vuông (tham khảo 1 1 1 1
hình vẽ dưới đây). Tính tổng diện tích các hình vuông này. Lời giải Trả lời: 8,33
Độ dài cạnh của các hình vuông lần lượt là 5 5 5
a = ; a = ; a = ; ... 1 2 3 2 4 8 2 2 2
Diện tích của các hình vuông lần lượt là 5 5 5 S ; S ; S = = = ; ... 1 2 3 2 4 8
Các diện tích S ; S ; S ; ... tạo thành cấp số nhân lùi vô hạn với số hạng đầu là 25 1 2 3 S = và 1 4 công bội là 1 q = . 4 25
Do đó, tổng diện tích các hình vuông là 4 25 S = 1 = 3 1− 4
---------- HẾT ---------- Page 12
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC ƠNG V GIỚI HẠN HÀM SỐ LIÊN TỤC CHƯ
BÀI: GIỚI HẠN CỦA DÃY SỐ ĐỀ TEST SỐ 02
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án. Câu 1: Tìm 1 lim 2 − ? n→+∞ n A. −∞ B. 1. C. 2 . D. +∞ .
Câu 2: Cho lim u = a
v = b . Trong các mệnh đề sau, mệnh đề nào sai? n , lim n n→+∞ n→+∞
A. lim (u − v = a −b
B. lim (u + v = a + b . n n ) n n ) n→+∞ n→+∞
C. lim (u v = a b .
D. lim un = a − b . n. n ) . n→+∞ n→+∞ vn Câu 3: Tìm 2n + 3 lim ? n→+∞ n −1 A. +∞ B. 3 − . C. −∞ . D. 2 . 2 Câu 4: Tính 4n + 5n + 2 lim + n n→+∞ n +1 A. 2 . B. 3. C. +∞ . D. 5.
Câu 5: Giá trị của giới hạn lim + − + bằng →+∞ ( n 9 n 4) n A. 1. B. 3. C. 5. D. 0.
Câu 6: Biểu diễn số 4,333333... dưới dạng phân số tối giản có dạng a , Tính a + b ? b A. 21. B. 30. C. 39. D. 48 . Câu 7: Tìm ( 5 3 lim 8n − n + ) 1 n→+∞ A. +∞ . B. 8 . C. 1. D. −∞ . 3 − +
Câu 8: Giá trị của n 2n 5 lim bằng n→+∞ 3+ 5n A. 5. B. 2 . C. −∞ . D. +∞ . 5 2 3 Câu 9: Tìm 7n − 2n +1 I = lim . 3 2 3n + 2n +1 A. 7 . B. 2 − . C. 0 . D. 1. 3 3 Page 1
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC n Câu 10: 2024 lim bằng 2025 A. 0 . B. +∞ . C. 1 . D. 2024 . 2 2025 Câu 11: Tính
1+ 3+ 5 +....+ (2n −1) lim 2.(n +1).(n + 2) A. 1 . B. 3 − . C. 3 . D. 5 . 2 4 2 n Câu 12: Tính 5 + 25 +...+ 5 lim 3.5n + 2.3n A. 5 . B. 6 . C. 1 . D. 1 − . 12 4 3
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời câu hỏi. Trong mỗi ý a), b), c), d) ở mỗi câu, thí
sinh chọn đúng hoặc sai.
Câu 1: Cho hai dãy số (u và (v với 3n +1 u − = , 5 4n v = . n ) n ) n n + 2 n n a) lim u = . n 3 n→+∞ b) lim un = 0 . n→+∞ 3n +1 c) lim v = . n 5 n→+∞ d) lim vn = 0 . n→+∞ n
Câu 2: Cho hai dãy số (u và (v với 2
u = n + n − n , 2
v = n − n − n n 8 n ) n ) n a) 1 lim u = . n n→+∞ 2
b) lim v = b > . n 0 n→+∞ c) lim un = 0 . n→+∞ n
d) Có hai giá trị nguyên dương của a để ( 2 2 lim
n −8n − n + a = . →+∞ ) 0 n
Câu 3: Cho hai dãy số (u và (v với 2
u = n + và v = n . n 2 n 1 n ) n ) a) lim v = +∞ . n n→+∞ b) lim u = +∞ . n n→+∞
c) lim (u − v = . n n ) 0 n→+∞ 2 5
− n (u − v n n ) d) lim = 0 . n→+∞ n +1 Page 2
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC
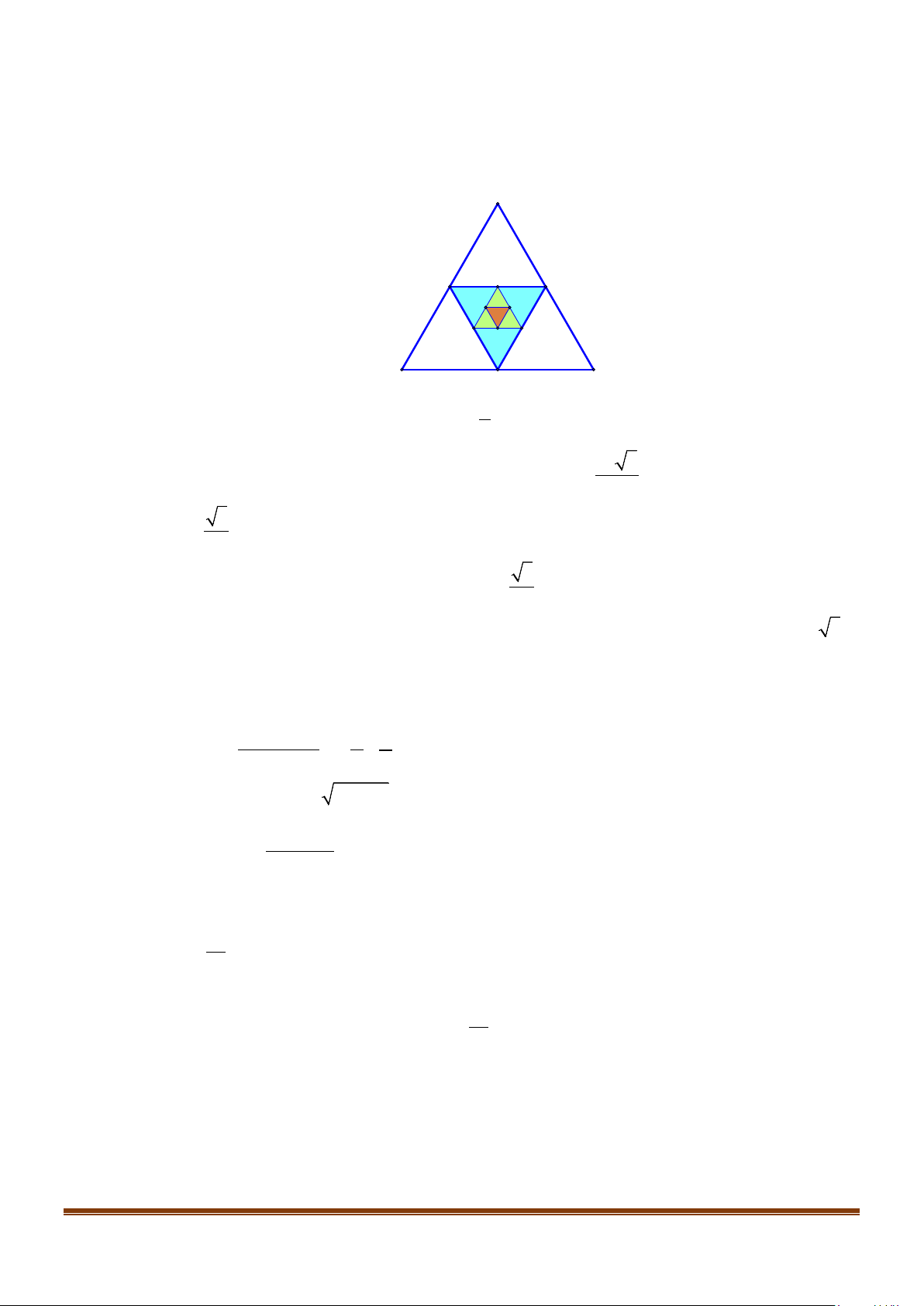
Câu 4: Cho tam giác đều ABC có độ dài cạnh bằng 1. Nối các trung điểm A , B ,C của các cạnh 1 1 1 BC,C ,
A AB ta được tam giác đều A B C . Tiếp tục nối các trung điểm A , B ,C của các cạnh 1 1 1 2 2 2
B C ,C A , A B ta được tam giác đều A B C , thực hiện quá trình này đến vô hạn. Gọi S lần là 1 1 1 1 1 1 2 2 2 n
diện tích của tam giác đều A B C . n n n A A2 C1 B1 C3 B3 B2 A C2 3 B C A1
a) Tam giác A B C có độ dài các cạnh bằng 1 . 1 1 1 2 2
b) Biết rằng tam giác đều có cạnh bằng a thì có diện tích là a 3 . Diện tích tam giác A B C 4 3 3 3 là: 3 S = . 3 64
c) Đặt u = S + S + S + + S . Khi đó 3 limu = . n ... 1 2 3 n n 12
d) Đặt h = AA ,h = A A ,h = A A ,...,h = A
và v = h + h + + h . Khi đó limv = . n 3 n ... − A 1 1 2 1 2 3 2 3 n n 1 n 1 2 n
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. 3 2 + + Câu 1: Biết n n 1 = lim a L = − ( a
T = a + b . 3 2018 − 3n b b tối giản, ; a b∈ ). Tính 3
Câu 2: Tính giới hạn sau: + − − ; →+∞ ( 2 lim n 2n n 2 n ) n+2 Câu 3: + Kết quả của 3 5 lim bằng 2n + 2.5n
Câu 4: Nam đang ngồi học thì nghe có tiếng mưa rơi. Tiếng mưa rơi lộp độp nhặt dần đến khi Nam nghe
gần như đều đặn. Thời gian đầu tiên Nam ước chừng khoảng 5 giây. Sau đó thời gian liên tiếp
giảm đi 11 giây. Thời gian Nam bắt đầu nghe các tiếng mưa rơi gần như đều đặn là………phút. 12
Câu 5: Từ độ cao 63m của một ngọn tháp, người ta thả một quả bóng cao su xuống đất. Giả sử mỗi lần
chạm đất quả bóng lại nảy lên độ cao bằng 1 độ cao mà quả bóng đạt được ngay trước đó. Độ 10
dài hành trình của quả bóng từ thời điểm ban đầu cho đến khi nó nằm yên trên mặt đất (khi
khoảng cách từ quả bóng đến mặt đất không đáng kể) là bao nhiêu mét? Page 3
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC
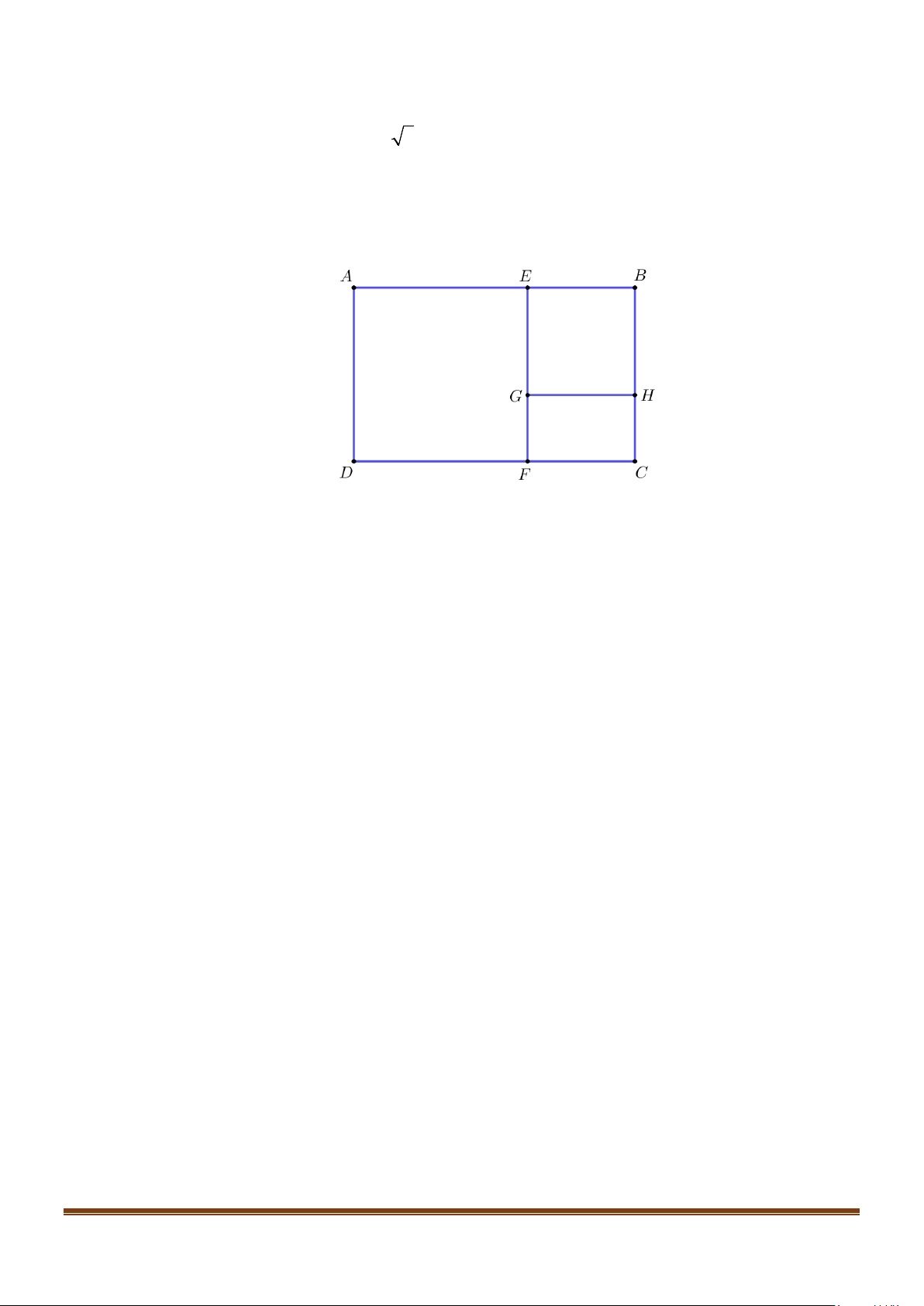
Câu 6: Ông An dự định dùng xen kẽ 2 màu vàng, xanh để sơn trang trí một bức tường hình chữ nhật theo
cách như sau: Đầu tiên dùng màu vàng sơn bức tường theo tấm bìa hình chữ nhật H có chiều dài, chiều 1
rộng tính theo đơn vị m lần lượt là 5 +1 và 2 , sau đó cắt hình H thành một hình vuông có cạnh 1
bằng chiều rông của H và hình chữ nhật H , rồi dùng màu xanh sơn tường theo hình H , …cứ tiếp 1 2 2
tục quá trình như vậy cho đến khi hình chữ nhật tạo ra có diện tích không đáng kể. Biết rằng tiền công để
sơn mỗi mét vuông tường như vậy là 21 nghìn đồng. Hỏi ông An cần chuẩn bị tối đa bao nhiêu tiền
công cho thợ sơn? (kết quả tính theo đơn vị nghìn đồng và làm tròn đến hàng nghìn).
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án. Câu 1: Tìm 1 lim 2 − ? n→+∞ n A. −∞ B. 1. C. 2 . D. +∞ . Lời giải 1 lim 2 − = 2 . n→+∞ n
Câu 2: Cho lim u = a
v = b . Trong các mệnh đề sau, mệnh đề nào sai? n , lim n n→+∞ n→+∞
A. lim (u − v = a −b
B. lim (u + v = a + b . n n ) n n ) n→+∞ n→+∞
C. lim (u v = a b .
D. lim un = a − b . n. n ) . n→+∞ n→+∞ vn Lời giải lim u a
n = (b ≠ 0) . n→+∞ v b n Câu 3: Tìm 2n + 3 lim ? n→+∞ n −1 A. +∞ B. 3 − . C. −∞ . D. 2 . Lời giải 3 2 2n 3 + + n 2 lim = lim = = 2 . n→+∞ n −1 n→+∞ 1 1 1− n 2 Câu 4: Tính 4n + 5n + 2 lim + n n→+∞ n +1 A. 2 . B. 3. C. +∞ . D. 5. Lời giải 5 2 2 4 + + +1 2 + + + Ta có 4n 5n 2 lim n = lim n n = 3 . n→+∞ n +1 1 1+ n
Câu 5: Giá trị của giới hạn lim + − + bằng →+∞ ( n 9 n 4) n A. 1. B. 3. C. 5. D. 0. Lời giải n + 9 − n + 4 Ta có: + − + = = = →+∞ ( n n ) ( ) 5 lim 9 4 lim lim 0. n n→+∞
n + 5 + n +1 n→+∞ 5 1 n 1+ + n + n n
Câu 6: Biểu diễn số 4,333333... dưới dạng phân số tối giản có dạng a , Tính a + b ? b A. 21. B. 30. C. 39. D. 48 . Lời giải Page 5
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC 3 3 3 3 1 1 1 1 S =1+ 3+ + + + ⋅⋅⋅ + + ... =1+ 3+ 3. + 3. + 3. + ⋅⋅⋅ + 3. + ... =1+ S ' 2 3 n 2 3 10 10 10 10 10 10 10 10n
Nhận thấy S ' tổng của cấp số nhân lùi vô hạn với 1 u = 3,q = . 1 10 Do đó u 3 30 39 1 S =1+ = 1+ = 1+ = 1− q 1 9 9 1− 10
Vậy a + b = 39 + 9 = 48 Câu 7: Tìm ( 5 3 lim 8n − n + ) 1 n→+∞ A. +∞ . B. 8 . C. 1. D. −∞ . Lời giải ( 5 3 n n ) 5 1 1 lim 8 1 lim n 8 − + = − + = +∞ 1 1 . Vì 5 lim n = ; +∞ lim 8 − + = 8 2 5 n→+∞ n→+∞ n n 2 5 n→+∞ n→+∞ n n 3 Câu 8: − + Giá trị của n 2n 5 lim bằng n→+∞ 3+ 5n A. 5. B. 2 . C. −∞ . D. +∞ . 5 Lời giải 2 5 2 5 3 1− + − + 1− + 2 3 n 2n 5 3 2 3 lim = lim n n n n 1 n ⋅ = +∞ Vì 3 lim n = ; +∞ lim = n→+∞ 3+ 5 n n →+∞ 3 + 5 n→+∞ n→+∞ 3 5 + 5 n n 2 3 Câu 9: Tìm 7n − 2n +1 I = lim . 3 2 3n + 2n +1 A. 7 . B. 2 − . C. 0 . D. 1. 3 3 Lời giải 7 1 2 3 − 2 + 3 Ta có 7n − 2n +1 n n 2 I = lim = lim = − . 3 2 3n + 2n +1 2 1 3 3+ + 3 n n n Câu 10: 2024 lim bằng 2025 A. 0 . B. +∞ . C. 1 . D. 2024 . 2 2025 Lời giải Áp dụng lim n q = 0, q <1. Câu 11: Tính
1+ 3+ 5 +....+ (2n −1) lim 2.(n +1).(n + 2) A. 1 . B. 3 − . C. 3 . D. 5 . 2 4 2 Lời giải
Ta có: u =1 và d = 2 nên 1+ 3+ 5 +....+ (2n −1) = [1+ (n −1).2].n 1 Page 6
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC Khi đó
1+ 3+ 5 +....+ (2n −1)
[1+ (n −1).2].n lim = lim 2.(n +1).(n + 2) 2.(n +1).(n + 2) 1 2 − 1 . (2n −1).n n 1 = lim = lim = 4.(n +1).(n + 2) 1 2 2 4. +1 . + 1 n n n Câu 12: Tính 5 + 25 +...+ 5 lim 3.5n + 2.3n A. 5 . B. 6 . C. 1 . D. 1 − . 12 4 3 Lời giải 5.(1−5n ) 5 − .(1−5n n )
Ta có: u = 5 và q = 5 nên 5 + 25 +...+ 5 = = 1 1− 5 4 Khi đó n 1 1 n − − − − n 5.5 . + + + − − 1 5. 1 5 25 ... 5 5.(1 5 ) 5n 5n 5 lim = lim = lim = lim = 3.5n + 2.3n 12.5n + 8.3n n n n 12 5 12 + 8 3 3 . . 2 1 + 8. 5n 5n
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời câu hỏi. Trong mỗi ý a), b), c), d) ở mỗi câu, thí
sinh chọn đúng hoặc sai.
Câu 1: Cho hai dãy số (u và (v với 3n +1 u − = , 5 4n v = . n ) n ) n n + 2 n n a) lim u = . n 3 n→+∞ b) lim un = 0 . n→+∞ 3n +1 c) lim v = . n 5 n→+∞ d) lim vn = 0 . n→+∞ n Lời giải a) Đúng b) Đúng c) Sai d) Đúng 1 3+ a) Đúng. Vì 3n +1 lim = lim n = 3. n→+∞ n + 2 n→+∞ 2 1+ n b) Đúng. Vì un 1 lim = lim = 0 .
n→+∞ 3n +1 n→+∞ n + 2 5 −4 − c) Sai. Vì 5 4 lim n = lim n = 4 − . n→+∞ n n →+∞ 1 5 4 − 2 − d) Đúng. Vì v n n 5 4 lim = lim = lim n n = 0. 2 n→+∞ n→+∞ n n n →+∞ 1 Page 7
Sưu tầm và biên soạn
ĐỀ TEST – CHUYÊN ĐỀ V – TOÁN – 11 – GIỚI HẠN VÀ HÀM SỐ LIÊN TỤC
Câu 2: Cho hai dãy số (u và (v với 2
u = n + n − n , 2
v = n − n − n n 8 n ) n ) n a) 1 lim u = . n n→+∞ 2
b) lim v = b > . n 0 n→+∞ c) lim un = 0 . n→+∞ n
d) Có hai giá trị nguyên dương của a để ( 2 2 lim
n −8n − n + a = . →+∞ ) 0 n Lời giải a) Đúng b) Sai c) Đúng d) Sai a) Đúng. Vì n
n + n − n = = = . n→∞ ( 2 ) 1 1 lim lim lim n→∞ 2 n n + n + n →∞ 1 2 1+ +1 n b) Sai. Vì − n n n n − − − = = = − < . n→∞ ( 2 ) 8 8 lim 8 lim lim 4 0 n→∞ 2 n −8 n n + n →∞ 8 1− +1 n 1 2 1+ −1 c) Đúng. Vì lim u
n + n − n n = lim = lim n = 0 . n→+∞ n→+∞ n n n →+∞ 1 2 2 2 ( 2 2a −8) 4 n − a d) Sai. Vì
n −8n − (n − a ) − − + = lim = lim →+∞ ( 2 2 lim n 8n n a n ) n→+∞ 2 2
n −8n + n − a n→+∞ 2 2
n −8n + n − a 4 2 2 −8 a a − = lim n 2
= a − 4 = 0 ⇔ a = 2
± . Mà a nguyên dương nên a = 2 . →+∞ 2 n 8 1− +1 a − n n (Hoặc − − + = − − + = − = ⇔ = ± ). →+∞ ( 2 2 n
n n a ) →+∞( 2n n n) 2 2 lim 8 lim 8 a a 4 0 a 2 n n
Câu 3: Cho hai dãy số (u và (v với 2
u = n + và v = n . n 2 n 1 n ) n ) a) lim v = +∞ . n n→+∞ b) lim u = +∞ . n n→+∞
c) lim (u − v = . n n ) 0 n→+∞ 2 5
− n (u − v n n ) d) lim = 0 . n→+∞ n +1 Lời giải a) Đúng b) Đúng c) Sai d) Sai a) Đúng. Vì lim v = n = +∞ . n lim (2 ) n→+∞ n→+∞ b) Đúng. Vì 2 1
lim n +1 = lim n 1+ = +∞ do 1 lim n = +∞, lim 1+ = 1. 2 n→+∞ n→+∞ n 2 n→+∞ n→+∞ n c) Sai. Vì (u −v = n + − n = n + − = −∞ n n ) n→+∞ n→+∞ ( 2 ) 1 lim lim 1 2 lim 1 2 2 n→+∞ n Page 8
Sưu tầm và biên soạn




