Đề kiểm tra Toán 10 lần 2 năm 2020 – 2021 trường THPT Quang Hà – Vĩnh Phúc

SỞ GD&ĐT VĨNH PHÚC
ĐỀ KIỂM TRA CHUYÊN ĐỀ LẦN II
TRƯỜNG THPT QUANG HÀ NĂM HỌC 2020 - 2021
Đề 1. Môn: Toán; Khối 10
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1. (4,5 điểm) Giải các bất phương trình sau: 2
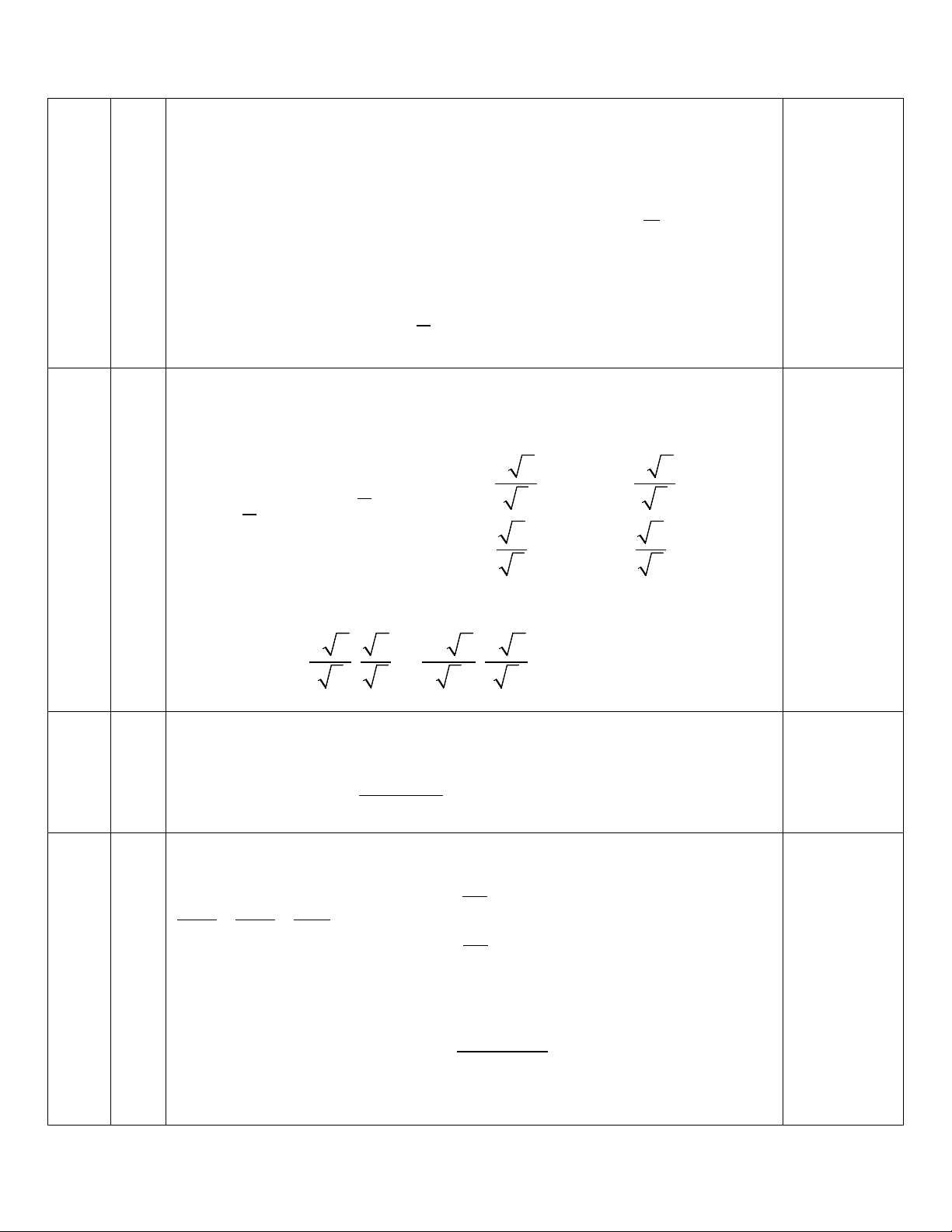
a / x − 4x − 5 < 0 2 x − 4x + 3 d/ ≥ 0 x − 2 − 2
b/ x + 3x − 2 ≥ 0 2
e/ 2x − 3x + 1 ≤ x − 1 x + 5 c/ ≥ 2 x + 2
f / x + 4 − 1− x ≤ 1− 2x
Câu 2. (1,0 điểm) Cho phương trình: 2
x + (m + 2)x + 2m + 1 = 0 . Tìm m để phương trình đã cho có 2 nghiệm phân biệt.
Câu 3. (1,0 điểm) Tìm m để bất phương trình sau nghiệm đúng với mọi x: (m + ) 2
1 x − 2 (3 − 2m)x + m + 1 ≥ 0
Câu 4. (1,5 điểm) Cho ∆ ABC có c = 35, b = 20, A = 600. Tính a; S; r. 2 2 3 5
 x y − 4xy + 3y − 2(x + y) = 0
Câu 5. (0,5 điểm) Giải hệ phương trình:  2 2 x + y = 2
Câu 6. (0,5 điểm) Xác định dạng của tam giác ABC biết các góc A,B, C của tam giác đó thỏa mãn hệ thức: sin C = 2 sin . A cosB
Câu 7. (1,0 điểm) Một xưởng sản xuất hai loại sản phẩm loại I và loại II từ 200kg nguyên liệu và một máy
chuyên dụng. Để sản xuất được một kilôgam sản phẩm loại I cần 2kg nguyên liệu và máy làm việc trong 3 giờ.
Để sản xuất được một kilôgam sản phẩm loại II cần 4kg nguyên liệu và máy làm việc trong 1,5 giờ. Biết một
kilôgam sản phẩm loại I lãi 300000 đồng, một kilôgam sản phẩm loại II lãi 400000 đồng và máy chuyên dụng
làm việc không quá 120 giờ. Hỏi xưởng cần sản xuất bao nhiêu kilôgam sản phẩm mỗi loại để tiền lãi lớn nhất?
_________________________ HẾT _________________________ SỞ GD&ĐT VĨNH PHÚC
ĐỀ KIỂM TRA CHUYÊN ĐỀ LẦN II
TRƯỜNG THPT QUANG HÀ NĂM HỌC 2020 - 2021
Đề 2. Môn: Toán; Khối 10
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1. (4,5 điểm) Giải các bất phương trình sau: 2
a / x + 3x − 4 > 0 2 x − 7x + 12 d/ ≥ 0 x − 5 − 2 b/
x − 6x + 7 > 0 2
e) x − 2x −15 ≤ x − 3 4x − 1 c/ ≥ 3
f / 5x −1 − x −1 > 2x − 4 x + 1
Câu 2. (1,0 điểm) Cho phương trình: 2
x + 2 (m + 1)x + 7m − 3 = 0 . Tìm m để phương trình đã cho có 2 nghiệm phân biệt.
Câu 3. (1,0 điểm) Tìm m để bất phương trình sau nghiệm đúng với mọi x: (m − ) 2
1 x + 2 (3 + 2m)x + m − 1 ≤ 0
Câu 4. (1,5 điểm) Cho ∆ ABC có c =10, b = 4 và A = 600. Tính a; S; r. 2 2
2x + 4xy + 5y = 5
Câu 5. (0,5 điểm) Giải hệ phương trình  2 2
x − 2y + 2x + y = 1 −
Câu 6. (0,5 điểm) Xác định dạng của tam giác ABC biết các góc A,B, C của tam giác đó thỏa mãn hệ thức: sinB = 2 sin . A cosC
Câu 7. (1,0 điểm) Một nông trại dự định trồng cà rốt và khoai tây trên khu đất có diện tích 5ha. Để chăm bón
các loại cây này, nông trại phải dùng phân vi sinh. Nếu trồng cà rốt trên 1 ha cần dùng 3 tấn phân vi sinh và thu
được 50 triệu đồng tiền lãi. Nếu trồng khoai tây trên 1 ha cần dùng 5 tấn phân vi sinh và thu được 75 triệu đồng
tiền lãi. Hỏi nông trại cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được tổng số tiền lãi cao nhất?
Biết rằng số phân vi sinh cần dùng không được vượt quá 18 tấn.
_________________________ HẾT _________________________
ĐÁP ÁN ĐỀ KSCĐ TOÁN 1O- LẦN 2 ĐỀ 1 Câu ý Nội dung Điểm 1 a 2
x − 4x − 5 < 0 1 ⇔ −1 < x < 5 b − 2
x + 3x − 2 ≥ 0 ⇔ 1 ≤ x ≤ 2 1 c x + 5 ≥ 2 x + 2 0,5 −x + ⇔ 1 ≥ 0 x + 2 ⇔ −2 < x ≤ 1 0,5 d 2 x − 4x + 3 ≥ 0 x − 2 x 1 2 3 2
x − 4x + 3 + 0 - - 0 + 0,25 x-2 - - 0 + + VT - 0 + - 0 +
KL: S = 1;2) ∪ 3;+∞ 0,25   ) e 2
2x − 3x + 1 ≤ x − 1 x ≥ 1   x − 1 ≥  0  0,25  1 2  x ≤  ⇔
2x − 3x + 1 ≥ 0 ⇔  2  2 x 1  2 2x 3x 1 (x 1)  ≥  − + ≤ −    2 x − x ≤  0 x ≥ 1    x ≤ 1  ⇔  2 ⇔ x = 0,25  1  x ≥  1 0 ≤ x ≤  1 1 KL: s = { } 1 f
x + 4 − 1− x ≤ 1− 2x 1  − x ≥ 0 1  − 2x ≥ 0 
⇔ x + 4 ≤ 1− x + 1− 2x ⇔ x + 4 ≥ 0  x + 4 ≤ 
( 1−x + 1−2x)2 0,25  1 4 − ≤ x ≤  ⇔  2  2
2x +1 ≤ 2x − 3x +1  1 − 4  ≤ x ≤  1 2 − 4   ≤ x ≤  1 2 x < − 2x +1 < 0  2 ⇔  ⇔  ⇔ 4 − ≤ x ≤ 0   1 2  x +1 ≥ 0  x ≥ − 0,25    2 2
 x − 3x +1 ≥ (2x + )2 2 1   7
− ≤ x ≤ 0  2 S=[-4;0]. 2 Cho phương trình: 2
x + (m + 2)x + 2m + 1 = 0 . Tìm m để phương trình đã cho có 2 nghiệm phân biệt.
Để phương trình có hai nghiệm phân biệt: 0,5 ∆ > 0
⇔ (m + 2)2 − 4.1.(2m + 1) > 0 ⇔= 2 m − 4m > 0 m < 0 ⇔  m >  4 0,5
KL: Vậy với m ∈ (−∞;0) ∪ (4;+∞) thì phương trình có hai nghiệm phân biệt 3
Tìm m để bất phương trình sau nghiệm đúng với mọi x: (m + ) 2
1 x − 2 (3 − 2m)x + m + 1 ≥ 0 (1) 2
TH1: Với: m + 1 = 0 ⇔ m = −1 0,25
BPT (1) ⇔ −10x ≥ 0 ⇔ x ≤ 0(loai)
TH2: m + 1 ≠ 0 ⇔ m ≠ −1
Để bất phương trình sau nghiệm đúng với mọi x:
(m +1) 2x − 2(3 − 2m)x + m +1 ≥ 0 (1) 0,25   m + 1 > m > − 0  1 ⇔  ⇔ 2 2  ' 0 ( ∆ ≤  3 − 
2m ) − (m + 1) ≤ 0 m > − m > −   1 1 0,25 ⇔ 2  ⇔ m 4 2  ⇔ ≤ ≤ m − m + ≤ 2 3 14 8 0 ≤ m ≤   4 3 3 2 
KL: Vậy với m ∈  ;4 0,25
3  thì bất phương trình nghiệm đúng với mọi x 4
Cho ∆ ABC có c = 35, b = 20, A = 600. Tính cạnh a; S; r.
AD định lí hàm số cosin ta có: 2 a = 2 b + 2 c − 2 2. . b . c c osA=35 + 2 20 − 2.35.20.c os60 = 925 0,5 ⇒ a ≈ 30, 1 4 0,5 S = 1 b c A = 1 . . .sin .35.20.sin 60 = 175 3 2 2 a + b + c 35 + 20 + 0,25 p = = 30, 41 = 42,705 2 2 0,25 = ⇒ = S S p r r = 175 3 . ≈ 7, 098 p 42,705 5 2 2 3 5
 x y − 4xy + 3y − 2(x + y) = 0
Giải hệ phương trình:  2 2 x + y = 2 2 2 3 2 2 5
 x y − 4xy + 3y − (x + y )(x + y) = 0 0,25 Hệ đã cho ⇔  2 2 x + y = 2 3 2 2 3 3
4x y − 5xy + 2y − x = 0 (*) ⇔  2 2 x + y = 2 y
Ta thấy x = 0 không là nghiệm của hệ nên từ PT (*) đặt: t = ta được PT: x t =1 3 2 2t 5t 4t 1 0  − + − = ⇔ 1  t =  2 y = x x =1 x = 1 − 0,25 Khi t = 1 ta có:  ⇔  ∨  2 2 x + y = 2 y =1 y = 1 −  2 2  2 2  1 x = x = − 1 y = x  5  5 Khi t = ta có:  2 ⇔  ∨ 2   2 2  2  2 x + y = 2 y = y = −  5    5
Vậy hệ đã cho có 4 nghiệm ( ; x y) là
( ) (− − )  2 2 2   2 − 2 − 2  1;1 ; 1; 1 ; ; ; ;   5 5   5 5  6
Xác định dạng của tam giác ABC biết các góc A,B, C của tam giác đó thỏa mãn hệ thức: sin C = 2 sin . A cosB
Áp dụng định lí hàm số sin : si  n a A = a b c  2 = = = 2 R R ⇒ sin A sin B sinC sin c C =  2R 0,25
AD định lí hàm số cosin ta có: 2 2 2 a + 2 c − 2 2 = + − b b a c 2.a . . c c osB ⇒ os c B= 2ac
Theo giả thiết ta có: 4 sin C = 2 sin . A cosB ⇔ sin C = 2sin . A cosB 2 2 2 c  + −  ⇔ = 2. a . a c b 2R 2R  2ac    0,25 2 2 2
a + c − b 2 2 2 2 ⇔ c =
⇔ c = a + c − b c 2 2
⇔ a = b ⇔ a = b
Vậy tam giác ABC cân tại C 7
Một xưởng sản xuất hai loại sản phẩm loại I và loại II từ 200kg nguyên liệu và
một máy chuyên dụng. Để sản xuất được một kilôgam sản phẩm loại I cần 2kg
nguyên liệu và máy làm việc trong 3 giờ. Để sản xuất được một kilôgam sản
phẩm loại II cần 4kg nguyên liệu và máy làm việc trong 1,5 giờ. Biết một
kilôgam sản phẩm loại I lãi 300000 đồng, một kilôgam sản phẩm loại II lãi
400000 đồng và máy chuyên dụng làm việc không quá 120 giờ. Hỏi xưởng cần
sản xuất bao nhiêu kilôgam sản phẩm mỗi loại để tiền lãi lớn nhất?
Giả sử sản xuất x(kg) sản phẩm loại I và y(kg) sản phẩm loại II.
Điều kiện x ≥ 0, y ≥ 0 và 2x + 4y ≤ 200 ⇔ x + 2y ≤ 100
Tổng số giờ máy làm việc: 3x +1,5y 0,25
Ta có 3x +1,5y ≤ 120
Số tiền lãi thu được là T = 300000x + 400000y (đồng).
Ta cần tìm x, y thoả mãn:
x ≥ 0, y ≥ 0 
x + 2y ≤100 (I) 0,25 3  x +1,5y ≤  120
sao cho T = 300000x + 400000y đạt giá trị lớn nhất.
Trên mặt phẳng tọa độ Oxy vẽ các đường thẳng
d : x + 2y =100; d : 3x +1,5y =120 1 2 0,25
Đường thẳng d cắt trục hoành tại điểm (
A 100;0), cắt trục tung tại điểm 1 B(0;50) . 5
Đường thẳng d cắt trục hoành tại điểm C(40;0) , cắt trục tung tại điểm 2 y D(0;80).
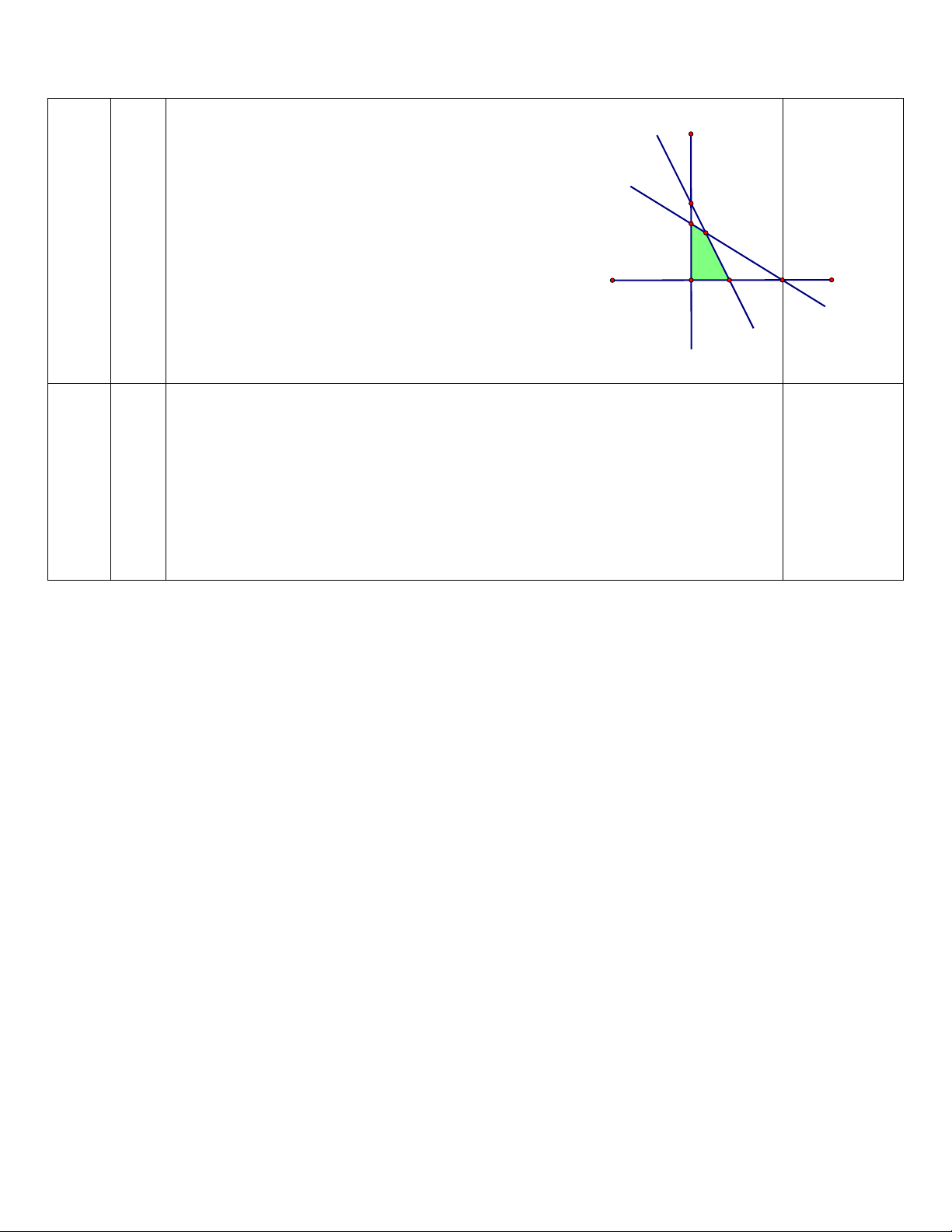
Đường thẳng d và d cắt nhau tại điểm E (20;40) . 1 2 D
Biểu diễn hình học tập nghiệm của B E
hệ bất phương trình (I) là miền đa giác OBEC . x O C A x = 0 x = 0 x = 20  ⇒ T = 0;  ⇒ T = 20000000 ;  ⇒ T = 22000000 ; y = 0 y = 50 y = 40 x = 40 0,25  ⇒ T = 12000000 y = 0
Vậy để thu được tổng số tiền lãi nhiều nhất thì xưởng cần sản xuất 20kg sản
phẩm loại I và 40kg sản phẩm loại II. 6 ĐÁP ÁN ĐỀ 2 Câu ý Nội dung Điểm 1 a x < −4 1,0 2
x + 3x − 4 > 0 ⇔  x >  1 b − 2
x − 6x + 7 > 0 ⇔ −7 < x < 1 1,0 c 4x − 1 ≥ 3 x + 1 0,5 x − ⇔ 4 ≥ 0 x + 1 x < −1 ⇔  0,5 x ≥  4 d 2 x − 7x + 12 ≥ 0 x − 5 X 3 4 5 2
x − 7x + 12 + 0 - 0 + + 0,25 x-5 - - - 0 + VT
- 0 + 0 - 0 + 0,25
KL: S = 3;4 ∪   (5;+∞ e 2
x − 2x − 15 ≤ x − 3 x ≥  3 x − 3 ≥ 0     x 3 0,25 2  ≤ −
⇔ x − 2x − 15 ≥ 0 ⇔ x ≥  5 2  2 x 2x 15 (x 3)  − − ≤ − x ≤  6 ⇔ 5 ≤ x ≤ 6 0,25 KL: S = 5;6   f
5x −1 − x −1 > 2x − 4 7 x −1 ≥ 0 5  x −1≥ 0 
⇔ 5x −1 > x −1 + 2x − 4 ⇔ 2x − 4 ≥ 0  5  x −1> 
( x−1+ 2x−4)2 0,25 x ≥1  1 x ≥  ⇔  5 x ≥ 2 
x + 2 > ( x − ) 1 (2x − 4)  x ≥ 2  x ≥ 2 ⇔ ( ⇔  ⇔ ≤ x <  x + 2  ) 2 10 2 > (x − ) 1 (2x − 4) 2
x −10x < 0 0,25 S = [2;10) 2 Cho phương trình: 2
x + 2 (m + 1)x + 7m − 3 = 0 . Tìm m để phương trình
đã cho có 2 nghiệm phân biệt.
Để phương trình có hai nghiệm phân biệt: ∆ > 0
⇔ (m + 1)2 − 1.(7m − 3) > 0 ⇔= 2
m − 5m + 4 > 0 0,5 m < 1 ⇔  m >  4 0,5
KL: Vậy với m ∈ (−∞;1) ∪ (4;+∞) thì phương trình có hai nghiệm phân biệt 3
Tìm m để bất phương trình sau nghiệm đúng với mọi x: (m − ) 2
1 x + 2 (3 + 2m)x + m − 1 ≤ 0 (1)
TH1: Với: m − 1 = 0 ⇔ m = 1 0,25
BPT (1) ⇔ 10x ≤ 0 ⇔ x ≤ 0(loai)
TH2: m − 1 ≠ 0 ⇔ m ≠ 1
Để bất phương trình sau nghiệm đúng với mọi x: 8
(m −1) 2x + 2(3 + 2m)x + m −1 ≤ 0 0,25   m − 1 < m < 0  1 ⇔  ⇔ 2 2  ' 0 ( ∆ ≤  3 + 
2m ) − (m − 1) ≤ 0 0,25 m < m <   1 1 ⇔ 2  ⇔ 4 m 2  ⇔ − ≤ ≤ −
3m + 14m + 8 ≤ 0 −4 ≤ m ≤ − 2   3  3  −2 0,25
KL: Vậy với m ∈ −  4;  
3  thì bất phương trình nghiệm đúng với mọi x 4
Câu 5. (1,5 điểm) Cho ∆ ABC có c =10, b = 4 và A = 600. Tính a; S; r.
AD định lí hàm số cosin ta có: 2 a = 2 b + 2 c − 2 2. . b . c c osA=1 + 2 0 4 − 2.4.10.c os 0 6 = 76 0,5 ⇒ a = 2 19 ≈ 8,72 0,5 S = 1 b c A = 1 . . .sin .4.10.sin 60 = 10 3 2 2 a + b + c 4 + 10 + 0,25 p = = 2 19 = 7 + 19 ≈ 11,36 2 2 0,25 = ⇒ = S S p r r = 10 3 . ≈ 1,525 p 7 + 19 5 2 2
2x + 4xy + 5y = 5
Giải hệ phương trình  2 2
x − 2y + 2x + y = 1 − (  2x + y 0,25  )2 − 2( 2 2 x − 2y ) = 5 Hệ phương trình ⇔ (  2x + y) +  ( 2 2 x − 2y ) = 1 −  u  =1  u  = 2x + y 2 u  − 2v = 5 v = 2 −  ⇔  ⇔ 2 2
v = x − 2y u  v 1  + = − u  = − Đặt: . Hệ trở thành: 3  v = 2 9 0,25 u =  =1 2x + y =1 x = 0; y 1   ⇔  ⇔  − 2 2 8 v = 2 − x − 2y = 2 − x = ; 9 y =  7 7 x = 2 u =  = 3 − 2x + y = 3 − ; y 1 −   ⇔  ⇔  − − 2 2 v = 2 x − 2y = 2 10 x = ; 1 y =  7 7
Vậy hệ phương trình có 4 nghiệm: ( ; x y) là: ( ) ( −  − − 0 )  8 2;1 ; ;1 ; ; 9 ; 10  ; 1 −  7 7 7 7      6
Xác định dạng của tam giác ABC biết các góc A,B, C của tam giác đó thỏa mãn hệ thức: sinB = 2 sin . A cosC
Áp dụng định lí hàm số sin : si  n a A = a b c  2 = = = 2 R R ⇒ sin A sin B sinC sinB b =  2R 0,25
AD định lí hàm số cosin ta có: 2 2 2 a + 2 b − 2 2 = + − c c a b 2.a .b.c osC ⇒ o c sC= 2ab
Theo giả thiết ta có: sinB = 2 sin . A cosC ⇔ sinB = 2sin . A cosC 2 2 2 b  + −  ⇔ = 2. a . a b c 2R 2R  2ab  0,25   2 2 2
a + b − c 2 2 2 2 ⇔ b =
⇔ b = a + b − c b 2 2
⇔ a = c ⇔ a = c
Vậy tam giác ABC cân tại B 10 7
Một nông trại dự định trồng cà rốt và khoai tây trên khu đất có diện tích 5ha. Để
chăm bón các loại cây này, nông trại phải dùng phân vi sinh. Nếu trồng cà rốt
trên 1 ha cần dùng 3 tấn phân vi sinh và thu được 50 triệu đồng tiền lãi. Nếu
trồng khoai tây trên 1 ha cần dùng 5 tấn phân vi sinh và thu được 75 triệu đồng
tiền lãi. Hỏi nông trại cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu
được tổng số tiền lãi cao nhất? Biết rằng số phân vi sinh cần dùng không được vượt quá 18 tấn.
Giả sử trồng x(ha) cà rốt và y(ha) khoai tây.
Điều kiện x ≥ 0, y ≥ 0 và x + y ≤ 5
Số phân vi sinh cần dùng là : 3x + 5y tấn 0,25
Ta có 3x + 5y ≤ 18
Số tiền thu được là T = 50x + 75y (triệu đồng).
Ta cần tìm x, y thoả mãn:
x ≥ 0, y ≥ 0  x + y ≤ 5 (I) 0,25 3  x +5y ≤  18
sao cho T = 50x + 75y đạt giá trị lớn nhất.
Trên mặt phẳng tọa độ Oxy vẽ các đường thẳng
d : x + y = 5; d : 3x + 5y =18 1 2
Đường thẳng d cắt trục hoành tại điểm C(5;0) , cắt trục tung tại điểm E(0;5). 1
Đường thẳng d cắt trục hoành tại điểm D(6;0) , cắt trục tung tại điểm 2 18 A0;  0,25  . 5    7 3 
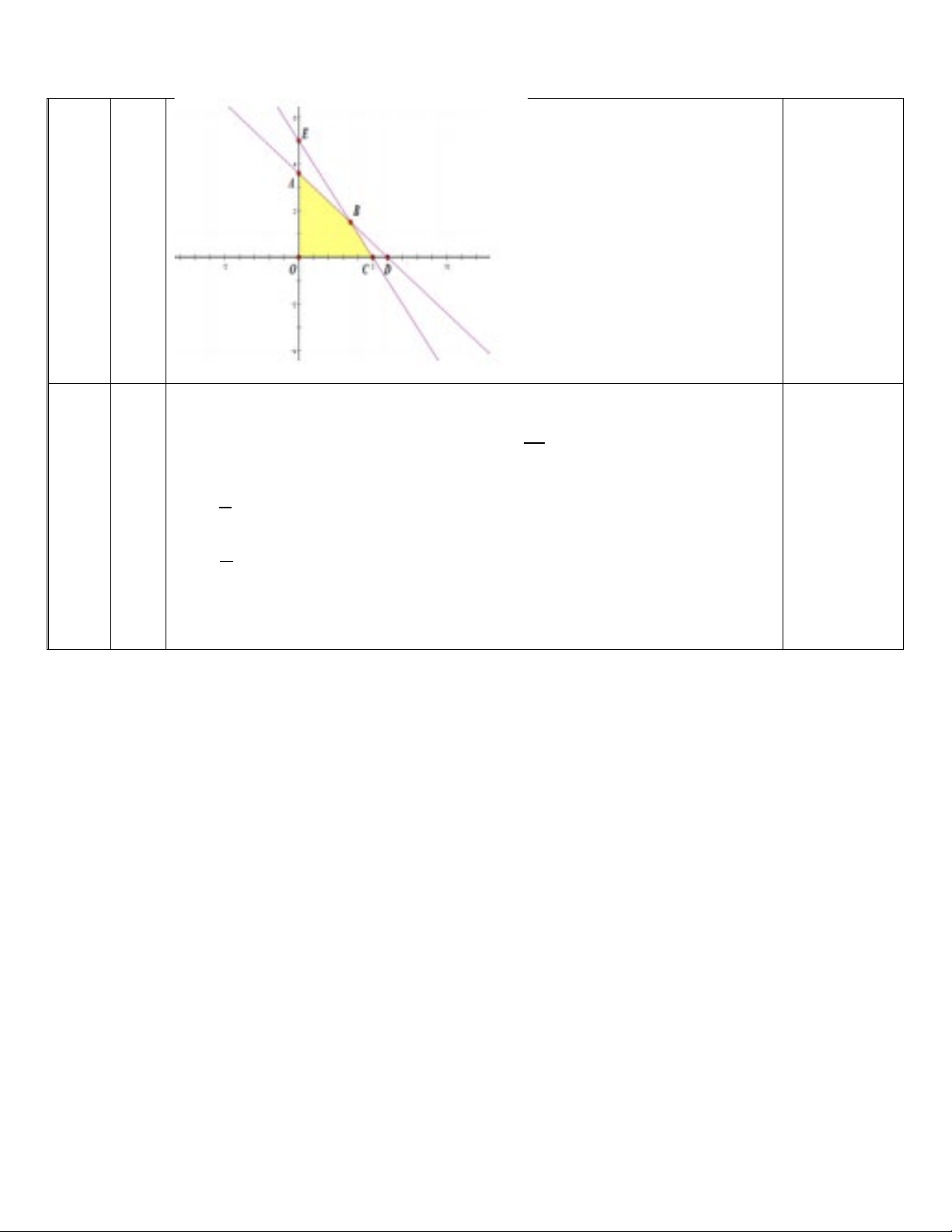
Đường thẳng d và d cắt nhau tại điểm B ; . 1 2 2 2   
Biểu diễn hình học tập nghiệm của
hệ bất phương trình (I) là miền đa giác OABC . 11 x = 0 x = 0 x = 5   ⇒ T = 0;  ⇒ T = 250 ;  18 ⇒ T = 270 ; y = 0 y = 0 y =  5  7 x =  2 0,25  ⇒ T = 287,5 3 y =  2
Vậy để thu được tổng số tiền lãi nhiều nhất thì nông trại cần trồng 3,5ha cà rốt và 1,5ha khoai tây. 12
Document Outline

• ĐỀ TOÁN 1O- KSCĐ LẦN 2
  • Câu 4. (1,5 điểm) Cho ABC có c = 35, b = 20, A = 600. Tính a; S; r.
  • Câu 4. (1,5 điểm) Cho ABC có c =10, b = 4 và A = 600. Tính a; S; r.
• ĐÁP ÁN KSCĐ TOÁN 1O LẦN 2