Đề KSCL đầu năm 2018 – 2019 môn Toán 12 trường THPT Lê Văn Thịnh – Bắc Ninh

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi khảo sát chất lượng theo định hướng thi tốt nghiệp THPT môn Toán 12 năm học 2018 – 2019.Mời bạn đọc đón xem.

18 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

25 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1/6 - Mã đề thi 132
SỞ GD VÀ ĐT BẮC NINH
TRƯỜNG THPT LÊ VĂN THỊNH
(Đề thi gồm 06 trang )
ĐỀ KHẢO SÁT CHẤT LƯỢNG ĐẦU NĂM
NĂM HỌC 2018-2019
Môn: TOÁN 12
Ngày thi: 16 tháng 9 năm 2018
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ, tên thí sinh:................................................ Số báo danh: ......................
Mã đề thi 132
Câu 1: Giá trị nhỏ nhất của hàm số
3
3 5y x x
trên đoạn
2;4
là:
A.
2; 4
min 3y
. B.
2; 4
min 7y
.
C.
2; 4
min 5.y
D.
2; 4
min 0.y
Câu 2: Cho hàm số
y f x
có đạo hàm trên đoạn
;a b
. Ta xét các khẳng định sau:
Nếu hàm số
f x
đạt cực đại tại điểm
0
;x a b
thì
0
f x
là giá trị lớn nhất của
f x
trên
;a b
.
2
Nếu hàm số
f x
đạt cực đại tại điểm
0
;x a b
thì
0
f x
là giá trị nhỏ nhất của
f x
trên
;a b
.
3
Nếu hàm số
f x
đạt cực đại tại điểm
0
x
và đạt cực tiểu tại điểm
1 0 1
, ;x x x a b
thì ta luôn có
0 1
f x f x
.
Số khẳng định đúng là?
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 3: Tiệm cận ngang của đồ thị hàm số
3
1
x
y
x
là đường thẳng có phương trình?
A.
5y
. B.
0y
. C.
1x
. D.
1y
.
Câu 4: Cho cấp số cộng
n
u
có số hạng tổng quát là
3 2
n
u n
. Tìm công sai
d
của cấp số cộng.
A.
2d
. B.
2d
. C.
3d
. D.
3d
.
Câu 5:
Đường cong trong hình bên là đồ thị của một hàm số trong
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào?
A.
2 1
1
x
y
x
. B.
1 2
1
x
y
x
.
C.
2 1
1
x
y
x
. D.
2 1
1
x
y
x
.
Câu 6:
Cho tứ diện
MNPQ
. Gọi
I
;
J
;
K
lần lượt là trung điểm
của các cạnh
MN
;
MP
;
MQ
. Tỉ số thể tích
MIJK
MNPQ
V
V
bằng
A.
1
4
. B.
1
3
.
C.
1
8
. D.
1
6
.
K
J
I
N
Q
P
M
Câu 7: Tập xác định của hàm số
tany x
là:
A.
\ ,
2
k k
. B.
\ ,k k
. C.
. D.
\ 0
.
O
x
y
1
1
2
Trang 2/6 - Mã đề thi 132
Câu 8: Cho hai đường thẳng phân biệt
,a b
và mặt phẳng
P
, trong đó
a P
. Chọn mệnh đề sai.
A. Nếu
//b a
thì
//
b P
. B. Nếu
//
b P
thì
b a
.
C. Nếu
//b a
thì
b P
. D. Nếu
b P
thì
//b a
.
Câu 9: Nghiệm của phương trình
2
cos
4 2
x
là
A.
2
2
x k
k
x k
. B.
2
2
x k
k
x k
.
C.
2
2
2
x k
k
x k
. D.
2
x k
k
x k
.
Câu 10: Dãy số nào sau đây có giới hạn bằng
0
?
A.
3
3
1
n
n n
u
n
. B.
6
5
n
n
u
. C.
2
4
n
u n n
. D.
2
3
n
n
u
.
Câu 11: Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng
phân biệt từ các điểm đã cho?
A.
3
. B.
6
. C.
4
. D.
2
.
Câu 12: Khối đa diện đều có
12
mặt thì có số cạnh là:
A.
. B.
60
. C.
12
. D.
24
.
Câu 13: Cho tập
0;2; 4;6; 8
A
;
3; 4;5;6; 7
B
. Tập
\A B
là
A.
0;6;8
. B.
0;2;8
. C.
3;6;7
. D.
0;2
.
Câu 14: Cho hàm số
3
3 .y x x
Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
; 1
và nghịch biến trên khoảng
1;

.
B. Hàm số nghịch biến trên khoảng
1;1
.
C. Hàm số đồng biến trên khoảng
( ; ). 
D. Hàm số nghịch biến trên khoảng
; 1
và đồng biến trên khoảng
1;

Câu 15: Hàm số
3 2
3 3 4y x x x
có bao nhiêu điểm cực trị?
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 16: Tìm hệ số của
6
x
trong khai triển thành đa thức của
10
2 3
x
.
A.
4
4 6
10
.2 . 3
C
. B.
6
6 4
10
.2 . 3
C
. C.
6 4 6
10
.2 .3
C
. D.
4
6 6
10
.2 . 3
C
.
Câu 17:
Cho hình lăng trụ
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
,
3
2
a
AA
. Biết rằng hình chiếu vuông góc của
A
lên
ABC
là trung điểm
BC
. Tính thể tích
V
của khối lăng trụ đó.
A.
3
2
3
a
V
. B.
3
3
4 2
a
V
.
C.
3
3
2
V a
. D.
3
V a
.
A
B
C
A
B
C
H
Trang 3/6 - Mã đề thi 132
Câu 18:
Cho hình chóp
.S ABCD
. Gọi
A
,
,
,
theo thứ tự là
trung điểm của
SA
,
SB
,
SC
,
SD
. Tính tỉ số thể tích của hai
khối chóp
.S A B C D
và
.S ABCD
.
A.
1
16
. B.
1
4
.
C.
1
8
. D.
1
2
.
D'
C'
B'
A'
D
C
B
A
S
Câu 19: Một tổ công nhân có
12
người. Cần chọn
3
người để đi làm cùng một nhiệm vụ, hỏi có bao
nhiêu cách chọn?
A.
3
12
C
. B.
3
12
. C.
12!
. D.
3
12
A
.
Câu 20: Phương trình
cos 2 4 sin 5 0x x
có bao nhiêu nghiệm trên khoảng
0;10
?
A.
5
. B.
2
. C.
4
. D.
3
.
Câu 21:
Cho hình chóp đều
.S ABCD
, cạnh đáy bằng
a
, góc giữa mặt bên
và mặt đáy là
60
. Tính khoảng cách từ điểm
B
đến mặt phẳng
SCD
.
A.
4
a
. B.
3
4
a
.
C.
3
2
a
. D.
2
a
.
D
A
B
C
S
Câu 22: Trong mặt phẳng
Oxy
cho đường thẳng
d
có phương trình
2 1 0x y
. Phép tịnh tiến theo
v
nào sau đây biến đường thẳng
d
thành chính nó?
A.
1;2
v
. B.
2; 4
v
. C.
2; 4
v
. D.
2;1
v
.
Câu 23: Cho cấp số nhân
n
u
có
1
3u
, công bội
2q
. Hỏi
192
là số hạng thứ mấy của
?
n
u
A. Số hạng thứ
7
. B. Số hạng thứ
6
. C. Số hạng thứ
8
. D. Số hạng thứ
5
.
Câu 24: Phát biểu nào sau đây là sai?
A.
1
lim 0
n
. B.
lim
n
u c
(
n
u c
là hằng số ).
C.
1
lim 0
k
n
1
k
. D.
lim 0
n
q
1
q
.
Câu 25: Tính đạo hàm của hàm số
tan
4
y x
:
A.
2
1
sin
4
y
x
. B.
2
1
sin
4
y
x
.
C.
2
1
cos
4
y
x
. D.
2
1
cos
4
y
x
.
Trang 4/6 - Mã đề thi 132
Câu 26: Cho hàm số
2
2
2
3 2
x x
y
x x
C
, đồ thị
C
có bao nhiêu đường tiệm cận?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 27:
Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành
tâm
O
. Gọi
,
N
,
P
theo thứ tự là trung điểm của
SA
,
SD
và
AB
. Khẳng định nào sau đây đúng?
A.
PON MNP NP
.
B.
//
NMP SBD
.
C.
//
MON SBC
.
D.
NOM
cắt
OPM
.
P
NM
O
C
S
B
D
Câu 28: Trên mặt phẳng toạ độ
Oxy
, cho tam giác
ABC
biết
1;3
A
,
2; 2
B
,
3;1
C
. Tính cosin
góc
A
của tam giác.
A.
2
cos
17
A
. B.
1
cos
17
A
.
C.
2
cos
17
A
. D.
1
cos
17
A
.
Câu 29: Cho hàm số
1
2
x
y
x
. Khẳng định nào sau đây đúng?
A. Hàm số đã cho đồng biến trên từng khoảng xác định của nó.
B. Hàm số đã cho đồng biến trên khoảng
;2 2;
 
.
C. Hàm số đã cho đồng biến trên
.
D. Hàm số đã cho nghịch biến trên từng khoảng xác định của nó.
Câu 30: Cho hàm số
1
x m
y
x
(
m
là tham số thực) thỏa mãn
0;1
min 3y
. Mệnh đề nào dưới đây
đúng?
A.
1 3m
. B.
6m
.
C.
1m
. D.
3 6m
.
Câu 31: Trên giá sách có
4
quyển sách toán, 3 quyển sách lý,
2
quyển sách hóa. Lấy ngẫu nhiên
3
quyển sách. Tính xác suất để trong ba quyển sách lấy ra có ít nhất một quyển là toán.
A.
2
.
7
B.
3
.
4
C.
37
.
42
D.
10
.
21
Câu 32: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
AB a
,
3BC a
,
SA a
và
SA
vuông góc với đáy
ABCD
. Tính
sin
, với
là góc tạo bởi giữa đường thẳng
BD
và mặt phẳng
SBC
.
A.
3
sin
5
. B.
7
sin
8
. C.
2
sin
4
D.
3
sin
2
.
Câu 33: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
cạnh
a
,
SO
vuông góc với mặt
phẳng
ABCD
và
.SO a
Khoảng cách giữa
SC
và
AB
bằng
A.
3
15
a
. B.
5
5
a
. C.
2 3
15
a
. D.
2 5
5
a
.
Trang 5/6 - Mã đề thi 132
Câu 34: Cho lăng trụ tam giác đều
.ABC A B C
có tất cả các cạnh đều bằng
a
. Khoảng cách giữa hai
đường thẳng
BC
và
AB
bằng
A.
3
2
a
. B.
21
7
a
. C.
7
4
a
. D.
2
2
a
.
Câu 35:
Cho hàm số
y f x
xác định trên
và hàm số
y f x
có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số
2
3
y f x
.
A.
3
. B.
2
.
C.
5
. D.
4
.
x
y
-2
2
O
1
Câu 36: Cho hàm số
2
2
mx
y
x m
,
m
là tham số thực. Gọi
S
là tập hợp tất cả các giá trị nguyên của
tham số
m
để hàm số nghịch biến trên khoảng
0;1
. Tìm số phần tử của
S
.
A.
2
. B.
5
. C.
1
. D.
3
.
Câu 37: Cho hàm số
2
1, 0
1, 0
ax bx x
f x
ax b x
. Khi hàm số
f x
có đạo hàm tại
0
0x
. Hãy tính
2T a b
.
A.
4T
. B.
0T
. C.
6T
. D.
4T
.
Câu 38: Đồ thị hàm số
2
5 1 1
2
x x
y
x x
có tất cả bao nhiêu đường tiệm cận?
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 39: Trong mặt phẳng với hệ tọa độ
Oxy
cho hình chữ nhật
ABCD
biết
2AD AB
, đường thẳng
AC
có phương trình
2 2 0x y
,
1;1
D
và
; , , 0
A a b a b a
. Tính
a b
.
A.
4a b
. B.
3a b
.
C.
4a b
. D.
1a b
.
Câu 40: Tổng tất cả các giá trị nguyên của
m
để phương trình
4 sin 4 cos 2 5 0
x m x m
có
nghiệm là:
A.
5
. B.
6
. C.
3
. D.
10
.
Câu 41: Biết
n
là số nguyên dương thỏa mãn
2
0 1 2
2 2 ... 2
n
n
n
x a a x a x a x
và
3
1 2 3
2 .192
n
a a a
. Mệnh đề nào sau đây đúng?
A.
9;16
n
. B.
8;12
n
.
C.
7;9
n
. D.
5;8
n
Câu 42: Giá trị nhỏ nhất
m
và giá trị lớn nhất
của hàm số
sin 2 cos 1
sin cos 2
x x
y
x x
là
A.
2m
;
1M
. B.
1m
;
2M
. C.
1
2
m
;
1M
. D.
1m
;
2M
.
Câu 43: Xét tứ diện
ABCD
có các cạnh
1AB BC CD DA
và
,AC BD
thay đổi. Giá trị lớn
nhất của thể tích khối tứ diện
ABCD
bằng
A.
4 3
27
. B.
4 3
9
. C.
2 3
9
. D.
2 3
27
.
Trang 6/6 - Mã đề thi 132
Câu 44:
Cho hàm số bậc ba
3 2
f x ax bx cx d
có đồ thị như
hình vẽ bên. Hỏi đồ thị hàm số
2
2
3 2 2 1
x x x
g x
x f x f x
có
bao nhiêu đường tiệm cận đứng?
A.
5
. B.
4
.
C.
6
. D.
3
.
Câu 45: Cho hàm số
4
1
x ax a
y
x
. Gọi
,M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm
số đã cho trên đoạn
1;2
. Có bao nhiêu giá trị nguyên của
a
để
2 .M m
A.
15
. B.
14
. C.
13
. D.
16
.
Câu 46: Cho hai đường thẳng cố định
a
và
b
chéo nhau. Gọi
AB
là đoạn vuông góc chung của
a
và
b
(
A
huộc
,a
B
thuộc
b
). Trên
a
lấy điểm
(khác
A
), trên
b
lấy điểm
N
(khác
B
) sao cho
, , 8.AM x BN y x y
Biết
6,AB
góc giữa hai đường thẳng
a
và
b
bằng
0
60 .
Khi thể tích
khối tứ diện
ABNM
đạt giá trị lớn nhất hãy tính độ dài đoạn
MN
(trong trường hợp
8MN
)
A.
13
. B.
12
. C.
2 39
. D.
2 21
.
Câu 47: Cho tập hợp
1;2;3;4...;100
A
. Gọi
S
là tập hợp gồm tất cả các tập con của
A
, mỗi tập con
này gồm 3 phần tử của
A
và có tổng bằng
91
. Chọn ngẫu nhiên một phần tử của
S
. Xác suất chọn được
phần tử có 3 số lập thành cấp số nhân bằng?
A.
1
645
. B.
3
645
. C.
4
645
. D.
2
645
.
Câu 48: Biết
m
là giá trị để hệ bất phương trình
0 1
2 1
x y
x y xy m
có nghiệm thực duy nhất.
Mệnh đề nào sau đây đúng?
A.
1 1
;
2 3
m
. B.
3
;0
4
m
. C.
1
;1
3
m
. D.
2; 1
m
.
Câu 49: Cho hàm số
3
3 2
y x x C
. Biết rằng đường thẳng
:d y ax b
cắt đồ thị
C
tại ba
điểm phân biệt
, ,M N P
. Tiếp tuyến tại ba điểm
, ,M N P
của đồ thị
C
cắt
C
tại các điểm
, ,M N P
(tương ứng khác
, ,M N P
). Khi đó đường thẳng đi qua ba điểm
, ,M N P
có phương trình là
A.
y ax b
. B.
4 9 18 8y a x b
.
C.
8 18 18 8y a x b
. D.
4 9 14 8y a x b
.
Câu 50: Cho phương trình:
3 3 3 3 2
sin 2 sin 3 2 cos 2 cos 2 2 cos cos
x x x m x m x x m
.
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình trên có đúng
1
nghiệm
2
0;
3
x
?
A.
4
. B.
2
. C.
3
. D.
1
.
-----------------------------------------------
----------- HẾT ----------
TÀI LIỆU ÔN THI THPT QG 2019 1
SỞ GD VÀ ĐT BẮC NINH
TRƯỜNG THPT LÊ VĂN THỊNH
ĐÁP ÁN ĐỀ KHẢO SÁT CHẤT LƯỢNG ĐẦU NĂM
NĂM HỌC 2018-2019
Môn: TOÁN 12
Ngày thi: 16 tháng 9 năm 2018
Đề gốc
I. NHẬN BIẾT
Câu 1: Tập xác định của hàm số
tan
y x
là:
A.
\ 0
. B. \ ,
2
k k
.
C.
. D.
\ ,k k
.
Lời giải
Chọn B.
Điều kiện xác định:
cos 0
x
2
x k
,
k
.
Vậy tập xác định là \ ,
2
k k
.
Câu 2: Nghiệm của phương trình
2
cos
4 2
x
là
A.
2
2
x k
k
x k
. B.
2
x k
k
x k
.
C.
2
2
x k
k
x k
. D.
2
2
2
x k
k
x k
.
Lời giải
Chọn D.
Phương trình
2
2
cos cos cos
4 2 4 4
2
2
x k
x x k
x k
.
Câu 3: Cho cấp số cộng
n
u
có số hạng tổng quát là
3 2
n
u n
. Tìm công sai
d
của cấp số cộng.
A.
3
d
. B.
2
d
. C.
2
d
. D.
3
d
.
Lời giải
Chọn A.
Ta có
1
3 1 2 3 2 3
n n
u u n n
Suy ra
3
d
là công sai của cấp số cộng.
Câu 4: Dãy số nào sau đây có giới hạn bằng
0
?
A.
2
3
n
n
u
. B.
6
5
n
n
u
. C.
3
3
1
n
n n
u
n
. D.
2
4
n
u n n
.
Lời giải:
Chọn A.
2
lim lim 0
3
n
n
n n
u
 
(Vì
2 2
1
3 3
).
TÀI LIỆU ÔN THI THPT QG 2019 2
Câu 5: Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng
phân biệt từ các điểm đã cho?
A.
6
. B.
4
. C.
3
. D.
2
.
Lời giải
Chọn B.
Vì
4
điểm không đồng phẳng tạo thành một tứ diện mà tứ diện có
4
mặt.
Câu 6: Cho hai đường thẳng phân biệt
,
a b
và mặt phẳng
P
, trong đó
a P
. Chọn mệnh đề sai.
A. Nếu
//
b a
thì
//
b P
. B. Nếu
//
b a
thì
b P
.
C. Nếu
b P
thì
//
b a
. D. Nếu
//
b P
thì
b a
.
Lời giải
Chọn A.
Nếu
a P
và
//
b a
thì
b P
.
Câu 7: Cho hàm số
3
3 .
y x x
Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
; 1

và nghịch biến trên khoảng
1;

.
B. Hàm số đồng biến trên khoảng
( ; ).
 
C. Hàm số nghịch biến trên khoảng
; 1

và đồng biến trên khoảng
1;

D. Hàm số nghịch biến trên khoảng
1;1
.
Lời giải
Chọn D.
Ta có
2
3 3 0 1
y x x
Bảng biến thiên
Dựa vào bảng biến thiên ta chọn đáp án D.
Câu 8: Cho hàm số
y f x
có đạo hàm trên đoạn
;
a b
. Ta xét các khẳng định sau:
1
Nếu hàm số
f x
đạt cực đại tại điểm
0
;
x a b
thì
0
f x
là giá trị lớn nhất của
f x
trên
đoạn
;
a b
.
2
Nếu hàm số
f x
đạt cực đại tại điểm
0
;
x a b
thì
0
f x
là giá trị nhỏ nhất của
f x
trên đoạn
;
a b
.
3
Nếu hàm số
f x
đạt cực đại tại điểm
0
x
và đạt cực tiểu tại điểm
1 0 1
, ;
x x x a b
thì ta
luôn có
0 1
f x f x
.
Số khẳng định đúng là?
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 9: Hàm số
3 2
3 3 4
y x x x
có bao nhiêu điểm cực trị?
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn C.
x

1
1

y
0
0
y

2
2

TÀI LIỆU ÔN THI THPT QG 2019 3
Ta có
2
2
3 6 3 3 1 0
y x x x
, x
. Hàm số đã cho có đạo hàm không đổi dấu
trên
nên nó không có cực trị.
Câu 10: Giá trị nhỏ nhất của hàm số
3
3 5
y x x
trên đoạn
2;4
là:
A.
2; 4
min 3
y
. B.
2; 4
min 7
y
. C.
2; 4
min 5.
y
D.
2; 4
min 0.
y
Lời giải
Chọn B.
Ta có:
2
3 3
y x
0
y
1 2;4
1 2;4
x
x
mà
2 7
4 57
f
f
2; 4
min 7
y
.
Câu 11: Tiệm cận ngang của đồ thị hàm số
3
1
x
y
x
là đường thẳng có phương trình?
A.
5
y
. B.
0
y
. C.
1
x
. D.
1
y
.
Lời giải
Chọn D.
Ta có
3
lim lim 1
1
x x
x
y
x
 
đường thẳng
0
y
là tiệm cận ngang của đồ thị hàm số.
Câu 12: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
2 1
1
x
y
x
. B.
1 2
1
x
y
x
. C.
2 1
1
x
y
x
. D.
2 1
1
x
y
x
.
Lời giải
Chọn A.
Đồ thị hàm số có đường tiệm cận đứng là
1
x
loại đáp án C.
Đồ thị hàm số đi qua điểm
0; 1A
loại đáp án B và D.
Câu 13: Khối đa diện đều có
12
mặt thì có số cạnh là:
A.
30
. B.
60
. C.
12
. D.
24
.
Lời giải
Chọn A.
Khối đa diện đều có
12
mặt là khối đa diện đều loại
5;3
thì có số cạnh là
30
.
Câu 14: Cho tứ diện
MNPQ
. Gọi
I
;
J
;
K
lần lượt là trung điểm của các cạnh
MN
;
MP
;
MQ
. Tỉ
số thể tích
MIJK
MNPQ
V
V
bằng
A.
1
3
. B.
1
4
. C.
1
6
. D.
1
8
.
Lời giải
Chọn D.
O
x
y
1
1
2
TÀI LIỆU ÔN THI THPT QG 2019 4
K
J
I
N
Q
P
M
Ta có:
.
.
1 1 1 1
. . . .
2 2 2 8
M IJK
M NPQ
V
MI MJ MK
V MN MP MQ
.
Câu 15: Cho tập
0;2;4;6;8
A
;
3;4;5;6;7
B
. Tập
\
A B
là
A.
0;6; 8
. B.
0;2;8
. C.
3;6;7
. D.
0;2
.
Lời giải
Chọn B.
Ta có
\ 0;2;8
A B .
II. THÔNG HIỂU
Câu 16: Phương trình
cos2 4 sin 5 0
x x
có bao nhiêu nghiệm trên khoảng
0;10
?
A.
5
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn A.
PT đã cho
2
2 sin 4 sin 6 0
x x
sin 1
sin 3
x
x VN
2 ,
2
x k k
.
Theo đề:
0;10
x
0 2 10
2
k
1 21
4 4
k .
Vì
k
nên
1;2;3;4;5
k
. Vậy PT đã cho có 5 nghiệm trên khoảng
0;10
.
Câu 17: Một tổ công nhân có
12
người. Cần chọn
3
người để đi làm cùng một nhiệm vụ, hỏi có bao
nhiêu cách chọn?
A.
3
12
A
. B.
12!
. C.
3
12
C
. D.
3
12
.
Lời giải
Chọn C.
Số cách chọn
3
người, là
3
12
C
(cách chọn)
Câu 18: Tìm hệ số của
6
x
trong khai triển thành đa thức của
10
2 3
x
.
A.
4
6 6
10
.2 . 3
C . B.
6
6 4
10
.2 . 3
C . C.
4
4 6
10
.2 . 3
C . D.
6 4 6
10
.2 .3
C
.
Lời giải
Chọn B.
Ta có:
10 10
10
10 10
10 10
0 0
2 3 .2 . 3 .2 . 3 .
k k
k k k k k
k k
x C x C x
Theo giả thiết suy ra:
6
k
.
TÀI LIỆU ÔN THI THPT QG 2019 5
Vậy hệ số của
6
x
trong khai triển là
6 6
6 10 6 6 4
10 10
.2 . 3 .2 . 3
C C
.
Câu 19: Cho cấp số nhân
n
u
có
1
3
u
, công bội
2
q
. Hỏi
192
là số hạng thứ mấy của
?
n
u
A. Số hạng thứ
6
. B. Số hạng thứ
7
. C. Số hạng thứ
5
. D. Số hạng thứ
8
.
Lời giải
Chọn B.
Giả sử
192
là số hạng thứ
n
của
n
u
với
*
n
.Ta có
1
1
192 .
n
u q
1
192 3 . 2
n
1
64 2
n
6 1
2 2
n
6 1
n
7
n
. Do đó
192
là số hạng thứ
7
của
n
u
.
Câu 20: Phát biểu nào sau đây là sai?
A.
lim
n
u c
(
n
u c
là hằng số ). B.
lim 0
n
q
1
q
.
C.
1
lim 0
n
. D.
1
lim 0
k
n
1
k
.
Lời giải
Chọn B.
Theo định nghĩa giới hạn hữu hạn của dãy số (SGK ĐS11-Chương 4) thì
lim 0
n
q
1
q
.
Câu 21: Tính đạo hàm của hàm số tan
4
y x
:
A.
2
1
cos
4
y
x
. B.
2
1
cos
4
y
x
.
C.
2
1
sin
4
y
x
. D.
2
1
sin
4
y
x
.
Giải:
Chọn A
2 2
1 1
.
4
cos cos
4 4
y x
x x
Câu 22: Trong mặt phẳng
Oxy
cho đường thẳng
d
có phương trình
2 1 0
x y
. Phép tịnh tiến
theo
v
nào sau đây biến đường thẳng
d
thành chính nó?
A.
2;4
v
. B.
2;1
v
. C.
1;2
v
. D.
2; 4
v
.
Lời giải
Chọn A.
Phép tịnh tiến theo
v
biến đường thẳng
d
thành chính nó khi vectơ
v
cùng phương với vectơ
chỉ phương của
d
. Mà
d
có VTCP
1;2
u
.
Câu 23: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành tâm
O
. Gọi
M
,
N
,
P
theo thứ tự
là trung điểm của
SA
,
SD
và
AB
. Khẳng định nào sau đây đúng?
A.
NOM
cắt
OPM
. B.
//
MON SBC
.
TÀI LIỆU ÔN THI THPT QG 2019 6
C.
PON MNP NP
. D.
//
NMP SBD
.
Hướng dẫn giải
Chọn B.
P
NM
O
C
S
B
D
A
Xét hai mặt phẳng
MON
và
SBC
.
Ta có:
//
OM SC
và
//
ON SB
.
Mà
BS SC C
và
OM ON O
.
Do đó
//
MON SBC
.
Câu 24: Cho hình chóp đều
.
S ABCD
, cạnh đáy bằng
a
, góc giữa mặt bên và mặt đáy là
60
. Tính
khoảng cách từ điểm
B
đến mặt phẳng
SCD
.
A.
4
a
. B.
3
4
a
. C.
3
2
a
. D.
2
a
.
Lời giải
Chọn C.
* Ta có:
;
2
;
d B SCD
BD
OD
d O SCD
; 2. ; 2
d B SCD d O SCD OH
. Trong đó
H
là
hình chiếu vuông góc của
O
lên
SCD
.
60
O
I
A
B
C
D
S
H
* Gọi
I
là trung điểm của
CD
ta có:
; ; 60
SI CD
SCD ABCD OI SI SIO
OI CD
.
Xét tam giác
SOI
vuông tại
O
ta có:
3
.tan 60
2
a
SO OI .
TÀI LIỆU ÔN THI THPT QG 2019 7
* Do
SOCD
là tứ diện vuông tại
O
nên:
2 2 2 2 2 2 2 2
1 1 1 1 2 2 4 16
3 3
OH OC OD OS a a a a
3 3
;
4 2
a a
OH d B SCD .
Câu 25: Cho hàm số
1
2
x
y
x
. Khẳng định nào sau đây đúng?
A. Hàm số đã cho đồng biến trên từng khoảng xác định của nó.
B. Hàm số đã cho đồng biến trên
.
C. Hàm số đã cho đồng biến trên khoảng
;2 2;
 
.
D. Hàm số đã cho nghịch biến trên từng khoảng xác định của nó.
Lời giải
Chọn A.
Ta có
2
1 1 3
0, 2.
2 2
2
x x
y x
x x
x
Do đó hàm số đã cho đồng biến trên các khoảng
;2

và
2;

.
Câu 26: Cho hàm số
1
x m
y
x
(
m
là tham số thực) thỏa mãn
0;1
min 3
y
. Mệnh đề nào dưới đây
đúng?
A.
1 3
m
. B.
6
m
. C.
1
m
. D.
3 6
m
.
Lời giải
Chọn D.
Tập xác định:
\ 1
D
.
Với
1
m
1
y
,
0;1
x
thì
0;1
min 3
y
.
Suy ra
1
m
. Khi đó
2
1
1
m
y
x
không đổi dấu trên từng khoảng xác định.
TH 1:
0 1
y m
thì
0;1
min 0 3
y y m
(loại).
TH 2:
0 1
y m
thì
0;1
min 1 5
y y m
( thỏa mãn).
Câu 27: Cho hàm số
2
2
2
3 2
x x
y
x x
C
, đồ thị
C
có bao nhiêu đường tiệm cận?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C.
Tập xác định
\ 1;2
D
Ta có
2
2
x
y
x
nên đồ thị hàm số có tiệm cận ngang của là
1
y
và là tiệm cận đứng là
2
x
Câu 28: Cho hình chóp
.
S ABCD
. Gọi
A
,
B
,
C
,
D
theo thứ tự là trung điểm của
SA
,
SB
,
SC
,
SD
. Tính tỉ số thể tích của hai khối chóp
.
S A B C D
và
.
S ABCD
.
A.
1
16
. B.
1
4
. C.
1
8
. D.
1
2
.
Lời giải
TÀI LIỆU ÔN THI THPT QG 2019 8
Chọn C.
D'
C'
B'
A'
D
C
B
A
S
Ta có
.
.
1
. .
8
S A B D
S ABD
V
SA SB SD
V SA SB SD
.
.
1
16
S A B D
S ABCD
V
V
.
Và
.
.
1
. .
8
S B D C
S BDC
V
SB SD SC
V SB SD SC
.
.
1
16
S B D C
S ABCD
V
V
.
Suy ra
. .
. .
1 1 1
16 1
6 8
S A B D S B D C
S ABCD S ABCD
V V
V V
.
.
1
8
S A B C D
S ABCD
V
V
.
Câu 29: Cho hình lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
,
3
2
a
AA
. Biết rằng
hình chiếu vuông góc của
A
lên
ABC
là trung điểm
BC
. Tính thể tích
V
của khối lăng trụ
đó.
A.
3
V a
. B.
3
2
3
a
V
. C.
3
3
4 2
a
V
. D.
3
3
2
V a
.
Lời giải
Chọn C.
Gọi
H
là trung điểm
BC
.
Theo giả thiết,
A H
là đường cao hình lăng trụ và
2 2
6
.
2
a
A H AA AH
Vậy, thể tích khối lăng trụ là
Δ
2 3
3 6 3 2
. .
4 2 8
ABC
a a a
V S A H
.
A
B
C
A
B
C
H
TÀI LIỆU ÔN THI THPT QG 2019 9
Câu 30: Trên mặt phẳng toạ độ
Oxy
, cho tam giác
ABC
biết
1;3
A ,
2; 2
B
,
3;1
C . Tính cosin
góc
A
của tam giác.
A.
2
cos
17
A . B.
1
cos
17
A . C.
2
cos
17
A . D.
1
cos
17
A .
Lời giải:
Chọn B.
3; 5
AB

,
2; 2
AC

.
. 3.2 5.2 1
cos cos ;
.
34.2 2 17
AB AC
A AB AC
AB AC
 
 
III. VẬN DỤNG
Câu 31: Tổng tất cả các giá trị nguyên của
m
để phương trình
4 sin 4 cos 2 5 0
x m x m
có nghiệm là:
A.
5
. B.
6
. C.
10
. D.
3
.
Lời giải
Chọn C.
4 sin 4 cos 2 5 0
x m x m
4 sin 4 cos 2 5
x m x m
.
Phương trình có nghiệm khi
2 2
2
4 4 2 5 0
m m
2
3 12 7 0
m m
6 57 6 57
3 3
m
Vì
m
nên
0,1,2, 3, 4
m .
Vây tổng tất cả các giá trị nguyên của
m
để phương trình có nghiệm là.
10
.
Câu 32: Giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của hàm số
sin 2 cos 1
sin cos 2
x x
y
x x
là
A.
1
2
m
;
1
M
. B.
1
m
;
2
M
. C.
2
m
;
1
M
. D.
1
m
;
2
M
.
Lời giải
Chọn C.
Ta có
sin 2 cos 1
1 sin 2 cos 1 2
sin cos 2
x x
y y x y x y
x x
*
Phương trình
*
có nghiệm
2 2 2
2
1 2 1 2 2 0 2 1
y y y y y y
.
Vậy
2
m
;
1
M
.
Câu 33: Trên giá sách có
4
quyển sách toán, 3 quyển sách lý,
2
quyển sách hóa. Lấy ngẫu nhiên
3
quyển sách. Tính xác suất để trong ba quyển sách lấy ra có ít nhất một quyển là toán.
A.
2
.
7
B.
3
.
4
C.
37
.
42
D.
10
.
21
Lời giải
Chọn C.
Số kết quả có thể khi chọn bất kì
3
quyển sách trong
9
quyển sách là
3
9
84.
C
Gọi
A
là biến cố ‘ Lấy được ít nhất
1
sách toán trong
3
quyển sách.’
A
là biến cố ‘ Không lấy được sách toán trong
3
quyển sách.’
TÀI LIỆU ÔN THI THPT QG 2019 10
Ta có xác sút để xảy ra
A
là
3
5
37
1 1 .
84 42
C
P A P A
Câu 34: Cho hàm số
2
1, 0
1, 0
ax bx x
f x
ax b x
. Khi hàm số
f x
có đạo hàm tại
0
0
x
. Hãy tính
2
T a b
.
A.
4
T
. B.
0
T
. C.
6
T
. D.
4
T
.
Lời giải
Chọn C.
Ta có
0 1
f
.
0
lim
x
f x
2
0
lim 1
x
ax bx
1
.
0
lim
x
f x
0
lim 1
x
ax b
1
b
.
Để hàm số có đạo hàm tại
0
0
x
thì hàm số phải liên tục tại
0
0
x
nên
0 0
0 lim lim
x x
f f x f x
. Suy ra
1 1
b
2
b
.
Khi đó
2
2 1, 0
1, 0
ax x x
f x
ax x
.
Xét:
+)
0
0
lim
x
f x f
x
2
0
2 1 1
lim
x
ax x
x
0
lim 2
x
ax
2
.
+)
0
0
lim
x
f x f
x
0
1 1
lim
x
ax
x
0
lim
x
a
a
.
Hàm số có đạo hàm tại
0
0
x
thì
2
a
.
Vậy với
2
a
,
2
b
thì hàm số có đạo hàm tại
0
0
x
khi đó
6
T
.
Câu 35: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông tâm
O
cạnh
a
,
SO
vuông góc với
mặt phẳng
ABCD
và
.
SO a
Khoảng cách giữa
SC
và
AB
bằng
A.
3
15
a
. B.
5
5
a
. C.
2 3
15
a
. D.
2 5
5
a
.
Lời giải
Chọn D.
Gọi
,
M N
lần lượt là trung điểm của các cạnh
,
AB CD
;
H
là hình chiếu vuông góc của
O
trên
.
SN
S
B
A
D
C
O
M
N
H
TÀI LIỆU ÔN THI THPT QG 2019 11
Vì
//
AB CD
nên
,SC ,( ) ,( ) 2 ,( )
d AB d AB SCD d M SCD d O SCD
(vì
O
là
trung điểm đoạn
MN
)
Ta có ( )
CD SO
CD SON CD OH
CD ON
Khi đó
( ) ;( ) .
CD OH
OH SCD d O SCD OH
OH SN
Tam giác
SON
vuông tại
O
nên
2 2 2 2 2 2
1 1 1 1 1 5
5
4
a
OH
OH ON OS a a a
Vậy
2 5
,SC 2
5
a
d AB OH .
Câu 36: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
AB a
,
3
BC a
,
SA a
và
SA
vuông góc với đáy
ABCD
. Tính
sin
, với
là góc tạo bởi giữa đường thẳng
BD
và
mặt phẳng
SBC
.
A.
7
sin
8
. B.
3
sin
2
. C.
2
sin
4
D.
3
sin
5
.
Lời giải
Chọn C
ABCD
là hình chữ nhật nên
2
BD a
, ta có
/ /
AD SBC
nên suy ra
, ,
d D SBC d A SBC AH
với
AH SB
. Tam giác
SAB
vuông cân tại
A
nên
H
là trung điểm của
SB
suy ra
2
2
a
AH
vậy
2
, ,
2
2
sin ,
2 4
a
d D SBC d A SBC
BD SBC
BD BD a
Câu 37: Cho hàm số
2
2
mx
y
x m
,
m
là tham số thực. Gọi
S
là tập hợp tất cả các giá trị nguyên của
tham số
m
để hàm số nghịch biến trên khoảng
0;1
. Tìm số phần tử của
S
.
A.
1
. B.
5
. C.
2
. D.
3
.
Lời giải
Chọn C.
TÀI LIỆU ÔN THI THPT QG 2019 12
Tập xác định \
2
m
D
2
2
4
2
m
y
x m
.
Yêu cầu bài toán
2
4 0
0;1
2
m
m
2 2
0
2
1
2
m
m
m
2 2
0
2
m
m
m
0 2
m
.
Câu 38: Cho hàm số
y f x
xác định trên
và hàm số
y f x
có đồ thị như hình vẽ. Tìm số
điểm cực trị của hàm số
2
3
y f x
.
x
y
-2
2
O
1
A.
4
. B.
2
. C.
5
. D.
3
.
Lời giải
Chọn D.
Quan sát đồ thị ta có
y f x
đổi dấu từ âm sang dương qua
2
x
nên hàm số
y f x
có một điểm cực trị là
2
x
.
Ta có
2 2
3 2 . 3
y f x x f x
2
2
0
0
0 3 2 1
2
3 1
x
x
x x
x
x
.
Mà
2
x
là nghiệp kép, còn các nghiệm còn lại là nghiệm đơn nên hàm số
2
3
y f x
có ba cực trị.
Câu 39: Đồ thị hàm số
2
5 1 1
2
x x
y
x x
có tất cả bao nhiêu đường tiệm cận?
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn D.
Tập xác định:
1; \ 0
D
.
lim
x
y

2
5 1 1
lim
2
x
x x
x x

2 3 4
5 1 1 1
lim
2
1
x
x
x x x
x

0
0
y
là đường tiệm
cận ngang của đồ thị hàm số.
TÀI LIỆU ÔN THI THPT QG 2019 13
0
lim
x
y
2
0
5 1 1
lim
2
x
x x
x x
2
0
2
5 1 1
lim
2 5 1 1
x
x x
x x x x
2
0
2
25 9
lim
2 5 1 1
x
x x
x x x x
0
25 9
lim
2 5 1 1
x
x
x x x
9
4
0
x
không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tất cả
1
đường tiệm cận.
Câu 40: Cho lăng trụ tam giác đều
.
ABC A B C
có tất cả các cạnh đều bằng
a
. Khoảng cách giữa hai
đường thẳng
BC
và
AB
bằng
A.
21
7
a
. B.
3
2
a
. C.
7
4
a
. D.
2
2
a
.
Lời giải
Chọn A.
I
A
C
B
C'
B'
A'
H
Ta có
//
BC B C
//
BC AB C
suy ra
,
d BC AB
,
d BC AB C
,
d B AB C
,
d A AB C
.
Gọi
I
và
H
lần lượt là hình chiếu vuông góc của
A
trên
B C
và
AI
.
Ta có
B C A I
và
B C A A
nên
B C A AI
B C A H
mà
AI A H
. Do
đó
AB C A H
Khi đó
,
d A AB C
A H
2 2
.
A A A I
A A A I
2
2
3
.
2
3
2
a
a
a
a
21
7
a
.
Vậy khoảng cách cần tìm là
21
7
a
.
Câu 41: Biết
n
là số nguyên dương thỏa mãn
2
0 1 2
2 2 ... 2
n
n
n
x a a x a x a x và
3
1 2 3
2 .192
n
a a a
. Mệnh đề nào sau đây đúng?
A.
9;16
n
. B.
8;12
n . C.
7;9
n
. D.
5;8
n .
Lời giải
Chọn B.
TÀI LIỆU ÔN THI THPT QG 2019 14
Ta có
2
0 1 1 2 2
2 2 .2 .2 2 .2 2 ... 2
n
n
n n n n n
n n n n
x x C C x C x C x
Do đó
3 1 1 2 2 3 3 3
1 2 3
2 .192 .2 .2 .2 2 .192
n n n n n
n n n
a a a C C C
1 2 3
.4 .2 192 9
n n n
C C C n
Câu 42: Trong mặt phẳng với hệ tọa độ
Oxy
cho hình chữ nhật
ABCD
biết
2
AD AB
, đường thẳng
AC
có phương trình
2 2 0
x y
,
1;1
D và
; , , 0
A a b a b a . Tính
a b
.
A.
4
a b
. B.
3
a b
. C.
4
a b
. D.
1
a b
.
Lời giải
Chọn D.
Gọi
;
A a b
. Vì
: 2 2 0
A AC x y
nên
2 2 0 2 2
a b a b
Do
0
a
nên
2 2 0 1
b b
*
Khi đó
2 2;
A b b
.
Ta có
2 3;1
AD b b

là véctơ chỉ phương của đường thẳng
AD
.
2; 1
u
là véctơ chỉ phương của đường thẳng
AC
.
Trên hình vẽ,
1 2
tan cos
2
5
DC
AD
1
Lại có
2
.
5 1
cos
5 2 2
. .
AD u
b
b b
AD u


2
Từ
1
và
2
suy ra
2
2
5 1
2
2 3 0 3
5
5 2 2
b
b b b
b b
(do
*
)
4
a
.
Khi đó
4; 3
A
, suy ra
1
a b
.
IV. VẬN DỤNG CAO
Câu 43: Xét tứ diện
ABCD
có các cạnh
1
AB BC CD DA
và
,
AC BD
thay đổi. Giá trị
lớn nhất của thể tích khối tứ diện
ABCD
bằng
A.
2 3
27
. B.
4 3
27
. C.
2 3
9
. D.
4 3
9
.
Lời giải
Chọn A.
Gọi
,
M N
lần lượt là trung điểm của
,
BD AC
. Đặt
2 , 2
BD x AC y
, 0
x y
.
;
A a b
1;1
D
C
B
TÀI LIỆU ÔN THI THPT QG 2019 15
Ta có
,
CM BD AM BD
BD AMC
.
Ta có
2
1
MA MC x
,
2 2
1
MN x y
,
1
.
2
AMN
S MN AC
2 2
1
. 1
2
y x y
.
1
. .
3
ABCD AMC
V DB S
2 2
1
.2 . 1
3
x y x y
2 2 2 2
2
. . 1
3
x y x y
3
2 2 2 2
1
2
3 27
x y x y
2 3
27
ABCD
V .
Câu 44: Cho hàm số
4
1
x ax a
y
x
. Gọi
,
M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm
số đã cho trên đoạn
1;2
. Có bao nhiêu giá trị nguyên của
a
để
2 .
M m
A.
15
. B.
14
. C.
15
. D.
16
.
Lời giải
Chọn A.
Xét hàm số
4
1
x ax a
f x
x
. Ta có
4 3
2
3 4
0, 1;2
1
x x
f x x
x
Do đó
1 2 , 1;2
f f x f x
hay
1 16
, 1;2
2 3
a f x a x
Ta xét các trường hợp sau :
Th1 : Nếu
1 1
0
2 2
a a
thì
16 1
;
3 2
M a m a
Theo đề bài
16 1 13
2
3 2 3
a a a
Do
a
nguyên nên
0;1;2;3; 4
a
.
Th2 : Nếu
16 16
0
3 3
a a thì
16 1
;
3 2
m a M a
Theo đề bài
1 16 61
2
2 3 6
a a a
Do
a
nguyên nên
10; 9;...; 6
a
.
Th3 : Nếu
1 16 16 1
0
2 3 3 2
a a a
thì
0; 0
M m
(Luôn thỏa mãn)
Do
a
nguyên nên
5; 4;...; 1
a
Vậy có
15
gái trị của
a
thỏa mãn yêu cầu bài toán.
Câu 45: Cho hàm số
3
3 2
y x x C
. Biết rằng đường thẳng
:
d y ax b
cắt đồ thị
C
tại ba
điểm phân biệt
, ,
M N P
. Tiếp tuyến tại ba điểm
, ,
M N P
của đồ thị
C
cắt
C
tại các điểm
, ,
M N P
(tương ứng khác
, ,
M N P
). Khi đó đường thẳng đi qua ba điểm
, ,
M N P
có
phương trình là
A.
4 9 18 8
y a x b
. B.
4 9 14 8
y a x b
.
TÀI LIỆU ÔN THI THPT QG 2019 16
C.
y ax b
. D.
8 18 18 8
y a x b
.
Lời giải
Chọn A.
Giả sử
1 1 2 2 3 3
; ; ; ; ;
A x y B x y C x y
. Ta có phương trình tiếp tuyến tại
A
của đồ thị
C
là
2 3
1 1 1 1 1
: 3 3 3 2
y x x x x x
Xét phương trình hoành độ giao điểm của đồ thị
C
và
1
là
2 3 3
1 1 1 1
3 3 3 2 3 2
x x x x x x x
2
1
1 1
1
2 0
2
x x
x x x x
x x
Do đó
3
1 1 1
2 ; 8 6 2
A x x x
Lại có
3 3
1 1 1 1 1 1 1
8 6 2 8 3 2 18 18 8 18 18
x x x x x ax b x
1 1 1
8 18 18 2 4 9 18 8
ax b x x a b
Khi đó
4 9 18 8
A A
y x a b
Vậy phương trình đường thẳng đi qua
3
điểm
, ,
A B C
là
4 9 18 8
y x a b
Câu 46: Cho hàm số bậc ba
3 2
f x ax bx cx d
có đồ thị như hình vẽ bên dưới:
Hỏi đồ thị hàm số
2
2
3 2 2 1
x x x
g x
x f x f x
có bao nhiêu đường tiệm cận đứng?
A.
5
. B.
4
. C.
6
. D.
3
.
Lời giải
Chọn A.
ĐK
1
; 0; 1
2
x f x f x
.
Xét phương trình
2
0
0, 5;1
2
0
1
1;2
2;3
x
x a a
x
x f x f x
x
x b b
x c c
Đồ thi hàm số có
4
đường tiệm cận đứng
; ; ; 2
x a x b x c x
Câu 47: Cho hai đường thẳng cố định
a
và
b
chéo nhau. Gọi
AB
là đoạn vuông góc chung của
a
và
b
TÀI LIỆU ÔN THI THPT QG 2019 17
(
A
huộc
,
a
B
thuộc
b
). Trên
a
lấy điểm
M
(khác
A
), trên
b
lấy điểm
N
(khác
B
) sao cho
, , 8.
AM x BN y x y
Biết
6,
AB
góc giữa hai đường thẳng
a
và
b
bằng
0
60 .
Khi
thể tích khối tứ diện
ABNM
đạt giá trị lớn nhất hãy tính độ dài đoạn
MN
(trong trường hợp
8
MN
)
A.
2 21
. B.
12
. C.
2 39
. D.
13
.
Lời giải
Chọn A.
Dựng hình chữ nhật
ABNC
.
0
, , 60
AM BN AM AC
Ta có
AB AM AB AM
AB ACM
AB BN AB AC
1 1 1 3 3
. . . sin .6. . .
3 6 6 2 2
ABNM MABC ACM
V V AB S AB AC AM CAM x y xy
2
3 3
8 3.
2 2 4
ABNM
x y
V xy
Dấu bằng xảy ra khi và chỉ khi
4.
x y
Khi đó
4
AM BN AC
Lại có
2 2 2
/ /
AB CN CN AMC CN CM MN CM CN
Mặt khác
0
60
MAC
hoặc
0
120
MAC
Trường hợp 1:
0
60
MAC
AMC
đều
2 2
4 4 6 2 13
CM MN
Trường hợp 2:
0
120
MAC
2 2 0 2
2 . cos120 48 48 6 2 41
CM AM AC AM AC MN
Câu 48: Cho tập hợp
1;2;3;4...;100
A
. Gọi
S
là tập hợp gồm tất cả các tập con của
A
, mỗi tập con
này gồm 3 phần tử của
A
và có tổng bằng
91
. Chọn ngẫu nhiên một phần tử của
S
. Xác suất
chọn được phần tử có 3 số lập thành cấp số nhân bằng?
A.
4
645
. B.
2
645
. C.
3
645
. D.
1
645
.
Lời giải
Chọn C.
Giả sử tập con bất kì
, ,
a b c S
1 , , 100
a b c
;
, ,
a b c
phân biệt.
a 91.
b c
Đây là bài toán chia kẹo Euler nên số bộ
, ,
a b c
là
3 1
91 1
C
Tuy nhiên trong các bộ trên vẫn chứa các bộ có 2 chữ số giống nhau, số bộ có 2 chữ số giống
nhau là
3.45 135
( bộ). Vậy
2
90
3.45 : 3! 645
n C .
Gọi
A
là biến cố: ”
, ,
a b c
lập thành cấp số nhân”
Gọi
q
là công bội của cấp số nhân theo bài ra ta có
0
q
2
91
a aq aq
2
1 1.91 13.7
a q q
Trường hợp 1:
2
1
1
9
1 91
a
a
q
q q
Trường hợp 2:
2
91
91
0
1 1
a
a
q
q q
(loại)
TÀI LIỆU ÔN THI THPT QG 2019 18
Trường hợp 3:
2
13
13
2
1 7
a
a
q
q q
(thỏa mãn)
Trường hợp 3:
2
7
7
3
1 13
a
a
q
q q
(thỏa mãn).
Vậy
3
n A
.
3
645
P A .
Câu 49: Biết
m
là giá trị để hệ bất phương trình
0 1
2 1
x y
x y xy m
có nghiệm thực duy nhất.
Mệnh đề nào sau đây đúng?
A.
1 1
;
2 3
m
. B.
3
;0
4
m
. C.
1
;1
3
m
. D.
2; 1
m
.
Lời giải
Chọn B.
Hệ phương trình tương đương với:
2
0 1
0 1
2 1
2 1 2 2
x y
x y
xy m x y
xy m x y x y
2 2
0 1 I
1 1 1 II .
x y
x y m
Tập nghiệm của (I) là phần nằm giữa hai đường thẳng
: ; ' : 1
d y x d y x
và trên
'.
d
Nếu
1
m
thì hệ phương trình vô nghiệm.
Nếu
1
m
thì tập nghiệm của (II) là hình tròn
( )
C
(kể cả biên)
có tâm
1;1
A bán kính
1
R m
.
Do đó hệ phương trình có nghiệm duy nhất khi
'
d
là tiếp tuyến của đường tròn
( )
C
.
Nghĩa là:
2 1
1 .
2 2
m m
Vậy hệ phương trình có nghiệm duy nhất khi
1
.
2
m
Câu 50: Cho phương trình:
3 3 3 3 2
sin 2 sin 3 2 cos 2cos 2 2 cos cos
x x x m x m x x m
.
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình trên có đúng
1
nghiệm
2
0;
3
x
?
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn D.
Ta có:
TÀI LIỆU ÔN THI THPT QG 2019 19
3
3 2 3 3 3
sin sin 2 sin 2 cos 2 2 cos 2 2 2 cos 2 1
x x x x m x m x m
Xét hàm số
3 2
2
f t t t t
có
2
6 2 2 0,f t t t t
, nên hàm số
f t
đồng
biến trên
.
Bởi vậy:
3
1 sin 2 cos 2
f x f x m
3
sin 2 cos 2 2
x x m
Với
2
0;
3
x
thì
2 3
2 sin 2 cos 2
x x m
3 2
2 cos cos 3 3
x x m
Đặt
cos
t x
, phương trình
3
trở thành
3 2
2 1 4
t t m
Ta thấy, với mỗi
1
;1
2
t
thì phương trình
cos
x t
cho ta một nghiệm
2
0;
3
x
Xét hàm số
3 2
2 3
g t t t
với
1
;1
2
t
.
Ta có
2
6 2
g t t t
,
0
0
1
3
t
g t
t
.
Ta có bảng biến thiên
Do đó, để phương trình đã cho có đúng
1
nghiệm
2
0;
3
x
điều kiện cần và đủ là phương
trình
4
có đúng một nghiệm
1
;1
2
t
3
3;2;1;0
80
0;
27
m
m
m
( Do
m
nguyên).
Chúc các em đạt kết quả cao trong kì thi THPT 2019!
t
1
2
1
3
0
1
g t
0
0
3
3
g t
80
27
0
| 1/25
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD VÀ ĐT BẮC NINH
ĐỀ KHẢO SÁT CHẤT LƯỢNG ĐẦU NĂM NĂM HỌC 2018-2019
TRƯỜNG THPT LÊ VĂN THỊNH Môn: TOÁN 12
(Đề thi gồm 06 trang )
Ngày thi: 16 tháng 9 năm 2018
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ, tên thí sinh:................................................ Số báo danh: ...................... Mã đề thi 132
Câu 1: Giá trị nhỏ nhất của hàm số 3
y x  3x  5 trên đoạn 2  ;4   là:
A. min y  3 .
B. min y  7 . 2; 4       2; 4     C. min y  5. D. min y  0. 2; 4      2; 4  
Câu 2: Cho hàm số y f x  có đạo hàm trên đoạn a  ;b
  . Ta xét các khẳng định sau:
 1Nếu hàm số f x đạt cực đại tại điểm x a;b thì f x là giá trị lớn nhất của f x trên a;b 0  0     .
2 Nếu hàm số f x đạt cực đại tại điểm x a;b thì f x là giá trị nhỏ nhất của f x trên a;b 0  0     .
3Nếu hàm số f x đạt cực đại tại điểm x và đạt cực tiểu tại điểm x x ,x a;b thì ta luôn có 1  0 1   0
f x f x . 0   1
Số khẳng định đúng là? A. 3 . B. 2 . C. 1 . D. 0 . x  3
Câu 3: Tiệm cận ngang của đồ thị hàm số y
là đường thẳng có phương trình? x  1 A. y  5 . B. y  0 . C. x  1 . D. y  1.
Câu 4: Cho cấp số cộng u có số hạng tổng quát là u  3n  2 . Tìm công sai d của cấp số cộng. n n A. d  2 . B. d  2 . C. d  3 . D. d  3 . Câu 5:
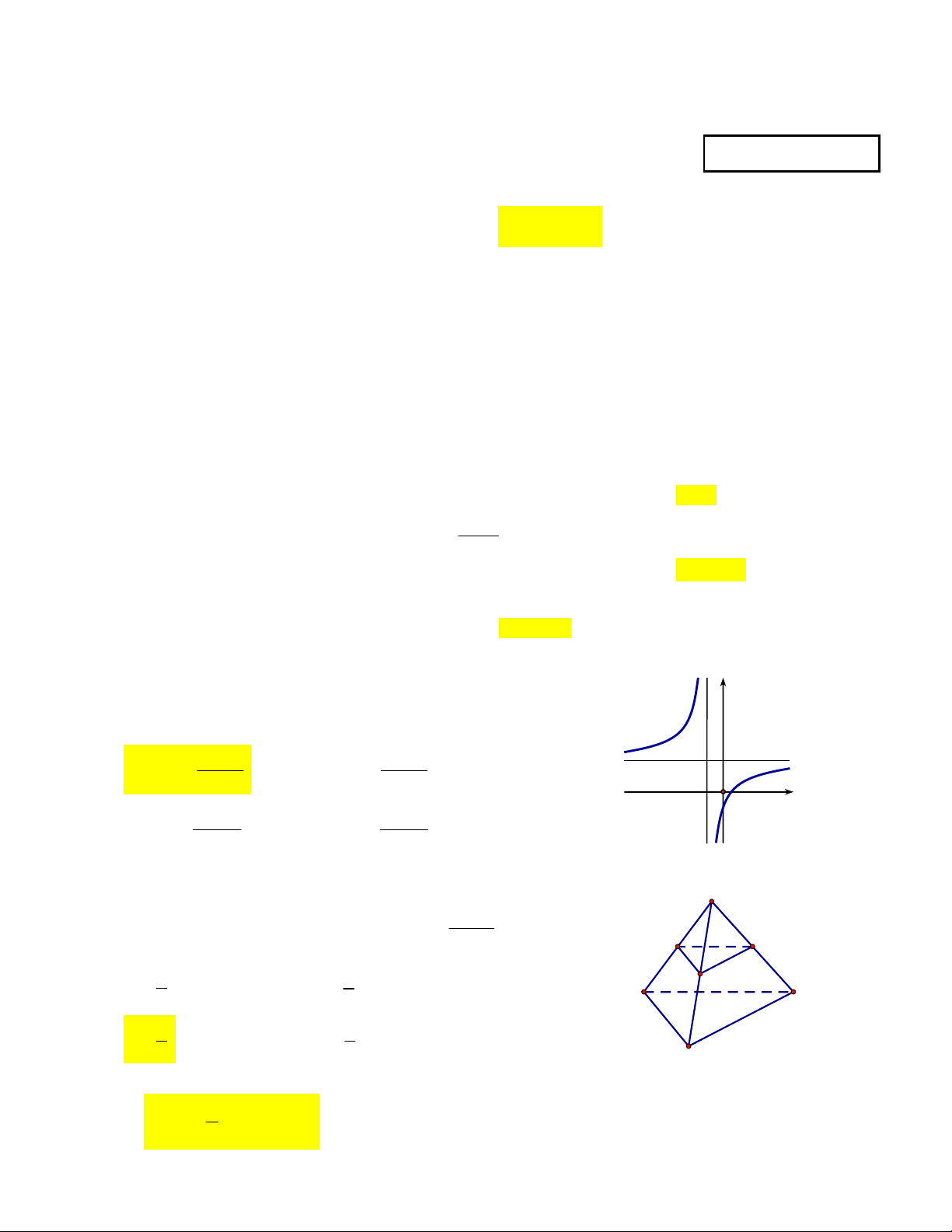
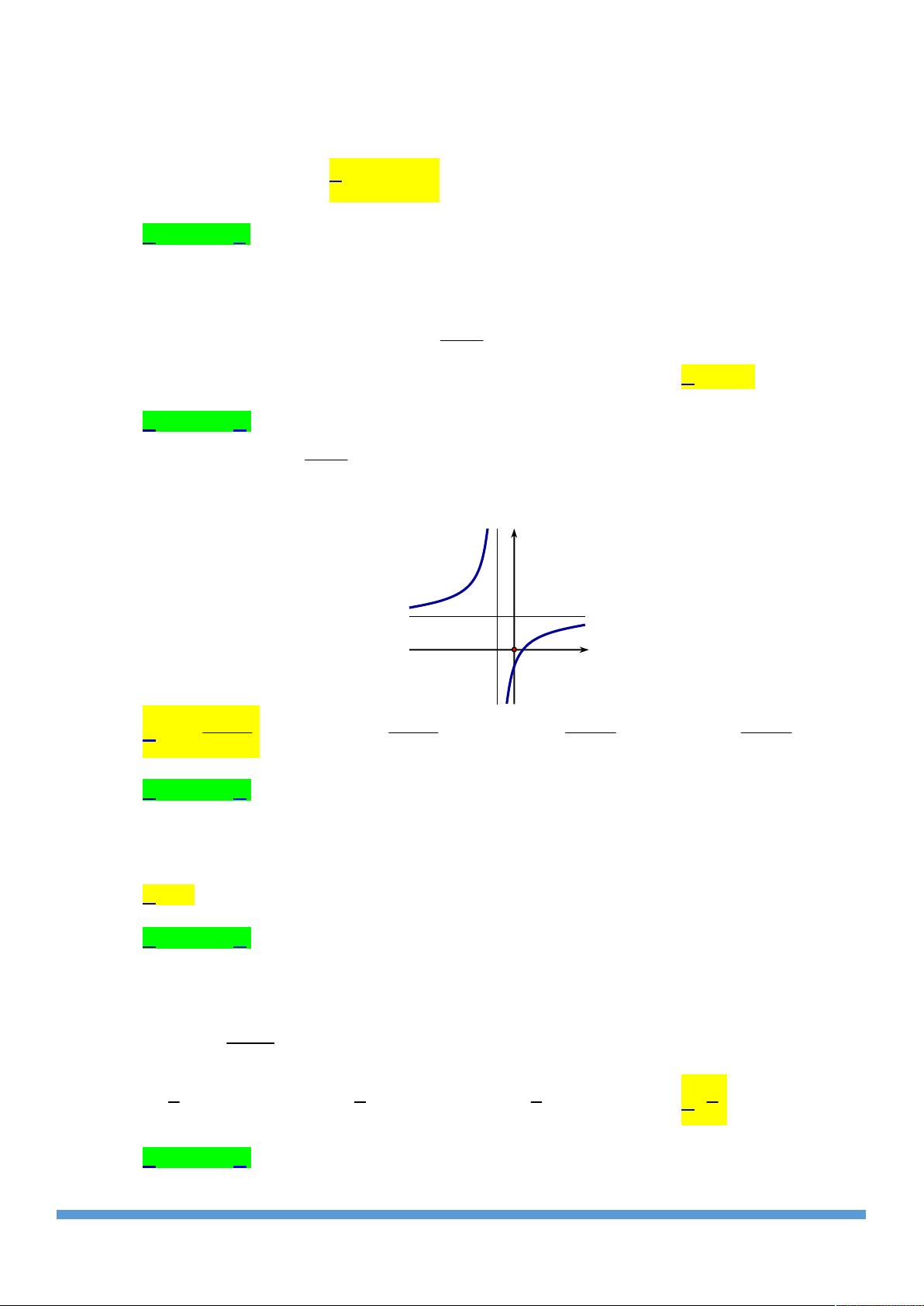
Đường cong trong hình bên là đồ thị của một hàm số trong y
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào? 2x  1 1  2x 2 A. y  . B. y  . x  1 x  1 1  O x 2x  1 2x  1 1  C. y  . D. y  . x  1 x  1 Câu 6:
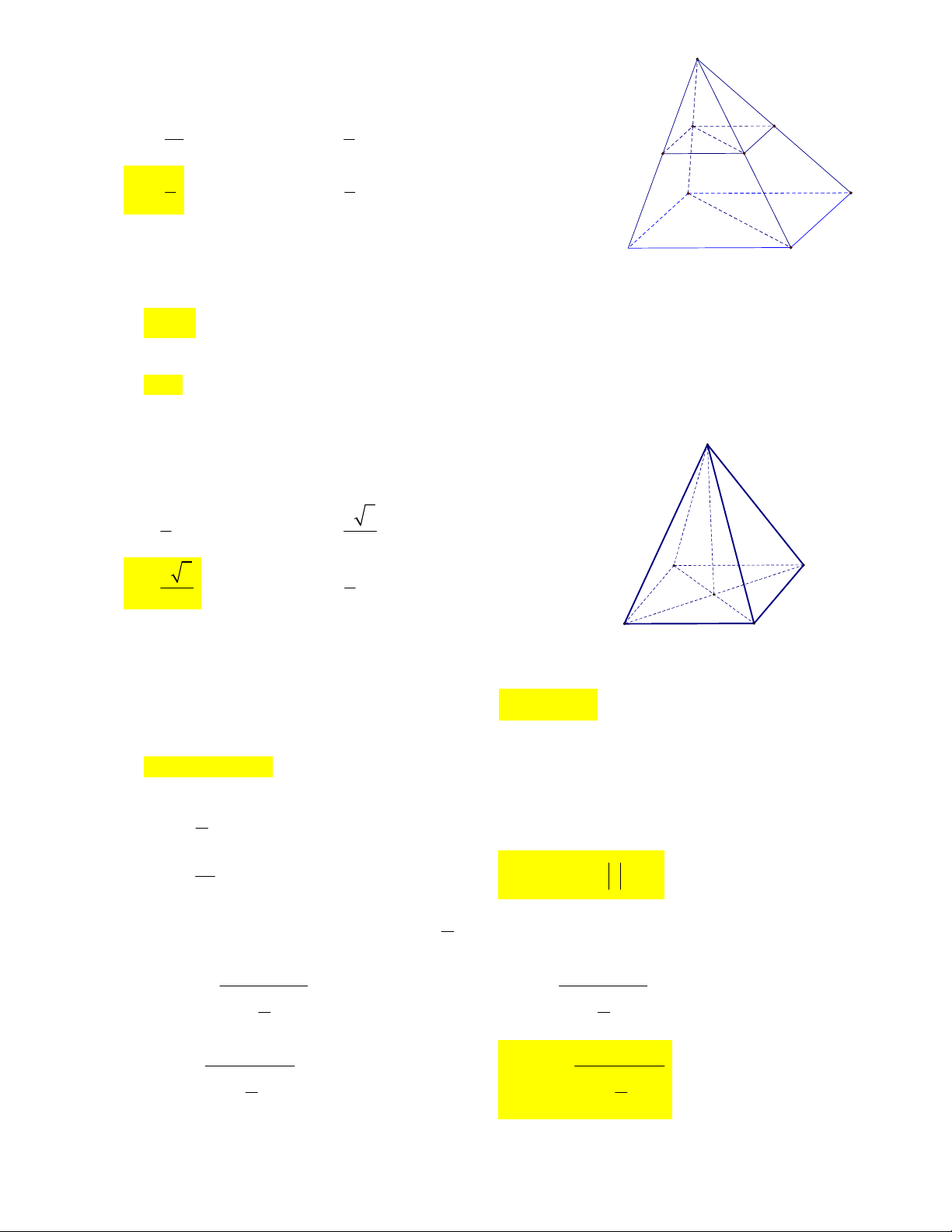
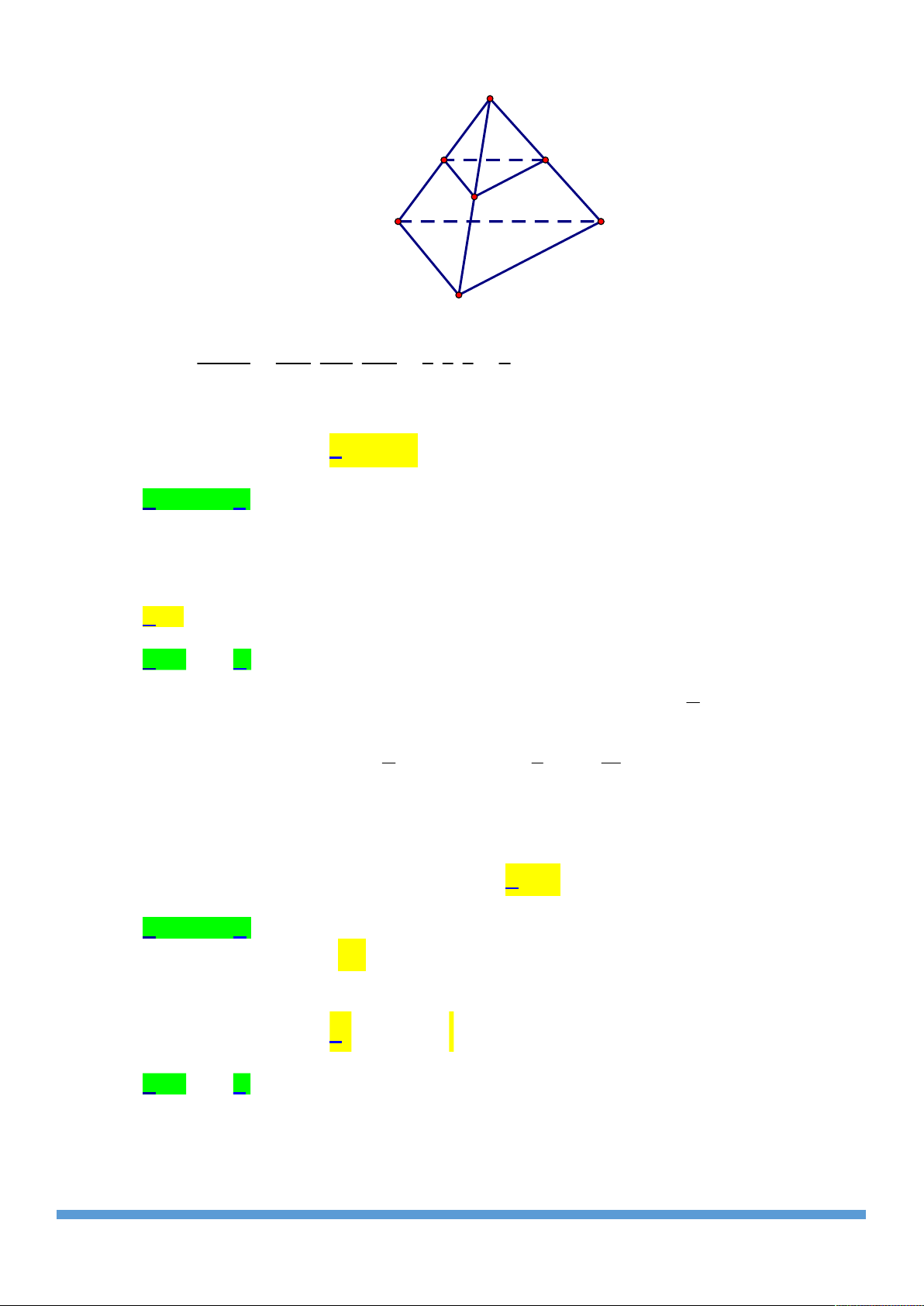
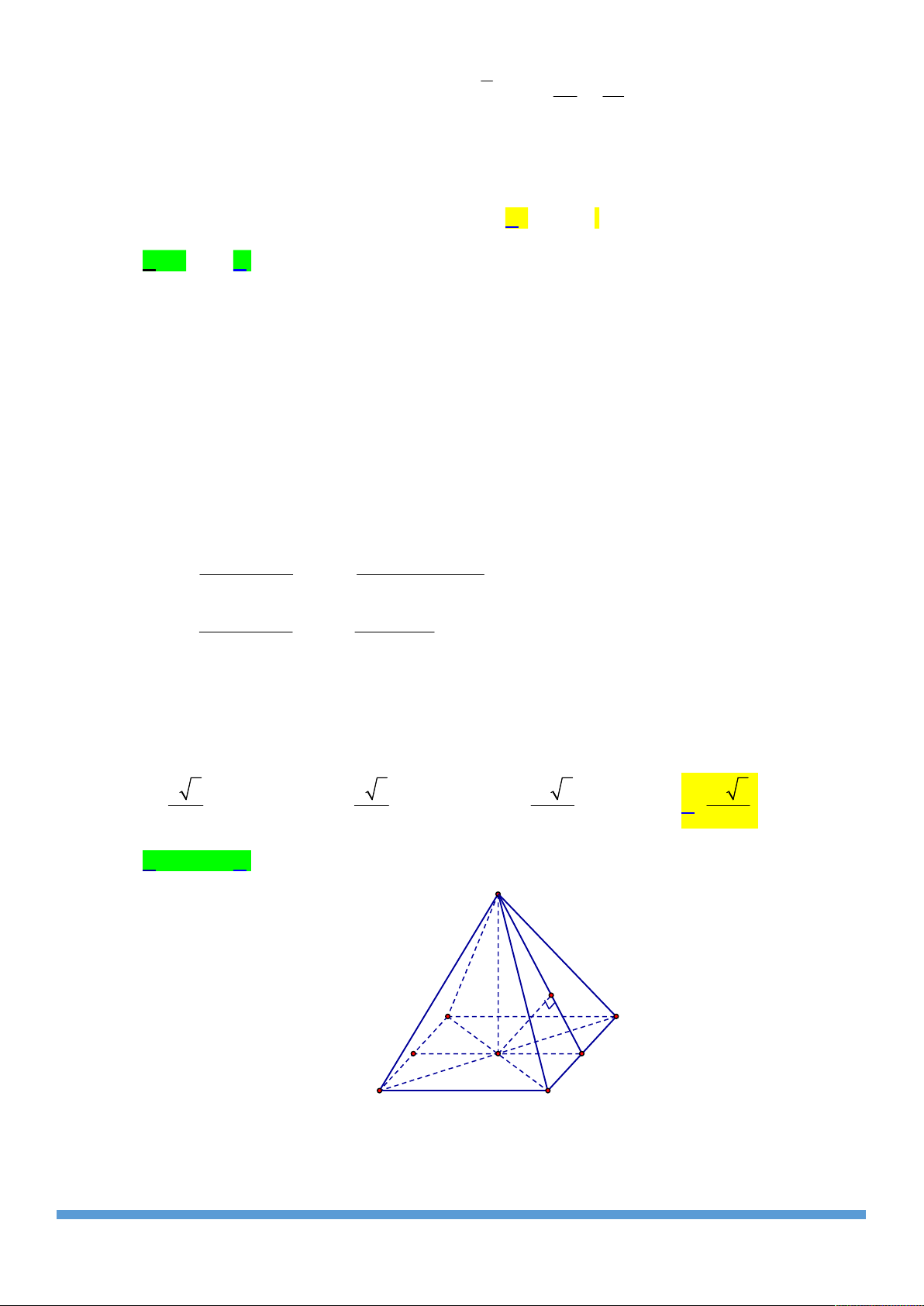
Cho tứ diện MNPQ . Gọi I ; J ; K lần lượt là trung điểm M V
của các cạnh MN ; MP ; MQ . Tỉ số thể tích MIJK bằng V I K MNPQ 1 1 A. . B. . J 4 3 N Q 1 1 C. . D. . 8 6 P
Câu 7: Tập xác định của hàm số y  tan x là:    
A.  \   k ,  k     \ k ,  k    \ 0  . B.  . C. . D.  . 2   
Trang 1/6 - Mã đề thi 132
Câu 8: Cho hai đường thẳng phân biệt a, b P a P
và mặt phẳng   , trong đó
 . Chọn mệnh đề sai.
A. Nếu b // a thì b // P .
B. Nếu b // P  thì b a .
C. Nếu b // a thì b  P  .
D. Nếu b  P  thì b // a .     2
Câu 9: Nghiệm của phương trình cos x      là  4  2 x   k  
x k2A. k  . B. k  . x
    k2  
x    k  2  2 x   k2   x kC. k  . D. k  . x
    k2  
x    k  2  2
Câu 10: Dãy số nào sau đây có giới hạn bằng 0 ? 3 n n n  3n 6    2    A. u  .
B. u    . C. 2
u n  4n . D. u    . n n  1 n 5 n n  3 
Câu 11: Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng
phân biệt từ các điểm đã cho? A. 3 . B. 6 . C. 4 . D. 2 .
Câu 12: Khối đa diện đều có 12 mặt thì có số cạnh là: A. 30 . B. 60 . C. 12 . D. 24 .
Câu 13: Cho tập A  0;2; 4;6;8 ; B  3; 4;5;6;7 . Tập A \ B là A. 0;6;8. B. 0;2; 8 . C. 3;6;7. D. 0;  2 . Câu 14: Cho hàm số 3
y x  3x. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng  ;   
1 và nghịch biến trên khoảng 1;.
B. Hàm số nghịch biến trên khoảng 1;  1 .
C. Hàm số đồng biến trên khoảng ( ;  )  .
D. Hàm số nghịch biến trên khoảng  ;   
1 và đồng biến trên khoảng 1; Câu 15: Hàm số 3 2
y x  3x  3x  4 có bao nhiêu điểm cực trị? A. 2 . B. 1 . C. 0 . D. 3 .
Câu 16: Tìm hệ số của 6
x trong khai triển thành đa thức của   10 2 3x . A. C  .2 . 3  4 4 6 . B. C .2 . 3  . C. 6 4 6 C  .2 .3 . D. C .2 . 3  . 10  4 6 6 10  6 6 4 10 10 Câu 17:
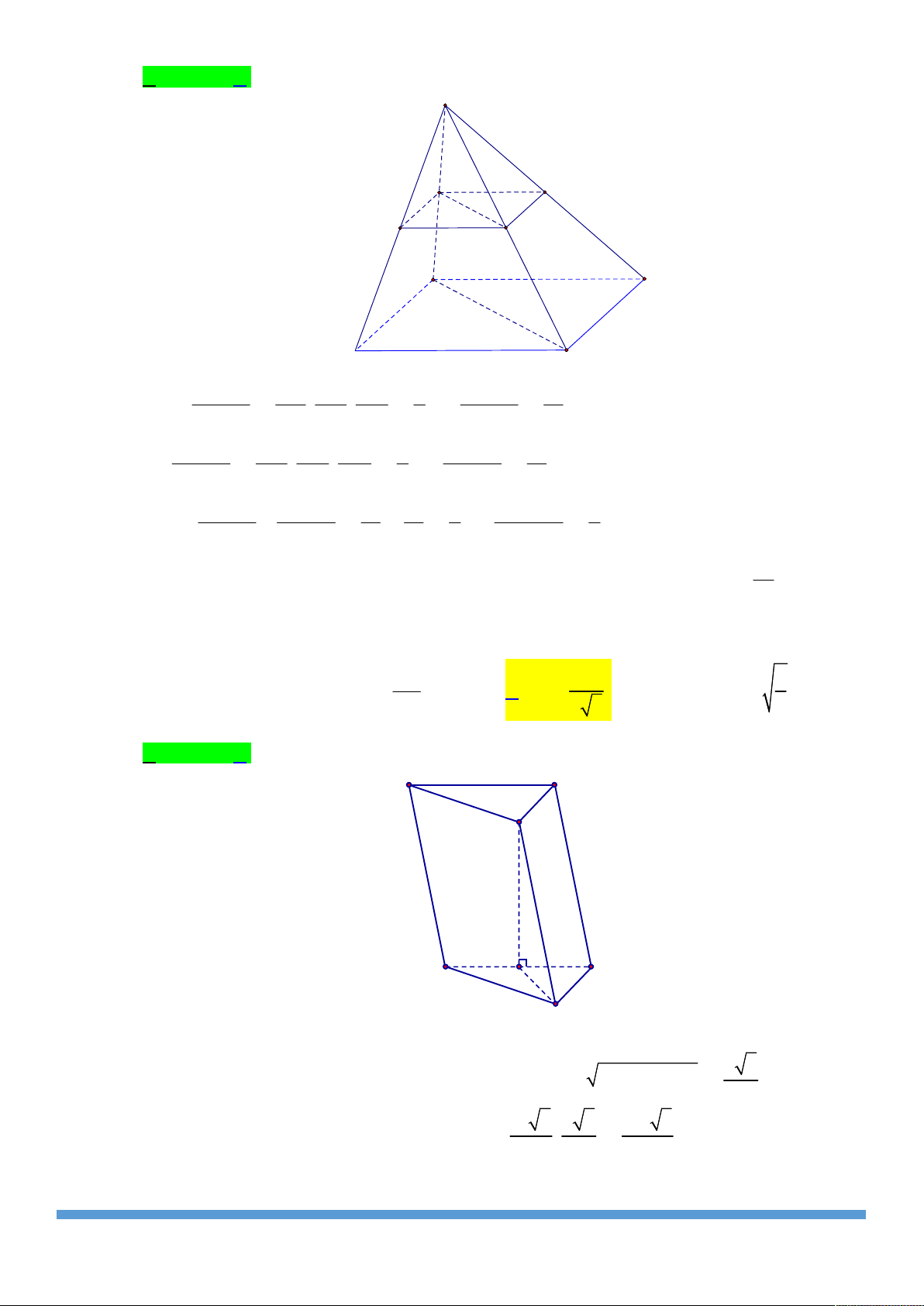
Cho hình lăng trụ ABC.AB C
  có đáy ABC là tam giác đều cạnh BC  3a a , AA 
. Biết rằng hình chiếu vuông góc của A lên ABC  2 A
là trung điểm BC . Tính thể tích V của khối lăng trụ đó. 3 2a 3 3a A. V  . B. V  . 3 4 2 3 C. 3 V a . D. 3 V a . 2 H C B A
Trang 2/6 - Mã đề thi 132 Câu 18:
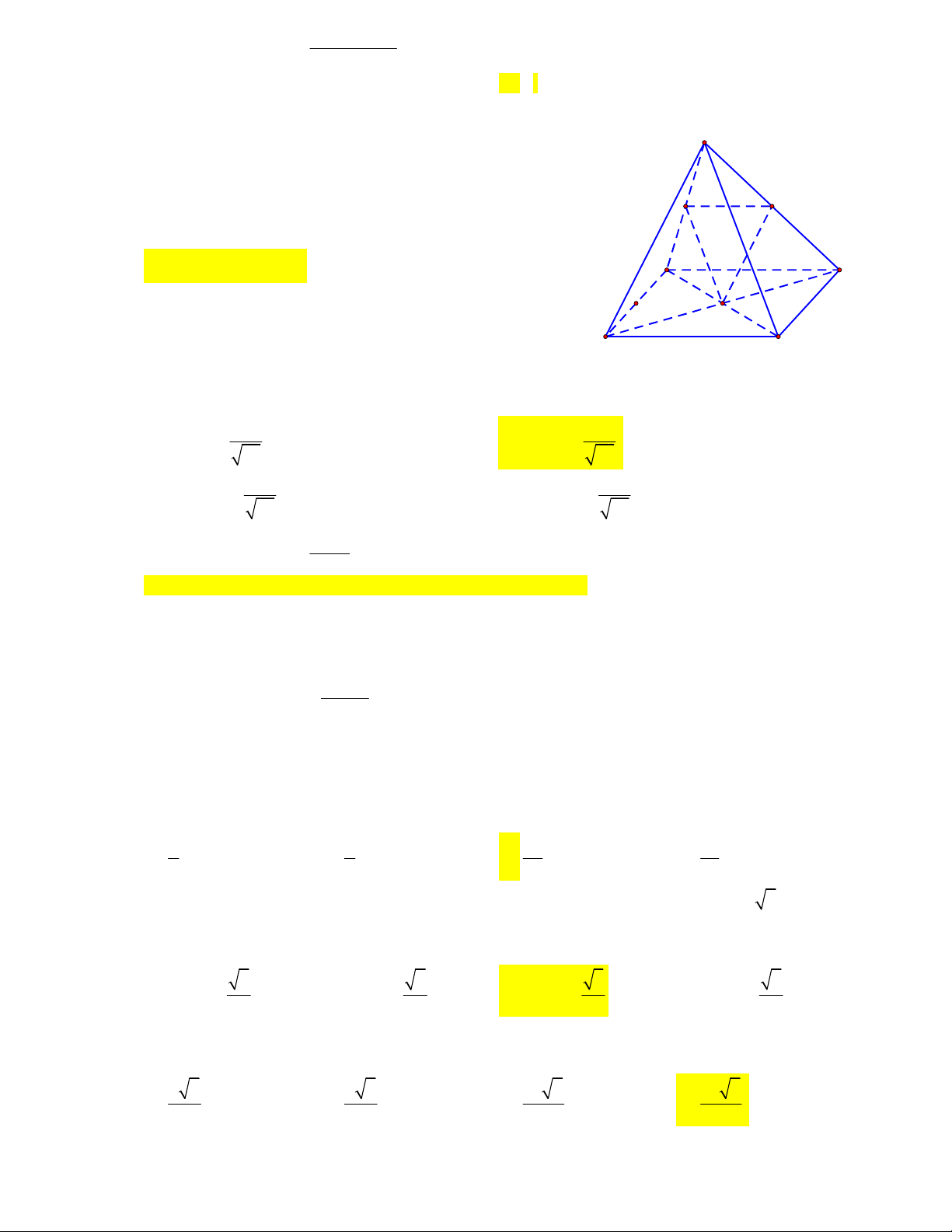
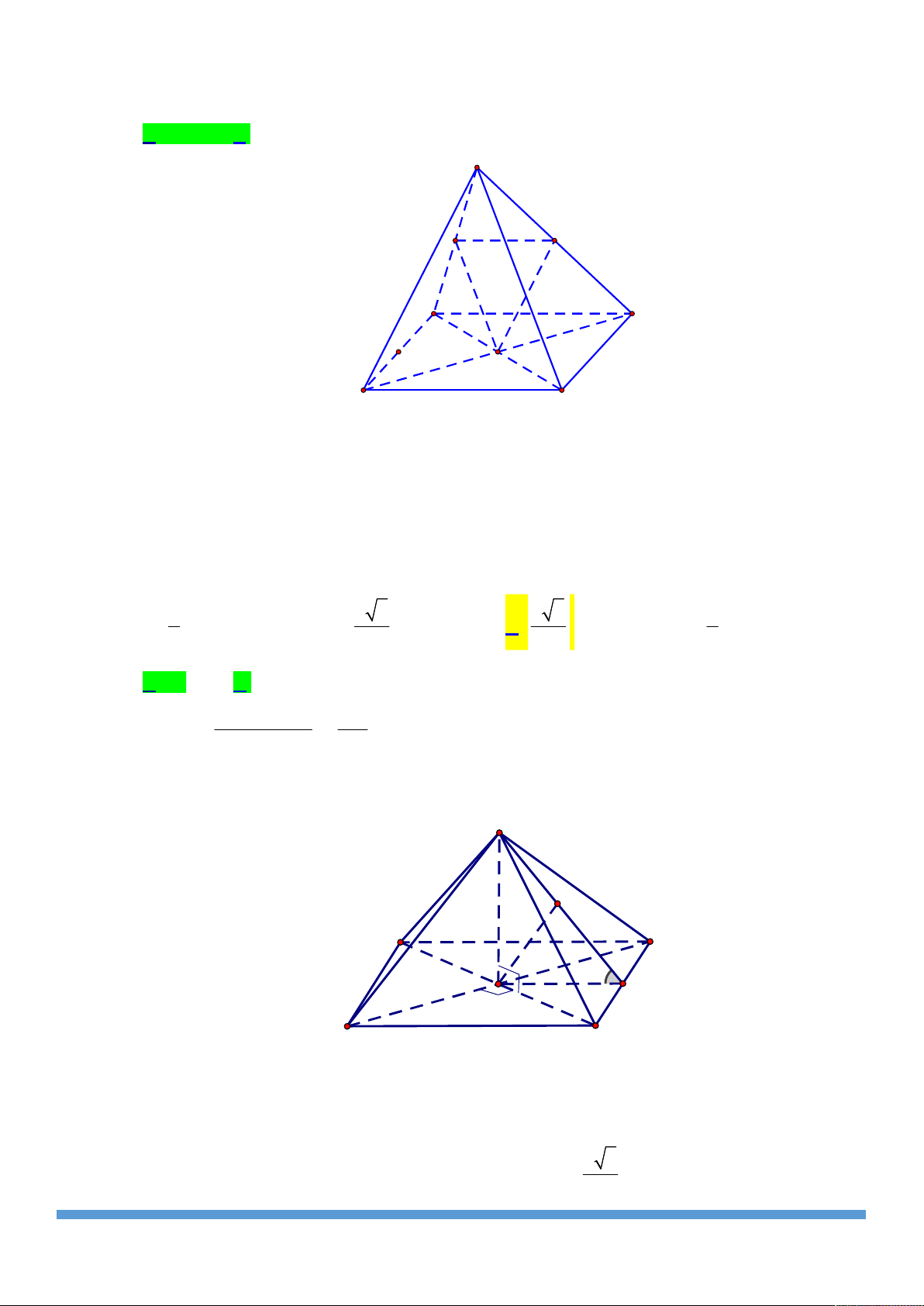
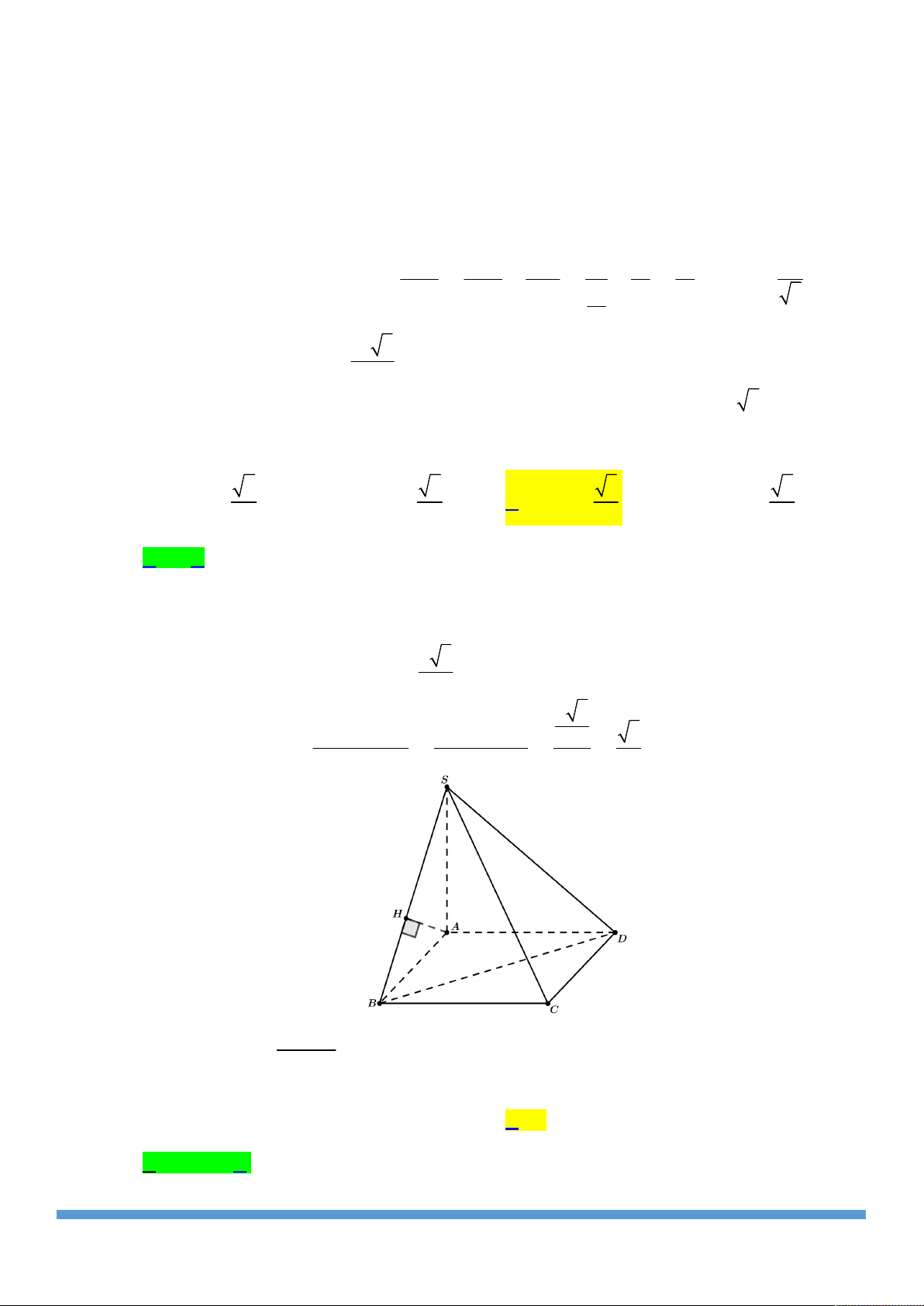
Cho hình chóp S.ABCD . Gọi A , B , C  , D theo thứ tự là S
trung điểm của SA , SB , SC , SD . Tính tỉ số thể tích của hai
khối chóp S.AB CD
  và S.ABCD . 1 1 D' C' A. . B. . 16 4 A' B' 1 1 C. . D. . D 8 2 C A B
Câu 19: Một tổ công nhân có 12 người. Cần chọn 3 người để đi làm cùng một nhiệm vụ, hỏi có bao nhiêu cách chọn? A. 3 C . B. 3 12 . C. 12 ! . D. 3 A . 12 12
Câu 20: Phương trình cos 2x  4 sin x  5  0 có bao nhiêu nghiệm trên khoảng 0;10 ? A. 5 . B. 2 . C. 4 . D. 3 . Câu 21:
Cho hình chóp đều S.ABCD , cạnh đáy bằng a , góc giữa mặt bên S
và mặt đáy là 60 . Tính khoảng cách từ điểm B đến mặt phẳng SCD. a a 3 A. . B. . 4 4 A a 3 a D C. . D. . 2 2 B C
Câu 22: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x y  1  0 . Phép tịnh tiến theo
v nào sau đây biến đường thẳng d thành chính nó?    
A. v  1;2.
B. v  2;4 .
C. v  2; 4 .
D. v  2;  1 .
Câu 23: Cho cấp số nhân u có u  3
 , công bội q  2 . Hỏi 192 là số hạng thứ mấy của u n  ? n  1
A. Số hạng thứ 7 .
B. Số hạng thứ 6 .
C. Số hạng thứ 8 .
D. Số hạng thứ 5 .
Câu 24: Phát biểu nào sau đây là sai? 1 A. lim  0 .
B. lim u c (u c là hằng số ). n n n 1 C. lim  0 k   1 . D. lim n
q  0 q   1 . k n   
Câu 25: Tính đạo hàm của hàm số y  tan   x  :  4  1 1 A. y    y   . B. .    2 sin   x 2    sin   x 4  4  1 1 C. y   y    . D. .    2 cos   x 2    cos   x 4  4 
Trang 3/6 - Mã đề thi 132 2 x x  2
Câu 26: Cho hàm số y
C , đồ thị C  có bao nhiêu đường tiệm cận? 2 x  3x  2 A. 0 . B. 1 . C. 2 . D. 3 . Câu 27:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành S
tâm O . Gọi M , N , P theo thứ tự là trung điểm của SA , SD
và AB . Khẳng định nào sau đây đúng?
A. PON   MNP   NP . M N
B. NMP // SBD .
C. MON  // SBC . A D
D. NOM  cắt OPM . P O B C
Câu 28: Trên mặt phẳng toạ độ Oxy , cho tam giác ABC biết A1; 3, B 2;2, C 3;  1 . Tính cosin
góc A của tam giác. 2 1 A. cos A  . B. cos A  . 17 17 2 1 C. cos A   . D. cos A   . 17 17 x  1
Câu 29: Cho hàm số y
. Khẳng định nào sau đây đúng? 2  x
A. Hàm số đã cho đồng biến trên từng khoảng xác định của nó.
B. Hàm số đã cho đồng biến trên khoảng  ;  2  2;.
C. Hàm số đã cho đồng biến trên  .
D. Hàm số đã cho nghịch biến trên từng khoảng xác định của nó. x m
Câu 30: Cho hàm số y
( m là tham số thực) thỏa mãn min y  3 . Mệnh đề nào dưới đây x  1 0;1   đúng?
A. 1  m  3 . B. m  6 . C. m  1 .
D. 3  m  6 .
Câu 31: Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3
quyển sách. Tính xác suất để trong ba quyển sách lấy ra có ít nhất một quyển là toán. 2 3 37 10 A. . B. . C. . D. . 7 4 42 21
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a , BC a 3 , SA a và
SA vuông góc với đáy ABCD . Tính sin , với là góc tạo bởi giữa đường thẳng BD và mặt phẳng SBC. 3 7 2 3 A. sin  . B. sin  . C. sin D. sin  . 5 8 4 2
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a , SO vuông góc với mặt
phẳng ABCD và SO a. Khoảng cách giữa SC và AB bằng a 3 a 5 2a 3 2a 5 A. . B. . C. . D. . 15 5 15 5
Trang 4/6 - Mã đề thi 132
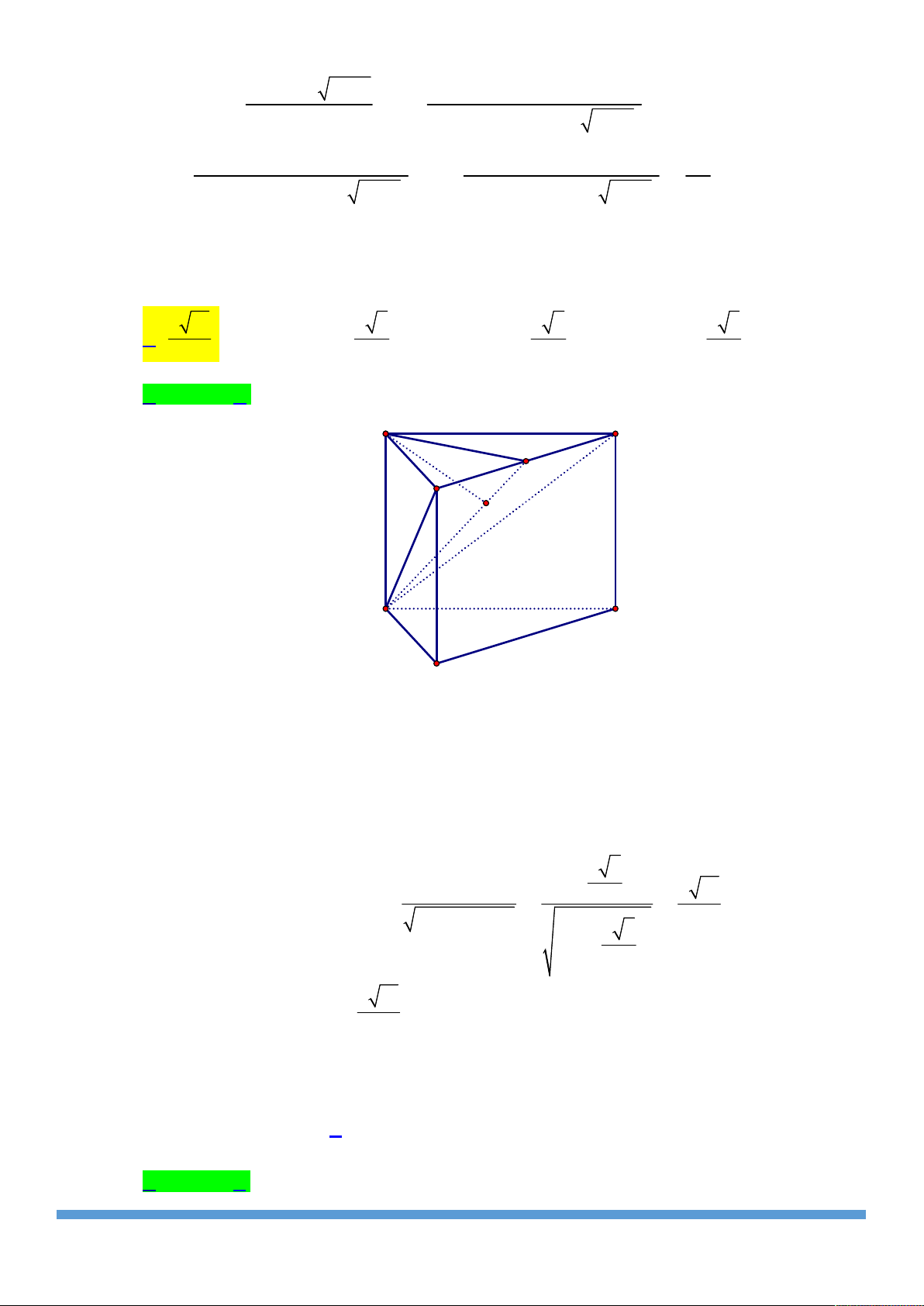
Câu 34: Cho lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh đều bằng a . Khoảng cách giữa hai
đường thẳng BC và AB bằng a 3 a 21 a 7 a 2 A. . B. . C. . D. . 2 7 4 2 Câu 35:
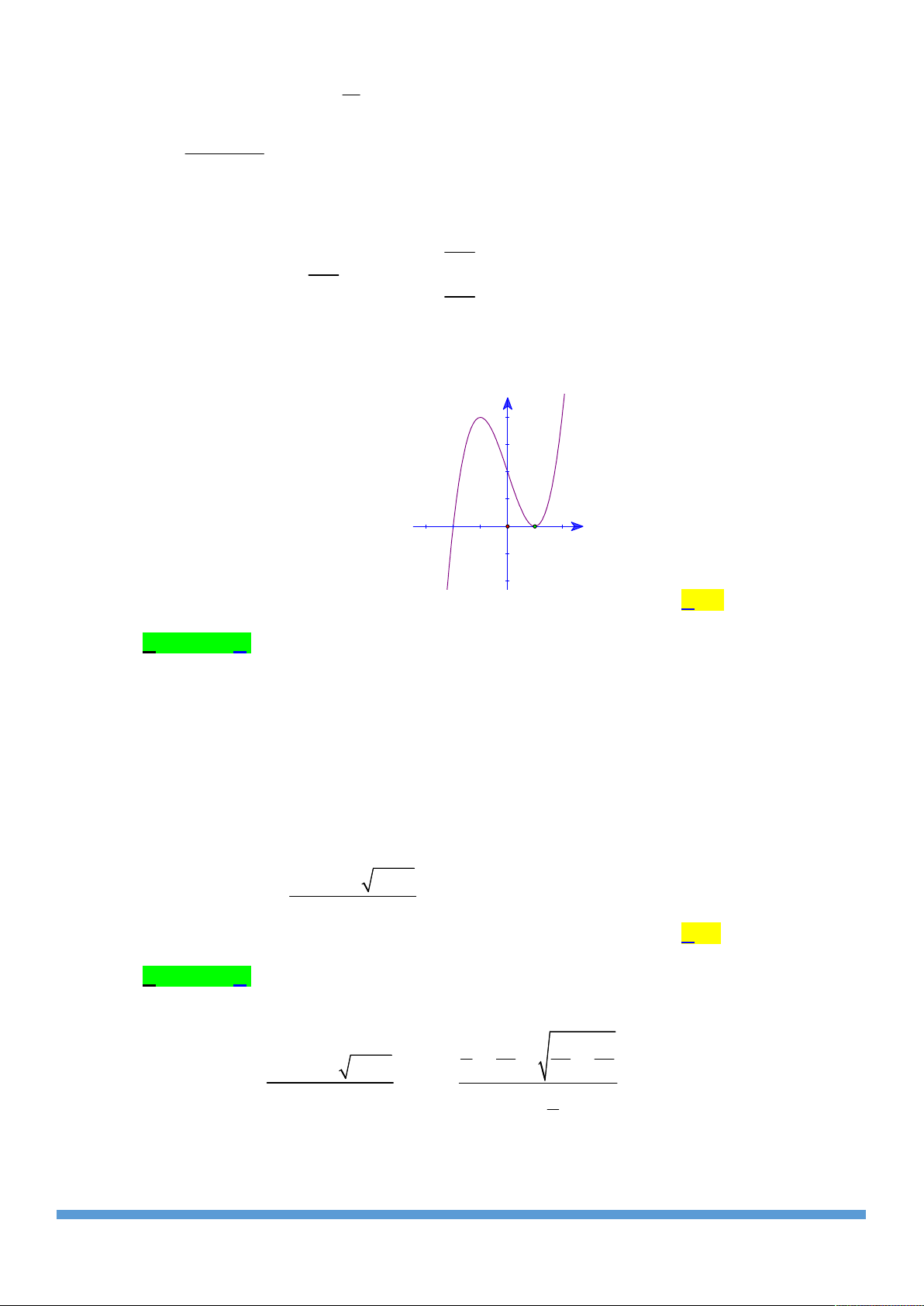
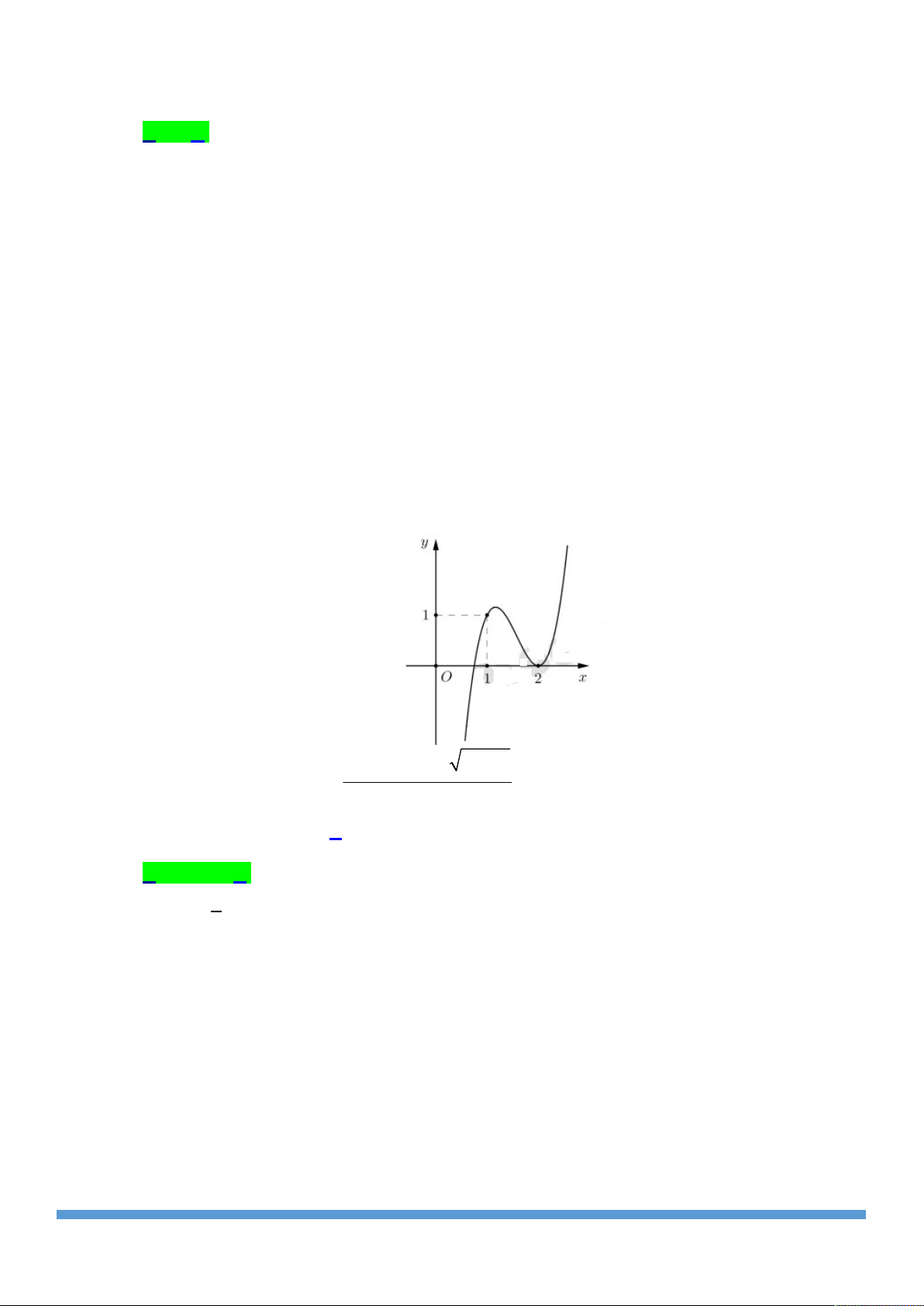
Cho hàm số y f x  xác định trên  và hàm số y f x y
có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số y f  2 x   3 . 2 A. 3 . B. 2 . 1 x -2 C. 5 . D. 4 . O mx  2
Câu 36: Cho hàm số y
, m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của 2x m
tham số m để hàm số nghịch biến trên khoảng 0; 
1 . Tìm số phần tử của S . A. 2 . B. 5 . C. 1 . D. 3 .  2 ax
bx  1,x  0 
Câu 37: Cho hàm số f x  
. Khi hàm số f x  có đạo hàm tại x  0. Hãy tính ax
b  1,x  0 0 
T a  2b . A. T  4 . B. T  0 . C. T  6 . D. T  4 .
5x  1  x  1
Câu 38: Đồ thị hàm số y
có tất cả bao nhiêu đường tiệm cận? 2 x  2x A. 3 . B. 0 . C. 2 . D. 1 .
Câu 39: Trong mặt phẳng với hệ tọa độ Oxy cho hình chữ nhật ABCD biết AD  2AB , đường thẳng
AC có phương trình x  2y  2  0 , D 1; 
1 và Aa;b a,b  , a  
0 . Tính a b .
A. a b  4  .
B. a b  3  .
C. a b  4 .
D. a b  1 .
Câu 40: Tổng tất cả các giá trị nguyên của m để phương trình 4 sin x  m  4cos x  2m  5  0 có nghiệm là: A. 5 . B. 6 . C. 3 . D. 10 . 2 n
Câu 41: Biết n là số nguyên dương thỏa mãn n
x a a x  2  a x  2  ...  a x  2 và 0 1   2   n   n 3 a a a 2    
.192 . Mệnh đề nào sau đây đúng? 1 2 3
A. n  9;16 .
B. n  8;1  2 .
C. n  7;9 .
D. n  5;  8
sin x  2 cos x  1
Câu 42: Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y  là
sin x  cos x  2 1
A. m  2 ; M  1.
B. m  1 ; M  2 .
C. m   ; M  1.
D. m  1; M  2 . 2
Câu 43: Xét tứ diện ABCD có các cạnh AB BC CD DA  1 và AC,BD thay đổi. Giá trị lớn
nhất của thể tích khối tứ diện ABCD bằng 4 3 4 3 2 3 2 3 A. . B. . C. . D. . 27 9 9 27
Trang 5/6 - Mã đề thi 132 Câu 44: Cho hàm số bậc ba   3 2
f x ax bx cx d có đồ thị như
 2x  3x  2 2x 1
hình vẽ bên. Hỏi đồ thị hàm số g x   có 2
x f xf x   
bao nhiêu đường tiệm cận đứng? A. 5 . B. 4 . C. 6 . D. 3 . 4
x ax a
Câu 45: Cho hàm số y
. Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm x  1  
số đã cho trên đoạn 1;2   
 . Có bao nhiêu giá trị nguyên của a để M  2m. A. 15 . B. 14 . C. 13 . D. 16 .
Câu 46: Cho hai đường thẳng cố định a và b chéo nhau. Gọi AB là đoạn vuông góc chung của a và b
( A huộc a, B thuộc b ). Trên a lấy điểm M (khác A ), trên b lấy điểm N (khác B ) sao cho
AM x,BN y,x y  8. Biết AB  6, góc giữa hai đường thẳng a và b bằng 0 60 . Khi thể tích
khối tứ diện ABNM đạt giá trị lớn nhất hãy tính độ dài đoạn MN (trong trường hợp MN  8 ) A. 13 . B. 12 . C. 2 39 . D. 2 21 .
Câu 47: Cho tập hợp A  1;2; 3;4...; 
100 . GọiS là tập hợp gồm tất cả các tập con của A , mỗi tập con
này gồm 3 phần tử của A và có tổng bằng 91 . Chọn ngẫu nhiên một phần tử của S . Xác suất chọn được
phần tử có 3 số lập thành cấp số nhân bằng? 1 3 4 2 A. . B. . C. . D. . 645 645 645 645 0
  x y  1 
Câu 48: Biết m là giá trị để hệ bất phương trình 
có nghiệm thực duy nhất. x
  y  2xy m  1 
Mệnh đề nào sau đây đúng?  1 1    3    1    A. m    ;   m    ; 0 m   ;1 m  2  ;1  . B. . C. . D.  .  2 3  4  3  Câu 49: Cho hàm số 3
y x  3x  2C . Biết rằng đường thẳng d :y ax b cắt đồ thị C  tại ba
điểm phân biệt M, N, P . Tiếp tuyến tại ba điểm M, N, P của đồ thị C  cắt C  tại các điểm M ,N ,P
(tương ứng khác M,N,P ). Khi đó đường thẳng đi qua ba điểm M ,
N ,P  có phương trình là
A. y ax b .
B. y  4a  9x  18  8b .
C. y  8a  18x  18  8b .
D. y  4a  9x  14  8b .
Câu 50: Cho phương trình: 3 x x    3 x m 3 3 2 sin 2 sin 3 2 cos
2 cos x m  2  2 cos x  cos x m .  2
Có bao nhiêu giá trị nguyên của tham số m để phương trình trên có đúng 1 nghiệm x  0;  ? 3     A. 4 . B. 2 . C. 3 . D. 1 .
----------------------------------------------- ----------- HẾT ----------
Trang 6/6 - Mã đề thi 132 SỞ GD VÀ ĐT BẮC NINH
ĐÁP ÁN ĐỀ KHẢO SÁT CHẤT LƯỢNG ĐẦU NĂM
TRƯỜNG THPT LÊ VĂN THỊNH NĂM HỌC 2018-2019 Môn: TOÁN 12
Ngày thi: 16 tháng 9 năm 2018 Đề gốc I. NHẬN BIẾT
Câu 1: Tập xác định của hàm số y  tan x là:   A.  \   0 . B.  \  k ,  k     . 2      C.  . D.  \ k ,k    . Lời giải Chọn B. 
Điều kiện xác định: cosx  0  x   k , k   . 2  
Vậy tập xác định là  \  k ,  k     . 2          2
Câu 2: Nghiệm của phương trình cos x       là  4 2 x  k2  x  k  A.   k  . B.   k  . x    k  x    k  2  2 x  k  x  k2  C.   k  . D.   k  . x    k2  x    k2  2  2 Lời giải Chọn D. x  k2     2          Phương trình cos x      cos x       cos    .               k   4 2 4
4 x   k2  2
Câu 3: Cho cấp số cộng u có số hạng tổng quát là u  3n 2 . Tìm công sai d của cấp số cộng. n  n A. d  3 . B. d  2. C. d  2 . D. d  3 . Lời giải Chọn A. Ta có u
 u  3 n  1  2  3n  2  3 n 1  n  
Suy ra d  3 là công sai của cấp số cộng.
Câu 4: Dãy số nào sau đây có giới hạn bằng 0 ? 2 n 6 n 3 n  3n A. u      . B. u      . C. u  . D. 2 u  n  4n . n  3  n 5 n n  1 n Lời giải: Chọn A. 2 n lim u  lim      0 2 2 (Vì   1). n n n  3  3 3
TÀI LIỆU ÔN THI THPT QG 2019 1
Câu 5: Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng
phân biệt từ các điểm đã cho? A. 6 . B. 4 . C. 3 . D. 2 . Lời giải Chọn B.
Vì 4 điểm không đồng phẳng tạo thành một tứ diện mà tứ diện có 4 mặt.
Câu 6: Cho hai đường thẳng phân biệt ,
a b và mặt phẳng P, trong đó a  P. Chọn mệnh đề sai.
A. Nếu b // a thì b // P.
B. Nếu b // a thì b  P.
C. Nếu b  P thì b // a .
D. Nếu b // P thì b  a . Lời giải Chọn A.
Nếu a  P và b // a thì b  P. Câu 7: Cho hàm số 3
y  x  3x. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng  ;
  1 và nghịch biến trên khoảng 1;.
B. Hàm số đồng biến trên khoảng ( ;   )  .
C. Hàm số nghịch biến trên khoảng  ;   
1 và đồng biến trên khoảng 1;
D. Hàm số nghịch biến trên khoảng 1;  1 . Lời giải Chọn D. Ta có 2
y  3x  3  0  x  1 Bảng biến thiên x  1 1  y  0  0  2  y  2
Dựa vào bảng biến thiên ta chọn đáp án D.
Câu 8: Cho hàm số y  f x có đạo hàm trên đoạn a;b
  . Ta xét các khẳng định sau:
 1Nếu hàm số f x đạt cực đại tại điểm x  a;b thì f x là giá trị lớn nhất của f x trên 0  0   đoạn a;b   .
2 Nếu hàm số f x đạt cực đại tại điểm x  a;b thì f x là giá trị nhỏ nhất của f x 0  0   trên đoạn a;b   .
3Nếu hàm số f x đạt cực đại tại điểm x và đạt cực tiểu tại điểm x x ,x  a;b thì ta 1  0 1   0 luôn có f x  f x . 0   1
Số khẳng định đúng là? A. 1. B. 2 . C. 0 . D. 3 . Câu 9: Hàm số 3 2
y  x  3x  3x  4 có bao nhiêu điểm cực trị? A. 1. B. 2 . C. 0 . D. 3 . Lời giải Chọn C.
TÀI LIỆU ÔN THI THPT QG 2019 2
Ta có y  x  x   x  2 2 3 6 3 3 1  0 , x
   . Hàm số đã cho có đạo hàm không đổi dấu
trên  nên nó không có cực trị.
Câu 10: Giá trị nhỏ nhất của hàm số 3
y  x  3x  5 trên đoạn 2;4   là: A. miny  3 . B. miny  7 . C. miny  5. D. miny  0. 2; 4          2; 4   2; 4   2; 4   Lời giải Chọn B. x  1  2;4 f  2 7 Ta có: 2
y  3x  3  y  0      mà   miny  7 . x  1  2;4      f  4  57 2; 4   x  3
Câu 11: Tiệm cận ngang của đồ thị hàm số y 
là đường thẳng có phương trình? x 1 A. y  5. B. y  0 . C. x  1 . D. y  1. Lời giải Chọn D. x  3 Ta có lim y  lim
 1  đường thẳng y  0 là tiệm cận ngang của đồ thị hàm số. x x x  1
Câu 12: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? y 2 1 O x 1 2x 1 1 2x 2x  1 2x  1 A. y  . B. y  . C. y  . D. y  . x  1 x  1 x 1 x  1 Lời giải Chọn A.
Đồ thị hàm số có đường tiệm cận đứng là x  1  loại đáp án C.
Đồ thị hàm số đi qua điểm A0; 1  loại đáp án B và D.
Câu 13: Khối đa diện đều có 12 mặt thì có số cạnh là: A. 30 . B. 60 . C. 12 . D. 24 . Lời giải Chọn A.
Khối đa diện đều có 12 mặt là khối đa diện đều loại 5; 
3 thì có số cạnh là 30 .
Câu 14: Cho tứ diện MNPQ . Gọi I ; J ; K lần lượt là trung điểm của các cạnh MN ; MP ; MQ . Tỉ V số thể tích MIJK bằng VMNPQ 1 1 1 1 A. . B. . C. . D. . 3 4 6 8 Lời giải Chọn D.
TÀI LIỆU ÔN THI THPT QG 2019 3 M I K J N Q P VM IJK MI MJ MK 1 1 1 1 Ta có: .  . .  . .  . V MN MP MQ 2 2 2 8 M .NPQ
Câu 15: Cho tập A  0;2;4;6; 
8 ; B  3;4;5;6;7. Tập A \ B là A. 0;6;8. B. 0;2;8. C. 3;6;7. D. 0;  2 . Lời giải Chọn B. Ta có A \ B  0;2;  8 . II. THÔNG HIỂU
Câu 16: Phương trình cos2x  4 sin x  5  0 có bao nhiêu nghiệm trên khoảng 0;10 ? A. 5 . B. 4 . C. 2 . D. 3 . Lời giải Chọn A. sinx  1  PT đã cho 2  2
 sin x  4 sinx  6  0     x    k2 ,  k  . sinx  3  VN 2  1 21
Theo đề: x  0;10  0    k2  10   k  . 2 4 4
Vì k   nên k  1;2;3;4; 
5 . Vậy PT đã cho có 5 nghiệm trên khoảng 0;10.
Câu 17: Một tổ công nhân có 12 người. Cần chọn 3 người để đi làm cùng một nhiệm vụ, hỏi có bao nhiêu cách chọn? A. 3 A . B. 12! . C. 3 C . D. 3 12 . 12 12 Lời giải Chọn C.
Số cách chọn 3 người, là 3 C (cách chọn) 12
Câu 18: Tìm hệ số của 6
x trong khai triển thành đa thức của   10 2 3x . A. C .2 . 4 6 6 3 . B. C .2 . 3 . C. C  .2 . 3 . D. 6 4 6 C  .2 .3 . 10  4 4 6 10  6 6 4 10 10 Lời giải Chọn B. 10 10 10 k k Ta có: 2  3x k 10  C .2 k.3x k 10  C .2 k. 3  . k x 10 10   k0 k0
Theo giả thiết suy ra: k  6.
TÀI LIỆU ÔN THI THPT QG 2019 4 6 6 Vậy hệ số của 6
x trong khai triển là 6 10 6 C .2  .3 6 4  C .2 . 3 . 10 10  
Câu 19: Cho cấp số nhân u có u  3
 , công bội q  2 . Hỏi 192 là số hạng thứ mấy của n  1 u ? n A. Số hạng thứ 6 . B. Số hạng thứ 7 . C. Số hạng thứ 5 . D. Số hạng thứ 8 . Lời giải Chọn B.
Giả sử 192 là số hạng thứ n của u với * n   .Ta có n  1 192 . n u q        1 192 3 . 2 n        1 64 2 n     6   1 2 2 n      6  n 1 1
 7  n . Do đó 192 là số hạng thứ 7 của u . n 
Câu 20: Phát biểu nào sau đây là sai?
A. limu  c (u  c là hằng số ). B. lim n q  0 q  1. n n 1 1 C. lim  0 . D. lim  0 k  1. n k n Lời giải Chọn B.
Theo định nghĩa giới hạn hữu hạn của dãy số (SGK ĐS11-Chương 4) thì lim n q  0 q  1.  
Câu 21: Tính đạo hàm của hàm số y  tan  x  : 4  1 1 A. y     . B. y    . 2 cos   x 2     cos  x 4  4  1 1 C. y    . D. y     . 2 sin   x 2     sin   x 4  4  Giải: Chọn A      1 1 y    x .    4      2   2 cos   x cos      x 4    4 
Câu 22: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x  y  1  0 . Phép tịnh tiến
theo v nào sau đây biến đường thẳng d thành chính nó?     A. v  2;4. B. v  2;  1 . C. v  1;2. D. v  2;4. Lời giải Chọn A.  
Phép tịnh tiến theo v biến đường thẳng d thành chính nó khi vectơ v cùng phương với vectơ 
chỉ phương của d . Mà d có VTCP u  1;2.
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M , N , P theo thứ tự
là trung điểm của SA, SD và AB . Khẳng định nào sau đây đúng?
A. NOM  cắt OPM. B. MON  // SBC .
TÀI LIỆU ÔN THI THPT QG 2019 5
C. PON  MNP  NP . D. NMP // SBD. Hướng dẫn giải Chọn B. S M N A D P O B C
Xét hai mặt phẳng MON và SBC .
Ta có: OM // SC và ON // SB .
Mà BS  SC  C và OM ON  O .
Do đó MON  // SBC .
Câu 24: Cho hình chóp đều S.ABCD , cạnh đáy bằng a , góc giữa mặt bên và mặt đáy là 60 . Tính
khoảng cách từ điểm B đến mặt phẳng SCD. a a 3 a 3 a A. . B. . C. . D. . 4 4 2 2 Lời giải Chọn C. d B;SCD BD * Ta có: 
  d B;SCD  2.dO;SCD  2OH . Trong đó H là d O SCD 2 ; OD
hình chiếu vuông góc của O lên SCD. S H A D 60 O I B C
* Gọi I là trung điểm của CD ta có: S  I CD    O  I  CD
SCD ABCD  OI SI  ; ;  SIO  60.  a 3
Xét tam giác SOI vuông tại O ta có: SO  OI.tan 60  . 2
TÀI LIỆU ÔN THI THPT QG 2019 6
* Do SOCD là tứ diện vuông tại O nên: 1 1 1 1 2 2 4 16        2 2 2 2 2 2 2 2 OH OC OD OS a a 3a 3a a 3  OH   d B SCD a 3 ;  . 4 2 x  1 Câu 25: Cho hàm số y 
. Khẳng định nào sau đây đúng? 2  x
A. Hàm số đã cho đồng biến trên từng khoảng xác định của nó.
B. Hàm số đã cho đồng biến trên  .
C. Hàm số đã cho đồng biến trên khoảng  ;  22;.
D. Hàm số đã cho nghịch biến trên từng khoảng xác định của nó. Lời giải Chọn A. x  1 x  1 3 Ta có y     0, x  2. 2  x x   2  x   22
Do đó hàm số đã cho đồng biến trên các khoảng  ;  2 và 2;. x  m Câu 26: Cho hàm số y 
(m là tham số thực) thỏa mãn miny  3 . Mệnh đề nào dưới đây x  1 0;1   đúng? A. 1  m  3 . B. m  6 . C. m  1 . D. 3  m  6 . Lời giải Chọn D.
Tập xác định: D   \   1 .
Với m  1  y  1, x  0;1
  thì miny  3 . 0;1   1m
Suy ra m  1. Khi đó y 
không đổi dấu trên từng khoảng xác định. x  21
TH 1: y  0  m  1 thì miny  y 0  m  3 (loại). 0;1    
TH 2: y  0  m  1 thì miny  y 1  m  5 ( thỏa mãn). 0;1     2 x  x  2 Câu 27: Cho hàm số y 
C, đồ thị C có bao nhiêu đường tiệm cận? 2 x  3x  2 A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn C.
Tập xác định D   \ 1;  2 x  2 Ta có y 
nên đồ thị hàm số có tiệm cận ngang của là y  1 và là tiệm cận đứng là x  2 x  2
Câu 28: Cho hình chóp S.ABCD . Gọi A, B , C  , D theo thứ tự là trung điểm của SA, SB , SC ,
SD . Tính tỉ số thể tích của hai khối chóp S.AB C  D   và S.ABCD . 1 1 1 1 A. . B. . C. . D. . 16 4 8 2 Lời giải
TÀI LIỆU ÔN THI THPT QG 2019 7 Chọn C. S D' C' A' B' D C A B V    V S AB D   SA SB SD 1 S AB D   1 Ta có .  . .  .   . V SA SB SD 8 V 16 S.ABD S.ABCD V    V S B D  C   SB SD SC 1 S B D  C   1 Và .  . .  .   . V SB SD SC 8 V 16 S.BDC S.ABCD V V    V S A B D S B D  C   1 1 1 S AB C  D   1 Suy ra . .     .   . V V 16 16 8 V 8 S.ABCD S.ABCD S.ABCD 3a
Câu 29: Cho hình lăng trụ ABC.AB C
  có đáy ABC là tam giác đều cạnh a , AA  . Biết rằng 2
hình chiếu vuông góc của A lên ABC  là trung điểm BC . Tính thể tích V của khối lăng trụ đó. 3 2a 3 3a A. 3 V  a . B. V  . C. V  . D. 3 3 V  a . 3 4 2 2 Lời giải Chọn C. B C  A H B C A
Gọi H là trung điểm BC . a
Theo giả thiết, AH là đường cao hình lăng trụ và 2 2 6 AH  AA  AH  . 2 2 3 a 3 a 6 3a 2
Vậy, thể tích khối lăng trụ là V  S .AH  .  . ΔABC 4 2 8
TÀI LIỆU ÔN THI THPT QG 2019 8
Câu 30: Trên mặt phẳng toạ độ Oxy , cho tam giác ABC biết A1;3, B2;2, C 3;  1 . Tính cosin góc A của tam giác. 2 1 2 1 A. cosA  . B. cosA  . C. cosA   . D. cosA   . 17 17 17 17 Lời giải: Chọn B.  
AB  3; 5, AC  2; 2.     A 
AB AC AB.AC 3.25.2 1 cos cos ;    AB.AC 34.2 2 17 III. VẬN DỤNG
Câu 31: Tổng tất cả các giá trị nguyên của m để phương trình 4 sin x  m  4cosx  2m  5  0 có nghiệm là: A. 5 . B. 6 . C. 10 . D. 3 . Lời giải Chọn C.
4 sinx  m  4cosx 2m  5  0  4sinx m  4cosx  2m  5 . 2 2
Phương trình có nghiệm khi 2
4  m  4 2m 5  0 2  3m  12m  7  0 6  57 6  57   m  3 3
Vì m   nên m  0,1,2,3,  4 .
Vây tổng tất cả các giá trị nguyên của m để phương trình có nghiệm là.10 . sinx  2 cosx  1
Câu 32: Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y  là sinx  cosx  2 1
A. m   ; M  1. B. m  1; M  2 .
C. m  2 ; M  1. D. m  1 ; M  2 . 2 Lời giải Chọn C. sinx  2cosx  1 Ta có y 
 y  1sinx y 2cosx  12y  * sinx  cosx  2 Phương trình  * có nghiệm
 y  2 y  2    y2 2 1 2 1 2
 y  y  2  0  2  y  1. Vậy m  2 ; M  1.
Câu 33: Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3
quyển sách. Tính xác suất để trong ba quyển sách lấy ra có ít nhất một quyển là toán. 2 3 37 10 A. . B. . C. . D. . 7 4 42 21 Lời giải Chọn C.
Số kết quả có thể khi chọn bất kì 3 quyển sách trong 9 quyển sách là 3 C  84. 9
Gọi A là biến cố ‘ Lấy được ít nhất 1 sách toán trong 3 quyển sách.’
A là biến cố ‘ Không lấy được sách toán trong 3 quyển sách.’
TÀI LIỆU ÔN THI THPT QG 2019 9 C
Ta có xác sút để xảy ra A là P   A   P   35 37 1 A  1  . 84 42 a  x bx  x 
Câu 34: Cho hàm số f x 2 1, 0  
. Khi hàm số f x có đạo hàm tại x  0. Hãy tính a  x b 1,x  0  0  T  a  2b . A. T  4 . B. T  0 . C. T  6 . D. T  4 . Lời giải Chọn C. Ta có f 0  1. lim f x  lim    1 .    2 ax bx 1 x 0    x0
lim f x  lim ax b   b  1.  1   x0 x0
Để hàm số có đạo hàm tại x  0 thì hàm số phải liên tục tại x  0 nên 0 0
f 0  lim f x  lim f x . Suy ra b
 1  1  b  2 .    x0 x0 a  x  x  x  Khi đó f x 2 2 1, 0   . a  x 1,x  0  Xét: f x f 0 2 ax  2x  11 +) lim  lim  lim   2 .  ax 2 x 0  x x 0  x x0 f x f 0 ax  11 +) lim  lim  lim a  a .   x 0  x x 0  x x0
Hàm số có đạo hàm tại x  0thì a  2. 0
Vậy với a  2,b  2 thì hàm số có đạo hàm tại x  0 khi đó T  6 . 0
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a , SO vuông góc với
mặt phẳng ABCD và SO  a. Khoảng cách giữa SC và AB bằng a 3 a 5 2a 3 2a 5 A. . B. . C. . D. . 15 5 15 5 Lời giải Chọn D. S H A D M O N B C
Gọi M,N lần lượt là trung điểm của các cạnhAB,CD ; H là hình chiếu vuông góc của O trên SN.
TÀI LIỆU ÔN THI THPT QG 2019 10
Vì AB//CD nênd AB,SC  d AB,(SCD )  d M,(SCD )  2d  , O (SCD ) (vì O là trung điểm đoạn MN ) C  D  SO Ta có   CD  (SON)  CD  OH C  D  ON  CD OH Khi đó 
 OH  (SCD)  d O;(SCD ) OH. O  H  SN  1 1 1 1 1 5 a
Tam giác SON vuông tại O nên       OH  2 2 2 2 2 2 OH ON OS a a a 5 4 a Vậy d AB  2 5 ,SC  2OH  . 5
Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a , BC  a 3 , SA  a và
SA vuông góc với đáy ABCD . Tính sin  , với  là góc tạo bởi giữa đường thẳng BD và mặt phẳng SBC . 7 3 2 3 A. sin   . B. sin   . C. sin   D. sin   . 8 2 4 5 Lời giải Chọn C
ABCD là hình chữ nhật nên BD  2a , ta có AD / /SBC nên suy ra d  , D  SBC d  , A   SBC    AH 
với AH  SB . Tam giác SAB vuông cân tại A nên H a 2
là trung điểm của SB suy ra AH  2 a d D SBC  d A  SBC  vậy sinB , D SBC        2 , ,  2 2     BD BD 2a 4 mx  2 Câu 37: Cho hàm số y 
, m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của 2x  m
tham số m để hàm số nghịch biến trên khoảng 0; 
1 . Tìm số phần tử của S . A. 1. B. 5 . C. 2 . D. 3 . Lời giải Chọn C.
TÀI LIỆU ÔN THI THPT QG 2019 11  m Tập xác định D  \     2      2 m  4 y  . 2x m2 2  m  2  2 m   4  0     2  m  2  m   Yêu cầu bài toán     m   0       m  0  0  m  2 .   0; 1  2     2  m     m  2   1   2
Câu 38: Cho hàm số y  f x xác định trên  và hàm số y  f x có đồ thị như hình vẽ. Tìm số
điểm cực trị của hàm số y  f  2 x  3. y 2 1 x -2 O A. 4 . B. 2 . C. 5 . D. 3 . Lời giải Chọn D.
Quan sát đồ thị ta có y  f x đổi dấu từ âm sang dương qua x  2 nên hàm số y  f x
có một điểm cực trị là x  2 . x  0 x  0     Ta có y  f  2 x    x f  2 3 2 . x      2  
3  0  x 3  2  x  1.  2 x  3  1 x  2  
Mà x  2 là nghiệp kép, còn các nghiệm còn lại là nghiệm đơn nên hàm số y  f  2 x  3 có ba cực trị. 5x  1 x 1
Câu 39: Đồ thị hàm số y 
có tất cả bao nhiêu đường tiệm cận? 2 x  2x A. 3 . B. 0 . C. 2 . D. 1. Lời giải Chọn D. Tập xác định: D   1;    \ 0 . 5 1 1 1    2 3 4  lim y 5x  1 x 1  lim  lim x x x
x  0  y  0 là đường tiệm x 2 x x  2x x 2 1  x
cận ngang của đồ thị hàm số.
TÀI LIỆU ÔN THI THPT QG 2019 12 5x  2 1  x 1  limy 5x  1 x 1  lim  lim x0 2 x0 x  2x
x0  2x  2x5x 1 x 1 2 25x  9  lim x 25x  9  lim 9   x  0
x0  2x  2x5x 1 x 1 x0 x 25x 1 x 1 4
không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tất cả 1 đường tiệm cận.
Câu 40: Cho lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh đều bằng a . Khoảng cách giữa hai
đường thẳng BC và AB bằng a 21 a 3 a 7 a 2 A. . B. . C. . D. . 7 2 4 2 Lời giải Chọn A. A' C' I B' H A C B Ta có BC//B C
   BC//AB C
suy ra d BC,AB  d BC,AB C
   d ,BAB C  dA,AB C .
Gọi I và H lần lượt là hình chiếu vuông góc của A trên B C   và AI . Ta có B C    AI và B C    AA nên B C
   AAI  B C  AH mà AI  AH . Do đó  AB C    AH a 3 A . AAI a. a 21 Khi đó d  A , AB C    AH  2   . 2 2 AA  AI 2   7 2 a 3 a      2    a 21
Vậy khoảng cách cần tìm là . 7 2
Câu 41: Biết n là số nguyên dương thỏa mãn x  a  a x  2  a x  2  ..  a x  2 n n và 0 1   2  n   n 3 a a a 2    
.192 . Mệnh đề nào sau đây đúng? 1 2 3 A. n  9;16. B. n  8;1  2 . C. n  7;9. D. n  5;8. Lời giải Chọn B.
TÀI LIỆU ÔN THI THPT QG 2019 13 n 2 n Ta có n x  x  0 n 1 n 1 C C   x  2 n 2 2 2 .2 .2 2 C .2           x 2 . . n C x    n n n n  2 Do đó n 3  1 n 1  2 n 2  3 n3 n 3 a a a 2 .192 C .2 C .2 C .2 2         .192 1 2 3 n n n 1 2 3
 C .4 C .2 C  192  n  9 n n n
Câu 42: Trong mặt phẳng với hệ tọa độ Oxy cho hình chữ nhật ABCD biết AD  2AB , đường thẳng
AC có phương trình x  2y  2  0 , D 1; 1 và Aa;b a,b  ,  a  0. Tính a b. A. a  b  4 . B. a  b  3 . C. a  b  4 . D. a b  1. Lời giải Chọn D.
Gọi Aa;b. Vì A  AC : x  2y  2  0 nên a  2b  2  0  a  2b  2
Do a  0 nên 2b  2  0  b  1   *
Khi đó A2b  2;b. 
Ta có AD  2b  3;1b là véctơ chỉ phương của đường thẳng AD .
u  2; 1 là véctơ chỉ phương của đường thẳng AC . DC 1 2 Trên hình vẽ, tan     cos   1 A ; a b D 1;  AD 2 1 5   AD.u 5 b  1
Lại có cos      2 2 AD . .u 5 b  2b  2 B C 5 b  1 2 Từ   1 và 2 suy ra 2 
 b  2b  3  0  b  3 (do  *) 2 5 b  2b  2 5  a  4 . Khi đó A4; 3
  , suy ra a b  1. IV. VẬN DỤNG CAO
Câu 43: Xét tứ diện ABCD có các cạnh AB  BC  CD  DA  1 và AC,BD thay đổi. Giá trị
lớn nhất của thể tích khối tứ diện ABCD bằng 2 3 4 3 2 3 4 3 A. . B. . C. . D. . 27 27 9 9 Lời giải Chọn A.
Gọi M , N lần lượt là trung điểm của B ,
D AC . Đặt BD  2x,AC  2y x, y  0 .
TÀI LIỆU ÔN THI THPT QG 2019 14 Ta có CM  B ,
D AM  BD  BD  AMC. 1 1 Ta có 2 MA  MC  1 x , 2 2 MN  1 x  y , S  MN.AC 2 2  y. 1 x  y . AMN 2 2 1 V  .DB.S 1 2 2  .2x.y 1 x y 2 2 2  x .y . 2 2 1 x y  ABCD 3 AMC 3 3 x y  x y 3 2 2 2 2 1 2  3 27 2 3 V  . ABCD 27 4 x ax a Câu 44: Cho hàm số y 
. Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm x  1
số đã cho trên đoạn 1;2
  . Có bao nhiêu giá trị nguyên của a để M  2m. A. 15 . B. 14 . C. 15 . D. 16 . Lời giải Chọn A. x  ax a 4 3 3x  4x Xét hàm số f x 4  . Ta có f x   0, x  1;2 x  1    x 21   1 16 Do đó f  
1  f x  f 2,x  1;2            hay a f x a , x 1;2 2 3  
Ta xét các trường hợp sau : 1 1 16 1
Th1 : Nếu a   0  a   thì M  a  ;m  a  2 2 3 2 16  1   13 Theo đề bài a   2 a     a  3  2 3
Do a nguyên nên a  0;1;2;3;4. 16 16  16    1 Th2 : Nếu a 
 0  a   thì m   a   ;M   a        3 3  3     2  1  16        61 Theo đề bài a  2 a       a     2    3  6
Do a nguyên nên a  10; 9  ;. .;  6 . 1 16 16 1
Th3 : Nếu a   0  a 
   a   thì M  0; m  0 (Luôn thỏa mãn) 2 3 3 2
Do a nguyên nên a  5; 4  ;. .;  1
Vậy có 15 gái trị của a thỏa mãn yêu cầu bài toán. Câu 45: Cho hàm số 3
y  x  3x  2C. Biết rằng đường thẳng d :y  ax b cắt đồ thị C tại ba
điểm phân biệt M,N,P . Tiếp tuyến tại ba điểm M,N,P của đồ thị C  cắt C  tại các điểm
M ,N ,P (tương ứng khác M,N,P ). Khi đó đường thẳng đi qua ba điểm M ,N ,P có phương trình là
A. y  4a  9x 18  8b .
B. y  4a  9x 14  8b .
TÀI LIỆU ÔN THI THPT QG 2019 15 C. y  ax  b .
D. y  8a 18x  18  8b . Lời giải Chọn A.
Giả sử Ax ;y ;B x ;y ;C x ;y . Ta có phương trình tiếp tuyến tại A của đồ thị C là 1 1  2 2  3 3  :y   2 3x  3x x  3  x  3x  2 1 1 1 1 1
Xét phương trình hoành độ giao điểm của đồ thị C  và  là 1  x  x 2 3x  3x x  3 3
 x  3x  2  x  3x  2 2 x x x 2x 0       1   1  1 1 1 1 1 x  2x  1  Do đó A 3 2x ; 8x  6x  2 1 1 1  Lại có 3
8x  6x  2  8 3x  3x  2 18x 18  8 ax b 18x 18 1 1 1 1  1  1  1
 8ax b 18x 18  2x 4a  9  18  8b 1  1 1   Khi đó y      x  4a 9 18 8b A A
Vậy phương trình đường thẳng đi qua 3 điểm A ,B ,C  là y  x 4a  9 18  8b
Câu 46: Cho hàm số bậc ba   3 2
f x  ax bx  cx  d có đồ thị như hình vẽ bên dưới: 2 x  3x  2 2x 1
Hỏi đồ thị hàm số g x   
có bao nhiêu đường tiệm cận đứng? 2 x f x f x    A. 5 . B. 4 . C. 6 . D. 3 . Lời giải Chọn A. 1
ĐK x  ; f x  0;f x  1. 2 x  0
x aa 0,5; 1 x  2 Xét phương trình 2
x f x f x  0    x  1 x bb   1; 2 x  c  c 2;3
Đồ thi hàm số có 4 đường tiệm cận đứng x  a;x  ; b x  ; c x  2
Câu 47: Cho hai đường thẳng cố định a và b chéo nhau. Gọi AB là đoạn vuông góc chung của a và b
TÀI LIỆU ÔN THI THPT QG 2019 16
(A huộc a, B thuộc b ). Trên a lấy điểm M (khác A ), trên b lấy điểm N (khác B ) sao cho
AM  x,BN  y,x  y  8. Biết AB  6, góc giữa hai đường thẳng a và b bằng 0 60 . Khi
thể tích khối tứ diện ABNM đạt giá trị lớn nhất hãy tính độ dài đoạn MN (trong trường hợp MN  8 ) A. 2 21 . B. 12 . C. 2 39 . D. 13 . Lời giải Chọn A.
Dựng hình chữ nhật ABNC . AM BN   AM AC  0 , ,  60 A  B  AM A  B  AM Ta có       AB  ACM A  B  BN A  B  AC   1 1  1 3 3 V V  AB.S
 AB.AC.AM sinCAM  .6.x.y.  xy ABNM MABC 3 ACM 6 6 2 2 x y2 3 3 V  xy 
 8 3. Dấu bằng xảy ra khi và chỉ khi x  y  4. ABNM 2 2 4
Khi đó AM  BN  AC  4 Lại có AB CN  CN  AMC  2 2 2 / /
 CN  CM  MN  CM CN Mặt khác  0 MAC  60 hoặc  0 MAC  120 Trường hợp 1:  0 MAC  60  A  MC đều 2 2
 CM  4  MN  4  6  2 13 Trường hợp 2:  0 MAC  120 2 2 0 2
 CM  AM  AC  2AM.AC cos120  48  MN  48  6  2 41
Câu 48: Cho tập hợp A  1;2;3;4. .;10 
0 . GọiS là tập hợp gồm tất cả các tập con của A , mỗi tập con
này gồm 3 phần tử của A và có tổng bằng 91 . Chọn ngẫu nhiên một phần tử của S . Xác suất
chọn được phần tử có 3 số lập thành cấp số nhân bằng? 4 2 3 1 A. . B. . C. . D. . 645 645 645 645 Lời giải Chọn C.
Giả sử tập con bất kì a, ,bc  S  1  a, ,bc  100 ;a, ,bc phân biệt. a b  c  91.
Đây là bài toán chia kẹo Euler nên số bộ a, , b c là 3 1 C  91 1 
Tuy nhiên trong các bộ trên vẫn chứa các bộ có 2 chữ số giống nhau, số bộ có 2 chữ số giống
nhau là 3.45  135 ( bộ). Vậy n      2 C  3.45 : 3!  645 . 90 
Gọi A là biến cố: ”a, ,
b c lập thành cấp số nhân”
Gọi q là công bội của cấp số nhân theo bài ra ta có q  0 2
a aq  aq  91  a  2
1 q q   1.91  13.7 a   1 a   1 Trường hợp 1:    2  1 q q  91 q     9   a   91 a   91 Trường hợp 2:    (loại) 2  1 q q  1 q     0  
TÀI LIỆU ÔN THI THPT QG 2019 17 a   13 a   13 Trường hợp 3:    (thỏa mãn) 2  1 q  q  7 q     2   a   7 a   7 Trường hợp 3:    (thỏa mãn). 2  1 q  q  13 q     3   Vậy n   A  3 . P   3 A  . 645 0   x  y  1
Câu 49: Biết m là giá trị để hệ bất phương trình 
có nghiệm thực duy nhất. x
 y  2xy m 1 
Mệnh đề nào sau đây đúng?  1 1  3  1  A. m     ;         . B. m    ;0. C. m   ;1. D. m   2  ; 1.  2 3  4  3  Lời giải Chọn B.
Hệ phương trình tương đương với: 0   x  y  1 0   x  y  1     2xy  m  1  x y   2
 xy m  12x 2y   x y2 0   x y 1  I    x  
21 y  21 m 1 II.
Tập nghiệm của (I) là phần nằm giữa hai đường thẳng d : y  x  ; d ' :y  x   1 và trên d '.
Nếu m  1 thì hệ phương trình vô nghiệm.
Nếu m  1 thì tập nghiệm của (II) là hình tròn (C )(kể cả biên)
có tâm A1; 1bán kính R  m 1 .
Do đó hệ phương trình có nghiệm duy nhất khi d ' là tiếp tuyến của đường tròn (C ). 2 1 Nghĩa là: m  1   m   . 2 2 1
Vậy hệ phương trình có nghiệm duy nhất khi m   . 2 Câu 50: Cho phương trình: 3 x  x    3 x  m 3 3 2 sin 2sin 3 2cos
2cos x  m  2  2cos x  cos x  m .
Có bao nhiêu giá trị nguyên của tham số m để phương trình trên có đúng 1 nghiệm  2  x  0;   ? 3    A. 2 . B. 1. C. 3 . D. 4 . Lời giải Chọn D. Ta có:
TÀI LIỆU ÔN THI THPT QG 2019 18 x  x  x   x  m  3 3 2 3   3 x  m   3 sin sin 2sin 2cos 2 2 cos
2  2 2cos x  m  2  1 Xét hàm số f t 3 2
 t  t  2t có f t 2
 6t  2t  2  0, t   , nên hàm số f t đồng biến trên  . Bởi vậy:
   f  x f  3 1 sin 2cos x  m  2 3
 sinx  2cos x  m  2 2  2 Với x  0;   thì 3      2 3
2  sin x  2 cos x  m  2 3 2  2
 cos x  cos x  3  m 3
Đặt t  cosx , phương trình 3 trở thành 3 2 2t t 1  m 4  1   2 Ta thấy, với mỗi t     ;1    
thì phương trình cosx  t cho ta một nghiệm x 0;   2     3     1  Xét hàm số g t 3 2
 2t t  3 với t     ;1  .  2  t  0  Ta có gt 2
 6t  2t , gt  0   1 . t    3 Ta có bảng biến thiên 1 1 t   0 1 2 3 gt  0  0  3 3 g t 80 0 27  2
Do đó, để phương trình đã cho có đúng 1 nghiệm x  0;  
điều kiện cần và đủ là phương 3     1 
trình 4 có đúng một nghiệm t     ;1   2  m   3    80  m   ( Do m nguyên).    3;2;1; 0 m 0;   27   
Chúc các em đạt kết quả cao trong kì thi THPT 2019!
TÀI LIỆU ÔN THI THPT QG 2019 19
Document Outline

  • Mađề132
  • Lời giải chi tiết đề lần 1. K12