Đề KSCL đội tuyển HSG Toán 11 năm 2017 – 2018 trường Minh Châu – Hưng Yên

SỞ GD&ĐT HƯNG YÊN
ĐỀ KSCL ĐỘI TUYỂN HỌC SINH GIỎI KHỐI 11
TRƯỜNG THPT MINH CHÂU
MÔN: TOÁN – NĂM HỌC 2017-2018
Thời gian làm bài: 120 phút, không kể thời gian phát đề Đề thi gồm: 01 trang 3
Câu 1 (1,0 điểm). Giải phương trình 2
cos 2x  cos 2x   0 4 x 
Câu 2 (1,0 điểm). Giải phương trình 2 sin 1
2(1 cos x)(1 cot x)  . sin x  cos x
Câu 3 (1,0 điểm). Cho hàm số 3 2
y = x -3x +1 có đồ thị (C). Viết phương trình tiếp tuyến của đồ
thị (C), biết tiếp tuyến vuông góc với đường thẳng D : x +9y = 0. 5 x  3 5x  2 2x  6x 
Câu 4 (1,0 điểm). Tính giới hạn: I  4 lim x 3 x  2 1 x  x  1
Câu 5 (1,0 điểm). Cho n là số nguyên dương thỏa mãn 1  3 5 n C
 C . Tìm hệ số của số hạng chứa 8 x n n 2 n  
trong khai triển nhị thức Niu-tơn của nx 1   , x   0 .  14 x   2
 4x  1x   y  3 5  2y  0
Câu 6 (1,0 điểm). Giải hệ phương trình  2 2
4x  y  2 3  4x  7
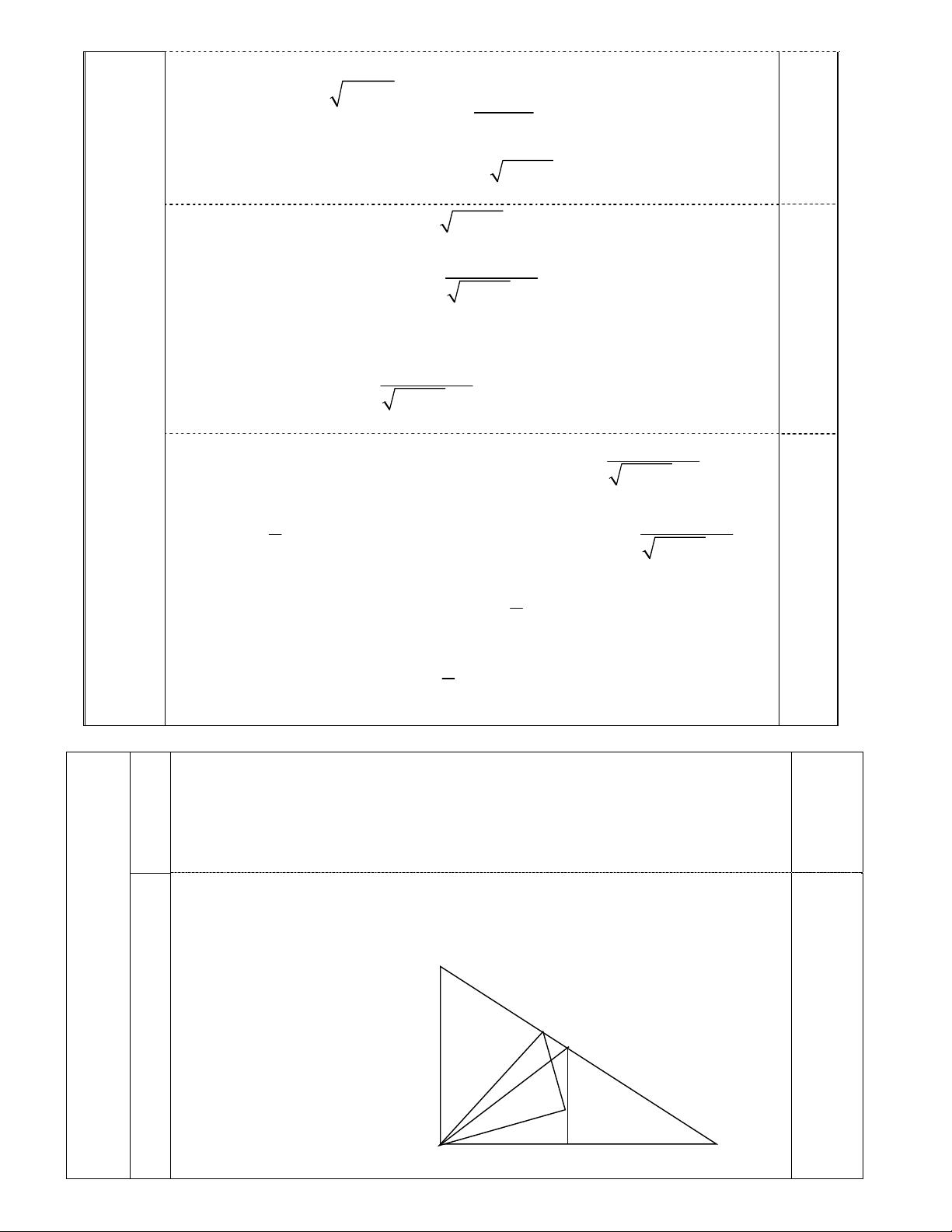
Câu 7 (1,0 điểm). Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm BC, G là trọng tâm
ABM ; điểm D(7; -2) nằm trên đoạn MC sao cho GA = GD. Viết phương trình đường thẳng AB,
biết hoành độ của A nhỏ hơn 4 và AG có phương trình 3x  y 13  0 .
Câu 8 (2,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thang cân (AD // BC), BC = 2a, AB
= AD = DC = a (a > 0). Mặt bên SBC là tam giác đều. Gọi O là giao điểm của AC và BD. Biết SD vuông góc với AC.
a) Chứng minh mặt phẳng (SBC) vuông góc mặt phẳng (ABCD). Tính độ dài đoạn thẳng SD.
b) Mặt phẳng   đi qua điểm M thuộc đoạn thẳng OD ( M khác O và D) và song song với
đường thẳng SD và AC. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng
  biết MD = x. Tìm x để diện tích thiết diện lớn nhất.
Câu 9 (1,0 điểm). Cho dãy số (u ) xác định bởi: n 2n   1 u  n 2 n u  1; 1 * u   , n
   . Tìm công thức số hạng tổng quát u theo n . 1 n n  n n  n  2 2 1 1
---------- HẾT ----------
Thí sinh không được sử dụng tài liệu.
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:…………………….………..…….; Số báo danh…………………… SỞ GD&ĐT HƯNG YÊN
ĐÁP ÁN KSCL ĐỘI TUYỂN HỌC SINH GIỎI
TRƯỜNG THPT MINH CHÂU KHỐI 11
MÔN: TOÁN – NĂM HỌC 2017-2018 Đáp án gồm: 06 trang I. LƯU Ý CHUNG:
- Hướng dẫn chấm chỉ trình bày một cách giải với những ý cơ bản phải có. Khi chấm bài học sinh
làm theo cách khác nếu đúng và đủ ý thì vẫn cho điểm tối đa.
- Điểm toàn bài tính đến 0,25 và không làm tròn.
- Với bài hình học nếu thí sinh không vẽ hình phần nào thì không cho điểm tương ứng với phần đó. II. ĐÁP ÁN: Câu Nội dung trình bày Điểm 1 (1,0 điểm)  1 cos 2x   2 PT   0,5 3
cos2x   L  2  
 2x    k2  x    k ,k   0,5 3 6 2 (1,0 điểm) x  k sin  x  0  ĐK:     , k  .  sin 
x  cos x  0
x    k  4 0,25 1 sin x 1
Pt  2(1 cos x).  2 sin x sin x  cos x 2 sin x 1  
 sin x  cos x  sin .
x cos x 1  0 1 cos x sin x  cos x 0,25 
Đặt t  sin x  cos x  2 sin(x  ),  2  t  2, Phương trình trở thành: 4 0,25 2 t 1 t 
1  0  t  1. 2    x     k2    1  4 4
x    k2 (tm) Với t  1,  ta có sin(x )        2 . 4 2  5  x    k2
x    k2 (l)  0,25  4 4 
Vậy phương trình có họ nghiệm x    k2. 2 3 (1,0 điểm) Đạo hàm 2 y ' = 3x -6 . x Gọi 3 2
M (a;a -3a +1) Î (C). Phương trình tiếp tuyến của (C) tại M là 0,25 3 2
y = f '(a)(x - a) + a -3a +1.
Tiếp tuyến vuông góc với đường x +9y = 0 nên 0,25 æ 1ö éa = -1 2 f '(a).ç ÷ - ç
÷ = -1  3a -6a = 9  ê . ç è 9÷ø êa = 3 ë
Với a = -1, phương trình tiếp tuyến là y = 9x + 6. 0,25
Với a = 3, phương trình tiếp tuyến là y = 9x-26. 0,25 Ta có : 5 3 2
x  x  x  x   x  2 x   2 5 2 6 4 1 2 x  2. 0.5 3 2 2
x  x  x  1  x  1 x  1 . 4. x x x x x  2 2 5 3 2 x      2 5 2 6 4  I     3 lim lim . x 3 2 1 x
x  x  x  1 1 x  1 2 0.5 Vậy I   3 . 2 (1,0 điểm)  
n  2 n 1 n n 7 n 1  3    Ta có 2 5C  C  5n 
 n  3n  28  0  . 0,25 n n  6 n  4   ktm 5. 7 7 7 2 2 7 k     Xét khai triển 7x 1 x 1  1  
       C    k k 142 1 k k x x 7  14 x   2 x  k 0  2  0,5 7 7  1 k   C    k k 143 1 k x . Ứng với 8
x suy ra 14  3k  8  k  2 . 7 k 0  2  5  1  21 Vậy hệ số của 8
x trong khai triển là: 2 C  0,25 7    2  32  2  4x  
1x y 3 5 2y  0  1
b)Giải hệ phương trình  2 2
4x  y  2 3  4x  7  2  5 y   a  x a  x Câu 6  2   Điều kiện:  Sau đó đặt  2   5  b 3  b   5  2y  y   (1,0 x    2 4 điểm)
Phương trình (1) trở thành 0,25 3 3
8a  2a  b  b  0  2a  b 2 2
4a  2ab  b   1  0 2a  b   2 2
4a  2ab  b 1  0  l x  0 
Với 2a  b  2x  5  2 y 2   5  4x y   2 0,25 Thay vào (2) ta có pt 4 2
16x  24x  3  8 3  4x  0 2  4x  2 4x   1  5 2 4x  
1  8 3  4x   1  0     2x   16 3 2
1 8x  4x 10x  5   0    3  4x 1 0,25 2x 1  0   16 3 2 8
 x  4x 10x  5   0 *  3  4x 1 16 Ta có * 2
 2x 4x  3  3x4x  3 2
 2x  x  5   0 3  4x 1 3 16 Với 0  x  có 2
2x 4x  3  3x4x  3 2
 2x  x  5   0 4 3  4x 1 0,25 3
Vậy (*) không có nghiệm thỏa mãn 0  x  4  
Kết luận hệ có nghiệm là x; y 1  ;2    2 
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm BC, G là trọng tâm
ABM ; điểm D(7; -2) nằm trên đoạn MC sao cho GA = GD. Viết phương
trình đường thẳng AB, biết hoành độ của A nhỏ hơn 4 và AG có phương trình 1.0
3x  y 13  0 .
Gọi I là trung điểm AB, dễ thấy GA  GB  GD  G là tâm đường tròn ngoại tiếp 0
ABD  AGD  2ABD  90  AG  DG 7 C 0.25 D M G A I B DG  d  ;
A AG  10  AD  2 5
Giả sử Aa a  
 a  2   a  2 ;3 13 , AD=2 5 7 3
11  20  a  3 (do a <4) 0.25  A3; 4    AI
AMB vuông tại M 3
 MI  IA  3IG  AG  10IG  cos BAG   AG 10  
Gọi na b  2 2 ;
a  b  0 là véc tơ pháp tuyến của AB, n 3; 1  là véc tơ pháp 1   0.25 tuyến của AG 3a  b 3 b  0
Áp dụng công thức tính góc ta được    2 2 a  b . 10 10 3a  4  b
Với b = 0 thì phương trình AB là x 3  0 Với 3a  4
 b thì AB : 4x-3y-24=0  D, G nằm về hai phía đối với AB G
nằm ngoài tam giác ABC(loại) 0.25
Kết luận: Phương trình AB là x 3  0.
*Chú ý: Nếu học sinh không loại nghiệm thì không cho điểm phần này. 5 2
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân (AD // BC), BC = 2a, AB =
(2 điểm) AD = DC = a (a > 0). Mặt bên SBC là tam giác đều. Gọi O là giao điểm của AC và
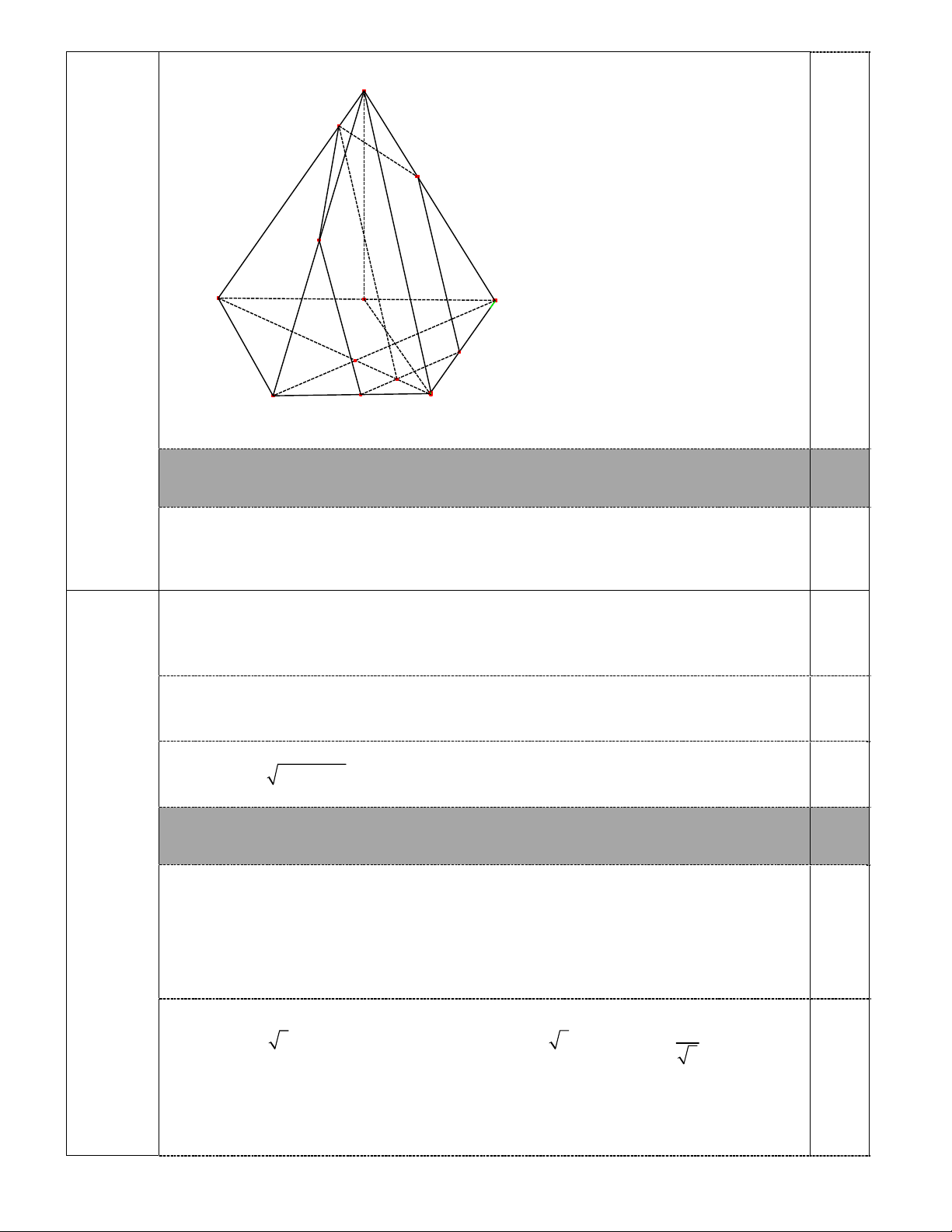
BD. Biết SD vuông góc với AC. S Q P E I B C O N M A G D 1 8a) 0,25
Gọi I là trung điểm của BC nên tứ giác ADCI là hình thoi cạnh a nên IA = IB = IC
= a thì tam giác ABC vuông tại A, suy ra AC vuông góc DI 0,25
AC  ID ID|| AB, AC  SD  AC  SID  AC  SI 0,25
Do AC  SI, BC  SI  SI   ABCD  (ABCD)  SBC 0,25 Ta có : 2 2
SD  SI  ID  2a 1 8b) 0,5
Từ M kẻ hai đường thẳng lần lượt song song với SD, AC chúng cắt theo thứ tự SB
tại Q và AB tại G, AC tại N. Từ G kẻ đường thẳng song song SD, cắt SA tại E,từ N
kẻ đường thẳng song song với SD cắt SC tại P. Ta được thiết diện là ngũ giác GNPQE. 0,25   Ta có x
BD  a 3 nên tính được EG  NP  2a  x 3,QM  2 a  
 , GN  3x  3 
Tứ giác EGMQ và MNPQ là hai hình thang vuông đường cao lần lượt là GM và NM nên S
 4x3a  2 3x MNPQE  0,25 3 3 a 3 Max 2 S  a tại x  MNPQE 2 4 9
Cho dãy số (u ) xác định bởi: n (1 điểm) 2n   1 u  n 2 n u  1; 1 * u   , n
   . Tìm công thức số hạng tổng 1 n n
n  n 2 2 1 1
quát u theo n . n 0,25 2n   2 1 u   n 1  2 n * 2n n u   , n
    nu  2 n 1 u  , n    . n 2 n   * n   n  n   n 1 1 1
n  n 2 2 2 1 1 2 2 n    n 
 nu  2 n  u  n    n   ( 1) 1 2( 1) * 1 , n 1   2n   2 1 [(n 1) 1] 0,25 1 1 1
 (n 1)u   [nu  ] (1) n 1  2 n 2 (n 1) 1 2 n 1 0,25 1 1 1 1
Đặt v  nu  . Khi đó (1)  v
 v (v   v  n n 2 n 1 n 1  2 n 1 2 n 2n 0,25 1 1 1 Vậy u  (  ) n 2 n n 1 2n