Đề KSCL giữa HK1 Toán 12 năm 2018 – 2019 trường THPT chuyên Đại học Vinh – Nghệ An

Đề KSCL giữa HK1 Toán 12 năm 2018 – 2019 trường THPT chuyên Đại học Vinh – Nghệ An mã đề 132 được biên soạn nhằm giúp nhà trường và giáo viên đánh giá khả năng của từng học sinh để có phương pháp dạy học phù hợp, đề gồm 5 trang với 50 câu hỏi và bài toán trắc nghiệm khách quan, học sinh có 90 phút để hoàn thành đề thi này.Mời bạn đọc đón xem.

38 19 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

28 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 1 Mã đề 132
Câu 1. Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 2. Cho hàm số
2
2
xx
y
x
+
=
−
có đồ thị
( )
C
. Phương trình tiếp tuyến tại điểm
( )
1; 2A −
của
( )
C
là
A.
35yx= − +
. B.
. C.
53yx= − +
. D.
.
Câu 3. Gọi
( )
P
là đồ thị hàm số
3
23y x x= − +
. Trong các đường thẳng sau, đường thẳng nào là tiếp
tuyến của
( )
P
?
A.
3.yx= − −
B.
11 4.yx=+
C.
3.yx= − +
D.
4 1.yx=−
Câu 4. Khối đa diện đều loại
4; 3
có bao nhiêu mặt?
A.
6.
B.
20.
C.
12.
D.
8.
Câu 5. Cho hình lăng trụ
. ' ' 'ABC A B C
có các mặt bên là hình vuông cạnh
2a
. Tính theo
a
thể tích
V
của khối lăng trụ
. ' ' 'ABC A B C
A.
3
6
2
a
V =
. B.
3
3
12
a
V =
. C.
2
3
4
a
V =
. D.
2
6
6
a
V =
.
Câu 6. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
2SA a=
và
SA
vuông góc với
()ABCD
. Góc giữa
SC
và
ABCD
bằng
A.
0
45
. B.
0
30
. C.
0
60
. D.
0
90
.
Câu 7. Cho hình lập phương
.ABCD A BC D
cạnh
.a
Tính khoảng cách giữa hai đường thẳng
AB
và
CD
.
A.
2
.
2
a
B.
.a
C.
2.a
D.
2.a
Câu 8. Giá trị cực đại
CD
y
của hàm số
3
12 20y x x= − +
là
A.
4.
CD
y =
B.
36.
CD
y =
C.
4.
CD
y =−
D.
2.
CD
y =−
Câu 9. Tập xác định của hàm số
1
sinx 1
y =
+
là
A.
\ 2 ,
2
kk

+


. B.
\ 2 ,
2
kk

− +


.
C.
\,
2
kk

− +


. D. .
Câu 10. Nghiệm âm lớn nhất của phương trình
2
3
3cot x 3
sin x
=+
là
A.
6
−
. B.
5
6
−
. C.
2
−
. D.
2
3
−
.
TRƯỜNG ĐẠI HỌC VINH
TRƯỜNG THPT CHUYÊN
-----------------------
ĐỀ KHẢO SÁT CHẤT LƯỢNG GIỮA HỌC KỲ 1
MÔN TOÁN - LỚP 12
NĂM HỌC 2018 - 2019
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
---------
(Đề thi gồm 05 trang, 50 câu trắc nghiệm)
MÃ ĐỀ THI
132
Họ và tên thí sinh: .................................................................. Số báo danh: ......................................
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 2 Mã đề 132
Câu 11. Cho cấp số cộng
( )
n
u
có các số hạng đầu lần lượt là
5
;
9
;
13
;
17
; … Tìm công thức số hạng
tổng quát
n
u
của cấp số cộng ?
A.
51
n
un=−
. B.
51
n
un=+
. C.
41
n
un=−
. D.
41
n
un=+
.
Câu 12. Tìm giá trị nhỏ nhất của hàm số
2
1yx=−
trên đoạn
3;2−
?
A.
3;2
min 3
−
=
. B.
3;2
min 3
−
=−
. C.
3;2
min 1
−
=−
. D.
3;2
min 8
−
=
.
Câu 13. Cho hàm số
2
1yx=−
. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
( )
0;+
. B. Hàm số nghịch biến trên khoảng
( )
;0−
.
C. Hàm số đồng biến trên khoảng
( )
1; +
. D. Hàm số đồng biến trên khoảng
( )
;− +
.
Câu 14. Khai triển
( )
100
3x −
ta được đa thức
( )
100
2 100
0 1 2 100
3 ...x a a x a x a x− = + + + +
, với
0
,a
1 2 100
, ,...,a a a
là các hệ số thực. Tính
0 1 2 99 100
...a a a a a− + − − +
?
A.
100
2−
. B.
100
4
. C.
100
4−
. D.
100
2
.
Câu 15. Nghiệm của phương trình lượng giác
2
cos cos 0xx−=
thỏa mãn điều kiện
0 x

là
A.
0x =
. B.
3
4
x
=
. C.
2
x
=
. D.
2
x
=−
.
Câu 16. Tất cả các nghiệm của phương trình
tan cotxx=
là
A.
,
44
x k k

= +
. B.
2,
4
x k k
= +
.
C.
,
4
x k k
= +
. D.
,
42
x k k

= +
.
Câu 17. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
2SA a=
và vuông góc
với
()ABCD
. Tính theo
a
thể tích
V
của khối chóp
.S ABC
A.
3
2
6
Va=
. B.
3
22
3
Va=
. C.
3
2Va=
. D.
3
2
3
Va=
.
Câu 18. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành,
AB a=
,
3SA a=
và vuông góc với
()ABCD
. Tính góc giữa hai đường thẳng
SB
và
CD
A.
0
60
. B.
0
30
. C.
0
45
. D.
0
90
.
Câu 19. Cho hàm số
31
3
x
y
x
−
=
−
có đồ thị
( )
C
. Mệnh đề nào sau đây sai?
A. Đồ thị
( )
C
có tiệm cận đứng và tiệm cận ngang.
B. Đồ thị
( )
C
không có tiệm cận đứng.
C. Đồ thị
( )
C
có tiệm cận ngang.
D. Đồ thị
( )
C
có tiệm cận.
Câu 20. Trong năm học
2018 2019−
trường THPT chuyên đại học Vinh có
13
lớp học sinh khối
10,
12
lớp học sinh khối
11,
.
12
lớp học sinh khối
12
. Nhân ngày nhà giáo Việt Nam
20
tháng
11
nhà
trường chọn ngẫu nhiên
2
lớp trong trường để tham gia hội văn nghệ của trường Đại học Vinh.
Xác suất để chọn được hai lớp không cùng khối là
A.
76
111
. B.
87
111
. C.
78
111
. D.
67
111
.
Câu 21. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
A
,
2BC a=
,
SA a=
và
SA
vuông góc
( )
ABC
. Tính góc giữa hai mặt phẳng
( )
SBC
và
( )
ABC
A.
0
45
. B.
0
30
. C.
0
60
. D.
0
90
.
Câu 22. Gọi
1 2 3
,,x x x
là các cực trị của hàm số
42
4 2019y x x= − + +
. Tính tổng
1 2 3
x x x++
bằng?
A.
0
. B.
22
. C.
1−
. D.
2
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 3 Mã đề 132
Câu 23. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
32
3 9 1y x x x= − − +
trên
đoạn
0;4
. Tính tổng
2mM+
.
A.
2 17mM+=
. B.
2 37mM+ = −
. C.
2 51mM+=
. D.
2 24mM+ = −
.
Câu 24. Cho cấp số nhân
( )
n
u
thỏa mãn
1 3 5
17
65
325
u u u
uu
− + =
+=
. Tính
3
.u
A.
3
15u =
. B.
3
25u =
. C.
3
10u =
. D.
3
20u =
.
Câu 25. Biết số tự nhiên
n
thỏa mãn
2
1
11
2 ... 45
n
nn
n
n
nn
CC
Cn
CC
−
+ + + =
. Tính
4
n
n
C
+
?
A.
715
. B.
1820
. C.
1365
. D.
1001
.
Câu 26. Tìm tất cả các giá trị của
m
để hàm số
1x
y
xm
−
=
+
đồng biến trên khoảng
( )
0;+
?
A.
( )
1;− +
. B.
)
0;+
. C.
( )
0;+
. D.
)
1;− +
.
Câu 27. Tìm tất cả các giá trị thực của tham số
m
sao cho điểm cực tiểu của đồ thị hàm số
32
1y x x mx= + + −
nằm bên phải trục tung?
A.
0m
. B.
1
0
3
m
. C.
1
3
m
. D.Không tồn tại.
Câu 28. Sinh nhật của An vào ngày 1 tháng 5. Bạn An muốn mua một chiếc máy ảnh giá khoảng
600.000
đồng để làm quà sinh nhật cho chính mình. Bạn ấy quyết định bỏ ống tiết kiệm
10.000
đồng vào
ngày 1 tháng 1 của năm đó, sau đó cứ tiếp tục những ngày sau, mỗi ngày bạn bỏ ống tiết kiệm
5.000
đồng. Biết trong năm đó, tháng 1 có 31 ngày, tháng 2 có 28 ngày, tháng 3 có 31 ngày và
tháng 4 có 30 ngày. Gọi
a
(đồng) là số tiền An có được đến sinh nhật của mình (ngày sinh nhật
An không bỏ tiền vào ống). Khi đó ta có:
A.
)
610000;615000a
. B.
)
605000;610000a
.
C.
)
600000;605000a
. D.
)
595000;600000a
.
Câu 29. Số nghiệm của phương trình
sin5 3cos5 2sin7x x x+=
trên khoảng
0;
2



là ?
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 30. Cho hàm số
()fx
có đạo hàm trên và
/
( ) 0,f x x
.Biết
(1) 2.f =
Hỏi khẳng định nào
sau đây có thể xảy ra ?
A.
(2) (3) 4.ff+=
B.
( 1) 2.f −=
C.
(2) 1.f =
D.
(2018) (2019).ff
Câu 31. Cho tập hợp
0,1,2,3,4,5,6A =
. Từ tập
A
lập được bao nhiêu số tự nhiên chẵn có
4
chữ số
khác nhau và nhỏ hơn
4012
A.
180
. B.
240
. C.
200
. D.
220
.
Câu 32. Một vật chuyển động theo quy luật
32
1
9
2
s t t
−
=+
, với
t
(giây) là khoảng thời gian tính từ lúc
vật bắt đầu chuyển động và
s
(mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi
trong khoảng thời gian
10
giây, kể từ lúc bắt đầu chuyển động vận tốc lớn nhất của vật đạt được
bằng bao nhiêu?
A.
216 ( / )ms
. B.
400 ( / )ms
. C.
54 ( / )ms
. D.
30 ( / )ms
.
Câu 33. Tất cả các giá trị của tham số
m
để hàm số
( )
4
1=−y m x
đạt cực đại tại
0=x
là
A.
1.m
B.
1.m
C. không tồn tại m. D.
1.=m
Câu 34. Tung hai con súc sắc
3
lần độc lập với nhau. Tính xác suất để có đúng một lần tổng số chấm
xuất hiện trên hai con súc sắc bằng
6.
Kết quả làm tròn đến
3
ba chữ số ở phần thập phân)
A.
0,120.
B.
0,319.
C.
0,718.
D.
0,309.
Câu 35. Hệ số của
5
x
trong khai triển
( )
9
2
1 2 3xx−−
là
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 4 Mã đề 132
A.
792
. B.
684−
. C.
3528
. D.
0
.
Câu 36. Cho một khối đa diện lồi có
10
đỉnh,
7
mặt. Hỏi khối đa diện này có mấy cạnh?
A.
20
. B.
18
. C.
15
. D.
12
.
Câu 37. Cho hình chóp
.S ABC
có
2 , 2 , 2 2SA a SB a SC a= = =
và
= = = 60ASB BSC CSA
. Tính
thể tích của khối chóp đã cho.
A.
3
4
3
a
. B.
3
23
3
a
. C.
3
2a
. D.
3
22
3
a
.
Câu 38. Cho hình lập phương
.ABCD A B C D
cạnh
a
. Gọi
,MN
lần lượt là trung điểm của
BC
và
DD
. Tính theo
a
khoảng cách giữa hai đường thẳng
MN
và
BD
.
A.
3a
. B.
3
2
a
. C.
3
3
a
. D.
3
6
a
.
Câu 39. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SAD
là tam giác đều và nằm
trong mặt phẳng vuông góc với
()ABCD
. Gọi
,,M N P
lần lượt là trung điểm các cạnh
,,SB BC CD
. Tính thể tích khối tứ diện
CMNP
.
A.
3
3
48
a
. B.
3
3
96
a
. C.
3
3
54
a
. D.
3
3
72
a
.
Câu 40. Số tiệm cận ngang của đồ thị hàm số
2018
2019
x
y
x
−
=
+
là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 41. Cho khối hộp
. ’ ’ ’ ’ABCD A B C D
có
M
là trung điểm
’’AB
. Mặt phẳng
( )
ACM
chia khối hộp đã
cho thành hai phần. Tỉ số thể tích của hai phần đó bằng?
A.
7
17
. B.
5
17
. C.
7
24
. D.
7
12
.
Câu 42. Đồ thị của hàm số
( )
32
f x x ax bx c= + + +
tiếp xúc với trục hoành tại gốc tọa độ và cắt đường
thẳng
1x =
tại điểm có tung độ bằng
3
khi
A.
0, 2a b c= = =
. B.
0, 2a c b= = =
. C.
2, 0a b c= = =
. D.
2, 1, 0a b c= = =
.
Câu 43. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
,
0
60ABC =
, cạnh bên
2SA a=
và
SA
vuông góc với
ABCD
.Tính góc giữa
SB
và
()SAC
.
A.
0
90
. B.
0
30
. C.
0
45
. D.
0
60
.
Câu 44. Gọi
m
là giá trị để đồ thị
(C )
m
của hàm số
22
2 2 1
1
x mx m
y
x
+ + −
=
−
cắt trục hoành tại hai điểm
phân biệt và các tiếp tuyến với
(C )
m
tại tại hai điểm này vuông góc với nhau. Khi đó ta có:
A.
( )
1;2m
. B.
( )
2; 1m − −
. C.
( )
0;1m
. D.
( )
1;0m−
.
Câu 45. Cho lăng trụ đứng
/ / /
.ABC A B C
có đáy ABC là tam giác cân tại C,
0
30BAC =
,
/
3, .AB a AA a==
Gọi M là trung điểm của
/
.BB
Tính theo a thể tích V khối tứ diện
/
.MACC
A.
3
3
12
a
V =
. B.
3
3
4
a
V =
.
C.
3
3
3
a
V =
. D.
3
3
18
a
V =
Câu 46. Cho hàm số
( )
.y f x=
Hàm số
( )
/
y f x=
có đồ thị như hình vẽ bên. Hỏi hàm số
( )
3y f x=−
đồng biến trên khoảng nào sau đây:
A.
( )
2;4
. B.
( )
1;3
. C.
( )
1;3−
. D.
( )
5;6
Câu 47. Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ sau:
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 5 Mã đề 132
Khi đó số nghiệm của phương trình
( )
2 2 3 5 0fx− − =
là:
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 48. Tìm số tiệm cận (bao gồm tiệm cận đứng và tiệm cận ngang) của đồ thị hàm số
2
45
2 1 1
x
y
xx
+
=
+ − −
A.3. B.1. C.2. D. 4.
Câu 49. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
D
,
2AB a=
,
AD CD a==
,
2SA a=
,
( )
SA ABCD⊥
. Tính côsin của góc tạo bởi
( )
SBC
và
( )
SCD
.
A.
6
6
. B.
6
3
. C.
2
3
. D.
3
3
.
Câu 50. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
3
2
7 14 2
3
mx
y mx x m= + + − +
nghịch
biến trên
)
1; +
.
A.
14
;
15

− −


. B.
14
;
15

− −

. C.
14
2;
15

−−


. D.
14
;
15

− +

.
ĐÁP ÁN
1-D
2-C
3-C
4-A
5-A
6-A
7-B
8-B
9-B
10-C
11-D
12-C
13-C
14-B
15-C
16-D
17-A
18-A
19-B
20-A
21-A
22-A
23-D
24-D
25-A
26-B
27-A
28-B
29-A
30-B
31-D
32-C
33-A
34-D
35-C
36-C
37-D
38-D
39-B
40-C
41-A
42-C
43-B
44-C
45-B
46-D
47-B
48-C
49-B
50-A
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 6 Mã đề 132
LỜI GIẢI
duongductri@gmail.com
Câu 1. Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
A.
3
. B.
1
. C.
2
. D.
4
.
Lời giải
Tác giả : Dương Đức Trí, FB: duongductric3ct
Chọn D
Gọi
, , , , , , , ,M N P E F I J G H
lần lượt là trung điểm các cạnh
,,AA CC BB
,
,AC A C

,
,BC B C

,
,AB A B

của lăng trụ tam giác đều
.ABC A B C
. Các mặt phẳng đối xứng của lăng
trụ tam giác đều
.ABC A B C
là
( )
MNP
,
( )
AIJA
,
( )
BEFB
,
( )
CGHC
.
duongductri@gmail.com
Câu 2. Cho hàm số
2
2
xx
y
x
+
=
−
có đồ thị
( )
C
. Phương trình tiếp tuyến tại điểm
( )
1; 2A −
của
( )
C
là
A.
35yx= − +
. B.
. C.
53yx= − +
. D.
.
Lời giải
Tác giả : Dương Đức Trí, FB: duongductric3ct
Chọn C
( )
2
2
42
2
xx
y
x
−−
=
−
;
( )
15y
=−
Phương trình tiếp tuyến tại điểm
( )
1; 2A −
của
( )
C
là
( )
5 1 2yx= − − −
53yx = − +
.
nguyenth4nhtr11ng@gmail.com
Câu 3. Gọi
( )
P
là đồ thị hàm số
3
23y x x= − +
. Trong các đường thẳng sau, đường thẳng nào là tiếp
tuyến của
( )
P
?
A.
3.yx= − −
B.
11 4.yx=+
C.
3.yx= − +
D.
4 1.yx=−
Lời giải
Tác giả : Nguyễn Thành Trung, FB: Nguyễn Thành Trung
Chọn C
2
' 3 1yx=−
Điều kiện đường thẳng
y ax b=+
là tiếp tuyến của hàm số
( ) ( )
y f x C=
:
( )
( )
0
00
'f x a
ax b f x
=
+=
có nghiệm. Kiểm tra các đáp án
Đáp án A:
2
0
0
3
0 0 0
3 1 1
0
33
3 2 3
x
x
x x x
− = −
=


−=
− − = − +
vô lí, đáp án A sai.
Đáp án B:
2
0
0
3
3
0 0 0
0 0 0
2
3 1 11
11 4 2 3
11 4 2 3
x
x
x x x
x x x
=
−=


+ − +
+ = − +
đáp án B sai.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 7 Mã đề 132
Đáp án C:
2
0
0
3
0 0 0
3 1 1
0
33
3 2 3
x
x
x x x
− = −
=


=
− + = − +
luôn đúng. Đáp án C đúng.
Do đáp án C đúng nên đáp án D sai.
Câu 4. Khối đa diện đều loại
4; 3
có bao nhiêu mặt?
A.
6.
B.
20.
C.
12.
D.
8.
Lời giải
Tác giả : Nguyễn Thành Trung, FB: Nguyễn Thành Trung
Chọn C
Khối đa diện đều loại
4; 3
là khối lập phương có 6 mặt.
Nvthang368@gmail.com
Câu 5. Cho hình lăng trụ
. ' ' 'ABC A B C
có các mặt bên là hình vuông cạnh
2a
. Tính theo
a
thể tích
V
của khối lăng trụ
. ' ' 'ABC A B C
A.
3
6
2
a
V =
. B.
3
3
12
a
V =
. C.
2
3
4
a
V =
. D.
2
6
6
a
V =
.
Lời giải
Tác giả: Nguyễn Văn Thắng; Fb: Nguyễn Thắng
Chọn A
Từ giả thiết suy ra đáy của hình lăng trụ là tam giác đều cạnh bằng
2a
⇒ Diện tích của đáy
là:
22
3.( 2 ) 3.
42
ABC
aa
S ==
⇒ Thể tích của lăng trụ là:
23
3. 6
.2
22
aa
Va==
⇒ Chọn A
Nvthang368@gmail.com
Câu 6. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
2SA a=
và
SA
vuông góc với
()ABCD
. Góc giữa
SC
và
ABCD
bằng
A.
0
45
. B.
0
30
. C.
0
60
. D.
0
90
.
Lời giải
Tác giả: Nguyễn Văn Thắng; Fb: Nguyễn Thắng
Chọn A
Vì SA vuông góc với đáy nên góc
( , ( ))SC ABCD SCA=
A
A'
C
C'
B
B'
S
A
D
C
B
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 8 Mã đề 132
Trong hình vuông ABCD có:
2AC a=
, theo giả thiết,
2SA a=
⇒ tam giác SAC vuông cân
tại A ⇒
0
45SCA =
⇒ Chọn A
Hungvn1985@gmail.com
Câu 7. Cho hình lập phương
.ABCD AB C D
cạnh
.a
Tính khoảng cách giữa hai đường thẳng
AB
và
CD
.
A.
2
.
2
a
B.
.a
C.
2.a
D.
2.a
Lời giải
Tác giả : Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng
Chọn B
Do
( )
'// ' ' '// ' 'AB C D AB DCC D
. Suy ra
( ) ( )
( )
( )
( )
'; ' '; ' ' ; ' 'd AB CD d AB DCC D d A DCC D AD a= = = =
Câu 8. Giá trị cực đại
CD
y
của hàm số
3
12 20y x x= − +
là
A.
4.
CD
y =
B.
36.
CD
y =
C.
4.
CD
y =−
D.
2.
CD
y =−
Lời giải
Tác giả : Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng
Chọn B
TXĐ:
D =
Ta có
22
2
3 12; 0 3 12 0
2
x
y x y x
x
=

= − = − =
=−
Bảng biến thiên
Suy ra
36.
CD
y =
diephd02@gmail.com
Câu 9. Tập xác định của hàm số
1
sinx 1
y =
+
là
A.
\ 2 ,
2
kk

+


. B.
\ 2 ,
2
kk

− +


.
C.
\,
2
kk

− +


. D. .
Lời giải
Tác giả : Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp
Chọn B
B'
C'
A'
D
A
B
C
D'
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 9 Mã đề 132
Hàm số
1
sinx 1
y =
+
xác định khi:
sinx 1 0 sinx 1 0 2
2
xk
−
+ + +
TXĐ:
\ 2 ,
2
D k k

= − +


.
Câu 10. Nghiệm âm lớn nhất của phương trình
2
3
3cot x 3
sin x
=+
là
A.
6
−
. B.
5
6
−
. C.
2
−
. D.
2
3
−
.
Lời giải
Tác giả : Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp
Chọn C
Điều kiện xác định của phương trình:
sinx 0
.
2
2
3
3cot x 3 3(1 cot ) 3cot x 3
sin
x
x
= + + = +
2
cotx = 0
3cot 3cot x 0
cotx = 3
x
− =
2
6
xk
xk
=+
=+
Họ nghiệm
2
xk
=+
có nghiệm âm lớn nhất
2
x
−
=
Họ nghiệm
6
xk
=+
có nghiệm âm lớn nhất
5
6
x
−
=
Vậy nghiệm âm lớn nhất của phương trình đã cho là
2
x
−
=
.
buinguyenphuong1991@gmail.com
Câu 11. Cho cấp số cộng
( )
n
u
có các số hạng đầu lần lượt là
5
;
9
;
13
;
17
; … Tìm công thức số hạng
tổng quát
n
u
của cấp số cộng ?
A.
51
n
un=−
. B.
51
n
un=+
. C.
41
n
un=−
. D.
41
n
un=+
.
Lời giải
Tác giả: Bùi Nguyên Phương, FB: Bùi Nguyên Phương
Chọn D
Ta có:
1
5u =
nên thay
1n =
vào 4 đáp án thấy chỉ có đáp án D đúng.
Câu 12. Tìm giá trị nhỏ nhất của hàm số
2
1yx=−
trên đoạn
3;2−
?
A.
3;2
min 3
−
=
. B.
3;2
min 3
−
=−
. C.
3;2
min 1
−
=−
. D.
3;2
min 8
−
=
.
Lời giải
Tác giả : Bùi Nguyên Phương, FB: Bùi Nguyên Phương
Chọn C
Tập xác định:
D =
. Hàm số
2
1yx=−
liên tục và có đạo hàm trên đoạn
3;2−
.
Đạo hàm:
2yx
=
. Xét
0 2 0 0 3;2y x x
= = = −
.
Ta có:
( )
01y =−
,
( )
38y −=
và
( )
23y =
. Vậy
3;2
min 1
−
=−
.
Tranthom275@gmail.com
Câu 13. Cho hàm số
2
1yx=−
. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
( )
0;+
. B. Hàm số nghịch biến trên khoảng
( )
;0−
.
C. Hàm số đồng biến trên khoảng
( )
1; +
. D. Hàm số đồng biến trên khoảng
( )
;− +
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 10 Mã đề 132
Lời giải
Tác giả : Trần Thị Thơm, FB: Tranthom275
Chọn C
Tập xác định:
( ; 1] [1; )D = − − +
2
1
x
y
x
=
−
,
( ; 1) (1; )x − − +
;
00yx
= =
(loại)
Bảng xét dấu
y
x
−
1−
1
+
y
−
+
Vậy hàm số đồng biến trên khoảng
( )
1; +
.
Câu 14. Khai triển
( )
100
3x −
ta được đa thức
( )
100
2 100
0 1 2 100
3 ...x a a x a x a x− = + + + +
, với
0
,a
1 2 100
, ,...,a a a
là các hệ số thực. Tính
0 1 2 99 100
...a a a a a− + − − +
?
A.
100
2−
. B.
100
4
. C.
100
4−
. D.
100
2
.
Lời giải
Chọn B
Ta có:
( )
100
2 100
0 1 2 100
3 ...x a a x a x a x− = + + + +
(1)
Thay
1x =−
vào hai vế của (1) ta được:
( ) ( ) ( ) ( ) ( ) ( )
100 2 3 99 100
0 1 2 3 99 100
1 3 1 1 1 ... 1 1a a a a a a− − = + − + − + − + + − + −
( )
100
0 1 2 99 100
4 ...a a a a a − = − + − − +
Vậy
100
0 1 2 99 100
... 4a a a a a− + − − + =
.
Cohangxom1991@gmail.com
Câu 15. Nghiệm của phương trình lượng giác
2
cos cos 0xx−=
thỏa mãn điều kiện
0 x

là
A.
0x =
. B.
3
4
x
=
. C.
2
x
=
. D.
2
x
=−
.
Lời giải
Tác giả : Phạm Văn Huy, FB: Đời Dòng
Chọn D
2
cos cos 0xx−=
cos 0
cos 1
x
x
=
=
;
2
2
xk
k
xk
=+

=
Với họ nghiệm
;
2
x k k
= +
Ta có
0
0
2
k
x
k

+
22
k
k

−
11
0
22
k
k
k
−
=
do đó chỉ có nghiệm
2
x
=
thỏa mãn
Với họ nghiệm
2;x k k
=
1
02
0
0
2
k
k
x
k
k




vô nghiệm
Vậy phương trình có một nghiệm
( )
0;
2
Cohangxom1991@gmail.com
Câu 16. Tất cả các nghiệm của phương trình
tan cotxx=
là
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 11 Mã đề 132
A.
,
44
x k k

= +
. B.
2,
4
x k k
= +
.
C.
,
4
x k k
= +
. D.
,
42
x k k

= +
.
Lời giải
Tác giả : Phạm Văn Huy, FB: Đời Dòng
Chọn D
Điều kiện
sin 0
sin2 0 ,
cos 0
2
x
x x m m
x
tan cot tan tan
2
x x x x

= = −


( )
2 4 2
x x k x k k
= − + = +
thỏa mãn điều
kiện.
ptpthuyedu@gmail.com
Câu 17. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
2SA a=
và vuông góc
với
()ABCD
. Tính theo
a
thể tích
V
của khối chóp
.S ABC
A.
3
2
6
Va=
. B.
3
22
3
Va=
. C.
3
2Va=
. D.
3
2
3
Va=
.
Lời giải
Tác giả : Phạm Thị Phương Thúy, FB: thuypham
Chọn A
Ta có
ABCD
là hình vuông cạnh
a
2
11
22
ABC ABCD
S S a = =
Thể tích khối chóp
.S ABC
là:
2
.
3
1
1 1 2
. . 2. .
3 2 6
3
S ABC ABC
V SA S a a a= = =
. Chọn A
Câu 18. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành,
AB a=
,
3SA a=
và vuông góc với
()ABCD
. Tính góc giữa hai đường thẳng
SB
và
CD
A.
0
60
. B.
0
30
. C.
0
45
. D.
0
90
.
Lời giải
Tác giả : Phạm Thị Phương Thúy, FB: thuypham
Chọn A
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 12 Mã đề 132
Ta có
ABCD
là hình bình hành
//AB CD
.
Do đó
( ) ( )
,,SB CD SB AB SBA==
Vì
()SA ABCD SA AB SAB⊥ ⊥
vuông tại A.
Xét tam giác vuông
SAB
ta có:
0
3
tan 3 60
SA a
SBA SBA
AB a
= = = =
Vậy
( )
0
, 60SB CD =
luulien1507@gmail.com
Câu 19. Cho hàm số
31
3
x
y
x
−
=
−
có đồ thị
( )
C
. Mệnh đề nào sau đây sai?
A. Đồ thị
( )
C
có tiệm cận đứng và tiệm cận ngang.
B. Đồ thị
( )
C
không có tiệm cận đứng.
C. Đồ thị
( )
C
có tiệm cận ngang.
D. Đồ thị
( )
C
có tiệm cận.
Lời giải
Tácgiả :Lưu Thị Liên, FB: Lotus
Chọn B
Ta có:
31
lim lim 3
3
xx
x
y
x
→ →
−
==
−
và
33
31
lim lim
3
xx
x
y
x
−−
→→
−
= = −
−
Nên đồ thị
( )
C
có tiệm cận đứng
3x =
và tiệm cận ngang
3y =
.
Câu 20. Trong năm học
2018 2019−
trường THPT chuyên đại học Vinh có
13
lớp học sinh khối
10,
12
lớp học sinh khối
11,
.
12
lớp học sinh khối
12
. Nhân ngày nhà giáo Việt Nam
20
tháng
11
nhà
trường chọn ngẫu nhiên
2
lớp trong trường để tham gia hội văn nghệ của trường Đại học Vinh.
Xác suất để chọn được hai lớp không cùng khối là
A.
76
111
. B.
87
111
. C.
78
111
. D.
67
111
.
Lờigiải
Tácgiả :Lưu Thị Liên, FB: Lotus
Chọn A
Số phần tử của không gian mẫu là số cách chọn
2
lớp trong số
37
lớp của trường để tham gia
hội văn nghệ:
2
37
()nC=
Số cách chọn
2
lớp cùng khối trong trường để tham gia hội văn nghệ của trường Đại học Vinh
là
222
12 12 13
CCC++
Số cách chọn
2
lớp không cùng khối trong trường để tham gia hội văn nghệ của trường Đại học
Vinh là
( )
2 2 2 2
37 12 12 13
C C C C− + +
Xác suất để chọn được hai lớp không cùng khối là:
( )
2 2 2 2
37 12 12 13
2
37
76
111
C C C C
C
− + +
=
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 13 Mã đề 132
trichinhsp@gmail.com
Câu 21. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
A
,
2BC a=
,
SA a=
và
SA
vuông góc
( )
ABC
. Tính góc giữa hai mặt phẳng
( )
SBC
và
( )
ABC
A.
0
45
. B.
0
30
. C.
0
60
. D.
0
90
.
Lời giải
Tác giả : Nguyễn Trí Chính, FB: Nguyễn Trí Chính
Chọn A
Gọi
I
là trung điểm
BC
,
ABC
vuông cân tại
A
nên
AI BC⊥
.
Có
( )
SA ABC⊥
SA BC⊥
.
Suy ra
( )
BC SAI⊥
. Suy ra
( ) ( )
( )
;SBC ABC SIA=
.
SIA
vuông tại A có
,SA a AI a==
. Suy ra
SIA
vuông cân tại
A
.
Suy ra
0
45SIA =
. Chọn A
Câu 22. Gọi
1 2 3
,,x x x
là các cực trị của hàm số
42
4 2019y x x= − + +
. Tính tổng
1 2 3
x x x++
bằng?
A.
0
. B.
22
. C.
1−
. D.
2
.
Lời giải
Tác giả : Nguyễn Trí Chính, FB: Nguyễn Trí Chính
Chọn A
+Cách trắc nghiệm: Có
. 4 0ab= −
. Nên hàm số có 3 cực trị
1
0x =
,
23
,xx
là 2 số đối nhau.
Suy ra
1 2 3
0x x x+ + =
+Cách tự luận
42
4 2019y x x= − + +
, TXĐ:
D =
.
/3
48y x x= − +
.
/3
0 4 8 0y x x= − + =
0
2
2
x
x
x
=
= −
=
Suy ra
1 2 3
0x x x+ + =
. Chọn A
vungoctan131@gmail.com
Câu 23. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
32
3 9 1y x x x= − − +
trên
đoạn
0;4
. Tính tổng
2mM+
.
A.
2 17mM+=
. B.
2 37mM+ = −
. C.
2 51mM+=
. D.
2 24mM+ = −
.
Lời giải
Tác giả : Vũ Ngọc Tân, FB: Vũ Ngọc Tân
Chọn D
Hàm số
32
3 9 1y x x x= − − +
xác định và liên tục trên , nên trên đoạn
0;4
hàm số luôn xác
định và liên tục.
I
B
C
S
A
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 14 Mã đề 132
Ta có:
( )
( )
2
1 0;4
3 6 9 0
3 0;4
x
y x x
x
= −
= − − =
=
.
Khi đó :
( ) ( ) ( )
0 1; 3 26; 4 19f f f= = − = −
.
So sánh các giá trị trên ta được :
0;4 0;4
1; 26M Maxy m Miny= = = = −
.
Suy ra:
2 26 2 24mM+ = − + = −
.
Vậy
2 24mM+ = −
.
Câu 24. Cho cấp số nhân
( )
n
u
thỏa mãn
1 3 5
17
65
325
u u u
uu
− + =
+=
. Tính
3
.u
A.
3
15u =
. B.
3
25u =
. C.
3
10u =
. D.
3
20u =
.
Lời giải
Tác giả : Vũ Ngọc Tân, FB: Vũ Ngọc Tân
Chọn D
Ta có:
( )
( )
24
24
1
1 3 5
1 1 1
6
6
17
11
1
1 65 (1)
65
. . 65
325
. 325
1 325 (2)
u q q
u u u
u u q u q
uu
u u q
uq
− + =
− + =
− + =


+=
+=
+=
Chia từng vế của
( )
1
cho
( )
2
ta được phương trình :
( )
24
6 4 2
6
11
5 5 4 0 *
15
qq
q q q
q
−+
= − + − =
+
Đặt
2
,0t q t=
.
Phương trình
( )
*
trở thành :
( )
( )
3 2 2
2
4
5 5 4 0 4 1 0
1 0( )
t
t t t t t t
t t vn
=
− + − = − − + =
− + =
Với
2
4 4 2t q q= = =
.
Với
2q =
thay vào
( )
2
ta được
1
5u =
.
Vậy
2
31
. 5.4 20.u u q= = =
anhtuanqh1@gmail.com
Câu 25. Biết số tự nhiên
n
thỏa mãn
2
1
11
2 ... 45
n
nn
n
n
nn
CC
Cn
CC
−
+ + + =
. Tính
4
n
n
C
+
?
A.
715
. B.
1820
. C.
1365
. D.
1001
.
Lời giải
Tác giả : Nguyễn Anh Tuấn, FB: Nguyễn Ngọc Minh Châu
Chọn A
Xét số hạng tổng quát:
( )
( ) ( )
1
.!
!!
!
1 ! 1 !
k
n
k
n
kn
k n k
C
k
n
C
k n k
−
−
=
− + −
1nk= + −
. với :
, ;1 .k n N k n
Do đó:
2
1
11
2 ... 45
n
nn
n
n
nn
CC
Cn
CC
−
+ + + =
( )
1 ... 1 45nn + − + + =
( )
1
45
2
nn+
=
2
90 0nn + − =
9
10( )
n
nl
=
=−
9n=
.Vậy
9
4 13
715
n
n
CC
+
==
.
Câu 26. Tìm tất cả các giá trị của
m
để hàm số
1x
y
xm
−
=
+
đồng biến trên khoảng
( )
0;+
?
A.
( )
1;− +
. B.
)
0;+
. C.
( )
0;+
. D.
)
1;− +
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 15 Mã đề 132
Lời giải
Tác giả : Nguyễn Anh Tuấn, FB: Nguyễn Ngọc Minh Châu
Chọn B
Tập xác định:
\Dm=−
.
( )
2
1
'
m
y
xm
+
=
+
.
Hàm số đồng biến trên khoảng
( )
0;+
0
10
m
m
−
+
0m
.
Congnhangiang2009@gmail.com
Câu 27. Tìm tất cả các giá trị thực của tham số
m
sao cho điểm cực tiểu của đồ thị hàm số
32
1y x x mx= + + −
nằm bên phải trục tung?
A.
0m
. B.
1
0
3
m
. C.
1
3
m
. D.Không tồn tại.
Lời giải
Tác giả : Hoàng Thị Thanh Nhàn, FB: Hoàng Nhàn
Chọn A
32
1y x x mx= + + −
2
32y x x m
= + +
.
Đồ thị hàm số có điểm cực tiểu khi và chỉ khi phương trình
0y
=
có hai nghiệm phân biệt
1 3 0m
= −
1
3
m
(1).
Khi đó, giả sử
1
x
,
2
x
là hai nghiệm của phương trình
0y
=
.
12
12
2
3
.
3
xx
m
xx
+ = −
=
Bảng biến thiên
Do
12
2
0
3
xx+ = −
nên hoặc nên điểm cực tiểu của đồ thị hàm số
32
1y x x mx= + + −
nằm
bên phải trục tung
12
.0xx
0
3
m

0m
(2).
( ) ( )
1 , 2 0m
.
Câu 28. Sinh nhật của An vào ngày 1 tháng 5. Bạn An muốn mua một chiếc máy ảnh giá khoảng
600.000
đồng để làm quà sinh nhật cho chính mình. Bạn ấy quyết định bỏ ống tiết kiệm
10.000
đồng vào
ngày 1 tháng 1 của năm đó, sau đó cứ tiếp tục những ngày sau, mỗi ngày bạn bỏ ống tiết kiệm
5.000
đồng. Biết trong năm đó, tháng 1 có 31 ngày, tháng 2 có 28 ngày, tháng 3 có 31 ngày và
tháng 4 có 30 ngày. Gọi
a
(đồng) là số tiền An có được đến sinh nhật của mình (ngày sinh nhật
An không bỏ tiền vào ống). Khi đó ta có:
A.
)
610000;615000a
. B.
)
605000;610000a
.
C.
)
600000;605000a
. D.
)
595000;600000a
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 16 Mã đề 132
Lời giải
Tác giả : Hoàng Thị Thanh Nhàn, FB: Hoàng Nhàn
Chọn B
Theo giả thiết An bỏ ống tiết kiệm từ ngày 1 tháng 1 đến ngày 30 tháng 4 nên tổng số ngày bỏ
tiết kiệm là
120
ngày.
Ngày thứ nhất An bỏ ống:
10000
đồng.
119 ngày sau An bỏ ống số tiền là:
119 5000 (120 1) 5000 600000 5000 = − = −
đồng.
Vậy tổng số tiền tiết kiệm là:
600000 5000 10000 605000a = − + =
đồng.
tranquocan1980@gmail.com
Câu 29. Số nghiệm của phương trình
sin5 3cos5 2sin7x x x+=
trên khoảng
0;
2



là ?
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Tác giả :Trần Quốc An, FB: TranQuocAn
Chọn A
Ta có :
sin5 3cos5 2sin7 sin 5 sin7
3
x x x x x

+ = + =


7 5 2
36
,
7 5 2
3 18 6
x x k x k
k
x x k x k




= + + = +



= − − + = +


TH1 :
11
00
6 2 6 3 6
k k k x
+ − = =
TH2 :
1 1 1 2 7
0 0 3 3 0,1,2 , , .
18 6 2 3 3 3 18 9 18
k k k k x
+ + − − = =
Vậy
27
,,,
18 9 18 6
x



.Chọn A
Câu 30. Cho hàm số
()fx
có đạo hàm trên và
/
( ) 0,f x x
.Biết
(1) 2.f =
Hỏi khẳng định nào
sau đây có thể xảy ra ?
A.
(2) (3) 4.ff+=
B.
( 1) 2.f −=
C.
(2) 1.f =
D.
(2018) (2019).ff
Lời giải
Tác giả :Trần Quốc An, FB: TranQuocAn
Chọn B
Xét đáp án A:
Ta có :
2 3 2 3
1 1 1 1
( ) ( ) 0 0 0 (2) (1) (3) (1) 0 4 4 0f x dx f x dx dx dx f f f f

+ + = − + − −
Vô
lý . Nên phương án A không thể xảy ra.
Xét đáp án C:
Ta có :
22
11
( ) 0 0 (2) (1) 0 1 2 0f x dx dx f f
= − −

Vô lý . Nên phương án C không thể
xảy ra.
Xét đáp án D :
Ta có :
2019 2019
2018 2018
( ) 0 0 (2019) (2018) 0 (2019) (2018)f x dx dx f f f f
= −

. Nên phương
án D không thể xảy ra.
Bằng phương pháp loại suy ,ta có đáp án B.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 17 Mã đề 132
Tuy nhiên , ta có thể chỉ ra một hàm
2
( ) 1f x x=+
thỏa mãn đáp án B vì
( ) 0,
( 1) 2
(1) 2
f x x
f
f
− =
=
Duanquy@gmail.com.
Câu 31. Cho tập hợp
0,1,2,3,4,5,6A =
. Từ tập
A
lập được bao nhiêu số tự nhiên chẵn có
4
chữ số
khác nhau và nhỏ hơn
4012
A.
180
. B.
240
. C.
200
. D.
220
.
Lời giải
Tác giả: Nguyễn Đức Duẩn, FB: Duan Nguyen Duc
Chọn D
Gọi số cần lập là
abcd
. Vì
4012 3abcd a
.
+) TH1: Nếu
1a =
khi đó số các số chẵn lập đc là
2
5
1.4.A 80=
.
+) TH2: Nếu
3a =
khi đó số các số chẵn lập đc là
2
5
1.4.A 80=
.
+) TH1: Nếu
2a =
khi đó số các số chẵn lập đc là
2
5
1.3.A 60=
.
Vậy số các số lập được thỏa mãn đề bài là
80 80 60 220+ + =
.
Câu 32. Một vật chuyển động theo quy luật
32
1
9
2
s t t
−
=+
, với
t
(giây) là khoảng thời gian tính từ lúc
vật bắt đầu chuyển động và
s
(mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi
trong khoảng thời gian
10
giây, kể từ lúc bắt đầu chuyển động vận tốc lớn nhất của vật đạt được
bằng bao nhiêu?
A.
216 ( / )ms
. B.
400 ( / )ms
. C.
54 ( / )ms
. D.
30 ( / )ms
.
Lời giải
Tác giả: Nguyễn Đức Duẩn, FB: Duan Nguyen Duc
Chọn C
Vì
3 2 2
13
9 18
22
s t t v t t
−−
= + = +
.
Xét hàm ,
'( ) 0 6f t t= =
.
BBT của hàm số
2
3
( ) 18
2
f t t t
−
=+
.
Dựa vào BBT ta thấy
(0;10)
max ( ) 54ft=
.
Vậy vận tốc lớn nhất vật đạt được là
max
54 ( / )v m s=
.
luuhuephuongtailieu@gmail.com
Câu 33. Tất cả các giá trị của tham số
m
để hàm số
( )
4
1=−y m x
đạt cực đại tại
0=x
là
A.
1.m
B.
1.m
C. không tồn tại m. D.
1.=m
Lời giải
Tác giả : Lưu Huệ Phương, FB: Lưu Huệ Phương
Chọn A
2
3
( ) 18 '(t) 3t 18
2
f t t t f
−
= + = − +
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 18 Mã đề 132
Trường hợp 1: Nếu
10= =my
→ Hàm số không có cực trị.
Vậy
1=m
không thỏa mãn.
Trường hợp 2: Nếu
1m
Ta có:
( )
3
4 1 , 0 0.

= − = =y m x y x
Để hàm số đạt cực đại tại
0=x
thì
y
phải đổi dấu từ
( )
+
sang
( )
−
qua
0.=x
Khi đó
( )
4 1 0 1.− mm
Vậy
1m
thỏa mãn yêu cầu bài toán.
luuhuephuongtailieu@gmail.com
Câu 34. Tung hai con súc sắc
3
lần độc lập với nhau. Tính xác suất để có đúng một lần tổng số chấm
xuất hiện trên hai con súc sắc bằng
6.
Kết quả làm tròn đến
3
ba chữ số ở phần thập phân)
A.
0,120.
B.
0,319.
C.
0,718.
D.
0,309.
Lời giải
Tác giả : Lưu Huệ Phương, FB: Lưu Huệ Phương
Chọn D
Khi gieo hai con súc sắc trong một lần gieo thì có tất cả
36
khả năng có thể xảy ra.
Gọi
A
là biến cố: “Có đúng một lần gieo tổng số chấm xuất hiện trên hai con súc sắc bằng
6
”
Ta có:
6 1 5 5 1 2 4 4 2 3 3.= + = + = + = + = +
Khi gieo hai con súc sắc trong cùng một lần gieo thì xác suất để tổng số chấm xuất hiện trên hai
con súc sắc bằng
6
là
5
36
và xác suất để tổng số chấm xuất hiện trên hai con súc sắc không bằng
6
là
31
.
36
Vậy xác suất cần tìm là:
( )
2
1
3
5 31 4805
. . 0,309.
36 36 15552

= =


P A C
nguyenthithutrang215@gmail.com
Câu 35. Hệ số của
5
x
trong khai triển
( )
9
2
1 2 3xx−−
là
A.
792
. B.
684−
. C.
3528
. D.
0
.
Lời giải
Tác giả : Nguyễn Thị Thu Trang, FB: Trang Nguyễn
Chọn C
Ta có:
( ) ( )
( )
( )
( )
( ) ( )
9
9
22
9 9 9
9
9
22
9 9 9
0 0 0
99
9
9
99
00
1 2 3 1 2 3
2 3 2 3
23
k
km
km
k k m
k
k k m
k
k m m
k m k m
k
km
x x x x
C x x C C x x
C C x
−
−
−−
−
= = =
−
−−
−+
−
==

− − = + − −

= − − = − −
= − −

Số hạng chứa
5
x
khi
09
0, 4
9
1, 5
95
2, 6
,
mk
mk
mk
mk
km
mk
mk
==
−
= =
− + =
==
Vậy hệ số của số hạng chứa
5
x
là:
( ) ( ) ( ) ( ) ( ) ( )
5 0 3 1 1 2
4 0 5 1 6 2
9 5 9 4 9 3
2 3 2 3 2 3 3528C C C C C C− − + − − + − − =
Câu 36. Cho một khối đa diện lồi có
10
đỉnh,
7
mặt. Hỏi khối đa diện này có mấy cạnh?
A.
20
. B.
18
. C.
15
. D.
12
.
Lời giải
Tác giả : Nguyễn Thị Thu Trang, FB: Trang Nguyễn
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 19 Mã đề 132
Chọn C
Ta có
2 15d m c c+ − = =
Vậy khối đa diện có
15
cạnh
kimoanh0102@gmail.com
Câu 37. Cho hình chóp
.S ABC
có
2 , 2 , 2 2SA a SB a SC a= = =
và
= = = 60ASB BSC CSA
. Tính
thể tích của khối chóp đã cho.
A.
3
4
3
a
. B.
3
23
3
a
. C.
3
2a
. D.
3
22
3
a
.
Lời giải
Tác giả: Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh
Chọn D
Cách 1
Gọi
H
là hình chiếu vuông góc của
A
lên mp
( )
SBC
. Gọi
,IK
lần lượt là hình chiếu vuông
góc của
H
lên
SB
và
SC
.
Ta có
SB HI
SB SI
SB SH
⊥
⊥
⊥
. Chứng minh tương tự ta được
SC SK⊥
.
= SAI SAK
(cạnh huyền – góc nhọn)
SI SK=
.
Khi đó
= SHI SHK
(cạnh huyền – cạnh góc vuông)
HI HK=
. Do đó
SH
là đường phân
giác trong của
BSC
, nên
=30HSI
.
Trong tam giác vuông
SAI
,
= = =
2
cos60 .cos60
2
SI a
SI SA
SA
.
Trong tam giác vuông
HIS
,
= = = =
2 3 6
cos30 :
cos30 2 2 3
SI SI a a
SH
SH
.
Khi đó
2
2 2 2
2 2 3
2
33
aa
AH SA SH a= − = − =
, và
= =
2
1
.2 .2 2 .sin60 6
2
SBC
S a a a
.
Vậy
3
2
.
1 1 2 3 2 2
. . 6
3 3 3 3
S ABC SBC
aa
V AH S a= = =
.
Cách 2: Sử dụng công thức tính nhanh
Nếu khối chóp
.S ABC
có
,,
, S , S
SA a SB b SC c
ASB B C C A
= = =
= = =
thì
2 2 2
.
1 cos cos cos 2cos cos cos
6
= − − − +
S ABC
abc
V
Áp dụng: Với
2 , 2 , 2 2SA a SB a SC a= = =
và
= = = 60ASB BSC CSA
, ta có
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 20 Mã đề 132
3
23
.
2 .2 .2 2 2 2
1 3.cos 60 2.cos 60
63
S ABC
a a a a
V = − + =
.
Cách 3
Trên các cạnh
SB
,
SC
lần lượt lấy các điểm

,BC
sao cho

= = = 2SB SC SA a
.
Khi đó chóp

.S AB C
là khối chóp tam giác đều. Đồng thời
= = = 60ASB BSC CSA
nên
= = = = 2AB B C AC SA a
.
Gọi
H
là hình chiếu của
S
lên mặt phẳng
( )

AB C
. Khi đó dễ dàng chứng minh được các tam
giác

,,SHA SHB SHC
bằng nhau. Suy ra

,,HA HB HC
bằng nhau. Hay
H
là tâm đường tròn
ngoại tiếp tam giác

AB C
. Vì tam giác

AB C
đều nên
H
cũng là trọng tâm tam giác

AB C
.
Ta có
= = = = − =
22
2 2 6 6 2 3
;
3 3 2 3 3
a a a
AH AI SH SA AH
( )

==
2
3
.
23
1 2 3
.
3 3 4 3
S AB C
a
aa
V
Ta có


= = =
.
.
2 2 2
..
24
22
S AB C
S ABC
V
SB SC a a
V SB SC a
a

= =
3
..
22
22
3
S ABC S AB C
a
VV
.
Câu 38. Cho hình lập phương
.ABCD A B C D
cạnh
a
. Gọi
,MN
lần lượt là trung điểm của
BC
và
DD
. Tính theo
a
khoảng cách giữa hai đường thẳng
MN
và
BD
.
A.
3a
. B.
3
2
a
. C.
3
3
a
. D.
3
6
a
.
Lời giải
Tác giả: Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh
Chọn D
Cách 1
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 21 Mã đề 132
Gọi P là trung điểm
BB
Ta có
( )
// //BD PN BD MPN
. Do đó
( ) ( )
( )
( )
( )
==; ; ;d MN BD d BD MPN d B MPN
.
3
..
1 1 1
. . . . . .
3 2 6 2 2 24
B PMN N BMP
a a a
V V CD BP BM a= = = =
.
2
2 2 2 2 2 2
26
; 2;
22
aa
MP BP BM PN BD a MN MD DN CM CD DN= + = = = = + = + + =
Nhận thấy
2 2 2
MP MN PN+=
nên tam giác
MPN
vuông tại
M
.
Do đó
2
1 1 2 6 3
..
2 2 2 2 4
MPN
a a a
S MP MN= = =
.
Ta có
( )
( )
( )
( )
= =
.
.
3
1
, . ,
3
B PMN
B PMN MPN
MPN
V
V d B MPN S d B MPN
S
( )
( )
=
3
,
6
a
d B MPN
.
Vậy
( )
=
3
,
6
a
d MN BD
.
Cách 2:
Gọi
P
là trung điểm
BB
. Ta có
( )
// //BD PN BD MPN
.
Đồng thời,
( ) ( )
// , // //MP CB PN B D MPN CB D
.
Do đó
( ) ( )
( )
( )
( )
( )
( )
= = =, , , ,d MN BD d BD MPN d B MPN d C MPN
(vì
PC
cắt
BC
tại trọng tâm của tam giác

BB C
).
Nhận thấy tứ diện
.C CB D
là tứ diện vuông tại
C
nên
( )
( )
= + + =
2 2 2 2
2
1 1 1 1 3
''
,
C C C B C D a
d C CB D
( )
( )
=
3
,
3
a
d C CB D
.
Vậy
( ) ( )
( )
==
13
,,
26
a
d MN BD d C CB D
.
Cách 3: Tọa độ hóa
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 22 Mã đề 132
Chọn hệ trục tọa độ
Oxyz
như hình vẽ. Khi đó,
( ) ( )
;0; , 0; ; , ; ; , 0; ;
22
aa
B a a D a a M a a N a
.
( )
= − = − − =
; ;0 , ; ; , 0; ;0
2 2 2
a a a
BD a a MN a BM
.

= − −



; ; ;
2 2 2
a a a
BD MN
;

=−

2
;.
4
a
BD MN BM
.
( )
2
;.
33
;:
4 2 6
;
BD MN BM
a a a
d BD MN
BD MN


= = =


.
Câu 39. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SAD
là tam giác đều và nằm
trong mặt phẳng vuông góc với
()ABCD
. Gọi
,,M N P
lần lượt là trung điểm các cạnh
,,SB BC CD
. Tính thể tích khối tứ diện
CMNP
.
A.
3
3
48
a
. B.
3
3
96
a
. C.
3
3
54
a
. D.
3
3
72
a
.
Lời giải
Tác giả : Nguyễn Hoàng Hưng, FB: Nguyễn Hưng
Chọn B
Gọi
H
là trung điểm của cạnh
AD
. Do tam giác
SAD
đều nên
SH AD⊥
.
( ) ( )
( ) ( )
( )
( )
,
SAD ABCD
SAD ABCD AD SH ABCD
SH SAD SH AD
⊥
= ⊥
⊥
Gọi
K
là trung điểm của
HB
//MK SH
.
Do đó:
( ) ( )
MK ABCD MK CNP⊥ ⊥
Vậy
MK
là chiều cao của khối tứ diện
CMNP
.
1 1 3 3
.
2 2 2 4
aa
MK SH= = =
2
11
. . . .
2 2 2 2 8
CNP
a a a
S CN CP= = =
Thể tích của khối tứ diện
CMNP
là
23
1 1 3 3
. . .
3 3 8 4 96
CMNP CNP
a a a
V S MK= = =
.
Câu 40. Số tiệm cận ngang của đồ thị hàm số
2018
2019
x
y
x
−
=
+
là
A.
1
. B.
3
. C.
2
. D.
0
.
P
K
N
M
H
S
A
B
C
D
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 23 Mã đề 132
Lời giải
Tác giả : Nguyễn Hoàng Hưng, FB: Nguyễn Hưng
Chọn C
Ta có:
2018
1
2018
2018
lim lim lim lim 1
2019
2019 2019
1
x x x x
x
x
x
y
xx
x
→+ →+ →+ →+
−
−
−
= = = =
++
+
2018
1
2018
2018
lim lim lim lim 1
2019
2019 2019
1
x x x x
x
x
x
y
xx
x
→− →− →− →−
−−
−
−−
= = = = −
++
+
Do đó đồ thị hàm số có hai tiệm ngang là các đường thẳng
1, 1yy= − =
.
anglenghia@gmail.com
Câu 41. Cho khối hộp
. ’ ’ ’ ’ABCD A B C D
có
M
là trung điểm
’’AB
. Mặt phẳng
( )
ACM
chia khối hộp đã
cho thành hai phần. Tỉ số thể tích của hai phần đó bằng?
A.
7
17
. B.
5
17
. C.
7
24
. D.
7
12
.
Lời giải
Tác giả : Trần Đắc Nghĩa, FB: Đ Nghĩa Trần
Chọn A
Gọi
N
là trung điểm
’’BC
và
E
là điểm đối xứng với
B
qua
’B
Khi đó khối hộp
. ’ ’ ’ ’ABCD A B C D
được mặt phẳng
( )
ACM
chia thành
2
khối đa diện
.’BAC B MN
và
’ ’ ’ACDMNC D A
Ta có
. . ' ' ' '
1
3
E BAC ABCD A B C D
VV=
và
. ' . . ’ .
17
88
E B MN E BAC BAC B MN E BAC
V V V V= =
Từ đó ta có
. ’ . ' ' ' ' . ’’' ' ' ' . ' ' ' '’
7 1 7 17
.
8 3 24 24
BAC B MN ABCD A B C D ABCD A B C D ACDM ANC D A BCD A B C D
V V V V V= = =
Nên:
.'
. ' ' ' '
7
17
BAC B MN
ABCD A B C D
V
V
=
anglenghia@gmail.com
Câu 42. Đồ thị của hàm số
( )
32
f x x ax bx c= + + +
tiếp xúc với trục hoành tại gốc tọa độ và cắt đường
thẳng
1x =
tại điểm có tung độ bằng
3
khi
A.
0, 2a b c= = =
. B.
0, 2a c b= = =
. C.
2, 0a b c= = =
. D.
2, 1, 0a b c= = =
.
Lời giải
Tác giả : Trần Đắc Nghĩa, FB: Đ Nghĩa Trần
Chọn C
Ta có :
( )
2
' 3 2f x x ax b=++
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 24 Mã đề 132
Đồ thị hàm số tiếp xúc với trục hoành tại gốc tọa độ
( )
0;0O
nên
( )
( )
00
0
0
' 0 0
f
c
b
f
=
=

=
=
Đồ thị hàm số đi qua điểm
( )
1;3A
nên
3 1 2aa= + =
nguyentuyetle77@gmail.com
Câu 43. Chuyên Vinh. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
,
0
60ABC =
, cạnh bên
2SA a=
và
SA
vuông góc với
ABCD
.Tính góc giữa
SB
và
()SAC
.
A.
0
90
. B.
0
30
. C.
0
45
. D.
0
60
.
Lời giải
Tác giả : NguyễnTuyết Lê, FB: Nguyên Tuyet Le
Chọn B
Gọi
O AC BD=
. Vì
ABCD
là hình thoi nên
(1)BO AC⊥
. Lại do:
( )
(2)SA ABCD SA AC⊥ ⊥
. Từ
(1)
và
(2)
ta có :
( ) ( ;( )) ( ; )BO SAC SB SAC SB SO BSO⊥ = =
.
Ta có:
22
3SB SA AB a= + =
. Vì
ABCD
là hình thoi có
0
60ABC =
nên tam giác
ABC
đều
cạnh
a
3
2
a
BO=
.Trong tam giác vuông
SBO
ta có:
3
1
2
sin
2
3
a
BO
BSO
SB
a
= = =
0
30BSO=
.
nguyentuyetle77@gmail.com
Câu 44. Gọi
m
là giá trị để đồ thị
(C )
m
của hàm số
22
2 2 1
1
x mx m
y
x
+ + −
=
−
cắt trục hoành tại hai điểm
phân biệt và các tiếp tuyến với
(C )
m
tại tại hai điểm này vuông góc với nhau. Khi đó ta có:
A.
( )
1;2m
. B.
( )
2; 1m − −
. C.
( )
0;1m
. D.
( )
1;0m−
.
Lời giải
Tác giả : NguyễnTuyết Lê, FB: Nguyên Tuyet Le
Chọn C .
Phương trình hoành độ giao điểm của
(C )
m
và trục
Ox
là:
22
2 2 1
0(1)
1
x mx m
x
+ + −
=
−
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 25 Mã đề 132
A
B
C
A'
C'
B'
M
(C )
m
cắt
Ox
tại hai điểm phân biệt
;AB
khi và chỉ khi phương trình
(1)
có hai nghiệm phân
biệt
22
( ) 2 2 1 0g x x mx m = + + − =
có hai nghiệm phân biệt
12
;1xx
2
2
11
10
11
(a)
1
0
(1) 2 2 0
0
g
m
m
m
m
m
g m m
m
−
= −
−

−
= +
.
Ta có :
22
'
2
(2 2 )( 1) (x 2 2 1)
( 1)
x m x mx m
y
x
+ − − + + −
=
−
Hệ số góc của
(C )
m
tại hai điểm
,AB
là:
22
1 1 1 1 1
1
2
11
(2 2 )( 1) (x 2 2 1) 2 2
( 1) 1
x m x mx m x m
k
xx
+ − − + + − +
==
−−
22
2 2 2 2 2
2
2
22
(2 2 )( 1) (x 2 2 1) 2 2
( 1) 1
x m x mx m x m
k
xx
+ − − + + − +
==
−−
Hai tiếp tuyến này vuông góc với nhau
12
.1kk = −
12
12
2 2 2 2
( ).( ) 1
11
x m x m
xx
++
= −
−−
2
1 2 1 2 1 2 1 2
4 . ( ) . ( ) 1(2)x x m x x m x x x x

+ + + = − + + −

.
Lại có:
12
2
12
2
. 2 1
x x m
x x m
+ = −
=−
. Do đó
2
1
(2) 6 2 4 0
2
3
m
mm
m
=−
+ − =
=
.
Đối chiếu điều kiện ta có
2
3
m =
.
tcdung.math@gmail.com
Câu 45. Cho lăng trụ đứng
/ / /
.ABC A B C
có đáy ABC là tam giác cân tại C,
0
30BAC =
,
/
3, .AB a AA a==
Gọi M là trung điểm của
/
.BB
Tính theo a thể tích V khối tứ diện
/
.MACC
A.
3
3
12
a
V =
. B.
3
3
4
a
V =
.
C.
3
3
3
a
V =
.D.
3
3
18
a
V =
Lời giải
Tác giả :TrầnCôngDũng, FB: trancong.dung.948
Chọn B
.
/ / /
3
0
.
1 3 3
3. 3.sin120 .
24
ABC A B C
a
V a a a==
.
Vì MB//(ACC’) nên
( )
( )
( )
( )
//
,,d M ACC d B ACC=
Do đó
/ / /
//
3
.
3
34
ABC A B C
MACC BACC
V
a
VV= = =
.
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 26 Mã đề 132
tcdung.math@gmail.com
Câu 46. Cho hàm số
( )
.y f x=
Hàm số
( )
/
y f x=
có đồ thị
như hình vẽ bên. Hỏi hàm số
( )
3y f x=−
đồng biến
trên khoảng nào sau đây:
A.
( )
2;4
. B.
( )
1;3
. C.
( )
1;3−
. D.
( )
5;6
Lời giải
Tác giả :TrầnCôngDũng, FB: trancong.dung.948
Chọn D
Nhận xét: Từ đồ thị f’(x), ta có
1
13
'(x) 0 [
x
x
f
−


Từ đó
( )
/
3 1 2
30
1 3 3 4 6
xx
fx
xx
− −

−

−

. Do đó chọn D.
thaygiaothaogiay@gmail.com
Câu 47. Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ sau:
Khi đó số nghiệm của phương trình
( )
2 2 3 5 0fx− − =
là:
A.
3
. B.
2
. C.
4
. D.
1
.
Lời giải
Tác giả :Đinh Phước Tân, FB: Tân Độc
Chọn B
Ta có
( )
( )
( )
53
23
23
22
2 2 3 5 0
5 2 3 3
23
22
a
f x x
xa
fx
x b b
f x x
+

− = =

−=
− − =

− = +

− = − =


Trong đó
0; 1ab
. Vậy phương trình đã cho có 2 nghiệm phân biệt.
thaygiaothaogiay@gmail.com
Câu 48. Tìm số tiệm cận (bao gồm tiệm cận đứng và tiệm cận ngang) của đồ thị hàm số
2
45
2 1 1
x
y
xx
+
=
+ − −
A.3. B.1. C.2. D. 4.
Lời giải
Tác giả : Đinh Phước Tân, FB: Tân Độc
Chọn C
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 27 Mã đề 132
Hàm số có tập xác định là
1
; \ 0
2

− +

.
Ta có
2
45
lim lim 2 2
2 1 1
xx
x
yy
xx
→+ →+
+
= = − = −
+ − −
là đường tiệm cận ngang của đồ thị hàm số đã
cho.
Mặt khác,
2
10
2 1 1 0
2 1 (x 1)
x
x x x
x
+
+ = + =
+ = +
Với mọi
0x
ta có
( )
2
22
0 2 1 2 1 1 2 1 1 2 1x x x x x x x x + + + + + + +
2
00
45
2 1 1 0 lim lim 0
2 1 1
xx
x
x x y x
xx
++
→→
+
+ − − = = − =
+ − −
là đường tiệm cận đứng của
đồ thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận.
Minhchung238@gmail.com
Câu 49. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
D
,
2AB a=
,
AD CD a==
,
2SA a=
,
( )
SA ABCD⊥
. Tính côsin của góc tạo bởi
( )
SBC
và
( )
SCD
.
A.
6
6
. B.
6
3
. C.
2
3
. D.
3
3
.
Lờigiải
Tác giả :Võ Minh Chung, FB: Võ Minh Chung
Chọn B
Chọn hệ trục tọa độ Oxyz như hình vẽ.
Ta có:
( )
( )
( ) ( ) ( )
0,0,0 , 0,0, 2 , 0,1,0 , 2,0,0 , 1,1,0A S D B C
.
Vecto pháp tuyến của
( )
SCD
:
( )
1
, 0, 2,1n SC SD

==

.
Vecto pháp tuyến của
( )
SBC
( )
2
, 2, 2,2n SB SC

==

.
Vậy:
( ) ( )
( )
12
12
6
cos ,
3
nn
SBC SDC
nn
==
.
Câu 50. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
3
2
7 14 2
3
mx
y mx x m= + + − +
nghịch
biến trên
)
1; +
.
A.
14
;
15

− −


. B.
14
;
15

− −

. C.
14
2;
15

−−


. D.
14
;
15

− +

.
O
z
y
x
S
D
C
B
A
Sản phẩm của Group FB: TEAM TOÁN VD–VDC Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 28 Mã đề 132
Lờigiải
Tác giả :Võ Minh Chung, FB: Võ Minh Chung
Chọn A
Ta có:
2
' 14 14y mx mx= + +
.
Hàm số đã cho nghịch biến trên
)
1; +
khi và chỉ khi
2
' 14 14 0,y mx mx x= + +
)
1; +
( )
)
)( )
2
2
14
14 14, 1; , 1; 1
14
m x x m x
x
−
+ − + +
+
.
Đặt
( )
2
14
14
fx
x
−
=
+
)
, 1;x +
( )
)
2
2
28
'( ) 0, 1;
14
x
f x x
x
= +
+
.
Do đó:
)
( ) ( ) ( )
1;
14
12
15
Min f x f
+
−
==
.
Từ
( ) ( )
1 , 2
suy ra giá trị
m
cần tìm là:
14
;
15
m

− −


.
| 1/28
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
TRƯỜNG ĐẠI HỌC VINH
ĐỀ KHẢO SÁT CHẤT LƯỢNG GIỮA HỌC KỲ 1 TRƯỜNG THPT CHUYÊN MÔN TOÁN - LỚP 12 ----------------------- NĂM HỌC 2018 - 2019
Thời gian làm bài: 90 phút (không tính thời gian phát đề) ---------
(Đề thi gồm 05 trang, 50 câu trắc nghiệm) MÃ ĐỀ THI 132
Họ và tên thí sinh: .................................................................. Số báo danh: ...................................... Câu 1.
Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng? A. 3 . B. 1. C. 2 . D. 4 . 2 x + x Câu 2. Cho hàm số y =
có đồ thị (C) . Phương trình tiếp tuyến tại điểm A(1; 2 − ) của (C) là x − 2
A. y = −3x + 5 . B. y = 5 − x + 7 .
C. y = −5x + 3 . D. y = 4 − x + 6 . Câu 3.
Gọi (P) là đồ thị hàm số 3
y = 2x − x + 3 . Trong các đường thẳng sau, đường thẳng nào là tiếp tuyến của (P) ?
A. y = −x − 3.
B. y = 11x + 4.
C. y = −x + 3.
D. y = 4x − 1. Câu 4.
Khối đa diện đều loại 4;  3 có bao nhiêu mặt? A. 6. B. 20. C. 12. D. 8. Câu 5.
Cho hình lăng trụ ABC. A ' B 'C ' có các mặt bên là hình vuông cạnh 2a . Tính theo a thể tích
V của khối lăng trụ ABC. A ' B 'C ' 3 6a 3 3a 2 3a 2 6a A. V = . B. V = . C. V = . D. V = . 2 12 4 6 Câu 6.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA = 2a và SA vuông góc với
( ABCD) . Góc giữa SC và ABCD bằng A. 0 45 . B. 0 30 . C. 0 60 . D. 0 90 . Câu 7.
Cho hình lập phương ABC . D A BCD
  cạnh a. Tính khoảng cách giữa hai đường thẳng AB và CD . 2a A. . B. a. C. 2 . a D. 2 . a 2 Câu 8.
Giá trị cực đại y của hàm số 3
y = x −12x + 20 là CD A. y = 4. B. y = 36. C. y = 4. − D. y = 2. − CD CD CD CD 1 Câu 9.
Tập xác định của hàm số y = là s inx +1      A.
\  + k2 , k   . B. \ −
+ k2,k  .  2   2     C. \ −
+ k,k  . D. .  2  3
Câu 10. Nghiệm âm lớn nhất của phương trình = 3cot x + 3 là 2 sin x  5  2 A. − . B. − . C. − . D. − . 6 6 2 3
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 1 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Câu 11. Cho cấp số cộng (u
có các số hạng đầu lần lượt là 5 ; 9 ; 13 ; 17 ; … Tìm công thức số hạng n )
tổng quát u của cấp số cộng ? n
A. u = 5n −1 .
B. u = 5n +1 .
C. u = 4n −1.
D. u = 4n +1. n n n n
Câu 12. Tìm giá trị nhỏ nhất của hàm số 2
y = x −1 trên đoạn  3 − ;2? A. min = 3 . B. min = 3 − . C. min = 1 − . D. min = 8 .  3 − ;2  3 − ;2  3; −  2  3 − ;2 Câu 13. Cho hàm số 2 y =
x −1 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng (0; +) .
B. Hàm số nghịch biến trên khoảng ( ;0 − ).
C. Hàm số đồng biến trên khoảng (1; +) .
D. Hàm số đồng biến trên khoảng (− ;  +) .
Câu 14. Khai triển ( x − )100 3
ta được đa thức (x −3)100 2 100
= a + a x + a x +...+ a x , với a , 0 1 2 100 0
a , a ,..., a
a − a + a − ... − a + a ? 1 2
100 là các hệ số thực. Tính 0 1 2 99 100 A. 100 2 − . B. 100 4 . C. 100 4 − . D. 100 2 .
Câu 15. Nghiệm của phương trình lượng giác 2
cos x − cos x = 0 thỏa mãn điều kiện 0  x   là 3  
A. x = 0 . B. x = . C. x = . D. x = − . 4 2 2
Câu 16. Tất cả các nghiệm của phương trình tan x = cot x là    A. x = + k ,k  . B. x =
+ k2 , k  . 4 4 4    C. x =
+ k , k  . D. x = + k , k  . 4 4 2
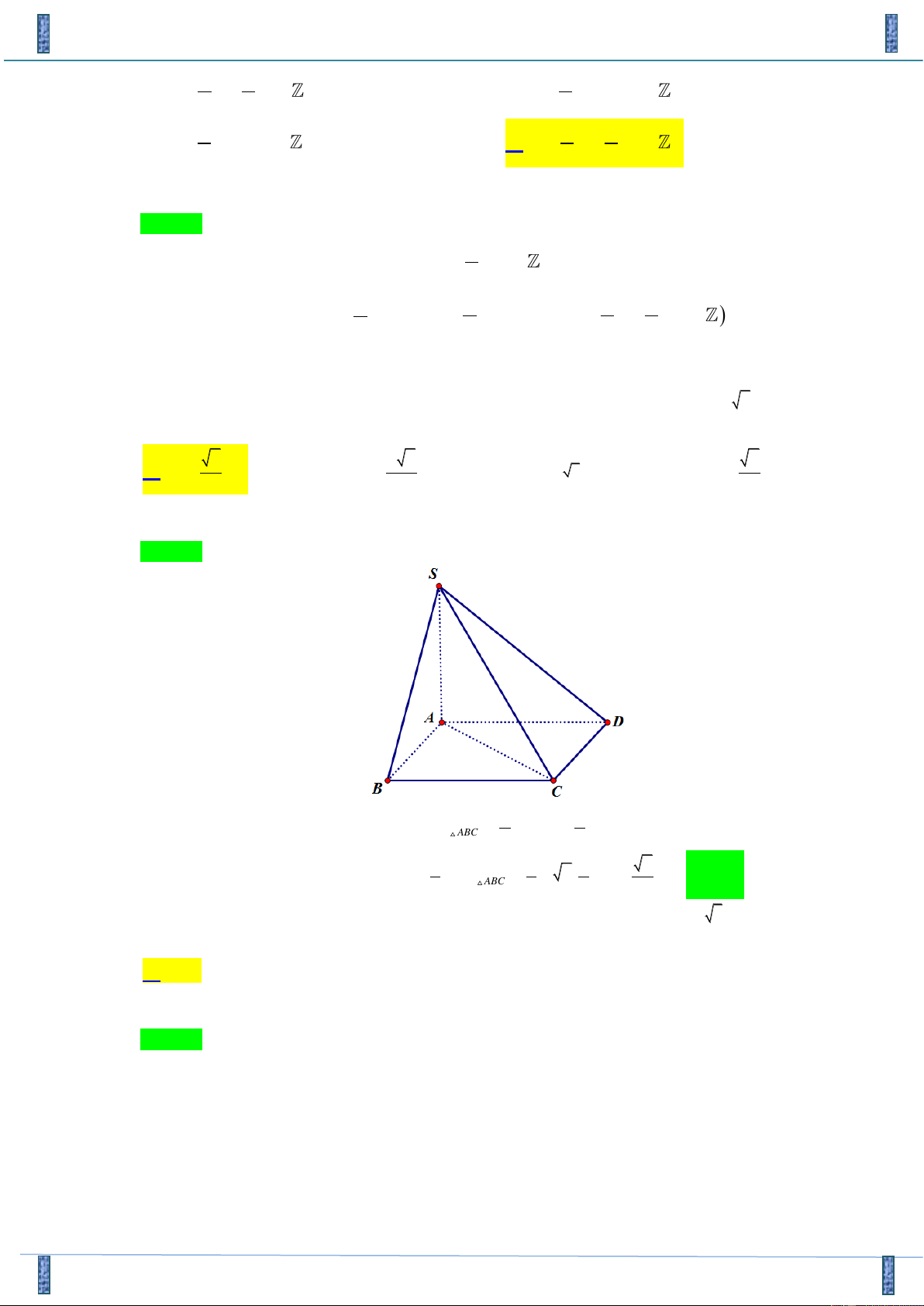
Câu 17. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA = a 2 và vuông góc
với ( ABCD) . Tính theo a thể tích V của khối chóp S.ABC 2 2 2 2 A. 3 V = a . B. 3 V = a . C. 3 V = 2a . D. 3 V = a . 6 3 3
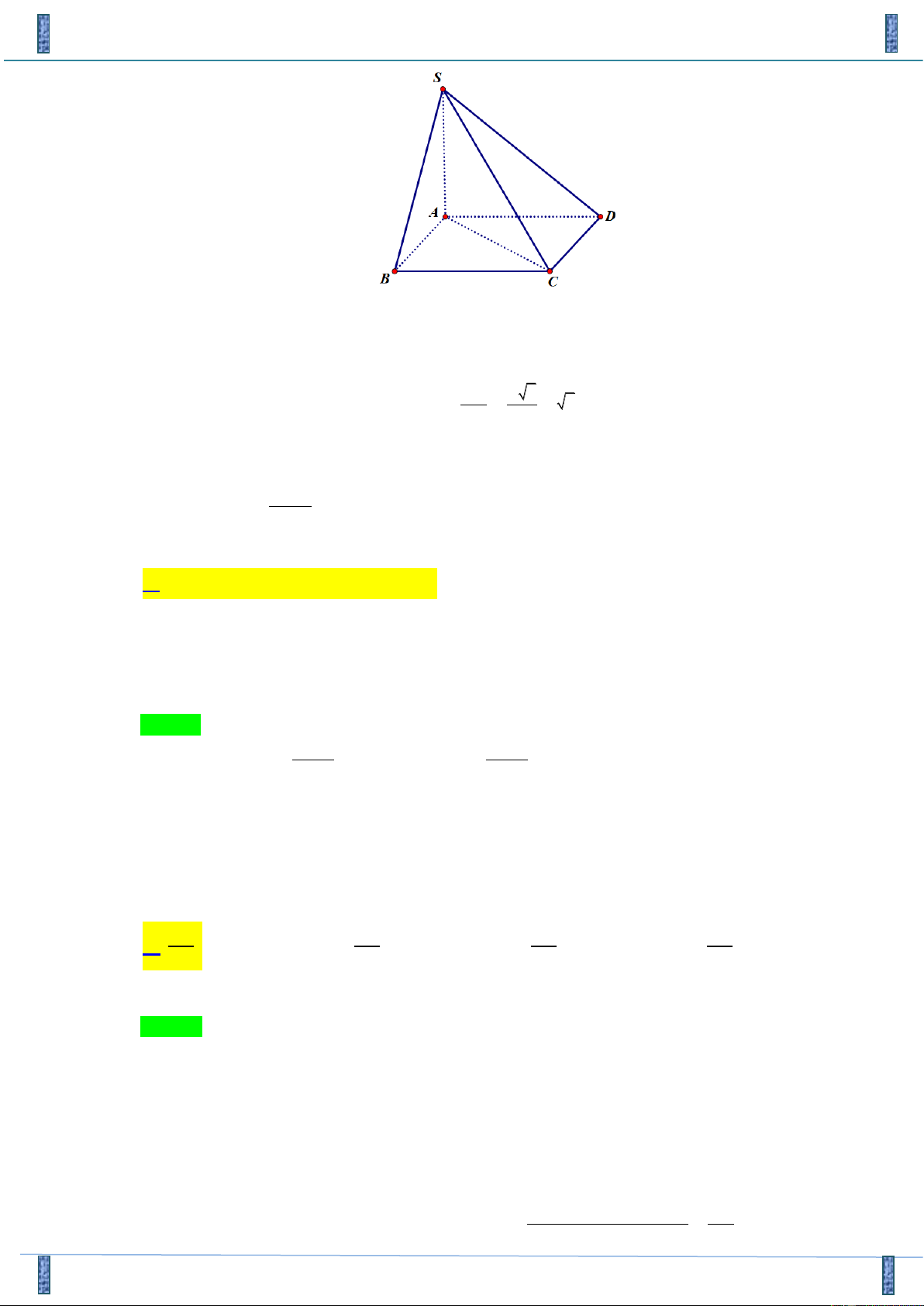
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AB = a , SA = a 3 và vuông góc với
( ABCD) . Tính góc giữa hai đường thẳng SB và CD A. 0 60 . B. 0 30 . C. 0 45 . D. 0 90 . 3x −1
Câu 19. Cho hàm số y =
có đồ thị (C) . Mệnh đề nào sau đây sai? x − 3
A. Đồ thị (C) có tiệm cận đứng và tiệm cận ngang.
B. Đồ thị (C) không có tiệm cận đứng.
C. Đồ thị (C) có tiệm cận ngang.
D. Đồ thị (C) có tiệm cận.
Câu 20. Trong năm học 2018 − 2019 trường THPT chuyên đại học Vinh có 13 lớp học sinh khối 10, 12
lớp học sinh khối 11, .12 lớp học sinh khối 12 . Nhân ngày nhà giáo Việt Nam 20 tháng 11 nhà
trường chọn ngẫu nhiên 2 lớp trong trường để tham gia hội văn nghệ của trường Đại học Vinh.
Xác suất để chọn được hai lớp không cùng khối là 76 87 78 67 A. . B. . C. . D. . 111 111 111 111
Câu 21. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , BC = 2a , SA = a và SA
vuông góc ( ABC) . Tính góc giữa hai mặt phẳng (SBC) và ( ABC) 0 0 0 0 A. 45 . B. 30 . C. 60 . D. 90 .
Câu 22. Gọi x , x , x
y = −x + x + x + x + x 1 2
3 là các cực trị của hàm số 4 2 4 2019 . Tính tổng 1 2 3 bằng? A. 0 . B. 2 2 . C. 1 − . D. 2 .
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 2 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Câu 23. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
y = x − 3x − 9x +1 trên
đoạn 0;4 . Tính tổng m + 2M .
A. m + 2M = 17 .
B. m + 2M = 37 − .
C. m + 2M = 51.
D. m + 2M = 24 − . u
 − u + u = 65
Câu 24. Cho cấp số nhân (u thỏa mãn 1 3 5  . Tính u . n ) u + u = 325  3 1 7
A. u = 15 .
B. u = 25 . C. u = 10 . D. u = 20 . 3 3 3 3 2 n C C
Câu 25. Biết số tự nhiên n thỏa mãn 1 C + 2 n + ... n + n = 45 . Tính n C n 1 n 1 + ? C C − n 4 n n A. 715. B. 1820 . C. 1365 . D. 1001. x −1
Câu 26. Tìm tất cả các giá trị của m để hàm số y =
đồng biến trên khoảng (0;+ ) ? x + m A. ( 1 − ;+ ) .
B. 0; + ) . C. (0; + ) . D.  1 − ;+ ) .
Câu 27. Tìm tất cả các giá trị thực của tham số m sao cho điểm cực tiểu của đồ thị hàm số 3 2
y = x + x + mx −1 nằm bên phải trục tung? 1 1
A. m  0 . B. 0  m  . C. m  . D.Không tồn tại. 3 3
Câu 28. Sinh nhật của An vào ngày 1 tháng 5. Bạn An muốn mua một chiếc máy ảnh giá khoảng 600.000
đồng để làm quà sinh nhật cho chính mình. Bạn ấy quyết định bỏ ống tiết kiệm 10.000 đồng vào
ngày 1 tháng 1 của năm đó, sau đó cứ tiếp tục những ngày sau, mỗi ngày bạn bỏ ống tiết kiệm
5.000 đồng. Biết trong năm đó, tháng 1 có 31 ngày, tháng 2 có 28 ngày, tháng 3 có 31 ngày và
tháng 4 có 30 ngày. Gọi a (đồng) là số tiền An có được đến sinh nhật của mình (ngày sinh nhật
An không bỏ tiền vào ống). Khi đó ta có:
A. a 610000;615000) .
B. a 605000;610000) .
C. a 600000;605000) .
D. a 595000;600000) .   
Câu 29. Số nghiệm của phương trình sin 5x + 3 cos 5x = 2sin 7x trên khoảng 0;    2  là ? A. 4 . B. 1. C. 3 . D. 2 .
Câu 30. Cho hàm số f (x) có đạo hàm trên và /
f (x)  0, x
  .Biết f (1) = 2. Hỏi khẳng định nào
sau đây có thể xảy ra ?
A. f (2) + f (3) = 4. B. f ( 1 − ) = 2. C. f (2) = 1.
D. f (2018)  f (2019).
Câu 31. Cho tập hợp A = 0,1, 2,3, 4,5, 
6 . Từ tập A lập được bao nhiêu số tự nhiên chẵn có 4 chữ số khác nhau và nhỏ hơn 4012 A. 180 . B. 240 . C. 200 . D. 220 . 1 − 3 2
Câu 32. Một vật chuyển động theo quy luật s =
t + 9t , với t (giây) là khoảng thời gian tính từ lúc 2
vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi
trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
A. 216 (m / s) .
B. 400 (m / s) .
C. 54 (m / s) .
D. 30 (m / s) .
Câu 33. Tất cả các giá trị của tham số m để hàm số y = (m − ) 4
1 x đạt cực đại tại x = 0 là A. m 1. B. m  1.
C. không tồn tại m. D. m = 1.
Câu 34. Tung hai con súc sắc 3 lần độc lập với nhau. Tính xác suất để có đúng một lần tổng số chấm
xuất hiện trên hai con súc sắc bằng 6. Kết quả làm tròn đến 3 ba chữ số ở phần thập phân) A. 0,120. B. 0, 319. C. 0, 718. D. 0, 309.
Câu 35. Hệ số của 5
x trong khai triển ( − x − x )9 2 1 2 3 là
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 3 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019 A. 792 . B. 684 − . C. 3528 . D. 0 .
Câu 36. Cho một khối đa diện lồi có 10 đỉnh, 7 mặt. Hỏi khối đa diện này có mấy cạnh? A. 20 . B. 18 . C. 15 . D. 12 .
Câu 37. Cho hình chóp S.ABC có SA = 2 , a SB = 2 ,
a SC = 2 2a và ASB = BSC = CSA =  60 . Tính
thể tích của khối chóp đã cho. 4 3 2 3 3 2 2 3 A. a a a 3 . B. 3 . C. 3 2a . D. 3 .
Câu 38. Cho hình lập phương ABC . D A B C
D cạnh a . Gọi M,N lần lượt là trung điểm của BC và
DD. Tính theo a khoảng cách giữa hai đường thẳng MN và BD . 3a 3a 3a A. 3a . B. . C. . D. . 2 3 6
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SAD là tam giác đều và nằm
trong mặt phẳng vuông góc với ( ABCD) . Gọi M , N , P lần lượt là trung điểm các cạnh
SB, BC, CD . Tính thể tích khối tứ diện CMNP . 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 48 96 54 72 x − 2018
Câu 40. Số tiệm cận ngang của đồ thị hàm số y = x + là 2019 A. 1. B. 3 . C. 2 . D. 0 .
Câu 41. Cho khối hộp ABC . D ’ A ’ B ’ C ’
D có M là trung điểm ’ A ’
B . Mặt phẳng ( ACM ) chia khối hộp đã
cho thành hai phần. Tỉ số thể tích của hai phần đó bằng? 7 5 7 7 A. . B. . C. . D. . 17 17 24 12
Câu 42. Đồ thị của hàm số ( ) 3 2
f x = x + ax + bx + c tiếp xúc với trục hoành tại gốc tọa độ và cắt đường
thẳng x = 1 tại điểm có tung độ bằng 3 khi
A. a = b = 0,c = 2 .
B. a = c = 0,b = 2 .
C. a = 2,b = c = 0 .
D. a = 2,b =1,c = 0 . 0
Câu 43. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , ABC = 60 , cạnh bên SA = a 2 và
SA vuông góc với ABCD .Tính góc giữa SB và (SAC) . A. 0 90 . B. 0 30 . C. 0 45 . D. 0 60 . 2 2
x + 2mx + 2m −1
Câu 44. Gọi m là giá trị để đồ thị (C ) của hàm số y = m x −
cắt trục hoành tại hai điểm 1
phân biệt và các tiếp tuyến với (C ) tại tại hai điểm này vuông góc với nhau. Khi đó ta có: m
A. m (1; 2) . B. m ( 2 − ;− ) 1 . C. m (0 ) ;1 . D. m ( 1 − ;0) .
Câu 45. Cho lăng trụ đứng / / / ABC.A B C
có đáy ABC là tam giác cân tại C, 0 BAC = 30 , /
AB = a 3, AA = .
a Gọi M là trung điểm của /
BB . Tính theo a thể tích V khối tứ diện / MACC . 3 a 3 3 a 3 A.V = . B.V = . 12 4 3 a 3 3 a 3 C.V = . D.V = 3 18
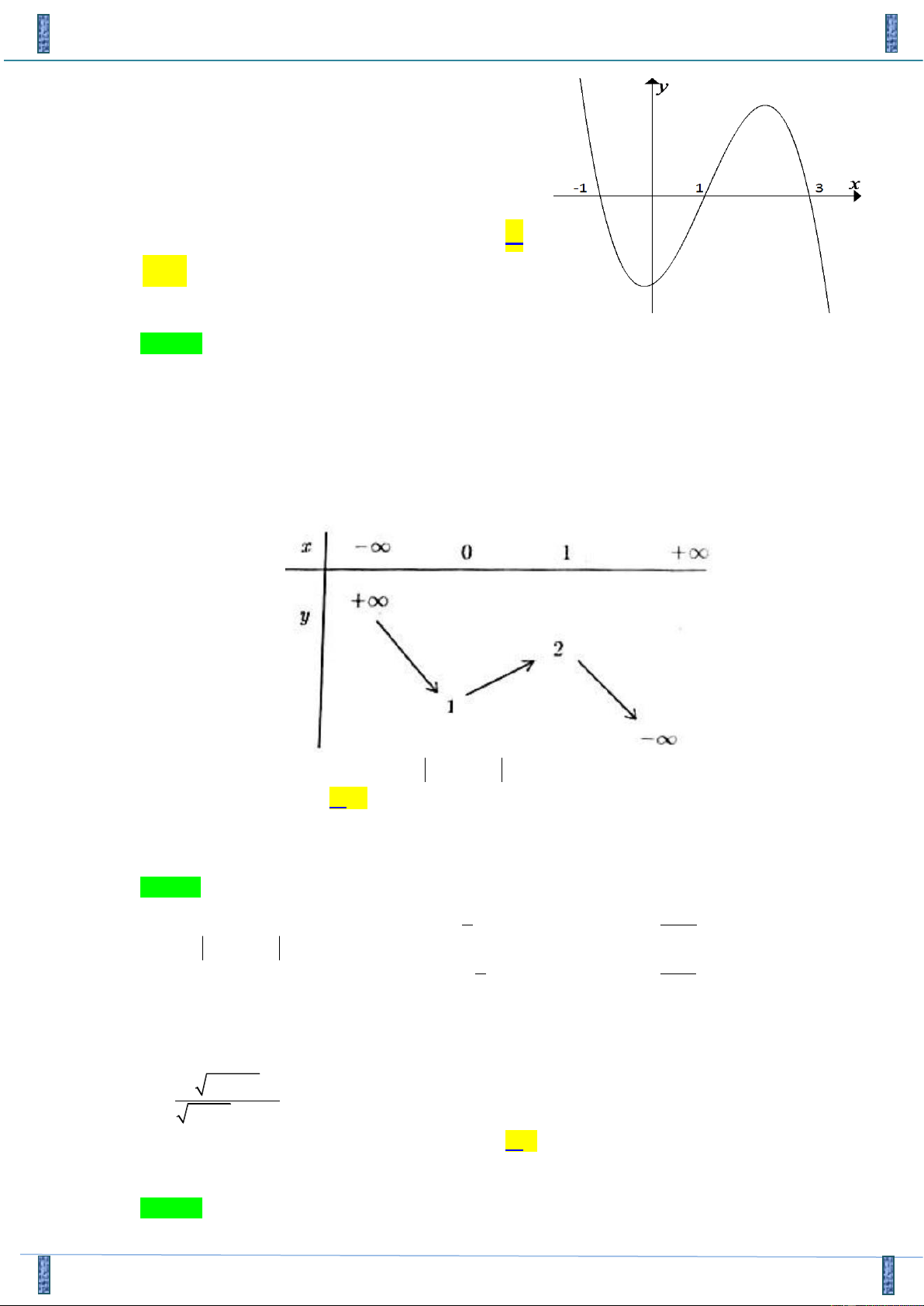
Câu 46. Cho hàm số y = f ( x). Hàm số /
y = f ( x) có đồ thị như hình vẽ bên. Hỏi hàm số y = f ( x − 3)
đồng biến trên khoảng nào sau đây: A. (2; 4) . B. (1;3) . C. (−1;3) . D. (5;6)
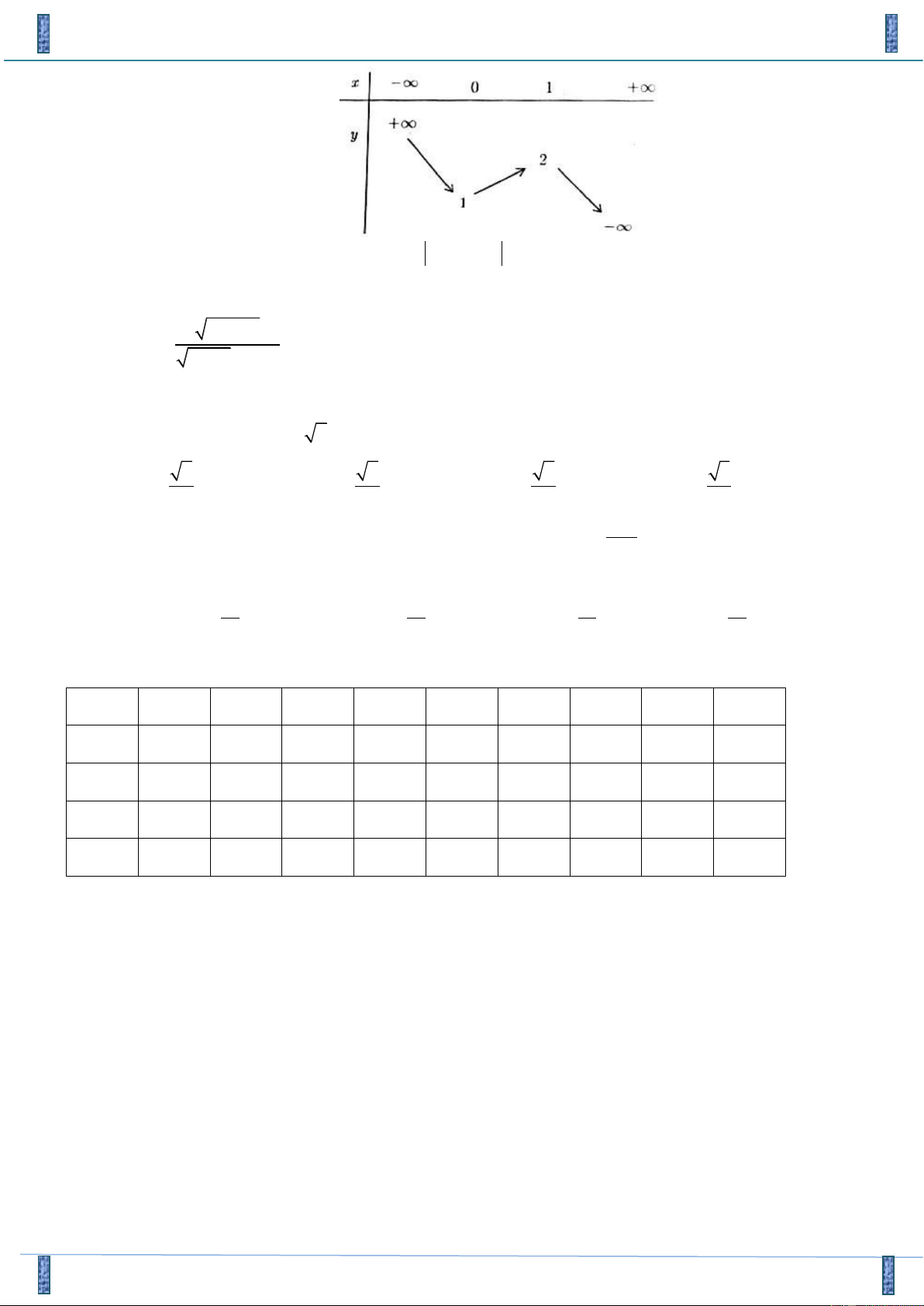
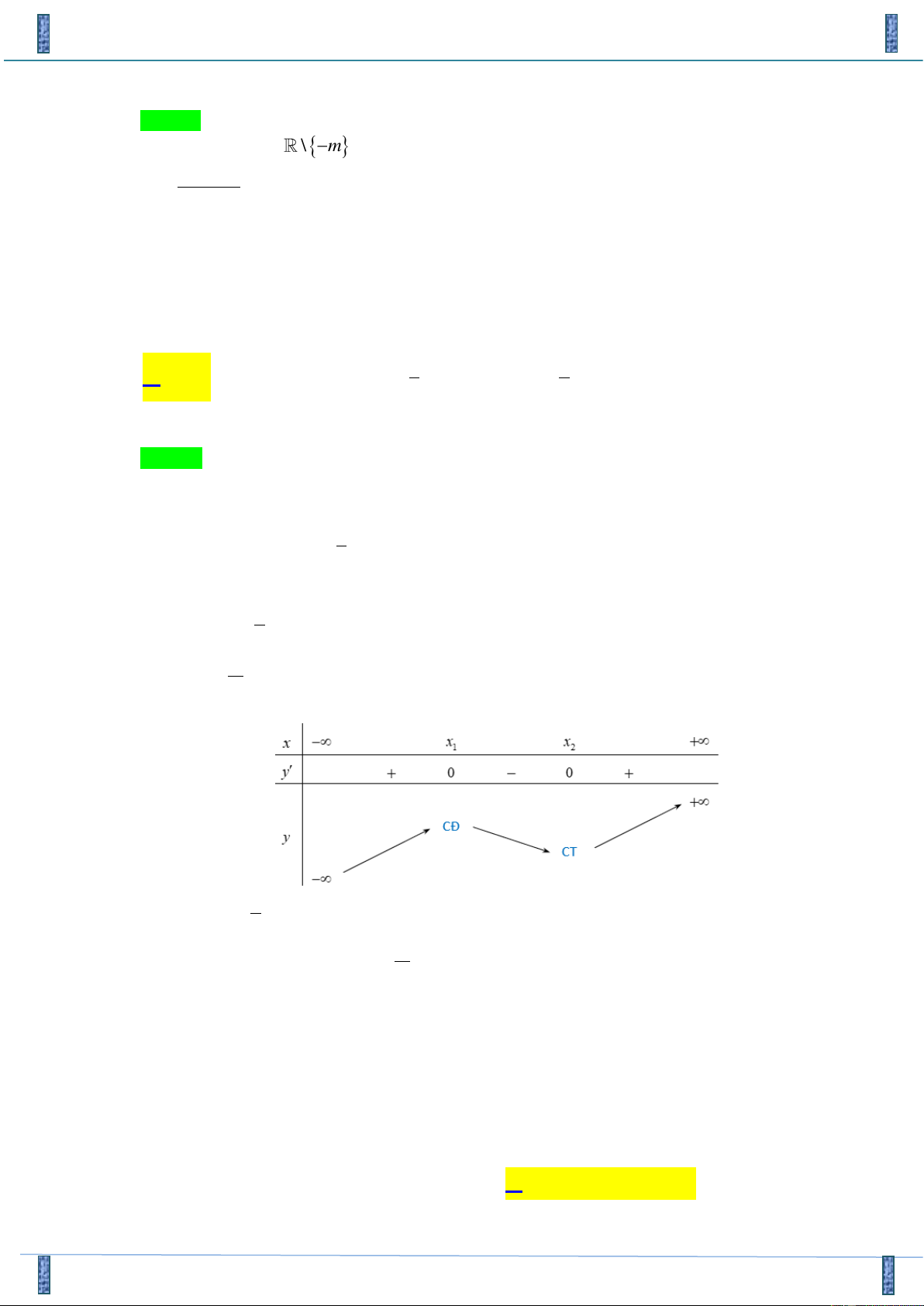
Câu 47. Cho hàm số y = f ( x) có bảng biến thiên như hình vẽ sau:
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 4 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Khi đó số nghiệm của phương trình 2 f (2x −3) −5 = 0 là: A. 3 . B. 2 . C. 4 . D.1.
Câu 48. Tìm số tiệm cận (bao gồm tiệm cận đứng và tiệm cận ngang) của đồ thị hàm số 2 4x + 5 y = 2x +1 − x −1 A.3. B.1. C.2. D. 4.
Câu 49. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D , AB = 2a ,
AD = CD = a , SA = 2a , SA ⊥ ( ABCD) . Tính côsin của góc tạo bởi (SBC) và (SCD) . 6 6 2 3 A. . B. . C. . D. . 6 3 3 3 3 mx
Câu 50. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 2 y =
+ 7mx +14x − m + 2 nghịch 3 biến trên 1; +) .  14   14   14   14  A. ; − −   . B. ; − −  . C. 2; − − . D. − ; +   .     15   15   15   15  ĐÁP ÁN 1-D 2-C 3-C 4-A 5-A 6-A 7-B 8-B 9-B 10-C 11-D 12-C 13-C 14-B 15-C 16-D 17-A 18-A 19-B 20-A 21-A 22-A 23-D 24-D 25-A 26-B 27-A 28-B 29-A 30-B 31-D 32-C 33-A 34-D 35-C 36-C 37-D 38-D 39-B 40-C 41-A 42-C 43-B 44-C 45-B 46-D 47-B 48-C 49-B 50-A
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 5 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019 LỜI GIẢI
duongductri@gmail.com Câu 1.
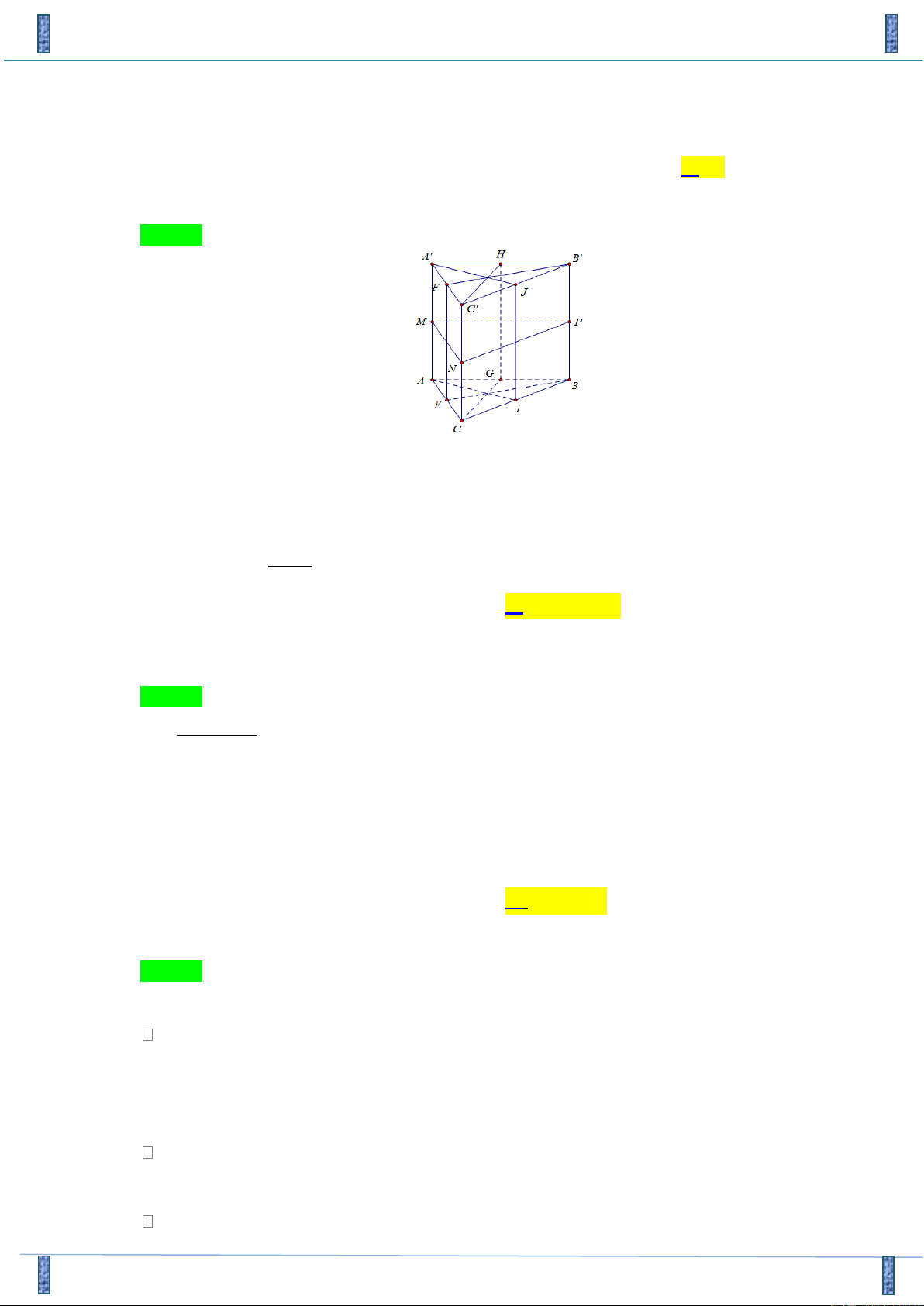
Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng? A. 3 . B. 1. C. 2 . D. 4 . Lời giải
Tác giả : Dương Đức Trí, FB: duongductric3ct Chọn D
Gọi M , N , P, E, F , I , J , G, H lần lượt là trung điểm các cạnh AA ,
CC , BB, AC, AC, BC, B C
  , AB, AB của lăng trụ tam giác đều AB . C A BC
 . Các mặt phẳng đối xứng của lăng
trụ tam giác đều AB . C A BC
  là (MNP) , ( AIJA) , (BEFB) , (CGHC).
duongductri@gmail.com 2 x + x Câu 2. Cho hàm số y =
có đồ thị (C) . Phương trình tiếp tuyến tại điểm A(1; 2 − ) của (C) là x − 2
A. y = −3x + 5 . B. y = 5 − x + 7 .
C. y = −5x + 3 . D. y = 4 − x + 6 . Lời giải
Tác giả : Dương Đức Trí, FB: duongductric3ct Chọn C 2 x − 4x − 2 y = = − ( ; y( ) 1 5 x − 2)2
Phương trình tiếp tuyến tại điểm A(1; 2
− ) của (C) là y = 5 − (x − ) 1 − 2  y = 5 − x + 3 .
nguyenth4nhtr11ng@gmail.com Câu 3.
Gọi (P) là đồ thị hàm số 3
y = 2x − x + 3 . Trong các đường thẳng sau, đường thẳng nào là tiếp tuyến của (P) ?
A. y = −x − 3.
B. y = 11x + 4.
C. y = −x + 3.
D. y = 4x − 1. Lời giải
Tác giả : Nguyễn Thành Trung, FB: Nguyễn Thành Trung Chọn C 2 y' = 3x − 1
Điều kiện đường thẳng y = ax + b là tiếp tuyến của hàm số y = f (x) (C) :  f '(x =  a 0 ) 
có nghiệm. Kiểm tra các đáp án ax + b =  f x  0 ( 0) 2 3x −1 = 1 − x = 0 Đáp án A: 0 0   
vô lí, đáp án A sai. 3
−x − 3 = 2x − x + 3    3 − = 3 0 0 0 2 3x −1 = 11 x = 2  Đáp án B: 0 0    đáp án B sai. 3 3 1
 1x + 4 = 2x − x + 3 1 
 1x + 4  2x − x + 3  0 0 0 0 0 0
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 6 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019 2 3x −1 = 1 − x = 0 Đáp án C: 0 0   
luôn đúng. Đáp án C đúng. 3
−x + 3 = 2x − x + 3   3 = 3 0 0 0
Do đáp án C đúng nên đáp án D sai. Câu 4.
Khối đa diện đều loại 4;  3 có bao nhiêu mặt? A. 6. B. 20. C. 12. D. 8. Lời giải
Tác giả : Nguyễn Thành Trung, FB: Nguyễn Thành Trung Chọn C
Khối đa diện đều loại 4; 
3 là khối lập phương có 6 mặt.
Nvthang368@gmail.com Câu 5.
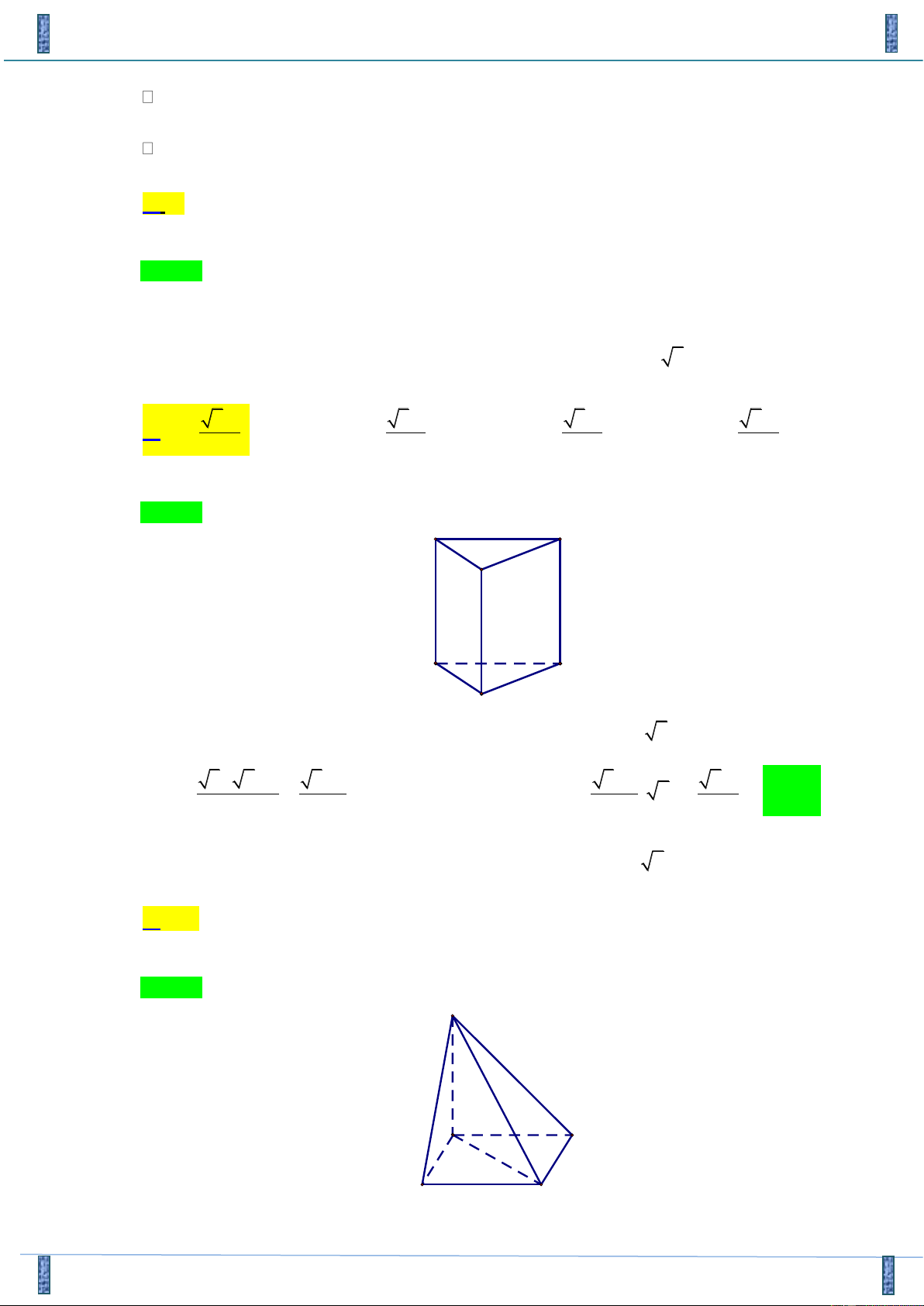
Cho hình lăng trụ ABC. A ' B 'C ' có các mặt bên là hình vuông cạnh 2a . Tính theo a thể tích
V của khối lăng trụ ABC. A ' B 'C ' 3 6a 3 3a 2 3a 2 6a A. V = . B. V = . C. V = . D. V = . 2 12 4 6 Lời giải
Tác giả: Nguyễn Văn Thắng; Fb: Nguyễn Thắng Chọn A A C B A' C' B'
Từ giả thiết suy ra đáy của hình lăng trụ là tam giác đều cạnh bằng 2a ⇒ Diện tích của đáy là: 2 2 3.( 2a) 3.a 2 3 3.a 6a S = =
⇒ Thể tích của lăng trụ là: V = . 2a = ⇒ Chọn A ABC 4 2 2 2
Nvthang368@gmail.com Câu 6.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA = 2a và SA vuông góc với
( ABCD) . Góc giữa SC và ABCD bằng A. 0 45 . B. 0 30 . C. 0 60 . D. 0 90 . Lời giải
Tác giả: Nguyễn Văn Thắng; Fb: Nguyễn Thắng Chọn A S A D B C
Vì SA vuông góc với đáy nên góc (SC, ( ABCD)) = SCA
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 7 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Trong hình vuông ABCD có: AC = a 2 , theo giả thiết, SA = 2a ⇒ tam giác SAC vuông cân tại A ⇒ 0 SCA = 45 ⇒ Chọn A
Hungvn1985@gmail.com Câu 7.
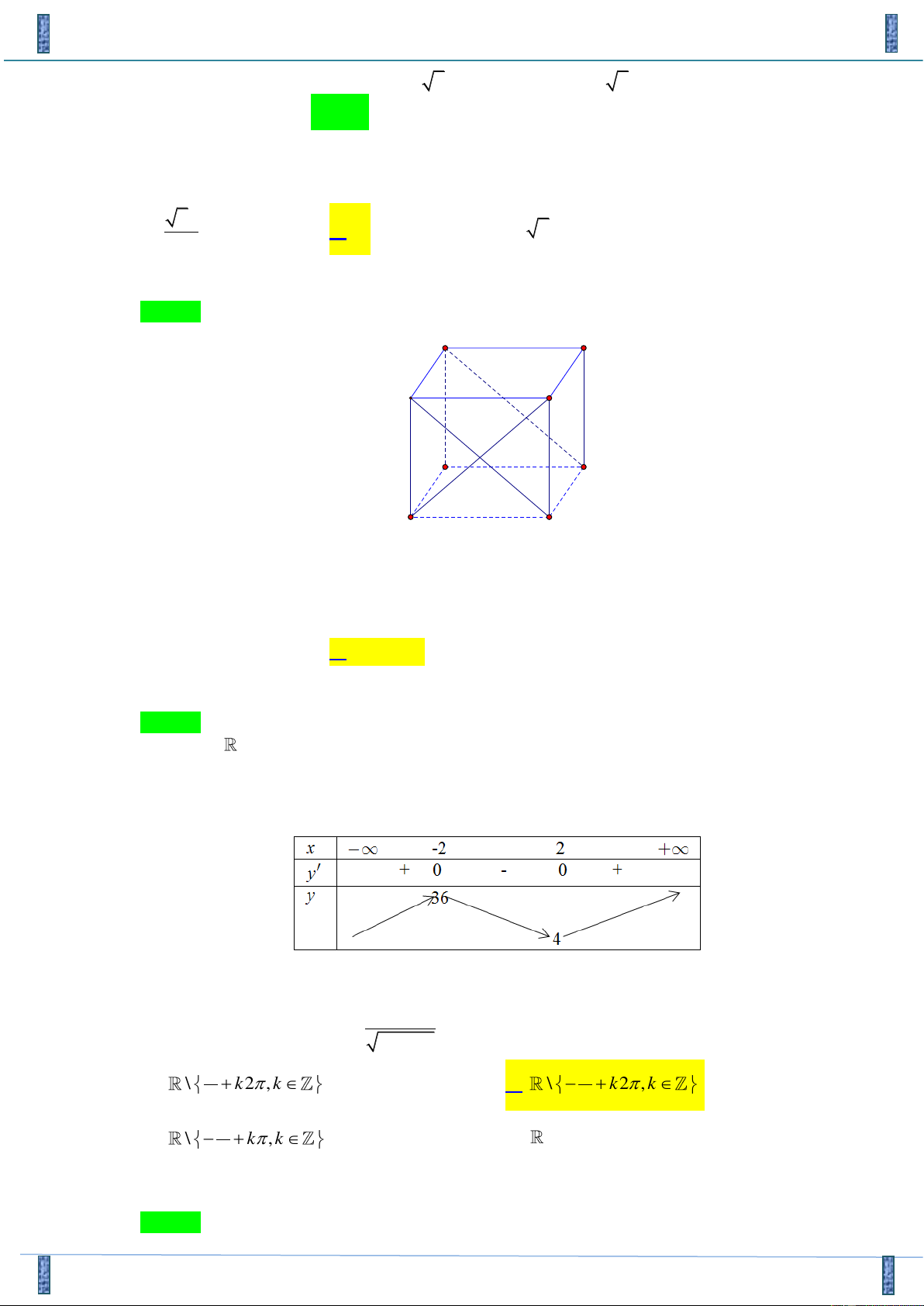
Cho hình lập phương ABC . D A BCD
  cạnh a. Tính khoảng cách giữa hai đường thẳng AB và CD . 2a A. . B. a. C. 2 . a D. 2 . a 2 Lời giải
Tác giả : Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng Chọn B A B D C B' A' D' C'
Do AB ' //C ' D '  AB ' // ( DCC ' D ') . Suy ra
d ( AB ';CD ') = d ( AB ';(DCC ' D')) = d ( ;
A (DCC ' D ')) = AD = a Câu 8.
Giá trị cực đại y của hàm số 3
y = x −12x + 20 là CD A. y = 4. B. y = 36. C. y = 4. − D. y = 2. − CD CD CD CD Lời giải
Tác giả : Phạm Ngọc Hưng, FB: Phạm Ngọc Hưng Chọn B TXĐ: D = x = 2 Ta có 2 2
y = 3x −12; y = 0  3x −12 = 0  x = 2 − Bảng biến thiên Suy ra y = 36. CD
diephd02@gmail.com 1 Câu 9.
Tập xác định của hàm số y = là s inx +1      A.
\  + k2 , k   . B. \ −
+ k2,k  .  2   2     C. \ −
+ k,k  . D. .  2  Lời giải
Tác giả : Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp Chọn B
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 8 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019 1  − Hàm số y =
xác định khi: s inx +1  0  s inx +1  0  x  + k2 s inx +1 2   TXĐ:  D = \ −
+ k2,k  .  2  3
Câu 10. Nghiệm âm lớn nhất của phương trình = 3cot x + 3 là 2 sin x  5  2 A. − . B. − . C. − . D. − . 6 6 2 3 Lời giải
Tác giả : Nguyễn Ngọc Diệp, FB: Nguyễn Ngọc Diệp Chọn C
Điều kiện xác định của phương trình: sinx  0 . 3 2
= 3cot x + 3  3(1+ cot x) = 3cot x + 3 2 sin x    = +  cotx = 0 x k  2  2
3 cot x − 3cot x = 0     cotx = 3  x = + k  6   − Họ nghiệm x =
+ k có nghiệm âm lớn nhất x = 2 2  −5 Họ nghiệm x =
+ k có nghiệm âm lớn nhất x = 6 6  −
Vậy nghiệm âm lớn nhất của phương trình đã cho là x = . 2
buinguyenphuong1991@gmail.com
Câu 11. Cho cấp số cộng (u
có các số hạng đầu lần lượt là 5 ; 9 ; 13 ; 17 ; … Tìm công thức số hạng n )
tổng quát u của cấp số cộng ? n
A. u = 5n −1 .
B. u = 5n +1 .
C. u = 4n −1.
D. u = 4n +1. n n n n Lời giải
Tác giả: Bùi Nguyên Phương, FB: Bùi Nguyên Phương Chọn D
Ta có: u = 5 nên thay n =1 vào 4 đáp án thấy chỉ có đáp án D đúng. 1
Câu 12. Tìm giá trị nhỏ nhất của hàm số 2
y = x −1 trên đoạn  3 − ;2? A. min = 3 . B. min = 3 − . C. min = 1 − . D. min = 8 .  3 − ;2  3 − ;2  3; −  2  3 − ;2 Lời giải
Tác giả : Bùi Nguyên Phương, FB: Bùi Nguyên Phương Chọn C Tập xác định: D = . Hàm số 2
y = x −1 liên tục và có đạo hàm trên đoạn  3 − ;2.
Đạo hàm: y = 2x . Xét y = 0  2x = 0  x = 0 3 − ;2. Ta có: y (0) = 1 − , y( 3
− ) = 8 và y(2) = 3 . Vậy min = 1 − .  3; −  2
Tranthom275@gmail.com Câu 13. Cho hàm số 2 y =
x −1 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng (0; +) .
B. Hàm số nghịch biến trên khoảng ( ;0 − ).
C. Hàm số đồng biến trên khoảng (1; +) .
D. Hàm số đồng biến trên khoảng (− ;  +) .
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán! Trang 9 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019 Lời giải
Tác giả : Trần Thị Thơm, FB: Tranthom275 Chọn C
Tập xác định: D = (− ;  −1] [1;+) x y = , x  (− ;
 −1)  (1;+); y = 0  x = 0 (loại) 2 x −1 Bảng xét dấu yx − −1 1 + y − +
Vậy hàm số đồng biến trên khoảng (1; +) .
Câu 14. Khai triển ( x − )100 3
ta được đa thức (x −3)100 2 100
= a + a x + a x +...+ a x , với a , 0 1 2 100 0
a , a ,..., a
là các hệ số thực. Tính a − a + a − ... − a + a ? 1 2 100 0 1 2 99 100 A. 100 2 − . B. 100 4 . C. 100 4 − . D. 100 2 . Lời giải Chọn B Ta có: ( x − )100 2 100 3
= a + a x + a x + ... + a x (1) 0 1 2 100 Thay x = 1
− vào hai vế của (1) ta được: ( 1 − − )100 3 = a + a (− ) 1 + a (− )2 1 + a (− )3 1 + ... + a (− )99 1 + a (− )100 1 0 1 2 3 99 100  ( 4
− )100 = a − a + a −... − a + a 0 1 2 99 100 Vậy 100
a − a + a − ... − a + a = 4 . 0 1 2 99 100
Cohangxom1991@gmail.com
Câu 15. Nghiệm của phương trình lượng giác 2
cos x − cos x = 0 thỏa mãn điều kiện 0  x   là 3  
A. x = 0 . B. x = . C. x = . D. x = − . 4 2 2 Lời giải
Tác giả : Phạm Văn Huy, FB: Đời Dòng Chọn D    x = x = + k 2
cos x − cos x = cos 0 0     2 ; k  cos x = 1  x = k2  Với họ nghiệm x = + k ; k  2        1 1 0  + k   −  k  −  k
Ta có 0  x     2   2 2   2 2  k = 0 k  k  k  
do đó chỉ có nghiệm x = thỏa mãn 2
Với họ nghiệm x = k 2 ; k   1 0  k2   0  k  0  x       2 vô nghiệm k  k 
Vậy phương trình có một nghiệm  (0; ) 2
Cohangxom1991@gmail.com
Câu 16. Tất cả các nghiệm của phương trình tan x = cot x là
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 10 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019    A. x = + k ,k  . B. x = + k2 , k  . 4 4 4    C. x =
+ k , k  . D. x = + k , k  . 4 4 2 Lời giải
Tác giả : Phạm Văn Huy, FB: Đời Dòng Chọn D s  in x  0  Điều kiện 
 sin 2x  0 x m , m cos x  0 2      
tan x = cot x  tan x = tan − x
  x = − x + k  x = + k
( k  ) thỏa mãn điều  2  2 4 2 kiện.
ptpthuyedu@gmail.com
Câu 17. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA = a 2 và vuông góc
với ( ABCD) . Tính theo a thể tích V của khối chóp S.ABC 2 2 2 2 A. 3 V = a . B. 3 V = a . C. 3 V = 2a . D. 3 V = a . 6 3 3 Lời giải
Tác giả : Phạm Thị Phương Thúy, FB: thuypham Chọn A 1 1
Ta có ABCD là hình vuông cạnh a 2  S = S = a ABC 2 ABCD 2 1 1 1 2
Thể tích khối chóp S.ABC là: 2 3 V = . SA S = .a 2. .a = a . Chọn A S . ABC ABC 3 2 6 3
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AB = a , SA = a 3 và vuông góc với
( ABCD) . Tính góc giữa hai đường thẳng SB và CD A. 0 60 . B. 0 30 . C. 0 45 . D. 0 90 . Lời giải
Tác giả : Phạm Thị Phương Thúy, FB: thuypham Chọn A
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 11 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Ta có ABCD là hình bình hành  AB / /CD . Do đó (S , B CD) = (S , B AB) = SBA
Vì SA ⊥ ( ABCD)  SA ⊥ AB   SAB vuông tại A. SA a 3
Xét tam giác vuông SAB ta có: 0 tan SBA = = = 3  SBA = 60 AB a Vậy (SB CD) 0 , = 60
luulien1507@gmail.com 3x −1
Câu 19. Cho hàm số y =
C . Mệnh đề nào sau đây sai? x − có đồ thị ( ) 3
A. Đồ thị (C) có tiệm cận đứng và tiệm cận ngang.
B. Đồ thị (C) không có tiệm cận đứng.
C. Đồ thị (C) có tiệm cận ngang.
D. Đồ thị (C) có tiệm cận. Lời giải
Tácgiả :Lưu Thị Liên, FB: Lotus Chọn B 3x −1 3x −1 Ta có: lim y = lim = 3 lim y = lim = − x→ x→ x − và 3 − − x→3 x→3 x − 3
Nên đồ thị (C) có tiệm cận đứng x = 3và tiệm cận ngang y = 3 .
Câu 20. Trong năm học 2018 − 2019 trường THPT chuyên đại học Vinh có 13 lớp học sinh khối 10, 12
lớp học sinh khối 11, .12 lớp học sinh khối 12 . Nhân ngày nhà giáo Việt Nam 20 tháng 11 nhà
trường chọn ngẫu nhiên 2 lớp trong trường để tham gia hội văn nghệ của trường Đại học Vinh.
Xác suất để chọn được hai lớp không cùng khối là 76 87 78 67 A. . B. . C. . D. . 111 111 111 111 Lờigiải
Tácgiả :Lưu Thị Liên, FB: Lotus Chọn A
Số phần tử của không gian mẫu là số cách chọn 2 lớp trong số 37 lớp của trường để tham gia hội văn nghệ: 2 ( n )  = C37
Số cách chọn 2 lớp cùng khối trong trường để tham gia hội văn nghệ của trường Đại học Vinh là 2 2 2 C + C + C 12 12 13
Số cách chọn 2 lớp không cùng khối trong trường để tham gia hội văn nghệ của trường Đại học Vinh là 2 C − ( 2 2 2 C + C + C 37 12 12 13 ) 2 C − ( 2 2 2 C + C + C 37 12 12 13 ) 76
Xác suất để chọn được hai lớp không cùng khối là: = 2 C 111 37
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 12 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
trichinhsp@gmail.com
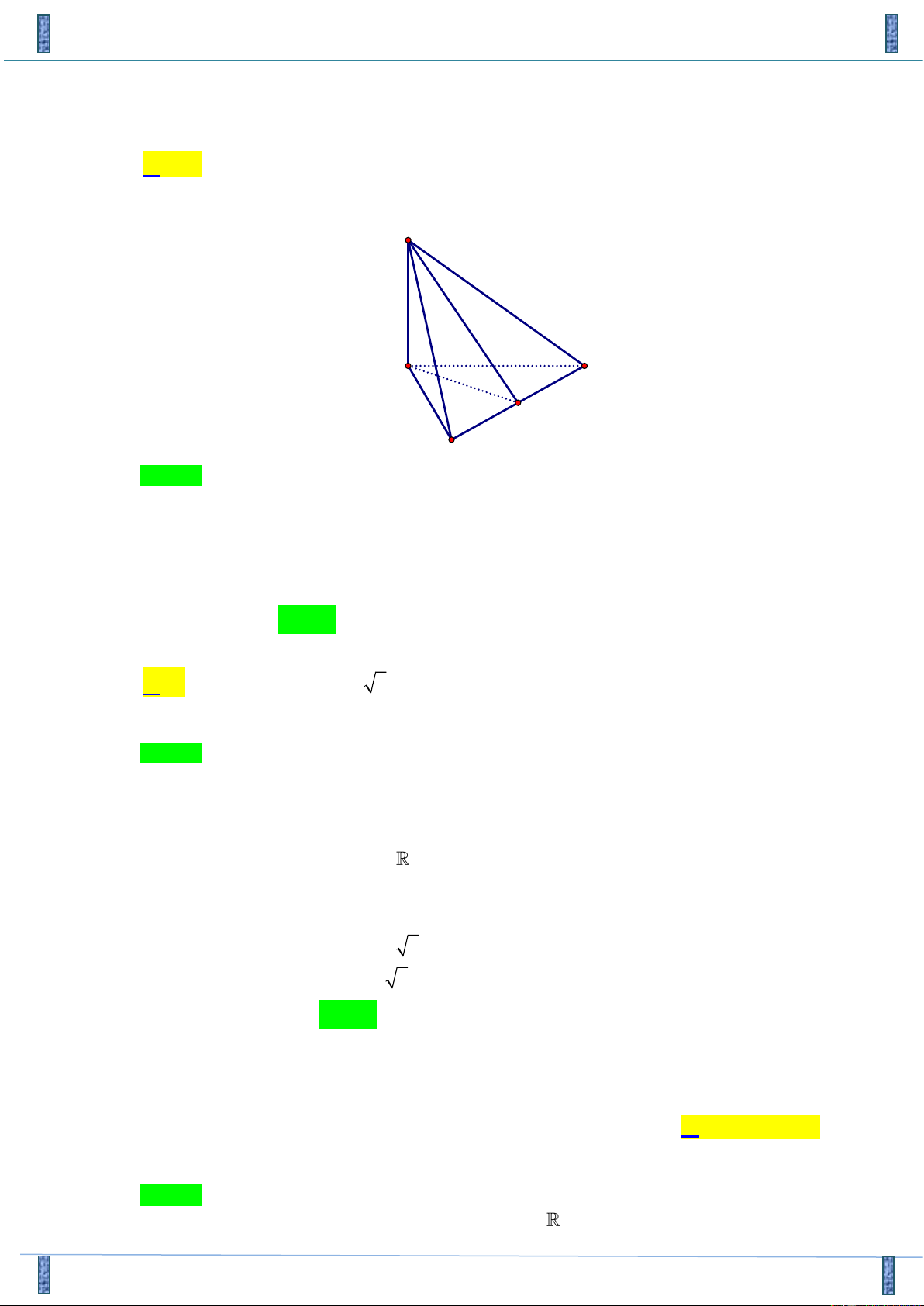
Câu 21. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , BC = 2a , SA = a và SA
vuông góc ( ABC) . Tính góc giữa hai mặt phẳng (SBC) và ( ABC) 0 0 0 0 A. 45 . B. 30 . C. 60 . D. 90 . Lời giải
Tác giả : Nguyễn Trí Chính, FB: Nguyễn Trí Chính S A C I B Chọn A
Gọi I là trung điểm BC , A
BC vuông cân tại A nên AI ⊥ BC .
Có SA ⊥ ( ABC)  SA ⊥ BC .
Suy ra BC ⊥ (SAI ) . Suy ra ( SBC);( ABC)) = SIA . S
IA vuông tại A có SA = ,
a AI = a . Suy ra S
IA vuông cân tại A . Suy ra 0 SIA = 45 . Chọn A
Câu 22. Gọi x , x , x
y = −x + x + x + x + x 1 2
3 là các cực trị của hàm số 4 2 4 2019 . Tính tổng 1 2 3 bằng? A. 0 . B. 2 2 . C. 1 − . D. 2 . Lời giải
Tác giả : Nguyễn Trí Chính, FB: Nguyễn Trí Chính Chọn A +Cách trắc nghiệm: Có . a b = 4
−  0 . Nên hàm số có 3 cực trị x = 0 x , x 1 , 2 3 là 2 số đối nhau.
Suy ra x + x + x = 0 1 2 3 +Cách tự luận 4 2
y = −x + 4x + 2019 , TXĐ: D = . / 3 y = 4 − x + 8x . x = 0  / 3 y = 0  4
− x + 8x = 0  x = − 2  x = 2 
Suy ra x + x + x = 0 1 2 3 . Chọn A
vungoctan131@gmail.com
Câu 23. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
y = x − 3x − 9x +1 trên
đoạn 0;4 . Tính tổng m + 2M .
A. m + 2M = 17 .
B. m + 2M = 37 − .
C. m + 2M = 51.
D. m + 2M = 24 − . Lời giải
Tác giả : Vũ Ngọc Tân, FB: Vũ Ngọc Tân Chọn D Hàm số 3 2
y = x − 3x − 9x +1 xác định và liên tục trên
, nên trên đoạn 0;4 hàm số luôn xác định và liên tục.
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 13 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019x = 1 − (0;4) Ta có: 2
y = 3x − 6x − 9 = 0   . x = 3  (0;4)
Khi đó : f (0) =1; f (3) = 26 − ; f (4) = 19 − .
So sánh các giá trị trên ta được : M = Maxy = 1; m = Miny = 26 − . 0;4 0;4
Suy ra: m + 2M = 26 − + 2 = 24 − .
Vậy m + 2M = 24 − . u
 − u + u = 65 1 3 5
Câu 24. Cho cấp số nhân (u thỏa mãn  . Tính u . n ) u + u = 325  3 1 7
A. u = 15 .
B. u = 25 . C. u = 10 . D. u = 20 . 3 3 3 3 Lời giải
Tác giả : Vũ Ngọc Tân, FB: Vũ Ngọc Tân Chọn D  − + =  − + = uu u u u u q u q  ( 2 4 2 4 1− q + q = 65 (1) 65 . . 65 1 ) Ta có: 1 3 5 1 1 1      6 u + u = 325  u  + u .q = 325  u  ( 6 + = 1 7 1 q 325 (2) 1 1 1 ) Chia từng vế của ( )
1 cho (2) ta được phương trình : 2 4 1− q + q 1 6 4 2
=  q − 5q + 5q − 4 = 0 * 6 ( ) 1+ q 5 Đặt 2
t = q , t  0 . t = 4
Phương trình (*) trở thành : 3 2
t − 5t + 5t − 4 = 0  (t − 4)( 2 t − t + ) 1 = 0   2
t − t +1 = 0(vn) Với 2
t = 4  q = 4  q = 2  . Với q = 2
 thay vào (2) ta được u = 5. 1 Vậy 2
u = u .q = 5.4 = 20. 3 1
anhtuanqh1@gmail.com 2 n C C
Câu 25. Biết số tự nhiên n thỏa mãn 1 C + 2 n + ... n + n = 45 . Tính n C n 1 n 1 + ? C C − n 4 n n A. 715. B. 1820 . C. 1365 . D. 1001. Lời giải
Tác giả : Nguyễn Anh Tuấn, FB: Nguyễn Ngọc Minh Châu Chọn A k.n! k C k ( ! n − k )!
Xét số hạng tổng quát: n k =
= n+1−k . với : k nN k n k 1 , ;1 . C − n! n (k − ) 1 ( ! n +1− k )! 2 n n (n + ) 1 Do đó: C C 1 C + 2 n + ... n + n
= 45  n + (n − ) 1 + ... +1 = 45  = 45 2
n + n − 90 = 0 n 1 n 1 C C − 2 n nn = 9  
n = 9 .Vậy n 9 C = C = 715.  + n = 1 − 0(l) n 4 13 x −1
Câu 26. Tìm tất cả các giá trị của m để hàm số y =
đồng biến trên khoảng (0;+ ) ? x + m A. ( 1 − ;+ ) .
B. 0; + ) . C. (0; + ) . D.  1 − ;+ ) .
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 14 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019 Lời giải
Tác giả : Nguyễn Anh Tuấn, FB: Nguyễn Ngọc Minh Châu Chọn B
Tập xác định: D = \ −  m . m +1 y ' = ( . x + m)2 −m  0
Hàm số đồng biến trên khoảng (0; + )    m  0 . m +1  0
Congnhangiang2009@gmail.com
Câu 27. Tìm tất cả các giá trị thực của tham số m sao cho điểm cực tiểu của đồ thị hàm số 3 2
y = x + x + mx −1 nằm bên phải trục tung? 1 1
A. m  0 . B. 0  m  . C. m  . D.Không tồn tại. 3 3 Lời giải
Tác giả : Hoàng Thị Thanh Nhàn, FB: Hoàng Nhàn Chọn A 3 2
y = x + x + mx −1 2
y = 3x + 2x + m .
Đồ thị hàm số có điểm cực tiểu khi và chỉ khi phương trình y = 0 có hai nghiệm phân biệt    =1−3m  1 0  m  (1). 3
Khi đó, giả sử x , x là hai nghiệm của phương trình y = 0 . 1 2  2 x + x = −  1 2  3   mx .x = 1 2  3 Bảng biến thiên 2 Do x + x = −
 0 nên hoặc nên điểm cực tiểu của đồ thị hàm số 3 2
y = x + x + mx −1 nằm 1 2 3 m
bên phải trục tung  x .x  0   0  m  0 (2). 1 2 3 ( )1,(2)  m  0 .
Câu 28. Sinh nhật của An vào ngày 1 tháng 5. Bạn An muốn mua một chiếc máy ảnh giá khoảng 600.000
đồng để làm quà sinh nhật cho chính mình. Bạn ấy quyết định bỏ ống tiết kiệm 10.000 đồng vào
ngày 1 tháng 1 của năm đó, sau đó cứ tiếp tục những ngày sau, mỗi ngày bạn bỏ ống tiết kiệm
5.000 đồng. Biết trong năm đó, tháng 1 có 31 ngày, tháng 2 có 28 ngày, tháng 3 có 31 ngày và
tháng 4 có 30 ngày. Gọi a (đồng) là số tiền An có được đến sinh nhật của mình (ngày sinh nhật
An không bỏ tiền vào ống). Khi đó ta có:
A. a 610000;615000) .
B. a 605000;610000) .
C. a 600000;605000) .
D. a 595000;600000) .
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 15 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019 Lời giải
Tác giả : Hoàng Thị Thanh Nhàn, FB: Hoàng Nhàn Chọn B
Theo giả thiết An bỏ ống tiết kiệm từ ngày 1 tháng 1 đến ngày 30 tháng 4 nên tổng số ngày bỏ tiết kiệm là 120 ngày.
Ngày thứ nhất An bỏ ống: 10000 đồng.
119 ngày sau An bỏ ống số tiền là: 119  5000 = (120 −1)  5000 = 600000 − 5000 đồng.
Vậy tổng số tiền tiết kiệm là: a = 600000 −5000 +10000 = 605000đồng.
tranquocan1980@gmail.com   
Câu 29. Số nghiệm của phương trình sin 5x + 3 cos 5x = 2sin 7x trên khoảng 0;    2  là ? A. 4 . B. 1. C. 3 . D. 2 . Lời giải
Tác giả :Trần Quốc An, FB: TranQuocAn Chọn A   
Ta có : sin 5x + 3 cos 5x = 2sin 7x  sin 5x + = sin 7x    3      7x = 5x + + k2 x = + k   3 6     , k      
7x =  − 5x − + k2 x = + k  3  18 6   1 1  TH1 : 0  + k 
 −  k   k = 0  x = 6 2 6 3 6    1 1 1  2 7 TH2 : 0  + k
 0  + k  3  −  k  3−  k = 0,1, 2  x = , , . 18 6 2 3 3 3 18 9 18   2 7   Vậy x   , , ,  .Chọn A 1  8 9 18 6 
Câu 30. Cho hàm số f (x) có đạo hàm trên và /
f (x)  0, x
  .Biết f (1) = 2. Hỏi khẳng định nào
sau đây có thể xảy ra ?
A. f (2) + f (3) = 4. B. f ( 1 − ) = 2. C. f (2) = 1.
D. f (2018)  f (2019). Lời giải
Tác giả :Trần Quốc An, FB: TranQuocAn Chọn B Xét đáp án A: 2 3 2 3 Ta có : f (
x)dx + f (x)dx  0dx + 0dx = 0  f (2) − f (1) + f (3) − f (1)  0  4 − 4  0     Vô 1 1 1 1
lý . Nên phương án A không thể xảy ra. Xét đáp án C: 2 2 Ta có : f (
x)dx  0dx = 0  f (2) − f (1)  0 1− 2  0  
Vô lý . Nên phương án C không thể 1 1 xảy ra. Xét đáp án D : 2019 2019 Ta có : f (  x)dx
0dx = 0  f (2019) − f (2018)  0  f (2019)  f (2018)   . Nên phương 2018 2018 án D không thể xảy ra.
Bằng phương pháp loại suy ,ta có đáp án B.
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 16 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Tuy nhiên , ta có thể chỉ ra một hàm 2
f (x) = x +1 thỏa mãn đáp án B vì
f (x)  0, x     f ( 1 − ) = 2  f (1) = 2
Duanquy@gmail.com.
Câu 31. Cho tập hợp A = 0,1, 2,3, 4,5, 
6 . Từ tập A lập được bao nhiêu số tự nhiên chẵn có 4 chữ số khác nhau và nhỏ hơn 4012 A. 180 . B. 240 . C. 200 . D. 220 . Lời giải
Tác giả: Nguyễn Đức Duẩn, FB: Duan Nguyen Duc Chọn D
Gọi số cần lập là abcd . Vì abcd  4012  a  3 .
+) TH1: Nếu a = 1 khi đó số các số chẵn lập đc là 2 1.4.A = 80 . 5
+) TH2: Nếu a = 3 khi đó số các số chẵn lập đc là 2 1.4.A = 80 . 5
+) TH1: Nếu a = 2 khi đó số các số chẵn lập đc là 2 1.3.A = 60 . 5
Vậy số các số lập được thỏa mãn đề bài là 80 + 80 + 60 = 220 . 1 − 3 2
Câu 32. Một vật chuyển động theo quy luật s =
t + 9t , với t (giây) là khoảng thời gian tính từ lúc 2
vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi
trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
A. 216 (m / s) .
B. 400 (m / s) .
C. 54 (m / s) .
D. 30 (m / s) . Lời giải
Tác giả: Nguyễn Đức Duẩn, FB: Duan Nguyen Duc Chọn C 1 − 3 − 3 2 2 Vì s =
t + 9t v = t + 18t . 2 2 3 − 2
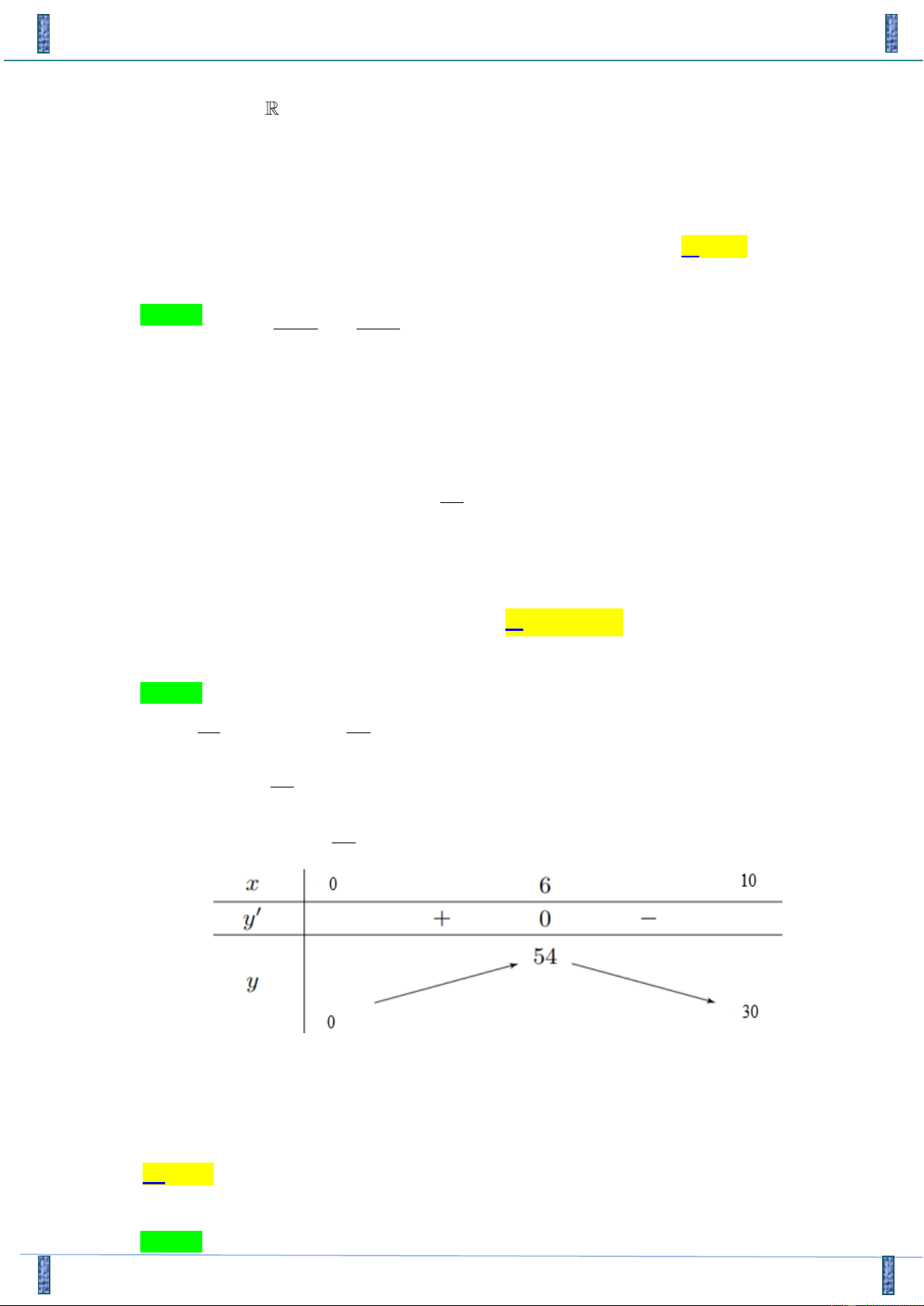
Xét hàm f (t) =
t +18t f '(t) = 3
− t+18 , f '(t) = 0  t = 6 . 2 3 − 2
BBT của hàm số f (t) = t + 18t . 2
Dựa vào BBT ta thấy max f (t) = 54 . (0;10)
Vậy vận tốc lớn nhất vật đạt được là v = 54 (m / s) max .
luuhuephuongtailieu@gmail.com
Câu 33. Tất cả các giá trị của tham số m để hàm số y = (m − ) 4
1 x đạt cực đại tại x = 0 là A. m 1. B. m  1.
C. không tồn tại m. D. m = 1. Lời giải
Tác giả : Lưu Huệ Phương, FB: Lưu Huệ Phương Chọn A
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 17 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Trường hợp 1: Nếu m = 1  y = 0 → Hàm số không có cực trị.
Vậy m =1 không thỏa mãn.
Trường hợp 2: Nếu m 1
Ta có: y = (m − ) 3 4
1 x , y = 0  x = 0.
Để hàm số đạt cực đại tại x = 0 thì y phải đổi dấu từ (+) sang (−) qua x = 0. Khi đó 4(m − ) 1  0  m  1.
Vậy m 1 thỏa mãn yêu cầu bài toán.
luuhuephuongtailieu@gmail.com
Câu 34. Tung hai con súc sắc 3 lần độc lập với nhau. Tính xác suất để có đúng một lần tổng số chấm
xuất hiện trên hai con súc sắc bằng 6. Kết quả làm tròn đến 3 ba chữ số ở phần thập phân) A. 0,120. B. 0, 319. C. 0, 718. D. 0, 309. Lời giải
Tác giả : Lưu Huệ Phương, FB: Lưu Huệ Phương Chọn D
Khi gieo hai con súc sắc trong một lần gieo thì có tất cả 36 khả năng có thể xảy ra.
Gọi A là biến cố: “Có đúng một lần gieo tổng số chấm xuất hiện trên hai con súc sắc bằng 6 ”
Ta có: 6 =1+ 5 = 5 +1 = 2 + 4 = 4 + 2 = 3+ 3.
Khi gieo hai con súc sắc trong cùng một lần gieo thì xác suất để tổng số chấm xuất hiện trên hai 5 con súc sắc bằng 6 là
và xác suất để tổng số chấm xuất hiện trên hai con súc sắc không bằng 36 31 6 là . 36 2 5  31  4805
Vậy xác suất cần tìm là: P ( A) 1 = C . . =  0,309. 3   36  36  15552
nguyenthithutrang215@gmail.com
Câu 35. Hệ số của 5
x trong khai triển ( − x − x )9 2 1 2 3 là A. 792 . B. 684 − . C. 3528 . D. 0 . Lời giải
Tác giả : Nguyễn Thị Thu Trang, FB: Trang Nguyễn Chọn C Ta có: (1−2x−3x )9 2 = 1  +  ( 2 2
− x − 3x ) 9 9 − − − − = C ( k k m k m k 2 − x − 3x ) 9 9 9 k m = C C − x − x −k ( 2 )9 2 ( 2 3 9 9 9 ) k =0 k =0 m=0 9 9−k − − = C C − − x − + −k ( k m m k m 2)9 ( 3) 9 k m 9 9 k =0 m=0
0  m k  9  m = 0,k = 4 m  9 − k  Số hạng chứa 5 x khi   m =1,k = 5 9 k m 5  − + =  m = 2,k = 6   , m k
Vậy hệ số của số hạng chứa 5 x là: C C ( 2 − )5 ( 3 − )0 +C C ( 2 − )3 ( 3 − )1 +C C ( 2 − )1 ( 3 − )2 4 0 5 1 6 2 = 3528 9 5 9 4 9 3
Câu 36. Cho một khối đa diện lồi có 10 đỉnh, 7 mặt. Hỏi khối đa diện này có mấy cạnh? A. 20 . B. 18 . C. 15 . D. 12 . Lời giải
Tác giả : Nguyễn Thị Thu Trang, FB: Trang Nguyễn
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 18 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019 Chọn C
Ta có d + m − c = 2  c =15
Vậy khối đa diện có 15 cạnh
kimoanh0102@gmail.com
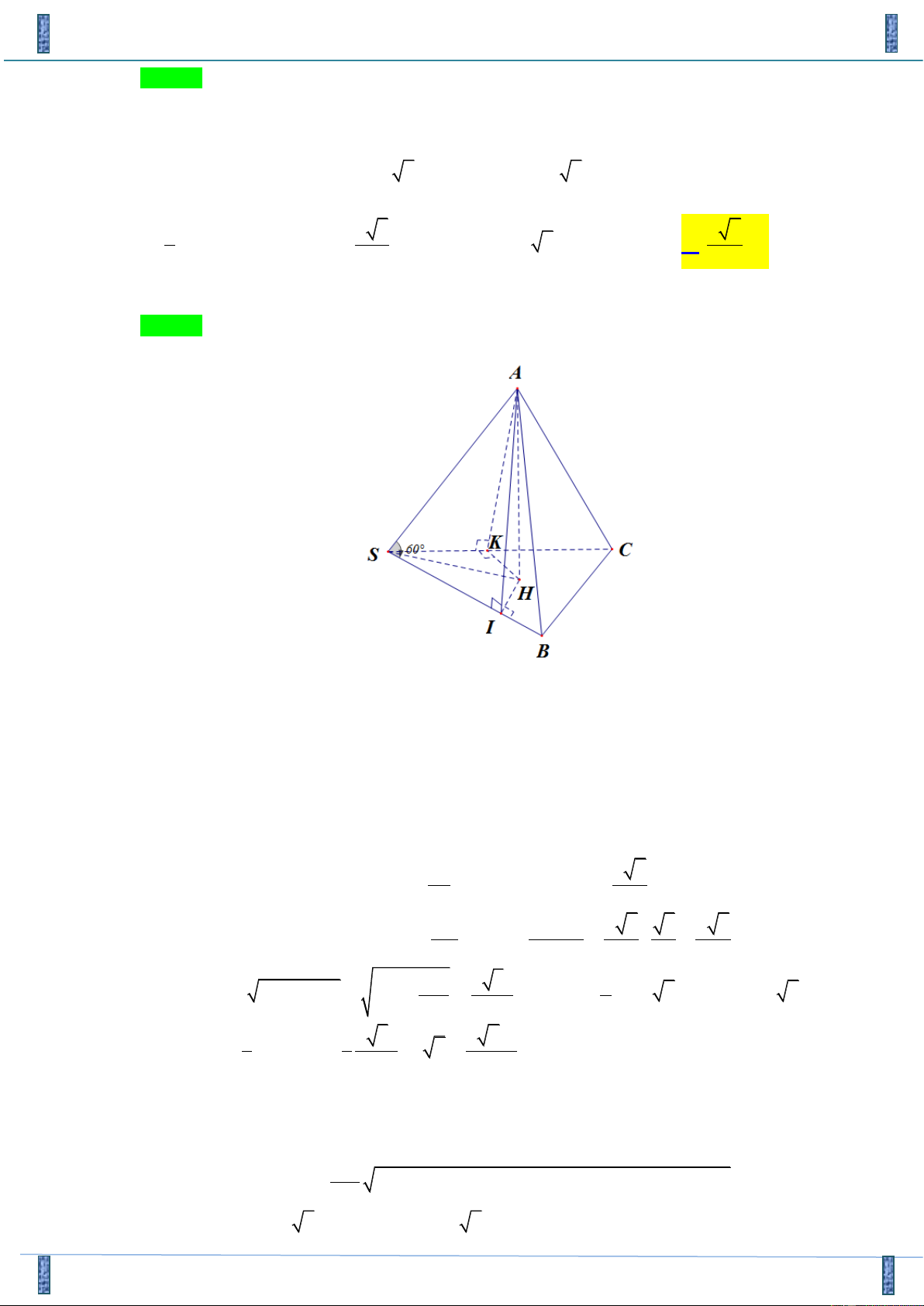
Câu 37. Cho hình chóp S.ABC có SA = 2 , a SB = 2 ,
a SC = 2 2a và ASB = BSC = CSA =  60 . Tính
thể tích của khối chóp đã cho. 4 3 2 3 3 2 2 3 A. a a a 3 . B. 3 . C. 3 2a . D. 3 . Lời giải
Tác giả: Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh Chọn D Cách 1
Gọi H là hình chiếu vuông góc của A lên mp (SBC) . Gọi I,K lần lượt là hình chiếu vuông
góc của H lên SB và SC . SB ⊥ HI Ta có 
SB ⊥ SI . Chứng minh tương tự ta được SC ⊥ SK . SB ⊥ SH
SAI = SAK (cạnh huyền – góc nhọn)  SI = SK .
Khi đó SHI = SHK (cạnh huyền – cạnh góc vuông)  HI = HK . Do đó SH là đường phân
giác trong của BSC , nên HSI =  30 . SI a 2
Trong tam giác vuông SAI , cos  60 =  SI = S . A cos  60 = SA 2 . SI SI a 2 3 a 6
Trong tam giác vuông HIS , cos  30 =  SH = = : = SH cos  30 2 2 3 . 2 a a 1 Khi đó 2 2 2 2 2 3
AH = SA − SH = 2a − = S .2 . a 2 2 . a sin60 a 6 3 3 , và =  = 2 SBC 2 . 3 1 1 2 3a 2 2 2a Vậy V = AH.S = .a 6 = S.ABC 3 SBC 3 3 3 .
Cách 2: Sử dụng công thức tính nhanh
SA = a, SB = , b SC = c
Nếu khối chóp S.ABC có  thì ASB = , S B C =  , S C A =  abc 2 2 2 V =
1 − cos  − cos  − cos  + 2 cos cos  cos S . ABC 6 Áp dụng: Với SA = 2 , a SB = 2 ,
a SC = 2 2a và ASB = BSC = CSA =  60 , ta có
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 19 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019 3 2 . a 2 . a 2 2a 2 2a 2 3 V =
1− 3.cos 60 + 2.cos 60 = . S.ABC 6 3 Cách 3
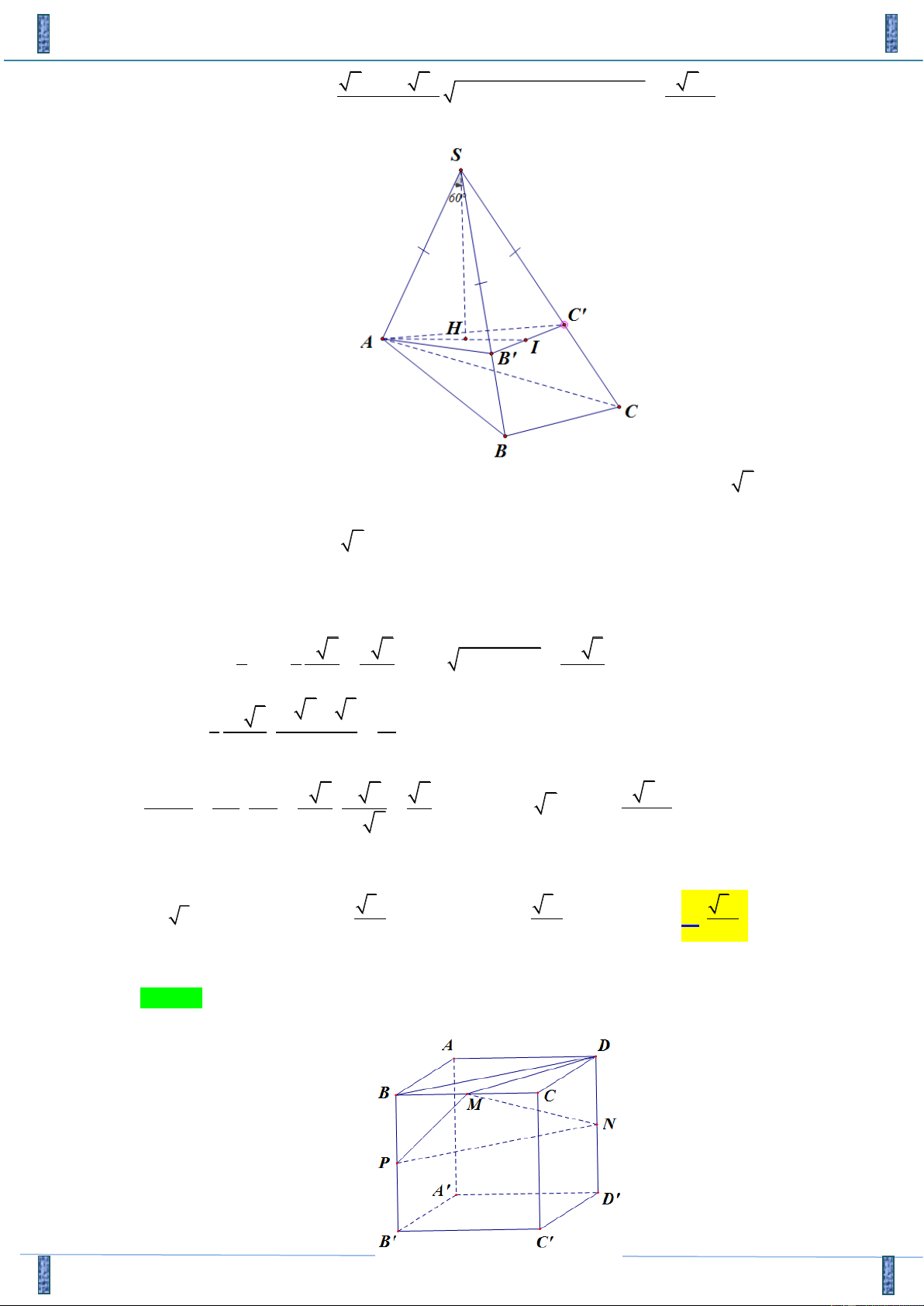
Trên các cạnh SB , SC lần lượt lấy các điểm B,C sao cho S
B = SC = SA = a 2 . Khi đó chóp . S A
B C là khối chóp tam giác đều. Đồng thời ASB = BSC = CSA =  60 nên A B = 
B C = AC = SA = a 2 .
Gọi H là hình chiếu của S lên mặt phẳng ( A
B C). Khi đó dễ dàng chứng minh được các tam giác SH , A SH
B ,SHC bằng nhau. Suy ra H , A H
B ,HC bằng nhau. Hay H là tâm đường tròn
ngoại tiếp tam giác A B
C . Vì tam giác A B
C đều nên H cũng là trọng tâm tam giác A B C . 2 2 a 6 a 6 2 2 2a 3 Ta có AH = AI = =
;SH = SA − AH = 3 3 2 3 3 1 2a 3 (a 2)2 3 3 a V = . =
S.ABC 3 3 4 3 Ta có V S
B SCa 2 a 2 2 3 2 2a
S.ABC = . = . =  V = 2 2V = V SB SC 2a S.ABC
S.ABC 3 . S ABC 2a 2 4 .
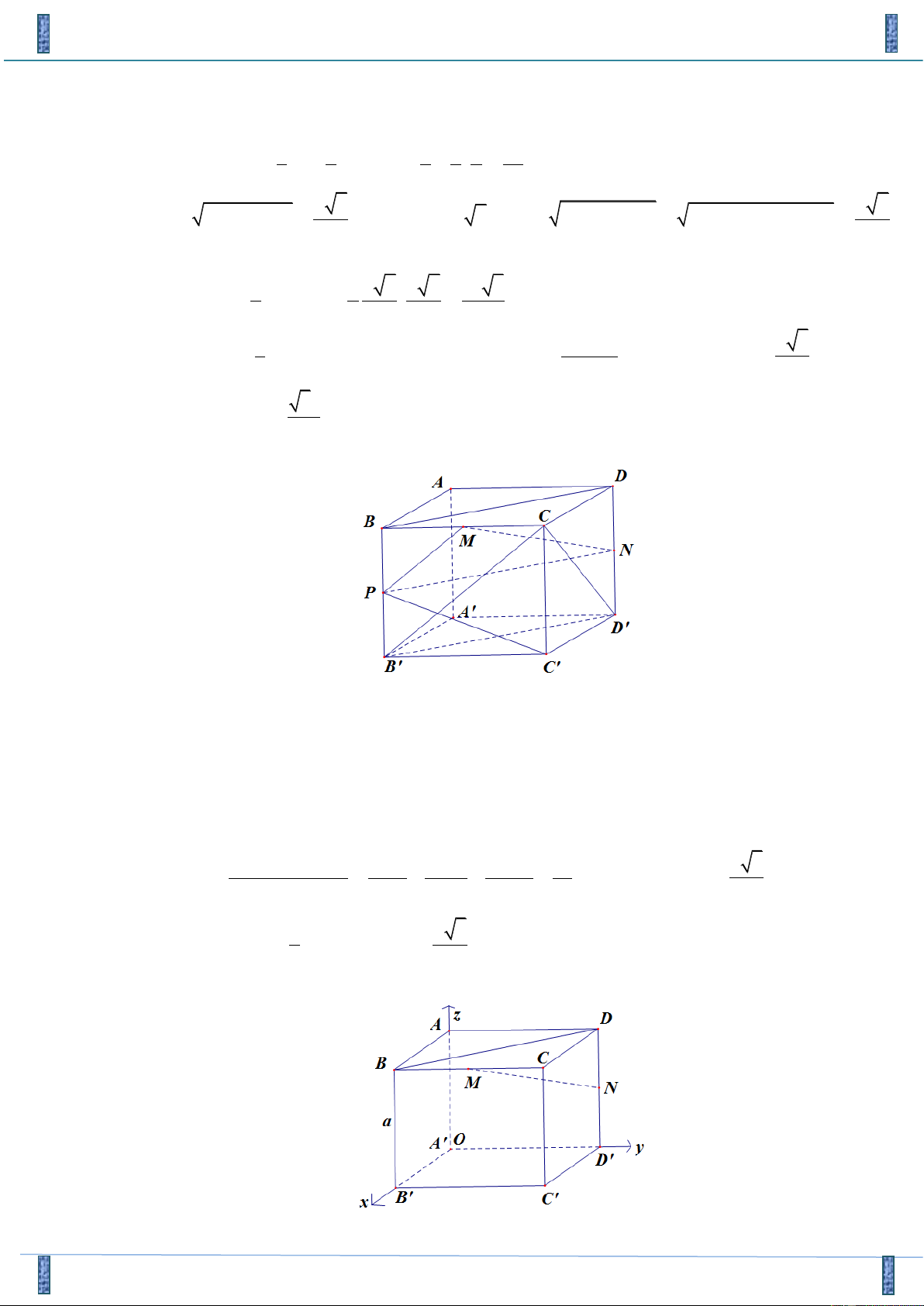
Câu 38. Cho hình lập phương ABC . D A B C
D cạnh a . Gọi M,N lần lượt là trung điểm của BC và
DD. Tính theo a khoảng cách giữa hai đường thẳng MN và BD . 3a 3a 3a A. 3a . B. . C. . D. . 2 3 6 Lời giải
Tác giả: Bùi Thị Kim Oanh, FB: Bùi Thị Kim Oanh Chọn D Cách 1
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 20 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
Gọi P là trung điểm BB Ta có BD // PN BD// (MPN ) . Do đó
d (MN;BD) = d(B ;
D (MPN)) = d( ; B (MPN)) . 3 1 1 1 = = . . . . = . a . a a V V CD BP BM a = B.PMN N .BMP 3 2 6 2 2 24 . a 2 2 2 2 2 2 2 2 a 6
MP = BP + BM =
; PN = BD = a 2; MN = MD + DN = CM + CD + DN = 2 2 2 2 2
Nhận thấy MP + MN = PN nên tam giác MPN vuông tại M . 2 1 1 a 2 a 6 a 3 Do đó S = MP.MN = . = MPN 2 2 2 2 4 . 1 3V a 3 Ta có V = d B MPN S d B MPN
d (B, MPN ) = PMN ( ,( )).  MPN ( ,( )) = B.PMN B. 3 S ( ) 6 . MPN 3a
Vậy d (MN,BD) = 6 . Cách 2:
Gọi P là trung điểm BB . Ta có BD // PN BD// (MPN ) .
Đồng thời, MP // C B ,PN //  B
D  (MPN) // (C B D ) . Do đó
d (MN,BD) = d(B ,
D (MPN)) = d( ,
B (MPN)) = d(C,(MPN)) (vì  PC cắt 
B C tại trọng tâm của tam giác B B C ). Nhận thấy tứ diện  C .C B
D là tứ diện vuông tại C nên 1 1 1 1 3 a 3
d (C,(CBD) = . 2
d (C,(C B D)) = + + = C 2 C C 2 B' C 'D2 2 a 3 1 a 3
Vậy d (MN,BD) = d (C,(CBD)) = 2 6 .
Cách 3: Tọa độ hóa
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 21 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019a   a
Chọn hệ trục tọa độ Oxyz như hình vẽ. Khi đó, B ( ;
a 0;a), D(0; ;aa), M ;a ;a , N 0; ;a  2   2  .     BD ( ; a ; a 0)  a a   a  = − , MN = − ; a ;− , BM =   0; ;0 .  2 2   2   a a a  2  a B ; D MN = − ;−  ;  B ; D MN .BM   ;   = − .  2 2 2    4 B ; D MN.BM d (BD MN) 2   a a 3 a 3 ; = = : = .   4 2 6 B ; D MN  
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SAD là tam giác đều và nằm
trong mặt phẳng vuông góc với ( ABCD) . Gọi M , N , P lần lượt là trung điểm các cạnh
SB, BC, CD . Tính thể tích khối tứ diện CMNP . 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 48 96 54 72 Lời giải
Tác giả : Nguyễn Hoàng Hưng, FB: Nguyễn Hưng Chọn B S M A B H K N D P C
Gọi H là trung điểm của cạnh AD . Do tam giác SAD đều nên SH ⊥ AD . (SAD) ⊥ (ABCD)  ( 
SAD)  ( ABCD) = AD  SH ⊥ ( ABCD) 
SH  (SAD), SH ⊥ AD
Gọi K là trung điểm của HB MK //SH .
Do đó: MK ⊥ ( ABCD)  MK ⊥ (CNP)
Vậy MK là chiều cao của khối tứ diện CMNP . 1 1 a 3 a 3 MK = SH = . = 2 2 2 4 2 1 1 a a a S = .CN.CP = . . = CNP 2 2 2 2 8 2 3 1 1 a a 3 3a
Thể tích của khối tứ diện CMNP là V = S .MK = . . = . CMNP 3 CNP 3 8 4 96 x − 2018
Câu 40. Số tiệm cận ngang của đồ thị hàm số y = x + là 2019 A. 1. B. 3 . C. 2 . D. 0 .
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 22 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019 Lời giải
Tác giả : Nguyễn Hoàng Hưng, FB: Nguyễn Hưng Chọn C 2018 1− x − 2018 x − 2018 Ta có: lim = lim = lim = lim x y =1 x→+
x→+ x + 2019
x→+ x + 2019 x→+ 2019 1+ x 2018 1 − − x − 2018 −x − 2018 lim = lim = lim = lim x y = 1 − x→−
x→− x + 2019 x→− x + 2019 x→− 2019 1+ x
Do đó đồ thị hàm số có hai tiệm ngang là các đường thẳng y = 1 − , y =1.
anglenghia@gmail.com
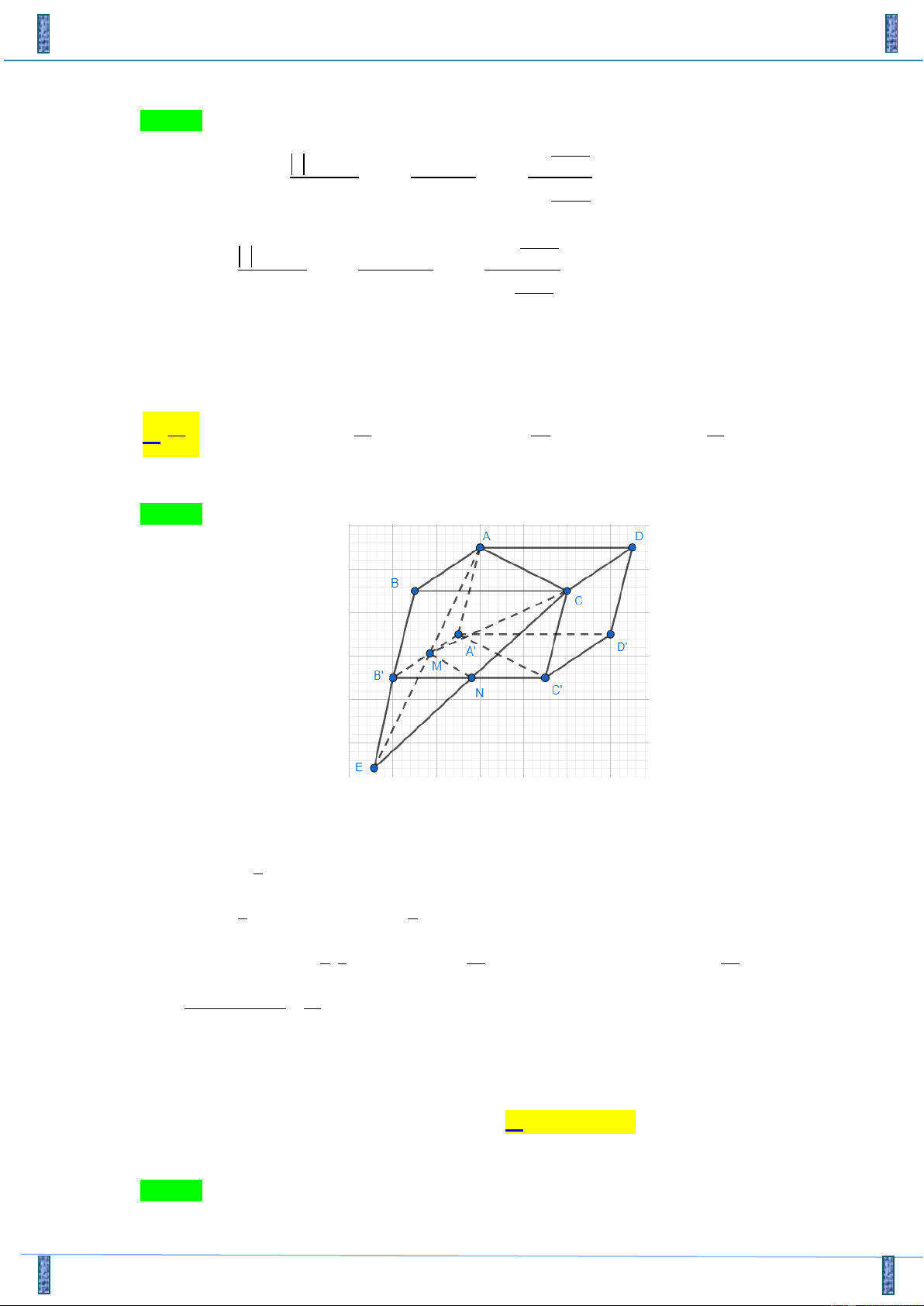
Câu 41. Cho khối hộp ABC . D ’ A ’ B ’ C ’
D có M là trung điểm ’ A ’
B . Mặt phẳng ( ACM ) chia khối hộp đã
cho thành hai phần. Tỉ số thể tích của hai phần đó bằng? 7 5 7 7 A. . B. . C. . D. . 17 17 24 12 Lời giải
Tác giả : Trần Đắc Nghĩa, FB: Đ Nghĩa Trần Chọn A
Gọi N là trung điểm ’
B C’ và E là điểm đối xứng với B qua ’ B
Khi đó khối hộp ABC . D ’ A ’ B ’ C ’
D được mặt phẳng ( ACM ) chia thành 2 khối đa diện BAC. ’ B MN và ACDMN ’ C ’ D ’ A 1 Ta có = E V .BAC A V BC .
D A' B 'C ' D ' 3 1 7 và =  = E V .B'MN E V .BAC B V AC. ’ B MN E V .BAC 8 8 7 1 7 17 Từ đó ta có = =  = B V AC. ’ . B MN A V BC .
D A' B 'C ' D ' A V BC .
D A' B 'C ' D ' A V CDMNC’ ’ D ’ A A V BC .
D A' B 'C ' D ' 8 3 24 24 V 7 Nên:
BAC.B ' MN = VABC .
D A' B 'C ' D ' 17
anglenghia@gmail.com
Câu 42. Đồ thị của hàm số ( ) 3 2
f x = x + ax + bx + c tiếp xúc với trục hoành tại gốc tọa độ và cắt đường
thẳng x = 1 tại điểm có tung độ bằng 3 khi
A. a = b = 0,c = 2 .
B. a = c = 0,b = 2 .
C. a = 2,b = c = 0 .
D. a = 2,b =1,c = 0 . Lời giải
Tác giả : Trần Đắc Nghĩa, FB: Đ Nghĩa Trần Chọn C Ta có : f ( x) 2 '
= 3x + 2ax + b
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 23 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019f  (0) = 0 c = 0
Đồ thị hàm số tiếp xúc với trục hoành tại gốc tọa độ O(0;0) nên     f '  (0) = 0 b  = 0
Đồ thị hàm số đi qua điểm A(1;3) nên 3 =1+ a a = 2
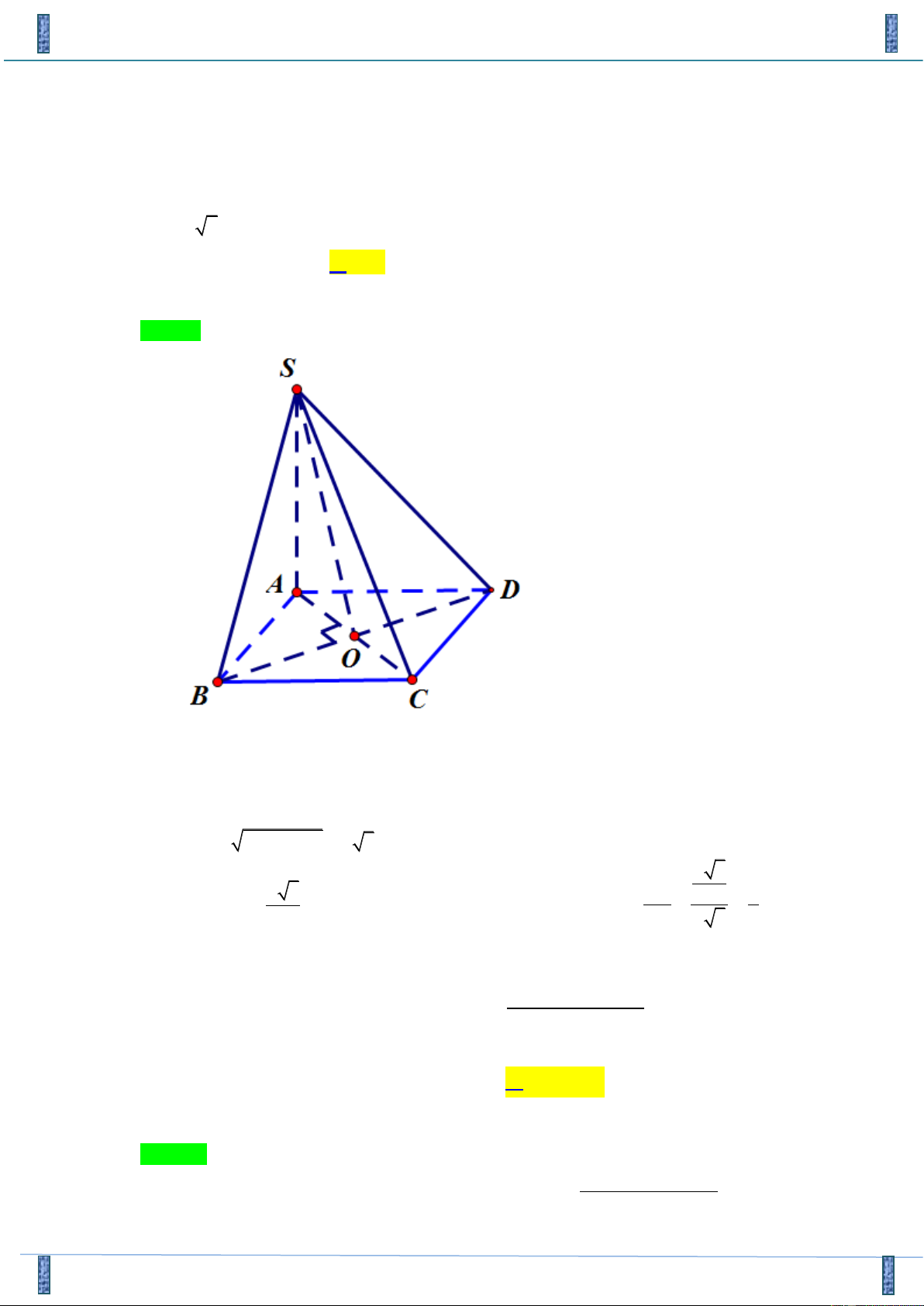
nguyentuyetle77@gmail.com 0
Câu 43. Chuyên Vinh. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , ABC = 60 , cạnh bên
SA = a 2 và SA vuông góc với ABCD .Tính góc giữa SB và (SAC) . A. 0 90 . B. 0 30 . C. 0 45 . D. 0 60 . Lời giải
Tác giả : NguyễnTuyết Lê, FB: Nguyên Tuyet Le Chọn B
Gọi O = AC BD . Vì ABCD là hình thoi nên BO ⊥ AC (1) . Lại do:
SA ⊥ ( ABCD)  SA ⊥ AC (2) . Từ (1) và (2) ta có :
BO ⊥ (SAC)  (S ;
B (SAC)) = (S ; B SO) = BSO . Ta có: 2 2 SB =
SA + AB = a 3 . Vì ABCD là hình thoi có 0
ABC = 60 nên tam giác ABC đều a 3 a 3 BO 1
cạnh a BO =
.Trong tam giác vuông SBO ta có: 2 sin BSO = = = 2 SB a 3 2 0  BSO = 30 .
nguyentuyetle77@gmail.com 2 2
x + 2mx + 2m −1
Câu 44. Gọi m là giá trị để đồ thị (C ) của hàm số y = m x −
cắt trục hoành tại hai điểm 1
phân biệt và các tiếp tuyến với (C ) tại tại hai điểm này vuông góc với nhau. Khi đó ta có: m
A. m (1; 2) . B. m ( 2 − ;− ) 1 . C. m (0 ) ;1 . D. m ( 1 − ;0) . Lời giải
Tác giả : NguyễnTuyết Lê, FB: Nguyên Tuyet Le Chọn C . 2 2 + + − Phương trình hoành độ x 2mx 2m 1
giao điểm của (C ) và trục Ox là: = 0(1) m x −1 .
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 24 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019 (C ) m
cắt Ox tại hai điểm phân biệt ;
A B khi và chỉ khi phương trình (1) có hai nghiệm phân 2 2  = + + − = x ; x  1 biệt g(x) x 2mx 2m 1
0 có hai nghiệm phân biệt 1 2  1 −  m 1 2  =1− m  0  −  m g 1 1    m  1 −   (a) 2  = +   m  0 g(1) 2m 2m 0 m  0 . 2 2
(2x + 2m)(x −1) − (x + 2mx + 2m −1) Ta có : ' y = 2 (x −1)
Hệ số góc của (C ) tại hai điểm , A B là: m 2 2 (2x + 2 )
m (x −1) − (x + 2mx + 2m −1) 2x + 2m 1 1 1 1 1 k = = 1 2 (x −1) x −1 1 1 2 2 (2x + 2 )
m (x −1) − (x + 2mx + 2m −1) 2x + 2m 2 2 2 2 2 k = = 2 2 (x −1) x −1 2 2
Hai tiếp tuyến này vuông góc với nhau  k .k = 1 − 1 2 2x + 2m 2x + 2m 1 2  ( ).( ) = 1 − x −1 x −1 1 2 2
 4 x .x + (
m x + x ) + m  = −x .x + (x + x ) −1(2)  1 2 1 2  1 2 1 2 .   = − x + x = 2 − m m 1 1 2 Lại có:  . Do đó 2 
(2)  6m + 2m − 4 = 0  2 . 2
x .x = 2m −1  m = 1 2  3 Đố 2
i chiếu điều kiện ta có m = . 3
tcdung.math@gmail.com
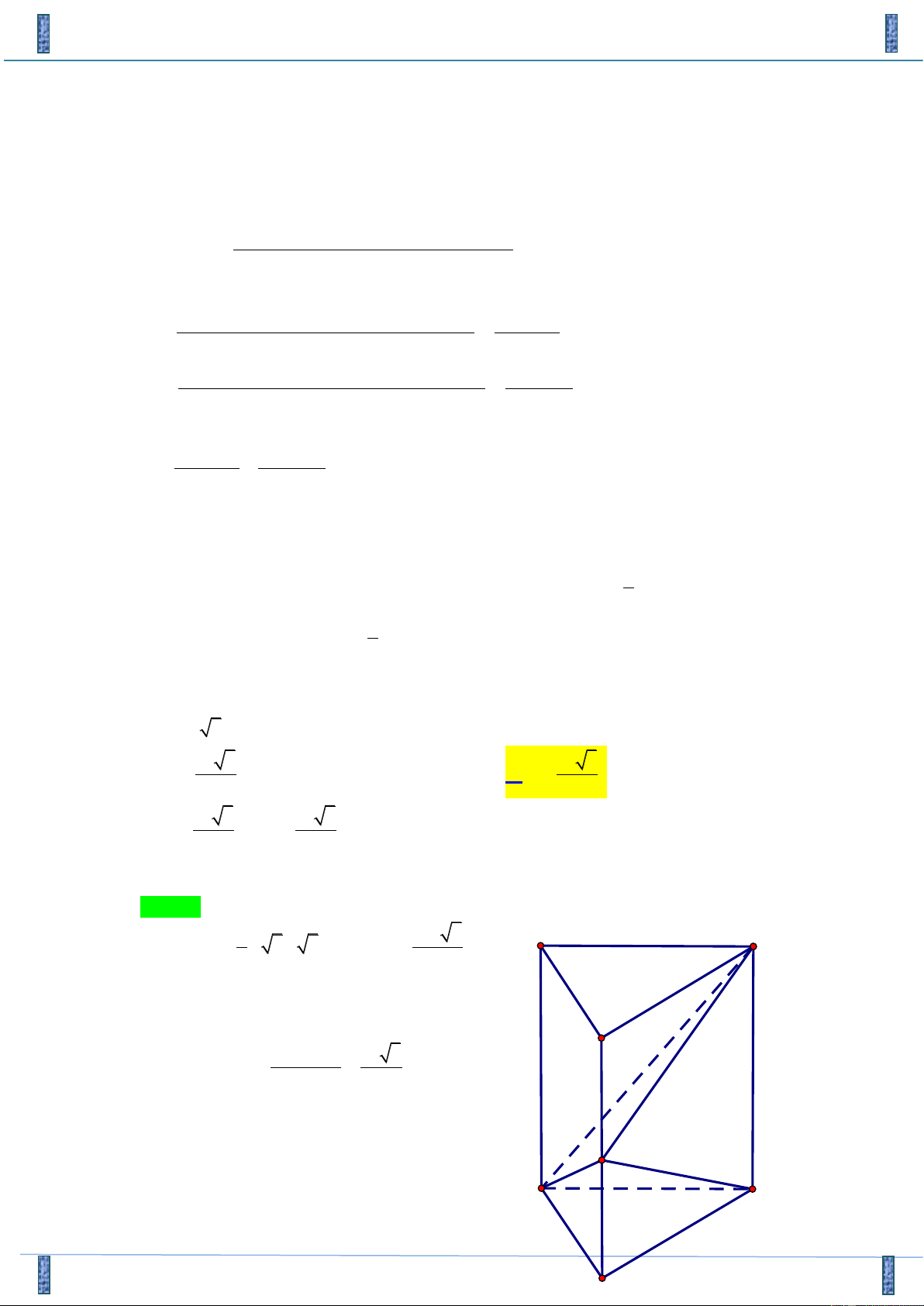
Câu 45. Cho lăng trụ đứng / / / ABC.A B C
có đáy ABC là tam giác cân tại C, 0 BAC = 30 , /
AB = a 3, AA = .
a Gọi M là trung điểm của /
BB . Tính theo a thể tích V khối tứ diện / MACC . 3 a 3 3 a 3 A.V = . B.V = . 12 4 3 a 3 3 a 3 C.V = .D.V = 3 18 Lời giải
Tác giả :TrầnCôngDũng, FB: trancong.dung.948 Chọn B 3 A' 1 3a 3 0 C' V
= a 3.a 3.sin120 .a = / / / ABC.A B C . 2 4 . d (M ( /
ACC ) = d (B ( / , , ACC ) Vì MB//(ACC’) nên Do đó 3 B' V / / / a 3 ABC. A B C V = V = = / / MACC BACC 3 4 . M A C
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 25 Mã đề 132 B
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019
tcdung.math@gmail.com
Câu 46. Cho hàm số y = f ( x). Hàm số /
y = f ( x) có đồ thị
như hình vẽ bên. Hỏi hàm số y = f ( x − 3) đồng biến
trên khoảng nào sau đây: A. (2; 4) . B. (1;3) . C. (−1;3). D. (5;6) Lời giải
Tác giả :TrầnCôngDũng, FB: trancong.dung.948 Chọn D 1
f '(x)  0  [x−
Nhận xét: Từ đồ thị f’(x), ta có 1x 3  x −3  1 − x  2 /
f ( x − 3)  0     1   x −3  3 4  x  6 Từ đó . Do đó chọn D.
thaygiaothaogiay@gmail.com
Câu 47. Cho hàm số y = f ( x) có bảng biến thiên như hình vẽ sau:
Khi đó số nghiệm của phương trình 2 f (2x −3) −5 = 0 là: A. 3 . B. 2 . C. 4 . D.1. Lời giải
Tác giả :Đinh Phước Tân, FB: Tân Độc Chọn B   + f ( x − ) 5 a 3 2 3 = x =  2x − 3 = a  Ta có f ( x − ) 2 2 2 2 3 − 5 = 0         − = +  f ( x − ) 5 2x 3 b b 3 2 3 = − x =  2  2
Trong đó a  0;b  1. Vậy phương trình đã cho có 2 nghiệm phân biệt.
thaygiaothaogiay@gmail.com
Câu 48. Tìm số tiệm cận (bao gồm tiệm cận đứng và tiệm cận ngang) của đồ thị hàm số 2 4x + 5 y = 2x +1 − x −1 A.3. B.1. C.2. D. 4. Lời giải
Tác giả : Đinh Phước Tân, FB: Tân Độc Chọn C
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 26 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019  1 
Hàm số có tập xác định là − ; +  \     0 .  2  2 4x + 5 Ta có lim y = lim = 2 −  y = 2
− là đường tiệm cận ngang của đồ thị hàm số đã x→+ x→+ 2x +1 − x −1 cho.  x +1  0
Mặt khác, 2x +1 = x +1    x = 0 2 2x +1= (x+1)
Với mọi x  0 ta có x   x + x +  x +  ( x + )2 2 2 0 2 1 2 1 1
 2x +1 x +1 2x +1 2 4x + 5
 2x +1 − x −1 0  lim y = lim
= −  x = 0 là đường tiệm cận đứng của + + x→0 x→0 2x +1 − x −1
đồ thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận.
Minhchung238@gmail.com
Câu 49. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D , AB = 2a ,
AD = CD = a , SA = 2a , SA ⊥ ( ABCD) . Tính côsin của góc tạo bởi (SBC) và (SCD) . 6 6 2 3 A. . B. . C. . D. . 6 3 3 3 Lờigiải
Tác giả :Võ Minh Chung, FB: Võ Minh Chung Chọn B z S B O x A D y C
Chọn hệ trục tọa độ Oxyz như hình vẽ.
Ta có: A(0, 0, 0), S (0,0, 2 ), D(0,1,0), B(2,0,0),C (1,1,0) .
Vecto pháp tuyến của (SCD) : n = SC, SD = 0, 2,1 . 1   ( )
Vecto pháp tuyến của (SBC ) n = SB, SC = 2, 2, 2 . 2   ( ) n n 6
Vậy: cos ((SBC ),(SDC )) 1 2 = = . n n 3 1 2 3 mx
Câu 50. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 2 y =
+ 7mx +14x − m + 2 nghịch 3 biến trên 1; +) .  14   14   14   14  A. ; − −   . B. ; − −  . C. 2; − − . D. − ; +   .     15   15   15   15 
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 27 Mã đề 132
Sản phẩm của Group FB: TEAM TOÁN VD–VDC
Đề Giữa HK1 Lớp 12 Chuyên ĐH Vinh 2018-2019 Lờigiải
Tác giả :Võ Minh Chung, FB: Võ Minh Chung Chọn A Ta có: 2
y ' = mx + 14mx + 14 .
Hàm số đã cho nghịch biến trên 1; +) khi và chỉ khi 2
y ' = mx + 14mx + 14  0, x   1;+) −  m( 14 2 x + 14)  14 − , x
 1;+)  m  , x   1;+ 1 . 2  )( ) x + 14 − Đặ 14 28x t f ( x) = , x
 1;+)  f '(x) =  0, x   1;+ . 2  ) 2 x + 14 ( 2x +14) −
Do đó: Min f ( x) = f ( ) 14 1 = (2) . 1;+) 15  14  Từ ( )
1 , (2) suy ra giá trị m cần tìm là: m  ; − −   .  15 
Group FB: STRONG TEAM TOÁN VD-VDC.- Group chỉ dành cho các Gv, Sv toán!
Trang 28 Mã đề 132