Đề KSCL giữa học kì 1 Toán 9 năm 2020 – 2021 phòng GD&ĐT Hà Đông – Hà Nội

Đề KSCL giữa học kì 1 Toán 9 năm 2020 – 2021 phòng GD&ĐT Hà Đông – Hà Nội gồm 01 trang với 05 bài toán dạng tự luận, thời gian học sinh làm bài thi là 60 phút. Mời bạn đọc đón xem.

23 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 9

Môn: Toán 9

Thông tin:

4 trang 7 tháng trước

Tác giả:

Profile Hà Việt Anh
HƯỚNG DẪN GIẢI
Bài 1: 1)
2 50
24.6
33
A

=+−



6 56
26.6
33
A

=+−



66
26.6
3
A

= −



( )
26 26.6A = −
0. 6 0A = =
.
2)
14 7 15 5 1
:
21 31 7 5
B

−−
= +


− −−

( )
( )
7 5. 7 5B =+−
752B =−=
.
Bài 2: 1) ĐKXĐ:
0x ≥
.
3 5 12 7 27 12xx x−+ =
3 5.2 3 7.3 3 12xxx⇔− + =
3 10 3 21 3 12xxx⇔− + =
12 3 12x⇔=
31x⇔=
31x⇔=
1
0
3
x⇔=>
(thỏa mãn điều kiện).
Vậy phương trình có tập nghiệm
1
3
S

=


.
2)
3
2
23x +=
22
2 27 25 5x xx⇔ += ⇔ = ⇔=±
.
Vậy phương trình có tập nghiệm
{ }
5S = ±
.
Bài 3: a) Thay
1, 44x =
(tmđk) vào biểu thức A ta được:
1,44 7 8,44 211
1, 2 30
1, 44
A
+
= = =
.
Vậy tại
1, 44x =
thì
211
30
A =
.
b) ĐKXĐ:
0; 9xx>≠
.
2 12 3
9
33
x x xx
B
x
xx
− −−
=+−
−
+−
( ) ( )( )
( )
( )
3 2 1 32 3
33
xx x x x x
B
xx
−+ − +− + +
=
+−
( )
( )
3 2 6 32 3
33
x xx xx xx
B
xx
− + + − −− + +
=
+−
( )
( )( )
3
33
xx
B
xx
+
=
+−
3
x
B
x
=
−
.
c) ĐKXĐ:
0; 9xx>≠
.
1 37 4 4
1
x x xx
SA x
B
xx x x
− + ++
=+= + = = + +
.
Vì
4
0; 0x
x
>>
nên áp dụng bất đẳng thức Côsi cho hai số dương
x
và
4
x
, ta được:
44
2.xx
xx
+≥
4
2.2x
x
⇒+ ≥
4
4x
x
⇒+ ≥
4
15x
x
⇔ + +≥
.
Dấu "=" xảy ra khi
4
4xx
x
= ⇒=
(thỏa mãn).
Vậy GTNN của
S
là 5 đạt được khi
4x =
.
Bài 4:
1) Xét
ABC∆
vuông tại
A
; đường cao
AH
.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
2
. 2.8 16 4AB BH BC AB=
==⇒=cm
( )
2
. . 6.8 48 4 3AC HC BC BC BH BC AC= = − ==⇒= cm
2
. 23AH HB HC AH= ⇒=cm
.
2) Xét tam giác vuông
ABK
, đường cao
AD
ta có:
2
.AB BD BK= (1)
Xét tam giác vuông
ABC
, đường cao
AH
ta có:
2
.AB BH BC= (2)
Từ
(1)
và
(2)
suy ra
2
..BD BK BH BC AB= =
(đpcm).
3) Gọi
E
là hình chiếu của
H
lên
BD
,
F
là hình chiếu của
C
lên
BK
. Ta có
1
..
2
1
..
2
BHD
BKC
HE BD
S
S
CF BK
=
2
.
...
HE BD BH BD BH BD BK
CF BK BC BK BC BK
= = =
2
2
1
. cos.
4
BH BA
ABD
BC BK
= =
2
1
cos
4
BHD BKC
S S ABD⇒=
.
Bài 5: ĐKXĐ:
9
5
x ≥
Với
9
5
x ≥
ta có:
( )
( )
22
593 359Kx x= −+ + − −
593359Kx x= −++ − −
.
Với
9
5
x ≥
ta có:
359359xx−−≥−−
593359 593359x xx x⇒ −++ − − ≥ −++− −
6K⇒≥
.
Dấu
""=
xảy ra
3 5 90x⇔− −≥
5 93x⇔ −≤
5 99x⇔ −≤
18
5
x⇔≤
.
Mà
9
5
x ≥
nên
9 18
55
x≤≤
.
Vậy
K
có giá trị nhỏ nhất là
6
đạt được khi và chỉ khi
9 18
55
x≤≤
.
HẾT
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

HƯỚNG DẪN GIẢI  2 50  Bài 1: 1) A =  + − 24 . 6   3 3    6 5 6  A =  + − 2 6 . 6   3 3    6 6  A =  − 2 6 . 6   3   A = (2 6 − 2 6 ). 6 A = 0. 6 = 0 .  14 − 7 15 − 5  1 2) B =  +  :   2 −1 3 −1 7 − 5  
 7 ( 2 − )1 5( 3 − )1 1 B   = + :  2 −1 3 −1  7 − 5   B = ( 7 + 5).( 7 − 5) B = 7 − 5 = 2 . Bài 2: 1) ĐKXĐ: x ≥ 0 .
3x − 5 12x + 7 27x = 12
⇔ 3x − 5.2 3x + 7.3 3x =12
⇔ 3x −10 3x + 21 3x =12 ⇔ 12 3x =12 ⇔ 3x =1 ⇔ 3x = 1 1
⇔ x = > 0 (thỏa mãn điều kiện). 3 1
Vậy phương trình có tập nghiệm S =   . 3 2) 3 2 x + 2 = 3 2 2
⇔ x + 2 = 27 ⇔ x = 25 ⇔ x = 5 ± .
Vậy phương trình có tập nghiệm S = {± } 5 . Bài 3:
a) Thay x = 1, 44 (tmđk) vào biểu thức A ta được: 1, 44 + 7 8, 44 211 A = = = . 1, 44 1, 2 30 211
Vậy tại x = 1, 44 thì A = . 30
b) ĐKXĐ: x > 0; x ≠ 9 . x 2 x −1 2x − x − 3 B = + − x + 3 x − 3 x − 9
x ( x − 3) + (2 x − )
1 ( x + 3) − 2x + x + 3 B = ( x +3)( x −3)
x − 3 x + 2x + 6 x − x − 3 − 2x + x + 3 B = ( x +3)( x −3) x ( x + 3)
B = ( x +3)( x −3) x B = . x − 3
c) ĐKXĐ: x > 0; x ≠ 9. 1 x − 3 x + 7 x + x + 4 4 S = + A = + = = x + +1. B x x x x 4 4 Vì x > 0;
> 0 nên áp dụng bất đẳng thức Côsi cho hai số dương x và , ta được: x x 4 4 x + ≥ 2 x. x x 4 ⇒ x + ≥ 2.2 x 4 ⇒ x + ≥ 4 x 4 ⇔ x + +1 ≥ 5 . x 4
Dấu "=" xảy ra khi x =
⇒ x = 4 (thỏa mãn). x
Vậy GTNN của S là 5 đạt được khi x = 4 . Bài 4: 1) Xét A
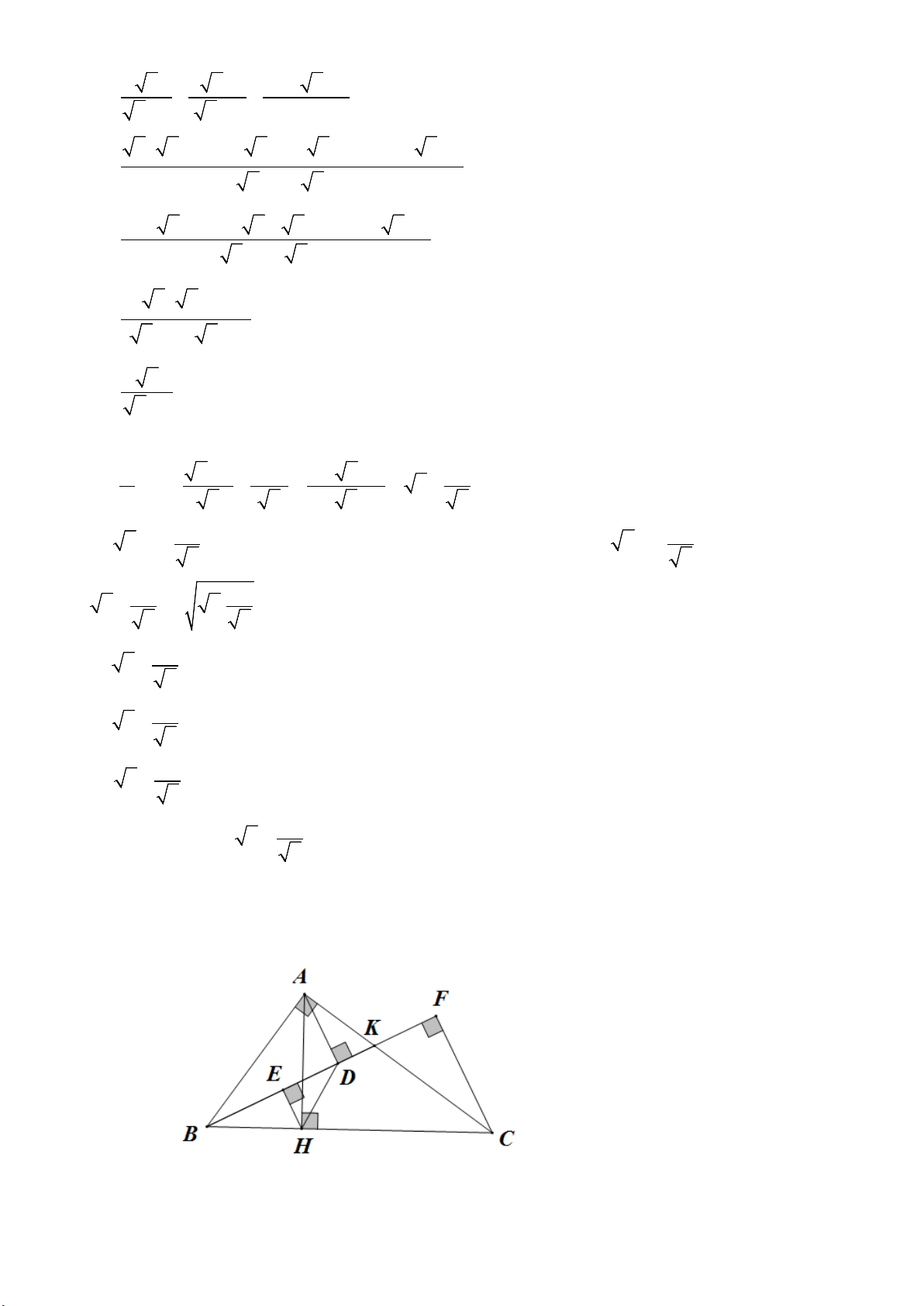
∆ BC vuông tại A ; đường cao AH .
Áp dụng hệ thức lượng trong tam giác vuông ta có: 2
AB = BH.BC = 2.8 = 16 ⇒ AB = 4 cm 2
AC = HC.BC = ( BC − BH ).BC = 6.8 = 48 ⇒ AC = 4 3 cm 2 AH = .
HB HC ⇒ AH = 2 3 cm .
2) Xét tam giác vuông ABK , đường cao AD ta có: 2 AB = B . D BK (1)
Xét tam giác vuông ABC , đường cao AH ta có: 2
AB = BH.BC (2) Từ (1) và (2) suy ra 2 B .
D BK = BH .BC = AB (đpcm).
3) Gọi E là hình chiếu của H lên BD , F là hình chiếu của C lên BK . Ta có 1 .HE.BD S HE BD BH BD BH B . D BK 2 BH BA 1 BHD 2 = = . = . = . = =  . cos.ABD S 1 2 CF BK BC BK BC BK 2 BC BK 4 BKC .CF.BK 2 1 2 ⇒ =  S S cos ABD . BHD 4 BKC Bài 5: ĐKXĐ: 9 x ≥ 5 9 Với x ≥ ta có: 5 K = ( x − + )2 + ( − x − )2 5 9 3 3 5 9
K = 5x − 9 + 3 + 3 − 5x − 9 . 9 Với x ≥ ta có: 5
3 − 5x − 9 ≥ 3 − 5x − 9
⇒ 5x − 9 + 3 + 3 − 5x − 9 ≥ 5x − 9 + 3 + 3 − 5x − 9 ⇒ K ≥ 6 .
Dấu " = " xảy ra ⇔ 3 − 5x − 9 ≥ 0 ⇔ 5x − 9 ≤ 3 ⇔ 5x − 9 ≤ 9 18 ⇔ x ≤ . 5 9 9 18 Mà x ≥ nên ≤ x ≤ . 5 5 5 9 18
Vậy K có giá trị nhỏ nhất là 6 đạt được khi và chỉ khi ≤ x ≤ . 5 5 HẾT
Document Outline

  • de-kscl-giua-hoc-ki-1-toan-9-nam-2020-2021-phong-gddt-ha-dong-ha-noi.pdf
  • QUẬN HÀ ĐÔNG - MÔN TOÁN 9.pdf