Đề KSCL học sinh giỏi Toán 8 năm 2024 – 2025 phòng GD&ĐT Kiến Xương – Thái Bình

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI KIẾN XƯƠNG
NĂM HỌC 2024 – 2025 ===***=== MÔN: TOÁN 8
(Thời gian làm bài 120 phút) Bài 1 (4,0 điểm). Cho biểu thức  x  2 2 2 1 1  2x  4x 1  x  x P      : với x  0; x  1  2 3 3 x  x  1 x 1 x 1 x  8x  
1) Rút gọn biểu thức P. Tìm x để P = 8.
2) Giả sử x  0; x  1. So sánh giá trị của biểu thức P và 4.
Bài 2 (4,5 điểm).
1) Tính giá trị của biểu thức: 2 2
A   x  y  5   x  y  58  2x  4  x tại 2025 y  10 1.
2) Cho x, y là các số thực thỏa mãn: x + y = 1.
Tìm giá trị nhỏ nhất của biểu thức: B   2 x  y 2 4
y  4x  20xy .
3) Tìm đa thức f(x) biết đa thức f(x) chia cho (x – 2) dư 5; f(x) chia cho (x – 3) dư 7
và f(x) chia cho (x – 2)(x – 3) được thương là x2 - 1 và còn dư.
Bài 3 (4,5 điểm).
1) Trong một hộp kín có 6 viên bi đỏ, 3 viên bi xanh, các viên bi có kích thước, khối
lượng và hình dạng như nhau chỉ khác màu sắc. Lấy ngẫu nhiên 1 viên bi từ trong hộp.
a) Tính xác suất của biến cố E: “Lấy được viên bi màu đỏ”.
b) Thêm vào hộp một số viên bi màu đỏ, màu xanh sao cho xác suất chọn được
một viên bi mỗi màu không đổi. Cần thêm ít nhất bao nhiêu viên bi mỗi màu?
2) Trong mặt phẳng tọa độ Oxy cho đường thẳng d: y = (m – 2)x - 2 (với m  2)
a) Giả sử d cắt trục Ox; Oy lần lượt tại A; B. Tìm m để AB = 2 2 .
b) Tìm điểm cố định mà tập hợp các đường thẳng d luôn đi qua khi giá trị của m thay đổi.
Bài 4 (6 điểm).
Cho tam giác ABC nhọn có các đường cao BD, CE cắt nhau tại H. Kẻ EK vuông
góc với AC tại K, DI vuông góc với EC tại I. Chứng minh: 1) CH.CE = CD.CA 2) IK vuông góc với BC. 1
3) Tam giác EIK đồng dạng tam giác ABC và S  S E  IK A  BC 4
Bài 5 (1 điểm).
Cho 2 số nguyên dương a,b thỏa mãn: a + b + 1 là một ước nguyên tố của 2(a2 + b2) - 1
Chứng minh rằng a.b là một số chính phương.
Họ và tên thí sinh:....................................................SBD:........
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM KHẢO SÁT CHẤT LƯỢNG HSG KIẾN XƯƠNG
NĂM HỌC 2024 – 2025 ===***=== MÔN TOÁN LỚP 8
Bài 1 (4,0 điểm). Cho biểu thức  x  2 2 2 1 1  2x  4x 1  x  x P      : với x  0; x  1  2 3 3 x  x  1 x 1 x 1 x  8x  
1) Rút gọn biểu thức P. Tìm x để P = 8.
2) Giả sử x  0; x  1. So sánh giá trị của biểu thức P và 4. Câu Đáp án Điểm  x  2 2 2 1 1  2x  4x 1  x  x Câu 1 P      : 2 3 3      (3đ) x x 1 x 1 x 1 x 8x   với x  0; x  1   x 2 2 1   1  2x  4x 1 x x   1 P      : 2 2 2  x  x 1 x   1 
x  x  1 x 1 x  x 8 0,5 x  3 1   2 1  2x  4x  2  x  x 1 x 1 P  :  x   1  2 x  x   2 1 x  8 2,0đ 3 2 2 2 2
x  3x  3x 1 1  2x  4x  x  x  1 x  8 0,5 P   x   1  . 2 x  x   1 x  1 3 2 x 1 x  8 P   0,5 x   1  . 2 x  x   1 x  1 2 x  8 2 x  8 P  Vậy với x  0; x  1  P  0,5 x  1 thì x  1 2 x  8 b) Ta có: P  với x  0; x  1  x  1 0,25 2 x  8 Để P = 8 thì  8 Suy ra 2 x  8  8x  8 x  1 1,0đ 2 x  8x  0     không tmđk    x 0 x 0 x x 8  0     x  8  0 x  8  0,5 tmđk  Vậy với x = 8 thì P = 8 0,25 Câu 2 2 x  8 1đ + Ta có: P  với x  0;x  1  x  1
+ Với x  0; x  1, Xét P – 4 ta có: x  8 x  8  4x  4   2 2 2 x 2 0,25 P  4   4   x 1 x 1 x 1 
 x  22  0 x  22
+ Vì x  0; x  1 nên    0 x 1 0 x  1 0,25
suy ra P  4  0 hay P  4 0,25
Dấu "= " xảy ra khi x=2(*) (TMĐK)
Vậy với x  0;x  1 thì P  4 . 0,25
Bài 2 (4,5 điểm).
1) Tính giá trị của biểu thức: 2 2
A   x  y  5   x  y  58  2x  4  x tại 2025 y  10 1.
2) Cho x, y là các số thực thỏa mãn: x + y = 1.
Tìm giá trị nhỏ nhất của biểu thức: B   2 x  y 2 4
y  4x  20xy .
3) Tìm đa thức f(x) biết đa thức f(x) chia cho (x – 2) dư 5; f(x) chia cho (x – 3) dư 7
và f(x) chia cho (x – 2)(x – 3) được thương là x2 - 1 và còn dư. Bài 2 Nội dung Điểm 1. Ta có:
A   x  y  52  2 x  y  54  x  4  x2 2
A   x  y  5)  (4  x   
A   x  y  5  4  x2 1,0 Câu 1.
A   y  2 1 (1,5đ)  Thay 2025 y  10
1 vào biểu thức A ta được:  0,25 A = ( 2025 10 1 – 1)2 = 4050 10
Vậy giá trị của biểu thức A = 4050 10 tại 2025 y  10 1 0,25 2. Ta có: 2 2
B   x  4y y  4x  20xy 2 2 3 3 2 2 3 3
 x y  4x  4y 16xy  20xy  x y  4(x  y )  36xy Câu 2)
Lại có: x  y   x  y3 3 3 3
 3xy(x  y)  1  3x .1 y  1 3xy 1,5đ) (vì x + y = 1) Do đó 2 2
B  x y  4(1 3xy)  36xy 2 2 2 2
B  x y  24xy  4  (x y  2.12xy  144) 140 0,75 2  (xy 12) 140 Có 2
(xy 12)  0 với mọi x, y nên 2 (xy 12) 140  1  40 với mọi x, y Dấu “=” xảy ra khi 2
(xy 12)  0 suy ra xy 12  0 hay xy  12  0,25 mà x + y = 1
Suy ra x = 4; y =  3 hoặc x =  3; y = 4 0,25
Vậy GTNN của biểu thức B là - 140 tại x = 4; y =  3 hoặc x =  3; 0,25 y = 4 Câu 3)
Tìm đa thức f(x) biết đa thức f(x) chia cho (x – 2) dư 5; f(x) chia cho (1,5đ)
(x – 3) dư 7 và f(x) chia cho (x – 2)(x – 3) được thương là x2 - 1 và còn dư.
+ Vì đa thức f(x) chia cho (x – 2)(x – 3) được thương là x2 - 1 và còn
dư, nên đa thức f(x) có dạng:
        2 f x x 2 x 3 x   1  ax  b x  0,5
Vì f  x  chia cho (x - 2) dư 5; f  x  chia cho (x - 3) dư 7 nên: f  2  5 2a  b  5  =>  f  3  7 3a  b  7 0,5
Học sinh giải tìm được a = 2; b = 1 0,25 Vậy đa thức 0,25
        2   4 3 2 f x x 2 x 3 x
1  2x 1  x  5x  5x  7x  5
Bài 3 (4,5 điểm).
1) Trong một hộp kín có 6 viên bi đỏ, 3 viên bi xanh, các viên bi có kích thước, khối
lượng và hình dạng như nhau chỉ khác màu sắc. Lấy ngẫu nhiên 1 viên bi từ trong hộp.
a) Tính xác suất của biến cố E: “Lấy được viên bi màu đỏ”.
b) Thêm vào hộp một số viên bi màu đỏ, màu xanh sao cho xác suất chọn được
một viên bi mỗi màu không đổi. Cần thêm ít nhất bao nhiêu viên bi mỗi màu?
2) Trong mặt phẳng tọa độ Oxy cho đường thẳng d: y = (m – 2)x - 2 (với m  2)
a) Giả sử d cắt trục Ox; Oy lần lượt tại A; B. Tìm m để AB = 2 2 .
b) Tìm điểm cố định mà tập hợp các đường thẳng d luôn đi qua khi giá trị của m thay đổi. Câu Đáp án Điểm 1) (2đ)
Tổng số viên bi trong hộp là: 6 + 3 = 9 (viên bi)
Lấy ngẫu nhiên 1 viên bi trong hộp 0,5 a) (0,5đ)
 Có 9 quả có thể xảy ra;
Số kết quả thuận lợi để lấy được viên bi đỏ là 6, nên xác suất lấy
được viên bi màu đỏ là 6 2  9 3 b) (1,5đ)
Số kết quả thuận lợi để lấy được viên bi xanh là 3, nên xác suất lấy 0,5
được viên bi màu xanh là 3 1  9 3
Gọi số bi đỏ, bi xanh cần thêm vào là x, y (x, y *  N )
Khi đó trong hộp có tất cả (9 + x + y) viên bi , trong đó có (6 + x)
viên bi đỏ và (3 + y) viên bi xanh
Do xác suất chọn được một viên bi mỗi màu không đổi nên ta có:  6  x 2  9 x  y 3 
 6  x  2(3  y)  x  2y 0,5 3  y 1   9  x  y 3 Do x, y *
 N và số bi cần thêm vào là ít
nhất nên y = 1 => x = 2;
Vậy cần phải thêm ít nhất 2 viên bi màu đỏ, 1 0,5 viên bi màu xanh. Câu 2
a) Xét đường thẳng d: y = (m – 2)x - 2 (với m  2): (2,5đ)
+ Cho x = 0, suy ra y = - 2 => d cắt Oy tại B(0; -2) 0,25  OB  2   2 a (1,75) 2 2 + Cho y = 0, suy ra x  => d cắt Ox tại A ( ; 0) m  2 m  2 0,25  2 OA  m  2 0,25
- Vì m  2 nên A; B không trùng O(0; 0);
Xét tam giác OAB vuông tại O có:
Ta có: AB2 = OA2 + OB2 (pytago) 2 2  2   2   2  (2 2)   4      m  22 2 2 1 Hay:  m  2   m  2  0,5
Giải, tìm được m =3; m = 1( thoả mãn điều kiện)
Vậy m = 3; m = - 1 thoả mãn đề bài. 0,5 b (0.75)
b) Ta có: đường thẳng d đi qua điểm B(0; -2),
toạ độ điểm B không phụ thuộc vào giá trị của m; Do đó điểm B(0; 0,5
- 2) là điểm cố định mà tập hợp các đường thẳng
d luôn đi qua khi giá trị của 0,25 m thay đổi.
Bài 4 (6 điểm).
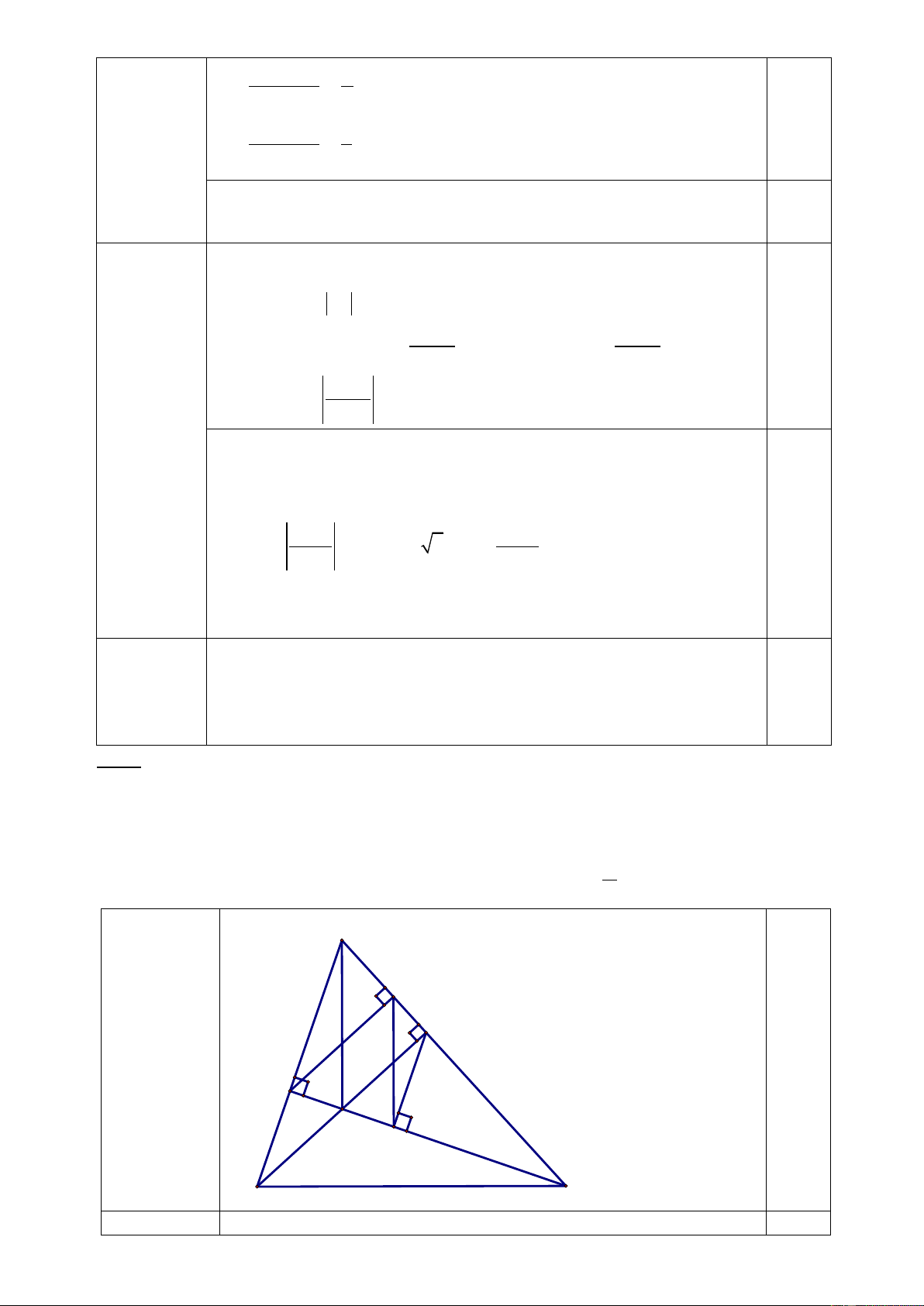
Cho tam giác ABC nhọn có các đường cao BD, CE cắt nhau tại H. Kẻ EK vuông
góc với AC tại K, DI vuông góc với EC tại I. Chứng minh: 1) CH.CE = CD.CA 2) IK vuông góc với BC. 1
3) Tam giác EIK đồng dạng tam giác ABC và S  S E  IK A  BC 4 A K D E H I C B
a) Xét  CHD và  CAE có: Câu 1   0 CDH CEA  90  (2,5đ) 1,5 ECA chung  ΔCHD ∽ CA  E(g - g) CH CD   CA CE 1,0 => CH.CE = CA.CD (đpcm) Xét  CID và  CKE có:   0 CID CKE  90  ECK chung 0,5  ΔCID ∽ C  KE(g - g) CI CD   CK CE Câu 2 CH CD CH CI CI CK (2đ) Mà  (cmt) =>    0,5 CA CE CA CK CH CA CI CK Xét  CAH, có  (cmt) CH CA 0,5
=> IK //AH ( định lý Ta lét đảo) (1)
Xét  ABC có đường cao BD và CE cắt nhau tại H, nên H là
trực tâm của  ABC, do đó AH  BC (2) 0,5
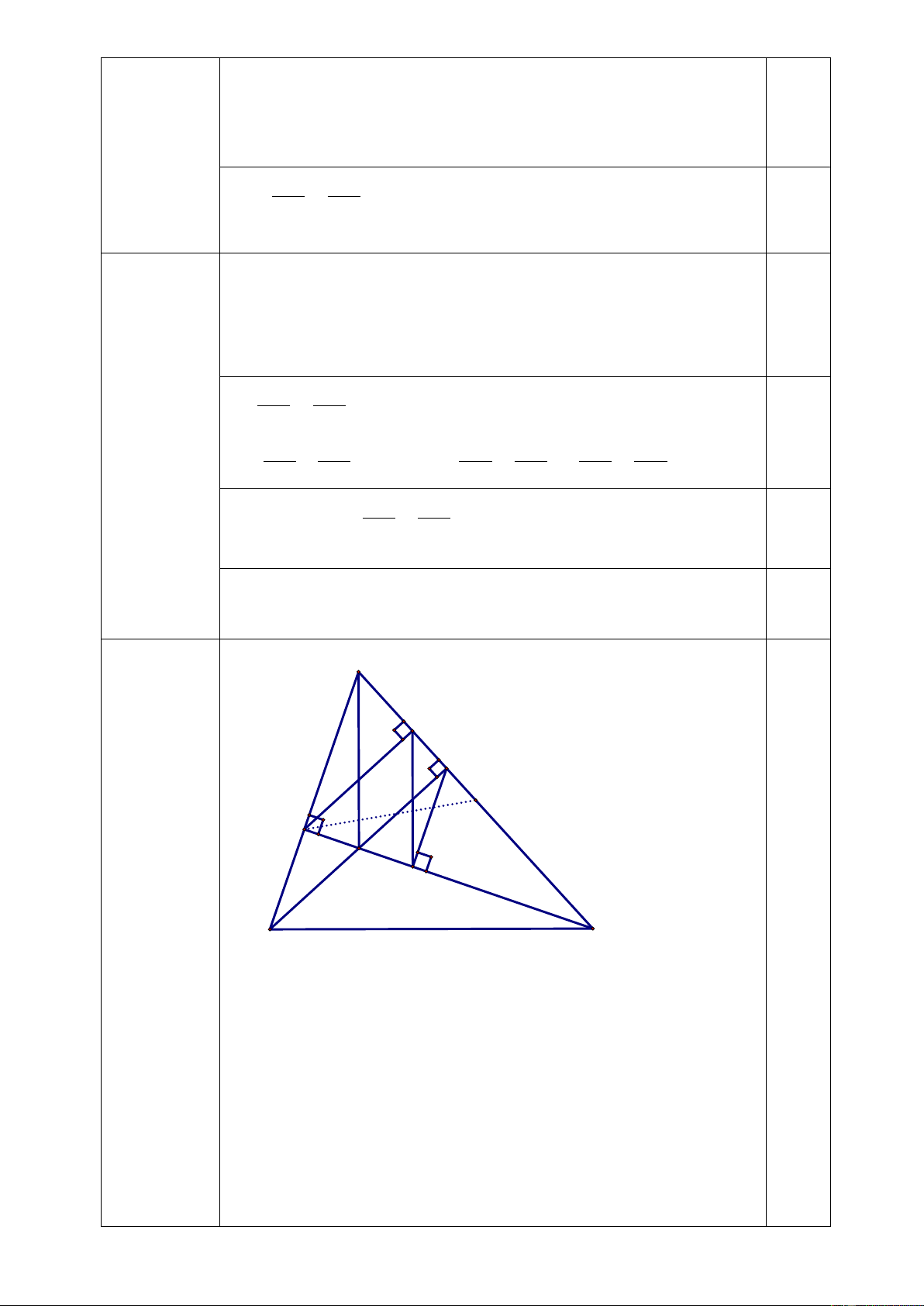
Từ (1) và (2), ta có IK  BC A K D M E 0,5 H I Câu 3 C B (1,5đ)
* Chứng minh cho tam giác EIK và tam giác ABC đồng dạng:
+ Ta có IK //AH (cmt) nên KIE  AHE (cặp góc đồng vị)
+ Do AH  BC (cmt) và CE  AB nên ABC  AHE ( cùng phụ EAH ) => ABC  KIE
+ Xét  EIK và  ABC có : KIE  ABC (cmt)
IEK  BAC (cùng phụ ACE )  ΔEIK ∽ A  BC(g - g) Ta có ΔEIK ∽ A  BC (cmt) 2 0,25 2 S  EK  EK => EIK     2 S  AC  AC A  BC
* Lấy M là trung điểm của AC, ta có: EK  EM
(Quan hệ giữa đường vuông góc và đường xiên)   1 EM  AC 
(T/c đường trung tuyến trong tam giác vuông)  2 2 1 EK 1  EK  AC   2 2 AC 4 S 1 => E  IK  0,5 S 4 A  BC
Dấu bằng xảy ra khi K trùng M
=> tam giác AEC vuông cân tại E => Góc A bằng 450 1 Vậy S  S E  IK A  BC 4 0,25
Bài 5 (1 điểm).
Cho 2 số nguyên dương a,b thỏa mãn: a + b + 1 là một ước nguyên tố của 2(a2 + b2) - 1
Chứng minh rằng a.b là một số chính phương.
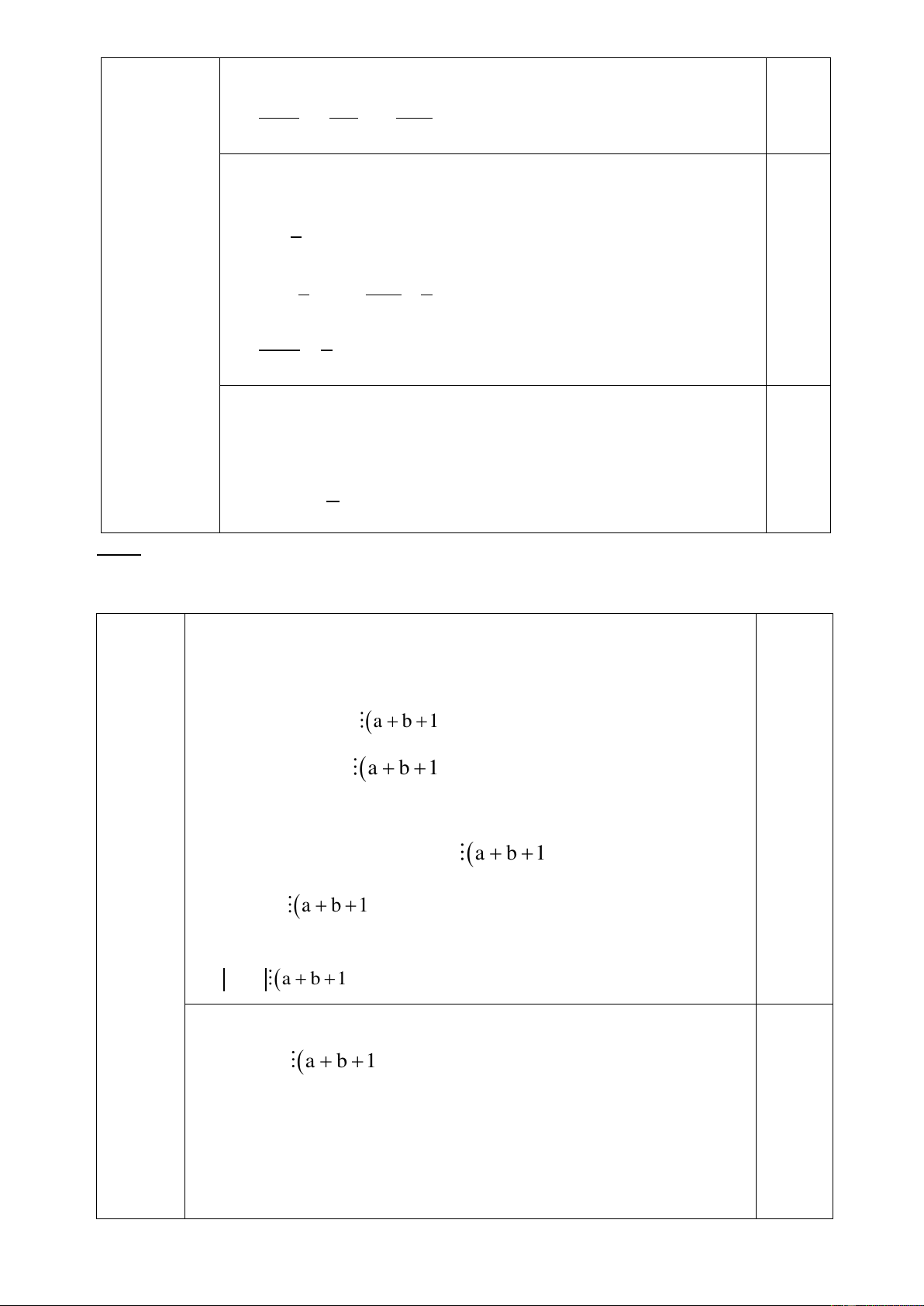
Giả sử a và b là 2 số nguyên dương khác nhau. Khi đó ta có: 1 đ 2
a  b 1  a  b   1 a  b   1 =>   2 a b 1 a  b   1   Mà  2 2
2. a  b  1 a  b  
1 ( vì a  b 1 là một ước nguyên tố của  2 2 2. a  b  1) 0,5
=>        2 2 2 2. a b 1 a b 1     a b  1 2
=> a  b a  b   1
Lại có a  b 1 là một số nguyên tố
=> a  b a  b   1
Không mất tính tổng quát, giả sử a > b, khi đó ta có :
a  b a  b   1
=> a  b  a  b  1  2b  1  0
Điều này là vô lý (vì b là số nguyên dương nên 2b + 1> 1) 0,5
Do đó điều giả sử a và b là 2 số nguyên dương khác nhau là sai => a = b Với a = b thì 2
a.b  a là một số chính phương (đpcm) Lưu ý:
- Học sinh làm theo cách khác đúng vẫn cho điểm tối đa
- Nếu học sinh không vẽ hình hoặc sai hình thì không chấm điểm bài hình
- Bài làm không chặt chẽ, không đủ cơ sở ở phần nào thì trừ nửa số điểm ở phần đó.
- Điểm bài thi là tổng điểm các bài thành phần, không làm tròn.
=============Hết ===========