Đề KSCL HSG Toán THPT năm 2022 – 2023 trường THPT Hà Văn Mao – Thanh Hóa

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi giao lưu khảo sát chất lượng học sinh giỏi cụm Bá Thước môn Toán THPT năm học 2022 – 2023 trường THPT Hà Văn Mao, tỉnh Thanh Hóa; đề thi hình thức trắc nghiệm với 50 câu hỏi và bài toán

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

36 trang 6 tháng trước

Tác giả:

Profile Nguyễn Vân
Trang 1/7 – Mã đề thi 123
TRƯỜNG THPT HÀ VĂN MAO
ĐỀ CHÍNH THỨC
Đề thi có 7 trang, 50 câu TNKQ
ĐỀ THI GIAO LƯU KSCL HSG - CỤM BÁ THƯỚC
NĂM HỌC 2022 - 2023
Môn thi: Toán - THPT
Khóa thi ngày: 12/11/2022
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên…………………..…………………………..
Số báo danh……………….…..……. Phòng thi….…..
Câu 1. Trong các hàm số sau đây, hàm số nào là hàm số chẵn?
A.
sin
2
yx



. B.
sin
yx
. C.
sin tan
yxx
. D.
sin .cosy xx
Câu 2. Một học sinh có
4
quyển sách Toán khác nhau và
5
quyển sách Ngữ văn khác nhau. Hỏi có
bao nhiêu cách xếp
9
quyển sách trên giá sao cho hai quyển sách kề nhau phải khác loại ?
A.
. B.
2880
. C.
362880
. D.
5760
.
Câu 3. Cho cấp số cộng
( )
n
u
với
1
6u =
;
9
d
=
. Khi đó số
2022
là số hạng thứ bao nhiêu của cấp
số?
A.
226
. B.
225
. C.
223
. D.
224
.
Câu 4. Tìm m để hàm số
( ) (
)
42
1 21 1ymx mx=−+−+
có đúng 3 điểm cực trị.
A.
1
1
2
m<<
. B.
1
1
2
m≤<
. C.
1
1
2
m<≤
. D.
1
1
2
m≤≤
.
Câu 5. Đặt
ln 2, ln 5= =ab
, hãy biểu diễn
1 2 3 98 99
ln ln ln ... ln ln
2 3 4 99 100
I = + + ++ +
theo
a
và
b
.
A.
(
)
2I ab=−+
B.
( )
2
I ab=−−
C.
( )
2I ab= +
D.
( )
2I ab
= −
Câu 6. Lăng trụ đứng có đáy là hình thoi có bao nhiêu mặt phẳng đối xứng?
A. 2. B. 9. C. 3. D. 5.
Câu 7. Cho đoạn thẳng
AB
có độ dài bằng
, vẽ tia
Ax
về phía điểm
B
sao cho điểm
B
luôn
cách tia
Ax
một đoạn bằng
a
. Gọi
H
là hình chiếu của
B
lên tia
Ax
, khi tam giác
AHB
quay quanh trục
AB
thì đường gấp khúc
AHB
vẽ thành mặt tròn xoay có diện tích xung
quanh bằng:
A.
2
32
2
a
π
. B.
( )
2
33
2
a
π
+
. C.
( )
2
13
2
a
π
+
. D.
( )
2
22
2
a
π
+
.
Câu 8. Cắt hình trụ
( )
T
bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện
tích bằng
30
2
cm
và chu vi bằng
26 cm
. Biết chiều dài của hình chữ nhật lớn hơn đường kính
mặt đáy của hình trụ
( )
T
. Diện tích toàn phần của
( )
T
là:
A.
( )
23
2
cm
π
. B.
( )
2
23
2
cm
π
. C.
( )
2
69
2
cm
π
. D.
( )
2
69 cm
π
.
Câu 9. Cho hàm số
()fx
xác định trên
1
\
2



thỏa mãn
( ) ( ) ( )
2
, 0 1, 1 2
21
fx f f
x
′
= = =
−
. Giá trị
của biểu thức
( ) ( )
13ff−+
bằng
A.
2 ln15+
B.
3 ln15+
C.
ln15
D.
4 ln15+
Mã đề thi: 123
Trang 2/7 – Mã đề thi 123
Câu 10. Cho
( )
2
0
3 2 1d 6
m
xx x−+ =
∫
. Giá trị của tham số
m
thuộc khoảng nào sau đây?
A.
( )
1;2−
. B.
(
)
;0
−∞
. C.
( )
0;4
. D.
( )
3;1−
.
Câu 11. Có bao nhiêu cách phân công 4 thầy giáo dạy toán vào dạy 12 lớp 12, mà mỗi thầy dạy đúng
3 lớp ?
A. 369600 B. 396900 C. 220 D. 369000
Câu 12. Giới hạn
( )
( )
42
3
2
lim
13 1
x
xx
xx
→+∞
++
+−
có kết quả là :
A.
3−
B.
3
3
C.
3
D.
3
3
−
Câu 13. Cho tứ diện
OABC
có
, ,
OA OB OC
đôi một vuông góc với nhau và
OA OB OC= =
. Gọi
M
là trung điểm của
BC
(tham khảo hình vẽ bên dưới). Góc giữa hai đường thẳng
OM
và
AB
bằng
A.
0
45
B.
0
90
C.
0
30
D.
0
60
Câu 14. Cho hàm số
( )
y fx
=
có đồ thị hàm
( )
y fx
′
=
như hình vẽ bên dưới.
Hàm số đã cho nghịch biến trên khoảng
A.
( )
;2−∞ −
. B.
( )
2;1−
. C.
( )
;4−∞ −
. D.
(
)
2;3−
.
Câu 15. Có bao nhiêu giá trị nguyên dương của
m
để khoảng cách từ gốc tọa độ
O
đến đường thẳng
đi qua 2 điểm cực trị của đồ thị hàm số
3
3y x xm=−+
nhỏ hơn hoặc bằng
5.
A. 5. B. 2. C. 11. D. 4.
Trang 3/7 – Mã đề thi 123
Câu 16. Giá trị nhỏ nhất và lớn nhất của hàm số
2
yx x
= −
trên đoạn
[0; 9]
lần lượt là
m
và
.
Giá trị của tổng
mM+
bằng
A. 2. B. 3. C. 0. D. 1.
Câu 17. Cho hàm số
1ax
y
bx c
+
=
+
(
,,abc
là các tham số) có bảng biến thiên như hình vẽ
Xét các phát biểu sau:
( )
( )
( )
(
)
1 : 1.
2 : 0 .
3 : 0 .
4 : 0.
c
ab
abc
a
>
+<
++=
>
Số phát biểu đúng là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 18. Đặt
3
log 2 a=
khi đó
16
log 27
bằng
A.
3
4
a
B.
3
4a
C.
4
3a
D.
4
3
a
Câu 19. Cho hai số thực dương
x
,
y
thỏa mãn
22
22
log 1 logx y xy 
. Mệnh đề nào dưới đây
đúng?
A.
xy
. B.
xy
. C.
xy
. D.
2
xy
.
Câu 20. Đặt
2
log 3a =
;
5
log 3b =
. Nếu biểu diễn
( )
( )
6
log 45
a m nb
ba p
+
=
+
thì
mnp++
bằng
A.
3
B.
4
C.
6
D.
3−
Câu 21. Một hình đa diện lồi có số mặt
, số đỉnh
D
và số cạnh
C
. Khi đó, hệ thức nào dưới đây là
đúng ?
A.
2DMC+ −=
B.
2DCM+− =
C.
2
MCD+− =
D.
MDC+=
Câu 22. Tính thể tích
V
của khối lăng trụ tam giác đều
.ABC A B C
′′′
có
5AC a
′
=
, cạnh đáy là
4a
.
A.
3
12Va=
. B.
3
20 3Va=
. C.
3
20Va=
. D.
3
12 3Va=
.
.Câu 23. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác cân tại
A
,
4; 6
AB AC a BC a
= = =
.Hình
chiếu vuông góc của
S
trên mặt phẳng
( )
ABC
nằm trong tam giác
ABC
. Các mặt bên của hình chóp
cùng tạo với đáy góc
0
60
. Tính thể tích khối chóp
.S ABC
.
A.
3
63a
. B.
3
3a
. C.
3
83a
. D.
3
33a
.
Câu 24. Cho hình nón đỉnh
I
, đường cao
(
O
là tâm của đáy) và có độ dài đường sinh bằng
3cm
,
góc ở đỉnh bằng
60°
. Gọi
K
là điểm thuộc đoạn
thỏa mãn
3
2
IO IK=
, cắt hình nón bằng
Trang 4/7 – Mã đề thi 123
mặt phẳng
()P
qua
K
và vuông góc với
IO
, khi đó thiết diện tạo thành có diện tích là
S
.
Tính
S
.
A.
(
)
2
3
S cm
π
=
. B.
( )
2
S cm
π
=
. C.
( )
2
3S cm
π
=
. D.
(
)
2
2
3
S cm
π
=
.
Câu 25. Cho
( )
2
Fx x=
là một nguyên hàm của hàm số
( )
2x
f xe
. Tìm nguyên hàm của hàm số
( )
2
'
x
f xe
.
A.
( )
22
' 22
x
f x e dx x x C=− ++
∫
. B.
( )
22
'2
x
f x e dx x x C
=−+ +
∫
.
C.
(
)
22
'
x
f x e dx x x C=− ++
∫
. D.
( )
22
' 22
x
f x e dx x x C= −+
∫
.
Câu 26. Có bao nhiêu số thực
a
để
1
2
0
1=
+
∫
x
dx
ax
.
A.
2
B.
1
C.
0
D.
3
Câu 27. Số giá trị nguyên của tham số
m
thuộc đoạn
[ ]
2022; 2022
−
để phương trình
( )
2
1 sin sin 2 cos 2 0m xx x+ −+ =
có nghiệm là:
A.
4045
. B.
4044
. C.
2023
. D.
2024
.
Câu 28. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với đáy và
3SA a=
. Gọi
α
là góc giữa
SD
và
( )
SAC
. Giá trị
sin
α
bằng
A.
2
4
. B.
2
2
. C.
3
2
. D.
2
3
.
Câu 29. Có bao nhiêu giá trị nguyên âm của tham số
m
để hàm số
( )
42
39
2 15 3 1
42
y x x m xm= − + + −+
đồng biến trên khoảng
( )
0; +∞
?
A.
2.
B.
3.
C.
5.
D.
4.
Câu 30. Cho hàm số
32
3
yx xm=−+
, với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của
tham số m để đồ thị hàm số có 5 điểm cực trị. Tổng tất cả các phần tử của tập S là
A. 3 B. 10 C. 6 D. 5
Câu 31. Cho hàm số
( )
y fx=
có bảng biến thiên như sau
Tập hợp tất cả các giá trị thực của tham số
m
để phương trình
() 0fx m+=
có 5 nghiệm
phân biệt là
A.
(
]
2; 1−−
. B.
[
)
1; 2−
. C.
( )
2; 1−−
. D.
(
)
2;1−
.
Câu 32. Cho hình chóp đều đỉnh S có đáy là đa giác đều 8 cạnh. Một hình nón đỉnh
S
có đáy
là đường tròn ngoại tiếp đáy hình chóp. Tính tỉ số thể tích của khối nón và khối chóp
tương ứng.
Trang 5/7 – Mã đề thi 123
A.
3
π
. B.
22
π
. C.
2
π
. D.
2
33
π
.
Câu 33. Số đường tiệm cận đứng của đồ thị hàm số
2
2
41 26
2
x xx
y
xx
−− + +
=
+−
là
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 34. Gọi
0
3ab
x
c
+
=
với (
,, ,
a
abc N
c
∈
tối giản) là một nghiệm lớn hơn
1
của phương trình
( )
1
1
2
1
2 3 12 1
3
x
x
xx
−


− += −





. Giá trị của
P abc=++
là
A.
6P
=
. B.
0P =
. C.
2P
=
. D.
4P =
.
Câu 35. Cho các hàm số
( ) ( ) ( )
12
,,,fxfxfx…
thỏa mãn:
(
) ( )
1
1
ln
1
x
x
e
fx fx
e
+
= =
−
;
( )
1
() (), 1;2;3;
nn
f x ffx n
+
= ∀= …
Khẳng định nào sau đây đúng?
A.
( )
2023
ln 2 ln 2f =
. B.
(
)
2023
ln 3 ln 4f =
. C.
( )
2023
ln 2 ln 3f =
. D.
( )
2023
ln 3 ln 3f =
.
Câu 36. Có bao nhiêu giá trị nguyên của m để phương trình
( )
( )
1 .log 2
x
x e mx
−
− +=−
có 2 nghiệm
thực phân biệt
A. Vô số. B. 11. C. 9. D. 10.
Câu 37. Cho hình hộp đứng
111 1
.ABCD A B C D
có cạnh
2AB AD= =
,
1
3AA =
và góc
60BAD = °
.
Gọi
M
,
N
lần lượt là trung điểm của các cạnh
11
AD
và
11
AB
. Tính thể tích
V
của khối chóp
.A BDMN
.
A.
5
2
V =
. B.
3
2
V =
. C.
4V =
. D.
2
V =
.
Câu 38. Một con quạ đang khát nước. Nó bay rất lâu để tìm nước nhưng chẳng thấy một giọt nước
nào. Mệt quá, nó đậu xuống cành cây nghỉ. Nó nhìn quanh và bỗng thấy một cái bình hình trụ
có bán kính đáy là
2cm
, chiều cao
21cm
ở dưới một gốc cây. Trong bình đang có một ít
nước, khoảng cách giữa đáy cốc và mặt nước là
12cm
(Hình vẽ). Nhìn chung quanh, quạ thấy
những viên đá nhỏ nằm lay lắt ở gần đấy. Lập tức, nó dùng mỏ gắp một viên đá hình cầu có
bán kính
0,6cm
thả vào bình. Cứ như vậy, nó gắp những viên đá khác và tiếp tục thả vào
bình. Giả sử các viên đá đều là hình cầu có bán kính
0,6
cm
Chẳng bao lâu, nước đã dâng lên.
Để uống được nước thì con quạ cần thả vào bình ít nhất bao nhiêu viên đá biết rằng quạ muốn
uống được nước trong cốc thì mặt nước phải cách miệng cốc không quá
6cm
?
Trang 6/7 – Mã đề thi 123
A.
. B.
41
. C.
30
. D.
27
.
Câu 39. Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng
9
, khối chóp có thể
tích lớn nhất bằng bao nhiêu ?
A.
576 2
. B.
144
. C.
576
. D.
144 6
.
Câu 40. Xét hàm số
(
)
fx
liên tục trên
[ ]
0;1
và thỏa mãn điều kiện
( )
( )
22
4. 3 1 1xf x f x x+ −=−
.
Tích phân
( )
1
0
dI fx x
=
∫
bằng:
A.
20
I
π
=
. B.
16
I
π
=
. C.
6
I
π
=
. D.
4
I
π
=
.
Câu 41. Cho
(
)
0fx≠
,
( ) ( )
42
2
2
31
.
xx
fx f x
x
+−
′
=
,
(
)
1
1
3
f = −
. Xét
( )
2022
1
1
1
2
k
b
S fk
a
=

= = −


∑
với
b
a
tối giản. Tính
ab+
.
A.
4092530
. B.
4090507
. C.
4088485
. D.
4086463
.
Câu 42. Một bàn cờ vua gồm
88
ô vuông, mỗi ô có cạnh bằng 1 đơn vị. Một ô vừa là hình vuông
hay hình chữ nhật, hai ô là hình chữ nhật,… Chọn ngẫu nhiên một hình chữ nhật trên bàn cờ.
Xác suất để hình được chọn là một hình vuông có cạnh lớn hơn 4 đơn vị bằng
A.
5
216
. B.
17
108
. C.
51
196
. D.
29
216
.
Câu 43. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật tâm
O
,
AB a=
,
3BC a=
. Tam
giác
ASO
cân tại
S
, mặt phẳng
( )
SAD
vuông góc với mặt phẳng
( )
ABCD
, góc giữa
SD
và
( )
ABCD
bằng
60°
. Khoảng cách giữa hai đường thẳng
SB
và
AC
bằng
A.
3
2
a
. B.
3
2
a
. C.
2
a
. D.
3
4
a
.
Trang 7/7 – Mã đề thi 123
Câu 44. Cho hàm số
32
1y ax x bx
= −+−
với
, ab
là các số thực,
0a ≠
,
ab≠
sao cho đồ thị hàm số
cắt trục
Ox
tại ba điểm có hoành độ dương. Tìm giá trị nhỏ nhất của biểu thức
(
)
2
2
532
a ab
P
aba
−+
=
−
.
A.
15 3.
B.
8 2.
C.
11 6.
D.
12 3.
Câu 45. Cho hàm số
( )
32
69fx x x x=−+
. Đặt
( ) ( )
( )
1kk
f x ff x
−
=
với
k
là số tự nhiên lớn hơn
1
.
Hỏi phương trình
( )
9
0fx=
có bao nhiêu nghiệm?
A.
19684
. B.
9841
. C.
19683
. D.
9842
.
Câu 46. Cho
;xy
∈
,
( )
0x ≥
thỏa mãn:
(
)
31 1
3
1
2021 2021 1 2021 3
2021
x y xy xy
xy
x yx
+ + −−
+
+ ++= + − +
.
Tìm giá trị nhỏ nhất của
2Tx y= +
.
A.
2
3
. B.
1−
. C.
2
3
−
. D.
1
.
Câu 47. Số nghiệm của phương trình
( )
2
2
ln 2 2022
2
x
xx+− − =
là
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 48. Xét các số thực dương
, xy
thỏa mãn
( ) ( )
22
3
log 3 3
2
xy
x x y y xy
x y xy
+
= −+ −+
+++
. Tìm
giá trị lớn nhất của
321
6
xy
P
xy
++
=
++
.
A.
2
B.
1
C.
3
D.
4
Câu 49. Cho hình chóp
.
S ABCD
có đáy là hình bình hành. Góc tạo bởi mặt bên
( )
SAB
với đáy bằng
α
. Tỉ số diện tích của tam giác
SAB
và hình bình hành
ABCD
bằng
k
. Mặt phẳng
( )
P
đi
qua
AB
và chia hình chóp
.S ABCD
thành hai phần có thể tích bằng nhau. Gọi
( )
β
là góc tạo
bởi mặt phẳng
( )
P
và mặt đáy. Tính
cot
β
theo
k
và
α
.
A.
51
cot cot
sink
βα
α
+
= +
B.
51
cot tan
sink
βα
α
+
= +
C.
51
cot cot
sink
βα
α
−
= +
D.
51
cot tan
sink
βα
α
−
= +
Câu 50. Cho tứ diện
ABCD
có thể tích là
V
. Điểm
M
thay đổi trong tam giác
BCD
. Các đường
thẳng qua
M
và song song với
AB
,
AC
,
AD
lần lượt cắt các mặt phẳng
( )
ACD
,
( )
ABD
,
( )
ABC
tại
N
,
P
,
Q
. Giá trị lớn nhất của thể tích khối tứ diện
MNPQ
là
A.
27
V
. B.
16
V
. C.
8
V
. D.
54
V
.
………………………HẾT…………………….
BẢNG ĐÁP ÁN
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
ĐA
A
B
B
A
A
C
B
C
B
C
A
B
D
Câu
14
15
16
17
18
19
20
21
22
23
24
25
26
ĐA
B
A
A
B
B
A
B
A
D
D
B
A
B
Câu
27
28
29
30
31
32
33
34
35
36
37
38
39
ĐA
D
A
D
C
A
B
C
D
C
D
B
A
C
Câu
40
41
42
43
44
45
46
47
48
49
50
ĐA
A
B
A
D
D
D
C
C
B
A
A
Xem thêm: ĐỀ THI HSG TOÁN 12
https://toanmath.com/de-thi-hsg-toan-12
Câu 1. Trong các hàm số sau đây, hàm số nào là hàm số chẵn?
A.
sin
2
yx



. B.
sin
yx
. C.
sin tanyxx
. D.
sin .cosy xx
Lời giải
Chọn A
Ta có
sin cos
2
yx x



nên
sin
2
yx



là hàm số chẵn.
Câu 2. Một học sinh có
4
quyển sách Toán khác nhau và
5
quyển sách Ngữ văn khác nhau. Hỏi có
bao nhiêu cách xếp
9
quyển sách trên giá sao cho hai quyển sách kề nhau phải khác loại ?
A.
. B.
2880
. C.
362880
. D.
5760
.
Lời giải
Chọn B
Để xếp
9
quyển sách trên giá sao cho hai quyển sách kề nhau phải khác loại, ta làm như sau:
Xếp
5
quyển sách Ngữ văn cạnh nhau có
5! 120
cách.
Giữa
5
quyển sách Ngữ văn trên có
4
chỗ trống, xếp
4
quyển sách Toán vào
4
chỗ trống đó
có
4! 24
cách.
Theo quy tắc nhân có
120.24 2880
cách sắp xếp thỏa điều kiện đề bài.
Câu 3. Cho cấp số cộng
( )
n
u
với
1
6u
=
;
9d =
. Khi đó số
2022
là số hạng thứ bao nhiêu của cấp số?
A.
226
. B.
225
. C.
223
. D.
224
.
Lời giải
Chọn B
Ta có:
( )
1
1
n
uu n d=+−
( )
2022 6 1 .9n⇔ =+−
225n
⇔=
.
Câu 4. Tìm m để hàm số
( ) (
)
42
1 21 1ymx mx=−+−+
có đúng 3 điểm cực trị.
A.
1
1
2
m<<
. B.
1
1
2
m
≤<
. C.
1
1
2
m<≤
. D.
1
1
2
m
≤≤
.
Lời giải
Chọn A
Cách 1:
( )( )
1
1 2 1 0 1.
2
Ycbt m m m⇔ − − <⇔ < <
Cách 2:
( ) ( ) ( )
32
'4 1 221 22 1 21y mx mxxmx m

= − + −= − +−

( )
2
0
'0
2 1 2 1 0 (1)
x
y
mx m
=
= ⇔
− + −=
Hàm số có đúng 3 điểm cực trị
'y⇔
có 3 nghiệm phân biệt
⇔
phương trình (1) có hai
nghiệm phân biệt khác 0
( )( )
1
1 2 1 0 1.
2
mm m⇔ − − <⇔ < <
Câu 5. Đặt
ln 2, ln 5= =ab
, hãy biểu diễn
1 2 3 98 99
ln ln ln ... ln ln
2 3 4 99 100
I = + + ++ +
theo
a
và
b
.
A.
( )
2I ab=−+
B.
( )
2I ab=−−
C.
( )
2I ab= +
D.
( )
2I ab= −
Lời giải
1 2 3 98 99
ln ln ln ... ln ln
2 3 4 99 100
I = + + ++ +
2
1 2 3 98 99 1
ln . . . .. . ln ln10
2 3 4 99 100 100
−

= = =


( ) ( )
2ln10 2 ln 2 ln5 2 ab=− =− + =−+
.
Câu 6. Lăng trụ đứng có đáy là hình thoi có bao nhiêu mặt phẳng đối xứng?
A. 2. B. 9. C. 3. D. 5.
Lời giải
Lăng trụ đứng có đáy là hình thoi có tất cả 3 mặt phẳng đối xứng (Hình vẽ).
Câu 7. Cho đoạn thẳng
AB
có độ dài bằng
2a
, vẽ tia
Ax
về phía điểm
B
sao cho điểm
B
luôn cách
tia
Ax
một đoạn bằng
a
. Gọi
H
là hình chiếu của
B
lên tia
Ax
, khi tam giác
AHB
quay
quanh trục
AB
thì đường gấp khúc
AHB
vẽ thành mặt tròn xoay có diện tích xung quanh
bằng:
A.
2
32
2
a
π
. B.
( )
2
33
2
a
π
+
. C.
( )
2
13
2
a
π
+
. D.
( )
2
22
2
a
π
+
.
Lời giải
Xét tam giác
AHB
vuông tại
H
. Ta có
22
3AH = AB HB a−=
Xét tam giác
AHB
vuông tại
H
,
HI AB⊥
tại
I
ta có
. 3. 3
22
AH HB a a a
HI =
AB a
= =
Khi tam giác
AHB
quay quanh trục
AB
thì đường gấp khúc
AHB
vẽ thành mặt tròn xoay (có
diện tích xung quanh là
S
) là hợp của hai mặt xung quanh của hình nón (N
1
) và (N
2
).
Trong đó:
A
B
I
H
x
(N
1
) là hình nón có được do quay tam giác
AHI
quanh trục
AI
có diện tích xung quanh là
2
1
33
.3
22
aa
S=π.HI.AH = . a
π
π
=
(N
2
) là hình nón có được do quay tam giác
BHI
quanh trục
có diện tích xung quanh là
2
2
33
.
22
aa
S=π.HI.BH = . a
π
π
=
( )
2
22
12
33
33
22 2
a
aa
S=S +S
π
ππ
+
⇒ =+=
.
Câu 8. Cắt hình trụ
( )
T
bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện
tích bằng
30
2
cm
và chu vi bằng
26
cm
. Biết chiều dài của hình chữ nhật lớn hơn đường kính
mặt đáy của hình trụ
(
)
T
. Diện tích toàn phần của
( )
T
là:
A.
( )
23
2
cm
π
. B.
( )
2
23
2
cm
π
. C.
( )
2
69
2
cm
π
. D.
( )
2
69
cm
π
.
Lời giải
Chọn C
Gọi
,hr
lần lượt là đường cao và bán kính đáy của hình trụ
( )
T
. Thiết diện của mặt phẳng và
hình trụ
( )
T
là hình chữ nhật
ABCD
. Khi đó theo giả thiết ta có
2
2 22 2
.2 30 15 13 2 13 2
2 13
2( 2 ) 26
5 3( )
2 15 15 0
3
10( )
2
ABCD
ABCD
hr hr hr hr
Shr hr hr hr
hr
C hr
r hl
rr
r h TM
> >> >

= = ⇔ = ⇔=− ⇔=−


+=
=+=
=⇒=
− + −=
=⇒=
Vậy .
Câu 9. Cho hàm số
()fx
xác định trên
1
\
2



thỏa mãn
( ) ( ) ( )
2
, 0 1, 1 2
21
fx f f
x
′
= = =
−
. Giá trị
của biểu thức
( ) ( )
13ff−+
bằng
A.
2 ln15+
B.
3 ln15+
C.
ln15
D.
4 ln15+
Lời giải
Chọn C
( )
2
ln 2 1
21
dx x C f x
x
= −+ =
−
∫
Với
1
2
x <
,
( )
01f =
1
C⇒=
nên
( )
1 1 ln 3f −=+
Với
( )
1
,12 2
2
xf C> =⇒=
nên
( )
3 2 ln 5f = +
Nên
( )
( )
1 3 3 ln15ff−+ =+
Câu 10. Cho
( )
2
0
3 2 1d 6
m
xx x−+ =
∫
. Giá trị của tham số
m
thuộc khoảng nào sau đây?
A.
( )
1;2−
. B.
(
)
;0
−∞
. C.
( )
0;4
. D.
( )
3;1−
.
Lời giải
Chọn C
Ta có:
( ) (
)
2 32 3 2
0
0
3 2 1d
m
m
x x x xxx mmm−+ = −+ = − +
∫
.
( )
2
0
3 2 1d 6
m
xx x−+ =
∫
( )
32
6 0 2 0;4mmm m⇔ − + −=⇔ =∈
.
Vậy
(
)
2 0;4
m
= ∈
.
Câu 11. Có bao nhiêu cách phân công 4 thầy giáo dạy toán vào dạy 12 lớp 12, mỗi thầy dạy đúng 3 lớp
?
A. 369600 B. 396900 C. 220 D. 369000
Lời giải
Chọn A
Giáo viên thứ nhất có
3
12
C
cách chọn.
Giáo viên thứ hai có
3
9
C
cách chọn.
Giáo viên thứ ba có
3
6
C
cách chọn.
Giáo viên thứ tư có
3
3
C
cách chọn.
Vậy số cách phân công 4 thầy giáo vào dạy 12 lớp 12 là:
3 333
12 9 6 3
. . . 369600C CCC
=
cách
Câu 12. Giới hạn
( )
( )
42
3
2
lim
13 1
x
xx
xx
→+∞
++
+−
có kết quả là :
A.
3−
B.
3
3
C.
3
D.
3
3
−
Lời giải
Chọn B
Ta có:
(
)
(
)
4
42
24 24
3
4
33
12 12
11
23
lim lim lim
11 11
3
13 1
13 13
xx x
x
xx
xx xx
xx
x
xx xx
→+∞ →+∞ →+∞
 
++ ++
 
++
 
= = =
 
+−
+− +−
 
 
.
Câu 13. Cho tứ diện
OABC
có
, ,
OA OB OC
đôi một vuông góc với nhau và
OA OB OC
= =
. Gọi
M
là trung điểm của
BC
(tham khảo hình vẽ bên dưới). Góc giữa hai đường thẳng
OM
và
AB
bằng
A.
0
45
B.
0
90
C.
0
30
D.
0
60
Lời giải
Chọn D
Đặt
OA a=
suy ra
OB OC a= =
và
2AB BC AC a= = =
Gọi
N
là trung điểm
AC
ta có
//MN AB
và
2
2
a
MN =
Suy ra góc
( )
( )
,,=OM AB OM MN
. Xét
OMN
Trong tam giác
OMN
có
2
2
a
ON OM MN= = =
nên
OMN
là tam giác đều
Suy ra
0
60OMN =
. Vậy
( )
( )
0
, , 60= =OM AB OM MN
Câu 14. Cho hàm số
( )
y fx=
có đồ thị hàm
( )
y fx
′
=
như hình vẽ bên dưới.
Hàm số đã cho nghịch biến trên khoảng
A.
( )
;2−∞ −
. B.
( )
2;1−
. C.
( )
;4−∞ −
. D.
( )
2;3−
.
Lời giải
Chọn B
Từ đồ thị hàm số
( )
y fx
′
=
ta thấy ngay hàm số nghịch biến trên các khoảng
( )
2;1−
.
Câu 15. Có bao nhiêu giá trị nguyên dương của
m
để khoảng cách từ gốc tọa độ
O
đến đường thẳng đi
qua 2 điểm cực trị của đồ thị hàm số
3
3y x xm=−+
nhỏ hơn hoặc bằng
5.
A. 5. B. 2. C. 11. D. 4.
Lời giải
Chọn A
3
3y x xm=−+
;
2
33yx
′
= −
;
1
0.
1
x
y
x
=
′
= ⇔
= −
⇒
Với mọi
m
phương trình
0y
′
=
có hai nghiệm phân biệt và
y
′
đổi dấu khi qua hai nghiệm.
⇒
Đồ thị hàm số có hai điểm cực trị với mọi
m
.
Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số đã cho là:
2y xm
=−+
(
)
∆
.
Khoảng cách từ
O
tới đường thẳng
∆
là
( )
;
5
m
dO∆=
.
Theo bài ra ta có:
( )
,5dO∆≤
⇔
5
5
m
≤
⇔
5m ≤
⇔
5 5.m−≤ ≤
Vì
m
nguyên dương nên
{ }
1; 2; 3; 4; 5 .m∈
Câu 16. Giá trị nhỏ nhất và lớn nhất của hàm số
2yx x= −
trên đoạn
[0; 9]
lần lượt là
m
và
M
. Giá
trị của tổng
mM+
bằng
A. 2. B. 3. C. 0. D. 1.
Lời giải
Chọn A
Đạo hàm
(
] [ ]
1
' 1 ; 0;9 y ' 0 1 0;9 .yx x
x
= − ∀ ∈ → = ⇔ = ∈
Ta có
( )
( )
( )
[ ]
( )
[ ]
( )
0;9
0;9
00
min 1
1 1 2.
max 3
93
f
m fx
f mM
M fx
f
=
= = −
= − → → + =

= =

=
Câu 17. Cho hàm số
1ax
y
bx c
+
=
+
(
,,abc
là các tham số) có bảng biến thiên như hình vẽ
Xét các phát biểu sau:
( )
( )
(
)
( )
1 : 1.
2 : 0.
3 : 0.
4 : 0.
c
ab
abc
a
>
+<
++=
>
Số phát biểu đúng là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Dựa vào bảng biến thiên ta có hàm số luôn đồng biến trên từng khoảng xác định, đồ thị hàm số
có tiệm cận đứng là đường thẳng
2x =
và tiệm cận ngang là đường thẳng
1y =
nên ta có hệ
2
2
01
22
1
10
2
02 0
1
0
0
2
0
c
c
b
cb cb
a
ab ab a
b
ac b b b
ac b
b
abc
−=
<<
=−=−


= ⇔ = ⇔ = ⇔−<<


−> − −>

−>

−<<

++=
Dựa vào hệ trên ta có các phát biểu
( ) ( )
1,4
là sai,
(
) (
)
2,3
đúng.
Câu 18. Đặt
3
log 2 a=
khi đó
16
log 27
bằng
A.
3
4
a
B.
3
4a
C.
4
3a
D.
4
3
a
Lời giải
Chọn B
Ta có
16 2
3
3 33
log 27 log 3
4 4.log 2 4a
= = =
Câu 19. Cho hai số thực dương
x
,
y
thỏa mãn
22
22
log 1 logx y xy 
. Mệnh đề nào dưới đây
đúng?
A.
xy
. B.
xy
. C.
xy
. D.
2
xy
.
Lời giải
Chọn A
Với
x
,
0y
ta có:
22 22
2 22 2
log 1 log log log 2
x y xy x y xy 
.
22
2x y xy
.
xy
.
Câu 20. Đặt
2
log 3a =
;
5
log 3b =
. Nếu biểu diễn
(
)
( )
6
log 45
a m nb
ba p
+
=
+
thì
mn p
++
bằng
A.
3
B.
4
C.
6
D.
3−
Lời giải
Chọn B
Ta có
( )
( )
3 33
6
3 33
1
2
21
log 45 log 9 log 5
log 45
1
log 6 log 2 log 3 1
1
ab
b
ba
a
+
+
+
= = = =
++
+
Suy ra
1, 2, 1 4m n p mn p= = =⇒ ++ =
Câu 21. Một hình đa diện lồi có số mặt
, số đỉnh
D
và số cạnh
C
. Khi đó, hệ thức nào dưới đây là
đúng ?
A.
2DMC+ −=
B.
2DCM+− =
C.
2MCD+−=
D.
MDC+=
Lời giải
Chọn A
Câu 22. Tính thể tích
V
của khối lăng trụ tam giác đều
.ABC A B C
′′′
có
5AC a
′
=
, cạnh đáy là
4a
.
A.
3
12Va=
. B.
3
20 3
Va=
. C.
3
20Va=
. D.
3
12 3Va=
.
Lời giải
Chọn D
Vì
.ABC A B C
′′′
là lăng trụ tam giác đều nên ta có
( )
CC ABC
′
⊥
và
ABC∆
đều cạnh là
.
Do đó:
22
25 16 3CC a a a
′
= −=
;
(
)
2
2
13
4 43
22
S aa
ABC
= =
∆
23
.
. 3 .4 3 12 3
ABC A B C ABC
V CC S a a a
′′′
∆
′
= = =
.
Câu 23. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác cân tại
A
,
4; 6AB AC a BC a= = =
.Hình
chiếu vuông góc của
S
trên mặt phẳng
( )
ABC
nằm trong tam giác
ABC
. Các mặt bên của
hình chóp cùng tạo với đáy góc
0
60
. Tính thể tích khối chóp
.S ABC
.
A.
3
63a
. B.
3
3a
. C.
3
83a
. D.
3
33a
.
Lời giải
Chọn D
5
a
4
a
A'
A
B'
B
C'
C
Gọi
H
là hình chiếu vuông góc của điểm
S
lên mặt phẳng
( )
ABC
,
,,MNP
lần lượt là hình
chiếu vuông góc của điểm
H
lên
,,AB BC CA
.
Khi đó ta có
SHM SHN SHP∆ =∆=∆
Suy ra
HM HN HP= =
Suy ra
H
là tâm đường tròn nội tiếp tam giác
ABC
2
63
ABC
Sa
∆
=
63
7
ABC
S
HN a
p
∆
= =
3 21
7
SH a=
Câu 24. Cho hình nón đỉnh
I
, đường cao
IO
(
O
là tâm của đáy) và có độ dài đường sinh bằng
3cm
,
góc ở đỉnh bằng
60°
. Gọi
K
là điểm thuộc đoạn
IO
thỏa mãn
3
2
IO IK=
, cắt hình nón bằng
mặt phẳng
()P
qua
K
và vuông góc với
, khi đó thiết diện tạo thành có diện tích là
S
. Tính
S
.
A.
( )
2
3
S cm
π
=
. B.
( )
2
S cm
π
=
. C.
( )
2
3S cm
π
=
. D.
( )
2
2
3
S cm
π
=
.
Lời giải
Chọn B
Thiết diện tạo thành là đường tròn tâm
K
, bán kính
KM
.
Ta có:
2 21
. .. 1
3 32
KM ON IN= = =
. Diện tích thiết diện là:
2
.S KM
ππ
= =
( )
2
cm
23
.
1 3 21
63 . 3 3 .
37
S ABC
V a aa= =
3 cm
30
°
M
K
O
N
I
Câu 25. Cho
( )
2
Fx x=
là một nguyên hàm của hàm số
( )
2x
f xe
. Tìm nguyên hàm của hàm số
( )
2
'
x
f xe
.
A.
( )
22
' 22
x
f x e dx x x C=− ++
∫
. B.
( )
22
'2
x
f x e dx x x C=−+ +
∫
.
C.
( )
22
'
x
f x e dx x x C=− ++
∫
. D.
( )
22
' 22
x
f x e dx x x C= −+
∫
.
Lời giải
Chọn A
( )
2
Fx x=
là một nguyên hàm của hàm số
( )
2x
f xe
2 2 22
1
'() (). 2 (). ().
x xx
F x fxe x fxe fxe dx x C⇒ = ⇒= ⇒ =+
∫
Đặt
22
22 2 2
2
2
'() ()
'( ). ( ). 2. ( ). 2 2
xx
xx x
u e du e dx
dv f x dx v f x
f xe dx fxe fxe dx C x x C

= =
⇒

= =

⇒ = − +=− ++
∫∫
Câu 26. Có bao nhiêu số thực
a
để
1
2
0
1=
+
∫
x
dx
ax
.
A.
2
B.
1
C.
0
D.
3
Lời giải
Chọn B
Điều kiện tích phân tồn tại là
[ ]
2
1
0, 0;1
0
<−
+ ≠ ∀∈ ⇒
>
a
ax x
a
Đặt
2
2d
t a x dt x x=+⇒=
. Khi đó
2
11
2
2
2
0
2
1
1
1 11
1
ln 1
1
22
1
1
+
=
+=
+
−
===⇔⇔
−
+
+=−
=
+
∫∫
a
a
a
a ea
x dt a
e
dx
ta
ax
a ea
a
e
So sánh điều kiện ta được
2
1
1
=
−
a
e
.
Câu 27. Số giá trị nguyên của tham số
m
thuộc đoạn
[ ]
2022; 2022−
để phương trình
( )
2
1 sin sin 2 cos 2 0m xx x+ −+ =
có nghiệm là:
A.
4045
. B.
4044
. C.
2023
. D.
2024
.
Lời giải
Chọn D
Ta có:
( )
2
1 sin sin 2 cos 2 0m xx x+ −+ =
( )
1 cos 2
1 sin 2 cos 2 0
2
x
m xx
−
⇔+ − + =
11
sin 2 cos 2
22
mm
xx
− −−
⇔− + =
.
Điều kiện để phương trình
sin cosa xb x c+=
có nghiệm là
222
abc+≥
ứng với phương trình
trên ta được
22
11
1
22
mm− −−

+≥


22
12 2 1
1
44
mm m m−+ ++
⇔+ ≥
44m⇔≤
1m⇔≤
.
Vậy các giá trị nguyên của tham số
m
thuộc đoạn
[ ]
2022; 2022−
thỏa mãn là
{ }
2022;...; 1;0;1−−
vậy có 2024 số.
Câu 28. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
vuông góc với đáy và
3SA a=
. Gọi
α
là góc giữa
SD
và
(
)
SAC
. Giá trị
sin
α
bằng
A.
2
4
. B.
2
2
. C.
3
2
. D.
2
3
.
Lời giải
Gọi
O AC BD= ∩
. Ta có:
(
)
( )
( )
DO AC
DO ABCD
DO SA SA ABCD
⊥
⇒⊥
⊥⊥
.
SO⇒
là hình chiếu của
SD
lên mặt phẳng
( )
SAC
( )
(
)
( )
;;SD SAC SD SO DSO
α
⇒===
.
Xét
SAD∆
vuông tại
A
:
22
32SD a a a= +=
.
Xét
SOD∆
vuông tại
O
: có
2SD a=
,
22
sin sin
24
a DO
OD DSO
SD
α
=⇒= ==
.
Câu 29. Có bao nhiêu giá trị nguyên âm của tham số
m
để hàm số
( )
42
39
2 15 3 1
42
y x x m xm= − + + −+
đồng biến trên khoảng
( )
0; +∞
?
A.
2.
B.
3.
C.
5.
D.
4.
Lời giải
Yêu cầu bài toán
(
)
3
3 9 2 15 0 0;y x xm x
′
⇔ = − + + ≥ ∀ ∈ +∞
và dấu bằng xảy ra tại hữu hạn
điểm thuộc
( )
0; +∞
( )
3
3 9 15 2 0;x x mx⇔ − + ≥ − ∀ ∈ +∞
.
Xét hàm số:
3
( ) 3 9 15gx x x= −+
trên
( )
0; +∞
.
Ta có:
2
() 9 9gx x
′
= −
( )
0gx
′
=
1
1( )
x
xl
=
⇒
= −
.
Bảng biến thiên:
Từ BBT ta có:
9
29
2
mm
− ≤ ⇔ ≥−
Vậy
{ 4; 3; 2; 1}m∈−−−−
.
Câu 30. Cho hàm số
32
3yx xm=−+
, với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của
tham số m để đồ thị hàm số có 5 điểm cực trị. Tổng tất cả các phần tử của tập S là
A. 3 B. 10 C. 6 D. 5
Lời giải:
Xét hàm số
32
() 3gx x x m=−+
có đồ thị như hình vẽ.
Để đồ thị hàm số
32
3yx xm=−+
có 5 điểm cực trị thì
4 <0
0
m
m
>
−+
⇔ 0 < m < 4 . Do đó S = {1;2;3}, tổng tất cả các giá trị
của S là 6 .
Cách khác:
(
)
2
32 32
3 3,yx xm x xm
=−+= −+
( )
(
)
(
)
32 2
2
32
3 36
'.
3
x xmx x
y
x xm
−+ −
=
−+
Đồ thị hàm số đã cho có 5 điểm cực trị khi và chỉ khi phương trình y’ = 0 có 5 nghiệm phân
biệt và y’ đổi dấu qua 5 nghiệm đó, điều này tương đương với
32
3x xm
−+
có ba nghiệm phân
biệt khác 0 và 2 .
Câu 31. Cho hàm số
( )
y fx=
có bảng biến thiên như sau
Tập hợp tất cả các giá trị thực của tham số
m
để phương trình
() 0fx m+=
có 5 nghiệm phân
biệt là
A.
(
]
2; 1−−
. B.
[
)
1; 2−
. C.
( )
2; 1−−
. D.
( )
2;1−
.
Lời giải
Từ bảng biến thiên của hàm số
( )
y fx=
.Ta có bảng biến thiên của hàm số
(
)
y fx=
Khi đó phương trình
() 0fx m+=
có 5 nghiệm khi phương trình
()fx m= −
có 5 nghiệm hay
đồ thị hàm số
( )
y fx=
và
ym
= −
cắt nhau tại 5 điểm phân biệt
Do vậy
1 22 1mm≤− < ⇔− < ≤−
.
Câu 32. Cho hình chóp đều đỉnh S có đáy là đa giác đều 8 cạnh. Một hình nón đỉnh
S
có đáy là
đường tròn ngoại tiếp đáy hình chóp. Tính tỉ số thể tích của khối nón và khối chóp
tương ứng.
A.
3
π
. B.
22
π
. C.
2
π
. D.
2
33
π
.
Lời giải
Chọn B
Gọi
;OR
lần lượt là tâm và bán kính đáy của hình nón đỉnh
S
,
h SO=
là độ dài
đường cao của hình nón
⇒
h
cũng là độ dài đường cao của hình chóp đều
12345678
.SAAAAAAAA
có đáy là đa giác đều
8
cạnh nội tiếp đáy của hình nón.
Ta có đáy nón ngoại tiếp đáy của hình chóp đều 8 cạnh như hình vẽ.
Ta thấy đa giác đều
12345678
AAAAAAAA
được chia thành 8 tam giác cân bằng nhau có
cạnh bên bằng
R
và góc ở đỉnh bằng
45°
⇒
Diện tích của đa giác đều
12345678
AAAAAAAA
là:
12
2
1 2 12
1
8. 8. . . .sin 2 2
2
OA A
S S OA OA A OA R
∆
= = =
.
Gọi
12
;VV
lần lượt là thể tích của khối chóp đều và khối nón đã cho.
Thể tích khối khối chóp đều đã cho là:
2
1
11
.. 2 2
33
V hS R h= =
.
Thể tích của khối nón đã cho là:
2
2
1
3
V Rh
π
=
.
Tỉ số thể tích của khối nón và khối chóp là:
2
2
2
1
1
3
1
22
22
3
Rh
V
V
Rh
π
π
= =
.
Câu 33. Số đường tiệm cận đứng của đồ thị hàm số
2
2
41 2 6
2
x xx
y
xx
−− + +
=
+−
là
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn C
Tập xác định
{ }
\ 1; 2D = −
{
}
0
\ 1; 2x∀∈ −
0
2
2
0 00
22
00
41 2 6
41 2 6
lim
22
xx
x xx
x xx
xx xx
→
−− + +
−− + +
=
+− + −
Suy ra tiệm cận đứng nếu có của đồ thị hàm số
2
2
41 2 6
2
x xx
y
xx
−− + +
=
+−
chỉ có thể là hai đường
thẳng
1; 2xx= = −
( )
( )
( )
( )
( )
( )(
)
(
)
( )
( )
( )( )
( )
( )
2
2
2
11
2
22
11
2
1
4 13 2 6
41 26
lim lim
2 12
9 26
13
41 41
3 26 3 26
lim lim
12 12
3
4
10
3 26
lim
29
xx
xx
x
x xx
x xx
xx x x
xx
xx
xx
xx xx
xx xx
x
xx
x
→→
→→
→
− +− + +
−− + +
=
+− − +
− ++
−+
−+ −−
+ ++ + ++
= =
−+ −+
+
−
+ ++
= =
+
Suy ra
1x =
không phải là đường tiệm cận đứng
Xét
2
2
2
41 2 6
lim
2
x
x xx
xx
+
→−
−− + +
+−
(
)
2
2
lim 4 1 2 6 9 6 0
x
x xx
+
→−
−− + + =−− <
( )( )
2
lim 1 2 0
x
xx
+
→−
− +=
, và
( )( )
1 20xx− +>
với mọi
x
thuộc lân cận của
nhưng nhỏ hơn
Suy ra
2
2
2
41 2 6
lim
2
x
x xx
xx
+
→−
−− + +
= −∞
+−
Vậy
2
x = −
là tiệm cận đứng
Kết luận: Đồ thị hàm số có một đường tiệm cận đứng.
Câu 34. Gọi
0
3ab
x
c
+
=
với (
,, ,
a
abc N
c
∈
tối giản) là một nghiệm lớn hơn
1
của phương trình
( )
1
1
2
1
2 3 12 1
3
x
x
xx
−


− += −





. Giá trị của
P abc
=++
là
A.
6P =
. B.
0P =
. C.
2P =
. D.
4P =
.
Lời giải
Chọn D
Điều kiện xác định:
0x ≠
.
( )
1
1
1
23 1
3
x
x
x
−


−+





2
21x= −
1
1
2
1
331
2
x
x
x
x
−
⇔ − += −
1
1
2
1
3 31
2
x
x
x
x
−
⇔ + = +−
( )
1
. Xét hàm số
( )
3
t
ft t= +
( )
0t ≠
,
( )
3 .ln 3 1 0
t
ft
′
= +>
( )
( )
1
11
2
f fx
x

⇔=−


1
1
2
x
x
⇔=−
13
2
x
±
⇔=
1
a⇒=
,
1
b =
,
2c =
. Vậy
4P =
.
Câu 35. Cho các hàm số
( ) ( )
( )
12
,,,fxfxfx
…
thỏa mãn:
(
) ( )
1
1
ln
1
x
x
e
fx fx
e
+
= =
−
;
( )
1
() (), 1;2;3;
nn
f x ffx n
+
= ∀= …
Khẳng định nào sau đây đúng?
A.
( )
2023
ln 2 ln 2f =
. B.
(
)
2023
ln 3 ln 4
f =
. C.
( )
2023
ln 2 ln 3f =
. D.
( )
2023
ln 3 ln 3f =
.
Lời giải
Chọn C
( ) ( )
1
1
ln
1
x
x
e
fx fx
e
+
= =
−
.
Ta có:
( ) ( )
( )
1
ln
1
1
ln
1
1
2
1
1
1
1
ln ln ln
1
1
1
1
x
x
x
x
x
e
e
x
x
x
e
e
x
e
e
e
fx ffx e x
e
e
e
+
−
+
−
+
+
+
−
= = = = =
+
−
−
−
.
( ) ( )
( )
32
1
ln
1
x
x
e
fx ffx
e
+
= =
−
.
( ) ( )
( )
43
fx ffx x= =
.
( ) ( )
( )
54
1
ln
1
x
x
e
fx ffx
e
+
= =
−
…
Bằng quy nạp ta chứng minh được
(
)
2023
1
ln
1
x
x
e
fx
e
+
=
−
.
Từ đó suy ra:
(
)
ln 2
ln
20
2
23
1
ln ln 32
1
lnf
e
e
+
==
−
;
( )
3
5
ln
ln 3
13
ln
12
ln 3f
e
e
+
==
−
.
Câu 36. Có bao nhiêu giá trị nguyên của m để phương trình
(
)
( )
1 .log 2
x
x e mx
−
− +=−
có 2 nghiệm
thực phân biệt
A. Vô số. B. 11. C. 9. D. 10.
Lời giải
Chọn D
Điều kiện:
0
x
em
−
+>
(*).
Vì
1x =
không là nghiệm nên phương trình nên:
2
1
2
log( ) 10
1
x
xx
x
x
em em
x
−
−−
−
−
+ = ⇔ +=
−
( thỏa mãn (*))
2
1
10
x
x
x
me
−
−
−
⇔= −
.
Đặt
2
1
( ) 10
x
x
x
y gx e
−
−
−
= = −
Ta có:
2
1
2
1
10 ln10 0, 1
( 1)
x
x
x
y ex
x
−
−
−
′
= + > ∀≠
−
Bảng biến thiên:
Vậy phương trình có 2 nghiệm thực phân biệt khi
1
10m
e
−< <
.
Suy ra các giá trị
m
cần tìm là: 0,1,2,3,4,5,6,7,8,9.
Câu 37. Cho hình hộp đứng
111 1
.ABCD A B C D
có cạnh
2AB AD= =
,
1
3AA =
và góc
60BAD = °
. Gọi
,
N
lần lượt là trung điểm của các cạnh
11
AD
và
11
AB
. Tính thể tích
V
của khối chóp
.A BDMN
.
A.
5
2
V =
. B.
3
2
V =
. C.
4V =
. D.
2V =
.
Lời giải
Gọi
E
là điểm đối xứng với
A
qua
1
A
, ta có:
1
1
//
2
A N AB
AB
AN
=
N
⇒
là trung điểm của đoạn
EB
1
1
//
2
A M AD
AD
AM
=
M⇒
là trung điểm của đoạn
ED
Ta có
1
. .sin
2
ABD
S AB AD BAD
∆
=
1
.2.2.sin 60
2
= °
3=
111 1
.
ABCD A B C D
là hình hộp đứng,
1
3AA =
23EA⇒=
.
1
.
3
E ABD ABD
V EA S
∆
⇒=
1
.2 3. 3 2
3
= =
.
.
1
.
4
E AMN
E ABD
V
EM EN
V ED EB
= =
..
1
4
E AMN E ABD
VV⇒=
..
3
4
A BDMN E ABD
VV⇒=
3
2
=
.
Câu 38. Một con quạ đang khát nước. Nó bay rất lâu để tìm nước nhưng chẳng thấy một giọt nước nào.
Mệt quá, nó đậu xuống cành cây nghỉ. Nó nhìn quanh và bỗng thấy một cái bình hình trụ có bán
kính đáy là
2cm
, chiều cao
21cm
ở dưới một gốc cây. Trong bình đang có một ít nước, khoảng
cách giữa đáy cốc và mặt nước là
12cm
(Hình vẽ). Nhìn chung quanh, quạ thấy những viên đá
nhỏ nằm lay lắt ở gần đấy. Lập tức, nó dùng mỏ gắp một viên đá hình cầu có bán kính
0,6cm
thả vào bình. Cứ như vậy, nó gắp những viên đá khác và tiếp tục thả vào bình. Giả sử các viên
đá đều là hình cầu có bán kính
0,6cm
Chẳng bao lâu, nước đã dâng lên. Để uống được nước
thì con quạ cần thả vào bình ít nhất bao nhiêu viên đá biết rằng quạ muốn uống được nước
trong cốc thì mặt nước phải cách miệng cốc không quá
6cm
?
N
M
B
A
D
C
B1
A1
D1
C1
E
A.
. B.
41
. C.
30
. D.
27
.
Lời giải
Ta có thể tích của mỗi viên đá là:
3
3
4 3 36
.. ( )
3 5 125
cm
π
π

=


.
Gọi
n
là số viên đá mà con quạ cần thả vào cốc (
*n ∈
). Khi thả vào số viên đá đó, thể tích
của nước được tăng thêm là:
3
.36
()
125
n
V cm
π
=
Để con quạ uống được nước trong cốc thì mực nước trong cốc cần dâng lên thêm ít nhất là:
21 12 6 3 ( )h cm= − −=
, tức là ứng với thể tích nước tăng lên là:
22
' . . 3. .2 12
V hr
πππ
= = =
Ta có điều kiện:
.36 125
' 12 41,66
125 3
n
VV n
π
π
≥ ⇔ ≥ ⇔≥ =
Vậy số viên đá tối thiểu con quạ cần bỏ vào cốc là
42
viên.
Câu 39. Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng
9
, khối chóp có thể
tích lớn nhất bằng bao nhiêu ?
A.
576 2
. B.
144
. C.
576
. D.
144 6
.
Lời giải
Chọn C
Giả sử khối chóp
.S ABCD
là khối chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng
9
.
Gọi
O
là tâm hình vuông
ABCD
thì
( )
SO ABCD⊥
.
M
là trung điểm của
SA
, kẻ
MI
vuông
góc với
SA
và cắt
SO
tại
I
thì
I
là tâm mặt cầu ngoại tiếp hình chóp
.S ABCD
, bán kính của
mặt cầu là
9IA IS= =
.
Đặt
IO x=
,
09x≤≤
, do
IAO∆
vuông tại
O
nên
22
AO AI IO= −
2
81
x
= −
, suy ra
2
2 81AC x= −
.
Do tứ giác
ABCD
là hình vuông nên
2
AC
AB =
2
2. 81 x= −
, suy ra
2
ABCD
S AB=
( )
2
2 81 x= −
.
Vậy
.
1
.
3
S ABCD ABCD
V S SO=
(
)
(
)
2
2
81 . 9
3
xx
=−+
( )
32
2
9 81 729
3
xx x= −− + +
.
Xét hàm số
( )
fx=
( )
32
2
9 81 729
3
xx x−− + +
với
[ ]
0;9x ∈
.
(
)
( )
2
2 6 27fx x x
′
=−− +
;
( )
0fx
′
=
⇔
( )
3
9
x
xl
=
= −
Bảng biến thiên :
Dựa vào bảng biến thiên ta thấy :
[
]
( )
( )
0;9
max 3
∈
=
x
fx f
576=
.
Vậy khối chóp có thể tích lớn nhất bằng
576
.
Câu 40. Xét hàm số
( )
fx
liên tục trên
[ ]
0;1
và thỏa mãn điều kiện
( )
( )
22
4. 3 1 1xf x f x x+ −=−
.
Tích phân
(
)
1
0
dI fx x
=
∫
bằng:
A.
20
I
π
=
. B.
16
I
π
=
. C.
6
I
π
=
. D.
4
I
π
=
.
Lời giải
Vì
( )
fx
liên tục trên
[ ]
0;1
và
( )
( )
22
4. 3 1 1xf x f x x+ −=−
nên ta có
(
)
( )
11
22
00
4. 3 1 d 1 dxf x f x x x x

+− =−

∫∫
( )
( )
11 1
22
00 0
4. d 3 1 d 1 dxf x x f x x x x⇔ + −=−
∫∫∫
( )
1
.
Mà
( )
1
2
0
4. dxf x x
∫
( ) ( )
1
22
0
2dfx x=
∫
( )
2
1
0
2d
tx
ft t
=
→
∫
2I=
và
( )
1
0
31 df xx−
∫
(
) ( )
1
0
3 1 d1fx x=−−−
∫
( )
1
1
0
3d
ux
fu u
= −
→
∫
3I=
Đồng thời
1
2
0
1dxx−
∫
2
sin
2
0
1 sin . cos d
xt
t tt
π
=
→ −
∫
2
2
0
cos dtt
π
=
∫
( )
2
0
1
1 cos 2 d
2
tt
π
= +
∫
4
π
=
.
Do đó,
(
)
1 ⇔
23
4
II
π
+=
hay
20
I
π
=
.
Câu 41. Cho
( )
0fx≠
,
(
) (
)
42
2
2
31
.
xx
fx f x
x
+−
′
=
,
( )
1
1
3
f = −
. Xét
( )
2022
1
1
1
2
k
b
S fk
a
=

= = −


∑
với
b
a
tối giản. Tính
ab+
.
A.
4092530
. B.
4090507
. C.
4088485
. D.
4086463
.
Lời giải
Ta có
( )
(
)
2
22
1
31
fx
x
fx x
′
= +−
( )
( )
2
22
1
d 31 d
fx
xx x
fx x
′

⇒ = +−


∫∫
( )
3
11
xx C
fx x
−
⇒ = ++ +
.
Mà
( )
1
10
3
fC
=−⇒ =
(
)
3
11
xx
fx x
−
⇒ = ++
.
( )
( )
2
42
22
12
12
1
xx
fx
xx
xx
−−
⇒= =
++
+−
( ) ( )
( )( )
22
22
22
11
1 11 1
.
2 21 1
11
xx xx
xx xx
xx xx
−+ − ++

= = −

++ −+
++ −+

.
( )
( ) (
)
11 1
2 11 11
fx
xx xx

⇒= −


++ −+

.
Khi đó :
( )
2022
1
11 1 1 1 1 1
...
2 1.2 1 0.1 1 2.3 1 1.2 1 2022.2023 1 2022.2021 1
k
S fk
=

= = − + − ++ −

++++ + +

∑
1 11
11
2 2022.2023 1 2
b
a

= −+ = −+

+

.
2022.2023 1,a⇒= +
1b
=
4090507ab⇒+=
.
Câu 42. Một bàn cờ vua gồm
88
ô vuông, mỗi ô có cạnh bằng 1 đơn vị. Một ô vừa là hình vuông hay
hình chữ nhật, hai ô là hình chữ nhật,… Chọn ngẫu nhiên một hình chữ nhật trên bàn cờ. Xác
suất để hình được chọn là một hình vuông có cạnh lớn hơn 4 đơn vị bằng
A.
5
216
. B.
17
108
. C.
51
196
. D.
29
216
.
Lời giải
Chọn A
Bàn cờ
88
cần 9 đoạn thẳng nằm ngang và 9 đoạn thẳng dọc. Ta coi bàn cờ vua được xác
định bởi các đường thẳng
0, 1,..., 8xx x
và
0, 1,..., 8yy y
.
Mỗi hình chữ nhật được tạo thành từ hai đường thẳng
x
và hai đường thẳng
y
nên có
22
88
.
CC
hình chữ nhật hay không gian mẫu là
22
99
. 1296n CC
.
Gọi
A
là biến cố hình được chọn là hình vuông có cạnh
a
lớn hơn 4.
Trường hợp 1:
5a
. Khi đó mỗi ô được tạo thành do 2 đường thẳng
x
cách nhau 5 đơn vị và
hai đường thẳng
y
cách nhau 5 đơn vị có
4.4 16
cách chọn.
Trường hợp 2:
6a
. Khi đó mỗi ô được tạo thành do 2 đường thẳng
x
cách nhau 6 đơn vị và
hai đường thẳng
y
cách nhau 6 đơn vị có
3.3 9
cách chọn.
Trường hợp 3:
7a
. Khi đó mỗi ô được tạo thành do 2 đường thẳng
x
cách nhau 7 đơn vị và
hai đường thẳng
y
cách nhau 7 đơn vị có
2.2 4
cách chọn.
Trường hợp 3:
8
a
. Khi đó mỗi ô được tạo thành do 2 đường thẳng
x
cách nhau 8 đơn vị và
hai đường thẳng
y
cách nhau 8 đơn vị có
1.1 1
cách chọn.
Suy ra
16 9 4 1 30
nA 
.
Xác suất để hình được chọn là một hình vuông có cạnh lớn hơn 4 đơn vị là
30 5
1296 216
nA
PA
n

.
Câu 43. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật tâm
O
,
AB a=
,
3BC a=
. Tam
giác
ASO
cân tại
S
, mặt phẳng
(
)
SAD
vuông góc với mặt phẳng
( )
ABCD
, góc giữa
SD
và
( )
ABCD
bằng
60°
. Khoảng cách giữa hai đường thẳng
SB
và
AC
bằng
A.
3
2
a
. B.
3
2
a
. C.
2
a
. D.
3
4
a
.
Lời giải
Ta có
( ) (
)
SAD ABCD⊥
,
( ) (
)
SAD ABCD AD
∩=
; trong mp
( )
SAD
, kẻ
SH AD⊥
thì
( )
SH ABCD⊥
Mặt khác
Gọi
I
là trung điểm
OA
, vì tam giác
ASO
cân tại
S
nên
AO SI⊥
,
AO SH⊥
HI OA⇒⊥
Tam giác
ADC
vuông tại
D
có
22
2
AC AD DC a
= +=
và
1
tan
3
DC
DAC
AD
= =
30DAC⇒=°
Tam giác
AHI
vuông tại
I
có
3
cos30 3
AI a
AH
= =
°
23
3
a
HD
⇒=
.
Tam giác
ABH
vuông tại
A
có
22
2
3
a
HB AH AB
= +=
,
2
.AB IB HB=
3
2
a
IB
⇒=
Trong mặt phẳng
( )
ABCD
, dựng hình bình hành
ABEC
thì
//BE AC
,
( )
BE SBE⊂
( )
//AC SBE
⇒
( ) ( )
(
)
( )
( )
,, ,d SB AC d AC SBE d I SBE= =
Mà
3
4
IB
HB
=
nên
( )
( )
( )
( )
3
,,
4
d I SBE d H SBE=
Lại có tam giác
OAB
là tam giác đều cạnh
a
nên
BI AC⊥
BI BE⇒⊥
,
BE SH⊥
( )
BE SBH⇒⊥
( ) ( )
SBE SBH⇒⊥
và
( )
( )
SBE SBH SB∩=
Trong mặt phẳng
( )
SBH
, kẻ
HK SB⊥
thì
( )
HK SBE⊥
( )
( )
,HK d H SBE⇒=
Tam giác
SBH
vuông tại
H
có
2 22
1 11
HK SH HB
= +
HK a⇒=
.
Vậy
( )
( )
,d H SBE HK a= =
và
(
)
( )
( )
(
)
33
,,
44
a
d I SBE d H SBE= =
.
Câu 44. Cho hàm số
32
1y ax x bx= −+−
với
, ab
là các số thực,
0a ≠
,
ab
≠
sao cho đồ thị hàm số cắt
trục
Ox
tại ba điểm có hoành độ dương. Tìm giá trị nhỏ nhất của biểu thức
(
)
2
2
532a ab
P
aba
−+
=
−
.
A.
15 3.
B.
8 2.
C.
11 6.
D.
12 3.
Lời giải
Xét phương trình
( )
32
1 0 *ax x bx− + −=
.
Gọi
,,mn p
là ba nghiệm dương của phương trình
( )
*
, khi đó
Ta có
1
1
1
mn p
a
mn np pm
a
mnp
a
++ =
++ =
=
Mặt khác
( ) ( )
2
3
3
3
m n p mn np pm
m n p mnp
++ ≥ + +
++ ≥
1
0
33
1
0
3
a
b
a
<≤
⇔
<≤
Xét hàm số
( )
( )
2
2
532 1
; b 0;
3
a ab
fb
aba a
−+

= ∈
−

là hàm số nghịch biến nên
( ) ( )
2
3
1 51
3. 3.
33
a
f b f ga
a aa
+

≥= =

−

Xét hàm số
( )
2
3
51 1
; a 0;
3
33
a
ga
aa
+

= ∈
−

, là hàm số nghịch biến nên ta có
( )
1
43
33
ga g

≥=


.
Vậy
3.4 3 12 3
P ≥=
.
Câu 45. Cho hàm số
( )
32
69fx x x x=−+
. Đặt
( ) ( )
( )
1kk
f x ff x
−
=
với
k
là số tự nhiên lớn hơn
1
.
Hỏi phương trình
(
)
9
0
fx
=
có bao nhiêu nghiệm?
A.
19684
. B.
9841
. C.
19683
. D.
9842
.
Lời giải
Chọn D.
Ta có
( )
2
3 12 9
fx x x
′
=−+
. Bảng biến thiên:
Từ bảng biến thiên ta có
( )
(
)
(
)
( )
( )
( )
( )
(
)
( )
(
)
( )
2
1
2
2
1
3
1
1
0
3
0
0
3
0 3 ...
3
3
3
3
k
k
kk
k
k
k
fx
fx
fx
fx
fx
fx f x
fx
fx
fx
fx
−
−
−
−
−
−
=
=
=
=
=
=⇔ ⇔ =⇔⇔
=
=
=
=
Bài toán sẽ được giải quyết nếu tìm được số nghiệm của phương trình
( )
3
k
fx=
.
+ Phương trình
( )
3fx=
có ba nghiệm thuộc
(
)
0; 4
.
+ Phương trình
( )
( )
( )
( ) ( )
( )
( ) (
) ( )
( ) ( )
( )
1
2
2
3
0; 1 0; 4
3 1; 3 0; 4
3;4 0;4
fx x
f x f fx fx x
fx x
=∈⊂
= =⇔ =∈⊂
=∈⊂
.
Từ bảng biến thiên ta có với mỗi giá trị
( )
123
, , 0; 4xxx∈
phương trình
( )
, 1, 3
i
f x xi= =
có ba
nghiệm thuộc
( )
0; 4
.
Như vậy phương trình
( )
2
3fx=
có 9 nghiệm thuộc
( )
0; 4
.
+ Bằng quy nạp ta chứng minh được phương trình
( )
3
k
fx=
có
3
k
nghiệm thuộc
( )
0; 4
.
Từ đó, số nghiệm của phương trình
( )
0
k
fx=
là
1
21
31
2 3 3 ... 3 2 3
2
k
k
−
−
−
++ + + =+
.
Vậy số nghiệm của phương trình
( )
9
0fx=
là
91
31
2 3 9842
2
−
−
+=
.
Câu 46. Cho
;
xy
∈
,
( )
0x ≥
thỏa mãn:
( )
31 1
3
1
2021 2021 1 2021 3
2021
x y xy xy
xy
x yx
+ + −−
+
+ ++= + − +
.
Tìm giá trị nhỏ nhất của
2Tx y= +
.
A.
2
3
. B.
1
−
. C.
2
3
−
. D.
1
.
Lời giải
Ta có
( )
31 1
3
1
2021 2021 1 2021 3
2021
x y xy xy
xy
x yx
+ + −−
+
+ ++= + − +
( )
( ) ( )
3
3 11
2021 2021 3 2021 2021 1 3 1
xy
x y xy xy
x y xy f x y f xy
−+
+ −− +
⇔ − + + = − − −⇔ + = − −
.
Với
(
)
2021 2021
tt
ft t
−
=−+
,
t
∈
.
( )
2021 ln 2021 2021 ln 2021 1 0
tt
ft
−
′
= + +>
,
t ∈
.
f
⇒
liên tục và đồng biến trên
. Do đó
( ) ( )
3 13 1f x y f xy x y xy+ = −−⇔+ =−−
( )
*
.
Với
1
y = −
:
(
)
* 31
⇔− =−
(vô lí).
Với
1
y
≠−
:
( )
13
*
1
y
x
y
−−
⇔=
+
. Vì
0x ≥
nên
1
1
3
y
− < ≤−
.
Từ
( )
*
ta có:
( )
2
3 12 12 22 1xy xy xy yxy xy xyyyy+ =− −⇔ + =−− −⇔ + =− + + − −
.
( )(
)
22
2
2121
21 2 1 2
11
yy yy
xy y yy xy T
yy
−− −−
⇔ + + = − −⇔ + = ⇔ =
++
.
Xét
( )
2
21
1
yy
fy
y
−−
=
+
,
1
1;
3
y

∈− −

.
( )
( )
2
2
24 1
0, 1;
3
1
yy
fy y
y
+

′
= < ∀∈− −

+
. Do đó
( )
1
1;
3
12
min
33
fy f

−−



=−=−


.
Vậy
1
2
min
3
3
0
y
T
x
= −
=−⇔
=
.
Câu 47. Số nghiệm của phương trình
( )
2
2
ln 2 2022
2
x
xx+− − =
là
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải
Xét hàm số
( )
( )
2
2
ln 2
2
x
fx x x= +− −
với
( ) ( )
; 2 2;x ∈ −∞ − ∪ +∞
.
Ta có
( )
2
2
1
2
x
fx x
x
′
= +−
−
;
( )
( )
( ) ( )
2
2
2
24
1 0, ; 2 2;
2
x
fx x
x
+
′′
= + > ∀ ∈ −∞ − ∪ +∞
−
.
Nên suy ra hàm số
( )
2
2
1
2
x
fx x
x
′
= +−
−
đồng biến trên mỗi khoảng
(
)
;2
−∞ −
và
( )
2;+∞
.
Mặt khác
( )
( )
( )
2 . 3 1. 1 3 0ff
′′
=−<
và
( )
( )
8
3 . 2 .1 0
7
ff
′′
− −=− <
nên
( )
fx
′
có đúng một
nghiệm
( )
;2a ∈ −∞ −
và đúng một nghiệm
( )
2;b ∈ +∞
.
Ta có bảng biến thiên
Ta có
( )
(
)
3
3 3 2022
2
fa f
<− =−<
và
(
)
( )
3
3 3 2022
2
fb f
< =+<
Nên từ bảng biến thiên suy ra phương trình
( )
2
2
ln 2 2022
2
x
xx+− − =
có
4
nghiệm.
Câu 48. Xét các số thực dương
, xy
thỏa mãn
( ) ( )
22
3
log 3 3
2
xy
x x y y xy
x y xy
+
= −+ −+
+++
. Tìm giá
trị lớn nhất của
321
6
xy
P
xy
++
=
++
.
A.
2
B.
1
C.
3
D.
4
Lời giải
Ta có
(
) ( )
22
3
log 3 3
2
xy
x x y y xy
x y xy
+
= −+ −+
+++
(
) ( )
( ) ( )
22 22
33
log 3 2 log 2 2
x y x y x y xy x y xy⇔ ++ ++= ++++ +++
( ) ( )
( ) ( )
22 22
3 33
log 3 log 3 log 2 2x y x y x y xy x y xy⇔ ++ ++ = ++++ +++
( ) ( )
( ) ( )
22 22
33
log 3 3 log 2 2x y x y x y xy x y xy⇔ + + += ++++ +++


( )
*
.
Xét hàm số
( )
3
logft t t= +
, với
0t >
.
có
( )
1
10
.ln 3
ft
t
′
= +>
,
0t∀>
.
Vậy hàm số
( )
ft
liên tục và đồng biến trên khoảng
( )
0; +∞
.
Do đó:
( )
( )
( )
( )
22 22
3 23 2+ = +++⇔ +=+++f x y f x y xy x y x y xy
( )
1
.
Từ
( )
1
( ) ( )
2
32⇔=+ − ++xy xy xy
.
Ta có
( )
2
1
1
2
++

=+ − = +− ≤ −


xy
x x xy xy x y xy xy
.
Đẳng thức xảy ra khi và chỉ khi
1= +xy
.
Do đó từ
( )
1
, suy ra:
( )
( ) ( )
2
2
1
32
4
++
≤ −+ + +−
xy
x xy xy
.
Đặt
= +txy
,
0
>t
.
Suy ra:
(
)
( )
(
)
(
)
2
2
2
1
21 32
21
3 22 3
4
6 6 46
+
++ − + −
+ ++
−+ −
=≤==
++ + +
t
t tt
xy x
tt
P ft
xy t t
.
Ta có:
( )
( )
2
2
3 36 135
03
46
−− +
′
= = ⇔=
+
tt
ft t
t
(nhận).
Bảng biến thiên
Dựa vào BBT, ta có
(
)
( ) (
)
0;
max max 3 1
+∞
= = =P ft f
khi và chỉ khi
12
31
=+=

⇔

+= =

xy x
xy y
.
Câu 49. Cho hình chóp
.
S ABCD
có đáy là hình bình hành. Góc tạo bởi mặt bên
( )
SAB
với đáy bằng
α
.
Tỉ số diện tích của tam giác
SAB
và hình bình hành
ABCD
bằng
k
. Mặt phẳng
( )
P
đi qua
AB
và chia hình chóp
.S ABCD
thành hai phần có thể tích bằng nhau. Gọi
( )
β
là góc tạo bởi mặt
phẳng
(
)
P
và mặt đáy. Tính
cot
β
theo
k
và
α
.
A.
51
cot cot
sink
βα
α
+
= +
B.
51
cot tan
sink
βα
α
+
= +
C.
51
cot cot
sink
βα
α
−
= +
D.
51
cot tan
sink
βα
α
−
= +
Lời giải
+∞
3
0
t
( )
ft
′
( )
ft
0
+
−
Giải sử mặt phẳng
( )
P
cắt
,SD SC
lần lượt tại
,MN
. Khi đó
//MN CD
.
Đặt:
0
SM SN
m
SD SC
= = >
Ta có:
( )
2
.
.
.
.
*
S MNB
SDCB
S AMB
S ABD
V
SM SN
m
V SD SC
V
SM
m
V SD
= =
= =
( )
22
.
.
51
10
22
S ABMN
S ABCD
V
mmmm m m
V
−
⇒ = +⇔ +=⇔= >
Từ
( )
( )
(
)
.
. . . M. ABD
.
15
* .. 1
12
S ABM
S ABM S ABD S ABM
M ABD
V
m
V mV m V V
Vm
+
⇒= = + ⇒ ==
−
Mặt khác:
( )
( )
.
.
.
2
.
SAB
S ABM
M ABD ABD
S Sin
V
V S Sin
αβ
β
−
=
Từ
( ) ( )
( )
. .sin
15 15
1 , 2 cot cot
1
2 .sin
. .sin
2
ABCD
ABCD
kS
k
S
αβ
βα
α
β
−
++
⇒ = ⇔=+
. Suy ra chọn A.
Câu 50. Cho tứ diện
ABCD
có thể tích là
V
. Điểm
thay đổi trong tam giác
BCD
. Các đường thẳng
qua
M
và song song với
AB
,
AC
,
AD
lần lượt cắt các mặt phẳng
( )
ACD
,
( )
ABD
,
( )
ABC
tại
N
,
P
,
Q
. Giá trị lớn nhất của thể tích khối tứ diện
MNPQ
là
A.
27
V
. B.
16
V
. C.
8
V
. D.
54
V
.
Lời giải
D
C
B
A
S
N
M
Tam giác
ABN
′
có
//MN AB
MN N M
AB N B
′
⇒=
′
.
Tam giác
ACP
′
có
//MP AC
MP P M
AC P C
′
=
′
.
Tam giác
ADQ
′
có
//QM AD
MQ Q M
AD Q D
′
⇒=
′
.
Khi đó:
MN MP MQ N M P M Q M
AB AC AD N B P C Q D
′′′
++ = + +
′′ ′
Mà
1
MCD MBC
MBD
BCD BCD BCD
SS
S
NM PM QM
NB PC QD S S S
′′′
++= ++=
′′ ′
nên
1
MN MP MQ
AB AC AD
++ =
Lại có
3
3
3
3
1 3 ..
MN MP MQ MN MP MQ
AB AC AD AB AC AD


= ++ ≥





(Cauchy)
1
.. ..
27
MN MP MQ AB AC AD⇔≤
..MN MP MQ⇒
lớn nhất khi
MN MP MQ
AB AC AD
= =
M⇒
là trọng tâm tam giác
BCD
1
3
MN MP MQ
AB AC AD
⇒===
( ) ( )
//
NPQ BCD⇒
,
2
2
3
NPQ
NPQ
S
S
′′ ′

=


, Mà
1
4
N P Q BCD
SS
′′ ′
=
nên
1
9
NPQ BCD
SS=
và
( )
( )
( )
( )
1
,,
2
d M NPQ d A BCD=
Vậy giá trị lớn nhất của thể tích khối tứ diện
MNPQ
là
( )
( )
1
.,
3
MNPQ NPQ
V S d M NPQ=
( )
( )
11 1
..,
3 9 3 27
MNPQ BCD
V
V S d A BCD⇔= =
, với
( )
( )
1
.,
3
ABCD BCD
V S d A BCD V= =
.
Q
N
P
Q'
N'
P'
A
B
C
D
M
| 1/36
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT HÀ VĂN MAO
ĐỀ THI GIAO LƯU KSCL HSG - CỤM BÁ THƯỚC NĂM HỌC 2022 - 2023 ĐỀ CHÍNH THỨC Môn thi: Toán - THPT
Đề thi có 7 trang, 50 câu TNKQ
Khóa thi ngày: 12/11/2022
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên…………………..…………………………..
Số báo danh……………….…..……. Phòng thi….….. Mã đề thi: 123
Câu 1. Trong các hàm số sau đây, hàm số nào là hàm số chẵn?   A. y sin  x     .
B. y  sin x .
C. y  sin x  tan x . D. y  sin . x cos x  2
Câu 2. Một học sinh có 4 quyển sách Toán khác nhau và 5 quyển sách Ngữ văn khác nhau. Hỏi có
bao nhiêu cách xếp 9 quyển sách trên giá sao cho hai quyển sách kề nhau phải khác loại ? A. 20 . B. 2880 . C. 362880 . D. 5760 .
Câu 3. Cho cấp số cộng (u với u = 6 ; d = 9 . Khi đó số 2022 là số hạng thứ bao nhiêu của cấp n ) 1 số? A. 226 . B. 225 . C. 223 . D. 224 .
Câu 4. Tìm m để hàm số y = (m − ) 4 x + ( m − ) 2 1 2
1 x +1 có đúng 3 điểm cực trị.
A. 1 < m <1.
B. 1 ≤ m <1.
C. 1 < m ≤1.
D. 1 ≤ m ≤1. 2 2 2 2
Câu 5. Đặt a = ln 2,b = ln 5, hãy biểu diễn 1 2 3 98 99
I = ln + ln + ln + ...+ ln + ln
theo a và b . 2 3 4 99 100 A. I = 2 − (a + b) B. I = 2 − (a −b)
C. I = 2(a + b)
D. I = 2(a −b)
Câu 6. Lăng trụ đứng có đáy là hình thoi có bao nhiêu mặt phẳng đối xứng? A. 2. B. 9. C. 3. D. 5.
Câu 7. Cho đoạn thẳng AB có độ dài bằng 2a , vẽ tia Ax về phía điểm B sao cho điểm B luôn
cách tia Ax một đoạn bằng a . Gọi H là hình chiếu của B lên tia Ax , khi tam giác AHB
quay quanh trục AB thì đường gấp khúc AHB vẽ thành mặt tròn xoay có diện tích xung quanh bằng: 2 ( + ) 2 3 3 π a ( + ) 2 1 3 π a ( + ) 2 2 2 π a A. 3 2π a . B. . C. . D. . 2 2 2 2
Câu 8. Cắt hình trụ (T ) bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện tích bằng 30 2
cm và chu vi bằng 26 cm . Biết chiều dài của hình chữ nhật lớn hơn đường kính
mặt đáy của hình trụ (T ). Diện tích toàn phần của (T ) là: A. 23π ( 2 cm ) . B. 23π ( 2 π cm ) . C. 69 ( 2 cm ) . D. π ( 2 69 cm ) . 2 2 Câu 9. Cho hàm số 2
f (x) xác định trên 1  \  
thỏa mãn f ′(x) =
, f (0) =1, f ( ) 1 = 2 . Giá trị 2   2x −1
của biểu thức f (− )
1 + f (3) bằng A. 2 + ln15 B. 3+ ln15 C. ln15 D. 4 + ln15
Trang 1/7 – Mã đề thi 123 m Câu 10. Cho ∫( 2 3x − 2x + )
1 dx = 6 . Giá trị của tham số m thuộc khoảng nào sau đây? 0 A. ( 1; − 2) . B. (−∞;0) . C. (0;4). D. ( 3 − ) ;1 .
Câu 11. Có bao nhiêu cách phân công 4 thầy giáo dạy toán vào dạy 12 lớp 12, mà mỗi thầy dạy đúng 3 lớp ? A. 369600 B. 396900 C. 220 D. 369000 4 2 Câu 12. Giới hạn x + x + 2 lim có kết quả là : x→+∞
( 3x + )1(3x− )1 A. − 3 B. 3 C. 3 D. 3 − 3 3
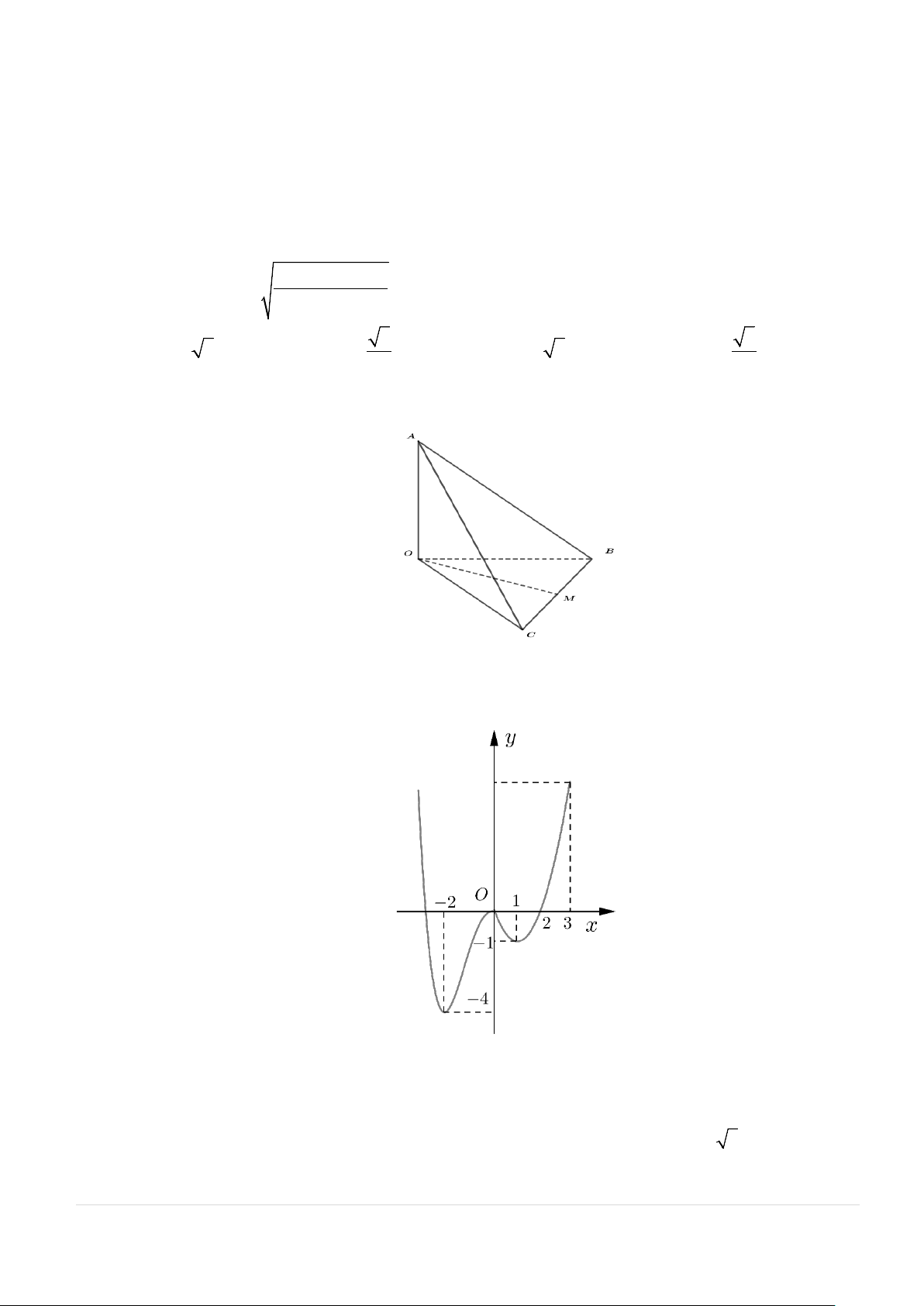
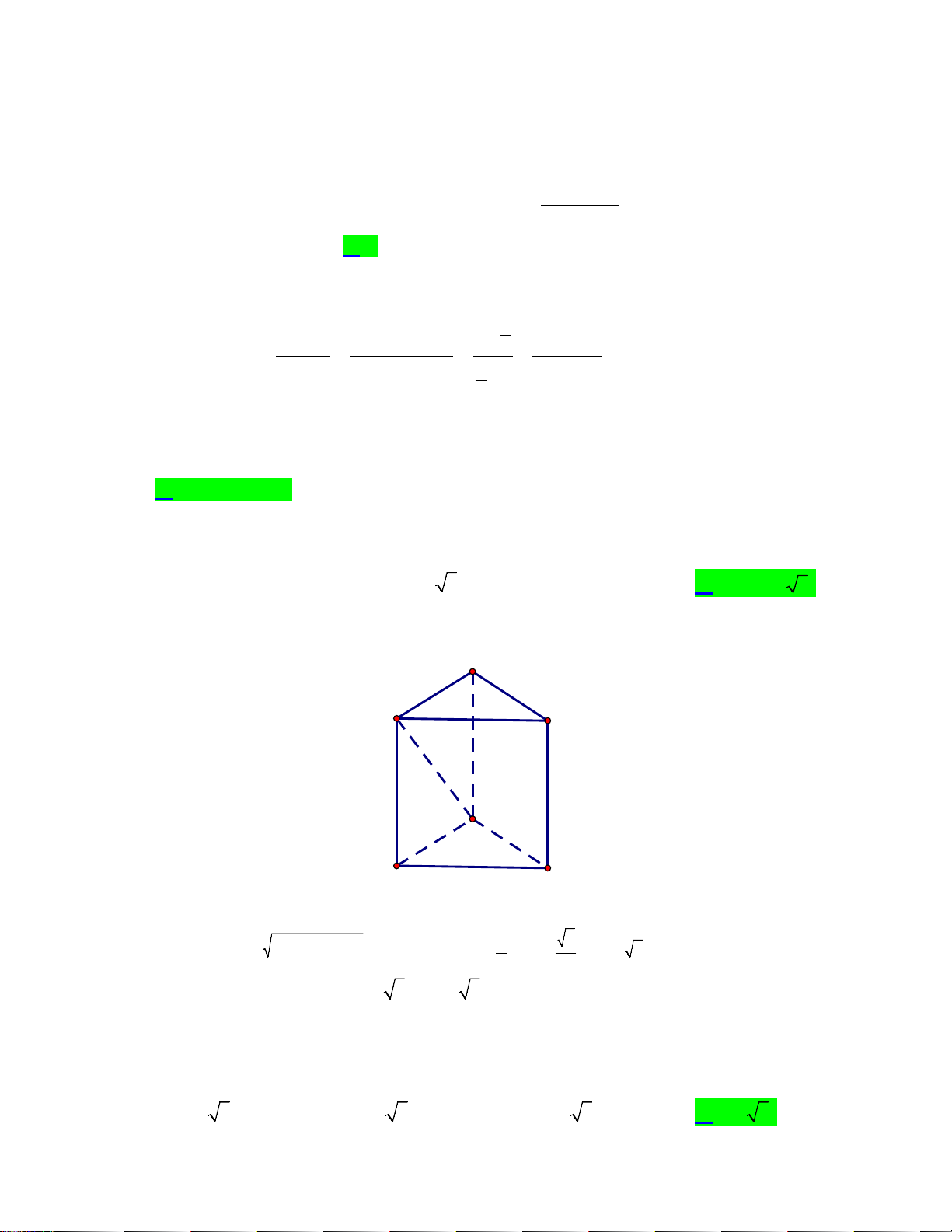
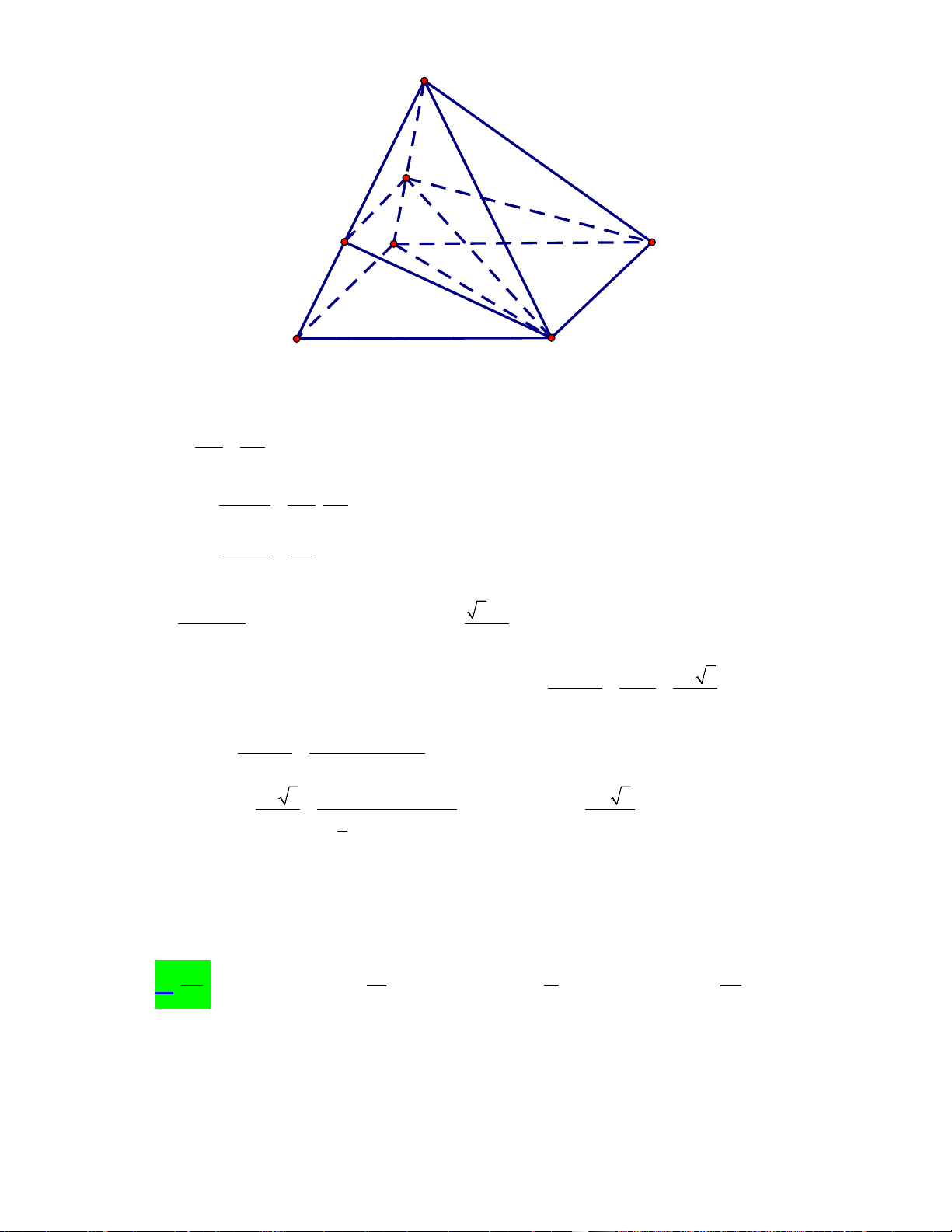
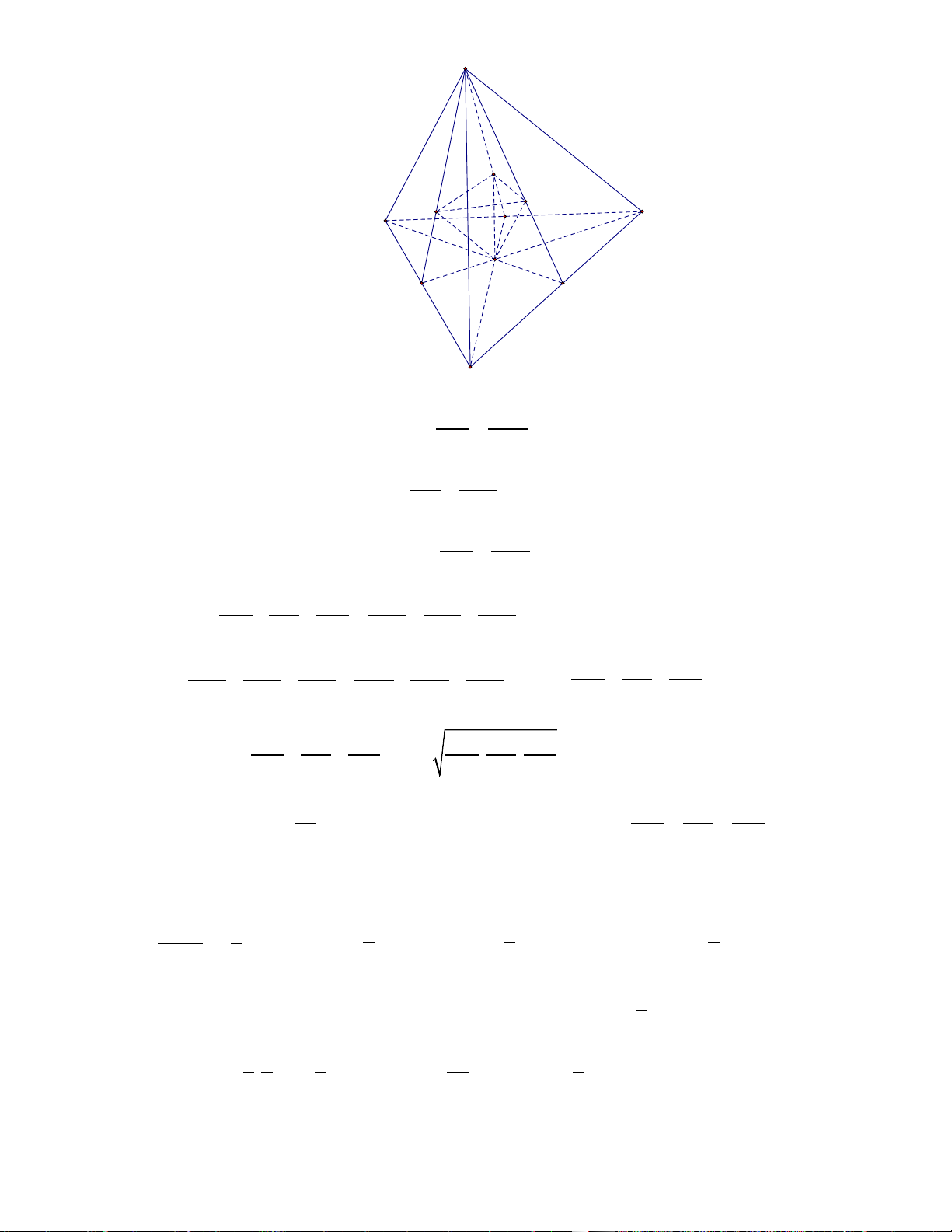
Câu 13. Cho tứ diện OABC có ,
OA OB, OC đôi một vuông góc với nhau và OA = OB = OC . Gọi
M là trung điểm của BC (tham khảo hình vẽ bên dưới). Góc giữa hai đường thẳng OM và AB bằng A. 0 45 B. 0 90 C. 0 30 D. 0 60
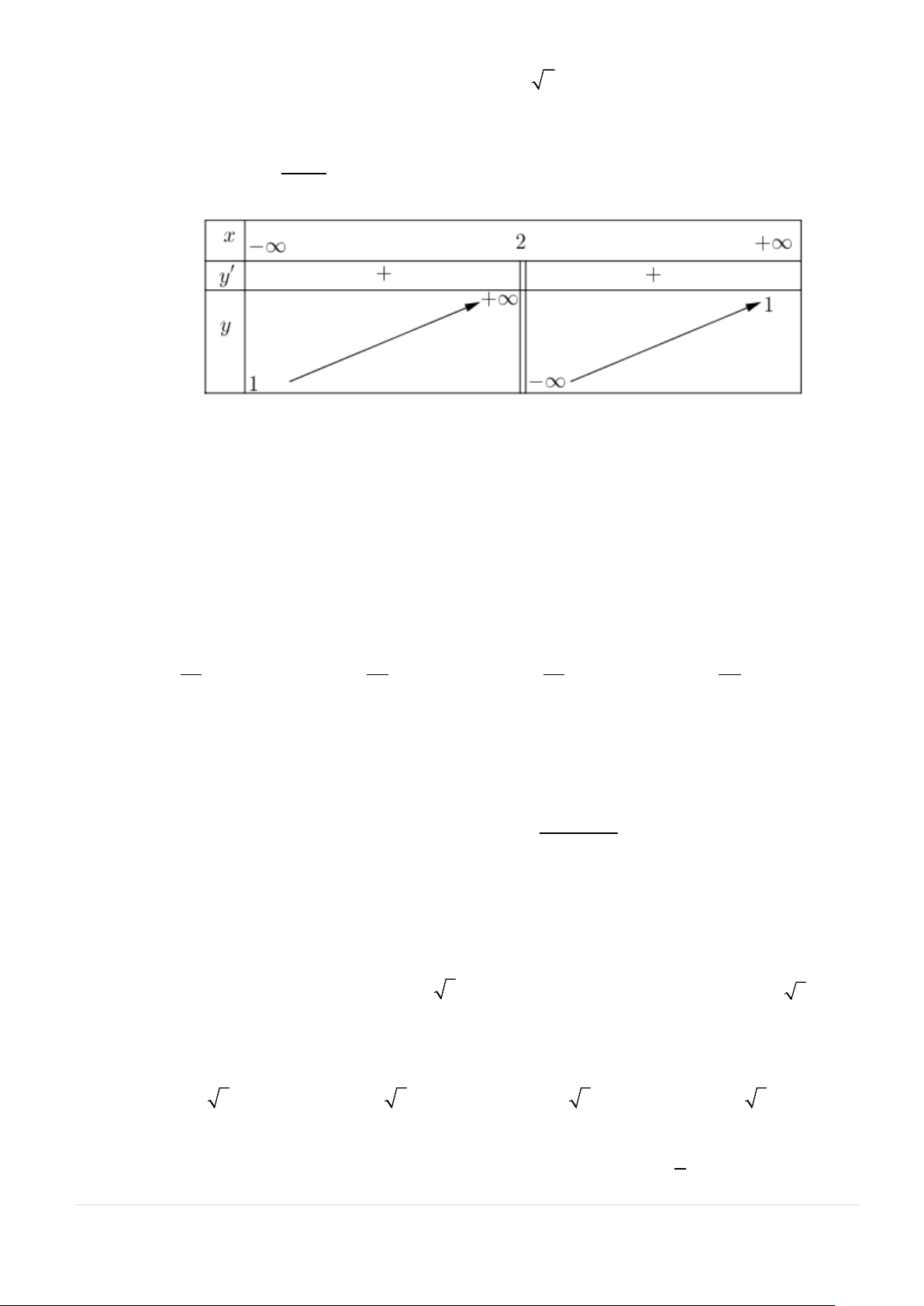
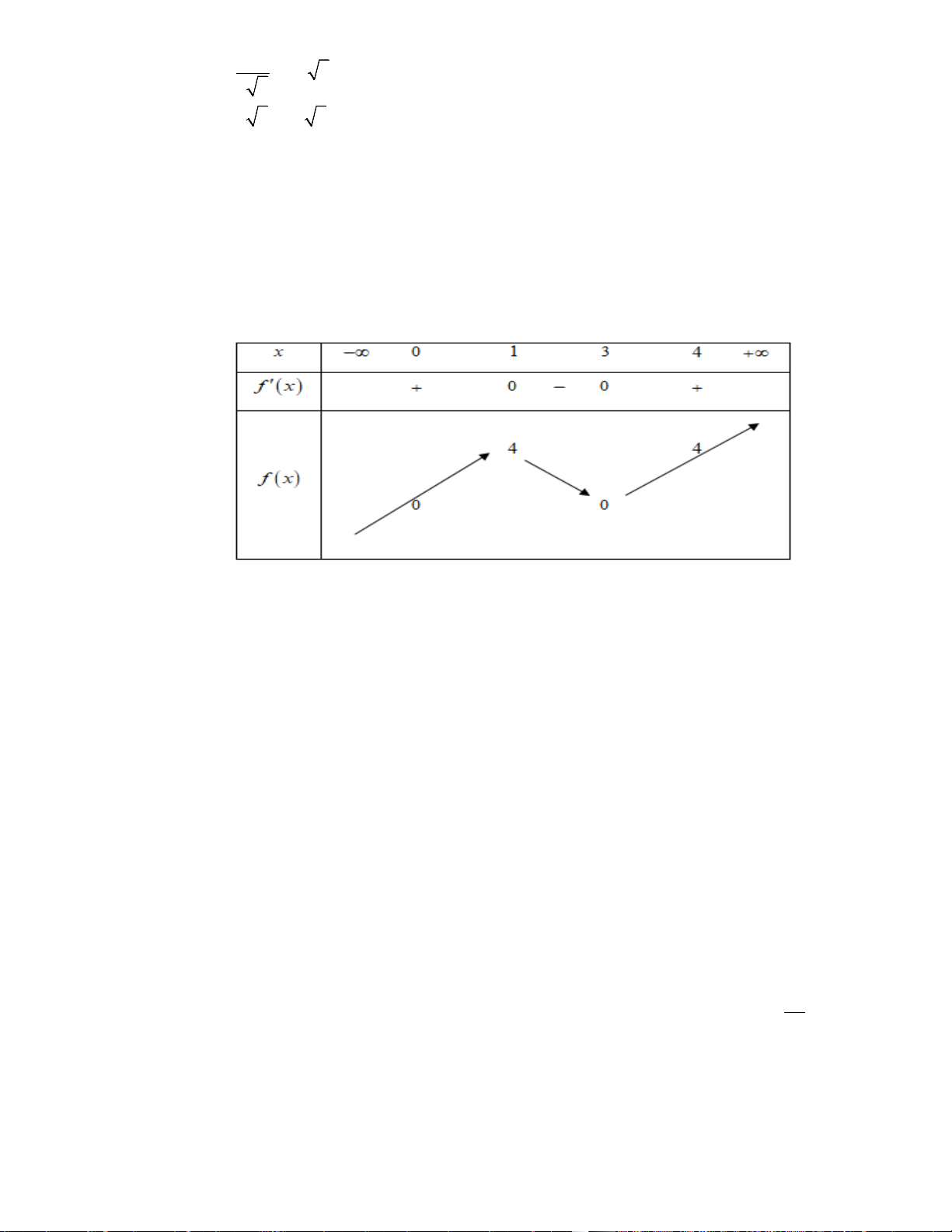
Câu 14. Cho hàm số y = f (x) có đồ thị hàm y = f ′(x) như hình vẽ bên dưới.
Hàm số đã cho nghịch biến trên khoảng
A. (−∞;− 2) . B. ( 2 − ) ;1 .
C. (−∞;− 4) . D. ( 2; − 3) .
Câu 15. Có bao nhiêu giá trị nguyên dương của m để khoảng cách từ gốc tọa độ O đến đường thẳng
đi qua 2 điểm cực trị của đồ thị hàm số 3
y = x − 3x + m nhỏ hơn hoặc bằng 5. A. 5. B. 2. C. 11. D. 4.
Trang 2/7 – Mã đề thi 123
Câu 16. Giá trị nhỏ nhất và lớn nhất của hàm số y = x − 2 x trên đoạn [0;9] lần lượt là m và M .
Giá trị của tổng m + M bằng A. 2. B. 3. C. 0. D. 1. ax +1
Câu 17. Cho hàm số y =
( a,b,c là các tham số) có bảng biến thiên như hình vẽ bx + c Xét các phát biểu sau: ( )1: c >1.
(2): a +b < 0. (
3): a + b + c = 0. (4): a > 0. Số phát biểu đúng là A. 1. B. 2 . C. 3. D. 4 .
Câu 18. Đặt log 2 = a khi đó log 27 bằng 3 16 A. 3a B. 3 C. 4 D. 4a 4 4a 3a 3
Câu 19. Cho hai số thực dương x , y thỏa mãn log  2 2
x y 1log xy . Mệnh đề nào dưới đây 2  2 đúng?
A. x y .
B. x y .
C. x y . D. 2 x y . a(m + nb)
Câu 20. Đặt a = log 3; b = log 3. Nếu biểu diễn log 45 =
thì m + n + p bằng 2 5 6 b(a + p) A. 3 B. 4 C. 6 D. 3 −
Câu 21. Một hình đa diện lồi có số mặt M , số đỉnh D và số cạnh C . Khi đó, hệ thức nào dưới đây là đúng ?
A. D + M − C = 2
B. D + C − M = 2
C. M + C − D = 2
D. M + D = C
Câu 22. Tính thể tích V của khối lăng trụ tam giác đều ABC.A′B C
′ ′ có AC′ = 5a , cạnh đáy là 4a . A. 3 V = 12a . B. 3 V = 20a 3 . C. 3 V = 20a . D. 3 V = 12a 3 .
.Câu 23. Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A , AB = AC = 4a; BC = 6a .Hình
chiếu vuông góc của S trên mặt phẳng ( ABC) nằm trong tam giác ABC . Các mặt bên của hình chóp cùng tạo với đáy góc 0
60 . Tính thể tích khối chóp S.ABC . A. 3 6a 3 . B. 3 a 3 . C. 3 8a 3 . D. 3 3a 3 .
Câu 24. Cho hình nón đỉnh I , đường cao IO (O là tâm của đáy) và có độ dài đường sinh bằng 3cm,
góc ở đỉnh bằng 60°. Gọi K là điểm thuộc đoạn IO thỏa mãn 3
IO = IK , cắt hình nón bằng 2
Trang 3/7 – Mã đề thi 123
mặt phẳng (P) qua K và vuông góc với IO , khi đó thiết diện tạo thành có diện tích là S . Tính S . A. π π S = ( 2 cm ). B. = π ( 2 S cm ). C. S = π ( 2 3 cm ) . D. 2 S = ( 2 cm ). 3 3 Câu 25. Cho ( ) 2
F x = x là một nguyên hàm của hàm số ( ) 2x
f x e . Tìm nguyên hàm của hàm số ( ) 2 ' x f x e . A. f ∫ (x) 2x 2 ' e dx = 2
− x + 2x + C . B. f ∫ (x) 2x 2 '
e dx = −x + 2x + C . C. ∫ ( ) 2 2 ' x
f x e dx = −x + x + C . D. f ∫ (x) 2x 2 '
e dx = 2x − 2x + C . 1
Câu 26. Có bao nhiêu số thực a để = 1 ∫ x dx . 2 a + x 0 A. 2 B. 1 C. 0 D. 3
Câu 27. Số giá trị nguyên của tham số m thuộc đoạn [ 2022 − ;2022] để phương trình (m + ) 2
1 sin x − sin 2x + cos 2x = 0 có nghiệm là: A. 4045 . B. 4044 . C. 2023. D. 2024 .
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy và
SA = a 3 . Gọi α là góc giữa SD và (SAC). Giá trị sinα bằng A. 2 . B. 2 . C. 3 . D. 2 . 4 2 2 3
Câu 29. Có bao nhiêu giá trị nguyên âm của tham số m để hàm số 3 4 9 2
y = x − x + (2m +15) x −3m +1 đồng biến trên khoảng (0;+∞)? 4 2 A. 2. B. 3. C. 5. D. 4. Câu 30. Cho hàm số 3 2
y = x − 3x + m , với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của
tham số m để đồ thị hàm số có 5 điểm cực trị. Tổng tất cả các phần tử của tập S là A. 3 B. 10 C. 6 D. 5
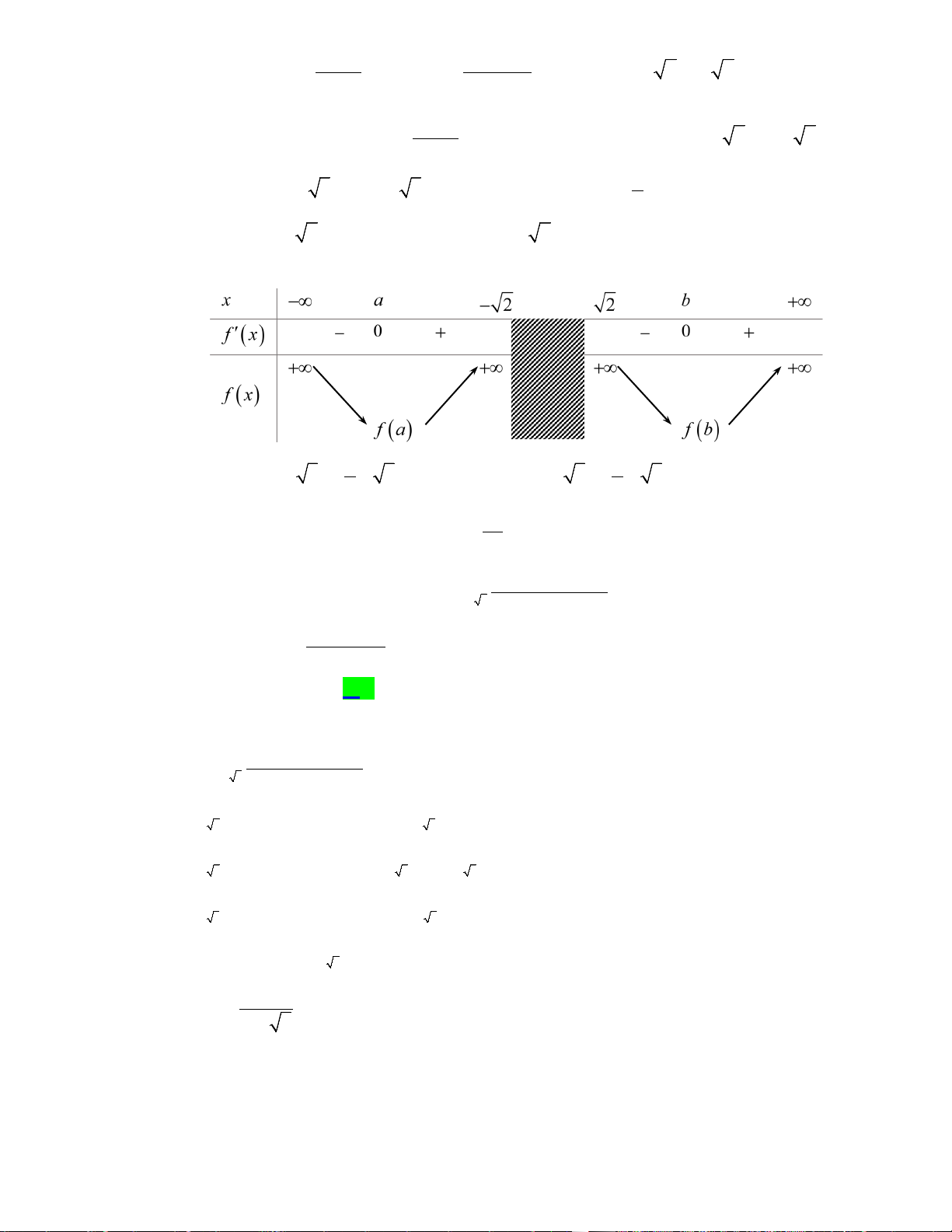
Câu 31. Cho hàm số y = f (x) có bảng biến thiên như sau
Tập hợp tất cả các giá trị thực của tham số m để phương trình f (x) + m = 0 có 5 nghiệm phân biệt là A. ( 2; − − ] 1 . B. [ 1; − 2) . C. ( 2; − − ) 1 . D. ( 2; − ) 1 .
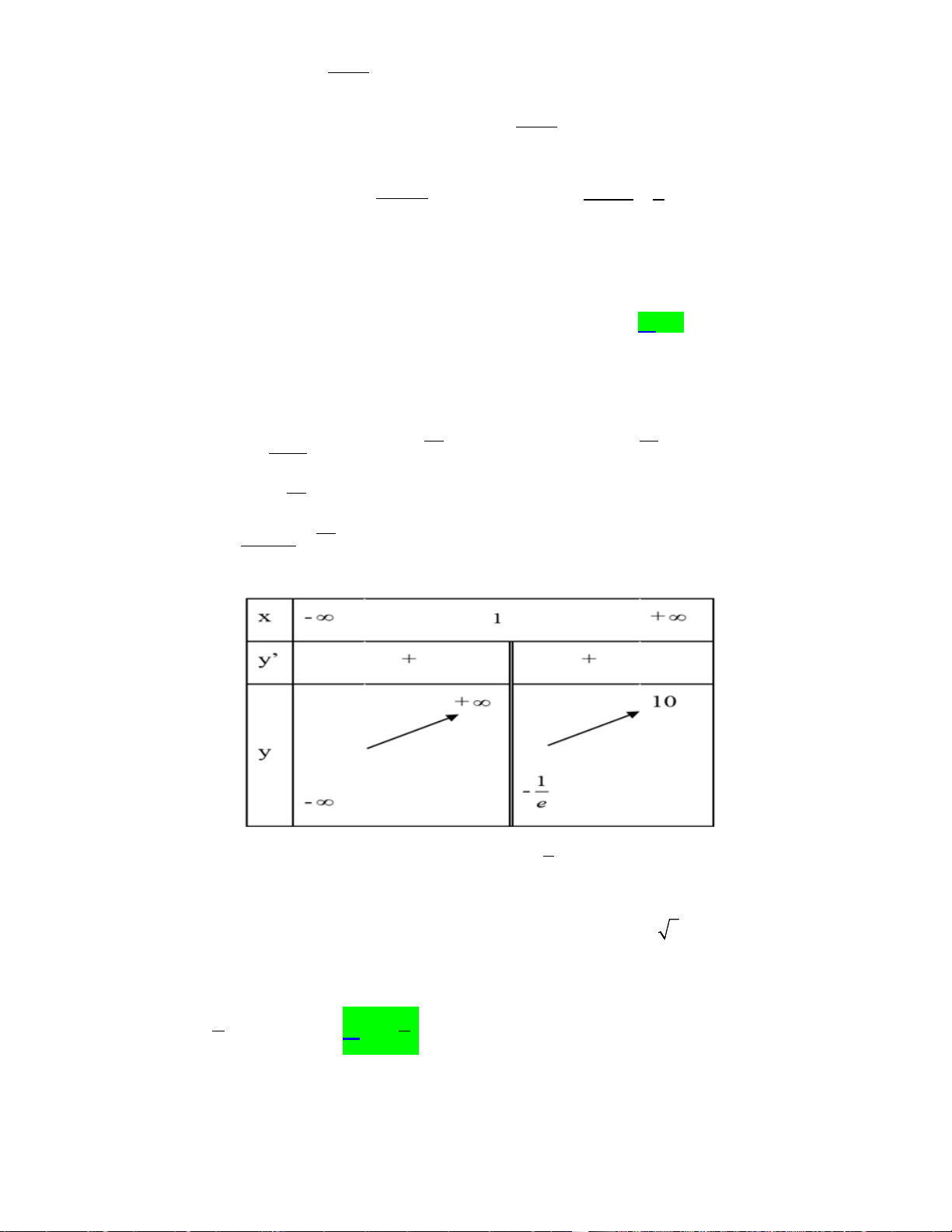
Câu 32. Cho hình chóp đều đỉnh S có đáy là đa giác đều 8 cạnh. Một hình nón đỉnh S có đáy
là đường tròn ngoại tiếp đáy hình chóp. Tính tỉ số thể tích của khối nón và khối chóp tương ứng.
Trang 4/7 – Mã đề thi 123 π π π π A. . B. . C. . D. 2 . 3 2 2 2 3 3 2
Câu 33. Số đường tiệm cận đứng của đồ thị hàm số
4x −1− x + 2x + 6 y = là 2 x + x − 2 A. 3. B. 2 . C. 1. D. 0 . Câu 34. Gọi a + b 3 x = với ( , , ∈ , a a b c N
tối giản) là một nghiệm lớn hơn 1 của phương trình 0 c c −x   2x ( 3)1 1 x  1  2 − +  
1 = 2x −1. Giá trị của P = a + b + c là   3   
A. P = 6 .
B. P = 0 .
C. P = 2 .
D. P = 4 .
Câu 35. Cho các hàm số f (x), f x , f x ,… thỏa mãn: 1 ( ) 2 ( ) x e +1 f x = f x = ln ; f = ∀ = … + x f f x n n ( ) n ( ) , 1;2;3; 1 ( ) 1 ( ) ( ) x e −1
Khẳng định nào sau đây đúng? A. f ln 2 = ln 2 f ln 3 = ln 4 f ln 2 = ln 3 f ln 3 = ln 3 2023 ( ) . B. 2023 ( ) . C. 2023 ( ) . D. 2023 ( ) .
Câu 36. Có bao nhiêu giá trị nguyên của m để phương trình ( − ) 1 .log( −x x
e + m) = x − 2 có 2 nghiệm thực phân biệt A. Vô số. B. 11. C. 9. D. 10.
Câu 37. Cho hình hộp đứng ABC .
D A B C D có cạnh AB = AD = 2 , AA = 3 BAD = °. 1 1 1 1 1 và góc  60
Gọi M , N lần lượt là trung điểm của các cạnh A D và A B . Tính thể tích V của khối chóp 1 1 1 1 . A BDMN . A. 5 V = . B. 3 V = . C. V = 4 . D. V = 2 . 2 2
Câu 38. Một con quạ đang khát nước. Nó bay rất lâu để tìm nước nhưng chẳng thấy một giọt nước
nào. Mệt quá, nó đậu xuống cành cây nghỉ. Nó nhìn quanh và bỗng thấy một cái bình hình trụ
có bán kính đáy là 2cm , chiều cao 21cm ở dưới một gốc cây. Trong bình đang có một ít
nước, khoảng cách giữa đáy cốc và mặt nước là 12cm (Hình vẽ). Nhìn chung quanh, quạ thấy
những viên đá nhỏ nằm lay lắt ở gần đấy. Lập tức, nó dùng mỏ gắp một viên đá hình cầu có
bán kính 0,6cm thả vào bình. Cứ như vậy, nó gắp những viên đá khác và tiếp tục thả vào
bình. Giả sử các viên đá đều là hình cầu có bán kính 0,6cm Chẳng bao lâu, nước đã dâng lên.
Để uống được nước thì con quạ cần thả vào bình ít nhất bao nhiêu viên đá biết rằng quạ muốn
uống được nước trong cốc thì mặt nước phải cách miệng cốc không quá 6cm ?
Trang 5/7 – Mã đề thi 123 A. 42 . B. 41. C. 30. D. 27 .
Câu 39. Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, khối chóp có thể
tích lớn nhất bằng bao nhiêu ? A. 576 2 . B. 144. C. 576. D. 144 6 .
Câu 40. Xét hàm số f (x) liên tục trên [0; ]
1 và thỏa mãn điều kiện x f ( 2
x ) + f ( − x) 2 4 . 3 1 = 1− x . 1
Tích phân I = f
∫ (x)dx bằng: 0 π π π π A. I = . B. I = . C. I = . D. I = . 20 16 6 4 4 2 2022 Câu 41. Cho 3x + x −1 1 f (x)  b
≠ 0 , f ′( x) 2 = . f x , f ( ) 1
1 = − . Xét S ∑ f (k)  1 = = − với b 2 ( ) x 3  k 1 = 2  aa
tối giản. Tính a + b . A. 4092530 . B. 4090507 . C. 4088485 . D. 4086463.
Câu 42. Một bàn cờ vua gồm 88 ô vuông, mỗi ô có cạnh bằng 1 đơn vị. Một ô vừa là hình vuông
hay hình chữ nhật, hai ô là hình chữ nhật,… Chọn ngẫu nhiên một hình chữ nhật trên bàn cờ.
Xác suất để hình được chọn là một hình vuông có cạnh lớn hơn 4 đơn vị bằng 5 17 51 29 A. . B. . C. . D. . 216 108 196 216
Câu 43. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O , AB = a , BC = a 3 . Tam
giác ASO cân tại S , mặt phẳng (SAD) vuông góc với mặt phẳng ( ABCD) , góc giữa SD và
(ABCD) bằng 60°. Khoảng cách giữa hai đường thẳng SB và AC bằng A. a 3 . B. 3a . C. a . D. 3a . 2 2 2 4
Trang 6/7 – Mã đề thi 123 Câu 44. Cho hàm số 3 2
y = ax − x + bx −1 với a, b là các số thực, a ≠ 0 , a ≠ b sao cho đồ thị hàm số
cắt trục Ox tại ba điểm có hoành độ dương. Tìm giá trị nhỏ nhất của biểu thức 2 5a − 3ab + 2 P = . 2
a (b − a) A. 15 3. B. 8 2. C. 11 6. D. 12 3.
Câu 45. Cho hàm số f (x) 3 2
= x − 6x + 9x . Đặt k
f (x) f ( k 1 f − =
(x)) với k là số tự nhiên lớn hơn 1. Hỏi phương trình 9
f (x) = 0 có bao nhiêu nghiệm? A. 19684. B. 9841. C. 19683. D. 9842. Câu 46. Cho x+ y xy+ − xy− 1 ;
x y ∈ , (x ≥ 0) thỏa mãn: 3 1 1 2021 + 2021 + x +1 = 2021 + − y x + 3 . x+3y ( ) 2021
Tìm giá trị nhỏ nhất của T = x + 2y . A. 2 . B. 1 − . C. 2 − . D. 1. 3 3 2
Câu 47. Số nghiệm của phương trình x + x − ( 2 ln x − 2) = 2022 là 2 A. 3. B. 1. C. 4 . D. 2 .
Câu 48. Xét các số thực dương +
x, y thỏa mãn log x y
= x x − 3 + y y − 3 + xy . Tìm 3 2 2 ( ) ( )
x + y + xy + 2 giá trị lớn nhất của 3x + 2y +1 P = . x + y + 6 A. 2 B. 1 C. 3 D. 4
Câu 49. Cho hình chóp S.ABCD có đáy là hình bình hành. Góc tạo bởi mặt bên (SAB) với đáy bằng
α . Tỉ số diện tích của tam giác SAB và hình bình hành ABCD bằng k . Mặt phẳng (P) đi
qua AB và chia hình chóp S.ABCD thành hai phần có thể tích bằng nhau. Gọi (β ) là góc tạo
bởi mặt phẳng (P) và mặt đáy. Tính cot β theo k và α . A. 5 +1 cot β + = cotα + B. 5 1 cot β = tanα + k sinα k sinα C. 5 −1 cot β − = cotα + D. 5 1 cot β = tanα + k sinα k sinα
Câu 50. Cho tứ diện ABCD có thể tích là V . Điểm M thay đổi trong tam giác BCD . Các đường
thẳng qua M và song song với AB , AC , AD lần lượt cắt các mặt phẳng ( ACD) , ( ABD),
( ABC) tại N , P , Q. Giá trị lớn nhất của thể tích khối tứ diện MNPQ là A. V . B. V . C. V . D. V . 27 16 8 54
………………………HẾT…………………….
Trang 7/7 – Mã đề thi 123 BẢNG ĐÁP ÁN
Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 ĐA A B B A A C B C B C A B D Câu 14 15 16 17 18 19 20 21 22 23 24 25 26 ĐA B A A B B A B A D D B A B Câu 27 28 29 30 31 32 33 34 35 36 37 38 39 ĐA D A D C A B C D C D B A C Câu 40 41 42 43 44 45 46 47 48 49 50 ĐA A B A D D D C C B A A
Xem thêm: ĐỀ THI HSG TOÁN 12
https://toanmath.com/de-thi-hsg-toan-12
Câu 1. Trong các hàm số sau đây, hàm số nào là hàm số chẵn?   A. y sin  x     .
B. y  sin x .
C. y  sin x  tan x . D. y  sin . x cos x  2 Lời giải Chọn A     Ta có y sin  x     cos x   
nên y  sinx   là hàm số chẵn.  2  2
Câu 2. Một học sinh có 4 quyển sách Toán khác nhau và 5 quyển sách Ngữ văn khác nhau. Hỏi có
bao nhiêu cách xếp 9 quyển sách trên giá sao cho hai quyển sách kề nhau phải khác loại ? A. 20 . B. 2880 . C. 362880 . D. 5760 . Lời giải Chọn B
Để xếp 9 quyển sách trên giá sao cho hai quyển sách kề nhau phải khác loại, ta làm như sau:
Xếp 5 quyển sách Ngữ văn cạnh nhau có 5! 120 cách.
Giữa 5 quyển sách Ngữ văn trên có 4 chỗ trống, xếp 4 quyển sách Toán vào 4 chỗ trống đó có 4! 24 cách.
Theo quy tắc nhân có 120.24  2880 cách sắp xếp thỏa điều kiện đề bài.
Câu 3. Cho cấp số cộng (u với u = 6 ; . Khi đó số n ) d = 9
2022 là số hạng thứ bao nhiêu của cấp số? 1 A. 226 . B. 225 . C. 223 . D. 224 . Lời giải Chọn B
Ta có: u = u + n − d ⇔ 2022 = 6 + (n − ) 1 .9 ⇔ = . n 1 1 ( ) n 225
Câu 4. Tìm m để hàm số y = (m − ) 4 x + ( m − ) 2 1 2
1 x +1 có đúng 3 điểm cực trị.
A. 1 < m <1.
B. 1 ≤ m <1.
C. 1 < m ≤1.
D. 1 ≤ m ≤1. 2 2 2 2 Lời giải Chọn A
Cách 1: Ycbt ⇔ (m − )( m − ) 1 1 2
1 < 0 ⇔ < m <1. 2
Cách 2: y = (m − ) 3
x + ( m − ) x = x  (m − ) 2 ' 4 1 2 2 1 2 2 1 x + 2m −1   x = 0 y ' = 0 ⇔  2  (m − ) 2
1 x + 2m −1 = 0 (1)
Hàm số có đúng 3 điểm cực trị ⇔ y ' có 3 nghiệm phân biệt ⇔ phương trình (1) có hai
nghiệm phân biệt khác 0 ⇔ (m − )( m − ) 1 1 2
1 < 0 ⇔ < m <1. 2
Câu 5. Đặt a = ln 2,b = ln 5, hãy biểu diễn 1 2 3 98 99
I = ln + ln + ln + ...+ ln + ln
theo a và b . 2 3 4 99 100 A. I = 2 − (a + b) B. I = 2 − (a −b)
C. I = 2(a + b)
D. I = 2(a −b) Lời giải 1 2 3 98 99
I = ln + ln + ln + ...+ ln + ln 2 3 4 99 100  1 2 3 98 99  1 2 = ln . . ... . = ln =   ln10−  2 3 4 99 100  100 = 2 − ln10 = 2 − (ln2 + ln5) = 2 − (a + b).
Câu 6. Lăng trụ đứng có đáy là hình thoi có bao nhiêu mặt phẳng đối xứng? A. 2. B. 9. C. 3. D. 5. Lời giải
Lăng trụ đứng có đáy là hình thoi có tất cả 3 mặt phẳng đối xứng (Hình vẽ).
Câu 7. Cho đoạn thẳng AB có độ dài bằng 2a , vẽ tia Ax về phía điểm B sao cho điểm B luôn cách
tia Ax một đoạn bằng a . Gọi H là hình chiếu của B lên tia Ax , khi tam giác AHB quay
quanh trục AB thì đường gấp khúc AHB vẽ thành mặt tròn xoay có diện tích xung quanh bằng: 2 ( + ) 2 3 3 π a ( + ) 2 1 3 π a ( + ) 2 2 2 π a A. 3 2π a . B. . C. . D. . 2 2 2 2 Lời giải A H I x B
Xét tam giác AHB vuông tại H . Ta có 2 2
AH = AB − HB = a 3
Xét tam giác AHB vuông tại H , HI ⊥ AB AH HB a a a tại I ta có . 3. 3 HI = = = AB 2a 2
Khi tam giác AHB quay quanh trục AB thì đường gấp khúc AHB vẽ thành mặt tròn xoay (có
diện tích xung quanh là S ) là hợp của hai mặt xung quanh của hình nón (N1) và (N2). Trong đó:
(N1) là hình nón có được do quay tam giác AHI quanh trục AI có diện tích xung quanh là 2 a 3 3π π . 3 a S = π.HI.AH = . a = 1 2 2
(N2) là hình nón có được do quay tam giác BHI quanh trục BI có diện tích xung quanh là 2 a 3 3π π . a S = π.HI.BH = . a = 2 2 2 (3 3 3 3 ) 2 2 2 π π π + a a a ⇒ S = S + S = + = . 1 2 2 2 2
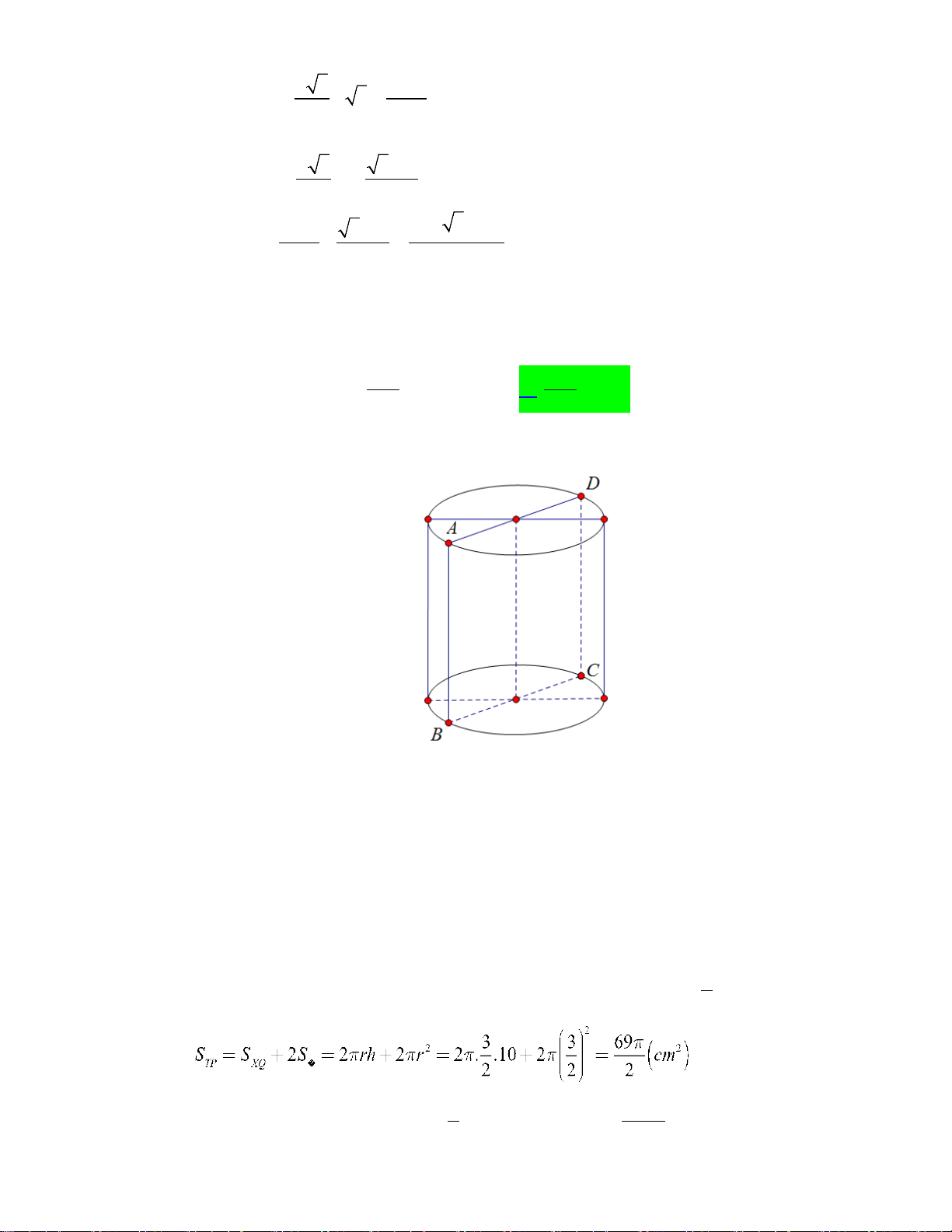
Câu 8. Cắt hình trụ (T ) bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện tích bằng 30 2
cm và chu vi bằng 26 cm . Biết chiều dài của hình chữ nhật lớn hơn đường kính
mặt đáy của hình trụ (T ). Diện tích toàn phần của (T ) là: A. 23π ( 2 cm ) . B. 23π ( 2 π cm ) . C. 69 ( 2 cm ) . D. π ( 2 69 cm ) . 2 2 Lời giải Chọn C
Gọi h,r lần lượt là đường cao và bán kính đáy của hình trụ (T ). Thiết diện của mặt phẳng và
hình trụ (T ) là hình chữ nhật ABCD . Khi đó theo giả thiết ta có    h > 2rh > 2rh > 2rh > 2r  S h r  hr  h r  = = ⇔ = ⇔ = − ⇔ h = − r ABCD .2 30 15 13 2 13 2    2 C =  h + r = h r  + = − + − =  = ⇒ = ABCD 2( 2 ) 26 2 13 2r 15r 15 0 r 5 h 3(l)   3 r = ⇒ h =  10(TM )  2 Vậy . Câu 9. Cho hàm số 2
f (x) xác định trên 1  \  
thỏa mãn f ′(x) =
, f (0) =1, f ( ) 1 = 2 . Giá trị 2   2x −1
của biểu thức f (− )
1 + f (3) bằng A. 2 + ln15 B. 3+ ln15 C. ln15 D. 4 + ln15 Lời giải Chọn C
2 dx = ln 2x−1 +C = f ∫ (x) 2x −1 Với 1
x < , f (0) =1 ⇒ C =1 nên f (− ) 1 =1+ ln 3 2 Với 1 x > , f ( )
1 = 2 ⇒ C = 2 nên f (3) = 2 + ln 5 2 Nên f (− ) 1 + f (3) = 3+ ln15 m Câu 10. Cho ∫( 2 3x − 2x + )
1 dx = 6 . Giá trị của tham số m thuộc khoảng nào sau đây? 0 A. ( 1; − 2) . B. (−∞;0) . C. (0;4). D. ( 3 − ) ;1 . Lời giải Chọn C m m Ta có: ∫( 2 3x − 2x + ) 1 dx = ( 3 2
x − x + x) 3 2
= m − m + m . 0 0 m ∫( 2 3x − 2x + ) 1 dx = 6 3 2
⇔ m − m + m − 6 = 0 ⇔ m = 2∈(0;4) . 0
Vậy m = 2∈(0;4) .
Câu 11. Có bao nhiêu cách phân công 4 thầy giáo dạy toán vào dạy 12 lớp 12, mỗi thầy dạy đúng 3 lớp ? A. 369600 B. 396900 C. 220 D. 369000 Lời giải Chọn A Giáo viên thứ nhất có 3 C cách chọn. 12 Giáo viên thứ hai có 3 C cách chọn. 9 Giáo viên thứ ba có 3 C cách chọn. 6 Giáo viên thứ tư có 3 C cách chọn. 3
Vậy số cách phân công 4 thầy giáo vào dạy 12 lớp 12 là: 3 3 3 3
C .C .C .C = 369600 cách 12 9 6 3 4 2 Câu 12. Giới hạn x + x + 2 lim có kết quả là : x→+∞
( 3x + )1(3x− )1 A. − 3 B. 3 C. 3 D. 3 − 3 3 Lời giải Chọn B 4  1 2   1 2 x 1  1  + + + + 4 2 2 4 2 4  Ta có: x + x + 2  x x   x x  3 lim = = = . x→+∞ ( lim lim 3 x + ) 1 (3x − ) 1 x→+∞ 4  1  1 x→+∞   1  1  3 x 1+ 3 −  1+ 3 −  3 3 x x x x       
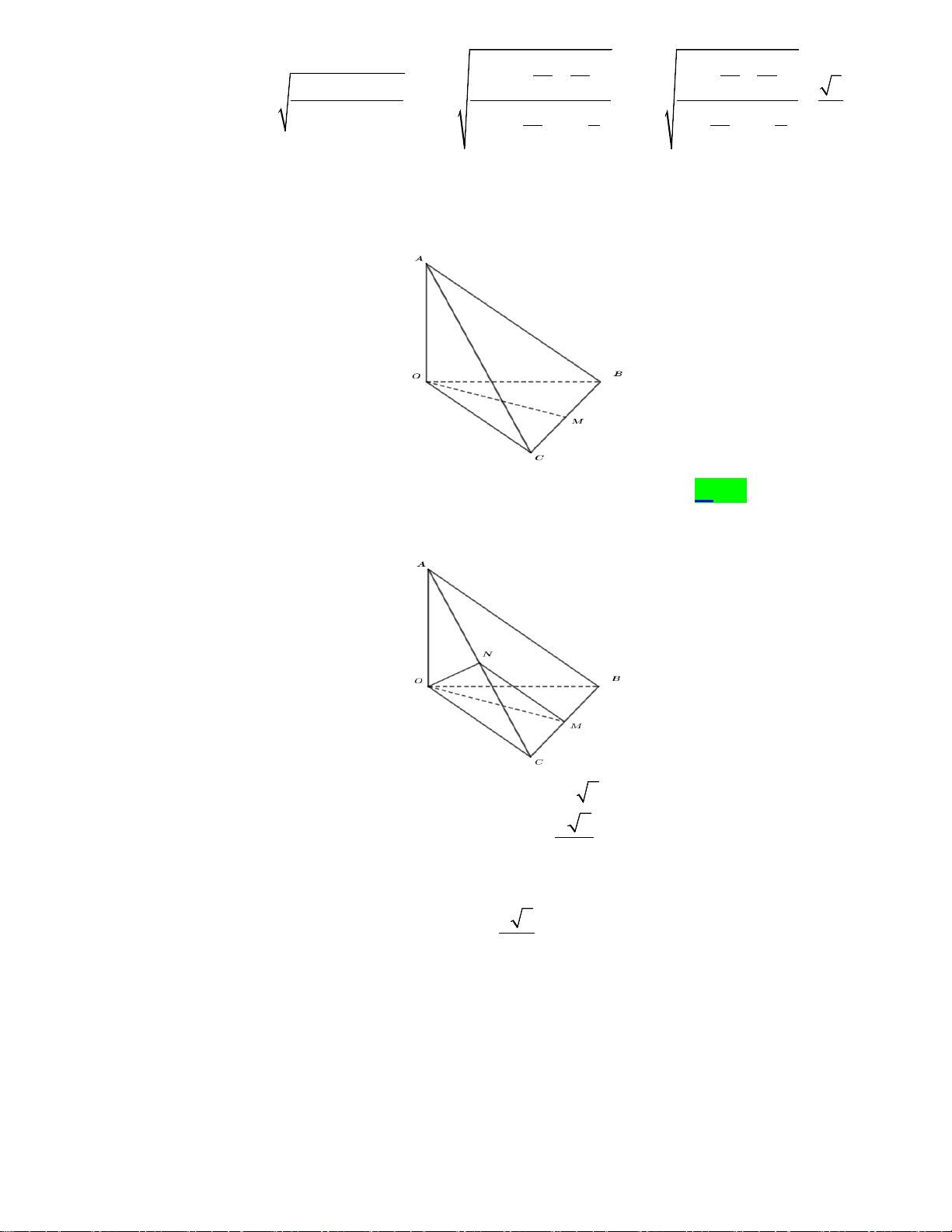
Câu 13. Cho tứ diện OABC có ,
OA OB, OC đôi một vuông góc với nhau và OA = OB = OC . Gọi M
là trung điểm của BC (tham khảo hình vẽ bên dưới). Góc giữa hai đường thẳng OM và AB bằng A. 0 45 B. 0 90 C. 0 30 D. 0 60 Lời giải Chọn D
Đặt OA = a suy ra OB = OC = a và AB = BC = AC = a 2 Gọi a
N là trung điểm AC ta có MN / / AB và 2 MN = 2 Suy ra góc (OM AB)  = (OM MN)  , , . Xét  OMN Trong tam giác a OMN có 2
ON = OM = MN =
nên OMN là tam giác đều 2 Suy ra  0
OMN = 60 . Vậy (OM AB)  = (OM MN)  0 , , = 60
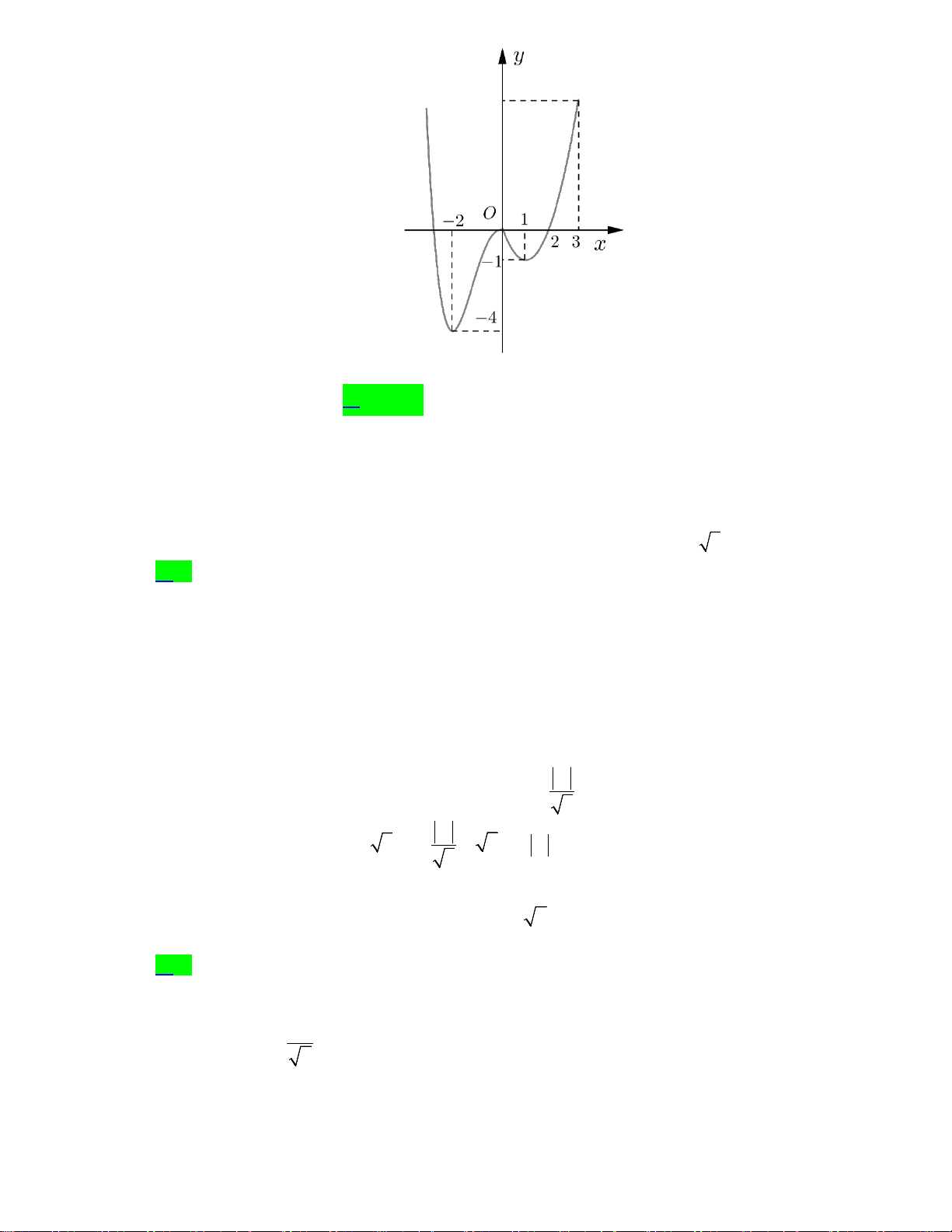
Câu 14. Cho hàm số y = f (x) có đồ thị hàm y = f ′(x) như hình vẽ bên dưới.
Hàm số đã cho nghịch biến trên khoảng
A. (−∞;− 2) . B. ( 2 − ) ;1 .
C. (−∞;− 4) . D. ( 2; − 3) . Lời giải Chọn B
Từ đồ thị hàm số y = f ′(x) ta thấy ngay hàm số nghịch biến trên các khoảng ( 2 − ) ;1 .
Câu 15. Có bao nhiêu giá trị nguyên dương của m để khoảng cách từ gốc tọa độ O đến đường thẳng đi
qua 2 điểm cực trị của đồ thị hàm số 3
y = x − 3x + m nhỏ hơn hoặc bằng 5. A. 5. B. 2. C. 11. D. 4.
Lời giải Chọn A x =1 3
y = x − 3x + m ; 2
y′ = 3x − 3 ; y′ = 0 ⇔  . x = 1 −
⇒ Với mọi m phương trình y′ = 0có hai nghiệm phân biệt và y′ đổi dấu khi qua hai nghiệm.
⇒ Đồ thị hàm số có hai điểm cực trị với mọi m .
Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số đã cho là: y = 2
− x + m (∆) . m
Khoảng cách từ O tới đường thẳng ∆ là d ( ; O ∆) = . 5 m
Theo bài ra ta có: d (O,∆) ≤ 5 ⇔ ≤ 5 ⇔ m ≤ 5 ⇔ 5 − ≤ m ≤ 5. 5
Vì m nguyên dương nên m∈{1;2;3;4; } 5 .
Câu 16. Giá trị nhỏ nhất và lớn nhất của hàm số y = x − 2 x trên đoạn [0;9] lần lượt là m và M . Giá
trị của tổng m + M bằng A. 2. B. 3. C. 0. D. 1. Lời giải Chọn A Đạo hàm 1 y ' =1− ; x ∀ ∈(0;9] 
→ y' = 0 ⇔ x =1∈[0;9]. xf (0) = 0
m = min f (x) = 1 −  Ta có  f ( )  [0;9] 1 = 1 −  →  →m + M =
M = max f ( x) 2. =  f  (9) 3 =  [0;9] 3 ax +1
Câu 17. Cho hàm số y =
( a,b,c là các tham số) có bảng biến thiên như hình vẽ bx + c Xét các phát biểu sau: ( )1: c >1.
(2): a +b < 0. (
3): a + b + c = 0. (4): a > 0. Số phát biểu đúng là A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn B
Dựa vào bảng biến thiên ta có hàm số luôn đồng biến trên từng khoảng xác định, đồ thị hàm số
có tiệm cận đứng là đường thẳng x = 2 và tiệm cận ngang là đường thẳng y =1nên ta có hệ  c   − = 2   b 0 < c <1   c = 2 − bc = 2 − b   a    1 
= 1 ⇔  a = b ⇔  a = b
⇔  − < a < 0 b 2    2 ac − b > 0 2 − b − b >   0 
ac − b > 0  1 − < b < 0    2 
a + b + c = 0
Dựa vào hệ trên ta có các phát biểu ( )
1 ,(4) là sai, (2),(3) đúng.
Câu 18. Đặt log 2 = a khi đó log 27 bằng 3 16 A. 3a B. 3 C. 4 D. 4a 4 4a 3a 3 Lời giải Chọn B Ta có 3 3 3 log 27 = log 3 = = 16 2 4 4.log 2 4a 3
Câu 19. Cho hai số thực dương x , y thỏa mãn log  2 2
x y 1log xy . Mệnh đề nào dưới đây 2  2 đúng?
A. x y .
B. x y .
C. x y . D. 2 x y . Lời giải Chọn A
Với x , y  0 ta có: log  2 2
x y 1log xy  log  2 2
x y  log 2xy . 2 2 2  2 2 2
x y  2xy . x y . a(m + nb)
Câu 20. Đặt a = log 3; b = log 3. Nếu biểu diễn log 45 =
thì m + n + p bằng 2 5 6 b(a + p) A. 3 B. 4 C. 6 D. 3 − Lời giải Chọn B 1 2 log 45 log 9 + log 5 + a 2b +1 3 3 3 ( ) Ta có log 45 b = = = = 6 log 6 log 2 + log 3 1 b 1+ a 3 3 3 ( ) +1 a
Suy ra m =1,n = 2, p =1⇒ m + n + p = 4
Câu 21. Một hình đa diện lồi có số mặt M , số đỉnh D và số cạnh C . Khi đó, hệ thức nào dưới đây là đúng ?
A. D + M − C = 2
B. D + C − M = 2
C. M + C − D = 2
D. M + D = C Lời giải Chọn A
Câu 22. Tính thể tích V của khối lăng trụ tam giác đều ABC.A′B C
′ ′ có AC′ = 5a , cạnh đáy là 4a . A. 3 V = 12a . B. 3 V = 20a 3 . C. 3 V = 20a . D. 3 V = 12a 3 . Lời giải Chọn D A' C' B' 5a A 4a C B
Vì ABC.A′B C
′ ′ là lăng trụ tam giác đều nên ta có CC′ ⊥ ( ABC) và ∆ ABC đều cạnh là 4a . Do đó: 2 2
CC′ = 25a −16a = 3a ; 1 S (4a)2 3 2 4a 3 ABC = = ∆ 2 2 2 3 V = ′ = = ′ ′ ′ CC S . ∆ a a a ABC A B C . ABC 3 .4 3 12 3 .
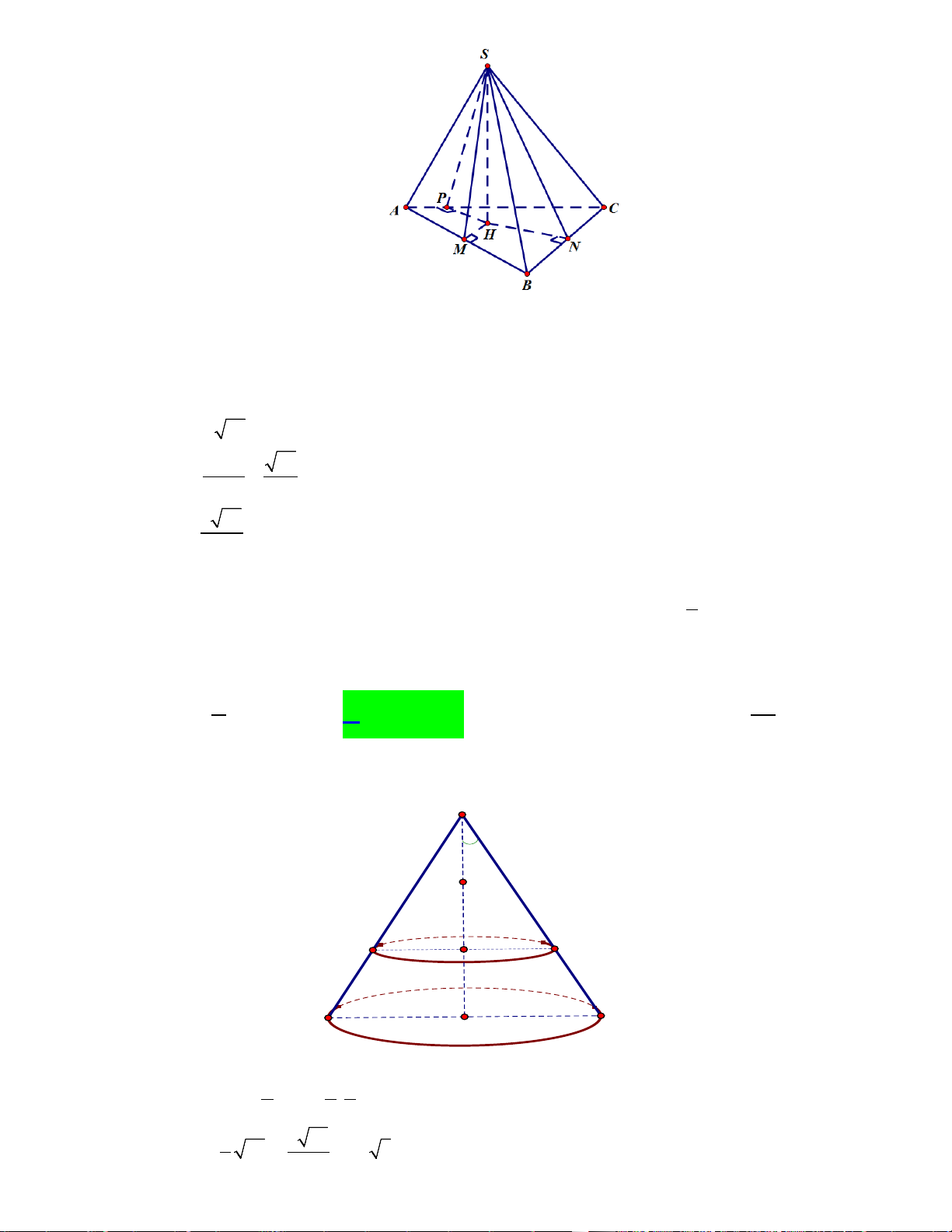
Câu 23. Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A , AB = AC = 4a; BC = 6a .Hình
chiếu vuông góc của S trên mặt phẳng ( ABC) nằm trong tam giác ABC . Các mặt bên của
hình chóp cùng tạo với đáy góc 0
60 . Tính thể tích khối chóp S.ABC . A. 3 6a 3 . B. 3 a 3 . C. 3 8a 3 . D. 3 3a 3 . Lời giải Chọn D
Gọi H là hình chiếu vuông góc của điểm S lên mặt phẳng ( ABC), M , N,P lần lượt là hình
chiếu vuông góc của điểm H lên AB,BC,CA . Khi đó ta có S ∆ HM = S ∆ HN = S ∆ HP
Suy ra HM = HN = HP
Suy ra H là tâm đường tròn nội tiếp tam giác ABC 2 S = ∆ a ABC 63 S ABC ∆ 63 HN = = a p 7 3 21 SH = a 7
Câu 24. Cho hình nón đỉnh I , đường cao IO (O là tâm của đáy) và có độ dài đường sinh bằng 3cm,
góc ở đỉnh bằng 60°. Gọi K là điểm thuộc đoạn IO thỏa mãn 3
IO = IK , cắt hình nón bằng 2
mặt phẳng (P) qua K và vuông góc với IO , khi đó thiết diện tạo thành có diện tích là S . Tính S . A. π π S = ( 2 cm ). B. = π ( 2 S cm ). C. S = π ( 2 3 cm ) . D. 2 S = ( 2 cm ). 3 3
Lời giải Chọn B I 30° 3 cm K M O N
Thiết diện tạo thành là đường tròn tâm K , bán kính KM . Ta có: 2 2 1
KM = .ON = . .IN =1. Diện tích thiết diện là: 2
S = π.KM = π ( 2 cm ) 3 3 2 1 2 3 21 3 V = a a = a S ABC 63 . 3 3 . . 3 7 Câu 25. Cho ( ) 2
F x = x là một nguyên hàm của hàm số ( ) 2x
f x e . Tìm nguyên hàm của hàm số ( ) 2 ' x f x e . A. f ∫ (x) 2x 2 ' e dx = 2
− x + 2x + C . B. f ∫ (x) 2x 2 '
e dx = −x + 2x + C . C. ∫ ( ) 2 2 ' x
f x e dx = −x + x + C . D. f ∫ (x) 2x 2 '
e dx = 2x − 2x + C . Lời giải Chọn A F (x) 2
= x là một nguyên hàm của hàm số ( ) 2x f x e 2x 2x 2x 2
⇒ F '(x) = f (x).e ⇒ 2x = f (x).e ⇒ f (x).e dx = x + C ∫ 1 Đặt 2x 2 u  = edu = 2 x e dx  ⇒ 
dv = f '(x)dx
v = f (x) 2x 2x 2x 2
⇒ f '(x).e dx = f (x).e − 2. f (x).e dx + C = 2
− x + 2x + C ∫ ∫ 2 1
Câu 26. Có bao nhiêu số thực a để = 1 ∫ x dx . 2 a + x 0 A. 2 B. 1 C. 0 D. 3 Lời giải Chọn B a < 1 −
Điều kiện tích phân tồn tại là 2
a + x ≠ 0,∀x ∈[0; ] 1 ⇒  a > 0 Đặt 2
t = a + x ⇒ dt = 2 d x x . Khi đó  1 1 1+a 2 a = x dt + a  + a = e a  2 1 1 1 1 e −1 dx = = ln = 1 ⇔ ∫ ∫  ⇔  2 2 a + x 2 t 2 a a 1  + a = −e a  1 − 0 a = 2  e +1
So sánh điều kiện ta được 1 a = . 2 e −1
Câu 27. Số giá trị nguyên của tham số m thuộc đoạn [ 2022 − ;2022] để phương trình (m + ) 2
1 sin x − sin 2x + cos 2x = 0 có nghiệm là: A. 4045 . B. 4044 . C. 2023. D. 2024 . Lời giải
Chọn D Ta có: (m + ) 2
1 sin x − sin 2x + cos 2x = 0 ⇔ ( + )1− cos2 1 x m
− sin 2x + cos 2x = 0 2 1− m −m −1 ⇔ −sin 2x + cos 2x = . 2 2
Điều kiện để phương trình asin x + bcos x = c có nghiệm là 2 2 2
a + b ≥ c ứng với phương trình trên ta được 2 2 1− m   −m −1 2 2 − + + + 1  1 2m m m 2m 1 + ≥  ⇔ 1+ ≥
⇔ 4m ≤ 4 ⇔ m ≤1. 2   2      4 4
Vậy các giá trị nguyên của tham số m thuộc đoạn [ 2022 − ;2022] thỏa mãn là { 2022 − ;...; 1 − ;0; } 1 vậy có 2024 số.
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy và
SA = a 3 . Gọi α là góc giữa SD và (SAC) . Giá trị sinα bằng A. 2 . B. 2 . C. 3 . D. 2 . 4 2 2 3 Lời giải DO ⊥ AC
Gọi O = AC ∩ BD . Ta có:  ⇒ ⊥ . DO ⊥ SA  (SA ⊥ 
( ABCD)) DO (ABCD)
⇒ SO là hình chiếu của SD lên mặt phẳng (SAC) ⇒ (SD (SAC))  = (SD SO)  =  ; ; DSO = α . Xét S
∆ AD vuông tại A : 2 2
SD = 3a + a = 2a . Xét S
∆ OD vuông tại O : có SD = 2a , a 2 = ⇒ α =  DO 2 OD sin sin DSO = = . 2 SD 4
Câu 29. Có bao nhiêu giá trị nguyên âm của tham số m để hàm số 3 4 9 2
y = x − x + (2m +15) x −3m +1 4 2
đồng biến trên khoảng (0;+∞)? A. 2. B. 3. C. 5. D. 4. Lời giải Yêu cầu bài toán 3
⇔ y′ = 3x − 9x + 2m +15 ≥ 0 x
∀ ∈(0;+∞) và dấu bằng xảy ra tại hữu hạn điểm thuộc (0;+∞) 3
⇔ 3x − 9x +15 ≥ 2 − m x ∀ ∈(0;+∞) . Xét hàm số: 3
g(x) = 3x −9x +15 trên (0;+∞). Ta có: 2
g (′x) = 9x −9 g′(x)  = = 0 x 1 ⇒  . x = 1 − (l) Bảng biến thiên: Từ BBT ta có: 9 2
− m ≤ 9 ⇔ m ≥ − 2
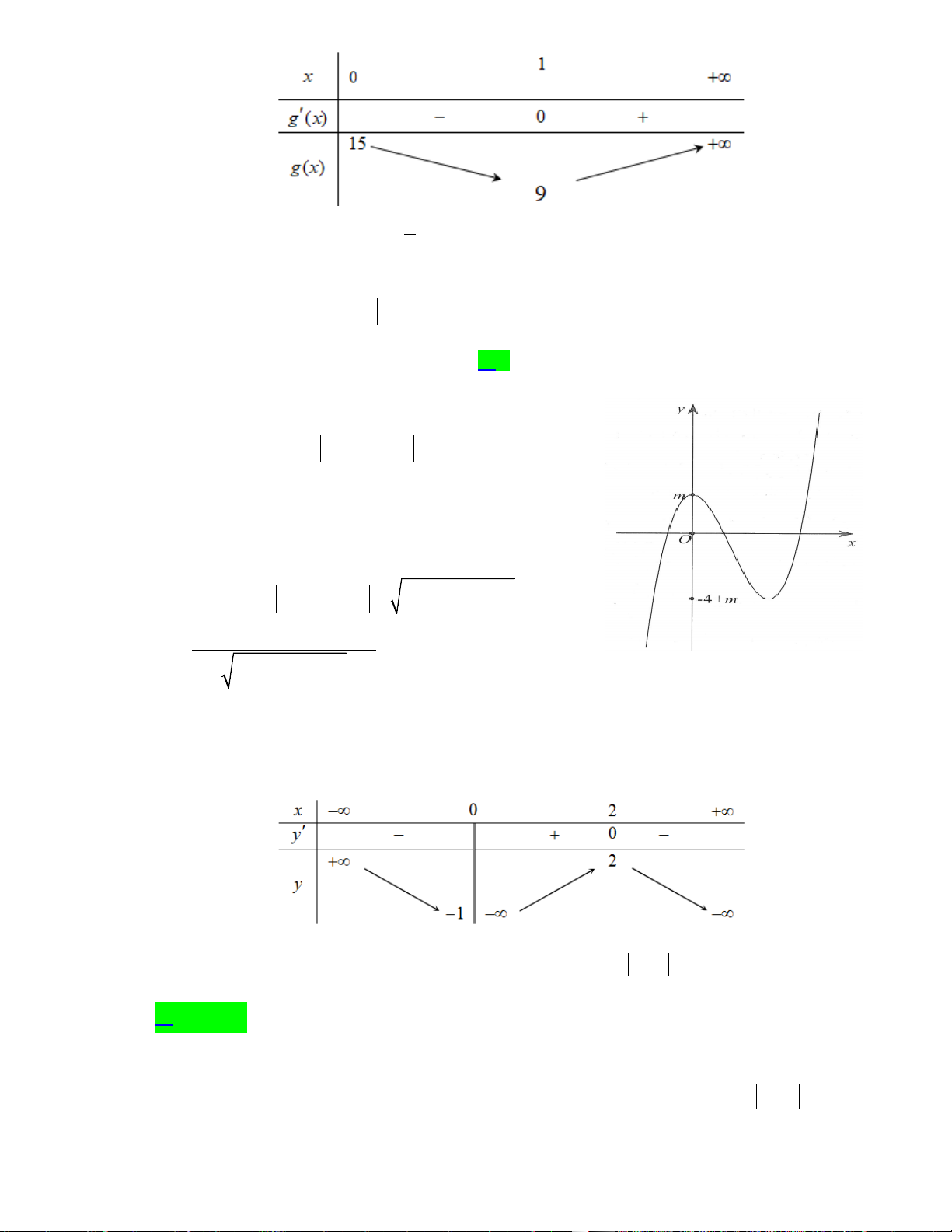
Vậy m∈{− 4;− 3;− 2;−1}. Câu 30. Cho hàm số 3 2
y = x − 3x + m , với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của
tham số m để đồ thị hàm số có 5 điểm cực trị. Tổng tất cả các phần tử của tập S là A. 3 B. 10 C. 6 D. 5 Lời giải: Xét hàm số 3 2
g(x) = x − 3x + m có đồ thị như hình vẽ. Để đồ thị hàm số 3 2
y = x − 3x + m có 5 điểm cực trị thì  4 − + m <0  m > 0
⇔ 0 < m < 4 . Do đó S = {1;2;3}, tổng tất cả các giá trị của S là 6 .
Cách khác: y = x − x + m = (x − x + m)2 3 2 3 2 3 3 , ( 3 2
x − 3x + m)( 2 3x − 6x) y ' = .
(x −3x +m)2 3 2
Đồ thị hàm số đã cho có 5 điểm cực trị khi và chỉ khi phương trình y’ = 0 có 5 nghiệm phân
biệt và y’ đổi dấu qua 5 nghiệm đó, điều này tương đương với 3 2
x − 3x + m có ba nghiệm phân biệt khác 0 và 2 .
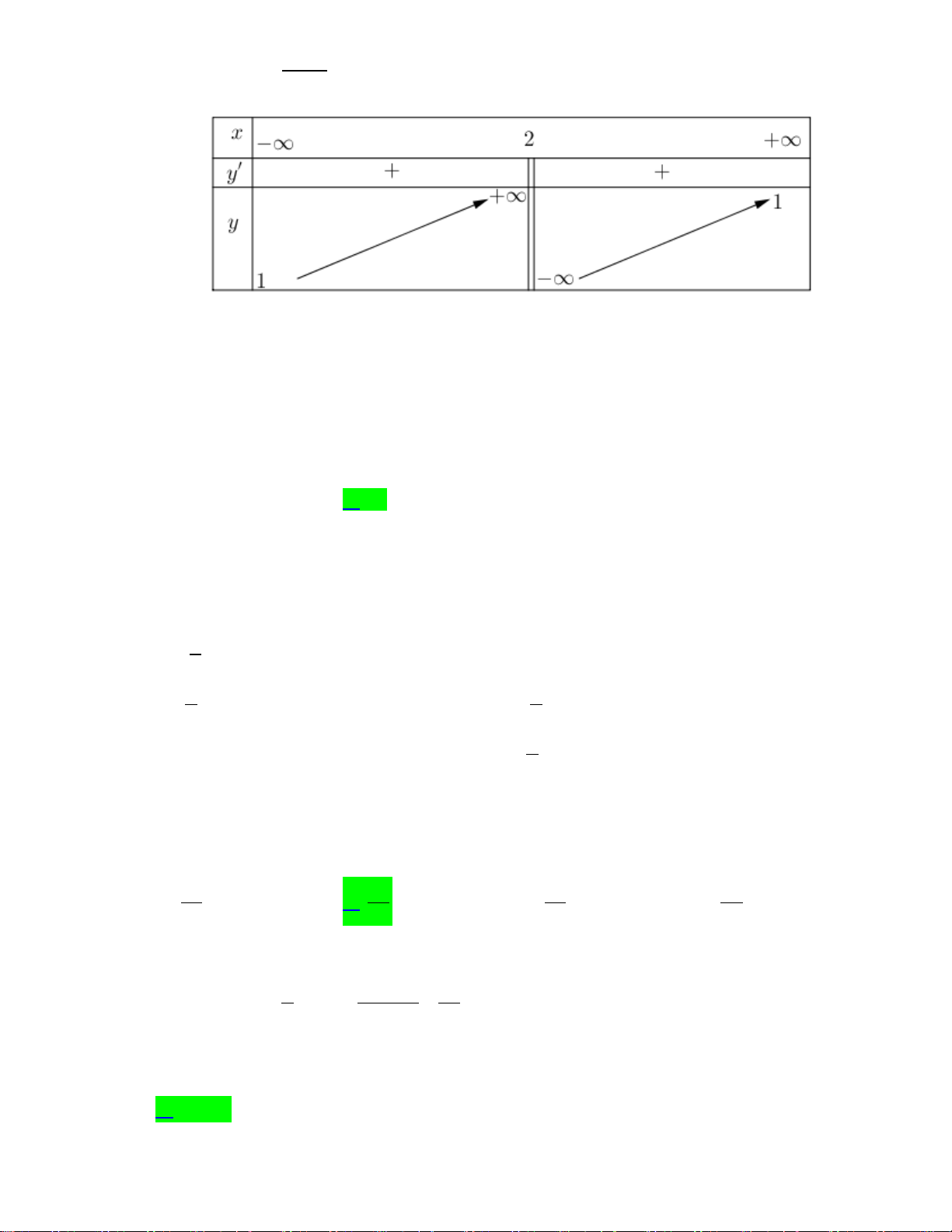
Câu 31. Cho hàm số y = f (x) có bảng biến thiên như sau
Tập hợp tất cả các giá trị thực của tham số m để phương trình f (x) + m = 0 có 5 nghiệm phân biệt là A. ( 2; − − ] 1 . B. [ 1; − 2) . C. ( 2; − − ) 1 . D. ( 2; − ) 1 . Lời giải
Từ bảng biến thiên của hàm số y = f (x) .Ta có bảng biến thiên của hàm số y = f (x)
Khi đó phương trình f (x) + m = 0 có 5 nghiệm khi phương trình f (x) = −mcó 5 nghiệm hay
đồ thị hàm số y = f (x) và y = −m cắt nhau tại 5 điểm phân biệt
Do vậy 1≤ −m < 2 ⇔ 2 − < m ≤ 1 − .
Câu 32. Cho hình chóp đều đỉnh S có đáy là đa giác đều 8 cạnh. Một hình nón đỉnh S có đáy là
đường tròn ngoại tiếp đáy hình chóp. Tính tỉ số thể tích của khối nón và khối chóp tương ứng. π π π π A. . B. . C. . D. 2 . 3 2 2 2 3 3 Lời giải Chọn B Gọi ;
O R lần lượt là tâm và bán kính đáy của hình nón đỉnh S , h = SO là độ dài
đường cao của hình nón⇒ h cũng là độ dài đường cao của hình chóp đều
S.A A A A A A A A có đáy là đa giác đều 8 cạnh nội tiếp đáy của hình nón. 1 2 3 4 5 6 7 8
Ta có đáy nón ngoại tiếp đáy của hình chóp đều 8 cạnh như hình vẽ.
Ta thấy đa giác đều A A A A A A A A được chia thành 8 tam giác cân bằng nhau có 1 2 3 4 5 6 7 8
cạnh bên bằng R và góc ở đỉnh bằng 45° ⇒ Diện tích của đa giác đều A A A A A A A A là: 1 2 3 4 5 6 7 8 1 = =  2 S 8.S = . ∆ OA OA AOA R OA A 8. . . .sin 2 2 1 2 1 2 1 2 2
Gọi V ;V lần lượt là thể tích của khối chóp đều và khối nón đã cho. 1 2
Thể tích khối khối chóp đều đã cho là: 1 1 2 V = . . h S = 2 2R h . 1 3 3
Thể tích của khối nón đã cho là: 1 2 V = π R h . 2 3 1 2 π R h
Tỉ số thể tích của khối nón và khối chóp là: V π 2 3 = = . V 1 2 1 2 2 2 2R h 3 2
Câu 33. Số đường tiệm cận đứng của đồ thị hàm số
4x −1− x + 2x + 6 y = là 2 x + x − 2 A. 3. B. 2 . C. 1. D. 0 . Lời giải Chọn C
Tập xác định D =  \{1;− } 2 x ∀ ∈  \ 1; 2 − 0 { } 2 2
4x −1− x + 2x + 6 4x −1− x + 2x + 6 0 0 0 lim = 2 2 x→ 0 x x + x − 2 x + x − 2 0 0 2
Suy ra tiệm cận đứng nếu có của đồ thị hàm số
4x −1− x + 2x + 6 y =
chỉ có thể là hai đường 2 x + x − 2
thẳng x =1; x = 2 − 2
4x −1− x + 2x + 6 4(x − ) 2
1 + 3− x + 2x + 6 lim = lim 2 x 1 → x 1 x + x − 2 → (x − ) 1 (x + 2) 9 − ( 2 x + 2x + 6) x − x + 4(x − ) 1 + 4(x − ) ( ) 1 ( 3) 1 − 2 2 3+ x + 2x + 6 3+ x + 2x + 6 = lim = lim x 1 → (x − ) 1 (x + 2) x 1 → (x − ) 1 (x + 2) (x +3) 4 − 2 3+ x + 2x + 6 10 = lim = x 1 → (x + 2) 9
Suy ra x =1 không phải là đường tiệm cận đứng 2 Xét
4x −1− x + 2x + 6 lim + 2 x→ 2 − x + x − 2 lim − − + + = − − < + →− ( 2 4x 1 x 2x 6 9 6 0 x 2 ) lim (x − )
1 (x + 2) = 0 , và (x − )
1 (x + 2) > 0 với mọi x thuộc lân cận của 2 − nhưng nhỏ hơn x 2+ →− 2 − 2 Suy ra
4x −1− x + 2x + 6 lim = −∞ + 2 x→ 2 − x + x − 2 Vậy x = 2 − là tiệm cận đứng
Kết luận: Đồ thị hàm số có một đường tiệm cận đứng. Câu 34. Gọi a + b 3 x = với ( , , ∈ , a a b c N
tối giản) là một nghiệm lớn hơn 1 của phương trình 0 c c −x   2x ( 3)1 1 x  1  2 − +  
1 = 2x −1. Giá trị của P = a + b + c là   3   
A. P = 6 .
B. P = 0 .
C. P = 2 .
D. P = 4 . Lời giải Chọn D
Điều kiện xác định: x ≠ 0 . −   1 x x x− 1 ( )1 1 x  1 x 2 3  − +   1 2 = 2x −1 2 1 ⇔ 3 − 3 +1 = x −   3    2x 1 1 2x x 1 3 3 − ⇔ + = + x −1 ( )
1 . Xét hàm số ( ) = 3t f t
+ t (t ≠ 0) , ′( ) = 3t f t .ln 3+1 > 0 2x ( )  1 1 1 f  ⇔ = f (x − 1 3   ) 1 ⇔ = x −1 x ± ⇔ =
⇒ a =1, b =1, c = 2 . Vậy P = 4 .  2x  2x 2
Câu 35. Cho các hàm số f (x), f x , f x ,… thỏa mãn: 1 ( ) 2 ( ) x e +1 f x = f x = ln ; f = ∀ = … + x f f x n n ( ) n ( ) , 1;2;3; 1 ( ) 1 ( ) ( ) x e −1
Khẳng định nào sau đây đúng? A. f ln 2 = ln 2 f ln 3 = ln 4 f ln 2 = ln 3 f ln 3 = ln 3 2023 ( ) . B. 2023 ( ) . C. 2023 ( ) . D. 2023 ( ) . Lời giải Chọn C x e +1 f x = f x = ln . 1 ( ) ( ) x e −1 Ta có: x x e 1 + e +1 ln x + e − 1 e +1 x e −1 f x = f f x = ln x = = e = x . x ln ln 2 ( ) ( 1( )) 1 e 1 + x ln e +1 x e 1 e − 1 − − 1 x e −1 x e +1 f x = f f x = ln . 3 ( ) ( 2 ( )) x e −1
f x = f f x = x . 4 ( ) ( 3 ( )) x e +1 f x = f f x = ln … 5 ( ) ( 4 ( )) x e −1 x
Bằng quy nạp ta chứng minh được e +1 f x = ln . 2023 ( ) x e −1 ln 2 e +1 ln3 Từ đó suy ra: f ln 2 = ln = ln 3 e +1 3 2023 ( ) ; f ln 3 = ln = . 5 ( ) ln 2 e −1 ln3 e −1 2
Câu 36. Có bao nhiêu giá trị nguyên của m để phương trình ( − ) 1 .log( −x x
e + m) = x − 2 có 2 nghiệm thực phân biệt A. Vô số. B. 11. C. 9. D. 10.
Lời giải Chọn D Điều kiện: −x
e + m > 0 (*).
Vì x =1không là nghiệm nên phương trình nên: x−2 x−2 − x x − 2 − x x 1 log(e + m) =
⇔ e + m =10 − ( thỏa mãn (*)) x 1 ⇔ m =10 − − x − e . x −1 x−2 Đặt x 1
y = g(x) =10 − − x − e x−2 Ta có: 1 x 1 y 10 − ′ = ln10 −x + e > 0, x ∀ ≠ 1 2 (x −1) Bảng biến thiên:
Vậy phương trình có 2 nghiệm thực phân biệt khi 1 − < m <10 . e
Suy ra các giá trị m cần tìm là: 0,1,2,3,4,5,6,7,8,9.
Câu 37. Cho hình hộp đứng ABC .
D A B C D có cạnh AB = AD = 2 , AA = 3 BAD = °. Gọi 1 1 1 1 1 và góc  60
M , N lần lượt là trung điểm của các cạnh A D và A B . Tính thể tích V của khối chóp 1 1 1 1 . A BDMN . A. 5 V = . B. 3 V = . C. V = 4 . D. V = 2 . 2 2 Lời giải B C A D B1 C1 N A1 M D1 E
Gọi E là điểm đối xứng với A qua A , ta có: 1 A N // AB 1  
AB ⇒ N là trung điểm của đoạn EB A N =  1  2 A M // AD 1  
AD ⇒ M là trung điểm của đoạn ED A M =  1  2 Ta có 1 =  S 1 = .2.2.sin 60° = 3 ∆ AB AD BAD ABD . .sin 2 2 ABC .
D A B C D là hình hộp đứng, AA = 3 ⇒ EA = 2 3 1 1 1 1 1 1 ⇒ V = EA S 1 = .2 3. 3 = 2 E ABD . . 3 ABD ∆ 3 V EM EN 1 3 3 E AMN 1 . = . = ⇒ V = V ⇒ V = V = . V ED EB E.AMN E. 4 ABD . A BDMN E. 4 ABD 2 E ABD 4 .
Câu 38. Một con quạ đang khát nước. Nó bay rất lâu để tìm nước nhưng chẳng thấy một giọt nước nào.
Mệt quá, nó đậu xuống cành cây nghỉ. Nó nhìn quanh và bỗng thấy một cái bình hình trụ có bán
kính đáy là 2cm , chiều cao 21cm ở dưới một gốc cây. Trong bình đang có một ít nước, khoảng
cách giữa đáy cốc và mặt nước là 12cm (Hình vẽ). Nhìn chung quanh, quạ thấy những viên đá
nhỏ nằm lay lắt ở gần đấy. Lập tức, nó dùng mỏ gắp một viên đá hình cầu có bán kính 0,6cm
thả vào bình. Cứ như vậy, nó gắp những viên đá khác và tiếp tục thả vào bình. Giả sử các viên
đá đều là hình cầu có bán kính 0,6cm Chẳng bao lâu, nước đã dâng lên. Để uống được nước
thì con quạ cần thả vào bình ít nhất bao nhiêu viên đá biết rằng quạ muốn uống được nước
trong cốc thì mặt nước phải cách miệng cốc không quá 6cm ? A. 42 . B. 41. C. 30. D. 27 . Lời giải 3
Ta có thể tích của mỗi viên đá là: 4  3  36π 3 .π. =   (cm ) . 3  5  125
Gọi n là số viên đá mà con quạ cần thả vào cốc ( n∈*). Khi thả vào số viên đá đó, thể tích
của nước được tăng thêm là: .36 n π 3 V = (cm ) 125
Để con quạ uống được nước trong cốc thì mực nước trong cốc cần dâng lên thêm ít nhất là:
h = 21−12 − 6 = 3 (cm) , tức là ứng với thể tích nước tăng lên là: 2 2 V ' = .
h π.r = 3.π.2 =12π Ta có điều kiện: .36 n π 125 V ≥ V ' ⇔ ≥ 12π ⇔ n ≥ = 41,66 125 3
Vậy số viên đá tối thiểu con quạ cần bỏ vào cốc là 42 viên.
Câu 39. Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, khối chóp có thể
tích lớn nhất bằng bao nhiêu ? A. 576 2 . B. 144. C. 576. D. 144 6 . Lời giải Chọn C
Giả sử khối chóp S.ABCD là khối chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9.
Gọi O là tâm hình vuông ABCD thì SO ⊥ ( ABCD) . M là trung điểm của SA , kẻ MI vuông
góc với SA và cắt SO tại I thì I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD , bán kính của
mặt cầu là IA = IS = 9 .
Đặt IO = x , 0 ≤ x ≤ 9 , do IA
∆ O vuông tại O nên 2 2
AO = AI − IO 2 = 81− x , suy ra 2
AC = 2 81− x .
Do tứ giác ABCD là hình vuông nên AC AB = 2 = 2. 81− x , suy ra 2 S = AB 2  ABCD = ( 2 2 81− x ) . Vậy 1 V = S SO 2 = ( 2
81− x ).(9 + x) 2 = ( 3 2
−x − 9x + 81x + 729) . S ABCDABCD . . 3 3 3
Xét hàm số f (x) = 2 ( 3 2
−x − 9x + 81x + 729) với x∈[0;9]. 3 x = 3 f ′(x) = ( 2
2 −x − 6x + 27) ; f ′(x) = 0 ⇔  x = 9 −  (l) Bảng biến thiên :
Dựa vào bảng biến thiên ta thấy : max f (x) = f (3) = 576 . x [ ∈ 0;9]
Vậy khối chóp có thể tích lớn nhất bằng 576.
Câu 40. Xét hàm số f (x) liên tục trên [0; ]
1 và thỏa mãn điều kiện x f ( 2
x ) + f ( − x) 2 4 . 3 1 = 1− x . 1
Tích phân I = f
∫ (x)dx bằng: 0 π π π π A. I = . B. I = . C. I = . D. I = . 20 16 6 4 Lời giải
Vì f (x) liên tục trên [0; ] 1 và x f ( 2
x ) + f ( − x) 2 4 . 3 1 = 1− x nên ta có 1 1 1 1 4 .x f ∫ 2 2  (x ) 1 2 + 3 f (1− x) 2  dx = 1− x dx  ∫ ⇔ 4 . x f ∫
(x )dx + 3f
∫ (1− x)dx = 1− x dx ∫ ( ) 1 . 0 0 0 0 0 1 1 1 Mà 4 . x f ( 2 x )dx ∫ = 2 f ∫ ( 2x)d( 2x) 2 t=x  →2 f
∫ (t)dt = 2I 0 0 0 1 1 1 và 3 f
∫ (1− x)dx = −3 f
∫ (1− x)d(1− x) u 1=−x →3 f
∫ (u)du = 3I 0 0 0 π π π 1 2 2 2 π Đồng thời 2 1 1− x dx ∫ x=sint 2 → 1− sin t.cos d t t ∫ 2 = cos d t t ∫
= ∫(1+ cos2t)dt = . 2 4 0 0 0 0 π π Do đó, ( )
1 ⇔ 2I + 3I = hay I = . 4 20 4 2 2022 Câu 41. Cho 3x + x −1 1 f (x)  b
≠ 0 , f ′( x) 2 = . f x , f ( ) 1
1 = − . Xét S ∑ f (k)  1 = = − với b 2 ( ) x 3  k 1 = 2  aa
tối giản. Tính a + b . A. 4092530 . B. 4090507 . C. 4088485 . D. 4086463. Lời giải f ′(x) f ′(x) Ta có 2 1 = 3x +1−  2 1 dx 3x 1  ⇒ = + − ∫ ∫ dx 2 f (x) 2 x 2 f (x) 2  x  1 − 3 1
⇒ ( ) = x + x+ +C . f x x Mà f ( ) 1 1 = − ⇒ C = 0 1 − 3 1 ⇒ = x + x + . 3 f (x) x ⇒ ( ) −x 1 2 − x f x = = 4 2
x + x +1 2 ( 2x + )2 2 1 − x 1 ( 2 x − x + ) 1 − ( 2 x + x + ) 1 1  1 1 .  = = − . 2 ( 2x + x + ) 1 ( 2 x − x + )  2 2 1 2  x x 1 x x 1 + + − +    ⇒ f (x) 1 1 1 =  − . 2 
x(x )1 1 x(x )1 1 + + − +   Khi đó : 2022
S ∑ f (k) 1  1 1 1 1 1 1 ...  = = − + − + + −   k 1 = 2 1.2 +1 0.1+1 2.3+1 1.2 +1 2022.2023+1 2022.2021+1 1  1  1  1    1 b  = − + = − + . 2  2022.2023 1 2  a  + 
⇒ a = 2022.2023+1, b =1 ⇒ a +b = 4090507.
Câu 42. Một bàn cờ vua gồm 88 ô vuông, mỗi ô có cạnh bằng 1 đơn vị. Một ô vừa là hình vuông hay
hình chữ nhật, hai ô là hình chữ nhật,… Chọn ngẫu nhiên một hình chữ nhật trên bàn cờ. Xác
suất để hình được chọn là một hình vuông có cạnh lớn hơn 4 đơn vị bằng 5 17 51 29 A. . B. . C. . D. . 216 108 196 216 Lời giải Chọn A
Bàn cờ 88 cần 9 đoạn thẳng nằm ngang và 9 đoạn thẳng dọc. Ta coi bàn cờ vua được xác
định bởi các đường thẳng x  0, x 1,..., x  8 và y  0, y 1,..., y  8.
Mỗi hình chữ nhật được tạo thành từ hai đường thẳng x và hai đường thẳng y nên có 2 2 C .C 8 8
hình chữ nhật hay không gian mẫu là n  2 2
  C .C 1296 . 9 9
Gọi A là biến cố hình được chọn là hình vuông có cạnh a lớn hơn 4.
Trường hợp 1: a  5. Khi đó mỗi ô được tạo thành do 2 đường thẳng x cách nhau 5 đơn vị và
hai đường thẳng y cách nhau 5 đơn vị có 4.4 16 cách chọn.
Trường hợp 2: a  6 . Khi đó mỗi ô được tạo thành do 2 đường thẳng x cách nhau 6 đơn vị và
hai đường thẳng y cách nhau 6 đơn vị có 3.3  9 cách chọn.
Trường hợp 3: a  7 . Khi đó mỗi ô được tạo thành do 2 đường thẳng x cách nhau 7 đơn vị và
hai đường thẳng y cách nhau 7 đơn vị có 2.2  4 cách chọn.
Trường hợp 3: a  8. Khi đó mỗi ô được tạo thành do 2 đường thẳng x cách nhau 8 đơn vị và
hai đường thẳng y cách nhau 8 đơn vị có 1.11 cách chọn. Suy ra n 
A 169 41 30 .
Xác suất để hình được chọn là một hình vuông có cạnh lớn hơn 4 đơn vị là n  P  A 30 5 A    . n   1296 216
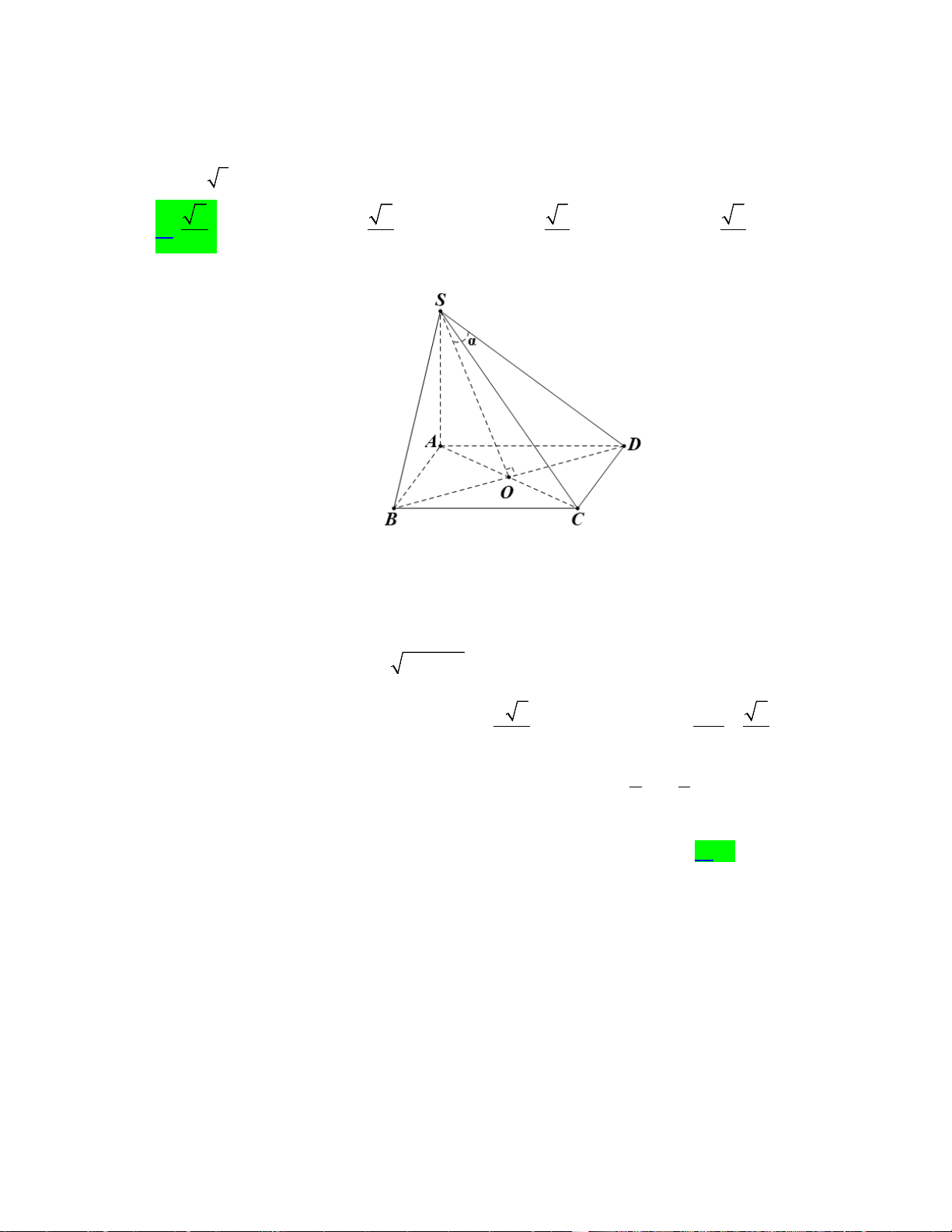
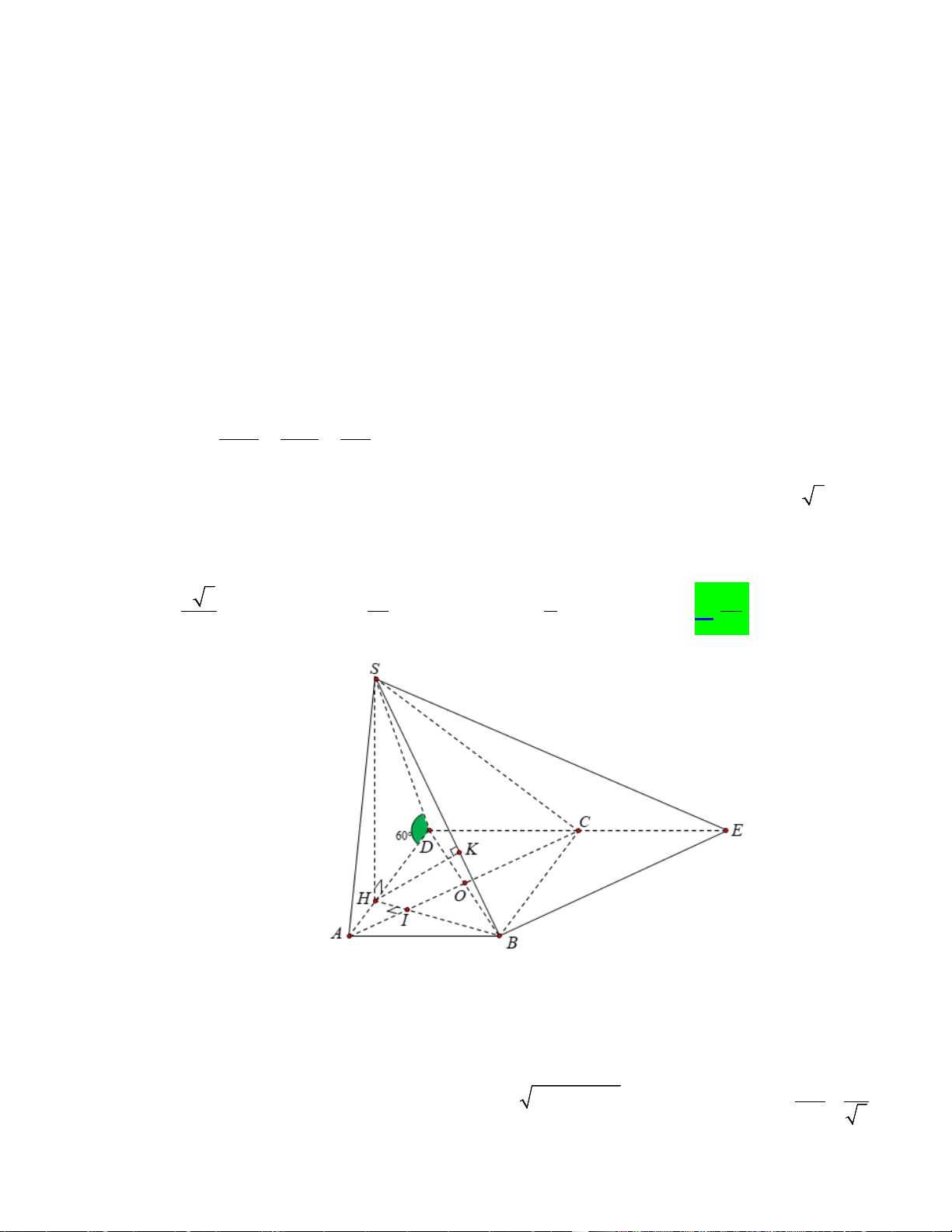
Câu 43. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O , AB = a , BC = a 3 . Tam
giác ASO cân tại S , mặt phẳng (SAD) vuông góc với mặt phẳng ( ABCD) , góc giữa SD và
( ABCD) bằng 60°. Khoảng cách giữa hai đường thẳng SB và AC bằng A. a 3 . B. 3a . C. a . D. 3a . 2 2 2 4 Lời giải
Ta có (SAD) ⊥ ( ABCD) , (SAD) ∩( ABCD) = AD ; trong mp(SAD), kẻ SH ⊥ AD thì SH ⊥ ( ABCD) Mặt khác
Gọi I là trung điểm OA, vì tam giác ASO cân tại S nên AO ⊥ SI , AO ⊥ SH ⇒ HI ⊥ OA
Tam giác ADC vuông tại D có 2 2
AC = AD + DC = 2a và  DC 1 tan DAC = = AD 3 ⇒  DAC = 30°
Tam giác AHI vuông tại I có AI a 3 AH = = 2a 3 ⇒ HD = . cos30° 3 3
Tam giác ABH vuông tại A có 2 2 2a
HB = AH + AB = , 2 AB = . IB HB a 3 ⇒ IB = 3 2
Trong mặt phẳng ( ABCD) , dựng hình bình hành ABEC thì BE // AC , BE ⊂ (SBE)
⇒ AC // (SBE) d (SB, AC) = d ( AC,(SBE)) = d (I,(SBE)) Mà IB 3
= nên d (I (SBE)) 3 ,
= d (H,(SBE)) HB 4 4
Lại có tam giác OAB là tam giác đều cạnh a nên BI ⊥ AC ⇒ BI ⊥ BE , BE ⊥ SH
⇒ BE ⊥ (SBH )
⇒ (SBE) ⊥ (SBH ) và (SBE) ∩(SBH ) = SB
Trong mặt phẳng (SBH ) , kẻ HK ⊥ SB thì HK ⊥ (SBE) ⇒ HK = d (H,(SBE))
Tam giác SBH vuông tại H có 1 1 1 = + ⇒ HK = a . 2 2 2 HK SH HB
Vậy d (H,(SBE)) = HK = a và ( ( )) 3 = ( ( )) 3 , , a d I SBE d H SBE = . 4 4 Câu 44. Cho hàm số 3 2
y = ax − x + bx −1 với a, b là các số thực, a ≠ 0 , a ≠ b sao cho đồ thị hàm số cắt 2 trục 5a − 3ab + 2
Ox tại ba điểm có hoành độ dương. Tìm giá trị nhỏ nhất của biểu thức P = . 2
a (b − a) A. 15 3. B. 8 2. C. 11 6. D. 12 3. Lời giải Xét phương trình 3 2
ax − x + bx −1 = ( 0 *) . Gọi , m ,
n p là ba nghiệm dương của phương trình (*) , khi đó  1
m + n + p =  a  Ta có  1
mn + np + pm = a   1 mnp =  a  1 (  0 < a ≤
m + n + p)2 ≥ 3(mn + np + pm)  Mặt khác  3 3  ⇔  3
m + n + p ≥ 3 mnp  1 0 < b ≤  3a 2
Xét hàm số f (b) 5a −3ab + 2  1 ; b 0;  = ∈
là hàm số nghịch biến nên 2 a (b a) 3a  −   2 f (b)  1  5a +1 ≥ f = 3. =   3.g a 3 ( )  3a a − 3a 2 5a +1  1 
Xét hàm số g (a) = ; a ∈0;
, là hàm số nghịch biến nên ta có 3 a 3a 3 3  −   g (a) 1 g   ≥ =   4 3 .  3 3 
Vậy P ≥ 3.4 3 =12 3 .
Câu 45. Cho hàm số f (x) 3 2
= x − 6x + 9x . Đặt k
f (x) f ( k 1 f − =
(x)) với k là số tự nhiên lớn hơn 1. Hỏi phương trình 9
f (x) = 0 có bao nhiêu nghiệm? A. 19684. B. 9841. C. 19683. D. 9842. Lời giải Chọn D.
Ta có f ′(x) 2
= 3x −12x + 9 . Bảng biến thiên:
Từ bảng biến thiên ta có  f (x) = 0   f x = 3 k−2  f (x) ( ) = 0 k 1  f − (x)  2 =  f x = k f (x) 0 3 k−2 0   f (x) ( ) 3 ...  = ⇔ ⇔ = ⇔ ⇔ k 1  f −  (x)  3 = 3  f x = 3 k 1  f − ( x) ( ) = 3     k 1  f −  (x) = 3
Bài toán sẽ được giải quyết nếu tìm được số nghiệm của phương trình k f (x) = 3 .
+ Phương trình f (x) = 3 có ba nghiệm thuộc (0;4) .
f (x) = x ∈ 0; 1 ⊂ 0; 4 1 ( ) ( )  + Phương trình 2
f (x) = f ( f (x)) = 3 ⇔  f (x) = x ∈ 1; 3 ⊂ 0; 4 . 2 ( ) ( )
f (x) = x ∈ 3; 4 ⊂ 0; 4 3 ( ) ( )
Từ bảng biến thiên ta có với mỗi giá trị x , x , x ∈ 0;4 phương trình f (x) = x i = có ba i , 1,3 1 2 3 ( ) nghiệm thuộc (0; 4). Như vậy phương trình 2
f (x) = 3 có 9 nghiệm thuộc (0; 4).
+ Bằng quy nạp ta chứng minh được phương trình k
f (x) = 3 có 3k nghiệm thuộc (0; 4). k 1 −
Từ đó, số nghiệm của phương trình k f (x) = 0 là 2 k 1 − 3 −1 2 + 3+ 3 +...+ 3 = 2 + 3 . 2 9 1 −
Vậy số nghiệm của phương trình 9 f (x) = 0 là 3 −1 2 + 3 = 9842 . 2 Câu 46. Cho x+ y xy+ − xy− 1 ;
x y ∈ , (x ≥ 0) thỏa mãn: 3 1 1 2021 + 2021 + x +1 = 2021 + − y x + 3 . x+3y ( ) 2021
Tìm giá trị nhỏ nhất của T = x + 2y . A. 2 . B. 1 − . C. 2 − . D. 1. 3 3 Lời giải Ta có x+3y xy 1 + − xy 1 − 1 2021 + 2021 + x +1 = 2021 + − y x + 3 x+3y ( ) 2021 x+3y −(x+3y) − xy 1 − xy 1 2021 2021 x 3y 2021 2021 + ⇔ − + + = −
− xy −1 ⇔ f (x + 3y) = f (−xy − ) 1 .
Với ( ) = 2021t − 2021−t f t
+ t , t ∈ . ( ) 2021t ln 2021 2021 t f t − ′ = +
ln 2021+1 > 0 , t ∈ .
⇒ f liên tục và đồng biến trên  . Do đó f (x + 3y) = f (−xy − )
1 ⇔ x + 3y = −xy −1 (*) . Với y = 1 − : (*) ⇔ 3 − = 1 − (vô lí). Với − − y y ≠ 1 − : ( ) 1 3 * ⇔ x = . Vì x ≥ 0 nên 1 1 − < y ≤ − . 1+ y 3 Từ (*) ta có:
x + y = −xy − ⇔ x + y = −y − xy − ⇔ x + y = −(x + y) 2 3 1 2 1 2
2 y + 2y − y −1. 2 2
⇔ (x + y)( + y) 2 2y − y −1 2y − y −1 2 1
= 2y − y −1 ⇔ x + 2y = ⇔ T = . y +1 y +1 2 − −
Xét f ( y) 2y y 1 = , 1 y  1;  ∈ − − . y +1 3   2
f ( y) 2y + 4y  1 0, y  1  2  1;  ′ = < ∀ ∈ − −
. Do đó min f ( y) = f − = − . (   y + )2 1 3    1 1;  − −  3  3  3    1 y = − Vậy 2 minT = − ⇔  3 . 3 x = 0 2
Câu 47. Số nghiệm của phương trình x + x − ( 2 ln x − 2) = 2022 là 2 A. 3. B. 1. C. 4 . D. 2 . Lời giải 2 Xét hàm số ( ) x f x = + x − ( 2
ln x − 2) với x∈( ; −∞ − 2)∪( 2;+∞) . 2 2 Ta có ′( ) 2 = +1 x f x x − ; f ′′(x) 2x + 4 = 1+ > 0, x ∀ ∈ ; −∞ − 2 ∪ 2;+∞ . 2 ( ) ( ) 2 x − 2 ( 2x −2) Nên suy ra hàm số ′( ) 2 = +1 x f x x −
đồng biến trên mỗi khoảng ( ; −∞ − 2) và ( 2;+∞) . 2 x − 2
Mặt khác f ′(2). f ′( 3) =1.(1− 3) < 0 và f ′(− ) f ′(− ) 8 3 .
2 = − .1< 0 nên f ′(x) có đúng một 7 nghiệm a ∈( ;
−∞ − 2) và đúng một nghiệm b∈( 2;+∞) . Ta có bảng biến thiên
Ta có f (a) < f (− ) 3
3 = − 3 < 2022 và f (b) < f ( ) 3 3 = + 3 < 2022 2 2 2
Nên từ bảng biến thiên suy ra phương trình x + x − ( 2
ln x − 2) = 2022 có 4 nghiệm. 2
Câu 48. Xét các số thực dương +
x, y thỏa mãn log x y
= x x − 3 + y y − 3 + xy . Tìm giá 3 2 2 ( ) ( )
x + y + xy + 2 trị lớn nhất của 3x + 2y +1 P = . x + y + 6 A. 2 B. 1 C. 3 D. 4 Lời giải Ta có log x + y
= x x − 3 + y y − 3 + xy 3 2 2 ( ) ( )
x + y + xy + 2
⇔ log (x + y) + 3(x + y) + 2 = log ( 2 2
x + y + xy + 2) + ( 2 2
x + y + xy + 2 3 3 )
⇔ log (x + y) + 3(x + y) + log 3 = log ( 2 2
x + y + xy + 2) + ( 2 2
x + y + xy + 2 3 3 3 ) ⇔ log 3
 ( x + y) + 3 
(x + y) = log ( 2 2
x + y + xy + 2) + ( 2 2
x + y + xy + 2 (*) . 3 3 )
Xét hàm số f (t) = log t + t , với t > 0. 3 có f ′(t) 1 = +1 > 0 , t ∀ > 0 . t.ln 3
Vậy hàm số f (t) liên tục và đồng biến trên khoảng (0;+∞).
Do đó: f ( (x + y)) = f ( 2 2
x + y + xy + ) ⇔ (x + y) 2 2 3 2 3
= x + y + xy + 2 ( ) 1 . Từ ( )
1 ⇔ xy = (x + y)2 −3(x + y) + 2 . 2  x + y +
Ta có x x xy xy x( y ) 1 1  = + − = + − xy ≤ −  xy . 2   
Đẳng thức xảy ra khi và chỉ khi x = y +1. (x + y + )2 1 Do đó từ ( ) 1 , suy ra: x ≤
− (x + y)2 + 3(x + y) − 2 . 4
Đặt t = x + y , t > 0 . (t + )2 1 2(x + y) 2 2t +1+ − t + 3t − 2 2 +1+ x Suy ra: 4 3
− t + 22t − 3 P = ≤ = = f t . x + y + 6 t + 6 4(t + 6) ( ) 2 Ta có: f ′(t) 3
− t − 36t +135 =
= 0 ⇔ t = 3 (nhận). 4(t + 6)2 Bảng biến thiên t 0 3 +∞ f ′(t) + 0 − f (t) x = y +1 x = 2
Dựa vào BBT, ta có max P = max f (t) = f (3) =1 khi và chỉ khi  ⇔  . (0;+∞) x + y = 3 y =1
Câu 49. Cho hình chóp S.ABCD có đáy là hình bình hành. Góc tạo bởi mặt bên (SAB) với đáy bằng α .
Tỉ số diện tích của tam giác SAB và hình bình hành ABCD bằng k . Mặt phẳng (P) đi qua AB
và chia hình chóp S.ABCD thành hai phần có thể tích bằng nhau. Gọi (β ) là góc tạo bởi mặt
phẳng (P) và mặt đáy. Tính cot β theo k và α . A. 5 +1 cot β + = cotα + B. 5 1 cot β = tanα + k sinα k sinα C. 5 −1 cot β − = cotα + D. 5 1 cot β = tanα + k sinα k sinα Lời giải S M N D A C B
Giải sử mặt phẳng (P) cắt SD,SC lần lượt tại M , N . Khi đó MN//CD . Đặt: SM SN = = m > 0 SD SCS V .MNB SM SN 2 = . = m  Ta có:  S V DCB SD SC   S V .AMB SM = = m(*)  S V .ABD SD S V .ABMN 2 2 5 −1 ⇒
= m + m ⇔ m + m =1 ⇔ m = (m > 0) 2 S V .ABCD 2 Từ ( ) V m + ⇒ S V ABM = . S mV ABD = . m ( S V ABM +V ) S.ABM 1 5 * . . . M.ABD ⇒ = = ( ) 1 M
V .ABD 1− m 2 S
V .ABM SSAB.Sin(α − β ) Mặt khác: = (2) M V .ABD SABD.Sinβ + α − β Từ ( ) ( ) 1 5 k.SABCD.sin( ) 1+ 5 1 , 2 ⇒ = ⇔ cot β = cotα + . Suy ra chọn A. 2 1 k.sin .S α ABCD.sin β 2
Câu 50. Cho tứ diện ABCD có thể tích là V . Điểm M thay đổi trong tam giác BCD . Các đường thẳng
qua M và song song với AB , AC , AD lần lượt cắt các mặt phẳng ( ACD) , ( ABD), ( ABC)
tại N , P , Q . Giá trị lớn nhất của thể tích khối tứ diện MNPQ là A. V . B. V . C. V . D. V . 27 16 8 54 Lời giải A P N Q P' D B M Q' N' C ′
 Tam giác ABN′ có MN // AB MN N M ⇒ = . AB N B ′ ′
 Tam giác ACP′ có MP // AC MP P M = . AC P C ′ ′
 Tam giác ADQ′ có QM // AD MQ Q M ⇒ = . AD Q D ′ ′ ′ ′
Khi đó: MN MP MQ N M P M Q M + + = + + AB AC AD N B ′ P C ′ Q D ′ ′ ′ ′ Mà N M P M Q M S S S MN MP MQ MCD MBD MBC + + = + + = 1 nên + + =1 N B ′ P C ′ Q D ′ S S S AB AC AD BCD BCD BCD 3 3     Lại có 3 MN MP MQ MN MP MQ = + + ≥ 3 1   3 . .  (Cauchy) AB AC ADAB AC AD      1 ⇔ MN. . MP MQ ≤ A .
B AC.AD ⇒ MN. .
MP MQ lớn nhất khi MN MP MQ = = 27 AB AC AD MN MP MQ
⇒ M là trọng tâm tam giác BCD 1 ⇒ = =
= ⇒ (NPQ) // (BCD) , AB AC AD 3 2 SNPQ  2  1 = , Mà 1 S = S = S
d (M , NPQ ) = d ( , A (BCD)) ′ ′ ′ S nên 1 và ( ) S   N P Q 4 BCD NPQ 9 BCD 2 N P ′ Q ′ ′  3 
Vậy giá trị lớn nhất của thể tích khối tứ diện 1 MNPQ là V = S d M NPQ MNPQ NPQ . ( ,( )) 3 1 1 1 V ⇔ V = S d A BCD = , với 1 V = S d A BCD = V . ABCD BCD . ( , ( )) MNPQ . BCD . ( ,( )) 3 9 3 27 3
Document Outline

  • Toán
  • Toán-BẢNG ĐÁP ÁN THI GIAO LƯU 2022
  • Toán-ĐÁP ÁN CHI TIẾT ĐỀ GIAO LƯU ĐT HSG 12-