Đề KSCL lần 1 năm học 2017 – 2018 môn Toán 10 trường THPT Nguyễn Viết Xuân – Vĩnh Phúc

Đề KSCL lần 1 năm học 2017 – 2018 môn Toán 10 trường THPT Nguyễn Viết Xuân – Vĩnh Phúc gồm 50 câu hỏi trắc nghiệm, thời gian làm bài 90 phút, mời các bạn đón xem

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 10

Môn: Toán 10

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GD VÀ ĐT VĨNH PHÚC
TRƯỜNG THPT LIỄN SƠN
ĐỀ THI KSCL KHỐI 10 LẦN 1 NĂM HỌC 2017 – 2018
MÔN : TOÁN
Thời gian làm bài : 90 phút
---------------o0o---------------
Câu 1. (1.0 điểm) Cho mệnh đề
P
: “
2
: 1 0
x x x
”. Phát biểu mệnh đề
P
, xác định tính
đúng – sai của mệnh đề
P
.
Câu 2. (1.0 điểm) Cho hai tập hợp
1;2;3;4;5 , 1;2;3;6
A B . Tìm tất cả các tập hợp
X
sao
cho
và
.
Câu 3. (1.0 điểm)
a. Trong một cuộc điều tra dân số, báo cáo dân số của tỉnh X là 2615473 người
300 người. Viết
số quy tròn của số gần đúng 2615473.
b. Chiều cao của một cây cổ thụ là
39,73 0,2
m m
. Viết số quy tròn của số gần đúng 39,73.
Câu 4. (1.0 điểm) Chứng minh rằng ít nhất 1 trong 3 phương trình bậc hai sau đây có nghiệm :
2 2 2
2 0, 2 0, 2 0
ax bx c bx cx a cx ax b
, (
x
là ẩn).
Câu 5. (1.0 điểm) Tìm tập xác định của hàm số :
2
20 11
2
9
x
y x
x
.
Câu 6. (1.0 điểm) Xét tính chẵn lẻ của hàm số :
2017
1
x
y
x
.
Câu 7. (1.0 điểm) Tìm Parabol (P) có đỉnh
2; 2
S
và đi qua điểm
4;2
M .
Câu 8. (1.0 điểm) Cho tam giác ABC vuông tại A và có
0
, 60
AB a ABC . Tính
AB AC
.
Câu 9. (1.0 điểm) Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AB và CD.
Chứng minh :
2
AD BC MN
.
Câu 10. (1.0 điểm) Cho tam giác ABC có trọng tâm G. Gọi D là điểm đối xứng của A qua B và E
là điểm trên đoạn AC sao cho
5 2
AE AC
. Chứng minh 3 điểm D, G, E thẳng hàng.
---------- HẾT ----------
Họ và tên : ……………………………………..………….…………… Lớp : ……………………
Đ
Ề
CHÍNH TH
Ứ
C
ĐÁP ÁN VÀ THANG ĐIỂM KSCL TOÁN 10 LẦN 1 NĂM HỌC : 2017 – 2018
CÂU NỘI DUNG ĐIỂM
Câu 1
Cho mệnh đề
P
: “
2
: 1 0
x x x
”. Phát biểu mệnh đề
P
, xác định tính
đúng – sai của mệnh đề
P
.
:
P
“
2
: 1 0
x x x
”
0.5
Ta có
2
2
1 3
1 0
2 4
x x x x
, suy ra
P
đúng
0.5
Câu 2
Cho hai tập hợp
1;2;3;4;5 , 1;2;3;6
A B . Tìm tất cả các tập hợp
X
sao
cho
và
.
, 1 , 2 , 3 , 1;2 , 1;3 , 2;3
X X X X X X X
1;2;3
X
(Viết được 2, 4, 6, 8 tập tương ứng cho 0.25, 0.5, 0.75, 1.0)
1.0
Câu 3 a. Trong một cuộc điều tra dân số, báo cáo dân số của tỉnh X là 2615473 người
300 người. Viết số quy tròn của số gần đúng 2615473.
b. Chiều cao của một cây cổ thụ là
39,73 0,2
m m
. Viết số quy tròn của số gần
đúng 39,73.
a. Vì độ chính xác đến hàng trăm
300
d , nên ta quy tròn đến hàng
nghìn. Số quy tròn là : 2615000
0.5
b. Vì độ chính xác đến hàng phần chục
0,2
d , nên ta quy tròn đến
hàng đơn vị. Số quy tròn là : 40
0.5
Câu 4 Chứng minh rằng ít nhất 1 trong 3 phương trình bậc hai sau đây có nghiệm :
2 2 2
2 0, 2 0, 2 0
ax bx c bx cx a cx ax b
, (
x
là ẩn).
Ba phương trình đã cho lần lượt có biệt thức :
' 2 ' 2 ' 2
1 2 3
, ,
b ac c ab a bc
Giả sử cả ba phương trình đều vô nghiệm khi đó
' ' '
1 2 3
0
0.5
2 2 2
2 2 2
0
1
0
2
a b c ab bc ca
a b b c c a
(điều này vô lí). Vậy ít nhất một trong ba phương trình đã cho có nghiệm
0.5
Câu 5
Tìm tập xác định của hàm số :
2
20 11
2
9
x
y x
x
.
ĐK:
2
3 3
9 0
2 2
2 0
x x
x
x x
x
0.5
TXĐ :
; 3 3;2
D 
0.5
Câu 6
Xét tính chẵn lẻ của hàm số :
2017
1
x
y
x
.
TXĐ :
D
,
x x
0.5
2017
2017
1 1
x
x
y x y x
x x
Vậy hàm số đã cho là hàm số lẻ
0.5
Câu 7
Tìm Parabol (P) có đỉnh
2; 2
S
và đi qua điểm
4;2
M .
Giả sử
2
: , 0
P y ax bx c a
. Từ giả thiết ta có
2
2
4 2 2
16 4 2
b
a
a b c
a b c
0.5
2
4 1
4 8 2 4 : 4 2
16 16 2 2
b a a
a a c b P y x x
a a c c
0.5
Câu 8
Cho tam giác ABC vuông tại A và có
0
, 60
AB a ABC . Tính
AB AC
.
AB AC CB BC
0.5
0
2
1
cos60
2
AB a
a
0.5
Câu 9 Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AB và CD.
Chứng minh :
2
AD BC MN
.
MN MA AD DN
MN MB BC CN
0.5
2
MN MA MB AD BC DN CN AD BC
0.5
a
60
A
C
B
M
N
B
A
D
C
Câu 10 Cho tam giác ABC có trọng tâm G. Gọi D là điểm đối xứng của A qua B và E
là điểm trên đoạn AC sao cho
5 2
AE AC
. Chứng minh 3 điểm D, G, E thẳng
hàng.
2 2 1
2 . 2
3 3 2
1 5
3 3
DG AG AD AM AB AB AC AB
AC AB
0.5
2 6 1 5 6
2
5 5 3 3 5
DE AE AD AC AB AC AB DG
Vậy
, ,
D E G
thẳng hàng
0.5
Người ra đề Người thẩm định Duyệt BGH
Lê Hồng Khôi Trần Quyết
G
M
B
A
D
C
E
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD VÀ ĐT VĨNH PHÚC
ĐỀ THI KSCL KHỐI 10 LẦN 1 NĂM HỌC 2017 – 2018
TRƯỜNG THPT LIỄN SƠN MÔN : TOÁN
Thời gian làm bài : 90 phút ĐỀ CHÍNH THỨC
---------------o0o---------------
Câu 1. (1.0 điểm) Cho mệnh đề P : “ 2 x
  : x x  1  0 ”. Phát biểu mệnh đề P , xác định tính
đúng – sai của mệnh đề P .
Câu 2. (1.0 điểm) Cho hai tập hợp A  1;2;3; 4; 
5 , B  1; 2;3; 
6 . Tìm tất cả các tập hợp X sao
cho X A và X B .
Câu 3. (1.0 điểm)
a. Trong một cuộc điều tra dân số, báo cáo dân số của tỉnh X là 2615473 người  300 người. Viết
số quy tròn của số gần đúng 2615473.
b. Chiều cao của một cây cổ thụ là 39, 73m  0, 2m . Viết số quy tròn của số gần đúng 39,73.
Câu 4. (1.0 điểm) Chứng minh rằng ít nhất 1 trong 3 phương trình bậc hai sau đây có nghiệm : 2 2 2
ax  2bx c  0, bx  2cx a  0, cx  2ax b  0 , ( x là ẩn). 20x 11
Câu 5. (1.0 điểm) Tìm tập xác định của hàm số : y   2  x . 2 x  9 2017 x
Câu 6. (1.0 điểm) Xét tính chẵn lẻ của hàm số : y  . x 1
Câu 7. (1.0 điểm) Tìm Parabol (P) có đỉnh S 2;2 và đi qua điểm M 4; 2 .  
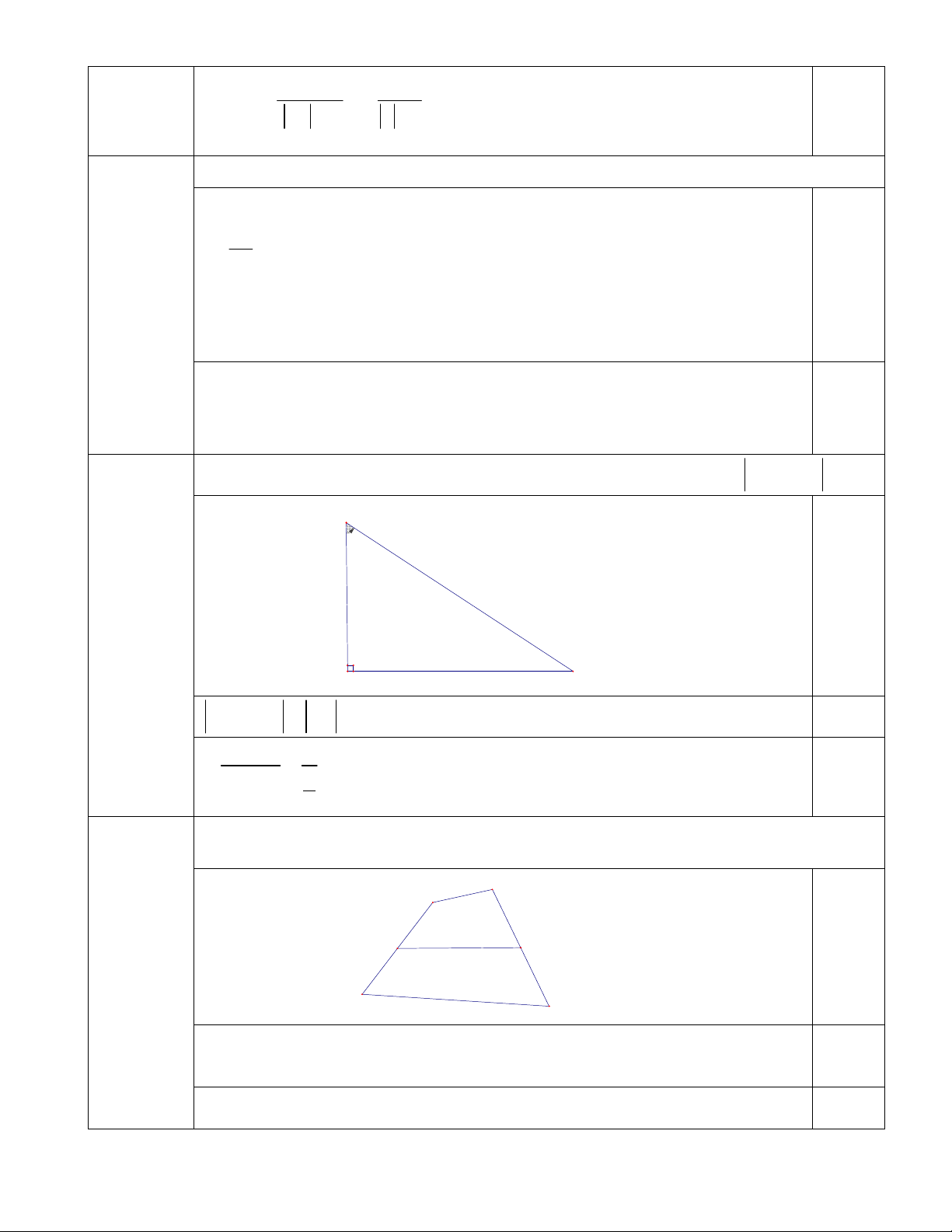
Câu 8. (1.0 điểm) Cho tam giác ABC vuông tại A và có  0
AB a , ABC  60 . Tính AB AC .
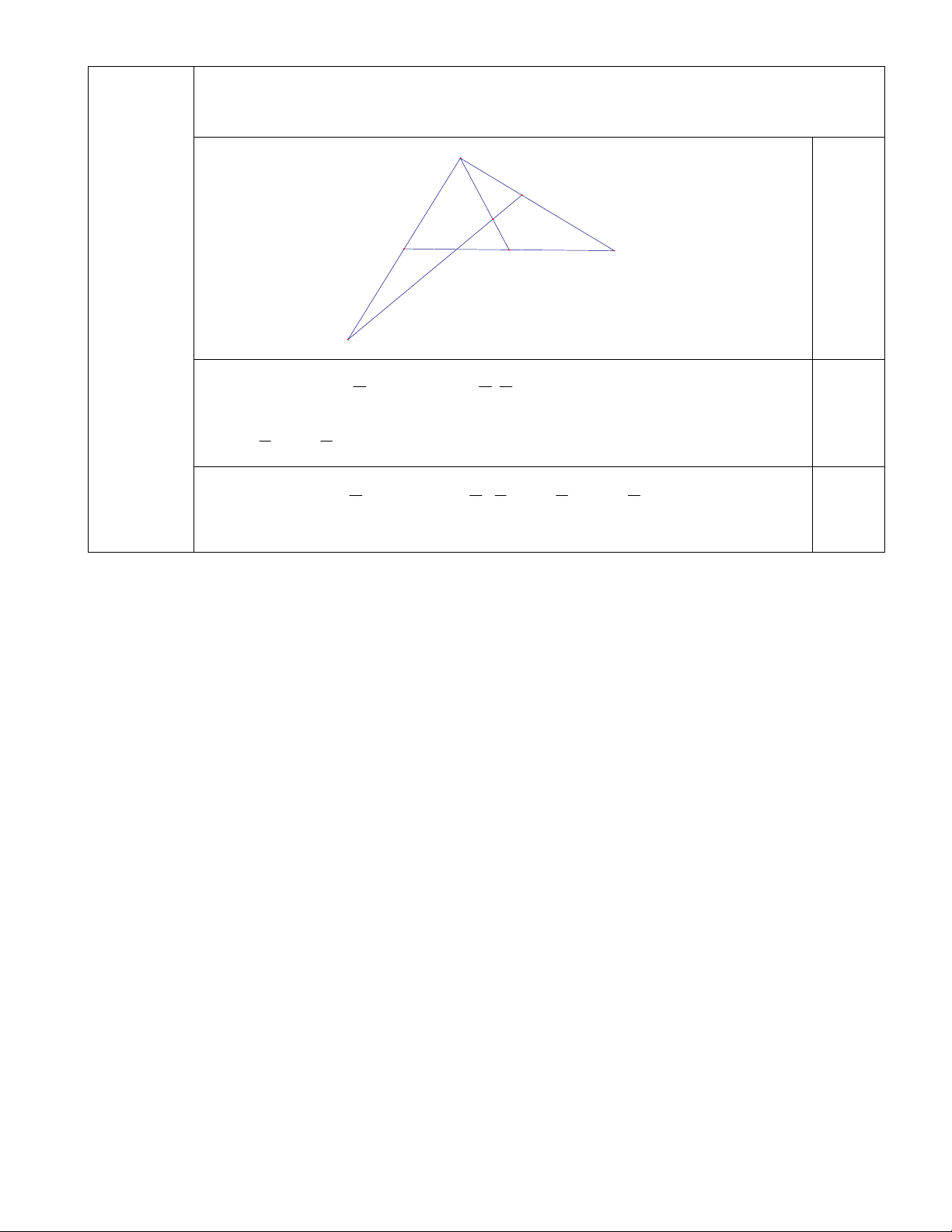
Câu 9. (1.0 điểm) Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AB và CD.   
Chứng minh : AD BC  2MN .
Câu 10. (1.0 điểm) Cho tam giác ABC có trọng tâm G. Gọi D là điểm đối xứng của A qua B và E
là điểm trên đoạn AC sao cho 5AE  2AC . Chứng minh 3 điểm D, G, E thẳng hàng.
---------- HẾT ----------
Họ và tên : ……………………………………..………….…………… Lớp : ……………………
ĐÁP ÁN VÀ THANG ĐIỂM KSCL TOÁN 10 LẦN 1 NĂM HỌC : 2017 – 2018 CÂU NỘI DUNG ĐIỂM Câu 1
Cho mệnh đề P : “ 2 x
  : x x  1  0 ”. Phát biểu mệnh đề P , xác định tính
đúng – sai của mệnh đề P . P: “ 2 x
  : x x 1  0 ” 0.5 2  1  3 0.5 Ta có 2
x x  1  x    0 x      , suy ra P đúng  2  4 Câu 2
Cho hai tập hợp A  1;2;3; 4; 
5 , B  1; 2;3; 
6 . Tìm tất cả các tập hợp X sao
cho X A và X B .
X   , X    1 , X    2 , X    3 , X  1;  2 , X  1;  3 , X  2;  3 1.0 X  1;2;  3
(Viết được 2, 4, 6, 8 tập tương ứng cho 0.25, 0.5, 0.75, 1.0) Câu 3
a. Trong một cuộc điều tra dân số, báo cáo dân số của tỉnh X là 2615473 người
300 người. Viết số quy tròn của số gần đúng 2615473.
b. Chiều cao của một cây cổ thụ là 39, 73m  0, 2m . Viết số quy tròn của số gần đúng 39,73.
a. Vì độ chính xác đến hàng trăm d  300 , nên ta quy tròn đến hàng 0.5
nghìn. Số quy tròn là : 2615000
b. Vì độ chính xác đến hàng phần chục d  0, 2 , nên ta quy tròn đến 0.5
hàng đơn vị. Số quy tròn là : 40 Câu 4
Chứng minh rằng ít nhất 1 trong 3 phương trình bậc hai sau đây có nghiệm : 2 2 2
ax  2bx c  0, bx  2cx a  0, cx  2ax b  0 , ( x là ẩn).
Ba phương trình đã cho lần lượt có biệt thức : 0.5 ' 2 ' 2 ' 2
  b ac ,   c ab ,   a bc 1 2 3
Giả sử cả ba phương trình đều vô nghiệm khi đó ' ' '       0 1 2 3 2 2 2
a b c ab bc ca  0 0.5 1
a b2 b c2 c a2         0 2  
(điều này vô lí). Vậy ít nhất một trong ba phương trình đã cho có nghiệm Câu 5 20x 11
Tìm tập xác định của hàm số : y   2  x . 2 x  9 2 x  9  0 x  3  x  3 0.5 ĐK:      2  x  0 x  2 x  2   
TXĐ : D  ;3   3  ; 2 0.5 Câu 6 2017 x
Xét tính chẵn lẻ của hàm số : y . x 1
TXĐ : D   , x
    x   0.5 x2017 2017 x 0.5 y x   
  y x x 1 x 1
Vậy hàm số đã cho là hàm số lẻ Câu 7
Tìm Parabol (P) có đỉnh S 2;2 và đi qua điểm M 4; 2 . Giả sử  P 2
: y ax bx c , a  0 . Từ giả thiết ta có 0.5  b   2  2a
4a  2b c  2 16 
a  4b c  2   b  4aa  1 0.5  
 4a  8a c  2  b
  4   P  2
: y x  4x  2 1  6a 16a c 2     c  2     Câu 8
Cho tam giác ABC vuông tại A và có  0
AB a , ABC  60 . Tính AB AC . B 60 a A C   
AB AC CB BC 0.5 AB a 0.5    2a 0 cos 60 1 2 Câu 9
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AB và CD.   
Chứng minh : AD BC  2MN . D A M N B C
   
MN MA AD DN 0.5
   
MN MB BC CN         
 2MN  MA MB   AD BC  DN CN   AD BC 0.5 Câu 10
Cho tam giác ABC có trọng tâm G. Gọi D là điểm đối xứng của A qua B và E
là điểm trên đoạn AC sao cho 5AE  2AC . Chứng minh 3 điểm D, G, E thẳng hàng. A E G B M C D
   2   2 1    0.5
DG AG AD AM  2AB
.  AB AC  2AB 3 3 2 1  5   AC AB 3 3
   2   6  1  5   6  0.5
DE AE AD AC  2 AB AC AB DG   5 5  3 3  5
Vậy D, E,G thẳng hàng Người ra đề
Người thẩm định Duyệt BGH Lê Hồng Khôi Trần Quyết